Summary
Decision making is often driven by the subjective value of available options, a value which is formed through experience. To support this fundamental behavior, the brain must encode and maintain the subjective value. To investigate the area specificity and plasticity of value coding, we trained mice in a value-based decision task and imaged neural activity in 6 cortical areas with cellular resolution. History- and value-related signals were widespread across areas, but their strength and temporal patterns differed. In expert mice, the retrosplenial cortex (RSC) uniquely encoded history and value-related signals with persistent population activity patterns across trials. This unique encoding of RSC emerged during task learning with a strong increase in more distant history signals. Acute inactivation of RSC selectively impaired the reward history-based behavioral strategy. Our results indicate that RSC flexibly changes its history coding and persistently encodes value-related signals to support adaptive behaviors.
Graphical Abstract
In Brief
During decision making values formed through experience are flexibly yet persistently maintained in the retrosplenial cortex over time to support adaptive behaviors
Introduction
The selection of an action among multiple possible options is influenced by a multitude of factors. In certain cases where there are external cues that determine the appropriate action (e.g. traffic lights), a simple association between the sensory cues and motor outputs may govern action selection. However, in many other situations there is no explicit cue that instructs the appropriate action, or the external cues are ambiguous. In these cases, internal, subjective processes may have a dominant role in biasing action selection. A major internal factor that biases action selection is the subjective value of each action. Individuals form such subjective values by integrating their personal experiences, and update these history-dependent values continuously based on the outcomes of their selected actions. To support such a behavior, the brain must maintain subjective values that are updated by each choice and its outcome.
Neural representations of value-related information have been intensely investigated. Neural recordings in animals performing decision making based on history-dependent value have been instrumental in this endeavor. These studies have identified individual neurons in multiple brain areas whose activity is modulated by history (Hwang et al., 2017; Kawai et al., 2015; Morcos and Harvey, 2016; Scott et al., 2017; Sugrue et al., 2004; Sul et al., 2011; Sul et al., 2010) and action values (Hamid et al., 2016; Kepecs et al., 2008; Padoa-Schioppa and Assad, 2006; Platt and Glimcher, 1999; Samejima et al., 2005; Stalnaker et al., 2014; Sugrue et al., 2004; Sul et al., 2011; Sul et al., 2010; Tsutsui et al., 2016). These results have thus established that information related to history-dependent value is widely distributed in many brain areas. However, a comprehensive understanding of across-area differences in population encoding is still lacking. Furthermore, little is known about whether and how the encoding is influenced by the learning of behavioral strategies.
In the current study, we sought to address two main questions about neural encoding of value: how does value encoding differ across cortical areas, and does their encoding of history information change across learning? First, we tested the potential differences across areas in the nature of their value coding. We reasoned that the brain must stably maintain value information to be able to retrieve it anytime as needed to bias action selection that may be prompted at unpredictable intervals. Therefore, we asked whether a certain area encodes value as a persistent population activity pattern that spans the entire period between one choice and the next. Second, we addressed the dynamics of history encoding over weeks of task learning. We hypothesized that, while animals learn to perform value-based decision making, specific areas preferentially enhance their encoding of choice-outcome history. We addressed these questions in mice performing a decision-making task based on history-dependent value. Mathematical modeling of behavior allowed an estimate of the value on a trial-by-trial basis with high accuracy. Using a chronic cranial window that exposed most of the dorsal cortex (Kim et al., 2016), we applied two-photon calcium imaging during the performance of this task in 6 dorsal cortical areas: anterior-lateral motor cortex (ALM) (Guo et al., 2014; Komiyama et al., 2010), posterior premotor cortex (pM2) (Yamawaki et al., 2016), posterior parietal cortex (PPC) (Harvey et al., 2012; Hwang et al., 2017; Morcos and Harvey, 2016; Raposo et al., 2014; Scott et al., 2017; Song et al., 2017), retrosplenial cortex (RSC) (Alexander and Nitz, 2015; Cembrowski et al., 2018; Czajkowski et al., 2014; Makino and Komiyama, 2015; Mao et al., 2017; Yamawaki et al., 2016), primary somatosensory cortex (S1), and primary visual cortex (V1). Although all the 6 cortical areas significantly encoded history- and value-related information, direct comparisons of population activity across areas revealed area specificity in the encoding of history and value-related information, and in the plasticity of history coding during task learning. In particular, we made a surprising finding that RSC uniquely and potently encodes value-related information in a persistent population activity pattern, and preferentially extends history coding during learning. Furthermore, acute optogenetic inactivation of RSC selectively impaired the reward history-based strategy. These results highlight RSC as a critical region for decision making based on history-dependent value.
Results
Decision making task based on history-dependent value in head-fixed mice
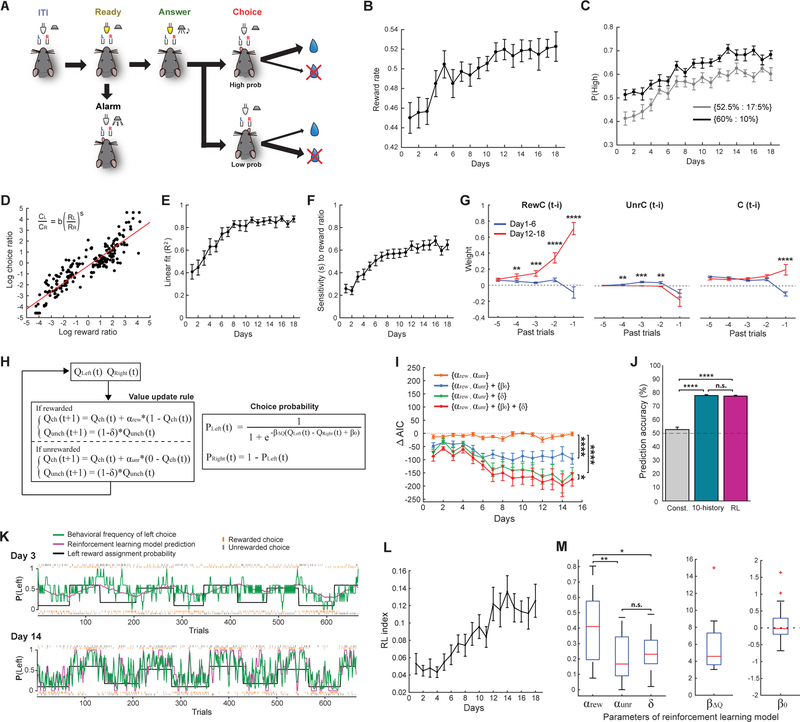
We sought to compare neural ensemble activity across cortical areas during decision making driven by history-dependent value. Towards this goal, we adapted a dynamic foraging task (Hamid et al., 2016; Johnson et al., 2016; Kawai et al., 2015; Samejima et al., 2005; Sugrue et al., 2004; Sul et al., 2011; Sul et al., 2010; Tsutsui et al., 2016) for mice under head fixation (Figure 1A). Each trial begins with a ready period (2 or 2.5 s, signaled by an LED light) during which mice need to withhold from licking. The ready period is followed by an answer period with an auditory cue. During the answer period, mice are free to choose between licking either the left or right lickport. The first lick triggers the delivery of a water reward at the lickport if it is assigned a reward. In each block of trials, a reward is assigned to each lickport based on predetermined probabilities: [60%, 10%], [52.5%, 17.5%], [17.5%, 52.5%], or [10%, 60%] probability combinations for [left, right]. Once a reward is assigned to a lickport, it remains assigned there until chosen in subsequent trials. Reward assignment probabilities change approximately every 60–80 trials, and there is no explicit cue indicating the changes. Therefore, mice need to adjust their choice preference based on the history of their choices and reward outcomes. During training with this task over weeks, mice learned to adjust their strategy and improved the fraction of trials in which they received a reward (Figure 1B). This learning accompanied an increase in the fraction of trials in which mice chose the side with a higher reward probability (Figure 1C). Mice also stochastically explored the alternative option at variable intervals (Figures S1A–S1D). Previous studies of dynamic foraging tasks have found that the ratio of two choices matches the ratio of the number of rewards from each alternative (‘Herrnstein’s matching law’) (Baum, 1974; Corrado et al., 2005; Herrnstein, 1970; Lau and Glimcher, 2005). We found that our head-fixed mice gradually developed matching behaviors during training (Figures 1D–1F), and their choice sensitivity to reward ratio reached the level equivalent to previous studies with monkeys (Corrado et al., 2005; Lau and Glimcher, 2005). To quantify the history dependency of their choices, we fit the behavior with a logistic regression model with 3 types of history predictors: rewarded choice history (RewC(t-i), 1 for rewarded left choice, −1 for rewarded right choice, and 0 otherwise), unrewarded choice history (UnrC(t-i), 1 for unrewarded left choice, −1 for unrewarded right choice, and 0 otherwise), and outcome-independent choice history (C(t-i), 1 for left choice, −1 for right choice) (Figure 1G and STAR Methods [eq. 2]). Information about past rewarded choices and unrewarded choices is essential for adaptive behavior in this task. This regression analysis revealed a dominant increase in the influence of rewarded choice history from 4 previous trials on decision making during learning (Figure 1G). This result indicates that mice improved the reward rate in the task by learning to adjust their strategy such that they preferentially chose the option that was more frequently rewarded in the recent trials.
Figure 1. Learning of a head-fixed dynamic foraging task.
(A) Task schematic.
(B) Fraction of rewarded trials in choice trials increases during learning (n = 21 mice, mean ± s.e.m.).
(C) Probability of choosing the lickport with higher reward assignment probability increases during learning (mean ± s.e.m.). (Some data points in early sessions are below 0.5 because of slow shifts in their choice preference after block transition.)
(D) Behavior of an example mouse showing a matching behavior (matching of the choice ratio with the reward ratio: note the reward ratio here is based on the actual reward frequencies the mice experienced, rather than the reward assignment probabilities). Each data point represents a single probability block. Block transition periods (20 trials after probability switch) were excluded from the analysis. All blocks from days 12–18 are shown. Red line is the linear fit.
(E) Goodness-of-fit of the matching law improves during learning (mean ± s.e.m.).
(F) Behavioral sensitivity to reward ratio increases during learning (mean ± s.e.m.).
(G) Weights from a logistic regression model that predicts each mouse’s choice with the 3 types of history (RewC(t-i): rewarded choice, UnrC(t-i): unrewarded choice, C(t-i): outcome-independent choice history) (mean ± s.e.m., Two-sided Wilcoxon signed-rank test).
(H) Our modified RL model.
(I) The effects of additional parameters on model fit were assessed with Akaike information criterion (AIC) (n = 21 mice, mean ± s.e.m., Two-way ANOVA with Tukey’s post-hoc test). ∆AIC indicates AIC difference from the standard RL model, and negative values indicate fit improvement beyond expected by overfitting. In the standard RL model, values update with a single learning rate α regardless of reward outcomes, unchosen value does not change, and constant value bias is zero. The RL model with two learning rates, bias, and forgetting rate best described the behavior in our task and thus we used this model in our study.
(J) Comparisons of choice prediction accuracies between a logistic regression model with a single constant bias term (Const.), a logistic regression model with rewarded choice, unrewarded choice, and outcome-independent history predictors from past 10 trials (31 parameters, [eq. 2] in STAR Methods), and our best RL model for expert imaging experiments (n = 83 sessions, mean ± s.e.m., One-way ANOVA with Tukey’s post-hoc test). Our best RL model with only 5 parameters performed as well as the logistic regression model with 31 parameters. Prediction accuracies were calculated by 2-fold cross-validation.
(K) Example performance of a mouse in early (day 3) and late (day 14) sessions. Black lines show reward assignment probability for left choice. Rewarded and unrewarded choice trials are marked by orange and grey ticks, respectively, for left choices (top) and right choices (bottom). Green lines show behavioral frequency of left choice within 5 trials (± 2 trials from each trial). Magenta lines show estimation of left choice probability by the RL model. Miss and alarm trials are not shown.
(L) Mice acquired RL strategy during task learning, shown by an increase in the RL index (n = 21 mice, mean ± s.e.m.).
(M) Distributions of RL model parameters in late session mice (day 12–18, n = 21 mice, One-way ANOVA with Tukey’s post-hoc test). The horizontal red lines indicate the medians, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points, excluding outliers. The red + symbols indicate outliers.
*P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.
See also Figure S1.
Reinforcement learning model to estimate subjective value
The behavioral results above suggest that expert mice used the recent choice-outcome history to form the subjective value of each option, and chose the option with a higher value. To study neural representations of value, which is an internal variable that is not directly measurable, we need to estimate the value on a trial-by-trial basis. The reinforcement learning (RL) theory (Sutton and Barto, 1998) provides a framework to estimate history-dependent value. Thus we fit the choice patterns of our expert mice with RL models. In the classic RL model (Sutton and Barto, 1998), value (Q) of the chosen option is updated by the difference between the actual outcome and the value of the chosen option (i.e. reward prediction error) multiplied by the learning rate α (STAR Methods [eq. 3]). The behavioral probability of choosing each option is estimated by a soft-max function based on the value difference between the two options (QL – QR, or ∆Q) and the parameter representing the sensitivity to the value difference (β∆Q) (STAR Methods [eq. 4]). We made several modifications to the classic RL model to improve the fit to the behavior (Figure 1H). First, we separated the learning rate for rewarded and unrewarded trials (αrew and αunr), as these two types of trials may have different levels of influence on value updates. Second, we included a forgetting rate (δ) to consider the possibility that the value of the unchosen option decayed (Barraclough et al., 2004; Ito and Doya, 2009). Third, we introduced a constant value bias term (β0) to account for a static preference for one option over the other. We quantified the fit by calculating the Akaike information criterion (AIC). The model that included all of these three modifications had the lowest AIC, indicating a significant improvement of the behavioral fit (Figure 1I). We note that AIC has a penalty for a larger number of parameters and thus the decrease in AIC represents a fit improvement beyond expected by the increased number of parameters. This modified RL model also outperformed the ‘local matching law’ model previously reported (Figures S1E–S1G) (Sugrue et al., 2004). This RL model with 5 parameters predicted choice patterns equally well as a logistic regression model with 10-trial history predictors (31 parameters in total) (Figure 1J), suggesting that the RL model indeed captures the behavioral strategy of the expert animals efficiently (Figure 1K).
To quantify the learning of the RL strategy, we defined the RL index as a measure of the degree to which the behavior resembled the RL strategy (STAR Methods [eq. 8]). The RL index gradually increased, indicating that mice acquired a RL-like strategy with learning (Figure 1L). In expert mice (RL index > 0.08), we found that αrew was significantly higher than αunr and δ (Figure 1M), indicating that the value difference between two options was more strongly updated after rewarded trials than unrewarded trials. This result is consistent with the dominant influence of rewarded choice history on upcoming choice (Figure 1G). The constant value bias β0 varied across sessions (Figure 1M). Expert mice showed high β∆Q, indicating that they indeed made decisions based on the value difference of the two options (Figure 1M). The forgetting rate δ was significantly above zero, indicating that the value of the unchosen option decayed (Figure 1M). Because an assigned reward remains assigned at the port until it is collected, the reward probability increases for the unchosen option in this task. Therefore, the ideal strategy is to increase the value of the unchosen option (δ < 0) instead of discounting it (δ > 0). The significantly positive δ suggests that their strategy was suboptimal. Nevertheless, stochastic exploration of the low-value option allowed the mice to achieve a relatively high reward rate.
In summary, this behavioral modeling provides two features that are critical for our study. First, the RL model confirmed that expert mice in our task indeed performed decision making based on history-dependent value. Second, the RL model provides a close estimate of their subjective value for each option on a trial-by-trial basis.
Heterogeneity of history coding across cortical areas in expert mice
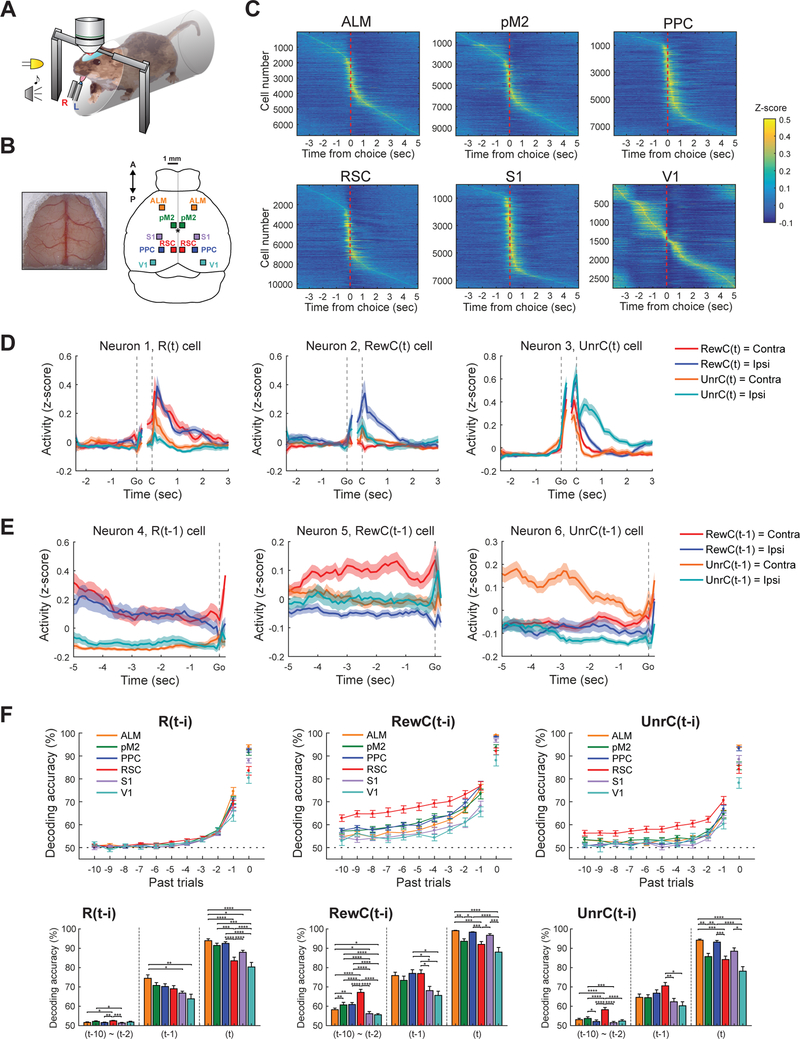
To study neural correlates of history and value signals during this history-dependent, value-based decision making task, we performed two-photon calcium imaging in task-performing mice (Figure 2A). We used CaMKIIa-tTA::tetO-GCaMP6s double transgenic mice that express GCaMP6s widely in cortical excitatory neurons (Wekselblatt et al., 2016). We adopted a surgical preparation that exposed most dorsal cortical areas for optical access (Kim et al., 2016), which allowed us to image multiple cortical areas in each mouse (Figure 2B). We focused on neurons in layer 2/3, and fluorescence signals from individual neurons were deconvolved to remove fluorescence decay and estimate spiking activity (Pachitariu et al., 2018) before all analyses. We first focused on expert sessions (defined as training day > 15 and RL index > 0.08) and imaged 6 dorsal cortical areas: ALM (n = 6,721 neurons from 13 fields in 7 mice), pM2 (n = 9,759 neurons from 17 fields in 10 mice), PPC (n = 7,703 neurons from 16 fields in 11 mice), RSC (n = 10,481 neurons from 17 fields in 9 mice), S1 (n = 7,576 neurons from 14 fields in 7 mice), and V1 (n = 2,767 neurons from 6 fields in 4 mice) (Figure 2B). We included only one image field for each cortical area per hemisphere per animal for analysis. In each behavioral session, we simultaneously imaged hundreds of neurons (542.3 ± 122.0 cells; mean ± SD) in one of the 6 cortical areas. Behavioral performance was equivalent in the sessions used to image each area (Figure S2).
Figure 2. Area specificity of history signals in expert mice.
(A) Schematic of two-photon imaging during task performance.
(B) Large craniotomy preparation that exposes most of the dorsal cortex for optical access (left) and locations of the 6 dorsal cortical areas imaged (right). Bregma is indicated with asterisk.
(C) Z-score normalized activity aligned to choice for all neurons imaged from expert mice. High activity during pre-choice period in V1 likely reflects visual response to ready cue (LED light).
(D) The activity of 3 example neurons in RSC tuned to the reward (Neuron 1, R(t) cell), rewarded choice (Neuron 2, RewC(t)), or unrewarded choice (Neuron 3, UnrC(t)) of the current trial.
(E) The activity of 3 example neurons in RSC tuned to the reward (Neuron 4, R(t-1) cell), rewarded choice (Neuron 5, RewC(t-1)), or unrewarded choice (Neuron 6, UnrC(t-1)) of the immediately preceding (t-1) trial.
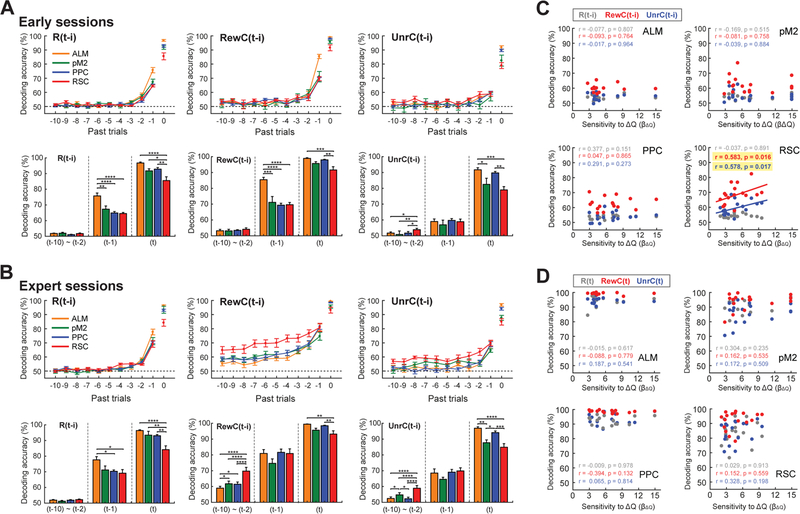
(F) Decoding accuracy for current and history information based on population activity of 200 neurons from each of the 6 cortical areas. Ready period activity (between −1.9 and −0.1 s from go cue) was used for history decoding ((t-10) to (t-1)), and post-choice period activity (between 0 and 1 s from choice) was used for current trial information decoding (t). Decoding accuracy was calculated by 10-fold cross-validation with PLS regression. Note that this analysis is potentially confounded by the autocorrelation of choice, which may inflate the length of encoded history. Thus we limit our interpretation to the differences across areas. Bar graphs show mean ± s.e.m. Two-way ANOVA with Tukey’s post-hoc test for (t-10)~(t-2), One-way ANOVA with Tukey’s post-hoc test for (t-1) and (t).
*P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001. All error bars are s.e.m.
See also Figure S2.
Each area contained many neurons with activity aligned to task epochs. Individual neurons showed heterogeneous activity patterns, and their peak timing tiled the entire trial period and inter-trial intervals in all 6 areas (Figure 2C). Many of these task-related neurons were tuned to specific task events. Figures 2D and 3E show 6 example neurons imaged in RSC that show specific tuning to task events. In Figure 2D, Neuron 1 was strongly activated during reward (R(t) cell), Neuron 2 was activated when ipsilateral choice was rewarded (RewC(t) cell), and Neuron 3 was particularly active when ipsilateral choice was unrewarded (UnrC(t) cell).
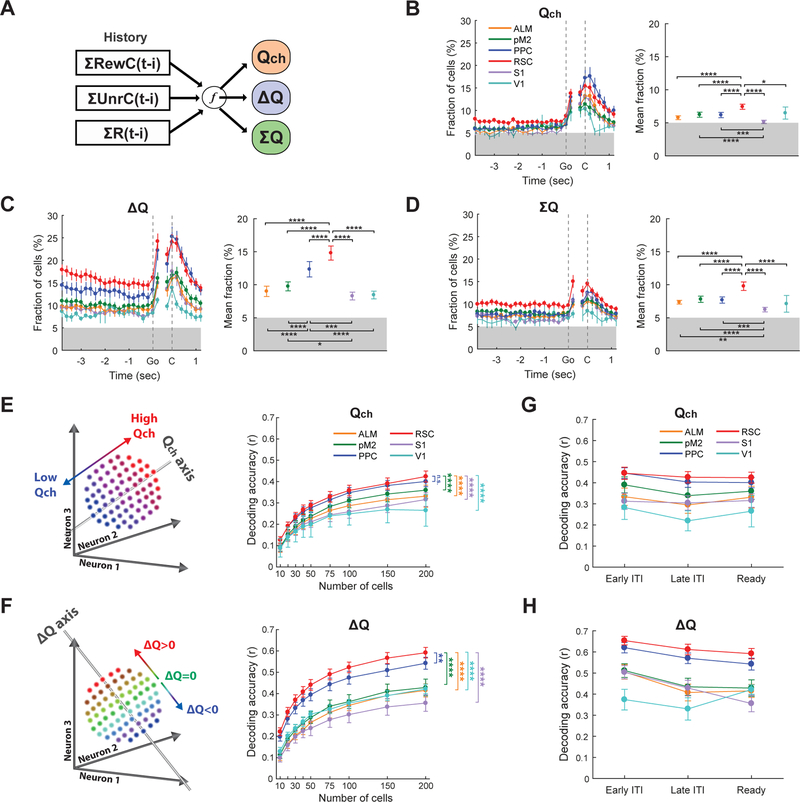
Figure 3. Preferential encoding of value-related information in retrosplenial cortex of expert mice.
(A) Value signals are constructed from a combination of the 3 types of history.
(B-D) Fractions of neurons that significantly encoded Qch (B), ∆Q (C), or ΣQ (D) (P < 0.05, Two-sided t-test of regression coefficients). Each fraction was calculated using 200 ms bin. Grey shading indicates 5% chance fraction. (Left) The fraction of significant neurons in each time bin. Data points with filled circles indicate the fractions that were significantly above the 5 % chance level (P < 0.05, One-sided t-test). (Right) Mean fraction during ready period (between −1.9 and −0.1 s from go cue) with statistics based on Two-way ANOVA with Tukey’s post-hoc test using the bins during the ready period.
(E-F) Decoding accuracy of Qch (E) or ∆Q (F) from population activity of variable numbers of neurons during ready period. Pearson correlation coefficient (r) was used as the decoding accuracy index (Two-way ANOVA with Tukey’s post-hoc test. Only the comparisons between RSC and the other areas are shown).
(G-H) Decoding accuracy of Qch (E) or ∆Q (F) from the activity of 200 cells during early ITI (between −5.9 and −4.1 s from go cue), late ITI (between −3.9 and −2.1 s from go cue), and ready period (between −1.9 and −0.1 s from go cue). Both ITIs and ready period encode the value-related information. Decoding was independently performed for each period.
*P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001. All error bars are s.e.m.
See also Figure S3.
In addition to such activity modulations based on ongoing task events, activity of many neurons was modulated by past events. The examples in Figure 2E show a neuron that was modulated by the reward history of the immediately preceding (t-1) trial (Neuron 4, R(t-1) cell) and neurons that were modulated by the rewarded choice (Neuron 5, RewC(t-1) cell) or unrewarded choice (Neuron 6, UnrC(t-1) cell) history from the preceding trial. To analyze how these history events modulated population activity in each area, we performed decoding analysis to classify various history and current events using population activity of 200 neurons from each area with multivariate partial least square (PLS) regressions. This method allows the decoding of multiple variables: in this case, multiple types of history information from multiple past trials, using a set of potentially collinear predictors (activity of individual neurons) (STAR Methods). This analysis revealed that the encoding of current and history events was area-specific. The encoding of current trial (t) events was generally strong in ALM and PPC. In contrast, history events, especially long (≤ t-2) history of rewarded choice and unrewarded choice, were most strongly encoded in RSC (Figure 2F). Long history modulation was weakest in primary sensory areas (V1 and S1, Figure 2F).
Retrosplenial cortex uniquely encodes value-related information as persistent activity
The results above indicate that history information is differentially represented across cortical areas in expert animals. This raises the possibility that these areas differentially encode value-related variables, since value in this task is a specific computational product of various types of history (Figure 3A). We focused on three types of value-related variables: 1) value difference between the two options (∆Q) which is the main driver of choice in this task and directly updated by rewarded and unrewarded choice history, 2) value of upcoming choice (Qch) which could contribute to whether the mouse chooses the high-value option (‘exploitive’ behavior) or the low-value option (‘explorative’ behavior) in each trial, and 3) the sum of the values for the two options (ΣQ) which may relate to the motivational state of the mouse (Tsutsui et al., 2016). We performed a multiple linear regression for the activity of each neuron with these three value-related variables. We also included the choice and reward information of the current trial in the regression to separate their contributions from history-dependent value (STAR Methods [eq. 12] and [eq. 13]). Regressions using the activity from each task-aligned time window identified individual neurons that were significantly modulated by value-related variables in each cortical area (Figures 3B–3D). The fractions of neurons varied across areas. In particular, RSC stood out as the area with the highest fractions of neurons encoding value-related variables among the 6 cortical areas.
We next examined how value-related information is encoded in each cortical area at the neural population level. Using neural population activity during the ready period, we performed linear decoding of ∆Q and Qch, two value-related variables important for value-based decision making (STAR Methods). All the 6 cortical areas encoded both Qch and ∆Q above chance level (Figure S3F), but the decoding accuracies varied across cortical areas. In particular, RSC had an especially high decoding accuracy for both Qch and ∆Q, followed closely by PPC (Figures 3E and 3F). Decoding accuracies were similar when we used neural activity during the inter-trial-interval (ITI) (Figures 3G and 3H). To examine whether the across-area differences depend on our decoder design, we repeated the decoding analysis using feedforward neural networks with a hidden layer for nonlinear decoding of value-related information (Figure S3). Similar to the linear decoding, RSC remained the area with particularly high decoding accuracies for Qch and ∆Q with the nonlinear model (Figure S3C). Furthermore, we found that the improvement in decoding accuracy by adding nonlinearity was marginal (Figures S3D and S3E). Thus it appears that the value-related information is largely encoded linearly in the 6 cortical areas.
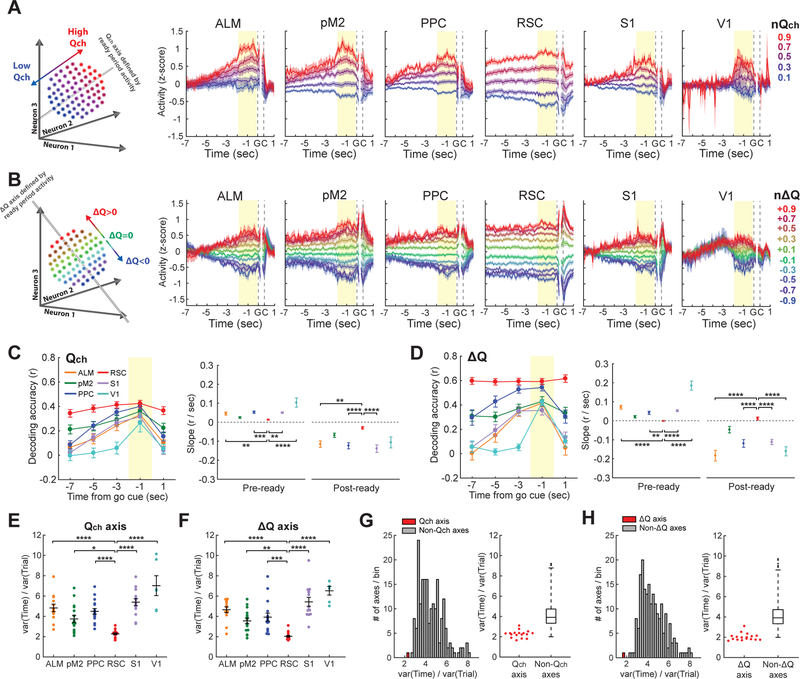
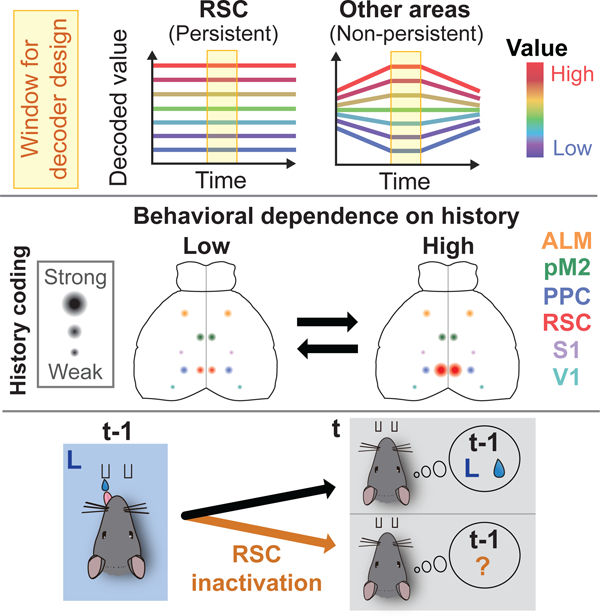
In order to use value-related information to reliably guide behavior, the brain needs to stably maintain the information over time. Thus, we tested whether value information is maintained as a stable population activity pattern across time. We did this by projecting the population activity from other time windows onto the value axes defined by the ready period activity. If, for example, an area encodes ∆Q in a persistent population activity pattern across time, population activity along the ∆Q axis (defined with the ready period activity) should consistently encode ∆Q even outside of the ready period. Alternatively, if ∆Q coding is temporally unstable, then the population activity along the ∆Q axis would not encode ∆Q outside of the ready period. In most of the areas, the separation of population activity according to ∆Q and Qch observed during the ready period decreased as the time window moved away from the ready period (Figures 4A and 4B). However, only in RSC, the population activity traces were nearly flat and persistently separated based on ∆Q and Qch throughout the ITI and ready period (Figures 4A and 4B). As a result, only in RSC, we could consistently decode value-related variables, especially ∆Q, across time along a single axis (Figures 4C and 4D). We also quantified the persistence of value coding using the temporal variance of activity along the ∆Q or Qch axis during the period spanning the ITI and ready period. The temporal activity variance along each axis was normalized by the across-trial activity variance along the same axis. This analysis revealed that RSC had the smallest temporal activity variance along the value-related axes (Figures 4E and 4F). Even though PPC and RSC had similar decoding accuracies when the decoders were trained with the activity during the tested period, their temporal persistence of value coding was strikingly different. These results indicate that RSC uniquely maintains value-related information in persistent population activity patterns.
Figure 4. Persistent population encoding of value-related information in retrosplenial cortex of expert mice.
(A-B) Projection of 200-cell population activity to Qch (A) or ∆Q (B) axis defined by ready period (yellow shading) activity. Qch was normalized such that it ranged from 0 to 1 for each session. ∆Q was normalized such that the negative and positive ∆Q ranged from −1 to 0 and from 0 to 1, respectively, for each session. Trials were averaged with 0.2 bin of the normalized Qch or ∆Q. Population activity along each axis was z-score normalized before averaging across sessions.
(C-D) (Left) Performance of decoders trained on ready period activity of 200 neurons at various time points (1.9-sec bins) in a trial. (Right) Slopes of the decoding accuracy curves before (−7 to −1 s, ‘pre-ready’) or after (−1 to 1 s, ‘post-ready’) the ready period (One-way ANOVA with Tukey’s post-hoc test for linear regression coefficients. Only the comparisons between RSC and the other areas are shown. The pre-ready slope for V1 was obtained using only −3 and −1 s.). Decoding accuracy quickly decays as the window moves away from ready period except for RSC, indicating value coding with persistent population activity pattern in RSC. (E-F) Temporal activity variance normalized by across-trial activity variance along Qch axis (E) or ∆Q axis (F) for 200-cell population from 6 cortical areas (One-way ANOVA with Tukey’s post-hoc test. Only the comparisons between RSC and the other areas are shown.). RSC shows the most persistent value coding.
(G-H) Temporal activity variance normalized by across-trial activity variance along Qch axis (G), ∆Q axis (H) or 199 axes orthogonal to either Qch or ∆Q axis for 200-cell RSC population activity. (Left) Distribution of variance along 200 axes in an example session. Qch and ∆Q axes are highlighted with red. (Right) Distributions of variance from all expert sessions. The horizontal lines of boxplots indicate medians, and the 25th and 75th percentiles. The whiskers extend to the most extreme data points, excluding outliers. The black dots indicate outliers.
*P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001. All error bars are s.e.m.
See also Figure S4.
Persistence of population activity along the value-related axes in RSC could result from population activity that is generally persistent. Alternatively, RSC population activity could be persistent specifically along the value-related axes, while maintaining variability along the other activity axes. To distinguish these possibilities, we examined the activity variance along different population activity axes. We used ready period activity of 200 neurons and defined the ∆Q or Qch axis as above. We then compared the temporal variance of activity during the period spanning the ITI and ready period along the ∆Q or Qch axis with the variance along the remaining 199 orthogonal axes (STAR Methods). Strikingly, this analysis revealed that the temporal activity variance along the value-related axes is smaller than the variance along almost all of the other orthogonal axes (Figures 4G and 4H). The results were similar with nonlinear decoders (Figure S4). Thus, the RSC population activity pattern is persistent specifically along the value-related axes.
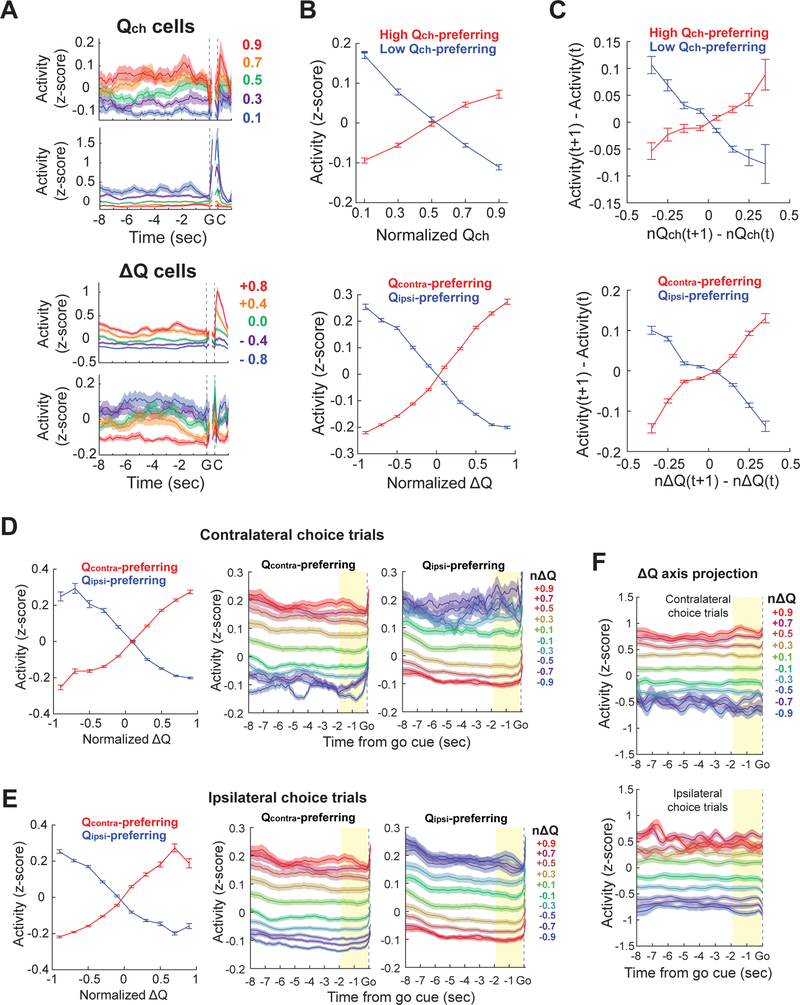
Consistent with the population analysis above, we were able to identify individual RSC neurons whose activity was persistently modulated according to the ∆Q and Qch values (Figure 5A). In contrast, neurons in the other areas that encoded ∆Q and Qch in the ready period did not consistently encode the value signals outside ready period (Figure S5), in line with the population analysis above (Figure 4). The RSC ∆Q and Qch neurons changed their activity depending on ∆Q and Qch in a graded manner (Figure 5B).
Figure 5. Graded and persistent encoding of value-related information by individual neurons in retrosplenial cortex of expert mice.
(A) Z-score normalized activity of two example Qch cells (top, a high Qch-preferring cell; bottom, a low Qch-preferring cell) and two example ∆Q cells (top, a contra-Q preferring cell; bottom, an ipsi-Q preferring cell) in RSC. Trials were averaged with 0.2 bin of normalized Qch or ∆Q. These cells encode Qch or ∆Q in a persistent and graded manner.
(B) Z-score normalized mean ready period activity of all RSC cells that significantly encoded Qch or ∆Q in their mean ready period activity (between −1.9 and −0.1 s from go cue). Activity was separately averaged according to the signs of activity modulations for Qch (high Qch-preferring, 4.95 ± 0.62 % of all imaged RSC cells; low Qch-preferring, 7.10 ± 0.66 %, mean ± s.e.m.) and ∆Q (Qcontra-preferring, 14.5 ± 1.58 %; Qipsi-preferring, 13.6 ± 0.88 %, mean ± s.e.m.). These cells encode Qch or ∆Q in a graded manner.
(C) Change across adjacent trials in Z-score normalized mean ready period activity of all RSC cells that significantly encoded Qch or ∆Q, plotted against the updates of Qch or ∆Q across adjacent trials. Population activity tracks updates of value-related variables on a trial-by-trial basis.
(D-E) ∆Q coding neurons reliably track ∆Q information within contralateral choice trials (D) and ipsilateral choice trials (E). (Left) Same as the bottom plot in (B), but separated based on the choice of the upcoming trials. (Middle and Right) Population-averaged activity of contra-preferring ∆Q neurons (Middle) and ipsi-preferring ∆Q neurons (Right) that were identified using ready period (yellow shading) activity (Trials were averaged with 0.2 bin of normalized ∆Q). These cells do not reflect the upcoming choice but instead encode ∆Q in a persistent and graded manner.
(F) 200-cell population activity projected to ∆Q axis in contralateral or ipsilateral choice trials. All traces were smoothed with a 500 ms moving average. All error bars are s.e.m.
See also Figure S5.
A recent study pointed out that slowly fluctuating neural activity can lead to spurious correlation with value (Elber-Dorozko and Loewenstein, 2018). However, in our data, ∆Q and Qch cells in RSC tracked value updates on individual trials, eliminating the possibility that activity of these neurons correlated with the value-related variables because of slow and random fluctuations (Figure 5C). Furthermore, when we separated trials based on the upcoming choice of the current trial, the RSC ∆Q cells still reliably encoded ∆Q (Figures 5D and 5E), excluding the possibility that the ∆Q cells simply encode motor plan. Similarly, population activity along ∆Q axis was not affected by upcoming choice in RSC (Figure 5F).
These results highlight RSC as a unique cortical area where value-related signals are potently and specifically encoded in a persistent population activity pattern across trials.
History coding preferentially increases in retrosplenial cortex with task learning
The results so far revealed heterogeneous encoding of history and value-related information across the cortex. We next asked if these features are stable across sessions, or if they emerge during learning of the task when mice gradually increased history dependency (Figure 1G). To examine potential plasticity of history coding, we performed two-photon calcium imaging in early sessions (≤ day 6) and compared the data with the expert sessions. For this longitudinal analysis, we only analyzed the neurons that were reliably imaged in both one early and one expert sessions, and focused on premotor and association areas, namely ALM (n = 3,526 neurons in 9 fields in 5 mice), pM2 (n = 2,906 neurons in 7 fields in 5 mice), PPC (n = 3,441 neurons in 11 fields in 9 mice), and RSC (n = 4,417 neurons in 8 fields in 4 mice). History-independent behavioral parameters were consistent between early and expert sessions (Figures S6A–S6C). We randomized the order of imaging of areas across animals. Consequently, similar to expert sessions, behavioral performance was equivalent across the early sessions used for imaging of each area (Figures S6D–S6G).
We analyzed history information in population activity from each area in early and expert sessions. We focused on history information instead of value for this analysis because the early session behavior was not fit by the RL model as well as expert sessions, making value estimates less reliable in early sessions (Figure 1L). We quantified population coding of each type of history information between early and expert sessions, with the same methodology used in Figure 2F. Strikingly, in early sessions, we found that long (≤ t-2) history coding in these areas was indistinguishable from each other, and short (t-1) history for rewarded choice and choice-independent reward outcome was most strongly encoded in ALM (Figure 6A). However, after learning, history coding increased in an area-specific manner, resulting in area differences of long (≤ t-2) history coding in expert sessions (Figure 6B). The area specificity in the expert sessions in this longitudinal dataset (Figure 6B) was similar to that of the analysis in Figure 2F that included all the neurons imaged in expert sessions. The increase in long (≤ t-2) history coding was particularly strong in RSC for rewarded choice history and unrewarded choice history (RSC increase was larger than ALM (P < 10−8), pM2 (P < 10−7), PPC (P < 10−8) for RewC history, and larger than ALM (P < 10−2), PPC (P < 10−3) for UnrC history. Two-way ANOVA with Tukey’s post-hoc test). These results indicate that specific cortical areas preferentially increase history signals when these signals are used for decision making. The potent history coding in RSC is a result of learning.
Figure 6. History coding of retrosplenial cortex reflects ongoing behavioral strategy.
(A-B) Decoding accuracy for current and history information based on population activity of 138 neurons from each of the 4 cortical areas in early (A) or expert (B) sessions. Only longitudinally tracked neurons were included in this analysis. Ready period activity (between −1.9 and −0.1 s from go cue) was used for history decoding ((t-10) to (t-1)), but post-choice period activity (between 0 and 1 s from choice) was used for current trial information decoding (t). Bar graphs show mean ± s.e.m. Two-way ANOVA with Tukey’s post-hoc test for (t-10)~(t-2), One-way ANOVA with Tukey’s post-hoc test for (t-1) and (t). *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001. All error bars are s.e.m.
(C) The relationship between the behavioral sensitivity to value difference based on the RL model and population encoding of history events (t-1 to t-10 trials) in mean ready period activity (between −1.9 and −0.1 s from go cue) in the expert sessions from the 4 cortical areas. Only the population encoding of rewarded and unrewarded choice history by RSC significantly correlates with the ongoing behavioral strategy (Spearman correlation).
(D) The relationship between the behavioral sensitivity to value difference based on the RL model and population encoding of the current trial events in mean post-choice period activity (between 0 and +1 s from choice) in the expert sessions from the 4 cortical areas. None of the comparisons shows significant correlations (Spearman correlation).
See also Figure S6.
The results above indicate that history coding in RSC is not fixed but is dynamically increased during task learning. This led us to wonder whether history coding in RSC is flexible even within expert sessions. Specifically, we asked whether history coding in RSC reflects the ongoing behavioral strategy in expert sessions. We analyzed how closely the population activity reflected history in individual sessions. This was done by a decoding analysis as above, and we averaged the decoding accuracy for t-1 to t-10 trials. The average decoding accuracy of RSC population activity for the rewarded choice history and unrewarded choice history showed significant correlations with β∆Q in the RL model, which is a measure of the behavioral sensitivity to the value difference of the two choices (Figure 6C). In other words, the RSC population better encoded the history information when the ongoing behavioral strategy relied more on history-dependent value. This correlation with behavioral strategy was specific, and not observed for choice-independent reward history information (Figure 6C) or for information about current trial (Figure 6D) in RSC. Furthermore, the other cortical areas did not show a correlation between behavioral strategy and population encoding (Figures 6C and 6D).
Taken together, these results indicate that RSC flexibly encodes history information depending on the ongoing behavioral strategy, and strongly encodes the specific history information required for that ongoing behavior.
Retrosplenial cortex is required for reward history-based strategy
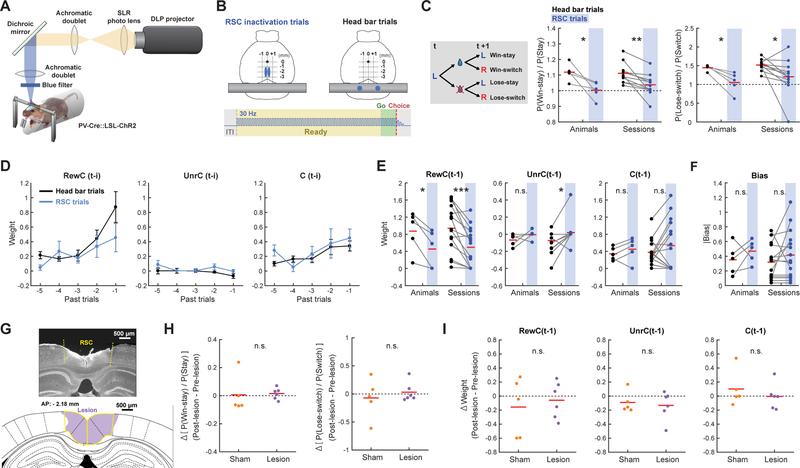
To examine whether RSC is necessary for the task performance, we performed optogenetic inactivation of RSC. We used PV-Cre::LSL-ChR2 double transgenic mice that express channelrhodopsin2 (ChR2) in parvalbumin-positive inhibitory neurons. By delivering blue light to activate inhibitory neurons, we bilaterally inactivated RSC from the onset of the ready period until the choice in a subset of trials. Since RSC is rostro-caudally elongated, we generated elliptical illumination patterns with a DLP projector (Figures 7A and 7B) (Dhawale et al., 2010; Haddad et al., 2013). In the other trials, the light was directed onto the head bar, away from RSC. We found that RSC inactivation decreased both the probability of repeating the same action after rewarded trials (‘win-stay’) and the probability of changing action after unrewarded trials (‘lose-switch’) (Figure 7C), suggesting that the RL strategy is impaired in trials with RSC inactivation. Furthermore, regression analysis revealed that RSC inactivation selectively impaired behavioral dependency on rewarded and unrewarded choice history, while preserving the dependency on outcome-independent choice history and choice bias (Figures 7D–7F). These results indicate that the activity of RSC is required for the reward history-based behavioral strategy.
Figure 7. Acute inactivation of RSC, but not its chronic lesion, impairs reward history-based strategy.
(A) Schematic of the projector-based optical stimulation system. Patterned light is resized and focused on cortex to optogenetically activate parvalbumin-positive inhibitory neurons.
(B) RSC was bilaterally inactivated in a small subset of trials within a session (5% or 15% of trials). In all other trials, the head bar was illuminated with the same light intensity and area. Elliptic illumination patterns were used for RSC inactivation trials to cover rostro-caudally elongated RSC. The illumination was applied from the onset of ready period until the choice at 30 Hz with a linear attenuation in the intensity after choice.
(C) Effects of RSC inactivation on the win-stay and lose-switch probabilities (Left: n = 5 mice; Right: n = 12 sessions). Red line indicates the mean of each condition. Only successive choice trials were used to derive the probabilities. P(Win-stay) was normalized by the overall stay probability (the average of P(Win-stay) and P(Lose-stay)). Similarly, P(Lose-switch) was normalized by the overall switch probability (the average of P(Win-switch) and P(Lose-switch)). For the n = animals plots (left), all sessions from each mouse were pooled to calculate the probabilities. For the n = sessions plots (right), only pairs from the 15% inactivation sessions were included. RSC inactivation made the stay and switch probabilities less dependent on the reward outcomes from the −1 trials. Paired t-test.
(D) Behavioral dependency on rewarded choice (RewC(t-i)), unrewarded choice (UnrC(t-i)) and outcome-independent choice (C(t-i)) history in head bar trials and RSC inactivation trials (STAR Methods [eq. 23]). (E) Effects of RSC inactivation on behavioral dependency on the 3 types of history from −1 trial (Left: n = 5 mice; Right: n = 15 sessions). Pairs of head bar trials (black) and RSC inactivation trials (blue) are shown. Red lines indicate the means. RSC inactivation reduced behavioral dependency on choice-reward history, especially for the rewarded choice history. Wilcoxon signed-rank test was used for non-normally distributed UnrC(t-1) weights of n = sessions, and paired t-test was used for the other comparisons.
(F) Effect of RSC inactivation to choice bias (Left: n = 5 mice; Right: n = 15 sessions). The absolute value of bias is shown for pairs of head bar trials (black) and RSC inactivation trials (blue). Red line indicates the mean of each condition. Paired t-test. The sign of the bias was also generally unaffected by inactivation (not shown).
(G) (Top) Example coronal section from a mouse with lesioned RSC. The section is stained with NeuN to visualize the presence of neurons. RSC largely lacks NeuN-positive neurons. Dashed lines indicate the borders of RSC. (Bottom) Corresponding brain atlas. Yellow lines outline RSC. Purple shading indicates lesioned area.
(H) Effects of RSC lesion on win-stay and lose-switch probabilities (Sham: n = 5 mice; Lesion: n = 6 mice). Difference between the mean of 7 sessions before sham/lesion and the mean of 7 sessions after sham/lesion is shown. Red lines indicate the means. Two-sided t-test.
(I) Effects of RSC lesion on behavioral dependency on the 3 types of history from −1 trial. Two-sided t-test.
*P < 0.05, **P < 0.01, ***P < 0.001.
See also Figure S7.
Our imaging results and previous studies suggested widespread encoding of history and value-related information across areas. To test the possibility that other areas can compensate for the function of RSC when it is removed chronically, we performed chronic, bilateral lesions of RSC by injecting NMDA to induce excitotoxicity (Figure 7G). In contrast to acute optogenetic inactivation, RSC lesion did not affect behavioral performance in subsequent sessions (Figures 7H, 7I and S7). These results suggest that while RSC is involved in the reward history-based strategy in normal mice, other areas can compensate for the chronic loss of RSC. We note, however, that the results do not exclude the possibility that the remaining neurons in RSC that survived the lesion were sufficient to support the behavior.
Discussion
By adapting the dynamic foraging task (Hamid et al., 2016; Johnson et al., 2016; Kawai et al., 2015; Samejima et al., 2005; Sugrue et al., 2004; Sul et al., 2011; Sul et al., 2010; Tsutsui et al., 2016) to head-fixed mice, we established a paradigm in which mice learn to perform decision making based on history-dependent value. We combined this behavior with two-photon calcium imaging to record the activity of hundreds of neurons simultaneously in each area at each learning stage, allowing the analysis of population coding of action value and plasticity of history coding. Equipped with this dataset of neural activity totaling 45,007 neurons, we found that the strength and temporal stability of history and value-related signals are heterogeneous across areas. Previous studies have revealed widespread activity related to history- and value-related information across many brain areas (Hamid et al., 2016; Hwang et al., 2017; Kawai et al., 2015; Kepecs et al., 2008; Morcos and Harvey, 2016; Padoa-Schioppa and Assad, 2006; Platt and Glimcher, 1999; Samejima et al., 2005; Scott et al., 2017; Stalnaker et al., 2014; Sugrue et al., 2004; Sul et al., 2011; Sul et al., 2010; Tsutsui et al., 2016), but the differences in the nature of population coding across individual brain areas have remained unclear. Here we found significant history- and value-related information in 6 dorsal cortical areas, even in primary sensory areas. However, we showed that only specific areas increase their encoding of history information when it is used for decision making, and maintain value-related information persistently.
A major finding in the current study is that RSC uniquely maintains persistent value-related population activity that tracked value updates on a trial-by-trial basis. Value-related information must be accessible to action selection circuitry even when actions are not on a fixed temporal schedule (e.g. variable inter-trial intervals as in our task). The persistent value coding in RSC may allow other brain areas to retrieve this information with a fixed read-out mechanism at any time. We note, however, that persistent population activity may not be the only mechanism by which value information is maintained in the brain. Persistent activity seems particularly suitable for short-term maintenance of value information when the brain needs to frequently retrieve value information and update it, as in our task in which mice are making hundreds of decisions in each behavioral session. We postulate that this mechanism may coexist with additional mechanisms that favor a more long-term, stable storage of value information when it may only need to be accessed in the distant future. Such long-term storage mechanisms may involve stable changes in synaptic weights.
Another main finding is that history coding in RSC is flexible. RSC increased history coding when mice learned to use history for decision making. Even within expert sessions, RSC history coding was the strongest in the sessions when the behavioral strategy relied more on the choice-outcome history. The other areas examined in this study did not show such correlations with the ongoing behavioral strategy. These results indicate that even though history coding is widespread, its flexibility is area-specific. History coding in RSC is particularly sensitive to the ongoing behavioral strategy.
We also found that RSC is required for the reward history-based decision making. Acute optogenetic inactivation of RSC during the pre-choice period selectively impaired behavioral dependence on rewarded and unrewarded choice history. These behavioral effects contrast with the previously reported effects of mouse mPFC inactivation, which specifically affected choice bias but not the dependence on reward history (Nakayama et al., 2018), indicating that different areas mediate different aspects of the behavior. We also presented evidence that chronically lost functions of RSC can be compensated for by other areas. This idea fits with our findings that history- and value-related information is widespread across many areas. The partial redundancy of value coding likely ensures the robustness of value-based decision making, a fundamental and evolutionarily conserved behavior.
To our knowledge, this is the first study to expose a unique coding of RSC in value-based decision making. RSC is heavily interconnected with many areas including the hippocampus and related cortical areas (Cembrowski et al., 2018; Ranganath and Ritchey, 2012), premotor cortex (Yamawaki et al., 2016), and the basal ganglia. With this hub-like connectivity (Vann et al., 2009), RSC may be an ideal area for the computation and persistent maintenance of history-dependent value, with access to choice and outcome information as well as action selection circuits. Our findings open an avenue for future investigations of circuit mechanisms for the plasticity and persistence of value coding, with RSC as a central locus.
STAR Methods
Contact for Reagent and Resource Sharing
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Takaki Komiyama (tkomiyama@ucsd.edu).
Experimental Model and Subject Details
All procedures were in accordance with the Institutional Animal Care and Use Committee at University of California, San Diego. Mice were obtained from The Jackson Laboratory (CaMKIIa-tTA: B6;CBA-Tg(Camk2a-tTA)1Mmay/J [JAX 003010]; tetO-GCaMP6s: B6;DBA-Tg(tetO-GCaMP6s)2Niell/J [JAX 024742]; PV-Cre: B6;129P2-Pvalbtm1(cre)Arbr/J [JAX 008069]; Ai32: B6.Cg-Gt(ROSA)26Sortm32(CAG-COP4*H134R/EYFP)Hze/J [JAX 024109]). All surgeries and experiments were carried out in adult mice (6 weeks or older). Mice were typically group housed in a plastic cage with bedding in a room with a reversed light cycle (12h-12h). All mice were prepared exclusively for the experiments described in this paper. Health conditions of mice were monitored daily during training. Both male and female healthy adult mice were used. Post hoc analysis revealed a tendency that males performed closer to our RL model than females in late (≥ day 14) sessions among CaMKIIa-tTA::tetO-GCaMP6s mice (Mean RL index, males: 0.1378 ± 0.0409 (n = 7 mice, mean ± SD), females: 0.0968 ± 0.0268 (n = 9 mice, mean ± SD), p = 0.0296 with two-sided t-test). However, of these late sessions, we only included sessions in which the performance was consistent (RL index > 0.08). In these sessions, the RL index did not significantly differ between sexes (p = 0.1272 with two-sided t-test).
Method Details
Surgery for imaging and optogenetics.
Adult mice were injected with dexamethasone (2 mg/kg) subcutaneously prior to surgery and continuously anesthetized with 1–2 % isoflurane during surgery. After cleaning the surface of dorsal skull with a razor blade, we applied saline on the skull and waited for a few minutes until the skull became transparent enough to visualize vasculature patterns. We recorded stereotactic coordinates of vasculature patterns through intact skull, and this information was used to identify imaging areas under the two-photon microscope. A craniotomy with a variable window size (ranging from a small circular window with ~2 mm diameter for imaging a single cortical area/mouse to a large hexagonal window for imaging multiple cortical areas/mouse) was performed on each mouse. The dura was left intact. A glass window was secured on the edges of the remaining skull using 3M Vetbond (Nishiyama et al., 2014) (WPI), followed by cyanoacrylate glue and dental acrylic cement (Lang Dental). The largest glass windows we used in this study were made by cutting a coverslip into a 5.5 × 7 mm rectangular glass and further cutting 2 frontal edges to make a hexagonal window. After the glass implantation, custom-built metal head-bar was secured on the skull above the cerebellum with cyanoacrylate glue and dental acrylic cement. Buprenorphine (0.1 mg/kg of body weight) and Baytril (10 mg/kg of body weight) were subcutaneously injected after surgery, and mice were monitored until they recovered from anesthesia.
Behavior.
Following a minimum of 5 days of recovery after surgery, mice were water-restricted at 1–2 ml/day. After at least a week of water-restriction, behavioral training began. Behavioral control was automated with a real-time system running on Linux communicating with Matlab (BControl, C Brody and Z Mainen). During behavioral sessions, two lickports were placed to the left and right sides of the head-fixed mouse and licking was monitored by IR beams. An amber LED was used as a ready cue (5mm diameter, placed ~5cm away from nose), and a speaker was used as a go cue (10 kHz tone). Each trial began with a ready period (2 or 2.5 s with LED light), followed by an answer period with an auditory go cue. The go cue was terminated when mice made a choice (the first lick to one of the two ports) or when the answer period exceeded the maximum duration of 2 s. Each choice triggered a 50 ms feedback tone (left, 5 kHz; right, 15 kHz). In rewarded trials, ~2.5 µ l of water reward was given immediately after the choice. Mice went through 3 phases of pre-training under head-fixation before starting the dynamic foraging task. In the first phase of pre-training (2–3 days), mice were rewarded for every left or right choice during the answer period with 100 % reward probability. Licking during ready period was not punished at this phase. We gradually increased mean ITI from 1 s to 6 s. In the second phase of pre-training (1–3 days), mice were trained in another task where reward was delivered alternately from left and right lickports following either choice (first lick during answer period). Beginning with this training phase, licking during ready period was punished by 500 ms white noise alarm and trial abort with an extra 2 s ITI. In the third phase of pre-training (1–2 weeks), mice were required to alternate their choices between left and right on every choice trial. Through the 3 phases of pre-training, mice learned the general task structure, including that only their first lick during answer period is associated with outcome, and that they need to withhold licking during ready period.
After the pre-training, mice started training in the dynamic foraging task where reward was probabilistic. Inter-trial intervals (ITI) varied randomly between 5–7 s. In a trial in which mice made a choice, ~2.5 µl of water reward was delivered immediately after choice if a reward had been assigned to the lickport on the trial. Reward was assigned at each lickport on every choice trial with a specific reward assignment probability for the lickport. Once a reward was assigned to a lickport, the reward was maintained until it was chosen. The combinations of reward assignment probabilities were either [60 %, 10 %] or [52.5 %, 17.5 %] in a trial, and reward assignment probability switched randomly every 60–80 trials in the order of [Left, Right] = …, [60 %, 10 %], [10 %, 60 %], [52.5 %, 17.5 %], [17.5 %, 52.5 %], [60 %, 10 %], …. The probability switch was postponed if the fraction of choosing the lickport with higher reward assignment probability was below 50 % in recent 60 trials until the fraction reached at least 50 %. Trials in which mice licked during ready period (‘alarm trials’) and the trials in which mice failed to lick during the answer period (‘miss trials’) were not rewarded. We did not include alarm and miss trials in neural activity analyses to ensure that the ready periods we analyzed were free of licking behaviors and that mice were engaged in the task in the trials. We defined expert sessions as the sessions in which the mice have been trained for at least 15 days in the dynamic foraging task and RL index was above 0.08 for the session. Expert mice typically performed > 600 trials in a session (711.5 ± 203.5 trials / session, 4.97 ± 3.29 % alarm rate and 4.51 ± 4.61 % miss rate in experts (mean ± SD)).
Two-photon calcium imaging.
Imaging was conducted with a commercial two-photon microscope (B-SCOPE, Thorlabs) running Scanimage using a 16× objective (0.8 NA, Nikon) with excitation at 925 nm (Ti-Sapphire laser, Newport). Six cortical areas investigated in this study are anterior lateral motor (ALM, 1.7 mm lateral and 2.25 mm anterior to bregma), posterior premotor (pM2, 0.4 mm lateral and 0.5 mm anterior to bregma), posterior parietal (PPC, 1.7 mm lateral and 2 mm posterior to bregma), retrosplenial (RSC, 0.4 mm lateral and 2 mm posterior to bregma), primary somatosensory (S1, 1.8 mm lateral and 0.75 mm posterior to bregma), and primary visual (V1, 2.5 mm lateral and 3.25 mm posterior to bregma) cortex. Images (512 × 512 pixels covering 524 × 564 µ m) were continuously recorded at ~29 Hz. Some of the mice were used for both early and expert session imaging. Areas that were not consistently imaged across frames were discarded from analyses (Typically ~10 pixels from each edge of the field of view).
Optogenetic inactivation.
To activate PV-positive inhibitory neurons in RSC of PV-Cre::LSL-ChR2 double transgenic mice using optogenetics, we generated elliptical illumination patterns with a DLP projector (Optoma X600 XGA). A single-lens reflex (SLR) lens (Nikon, 50 mm, f/1.4D, AF) was coupled with 2 achromatic doublets (Thorlabs, AC508–150-A-ML, f=150 mm; Thorlabs, AC508–075-A-ML, f=75 mm) to shrink and focus illumination patterns on RSC. A dichroic mirror (Thorlabs, DMLP490L) and a blue filter (Thorlabs, FESH0450) were placed between the 2 achromatic doublets and after the 2nd achromatic doublet, respectively, to pass only blue light (400–450 nm). Illumination patterns were generated with Psychtoolbox in MATLAB (http://psychtoolbox.org/). In RSC inactivation trials, a 2 mm × 0.5 mm ellipse was focused on RSC in each hemisphere (Center at 0.3 mm lateral and 2 mm posterior to bregma). In all other trials, two 1 mm × 1 mm circles were focused on the head bar (‘head bar trials’). The total light intensity was equivalent between RSC inactivation trials and head bar trials. We projected the patterns at 30 Hz as a sequence of square pulses from the onset of the ready period until the choice, with a linear attenuation in intensity over the last 100 ms. The intensity at the focus ranged between 2.5–6 mW/mm2 to moderately activate ChR2-expressing neurons (Dhawale et al., 2010; Haddad et al., 2013). We set the frequency of RSC inactivation trials within a session to either 15% (12 sessions) or 5% (3 sessions) with the constraint that each RSC inactivation trial must be followed by at least 3 head bar trials to avoid excessive perturbation of reinforcement learning. We inactivated RSC through a glass window for 4 mice and through the skull for 1 mouse. The skull for the through-skull inactivation was made semi-transparent by covering the dorsal skull surface with a layer of cyanoacrylate glue (Makino et al., 2017).
Lesion.
Twelve adult mice were trained to perform the task, and after at least 7 days of stable performance underwent excitotoxic-lesion or sham-lesion surgery. Stable, expert performance for this task was determined to be choice prediction accuracy of a standard RL model ([eq.3], [eq.4]) > 65 % in at least 6 sessions during the 7 days; these sessions also met the > 0.08 RL index criterion for imaging mice in at least 6 sessions during the 7 days. Mice were anesthetized with 1–2% isoflurane during surgery. Three burr-hole craniotomies per hemisphere (6 total) were opened on the dorsal skull over RSC. A tapered glass pipette was inserted to perform the cortical microinjection. Injection sites were, in mm and relative to Bregma: AP = −1.6, −2.3, −3.0, ML = ± 0.3, ±0.35, ±0.4, and DV = −0.4 from the dura surface in all sites. Injection was of 50 nl/site of either NMDA in sterile saline (20 µ g/µl or 10 µ g/µ;l Sigma) or sterile saline, at a rate of 0.05–0.1 µl/min. After injection, the pipette was left for 5 minutes to ensure diffusion of the solution. Buprenorphine (0.1 mg/kg of body weight) and Baytril (10 mg/kg of body weight) were subcutaneously injected after surgery. Following surgery, the mouse resumed the behavioral task on the next day, and thereafter every day. Both the surgeon and the experimenter for the behavior were blind to the identity of the substance that was injected, and became unblinded only after the last day of data collection. Of the 12 mice, 5 received saline, 7 received NMDA. One of the NMDA mice was excluded due to small and off-target lesion, as quantified by histology.
Brains of lesion and saline mice were collected at 21–25 days post injection. To quantify the lesion size, 50 µm-thick coronal sections were prepared with a microtome (Thermo Fisher Scientific) and blocked with 10% goat serum, 1% bovine serum albumin, and 0.3% Triton X-100 in PBS. Immunostaining was then performed with anti-NeuN primary antibody (1:400; Mouse, Millipore) and anti-mouse Alexa Fluor 488 secondary antibody (1:1000; Goat, Thermo Fisher Scientific). Both missing areas and areas that lacked NeuN-positive neurons were considered lesioned. Images of coronal sections with RSC and the corresponding brain atlas (Paxinos and Franklin, 2001) were superimposed to quantify the % of lesion within RSC.
Quantification and Statistical Analysis
Generalized matching law.
Generalized matching law (Baum, 1974) is an extension of the original Herrnstein’s matching law (Herrnstein, 1970) to describe behavior in which animals match the relative frequency of responding with that of reinforcement. We formulated the relationship for our task as follows:
| [eq. 1] |
where CL and CR are the number of left and right choices, respectively, RL and RR are the number of reinforcers (rewards) from left and right, respectively, s is the sensitivity of choice patterns to the reward ratio, and b is the choice bias. For each session, we calculated the choice and reward ratios for each probability block, excluding the first 20 trials at the beginning of each block. The logarithmic version of the model was fit with ordinary least squares.
Quantification of behavioral history dependency.
To quantify dependency of decision making on history, we fit the following logistic regression model with 3 types of history predictors:
| [eq. 2] |
where RewC(t − i) is the rewarded choice history on trial t − i (1 if rewarded left choice, −1 if rewarded right choice, 0 otherwise), UnrC(t − i) is the unrewarded choice history on trial t − i (1 if unrewarded left choice, −1 if unrewarded right choice, 0 otherwise), C(t − i) is the outcome-independent choice history on trial t − i (1 if left choice, −1 if right choice, 0 otherwise). βRewC(t–i), βUnrC(t–i) and βC(t–i) are the regression weights of each history predictor, and β0 is the history-independent constant bias term. The model was regularized with L1-penalty where the regularization parameter was selected by 10-fold cross-validation (minimum cross-validation error plus one standard error). The prediction accuracy of choice was calculated by 2-fold cross-validation to separate the test trial sets from the training trial sets.
Reinforcement learning model.
In a standard RL model (Sutton and Barto, 1998), action value for the chosen option is updated as follows:
| [eq. 3] |
where Qch(t) is the subjective action value of the chosen option on trial t, R(t) is the reward outcome on trial t (1 if rewarded, 0 if unrewarded), and α is the learning rate. The probability of choosing left on trial t is estimated by a softmax function as follows:
| [eq. 4] |
where QL(t) and QR(t) are the action values of the left and right choices on trial t respectively, and β∆Q defines the sensitivity of decision making to the value difference.
We made several modifications to the above standard Rescorla-Wagner RL model to improve the prediction accuracy for our mouse behaviors. We validated each additional parameter using Akaike information criterion (AIC) and only used the additional parameters that improved (decreased) AIC for the behavior in the current task (Figure 1I). In our final model, action values of chosen (Qch) and unchosen (Qunch) options are updated as follows:
| [eq. 5] |
| [eq. 6] |
where we prepared separate learning rates for rewarded (αrew) and unrewarded (αunr) trials, δ is the forgetting rate for the unchosen option (Barraclough et al., 2004; Ito and Doya, 2009), R(t) is reward outcome on t (1 for rewarded, 0 for unrewarded trials). The learning rates and the forgetting rate were constrained between 0 and 1. However, even without the positive constraint, the forgetting rate never took a negative value in any of the late sessions (≥ Day 12, n = 460 sessions). In alarm and miss trials, values of both options were discounted by δ. The probability of choosing left (PL) on trial t is estimated using left (QL) and right (QR) action values as follows:
| [eq. 7] |
where β0 is the value bias which is constant within each session, and β∆Q is the sensitivity to value difference. The RL model was fit to the behavioral choice patterns by maximum likelihood estimation. Using the maximum likelihood of the model, we quantified how closely the value update rule of the RL model captured the mouse strategy by defining the RL index as follows:
| [eq. 8] |
where n is the number of choice trials in a session, and the likelihood explained by β0 was calculated using the following choice probability:
| [eq. 9] |
where both β∆Q and β0 are fit parameters from the above RL model.
The prediction accuracy of choice was calculated by 2-fold cross-validation.
Local matching law and its generalization.
Local matching law (Sugrue et al., 2004) is an extension of the Herrnstein’s matching law (Herrnstein, 1970) to estimate the trial-by-trial choice probability in a dynamic environment. The local matching law estimates the choice probability on each trial by integrating reward history of each action with exponential functions. The instantaneous choice probability ratio is estimated as follows:
| [eq. 10] |
where PL and PR are the probability of choosing left and right, respectively, RL and RR are the number of rewards from left and right, respectively (1 if rewarded, 0 if unrewarded), and τ is the time constant for the exponential functions.
We also generalized this local matching law such that it can account for choice bias and imperfect sensitivity of animals to reward ratio (Baum, 1974) as follows:
| [eq. 11] |
where s is the sensitivity of choice patterns to the reward ratio, and b is the choice bias. The generalized local matching law outperformed the local matching law (Figure S1F). The local matching law and generalized local matching law were fit to the behavioral choice patterns by maximum likelihood estimation.
Two-Photon Image Processing
Slow drifts in the imaging field were manually corrected during imaging. Acquired images were motion corrected by a custom-written motion correction algorithm (Mitani and Komiyama, 2018) offline, and slow image distortions were corrected by affine transformations based on enhanced correlation coefficients between frames (Evangelidis and Psarakis, 2008). After motion correction, we used Suite2P (Pachitariu et al., 2016) to generate regions of interest (ROIs) corresponding to individual neurons and extract their fluorescence. ROI classifications by the automatic classifier were further refined by manual inspection. We excluded ROI pixels that overlap with the other ROIs, and linear trends in fluorescence signals were removed before further processing. The de-trended signals from cellular ROIs were deconvolved with a non-negative deconvolution algorithm to remove fluorescence decay and estimate underlying spiking activity (Pachitariu et al., 2018). This published method also removes contamination of activity of neuropil structures surrounding each cellular ROI. The deconvolved signals were used for all neural activity analyses. For a subset of mice, imaging was conducted in the same cortical areas from both left and right hemispheres. To avoid overrepresentation of a local population that could skew our results, we only included imaging data from one image session per cortical area per hemisphere in each mouse for analyses of neural activity. We excluded sessions if bone re-growth covered the areas of interest.
Multiple regression analysis of cellular activity.
To quantify the fraction of neurons that significantly encode value-related information at each time point in a trial, we first averaged neural activity with non-overlapping moving windows (200 ms bins) starting from either go cue or choice (first lick). The first bins at the go cue or choice are the averages between the go cue ± 100 ms or choice ± 100 ms. After the binning, value-related modulation of neural activity within each bin was analyzed using the following 2 models for pre-choice period ([eq. 12]) and post-choice period ([eq. 13]):
| [eq. 12] |
| [eq. 13] |
where C(t) is the choice on trial t (1 if contralateral choice, −1 if ipsilateral choice, 0 otherwise), R(t) is the reward outcome on trial t (1 if rewarded choice, −1 if unrewarded choice, 0 otherwise), RewC(t) is the rewarded choice on trial t (1 if rewarded contralateral choice, −1 if rewarded ipsilateral choice, 0 otherwise), UnrC(t) is the unrewarded choice on trial t (1 if unrewarded contralateral choice, −1 if unrewarded ipsilateral choice, 0 otherwise), Qch(t) is the value of chosen option on trial t, ∆Q(t) is the value difference between contralateral and ipsilateral options on trial t, and ∑ Q (t) is the sum of values of both options on trial t. For some analyses (Figures 5A–E and Figure S5), averaged ready period activity (averaged between −1.9 and −0.1 s from go cue) was used instead of 200 ms bin. We tested the significance of each regression weight using Two-sided t-test to classify cells with significant history or value information. The median variance inflation factors for βC(t), βQch(t), β∆Q(t), β∑ Q(t) in [eq.12] were 1.7174, 3.8833, 1.8048, 3.7684, respectively. The median variance inflation factors forβRewC(t), βUnrC(t), βR(t), βQch(t), β∆Q(t), β∑ Q(t) in [eq.13] were 1.4099, 1.3860, 1.0411, 3.8926, 1.8124, 3.8648, respectively. To minimize the effects of multicollinearity, we focused our analysis on the fractions of statistically significant coefficients instead of using the raw coefficients for these multiple regression analyses.
Decoding of history information from population activity.
We used a multivariate partial least square (PLS) regression model (Wold et al., 2001) to build a multivariate decoder that would decode various history information in multiple past trials based on the activity of neural ensembles that include interneuronal correlations (i.e. multicollinearity). PLS regression projects both response and predictor variables into new orthogonal spaces with reduced dimensions such that the covariance between response and predictor variables is maximized. We first built a predictor matrix X of size [Number of trials for model training] × [Number of neurons] where each element is the average of z-score normalized deconvolved neural activity during either ready period or post-choice period. The size of response matrix Y was [Number of trials for model training] × [Number of current/history events to decode]. The column size was 61 for ready period decoding (upcoming choice C, and −20 to −1 trial history for RewC, UnrC and R) and 63 for post-choice period decoding (RewC, UnrC and R of current trial, and −20 to −1 trial history for RewC, UnrC and R). C, RewC, UnrC and R of current/history events take −1, 0 or 1 as described in the section of multiple regression analysis above. PLS regression decomposes predictor matrix X and response matrix Y into a lower-dimensional space as follows:
| [eq. 14] |
| [eq. 15] |
where T and U are projections of X and Y, respectively, to new low-dimensional spaces, P and Q are orthogonal loading matrices with reduced dimensions, and E1 and E2 are error terms. Then a least square regression was performed between T and U as follows:
| [eq. 16] |
where B is a matrix with a set of regression coefficients and E3 is the error term. We obtained solutions of PLS regression with the nonlinear iterative partial least squares (NIPALS) method such that covariance between T and U is maximized. After fitting the model to training set trials, we decoded information of current and past trial events using activity of test trial sets as follows:
| [eq. 17] |
where Xtest and Ytest are predictor matrix and response matrix for test trial set, respectively. The elements in the decoded response matrix Ytest were further binarized for binary classification of current and history events based on the sign of the decoded elements. Each decoding was performed by 10-fold cross-validation. For each image field, we subsampled either 200 cells (Figure 2F) or 138 cells (Figures 6A and 6B) in each iteration allowing repetitions with the smallest number of iterations to include every cell at least once for decoding, and the decoding accuracy from the iterations were averaged. 138 was the smallest number of neurons that we longitudinally tracked between early and expert sessions within the same field of view.
Linear decoding of value-related information from population activity.
To decode information of Qch and ∆Q from population activity during ready period or ITI, we used the following linear decoders:
| [eq. 18] |
| [eq. 19] |
These equations decode Qch and ∆Q using a weighted linear sum of the activity of a neural population (n neurons) during early ITI (between −5.9 and −4.1 s from go cue), late ITI (between −3.9 and −2.1 s from go cue) or ready period (average between −1.9 and −0.1 s from go cue). These linear models were regularized with L1-penalty where the regularization parameter was selected by 10-fold cross-validation so that the cross-validated mean squared error is minimized. The objective functions of the models were minimized by Sparse Reconstruction by Separable Approximation (SpaRSA) (Wright et al., 2009). The decoding was performed by 10-fold cross-validation. We quantified decoding accuracy using Pearson correlation coefficient between the decoded values and behaviorally estimated values from the RL model. The decoding analyses were repeated until all cells were used at least once, as described in the PLS regression section, and decoding accuracies from multiple iterations were averaged for each session. The Qch and ∆Q axes were defined using regularized regression coefficients from the above decoders as follows:
| [eq. 20] |
| [eq. 21] |
Population activity at different time points was projected to these axes by taking the inner product of the population activity vector and these axis vectors. The constant bias coefficient β0 from each decoder was added to the inner product to derive the final projected population activity. However, the inclusion of β0 did not significantly affect the final results (not shown). Projected population activities of multiple 200-cell sets were averaged within each session. The chance level of decoding accuracy was calculated by shuffling the trial labels of the test set trials 1,000 times.
Nonlinear decoding of value-related information from population activity.
To decode information of Qch and ∆Q from population activity without assuming a linear neural code, we trained feedforward neural networks with a hidden layer for nonlinear decoding of value-related information. The hidden layer consisted of 10 sigmoid neurons, which conferred on the networks the ability to learn complex nonlinear relationships between population activity and the value-related information. The neural networks were trained by Bayesian regularization backpropagation with Levenberg-Marquardt optimization. The decoding was performed by 10-fold cross-validation. The decoding analyses were repeated until all cells were used at least once, as described in the PLS regression section, and decoding accuracies from multiple iterations were averaged for each session.
Temporal activity variance along value-related axes and their orthogonal axes.
The population activity of 200 neurons that we used to identify value-related axes has 200 dimensions. To identify 199 axes that are orthogonal to each value-related axis, we performed singular value decomposition (SVD) of each axis vector as follows:
| [eq. 22] |
where U is a left singular matrix, Σ is a diagonal matrix with singular values, and V is a right singular matrix. The first column of V is the normalized value-related axis vector, and the other columns are 199 axis vectors that are orthonormal to the value-related axis vector and to each other. To calculate the activity variance, we first projected population activity of each trial between −6 and 0 s from go cue (smoothed with 500 ms moving averaging) to the 200 orthonormal axes. To obtain temporal activity variance, we subtracted the mean activity during the time window from projected activity trace for each trial to remove across-trial activity variance, and then concatenated these mean-centered activity traces of all trials. Variance across time of the concatenated trace was used as the temporal activity variance along each axis. This temporal activity variance was normalized by dividing with the across-trial activity variance, which is the variance of mean activity during the time window across trials along each axis.
Effects of optogenetic RSC inactivation on behavioral history dependency.
To quantify the effects of RSC inactivation on the behavioral history dependency, we fit the following logistic regression model:
| [eq. 23] |
where RewC(t − i) is the rewarded choice history on trial t − i (1 if rewarded left choice, −1 if rewarded right choice, 0 otherwise), UnrC(t − i) is the unrewarded choice history on trial t − i (1 if unrewarded left choice, −1 if unrewarded right choice, 0 otherwise), C(t − i) is the outcome-independent choice history on trial t − i (1 if left choice, −1 if right choice, 0 otherwise). HB(t) is 1 on head bar trials and 0 on RSC inactivation trials. RSC(t) is 1 on RSC inactivation trials and 0 on head bar trials. βRewC(t–i), βUnrC(t–i), and βC(t–i) are the regression weights of each history predictor, and β0 is the history-independent constant bias. The model has separate regression weights for head bar and RSC inactivation trials. The model was regularized with L1-penalty where the regularization parameter was selected by 10-fold cross-validation (minimum cross-validation error). To prevent overpenalization of regression weights for less frequent RSC inactivation trials, we matched the number of head bar trials to the number of RSC inactivation trials for each fitting by randomly subsampling head bar trials. The subsampling and fitting were repeated with the smallest number of iterations to include every head bar trial at least once, and the regression weights from the iterations were averaged.
Effects of RSC lesion to behavioral history dependency.
To quantify the effects of RSC lesion to the behavioral history dependency, we fit the following logistic regression model:
| [eq. 24] |
The model was regularized with L1-penalty where the regularization parameter was selected by 10-fold cross-validation (minimum cross-validation error). The model was fit to the choice patterns of each session.
Statistical analysis.
Normality of distributions was tested for each dataset using Lilliefors test to decide whether to use parametric or non-parametric tests. Tukey–Kramer method was used for post hoc multiple comparison tests. For all statistical analyses, we calculated a single value for each session. For example, we calculated cell fractions per cortical area in a session and did not pool cells from different mice or sessions to calculate the cell fractions. All statistical and data analyses were performed in MATLAB. The numbers of cells, animals, and sessions for each experiment are provided in the text and figure legends.
Data and Software Availability
All data and analysis code are available upon reasonable request to the Lead Contact, Takaki Komiyama (tkomiyama@ucsd.edu).
Supplementary Material
(A-D) Distributions of run-lengths (the number of consecutive choices to the same side before exploring the other side) of an example mouse for the option with higher probability in [0.6:0.1] block (A), the option with higher probability in [0.525:0.175] block (B), the option with lower probability in [0.525:0.175] block (C), the option with lower probability in [0.6:0.1] block (D). All run-lengths from ≥ day 14 sessions are pooled. The run-length distributions follow a gamma distribution which is expected for stochastic Poisson processes. This argues against the possibility that mice employed fixed strategies such as exploring the low probability option after a set number of consecutive choices to the high probability option.
(E) Schematic of the local matching law (LML). The LML estimates the action value on each trial by integrating reward history with exponential functions. The local matching law assumes that the choice probability ratio exactly matches the ratio of integrated reward history ratio (STAR Methods [eq. 10]). We also considered a model with the assumption that the matching between choice probability ratio and the reward history ratio is not exact, which we termed the generalized local matching law (GLML, STAR Methods [eq. 11]).
(F) Akaike Information Criteria (AIC) difference between the LML and the GLML. The GLML shows lower AIC throughout training days, indicating a better behavioral fit.
(G) AIC difference between our best RL model and the GLML. The RL model shows lower AIC throughout training days.
All error bars are s.e.m.
(A) The accuracy of the RL model in correctly predicting the behavioral choices.
(B) The accuracy of the history regression model with rewarded choice, unrewarded choice, and outcome-independent history predictors from past 10 trials and a constant bias term in correctly predicting the behavioral choices.
(C) Reinforcement learning index (STAR Methods [eq. 8]).
(D) The fraction of rewarded trials.
One-way ANOVA with Tukey’s post-hoc test (*P < 0.05, n.s. P > 0.05). All error bars are s.e.m.
(A) Schematic of the linear decoders. The linear decoders decode value-related information by a weighted linear sum of neural activity.
(B) Schematic of the feedforward neural network for nonlinear decoding. The network has a hidden layer with 10 sigmoid neurons, which confers on the network the ability to learn complex nonlinear relationships between population activity and the value-related information.
(C) Decoding accuracy of Qch and ∆Q from population activity of variable numbers of neurons during ready period with the nonlinear model. (Two-way ANOVA with Tukey’s post-hoc test. Only the comparisons between RSC and the other areas are shown).
(D-E) Comparisons of the decoding accuracy between the linear model and the nonlinear model for Qch (D) and ∆Q (E) (Two-way ANOVA with Tukey’s post-hoc test).
(F-G) The distributions of the chance decoding accuracy for linear models (F) and nonlinear models (G). Each decoder was trained with ready period activity (yellow shading) of a subset of trials, and the decoding accuracy was calculated by shuffling the trial labels of the test set trials 1,000 times for different trial periods. 99th percentile, 95th percentile, 5th percentile and 1st percentile of each session were averaged across sessions. All error bars are s.e.m.
*P < 0.05, **P < 0.01, ****P < 0.0001. All error bars are s.e.m.
(A-B) (Left) Performance of nonlinear decoders trained on ready period activity of 200 neurons at various time points (1.9-sec bins) in a trial. (Right) Slopes of the decoding accuracy curves before (−7 to −1 s, ‘pre-ready’) or after (−1 to 1 s, ‘post-ready’) the ready period (One-way ANOVA with Tukey’s post-hoc test for linear regression coefficients. Only the comparisons between RSC and the other areas are shown. The pre-ready slope for V1 was obtained using only −3 and −1 s).
(C-D) Temporal activity variance normalized by across-trial activity variance along nonlinear Qch axis (C) or ∆Q axis (D) for 200-cell population from 6 cortical areas (One-way ANOVA with Tukey’s post-hoc test. Only the comparisons between RSC and the other areas are shown). RSC shows the most persistent value coding.
*P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001. All error bars are s.e.m.
(A) Population averages of the activity of all neurons that significantly encoded Qch during ready period (yellow shading) in each area. Top, high Qch-preferring neurons (2.97 ± 0.41 % of imaged neurons in ALM, 3.88 ± 0.64 % in pM2, 3.76 ± 0.57 % in PPC, 4.95 ± 0.62 % in RSC, 3.24 ± 0.82 % in S1, 3.75 ± 2.30 % in V1, mean ± s.e.m.); bottom, low Qch-preferring neurons (5.17 ± 0.60 % in ALM, 5.82 ± 0.58 % in pM2, 7.09 ± 1.28 % in PPC, 7.10 ± 0.66 % in RSC, 4.27 ± 0.50 % in S1, 7.61 ± 2.76 % in V1, mean ± s.e.m.). Trials were averaged with 0.2 bin of normalized Qch.
(B) Population averages of the activity of all neurons that significantly encoded ∆Q during ready period in each area. Top, Qcontra-preferring neurons (8.53 ± 0.99 % in ALM, 8.77 ± 1.02 % in pM2, 13.00 ± 1.63 % in PPC, 14.50 ± 1.58 % in RSC, 9.24 ± 1.80 % in S1, 8.45 ± 1.92 % in V1, mean ± s.e.m.); bottom, Qipsi-preferring neurons (9.66 ± 1.09 % % in ALM, 9.87 ± 0.85 % in pM2, 15.30 ± 2.46 % in PPC, 13.60 ± 0.88 % in RSC, 8.52 ± 0.98 % in S1, 7.94 ± 1.58 % in V1, mean ± s.e.m.). Trials were averaged with 0.2 bin of normalized ∆Q. All error bars are s.e.m.
(A-C) Consistency of the history-independent behavioral measurements between early and expert sessions of imaging data used in Figure 6. Fractions of miss trials (A), fractions of alarm trials (B), number of trials per session (C). n = 35 sessions for both early and expert sessions. Paired t-test (n.s. P > 0.05).
(D-G) Equivalent behavioral performance in the early sessions used for imaging of each cortical area. The accuracy of the RL model in correctly predicting the behavioral choices (D). The accuracy of the history regression model with rewarded choice, unrewarded choice, and outcome-independent history predictors from past 10 trials and a constant bias term in correctly predicting the behavioral choices (E). Reinforcement learning index (F). The fraction of rewarded trials (G). One-way ANOVA with Tukey’s post-hoc test (n.s. P > 0.05).
All error bars are s.e.m.
(A) Relationship between RSC lesion size and the effect on win-stay and lose-switch probabilities. Difference between the mean of 7 sessions before lesion and the mean of 7 sessions after lesion is shown. Pearson’s correlation coefficients and their p-values are shown.
(B) Behavioral dependency on rewarded choice (RewC(t-i)), unrewarded choice (UnrC(t-i)), and outcome-independent choice (C(t-i)) history before and after sham/lesion surgery. The mean of 7 sessions before sham/lesion and the mean of 7 sessions after sham/lesion are shown. The means were averaged across mice (n = 5 sham mice; n = 6 lesion mice). Error bars are s.e.m.
(C) Relationship between RSC lesion size and the effects on behavioral dependency on the 3 types of history from −1 trial. Difference between the mean of 7 sessions before lesion and the mean of 7 sessions after lesion is shown. Pearson’s correlation coefficients and their p-values are shown.
(D) Effects of RSC lesion on win-stay and lose-switch probabilities on day 1 after lesion. (Top) Difference between the mean of 7 sessions before sham/lesion and day 1 after sham/lesion is shown (Two-sided t-test). Red lines indicate the means. (Bottom) Relationship between RSC lesion size and the effects on win-stay and lose-switch probabilities. Difference between the mean of 7 sessions before lesion and day 1 after lesion is shown. Pearson’s correlation coefficients and their p-values are shown.
(E) Effects of RSC lesion on behavioral dependency on the 3 types of history from −1 trial. (Top) Difference between the mean of 7 sessions before sham/lesion and day 1 after sham/lesion is shown (Two-sided t-test). Red lines indicate the means. (Bottom) Relationship between RSC lesion size and the effects on behavioral dependency on the 3 types of history from −1 trial. Pearson’s correlation coefficients and their p-values are shown.
n.s. P > 0.05.
Highlights.
History and value-related information was widespread across 6 dorsal cortical areas
Retrosplenial cortex (RSC) encoded value signals as persistent population activity
RSC history coding increased with learning, reflecting ongoing behavioral strategy
Acute inactivation of RSC selectively impaired the reward history-based strategy
Acknowledgements
We thank K. O’Neil, O. Arroyo, Q. Chen, L. Hall, A. Kim and T. Loveland for technical assistance, A. Mitani for motion correction algorithm, and the rest of the members of the Komiyama lab, especially E.J. Hwang, H. Liu, A. Mitani, and C. Ren for discussions. The research was supported by grants from NIH (R01 NS091010A, R01 EY025349, R01 DC014690, U01 NS094342, and P30EY022589), Pew Charitable Trusts, David and Lucile Packard Foundation, McKnight Foundation, New York Stem Cell Foundation, Kavli Institute for Brain and Mind, and NSF (1734940) to T.K. R.H., B.D., and N.M. are respectively supported by the Uehara Memorial Foundation Postdoctoral Fellowship, NIH (F31 MH116613) and the ARCS Foundation, and the San Diego Fellowship associated with the UCSD Q-Bio TG (NIH 1T32GM127235-01).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no competing interests.
References
- Alexander AS, and Nitz DA (2015). Retrosplenial cortex maps the conjunction of internal and external spaces. Nat Neurosci 18, 1143–1151. [DOI] [PubMed] [Google Scholar]
- Barraclough DJ, Conroy ML, and Lee D (2004). Prefrontal cortex and decision making in a mixed-strategy game. Nat Neurosci 7, 404–410. [DOI] [PubMed] [Google Scholar]
- Baum WM (1974). On two types of deviation from the matching law: bias and undermatching. J Exp Anal Behav 22, 231–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cembrowski MS, Phillips MG, DiLisio SF, Shields BC, Winnubst J, Chandrashekar J, Bas E, and Spruston N (2018). Dissociable Structural and Functional Hippocampal Outputs via Distinct Subiculum Cell Classes. Cell 173, 1280–1292.e1218. [DOI] [PubMed] [Google Scholar]
- Corrado GS, Sugrue LP, Seung HS, and Newsome WT (2005). Linear-Nonlinear-Poisson models of primate choice dynamics. J Exp Anal Behav 84, 581–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czajkowski R, Jayaprakash B, Wiltgen B, Rogerson T, Guzman-Karlsson MC, Barth AL, Trachtenberg JT, and Silva AJ (2014). Encoding and storage of spatial information in the retrosplenial cortex. Proc Natl Acad Sci U S A 111, 8661–8666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhawale AK, Hagiwara A, Bhalla US, Murthy VN, and Albeanu DF (2010). Non-redundant odor coding by sister mitral cells revealed by light addressable glomeruli in the mouse. Nat Neurosci 13, 1404–1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elber-Dorozko L, and Loewenstein Y (2018). Striatal action-value neurons reconsidered. Elife 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evangelidis GD, and Psarakis EZ (2008). Parametric image alignment using enhanced correlation coefficient maximization. IEEE Trans Pattern Anal Mach Intell 30, 1858–1865. [DOI] [PubMed] [Google Scholar]
- Guo ZV, Li N, Huber D, Ophir E, Gutnisky D, Ting JT, Feng G, and Svoboda K (2014). Flow of cortical activity underlying a tactile decision in mice. Neuron 81, 179–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haddad R, Lanjuin A, Madisen L, Zeng H, Murthy VN, and Uchida N (2013). Olfactory cortical neurons read out a relative time code in the olfactory bulb. Nat Neurosci 16, 949–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamid AA, Pettibone JR, Mabrouk OS, Hetrick VL, Schmidt R, Vander Weele CM, Kennedy RT, Aragona BJ, and Berke JD (2016). Mesolimbic dopamine signals the value of work. Nat Neurosci 19, 117–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Coen P, and Tank DW (2012). Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein RJ (1970). On the law of effect. J Exp Anal Behav 13, 243–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Dahlen JE, Mukundan M, and Komiyama T (2017). History-based action selection bias in posterior parietal cortex. Nat Commun 8, 1242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito M, and Doya K (2009). Validation of decision-making models and analysis of decision variables in the rat basal ganglia. J Neurosci 29, 9861–9874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson CM, Peckler H, Tai LH, and Wilbrecht L (2016). Rule learning enhances structural plasticity of long-range axons in frontal cortex. Nat Commun 7, 10785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai T, Yamada H, Sato N, Takada M, and Matsumoto M (2015). Roles of the Lateral Habenula and Anterior Cingulate Cortex in Negative Outcome Monitoring and Behavioral Adjustment in Nonhuman Primates. Neuron 88, 792–804. [DOI] [PubMed] [Google Scholar]
- Kepecs A, Uchida N, Zariwala HA, and Mainen ZF (2008). Neural correlates, computation and behavioural impact of decision confidence. Nature 455, 227–231. [DOI] [PubMed] [Google Scholar]
- Kim TH, Zhang Y, Lecoq J, Jung JC, Li J, Zeng H, Niell CM, and Schnitzer MJ (2016). Long-Term Optical Access to an Estimated One Million Neurons in the Live Mouse Cortex. Cell Rep 17, 3385–3394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komiyama T, Sato TR, O’Connor DH, Zhang YX, Huber D, Hooks BM, Gabitto M, and Svoboda K (2010). Learning-related fine-scale specificity imaged in motor cortex circuits of behaving mice. Nature 464, 1182–1186. [DOI] [PubMed] [Google Scholar]
- Lau B, and Glimcher PW (2005). Dynamic response-by-response models of matching behavior in rhesus monkeys. J Exp Anal Behav 84, 555–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makino H, and Komiyama T (2015). Learning enhances the relative impact of top-down processing in the visual cortex. Nat Neurosci 18, 1116–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makino H, Ren C, Liu H, Kim AN, Kondapaneni N, Liu X, Kuzum D, and Komiyama T (2017). Transformation of Cortex-wide Emergent Properties during Motor Learning. Neuron 94, 880–890.e888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mao D, Kandler S, McNaughton BL, and Bonin V (2017). Sparse orthogonal population representation of spatial context in the retrosplenial cortex. Nat Commun 8, 243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitani A, and Komiyama T (2018). Real-Time Processing of Two-Photon Calcium Imaging Data Including Lateral Motion Artifact Correction. Front Neuroinform 12, 98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morcos AS, and Harvey CD (2016). History-dependent variability in population dynamics during evidence accumulation in cortex. Nat Neurosci 19, 1672–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakayama H, Ibañez-Tallon I, and Heintz N (2018). Cell-Type-Specific Contributions of Medial Prefrontal Neurons to Flexible Behaviors. J Neurosci 38, 4490–4504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiyama N, Colonna J, Shen E, Carrillo J, and Nishiyama H (2014). Long-term in vivo time-lapse imaging of synapse development and plasticity in the cerebellum. J Neurophysiol 111, 208–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pachitariu M, Stringer C, and Harris KD (2018). Robustness of Spike Deconvolution for Neuronal Calcium Imaging. J Neurosci 38, 7976–7985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pachitariu M, Stringer C, Schröder S, Dipoppa M, Rossi LF, Carandini M, and Harris KD (2016). Suite2p: beyond 10,000 neurons with standard two-photon microscopy 061507.
- Padoa-Schioppa C, and Assad JA (2006). Neurons in the orbitofrontal cortex encode economic value. Nature 441, 223–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, and Franklin KBJ (2001). The mouse brain in stereotaxic coordinates, 2nd edn (San Diego, Calif.; London: Academic; ). [Google Scholar]
- Platt ML, and Glimcher PW (1999). Neural correlates of decision variables in parietal cortex. Nature 400, 233–238. [DOI] [PubMed] [Google Scholar]
- Ranganath C, and Ritchey M (2012). Two cortical systems for memory-guided behaviour. Nat Rev Neurosci 13, 713–726. [DOI] [PubMed] [Google Scholar]
- Raposo D, Kaufman MT, and Churchland AK (2014). A category-free neural population supports evolving demands during decision-making. Nat Neurosci 17, 1784–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samejima K, Ueda Y, Doya K, and Kimura M (2005). Representation of action-specific reward values in the striatum. Science 310, 1337–1340. [DOI] [PubMed] [Google Scholar]
- Scott BB, Constantinople CM, Akrami A, Hanks TD, Brody CD, and Tank DW (2017). Fronto-parietal Cortical Circuits Encode Accumulated Evidence with a Diversity of Timescales. Neuron 95, 385–398.e385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song YH, Kim JH, Jeong HW, Choi I, Jeong D, Kim K, and Lee SH (2017). A Neural Circuit for Auditory Dominance over Visual Perception. Neuron 93, 940–954.e946. [DOI] [PubMed] [Google Scholar]
- Stalnaker TA, Cooch NK, McDannald MA, Liu TL, Wied H, and Schoenbaum G (2014). Orbitofrontal neurons infer the value and identity of predicted outcomes. Nat Commun 5, 3926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugrue LP, Corrado GS, and Newsome WT (2004). Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787. [DOI] [PubMed] [Google Scholar]
- Sul JH, Jo S, Lee D, and Jung MW (2011). Role of rodent secondary motor cortex in value-based action selection. Nat Neurosci 14, 1202–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sul JH, Kim H, Huh N, Lee D, and Jung MW (2010). Distinct roles of rodent orbitofrontal and medial prefrontal cortex in decision making. Neuron 66, 449–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, and Barto AG (1998). Reinforcement learning : an introduction (Cambridge, Mass: MIT Press; ). [Google Scholar]
- Tsutsui K, Grabenhorst F, Kobayashi S, and Schultz W (2016). A dynamic code for economic object valuation in prefrontal cortex neurons. Nat Commun 7, 12554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vann SD, Aggleton JP, and Maguire EA (2009). What does the retrosplenial cortex do? Nat Rev Neurosci 10, 792–802. [DOI] [PubMed] [Google Scholar]
- Wekselblatt JB, Flister ED, Piscopo DM, and Niell CM (2016). Large-scale imaging of cortical dynamics during sensory perception and behavior. J Neurophysiol 115, 2852–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wold S, Sjöström M, and Eriksson L (2001). PLS-regression: a basic tool of chemometrics. Chemometrics and Intelligent Laboratory Systems 58, 109–130. [Google Scholar]
- Wright SJ, Nowak RD, and Figueiredo MA (2009). Sparse Reconstruction by Separable Approximation. IEEE Transactions on Signal Processing 57, 2479–2493. [Google Scholar]
- Yamawaki N, Radulovic J, and Shepherd GM (2016). A Corticocortical Circuit Directly Links Retrosplenial Cortex to M2 in the Mouse. J Neurosci 36, 9365–9374. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(A-D) Distributions of run-lengths (the number of consecutive choices to the same side before exploring the other side) of an example mouse for the option with higher probability in [0.6:0.1] block (A), the option with higher probability in [0.525:0.175] block (B), the option with lower probability in [0.525:0.175] block (C), the option with lower probability in [0.6:0.1] block (D). All run-lengths from ≥ day 14 sessions are pooled. The run-length distributions follow a gamma distribution which is expected for stochastic Poisson processes. This argues against the possibility that mice employed fixed strategies such as exploring the low probability option after a set number of consecutive choices to the high probability option.
(E) Schematic of the local matching law (LML). The LML estimates the action value on each trial by integrating reward history with exponential functions. The local matching law assumes that the choice probability ratio exactly matches the ratio of integrated reward history ratio (STAR Methods [eq. 10]). We also considered a model with the assumption that the matching between choice probability ratio and the reward history ratio is not exact, which we termed the generalized local matching law (GLML, STAR Methods [eq. 11]).
(F) Akaike Information Criteria (AIC) difference between the LML and the GLML. The GLML shows lower AIC throughout training days, indicating a better behavioral fit.
(G) AIC difference between our best RL model and the GLML. The RL model shows lower AIC throughout training days.
All error bars are s.e.m.
(A) The accuracy of the RL model in correctly predicting the behavioral choices.
(B) The accuracy of the history regression model with rewarded choice, unrewarded choice, and outcome-independent history predictors from past 10 trials and a constant bias term in correctly predicting the behavioral choices.
(C) Reinforcement learning index (STAR Methods [eq. 8]).
(D) The fraction of rewarded trials.
One-way ANOVA with Tukey’s post-hoc test (*P < 0.05, n.s. P > 0.05). All error bars are s.e.m.
(A) Schematic of the linear decoders. The linear decoders decode value-related information by a weighted linear sum of neural activity.
(B) Schematic of the feedforward neural network for nonlinear decoding. The network has a hidden layer with 10 sigmoid neurons, which confers on the network the ability to learn complex nonlinear relationships between population activity and the value-related information.
(C) Decoding accuracy of Qch and ∆Q from population activity of variable numbers of neurons during ready period with the nonlinear model. (Two-way ANOVA with Tukey’s post-hoc test. Only the comparisons between RSC and the other areas are shown).
(D-E) Comparisons of the decoding accuracy between the linear model and the nonlinear model for Qch (D) and ∆Q (E) (Two-way ANOVA with Tukey’s post-hoc test).
(F-G) The distributions of the chance decoding accuracy for linear models (F) and nonlinear models (G). Each decoder was trained with ready period activity (yellow shading) of a subset of trials, and the decoding accuracy was calculated by shuffling the trial labels of the test set trials 1,000 times for different trial periods. 99th percentile, 95th percentile, 5th percentile and 1st percentile of each session were averaged across sessions. All error bars are s.e.m.
*P < 0.05, **P < 0.01, ****P < 0.0001. All error bars are s.e.m.
(A-B) (Left) Performance of nonlinear decoders trained on ready period activity of 200 neurons at various time points (1.9-sec bins) in a trial. (Right) Slopes of the decoding accuracy curves before (−7 to −1 s, ‘pre-ready’) or after (−1 to 1 s, ‘post-ready’) the ready period (One-way ANOVA with Tukey’s post-hoc test for linear regression coefficients. Only the comparisons between RSC and the other areas are shown. The pre-ready slope for V1 was obtained using only −3 and −1 s).
(C-D) Temporal activity variance normalized by across-trial activity variance along nonlinear Qch axis (C) or ∆Q axis (D) for 200-cell population from 6 cortical areas (One-way ANOVA with Tukey’s post-hoc test. Only the comparisons between RSC and the other areas are shown). RSC shows the most persistent value coding.
*P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001. All error bars are s.e.m.
(A) Population averages of the activity of all neurons that significantly encoded Qch during ready period (yellow shading) in each area. Top, high Qch-preferring neurons (2.97 ± 0.41 % of imaged neurons in ALM, 3.88 ± 0.64 % in pM2, 3.76 ± 0.57 % in PPC, 4.95 ± 0.62 % in RSC, 3.24 ± 0.82 % in S1, 3.75 ± 2.30 % in V1, mean ± s.e.m.); bottom, low Qch-preferring neurons (5.17 ± 0.60 % in ALM, 5.82 ± 0.58 % in pM2, 7.09 ± 1.28 % in PPC, 7.10 ± 0.66 % in RSC, 4.27 ± 0.50 % in S1, 7.61 ± 2.76 % in V1, mean ± s.e.m.). Trials were averaged with 0.2 bin of normalized Qch.
(B) Population averages of the activity of all neurons that significantly encoded ∆Q during ready period in each area. Top, Qcontra-preferring neurons (8.53 ± 0.99 % in ALM, 8.77 ± 1.02 % in pM2, 13.00 ± 1.63 % in PPC, 14.50 ± 1.58 % in RSC, 9.24 ± 1.80 % in S1, 8.45 ± 1.92 % in V1, mean ± s.e.m.); bottom, Qipsi-preferring neurons (9.66 ± 1.09 % % in ALM, 9.87 ± 0.85 % in pM2, 15.30 ± 2.46 % in PPC, 13.60 ± 0.88 % in RSC, 8.52 ± 0.98 % in S1, 7.94 ± 1.58 % in V1, mean ± s.e.m.). Trials were averaged with 0.2 bin of normalized ∆Q. All error bars are s.e.m.
(A-C) Consistency of the history-independent behavioral measurements between early and expert sessions of imaging data used in Figure 6. Fractions of miss trials (A), fractions of alarm trials (B), number of trials per session (C). n = 35 sessions for both early and expert sessions. Paired t-test (n.s. P > 0.05).
(D-G) Equivalent behavioral performance in the early sessions used for imaging of each cortical area. The accuracy of the RL model in correctly predicting the behavioral choices (D). The accuracy of the history regression model with rewarded choice, unrewarded choice, and outcome-independent history predictors from past 10 trials and a constant bias term in correctly predicting the behavioral choices (E). Reinforcement learning index (F). The fraction of rewarded trials (G). One-way ANOVA with Tukey’s post-hoc test (n.s. P > 0.05).
All error bars are s.e.m.
(A) Relationship between RSC lesion size and the effect on win-stay and lose-switch probabilities. Difference between the mean of 7 sessions before lesion and the mean of 7 sessions after lesion is shown. Pearson’s correlation coefficients and their p-values are shown.
(B) Behavioral dependency on rewarded choice (RewC(t-i)), unrewarded choice (UnrC(t-i)), and outcome-independent choice (C(t-i)) history before and after sham/lesion surgery. The mean of 7 sessions before sham/lesion and the mean of 7 sessions after sham/lesion are shown. The means were averaged across mice (n = 5 sham mice; n = 6 lesion mice). Error bars are s.e.m.
(C) Relationship between RSC lesion size and the effects on behavioral dependency on the 3 types of history from −1 trial. Difference between the mean of 7 sessions before lesion and the mean of 7 sessions after lesion is shown. Pearson’s correlation coefficients and their p-values are shown.
(D) Effects of RSC lesion on win-stay and lose-switch probabilities on day 1 after lesion. (Top) Difference between the mean of 7 sessions before sham/lesion and day 1 after sham/lesion is shown (Two-sided t-test). Red lines indicate the means. (Bottom) Relationship between RSC lesion size and the effects on win-stay and lose-switch probabilities. Difference between the mean of 7 sessions before lesion and day 1 after lesion is shown. Pearson’s correlation coefficients and their p-values are shown.
(E) Effects of RSC lesion on behavioral dependency on the 3 types of history from −1 trial. (Top) Difference between the mean of 7 sessions before sham/lesion and day 1 after sham/lesion is shown (Two-sided t-test). Red lines indicate the means. (Bottom) Relationship between RSC lesion size and the effects on behavioral dependency on the 3 types of history from −1 trial. Pearson’s correlation coefficients and their p-values are shown.
n.s. P > 0.05.
Data Availability Statement
All data and analysis code are available upon reasonable request to the Lead Contact, Takaki Komiyama (tkomiyama@ucsd.edu).