A Statistical Model-based Technique for Accounting for Prostate Gland Deformation in Endorectal Coil-based MR Imaging

Abstract

In prostate brachytherapy procedures, combining high-resolution endorectal coil (ERC)-MRI with Computed Tomography (CT) images has shown to improve the diagnostic specificity for malignant tumors. Despite such advantage, there exists a major complication in fusion of the two imaging modalities due to the deformation of the prostate shape in ERC-MRI. Conventionally, nonlinear deformable registration techniques have been utilized to account for such deformation. In this work, we present a model-based technique for accounting for the deformation of the prostate gland in ERC-MR imaging, in which a unique deformation vector is estimated for every point within the prostate gland. Modes of deformation for every point in the prostate are statistically identified using a set of MR-based training set (with and without ERC-MRI). Deformation of the prostate from a deformed (ERC-MRI) to a non-deformed state in a different modality (CT) is then realized by first calculating partial deformation information for a limited number of points (such as surface points or anatomical landmarks) and then utilizing the calculated deformation from a subset of the points to determine the coefficient values for the modes of deformations provided by the statistical deformation model. Using a leave-one-out cross-validation, our results demonstrated a mean estimation error of 1mm for a MR-to-MR registration.

I. INTRODUCTION

Prostate cancer is the most common non-skin cancer and is recognized as the second deadliest cancer in men in the Western world. Current radiation-based treatment planning of the prostate cancer is conducted using Computed Tomography (CT) images of the prostate. CT images provide high geometric accuracy and electron density information that is required for accurate dose calculation. In spite of the aforementioned advantages, the delineation of the prostate gland in CT images is quite poor due to small differences in tissue density within and surrounding the prostate gland. On the other hand, magnetic resonance imaging (MRI) provides a high-resolution anatomical detailing of the prostate. Furthermore, the introduction of endorectal coil (ERC) in MR imaging of the prostate has significantly improved the spatial resolution and signal-to-noise ratio in prostate MR images [1]. The enhanced detailing of the prostate gland provided by ERC-based MRI has proven to provide valuable information for cancer staging and image-based guidance during the diagnosis and treatment procedures of the prostate cancer [2]. Fusion of ERC-MRI with CT images provides a better delineation of the prostate during radiation treatment planning. However, the use of ERC in MR imaging poses a major challenge in the fusion of the two imaging modalities by deforming the prostate shape (Figure 1).

Fig. 1.

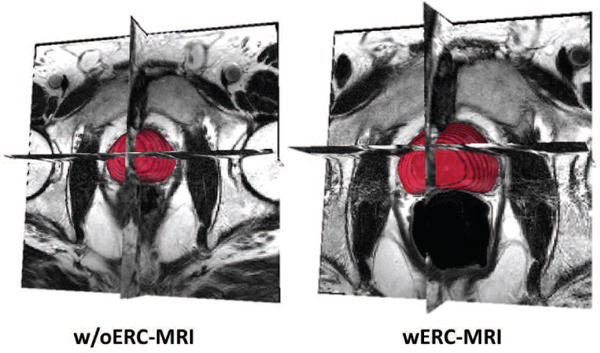
MRI with and without ERC.

It is shown that the deformation of the prostate in ERC-MRI cannot be accounted for by just simple linear rotation and translation transformations [3], [4]. A number of researchers have proposed several nonlinear registration techniques for fusing ERC-MRI with CT images. The use of intensity-based metrics is not feasible for MR-to-CT image registration as the contrast variation is limited in CT images of the prostate. Fei et al. [5], Lian et al. [6], and Venugopal et al. [7], separately, proposed thin plate spline (TPS) point-based transformations. The transformation is calculated for a set of control points that were selected along the contour of the prostate in corresponding MR and CT images. Others have proposed the use of finite element method (FEM) for determining the motion and deformation of the prostate gland [8], [9]. A major shortcoming of all these frameworks is that the biomechanical properties of the prostate tissue are assumed to be the same within the entire prostate gland and accordingly, the tissue deformation is considered as uniform across the whole prostate. A quantitative shape and volume analysis of the prostate using MR images by Hirose et al. [10] showed that this assumption is incorrect. In a study using 10 patients, they demonstrated that the peripheral zone undergos significantly greater deformation than the central gland during ERC-based MR imaging.

In this work, a novel solution for fusing MR-to-CT images of the prostate is proposed that accommodates for nonlinear deformation differences between the two modalities for every point of the prostate. The proposed technique consists of a training phase and an estimation phase. In the training phase, a set of deformed (ERC-MRI) and non-deformed (MRI without ERC) prostate image data are used to generate the deformation model of the prostate. Deformation field maps are calculated from intensity-based nonlinear registration of without ERC (w/oERC) to with ERC (wERC) MRI datasets. Principal component analysis (PCA) is then utilized on the resulting deformation fields to extract the statistical mean deformation as well as the most significant modes of deformation for every point of the prostate. Given a new registration problem, such as mapping a deformed prostate image in ERC-MRI to a non-deformed prostate image in CT for a new subject, first a nonlinear registration is calculated for a limited number of corresponding landmarks in both modalities (such as surface contours or anatomical landmarks). The deformation field values at the known points are then used to calculate the eigen coefficients corresponding to the deformation modes. Finally, an estimate of the deformation field for every point constituting the prostate gland is computed as the summation of the mean deformation plus a linear combination of the deformation modes with the calculated eigen coefficients as the weights.

II. MATERIALS AND METHOD

The imaging study was approved by the institutional review board of the National Cancer Institute of the National Institutes of Health. Informed written consent was obtained from volunteer patients. Multi-parametric MR images were acquired from each patient using a 3.0 T whole body clinical MR scanner (Achieva, Philips Healthcare, Best, The Netherlands). T2-weighted MR images covering whole prostate were collected twice. First, with 6-channel cardiac coil (SENSE, Philips Healthcare, Best, the Netherlands), then, with a 16-channel anterior cardiac coil (SENSE, Philips Healthcare, Best, the Netherlands) and an endorectal coil (BPX-30, Medrad, Pittsburgh, PA, USA). A brief summary of the proposed method is depicted in Figure 2.

Fig. 2.

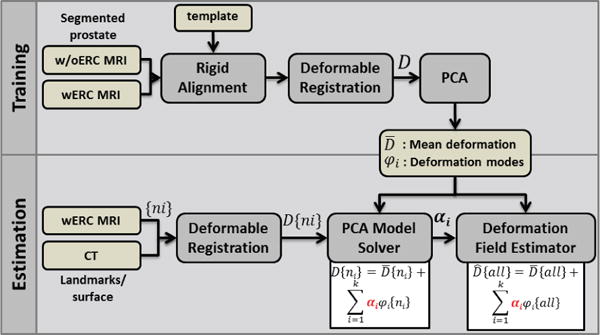
Flowchart of the proposed method. See Section II for details.

A. Deformable Registration

Prostate gland was segmented in both wERC and w/oERC MR images. All w/oERC segmented prostate images were rigidly aligned to the average of all w/oERC segmented images. Each individual’s wERC prostate image was then rigidly aligned with the corresponding w/oERC image. Next, the w/oERC prostate image was nonlinearly registered to the corresponding wERC segmented image using a BSpline-based deformable registration. The registration runs in a multi-resolution framework, starting with a coarse grid size followed by a finer grid.

B. Phase I: Statistical Deformation Modeling

The principal component analysis was used to derive the linear deformation modes from the displacement fields of the available samples in the following fashion.

Given a subset F in R³, the calculated displacement fields (with three x, y, and z components) is shown as:

$${\mathcal{D}}_i^{<j>}:F\to {\mathbf{R}}^3$$ (1)

where i = 1, …, m refers to the indices of the data points, P, lying within the M_w/oERC mask, and j = 1, …, n refers to the dataset index. m, and n refer to the total number of data points (within M_w/oERC), and datasets, respectively.

Each deformation field is reformatted to a 1-D vector by concatenating x, y, and z components from all data points $({\mathcal{D}}_{m\times 3}^{<j>}\Rightarrow {\mathbf{d}}_{3m\times 1}^{<j>})$. The covariance matrix, Σ, is calculated as following:

$${\stackrel{\sim }{\mathbf{d}}}^{<i>}={\mathbf{d}}^{<i>}-\overline{\mathbf{d}}$$ (2)

where $\overline{\mathbf{d}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\mathbf{d}}^{<i>}}$.

$${\mathbf{D}}_{3m\times n}=[{\stackrel{\sim }{\mathbf{d}}}^{<1>}{\stackrel{\sim }{\mathbf{d}}}^{<2>}\mathrm{..}{\stackrel{\sim }{\mathbf{d}}}^{<n>}]$$ (3)

$$\sum ={\mathbf{D}}^T\mathbf{D}$$ (4)

The matrix of deformation eigenvectors, Ψ, which diagonalizes the covariance matrix Σ is found as:

$${\mathbf{\Psi }}^{-1}\sum \mathbf{\Psi }=\mathrm{\Lambda }$$ (5)

where Λ = [λ_i]_n×n is a diagonal matrix with eigenvalues of Σ, as its diagonal elements. Finally, the eigenvectors of the displacement field matrix (D_3m×n) is found by:

$$\mathbf{\Phi }=\mathbf{D}\mathbf{\Psi }{\mathrm{\Lambda }}^{-\frac{1}{2}}$$ (6)

Any displacement field can be estimated from the linear combination of the deformation modes (ϕ_i) as following:

$${\widehat{\mathbf{d}}}^{<j>}=\overline{\mathbf{d}}+{\displaystyle \sum _{i=1}^k{{\alpha }_i}^{<j>}}{\varphi }_i,k<n$$ (7)

C. Phase II: Estimation

Let P, and S denote all the data points constituting the prostate gland and the surface points of the prostate, respectively. Given the displacement field values at the surface points, S, the eigen coefficients, α_i, i = 1, …, k, corresponding to k deformation modes are found by solving the following matrix of equations:

$${\mathbf{d}}^{<j>}\{S\}=\overline{\mathbf{d}}\{S\}+{\displaystyle \sum _{i=1}^k{{\alpha }_i}^{<j>}}{\varphi }_i\{S\}$$ (8)

Having found the {α_i}, the deformation field value for the rest of the points within the prostate, P − S, is calculated from:

$${\widehat{\mathbf{d}}}^{<j>}\{P-S\}=\overline{\mathbf{d}}\{P-S\}+{\displaystyle \sum _{i=1}^k{{\alpha }_i}^{<j>}}{\varphi }_i\{P-S\}$$ (9)

III. RESULTS

wERC and w/oERC T2-weighted MRI available from 77 patients were used in this study. Prostate gland was segmented in MR images using iCAD segmentation tool (iCAD Inc., Nashua, NH, USA) with manual corrections. The segmented prostate from w/oERC images were rigidly aligned to an average template. Segmented prostate images from wERC data were also rigidly aligned to the w/oERC prostate image from the same individual. A multi-resolution BSpline-based deformable registration, implemented in ITK (Insight Toolkit version 4.0, Kitware Inc.), was used to register w/oERC to wERC prostate images resulting in a three-component displacement vector for every voxel. The registration consists of two resolutions: a coarse grid of 5 × 5 × 5 voxels followed by a finer grid of 20 × 20 × 20 voxels. Mutual information was used as the image similarity metric. The calculated displacement field was used to warp the w/oERC image data. The registration resulted in poor matching for five datasets. These five datasets were excluded from the rest of the experiment. In order to assess the performance of the registration, the similarity between warped w/oERC and wERC images within the prostate mask was measured using normalized cross-correlation (NCC) metric (mean ± std for 72 cases: 96.0 ± 1.0%):

$$\mathit{NCC}=\frac{E\left[\left(S_{w/\mathit{oERC}}-{\overline{S}}_{w/\mathit{oERC}}\right)\left(S_{\mathit{wERC}}-{\overline{S}}_{\mathit{wERC}}\right)\right]}{\sigma \left(S_{w/\mathit{oERC}}\right)\sigma \left(S_{\mathit{wERC}}\right)}$$ (10)

Next, the calculated displacement fields were reformatted and used in a principal component analysis to compute the deformation modes as described in the previous section. Based on the calculated eigenvalues, at least 29 modes are required to capture more than 95% of the variability in the sample. Such high number of modes could be due to the following reasons: 1) error in the segmentation of the prostate; and/or 2) error in the nonlinear registration, as for every 16 voxels a single displacement vector was considered in the registration.

In order to validate the accuracy of the proposed technique in estimating the displacement field from partial available displacement field data (e.g., surface points) and eigen modes of deformation generated using PCA on displacement fields, a leave-one-out (LOO) cross-validation scheme was utilized. Out of 72 datasets, one dataset was excluded at a time and the rest were passed through PCA to generate the eigen deformation modes (overall 72 cases). The displacement field values at surface points from the excluded data together with the resulting mean displacement field and eigenvectors from the PCA were plugged in Eq. 7 to estimate the displacement field at the rest of the voxels. On average, surface points constitute 4% of the total number of voxels within the prostate mask. Figure 3 demonstrates the mean ± std of the normalized eigen coefficient calculated from the 72 leave-one-out cases.

Fig. 3.

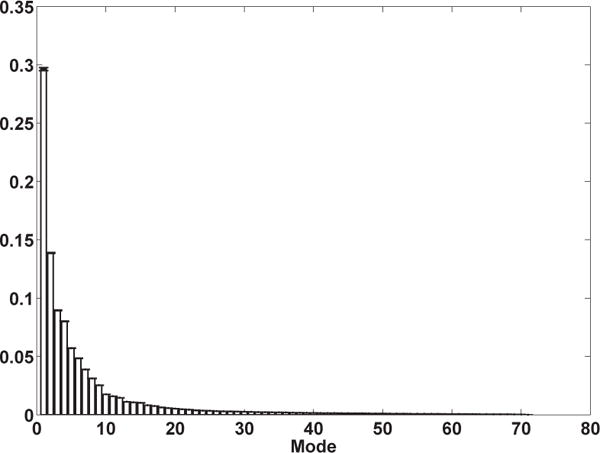
Mean±std of the normalized eigen coefficients from 72 cases calculated in a leave-one-out framework.

For each LOO case, the estimation error was calculated as the mean square difference between the estimated displacement field and the displacement field resulting from the nonlinear registration between w/oERC and wERC image data. Figure 4(a) shows the distribution of the error from all voxels within the prostate mask, collapsed across all 72 cases. Figure 4(b) demonstrates the localization of the error across the prostate gland.

Fig. 4.

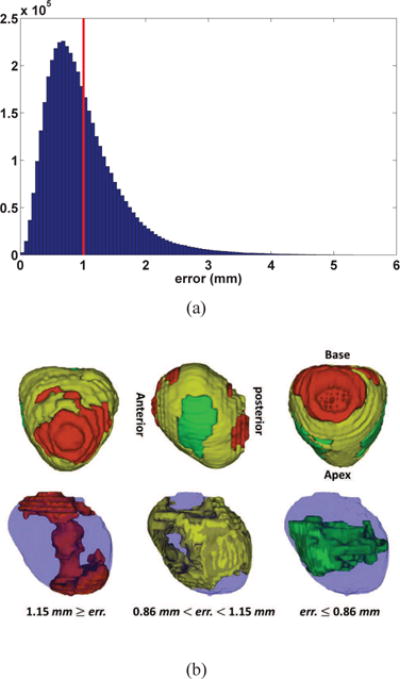
(a) Distribution of error between the estimated and the actual deformation field combining all 72 cases from the leave-one-out cross-validation. Mean error is depicted by a red vertical line; (b) Localization of the distribution of error between the estimated and the actual deformation field combining all 72 cases from the leave-one-out cross-validation. The distribution is thresholded at 0.25th and 0.75th quantiles.

In order to evaluate the sensitivity of the proposed technique to the number of deformation modes considered in estimation (k in Eq. 7) the LOO was repeated using a range of values for the number of modes, 10 up to 70 modes with step size of 10. Figure 5 shows the estimation error collapsed across all LOO cases for different number of deformation modes. As can be seen in the figure, the minimum error occurs when using 40 modes. This may imply that using higher number of modes may result in overfitting. One-way ANOVA analysis demonstrated a significant difference between the distribution of error among different number of modes. Further post-hoc multiple comparisons revealed that the error distribution from all 7 modes are significantly different from one another (F (6, 3 × 10⁷) = 134261, p < 0.0001).

Fig. 5.

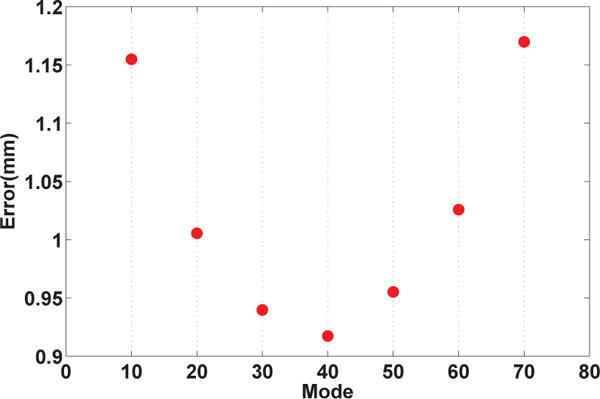
Error of estimation from the leave-one-out cross-validation for different number of deformation modes.

IV. DISCUSSION

A model-based approach for accounting for the deformation of the prostate caused by using an ERC in MR imaging is proposed. The proposed model-based approach overcomes the current limitations in fusing ERC-MRI with other modalities such as CT in brachytherapy procedures by providing a nonlinear mapping for every point of the prostate rather than a limited number of landmarks such as conventional surface-to-surface registration techniques.

A statistical model of the prostate gland deformation is generated using PCA on displacement fields provided by nonlinear registration of w/oERC to wERC MR images for a large sample. Performing a nonlinear intra-modality registration using an intensity-based metric guarantees an accurate match between non-deformed (w/oERC) and deformed (wERC) state of the prostate. To be able to utilize PCA in this framework, a point-to-point correspondence is required between all datasets within the training sample. In this study, a rough correspondence between training data (w/oERC MRI) required for the principal component analysis is achieved by a rigid alignment. The PCA performance in this study is affected by: 1) way of realizing correspondence among sample points (rigid registration); 2) the prostate segmentation accuracy; and 3) nonlinear registration between w/oERC and wERC image data. A few alternative techniques are currently being investigated to improve the data correspondence, the segmentation and registration accuracies.

As demonstrated in Figure 5, the estimation error significantly changes with the number of deformation modes. The increase in the estimation error seen by using more than 40 modes could also be explained by the prostate segmentation and registration error, which causes overfitting of the model.

In order to use the proposed framework for a nonlinear registration between ERC-MRI and any other modality such as CT images, a set of landmarks that are identifiable in both modalities are extracted and nonlinearly registered (using a point-based registration technique). Such set of landmarks could be a few control points on the contour of the prostate, anatomical landmarks that are visible in both modalities or artificial fiducials such as radioactive seeds. A deformation field that matches the prostate at every point in both modalities is then realized by inserting the calculated deformation values at the selected landmarks into the PCA deformation model of the prostate and solving for the eigen coefficients of the deformation modes.