Invited Commentary: Selection Bias Without Colliders

Abstract

In causal analyses, conditioning on a collider generally results in selection bias. Conditioning on a prognostic factor that is independent of the exposure—and therefore is not a collider—can also result in selection bias when 1) the exposure has a non-null effect on the outcome and 2) the association between the noncollider and the outcome is heterogenous across levels of the exposure. This result was empirically demonstrated by Greenland in 1977 (Am J Epidemiol. 1977;106(3):184–187).

Forty years ago, Sander Greenland was busy describing the conditions under which selection bias may arise in follow-up studies (1). As someone who has more recently engaged in similar undertakings, I am honored by the invitation to comment on the article published by Greenland in 1977. I am also humbled: I could not read the article at the time of its publication because I was 6 years old and had yet to take my first English lesson. When I first met Sander at a meeting of the Society for Epidemiologic Research, he had already been thinking about selection bias for more than 2 decades. Also, he was about to publish, together with Judea Pearl and Jamie Robins, the first description of causal diagrams for epidemiologic research (2). Below I map the ideas described by Greenland in 1977 to structural representations of selection bias using causal diagrams.

An initial clarification: I use the term selection bias to refer to the bias that arises when the parameter of interest in a population differs from the parameter in the subset of individuals from the population that is available for analysis (3). For example, we can have selection bias for descriptive measures (e.g., prevalence) because of nonrandom sampling or for effect measures (e.g., causal risk ratio) because of differential loss to follow-up. In this commentary, I discuss selection bias for causal effect measures. Note that some scientific disciplines (e.g., econometrics, statistics) have historically used a different definition of selection bias that is essentially equivalent to the epidemiologic term confounding: bias due to the way in which individuals in the population are selected or select themselves into each treatment or exposure level. Here I will assume, like Greenland did in 1977, that no confounding for the effect of treatment or exposure exists.

Greenland presented a hypothetical example in which the causal risk ratio of disease for the exposed versus the unexposed was 1.69 in the entire population of interest. This risk ratio, however, was unknown to the investigators because approximately 28% of the individuals in the population refused to participate in the study or were lost to follow-up and therefore had an unknown (censored) outcome. The risk ratio in the uncensored individuals was 2.05; that is, selection resulted in selection bias, which in this case manifested itself as an overestimation of the population risk ratio. (Incidentally, there is a typo in Table 3 of the article: The risk ratio in the censored individuals was 0.70, not 70.)

What makes this example interesting is that the proportions of exposed and unexposed who were censored were approximately the same (≈28%). That is, selection was independent of the exposure and yet the effect measure was biased. Greenland was arguing that the old adage that there is only bias when censoring is associated with both exposure and outcome was false. In his example, censoring was nondifferential because it was associated with the outcome (the risk ratio was 1.36) but not with the exposure (the risk ratio was 1.02).

Let us draw a causal diagram that represents Greenland's example. We have 3 variables: a randomly assigned exposure E, censoring (or, more generally, selection) C, and the disease D that would have been observed in the absence of censoring. There is an arrow from E to D because the causal risk ratio is 1.69. There is no arrow from E to C because the causal risk ratio is effectively 1. Also, unknown to the investigators, there is an association between C and D within at least 1 level of E (risk ratio = 2.93 in the exposed and 0.99 in the unexposed). This association can be represented by an unmeasured common cause U of both C and D, because we usually expect that censoring will be a marker of prognostic factors U rather than having a direct causal effect on the value of the outcome that would have been observed under no censoring. Figure 1 depicts the causal diagram. The box around C indicates that the analysis is conditional on being uncensored.

Figure 1.

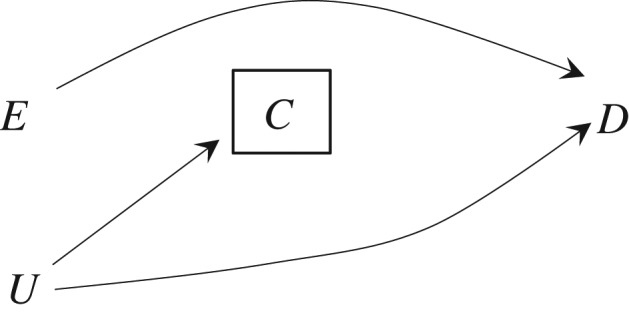
Causal directed acyclic graph off the null where E is exposure, D is disease, C is censoring, and U is the unmeasured common causes of C and D. The box around C indicates that the analysis is conditional on being uncensored.

Greenland's example demonstrates that selection bias may arise when conditioning on a variable C that is not a collider. The inescapable conclusion is that collider stratification is not a necessary condition for selection bias. Yet, in the absence of collider stratification, selection bias is not guaranteed to arise. To see why, let us consider 2 settings: Figure 1, in which the exposure E has a non-null causal effect on disease D for some individuals in the population (and therefore the causal risk ratio is different from 1), and Figure 2, in which the exposure E has a null causal effect on the disease D of all individuals in the population (and therefore the causal risk ratio equals 1). In both figures, censoring is independent of the exposure.

Figure 2.

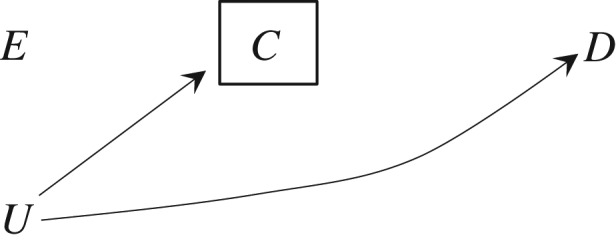
Causal directed acyclic graph under the null where E is exposure, D is disease, C is censoring, and U is the unmeasured common causes of C and D. The box around C indicates that the analysis is conditional on being uncensored.

The application of the rules of d-separation (4) to Figure 2 shows that E and D are independent whether the analysis includes all individuals in the population (no box around C) or is restricted to the uncensored individuals (box around C); that is, no selection bias arises when the sharp null hypothesis holds—the exposure has no effect on the outcome of any individuals—and censoring is independent of the exposure. We say that conditioning on the non-collider C does not induce selection bias under the null. Table 1 provides a numerical example so that interested readers can check that indeed no selection bias is introduced by censoring in this setting. Unlike in Greenland's 1977 example, the causal risk ratio of disease for exposure versus no exposure is 1 in the population of Table 1.

Table 1.

Data From a Hypothetical Cohort Study With No Confounders of the Effect of E on D

C	D
	1	0
0
E = 1	40	160
E = 0	120	480
1
E = 1	5	45
E = 0	15	135

Abbreviations: E, exposure; D, disease; C, censoring status.

In contrast, applying d-separation to Figure 1 shows that E and D are associated whether the analysis includes all individuals in the population (no box around C) or is restricted to the uncensored individuals (box around C). We will say that there is selection bias for the population parameter whenever the association in the uncensored individuals is different from the association in the entire population. In that case, we will say that conditioning on the noncollider C induces selection bias under the alternative hypothesis of a non-null effect of the exposure on the outcome, or selection bias off the null. In fact, as Greenland explained in 1977 and again in 2011 with Judea Pearl (5), selection bias off the null further requires that the association between C and D varies across levels of E on the scale (e.g., risk ratio, risk difference) used to measure the population effect of E on D. That is precisely what happened in the 1977 example: the risk ratio of D for censoring versus no censoring varies by levels of E. This heterogeneity of the C-D association across levels of E can be attributed to an interaction between E and U on the risk ratio scale.

Importantly, were there no such heterogeneity on the risk ratio scale, there would have been no selection bias for the population risk ratio, but there would have been selection bias for the population risk difference (because, off the null, no heterogeneity for the causal risk ratio implies heterogeneity for the causal risk difference). This dependence of the bias on the parameter used to quantify the effect explains why causal diagrams fail to depict selection bias off the null: Causal directed acyclic graphs are nonparametric and thus cannot generally encode biases that depend on a particular parameterization of the effect. This is also the reason why the distinction between bias under the null and bias off the null is important for selection bias but not for confounding. The presence of common causes of exposure and outcome is expected to induce an association (confounding bias) between treatment and outcome on all scales (risk ratio, risk difference, etc.), regardless of whether the exposure does or does not have an effect on the outcome.

In 2004, my colleagues and I described the structure of selection bias and equated it to conditioning on a common effect of (a cause of) the exposure and (a cause of the) outcome, that is, to conditioning on a collider (6). Although we were only considering selection bias under the null (none of the causal diagrams in the article included an arrow from E to D), we did not explicitly say so. As a result, our equating collider stratification and selection bias (under the null) was construed by some readers as meaning that collider stratification is needed for all forms of selection bias in causal inference. Clearly, collider stratification is not needed for selection bias to arise when the treatment has a non-null effect on the outcome. Sander Greenland had already proved it with an example in 1977.

This discussion has thus far revolved around studies in which investigators aimed at estimating the causal effect of E on D in the entire study population. As we have discussed, when C is a collider, restriction to uncensored individuals yields an association measure that is biased for both the effect in the entire population and the effect in uncensored individuals (6). On the other hand, when C is not a collider, as in Figure 1, restriction to uncensored individuals yields an association measure that is biased for the effect in the entire population but unbiased for the effect in uncensored individuals. Under Figure 1, we say that there is selection bias (off the null) because our target population for causal inference was the entire study population (3), but the association measure from an analysis restricted to uncensored individuals is a valid estimate of the effect in the subset of uncensored individuals. See the Appendix of the article by Murray et al. (7) for a systematic exploration of the settings under which selection will induce bias.

In summary, conditioning on a collider will induce a noncausal association between exposure and outcome, even if no causal association existed at the start (selection bias under the null), whereas conditioning on a noncollider may at most alter an existing association between exposure and outcome (selection bias off the null). Thus, the selection bias induced by conditioning on a prognostic factor that is not an effect of exposure, as represented in Figure 1, resembles selection bias for descriptive measures such as prevalence. The question is not whether a nonrandom selection mechanism would create a noncausal association between exposure and outcome even if the exposure had no effect on the outcome, but rather whether a nonrandom selection mechanism prevents the generalizability or transportability of the effect measure in a subset of the population to the entire target population.