The Geometry of Perisaccadic Visual Perception

Abstract

Our ability to explore our surroundings requires a combination of high-resolution vision and frequent rotations of the visual axis toward objects of interest. Such gaze shifts are themselves a source of powerful retinal stimulation, and so the visual system appears to have evolved mechanisms to maintain perceptual stability during movements of the eyes in space. The mechanisms underlying this perceptual stability can be probed in the laboratory by briefly presenting a stimulus around the time of a saccadic eye movement and asking subjects to report its position. Under such conditions, there is a systematic misperception of the probes toward the saccade end point. This perisaccadic compression of visual space has been the subject of much research, but few studies have attempted to relate it to specific brain mechanisms. Here, we show that the magnitude of perceptual compression for a wide variety of probe stimuli and saccade amplitudes is quantitatively predicted by a simple heuristic model based on the geometry of retinotopic representations in the primate brain. Specifically, we propose that perisaccadic compression is determined by the distance between the probe and saccade end point on a map that has a logarithmic representation of visual space, similar to those found in numerous cortical and subcortical visual structures. Under this assumption, the psychophysical data on perisaccadic compression can be appreciated intuitively by imagining that, around the time of a saccade, the brain confounds nearby oculomotor and sensory signals while attempting to localize the position of objects in visual space.

Introduction

Reaching or navigating toward an object of interest requires accurate estimates of the spatial layout of the immediate environment. When these estimates are informed by vision, the brain must combine retinal information with extraretinal signals that encode the position of the eye, head, and body to obtain accurate representations of objects in space.

A more subtle problem for object localization arises from the structure of the retina itself. Relative to the retinal periphery, the fovea contains an extremely high density of cones (Curcio and Allen, 1990), and this asymmetry is maintained and amplified in retinotopic maps found throughout the brain (Talbot and Marshall, 1941; Daniel and Whitteridge, 1961; Hubel and Wiesel, 1974; Tootell et al., 1982; Ottes et al., 1986). In such maps, the foveal region is vastly overrepresented, leading to a distorted representation of visual space.

Under normal circumstances the brain compensates for both gaze shifts and retinotopic map structure. However, in the laboratory it becomes possible to induce highly inaccurate spatial percepts that may provide insights into the brain mechanisms that underlie the perception of visual space. Specifically, previous work has shown that visual localization for probe stimuli presented briefly near the onset of saccades are characterized by a shift of the perceived position of the probe in the direction of the saccade (Matin and Pearce, 1965; Mateeff, 1978; Honda, 1989, 1991; Schlag and Schlag-Rey, 1995; Lappe et al., 2000), and a compression of visual space, wherein subjects report that probe stimuli are closer to the saccade target than they really are (Honda, 1993; Morrone et al., 1997; Ross et al., 1997; Lappe et al., 2000; Kaiser and Lappe, 2004).

Although the perceived shift of visual objects may be attributed primarily to delays in the processing of visual information relative to eye movement signals (Schlag and Schlag-Rey, 2002; Pola, 2004) (but see Boucher et al., 2001), the mechanism underlying perceptual compression remains relatively elusive. In this work, we suggest that perisaccadic compression is linked directly to the problem of recovering accurate spatial representations from distorted retinotopic maps. This hypothesis is not entirely new—the idea that perceptual distortions are related to the structure of retinotopic visual maps has been suggested previously (Johnston and Wright, 1983; Stevenson et al., 1992; Ross et al., 1997; Westheimer, 2003; VanRullen, 2004; Hamker et al., 2008). However, we have derived a novel formulation that captures the interaction between oculomotor and visual signals on a retinotopic map and have tested this hypothesis psychophysically across a wide range of conditions. We find that the model accounts for the data remarkably well with a very small number of free parameters. Importantly, because our model can be characterized by a simple closed-form expression, it also makes specific predictions about the outcome of future psychophysical experiments and the characteristics of brain structures that might be involved in perceptual estimates of the metrics of visual space.

Materials and Methods

Subjects.

Data were collected from four male subjects (two authors and two naive; mean age, 36), each of whom had normal vision. Informed consent was obtained from the subjects before study participation, and all experimental protocols were approved by the Montreal Neurological Institute and Hospital Research Ethics Committee. Subjects participated in 16–20 experimental sessions, each lasting ∼1 h.

Stimuli and experimental setup.

Experiments were conducted in a dark room. Subjects were seated in front of a semitransparent screen subtending 90 × 40° of visual angle, and viewing was binocular at a distance of 56 cm. The head was stabilized with an adjustable head strap and bite bar. Stimuli were generated in Matlab using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) and backprojected onto the screen at 85 Hz with an Electrohome Marquee 8000 projector (projector resolution, 1024 × 768 pixels) against a homogenous black background. This type of projector assures a very black background (screen luminance, <0.01 cd/m²). In line with previous studies of the compression effect, we presented a horizontal reference ruler, with vertical ticks and numbers ordinally arranged at 10° intervals (luminance, 118.4 cd/m²) for the duration of each trial (Ross et al., 1997; Lappe et al., 2000). Eye position was monitored continuously at 120 Hz using infrared oculography (ASL Laboratories Eye Tracker). Event timing, on-line displays, and the data acquisition were controlled using REX, a QNX-based real-time data acquisition system (Hayes et al., 1982).

Experimental protocol.

The beginning of each trial was marked by the presentation of a fixation cross [fixation point (FP), 1° in diameter] at a certain distance ranging from 7 to 20° to the left of screen center. After a brief period of fixation, the FP disappeared, and at the same time a saccade target (ST, 1° in diameter) was flashed for 24 ms at a position to the right of screen center.

At an unpredictable time (12–390 ms) after the saccade target was flashed, a localization target (LT) in the form of a vertical bar 20° in length was presented for 12 ms at one of four locations positioned around the saccade target. The distribution of the LTs was symmetrical around the saccade target in experiment 1 (see Fig. 2A, top left), whereas in experiment 2 the spatial location of the LTs was held constant relative to the FP across amplitudes (see Fig. 2B, bottom left). Unless otherwise noted, the luminance of the LT was always 118.4 cd/m², and LT presentation time ranged between ±200 ms relative to the onset of saccades. In a third experiment, we varied the luminance of the LT among low (5.9 cd/m²), medium (12.3 cd/m²), and high (118 cd/m²) values.

Figure 2.

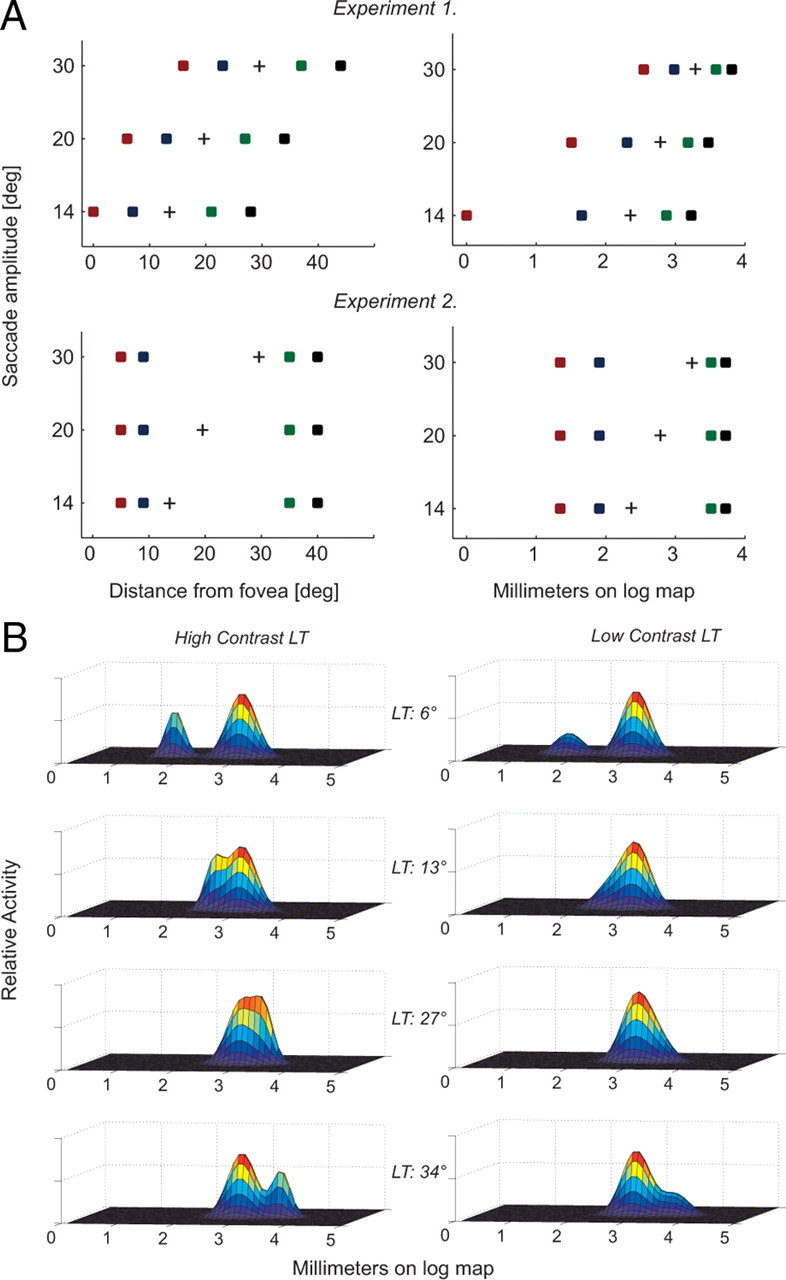
A, Stimulus positions transformed from visual coordinates to logarithmic coordinates. The left column represents stimulus geometry for experiments 1 and 2 in visual space, whereas the right column shows how the same stimulus configuration would be represented on logarithmic maps in areas such as V1. B, A schematic of how the neural activity attributable to the LT and gaze command to the ST might look if both were represented in a common reference frame, for a 20° saccade in experiment 1 (LT positions 6, 13, 27, and 34°). For each diagram, the smaller hill represents the neural activity attributable to the LT, which can vary in amplitude (or firing frequency) depending on the luminance.

Figure 1A depicts the sequence of monitor frames for a typical trial. Figure 2A, left column, shows the retinal layout of the saccade end point and bar positions relative to the initial fixation point for the two experiments. Figure 1B shows eye movement traces along with the sequence of events for a typical 20° saccade trial. The saccade latency across subjects for all experiments was 206 ± 47 ms (mean ± SD).

Figure 1.

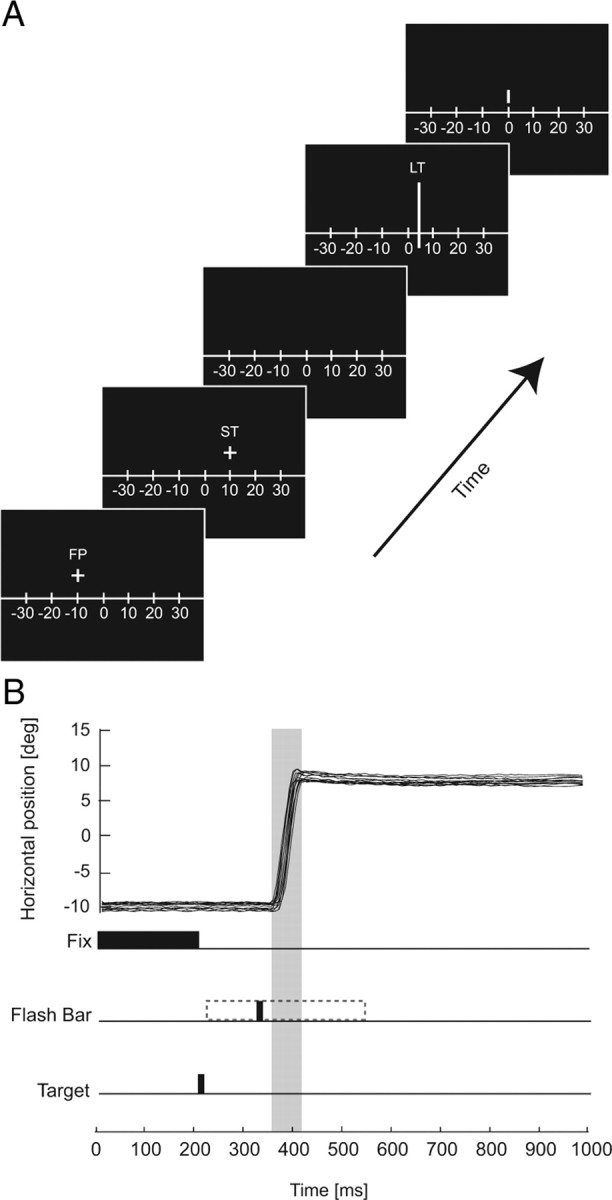
Sequence of events for an example 20° saccade. A, Experiment frames depicting the events on the screen for a given trial. After a brief fixation period (FP), the ST is flashed for two frames (24 ms), and the LT is flashed for one frame (12 ms) after a variable delay (blank screen from 12 to 390 ms). After successful completion of a saccade, the observer was cued to manually report the apparent position of the LT by the appearance of a mouse cursor on the screen. B, Analog eye movement traces for a 20° saccade trial, with trial events and corresponding times below.

The successful completion of a saccade was followed by the appearance of a cursor, which subjects could move horizontally by means of a mouse. Subjects indicated the perceived location of the LT by moving the cursor to the appropriate location and clicking the left mouse button. During this part of each trial, subjects were free to move their eyes. Subjects performed two blocks of 300 successful trials for most experimental conditions, with saccade amplitude remaining constant for the duration of each block.

Data analysis.

Calibration of eye movements was performed at the beginning of each experimental session. Analog eye position signals were analyzed off-line using Matlab (Mathworks). The onset and offset of saccades were determined using a variation of the method described by Carl and Gellman (1987). The starting time of a saccade was calculated as the intersection between the linear regression of a data sample obtained after a velocity criterion (100°s⁻¹) was reached, and the averaged eye position during the previous fixation. Trials were automatically discarded if any of the following occurred: if the reaction time exceeded 500 ms; if the saccade end point fell outside ±2.5° of the saccade target; if a blink occurred around the time of bar presentation; or if a saccade occurred before target onset. On average, 5% of all trials were discarded per experiment. The saccadic main sequence was computed for trials that met task requirements (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). Importantly, the relationship between peak saccade velocity and amplitude did not differ significantly between experiments 1 and 2 across all observers (two-sample t test, α = 0.05). Data from separate blocks of the same experiment were pooled for each subject.

For some of our analyses, we followed Lappe et al. (2000) and calculated a global compression index (CI) as the SD of the perceived positions of the four LTs normalized to the average of the SDs during the periods from 150 to 100 ms before the saccade, and 100–150 ms after the saccade. We also described the mislocalization of LTs for individual LT locations by calculating the absolute deviation in degrees of the perceived position of LT from the saccade target (see below, Eq. 1). To quantify the extent of mislocalization on a normalized scale, this deviation was divided by the actual distance between the saccade target and the LT. Thus, similar to the global CI defined by Lappe et al. (2000), our CI for individual LTs varied between 0 and 1 for full and no compression, respectively. All modeling computations were performed in Matlab (Mathworks).

Goodness of the fit of the model to the data was analyzed using a reduced χ² statistic (Bevington and Robinson, 1992; Taylor, 1997; Cavanaugh et al., 2002). This method permits the comparison of model fits that involve different numbers of free parameters. The statistic produces a χ²_R value and a p value, with the latter corresponding to the probability that the data points and the model output came from the same distribution.

Model.

Figure 2B shows a hypothetical example of how the saccade target and LT might be encoded on a retinotopic map of the kind that has been found in the visual cortex, and in visuomotor areas of the primate brain such as the superior colliculus and LIP. Each panel in the figure shows the representation of a single LT presented at the positions used in experiment 1 in the 20° saccade condition (Fig. 2A, top left). Because of the logarithmic manner with which visual space is mapped (Schwartz, 1977; Ottes et al., 1986), the representation of the LTs is compressed substantially (Fig. 2A, top right). Indeed, for some experimental configurations in the diagram representation of Figure 2B, the visual and oculomotor activity attributable to the LT and the intended saccade location, respectively, cannot be discerned from each other. This situation might be expected to result in a mislocalization bias of the LT toward the saccade target. In reality, the degree to which oculomotor activity obscures visual activity will of course depend on a number of unknown factors, including the amplitude, width, and relative timing of the two types of representations on the map. Nevertheless, even in the absence of detailed information on these quantities, the geometry of Figure 2B suggests that perceptual compression will depend on the relationship between the spatial positions of visual and oculomotor representations in logarithmic coordinates. Specifically, we hypothesize that perceptual compression is related to a single quantity: the distance on a logarithmically encoded retinotopic map between the saccade vector and LT representation relative to the fovea. As can be seen in Figure 2A, right column, this distance depends heavily on both saccade amplitude and the retinal position of the LT.

To test our model, we performed a series of psychophysical experiments using different LT positions and saccade amplitudes (Fig. 2A, left column). Previous studies have quantified compression by combining data across LT positions (Lappe et al., 2000), but we wanted to test the specific predictions of the model about mislocalization for different LT positions. We therefore defined a new compression index that considers the mislocalization of each LT as the distance between the perceived position P of the LT and the saccade target S, normalized by the difference between the actual LT position B and the saccade target as follows:

This metric captures the intuition that perceptual compression should result in a bias of the perceived position of the LT toward the saccade target. A complete compression would thus result in a value of 0, and no compression would have a value of 1.

We hypothesized that the quantity defined in Equation 1 would relate to the distance between the saccade target and each individual LT in a coordinate system defined by the retinotopic mapping of visual space onto visual structures in the primate brain. Previous work (Schwartz, 1977) has shown that this mapping can be captured by the following equation:

where x is distance on the log map in millimeters, z is the retinal eccentricity of a point on the retina, k₁ is a constant that scales the map without changing its shape, and a defines the size of the foveal region of the map (where the relationship between cortical distance in millimeters and visual distance in degrees is approximately linear). In primates, a has been estimated to be ∼1 for primary visual cortex (Daniel and Whitteridge, 1961; Dow et al., 1981, 1985; Schwartz, 1994), and we have used this value in all of our simulations. Changing the value of a to be more consistent with values observed in extrastriate cortex (Polimeni et al., 2006) had very little effect on any of the simulations described below. Thus, using the variables defined above, the distance between the saccade target and a given LT at position B was given by the following:

which simplifies to the following:

We suggest that perceptual compression (defined as in Eq. 1) is proportional to the proximity of the LT to the saccade target in a logarithmic coordinate system. Therefore, by combining Equations 1 and 4, we get the following:

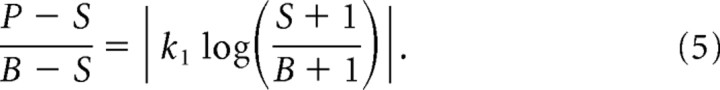This formulation has one free parameter, the map constant k₁, which absorbs the constant of proportionality between the two sides of Equation 5. Consequently, the value of k₁ in this formulation is not meant to have any physiological significance, as it merely scales the relationship between two dimensionless quantities.

Equation 5 does not account for an important feature of the data, namely the unidirectional shift in perceived LT position that accompanies perisaccadic compression (Matin and Pearce, 1965; Mateeff, 1978; Honda, 1989, 1991; Schlag and Schlag-Rey, 1995; Lappe et al., 2000) (see Introduction). As the shift phenomenon appears to depend far more on the temporal than the spatial structure of the stimulus (Schlag and Schlag-Rey, 1995; Pola, 2004), we have not attempted to incorporate it explicitly into our space-domain model. Instead, we simply extended the model to include a free parameter k₂ that represents a shift in retinal coordinates that potentially varies across LT positions and saccade amplitudes. This was added to the LT position B, but the model was otherwise unchanged. The complete model is thus the following:

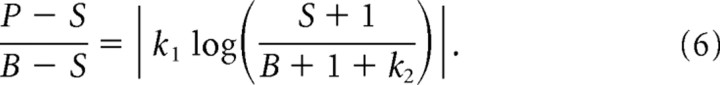As we show in Results, the value of k₂ has surprisingly little impact on any conclusions related to the compression model, consistent with the finding (Boucher et al., 2001; van Wetter and van Opstal, 2008a,b) that the shift is mostly unaffected by the parameters (LT contrast and saccade amplitude) that were manipulated in our experiments.

Rearranging the terms in this model allows us to predict the relationship between perceived and actual bar position as follows:

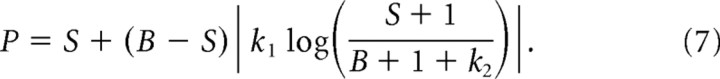Note that the prediction of Equation 7 is undefined for LTs presented at locations that are positioned far into the hemifield opposite the saccade target (when B < −k₂ − 1). We have not tested such conditions in our experiments, but such data would constrain future elaborations to the model.

We tested our model by collecting data from four subjects (two authors and two naive), using the stimulus configurations shown in Figure 2A. We then optimized parameters k₁ and k₂ to account for each subject's data in both experiments 1 and 2, using data taken from the time window spanning the 60 ms before saccade onset. This time window had the virtue of separating the mislocalization effects that could be attributed to the relative positions of the LT and the saccade target from optical effects that occur during the eye movement (Burr and Ross, 1982; Burr et al., 1982, 1994).

The model fits obtained with the presaccadic data were then used to predict the time course of the compression effect for each observer. We did this by examining the data in three time windows following saccade onset (10–25, 25–50, and 90–120 ms). These windows were chosen to test the model early in the saccade, late in the saccade, and after the saccade; with nearly identical results obtained for modest changes in the position or width of the windows. Within each window, the model output was taken from Equation 7, using the retinal position of the bar (adjusted, per observer, for mean instantaneous eye position), and the parameters k₁ and k₂ obtained for each observer from the presaccadic model fits.

Extension of model to LTs of different contrasts.

Our model provides a simple explanation of perceptual compression based on the relative positions of two types of signals on a logarithmic map of visual space (Fig. 2B). The underlying intuition is that strong oculomotor activity on such a map influences the ability of the brain to extract visual signals from the same map.

We can extend this reasoning further to include variations in the relative amplitude of the two signals. Although there is no obvious way to manipulate the amplitude of the oculomotor signal substantially, the strength of the visual signal can be altered by simply changing the salience of the LT. As in Figure 2B, right, we can predict that a smaller visual signal will lead to greater compression, since in this case the influence of the oculomotor activity will be even stronger. For example, in Figure 2B, second row, the representation of the LT (left bump on the map) is more easily discerned at high contrast (left) than at low contrast (right). We therefore propose that, for a LT of luminance L, compression will be determined by a straightforward extension to Equation 5 as follows:

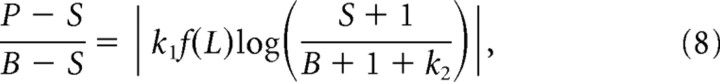where f(L) = L^k₃ captures the power-law relationship between luminance and the response of the early visual system (Purpura et al., 1988). For the highest LT luminance, we define f(L) = 1 so that Equation 7 holds for all simulations.

Results

Our goal was to characterize the geometry of perisaccadic distortions in the perception of visual space. To this end, we performed two sets of experiments that involved saccades of varying amplitudes. In the first set of experiments, visual space was probed in a fixed region relative to different saccade targets (Fig. 2A, top left). In the second set of experiments, we probed visual space in a fixed region relative to the fovea, independent of saccade amplitude (Fig. 2A, bottom left). Our simple model makes very specific predictions about the dependence of compression on the distance on a log map between the saccade target and LT. In the following sections, we show that this model fits all our results remarkably well.

Experiment 1: perception of visual space around the saccade target

In the first set of experiments, subjects were asked to report the position of a high-contrast LT presented briefly (∼12 ms) around the time (±200 ms) of mean saccade onset. In separate blocks of trials, subjects were cued to make saccades of 14, 20, or 30°. The LTs were always distributed symmetrically at a constant distance (−14, −7, 7, and 14°) around the saccade target for each saccade amplitude (Fig. 2A, top left). For simplicity, LT positions lying between the initial fixation point and the saccade target will be referred to as inboard, whereas those beyond the saccade target will be called outboard.

Representative data for one subject (C.P.), aligned to the time of saccade onset, are shown in Figure 3A (data for remaining observers are in supplemental Figs. 5–7, available at www.jneurosci.org as supplemental material). Each point indicates the perceived position of the LT as a function of LT presentation time on a given trial, and the thick, hatched black line indicates the position of the saccade target. Position lines were calculated as running averages obtained with a Gaussian filter (σ = 15 ms). In each condition, there is a systematic mislocalization of the LT that begins ∼50 ms before saccade onset and continues throughout the saccade. In agreement with previous results (Ross et al., 1997, 2001; Lappe et al., 2000), localization errors are of two main types: a mislocalization in the direction of the saccade for inboard LTs and a mislocalization in the direction opposite the saccade for outboard LT positions. Together, these effects comprise the perisaccadic compression of perceived visual space described previously (Honda, 1993; Ross et al., 1997; Lappe et al., 2000; Ostendorf et al., 2007).

Figure 3.

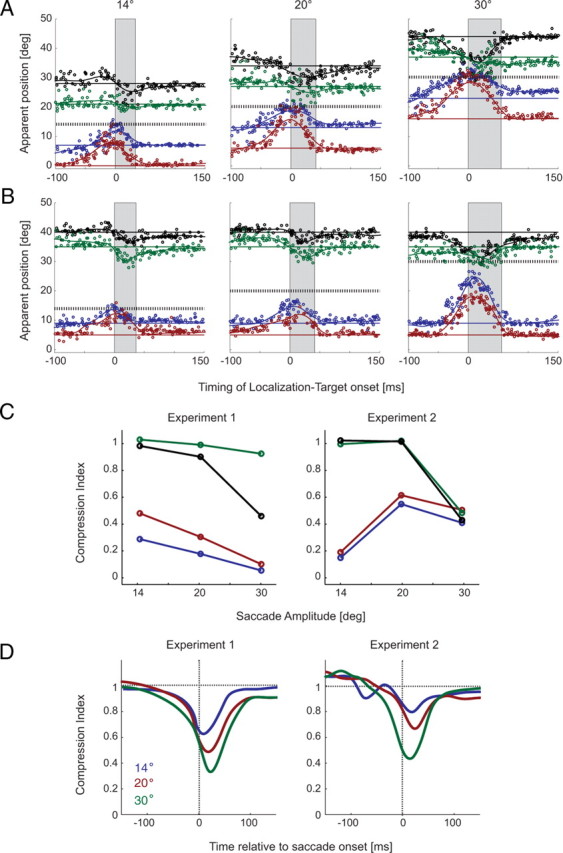
Raw data for experiments 1 (A) and 2 (B). Apparent positions of a briefly flashed bar (12 ms) are aligned on saccade onset. Data were collected for three different saccade sizes (14, 20, and 30°) on both experiments. The black hatched line indicates the saccade target position, and the gray area highlights the average saccade duration for a given amplitude. Data points (each color indicating a different LT position) represent responses for the four LT positions tested, which could either be distributed symmetrically around the saccade end point (experiment 1) (A) or held a constant distance relative to fixation (experiment 2) (B). Position lines were calculated as running averages for each LT position, obtained with a Gaussian filter (σ = 15 ms). C, The value of the compression index defined in Equation 1, for each LT position (color-coded as in A and B), for the maximum mislocalization that occurs in the −60 to 0 ms time interval before saccade onset. D, Compression as a function of time relative to saccade onset, based on the compression index defined initially by Lappe et al. (2000) for experiments 1 and 2 (saccade sizes of 14, 20, and 30°). All data shown are from observer C.P.; for other observers, see supplemental Figures 5–7 (available at www.jneurosci.org as supplemental material).

From inspection of Figure 3A, it appears that perceptual compression increases with saccade amplitude across the range of amplitudes we have tested. That is, the perceived distance between the LT and the saccade target decreases with increasing saccade amplitude. From these results, one might conclude that compression depends on saccade amplitude, but Figure 2A, right column, suggests another possibility: on a logarithmic map the distance between the LTs and the saccade target decreases dramatically with increasing saccade amplitude (whereas they are constant in visual space). This implies that the distance between the LT and saccade target representations in logarithmic coordinates may account for the observed relationship between compression strength and saccade amplitude, as indicated in the diagram representation of Figure 2B. The results of experiment 1 do not distinguish between the two possibilities. We therefore conducted a second series of experiments in which the retinal eccentricity of the LTs was held constant while saccade amplitude was varied.

Experiment 2: perception of visual space with probe eccentricity held constant

The spatial conditions of experiment 2 are depicted in Figure 2A, bottom row, which shows the relative positions of the saccade targets and LTs in the retinal (left column) and logarithmic (right column) coordinate systems described previously for experiment 1. In contrast to this previous experiment, the distance between the saccade target and a given LT does not necessarily decrease with increasing saccade amplitude, and in some cases (i.e., the inboard LTs), it actually increases. At the same time, the opposite relationship holds for outboard bars: the distance between the LT and the saccade target on the logarithmic map decreases as saccade amplitude increases.

Figure 3B shows data from experiment 2 for the same subject and in the same format as in Figure 3A. Here again, each point corresponds to the perceived location of the LT on a single trial, and the four black lines correspond to the actual positions of the LTs. As in experiment 1, the data indicate a compression of visual space that begins before saccade onset, peaks close to saccade onset, and varies across experimental conditions.

At first glance, the results of experiment 2 appear to be similar to those of experiment 1, as the perceptual displacement of the LT increases with saccade amplitude. Indeed, when data are pooled across LT positions using standard measures (Lappe et al., 2000), the magnitude of compression unambiguously increases with saccade amplitude for both experiments 1 and 2 (Fig. 3D). However, closer inspection of individual LT positions reveals important differences between the results of experiments 1 and 2. Consider, for example, the distance between the perceived position of the inboard LT that is closest to the fovea (Fig. 3A, red lines) and the saccade target (hatched horizontal line). This quantity decreases with increasing saccade amplitude in experiment 1 (Fig. 3A) but increases with saccade amplitude in experiment 2 (Fig. 3B). Similarly, the perceived positions of both outboard bars change far more with saccade amplitude in experiment 1 than in experiment 2. To make these differences more apparent, we developed a new metric of perceptual compression that takes into account the positions of individual LTs (Eq. 1). A key feature of the new metric is that it represents the perceived displacement of each LT as a function of the actual difference between the LT and the saccade target (Eq. 1).

Figure 3C plots our compression index for each LT position as a function of saccade size in both experiments. Here, as with previous metrics (Lappe et al., 2000), increased compression is indicated by decreasing values of the compression index. In experiment 1, there is a clear trend of increasing compression with saccade amplitude for each LT position, whereas in experiment 2 compression actually decreases when saccade amplitude is increased from 14 to 20° for the inboard bars (red and blue lines, right panel). For the outboard bars, compression increases with saccade amplitude in both experiments. Thus, a more detailed examination of the perceived positions of individual LTs reveals a complex pattern of perisaccadic mislocalization that would be obscured by pooling across LT positions. We next examined the extent to which the model derived in Materials and Methods can account for these results.

Model results: LTs flashed before saccade onset

Figure 4 shows plots of perceived LT position versus real LT position for the four observers. In these plots, the unity line represents accurate perception, whereas deviation away from it reflects mislocalization. Complete compression would thus be represented as a horizontal line through the ST (red star symbol). However, our data show a more complex, nonlinear relationship between real and perceived LT positions.

Figure 4.

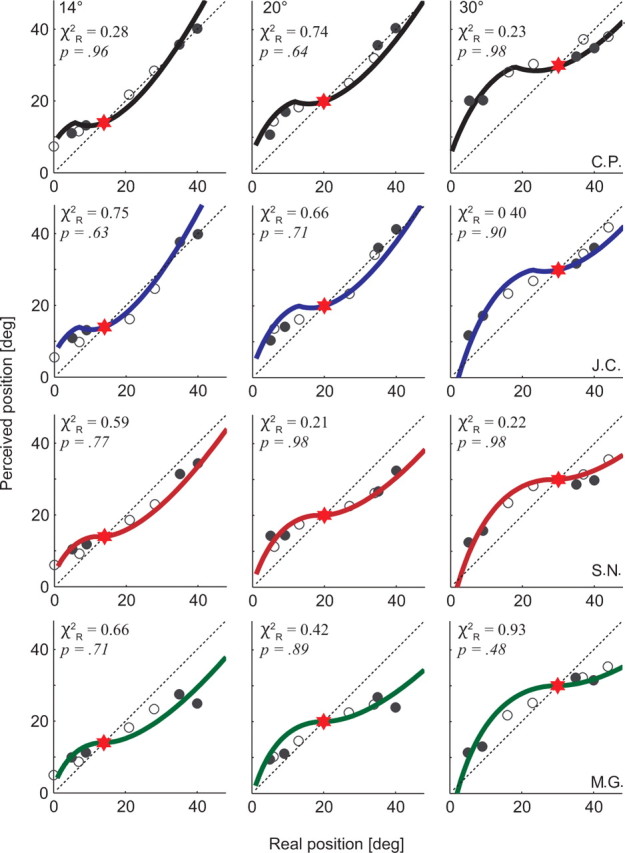
Model fits for experiments 1 (unfilled circles) and 2 (filled circles) combined. Each data point represents the perceived position corresponding to the maximal mislocalization that occurs for each LT (4 bars × 2 experiments), in the −60 to 0 ms time epoch before eye movement onset. Data are shown for four different observers (rows, top to bottom, C.P., J.C., S.N., M.G.) for each saccade amplitude tested (columns, 14, 20, 30°). Model fits for each observer are colored lines (Eq. 7, with k₁ values fixed per observer, and k₂ adjusted for each fit) (for values, see Table 1). All p values are given for 7 df. The red star symbols refer to saccade target position, and the dashed oblique line represents a unity relationship for real versus perceived LT position.

We fit the model described by Equation 7 to the data corresponding to the time period 60 ms before saccade onset for each observer (Fig. 4). In these plots, k₁ has been optimized globally for each observer (Table 1). The parameter k₂ represents a unidirectional shift in perceived LT position, which may be expected to change with saccade amplitude (Richard et al., 2008a,b; van Wetter and van Opstal, 2008a). Consequently k₂ was adjusted for each panel. Despite this modest number of free parameters, the model fits the data extremely well in all cases.

Table 1.

k₁ and k₂ values for all subjects in experiments 1 and 2

Amplitude (°)	C.P.		J.C.		S.N.		M.G.
	k1	k2	k1	k2	k1	k2	k1	k2
14	0.9348	6.6553	1.0101	6.6926	0.9487	4.3519	0.7375	2.1591
20	1.3398	5.7051	1.3210	5.5113	0.8819	3.1569	0.7367	1.5498
30	1.1091	12.7213	1.3049	9.4366	0.9629	5.3812	0.8245	1.7382
Mean	1.1279	8.3606	1.2120	7.2135	0.9312	4.2967	0.7662	1.8157
All values mean				k1: 1.0093
				k2: 5.4216

We used the reduced χ² test (the Pearson's χ² value normalized by the number of degrees of freedom in the model being tested) to assess the goodness of fit of our model to the experimental data (Bevington and Robinson, 1992; Taylor, 1997; Cavanaugh et al., 2002), as this method had the benefit of allowing us to compare fits generated with different numbers of free parameters. Degrees of freedom were defined as the number of observed data points minus the number of free parameters computed from the data and used in the calculation. This calculation confirms that the model fits the data extremely well for all observers across the three amplitude conditions tested (Fig. 4) (min < χ²_R < max, 0.21 < χ²_R < 0.93; df = 7).

Interestingly, the optimal k₂ is much less than saccade amplitude for all observers (Table 1). This predicts that the previously observed shift in perceived LT position does not scale linearly with saccade amplitude, in agreement with the observations of van Wetter and van Opstal (2008a,b), who showed that the shift reaches a maximum value of ∼10° even for very large gaze shift amplitudes (>50°).

To test the generality of our modeling results, we acquired data from a previously published experiment (Morrone et al., 1997) (Fig. 5) that examined the perceptual mislocalization of LTs presented at various positions just before the onset of a 20° saccade. Figure 5 shows the data along with our model fits for both observers. Again, the model fit the data very well (χ²_R = 1.53 and 0.21; df = 57 and 37; p = 0.54 and 0.64 for subjects M.C.M. and J.R., respectively), yielding the following optimal parameter values: k₁ = 0.4 (M.C.M.) and 0.5 (J.R.); k₂ = 9.1 (M.C.M.) and 7.2 (J.R.). These values can be compared, in Table 1, to those obtained from our own observations. The value of k₂ in our model fits to the data of Morrone et al. (1997) was within the range calculated for our subjects. In comparison, the value of k₁ for the Morrone data was approximately one-half of ours. As mentioned in Materials and Methods, k₁ has no obvious physiological interpretation so we can offer no strong explanation as to why its value is relatively homogeneous in each laboratory, but different across laboratories. We note, however, that the value of k₁ was of the same order of magnitude across all experiments and that the model was able to accommodate a range of variability across observers and experimental conditions.

Figure 5.

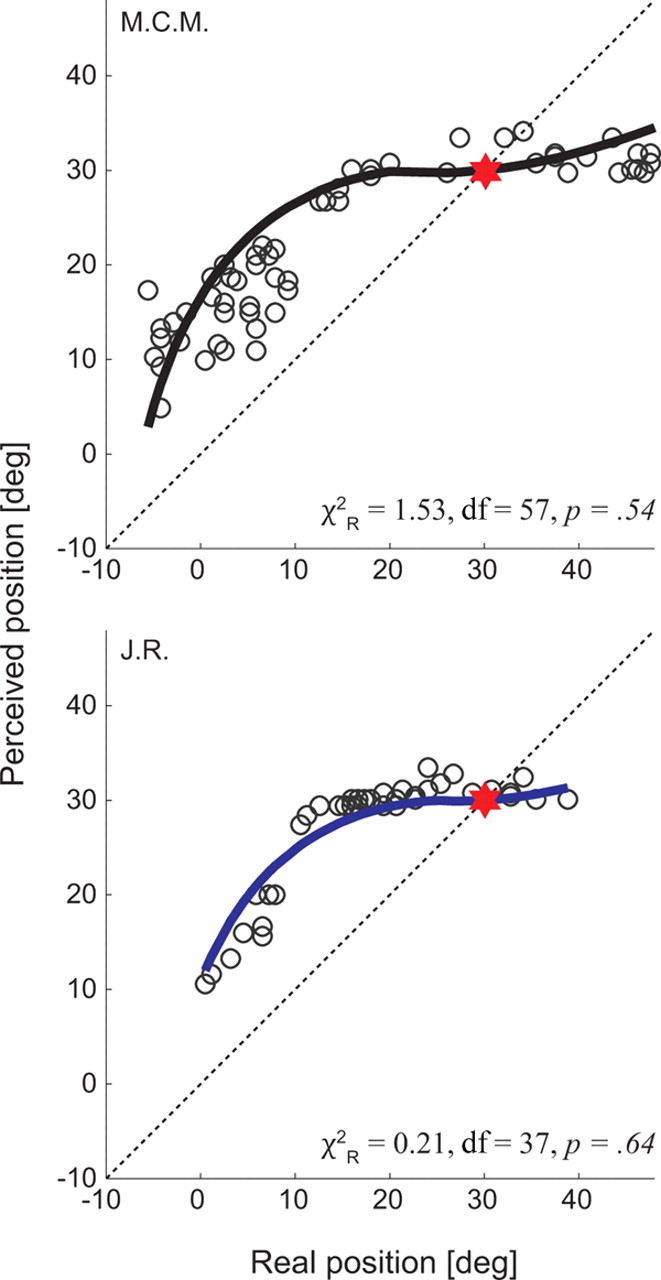
Model fits for previously published data [acquired from Morrone et al. (1997)]. The data show the perceived position of bars flashed in the −25 to 0 ms interval before saccade onset for a 20° saccade in two observers (M.C.M. in black and J.R. in blue). The abscissa shows the position of the flashed bar in retinotopic coordinates, for a saccade made from 10 to 30°. The red star symbols refer to saccade target position, and the dashed oblique line represents a unity relationship for real versus perceived LT position. The superimposed solid lines are the model predictions made by Equation 8.

Model results: LTs flashed after saccade onset

The results from Figures 4 and 5 suggest that the model was able to predict the perceived mislocalizations for LTs flashed at various retinal positions just before the onset of saccades of various amplitudes. However, as shown in Figure 3D, the magnitude of the compression effect changes substantially over time, and in some cases it peaks after saccade onset. Movement of the eye alters the retinal position of the LT, and hence the distance between the representation of the saccade target and the LT on the logarithmic map that forms the core of the model (Fig. 2). Thus, the model makes specific predictions about how the perceived position of the LT should depend on the time at which it is presented relative to saccade onset. In particular, because in our model an eye movement is equivalent to presenting an LT at a different retinal position, we predict that Equation 7 with the same model parameters will be sufficient to fit the localization data for a given observer at any point during the saccade.

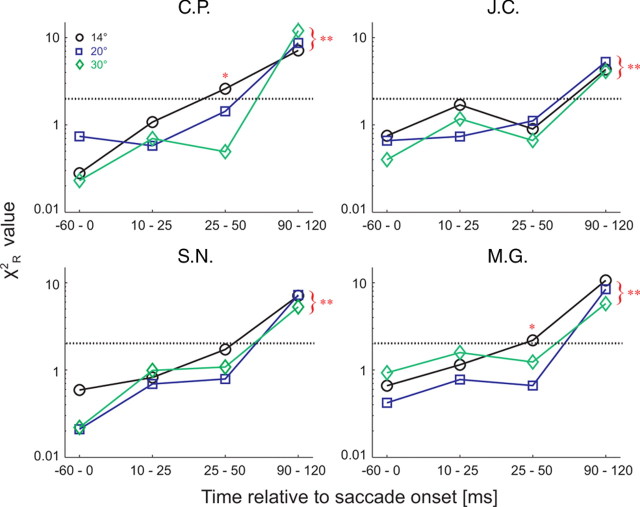
To test these model predictions, we sampled our data at four different time epochs relative to saccade onset (−60 to 0, 10–25, 25–50, and 90–120 ms) and plotted the perceived position for each LT as a function of its average position on the retina for each observer. These data are shown in Figure 6 for observer C.P., along with the model curve obtained by optimizing the parameters for the presaccadic data reported above. The same analysis for the three other observers is shown in supplemental Figures 2–4, available at www.jneurosci.org as supplemental material. Remarkably, the model fit the data nearly as well during the two intrasaccadic time epochs (Fig. 6, rows 2, 3), as revealed by the χ²_R and p values for all fits (df = 7), despite the fact that no free parameters were manipulated beyond the optimization of k₁ and k₂ for the data from the presaccadic epoch. Figure 7 summarizes these findings for all observers by plotting the mean χ²_R for each epoch, including the postsaccadic epoch when perception was essentially veridical (Fig. 6, last row).

Figure 6.

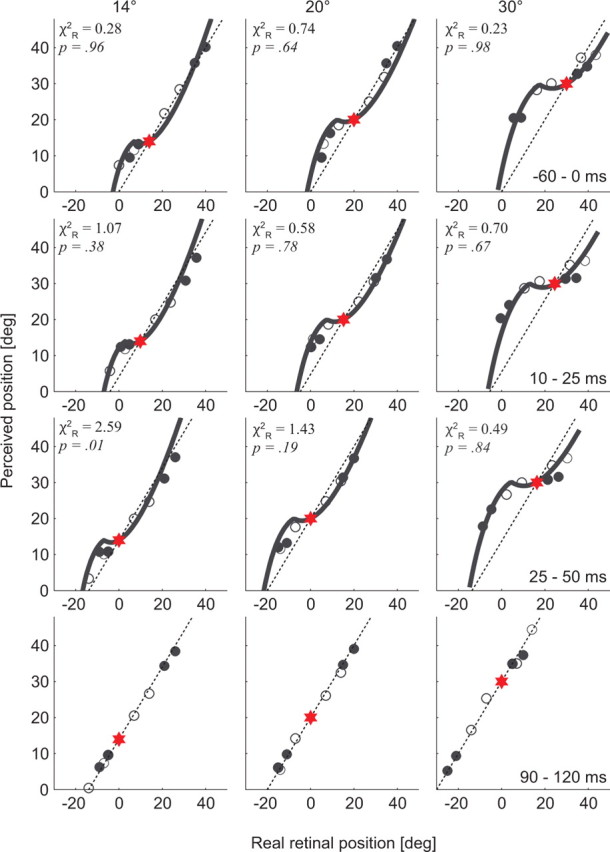
Model fits for experiments 1 and 2, for different times epochs relative to saccade onset (data from observer C.P. are shown) (for other observers, see supplemental Figs. 2–4, available at www.jneurosci.org as supplemental material). As in previous figures, each data point represents the perceived position corresponding to the maximal mislocalization that occurs for each LT (4 bars × 2 experiments), during the specified perisaccadic time epoch (each row; −60 to 0, 10–25, 25–50, and 90–120 ms). The unfilled circles refer to experiment 1, and the filled circles refer to experiment 2. For each time epoch, the retinal position of the LT is adjusted for the average amount the eye has moved. Data are shown for 14, 20, and 30° saccade amplitudes (columns). Model fits are solid lines (Eq. 7, with fixed k₁, whereas k₂ is adjusted for each fit) (for values, see Table 1). All p values are given for 7 df. The red star symbols refer to saccade target position, and the dashed oblique line represents a unity relationship for real versus perceived LT position.

Figure 7.

Statistics summary for all observers. Model goodness of fit (χ²_R) is plotted for different time epochs before, during, and after the saccade. All points that lie beneath the black dashed line (p = 0.05) represent instances where the model fit the data. For cases when the model did not fit the data, significance levels are designated by single (p < 0.05) or double (p < 0.01) asterisks.

Effects of varying the luminance of LT

The same reasoning that led us to derive the model used in Figure 4 suggests that perisaccadic visual perception should depend on the luminance of the LT. Specifically, the influence of the oculomotor signal on the readout of LT position should depend on an interaction between visual and oculomotor signals, both of which are represented on a logarithmic retinotopic map. The strength of the interaction would then depend on the distance between these two representations, and our results in the previous section are consistent with this idea. However, the interaction might also depend on the magnitude of the neural activity related to each signal, since a weak visual signal would be more easily obscured by oculomotor activity. As described in Materials and Methods, this idea can be incorporated into the existing model by the addition of a single additional parameter k₃ that represents the strength of the visual signal relative to that of the oculomotor signal.

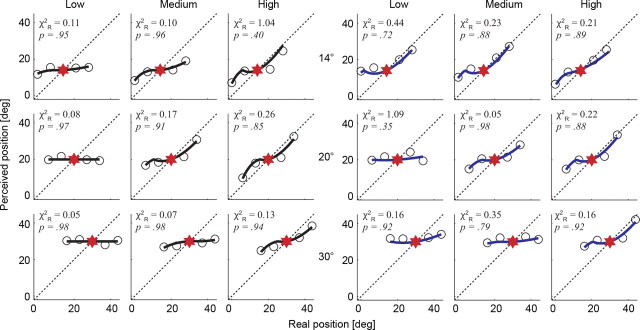
We repeated experiment 1 in two subjects, but this time we varied the luminance of the LT among three values (5.9, 12.3, and 118 cd/m²). Figure 8 shows the results along with the fits of the extended model that contains an expression for relating stimulus luminance to a visual response via a power-law relationship. Again, we found excellent fits to all our data (range across subjects, 0.05 < χ²_R < 1.09; df = 3) with the additional striking feature that optimal values of k₃ were nearly identical between subjects (mean ± SE, 0.51 ± 0.06) (Table 2). In both cases, we found that the optimal k₃ was ∼0.5, which suggests a saturating nonlinearity similar to that found in the early visual system (Purpura et al., 1988).

Figure 8.

Model fits for experiment 1, redone with variable LT luminance (columns; low, 5.9 cd/m²; medium, 12.3 cd/m²; and high, 118 cd/m²). As in Figure 4, data points represent the maximal mislocalization for each bar position (4 LTs, symmetrically distributed around the saccade target), in the −60 to 0 ms time epoch before eye movement onset, for 14, 20, and 30° saccades (rows). Data from two observers are shown, and model fits are solid lines (C.P. in black, left; J.C. in blue, right). Using Equation 8, k₁ and k₂ values were fixed per subject (Table 1), whereas k₃ was adjusted for each fit (Table 2). All p values are given for 3 df. The red star symbols refer to saccade target position, and the dashed oblique line represents a unity relationship for real versus perceived LT position.

Table 2.

k₃ values for experiment 3

Amplitude (°)	C.P.			J.C.
	Low	Medium	High	Low	Medium	High
14	0.5007	0.4997	0.4996	0.5018	0.4994	0.4999
20	0.4997	0.6038	0.5007	0.3432	0.5002	0.5005
30	0.7899	0.5006	0.5000	0.4997	0.4998	0.4999
Mean	0.5968	0.5347	0.5001	0.4482	0.4998	0.5001
All values mean			k3: 0.5133

Discussion

We have shown that the perceived position of a visible object presented just before a saccade can be predicted by a simple model that takes into account the logarithmic mapping of the retinal image onto the visual cortex. On a logarithmic map, contours separated by a fixed distance in the visual field are closer together at large than at small retinal eccentricities. Consequently, the representation of the distance between saccade vectors and visual targets is compressed in the periphery of the map, and we have shown how a simple, closed-form expression based on this idea can account for data obtained over a wide range of experimental conditions.

Comparison to other models

Perhaps the most detailed conceptual framework for explaining perisaccadic perceptual phenomena is the model developed by Hamker et al. (2008). These authors present a computational theory that also predicts two other phenomena known to occur perisaccadically: receptive field shifts (Duhamel et al., 1992) and enhanced visual discrimination at the saccade target (Kowler et al., 1995; Deubel and Schneider, 1996; Castet et al., 2006; Montagnini and Castet, 2007). The model incorporates a detailed mathematical description of the spatial and temporal factors that affect perisaccadic perception, and relates these factors to specific brain structures. Importantly, the model hypothesizes that oculomotor signals interact with visual signals through a space-varying gain modulation akin to that previously reported for attention signals in the visual cortex (Martínez-Trujillo and Treue, 2002; Reynolds and Desimone, 2003). We suggest that this mechanism could also underlie the interaction between visual and oculomotor signals in our model.

Another similarity between our model and that of Hamker et al. (2008) is the representation of spatial positions in a coordinate system defined by the cortical magnification factor. Given these similarities, we suggest that the main advantage of our model is that it accounts for the effects of LT luminance, LT position, the time of LT presentation, and saccade amplitude with a simple closed-form expression that has very few free parameters. Although the simplicity of this formulation naturally comes at the expense of detailed correspondence to biological mechanisms, it does make very specific predictions about the brain regions that could be responsible for perisaccadic visual perception (see below). Moreover, the conceptual basis for the model yields the prediction that similar perceptual compression should be observed for eye-head gaze shifts, as many oculomotor structures also control head movements. We are currently testing this prediction.

An even simpler model that also incorporates the cortical magnification factor was proposed by VanRullen (2004). In this formulation, perceptual compression is attributable to a translation of the origin of the logarithmic coordinate system. This model has no free parameters and qualitatively matches some data on perceptual compression. However, the model predicts near total compression for LTs at any position, as well as a linear relationship between perceived and actual LT position, neither of which are observed in the data. Thus, although the model offers a compelling demonstration of how the cortical magnification factor can be related to perisaccadic localization errors, its quantitative predictions depart significantly from psychophysical findings. Finally, there is the model of Ross et al. (1997), which generally fits our psychophysical data to an equivalent or slightly lesser extent (range across subjects, 0.33 < χ²_R < 2.86; df = 2) (supplemental Fig. 8, available at www.jneurosci.org as supplemental material), but requires six free parameters and has no explicit mechanistic interpretation.

Neurophysiological implications

A straightforward prediction of our modeling work is that object location is computed by brain regions that represent both visual space and saccade vectors on a logarithmic map. This would seem to exclude high-level visual areas such as the dorsal medial superior temporal area (MSTd), where retinotopy is crude (Saito et al., 1986), and V1, where saccade-related activity is minimal (Wurtz and Mohler, 1976). Cortical areas such as V3, V4, and the middle temporal area (MT) thus appear to be reasonable candidates, as all three have an approximately logarithmic map of visual space (Albright and Desimone, 1987; Gattass et al., 1988; Motter, 2009) and receive extraretinal signals related to saccadic eye movements (Nakamura and Colby, 2000; Tolias et al., 2001; Thiele et al., 2002; Ibbotson et al., 2007). Indeed, Krekelberg et al. (2003) have reported that the population output of MT appears to exhibit a neuronal correlate of perceptual compression. The same study found that neurons in higher areas such as the medial superior temporal area (MST) and the ventral intraparietal area (VIP) also show compression effects, and we suggest that these response properties are likely inherited from areas such as V3 and MT.

Another brain region that would appear to be a candidate for a neuronal correlate of perceptual mislocalization is the superior colliculus (SC), a brainstem region involved in the generation of saccades. The SC contains a logarithmic map of visual space (Ottes et al., 1986; Marino et al., 2008), with the superficial layers devoted primarily to the representation of visual targets, whereas the deeper layers contain individual neurons that encode visual targets, saccade vectors, or both. However, the timing of responses in the SC appears to be inconsistent with the various phenomena on perceptual mislocalization. Specifically, the strongest perisaccadic compression is found for LTs presented near or just after saccade onset (Morrone et al., 1997; Lappe et al., 2000), which, given the latencies of visual responses, means that information about the position of the LT reaches the SC near the end of the saccade. By this time, saccade-related SC activity has dropped substantially (Munoz and Wurtz, 1995), suggesting that visual and extraretinal signals during experiments on perisaccadic perception are temporally offset in the SC. Thus, the neuronal correlate of any model based on their interaction is unlikely to reside in the SC. Perhaps more importantly, subjects are not generally aware of visual activity that occurs in subcortical areas like the SC, although there are interesting exceptions (Binsted et al., 2007; Stoerig and Cowey, 2007). Thus, the various phenomena related to perisaccadic mislocalization are unlikely to be directly related to neural activity on the collicular map.

Extraretinal signals from the SC reach a number of cortical structures, notably the frontal eye fields (FEF) (Sommer and Wurtz, 2002). Sommer and Wurtz (2004a,b) have suggested that the FEF might distribute these signals to parietal brain regions, and given the timing considerations mentioned above, this relatively lengthy pathway may compensate for the offset between visual and oculomotor signals found in the SC. Neurons in the SC and FEF also exhibit a remapping of visual space that begins around the time of a saccade (Walker et al., 1995; Umeno and Goldberg, 1997), and similar effects are found in V3 (Nakamura and Colby, 2000) and parietal cortex (Duhamel et al., 1992). In the model of Hamker et al. (2008), this remapping is caused by the same mechanism (gain modulation) that generates perceptual compression.

Functional considerations

Our model suggests that oculomotor signals interfere with the readout of the position of visual stimuli presented around the time of a saccade. This raises the question of why the visual system would use a map that is corrupted by oculomotor signals to localize the positions of objects in space. We suggest that, under normal circumstances, oculomotor signals increase neuronal activity related to objects near the saccade target. Because primates typically make saccades to objects of interest, this property would be functionally adaptive in natural settings.

Perceptually, saccades are accompanied by shifts in the locus of covert attention (Kowler et al., 1995), and this effect has also been observed in single neurons of the superior colliculus (Kustov and Robinson, 1996; Carello and Krauzlis, 2004; Ignashchenkova et al., 2004). Moreover, the effects of attentional shifts on neurons in the visual cortex can be mimicked by microstimulating in the superior colliculus (Müller et al., 2005). Thus, it appears that neuronal signals originating in oculomotor centers can trigger the effects of covert attention near the spatial position encoded by the stimulated neurons (Cutrell and Marrocco, 2002; Moore and Armstrong, 2003), even in the absence of an eye movement. This suggests that the pathways conveying extraretinal signals related to the saccade are responsible for psychophysical observations on the increased perceptual saliency of visual objects near the saccade target (Kowler et al., 1995; Deubel and Schneider, 1996; Castet et al., 2006; Montagnini and Castet, 2007).

In the visual cortex, voluntary attention generally has the effect of increasing the gain of visual responses to stimuli presented near the attended target (for review, see Maunsell and Cook, 2002). Importantly, the effect of attention is stronger for low-contrast stimuli (Reynolds et al., 2000; Martínez-Trujillo and Treue, 2002). Thus, the consequence of a saccade would be to increase the neuronal response to visual stimuli near the target location, particularly those that are low in salience. This may explain why compression is stronger for low-contrast LTs (Fig. 8) (Michels and Lappe, 2004). Furthermore, signals related to spatial attention may be useful for computing translation-invariant representations of visual objects (Olshausen et al., 1993; Salinas and Abbott, 1997). Many of these ideas can be linked to the perisaccadic compression of visual space, as demonstrated by the recent modeling work of Hamker et al. (2008).