Abstract
To understand the mechanisms of fast information processing in the brain, it is necessary to determine how rapidly populations of neurons can respond to incoming stimuli in a noisy environment. Recently, it has been shown experimentally that an ensemble of neocortical neurons can track a time-varying input current in the presence of additive correlated noise very fast, up to frequencies of several hundred hertz. Modulations in the firing rate of presynaptic neuron populations affect, however, not only the mean but also the variance of the synaptic input to postsynaptic cells. It has been argued that such modulations of the noise intensity (multiplicative modulation) can be tracked much faster than modulations of the mean input current (additive modulation). Here, we compare the response characteristics of an ensemble of neocortical neurons for both modulation schemes. We injected sinusoidally modulated noisy currents (additive and multiplicative modulation) into layer V pyramidal neurons of the rat somatosensory cortex and measured the trial and ensemble-averaged spike responses for a wide range of stimulus frequencies. For both modulation paradigms, we observed low-pass behavior. The cutoff frequencies were markedly high, considerably higher than the average firing rates. We demonstrate that modulations in the variance can be tracked significantly faster than modulations in the mean input. Extremely fast stimuli (up to 1 kHz) can be reliably tracked, provided the stimulus amplitudes are sufficiently high.
Keywords: transfer function, linear response, population rate, multiplicative noise, pyramidal cell, ensemble
Introduction
The dynamics of cortical networks is often described in terms of population firing rate models. The construction of such network models relies on the knowledge of the response properties of ensembles of unconnected neurons. Theoretical studies (Knight, 1972a; van Vreeswijk and Sompolinsky, 1996; Gerstner, 2000 and references therein; Lindner and Schimansky-Geier, 2001) have suggested that ensembles of neurons can track noisy time-varying inputs considerably faster than single neurons. The transmission characteristics of neuronal populations crucially depend on single-neuron properties, in particular on the filter characteristics of the membrane (Knight, 1972a) and the synapses (Brunel et al., 2001; Fourcaud and Brunel, 2002) and on the dynamics of the action potential generation (Fourcaud-Trocmé et al., 2003; Naundorf et al., 2005). Depending on the considered neuron model, different theoretical studies have therefore predicted different transmission scenarios. The seminal work of Knight (1972a) has shown that an ensemble of perfect integrators (simple integrate-and-fire neurons) can replicate a stimulus without distortion. Leak currents (leaky integrate-and-fire neuron; LIF) lead to resonances at multiples of the stationary single-neuron firing rate at which the cell ensemble tends to synchronize. Knight (1972a) showed that noise can break this synchrony and suppress the resonances of the population activity. Several theoretical studies (Brunel and Hakim, 1999; Brunel et al., 2001; Lindner and Schimansky-Geier, 2001) pointed out that ensembles of leaky integrate-and-fire neurons act as low pass filters if the synaptic noise is treated as additive white noise. In contrast, the response amplitudes remain finite even for infinitely high frequencies if the noise is correlated, for example due to low-pass filtering by the synapses (Brunel et al., 2001; Fourcaud and Brunel, 2002). This finding, however, turned out to be the result of an oversimplification: realistic neuron models, which take the dynamics of action-potential generation into account, exhibit low-pass characteristics, independently of the spectrum of the noise. It has been shown that the speed of the action-potential onset is the main parameter determining how fast the populations of cells can track a time-varying input (Fourcaud-Trocmé et al., 2003; Naundorf et al., 2005).
Most previous studies have focused on an additive superposition of signal and noise (modulation of the mean input). In a realistic scenario, however, not only the mean but also the intensity of the noise will be affected by modulations of the firing rate of presynaptic neuron populations. It has been demonstrated that an ensemble of LIF neurons can track a stimulus much faster if it is constructed as a white-noise current modulated in the variance (multiplicative modulation) (Lindner and Schimansky-Geier, 2001), rather than in the mean. For correlated (colored) noise, however, the two stimulus paradigms become less distinct (Fourcaud-Trocmé et al., 2003; Naundorf et al., 2005). Ensembles of model neurons with finite action-potential onset speed exhibit low-pass behavior for both modulation paradigms.
Despite the rich theoretical background, experimental evidence on the transmission properties of neuronal ensembles is only recently becoming available. For additive input modulation, it has been demonstrated that ensembles of neocortical neurons can track stimuli in the presence of colored noise very fast: up to frequencies of 200 Hz (Köndgen et al., 2008). In accordance with theoretical predictions, the work of Silberberg et al. (2004) indicated that a multiplicative modulation speeds up the population response considerably, if the noise is (quasi) white. Here, we assessed the transmission properties for multiplicative modulation for the case of colored noise and over a wide range of frequencies and modulation depths, and compared them to the additive scenario. To this end, we measured transfer functions of ensembles of layer V pyramidal neurons from rat somatosensory cortex for the two different stimulation paradigms (additive and multiplicative). For both modulation paradigms we observed low-pass behavior. The cutoff frequencies were, however, significantly higher for modulations of the noise variance than for modulations of the mean input. Our results experimentally confirm the theoretical predictions for the response properties of neurons with finite but large action-potential onset speed.
Materials and Methods
Electrophysiology.
Acute slices of 350 μm thickness were prepared from somatosensory cortex of rats (Long–Evans; postnatal days 16–24) as described previously (Boucsein et al., 2005). Whole-cell patch-clamp recordings (pipette resistance 2–6 MΩ, capacitance 13–17 pF) were made from visually identified layer V pyramidal neurons (N = 23) using infrared video microscopy (Dodt and Zieglgänsberger, 1998). Cells were routinely filled with biocytin via the patch pipette and, after fixation, processed with a silver-enhanced DAB-reaction (Horikawa and Armstrong, 1988) to confirm their identity. Control signals for current injection were sampled at 20 kHz and low-pass filtered at 3–10 kHz before application via the patch-clamp amplifier (BVC-700A, Dagan). Low-pass properties of patch pipettes were compensated for by using the capacitance neutralization circuits of the amplifier. Voltage recordings were low-pass filtered at 3–5 kHz before sampling at 20 kHz (micro-1401, Cambridge Electronic Design). Animal treatment was according to the Freiburg University's and German guidelines on the use of animals in research.
Stimuli.
Synaptic input currents I(t) were synthesized as Ornstein-Uhlenbeck noise z(t) (i.e., low-pass filtered white noise x(t), τ · dz / dt = −z(t) + x(t), time constant τ = 1 ms) with a sinusoidal modulation of the mean (additive modulation),
or of the variance of the noise (multiplicative modulation),
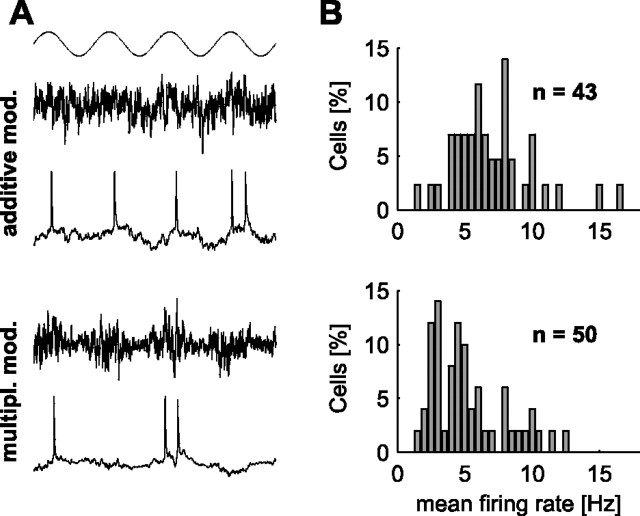
Four different modulation depths (I 1 = 0.1, 0.2, 0.5, 1) and modulation frequencies ranging from 1–1000 Hz were used. To reduce the number of parameters, we set the offset I 0 to zero. To keep the ensemble of cells close to a defined working point, we scaled the amplitude of the input currents such that the time-averaged firing rates of individual cells remained in the range between 5 and 10 spikes/s (Fig. 1 B). This way we make sure that the additive and the multiplicative modulation scheme have the same effect at zero frequency. Each stimulation frequency was applied for 50 s, with 0.5 s gaps between trials for the different frequencies, and only data from cells where all frequencies could be applied were analyzed. In a subset of cells (N = 4), frequency order was randomly shuffled, but since frequency tuning curves did not show differences in shape compared with those derived from ascending frequency order stimulation, data were pooled. Stimuli with the four different modulation depths I 1 were applied to 7, 12, 11, 13 cells and 7, 15, 14, 13 cells for mean and variance modulation, respectively. Cells had an input resistance of 80 ± 57 MΩ (27–270 MΩ), access resistance was 19 ± 6 MΩ (10–32 MΩ). Liquid junction potentials were left uncorrected.
Figure 1.
A, Stimulation paradigms used in the present study. The top trace shows the phase of the sine wave, with which the injected noisy currents were modulated. Below, Examples of injected currents (top traces) and resulting membrane potential fluctuations (bottom traces) are shown for both additive and multiplicative modulation. B, Histograms of average firing rates for all cells used for the additive (top) and multiplicative (bottom) modulation.
Data analysis.
Spikes were detected using a combined threshold and dead-time criterion (Voltage >0 mV and a minimal interspike interval of 2 ms). The spike phase was determined using the period histogram (bin size 0.1/f), i.e., the stimulus sine-wave triggered histogram for each trial and each neuron. A sinusoidal function of the form
was fitted to the period histogram by minimizing the squared deviations of r(t) from the actual data (least square fit, Levenberg–Marquardt algorithm). The goodness of the fit was quantified by the confidence interval (68.2% range) for each fit parameter r 0, r 1 and φ, respectively. To obtain estimates of the population responses, we averaged the complex transfer functions defined by
with
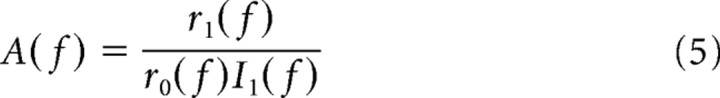 |
across the ensemble of cells and extracted the amplitudes (Figs. 2, 3, thick black curves) and phases of the resulting population transfer functions for further data analysis (Fig. 4). The fit errors of the single cell data gave rise to the confidence interval of the population amplitudes (Figs. 2, 3, gray bands) and phases via error propagation. To evaluate the significance of the measured responses, we generated ensembles of stationary Poissonian spike trains with rates according to the population averaged firing rates for each stimulus condition. By repeating the analysis described above for these surrogate data, we obtained significance levels for the single-cell and population data (Figs. 2, 3, gray lines). The response characteristics of the neuron ensembles were quantified by fitting a function of the form
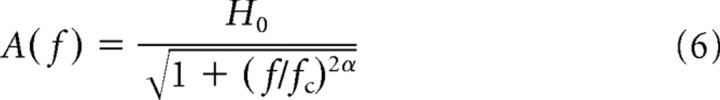 |
to the amplitude of the population averaged transfer function (least-square fit, Levenberg–Marquardt). Here, H 0 corresponds to the response amplitude for small frequencies (f ≪ f c), f c is the cutoff frequency defined by H(f c) = H 0/, and α measures how the response amplitudes decay at large frequencies (f ≫ f c) (Fig. 4). To test for the presence of transmission delays d between input currents and spike responses, we fitted a linear decay,
to the phase of the population averaged transfer function at high frequencies (800–1000 Hz).
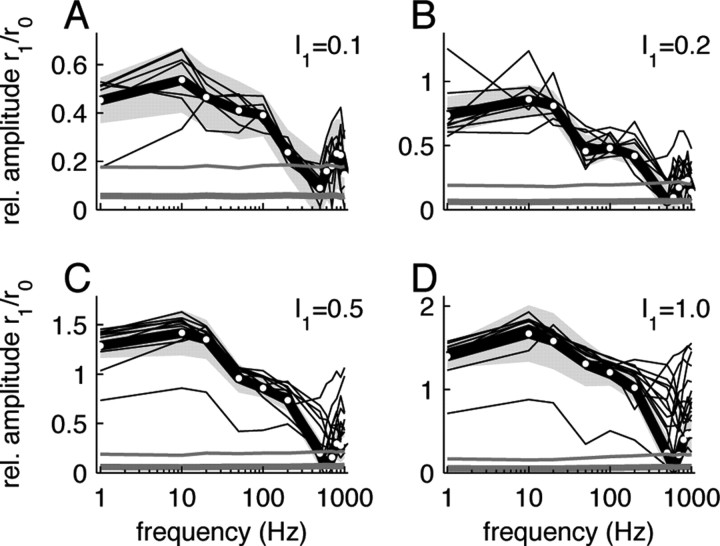
Figure 2.
Response tuning curves for stimuli with additive modulation (A: I 1 = 0.1, B: I 1 = 0.2, C: I 1 = 0.5 and D: I 1 = 1.0). Amplitudes of single cell (thin black lines) and population responses (thick black line, white symbols) are shown for different stimulus frequencies. The light gray area represents the 95% confidence interval of the population average. Significance levels (5%) for the single cell (thin gray line) and population data (thick gray line) were obtained from randomly shuffled spike data.
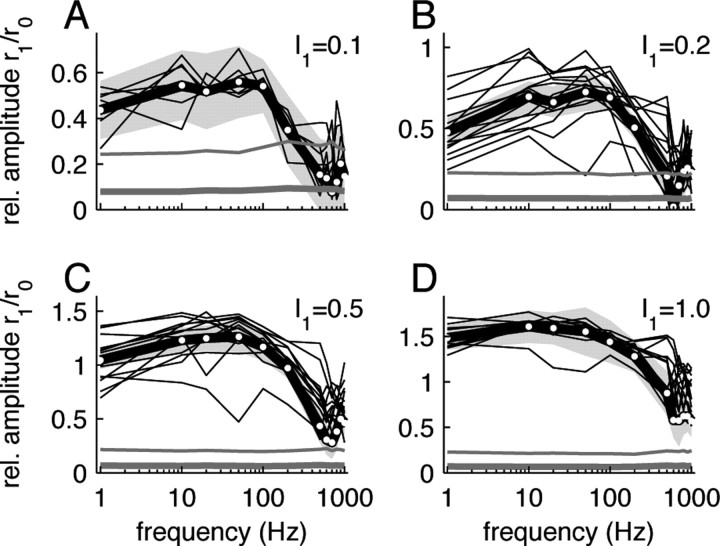
Figure 3.
Response tuning curves for stimuli with multiplicative modulation, details as in Figure 2.
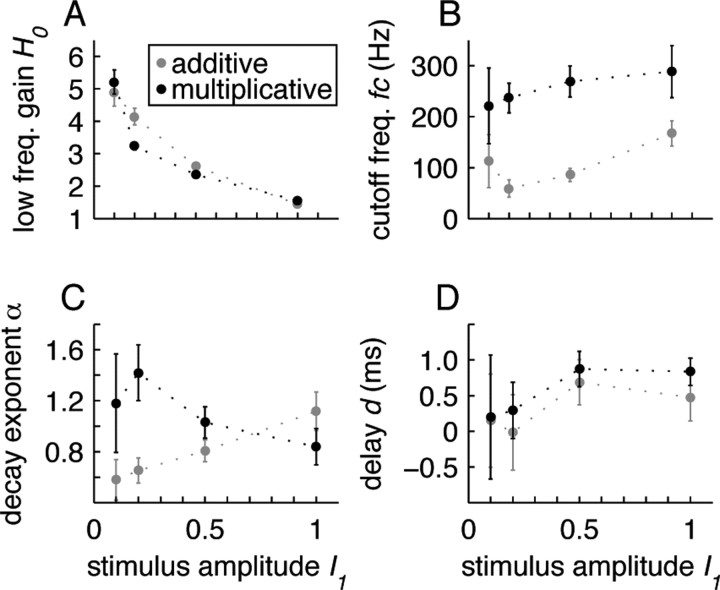
Figure 4.
Results of transfer function fit (cf. Eqs. 6, 7). Dependence of low-frequency gain H 0 (A), cutoff frequency f c (B), decay exponent α (C) and transmission delay d (D) on stimulus amplitude I 1 for additive (gray) and multiplicative (black) modulation. Data obtained from ensemble averaged transfer functions. Symbols indicate best-fit parameters. Error bars represent 68.2% confidence intervals.
Results
We assessed the transmission properties of an ensemble of cortical neurons in a moderately active regime, which allows for both an increase and a decrease of the firing rate. Since neocortical neurons in acute brain slices are usually not spontaneously active, we scaled the injected noisy currents appropriately to keep the average firing rates r 0 in a low narrow range (Fig. 1 B) (7 ± 3 spikes/s for additive modulation, 5 ± 3 spikes/s for multiplicative modulation). Throughout each trial, firing rates varied only little and were neither correlated with the stimulus amplitude I 1 nor the frequency f (data not shown).
The normalized response amplitudes r 1(f)/r 0(f) revealed low-pass characteristics for both the additive (Fig. 2) and the multiplicative modulation (Fig. 3). The fitted cutoff frequencies f c (cf. Eq. 6) were generally high and ranged from ∼60–300 Hz (Fig. 4 B). They were significantly higher for the multiplicative modulation (220 ± 70 Hz for I 1 = 0.1) compared with the additive modulation paradigm (110 ± 50 Hz for I 1 = 0.1) (Fig. 4 B). Overall, the cutoff frequencies increased with the stimulus amplitude I 1. For the largest amplitude (I 1 = 1.0) we observed f c = 290 ± 50 Hz for the multiplicative and f c = 170 ± 30 Hz for the additive modulation.
The comparison between the single cell response amplitudes (Figs. 2, 3, thin black lines) and the corresponding significance levels (Figs. 2, 3, thin gray lines) shows that for small stimulus amplitudes (I 1 = 0.1) individual cells could reliably track the stimuli up to frequencies of ∼200 Hz for both the additive (Fig. 2 A) and the multiplicative (Fig. 3 A) modulation scheme. For higher frequencies, the distribution of fitted amplitudes r 1 did not significantly differ from the one obtained from the surrogate spike data. Significant single cell responses at higher frequencies (f > 200 Hz) could only be observed for larger stimulus amplitudes I 1 (Figs. 2 B–D, 3 B–D). Population averaging can further increase the signal-to-noise ratio, provided noise correlations can be neglected (Zohary et al., 1994). At the population level, we find significant responses for the smallest modulation depth I 1 = 0.1 for frequencies <300 Hz (Figs. 2, 3, compare gray bands and thick gray lines). For multiplicative modulation with large modulation depths (I 1 = 0.5, 1.0), we observe reliable population responses up to 1 kHz. Note, that these data were obtained for a small population of N cells by averaging over many stimulus periods over a rather long, physiologically nonrelevant, time window of T = 50 s. One may ask how reliable a population of M cells can respond to a single stimulus period. If we assume that we can replace the time average (average over stimulus periods) by an ensemble average, we may associate the total number of periods M = N · f · T by the size of a hypothetical cell population. For I 1 = 0.1, for example, we obtained data from N = 7 cells. For a stimulus frequency of f = 300 Hz and a trial duration of T = 50 s, this accounts for an ensemble size of about M = 100,000. Our data suggest that even such large populations cannot reliably track weak (I 1 = 0.1) high-frequency (f > 300 Hz) stimuli. Increasing the ensemble size even further may lead to significant responses, but the biological relevance of this result would appear questionable. It is therefore necessary to consider larger stimulus amplitudes I 1 > 0.1.
With increasing stimulus amplitudes, it becomes more likely that the system leaves the linear regime, i.e., the response amplitudes r 1(f)/r 0(f) would not grow linearly with the stimulus amplitude I 1. Figure 4 A shows, indeed, that the low-frequency gain H 0 decreased with I 1, i.e., the amplitudes r 1(f)/r 0(f) grew sublinearly with I 1. For I1 > 0.2, this nonlinear behavior resulted at least partly from a rectification of the firing rates, because here the fitted response modulation depth r 1(f) exceeded the response offset r 0(f) for a broad frequency range (Figs. 2, 3).
For the additive modulation paradigm, our data analysis shows that the response amplitudes decay generally slower than 1/f at high frequencies: the decay exponent α (cf. Eq. 6) is smaller than 1 for small stimulus amplitudes I 1 (Fig. 4 C). It grows for increasing modulation depths and approaches 1 for I 1 = 1.0. If we restrict the analysis to frequencies <600 Hz, we obtain decay exponents close to 1 for all stimulus amplitudes (data not shown). If the stimulus modulates the variance of the noise rather than its mean, α is always close to 1. In the high-frequency limit, Fourcaud-Trocmé et al. (2003) and Naundorf et al. (2005) predicted a decay exponent α = 1 or larger. It is unclear, however, to which frequencies this limit actually applies. A comparison between these predictions with the exponent α measured here (in the frequency range up to 1 kHz) is, therefore, difficult.
At high frequencies f > 700 Hz, the phase φ(f) of the population averaged transfer function generally showed a linear decay, thereby indicating the presence of a constant time delay d. The fitted values of d (cf. Eq. 7) were in the range between 0 and 0.9 ms (Fig. 4 D) and did not significantly differ in the additive and the multiplicative modulation paradigm. These small delays can at least partly be explained by the time between the action potential onset and the spike detection threshold (0 mV).
Discussion
In the presence of transient stimuli, cortical neurons receive noisy input currents with modulations not only in the mean, but also in the variance of the noise. We have shown that ensembles of pyramidal cells exhibit low-pass characteristics for both additive and multiplicative modulation of the input noise. The observed cutoff frequencies are markedly high, considerably higher than the average firing rates. Moreover, we demonstrated that modulations in the noise variance can be tracked significantly faster than modulations in the mean input. Extremely fast stimuli (up to 1 kHz) can be reliably tracked, provided the stimulus amplitudes are sufficiently high.
The transmission properties of ensembles of neurons have been frequently discussed in previous theoretical and experimental studies. The majority of these studies focused on the transmission of signals superimposed by additive noise. For this additive stimulation paradigm, Köndgen et al. (2008) recently showed that ensembles of cortical neurons exhibit low-pass characteristics with high cutoff frequencies, thereby confirming the predictions of the theoretical studies of Fourcaud-Trocmé et al. (2003) and Naundorf et al. (2005): in contrast to simple linear integrate-and-fire models, neurons with continuous action-potential onset dynamics (like the quadratic or exponential integrate-and-fire neuron or conductance-based models) exhibit a finite tracking speed which crucially depends on the speed of the action-potential onset dynamics (see also Naundorf et al., 2006).
Modulations of presynaptic firing rates, however, affect not only the population averaged (mean) input current, but also its variance. Lindner and Schimansky-Geier (2001) pointed out that a population of leaky integrate-and-fire neurons can faithfully track signals at arbitrarily high frequencies, if the signal modulates the variance of a white-noise carrier, rather than its mean. According to Naundorf et al. (2005), neurons with finite action-potential onset speed exhibit low-pass behavior for both modulation schemes, independently of the time constant of the noise. The cutoff frequencies, however, are larger in the multiplicative case. Our results clearly confirm these predictions for colored noise and a variety of stimulus amplitudes. Similar results were obtained earlier by Silberberg et al. (2004) for white noise. While they used broad-band stimuli (steps, frozen noise), we performed a frequency resolved analysis. Measuring response amplitudes for each stimulus frequency separately allowed us to make a more direct comparison with the theoretically predicted transfer functions. For linear systems, the two approaches are equivalent. As we have shown, linearity can, however, not be guaranteed for stimulus amplitudes required to obtain significant responses.
Theoretical studies (Brunel and Hakim, 1999; Brunel et al., 2001; Lindner and Schimansky-Geier, 2001; Fourcaud and Brunel, 2002; Fourcaud-Trocmé et al., 2003; Naundorf et al., 2005) typically restrict the mathematical analysis of population responses to the linear regime, i.e., to the case of infinitely small stimulus amplitudes. By means of simulations, most of these studies have, however, shown that the linear response analysis correctly predicts population responses for a large range of amplitudes. For biologically relevant stimulus amplitudes (i.e., amplitudes which are large enough to elicit significant responses) we observed signs of nonlinearity: the response amplitudes grew sublinearly with the stimulus amplitude. Although the shape of the measured transfer functions changed for different stimulus amplitudes, the main features remained, however, qualitatively the same.
In the present study, we probed a rather small number of neurons (7–15 cells for each modulation depth). Conclusions on the response properties of large populations of layer V pyramidal cells were drawn by replacing the population average by a combination of an ensemble average (average over the small tested ensemble of cells) and a time average (average over many stimulus periods). This approach has often been used in the past (Knight, 1972b; Silberberg et al., 2004; Köndgen et al., 2008), but it has its limitations. An underlying assumption here is that the ensemble of tested cells can be considered as a representative subset. The role of heterogeneity in cell parameters may be underestimated. In the small ensemble of cells tested here, the variability across cells is relatively small (Figs. 2, 3, thin black lines). The transfer functions obtained from single cells by averaging over stimulus periods are qualitatively identical to those obtained by population averaging (Figs. 2, 3, thick black lines).
Footnotes
This work was partially supported by the German Federal Ministry of Education and Research (BMBF Grant 01GQ0420 to the Bernstein Center for Computational Neuroscience Freiburg), the European Union (EU Grant 15879, FACETS), and the Research Council of Norway (eVITA program). We thank Helena Gavrilova and Susanne Reichinnek for support with the experimental data acquisition.
References
- Boucsein C, Nawrot M, Rotter S, Aertsen A, Heck D. Controlling synaptic input patterns in vitro by dynamic photo stimulation. J Neurophysiol. 2005;94:2948–2958. doi: 10.1152/jn.00245.2005. [DOI] [PubMed] [Google Scholar]
- Brunel N, Hakim V. Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Comput. 1999;11:1621–1671. doi: 10.1162/089976699300016179. [DOI] [PubMed] [Google Scholar]
- Brunel N, Chance FS, Fourcaud N, Abbott LF. Effects of synaptic noise and filtering on the frequency response of spiking neurons. Phys Rev Lett. 2001;86:2186–2189. doi: 10.1103/PhysRevLett.86.2186. [DOI] [PubMed] [Google Scholar]
- Dodt HU, Zieglgänsberger W. Visualization of neuronal form and function in brain slices by infrared videomicroscopy. Histochem J. 1998;30:141–152. doi: 10.1023/a:1003291218707. [DOI] [PubMed] [Google Scholar]
- Fourcaud N, Brunel N. Dynamics of the firing probability of noisy integrate-and-fire neurons. Neural Comput. 2002;14:2057–2110. doi: 10.1162/089976602320264015. [DOI] [PubMed] [Google Scholar]
- Fourcaud-Trocmé N, Hansel D, van Vreeswijk C, Brunel N. How spike generation mechanisms determine the neuronal response to fluctuating inputs. J Neurosci. 2003;23:11628–11640. doi: 10.1523/JNEUROSCI.23-37-11628.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W. Population dynamics of spiking neurons: fast transients, asynchronous states, and locking. Neural Comput. 2000;12:43–89. doi: 10.1162/089976600300015899. [DOI] [PubMed] [Google Scholar]
- Horikawa K, Armstrong WE. A versatile means of intracellular labeling: injection of biocytin and its detection with avidin conjugates. J Neurosci Methods. 1988;25:1–11. doi: 10.1016/0165-0270(88)90114-8. [DOI] [PubMed] [Google Scholar]
- Knight BW. Dynamics of encoding in a population of neurons. J Gen Physiol. 1972a;59:734–766. doi: 10.1085/jgp.59.6.734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight BW. The relationship between the firing rate of a single neuron and the level of activity in a population of neurons. J Gen Physiol. 1972b;59:767–778. doi: 10.1085/jgp.59.6.767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Köndgen H, Geisler C, Fusi S, Wang XJ, Lüscher HR, Giugliano M. The dynamical response properties of neocortical neurons to temporally modulated noisy inputs in vitro . Cereb Cortex. 2008;18:2086–2097. doi: 10.1093/cercor/bhm235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindner B, Schimansky-Geier L. Transmission of noise coded versus additive signals through a neuronal ensemble. Phys Rev Lett. 2001;86:2934–2937. doi: 10.1103/PhysRevLett.86.2934. [DOI] [PubMed] [Google Scholar]
- Naundorf B, Geisel T, Wolf F. Action potential onset dynamics and the response speed of neuronal populations. J Comput Neurosci. 2005;18:297–309. doi: 10.1007/s10827-005-0329-8. [DOI] [PubMed] [Google Scholar]
- Naundorf B, Wolf F, Volgushev M. Unique features of action potential initiation in cortical neurons. Nature. 2006;440:1060–1063. doi: 10.1038/nature04610. [DOI] [PubMed] [Google Scholar]
- Silberberg G, Bethge M, Markram H, Pawelzik K, Tsodyks M. Dynamics of population rate codes in ensembles of neocortical neurons. J Neurophysiol. 2004;91:704–709. doi: 10.1152/jn.00415.2003. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science. 1996;274:1724–1726. doi: 10.1126/science.274.5293.1724. [DOI] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, Newsome WT. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature. 1994;370:140–143. doi: 10.1038/370140a0. [DOI] [PubMed] [Google Scholar]