Embedding Multiple Trajectories in Simulated Recurrent Neural Networks in a Self-Organizing Manner

Abstract

Complex neural dynamics produced by the recurrent architecture of neocortical circuits is critical to the cortex's computational power. However, the synaptic learning rules underlying the creation of stable propagation and reproducible neural trajectories within recurrent networks are not understood. Here, we examined synaptic learning rules with the goal of creating recurrent networks in which evoked activity would: (1) propagate throughout the entire network in response to a brief stimulus while avoiding runaway excitation; (2) exhibit spatially and temporally sparse dynamics; and (3) incorporate multiple neural trajectories, i.e., different input patterns should elicit distinct trajectories. We established that an unsupervised learning rule, termed presynaptic-dependent scaling (PSD), can achieve the proposed network dynamics. To quantify the structure of the trained networks, we developed a recurrence index, which revealed that presynaptic-dependent scaling generated a functionally feedforward network when training with a single stimulus. However, training the network with multiple input patterns established that: (1) multiple non-overlapping stable trajectories can be embedded in the network; and (2) the structure of the network became progressively more complex (recurrent) as the number of training patterns increased. In addition, we determined that PSD and spike-timing-dependent plasticity operating in parallel improved the ability of the network to incorporate multiple and less variable trajectories, but also shortened the duration of the neural trajectory. Together, these results establish one of the first learning rules that can embed multiple trajectories, each of which recruits all neurons, within recurrent neural networks in a self-organizing manner.

Introduction

Complex neural dynamics produced by the recurrent architecture of neocortical circuits is critical to the cortex's computational properties (Ringach et al., 1997; Sanchez-Vives and McCormick, 2000; Wang, 2001; Vogels et al., 2005). Rich dynamical behaviors, in the form of spatiotemporal patterns of neuronal spikes are observed in vitro (Beggs and Plenz, 2003; Shu et al., 2003; Johnson and Buonomano, 2007) and in vivo (Wessberg et al., 2000; Churchland et al., 2007; Pastalkova et al., 2008), and have been shown to code information about sensory inputs (Laurent, 2002; Broome et al., 2006), motor behaviors (Wessberg et al., 2000; Hahnloser et al., 2002), as well as memory and planning (Euston et al., 2007; Pastalkova et al., 2008). Although it is clear that the neural dynamics that emerges as a result of the recurrent architecture of cortical networks is fundamental to brain function, relatively little is known about how recurrent networks are set up in a manner that support computations, yet avoid pathological states, including runaway excitation and epileptic activity. Particularly, what are the synaptic learning rules that guide recurrent networks to develop stable and functional dynamics? Traditional learning rules, including Hebbian plasticity, spike-timing-dependent plasticity (STDP), and synaptic scaling, have been primarily studied in the context of feedforward networks, or at least in networks that do not exhibit significant temporal dynamics.

It is well established that randomly connected recurrent neural network models can exhibit chaotic regimes (van Vreeswijk and Sompolinsky, 1996; Brunel, 2000; Banerjee et al., 2008) when driven by continuous Poisson inputs. In response to simple external inputs, such as a brief activation of a subset of the neurons in the network, randomly connected neural networks generally lead to unphysiological behavior, including runaway excitation, or what has been termed a “synfire explosion” (Mehring et al., 2003; Vogels et al., 2005). One difference between many of the simulations and biological networks relates precisely, to the random connectivity. Structural analyses (Song et al., 2005; Cheetham et al., 2007) and the universal presence of synaptic learning rules (Abbott and Nelson, 2000; Dan and Poo, 2004) indicate that network connectivity is not random, but rather sculpted by experience. A few studies have incorporated STDP into initially random recurrent networks and analyzed the dynamics driven by spontaneous background activity (Izhikevich et al., 2004; Izhikevich and Edelman, 2008; Lubenov and Siapas, 2008). And, Izhikevich (2006) has shown that STDP coupled with long synaptic delays can be used to generate reproducible spatiotemporal patterns of activity within recurrent networks.

Experimental studies using organotypic cortical slices have shown that during the first week of in vitro development, a brief stimulus does not lead to any propagation, but at later stages stimulation elicits spatiotemporal patterns of activity lasting up to a few hundred milliseconds (Buonomano, 2003; Johnson and Buonomano, 2007). Here, we sought to examine the learning rules that could lead to this type of evoked propagation. STDP is not effective, in part because it requires the presence of spikes to be engaged, and in part because it inherently shortens the propagation time of neural trajectories. Previous studies showed that a form of homeostatic plasticity, synaptic scaling, generates stable evoked patterns in feedforward networks (van Rossum et al., 2000), but is unstable in recurrent networks (Buonomano, 2005; Houweling et al., 2005). A modified form of synaptic scaling termed presynaptic-dependent scaling (PSD), however, was shown to guide initially randomly connected neural networks to develop stable dynamic states in response to a single input stimulus (Buonomano, 2005). Here, we establish that PSD can embed more than one neural trajectory in a network, and that as the number of embedded trajectories increases so does network recurrency. This is one of the first learning rules that accounts for the generation of multiple patterns—each of which engages all neurons—in recurrent networks in a self-organizing manner.

Materials and Methods

All simulations were performed using NEURON (Hines and Carnevale, 1997).

Neuron dynamics.

Excitatory (Ex) and inhibitory (Inh) neurons were simulated as single compartment integrate-and-fire neurons. As described previously, each unit contained a leak (E_L= −60 mV), afterhyperpolarization (E_AHP= −90 mV), and noise current. Ex (Inh) units had a membrane time constant of 30 (10) ms. Spike thresholds were set from a normal distribution (σ² = 5%), with means of −40 and −45 mV, for Ex and Inh units, respectively. When threshold was reached, V was set to 40 mV for the duration of the spike (1 ms). At offset, V was set to −60 and −65 mV for the Ex and Inh units, respectively, and a afterhyperpolarization conductance (g_AHP) was activated and decayed with a time constant 10 (2) ms for the Ex (Inh) units. Whenever a spike occurred, there was a stepwise increment of g_AHP = 0.07(0.02) mS/cm² for the Ex (Inh) units at spike offset.

Synaptic currents.

Two excitatory (AMPA and NMDA) and one inhibitory (GABAa) current were simulated using a kinetic model (Destexhe et al., 1994; Buonomano, 2000; Lema et al., 2000). Synaptic delays were set to 1.4 ms for excitatory synapses and 0.6 ms for inhibitory synapses. The ratio of NMDA to AMPA weights was fixed at g_NMDA = 0.6 g_AMPA for all excitatory synapses. Short-term synaptic plasticity was incorporated in all synapses as modeled previously (Markram et al., 1998; Izhikevich et al., 2003). Specifically, the Ex→Ex synapses exhibited depression, U = 0.5, τ_rec = 500 ms, τ_fac = 10 ms; Ex→Inh synapses exhibited facilitation, U = 0.2, τ_rec = 125 ms,τ_fac = 500 ms; and Inh→Ex synapses exhibited depression (Gupta et al., 2000), U = 0.25, τ_rec = 700 ms, τ_fac = 20 ms. It should be noted that while short-term plasticity was incorporated, its presence was not critical to the results described here.

Presynaptic-dependent synaptic scaling.

We used a modified homeostatic synaptic scaling rule, termed presynaptic-dependent scaling (Buonomano, 2005) as follows:

Where W_ij^τ represents the synaptic weight from neuron j to i at trial τ. α_W is the learning rate (0.01), and A_goal is the target activity (mean number of spikes per trial); set to 1 for Ex cells and 2 for Inh cells. A_i^τ is the average activity of neuron i at trial τ, given by the following:

in which α_A = 0.05 defined across-trial integration of activity. Therefore, learning dynamics and neural dynamics were coupled via S^τ, the number of spikes in the τth trial for each cell. In the present study the duration of a trial was 250 ms, and in between trials all state variables were considered to have decayed back to their initial values. This scheme for trial-based learning dynamics was used since the time scale of homeostatic plasticity and neural activation is not agreed upon (Buonomano, 2005; Fröhlich et al., 2008).

Spike-timing-dependent plasticity.

STDP was implemented in a multiplicative form (van Rossum et al., 2000):

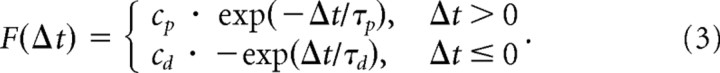Where Δt = t_post−t_pre. The above function was used for Ex→Ex synapse pairs. Here, we used the following: τ_p = 20 ms, τ_d = 40 ms, c_p = c_d = 0.0001. Synaptic weights modified by STDP were updated as follows:

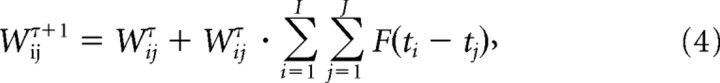where J was the number of spikes for neuron j and I the number of spikes for neuron i in the τth trial, and t_j and t_i the respective spikes times.

Output layer.

The output layer consisted of five IAF neurons that received inputs from all Ex neurons of the network. Each output unit was trained to fire at one of the randomly assigned target times: 20, 40, 60, 80, and 100 ms. Each output unit was randomly assigned one of the target times, resulting in different random sequences of five elements. Synaptic weights were adjusted using a simple supervised learning rule: if a presynaptic neuron fired at the target time (actually a time window equal to the target time ± 10%) its synapse onto the corresponding target output unit was potentiated (assuming the output neuron did not fire). If the output neuron fired outside the target window and the presynaptic neuron fired, that synapse was depressed. Training of the output units consisted of the presentation of 170 trials, and 30 trials were used to test the performance. A performance value of p = 1 means that each motor neuron fired at its correct target time window for all 30 test trials.

Neural trajectories in state space.

To visualize the different neural trajectories in neuron state space, we used principal component analysis to reduce the dimensionality of the network state. This analysis relied on the average activity (the PSTH of each Ex unit; see Fig. 6) over 200 trials after training. The data were normalized and the principal components were calculated using the PROCESSPCA function in MATLAB 2007a.

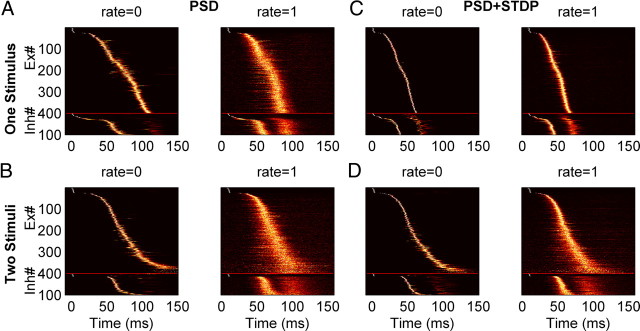
Figure 6.

Sensitivity to background spiking noise with different learning rules. A–D, Neurograms of the trajectories produced by training with one (A, C) and two stimuli (B, D) averaged over 200 posttraining trials. Each line represents the normalized PSTH of a single unit. Simulations were performed without spontaneous spiking activity (rate = 0) or with spontaneous spikes (1 Hz Poisson noise). Neurograms show the increased jitter in the presence of noise [performance: (A) p = 0.99 (left), p = 0.49 (right); (C) p = 0.6 (left), p = 0.57 (right); (B) p = 0.87 (left), p = 0.32 (right); (D) p = 0.92 (left), p = 0.45 (right)]. Compared with PSD, the neural trajectories of networks trained with PSD+STDP were more robust because they exhibited less jitter.

Network structure analysis.

To analyze the network structure, two measures were used: efficiency (E) and the recurrence index (RI). Efficiency was defined as follows:

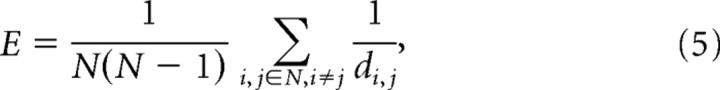where N was the number of Ex cells and d_ij was the shortest path from neuron i to neuron j. In a binary graph, in which all weights were equal, the distance corresponds to minimal path length. In a weighted graph the distance between nodes 1 and 3 through path 1→2→3 corresponds to the following:

Thus, a longer path with stronger weights can be more efficient than a shorter path with weaker weights (Boccaletti et al., 2006). The following is an instance:

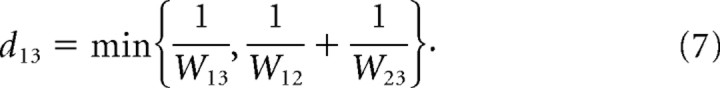Dijkstra's algorithm was used to calculate the shortest path for a graph, and the Brain Connectivity Toolbox was used to calculate efficiency (http://www.indiana.edu/∼cortex). The recurrence index (RI) is conceptually related to E, but takes the perspective of each synapse, specifically as follows:

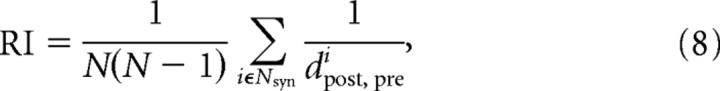where N_syn was the number of synapses within the network, d_{post, pre}ⁱ was the shortest length from the postsynaptic neuron of synapse i back to its presynaptic neuron. Here, the shortest path in RI was defined as the binary path.

Input stimulus patterns.

The stimuli consisted of 24 and 12 randomly selected Ex and Inh neurons, respectively, that fired at 0 ± 1 ms (mean ± SD) following a Gaussian distribution, thus only a small subset of neurons fired at the beginning of each trial. Qualitatively similar results were obtained when the SD of the Gaussian time window was increased. We used a small SD to simulate a brief highly synchronous input to the network (Mehring et al., 2003).

Model parameters and initial conditions.

Unless stated otherwise, all simulations were performed using a network with 400 Ex units and 100 Inh units connected with a probability 0.12 for Ex→Ex, and 0.2 for both Ex→Inh and Inh→Ex, which results in each postsynaptic Ex unit receiving 48 inputs from other Ex units, and 20 inputs from Inh units; each postsynaptic Inh unit received 80 inputs from Ex units. Initial synaptic weights were chosen from a normal distribution with the mean as W_EE = 2/48 nS, W_EI = 1/80 nS and W_IE = 2/20 nS, respectively. The SD of the distributions were σ_EE = 2W_EE, σ_EI = 8W_EI and σ_IE = 2W_IE. If the initial weights were nonpositive, they were reset to a uniform distribution from 0 to twice the mean. To avoid the induction of unphysiological states in which a single presynaptic neuron fired a postsynaptic neuron, the maximal Ex→Ex AMPA synaptic weights were W_EE^max = 1.5 nS except as stated in Figure 6. The maximal Ex→Inh AMPA synaptic weights were set as W_EI^max = 0.4 nS. All inhibitory synaptic weights were fixed. All simulations were done with a time step Δt = 0.1 ms.

Results

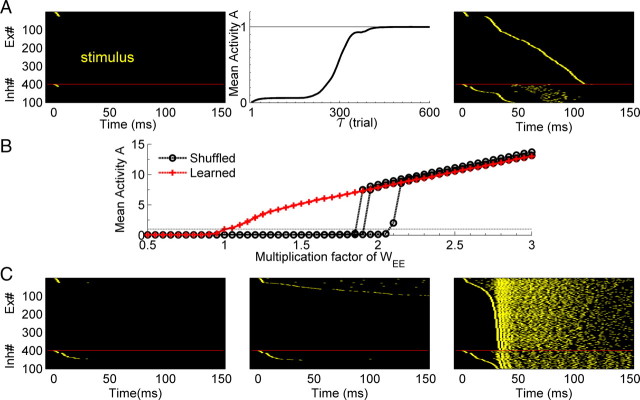
We used an artificial neural network composed of 400 Ex and 100 Inh integrate-and-fire units. As described in Materials and Methods, the connection probability between Ex neurons was 12%, and each unit contained an independent noise current. The network was driven by a brief stimulus at t = 0 that consisted of a single spike in 24 Ex and 12 Inh units. As observed during early development (Muller et al., 1993; Echevarría and Albus, 2000), the initial weights of the recurrent network were weak and thus not capable of supporting any network activity—that is, the input stimulus did not elicit any propagation (Fig. 1A, left). Training consisted of hundreds of presentations of the input stimulus in the presence of the PSD learning rule (Eq. 1). Like synaptic scaling, PSD will increase the weights onto a postsynaptic neuron that has a low level of average activity across trials (see Materials and Methods). In contrast to synaptic scaling however, PSD will preferentially potentiate synapses from presynaptic neurons that have a higher average activity rate across the preceding trials. As shown in Figure 1A (middle panel), over the course of training PSD guides the network to a stable state, where each neuron's activity within one trial reached the target level of one spike per trial. Thus, as a result of training, a stable neural trajectory lasting ∼120 ms emerged (Fig. 1A, right). Throughout this paper we will use the term neural trajectory to refer to the spatiotemporal pattern of activity observed in the network. Specifically, the trajectory is defined by the path network activity takes through N-dimensional state space (where N equals the total number of cells). Note that in general, every neuron in the network participates in each trajectory.

Figure 1.

PSD creates stable propagation of activity. A, Left, In the initial state a brief stimulus does not produce network activity because of the weak synaptic weights. Middle, The mean activity of the network over all Ex neurons converges to the target level (one spike/trial) after training with PSD over hundreds of trials. Right, The pattern of activity (the neural trajectory) to which the network converged to during training (Ex and Inh units fired once and twice per trial, respectively). Units were sorted by their latency. B, Mean activity as a function of synaptic strength of trained matrix (unshuffled, red), and shuffled weight matrices (black). The x-axis reflects the gain factor by which the weight matrices were multiplied. The shuffled case shows a sharp transition, whereas the trained case shows a linear increase in activity. Each red line is a simulation with a different random seed, and each black line results from shuffling the matrix of one of the red line simulations. There are three overlapping red lines. The dashed line is the target activity, A = 1. C, Three examples of the raster plots of a shuffled matrix: left, multiplication factor = 1; middle, ×2; right; ×3. Only the weights of Ex→Ex synapses are shuffled. Raster plots are sorted by the latency of the spike time (the first spike for Inh neurons).

To determine the importance of the precise structure of the weight matrix between the Ex neurons, compared with the contribution of the mean weights and their statistical distribution, we shuffled the synaptic weight matrix and examined the network response to the same input. As expected, shuffled weights produced no network activity (Fig. 1C, left). We next progressively scaled the shuffled Ex→Ex matrix. A scale factor of 2 resulted in suprathreshold activity in a few neurons (Fig. 1C, middle), a factor of 3 produced runaway excitation (Fig. 1C, right). The average number of spikes per neuron as a function of the scaling of the weight matrix is shown in Figure 1B; a sharp transition occurs between low activity and “explosive” regimes, suggestive of a phase transition where the scaling factor represents an order parameter. In contrast, when the weights of the nonshuffled matrix were scaled, activity increased in a fairly linear manner (Fig. 1B). These results indicate that the learning generated dynamics was specific to the structure of the network, and not a result of the statistical properties of the weight matrix, such as the mean synaptic weights.

Training with two stimuli produces two distinct neural trajectories

Biological recurrent neural networks can generate multiple distinct neural trajectories in response to different stimulus patterns (Stopfer et al., 2003; Broome et al., 2006; Durstewitz and Deco, 2008; Buonomano and Maass, 2009). Thus we next examined whether PSD could embed more than one neural trajectory by training it with two input patterns.

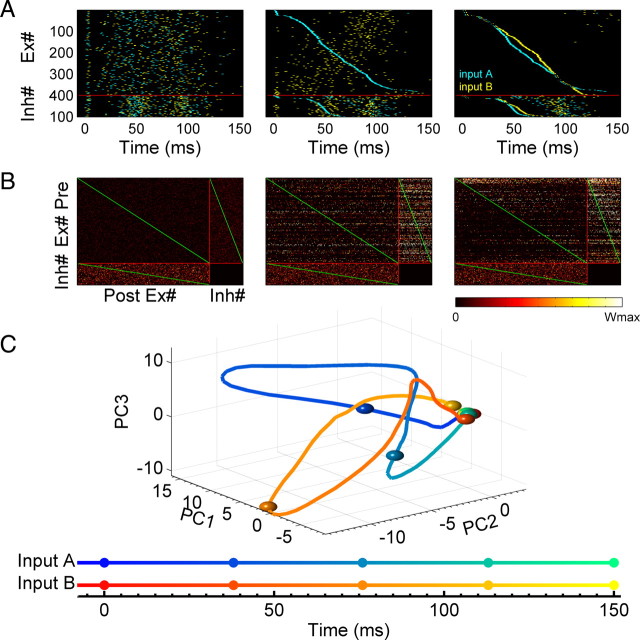
Each of the two input patterns were composed of a subset of randomly selected Ex and Inh units, which as above fired as a brief “pulse.” Every “block” consisted of a sequence of two trials, and within a block this sequence of stimuli was presented in each trial, but in random order. As shown in Figure 2A, training resulted in the emergence of two distinct neural trajectories within the network (see Movie in supplemental material, available at www.jneurosci.org). Specifically, each of the two input patterns elicited a distinct spatiotemporal pattern of activity—a behavior that requires the presence of functional recurrent connections. The fact that both trajectories were distinct can be visualized by sorting the units according the spike latency generated by one or both of the patterns (Fig. 2A, middle and right panels). The initial and final weight matrices are shown in Figure 2B. When sorted by spike latency one can see that the upper triangle blocks of Ex→Ex and Ex→Inh have stronger weights than the lower triangles; reflecting a functional feedforward structure within the recurrent network. However, one can also see the presence of significant recurrent structure (recurrence is quantified below). The two distinct neural trajectories can also be visualized using principle component analysis to reduce the high dimension state space into three-dimensional (3D) space (Fig. 2C); both trajectories start from the same location at t = 0, but traveled through different regions of state space before returning to the initial rest state ∼120 ms later.

Figure 2.

Two distinct neural trajectories are produced by training the network with two stimuli. A, Raster plots of unsorted (left), sorted by input A (middle) and by both inputs separately (right) after training with two different input patterns (cyan: input A; yellow: input B) presented at t = 0. B, The corresponding weight matrix before and after training. Initial weights are weak (left); weights after training (middle); weight matrix sorted using neural indexes from the middle of A (right) for both presynaptic and postsynaptic neurons. The weights in the upper triangle blocks of the Ex→Ex and Ex→Inh connections are stronger than those in the lower triangle blocks. The red line divides the matrix into three matrices: Ex→Ex, Ex→Inh, Inh→Ex. The green lines establish a visual reference of the diagonal of the matrices. The color bar shows the range of weights from zero to their maximum. The submatrices are normalized by the maximum weight of each type of synapse: AMPA for Ex→Ex and Ex→Inh, GABAa for Inh→Ex connections. Only excitatory synapses are plastic, GABAa synapses are fixed. The Inh→Inh block is empty since there are no Inh→Inh synapses. C, Two neural trajectories (solid line: input A; dashed line: input B) averaging 200 trials are visualized in the PCA-reduced 3D network state space. Both trajectories start at the same initial point and rapidly diverge, until returning to the initial state.

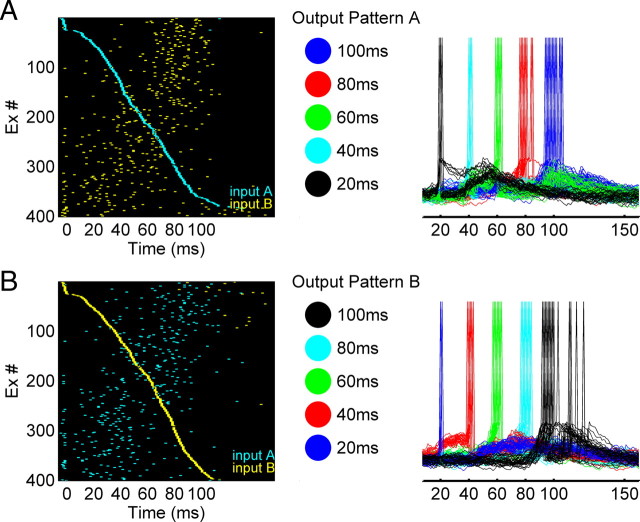
The trajectories observed above allow neural networks to generate complex spatiotemporal output patterns in response to different stimuli. To quantify this ability we can think of the recurrent circuit as a premotor network and add a small number of output neurons, each of which receives input from all the Ex units in the recurrent network. We asked whether it is possible to use distinct neural trajectories to generate different spatiotemporal output motor patterns. To answer this question, we used a supervised learning rule to train the output units to fire in a specific temporal sequence (see Materials and Methods)—note that we are using a supervised learning rule to train the output units as a method to study the behavior of the recurrent network, not necessarily because it reflects biologically plausible mechanisms, or a plausible mechanism to decode temporal information (Buonomano and Merzenich, 1999). The output layer was composed of five integrate-and-fire units. As shown in Figure 3, input pattern A generated an output A′ (O₁→O₂→O₃→O₄→O₅), while input B generated the output pattern B′: O₅→O₄→O₃→O₂→O₁ (one could think of these patterns as five fingers playing a specific sequence of notes on a keyboard). The transformation of the neural trajectories into a simpler output pattern facilitates the quantification of the robustness of the neural trajectories, and provides a measure of how well these trajectories could be used by downstream neurons for motor control. We defined a performance measure (P) as the percentage of spikes of all five output neurons that occurred at the target time window (±10%), such that p = 1 corresponds to the optimal performance (see Materials and Methods). Thus, P can be used to quantify both the reproducibility of the neural trajectories in the recurrent network, as well as how this information could be used to generate precise motor output patterns.

Figure 3.

Different trajectories can drive multiple spatiotemporal patterns in output neurons. A, Trajectory A drives output neurons to generate output pattern A'. Raster plots of two trajectories (cyan: input A; yellow: input B) sorted by the trajectory A (left); output pattern A in which five output neurons fire at different times (middle); voltage traces of the output neurons show that they fire at their target time during the test trials (right). B, Similar to A, trajectory B drives the same five output neurons to generate a different spatiotemporal output pattern B'. Raster plots of same two trajectories sorted by trajectory B (left); the reversed temporal patterns from that in A was used as the target (middle and right).

STDP improves the embedding of multiple trajectories

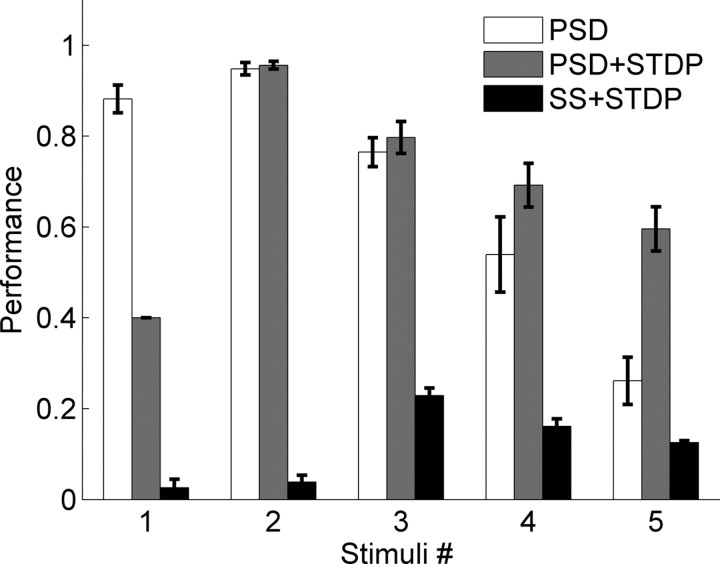
We next examined and quantified the ability of the network to learn 1–5 different patterns. Figure 4(open bars) shows the mean performance of the network after training with PSD across different numbers of input stimuli—above 4 patterns performance falls close to 0.5. Much of this decrease was a result of increasing jitter and the high variability across trials, particularly of the spikes late in the sequence. Thus, it seemed that a learning rule which further strengthened the synapses between neurons that were being sequentially activated would be beneficial in decreasing this variability, and improving performance. To test this hypothesis we incorporated both PSD and STDP into the network (Abbott and Nelson, 2000; Karmarkar et al., 2002; Dan and Poo, 2004). PSD+STDP resulted in a significant improvement in performance, particular in the five-stimulus case, reflecting less variable neural trajectories across trials. There was however a tradeoff; as expected, STDP tended to shorten the time span over which the trajectory unfolds, because strengthening the sequentially activated synapses decreases spike latency. This was the cause of the decreased performance when the network was trained on only one stimulus (note the first gray bar in Fig. 4). Specifically, there was a well embedded trajectory, however it was over in <50 ms, and thus output spikes cannot be generated at the 60, 80 and 100 ms time points. Interestingly, in the PSD+STDP condition, performance was dramatically better when the network was trained with two inputs compared with one. We also included stimulations with conventional synaptic scaling (SS) (van Rossum et al., 2000) and STDP, which resulted in poor performance independent of the number of stimuli. Note that we did not examine the performance of STDP alone in the current study, because, guided by our developmental experimental data (Johnson and Buonomano, 2007) the initial synaptic weights were very weak and incapable of eliciting spiking activity, and since STDP requires spikes, analyses of STDP alone would require an additional set of assumptions.

Figure 4.

Performance with and without STDP when training with different number of stimuli. When training with more than one stimulus, performance in networks trained with PSD or PSD+STDP decreased with increasing stimulus number. Additionally, for >4 stimuli performance was higher in networks trained with PSD+STDP. We also examined performance using traditional SS and STDP. Error bars represent the SEM, and were calculated from 10 simulations with different random seeds. A two-way ANOVA over the multiple stimuli conditions (2–5) reveled a significant interaction between number of stimuli and the presence or absence of STDP (F_(3,72) = 5.3, p = 0.002).

Parameter robustness and sensitivity to random spikes

The above results show that PSD can embed multiple neural trajectories in recurrent networks. However, an important question is how dependent are these results on the parameters used in the simulations, and how robust is performance in response to increased levels of noise. We examined these issues by (1) parametrically varying the connection probability P_EE and the maximal excitatory synaptic weight of the Ex→Ex connections (W_EE^max); and (2) adding background Poisson activity.

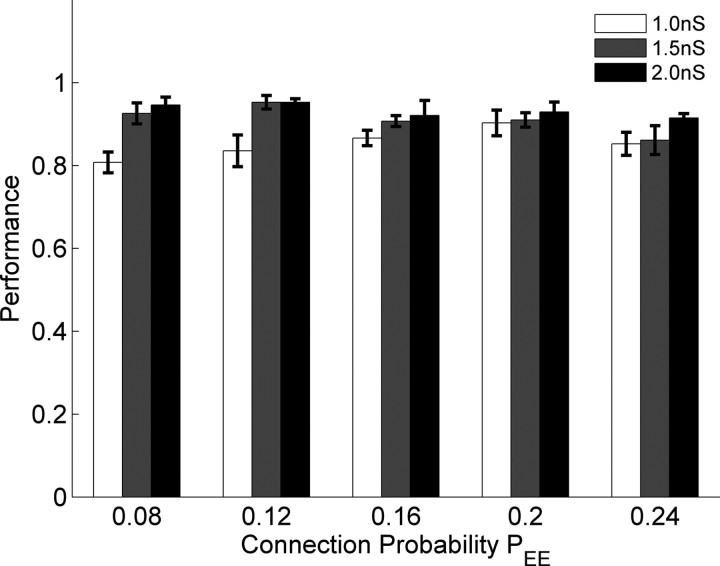
Physiologically, the strength of excitatory synapses exhibits an upper bound. Generally the strength of a single connection between any two Ex neurons is well below threshold, and thus many presynaptic neurons must cooperate to fire a postsynaptic cell (Markram et al., 1997; Koester and Johnston, 2005). In the above simulations the maximal Ex→Ex weight was W_EE^max = 1.5 nS, a value that required at least 2 synchronous excitatory inputs in the absence of any inhibition to fire a postsynaptic cell. Figure 5 shows the network performance after training with two stimuli and the PSD learning rule while both W_EE^max and P_EE were varied. The overall performance was larger than 80% for all parameters. Performance was slightly lower when W_EE^max = 0.8 nS and P_EE was small. Performance was fairly robust to the variations of P_EE, particularly given that the conservative experimental estimate of connectivity between pyramidal neurons is 10% (Mason et al., 1991; Holmgren et al., 2003; Song et al., 2005).

Figure 5.

Performance in response to different parameter values. With W_EE^max values of 1, 1.5, and 2nS, performance was robust over different connection probabilities (P_EE). Error bars represent the SEM calculated from 10 simulations with different random seeds. Data were obtained with training with two stimuli and PSD.

All of the above simulations included a current that injected independent noise into each unit. While this current induced fluctuations in the membrane voltage and was responsible for the jitter seen across trials it did not elicit spikes by itself. Thus we next examined performance in the presence of additional random spiking activity. We added background Poisson activity during the training and testing of the network. Figure 6 shows a typical neurogram after training the network with one stimulus (Fig. 6A,C) or two stimuli (Fig. 6B,D) in presence of 0 (“control”) or 1 Hz Poisson noise. With PSD alone, training without random spikes (Fig. 6, rate = 0) resulted in a small degree of jitter of the neural trajectories; the introduction 1 Hz noise, however, induced a significant increase in jitter as evidenced by the width of the diagonal band. Since STDP further enhanced the synaptic strength of sequentially activated neurons, the PSD+STDP condition was less sensitive to the presence of 1 Hz background activity. These results suggest that STDP may play an important role in creating robust noise-insensitive neural trajectories, even though it may not initially underlie their actual formation.

Network structure analysis

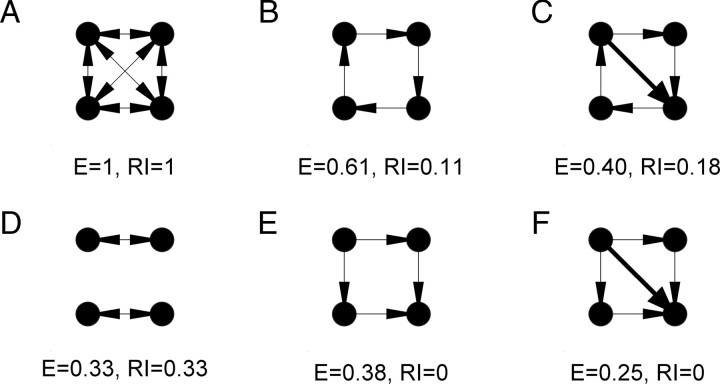
Training with different numbers of stimuli resulted in qualitatively different behavior, specifically, multiple embedded trajectories. Thus, we next asked: what is the structural difference between networks trained with different numbers of stimuli? Visual inspection of the weight matrices trained with one stimulus reveal that they function primarily in a feedforward mode—i.e., an initially recurrent network with weak random weights, became a functionally feedforward network after training. However, when multiple trajectories were present, it was clear that some degree of recurrence is necessary, because each neuron participated in more than one trajectory. To analyze and quantify the structure of the trained networks we used two measures to characterize the weight matrix: E and RI. Both measures were based on the mathematical description of neural networks as a directed graph (see Materials and Methods). Efficiency is a generalization of the standard measure of the shortest path of the graph, which takes into account the connection weight to describe the average shortest length between any two nodes of a network (Boccaletti et al., 2006). While this is a useful measure it does not directly capture what many neuroscientists mean when they refer to recurrence, which relates to the ability of a neuron to “loop back” upon itself. For example, the efficiency in a feedforward network can be larger than that in a network with some degree of recurrence (even if the number of synapses is the same, Fig. 7E vs D). Thus, we introduced the RI measure, which was based on the shortest directed path it took an individual synapse to return to itself. As illustrated using simple networks in Figure 7A, both efficiency and RI are 1 in a fully connected network, however, in contrast to efficiency, RI will always be zero in a feedforward architecture (Fig. 7E,F).

Figure 7.

Examples of the efficiency and RI measures using simple networks. Arrows indicate the direction of synaptic connections from pre- to postsynaptic neurons. Note that E decreases from B to C, and E to F, because the weights are normalized to the maximum. Assigned weights are equal to 1 and 2, for the thin and thick lines, respectively.

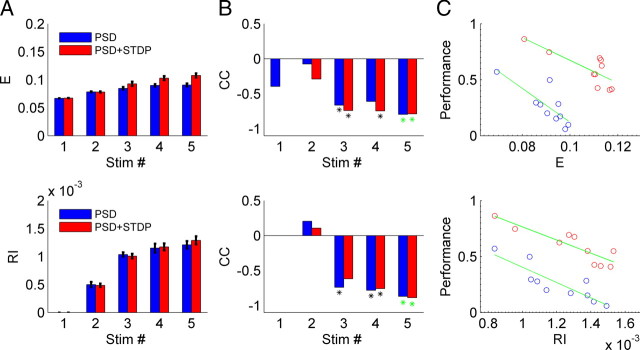
We first analyzed the mean efficiency and RI in networks trained with 1–5 inputs. Both the efficiency and RI increased with the number of training patterns (Fig. 8A), and as expected the RI was close to 0 when the network was trained with a single pattern, consistent with the notion that this network was essentially a feedforward one. This implies that the network structure becomes more complex when multiple stimuli are presented. Specifically, when the same network was trained with different number of stimuli, it became structurally more complex—even though the “skeleton” of the synaptic connections remained the same—because the initial connectivity patterns were the same for a given simulation random number generator seed.

Figure 8.

Network recurrence increases with increasing number of stimuli and is inversely correlated with the performance. A, Both E and RI increase as the number of stimuli used to train the network increases – independently of whether PSD (blue) or PSD+STDP (red) was used. B, Correlation coefficients between E and RI and the performance for a given stimulus number are negative. The asterisk represents a significant correlation (p < 0.05). The green asterisks indicate the data shown in C. C, An example of the data for the correlations shown in B. E (top) or RI (bottom) are plotted against performance for networks trained with five stimuli. The green line represents the linear fit of the 10 points, each of which represents a simulation with different random seeds.

Even for a given number of training stimuli performance of a network varied significantly depending on the random “seed” chosen to build the network, that is, on the relationship between which units were physically connected and the chosen input patterns. For example, for a PSD+STDP simulation using 5 stimuli, performance could range from ∼0.5 to 0.9 (Fig. 8C, y-axis). Correlation coefficients (CC) between the performance and the structural indices, calculated using 10 replications with different random number generator seeds, established that there was an inverse relationship. When the stimulus number was three or more, this relationship was significant (Fig. 8B). Thus, while the higher degree of recurrence was observed when multiple trajectories were embedded, each trajectory was less robust with higher degrees of recurrence.

Discussion

Our results demonstrate how simple synaptic learning rules can lead to the embedding of multiple neural trajectories in a recurrent network in a self-organizing manner. Analysis of the structure of the network revealed that, depending on the number of stimuli used during training, qualitatively different configurations emerged. Recurrence increased as a function of the number of input stimuli used for training. However, for a given number of input patterns, the networks ability to reliably generate multiple trajectories was inversely related to the degree of recurrence.

Neural dynamics in recurrent networks

It is widely accepted that the recurrent architecture of neural networks is of fundamental importance to the brain's ability to perform complex computations. First, the generation of complex spatiotemporal patterns of action potentials that underlie motor behavior is assumed to rely on the recurrent nature of motor and premotor cortical circuits (Wessberg et al., 2000; Hahnloser et al., 2002; Churchland et al., 2007; Long and Fee, 2008). Second, it has been proposed that many forms of sensory processing rely on the interaction between incoming stimuli and the internal state of recurrent networks (Mauk and Buonomano, 2004; Durstewitz and Deco, 2008; Rabinovich et al., 2008; Buonomano and Maass, 2009). However, relatively little progress has been made toward understanding how cortical circuits generate and control neural dynamics. Most studies of neural dynamics within recurrent networks have focused on the dynamic behavior of networks in which the weights are randomly assigned (in the absence of synaptic learning rules), and activity is driven by spontaneous background activity as opposed to transiently evoked external inputs representing sensory stimuli (van Vreeswijk and Sompolinsky, 1996; Brunel, 2000; Mehring et al., 2003). Depending on the strength of recurrent connections and the relative balance between excitation and inhibition, these networks typically exhibit a number of regimes including complex irregular and asynchronous activity, which resembles in vivo patterns of spontaneous activity (Brunel, 2000). It has been proposed that regimes near where these networks exhibit phase transitions similar to that shown in Figure 1B (Haldeman and Beggs, 2005) are optimal for storage capacity and dynamics, however, how such regimes would be achieved has not been clear. Mehring and colleagues have shown that recurrent networks tend to exhibit the “explosive” type of behavior shown in Figure 1C, when they were stimulated with a brief external stimulus (Mehring et al., 2003). A later study showed that it was possible to embed two neural trajectories with a randomly connected recurrent network in a manual manner, that is, when the synaptic weights were explicitly assigned between subgroups of neurons in a feedforward manner (Kumar et al., 2008). While controlling dynamics and adjusting the weights of synapses in recurrent networks remains a fundamental challenge, it should be pointed out that theoretical studies have shown that even recurrent networks with random weights can be used to perform functional computations (Buonomano, 2000; Medina and Mauk, 2000; Maass et al., 2002), and that carefully controlling the feedback from output units into the recurrent network offers a promising way to control dynamics in the absence of synaptic plasticity within the recurrent network (Jaeger and Haas, 2004; Maass et al., 2007).

Synaptic learning rules in recurrent networks

Traditional learning rules such as STDP (Song et al., 2000; Song and Abbott, 2001), and synaptic scaling (van Rossum et al., 2000) have been studied primarily in feedforward networks (and/or networks that do not exhibit temporal dynamics). A number of recent studies have incorporated synaptic learning rules into networks driven by spontaneous activity and shown that in some cases stable firing rates or spike patterns can be observed (Renart et al., 2003; Izhikevich et al., 2004; Izhikevich, 2006; Izhikevich and Edelman, 2008; Lubenov and Siapas, 2008). One synaptic learning rule that would appear to be well suited to guide network dynamics to stable dynamical regimes is synaptic scaling (van Rossum et al., 2000). However, it has been previously shown that, when recurrent networks are driven by transient synaptic activity, synaptic scaling is inherently unstable (Buonomano, 2005), and can underlie repeating pathological burst discharges (Houweling et al., 2005; Fröhlich et al., 2008). Additionally, a number of experimental studies have shown that while synapses may be up or downregulated in a homeostatic manner, this form of plasticity does not always obey synaptic scaling (Thiagarajan et al., 2005, 2007; Goel and Lee, 2007). Interestingly, feedforward and recurrent networks may exhibit fundamentally different forms of homoeostatic plasticity; Kim and Tsien (2008) reported that while inactivity increases the strength of CA3→CA1 (feedforward) synapses, the same was not true in CA3→CA3 (recurrent) synapses. Consistent with the theoretical studies cited above, it was suggested that this difference was related to the fact that synaptic scaling could contribute to the induction of epileptic like activity. The reason synaptic scaling is unstable in recurrent networks is precisely because the ratio of all the synaptic strengths onto a given postsynaptic neuron is constant (i.e., they are scaled). The presynaptic-dependent scaling rule used here relies on a modification of the conventional synaptic scaling rule in which the postsynaptic neuron preferentially changes the weight of those presynaptic neurons that have high average (cross-trial) levels of activity. We have shown that this learning rule can lead to multiple neural trajectories within recurrent networks. PSD by itself, however, is limited in its ability to embed multiple neural trajectories and in the sensitivity of these trajectories to noise. Interestingly, PSD together with STDP generated more robust neural trajectories, Thus, in this framework STDP played an important role in tuning or “burning in” the trajectories generated by PSD, but was not actually necessary for their formation.

Biological plausibility of PSD and experimental predictions

While distinct from the traditional description of homeostatic plasticity in the form of synaptic scaling (van Rossum et al., 2000), PSD is nevertheless a extension of synaptic scaling that includes a term that captures the average levels of presynaptic activity. Consequently, PSD predicts that not all synapses will be scaled equally, rather that those synapses from presynaptic neurons that have higher average rates of activity will be increased more than others. It is important to note that this prediction is not inconsistent with the current experimental findings that support synaptic scaling. Specifically, for the most part these studies have relied primarily on global pharmacological manipulations that would be expected to the level of activity of all neurons equally (Turrigiano et al., 1998; Karmarkar and Buonomano, 2006; Goel and Lee, 2007). Under these conditions synaptic scaling and presynaptic-dependent scaling are essentially equivalent since the presynaptic term in Equation 1 will on average be the same for all synapses.

The experimentally testable prediction generated by PSD is that if during a global decrease in activity, some neurons nevertheless exhibit higher than average levels of activity, the synapses from these neurons will be preferentially potentiated. This prediction could be tested in a number of ways. First, partially blocking network activity with glutamatergic antagonists, while electrically or optically stimulating a subset of neurons in the network. Second, it has been shown that overexpressing a delayed rectifier potassium channel causes cells to exhibit decreased activity (Burrone et al., 2002), PSD predicts that coupled with partial activity blockade these cells would on average would generate weaker synapses onto postsynaptic neurons.

Implicit in the notion synaptic of scaling, PSD, or any other form of homeostatic plasticity, is that cells must be able to track their average levels of activity over windows of minutes or hours to trigger synaptic and cellular mechanisms to upregulate or downregulate activity. The mechanisms that allow neurons to do this remain unidentified, but it is suggested that this may be accomplished by Ca²⁺-sensors with long integration times (Liu et al., 1998), and that activity-dependent changes in the release of growth factors, such as BDNF and TNFα, may signal changes in neuronal activity levels (Stellwagen and Malenka, 2006; Turrigiano, 2007).

Network recurrency

In recent years there has been an increased interest in understanding the relationship between network structure and the functional properties of networks. These analyses have been performed in the context of mathematical graph theory of complex networks (Sporns et al., 2004), where a number of measures have been developed to characterize the degree of complexity of neural networks from the viewpoint of the small-world network topology (Watts and Strogatz, 1998; Bassett et al., 2008), and network motifs analysis (Sporns and Kötter, 2004). Most of these studies have focused on binary networks, that is, connections between nodes are either present or absent. Some recent studies, however, have began to address more complex networks as directed weighted graphs (Boccaletti et al., 2006), which is particularly important for neural networks. To date, however, few studies have attempted to relate the architecture of recurrent neural networks with their neural dynamics. The efficiency measure used in the present study relates to the “interconnectedness” and complexity of networks (Latora and Marchiori, 2001) (Fig. 8). We also introduced a new measure, the recurrence index, which provides a more direct measure of what neuroscientists refer to as recurrence. As with efficiency, the RI could be modified to incorporate the weights of the synaptic connections, however, in the current study we used a threshold of 25% of the maximum value to generate a binary representation of the network.

In our study both the efficiency and RI measures generated similar conclusions, although we find the RI measure is more meaningful. For example it insures a value of zero for a feedforward network. The RI measure revealed that when trained on a single stimulus, the network was essentially functionally feedforward. However, the complexity of the networks, as well their RI, increased with the number of trained stimuli and embedded trajectories. Furthermore, there was a significant variation in network structure, revealed by E and RI, over different replications (i.e., different random number generator seeds). The fact that the efficiency and RI were inversely correlated with performance within an experimental condition indicates that these measures, do indeed, capture a fundamental property of network structure.

Future directions

Two important issues that should be addressed in future studies relate to the trajectory capacity and the maximal time intervals that can be encoded in these trajectories. The capacity of the network was fairly low (Fig. 4), only 4 or 5 trajectories in a network of 500 units. We speculate that incorporation of inhibitory plasticity, which was absent in our simulations, may play an important role in embedding a larger number of trajectories and thus the capacity of these networks. Additionally, it is important to note that each trajectory recruits every neuron in the network, that is, each trajectory was of length N. While this number is on the same order of some theoretical estimates (Herrmann et al., 1995), others have shown that networks of similar size can generate thousands of trajectories; however, in this case each was of length on the order of 10 neurons (Izhikevich, 2006). Indeed, an important question relates to the numbers of neurons that participate in a given trajectory. While this issue remains to be resolved it appears that in some cortical areas, such as premotor cortex, it is indeed the case that a large percentage of local neurons participate in the production of a given motor pattern (Moran and Schwartz, 1999; Churchland et al., 2006).

The time span of each trajectory was also relatively short, between 100 and 200 ms. This is the time scale of the evoked neural patterns observed in vitro (Buonomano, 2003; Beggs and Plenz, 2004; Johnson and Buonomano, 2007). It is clear, however, that in vivo the generation of longer neural trajectories is critical for many types of timing and motor control. Future studies must examine how longer trajectories emerge in a self-organizing manner. It has been suggested that the inclusion of longer, yet experimentally derived, synaptic delays (Izhikevich, 2006), or that appropriately controlling feed-back within recurrent networks (Maass et al., 2007), may play a critical role in allowing recurrent networks to generate long-lasting patterns of activity. Additionally, it is possible that the recurrent structure of cortical networks are composed of embedded feedforward architectures, that are better suited for encoding trajectories lasting on the order of seconds (Ganguli et al., 2008; Goldman, 2009).

Undoubtedly, the brain relies on a number of synaptic learning rules operating in parallel to control and generate neural trajectories within recurrent networks. It is likely that many of these rules remain to be elucidated both at the experimental and theoretical level. However, the results described here demonstrate that PSD is capable of leading to stable dynamical behavior in recurrent networks in a unsupervised manner. Furthermore, the trajectories capture some of the features observed in in vitro cortical networks (Buonomano, 2003; Beggs and Plenz, 2004; Johnson and Buonomano, 2007).