Rod Phototransduction Determines the Trade-Off of Temporal Integration and Speed of Vision in Dark-Adapted Toads

Abstract

Human vision is ∼10 times less sensitive than toad vision on a cool night. Here, we investigate (1) how far differences in the capacity for temporal integration underlie such differences in sensitivity and (2) whether the response kinetics of the rod photoreceptors can explain temporal integration at the behavioral level. The toad was studied as a model that allows experimentation at different body temperatures. Sensitivity, integration time, and temporal accuracy of vision were measured psychophysically by recording snapping at worm dummies moving at different velocities. Rod photoresponses were studied by ERG recording across the isolated retina. In both types of experiments, the general timescale of vision was varied by using two temperatures, 15 and 25°C. Behavioral integration times were 4.3 s at 15°C and 0.9 s at 25°C, and rod integration times were 4.2–4.3 s at 15°C and 1.0–1.3 s at 25°C. Maximal behavioral sensitivity was fivefold lower at 25°C than at 15°C, which can be accounted for by inability of the “warm” toads to integrate light over longer times than the rods. However, the long integration time at 15°C, allowing high sensitivity, degraded the accuracy of snapping toward quickly moving worms. We conclude that temporal integration explains a considerable part of all variation in absolute visual sensitivity. The strong correlation between rods and behavior suggests that the integration time of dark-adapted vision is set by rod phototransduction at the input to the visual system. This implies that there is an inexorable trade-off between temporal integration and resolution.

Introduction

In vision as in photography, discrimination of objects in dim light can be improved by prolonging the exposure time (i.e., summing photon traces over longer intervals), but this advantage is bought at the expense of temporal resolution. Under strict serial processing, information sacrificed at one stage is irretrievably lost. Only by investing in parallel channels with different temporal properties is it possible to circumvent such obligate trade-offs. Because the responses of the primary input neurons, the photoreceptor cells, set absolute limits for performance in any visual task, most vertebrates invest in parallel photoreceptor systems to deal with the very different optimizations faced in dim and bright light. Rods set up a large but slow signal in response to each photon; cones (usually of several spectral classes) give smaller but faster single-photon responses. In very dim light, cones are generally useless and vision relies entirely on rods.

When studying fundamental constraints on performance, interspecies comparisons are generally illuminating. The sensitivity of the toad is 10-fold higher than that of humans for detection of an extended, moving object at night (Aho et al., 1988, 1993a). This is thought to depend on two factors, both of which are partly connected with the low natural body temperature of the toad. One is low thermal noise in the retina, implying that relatively small numbers of captured photons can provide sufficient signal-to-noise ratios (Baylor et al., 1980; Donner, 1989a). The other factor assumed to be important is extended temporal integration of photon signals.

In this work, we provide direct evidence that temperature-dependent temporal integration is a key factor for the high absolute visual sensitivity of toads. We then proceed to identify the neural stage that determines the integration time. Assuming that it resides in the retina (cf. Aho et al., 1993a,b), we distinguish two main possibilities with different consequences for other aspects of vision: (1) temporal integration is set at the very first stage, by rod phototransduction, which will necessarily limit all other temporal aspects of rod-mediated vision; (2) it is set by postreceptoral processing resulting in particularly long integration times in at least some ganglion cells at the retinal output. Rod responses could then be “faster” and allow vision at higher temporal frequencies, mediated by other types of ganglion cells.

We measured temporal properties of visual responses at the behavioral “output” and the rod “input” levels of toad vision. The general timescale was manipulated by using two different experimental temperatures (15 and 25°C). A close agreement was found between the two levels, suggesting that temporal integration in the task studied is determined by the kinetics of rod responses. Current evidence on the relationship between temporal properties of human rod vision and rod photoreceptors is inconclusive, but consistent with the idea that the dark-adapted integration time is constrained by rod kinetics.

Materials and Methods

Animals

Toads (Bufo bufo) were caught in the autumn in southern Finland. They were kept in hibernating conditions until late March next year, after which they were transferred to terrariums at 15–20°C with natural light/dark cycle (∼14/10 h) and access to dark shelters. In the terrariums, the toads were fed mealworms ad libitum overnight twice a week except at the time of experiments when they were only given one worm after each experiment. The time between experiments varied from 1 d to 1 week, so at the time of experiments toads were always hungry, but not starving.

Use and handling of the toads were in accordance with the Finnish Animal Welfare Act of 1986 and with the guidelines of the Animal Experimentation Committee of the University of Helsinki.

Behavioral experiments

The experiments were performed in the daytime. A toad that had been dark-adapted overnight was placed in the snapping chamber (Larsen and Pedersen, 1982; Aho et al., 1988, 1993a) in a dark room. The toad was moving freely in a black plastic box with an 80-mm-wide transparent window of antireflex glass in the floor. One millimeter beneath the floor, over a background of black cardboard, white worm dummies (3 × 12 mm) made of plastic tubing attached to a black string were driven by an electric motor at different velocities. Only one dummy was visible at a time. The snapping box was illuminated by a 20 W halogen lamp through an interposed matte plastic diffuser screen and a 525 nm interference filter placed 120 cm above the toad. The intensity was controlled with calibrated neutral density filters.

A toad was removed from the box as soon as it had snapped four times or after a maximum of 3 min to avoid habituation after unsuccessful snapping. The snapping process was watched on a video monitor by a second experimenter sitting behind black screens. The sessions were video recorded in their entirety and for each snap the tongue hit position relative to the worm was measured from the video images. Snaps at dummies that were partly disappearing from the window were not included in the study.

The video camera was a black-and-white Panasonic WV-BL600 sensitive to wavelengths from 400 to 1000 nm provided with a zoom objective M6Z1212. The system recorded 50 frames/s, each covering 4 ms. Infrared light for video recording came from a separate 20 W halogen lamp (maximum emission, ∼900 nm) provided with a Schott RG edge filter transmitting wavelengths >850 nm. Although no significant effect on the toad's snapping threshold at 15°C caused by this infrared illumination was found, it will contribute a quantal background noise, estimated to be of approximately the same order of magnitude as that from spontaneous thermal rhodopsin activations. The consensus estimate for the rate of discrete “dark” events in Bufo bufo rods at 15°C is ∼0.013 Rh*s⁻¹ (Fyhrquist et al., 1998; Firsov et al., 2002). Applying the temperature dependence measured in Bufo marinus rods by Baylor et al. (1980), the rate is expected to be ∼0.05 Rh*s⁻¹ at 25°C. Calculation of photoisomerization rates in rods in the toad's eye because of the infrared light (>850 nm) contains large uncertainties. Some inevitable, although very small, reflection of 525 nm photons even from the antireflex glass floor should also be considered. Our best estimates for the background rate of photoisomerizations lie between the 15 and 25°C rates of thermal isomerizations.

The ambient temperature was adjusted to either 15 or 25°C. In separate measurements with a thermocouple attached to the scalp between the eyes, it was confirmed that the temperature of the toad in this region was very close to the ambient temperature.

Snapping threshold.

For each worm velocity at both experimental temperatures, a frequency of seeing function was obtained by calculating the percentage of “positive” sessions at each of five to six different light intensities spanning 4 log units from ∼3 × 10⁻⁴ to 3 Rh*s⁻¹. A “positive” session was one in which the toad snapped at least once (during the maximal session duration of 3 min). The percentages of positives in all sessions pooled across one condition (i.e., combination of temperature, worm velocity, and light intensity) were plotted as functions of log light intensity and connected by straight lines. Threshold was taken as the intensity at which the curve thus obtained crossed the 50% snapping level.

Error estimates for the thresholds in Figure 2 were obtained as follows. In most cases, the data consisted of several sets of sessions in the same condition conducted on different days. The result (the percentage of positive sessions) from each day was considered as one independent value. For the experiments at 15°C, frequency-of-snapping functions were then plotted separately for every possible combination of single-day percentages at a given velocity, and for each of these frequency-of-snapping functions the 50% threshold was determined. The error bars associated with the 15°C data points in Figure 2 are the SEMs of all thresholds thus obtained at the given velocity. At 25°C, almost all sessions gave either 0 or 100% snapping and other outcomes were obtained only at two of the intermediate velocities. Thus, the uncertainty of the threshold determination at this temperature is directly evident from the variability of the five “warm” data points in Figure 2 and no error bars have been plotted.

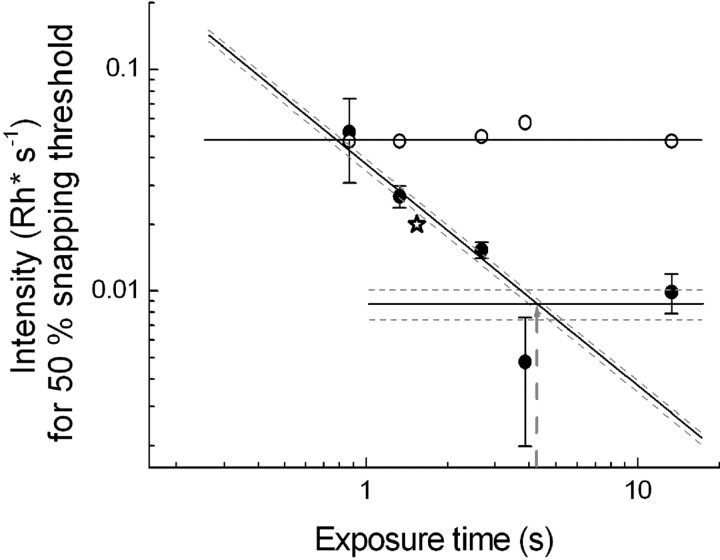
Figure 2.

Behavioral integration times estimated from the dependence of snapping thresholds on exposure time at 15°C (solid symbols) and 25°C (open symbols). A 45° straight line has been fitted by a least-squares criterion to the four 15°C data points (weighted in inverse proportion to the error bars) at which thresholds decrease with increasing exposure time. The intersection of this line and the horizontal straight line fitted by a least-squares criterion to the two lowest data points (weighted in inverse proportion to the error bars) gives the integration time at 15°C (shown by a gray dashed arrow). The dashed lines give SDs for the line fits, and taking the farthest intersection points of these as error limits, the 15°C integration time is 4.3 ± 0.9 s. The integration time at 25°C (open circles) is ≤0.87 s (i.e., at least fivefold shorter). The open star shows for comparison a threshold determined at 15°C with a 3 × 20 mm dummy moving at the speed 13.8 mm/s, indicating that the results are not sensitive to moderate changes in the spatial parameters of the stimulus.

Exposure time.

Temporal integration was determined as a “critical duration” of the stimulus. For toad snapping, this cannot be measured as the duration of square-wave light pulses (as for rods and in human psychophysics), because toads snap only at moving prey. Instead, the velocity of the dummy was varied, and stimulus duration was taken as the time for which any given retinal point under the trajectory of the dummy was illuminated. This was termed “exposure time,” calculated as the length of the dummy (in millimeters) divided by its velocity (in millimeters per second).

Woodlouse observations

To relate the laboratory observations to the timescale that a hunting toad encounters in nature, we measured the speed of woodlice Porcellio scaber, a common prey item, as function of temperature. The woodlice were moving on a relatively smooth horizontal bark surface at 10, 15, and 25°C in very weak illumination. The time taken to traverse a distance of 100 mm was recorded in 10 runs each of 10 individuals (mean body length, 15 mm).

Electroretinogram recordings

Animals.

The toads used in the electrophysiological experiments came from the same population and had been kept in similar conditions as those used in the behavioral experiments.

Preparation and recording.

Dark-adapted toads were decapitated and double-pithed, and retinas were isolated under dim red light in cooled Ringer's solution. The isolated retina was mounted in a specimen holder (Donner et al., 1988) with the photoreceptor side upwards. A flat circular area (diameter, 2.0 mm) was exposed to perpendicularly incident stimulus light and was continuously superfused (∼1.4 ml/min) with Ringer's solution containing the following (in mm): 111.3 Na⁺, 2.5 K⁺, 1.5 Mg²⁺, 1.0 Ca²⁺, 113.0 Cl⁻, 10.0 glucose, 0.01 EDTA, 12.0 HEPES. The solution was buffered to pH 7.5 (at room temperature). Leibovitz culture medium L-15 (Sigma-Aldrich) (0.72 mg/ml) was added to improve the viability of the retina and sodium-l-aspartate (2 mm) to block synaptic transmission to second-order neurons. In addition, BaCl₂ (10 mm) was added in the lower electrode space, from where it would diffuse into the retina to suppress glial currents by blocking potassium channels located mainly at the end feet of Müller cells (Donner and Hemilä, 1985; Newman, 1989; Nymark et al., 2005). The temperature at the retina was controlled by a heat exchanger below the specimen holder and monitored with a thermistor in the bath close to the retina (Ala-Laurila et al., 2002).

The transretinal potential was recorded over the effective circular measurement area with two Ag–AgCl electrodes, one in the space under the retina and the other in chloride solution connected to the perfusion Ringer's through a porous plug. The DC signal was amplified 10,000 times, digitized at 200 Hz, and stored on a computer hard disk for additional analysis. Homogeneous full-field illumination was provided by a dual-beam optical system (Donner et al., 1988). The light source was a 543.5 nm He–Ne laser (Melles Griot 05 LGR 173; 0.8 mW). The light intensity was controlled with calibrated neutral density wedges and filters. The 20 ms pulses of stimulus light (“flashes”) were provided by a computer-controlled Compur shutter.

Experimental protocol.

Recording was started after the isolated retina had recovered from the dissection and adapted for 1–2 h in darkness. Likewise, before starting measurements after a temperature change, the retina was allowed to adapt in darkness for 1–2 h. The experimental temperatures were 15 and 25°C. Rod response families to 20 ms flashes of increasing intensity (covering the dynamic range of the rods) and responses to dim light pulses of successively increasing duration (from 20 ms up to even 25,000 ms) were recorded. In the latter type of recordings, stimulus intensity was reduced as duration was increased so as to keep the responses within the linear response range. Finally, a range was reached at which the intensity needed to elicit a linear-range response of criterion amplitude (∼10% of the saturating amplitude) stayed constant independent of increasing pulse duration. By accurate mapping of the range at which the stimulus intensity needed for a criterion response changed inversely to stimulus duration and the range at which it was duration independent, we could determine the integration time as a “critical duration,” in analogy with psychophysics (see Fig. 5).

Figure 5.

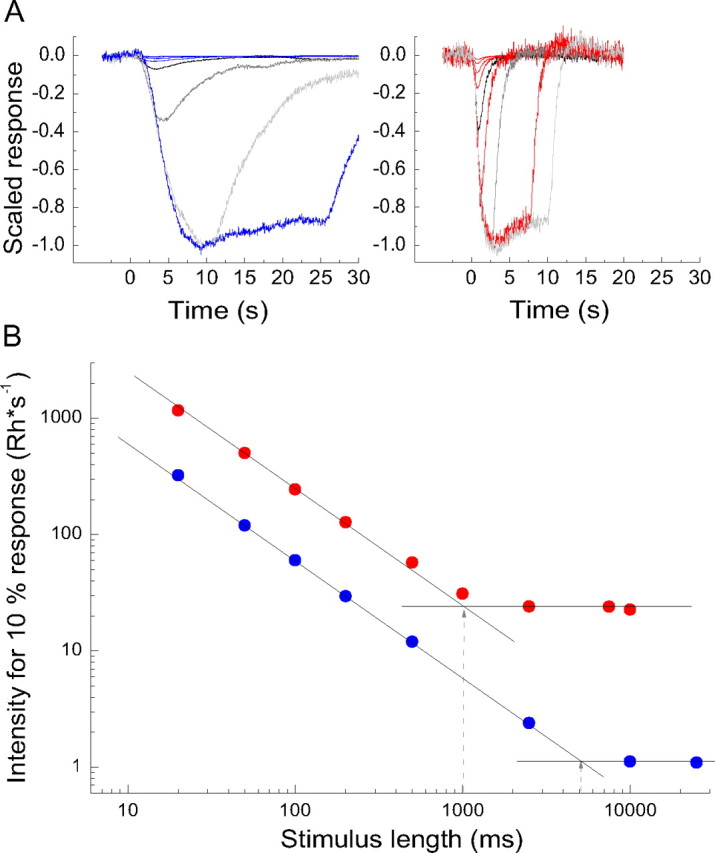
A, Linear-range responses (averages of 3 single responses) to square-wave light pulses of different durations recorded at 15°C (left panel) and at 25°C (right panel). In the figure, the responses have been scaled by the inverse value of the stimulus intensity (Rh*s⁻¹) used in each case and then normalized to unity peak amplitude of the largest response. The duration of the light pulse was 20, 50, 100, 200, 500 ms (black trace), 1000 ms (only at 25°C), 2500 ms (dark gray trace), 7500 ms (only at 25°C), 10,000 ms (light gray trace), and 25,000 ms (only at 15°C). B, Log light intensity (Rh*s⁻¹) needed to evoke responses with peak amplitude of 10% of the saturated rod response amplitude, plotted as function of log pulse duration; data from the same retina as the responses in A. A 45° straight line has been fitted by a least-squares criterion to the red (25°C) and blue (15°C) data points for shorter pulse durations, at which thresholds decreased with increasing pulse length. The points of intersection of the 45° lines and the horizontal straight lines for each set of data (shown by gray dashed arrows) show the critical durations.

Analysis of the dim-flash responses.

Responses to dim, brief (20 ms) flashes were fitted with the “independent activation” multistage filter model of Baylor et al. (1974, 1979) as follows:

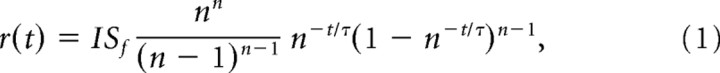where r(t) is the response, I is flash intensity (in photons per square micrometer), S_f is flash sensitivity [in microvolts/(photons per square micrometer)], n is the number of stages (here n = 4), and τ is the general time constant of the response. The model fits were used to estimate the integration time (t_i) (Baylor and Hodgkin, 1973) as follows:

where r(t) gives the temporal waveform of the response (Eq. 1) and r_peak is the amplitude at the peak of the response. Substituting r(t) from Equation 1 into Equation 2 and performing the integration gives t_i as follows:

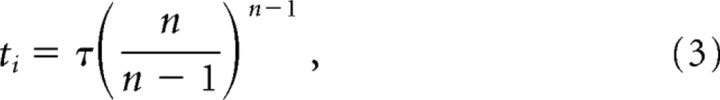Equation 3 allows the integration time to be calculated from the directly observable parameter time-to-peak (t_p) by substituting for τ the following expression:

Calibration of light intensities in terms of photoisomerization rates (Rh*s⁻¹) in rods

ERG recordings.

The absolute intensity of the unattenuated laser beam (photons per square millimeter per second incident on the retina) was measured in each experiment with a calibrated photodiode (EG&G HUV-1000B; calibration by the National Standards Laboratory of Finland). Conversion into photoisomerizations per rod per second (Rh*s⁻¹) was done as described by Aho et al. (1993a). For Bufo bufo of the same population as used here, they concluded that 34% of incident 525 photons cause isomerizations in rods. Recalculated for the stimulus wavelength used in the ERG experiments (λ_stim = 543.5) according to the Govardovskii et al. (2000) template (A1 pigment, λ_max = 501.4), this corresponds to 27% (or 40% at λ_max).

Behavioral experiments.

The retinal isomerization rates produced by the white worm dummies in the snapping experiments were calculated as described by Aho et al. (1988, 1993a). The unattenuated 525 nm light illuminating the arena was measured with a calibrated Airam UVM-8 radiometer and the reflectance of the white plastic surface of the dummies by a LOMO SF-10 spectrophotometer with magnesium oxide as white reference. The surface was assumed to act as a perfectly diffuse reflector. The photoisomerization rate in rods covered by the image of the dummy was estimated by calculating the acceptance angle of the pupil (based on the toad's viewing distance and pupil size determined from photographs in frontal projection) and the size of the retinal image based on a model eye, with correction for corneal reflection (Aho et al., 1988, 1993a). Under unattenuated illumination, the photoisomerization rate in each rod under the image of the dummy was thus estimated to be 200 Rh*s⁻¹.

Results

Snapping thresholds

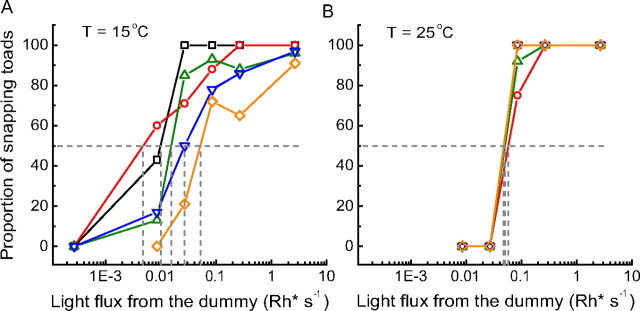
Figure 1 summarizes the results of the behavioral experiments, A for 15°C (denoted “C” for “cold”) and B for 25°C (denoted “W” for “warm”). In both panels, the abscissa gives log light intensity in terms of retinal illumination over the area covered by the image of the worm dummy in units of photoisomerizations per rod per second (Rh*s⁻¹). The ordinate gives the fraction of sessions in which the toad snapped at least once. Each curve (identified by one symbol type connected by straight lines of one color) refers to experiments with one worm velocity.

Figure 1.

Fraction of sessions in which toads snapped at least once toward the worm dummy plotted as function of light intensity at 15°C (A) and 25°C (B). Each symbol type and color represents results from experiments with one worm velocity: 0.9 mm/s (black squares), 3.1 mm/s (red circles), 4.5 mm/s (green upward triangles), 9.0 mm/s (blue downward triangles), and 13.8 mm/s (yellow diamonds).

In all situations, the fraction of sessions in which the toad snapped shows a practically monotonic increase with increasing light intensity (two single data points in the C experiments being the sole exceptions). All curves except one reach 100% snapping in the brightest illumination tested. Together, these observations indicate that prey visibility rather than some inherent velocity preference determines the inclination of the toads to snap in this range of experimental parameters. Threshold in each situation was defined as the intensity at which the curve crosses the 50% snapping level. A qualitative difference between C and W data is immediately evident. Whereas the curves for all worm velocities are virtually superimposed at 25°C, at 15°C they are spaced over a wide interval on the log intensity axis, so that the curve for the lowest velocity spans a much lower range of light intensities than that for the highest velocity. In other words, cool toads were able to benefit from the longer exposures afforded by slower worms, whereas warm toads were not.

This can be seen more clearly in Figure 2, in which the 50% snapping thresholds are plotted (on logarithmic scales) against the time for which any retinal point traversed by the image of the worm was exposed. The W thresholds (open circles) stay practically constant all the way from the shortest exposure time tested (0.87 s). In contrast, the C thresholds are highest at the shortest exposure time and fall with increasing exposure time (lower worm velocity). In a certain interval, a 45° straight line fits the data quite well, indicating full reciprocity between light intensity and exposure time, often referred to as “complete temporal summation” (I × t = constant) (Barlow, 1953). In this range, detection depends only on the number of photons collected, not on their temporal distribution. With additional increases in exposure time, a limit is reached at which threshold intensity no longer changes. In Figure 2, a horizontal straight line, representing the assumption that threshold is independent of exposure time, has been fitted by a least-squares criterion to the two lowest threshold intensities (weighted in inverse proportion to the error bars). The point of intersection of the 45° and horizontal lines gives the “critical duration,” a conventional psychophysical measure of temporal integration. At 15°C (solid circles), the critical duration is 4.3 ± 0.9 s; at 25°C, it is ≤0.87 s, because prolonging the exposure time beyond this did not lower threshold. Although it could in principle be shorter, it is in fact likely to be close to 0.87 s, because at that value W and C thresholds approximately coincide.

The regular behavior of thresholds seen in Figure 2 also gives support to the underlying assumption that the experiments really isolate “exposure time” as a simple threshold-determining variable. In principle, there might have been several confounding factors (e.g., if the toads had shown some velocity preference or if spatiotemporal interactions had entered as a variable that differed between velocities). We had made a rough test of such possibilities in pilot experiments in which similar exposure times were achieved with different combinations of dummy length and velocity. No spatial effects were detected. In Figure 2, a threshold carefully determined with a 3 × 20 mm dummy moving at the maximum speed (13.8 mm/s) has been plotted as a star. This threshold for a 67% longer worm providing an exposure time of 1.45 s is in line with the rest and near that for exposure time of 1.33 s produced by the 12 mm worm moving at a slower speed.

The slopes of frequency-of-seeing curves together with the threshold intensities (Figs. 1, 2) are in principle informative, on one hand, of the amount of noise integrated with the signal in each situation and, on the other hand, of the criterion for detection (signal-to-noise ratio or signal amplitude) (Barlow, 1956). At any given 50% threshold, the amount of noise summed with the signal will be reflected in the steepness of the frequency-of-seeing curve, a noise increase making the curve shallower, a noise decrease making it steeper. The C curves in Figure 1 are affected by too much experimental variability to allow reliable comparison of their slopes. However, the W curves seem to be systematically steeper than the C curves, including those for the shortest exposure time, at which W and C thresholds were the same. This suggests that less noise is summed with the signal at 25°C, implying that the integration time for noise as well as signal shortens with warming. Moreover, the fair fit of the 45° line to the 15°C data for short-to-medium exposure times suggests that threshold depends mainly on signal amplitude, whether or not the amount of noise summed with the signal varies with exposure time.

These observations underscore that the threshold data in Figure 2 are not consistent with any purposeful “optimization” of temporal integration (e.g., in terms of signal/noise). It would certainly have been useful for the warm toad to have as long integration times as the cool toad has: the advantage in visual sensitivity would have been similar, and a warm toad would not be less successful than a cool (slower) toad in catching a worm moving at any given speed. Yet the warm toad never integrated over more than ∼0.9 s. Its failure to do so suggests that temporal integration is mechanistically limited by some distal stage in the visual system. We hypothesized that the dominant constraint is the kinetics of rod photoresponses.

Rod responses

The ERG mass rod response recorded across the intact, isolated retina (see Materials and Methods) is particularly suitable for our present purposes for two main reasons.

First, transretinal ERG is a comparatively noninvasive technique. The photoreceptors remain embedded in the retinal tissue, retaining more natural function regarding, for example, response shutoff than with some single-cell techniques (Nymark et al., 2005). Thus, kinetics is likely to be close to that in the living animal.

Second, the ERG gives an average response from many rods, which is appropriate for comparison with behavior. The 15°C snapping thresholds in Figure 2 correspond to ∼0.03 photoisomerizations per exposure time per rod under the retinal image of the dummy. Typical sensitive ganglion cells in the toad retina have receptive field diameters ∼80% of the width of the image, collecting signals from ∼1000 rods (cf. Aho et al., 1993a). The response of each ganglion cell that mediates the threshold information in vivo would then be based on photoisomerizations in ∼30 rods randomly sampled by photons impinging on the ganglion cell receptive field. (If the behavior somehow had direct recourse to a signal summed over the entire dummy image, the averaging would be still more effective, being based on photoisomerizations in ∼240 rods randomly sampled from a total of ∼8000.) It should be noted that rods in the toad retina are extensively coupled by gap junctions, forming “signal-to-noise-equivalent rod receptive fields” encompassing some 30 rods (Copenhagen et al., 1990; Hemilä et al., 1998). Each single-photon response will be distributed as a temporally coherent, low-amplitude hyperpolarization in all these rods, excluding the possibility (suggested in mammalian retina) that a substantial fraction of single-photon responses from the low end of the response amplitude distribution could be discarded by thresholding in the first synapse (Field and Rieke, 2002; Sampath and Rieke, 2004; Field et al., 2005). Thus, it seems justified to assume that the retinal ganglion cells that underlie the behavioral response have access to a linear sum of the full number of single-photon responses estimated from absorptive quantum efficiency. Mean kinetics in random samples of n = 30 or even n = 240 will be close to the population mean reflected by the ERG signal.

Figure 3 shows families of rod responses to brief flashes of light of increasing intensities, recorded at the same two experimental temperatures as used in the behavioral experiments, 15°C (A) and 25°C (B). The flash intensities increase in 0.5 log unit steps from 6 to 60,000 Rh* in A and from 19 to 60,000 Rh* in B. The two or three smallest responses in each panel have approximately the same temporal waveform, whereas their amplitudes grow proportionally to flash intensity, indicating that they are in the linear response range. With stronger flashes, response amplitudes grow less than proportionally to intensity, indicating incipient saturation. Finally, when flash intensity is increased even further, the amplitude of the rod response no longer grows, only the time spent in saturation, evident as a horizontal plateau. On top of the rod plateau there appears a fast “nose” of complex origin, the main component being a cone response (Green and Kapousta-Bruneau, 1999).

Figure 3.

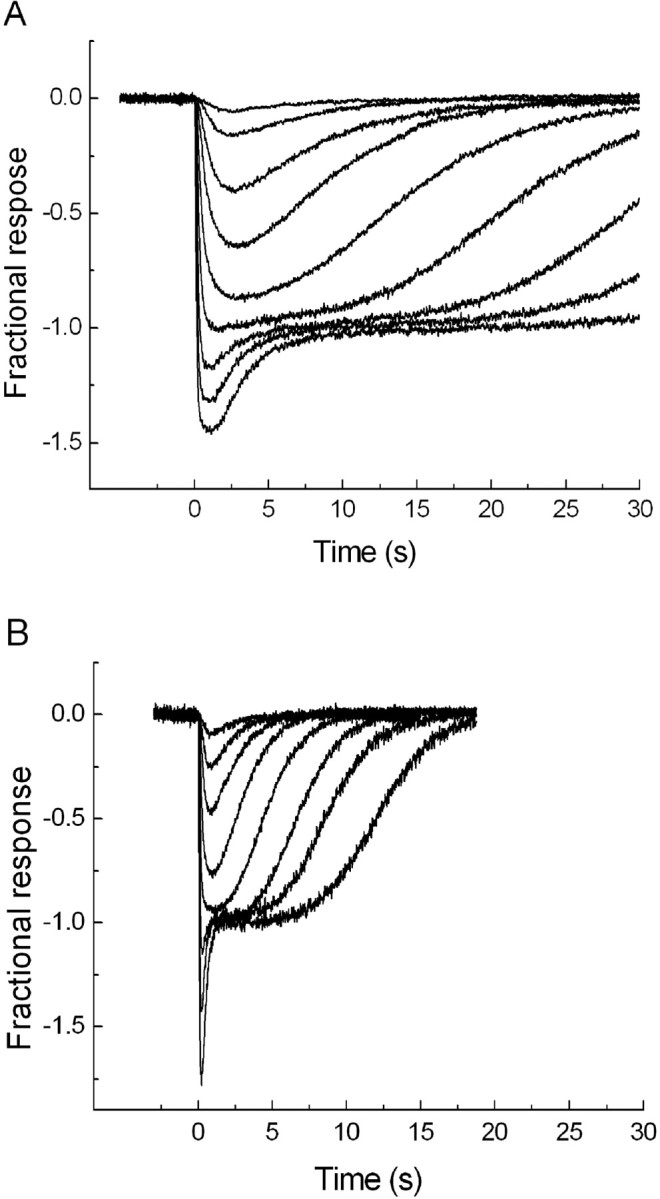
Rod response families to 20 ms flashes of light. The amplitude scale (ordinates) has been normalized to unity at the saturation level of rods. The flash intensities at 15°C (A) range from 6 to 60,000 Rh* in 0.5 log unit steps; those at 25°C (B) range from 19 to 60,000 Rh* in 0.5 log unit steps.

The main observation in Figure 3 is the general extension of response timescale at 15°C compared with 25°C. For vision at the absolute snapping threshold, at which each rod covered by the worm image receives, on average, approximately one photoisomerization per minute (∼0.01 Rh*s⁻¹) (Fig. 2), only the kinetics of the smallest, linear-range responses is relevant. These responses have the same waveform as the response to a single photon (the quantal response), which is of very similar shape across most vertebrate species and can often be phenomenologically modeled as the impulse response of some version of a linear filter cascade, such as the “Poisson” model or the “independent activation” model introduced by Baylor et al. (1974). In these models, the response (when normalized to unity peak amplitude) is fully described by two parameters, the number of filter stages n and a general time constant τ. Temperature-dependent changes of dim-flash responses can, within certain limits, be described simply as a decrease of the time constant τ with warming (Baylor et al., 1983; Lamb, 1984; Donner et al., 1988).

Figure 4, A and B, exemplifies this. Linear-range responses recorded at 15 and 25°C have been fitted with the independent activation model with the same number of filter stages in both cases (n = 4), but with 4.3-fold larger τ at 15°C. This confirms that changing temperature mainly acts to extend or compress the general timescale of responses. Such changes can be fully captured by comparing the timing of any well defined point of the responses. The time-to-peak (t_p) is a convenient measure, because it is easy to read from recorded waveforms. Figure 4C plots t_p of linear-range responses (mean ± SEM) at three temperatures. The dependence can be described by a Q₁₀ of ∼3, in agreement with previous work on rat, toad, and frog retina (Baylor et al., 1983; Lamb, 1984; Donner et al., 1988; Nymark et al., 2005).

Figure 4.

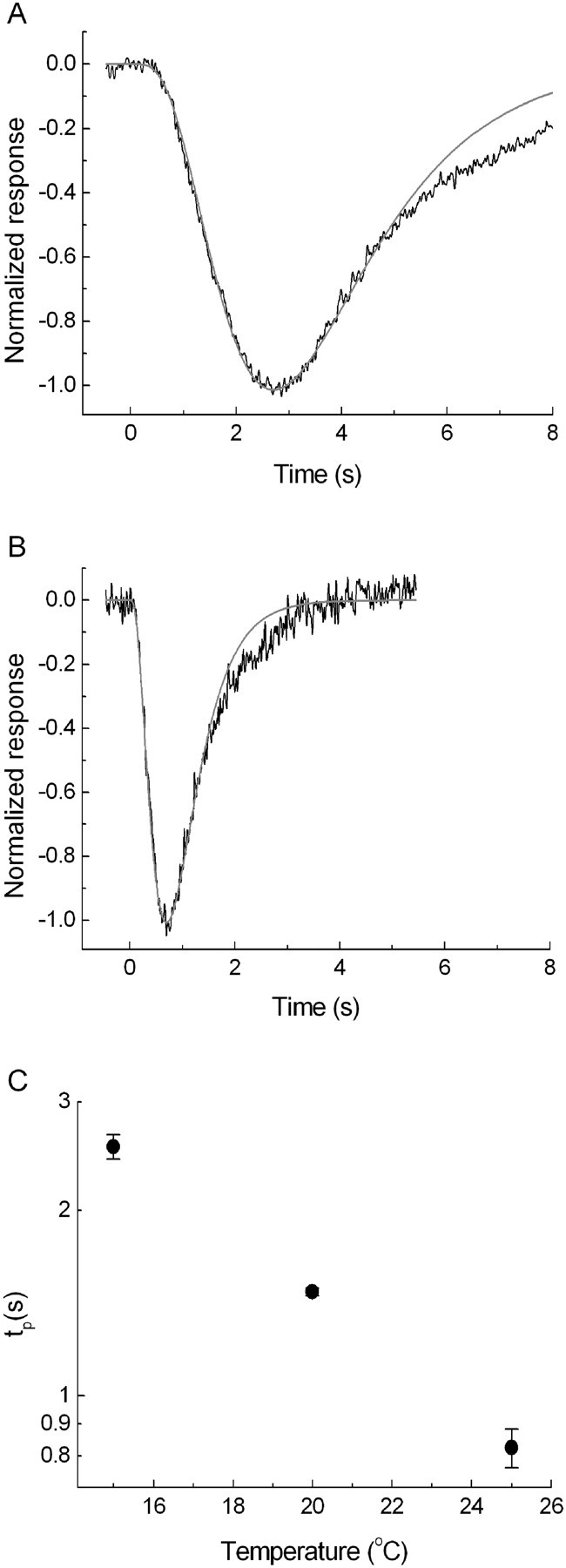
Linear-range responses to brief light flashes at 15°C (A) and 25°C (B), normalized to unity at peak (the actual flash intensities were 7 Rh* and 15 Rh*, respectively). The responses have been fitted with the “independent activation” model of Baylor et al. (1974) with the number of filter stages n = 4 (gray curves). C, Times to peak of linear-range responses as function of temperature. The values are means of measurements in 10 retinas at 15°C, 4 at 20°C, and 10 at 25°C. Error bars indicate SEM.

The integration time t_i of shape-invariant responses is directly proportional to τ or to any other well defined time measure (e.g., t_p). Filter models such as that used in Figure 4 provide simple analytical expressions for the proportionality constant relating t_i to t_p. For the independent activation model with four filter stages, t_i = 1.71 t_p (see Materials and Methods, Eqs. 3 and 4). For the mean time-to-peak values shown in Figure 4C, we get t_i = 4.2 at 15°C and t_i = 1.3 at 25°C.

We also determined the integration time of rods as a “critical duration” by measuring threshold intensity as a function of stimulus duration. Threshold was defined as the stimulus intensity that elicited a linear-range response of criterion peak amplitude (in our case chosen to be 10% of the saturated rod response amplitude). To stay within the linear response range, it was of course generally necessary to use lower intensities for longer light pulses than for the shortest ones. Figure 5A displays linear-range responses to light pulses of different durations. The amplitudes have been divided by the stimulus intensity used in each case (Rh*s⁻¹), and normalized to unity peak amplitude of the largest response. The range of temporal integration now appears as the range over which peak response amplitude grows with increasing stimulus pulse duration. The threshold intensity is inversely proportional to the peak response amplitude in Figure 5A. Relative threshold intensities thus obtained are plotted against stimulus duration on logarithmic scales in Figure 5B. This plot is directly comparable with the plot of behavioral thresholds versus exposure time in Figure 2. Again, the critical duration can be determined as the point of intersection of a 45° and a horizontal line fitted to the data. In the experiment of Figure 5, the critical durations are 5 s at 15°C and 1 s at 25°C. The mean ± SEM values thus obtained from three retinas were 4.3 ± 0.4 and 1.0 ± 0.1 s at 15 and 25°C, respectively (Table 1).

Table 1.

Integration times at 15 and 25° C determined (1) from the behavioral experiments, (2) from the shape of linear-range rod responses to brief flashes, and (3) from the light intensities needed at different stimulus pulse durations to produce a rod response of criterion peak amplitude in the linear range

Temperature (°C)	Behavior	Rods
		From model fits to responses to brief flashes	From threshold intensity versus stimulus duration
15	4.3 ± 0.9	4.2 ± 0.3	4.3 ± 0.4
25	≤0.9	1.3 ± 0.1	1.0 ± 0.1

Data are expressed as mean ± SEM.

Rod responses recorded by ERG basically reflect the kinetics of the photocurrent. In the rods of some amphibians, the photovoltage, which controls transmitter release and thus the visual signal, has been found to be somewhat faster than the photocurrent [salamander (Baylor and Nunn, 1986); frog (Donner et al., 1995)]. We lack accurate data on the voltage response of Bufo bufo rods, but in the closely related toad Bufo marinus there appears to be no significant difference between the kinetics of voltage and current responses. The integration time of current responses calculated from Table 1 in Baylor et al. (1979) is 1.89 ± 0.24 s (mean ± SEM; n = 9; “room temperature,” 18–25°C), not different from the integration time of voltage responses in the same species, given in Table 1 of Donner et al. (1990) (1.89 ± 0.11 s; n = 11; temperature, 20°C). Thus, the rod values in our Table 1 are likely to be representative of the rod signals transmitted to higher-order cells.

The cost of slowness

A long integration time at threshold necessarily entails a corresponding delay in any behavioral reaction at threshold. For reaction times to suprathreshold stimuli, however, the relationship to the integration time recorded at threshold is not self-evident, but will depend on what aspect of the (larger) neural response triggers the reaction. Generally, latencies can be explained as the time it takes for a rod signal summed over a certain area to rise to criterion amplitude (Donner, 1989b). If differences in integration time are attributable to differences in the general timescale of otherwise shape-invariant rod responses, a longer integration time at threshold will inevitably correlate with longer latencies and longer reaction times for suprathreshold stimuli as well. The prediction in our present experiments is that the snap of the cool toad will be more strongly delayed than that of the warm toad even when thresholds are similar and the light intensity (worm contrast) is the same relative to threshold.

Figure 6 shows the positions at which the tongue of the toad hit the floor of the chamber relative to the position of the worm (shown as a gray rectangle) moving at the highest velocity, whereby the threshold intensity was practically equal for C and W toads (Fig. 2, compare the leftmost snapping threshold points). The difference in snapping accuracy in the direction of movement is immediately obvious: only 1 of 28 snaps (<4%) by the C toad (Fig. 6A, solid circles) fell within the longitudinal compass of the worm, compared with 10 snaps of 30 (33%) for the W toad (Fig. 6B, open circles). The dispersion of points in the transverse direction (y-axis) does not differ between the two temperatures. With slow worms, there was no difference in longitudinal snapping accuracy between the two temperatures (data not shown in the figure). For example, with worm velocity 0.9 mm/s the longitudinal hit rate was 80% for C toads and 69% for W toads. The results demonstrate that the long integration time enabling high sensitivity at the lower temperature comes with a cost: vision becomes so slow that it will finally become useless for catching fast prey.

Figure 6.

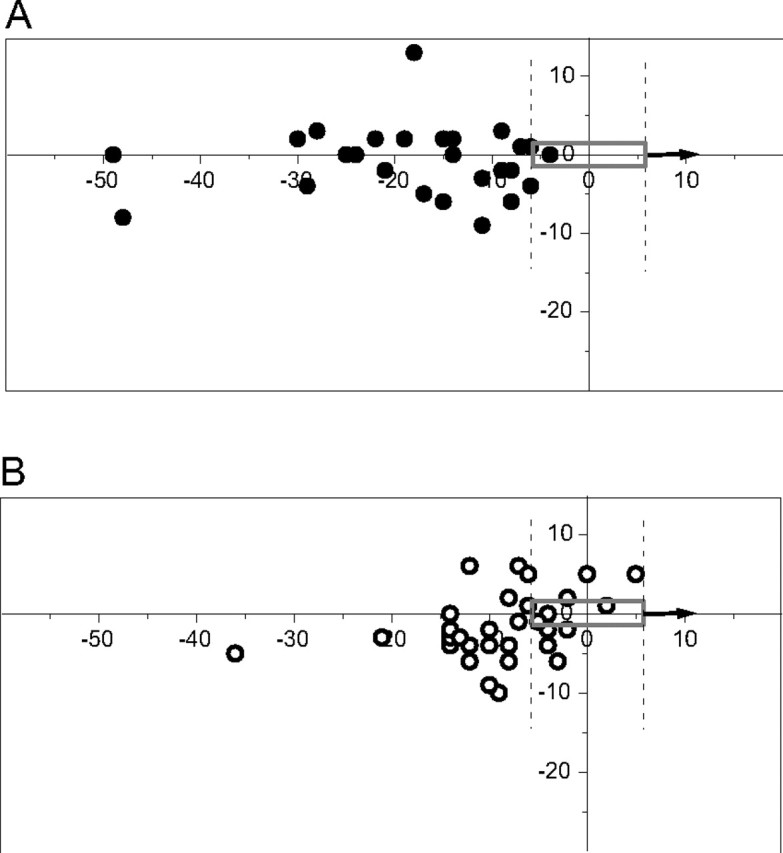
Tongue hit positions relative to worm dummy, moving toward the right at velocity 13.8 mm/s at 15°C (A) and 25°C (B). The vertical dashed lines show the horizontal extension of the worm.

Yet it should be observed that most processes in the biological environment, including prey locomotion, slow down similarly with falling temperature. We studied this semiquantitatively by measuring the running speed of woodlice at three temperatures (see Materials and Methods). The results (mean ± SEM) were 12 ± 4 mm s⁻¹ at 10°C, 14 ± 2 mm s⁻¹ at 15°C, and 27 ± 17 mm s⁻¹ at 25°C. Thus, the mean running speed of real woodlice at 15°C was approximately the same as the highest dummy speed used in the present experiments, but at 25°C it was twice as high on average.

Discussion

Visual sensitivity is favored by long integration times and low intrinsic noise

Cooling the eye increases the absolute sensitivity of vision. The improvement could depend on two factors: (1) a decrease in intrinsic noise and (2) an increase in temporal integration as neural signals slow down. The importance of temperature-dependent noise has been quite firmly established. Rates of thermal “dark” events in rods (Baylor et al., 1980; Fyhrquist et al., 1998; Firsov et al., 2002) agree with performance-limiting noise in retinal ganglion cells (Copenhagen et al., 1987), and both are consistent with the absolute behavioral sensitivity limit (Aho et al., 1988, 1993a). However, the importance of varying integration time has been only an assumption. Here, we found that the behaviorally measured seeing threshold of a toad at 15°C grew proportionally to exposure time up to ∼4.3 s, but at 25°C, the “critical duration” was <0.9 s. The advantage in temporal integration at the lower temperature correlated rather precisely with the higher visual sensitivity to real objects.

Temporal integration versus resolution at different levels in the visual system

Temporal integration reflects the persistence of the neural memory trace left by each photon. The trace can be lengthened or shortened at any level of the system by operations resembling integration or differentiation of an input signal by a neuron, so there is no necessary relationship between the speed of photoreceptor responses and the integration time measured at higher levels. Still, under serial processing, the stage with the longest integration time will necessarily limit the high-frequency response of the whole “channel.”

In the second part of this study, we showed a close correlation between rods and behavior, suggesting that the integration time is mainly set by rod phototransduction right at the input to the scotopic visual system. This implies that the slowness must affect all rod-mediated visual tasks, and evolution has had to strike a sensitive balance between gains in sensitivity and concomitant losses in temporal resolution. The payoff of increasing temporal integration at the expense of response speed will turn zero or negative at a point at which vision becomes too slow to serve a relevant biological purpose, such as catching food. As shown by Figure 6, dark-adapted toad vision operates near that limit (cf. Warrant, 1999). Mammalian rods are as slow as toad rods when cooled to the same temperatures (Nymark et al., 2005), but “warm-blooded” animals cannot be active at body temperatures of 15°C or even 25°C. To amphibians, the sensitivity advantage that this confers opens up a deep-night ecological niche for visual activity inaccessible to mammalian or avian predators.

The acceleration of rod responses under light adaptation, as well as the generically faster timescale of cones, is achieved by acceleration of response recovery (cf. Baylor and Hodgkin, 1974). The initial rise of the photoreceptor response remains rather constant under moderate adaptation (Thomas and Lamb, 1999; Friedburg et al., 2001; Nymark et al., 2005) and is similar in cones as well (Soo et al., 2008). Because visual latency (or reaction time) is basically determined by the rising edge of responses (Donner, 1989b), delaying recovery kinetics alone need not slow down reactions to moving contrast borders. Thus, the long integration time and poor high-frequency response associated with dark adaptation need not imply long visual reaction times. In contrast, the long integration time associated with cooling depends on retardation of the entire rod response (Fig. 3) and will increase the photoreceptor-dependent part of reaction time proportionally to the increase in time-to-peak of the quantal response (Fig. 4C). This will degrade localization of moving object borders (Fig. 6).

The diversity of retinal ganglion cells

Parallel processing of rod signals in the vertebrate retina begins in the first synapse (Werblin and Dowling, 1969; Soucy et al., 1998) and is finally expressed as the rich diversity of response properties found in the retinal output cells, the ganglion cells (Masland and Martin, 2007). The frog retina is the locus classicus for studies of parallel processing (Barlow, 1953; Lettvin et al., 1959; Maturana et al., 1960), and the toad retina is organized on similar principles (Ewert, 1970; Ewert and Hock, 1972). The specializations associated with “feature extraction” properties are also attended by differences in basic temporal transfer characteristics. On one hand, most dark-adapted ganglion cells in the frog have somewhat shorter integration times than rods (Donner, 1987). This is consistent with signal differentiation during signal transmission in the vertebrate retina (Baylor and Fettiplace, 1977; Schnapf and Copenhagen, 1982). However, there might be a small population of ganglion cells with longer integration times supporting, for example, simple light detection underlying frog phototaxis (Donner, 1989a; Aho et al., 1993b).

The present behavioral experiments gave no indication of postreceptoral temporal integration in the rod system of the toad. This does not exclude the possibility that there could be some subset of ganglion cells that play no role in prey-catching but provide increased temporal integration (e.g., for phototaxis). Prey-catching requires movement detection as well as reasonably accurate localization of the target and probably relies on the “conventional” on–off cell classes 1–3 (Grüsser and Grüsser-Cornehls, 1976).

Comparison with humans

The dim-flash photocurrent response of dark-adapted human rods recorded in single cells peaks at t_p = 145–190 s (Kraft et al., 1993), whereas whole-eye ERG indicates t_p ≈ 120 ms (Friedburg et al., 2001). The difference is not surprising, because retardation of responses is a common observation in isolated rods compared with more integral preparations.

Psychophysical measures of temporal performance near threshold may be translated into conceptual times-to-peak of the dim-flash response of the photoreceptor by means of some conventional model waveform. The “Poisson” model (Baylor et al., 1974) with the number of filter stages of n = 4 or 5 has been found to fit current responses of human rods (Kraft et al., 1993). Critical duration in dark-adapted humans with normal vision lies in the range 100–150 ms (Barlow, 1958; Baumgardt and Hillmann, 1961; Sharpe et al., 1988, 1993), whereas 200 ms was found in a rod monochromat (Sharpe et al., 1988). The range for normal observers would correspond to rod t_p = 67–101 ms (Poisson; n = 4) or 78–117 (n = 5), all below the range of electrophysiological values. Only the rod monochromat with conceptual rod t_p = 134 ms (n = 4) or 156 ms (n = 5) seems to agree with electrophysiology. If the voltage response of human rods (which modulates transmitter release and thus the visual signal) were faster than the corresponding current response, as in some species (Baylor and Nunn, 1986; Donner et al., 1995), this could explain (part of) the discrepancies. However, such a difference between photovoltage and photocurrent has not been clearly seen in rods of monkey (Baylor et al., 1984; Schneeweis and Schnapf, 1995, 1999) or toad [Bufo marinus (Baylor et al., 1979; Donner et al., 1990)].

Other psychophysical measures add to the contradictory picture. The temporal contrast modulation sensitivity function of nearly dark-adapted humans (Sharpe et al., 1989) suggests rod t_p ≈ 50–60 ms, whereas dark-adapted reaction times would indicate t_p ≈ 140 ms (Mansfield, 1973; Donner, 1989). By most criteria, dark-adapted scotopic vision seems somewhat faster than rod photoreceptors, and generalizations about determinants of temporal vision in dark-adapted humans must be made with caution.

Still, it is worth noting that the fixed, restricted capacity for temporal integration strongly suggests a mechanistic constraint near the input to the system. Certainly, human night vision would benefit from having recourse to longer “exposure times” than 100–150 ms in many situations. However, there are additional mechanisms allowing light integration over longer times for purposes other than seeing objects. For example, plain detection of large, persistent light fields is supported by a higher-level memory spanning several seconds (Denton and Pirenne, 1954), and melanopsin ganglion cells, which measure light for the circadian clock, have much more extended temporal integration than conventional visual functions (Berson et al., 2002).

Different roles of rods and cones as determinants of the temporal properties of vision

As opposed to the situation in rod vision, photoreceptor electrophysiology is of little help for explaining absolute temporal parameters of cone vision. The dim-flash voltage response of dark-adapted cones in the macaque retina peaks at 30–40 ms (Schneeweis and Schnapf, 1995, 1999) and the current response of human cones ∼15–20 ms [whole-eye ERG in a weakly light-adapted state (Friedburg et al., 2004)]. Different classes of psychophysical data suggest the following “cone” times-to-peak (Poisson model; n = 5): t_p = 78 ms [from critical duration of 100 ms; data summarized by Donner (1992)], t_p = 125 ms [from the contrast modulation transfer function (Rovamo et al., 1999)], or t_p ≈ 120 ms [from reaction time (Donner and Fagerholm, 2003)]. At least foveal cone vision is consistently slower than would be predicted from available cone electrophysiology. The retardation seems to occur primarily in the retina, being evident already in retinal ganglion cell responses both in primates (Purpura et al., 1990; Lee et al., 1994) and amphibians (Donner et al., 1998).