Neural Control of Unloaded Leg Posture and of Leg Swing in Stick Insect, Cockroach, and Mouse Differs from That in Larger Animals

Abstract

Stick insect (Carausius morosus) leg muscles contract and relax slowly. Control of stick insect leg posture and movement could therefore differ from that in animals with faster muscles. Consistent with this possibility, stick insect legs maintained constant posture without leg motor nerve activity when the animals were rotated in air. That unloaded leg posture was an intrinsic property of the legs was confirmed by showing that isolated legs had constant, gravity-independent postures. Muscle ablation experiments, experiments showing that leg muscle passive forces were large compared with gravitational forces, and experiments showing that, at the rest postures, agonist and antagonist muscles generated equal forces indicated that these postures depended in part on leg muscles. Leg muscle recordings showed that stick insect swing motor neurons fired throughout the entirety of swing. To test whether these results were specific to stick insect, we repeated some of these experiments in cockroach (Periplaneta americana) and mouse. Isolated cockroach legs also had gravity-independent rest positions and mouse swing motor neurons also fired throughout the entirety of swing. These data differ from those in human and horse but not cat. These size-dependent variations in whether legs have constant, gravity-independent postures, in whether swing motor neurons fire throughout the entirety of swing, and calculations of how quickly passive muscle force would slow limb movement as limb size varies suggest that these differences may be caused by scaling. Limb size may thus be as great a determinant as phylogenetic position of unloaded limb motor control strategy.

Introduction

Understanding how nervous systems control posture and movement is a fundamental goal of neurobiology. Muscle transforms neural output into action. The consequences of motor neuron activity therefore cannot be understood without understanding this transformation (see Chiel and Beer, 1997, for a full discussion of this issue). Work on the pyloric muscles of the lobster stomatogastric system well demonstrates this issue (Morris and Hooper, 1998; Morris et al., 2000; Thuma et al., 2003). Pyloric motor neurons fire bursts of action potentials approximately once per second. Pyloric muscles might therefore be assumed to shorten and lengthen with each motor neuron burst. However, these muscles are much too slow to do so, and instead either produce sustained, tonic contractions, or contract and relax in phase with modulations imposed on pyloric motor neuron activity by other, more slowly cycling, stomatogastric neural networks. Understanding the functional consequences of motor neuron activity in this system is thus impossible without knowing muscle response to motor neuron input.

It could be argued that this example is a special case. Muscles controlling limbs, which in general can move rapidly, and whose movements are believed to be often subject to moment-by-moment control, might be expected to respond rapidly to changes in motor neuron activity. We were therefore surprised to find that stick insect leg muscles are slow (Guschlbauer et al., 2007; Hooper et al., 2007a,b). These data suggested that it was important to reexamine neural control of limb posture and movement in this species (for review of previous work see Bässler and Büschges, 1998, and Büschges and Gruhn, 2008). To limit these investigations to particularly simple situations, we examined neural control under conditions (unloaded limb posture, swing phase in walking) in which only the limb's own mass is controlled. We report here that neural control in stick insect indeed differs from that in several species with more rapid muscles (Prochazka et al., 1989; Tokuriki and Aoki, 1995). However, these organisms are also much larger then stick insects. To control for this size difference, we examined neural control of unloaded leg posture in cockroach and leg swing in mouse, which have more rapid muscles. Cockroach and mouse motor control mirrored that found in stick insect. Furthermore, comparing motor control strategy across several animals with rapid muscles showed a graded, size-dependent transition in swing motor control strategy. These observations suggest that this transition is a scaling phenomenon, and that limb size is a major determinant of neural control strategy of unloaded limb posture and movement.

Preliminary reports of these data have appeared in abstract form (Guschlbauer et al., 2005; Blümel et al., 2007a,b).

Materials and Methods

Extracellular recordings of Carausius morosus muscle activity (EMGs).

Techniques to record C. morosus muscle activity during walking are described in detail by Gruhn et al. (2006) (see Figs. 1, 4). In brief, adult female C. morosus from the laboratory's (Universität zu Köln) colony that showed robust responses to handling were glued (ProTempII; 3M ESPE) ventral side down to a balsa rod, and all but the middle legs were removed. Activity was recorded from the protractor and retractor coxae or flexor and extensor muscles by inserting fine wires into each muscle and a reference electrode into the abdomen. EMGs were amplified 100-fold with a preamplifier (electronics workshop, Zoologisches Institut, Köln), bandpass filtered (100 Hz to 2 kHz), further amplified 20-fold, and transferred to a computer using a Micro 1401 II data acquisition system and Spike 2 (version 5.05) software (both Cambridge Electronic Design).

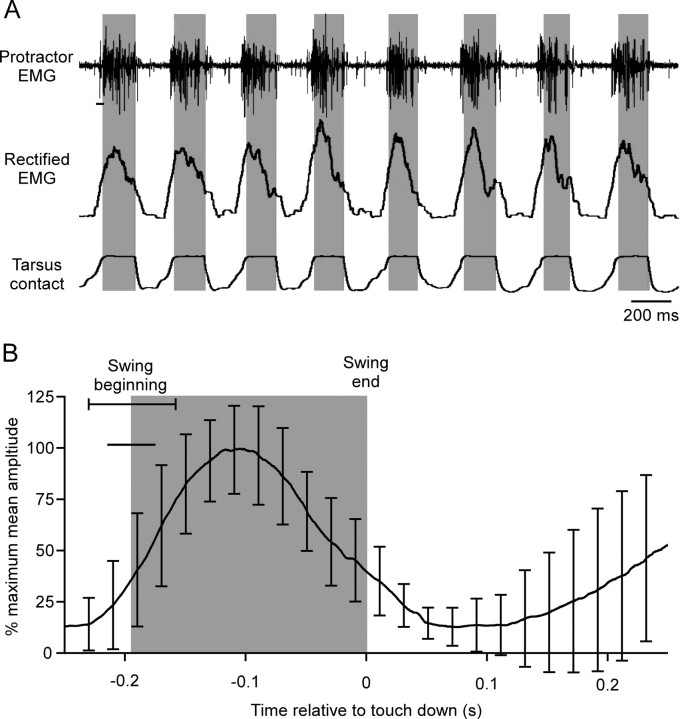
Figure 1.

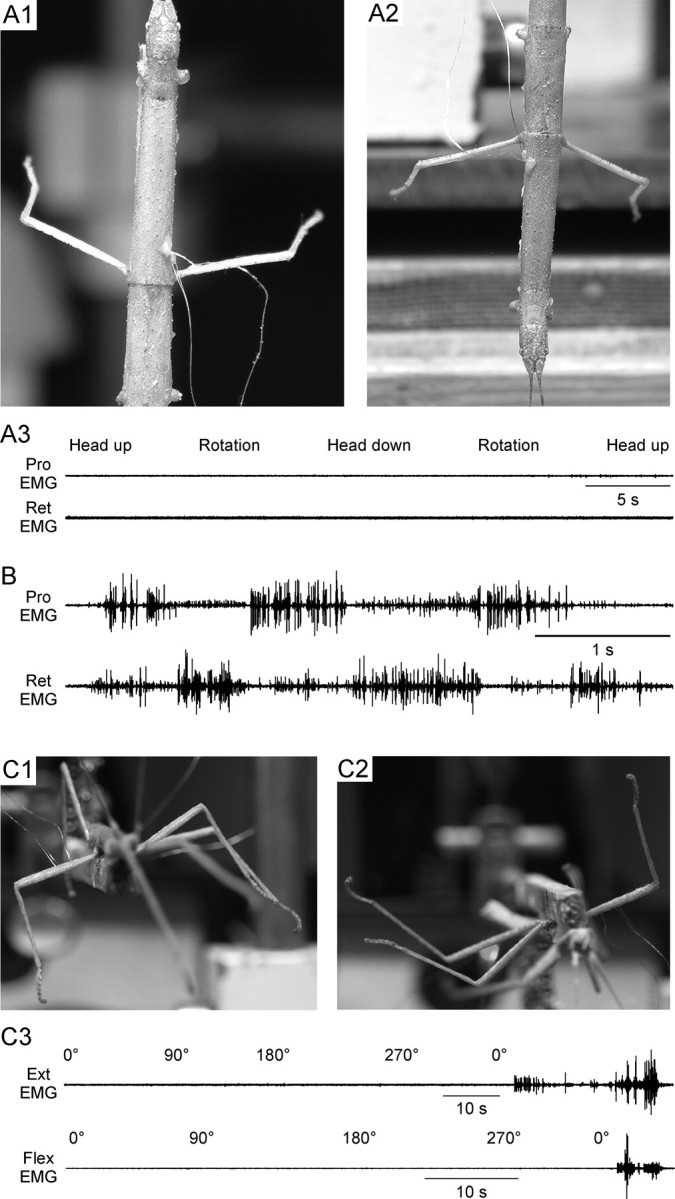
C. morosus legs assume constant, gravity-independent postures in the absence of leg muscle nerve activity. A, Photographs of an animal in head-up (A1) and head-down (A2) positions with the long axis of the body positioned parallel to gravity (i.e., in A1 the animal is oriented similar to a standing human). The left side of the animal was opened ventrally and all nerves innervating the middle leg muscles, including the protractor and retractor coxae muscles, were severed. The innervations of the muscles on the right side were left intact and EMGs recorded from the protractor and retractor muscles. Both legs remained almost perpendicular to the body's long axis regardless of animal position. Simultaneous recordings (A3) of activity in the protractor and retractor muscles, which control leg position in this plane, showed that maintenance of these postures was not associated with measurable muscle activity, which was absent at all head orientations and during rotations between orientations. B, Recordings of protractor and retractor activity during walking induced by touching the animal showed that the recording electrodes were functioning. C, Photographs of an animal ventral (C1) and dorsal (C2) side down. Femur–tibia joint (the femur is the portion of the leg lying relatively horizontally and the tibia the portion lying vertically, pointing downward, in C1) angle did not change when animal position relative to gravity was changed. Recordings from the flexor and extensor muscles (which control this joint) showed that this maintenance of femur–tibia joint angle was not associated with measurable muscle activity (C3). The last portions of the recordings were the activity that occurred when the animal was induced to walk, and show that the EMG electrodes were functioning. The recordings in C3 were from the same animal but are not simultaneous (first the extensor muscle was recorded from and the animal rotated 360° and then the flexor was recorded from and the animal again rotated 360°).

Figure 4.

C. morosus protractor (swing) motor neuron activity continues throughout the entirety of swing. A, EMG recordings of middle leg protractor coxae (Protractor) activity (top trace), rectified and smoothed (τ = 0.02 s) EMGs (middle trace), and record of tarsus contact (third trace) while animal stepped on a slippery surface (Gruhn et al., 2006). Gray shadings indicate swing duration. The rectified EMG begins to rise before the EMG spikes because of the 20 ms smoothing window (horizontal line under first spike in top trace). Tarsus contact trace shows graded onset and offset because of changing tarsus area in contact with the plate during tarsus set-down and lift-off. B, Mean protractor EMG activity from one animal (54 steps, error bars are SD) averaged using swing end as time 0. Gray shading indicates swing duration. Horizontal line under swing beginning SD line is EMG smoothing window duration.

Stance and swing were detected as follows. Electrode cream (GE Medical Systems) was applied to the tibia cuticle, and a portion of a copper wire from which the insulation had been removed was wrapped around the tibia. The other end of the wire was connected to a differential amplifier (electronics workshop, Zoologisches Institut, Köln). The animals were then situated so that when they were not walking, their feet touched a metal plate coated with an electrically conductive, slippery (5% NaCl, 95% glycerin) solution, and low-voltage square-wave pulses were applied to the plate using a pulse generator (model MS501, electronics workshop, Zoologisches Institut, Köln). During walking (induced by touching the animal's abdomen) (Bässler and Wegner, 1983), the electric circuit only became closed, and the square-wave pulses were thus detectable by the differential amplifier, when the leg touched the plate (stance). Swing phase start and end were defined by setting thresholds in the tarsal contact trace. Steps without clearly alternating antagonistic muscle activity were excluded from analysis.

The effect of gravity on leg motor nerve activity (see Fig. 1) was determined by lifting the animals from the plate so that the legs were not in contact with a substrate and manually rotating the balsa rod to which the animals were glued to bring the animals to different orientations relative to gravity. Deafferentation and efferentation of the mesothoracic leg (protractor and retractor experiments) on one side of the animal were achieved by making a small incision on the ventral side of the animal and cutting all nerves on one side of the mesothoracic ganglion with fine scissors. The completeness of the procedure was confirmed by failure to elicit reflex responses in the leg in question.

Measuring isolated stick insect leg rest femur–tibia and cockroach joint angles.

Stick insects were induced to autotomize a middle leg (see Figs. 2, 5). C. morosus leg flexion axons can spontaneously generate action potentials for a considerable time after leg autotomy (Schmidt and Grund, 2003). However, the movements these spikes induce are visually apparent, and all isolated leg experiments were performed after they had ceased (5–10 min post autotomy). The leg was then mounted in a stand under a tripod-fixed Fujifilm FinePix S602 Zoom camera, and the femur–tibia joint alternately was maximally flexed (to 20–30°) and extended (to 180°) by hand, and joint return angles were photographed. No limb was used >30 min; control experiments showed that robust return movements continued at least an hour after autotomy. Exactly analogous procedures were used in examining Periplaneta americana isolated leg femur–tibia joint passive properties, except that the leg was removed by cutting through the thorax–coxa joint and an Olympus E-330 camera was used. C. morosus leg flexor and extensor muscles were ablated by inserting a hot needle into the femur up to (but not into) the femur–tibia joint and moving it along the interior walls of the femur. Flexions and extensions were then performed again as above. In all cases the returns were photographed 5 s after the flexion or extension. Data on the time course of the returns were not obtained, but visual observations indicate that return velocity was highest at return beginning and decreased as the joint equilibrium angle was approached. Pictures were transferred to a personal computer and joint angles were measured in Canvas (ACD Systems). Data were analyzed and plotted in KaleidaGraph (Synergy Software) and final figures were prepared in Canvas for these and all other data presented here.

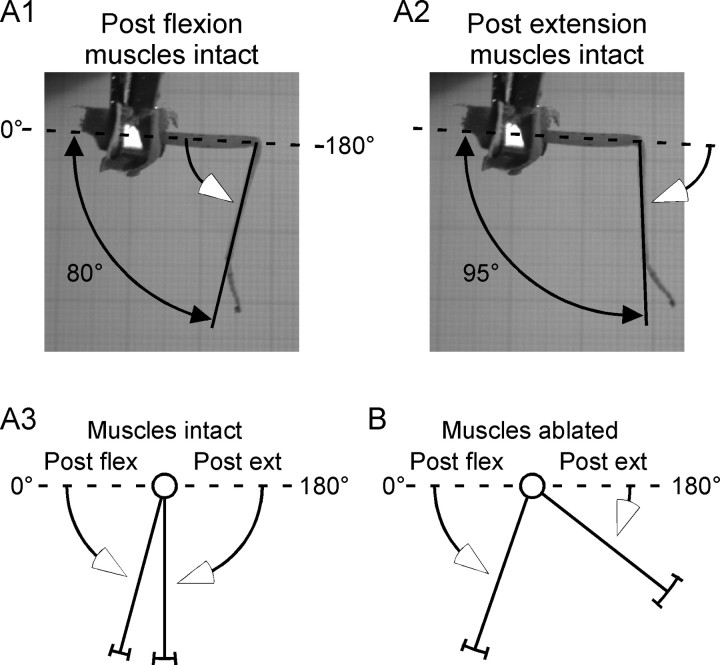
Figure 2.

Isolated C. morosus femur–tibia joints drive to constant angles after flexion or extension. Photographs of C. morosus returns after flexion (A1) and extension (A2). Lines with open arrows indicate direction of leg movement during passive returns. A3, Mean data. B, Mean data after extensor and flexor muscle ablation. Means and SDs were (muscles intact) postextension, 90 ± 8°, postflexion, 75 ± 6° (muscles ablated), postextension, 142 ± 12°, postflexion, 71 ± 9°. N = 6. Intact and ablated postextension returns differed at p < 0.0001; intact and ablated postflexion returns did not differ (p = 0.99) (repeated measure Student's t test).

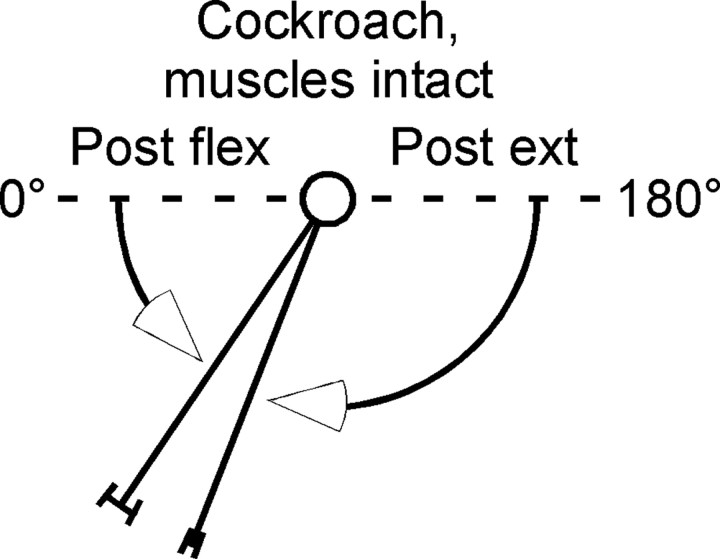
Figure 5.

Cockroach femur–tibia joints drive to constant angles after flexion or extension. Figure conventions same as in Figure 2A3. Means and SDs were: postextension, 68 ± 3°; postflexion, 56 ± 6° (N = 3).

Passive muscle force measurements.

For detailed methods of measuring C. morosus leg muscle properties (see Fig. 3), see Guschlbauer et al. (2007). In brief, the thorax was opened by cutting along the animal's longitudinal axis, and gut and fat tissue was removed. Nerves nl3 (for the extensor tibiae) or ncr [for the flexor tibiae; nomenclature according to Marquardt (1940)] were either crushed or cut to prevent motor neuron activity from reaching the leg muscles. Animals were pinned ventral side down on a balsa wood platform with all legs except the right middle cut at mid-coxa. The femur was embedded in dental cement (two-component glue, ProTempII; 3M ESPE), opened distally, and carefully dissected to access the extensor or flexor tibiae tendon. In both cases the tendon was cut with the femur–tibia joint at 90° (the muscle reference length) and perforated with a hook-shaped insect pin that connected the muscle to the lever arm of an Aurora 300 B dual-mode lever system (Aurora Scientific Inc.). Muscles were stretched with SPIKE2 (Cambridge Electronic Design) Sequencer-generated ramps, and passive muscle forces were determined after the initial force response had decayed to approximately steady state. Drops of stick insect saline (in mm: 178.54 NaCl, 10 HEPES, 7.51 CaCl₂·2H₂O, 17.61 KCl, 25 MgCl₂·6H₂O, pH 7.2) (Weidler and Diecke, 1969) were applied to the distal muscle end throughout the experiment.

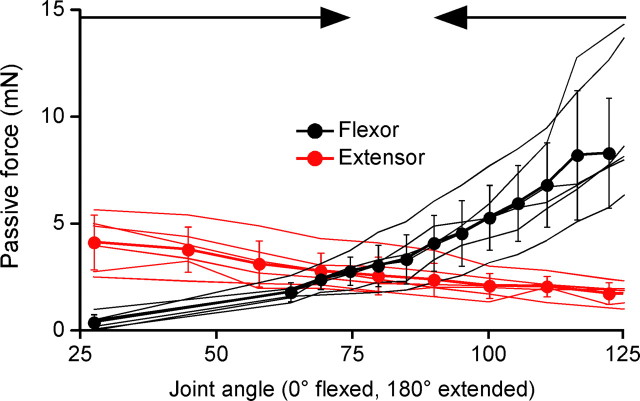
Figure 3.

Isolated stick insect femur–tibia joint muscles develop large passive forces that are approximately equal at the rest joint angles observed in intact legs. Flexor (black) and extensor (red) static passive length-tension curves (N = 6 for each muscle) overlap at the same angle range that intact legs return to after perturbation (Fig. 2A3). Thin lines are data from individual muscles, thick lines with closed circles are mean data, error bars are SDs. Joint angles were calculated from stretched muscle lengths using moment arms measured in Guschlbauer et al. (2007). Arrows at top of panel show the angles (75° and 90°, respectively) that legs with intact muscles drove to after flexion and extension.

Extracellular recordings of mouse muscle activity.

EMG recordings during walking on a treadmill (speed, 0.2 m/s) were made (Columbia University, New York, NY) from left hind leg hip (iliopsoas) and ankle (tibialis anterior) flexor muscles in three male and two female adult (50- to 90-d-old) mice (see Fig. 6). Data were recorded to a computer using a Power1401 data acquisition system and Spike 2 (version 6.02) software. EMG electrode fabrication and implantation are described in detail by Akay et al. (2006) and Pearson et al. (2005). Leg movement data were obtained by attaching custom-made cone-shaped reflective markers to the skin of the left hind leg above the level of the anterior end of the iliac crest, hip, knee, ankle, the fifth toe joint, and the tip of the fourth toe (Pearson et al., 2005; Akay et al., 2006) and recording marker movement using a high-speed (250 frames/s) Fastcam PCI R2 video camera (Photron USA). Video data were analyzed using Peak Motus 8.2 (Peak Performance Technologies Inc.) motion analysis software. Swing onset and offset were defined as the times when the toe marker began moving forward or backward, respectively. Kinematic and EMG data were synchronized by matching a light-emitting diode flash in the video files with a simultaneous voltage step in the EMG recordings (Pearson et al., 2005; Akay et al., 2006). All data were obtained 2 d after the implantation surgery.

Figure 6.

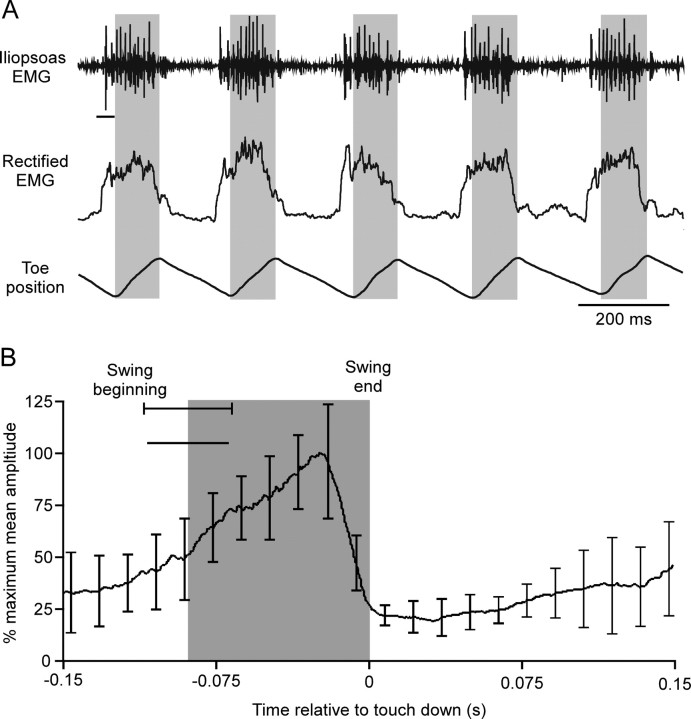
Mouse hip flexor (iliopsoas) activity begins before swing and continues throughout the entirety of swing. A, EMG recordings of left hind leg iliopsoas activity (top trace), rectified and smoothed EMGs (middle trace), and record of toe movement (third trace) while animal stepped on a treadmill. Gray shadings indicate swing phase. The rectified EMG begins to rise before the EMG spikes because of the 20 ms smoothing window (horizontal line under first spike in top trace). B, Mean protractor EMG activity from one animal (27 steps, error bars are SD) averaged using swing end as time 0. Gray shading indicates swing duration. Horizontal line under swing beginning SD line is EMG smoothing window duration.

Calculating mean EMG activities and phase normalization to cycle period.

Mean EMG activities (see Figs. 4, 6) were calculated in Spike 2 by marking swing end in each cycle from either the tarsus or toe movement data and using a built-in function to perform the averages (see Figs. 4, 6, 7). The data shown are mean data (Fig.4, 54 steps; Fig. 6, 27 steps) from the same animals for which the EMG data in the figures were obtained. Data from other animals (N = 4 for C. morosus, N = 5 for mouse) were similar and, in particular, in all cases showed swing motor neuron activity that continued throughout swing duration. For the mouse, phase normalization (see Fig. 7) was performed by dividing each step cycle into 50 subdivisions. The rectified and lowpass-filtered EMG traces in each subdivision of the 27 steps were averaged to obtain mean EMG values in each time subdivision, and hence a mean EMG trace versus time. The time value of each subdivision was then divided by average step cycle period to transform the time values to phase.

Figure 7.

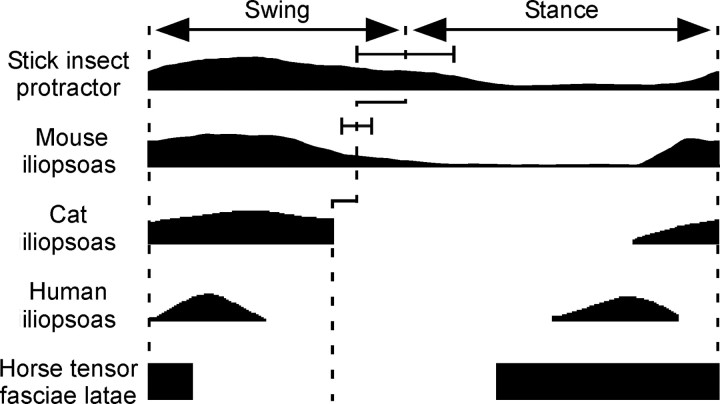
Comparison of C. morosus, mouse, cat, human, and horse (horse data are the mean of the activities observed during walk, trot, and cantor) swing motor neuron activity. C. morosus, mouse, and cat swing motor neurons are active throughout swing, human and horse swing motor neurons are active only at swing beginning. See Results for discussion of stance phase activities. For the horse data, the rectangles show only when swing motor neurons are active, not the amplitude of the activity; for the other traces, the varying heights of the traces show how the activity's amplitude varied in the step cycle. Cat, human, and horse data modified from Prochazka et al. (1989) and Tokuriki and Aoki (1995). Error bars on C. morosus and mouse data are SDs.

Because of large step-to-step variation in cycle period in stick insect walking, phase normalization for C. morosus was performed individually for each step using GNU Octave as follows. Step cycle period was first defined as beginning at each swing beginning. Each step's rectified EMG was then resampled at 10 kHz. A step with a cycle period of 1.234 s would thus have 12,340 EMG values, each associated with a time value of 0 s, 0.0001 s, 0.0002 s, etc. We chose to build the phase plots using 200 points each, and hence wanted the EMG value at phases of 0, 0.005, 0.01, etc. The task was thus to identify which samples in the resampled EMG corresponded most closely to these phase values. This was determined by multiplying the total number of EMG values by the desired phase. For example, for phase 0.005, the desired sample number would be 0.005 × 12,340 = 61.7. Because there were only integer sample numbers, an integer function that truncated the decimal portion was used to transform the decimal values into integers. Thus, in the case at hand, the EMG value associated with sample 61 was used as the EMG value at phase 0.005. Each sample number's EMG value was then averaged across the 54 steps.

Results

The work reported here was triggered by the observation that at least one C. morosus leg muscle contracts and relaxes very slowly (Hooper et al., 2007a,b). These data suggested that neural control of this muscle in posture and walking might differ from that in systems with more rapid muscles. Simultaneously with work investigating this issue, we were independently performing experiments defining extensor muscle properties in greater detail (Guschlbauer et al., 2007). As we obtained the C. morosus data, it became clear that work in other species (cockroach and mouse) would also be necessary. Thus, the work on these four projects was not performed in a species-specific order, but instead was performed incrementally, moving back and forth between species and projects as our understanding advanced. Consequently, we do not present the data in the order in which the experiments were performed, but instead organize them logically: neural control of posture in C. morosus, neural control of swing phase in C. morosus, and comparison of C. morosus data and data from other animals.

Neural control of posture in C. morosus

When intact C. morosus were glued to a wooden dowel and the animal was lifted into the air so that its legs were not in contact with a substrate, the legs assumed characteristic postures, with the femurs positioned perpendicular to the body's long axis (Fig. 1A1, right leg; for left leg, see below). These postures were not altered by changing the animal's position relative to gravity (in Fig. 1A1 the animal was head up with the body's long axis parallel to gravity, like a standing human, and in Fig. 1A2 the animal had been rotated 180° so that the head pointed down, like a human suspended from her/his feet; these changes would be expected to alter femur position relative to the body's long axis if the direction of the gravity vector affected the angle of the thorax–coxa joint).

Maintaining perpendicular joint postures with human shoulders or hips (roughly equivalent to the thorax–coxa joint) would require continuous muscle activity to counteract gravity, and the pattern of muscle activation would change as the human was rotated heels over head. However, simultaneous recordings of protractor and retractor muscle activity (the muscles responsible for controlling the thorax–coxa joint) showed that in C. morosus, there was no activity in these muscles regardless of the animal's position relative to gravity. (Fig. 1A3 shows activity in these muscles in the right leg with the body in the original head-up position, during counterclockwise rotation of the animal to the head-down position, and further counterclockwise rotation to return to the head-up position; Fig. 1B shows that inducing the animal to walk resulted in robust protractor and retractor activity, and thus that the EMG electrodes were functioning properly.) One explanation for these data was that muscle activity was occurring in these experiments, but the amplitude of the units being activated was too small to be recorded by the EMG electrodes. However, deafferented and de-efferented legs (the left leg in Fig. 1A) continued to assume constant, gravity-independent postures. Although these data do not prove that small-amplitude units were not active during these experiments, they do show that this activity is not necessary for the legs to assume and maintain these postures.

These constant, gravity-independent postures occurred not only at the thorax–coxa joint, but also at a more distal joint, the femur–tibia joint (roughly equivalent to human elbow or knee joints). When the body was rotated around the body's long axis, the femur–tibia joint angle did not change (rotation about this axis would be expected to alter the femur–tibia joint angle if the direction of the gravity vector affected the angle of this joint) (Fig. 1C1,C2). The femur–tibia joint is controlled by the extensor and flexor muscles, and recordings from these muscles showed that this maintenance of femur–tibia joint angle, regardless of position relative to gravity, was not associated with measurable activity in the muscles (Fig. 1C3).

We have well developed techniques for working with the extensor and flexor muscles (Guschlbauer et al., 2007; Hooper et al., 2006, 2007a,b) and, therefore, used this joint to study the mechanisms underlying the constant, gravity-independent leg postures. We first verified that the constant, gravity-independent postures of this joint did not depend on neural activity by removing the leg from the animal. Isolated leg femur–tibia joints assumed a constant angle of ∼90°, and rotating the femur so that the tibia had different orientations relative to gravity had no effect on this angle (data not shown). Moving the tibia showed that after either flexion (Fig. 2A1) or extension (Fig. 2A2), the tibia returned to femur–tibia angles between 75° and 90° (Fig. 2A3, grouped data).

These constant, gravity-independent, passively determined joint angles could arise from at least two mechanisms. The first is the cuticular structures of the joints having a preferred joint angle. This mechanism could arise because insect joint cuticular tissues are less flexible than, for instance, human skin and connective tissues. Compression of C. morosus joint interior cuticular tissues and stretch of joint exterior cuticular tissues, as would occur with joint flexion, and stretch of interior cuticular tissues and compression of exterior cuticular tissues, as would occur with joint extension, could therefore generate forces that help restore joint angle after perturbations from the rest angle. We tested the role of cuticular structures by ablating the extensor and flexor muscles (Fig. 2B). Muscle ablation little altered postflexion returns, suggesting that cuticle-generated forces play a major role in restoring joint angle after flexion. However, muscle ablation strongly reduced postextension returns, suggesting that cuticle-generated forces play a minor role in restoring joint angle after extension. In one experiment in which the muscles were cut from their attachment points to the cuticle (the apodemes), as opposed to being ablated, similar changes in returns were observed. In this experiment we also tested the role of the cuticular tissue directly by removing the cuticle from the interior and exterior of the joint after the muscles had been cut from the apodemes, leaving only the medial joint cuticle intact. In this case the joint appeared to no longer have a preferred angle to which it returned, instead remaining at whatever angle it was placed.

A second mechanism for these constant rest joint angles arises from muscles being spring-like entities that generate passive restoring forces when stretched beyond their rest length. Muscles could thus give rise to constant rest joint angles if the flexor and extensor muscles generated approximately equal passive forces at the rest angles, and net restoring forces at other angles. Experiments on isolated flexor and extensor muscles (Fig. 3) showed that the muscles generated equal forces at angles between 70° and 90°, in good agreement with the data from intact legs. For such forces to result in gravity-independent rest joint angles, the net difference between flexor and extensor muscle passive forces at other angles would need to be large compared with leg weight. The parts of the limb that these muscles move, the tibia and tarsus, have a combined mass of 3.3 ± 0.2 mg (SD, N = 5), on which the force of gravity is 0.03 mN. The difference in flexor and extensor passive force as the joint was perturbed could be as large as 6 mN (Fig. 3, 125° joint angle), and was >1 mN for all angles outside the 70–90° range. Muscle-derived net restoring forces were thus 30- to 200-fold greater than the force of gravity on the leg segments in question, clearly sufficient to contribute to gravity-independent joint positions.

Neural control of swing phase in C. morosus

We next measured protractor (swing) motor neuron firing during walking (Fig. 4). The upper three traces show raw and rectified protractor EMG data and tarsus contact (gray shading marks swing phase) for eight steps, and the bottom plot shows mean data from 54 steps (gray shading again indicates swing duration). Protractor motor neurons began to fire shortly before full tarsus liftoff (horizontal upper portion of tarsus contact trace) and continued to fire throughout the entirety of swing.

Comparison of C. morosus data to those from other animals

The work examining neural control mechanisms in C. morosus was motivated by the presence of at least one very slow leg muscle in this animal (Hooper et al., 2007a,b). C. morosus also moves very slowly, and freezes as a protective mechanism when threatened (Bässler, 1972, 1983; Godden, 1974). Similar fixed joint rest angles, perhaps gravity-independent and likely attributable to an equilibrium point of agonist and antagonist passive forces, have also been seen in crustacea (Yox et al., 1982), which suggests that the data presented above were probably not limited to stick insects. Nonetheless, to ensure that the data in Figures 1 and 2 were not attributable to C. morosus ' specialized behavior, we repeated the isolated leg experiments on an animal renowned for its locomotory speed and versatility, the cockroach, P. americana. These experiments showed that, despite the speed difference between the two species, P. americana isolated femur–tibia joints also had constant, gravity-independent rest positions to which they returned after perturbation (Fig. 5).

To further test whether the C. morosus data were the result of this animal's slow properties, we examined swing motor control in mouse hind leg (Fig. 6). The justification for performing these experiments was that, although mammals do have fast and slow skeletal muscle fibers, even the slowest of these are much faster than stick insect extensor and other slow invertebrate nonspiking muscles, which can take hundreds to thousands of milliseconds to reach steady-state contraction levels in response to tonic motor neuron firing at physiological spike frequencies (Morris and Hooper, 1997; Hooper et al., 2007b). As such, if the slow properties of C. morosus muscles gave rise to unusual motor control strategies, these should be clearly shown by comparing motor control in C. morosus and animals, such as mammals, with much more rapidly contracting muscles. The top trace of Figure 6A shows mouse hip flexor (swing) muscle raw EMG activity, the second, rectified and smoothed EMG activity, and the third, toe position. The gray shading again marks swing phase. Figure 6B shows mean activity from 27 steps, with the gray shading showing swing duration. Mouse hip flexor activity slightly preceded swing beginning and, exactly as in C. morosus, continued throughout swing. Recordings from mouse ankle flexor muscles showed that these muscles were also active throughout the entirety of ankle flexion (data not shown).

These results suggested that the C. morosus data were unlikely attributable to this animal's slow properties. To gain insight into this issue, we compared mean C. morosus protractor and mouse hip flexor motor neuron activity during swing and stance to data from the literature for cat, human, and horse hip flexors (Fig. 7). The stick insect, mouse, and cat data differed markedly from the human and horse data, with the smaller animals having swing motor neuron activity that continued throughout swing and the larger ones having swing activity only at swing beginning. Swing motor neuron activity also continues throughout the entirety of swing in guineafowl (Gatesy, 1999), chick (Jacobson and Hollyday, 1982), and newt (Székely et al., 1969) legs and small (ankle) limb segments in humans (Prochazka et al., 1989; Halliday et al., 2003; Cappellini et al., 2006).

The data in Figure 7 are in the phase (normalized to cycle period) domain, and thus contain no information about cycle period, swing, or swing EMG activity durations. Examining actual durations, as well, is interesting for two reasons. First, in mouse, cat, human, and horse, the legs are beneath the body (as opposed to the sprawling posture of the stick insect) and thus their swings could be at least partially pendular, and hence governed by the relationship cycle period = 2π√limb length/g. Second, such an analysis might reveal whether there is some simple relationship between swing motor neuron activity (EMG duration) and other motor pattern parameters (cycle period, swing duration) or limb length.

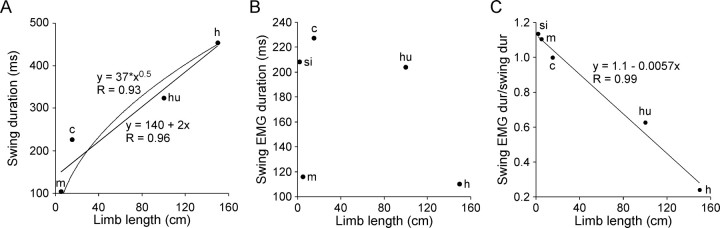
With respect to the first point, mouse, cat, human, and horse legs [using leg lengths of 5 cm (mouse), 15 cm (cat), 100 cm (human), and 150 cm (horse)] would have pendulum-alone swing durations (one-half of pendulum cycle period) of 200 ms (mouse), 400 ms (cat), 1000 ms (human), and 1200 ms (horse). Actual swing durations are 105 ms (mouse), 227 ms (cat), 325 ms (human), and 455 ms (horse). In all cases, swing motor neuron activity thus accelerates limb swing to faster velocities than those that would occur from simple pendulum dynamics alone. Figure 8A plots swing durations in these animals versus leg length, and shows linear and square root fits to the data. The fits are equally good. These data thus cannot rule out that pendular dynamics play some role in swing in these limbs (the acceleration noted above that occurs during swing in these limbs is the reason for the value of “37” in the square root fit; with the units used in this figure, this parameter would be “100” if the limbs moved only as pendulums during swing).

Figure 8.

Plots of swing duration (A) (mouse, cat, human, and horse data), swing EMG duration (B) (all five species), and swing EMG duration divided by swing duration (C) (all five species) versus limb length. For mouse, cat, human, and horse limb the entire leg is indicated; for stick insect limb the tibia and tarsus are indicated. See Results for explanation. si (stick insect), m (mouse), c (cat), hu (human), and h (horse) indicate which species the data in question are from.

With respect to the second point, swing EMG durations are 208 ms (stick insect), 116 ms (mouse), 227 ms (cat), 204 ms (human), and 110 ms (horse). Despite the monotonic increase in swing duration as limb length increases (Fig. 8A), plotting swing EMG duration versus limb length shows no monotonic relationship (Fig. 8B; note that in this plot the stick insect data have been included, but that the nonmonotonic relationship remains even without the stick insect data). Swing EMG duration shows a similar nonmonotonic dependence when plotted against swing duration or step cycle period (stick insect, 410 ms; mouse, 290 ms; cat, 700 ms; human, 1000 ms; horse, 1400 ms) (data not shown). Figure 7 shows that swing EMG activity occupies an increasing proportion of swing duration as animal size decreases. Figure 8C quantitates this relationship by plotting swing EMG duration divided by swing duration versus limb length, and shows that these parameters are linearly related. This analysis shows that although swing duration increases monotonically with leg length, swing EMG duration shows no simple dependence on limb length. However, the percentage of swing duration that swing motor neurons fire depends linearly on limb length, decreasing as limb length increases.

We present in the Discussion a general hypothesis for why the duration of swing muscle activation should occupy an increasingly large proportion of swing duration as limb length decreases. With respect to the data specifically shown in Figure 7, however, a reason for the different swing motor neuron activation durations in stick insect and humans can be understood by using the data presented in Figure 3 for passive stick insect muscle forces and data from human lower leg to calculate (Appendix) how quickly passive muscle force caused by antagonist (stance) muscle stretch would stop leg swing in the two animals if swing motor neurons were to stop firing. These calculations show that human lower leg velocity would decrease because of antagonist muscle stretch only 63% in 0.8 s, whereas in C. morosus muscle passive forces would completely stop tibia/tarsus momentum-based swing in 0.09 ms. The magnitude of this difference can be appreciated by noting that, if protractor motor neurons stopped firing at any time, stick insect limb movement would cease in less time than the width of the dashed lines in Figure 7 marking swing-stance transitions. Alternatively, without the gluteus maximus activity that slows human leg movement at the end of swing (Lieberman et al., 2006), human swing would decrease only 63% in a time 25% longer than the entire time shown in the figure. C. morosus swing motor neuron activity must therefore continue throughout swing because otherwise leg swing would instantaneously end, whereas in humans swing motor neuron activity can cease shortly after the initial acceleration of the leg because leg momentum can finish the swing movement.

In all animals in Figure 7 there is also swing motor neuron activity late in stance. In stick insect this early firing possibly occurs because the protractor muscle, similar to the extensor (Guschlbauer et al., 2005, 2007; Hooper et al., 2007a,b), only slowly relaxes, which might result in insufficiently rapid swings if the extensor muscle were not “precontracted” before swing beginning. Although mouse and cat muscles contract much faster than do stick insect muscles, the timing of the early swing motor neuron activity (just before swing beginning) in these animals nonetheless suggests that it may serve a similar purpose in them. The motor neuron burst in the middle of stance in humans, ending as it does well before swing beginning, is likely attributable to the muscle in question being bifunctional, and serving as a hip flexor during swing (Hamilton, 1972; Warwick and Williams, 1980; Moore, 1983) but a lumbar spine flexor (Hamilton, 1972; Woodburne and Burkel, 1988) or stabilizer (Nachemson, 1966, 1968; Crisco and Panjabi, 1990; Santaguida and McGill, 1995) or even power muscle (Gracovetsky et al., 1986) during stance. The extent to which the stance phase activity in horse, which begins in the middle of swing and continues without stopping until approximately one-third of the way into swing, is attributable to similar bifunctionality versus preparing for leg swing is unclear.

Together, these data suggest that the different motor control strategies seen in the small and large animals result from the different sizes of the limbs being moved (see Discussion), not whether the muscles are slow or fast. Nonetheless, the insect data may have relevance to two characteristics often seen in invertebrate slow muscle, the presence of high resting muscle tension (tonus) (Hoyle, 1978) and of inhibitory motor neurons (Pearson and Bergman, 1969; Pearson and Fourtner, 1973; Hale and Burrows, 1985; Rathmayer and Bevengut, 1986; Allgäuer and Honegger, 1993) and peripheral modulation of muscle properties (Evans and O'Shea, 1978; Cropper et al., 1987, 1990; Weiss et al., 1992; Evans et al., 1999), including increased relaxation rate. The hypothesis here is that, because in these limbs the joints will have gravity-independent rest positions and require continuous (excitatory) motor neuron activation to move in any case, (1) evolution may have taken advantage of this characteristic by increasing muscle resting tension to accentuate these properties and hence to have the limbs stably assume a particularly useful posture (e.g., appropriate for quiet standing) in the absence of motor neuron activity and (2) the common inhibitor motor neurons and neuromodulatory inputs may have evolved to decrease the interfering opposition of antagonistic muscles during active movement.

Discussion

Intact, unloaded C. morosus legs assumed constant, gravity-independent postures without any activity in leg motor nerves (Fig. 1). Isolated C. morosus and P. americana legs (Figs. 2, 5) assumed constant, gravity-independent postures and returned to them when perturbed. These postures in C. morosus were caused in part by the muscles controlling the joints generating equal passive forces at these angles (Figs. 2B, 3). Swing motor neurons fired throughout the entirety of swing in C. morosus, mouse, and cat but only at swing beginning in human and horse (Figs. 4, 6, 7).

Gravity-independent rest positions and muscle passive force in other animals

Isolated Periplaneta, Blaberus, and Carcinus legs passively return to constant postures after perturbation (Fourtner, 1981; Yox et al., 1982; Dudek and Full, 2007). However, the Periplaneta and Carcinus leg positions relative to gravity were unspecified and the Blaberus legs were arranged horizontally “to remove the effect of gravity from the leg response” [Dudek and Full (2007), p 3211]. Whether these returns were gravity independent was thus unknown. Experiments on isolated Periplaneta legs showed that their returns are indeed gravity independent, and Carcinus passive muscle forces relative to leg mass are large enough that they should be as well. Multiple (ankle extensor, biceps femoris anterior, caudofemoralis, medial gastrocnemius, sartorius anterior, semitendinosus, tenuissimus) cat leg muscles develop passive forces (Grillner, 1972; Stephens et al., 1975; Brown et al., 1996) equal to the force of gravity on masses much larger (0.8–4 kg) than those of the limbs the muscles move, and these limbs should thus also have gravity-independent rest postures. Relaxed human fingers assume a “C”-shaped configuration regardless of hand position relative to gravity. These small limbs may thus also have gravity-independent rest postures.

Use of gravity-independent rest positions in movement control

At stance end, C. morosus ' middle legs are retracted far behind the thorax–coxa joint rest positions shown in Figure 1 (Wendler, 1964; Cruse and Bartling, 1995). One might therefore predict that C. morosus protractor motor neurons would not need fire at swing beginning because the initial portion of swing could occur from passive muscle forces alone. Protractor motor neuron activity nonetheless does occur in early swing (Fig. 4), and in this species all aspects of swing are thus actively driven. Other nervous systems, however, clearly take functional advantage of small limbs having gravity-independent rest positions. Locust leg movements against gravity, presumably passive returns to gravity-independent rest angles, can occur without motor neuron activity (Berkowitz and Laurent, 1996; Zakotnik et al., 2006; Page et al., 2008). Passive forces slow leg velocity during swing phase in turkey (Roberts et al., 1997). When extensor motor nerves in the related stick insect Cuniculina impigra are cut, extensor muscle passive force increases over several days (Bässler et al., 2007). This change shifts joint rest position to 180°, allowing the animals to make extension and flexion movements by activating the flexor muscle alone. A similar situation exists in the cockroach trochanter–femur joint, in which extension occurs solely because of passive joint properties (Watson et al., 2002).

Does scaling explain the size dependence of gravity-independent joint posture and swing motor neuron firing differences?

C. morosus, P. americana, Carcinus, and cat legs, and human ankles and fingers, either do or likely have gravity-independent rest positions, but human elbows, shoulders, knees, and hips do not. Stick insect, mouse, and cat swing motor neurons fire throughout swing, whereas human and horse hip swing motor neurons fire only at swing beginning. The dependence of these differences on limb size, and independence of whether the animals are vertebrate or invertebrate or the muscles are slow or fast, suggest the differences may result from a general scaling phenomenon.

This scaling would arise because muscle passive force varies with muscle cross-sectional area, but limb mass varies with limb volume. In large limbs, muscle passive forces would consequently be so small relative to limb mass that momentum and gravity would dominate limb mechanics: very heavy pendulums with very weak springs oscillate for long periods before stopping, and at rest hang essentially parallel to gravity. In small limbs, alternatively, muscle passive force would be so great relative to limb mass that gravity and momentum would be inconsequential: very light pendulums with very strong springs quickly cease to move, and have rest positions determined by spring forces, not gravity. For joints such as those in invertebrates in which joint tissues might exert restoring forces, analogous arguments apply because the force-generating tissue (the cuticle) is again fundamentally two-dimensional.

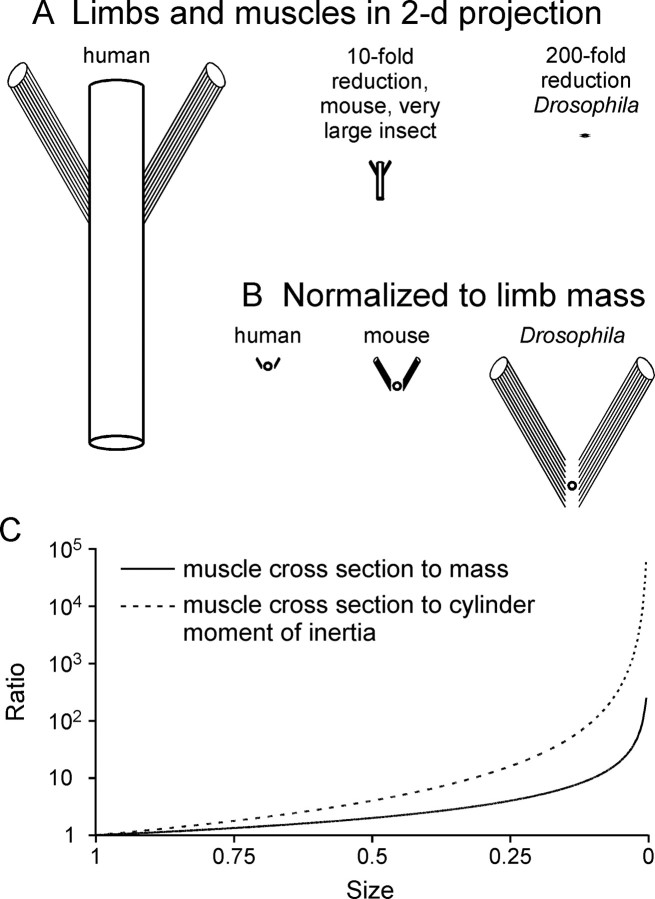
Figure 9 illustrates this idea. Figure 9A shows a two-dimensional schematic of a human leg with two attached muscles and 10-fold (mouse, very large insect legs) and 200-fold (Drosophila legs) reductions. In Figure 9B the cylinders have been replaced with circles whose areas are proportional to cylinder mass, and the schematics normalized to limb mass (circle area). The ratio of muscle cross-sectional area to limb mass is much greater in Drosophila than in humans. Because muscle cross-section varies as size squared, but limb mass as size cubed, their ratio varies as 1/size (Fig. 9C, solid line). For cylindrical limbs this scaling effect is even greater, varying as size to the −2nd power (Fig. 9C, dashed line), because the relevant ratio is cross-section to moment of inertia, which varies as size to the 4th power for cylinders.

Figure 9.

Muscles dominate limb-muscle systems at small limb sizes. Size scaling is accurate, animal identification is approximate.

Changes in other aspects of animal anatomy or physiology could of course alter these scaling effects. Size-dependent changes in moment arm length or muscle physiology (Nauen and Shadwick, 1999, 2001; Van Wassenbergh et al., 2007) could lessen the predicted shift of mass versus muscle in controlling limb rest posture and movement. Bird and mammal muscle cross-section varies as body mass raised to the 0.7th to 0.9th power (Alexander, 1977; Maloiy et al., 1979; Pollock and Shadwick, 1994), larger than the 0.67 expected for the proportional scaling in Figure 9. To create large grip strength, human fingers may be driven by larger muscles than scaling alone would predict. Nonetheless, given the several hundredfold size variation present in limbed animals and the data presented here, it is likely that scaling plays a major role in determining how nervous systems control limbs.

The ideas in Figure 9 are straightforward. We therefore extensively searched for them in the scaling, large and small vertebrate limb, invertebrate limb, energy and locomotion, inverted pendulum, large and insect-inspired robot, and general and textbook literatures (see supplemental material, available at www.jneurosci.org). In these literatures only one article specifically deals with muscle and limb scaling (Garcia et al., 2000). In this study, limb muscles were mimicked by a lumped single muscle rather than considering agonist and antagonist muscles separately. This work consequently could not predict two central issues: (1) that small limbs have gravity-independent rest positions (instead ascribing limb returns to being “mainly due to gravity”) and (2) that muscle passive forces prevent small limbs from making momentum-based movements (instead predicting these movements would be powered by “short, quick [motor neuron] bursts”).

Whether the scaling arguments made here are implicitly contained in this literature is impossible to disprove. However, we can state with certainty that they are never explicitly made, including in textbooks and lay treatments in which such explanation would be expected. Considerations of scaling effects are similarly lacking in explanations of biphasic agonist–antagonist and triphasic agonist–antagonist–agonist muscle activation patterns in limb movements. These motor neuron firing patterns make sense for only momentum-based movement control strategies, in which limb momentum induced by the initial agonist contraction must be diminished by subsequent antagonist activity. However, these authors never mention that these patterns are therefore expected to be used only to control large limbs, and that in small limbs agonist activation must instead continue throughout movement duration because, otherwise, antagonist passive force would prematurely stop limb movement.

This literature does extensively investigate the role of momentum and across-phase energy storage and release in locomotion (see supplemental material, available at www.jneurosci.org). Because this work studies whole body locomotion, not how nervous systems control movements of single unloaded limbs, the data presented here in no way contradict its conclusions. Indeed, small limbs having constant rest postures determined by muscle passive properties is completely consistent with much work in this field, as deflections from these postures in one movement phase would provide an excellent mechanism for storing energy for use in later phases.

Evolutionary implications

It is natural to assume that vertebrate motor neural networks and control strategies will resemble each other more than they do invertebrate ones. However, the data and ideas presented here suggest that limb size may be as important as phylogenetic position in determining motor control strategy. The neural control strategies of human fingers and ankles, and mouse, cat, and all invertebrate limbs may thus resemble each other more than any of them do human shoulder, elbow, hip, knee, and other large-limb control strategies. Furthermore, given that the first limbed animals were small, gravity-independent joint rest positions and non-momentum-based neural control strategies may represent the ur-state from which large-limb control strategies are a derived specialization.

Appendix

Calculating human knee oscillation decay time constant

Calculating how quickly resistive forces slow human knee movement requires deriving the equations governing the movements of damped cylinders such as those in Figure 9. To avoid using moments of inertia and torques or needing to consider where on the cylinder the muscles attach, we replaced the cylinders with point–mass pendulums. The equation of motion of an undamped pendulum is m · l · d²θ/dt² = m · g · sinθ, where m and l are pendulum mass and length, θ is the angle the pendulum makes to the vertical, and g is the gravitational constant. Muscle and joint passive forces are F_r = −b · l · dθ/dt − k · l · Δθ, where l · dθ/dt is muscle stretch or joint velocity and l · Δθ is displacement from muscle or joint rest position. Incorporating these terms, replacing g/l with ω₀², and rearranging gives d²θ/dt² + b/m · dθ/dt + k/m · Δθ + ω₀²θ sinθ = 0.

This equation is not integrable. The equation of motion of a damped harmonic oscillator, d²θ/dt² + (b/m)dθ/dt + ω₀²θ = 0, is an approximation valid for small θ that is integrable. Not including the displacement-dependent resistive forces is justified because we consider here a moving leg, and muscle velocity-dependent forces are typically much greater than displacement-dependent ones. For values of b and m (b/m < 2ω₀) that allow oscillation, a solution to this equation is θ = e^t/2τ (Acos γt + Bsin γt, where τ = m/b, A and B are initial condition-dependent constants, and γ = (ω₀² − b²/4m)^1/2. This function is a sinusoid of exponentially decreasing amplitude with time constant τ. Measuring τ thus determines how quickly passive resistance alone decreases oscillation amplitude, and thus how quickly the oscillation ceases.

τ was calculated by measuring the amplitude decrease over the first oscillation cycle of a male adult knee after release of the foot from a raised position (zero initial velocity, movement due to gravity alone). This value is technically valid only for this particular set of conditions. For instance, if resistance to movement is greater at the higher velocities that occur during swing, this technique would underestimate how quickly passive properties slow the lower limb during walking. However, given the ∼9000-fold difference between the human and stick insect values, any errors so introduced are unlikely to affect article conclusions.

Calculating how quickly flexor muscle passive force would stop tibia swing

Because stick insect legs do not oscillate after perturbation, the method explained above was not used. Flexor muscle passive force during 0.1 s, 0.5 mm linear ramp stretches mimicking those occurring during tibia extension were instead directly measured with an Aurora Scientific 300B dual-mode lever arm system. C. morosus muscles respond to stretch by producing an initial large force (the dynamic force) that then declines to a steady-state value (the static force) after ramp end (Guschlbauer et al., 2007). The forces shown in Figure 3 are the static forces, but because we are here examining the effect of changes of muscle force on a moving leg, we use here the average of the dynamic forces immediately at ramp end, 67 ± 29 mN (SD, N = 12). The flexor muscle works over a moment arm of 0.56 mm (Guschlbauer et al., 2007), and 67 mN thus delivers a torque to the tibia of 38 × 10⁻⁶ N/m. The tibia's moment of inertia is 0.32 × 10⁻⁹ kg m² (Guschlbauer et al., 2007), and thus flexor passive force results in an initial angular deceleration of −117 × 10³ rad/s², or −6.71 × 10⁶°/s². The highest angular velocity during swing is 11 rad/s (516°/s). Flexor passive force would thus stop tibia motion in 0.09 ms if the deceleration were linear. Flexor force production did not change within 0.5 ms after ramp end, and so this linear approximation was accepted.