Does Asynchronous Neuronal Activity Average out on a Macroscopic Scale?

The integration of related findings from different levels of observation is a prerequisite for a comprehensive understanding of brain activity. Although a central question in neuroscience, it remains unclear how the neuronal dynamics observed by single-cell recordings relates to modalities such as functional magnetic resonance imaging and electroencephalography. It is generally assumed that the occurrence of recordable amplitude fluctuations in macroscopic recordings reflects coherent activation of a large number of neurons synchronized at a specific frequency (Singer, 1993). Electrophysiological recordings, on the other hand, also exhibit a slowly decreasing power law in the spectral domain (Novikov et al., 1997) (cf. Fig. 1). It has been argued that the brain does not generate this complex 1/f noise directly, but instead generates a large family of narrow frequency-band oscillations whose spatiotemporal integration gives rise to the observed power law (Buzsáki, 2006).

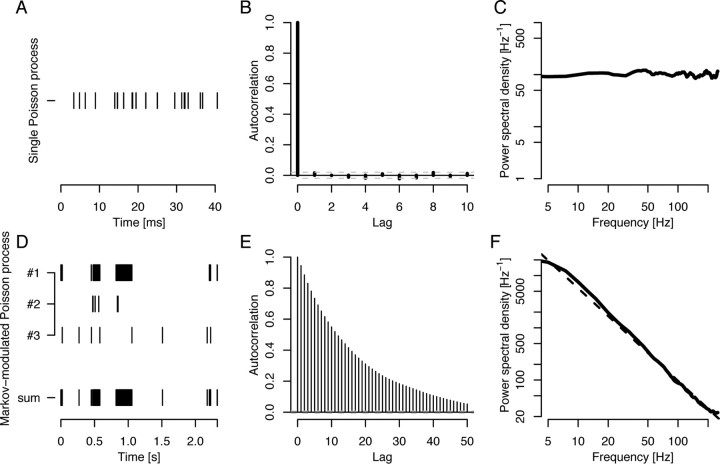
Figure 1.

Spectral analysis of simple models of neuronal activity. A, Typical spike train generated by a single Poisson process. B, The interarrival times of spikes in the Poisson process are independent of earlier interarrival times, i.e., the Poisson process is memoryless. This implies that spikes are not correlated in time, and the autocorrelation function of the signal is zero for positive time lags. C, The power spectral density is the Fourier transform of the autocorrelation function and quantifies the amount of variance (“power”) per frequency component. For the Poisson process the power spectral density is flat. D, Three Poisson processes (#1–3) with distinct intensities (“firing rates”) contribute to the total signal (bottom). Only one process is active at each time, as determined by a hidden Markov process. The time series to be analyzed is the number of spikes in each fixed, small time interval along the time axis (interval length 2 ms, not shown). E, The autocorrelation function of the spike count time series falls off slowly for increasing time lags and indicates long-range correlations. F, The estimated power spectral density of the spike count time series seemingly follows a 1/f^α power-law, as assessed by fitting a line (dashed, slope −α ≈ −1.8) in a double-logarithmic plot. Similar power law behavior is often seen in spectral densities from electrophysiological recordings. Note that both power spectral densities have been smoothed by a moving average filter for easier visualization.

The recent findings of Miller et al. (2009) are important in this regard, since the authors report a broadband power increase during finger movements as obtained by electrocorticography (ECoG). If the validity of the employed method can be confirmed, the spatial resolution of the ECoG electrodes (2–7 mm) would challenge the above views. That is, such a short time interval and small volume would only allow integration over a limited number of neural ensembles, and if these ensembles generate narrow frequency-band oscillations, this might not result in a power-law distribution. The results of Miller et al. (2009) therefore suggest that the observed short-term macroscopic responses partially arise through increased firing rate, i.e., neuronal rate coding, instead of by the activity of locally synchronized neuronal populations.

To discuss the findings of Miller et al. (2009) in this light, we shortly describe the background and the analysis of their experiment. During movements, macroscopic recordings show characteristic power decreases in the alpha (8–12 Hz) and beta (13–30 Hz) frequency bands over the sensorimotor cortex (Pfurtscheller and Lopes da Silva, 1999). The reduction in power is generally thought to reflect desynchronization of neuronal activity and cannot be directly explained by increased neuronal firing rate, as evidenced by microscopic recordings (Georgopoulos et al., 1982). Using ECoG, an increase in gamma band (30–100 Hz) was also reported during motor responses (Crone et al., 1998). Compared with the alpha and beta decrease, the increase in gamma power was more localized in time and somatotopically specific. The neuronal mechanisms responsible for generating activity in these different frequency bands may be partly independent and therefore occupy distinct functional roles.

Miller et al. (2009) argue that this increase is not specifically restricted to the gamma frequency range, but rather is part of a broadband increase in power with a power-law distribution. They arrive at this conclusion based on principal component analysis (PCA) of ECoG recordings in 10 epileptic patients. Each had subdural ECoG grids placed on the surface of the brain overlying the motor cortex. Participants were asked to move fingers independently during 2 s movement trials. Power spectral density was calculated for each electrode from 1 s epochs centered at the time of maximum flexion during each movement and intermediate rests. The power spectral densities were mean centered independently per frequency before applying the logarithmic transform [Miller et al. (2009), their supplemental Eq. 3] and then submitted to PCA for unsupervised (blind) classification of different movement conditions based on covariation of power at different frequencies. The analysis resembles partial least squares using a mean-centering approach, but with one crucial difference: covariances were not computed between spectra of different trials but on the transposed matrix, to “identify motifs of movement-related change in the PSD [power spectral density].” Thereby, the principal components correspond to linear combinations of “spectral densities” instead of trials and/or conditions.

The main finding was that the first principal component corresponds to a broadband increase in power spectral density, as reflected by nonzero frequency element magnitudes (eigenvector coefficients), and the second and third modes represent beta and alpha modulations [Miller et al. (2009), their Fig. 1A,C–G]. These results were highly consistent over subjects and electrodes as evidenced by an almost identical mode separation [Miller et al. (2009), their supplemental Fig. S4]. The projection weights in the first mode were mirrored in the second mode [Miller et al. (2009), their Fig. 1B], reflecting a simultaneous broadband power increase and a decrease in the lower frequency range during finger movements. The relative strength of the first principal mode revealed separable individual finger somatotopy in all subjects and was more focally distributed than the second and third modes, as reflected by the distribution of projection weights over neighboring electrodes [Miller et al. (2009), their Fig. 2, Fig. 3, and supplemental Fig. S5]. To address the relation between the obtained principal components and the movement trajectories, separately computed time-resolved power spectral densities from wavelet decomposition were projected onto the first three eigenvectors. The resulting time course of the first principal component was correlated with finger position and was specific for individual digits [Miller et al. (2009), their Fig. 2, Fig. 4]. The observed broadband power increase might therefore be used as a macroscopic measure to assess the activity of local cortical populations.

These conclusions critically depend on the specific application of PCA, and there are several methodological considerations that need to be addressed. First, applying the logarithmic transform strongly affects the signal's distribution, but can be justified from a statistical perspective to stabilize variance (Bartlett, 1947). The decomposition of the transformed power spectral densities is based on what the authors refer to as “covariance matrix.” This is, however, not a covariance measure but a mere inner product, since the deviation from the logarithmic transform of the mean is used (as opposed to the mean of the logarithms). In practice this means that the first mode describes the baseline (mean) of the (logarithms of) frequency-wise relative power, a quantity that is difficult to interpret. A nonzero first mode, as reported by Miller et al. (2009), might thus result from the manner in which the data are normalized. The linear combination of the “spectral densities” in an eigenmode corresponds to a nonlinear combination of the spectral densities when transformed back. Explicitly, considering just two spectral densities P₁(f) and P₂(f), the combination αlog(P₁(f)/μ(f)) + βlog(P₂(f)/μ(f)) results in (P₁(f)/μ(f))^α(P₂(f)/μ(f))^β when exponentiated. It is therefore not clear how the proposed “principal spectral components” relate to the original spectral densities. Put differently, since the back transformation is multiplicative, even small projection weights (α and β) can have a large influence on the composite, projected spectral density. In combination with the omitted eigenvalues, the interpretation of the reported principal components is difficult, that is, it remains unclear whether the first mode is necessarily caused by a broadband increase in power during finger movements.

Another issue is that the authors seem to regard all samples as independent, although there might well be low-frequency fluctuations. In fact, this would be a consequence of the assumed power law because the autocorrelation function of such a signal would exhibit long-range correlations. As the timing of beta amplitude is related to the movement frequency, high-pass filtering (as the authors did) will not exclude all movement-frequency related effects. The analysis of Miller et al. (2009) is insensitive to changes related to the movement trajectory because their method does not capture changes in power relative to the onset of movement, but rather uses an average of the total power during a single time window around each event. To overcome this limitation, the authors used the above mentioned wavelet approach, but only after the identification of spectral modes.

Other analyses might be better suited to identify motifs of movement-related power changes. For instance, PCA in the frequency domain is well known for its capacity to separate conditions based on the principal components' contribution to the spectral content. This is related to conventional PCA in the time domain in that the frequency domain PCA can be obtained by decomposing the covariance matrix of the time series and their Hilbert transforms (Brillinger, 1981). Thereby, the cross-spectral densities of a multivariate signal, which in the case of Miller et al. (2009) are the cross-spectra between all combinations of epochs, are decomposed by PCA for each frequency separately. When transformed back into the time domain, this results in a set of time series, called principal component series, whose spectral densities are uncorrelated. In contrast, when using PCA on power spectral densities to blindly identify principal components separating frequencies between conditions, the resulting decomposition cannot immediately be interpreted as an actual spectrum. It would indeed be interesting to submit the data of Miller et al. (2009) to comparable analyses whose outcome measures are readily interpretable.

Regardless of alternative methods, genuine “power-law” increases are difficult to prove. Even when assuming that the true spectral densities exhibit power-law behavior, it is not enough to simply fit a regression line to the logarithm of the spectrum (Miller et al., 2007). At the very least, one should search for self-similar behavior in the time domain by calculating the Hurst exponent (see Table 1). The authors mention that such a power spectral distribution could be obtained from an average of a large number of Poisson-distributed neuronal activities without a preferred timescale, i.e., such that their sum does not display frequency-specific oscillations. We should remark here that even simpler models could explain such an observation. One example is a Markov-modulated Poisson process, in which distinct Poisson distributions are switched on or off by a continuous-time Markov chain in a purely random manner. For finite time series, such a nonstationary mixture of stochastic processes exhibits power-law behavior and seems to be long-range dependent (Robert and Le Boudec, 1996) (cf. Fig. 1 for an example). This does offer an alternative explanation for the observed phenomenon that appears more physiologically feasible: instead of a large number of asynchronous neurons, a few synchronized neural clusters may generate the signal in question.

Table 1.

Glossary of technical terms

Term	Description
1/f noise	A signal with a frequency content such that its power spectral density S(f) is proportional to a small power α of the reciprocal of the frequency, i.e., S(f) ≈ 1/fα, where the exponent α satisfies 0 ≤ α ≤ 3. Such signals are characteristic of complex processes without a preferred timescale, e.g., long-range-dependent signals.
Continuous-time Markov chain	A stochastic process X(t) in continuous time for which the conditional probability distribution at time t depends only on a finite number n of values X(s1), X(s2), …, X(sn) from its past, s1 < s2 < … < sn < t. Such a process is also called a process with finite memory. The special case where n = 0 is a memoryless process.
Eigenvalue	Principal component analysis decomposes the covariance matrix of a multivariate data set into an ordered set of eigenvectors along which the data varies the most. The corresponding eigenvalues represent the variance of the data explained by each eigenvector.
Eigenvector coefficients	The components of a principal mode (or eigenmode), i.e., of an eigenvector of the covariance matrix in principal component analysis.
Hilbert transform	A tool from signal processing that shifts the phase factors of a bandpass-filtered signal. Adding the Hilbert transform as imaginary part to the original signal results in an analytic signal, from which the instantaneous phase and the envelope of the signal can be calculated.
Hurst exponent	The Hurst exponent H (where 1/2 ≤ H ≤ 1) quantifies the self-similarity of a signal. A stochastic process X(t) is called self-similar if X(at) has the same probability distribution as aHX(t) for each a > 0. Long-range-dependent signals (e.g., arising from a process with a 1/f power spectral density) exhibit values of H close to 1.
Long-range dependence	A stochastic process is long-range dependent if its autocorrelation function R(τ) falls off slower than exponentially for large values of the lag τ. Such processes have infinite memory and typically give rise to power spectral densities with a 1/f distribution.
Power spectral density	The power spectral density S(f) is the Fourier transform of the autocorrelation function of a stochastic process X(t). It is closely related to the Fourier transform of the signal (which does not exist if X(t) is long-range dependent) and quantifies the frequency content of X(t), i.e., S(f) is the contribution to the variance (or ″power″) of X(t) at the frequency f.
Projection weight	The scalar product of the original signal with an eigenvector of the covariance matrix in principal component analysis, i.e., the coefficient the eigenvector has when the signal is written as a linear combination of all eigenvectors. This quantifies the amount the eigenvector in question contributes to the signal.
Wavelet decomposition	A time–frequency representation of a signal X(t) that quantifies its local frequency content, similar to windowed Fourier analysis. The signal X(t) is convolved with a family of short test signals that are rescaled and translated copies of a single ″mother″ signal (wavelet).

To summarize, if the movement-related power increases are broadband in nature, as Miller et al. (2009) suggest, this seemingly implies that ECoG can pick up the effect of asynchronous neuronal activity. This contradicts common ideas about the nature of electrophysiological signals (e.g., Buzsáki, 2006). Given the small time window (<1 s) and the small spatial scale (<1 cm) it is questionable that such averages yield a broadband spectrum. We offer a more realistic alternative in the form of nonstationary behavior from a few synchronized clusters. Although the possibility of measuring asynchronous activity cannot be excluded and remains intriguing, we believe that more substantial evidence is needed before that conclusion can be reached.