Abstract
Discrimination of stimulus duration on the order of milliseconds has been observed in behavioral and neurophysiological studies across a variety of species and taxa. Several studies conducted in mammals have found neurons in the auditory midbrain (inferior colliculus) that are selective for signal duration. Duration selectivity in these cells arises from an interaction of excitatory and inhibitory events occurring at particular latencies from stimulus onset and offset. As previously shown in barn owls, coincidence of delayed, excitatory events can be used by the CNS to respond selectively to specific stimuli in auditory space. This study formulates several computational models of duration tuning that combine existing conceptual models with observed physiological responses in the auditory brainstem and midbrain to evaluate the plausibility of the proposed neural mechanisms. The computational models are able to reproduce a wide range of in vivo responses including best duration tuning, duration-selective response classes, spike counts, first-spike latencies, level tolerance to changes in signal amplitude, and neuropharmacological effects of applying inhibitory neurotransmitter antagonists to duration-tuned neurons. A unified model of duration tuning is proposed that enhances classic models of duration tuning, emphasizes similarities across the models, and simplifies our understanding of duration tuning across species and sensory modalities.
Introduction
Stimulus duration can encode information about the source and meaning of a signal. To use temporal information, the CNS employs mechanisms that can discriminate temporal intervals over several orders of magnitude. Numerous neurophysiological studies in frogs (Potter, 1965; Gooler and Feng, 1992; Leary et al., 2008), rats (Pérez-González et al., 2006), mice (Brand et al., 2000), guinea pigs (Wang et al., 2006), cats (He et al., 1997), and bats (Ehrlich et al., 1997; Casseday et al., 2000; Faure et al., 2003; Mora and Kössl, 2004; Fremouw et al., 2005) reveal the presence of auditory duration-tuned neurons (DTNs) with precise millisecond level response discrimination (tuning) to stimulus durations typical of species-specific vocalizations. Visually oriented DTNs have also been reported in areas 17 and 18 of the cat visual cortex (Duysens et al., 1996). Duration-tuned neurons were first observed in the torus semicircularis of amphibians (Potter, 1965) and later in the inferior colliculus (IC) of mammals (Casseday et al., 1994). Their physiological responses can be characterized by having a maximum spike count at a best duration (BD) and a temporal response bandwidth, typically to pure tones or species-specific frequency-modulated (FM) signals (Casseday et al., 1994, 2000; Fremouw et al., 2005).
Temporal selectivity in the CNS can be conceptualized to arise out of internal state changes in neural networks between two temporally separated events such as a stimulus onset and offset (Buonomano and Maass, 2009). For example, a counting mechanism coupled to an internal clock has been hypothesized to provide temporal discrimination on the order of seconds to minutes (Roberts, 1981; Church, 1984; Meck, 2006). Singh and Mountain (1997) demonstrated millisecond level selectivity for bandpass duration tuning using rate coded model neurons and a coincidence detection mechanism of delayed onset- and offset-evoked excitatory events.
Whole-cell patch and extracellular recordings in the amphibian and mammalian auditory midbrain provided evidence that duration tuning results from the interaction of early postsynaptic inhibition and delayed postsynaptic excitation (Fuzessery and Hall, 1999), and/or from the interaction of sustained postsynaptic inhibition and multiple postsynaptic excitations (Covey et al., 1996; Casseday et al., 2000; Faure et al., 2003; Leary et al., 2008). A similar coincidence detection mechanism has been described for microsecond level timing in the nucleus laminaris of barn owls (Carr and Konishi, 1990), suggesting the mechanism may be used generally by the CNS to encode and discriminate temporal signals.
Here, we amalgamate conceptual models of duration tuning with observed neuronal response characteristics to produce formal, detailed, and biologically plausible computational models of DTNs. Our goals were to evaluate the plausibility of each model and to explore their response dynamics. We propose that each conceptual model can be described by a single, overarching model, and then demonstrate how each duration-tuning response class can arise by simple parameter adjustments in the unified model.
Materials and Methods
Conceptual models.
Responses of DTNs can be divided into three electrophysiological response classes (Jen and Zhou, 1999; Faure et al., 2003). (1) Short-pass DTNs have spike counts that peak at BD and drop to ≤50% of the peak at durations longer than BD, whereas stimuli shorter than BD continue to elicit strong spiking. (2) Bandpass DTNs also have a peak spike count to a BD, but their spike counts drop to ≤50% of the peak count at durations both shorter and longer than BD. (3) Long-pass DTNs do not have a BD and are characterized by responding only when the stimulus exceeds a minimum duration. Moreover, the minimum stimulus duration required to elicit a response does not continue to decrease as signal energy increases (Brand et al., 2000; Faure et al., 2003; Pérez-González et al., 2006) even though central auditory neurons tend to respond with more spikes at a short latency to higher amplitude stimuli (Kiang, 1965). Spikes for short-pass and bandpass DTNs typically occur after stimulus offset, whereas spikes for long-pass cells can occur during the ongoing portion of the stimulus (Faure et al., 2003; Pérez-González et al., 2006).
Three conceptual models have been proposed to explain the neural mechanisms underlying short-pass, bandpass, and long-pass duration tuning in the auditory midbrain of amphibians and mammals, and all rely on the temporal interaction of synaptic excitation and inhibition (Fig. 1). The first model is a coincidence detection mechanism that suggests a transient, onset-evoked excitation coinciding with an offset-evoked excitation could produce cells with responses tuned to specific stimulus durations. If the onset-evoked excitation arrived either before or after the offset-evoked excitation, there would be no temporal coincidence of the excitations and the DTN would fail to respond (Potter, 1965; Narins and Capranica, 1980). Whole-cell patch recordings indicated that DTNs received an onset-evoked IPSP that preceded an onset-evoked EPSP (Casseday et al., 1994; Covey et al., 1996). Paired tone stimulation experiments confirmed that DTNs received inhibition that preceded excitation, and that the inhibition was sustained for as long or longer than the duration of the stimulus (Faure et al., 2003). Many DTNs lost their selectivity and responded to all stimulus durations when inhibition to the cell was blocked with neurotransmitter antagonists (Casseday et al., 1994). The cells also changed the timing of their spikes from offset-following to a fixed latency from stimulus onset (Fuzessery and Hall, 1999; Casseday et al., 2000). Because in vivo single-unit recordings and neuropharmacological experiments revealed that many DTNs received a suprathreshold, onset-evoked excitation (Casseday et al., 2000; Faure et al., 2003), this contradicted the original coincidence detection mechanism of duration tuning that assumed both the onset- and offset-evoked excitations were subthreshold.
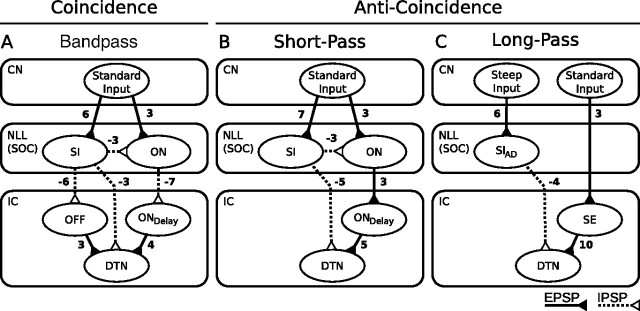
Figure 1.
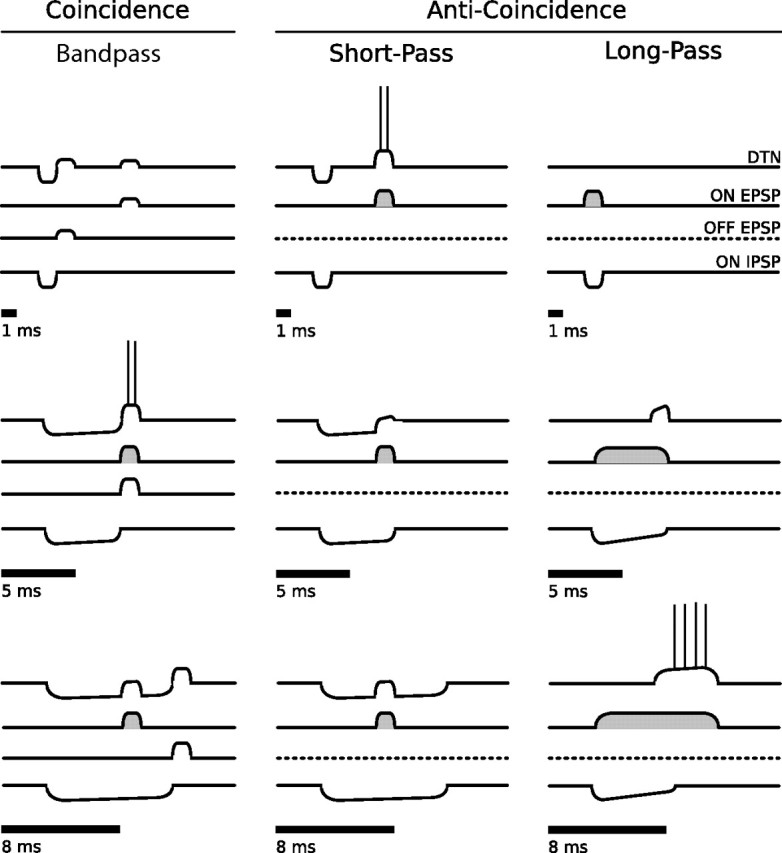
Coincidence and anti-coincidence conceptual models for the creation of bandpass, short-pass, and long-pass DTNs. Four traces are shown above each stimulus (black bars). The top traces show the membrane potentials from the summation of synaptic inputs and, if suprathreshold, the spike output of the DTN. The second, third, and bottom traces represent hypothetical synaptic inputs to a DTN. Each model has two or three inputs illustrated as EPSPs or IPSPs: (1) onset-evoked EPSP (ON EPSP; second trace); (2) offset-evoked EPSP (OFF EPSP; third trace; coincidence detection model only); (3) onset-evoked IPSP (ON IPSP; bottom trace). In the coincidence detection model, the DTN spikes only when the ON EPSP coincides with the OFF EPSP. This occurs for the 5 ms stimulus but not for the 1 or 8 ms stimuli. For the 1 ms stimulus, the ON and OFF EPSPs are absent or weak. For the 8 ms stimulus, the ON and OFF EPSPs do not coincide and the ON EPSP is rendered subhreshold by the ON IPSP. In the anti-coincidence models, the DTN spikes only when the ON EPSP does not coincide with the sustained ON IPSP. In the short-pass anti-coincidence model, this occurs for the 1 ms stimulus but not for the 5 or 8 ms stimuli. For the long-pass anti-coincidence model, this occurs only for the 8 ms stimulus. In the long-pass model, the ON EPSP is sustained, whereas the ON IPSP adapts. Suprathreshold EPSPs are illustrated with gray shading. The OFF EPSP is absent in both anti-coincidence models (dashed lines). Models were adapted and modified from Fuzessery and Hall (1999), Faure et al. (2003), and Leary et al. (2008).
Here, we propose a new version of the coincidence detection model of duration tuning that is consistent with the in vivo data. Our model employs suprathreshold, onset-evoked excitation at all but the shortest stimulus duration (i.e., 1 ms); however, this excitation can be rendered subthreshold when it interacts (coincides) with inhibition. Later, we demonstrate that inhibition is crucial for controlling the temporal specificity (i.e., window of temporal coincidence) for the onset- and offset-evoked EPSPs. In our new version of the bandpass coincidence detection model, a DTN fails to spike at 1 ms because there is insufficient stimulus energy to evoke reliable firing in the cells providing the onset- and offset-evoked excitations. In the new version of the short-pass coincidence detection model, the spiking threshold of the cells providing the onset-evoked excitation was lowered and this permitted responses from the DTN at 1 ms.
The second conceptual model is an anti-coincidence mechanism described specifically for short-pass duration tuning (Fuzessery and Hall, 1999). This model suggests a short-latency, onset-evoked IPSP, lasting the duration of the stimulus, occurs at a fixed latency from stimulus onset, and that a delayed, suprathreshold, onset-evoked EPSP arrives after the IPSP when the stimulus is shorter than some duration. When the stimulus duration is longer, the IPSP now overlaps with the delayed EPSP and this prevents the DTN from reaching spike threshold. The anti-coincidence model does not rely on an offset-evoked response or the coincidence of excitatory events (i.e., EPSPs).
The third model, also an anti-coincidence mechanism, is specific to long-pass duration tuning and suggests that a suprathreshold, onset-evoked EPSP provides sustained excitation to the DTN throughout the stimulus (Brand et al., 2000; Faure et al., 2003; Pérez-González et al., 2006). A strong, onset-evoked IPSP is also present and overlaps with the suprathreshold EPSP, and this prevents action potentials in the DTN for the first several milliseconds. When the IPSP ends, or when its strength decreases (adapts), the suprathreshold EPSP evokes action potentials in the DTN for the remainder of the stimulus. Because the DTN spikes only when there is no significant interaction between the EPSP and IPSP, this model is also classified as anti-coincidence.
Computational model components.
Our computational models simulate cells from subpopulations of neurons in the mammalian central auditory system that differ in their physiological response properties. For convenience, we have suggested possible anatomical locations for these neural populations, although the performance of the models is not dependent on their exact locations. Model performance is also independent of stimulus frequency, but we assume that all input populations are excited at their characteristic frequency. Furthermore, we only consider monaural auditory pathways at this time because the majority of in vivo data on the responses of DTNs have been collected using monaural, contralateral acoustic stimulation (i.e., acoustic stimuli were presented to the ear contralateral to the electrode recording site).
Each model cell population, other than the single DTN in the IC and the afferent input population in the cochlear nucleus (CN), was composed of 10 model neurons. Sound input to the system was modeled by simulating driven (evoked) CN activity with 25 Poisson distributed random spiking processes with a mean firing rate (μ) that exceeded 0 Hz during the stimulus (25 Poisson processes each with mean spiking rate μ is equivalent to a single Poisson process with mean spiking rate of 25μ). We incorporated a larger number of neurons in the CN input responses so that individual spiking rates could be described at physiologically plausible rates. An initial burst of spikes lasting 2 ms that grows with stimulus amplitude was modeled to mimic the onset burst response of auditory nerve fibers (Kiang, 1965) and CN neurons (Rhode and Greenberg, 1992). Additionally, a 0.2 ms onset and offset ramp was applied to μ to simulate the energy envelope of mechanically generated acoustic signals.
The complete input firing rate for simulated CN evoked activity is characterized for 100 Hz < μ < 500 Hz by the equations below, where t is time in milliseconds relative to stimulus onset, μ0 is the mean firing rate of a CN neuron after its initial onset burst of activity, d is the stimulus duration, r (μ(t), t) is a linear energy envelope ramp function of 0.2 ms, and μr(t) is the mean spiking rate after the onset burst and ramp functions have been applied as follows:
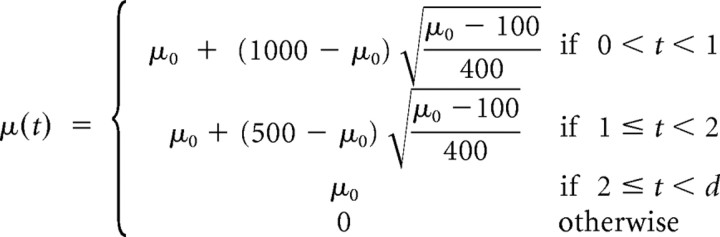 |
An example peristimulus time histogram (PSTH) of the Poisson process for the simulated evoked CN activity is shown in Figure 2A. For rates >500 Hz, the initial onset burst of spikes was capped at a firing rate of 1000 Hz. Although auditory neurons are known to phase lock to stimulus frequency, this ability is greatly diminished at carrier frequencies ≥3 kHz (Covey and Casseday, 1999). Because in vivo DTNs show little to no spontaneous activity (Casseday et al., 1994; Faure et al., 2003), our models have, for the most part, ignored spontaneous input; however, for instances in which we wanted to model a DTN with spontaneous activity, we included an additional population of Poisson spiking processes to excite the DTN directly for the entire simulation (e.g., see below, Anti-coincidence model).
Figure 2.
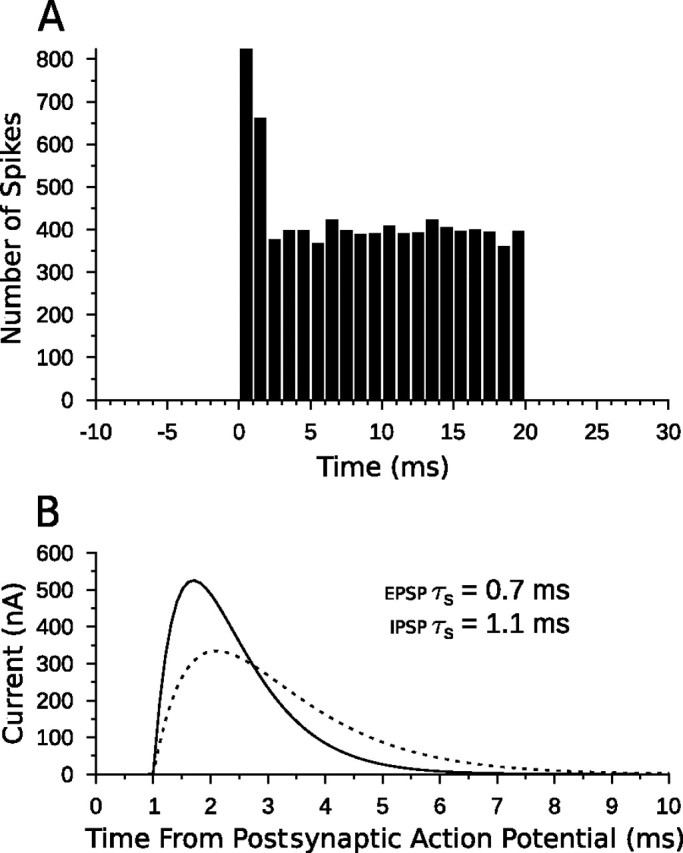
Model CN afferent input and postsynaptic α-functions. A, PSTH of spike counts for 25 model CN Poisson neurons over 40 trials with a mean firing rate μ0 of 400 Hz. The stimulus occurs from 0 to 20 ms. Each time bin is 1 ms and there are 25 × 40 = 1000 neuron trials per bin, so the spike count can be interpreted as an averaged, instantaneous firing rate in hertz. The onset burst in the CN neurons is easily seen in the first and second bins. B, The α-function of the model with τs = 0.7 ms (EPSP; solid line) and τs = 1.1 ms (IPSP; dashed line) plotted as a function of time since the postsynaptic neuron generated an action potential. A 1 ms delay was added to simulate the axonal delays of each neuron in the circuit. Each function is normalized to an area of 1 before being scaled by q to ensure the same total energy for each spike regardless of τs. Increased or decreased levels of current can be implemented by multiplying the α-functions by a scaling factor (connection weight).
Although rate level functions of mammalian CN neurons vary, for consistency of comparison, our chosen values of 350, 400, 450, and 500 Hz were used for all simulations. These values are on the same order as for CN neurons from horseshoe bats, Rhinolophus ferrumequinum (Vater, 1982), and correspond to an input stimulus dynamic range of ∼30–40 dB.
An adaptive exponential integrate-and-fire (aEIF) single neuron model (Brette and Gerstner, 2005) was used for all other model neurons with parameters set so that model output was qualitatively comparable with response characteristics observed for in vivo and in vitro neurons. Parameters for each model neuron within a population were often drawn from a normal distribution with a mean (μ) and variance (ς) to simulate the varying nature of real neural systems. Each population was fully and unidirectionally connected with neurons between populations. The connection strength was characterized by a weight, W, that was divided evenly between each individual connection. This allowed a population to have an arbitrary number of model neurons without changing the total summed connection strength. The membrane potentials of postsynaptic cells were modified with a current injecting α-function (Fig. 2B), multiplied by W, as described by Gerstner and Kistler (2002). Full implementation details are given in Appendix.
The aEIF model is defined by the following differential equations:
 |
where C is the cell membrane capacitance, V is the membrane potential, t is time, gL is the leak conductance, EL is the leak reversal potential, w is an adaptation parameter with dynamics characterized by time constant τw, a is a subthreshold adaptation value, I is the input current, and s(V) is an exponential spiking mechanism characterized by a slope factor, ΔT, and a threshold value, VT. An exponential spiking mechanism is said to reach threshold when the rate of change in membrane voltage approaches infinity. In practice, spikes in our model were triggered when the membrane potential reached an absolute value of +20 mV because the rate of change was always satisfactorily steep at this point. Changing this hard threshold only modifies spike times by a fraction of a millisecond (Gerstner and Kistler, 2002). To confirm this, we reran several simulations with a hard threshold of −20 mV, and no differences in spike timing or response characteristics were observed. When a spike occurred, the time was recorded and the membrane potential was reset to a predetermined value, VR.
Coincidence detection model.
The coincidence detection model defines three events responsible for causing a DTN to selectively produce action potentials in response to a stimulus of appropriate duration (Faure et al., 2003; Leary et al., 2008): (1) a short-latency, onset-evoked inhibition (IPSP) that is sustained for at least the duration of the stimulus; (2) a longer latency (delayed), onset-evoked excitation (EPSP); and (3) an offset-evoked excitation (EPSP). At the shortest stimulus duration (1 ms), the onset- (2) and offset-evoked EPSPs (3) are either absent or subthreshold. At longer durations (≥2 ms), the onset-evoked EPSP is suprathreshold on its own but is rendered subthreshold when interacting with the onset-evoked IPSP (1). The offset-evoked EPSP is subthreshold. When events (2) and (3) coincide, the membrane potential of the neuron is likely to rise above the spike generation threshold, resulting in action potentials in the DTN. In Figure 1, we illustrate (3) as an independent offset-evoked EPSP, but this event could also be modeled as postinhibitory rebound excitation in the model DTN, and later we explicitly explore this possibility (see Results, Relevance of model components). This model is naturally conducive to producing bandpass duration tuning because short stimulus durations cause the onset- and offset-evoked EPSPs to be weak or absent and long signal durations cause the offset-evoked EPSP (3) to occur after the delayed, onset-evoked EPSP (2).
A schematic illustrating the network connections of our bandpass coincidence detection model is shown in Figure 3A. First, the CN excites two populations of neurons that for our purposes have been hypothesized to reside in the nucleus of the lateral lemniscus (NLL) because of its inhibitory connections to the IC (Schofield, 2005); however, neurons with similar response characteristics and inhibitory connections to the IC are also found in the superior olivary complex (SOC) (Schofield, 2005). Hence, the model is not dependent on input from particular auditory nuclei. The first population provides sustained inhibition (SI) to its target cells: an onset-evoked population of cells (ON) in the NLL, an offset-evoked population of cells (OFF) in the IC, and to the single model DTN in the IC. When the stimulus ends, the sustained inhibition ends and the targets of the SI units are released from inhibition. This results in postinhibitory rebound spikes in the population of OFF cells that provide subthreshold excitation to the model DTN, and also marks the offset of the stimulus. For additional details on the physiological characteristics of postinhibitory rebound of in vitro IC neurons, see Peruzzi et al. (2000) and Sun and Wu (2008). Offset responding cells have also been found in the SOC of bats (Grothe, 1994) and rabbits (Kuwada and Batra, 1999), and in the superior paraolivary nucleus of rats (Kadner et al., 2006). The sustained inhibitory input to the DTN prevents action potentials from being evoked during the stimulus and plays a key role in refining the duration-tuning curve (see Results, Relevance of model components).
Figure 3.
Network flow diagrams for three computational models of duration tuning. The rectangles define nuclei of the mammalian central auditory system in which the proposed model components may exist in vivo. The solid lines with filled triangles connecting populations represent EPSPs, and the dashed lines with open triangles represent IPSPs, with connection weights as shown. The ovals represent subpopulations of neurons that share similar response characteristics. Standard Input, Acoustic input implemented as a Poisson spiking process in CN afferents (Fig. 2A); Steep Input, acoustic input to inhibitory components in the long-pass model implemented as a Poisson spiking process with a mean firing rate that grows steeply as stimulus intensity increases; SI, cells that provide sustained inhibition during a stimulus; ON, cells that respond with one or two spikes to stimulus onset; OFF, cells that respond with one or two spikes to stimulus offset via a postinhibitory rebound mechanism; ONdelay, onset cells that respond with one or two spikes after some delay; SIAD, cells that provide adapting sustained inhibition during a stimulus; SE, cells that provide sustained excitation during a stimulus. A, In the bandpass coincidence detection model, the DTN responds only when the stimulus duration results in the production of spikes in the ON cells and EPSPs from the ONdelay and OFF cells coincide. B, In the short-pass anti-coincidence model, the DTN responds only when the EPSP from the ONdelay cells does not coincide with the IPSP from the SI cells. C, In the long-pass anti-coincidence model, the DTN responds only when the EPSP from the SE cells is not suppressed by the adapting IPSP from the SIAD cells.
The CN also drives a population of onset responding cells (ON) that provide a transient, onset-evoked inhibition to a population of delayed onset responding cells (ONdelay) in the IC. When ONdelay cells are released from inhibition, they rebound with one or two action potentials that provide suprathreshold excitation to the DTN for durations ≥2 ms; however, when coinciding with inhibition from the SI population, the postinhibitory rebound excitation is rendered subthreshold. Because the response characteristics of the ON population are mostly independent of stimulus duration, the ONdelay population will be released from inhibition at a fixed latency from stimulus onset. Each cell in the ON population produces only one or two action potentials at stimulus onset and then ceases to fire for the remainder of the stimulus. Inhibition from the SI population ensures that ON cells do not produce action potentials after their initial onset burst of spikes. Onset cells in the bandpass coincidence model were tuned with a higher spiking threshold and required stimulus durations ≥2 ms before producing spikes. For an overview of onset responses of in vivo NLL neurons, see Covey and Casseday (1991). Onset-bursting cells with similar behavior are also found in the IC (Xie et al., 2008).
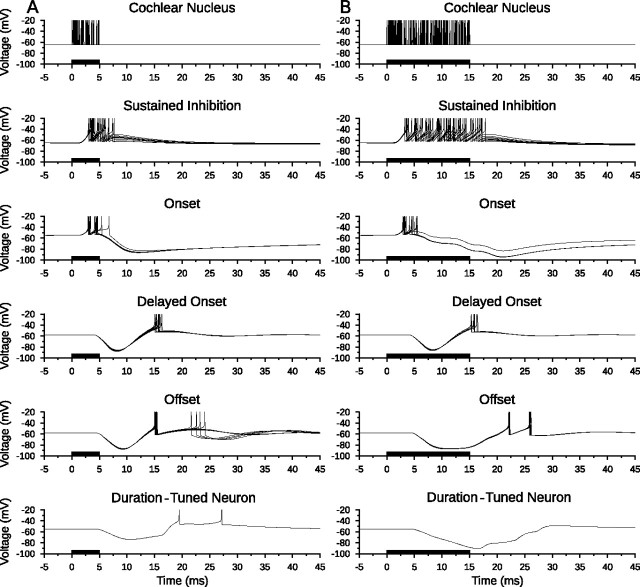
To illustrate responses of each cellular population, Figure 4A shows the membrane voltage traces of each neuron in the coincidence detection model for a single stimulus presentation at the BD of the network (in this case, 5 ms). Figure 4B demonstrates the response of the model to a longer stimulus (15 ms) that is not at BD and clearly shows a lack of spiking in the model DTN when responses from the ONdelay and OFF cells fail to coincide.
Figure 4.
Bandpass coincidence detection duration tuning. Shown are model neuron responses to a single standard input stimulus from the cochlear nucleus at 400 Hz for a duration of 5 ms (A) and 15 ms (B) to illustrate model responses to a BD stimulus and a longer duration stimulus. Membrane potential (voltage) traces of every neuron in the model are shown with action potentials truncated for improved subthreshold clarity. Action potentials from the cochlear nucleus Poisson spiking processes are drawn as instantaneous spikes. A, The duration-tuned neuron produced action potentials when there was a coincidence of spikes from the delayed onset and offset populations. B, When excitations from the delayed onset and offset populations did not coincide, the membrane potential of the DTN remained subthreshold and no action potentials were produced. Stimulus duration is illustrated as black bars on the time axis.
Assuming the first-spike latency of OFF cells (re stimulus offset) is consistent across all durations, then it is the response latency of the ONdelay cells (re stimulus onset) that ultimately determines the BD of the coincidence detection network. The temporal bandwidth of duration tuning is determined by the duration and strength of the ONdelay and OFF EPSPs as these define the window of coincidence. The DTN produces spikes only when the stimulus is long enough to evoke spikes in the ON population and short enough such that the ONdelay and OFF EPSPs coincide. Our computational model is similar to the coincidence detection model originally postulated by Potter (1965) and later by Narins and Capranica (1980) but differs in one key characteristic. In the new model, the onset-evoked EPSP is always suprathreshold except when it coincides with inhibition or for a 1 ms stimulus when it is weak or absent. Classic presentations of the coincidence detection model suggested that the onset-evoked EPSP was always subthreshold and did not include a role for inhibition. As shown later, these modifications were critical for reproducing results from in vivo neuropharmacological experiments (see Results, Relevance of model components).
Anti-coincidence model.
The anti-coincidence model suggests a mechanism in which suprathreshold, onset-evoked excitation causes action potentials in the model DTN only if it arrives after the onset-evoked, sustained inhibition (Fig. 1). Thus, the anti-coincidence model defines two key events responsible for producing selectivity to short stimulus durations (Fuzessery and Hall, 1999): (1) a short-latency, onset-evoked inhibition (IPSP) that is sustained for at least the duration of the stimulus, and (2) a longer latency (delayed), suprathreshold, onset-evoked transient excitation (EPSP). When event (2) occurs after event (1), the membrane potential of the DTN is likely to rise above the spike generation threshold, resulting in action potentials. At longer durations, the sustained IPSP coincides with the onset-evoked EPSP and this suppresses suprathreshold activity in the model DTN.
The network structure of an anti-coincidence short-pass duration-tuned neural circuit is shown in Figure 3B. Simply removing the offset excitation component from the coincidence detection model in Figure 3A without other modifications caused the model DTN to respond with few or no spikes. This was because excitation from the ONdelay population was rendered subthreshold when combined with the sustained inhibition. In the short-pass anti-coincidence model, we increased the ONdelay to DTN connection weight from 4 to 5 to provide suprathreshold excitation to the DTN even when a small amount of inhibition coincided with the arrival of the EPSP at shorter durations. At longer durations when the inhibition was stronger, the ONdelay was still rendered subthreshold. In the bandpass coincidence detection model, the ON population was tuned with a high spiking threshold to prevent spiking to short stimulus durations. To permit sensitivity to short stimulus durations in the short-pass anti-coincidence model, ON cells were tuned with a lower spiking threshold by changing the leak reversal potential (EL) and spike threshold (VT) parameters by 2 mV. We found that the onset bursting behavior of the input CN population was critical for evoking spikes in DTNs at short (1–2 ms) stimulus durations. At longer stimulus durations (≥3 ms), the onset bursting behavior in the CN afferents was less critical. We also changed the inhibitory connection between the ON and the ONdelay population to an excitatory connection. The reason for doing this was to account for the shorter first-spike latencies and sharper temporal response bandwidths observed in many in vivo short-pass DTNs (Faure et al., 2003).
A postinhibitory rebound mechanism in the ONdelay population, as described in the coincidence detection model, could also be implemented in an anti-coincidence model to produce a short-pass DTN. The postinhibitory rebound would delay the arrival of suprathreshold excitation to the DTN; hence longer duration stimuli would be required before sustained inhibition from the SI population would overlap with the EPSP from the ONdelay population. This would result in a short-pass DTN with a wider temporal response bandwidth and longer first-spike latency (data not shown).
Many in vivo DTNs elicit several action potentials in response to short duration stimuli, and the spikes tend to be spread apart by several milliseconds (Faure et al., 2003). To account for this, we hypothesized that such cells received subthreshold, spontaneous activity acting as an additional source of excitation (i.e., EPSPs) riding on top of the excitation from the onset-evoked EPSP to produce longer latency action potentials at short durations. To model this, we generated random Poisson spikes for the entire run of the simulation in a population of five neurons, each with a mean firing rate of 50 Hz. This population synapsed directly on the DTN with an excitatory connection weight of 1.
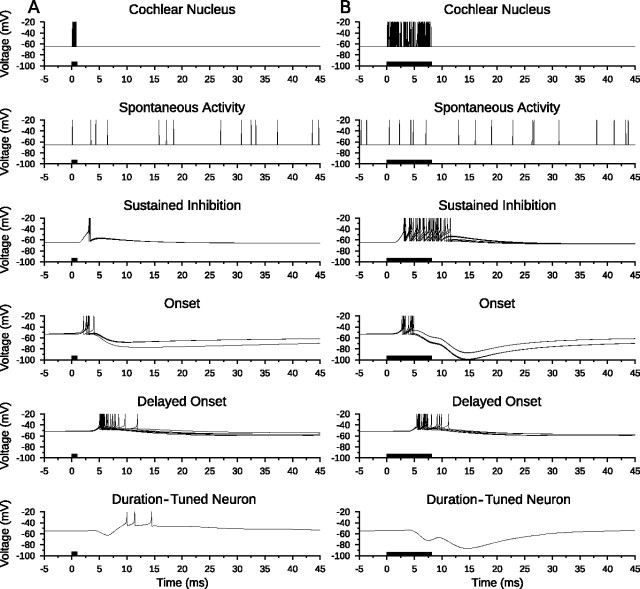
In the anti-coincidence model of duration tuning, the ON population excited the ONdelay population after stimulus onset, and the ONdelay population provided suprathreshold excitation to the DTN. Figure 5 shows the membrane potential traces of each neuron in a short-pass anti-coincidence model to a single stimulus presentation at BD (1 ms) and at a longer duration (8 ms). The SI population provided sustained inhibition to the model DTN beginning shortly after stimulus onset and lasting throughout the stimulus. At short durations, spiking was evoked in the SI population for only a short time period. As a result, inhibition from the SI population ended before excitation from the ONdelay population arrived. This allowed for the production of action potentials in the model DTN. When the duration of the stimulus was lengthened, sustained inhibition from the SI population coincided with excitation from the ONdelay population and this prevented action potentials in the model DTN.
Figure 5.
Short-pass anti-coincidence duration tuning. Shown are model neuron responses to a single standard input stimulus from the cochlear nucleus at 400 Hz for a duration of 1 ms (A) and 8 ms (B) to illustrate model responses to a BD stimulus and a longer duration stimulus. Spontaneous activity to the DTN from five Poisson spiking processes each with a mean firing rate of 50 Hz is also shown. Membrane potential (voltage) traces of every neuron in the model are shown with action potentials truncated for improved subthreshold clarity. Action potentials from the cochlear nucleus Poisson spiking processes and from spontaneous activity are drawn as instantaneous spikes. A, Excitation from the delayed onset cells was suprathreshold unless it overlapped with inhibition. Therefore, the duration-tuned neuron produced action potentials when there was an anti-coincidence of spikes in the sustained inhibition and delayed onset populations. B, When responses of the delayed onset and sustained inhibition populations overlapped, the membrane potential of the duration-tuned neuron remained subthreshold and no action potentials were produced. Stimulus duration is illustrated as black bars on the time axis.
Long-pass model.
Unlike typical sensory neurons that show a decrease in first-spike latency in response to increasing stimulus intensity (Kitzes et al., 1978; Heil, 1997), some long-pass DTNs in the mammalian IC show an increase in first-spike latency at higher sound pressure levels (SPLs) (Faure et al., 2003; Pérez-González et al., 2006). The response characteristics of long-pass DTNs differ both qualitatively and quantitatively from bandpass and short-pass DTNs in that (1) spikes are evoked by the onset of the stimulus, (2) spikes occur during the ongoing portion of the stimulus, and (3) the number of spikes tends to increase with stimulus duration. To model these responses, we instantiated an anticoincidence tuning mechanism proposed by Brand et al. (2000), Faure et al. (2003), and Pérez-González et al. (2006) with the components illustrated in Figure 3C.
The long-pass model used our standard CN Poisson input spiking process to provide excitation throughout the duration of the stimulus to sustained excitation (SE) cells in the IC, which then relayed excitation to the model DTN in the IC. Additionally, a second population of CN afferents with a steeper rate level function (i.e., afferents with a larger increase in spiking rate as a function of stimulus magnitude) excited cells in the NLL (or SOC) that provided adapting, sustained inhibition (SIAD) to the DTN. We used two different CN rate level functions (standard and steep) to account for the in vivo responses of long-pass DTNs at higher SPLs. For a stimulus of fixed duration, the strength of inhibition received by the model DTN grew faster than the strength of the excitation as stimulus magnitude increased, resulting in decreased spike counts and longer first-spike latencies as observed in vivo. Recruiting afferent input to the model at different rates is biologically plausible because a wide variety of rate level functions exist in the mammalian central auditory system [for auditory nerve fibers, see Kiang (1965); for CN afferents, see Rhode and Greenberg (1992)].
The long-pass model incorporates neurons with adapting, sustained inhibition (SIAD) to inhibit the model DTN. This is in contrast to the short-pass and bandpass models, which used nonadapting inhibitory inputs. Neurons with adapting responses are referred to as “primary-like” and have been observed in the NLL (Covey and Casseday, 1991) and the SOC (Guinan et al., 1972).
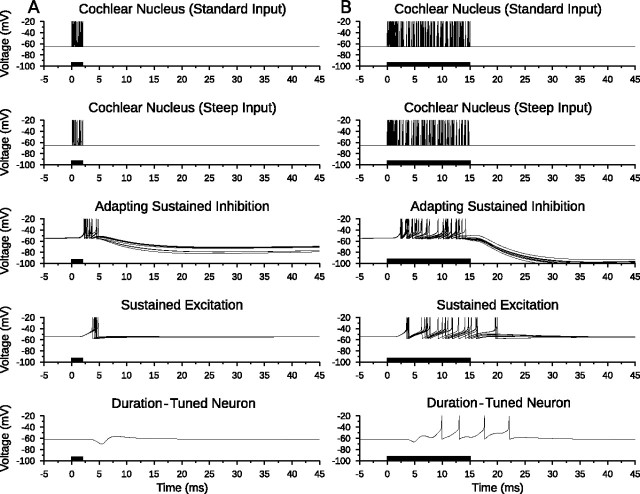
Figure 6A shows the membrane potential traces of each neuron in the long-pass model in response to a 5 ms stimulus. Inhibition from the SIAD population was strong and suppressed spiking that might otherwise have been induced in the DTN by excitation from the SE population. Figure 6B shows the membrane potential traces of the same long-pass model network in response to a 15 ms stimulus. Starting at ∼10 ms after stimulus onset, the SIAD population had adapted sufficiently so that excitation from the SE cells was able to evoke action potentials in the DTN. Note the subthreshold change in the membrane potential of the model DTN from 4 to 8 ms after stimulus onset caused by the SIAD cells overpowering the sustained excitation. Faure et al. (2003) and Pérez-González et al. (2006) observed longer first-spike latencies in some long-pass DTNs as stimulus magnitude increased. To account for this, we hypothesized that CN afferent input to the SIAD population grew more quickly than CN afferent input to the SE population; thus, increasing stimulus energy caused the SIAD-evoked inhibition to lengthen in duration and overlap with the initial portion of the onset-evoked EPSP. This resulted in longer first-spike latencies in the model cell, reproducing the so-called “paradoxical latency shift” (Heil, 2004) that has been observed in some long-pass DTNs and other IC neurons (Wang et al., 2007).
Figure 6.
Long-pass anti-coincidence duration tuning. Shown are model neuron responses to a single input stimulus that recruits standard input at 400 Hz and steep input at 250 Hz from the cochlear nucleus to illustrate model responses to a 2 ms (short) stimulus (A) and a 15 ms (long) stimulus (B). Membrane potential (voltage) traces of every neuron in the model are shown with action potentials truncated for improved subthreshold clarity. Action potentials from the cochlear nucleus Poisson spiking processes are drawn as instantaneous spikes. A, Excitation from the sustained excitation cells was suprathreshold unless it overlapped with inhibition. Therefore, the duration-tuned neuron did not fire action potentials when there was a coincidence of spikes from the adapting sustained inhibition and sustained excitation populations. B, When inhibition from the adapting sustained inhibition population decreased, excitation from the sustained excitation population broke through and produced action potentials in the duration-tuned neuron. Note how the membrane potential of the DTN at 7 ms (both stimuli) was raised by excitatory input from the sustained excitation population but did not reach threshold. Sustained excitation neurons driven by the standard cochlear nucleus Poisson spiking process; adapting sustained inhibition neurons driven by the steep cochlear nucleus Poisson spiking process (Fig. 3C). Stimulus duration is illustrated as black bars on the time axis.
Alternatively, long-pass selectivity could arise from a duration-dependent enhancement of excitation rather than through a reduction of inhibition as proposed above. For paradoxical latency shift to occur in this case, there would also need to be an inverse relationship between stimulus input energy and the strength of excitation to the DTN; as stimulus energy increased, the strength of the excitatory input to the long-pass cell would need to decrease (to a point), resulting in fewer spikes at longer latencies.
Results
To evaluate the biological plausibility of our computational networks, we compared responses of model neurons to responses of in vivo extracellular recordings of DTNs from the IC of the big brown bat, Eptesicus fuscus (Casseday et al., 2000; Faure et al., 2003). In vivo responses were measured with pure tones or linear FM sweeps that were randomly varied in duration and presented at 10–40 dB above threshold at the characteristic frequency of the DTN. Acoustic stimuli were presented monaurally to the ear contralateral to the recording site. To simulate increases in SPL for model input, we chose CN rate level functions appropriate for bats (see Materials and Methods).
Transitioning between short-pass and bandpass responses
Historically, the labels “short-pass” and “bandpass” were used to describe the temporal selectivity and response classes of DTNs in a manner analogous to the filter frequency selectivity of resonant electronic circuits. A coincidence detection mechanism was suggested to produce cells in both classes (Ehrlich et al., 1997; Faure et al., 2003), whereas an anti-coincidence mechanism was suggested for short-pass responses (Fuzessery and Hall, 1999). In this section, we demonstrate that neither mechanism is necessarily mutually exclusive and that hybrid models can produce short-pass and bandpass duration-tuned responses by modifying various model connection weights and response parameters.
To demonstrate that an anti-coincidence mechanism can produce model neurons with bandpass duration tuning, we changed the original bandpass coincidence detection model into a bandpass anti-coincidence model by removing the OFF population and increasing the ONdelay to DTN connection weight from 4 to 8. As in our bandpass coincidence detection model, very short stimulus durations (i.e., 1 ms) failed to evoke spikes in the ON population and thus the DTN did not respond. Therefore, a minimum stimulus duration was required to evoke spikes in the DTN in both the coincidence detection and anti-coincidence bandpass models. At longer stimulus durations (i.e., ≥10 ms), inhibition from the SI population was strong and rendered the suprathreshold excitation from the ONdelay population subthreshold. At stimulus durations near the BD of the model cell (∼5 ms), suprathreshold excitation from the ONdelay population was not sufficiently coincident with inhibition from the SI population, and therefore the model DTN was able to produce action potentials.
To demonstrate that a coincidence detection mechanism can produce model neurons with short-pass duration tuning, we transformed the original short-pass anti-coincidence model into a short-pass coincidence detection model by reducing the ONdelay to DTN connection weight from 5 to 4, adding a population of offset (OFF) responding cells with parameters equivalent to the OFF population in our bandpass coincidence detection model (along with the afferent and efferent connections), and by removing the spontaneous afferent input that was included in the short-pass anti-coincidence model (see Materials and Methods, Anti-coincidence model). In the original short-pass anti-coincidence model, suprathreshold excitation from the ON population was capable of producing spikes in the DTN at durations of 1–4 ms even when there was a small overlap with inhibition. In the short-pass coincidence detection model, the ONdelay to DTN connection weight was reduced so the ONdelay excitation was now rendered subthreshold by inhibition from the SI population for stimulus durations ≥2 ms. At 1 ms, the ONdelay excitation could still evoke spikes in the DTN on its own because the overlap with inhibition was insignificant. At stimulus durations ≥2 ms, the ONdelay excitation required coincidence with the OFF excitation to evoke spikes in the DTN. Therefore, this alternative model of short-pass duration tuning was a hybrid of anti-coincidence and coincidence detection mechanisms. We refer to this model as a coincidence detection model because the majority of responses (stimulus durations ≥2 ms) required coincidence of the ONdelay and OFF excitations. In contrast to the short-pass anti-coincidence model, the short-pass coincidence detection model produced more spikes at longer stimulus durations (see below, Model response characteristics). This was attributable to the window of coincidence being sufficiently wide to facilitate coincidence at stimulus durations up to 9 ms. Increasing the SI to DTN connection weight strengthened inhibition to the DTN, and this narrowed the window of coincidence between the onset- and offset-evoked excitations but also decreased the number of spikes at all durations.
Model response characteristics
For each figure in this section, two types of plots are presented. The first shows a dot raster display of the spikes evoked by a DTN in response to stimuli that were randomly varied in duration from 1 to 25 ms at a constant mean Poisson input rate or acoustic SPL. The ordinate shows stimulus duration and the abscissas show time relative to stimulus onset. The black lines represent the duration of the stimulus, and the dots represent the time of occurrence of individual spikes. The second plot shows the mean ± SE number of spikes per stimulus at each duration and stimulus level. Model and in vivo bandpass plots were composed of 20 trials per stimulus, whereas short-pass and long-pass plots were comprised of 15 trials per stimulus. This was done so that the number of trials was the same when comparing model and in vivo responses.
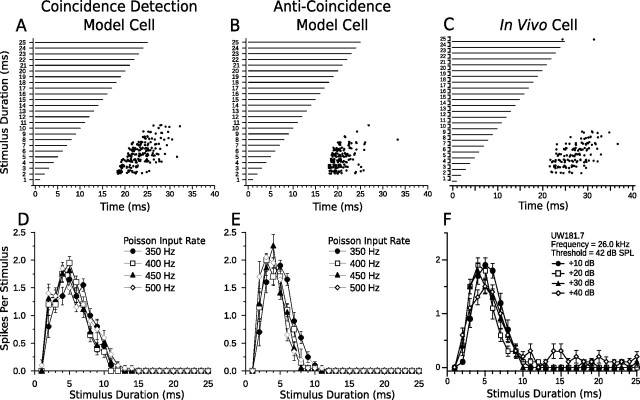
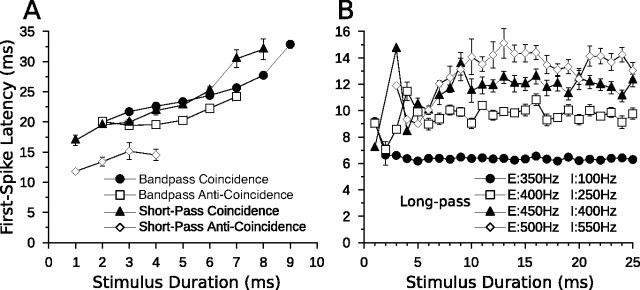
First, we compare bandpass responses from the coincidence detection and anti-coincidence models with bandpass responses from an in vivo DTN (Fig. 7). Notice how both the coincidence detection and anti-coincidence models accurately reproduced the spike counts, first-spike latencies, and amplitude tolerance of the in vivo bandpass DTN (Fig. 7, compare A, B, with C). At durations above ∼11 ms, the models failed to spike even though the in vivo bandpass neuron occasionally produced action potentials, especially at the highest stimulus amplitudes (Fig. 7, compare D, E, with F). Although the +40 dB raster data from Figure 7F are not shown, the few additional spikes that were evoked by stimulus durations ≥11 ms consistently occurred between 20 and 30 ms re stimulus onset and did not follow stimulus offset, thus confirming the existence of an onset-evoked excitation. The default parameters we used did not reproduce onset breakthrough in our models; however, slight modifications permit for such occurrences (see Fig. 11A). A primary difference between responses from the bandpass coincidence detection and anti-coincidence model neurons was in first-spike latency; because of the offset component in the coincidence detection model, spikes followed the offset of the stimulus more faithfully than in the anti-coincidence model. This difference is discussed further below (see Relevance of model components). The temporal response bandwidth was also 1–2 ms larger in the coincidence detection model DTN.
Figure 7.
Comparison of model and in vivo bandpass duration tuning. Shown are dot raster displays of the responses of a bandpass coincidence detection (A) and anti-coincidence (B) model cell to different stimulus durations (20 trials per stimulus; mean Poisson input firing rate, 400 Hz). Model cells have a BD of 5 ms. C, Dot raster display of the responses of an in vivo bandpass DTN with a BD of 5 ms to variable duration pure tones presented at the characteristic frequency of the cell (20 trials per stimulus; 30 dB above threshold). D–F, Mean ± SE spikes per stimulus as a function of stimulus duration (i.e., duration-tuning curves) at four different CN Poisson input firing rates (D, E) or different SPLs relative to threshold (F). Four different Poisson firing rates were chosen to be analogous to four different acoustic SPLs. Refer to Materials and Methods for additional details. Note the response tolerance to changes in stimulus magnitude in both model and in vivo cells. Coincidence detection model responses follow offset of the stimulus more faithfully than anti-coincidence model responses and have a slightly wider temporal bandwidth. C and F were reprinted with permission [Faure et al. (2003), their Fig. 4B].
Figure 11.
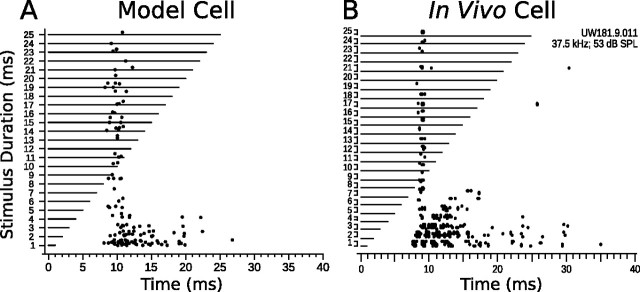
Onset excitation breakthrough in model and in vivo DTNs. A, Dot raster display of an onset breakthrough response in a short-pass anti-coincidence model neuron (BD, 1 ms) with the SI to DTN connection weight decreased from −5 to −4.3 and the SI to DTN axonal delay increased from 1 to 2.8 ms (15 trials per stimulus; mean Poisson input firing rate, 400 Hz). B, Dot raster display of an onset breakthrough response in an in vivo short-pass DTN (BD, 1 ms; 15 trials per stimulus; 30 dB above threshold). B was reprinted with permission [Faure et al. (2003), their Fig. 6B].
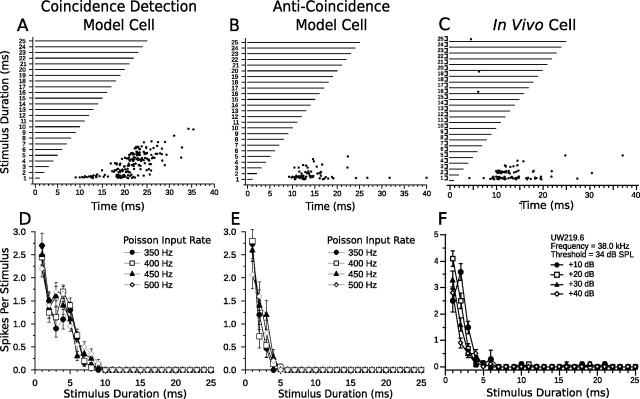
Figure 8 compares short-pass model responses from the coincidence detection and anti-coincidence models with short-pass responses from an in vivo DTN. Although the coincidence detection model reproduced the first-spike latency and amplitude tolerance of the in vivo short-pass DTN, it also produced spikes at longer stimulus durations (i.e., 5–8 ms), whereas the anti-coincidence model did not (Fig. 8, compare A, D, with C, F). This is because the window of coincidence between the ONdelay and OFF populations was wide enough to evoke suprathreshold responses to durations <10 ms. To narrow the window of coincidence, the offset excitation would either have to be shorter in duration or weaker in amplitude than in our model network. The brief increase in spike count in the coincidence model at 4 and 5 ms was caused by a stronger offset response to longer stimulus durations, but at 6 ms there was less coincidence between the onset- and offset-evoked EPSPs so spike counts again decreased.
Figure 8.
Comparison of model and in vivo short-pass duration tuning. Shown are dot raster displays of the responses of a short-pass coincidence detection (A) and anti-coincidence (B) model cell to different stimulus durations (15 trials per stimulus; mean Poisson input firing rate, 400 Hz). Model cells have a BD of 1 ms. C, Dot raster display of the responses of an in vivo short-pass DTN with a BD of 1 ms to variable duration pure tones presented at the characteristic frequency of the cell (15 trials per stimulus; 30 dB above threshold). D–F, Mean ± SE spikes per stimulus as a function of stimulus duration at four different CN Poisson input firing rates (D, E) or different SPLs relative to threshold (F). Four different Poisson firing rates were chosen to be analogous to four different acoustic SPLs. Refer to Materials and Methods for additional details. Note the response tolerance to changes in stimulus magnitude in both model and in vivo cells. Coincidence detection model DTN has a wider temporal response bandwidth than the anti-coincidence model neuron. C and F were reprinted with permission [Faure et al. (2003), their Fig. 4A].
Neural responses similar to the output of the coincidence detection and anti-coincidence short-pass models have been observed from in vivo DTNs exhibiting a wide range of temporal bandwidths (Jen and Zhou, 1999; Fremouw et al., 2005). The anticoincidence model accurately reproduced the spike counts, first-spike latencies, and amplitude tolerance of the in vivo short-pass cell (Fig. 8, compare B, E, with C, F). The inclusion of spontaneous input directly to the DTN in the short-pass anti-coincidence model (see Materials and Methods) caused additional action potentials at latencies >15 ms re stimulus onset. This mirrors the in vivo responses of some short-pass DTNs (Faure et al., 2003). Removal of the spontaneous activity resulted in fewer spikes at the BD of the model neuron.
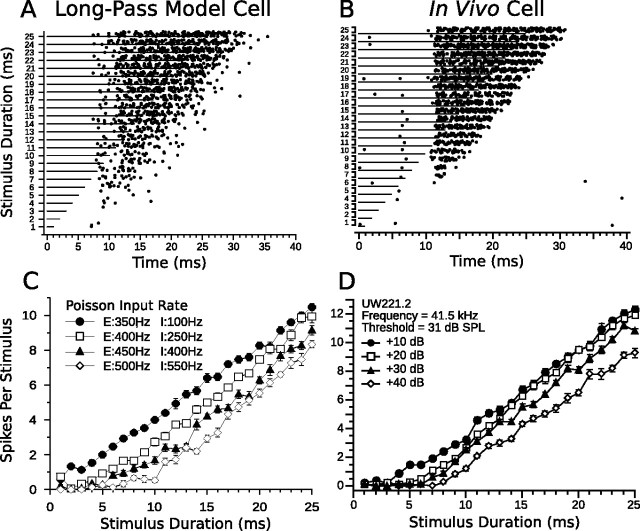
Long-pass model responses and in vivo long-pass data are compared in Figure 9. The model cell accurately reproduced the spike counts and first-spike latencies of the in vivo long-pass cell (Fig. 9A–D). Sustained excitation resulted in linearly increasing spike counts in the model DTN with increasing stimulus duration. The delay in first-spike latency in the model long-pass DTN at high stimulus amplitudes (shown explicitly in Fig. 13B) occurred because the strength of the adapting sustained inhibition from the SIAD cells grew more rapidly for increases in stimulus magnitude than the sustained excitation from the SE cells. As the SIAD cells adapted, the sustained excitation (driven by the standard CN input) broke through the adapting sustained inhibition (driven by the steep CN input), and action potentials were produced. This resulted in paradoxical latency shift that has been observed for some long-pass DTNs in the IC of the bat (Faure et al., 2003) and rat (Pérez-González et al., 2006).
Figure 9.
Comparison of model and in vivo long-pass duration tuning. A, Dot raster display of the responses of a long-pass anti-coincidence model cell to different stimulus durations (15 trials per stimulus; mean standard input Poisson firing rate, 400 Hz; mean steep input Poisson firing rate, 250 Hz). B, Dot raster display of the responses of an in vivo long-pass DTN to variable duration pure tones presented at the characteristic frequency of the cell (15 trials per stimulus; 30 dB above threshold). C, D, Mean ± SE spikes per stimulus as a function of stimulus duration at four different CN Poisson input firing rates (C) or different SPLs relative to threshold (D). Four different Poisson firing rates were chosen to be analogous to four different acoustic SPLs. The legend in C lists the standard CN input Poisson firing rates driving the sustained excitation cells (prefaced with an “E”) and the steep CN input Poisson firing rates driving the adapting sustained inhibition cells (prefaced with an “I”). Refer to Materials and Methods for additional details. Note the decreased spike counts of both the model and in vivo long-pass DTNs as the stimulus magnitude increases. B and D were reprinted with permission [Faure et al. (2003), their Fig. 4C].
Figure 13.
Mean ± SE first-spike latencies of the coincidence detection, anti-coincidence (A), and long-pass (B) duration-tuning models. A, Responses of the coincidence and anti-coincidence model cells followed the offset of the stimulus. In the anti-coincidence models, the sustained inhibition to the model DTN caused a longer first-spike latency even though the onset-evoked EPSP arrived at approximately the same time at all durations. The coincidence detection models followed signal offset more reliably than the anti-coincidence models (see Results, Relevance of model components). B, First-spike latencies of the long-pass model at four Poisson input firing rates. Note how first-spike latency increased with stimulus magnitude at durations ca. ≥6 ms. Action potentials occurred less frequently and with more variable timing at shorter durations (Fig. 9). Each model was run 20 times with a mean Poisson input rate of 400 Hz (A) or as shown in the legend (B).
Relevance of model components
To assess the relevance of various components, we ran simulations with each model while varying a single parameter across a range of values. In both the coincidence detection and anti-coincidence models, inhibition from the SI population played a key role in defining spike counts and temporal response bandwidths of DTNs. To study the role of inhibition in duration tuning, Casseday et al. (2000) iontophoretically applied two types of inhibitory neurotransmitter antagonists while simultaneously recording acoustically evoked responses from DTNs in the IC of the bat. Responses were recorded before, during, and after the blocking of synaptic inhibition at the DTN with bicuculline, a GABAA antagonist, and strychnine, a glycine antagonist. They found that when inhibition was blocked, duration selectivity vanished in 71% of cells tested with bicuculline and in 40% of cells tested with strychnine. In the remaining units, the temporal bandwidth of the duration-tuning curve broadened or no changes were observed.
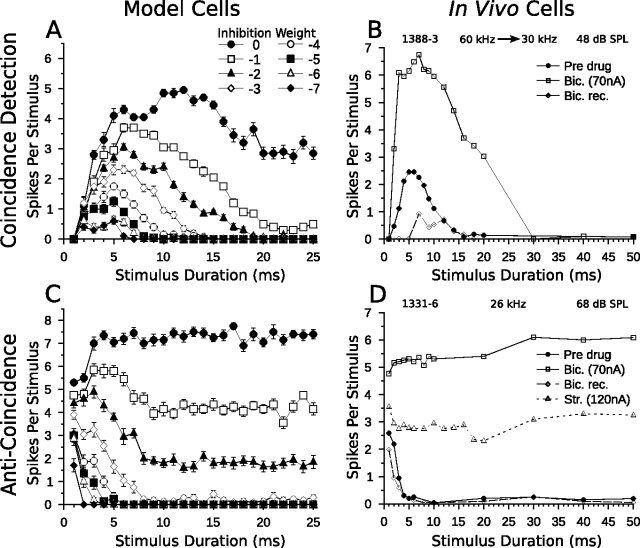
To simulate the effects of applying inhibitory neurotransmitter antagonists, we modified the coincidence detection and anticoincidence models by adjusting the inhibitory connection weight between the SI population and the DTN (Fig. 3A,B). This effectively blocked some or all inhibition to the model DTN. Figure 10, A and B, compares coincidence detection model cell responses with decreasing levels of inhibition to in vivo responses of a bandpass DTN when inhibition was blocked iontophoretically. As the inhibitory connection weight in the coincidence model decreased, the temporal selectivity of the DTN decreased. Eventually, its bandpass tuning was abolished when inhibition was removed completely. This occurred because all onset excitation to the model DTN evoked spiking. Therefore, inhibition was critical for ensuring the onset-evoked excitation remained subthreshold. The BD of the network, however, remained fairly stable, increasing only slightly from 5 to 7 ms when inhibition was present. This happened because peak spiking still occurred when the onset- and offset-evoked excitations coincided. Again, the model DTN did not respond to 1 ms stimuli when inhibition was completely removed because of the high spiking threshold of the ON population (see Materials and Methods, Coincidence detection model). Casseday et al. (2000) reported that blocking inhibition with bicuculline resulted in either a broadening of the duration-tuning curve (Fig. 10B) or loss of temporal selectivity.
Figure 10.
Blocking inhibition in model and in vivo DTNs. Shown are mean ± SE (A, C) and mean spikes per stimulus (B, D) as a function of stimulus duration. A, Duration-tuning curves of a bandpass coincidence detection model neuron (20 trials per stimulus; mean Poisson input firing rate, 400 Hz) with the SI to DTN connection weight varied from −7 to 0 (Fig. 3A). As inhibition decreased, spike counts increased, the BD of the neuron remained fairly stable, and the temporal response bandwidth increased until eventually duration tuning was lost. B, Duration-tuning curves of an in vivo bandpass DTN in response to downward frequency modulated sweeps (60–30 kHz) before, during, and after application of bicuculline, a GABAA antagonist that blocks inhibition. Before drug application (solid circles), the cell had a BD of 5 or 6 ms and did not respond reliably to sounds longer than 14 ms. During application of bicuculline (open squares), spike counts grew considerably, BD remained unchanged, and the temporal response bandwidth increased. C, Duration-tuning curves of a short-pass anti-coincidence model neuron (20 trials per stimulus; mean Poisson input firing rate, 400 Hz) with the SI to DTN connection weight varied from −7 to 0 (Fig. 3B). Once again, as inhibition decreased, spike counts increased and short-pass duration tuning was eventually lost. D, Duration-tuning curves of an in vivo short-pass DTN in response to pure tones (characteristic frequency, 26 kHz) at varying stimulus durations before (closed circles), during (open squares), and after (open diamonds) application of bicuculline, and during application of strychnine, a glycine antagonist (open triangles). When inhibition was blocked, spike counts increased considerably and duration tuning was eventually abolished. B and D were reprinted with permission [Casseday et al. (2000), their Figs. 5A, 2A].
As inhibition was removed in the anti-coincidence model, the duration turning curve of the short-pass model cell broadened and eventually its temporal selectivity was abolished (Fig. 10C). This occurred because spiking from the ONdelay population provided suprathreshold excitation to the model DTN at a fixed latency from stimulus onset at all durations when inhibition was no longer available to render it subthreshold. Again, our simulations mirrored the in vivo results of Casseday et al. (2000) who reported that some short-pass cells bathed in bicuculline and/or strychnine lost their temporal response specificity (Fig. 10D). When spikes were observed for in vivo cells, they tended to occur at a fixed latency from stimulus onset.
The standard parameters of our bandpass coincidence detection model produced a DTN with a BD tuned between 4 and 6 ms, whereas the standard anti-coincidence model resulted in a short-pass cell with a BD of 1 or 2 ms. These BDs are typical for DTNs recorded in the IC of bats (Faure et al., 2003) and mice (Brand et al., 2000). When in vivo DTNs with longer BDs were reported, they typically had a wider temporal response bandwidth. That is, the width at half-height of the duration-tuning function was wider and shifted toward longer durations (Fremouw et al., 2005). As seen in our simulations, dampening inhibition in the coincidence detection and anti-coincidence models produced similar behavior. Therefore, we conclude that inhibition plays a critical role in determining the BD of both model and in vivo DTNs.
Onset excitation breakthrough has been observed in as many as 49% of DTNs (Faure et al., 2003). The breakthrough was interpreted as evidence for an onset-evoked excitation that was able to break through a weaker, sustained inhibition during the stimulus, resulting in spikes with a (more or less) constant first-spike latency re stimulus onset rather than a latency that tracks stimulus offset. To reproduce this behavior in the short-pass anti-coincidence model neuron, we decreased the magnitude of the SI to DTN inhibitory connection weight from −5 to −4.3 and increased the axonal delay from 1 to 2.8 ms (i.e., we weakened and delayed synaptic inhibition to the DTN) (Fig. 3B) while keeping all other model parameters unchanged. Figure 11 compares the results of a modified short-pass anti-coincidence model cell to an in vivo short-pass DTN exhibiting onset excitation breakthrough. By slightly weakening the onset-evoked sustained inhibition to the model DTN, we were able to reproduce the onset-evoked excitation breakthrough that has been observed in vivo.
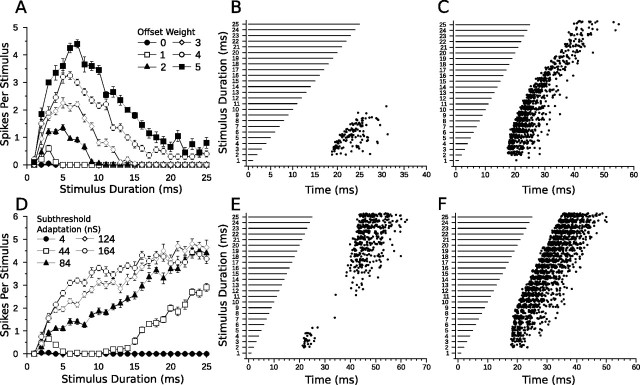
In the coincidence detection model, the latency of the offset-evoked EPSP (re stimulus onset) increases with stimulus duration. Indeed, it is the timing of the offset-evoked excitation that determines when a DTN will spike because the onset-evoked excitation occurs at a fixed latency (re stimulus onset). To evaluate how the strength of the offset-evoked excitation affected responses of the bandpass coincidence detection model, we varied the OFF to DTN connection weight from 0 to 5 (with 3 being the value in the standard model) (Fig. 7A). When the connection weight was 0 (i.e., the offset-evoked excitation was removed), spiking in the DTN was effectively abolished (Fig. 12A) despite the onset-evoked EPSP being suprathreshold in the absence of inhibition (Fig. 10A). Even at short durations, when the sustained inhibitory input to the DTN had ended before the arrival of the suprathreshold, onset-evoked EPSP, the excitation was still rendered subthreshold because the recovery of the model neuron from inhibition was not instantaneous. In vivo recordings from IC neurons have shown that the effects of inhibition can persist beyond the duration of the stimulus (Klug et al., 1999). This emphasized the need for a coincidence between the onset- and offset-evoked EPSPs. When the connection weight was 1 (Fig. 12A), responses from the model DTN started to become bandpass. Figure 12, B and C, shows dot rasters when the OFF to DTN connection weights were 2 and 5, respectively. Increasing the offset connection weight caused the subthreshold, offset-evoked EPSP to become suprathreshold, resulting in spikes that followed stimulus offset at all durations, although peak counts still occurred when the onset- and offset-evoked EPSPs coincided. Additional spikes also occurred when the SI to DTN inhibitory connection weight was decreased (Fig. 10A), but in this case, the relative timing of the spikes differed. As inhibition to the DTN was weakened, the onset-evoked EPSP was no longer rendered subthreshold by the sustained inhibition. Therefore, the additional spikes occurred at a fixed latency from stimulus onset (Fig. 11A) rather than from stimulus offset.
Figure 12.
Offset excitation in the bandpass coincidence detection model. A, Mean ± SE duration-tuning curves of a bandpass coincidence detection model cell with the OFF to DTN connection weight varied from 0 to 5 (Fig. 3A) and a mean Poisson input rate of 400 Hz (20 trials per stimulus). B, C, Dot raster displays showing responses of the bandpass coincidence model with the OFF to DTN connection weight set to 2 (B) and 5 (C). D, Mean ± SE duration-tuning curves of a bandpass coincidence model with postinhibitory rebound and increasing levels of subthreshold adaptation in the model neuron (see Results, Relevance of model components). E, F, Dot raster displays showing responses of the bandpass coincidence model with postinhibitory rebound and subthreshold adaptation levels of 44 nS (E) and 164 nS (F). In E, note the bimodal pattern of action potentials. The model cell reliably spiked in response to stimulus durations between 2 and 4 ms and at durations >15 ms. The band-reject selectivity resulted from the failure of the model cell to produce spikes from postinhibitory rebound at short durations unless the rebound coincided with the onset-evoked excitation; however, at longer durations, the rebound was strong and spikes were produced in the model DTN. In F, the high level of subthreshold adaptation allowed the model cell to spike via postinhibitory rebound at all but the shortest duration; hence the cell lost its duration selectivity.
It is also plausible that the offset excitation observed from in vivo recordings of DTNs does not arise from an external synaptic input, but instead arises from a postinhibitory rebound mechanism. Postinhibitory rebound, likely facilitated by an Ih current, has been observed in the mammalian IC (Peruzzi et al., 2000; Koch and Grothe, 2003; Tan et al., 2007; Sun and Wu, 2008). To examine response characteristics of model DTNs with postinhibitory rebound, we removed the OFF population from the coincidence detection model and increased the subthreshold adaptation parameter (a) of the model DTN (Brette and Gerstner, 2005). Figure 12 D–F shows spike counts and dot raster displays for several values of a. With a small amount of adaptation (a = 44 nS), the model cell produced band-reject duration tuning. That is, the cell reliably responded only to short (2–4 ms) or long signals (≥15 ms). For stimulus durations between 5 and 14 ms, there were few or no spikes. At short durations, the model DTN was not sufficiently hyperpolarized to evoke postinhibitory rebound spiking unless excitation from the delayed onset-evoked EPSP coincided with the rebound. This occurred between 2 and 4 ms. At durations ≥15 ms, the model cell was hyperpolarized for a sufficient time such that the postinhibitory rebound was stronger and produced action potentials in the model DTN, even in the absence of coincident excitation from the onset-evoked EPSP. Therefore, for a postinhibitory rebound mechanism to replace the offset excitation in the coincidence detection model and reproduce typical in vivo responses, the rebound must be subthreshold at all durations. Leary et al. (2008) found no evidence of postinhibitory rebound in short-pass DTNs in amphibians, although it may still play a role in the DTNs of mammals.
Finally, we examined first-spike latencies in each duration-tuning model. Figure 13A shows first-spike latencies of bandpass and short-pass model DTNs implemented with coincidence detection and anti-coincidence mechanisms. Both short-pass and bandpass model cells had first-spike latencies that tracked stimulus offset. This was expected for the coincidence detection models because the overlap between the onset- and offset-evoked excitations would occur later in time as stimulus duration increased. We also found that both anti-coincidence models produced first-spike latencies that tracked stimulus offset. This was somewhat surprising because, conceptually, the kinetics of the anti-coincidence mechanism depends primarily on a single, fixed-latency, onset-evoked EPSP. We hypothesized that the offset following response in both the short-pass and bandpass anticoincidence networks resulted from sustained inhibition; because the duration of the sustained IPSP increased with stimulus duration, this increased first-spike latencies in both the short-pass and bandpass anti-coincidence networks. In short, the spikes were delayed by the recovery of the DTN from hyperpolarization. Not surprisingly, we found that the shortest first-spike latencies occurred in short-pass DTNs for the anti-coincidence network when the onset-evoked excitation was early and suprathreshold (Fig. 13A). The coincidence detection models of duration tuning had consistently longer first-spike latencies because spikes in these models explicitly required the coincidence of onset- and offset-evoked EPSPs. Longer first-spike latencies were also observed in the bandpass anti-coincidence model because spikes in the ONdelay cells were evoked by a postinhibitory rebound mechanism and this delayed the arrival of onset-evoked excitation to the model DTN.
Variability of first-spike latency between different computational models was consistent with in vivo data in which a wide range of first-spike latencies has been observed between but not within cells tuned to similar BDs. Leary et al. (2008) reported first-spike latencies from ∼55 to 150 ms in frog DTNs with BDs tuned from 10 to 12 ms. Faure et al. (2003) found that DTNs of big brown bats had first-spike latencies ranging from 8 to 27 ms in cells with a 2 ms BD, and 13 to 24 ms in cells with a 5 ms BD. Such large variation in first-spike latency between cells with the same BD suggests the existence of multiple neural mechanisms underlying in vivo duration selectivity, and/or that there is variability within a single mechanism across networks.
First-spike latencies in the long-pass model of duration tuning clearly showed a paradoxical latency shift at stimulus durations >10 ms (Fig. 13B). At shorter durations, action potentials were infrequent and first-spike latencies had more variable timing. Recall that paradoxical latency shift occurred in our long-pass model because inhibitory inputs increased in strength faster than excitatory inputs.
Discussion
In general, the computational models presented here support previously hypothesized conceptual models proposed for creating duration-selective neural responses in the auditory system of amphibians (Leary et al., 2008) and mammals (Casseday et al., 1994, 2000; Mora and Kössl, 2004). One notable advancement is the introduction of a suprathreshold, onset-evoked excitation that can be rendered subthreshold by onset-evoked inhibition when it does not coincide with subthreshold, offset-evoked excitation. This is in contrast to the original versions of the coincidence detection model in which it was explicitly stated that the onset- and offset-evoked excitations were subthreshold even in the absence of inhibition (Casseday et al., 1994; Faure et al., 2003; Mora and Kössl, 2004). With this simple enhancement, our new version of the coincidence detection model was able to reproduce a wider range of in vivo response characteristics.
The power of these computational models is their simplicity and biological plausibility in both the individual neuron response characteristics and the proposed neuroanatomical network connections. To showcase the predictive and concordant responses of each model, comparisons were made with in vivo data. First, the number of action potentials evoked by model neurons was on the same order as those observed for in vivo DTNs. Second, model DTNs had first-spike latencies that tracked signal offset as reported for in vivo DTNs in both the amphibian and mammalian auditory midbrain (Brand et al., 2000; Casseday et al., 2000; Leary et al., 2008) and the mammalian (cat) visual cortex (Duysens et al., 1996). We demonstrated that variation in first-spike latency, which correlates with neuronal BD and the strength of leading inhibition in vivo (Faure et al., 2003), can easily be altered by simple changes to excitatory or inhibitory connection weights (e.g., compare bandpass coincidence detection model with short-pass anti-coincidence model in Fig. 3). Our computational models were also capable of reproducing the variation in first-spike latency that is observed between cells tuned to similar BDs. Third, responses from our model neurons were robust to changes in stimulus input firing rates (analogous to changes in acoustic SPL) and showed amplitude tolerance similar to in vivo DTNs (Zhou and Jen, 2001; Fremouw et al., 2005). Fourth, we found that the strength and timing of inhibition and excitation could be tuned to produce model cells with a range of neuronal BDs and temporal response bandwidths. Fifth, our models were capable of replicating additional in vivo neurophysiological responses such as onset excitation breakthrough and the effects of blocking local synaptic inhibition with neuropharmacological agents.
Comparison with other timing mechanisms
Significant behavioral and neurophysiological research has been conducted on the perception of stimulus duration in human and nonhuman animals. The pacemaker–accumulator model (for review, see Buhusi and Meck, 2005) proposes that an internal clock (e.g., spiking neurons) provides regularly spaced pulses that accumulate over time. In this model, the duration of an event is calculated by multiplying the number of pulses received during an event by the discharge frequency of the internal clock. This simple model has been successful in explaining many behavioral results on a timescale of hundreds or thousands of milliseconds, but fails to explain the millisecond level discrimination observed for in vivo DTNs. Additionally, because spike counts in most auditory midbrain neurons (but not all DTNs) tend to increase with stimulus amplitude (Potter, 1965; Covey and Carr, 2005), this would hinder a pacemaker–accumulator mechanism because it relies on a constant spiking frequency to calculate the duration of an event.
Carr and Konishi (1990) described a coincidence detection timing mechanism that used axonal delay lines of cochlear nucleus magnocellularis neurons to facilitate microsecond, interaural interval tuning in the nucleus laminaris of barn owls (Tyto alba). The coincidence detection mechanism described by our models is similar in that it requires two excitatory inputs to coincide, although it is unlikely that simple axonal delays can explain first-spike latencies of 20+ ms observed for in vivo DTNs (Faure et al., 2003).
A previous model of duration tuning, the slow conductance model, suggested that duration-selective responses resulted from slowly changing ionic currents induced in a cell by hyperpolarization (Hooper et al., 2002). This model was especially tailored for sound durations >50 ms and relied on inhibition that was sustained throughout the stimulus. The slow conductance model and our network models are not mutually exclusive mechanisms because they invoke explanations at different levels of analyses. Both models produce offset responding cells tuned to a range of BDs, and both predict that the range of excitatory durations (i.e., temporal bandwidth) increases as a function of BD. However, the slow conductance model does not reproduce several key in vivo results observed in DTNs with BDs <50 ms. First, onset- and (sometimes) offset-evoked excitatory inputs are known to occur in midbrain DTNs of amphibians (Leary et al., 2008) and mammals (Covey et al., 1996; Casseday et al., 2000; Faure et al., 2003); the slow conductance model includes an offset-evoked rebound excitation (i.e., postinhibitory rebound) but does not include an onset-evoked excitation. Second, Fuzessery and Hall (1999) and Casseday et al. (2000) showed that pharmacologically blocking inhibition increased spike counts and broadened or abolished the duration-selective responses of some DTNs. The slow conductance model should cease responding entirely when inhibition is removed because the only input is an IPSP that lasts for the duration of the stimulus. Third, first-spike latencies of in vivo DTNs with the same BD can be quite variable, ranging from 7 to 27 ms after stimulus onset in bats (Faure et al., 2003). Variation in first-spike latency of DTNs in the IC of the bat also correlates with the magnitude of leading inhibition (i.e., the difference in time between when the onset-evoked IPSP and the onset-evoked EPSP arrives at the DTN) (Faure et al., 2003). The slow conductance model does not explicitly account for variation in first-spike latency of DTNs with the same or with different BDs.
Model generalization
The coincidence detection and anti-coincidence models in no way limit the range of stimulus durations that can be successfully discriminated; however, neural instantiations restrict their use to short timescales (i.e., millisecond to tens of milliseconds). For both the coincidence and anti-coincidence models to discriminate long duration stimuli, the latency of the onset-evoked events would have to scale proportionally. That is, for a neuron to have a BD of 50 ms, the onset-evoked excitation (re stimulus onset) would have to be delayed by ∼50 ms. Accounting for such a long delay would necessitate mechanisms not included in the present computational models, such as slowly changing ionic currents (Hooper et al., 2002) or unrealistic axonal delays. The long-pass model, however, may be able to explain preferences for long duration stimuli. Increasing the adaptation time of the onset-evoked inhibition in the long-pass model could produce a DTN with a preference for arbitrarily long duration stimuli.
Unifying the conceptual models
Duration-tuned neurons are among the most complex cells in the central auditory pathway because they are tuned to stimulus frequency, amplitude, and duration. Three conceptual models were proposed to describe the underlying neural mechanisms of duration selectivity, and in this study we have formulated each model computationally. Here, we combine the models into a single, unified conceptual model that encompasses all duration-tuning response classes.
The unified model consists of three components (inputs) to the DTN, each with parameters that can be tuned to produce different response characteristics: (1) onset-evoked excitation, (2) offset-evoked excitation (which may be an external synaptic connection to the DTN or rebound from inhibition within the DTN), and (3) onset-evoked inhibition. Parameters to adjust in all three components include the following: the synaptic connection strength to the DTN, the latency of the component relative to other components, the duration and rate of adaptation of the component, and the minimum stimulus energy required for evoking the component (i.e., low or high spiking threshold). Table 1 suggests how the parameters of the unified model may be tuned generally to create each duration-tuning response class.
Table 1.
Parameters of the unified conceptual model to produce three classes of duration tuning
| Onset EPSP | Offset EPSP | Onset IPSP | Conceptual model |
|---|---|---|---|
| Short-pass | |||
| Supra-; low; transient | None | Sustained | Anti-coincidence |
| Supra-; low; transient | Sub-; low; transient | Sustained | Coincidence |
| Bandpass | |||
| Supra-; high; transient | None | Sustained | Anti-coincidence |
| Supra-; high; transient | Sub-; high; transient | Sustained | Coincidence |
| Long-pass | |||
| Supra-; low/high; sustained | None | Sustained; adapting | Anti-coincidence |
| Supra-; low/high; sustained; augmenting | None | Sustained | Alternative anti-coincidence |
Supra-, Suprathreshold synaptic input to the DTN; sub-, subthreshold input to the DTN (i.e., requires coincidence with an additional excitatory event); low, low spiking threshold (i.e., neurons providing this input spike with low stimulus input energy); high, high spiking threshold spiking (i.e., neurons providing this input spike only with high stimulus input energy); transient, duration of the synaptic input is transient; sustained, synaptic input lasting as long or longer than the stimulus; augmenting, input strengthens over time; adapting, input weakens (adapts) over time.
Short-pass duration tuning can arise when the suprathreshold, onset-evoked excitation (component 1) has a low spiking threshold (i.e., the neurons providing this input spike with low stimulus input energy) and occurs after the onset-evoked inhibition (component 3). This is the anti-coincidence mechanism of short-pass duration tuning. Alternatively, if the onset-evoked excitation (1) is rendered subthreshold at short durations by sustained, onset-evoked inhibition (3), then it must also coincide with subthreshold, offset-evoked excitation (component 2) to produce spikes in the DTN. This is the coincidence detection mechanism of short-pass duration tuning.
Bandpass duration tuning can arise when suprathreshold, onset-evoked excitation (1) has a high spiking threshold (i.e., the neurons providing this input spike only with high stimulus input energy) and occurs after the onset-evoked inhibition (3). This is the anti-coincidence mechanism of bandpass duration tuning. If the onset-evoked excitation (1) is rendered subthreshold by sustained, onset-evoked inhibition (3), then it must also coincide with subthreshold, offset-evoked excitation (2) to produce spikes in the DTN. This is the coincidence detection mechanism of bandpass duration tuning.
Long-pass duration tuning can arise when suprathreshold, onset-evoked excitation (1) persists for as long or longer than the duration of the stimulus and is rendered subthreshold for the first several milliseconds of a stimulus by onset-evoked inhibition (3). For this to occur, either the onset-evoked inhibition (3) must adapt and weaken over time, or the onset-evoked excitation (1) must strengthen over time. This is the anti-coincidence mechanism of long-pass duration tuning.
In all cases, the connection strength of the excitatory events (components 1 and 2) can vary as a function of the inhibitory connection strength (component 3). Hybrid mechanisms might employ an anti-coincidence mechanism for short stimulus durations and a coincidence detection mechanism for longer durations. Increasing stimulus energy can decrease spike counts in the DTN if the input to the onset-evoked inhibition has a steeper rate level function than to the onset-evoked excitation. This is explicitly formulated in the long-pass model but could also exist in the short-pass and bandpass models.
Encompassing each conceptual model of duration tuning under a single, unifying model simplifies our understanding of neural selectivity for stimulus duration. Rather than distinct mechanisms for each class of duration tuning, we present a gradient across models, unified with common components and parameters. With such an understanding, it is now possible to investigate how duration tuning could generalize within and across species and sensory modalities. Indeed, simple parameter adjustments to the model can reproduce the variation observed within and between duration-tuning response classes, both within and across species (e.g., DTNs in bats vs mice vs frogs). This is the subject of a future investigation.
Appendix
Neural model
The goal of our computational models was to evaluate the plausibility of previously proposed conceptual models of duration tuning in the central auditory system (Potter, 1965; Narins and Capranica, 1980; Fuzessery and Hall, 1999; Faure et al., 2003). To model neuronal circuits with realistic temporal dynamics while retaining tractability and simplicity, we used individual neuron models that have an aEIF mechanism (Brette and Gerstner, 2005), except for the stimulus input to the cochlear nucleus, which was modeled with Poisson spiking processes. The aEIF model is a single compartment cellular model extending the classic integrate-and-fire model with exponential spike generation, subthreshold adaptation, and spike adaptation. It is defined by the following differential equations:
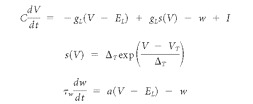 |
with model parameters for each model shown in Tables 2–4. The VT parameter, unlike a standard integrate-and-fire model, is not a hard set spiking threshold. Instead, it defines a point at which the membrane potential begins to rise rapidly, similar to a real action potential. Formally, a spike is said to have occurred when the membrane potential, V, rises rapidly to infinity. The exact spike threshold is a function of VT and ΔT, which defines the slope of the exponential curve immediately before a spike is triggered. Following Brette and Gerstner (2005), we defined a spike to have occurred when the membrane potential reached an absolute value of +20 mV, but the exact value was not critical because it changed spike times by only a fraction of a millisecond. After spiking, the membrane potential of the neuron was set to VR. The w term provides both the subthreshold adaptation and spike adaptation. For spike adaptation, the value of w was increased by b immediately after each spike. The initial values of the free variables were w = 0 and V = EL.
Table 2.
aEIF parameters for the coincidence detection model chosen from a normal distribution with parameters (μ,ς) and when not shown, ς = 0
| Parameter | SI | ON | ONdelay | OFF | DTN | |
|---|---|---|---|---|---|---|
| C (pF) | Membrane capacitance | (220, 5) | (200, 2) | (250, 10) | (250, 5) | 260 |
| gL (nS) | Leak conductance | 30 | 30 | 30 | 30 | 30 |
| EL (mV) | Leak reversal potential | (−65,1) | −55 | −58 | −58 | −55 |
| VT (mV) | Spike threshold | (−52,3) | (−52,1) | −50 | −55 | −48 |
| VR (mV) | Spike reset level | −63 | −54 | −53 | −62 | −47 |
| Δ T (mV) | Slope factor | 2 | 2 | 2 | 2 | 2 |
| τ w (ms) | Slope factor | 250 | 100 | 10 | 10 | 30 |
| a (nS) | Subthreshold adaptation | 40 | 10 | (200, 2) | (200, 2) | 4 |
| b (nA) | Spike-triggered adaptation | (10, 2) | 400 | 500 | 1000 | 10 |
Table 3.
aEIF parameters for the anticoincidence model chosen from a normal distribution with parameters (μ,ς) and when not shown, ς = 0
| Parameter | SI | ON | ONdelay | DTN | |
|---|---|---|---|---|---|
| C (pF) | Membrane capacitance | (220, 5) | (200, 5) | (250, 5) | 280 |
| gL (nS) | Leak conductance | 30 | 30 | 30 | 30 |
| EL (mV) | Leak reversal potential | −65 | −53 | −52 | −55 |
| VT (mV) | Spike threshold | (52, 1) | (−50, 1) | (−50, 1) | −48 |
| VR (mV) | Spike reset level | −63 | −54 | −49 | −46 |
| Δ T (mV) | Slope factor | 2 | 2 | 2 | 2 |
| τ w (ms) | Slope factor | 250 | 100 | 100 | 30 |
| a (nS) | Subthreshold adaptation | 40 | 10 | 10 | 4 |
| b (nA) | Spike-triggered adaptation | (10, 2) | 400 | 100 | 1 |
Table 4.
aEIF parameters for the long-pass model chosen from a normal distribution with parameters (μ,ς) and when not shown, ς = 0
| Parameter | SIAD | SE | DTN | |
|---|---|---|---|---|
| C (pF) | Membrane capacitance | (220, 10) | (280, 7) | 260 |
| gL (nS) | Leak conductance | 30 | 30 | 30 |
| EL (mV) | Leak reversal potential | −55 | −55 | −62 |
| VT (mV) | Spike threshold | (−51, 1) | (−50, 1) | −52 |
| VR (mV) | Spike reset level | −56 | −58 | −62 |
| Δ T (mV) | Slope factor | 2 | 2 | 2 |
| τ w (ms) | Slope factor | 250 | 250 | 30 |
| a (nS) | Subthreshold adaptation | 40 | 40 | 4 |
| b (nA) | Spike-triggered adaptation | (300, 20) | 0 | 4 |
Differential equations were solved in a C++ program compiled with GCC 4.3.2 via the fourth-order Runge–Kutta method and a constant time step of 0.05 ms. To obtain the source code, please contact the corresponding author.
Network modeling
Except for Poisson spiking processes in the CN afferents, membrane potential changes in model neurons were evoked by action potentials in “synaptically” connected neurons. When a model neuron produced an action potential, the time was recorded in memory. The current induced in a postsynaptic neuron was then calculated by an α-function (equations below), which takes the time interval between a simulation time step and a spike time and returns the magnitude of the postsynaptic input current for that time step and spike, where s is (current time − spike time), W is the connection weight, Δax is the axonal delay, q is the scaling factor, and τs is the rise/fall time constant (Gerstner and Kistler, 2002). All models used a constant axonal delay of 1 ms (unless otherwise stated), a scaling factor of q = 1000, and a time constant (τs) of 0.7 ms for EPSP connections and 1.1 ms for IPSP connections (Fig. 2B) as follows:
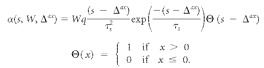 |
Footnotes
This research was supported by Discovery Grants from the Natural Sciences and Engineering Research Council (NSERC) of Canada (S.B., P.A.F.). B.A. was supported by a NSERC Canada Graduate Scholarship. Research in the McMaster Bat Laboratory was also supported by infrastructure grants from the Canada Foundation for Innovation and the Ontario Innovation Trust.
References
- Brand A, Urban R, Grothe B. Duration tuning in the mouse auditory midbrain. J Neurophysiol. 2000;84:1790–1799. doi: 10.1152/jn.2000.84.4.1790. [DOI] [PubMed] [Google Scholar]
- Brette R, Gerstner W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J Neurophysiol. 2005;94:3637–3642. doi: 10.1152/jn.00686.2005. [DOI] [PubMed] [Google Scholar]
- Buhusi CV, Meck WH. What makes us tick? Functional and neural mechanisms of interval timing. Nat Rev Neurosci. 2005;6:755–765. doi: 10.1038/nrn1764. [DOI] [PubMed] [Google Scholar]
- Buonomano DV, Maass W. State-dependent computations: spatiotemporal processing in cortical networks. Nat Rev Neurosci. 2009;10:113–125. doi: 10.1038/nrn2558. [DOI] [PubMed] [Google Scholar]
- Carr CE, Konishi M. A circuit for detection of interaural time differences in the brainstem of the barn owl. J Neurosci. 1990;10:3227–3246. doi: 10.1523/JNEUROSCI.10-10-03227.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casseday JH, Ehrlich D, Covey E. Neural tuning for sound duration: role of inhibitory mechanisms in the inferior colliculus. Science. 1994;264:847–850. doi: 10.1126/science.8171341. [DOI] [PubMed] [Google Scholar]
- Casseday JH, Ehrlich D, Covey E. Neural measurement of sound duration: control by excitatory-inhibitory interactions in the inferior colliculus. J Neurophysiol. 2000;84:1475–1487. doi: 10.1152/jn.2000.84.3.1475. [DOI] [PubMed] [Google Scholar]
- Church RM. Properties of the internal clock. Ann N Y Acad Sci. 1984;423:566–582. doi: 10.1111/j.1749-6632.1984.tb23459.x. [DOI] [PubMed] [Google Scholar]
- Covey E, Carr C. The auditory midbrain in bats and birds. In: Winer JA, Schreiner CE, editors. The inferior colliculus. New York: Springer; 2005. pp. 493–536. [Google Scholar]
- Covey E, Casseday JH. The monaural nuclei of the lateral lemniscus in an echolocating bat: parallel pathways for analyzing temporal features of sound. J Neurosci. 1991;11:3456–3470. doi: 10.1523/JNEUROSCI.11-11-03456.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covey E, Casseday JH. Timing in the auditory system of the bat. Annu Rev Physiol. 1999;61:457–476. doi: 10.1146/annurev.physiol.61.1.457. [DOI] [PubMed] [Google Scholar]
- Covey E, Kauer JA, Casseday JH. Whole-cell patch-clamp recording reveals subthreshold sound-evoked postsynaptic currents in the inferior colliculus of awake bats. J Neurosci. 1996;16:3009–3018. doi: 10.1523/JNEUROSCI.16-09-03009.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duysens J, Schaafsma SJ, Orban GA. Cortical off response tuning for stimulus duration. Vision Res. 1996;36:3243–3251. doi: 10.1016/0042-6989(96)00040-5. [DOI] [PubMed] [Google Scholar]
- Ehrlich D, Casseday JH, Covey E. Neural tuning to sound duration in the inferior colliculus of the big brown bat, Eptesicus fuscus. J Neurophysiol. 1997;77:2360–2372. doi: 10.1152/jn.1997.77.5.2360. [DOI] [PubMed] [Google Scholar]
- Faure PA, Fremouw T, Casseday JH, Covey E. Temporal masking reveals properties of sound-evoked inhibition in duration-tuned neurons of the inferior colliculus. J Neurosci. 2003;23:3052–3065. doi: 10.1523/JNEUROSCI.23-07-03052.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fremouw T, Faure PA, Casseday JH, Covey E. Duration selectivity of neurons in the inferior colliculus of the big brown bat: tolerance to changes in sound level. J Neurophysiol. 2005;94:1869–1878. doi: 10.1152/jn.00253.2005. [DOI] [PubMed] [Google Scholar]
- Fuzessery ZM, Hall JC. Sound duration selectivity in the pallid bat inferior colliculus. Hear Res. 1999;137:137–154. doi: 10.1016/s0378-5955(99)00133-1. [DOI] [PubMed] [Google Scholar]
- Gerstner W, Kistler W. Cambridge, UK: Cambridge UP; 2002. Spiking neuron models: single neurons, populations, plasticity. [Google Scholar]
- Gooler DM, Feng AS. Temporal coding in the frog auditory midbrain: the influence of duration and rise-fall time on the processing of complex amplitude-modulated stimuli. J Neurophysiol. 1992;67:1–22. doi: 10.1152/jn.1992.67.1.1. [DOI] [PubMed] [Google Scholar]
- Grothe B. Interaction of excitation and inhibition in processing of pure tone and amplitude-modulated stimuli in the medial superior olive of the mustached bat. J Neurophysiol. 1994;71:706–721. doi: 10.1152/jn.1994.71.2.706. [DOI] [PubMed] [Google Scholar]
- Guinan JJ, Guinan SS, Norris BE. Single auditory units in the superior olivary complex. I: Responses to sounds and classifications based on physiological properties. Int J Neurosci. 1972;4:101–120. [Google Scholar]
- He J, Hashikawa T, Ojima H, Kinouchi Y. Temporal integration and duration tuning in the dorsal zone of cat auditory cortex. J Neurosci. 1997;17:2615–2625. doi: 10.1523/JNEUROSCI.17-07-02615.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heil P. Auditory cortical onset responses revisited. I. First-spike timing. J Neurophysiol. 1997;77:2616–2641. doi: 10.1152/jn.1997.77.5.2616. [DOI] [PubMed] [Google Scholar]
- Heil P. First-spike latency of auditory neurons revisited. Curr Opin Neurobiol. 2004;14:461–467. doi: 10.1016/j.conb.2004.07.002. [DOI] [PubMed] [Google Scholar]
- Hooper SL, Buchman E, Hobbs KH. A computational role for slow conductances: single-neuron models that measure duration. Nat Neurosci. 2002;5:552–556. doi: 10.1038/nn0602-838. [DOI] [PubMed] [Google Scholar]
- Jen PHS, Zhou XM. Temporally patterned pulse trains affect duration tuning characteristics of bat inferior collicular neurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1999;185:471–478. doi: 10.1007/s003590050408. [DOI] [PubMed] [Google Scholar]
- Kadner A, Kulesza RJ, Jr, Berrebi AS. Neurons in the medial nucleus of the trapezoid body and superior paraolivary nucleus of the rat may play a role in sound duration coding. J Neurophysiol. 2006;95:1499–1508. doi: 10.1152/jn.00902.2005. [DOI] [PubMed] [Google Scholar]
- Kiang NYS. Cambridge, MA: MIT; 1965. Discharge patterns of single fibers in the cat's auditory nerve. [Google Scholar]
- Kitzes LM, Gibson MM, Rose JE, Hind JE. Initial discharge latency and threshold considerations for some neurons in cochlear nuclear complex of the cat. J Neurophysiol. 1978;41:1165–1182. doi: 10.1152/jn.1978.41.5.1165. [DOI] [PubMed] [Google Scholar]
- Klug A, Bauer EE, Pollak GD. Multiple components of ipsilaterally evoked inhibition in the inferior colliculus. J Neurophysiol. 1999;82:593–610. doi: 10.1152/jn.1999.82.2.593. [DOI] [PubMed] [Google Scholar]
- Koch U, Grothe B. Hyperpolarization-activated current (Ih) in the inferior colliculus: distribution and contribution to temporal processing. J Neurophysiol. 2003;90:3679–3687. doi: 10.1152/jn.00375.2003. [DOI] [PubMed] [Google Scholar]
- Kuwada S, Batra R. Coding of sound envelopes by inhibitory rebound in neurons of the superior olivary complex in the unanesthetized rabbit. J Neurosci. 1999;19:2273–2287. doi: 10.1523/JNEUROSCI.19-06-02273.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leary CJ, Edwards CJ, Rose GJ. Midbrain auditory neurons integrate excitation and inhibition to generate duration selectivity: an in vivo whole-cell patch study in anurans. J Neurosci. 2008;28:5481–5493. doi: 10.1523/JNEUROSCI.5041-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meck WH. Neuroanatomical localization of an internal clock: a functional link between mesolimbic, nigrostriatal, and mesocortical dopaminergic systems. Brain Res. 2006;1109:93–107. doi: 10.1016/j.brainres.2006.06.031. [DOI] [PubMed] [Google Scholar]
- Mora EC, Kössl M. Ambiguities in sound duration selectivity by neurons in the inferior colliculus of the bat Molossus molossus from Cuba. J Neurophysiol. 2004;91:2215–2226. doi: 10.1152/jn.01127.2003. [DOI] [PubMed] [Google Scholar]
- Narins PM, Capranica RR. Neural adaptations for processing the two-note call of the Puerto Rican treefrog, Eleutherodactylus coqui. Brain Behav Evol. 1980;17:48–66. doi: 10.1159/000121790. [DOI] [PubMed] [Google Scholar]
- Pérez-González D, Malmierca MS, Moore JM, Hernández O, Covey E. Duration selective neurons in the inferior colliculus of the rat: topographic distribution and relation of duration sensitivity to other response properties. J Neurophysiol. 2006;95:823–836. doi: 10.1152/jn.00741.2005. [DOI] [PubMed] [Google Scholar]
- Peruzzi D, Sivaramakrishnan S, Oliver DL. Identification of cell types in brain slices of the inferior colliculus. Neuroscience. 2000;101:403–416. doi: 10.1016/s0306-4522(00)00382-1. [DOI] [PubMed] [Google Scholar]
- Potter HD. Patterns of acoustically evoked discharges of neurons in the mesencephalon of the bullfrog. J Neurophysiol. 1965;28:1155–1184. doi: 10.1152/jn.1965.28.6.1155. [DOI] [PubMed] [Google Scholar]
- Rhode WS, Greenberg S. Physiology of the cochlear nuclei. In: Popper AN, Fay RR, editors. The mammalian auditory pathway: neurophysiology. New York: Springer; 1992. pp. 94–152. [Google Scholar]
- Roberts S. Isolation of an internal clock. J Exp Psychol Anim Behav Process. 1981;7:242–268. [PubMed] [Google Scholar]
- Schofield BR. Superior olivary complex and lateral lemniscal connections of the auditory midbrain. In: Winer JA, Schreiner CE, editors. The inferior colliculus. New York: Springer; 2005. pp. 132–154. [Google Scholar]
- Singh S, Mountain DC. A model for duration coding in the inferior colliculus. In: Bower JM, editor. Computational neuroscience, trends in research. New York: Plenum; 1997. pp. 497–503. [Google Scholar]
- Sun H, Wu SH. Physiological characteristics of postinhibitory rebound depolarization in neurons of the rat's dorsal cortex of the inferior colliculus studied in vitro. Brain Res. 2008;1226:70–81. doi: 10.1016/j.brainres.2008.06.010. [DOI] [PubMed] [Google Scholar]
- Tan ML, Theeuwes HP, Feenstra L, Borst JGG. Membrane properties and firing patterns of inferior colliculus neurons: an in vivo patch-clamp study in rodents. J Neurophysiol. 2007;98:443–453. doi: 10.1152/jn.01273.2006. [DOI] [PubMed] [Google Scholar]
- Vater M. Single unit responses in cochlear nucleus of horseshoe bats to sinusoidal frequency and amplitude modulated signals. J Comp Physiol. 1982;149:369–388. [Google Scholar]
- Wang J, van Wijhe R, Chen Z, Yin S. Is duration tuning a transient process in the inferior colliculus of guinea pigs? Brain Res. 2006;1114:63–74. doi: 10.1016/j.brainres.2006.07.046. [DOI] [PubMed] [Google Scholar]
- Wang X, Galazyuk AV, Feng AS. FM signals produce robust paradoxical latency shifts in the bat's inferior colliculus. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2007;193:13–20. doi: 10.1007/s00359-006-0167-9. [DOI] [PubMed] [Google Scholar]
- Xie R, Gittelman JX, Li N, Pollak GD. Whole cell recordings of intrinsic properties and sound-evoked responses from the inferior colliculus. Neuroscience. 2008;154:245–256. doi: 10.1016/j.neuroscience.2008.02.039. [DOI] [PubMed] [Google Scholar]
- Zhou X, Jen PHS. The effect of sound intensity on duration-tuning characteristics of bat inferior collicular neurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2001;187:63–73. doi: 10.1007/s003590000179. [DOI] [PubMed] [Google Scholar]