Abstract
There are clusters of slowly adapting (SA) mechanoreceptors in the skin folds bordering the nail. These “SA-IInail” afferents, which constitute nearly one fifth of the tactile afferents innervating the fingertip, possess the general discharge characteristics of slowly adapting type II (SA-II) tactile afferents located elsewhere in the glabrous skin of the human hand. Little is known about the signals in the SA-IInail afferents when the fingertips interact with objects. Here we show that SA-IInail afferents reliably respond to fingertip forces comparable to those arising in everyday manipulations. Using a flat stimulus surface, we applied forces to the finger pad while recording impulse activity in 17 SA-IInail afferents. Ramp-and-hold forces (amplitude 4 N, rate 10 N/s) were applied normal to the skin, and at 10, 20, or 30° from the normal in eight radial directions with reference to the primary site of contact (25 force directions in total). All afferents responded to the force stimuli, and the responsiveness of all but one afferents was broadly tuned to a preferred direction of force. The preferred directions among afferents were distributed all around the angular space, suggesting that the population of SA-IInail afferents could encode force direction. We conclude that signals in the population of SA-IInail afferents terminating in the nail walls contain vectorial information about fingertip forces. The particular tactile features of contacted surfaces would less influence force-related signals in SA-IInail afferents than force-related signals present in afferents terminating in the volar skin areas that directly contact objects.
Introduction
One of the two classes of slowly adapting, low-threshold mechanoreceptors found in human glabrous skin are the slowly adapting type II afferents (SA-II), which are thought to innervate Ruffini-like nerve endings that respond to tension in collagenous fiber strands running in and between dermal and subdermal tissues (Vallbo and Johansson, 1984) (see also Chambers et al., 1972). While these afferents are distributed uniformly over the glabrous skin of the hand, there is an accumulation of slowly adapting afferents with similar discharge properties in the soft tissue surrounding the lateral borders of the nail (Knibestöl, 1975; Johansson, 1978; Johansson and Vallbo, 1979), i.e., in the paronychium where the fingertip skin is anchored to the distal phalanx via the nail bed (Zook, 2003; Schmidt and Lanz, 2004). Indeed, Ruffini-like structures in the human fingertips skin are most easily found around the nails (Paré et al., 2003). As typical SA-II afferents, these SA-IInail afferents show a modest dynamic sensitivity and a regular static discharge; some also show an ongoing impulse activity in the absence of external stimuli (Knibestöl, 1975).
Relatively little is known about the function of the SA-IInail afferents, although they constitute some 17% of the tactile afferents that innervate the distal segment of a finger, which corresponds to ∼200 afferents/digit (Johansson and Vallbo, 1979). It has been proposed that they can signal forces applied to the nails (Johansson, 1978) and, since their firing rate can be modulated with the position of the distal interphalangeal joint, that they play a role in proprioception (Knibestöl, 1975). Given their abundance, in the present study we asked whether the SA-IInail afferents might contribute important information about mechanical events at volar skin areas of the fingertips that directly contact objects during natural use of the digits. Because widespread complex stresses and strains occur all over the fingertip when it deforms in response to forces applied on objects, tactile afferents not only in the skin area contacting an object, but also at the end and sides of the fingertip, can convey information about contact forces (Bisley et al., 2000; Birznieks et al., 2001; Jenmalm et al., 2003; Johansson and Birznieks, 2004). We hypothesized that also SA-IInail afferents might encode fingertip forces because of significant changes of the tension in collagenous fiber strands of the paronychium where their end organs are situated. Specifically, we asked whether SA-IInail afferents reliably respond to forces applied to the fingertip, and, in particular, whether they can transmit complex force information; namely, direction of fingertip forces. Vectorial force information is not only important for planning and control of object manipulation tasks (for review, see Johansson and Flanagan, 2008, 2009) but also in haptics perception, where people actively explore an object to identify and locate shape features based on force cues (Robles-De-La-Torre and Hayward, 2001). Encoding fingertip forces in afferents that terminate dorsally in fingertip might be advantageous because fine-form features of the contacted surfaces would less influence the afferent signals than with afferents terminating in the finger pulp.
Materials and Methods
Participants and general procedure.
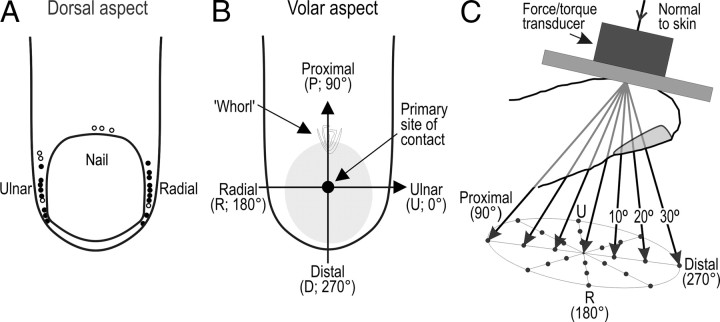
Three females and eight males (20–26 years of age) participated after providing written informed consent in accordance with the Declaration of Helsinki. Participants sat in a dentist's chair with the forearm and wrist supported by an evacuated vacuum cast. Impulses in single tactile afferents that terminated in the distal segment of the index, long or ring finger were recorded with tungsten microelectrodes (Vallbo and Hagbarth, 1968) inserted into the median nerve ∼2 cm proximal to the wrist. The median nerve was located by electrical stimulation and the position of the microelectrode tip manually adjusted until unitary action potentials could be discriminated. Afferents were classified according to criteria described previously (Johansson and Vallbo, 1983; Vallbo and Johansson, 1984). Twenty-four of the afferents encountered were classified as SA-II afferents that terminated around the borders of the nail as assessed by the locus of maximum sensitivity defined by pointed indentations with calibrated nylon filaments (von Frey hairs) (Fig. 1A). Seventeen of these 24 SA-IInail afferents constituted the afferents subjected to quantitative analyses in the present study (Fig. 1A, black dots); insufficient data were obtained from the remaining seven afferents.
Figure 1.
Experimental protocol and afferent sample. A, Distribution of loci of maximum sensitivity to pointed skin indentation for all SA-IInail afferents projected on the dorsal aspect of the fingertip. The black dots indicate the 17 afferents for which the recordings were stable enough that sufficient data were collected for statistical analyses. B, Outline of a fingertip showing the primary site of stimulation (filled circle). Note the polar coordinate conventions; U (0°), P (90°), R (180°), and D (270°). Gray zone on the finger drawings indicate an estimate of the area of contact at 4 N plateau normal force (Birznieks et al., 2001). C, The flat stimulus surface was parallel to the flat portion of skin. Force stimuli were delivered normal to the skin over the center of the finger pad, and at 10, 20, or 30° to the normal (vertical angle) in eight radial directions (total number of stimuli = 25) as exemplified by the arrows along distal-proximal axes; the normal force was always 4 N.
Stimulation procedures.
Mechanical stimuli were delivered to the tip of the receptor-bearing finger (i.e., right index, middle, or ring finger) using a custom-built computer-controlled stimulator that allowed control of force or position in three dimensions. A previous report describes in detail the apparatus used to deliver the mechanical stimuli (Birznieks et al., 2001).
A 30° wedge of wood held the receptor-bearing digit extended at ∼150°. Lateral bars held the adjacent fingers extended at ∼180°. To enhance reproducibility of the delivery of stimuli across multiple trials, the receptor-bearing digit was mechanically stabilized at the nail. The center of the nail of the digit was glued by cyanoacrylate cement to a 6-mm-wide aluminum plate shaped to accommodate the curvature of the nail. This plate was fixed to the end of the wooden wedge via a small post such that the distal segment of the receptor-bearing finger completely rested on the nail and did not contact the wedge, thereby allowing the fingertip to deform as it might if it were actively pressed against a surface (see Discussion). Thus, there was no incidental contact between the skin of distal segment of the receptor-bearing digit and the underlying support when stimulated by forces applied to the finger pad. We applied the stimulus to a standard test site on the tip of the receptor-bearing finger, defined as the midpoint of a line extending in the proximal–distal direction from the whorl of the papillary ridges to the distal end of the fingertip (Fig. 1B). This primary site of stimulation was located approximately in the center of the rather flat portion of the volar surface of the fingertip that serves as a primary target for object contact in precise object manipulation tasks (Christel, 1993). We oriented the stimulus surface such that it was parallel to the skin surface at the primary site of contact with the fingertip (Fig. 1C).
The surface that contacted the finger pad was flat and circular (diameter, 5 cm). A latex rubber membrane (25 μm thick) was glued onto the surface to obtain sufficiently high and stable friction between the contact surface and the skin to prevent slippage of the surface during the stimulation protocol. To measure the force applied to the fingertip, a six-axis force/torque transducer (Nano F/T transducer; ATI Industrial Automation) was attached between the contact surface and the effector element of the stimulator (Fig. 1C). The contact force was measured as three orthogonal components—two in the horizontal plane of the contact surface (along the distal-proximal direction and along the radial-ulnar direction of the fingertip) (Fig. 1B) and one normal to the surface. By using custom-made electronics for the Nano F/T transducer, we obtained a resolution <0.9 mN (RMS) in all directions and a bandwidth of 0–2.9 kHz.
Each stimulus consisted of a force protraction phase lasting 0.4 s, a plateau phase of constant force for 0.5 s, and a force retraction phase lasting 0.4 s (see Fig. 3). Starting above the fingertip, the manipulator moved the stimulus surface, under position control, perpendicularly toward the primary site of stimulation at a constant velocity of 2 mm/s. After the surface contacted the skin and the normal force reached 0.2 N, the servo switched from position control to force control. During the force protraction phase the normal force increased linearly at 10 N/s to 4 N and was maintained at this level during the plateau phase. During the force retraction phase the contact force decreased linearly at 10 N/s until the contact with the skin was broken and the stimulator switched back to position control. A stimulation cycle was repeated every 2 s. Force stimuli were delivered three times in the normal direction (referred to as 0° “vertical angle”) and, at an angle 30° to the normal (30° vertical angle), with tangential components in the eight radial directions with reference to the location of the primary contact site (0, 45, 90, 135, 180, 225, 270, 315°) (Fig. 1C). Stimuli with tangential components in the same eight radial directions were then applied at a vertical angle of 20° and then at 10°. Thus, we used 25 force directions in total (Fig. 1C). For each afferent the entire stimulation sequence was repeated 3–7 times (on average 4.6 times), depending on the stability of the recording.
Figure 3.
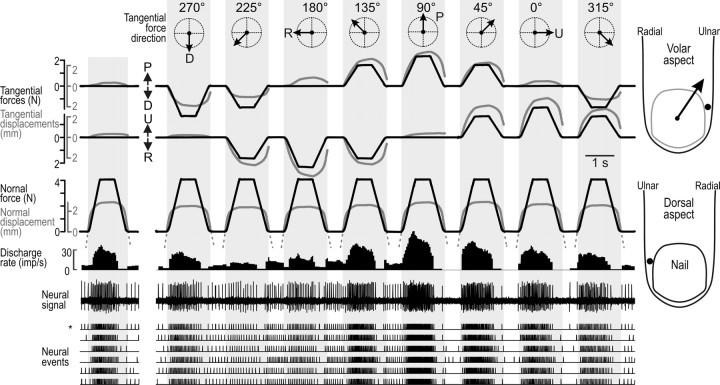
Force stimuli applied to the standard test site at the center of the fingerpad while recording action potentials in a single SA-IInail afferent. Stimuli were delivered with normal force only (far left) and with tangential force components in eight directions (arrows in the circular coordinate system in the top row; D, R, P, and U refer to distal, radial, proximal, and ulnar direction). Overlaid black and gray lines represent force and position signals, respectively. Position signals indicated by solid lines show displacement of the stimulation surface when in contact with the skin; broken lines indicate the position of the surface along the axis normal to the skin when the surface moves in the air between force stimuli. Note that the position signal in tangential directions is not shown when the stimulation surface is not in contact with the skin. The gray shaded areas indicate the periods when the stimulation surface made contact with the fingertip skin. The normal force component was 4 N, and when tangential force component was present, the force vector angle relative to the normal was 30°. Data correspond to a single stimulation sequence, except the nerve impulse ensembles, which show the current stimulation sequence (indicated by an asterisk) as well as data from five repetitions of the same sequence. This unit was maximally responsive to forces with a tangential component applied between the proximal and proximal-ulnar directions and weakest when applied in distal-radial directions. The arrow originating from the primary site of stimulation shows its preferred direction. Insets on the right show the most sensitive spot of the afferent to point indentations of the skin, projected onto the fingertip outline from the volar and dorsal aspects. The gray line on the volar aspect indicates the outline of the nail as if seen through the fingertip.
Data collection and analysis.
The neural signals (bandwidth 0.5–5 kHz; 10 bits resolution) were sampled at 12.8 kHz using the SC/ZOOM data acquisition and analysis system (Physiology Section, Department of Integrative Medical Biology, University of Umeå, Umeå, Sweden). Mechanical signals were simultaneously sampled (16 bits resolution) by the same system at 400 Hz after low-pass filtered at 200 Hz. Action potentials were detected using an algorithm based on differences in spike morphology, which was verified for each action potential off-line (Edin et al., 1988). The instantaneous frequency of the action potentials was defined as the inverse of the interval between consecutive impulses for the duration of the interval.
For each stimulus, we calculated four measures of the response of the afferent, given by the number of nerve impulses recorded during (1) the protraction phase (400 ms duration), (2) the plateau phase (500 ms duration), and (3) the retraction phase (400 ms duration). The first two stimuli of each stimulus sequence with normal force only were ignored, so as to allow effects of viscoelastic properties of the fingertip pulp to stabilize. For each afferent and angle to the normal (10, 20, and 30°) we used the Kruskal–Wallis one-way ANOVA by ranks to test whether the direction of the tangential force component reliably influenced the response. For conditions in which the direction of the tangential force component influenced the response, we used three quantitative measures to characterize the directional effect: (1) the preferred direction, (2) a directional sensitivity index, and (3) a measure of broadness of tuning toward the preferred direction. These measures were all based on the mean value of the responses to all stimuli delivered in a particular direction. We estimated the preferred direction of tangential force by the vector sum of the responses in the eight directions of tangential forces. We represented the preferred direction geometrically by a vector that originated from the primary site of stimulation and pointed in the direction of the estimated preferred stimulation. The directional sensitivity index reflects the depth of the tuning of the afferent response to the preferred direction (Birznieks et al., 2001). This index was defined as the magnitude of the vector sum of the responses to forces with tangential components in the eight directions divided by the scalar sum of the response magnitudes in the eight directions, i.e., as follows:
 |
where ri is the afferent response in one of eight tested force directions. The directional sensitivity index ranges between 0 and 1, and is a measure of tuning independent of the responsiveness of the afferent. Broadness of tuning was calculated based on a tuning curve mapping the afferent response as a function of the direction (°) of the tangential force component (see Fig. 7). We defined the broadness index as the angular width of the tuning curve around the direction of the strongest response at half-height of the modulation. To this end, we first subtracted the response in each tangential direction by the mean response computed across all eight directions. We then measured the angular width of the part of the tuning curve for which the response values exceeded the mean response, using linear interpolation between responses to adjacent tangential angles (see Fig. 7A, B, black segments of curves).
Figure 7.

Tuning curves illustrating the afferent responses as a function of the direction of the tangential force component relative to the direction of the strongest response (0°) provided by stimuli delivered at angle 30° to the normal (vertical angle). A, B, Data from two single afferents and for all three vertical angles of force stimulation (10, 20, 30°). The vertical position of the dashed lines represents for each vertical angle the mean response computed across eight tangential directions. The broadness of tuning was defined as the width of the tuning curve (°) at this line and corresponds to the black segments of the curve, for which the response values exceeded the mean response. C, D, Tuning curves as in A and B superimposed for all afferents, where the top, middle, and bottom panels refer to data obtained with a vertical angle of 30, 20, and 10°, respectively. Graphs in C show data from the eight afferents with the lowest overall responsiveness and in D for the remaining eight afferents with higher overall responsiveness. The gray curves and symbols refer to single afferents and the black curve to the mean across afferents, with vertical lines representing ±1 SEM.
As nonparametric measures of correlation, we used the Spearman rank correlation coefficient (rs) and nonparametric angular-angular correlation (raa) (Zar, 1996). The Rayleigh test of circular distribution uniformity was used for analyses of vector data (Zar, 1996). We used the Watson U2 test to test for differences between two groups of angular data. In addition to nonparametric statistics, we used angular-linear correlation analysis for correlating an angular variable with a linear variable (Zar, 1996). Repeated measures ANCOVA was used to examine effects at the population level of the vertical angle of force stimulation (0, 10, 20, 30°; fixed effect) and of afferents' overall responsiveness (covariate; quantitative predictor) on the measures of directionality of afferent responses (directional sensitivity index and broadness of tuning). For each afferent we defined its overall responsiveness as the mean value of the responses obtained across all 25 directions of stimulation (see Fig. 1C). In all tests, the level of probability selected as significant was p < 0.05.
Results
We classified an SA-II afferent as an SA-IInail type if it responded to a sustained pointed indentation to the soft tissue surrounding the nail and showed a single locus of maximum sensitivity within ∼2 mm of the borders of the nail (Fig. 1A). In agreement with previous studies (Knibestöl, 1975; Johansson and Vallbo, 1979), for most of the SA-IInail afferents that we encountered this locus of maximum sensitivity was situated in the skin folds along the lateral borders of the nail, indicating that these afferents terminated in the nail walls (Fig. 1A). The SA-IInail afferents shared many general response features with SA-II afferents that terminate elsewhere in the glabrous skin of the hand and that distinguish SA-II afferents from SA-I afferents: a single zone of maximum sensitivity to punctate indentation of the skin, poor dynamic sensitivity, a regular discharge during sustained skin indentation, and often an ongoing discharge in the absence of external stimuli (Vallbo and Johansson, 1984). Just over one-half (14/24) of the SA-IInail afferents showed a regular ongoing discharge in the absence of external stimuli, with typical firing rates ∼10 imp/s. However, the SA-IInail afferents appeared to respond comparatively poorly to planar skin stretch applied remote from the end-organs, which agrees with previous findings (Knibestöl, 1975; Johansson, 1978). Nevertheless, all SA-IInail afferents could respond to the force stimuli applied to the finger pad. Our analyses are based on data obtained from 17 of the SA-II nail afferents for which the recordings were stable enough to collect sufficient data for statistical analyses of effect on the afferent responses by direction of fingertip forces (see Fig. 1C), which is the prime subject of this report. Sixteen of the 17 SA-IInail afferents analyzed (94%) were sensitive to the direction of the tangential force component applied with the most oblique angle from normal, i.e., at 30° vertical angle (p < 0.05 in all cases; Kruskal–Wallis test). That is, for all but one afferent, the direction of the tangential force component influenced the number of impulses elicited during the force protraction phase (lasting for 0.4 s). All 16 afferents showing directionality at the 30° vertical angle retained this directional sensitivity when the stimuli were applied at more acute angles (10° and 20°; p < 0.05 in all 32 cases; Kruskal–Wallis test).
The remainder of the Results primarily concerns the 16 afferents showing directionality. Focusing on the force protraction phase, we will first characterize the responsiveness of afferents to the magnitude of the tangential force component generalized across all radial directions. Then we will analyze how the direction of force influenced the afferent responses during the force protraction phase. In the third part of Results, we compare the directionality of the afferent responses recorded during the different phases of the stimulus, i.e., protraction, plateau, and retraction phases. Finally, we briefly address the receptiveness of the SA-IInail afferents to forces applied to the finger pad by reporting on the threshold sensitivity to normal force stimulation.
General effect of tangential force on afferent responses
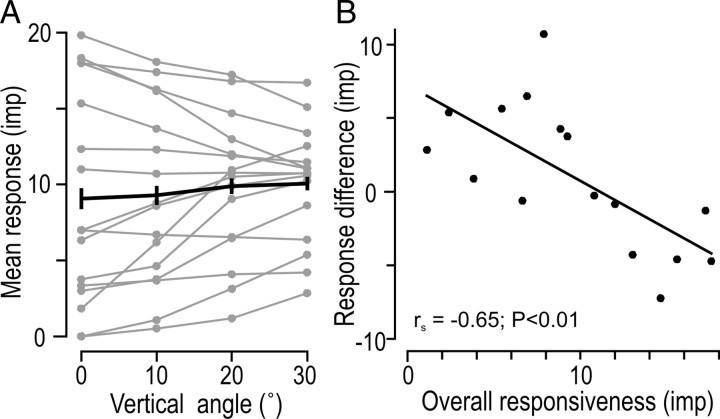
To assess the effect of the tangential force components as such on the afferent responses, for each afferent we looked for effect of the vertical angle (0, 10, 20, 30°) on the mean intensity of the responses averaged across all radial directions during the force protraction phase. Inspection of single afferent data indicated no systematic effect of the vertical angle across afferents, but suggested that afferents with overall lower responsiveness to fingertip forces tended to show increased discharge rates with increased angle of stimulation and vice versa for afferents showing weaker responsiveness (Fig. 2A). This impression was verified in an ANCOVA with vertical angle as a fixed effect and the overall responsiveness of the afferents (mean value of the responses obtained across all 25 directions of stimulation) as covariate. That is, there was a significant interaction between angle and the overall responsiveness to fingertip forces (F(3,42) = 11.0; p < 0.0001). Figure 2B illustrates the effect by plotting, for each afferent, the difference between the response at 30° angle from normal and that at normal force only (0°) as a function of the overall responsiveness.
Figure 2.
Overall responsiveness of afferents with directional stimuli. A, Mean number of impulses elicited during the force protraction phase (0.4 s duration) function of force angle relative to normal (vertical angle). For vertical angles different from zero (normal-force-only) the data were averaged across all 8 radial force directions. Each gray curve refers to a single afferent and the black curve to the grand mean across all afferents; vertical lines represent ±1 SEM. B, Difference in mean responses elicited at 30° and 0° vertical angles as a function of overall responsiveness (mean response averaged across all 25 stimulation directions). Each symbol represents a single afferent and the line show the linear regression.
Directional tuning characteristics of afferent responses during the force protraction phase
Figure 3 shows the responses of one representative afferent to ramp-and-hold forces applied to the finger pulp normal to the skin (0°), and at 30° vertical angle with the tangential force component in eight radial directions, relative to the primary site of contact (see Fig. 1C). The firing rate of this afferent, located on the ulnar side of the nail of the middle finger, was tuned broadly toward a preferred direction of tangential force: the afferent showed the strongest response to tangential forces applied in the proximal direction (90°) and the weakest response when the tangential force component was in between the distal and radial direction (225°). Thus, the directions to which the afferent responded with the highest and lowest firing rates were approximately opposite; responses of intermediate strengths were observed in the directions between these extremes. This pattern was consistent across the six trials in which the same sequence of stimuli was delivered, yet some intertrial variability was observed (Fig. 3, see ensembles of neural events). In the intervals between stimuli, the afferent could show an ongoing discharge, the rate of which appeared to be inversely related to the intensity of the response to the preceding stimulus. That is, like SA-II afferents in general (Knibestöl and Vallbo, 1970; Chambers et al., 1972; Burgess and Perl, 1973), the SA-IInail afferents were subject to pronounced poststimulation depression. Furthermore, the postexcitatory depression was also manifested by the afferent typically ceasing to fire during the later parts of the force retraction phases, before the background activity resumed during unloading.
Figure 3 also illustrates aspects of the mechanical complexity of the fingertip by showing the displacement of the contact surface in the direction normal to the skin and in the plane tangential to the skin for forces applied in each of the nine test directions. In agreement with our previous observations (Birznieks et al., 2001; Jenmalm et al., 2003), we noted that the fingertip shows marked viscoelastic and anisotropic mechanical properties. The viscoelastic properties resulted in pronounced hysteresis especially in the tangential plane between the force and position signals. The anisotropic properties of the fingertip implied that the displacements of the contact surface differed in the tangential directions although the magnitude of the tangential force component was the same. For example, the tangential displacement was greater for tangential forces of a given magnitude if they involved a proximal component compared with a distal component.
Preferred direction of tangential force
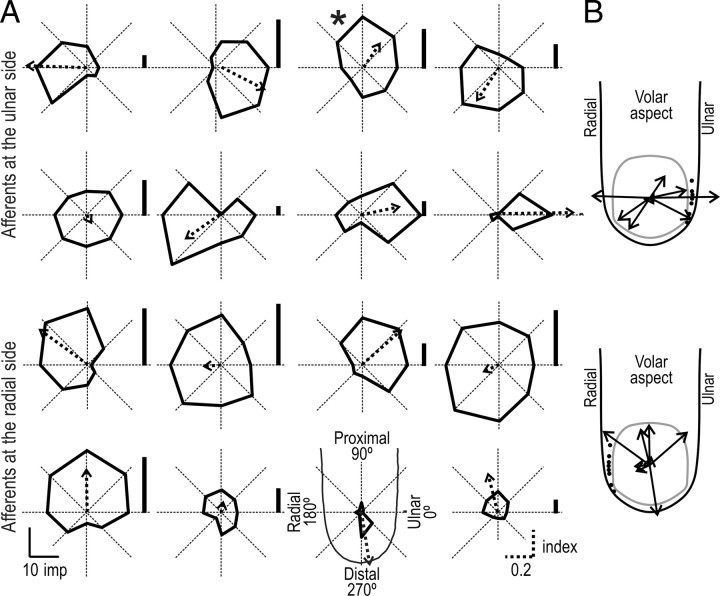
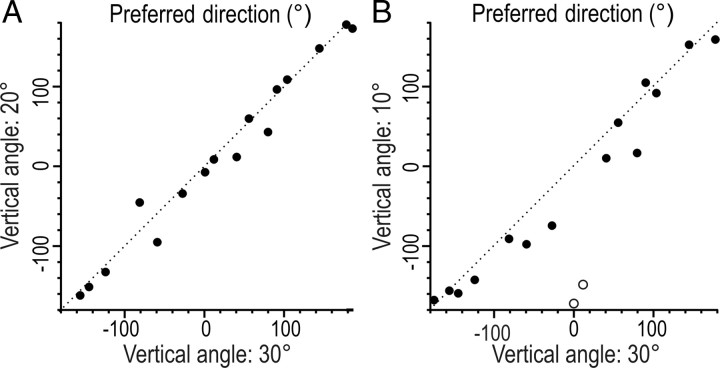
Figure 4A shows polar plots of the directionality for each the 16 directional sensitive SA-IInail afferents when tested with tangential forces delivered 30° from normal. The two upper rows illustrate the eight afferents that terminated on the ulnar side of the nail, and the two bottom rows the eight afferents that terminated on the radial side (compare Fig. 1A). For all of these afferents, the response magnitude was broadly tuned to a particular direction of stimulation. Preferred directions, computed as the vector sum of the responses to stimuli in the eight tangential directions, were essentially evenly distributed in all angular directions (p > 0.05; Rayleigh test). Figure 4B illustrates the preferred directions of the afferents terminating on the radial and ulnar side of the nail in separate panels. Possible differences in preferred directions of afferents terminating on the radial and ulnar side failed to reach statistical significance (p > 0.05; Watson U2 test). Across afferents there was a strong correlation between the preferred directions obtained with the two most oblique angles, i.e., 30° and 20° (Fig. 5A). With an angle of 10° to the normal, the correlation was weaker but still significant (Fig. 5B). The behavior of two afferents principally accounted for this weaker correlation (Fig. 5B, open circles).
Figure 4.
Polar plots of the directionality of the responses during the protraction phase for each the 16 directional sensitive SA-IInail afferents when tested with tangential forces delivered 30° from normal. A, The polar plot consists of eight solid straight lines joining the response magnitudes in the eight tangential force directions (45° apart) measured as the number of impulses evoked during the protraction phase. The origin of the coordinate system is at the primary site of stimulation. Arrows show the preferred directions of the 16 afferents. The length of the vector represents the directional sensitivity index. The vertical bar next to each polar plot shows the afferent response during the normal-force-only stimulation. The two upper rows show afferents terminating on the ulnar side of the nail, and the two bottom rows represent afferents terminating on the radial side (compare Fig. 1A). The asterisk refers to the afferent featured in Figure 4. B, Preferred direction vectors originating from the primary site of contact are shown divided into two groups, according to whether the afferent terminated on the ulnar or radial side of the nail (black dots projected on the contours of the fingertip). Finger and nail projections are viewed from the volar aspect of the finger.
Figure 5.
Comparison of estimates of preferred directions to tangential force component applied at different vertical angles for 16 SA-IInail afferents. A, B, Scatter plots showing the relationship between the preferred directions estimated with stimulation forces applied at 30° versus 20° vertical angles (raa = 0.96, p < 0.001), and at 30° versus 10° vertical angles (raa = 0.48, p < 0.01), respectively. Two outliers are coded by open circles in B. The dotted line is a unity line showing equivalent preferred direction on the ordinate and abscissa. Polar coordinate as in Figures 1B and 4A.
Directional sensitivity
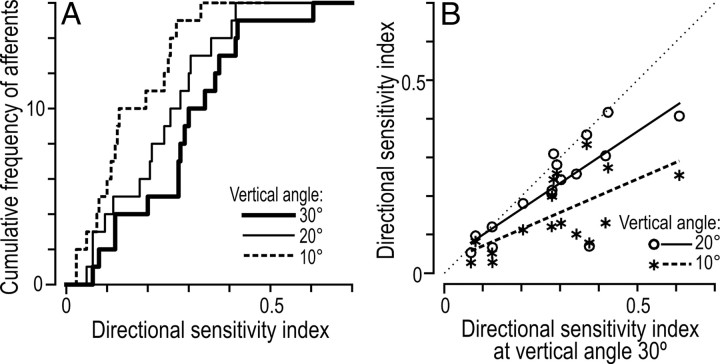
The length of the vectors indicating afferents preferred directions in Figure 4 represents the directional sensitivity index. This index, which ranges between 0 and 1, reflects in relative terms the depth of modulation of an afferent's response with reference to the preferred direction; an index of 0 indicates that the response is the same in all eight directions, and 1 indicates that the afferent responds in only one direction (see Materials and Methods). Figure 6A shows for each of the three vertical angles of force stimulation (10, 20, and 30°) the distribution of directional sensitivity indices for the 16 SA-IInail afferents sensitive to the direction the tangential force component for the responses elicited during the protraction phases. When afferents were stimulated at an angle of 30° from normal, the directional sensitivity index was, on average, 0.29 ± 0.14. However, as might be expected, when the angle of the stimulation force was more acute, the directional sensitivity index decreased (Fig. 6A). The mean directional sensitivity index was 0.22 ± 0.12 and 0.15 ± 0.10 for 20° and 10°, respectively. A repeated measures ANCOVA verified an effect of vertical angle on the afferents' sensitivity to direction of tangential force (F(2,28) = 7.7; p < 0.01). The overall responsiveness of the afferents did not reliably affect the directional sensitivity index (p = 0.10) and there was no significant interaction between angle and overall responsiveness on the directional sensitivity index (p = 0.28). Across afferents, there was a significant correlation between the directional sensitivity index obtained with the different vertical angles of force stimulation (Fig. 6B).
Figure 6.
Directional sensitivity index at three different vertical angles of force stimulation (10, 20, and 30°) for 16 SA-IInail afferents. A, Cumulative frequency distribution of the directional sensitivity indices. B, Scatter plots show the relationship between indices estimated with stimulation forces applied at 30° versus 20° vertical angles (rs = 0.77, p < 0.001; open circles), and at 30° versus 10° vertical angles (rs = 0.67, p < 0.005; asterisks). Each symbol represents a single afferent and the line shows the linear regression; the thin dotted line is the line of unity, showing equivalent directional sensitivity on the ordinate and abscissa.
Interestingly, the directional sensitivity indices of the SA-IInail afferents estimated with forces 20° from the normal were very similar to indices estimated at the same vertical angle for populations of SA-II (0.24 ± 0.20), SA-I (0.23 ± 0.18), and fast-adapting type I (FA-I; 0.24 ± 0.18) afferents distributed over the entire volar aspect of the fingertip using similar stimuli (Birznieks et al., 2001).
Tuning of responses to force direction
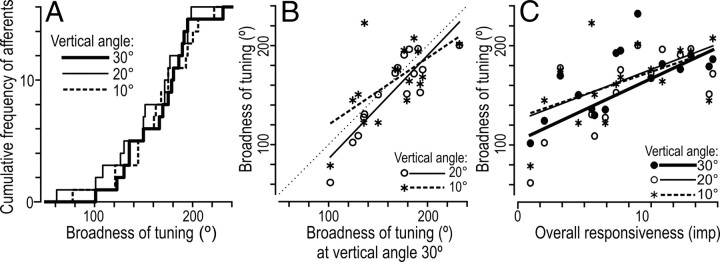
To enhance the appreciation of the tuning of the afferent responses to direction of the tangential force component, for each afferent and angle to the normal, we constructed a tuning curve showing the response as a function of the force direction in the plane of the skin surface (Fig. 7). We centered these curves on the tangential direction that provided the strongest response when tested at the most oblique angle from the normal (30°). For each afferent and vertical angle (10, 20, and 30°), we assessed the broadness of tuning as the width of the part of the tuning curve for which the response values exceeded the mean response computed across all eight directions of tangential force (Figs. 7A, B, black segments of curves). Although the broadness of tuning varied among afferents, it appeared little influenced by the vertical angle (Figs. 7, 8A). For stimuli delivered 30° from the normal, it ranged between 102° and 232° and, on average, it was 166°. The corresponding data for stimuli delivered 10° from the normal were 79° and 223°, and 164°. Likewise, there was a significant correlation between the broadness of tuning assessed for the different vertical angles (Fig. 8B). The broadness of tuning, however, tended to increase with the overall responsiveness of the afferents (Fig. 8C). This can also be appreciated in Figure 7, C and D, which shows afferent tuning curves after dividing the afferents into two equal sized groups (n = 8) based on their overall responsiveness. A repeated measures ANCOVA verified that the broadness of tuning it was related to the overall responsiveness of the afferents (F(1,14) = 12.7; p < 0.01), but failed to show an effect of the vertical angle of force stimulation. There was no significant interaction between vertical angle and overall responsiveness.
Figure 8.
Broadness of tuning for 16 SA-IInail afferents to the direction of tangential force at three different vertical angles of force stimulation (10, 20, and 30°). A, Cumulative frequency distribution of the broadness of tuning. B, Scatter plot displaying the relationship between the broadness of tuning at 30° vertical angle versus broadness of tuning with forces applied at 20° vertical angle (rs = 0.82; p < 0.001; open circles) and at 10° vertical angle (rs = 0.51; p < 0.05; asterisks). The thin dotted line is the line of unity, showing equivalent broadness on the ordinate and abscissa. C, Broadness of tuning as a function of the afferents' overall responsiveness. B, C, Each symbol represents a single afferent and the related line shows the linear regression.
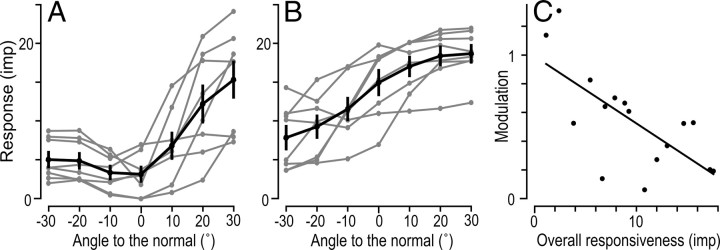
We also analyzed the effect of the angle from the normal on the responses of SA-II-nail afferents by constructing tuning curves along the axis of most-least preferred direction (Fig. 9A, B). In this analysis, we centered the data at the normal (0°) orientation and gave the most preferred direction positive angles (10, 20, and 30°) and the opposite orientation negative angles (−10, −20, and −30°). Figure 9, A and B, shows the eight afferents with lowest and highest overall responsiveness, respectively (compare Fig. 7C, D). A repeated measured ANCOVA with vertical angle as fixed effect and the afferents' overall responsiveness as covariate, showed, as expected, a main effect of vertical angle on the afferents' firing rates (F(6,84) = 10.4; p < 0.0001). Furthermore, there was a significant interaction between vertical angle and the overall responsiveness of afferents to fingertip forces (F(6,84) = 5.71; p < 0.0001). That is, afferents with overall lower responsiveness to fingertip forces tended to show a stronger modulation with changes in vertical angle than afferents showing higher overall responsiveness (Fig. 9C; also compare Fig. 9A, B).
Figure 9.
Tuning curves illustrating the afferent's response as a function of direction of the force relative to the normal (0°) along the axis of the “least–most” preferred direction represented by −30 to 30°. A, B, Number of impulses elicited as a function of vertical force angle in relative to normal (vertical angle) for the eight afferents with the lowest overall responsiveness (A) and for the remaining eight afferents with higher overall responsiveness (B). The gray curves refer to single afferents and the black curve to means across afferents with vertical lines representing ± 1 SEM. C, Correlation between afferents' overall responsiveness and the modulation of their responses by direction of vertical force along the axis of the “least–most” preferred direction (rs = −0.63; p < 0.01). The modulation was computed as the ratio between the SD of the responses to stimuli with forces in all seven vertical angles and the mean response to stimuli in all seven angles (cf. coefficient of variation). Each symbol represents a single afferent and the line show the linear regression.
Together, these findings indicate that the overall responsiveness of an afferent influenced its tuning properties to direction of force. That is, compared with afferents with higher overall responsiveness, afferents with an overall lower responsiveness were more sharply tuned to the direction of the tangential force component and the responses were more influenced by the vertical angle of the force, i.e., the magnitude of the tangential force component.
Directionality of afferent responses during the different phases of force stimuli
So far, we have reported on directionality of responses in SA-IInail afferents during the force protraction phases. We also examined directionality of responses during the plateau and retraction phases of the force stimuli, focusing on stimuli delivered at an angle of 30° from the normal. The slowly adapting characteristics of the SA-IInail afferents inferred that they responded reliably during the plateau phase, which would resemble force stimulations occurring during the static phases of object manipulation tasks, such as when we hold an object in the air. Although the SA-IInail afferents tended to cease responding during the force retraction phase (Fig. 3), which corresponds to the force changes that occur when releasing a grasped object, there was nevertheless impulse activity available for analysis of directionality. All 16 SA-IInail afferents that were significantly influenced by the direction of the tangential force component during the protraction phase also showed directionality during the plateau and retraction phases (p <0.05 in all 32 instances; Kruskal–Wallis). There was a correspondence between the preferred directions estimated for the plateau phase and the protraction phase across afferents (Fig. 10A). Likewise, there was a correspondence between the preferred directions estimated for the protraction and retraction phases, although this was less impressive (Fig. 10B). Although the magnitude of the directional sensitivity index could vary for individual afferents across phases, across afferents it was positively correlated for the protraction and the plateau phases (Fig. 10C), but not reliably for the protraction and the retraction phases (Fig. 10D). Overall, the distributions of directional sensitivity indices across afferents were similar across the three phases (Fig. 10E).
Figure 10.
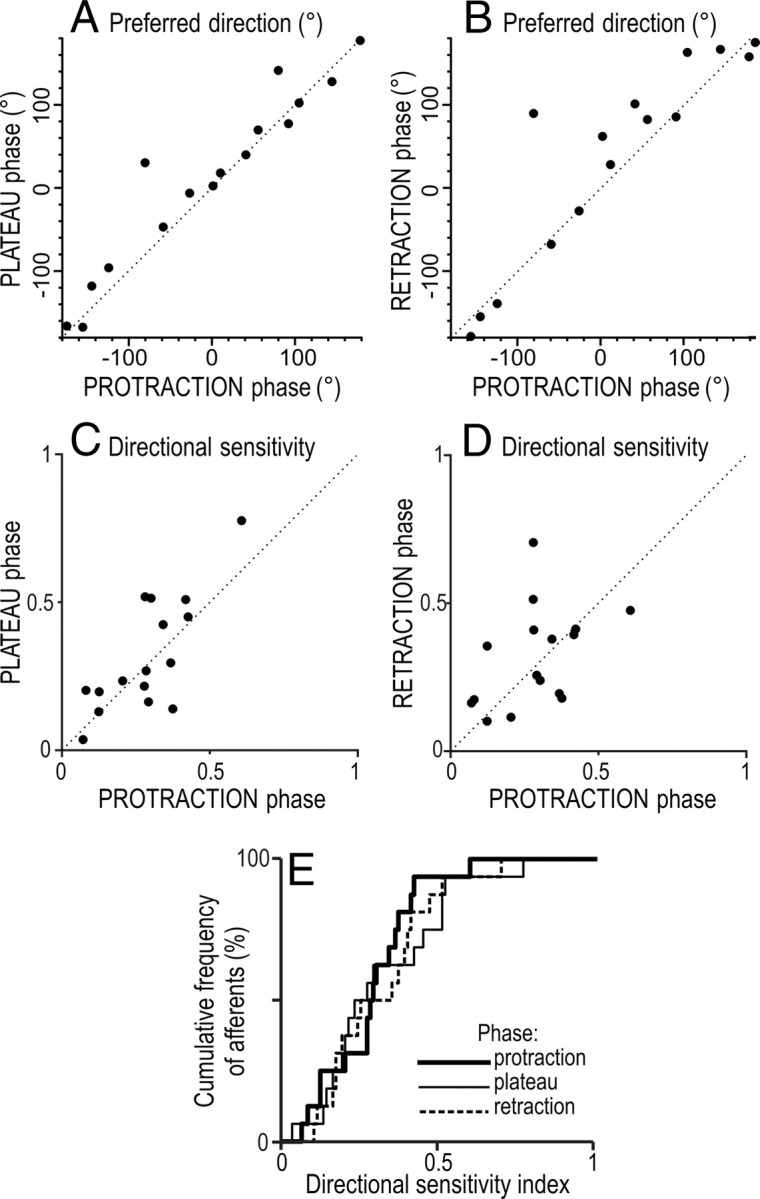
Comparison of directionality of 16 SA-IInail afferents during different phases of the stimulus applied at 30° angle relative to normal. A, B, Relationship between preferred direction during the protraction phase and that during the plateau phase (raa = 0.73, p <0.01) and during the retraction phase (raa = 0.45, p <0.05). C, D, Relationship between the directional sensitivity indices during protraction versus the plateau phase (rs = 0.64, p <0.01) and versus the retraction phases (rs = 0.48, p = 0.06). E, Cumulative distribution of directional sensitivity indices during different phases of stimulation. A–D, The dotted line is a unity line showing equivalent preferred direction on the ordinate and abscissa. Polar coordinates as in Figures 1B and 4A.
Receptiveness to forces applied to the finger pad
We estimated the threshold sensitivity of SA-IInail afferents to fingertip forces focusing on stimuli in the normal-force-only condition. To that end, we measured the amplitude of the normal force during the protraction phase 10 ms before detection of the afferent response to the ramp force increase. The 10 ms time advance was applied to account approximately for nerve conduction delays. For seven afferents that did not show ongoing impulse activity in periods between force stimuli, the appearance of the first spike defined the onset-time of the response. For the remaining afferents that showed background discharges, we arbitrarily defined the response onset time as the time when a spike appeared after which the firing rate persistently changed by >20% with reference to the background firing rate. The force threshold, estimated for each afferent as the mean threshold value computed across all normal-force stimulations (see stimulation sequences in Materials and Methods), ranged between 0.12 and 0.67 N (mean = 0.35 N) and between 0.27 and 1.68 N (mean = 0.92 N) for afferents without and with ongoing background discharges, respectively. The variability in the threshold estimates across the repeated normal-force stimulations, computed as the coefficient of variation for each afferent was, on average, 13% and 22% for afferents without and with background discharges, respectively.
Discussion
We have demonstrated that SA-IInail afferents, located in skin bordering the lateral edges of the nails, respond reliably to forces applied to the volar area of the fingertips that primarily contacts objects in manipulation and exploration tasks. Furthermore, signals in populations of SA-IInail afferents contain directional information about fingertip forces. That is, force direction reliably influenced the responses in nearly all SA-IInail afferents and the preferred direction to tangential force components was distributed in all angular directions across afferents.
The nerve endings of the SA-IInail afferents are presumably located in the collagenous fiber strands that anchor pulp tissues, including the skin, to the perimeter of the nail (see Introduction). Their general discharge characteristics are shared with afferents with Ruffini-like endings that innervate fibrous tissues throughout the body, including glabrous and hairy skin, interosseous membranes, tendons, tendon sheaths, muscle fasciae, joint capsules and ligaments (for review, see Darian-Smith, 1984). Thus, the SA-IInail afferents apparently belong to a universal mechanoreceptive system, in which Ruffini-like endings have been shown to encode tensile stress in collagenous bundles (Chambers et al., 1972; Fuller et al., 1991; Grigg, 1996; Khalsa et al., 1996). Indeed, SA-IInail afferents not only respond to fingertip forces as we have demonstrated but can also respond to the flexion state of the distal interphalangeal joint (Knibestöl, 1975), which presumably influences the tension in the receptor-bearing collagenous strands.
SA-IInail afferents and deformations of the paronychium
Visual monitoring of the fingertip when it applies forces to a flat surface provides some clues about the mechanisms that underlie the responses of the SA-IInail afferents to fingertip forces. During application of forces normal to the skin, the increase in pressure in the pulp causes symmetrical bulging of the pulp tissue at the end and sides of the fingertip. This increases the strain in the skin and the stress in the fibrous tissues that anchor the skin to the terminal phalanx. In particular, significant tensile strain arises around the nail walls and in the skin along the distal margin of the nail bed where the skin is anchored to nail, which is mechanically constrained (Shimawaki and Sakai, 2007). Consequently, if SA-IInail afferents terminating in the nail walls were excited by tensile stress, they would respond to compression of the pulp, which is exactly what we observed. The direction of the tangential force influencing the transformation of the fingertip would account for the directionality of the afferent responses. That is, the sliding of the fingertip pulp over the phalanx caused by the tangential force component (see Fig. 3, tangential displacements) tends to enhance the bulging of the nail wall at locations in the direction of the force, while also tending to stretch the skin at locations on the opposite side of the nail. Such compound direction-dependent effects on the nail walls, together with the particular localization of the afferents' in the highly intricate networks of collagenous fibers that anchor the pulp tissue to the perimeter of the nail (Sangiorgi et al., 2005), would explain that afferents located in the same nail wall could show quite different directional preferences (Fig. 4B).
In the present experiments, forces applied to the fingertip operated between its volar surface and the mechanically stabilized nail. However, forces naturally applied against objects operate primarily between the volar surface and the distal phalanx. Hence, one may question whether signals in the SA-IInail afferents that we observed are representative for natural use of the digits. There is however solid evidence supporting our view. First, the nail is firmly fixed to the periosteum by a dense mesh of criss-crossed strands of collagen (unguinal retinacula), which implies that the nail, the nail bed and terminal phalanx behave practically as a rigid object (Schmidt and Lanz, 2004) (see also Birznieks et al., 2001). Second, the SA-IInail afferents that we have analyzed terminated in the nail walls rather than in the nail bed, where the stress might differ between active and passive force generation. Third, there is direct evidence that SA-IInail afferents respond to fingertip forces during natural manipulation task (Westling and Johansson, 1987). For a few SA-IInail afferents, it was reported that both forces normal and tangential to the contacted surfaces could influence the responses, but no quantitative data were provided.
What do the SA-IInail afferents tell the CNS?
The relatively low dynamic sensitivity, the well sustained tonic response to maintained stimulation and the poststimulation depression suggest that the SA-II afferents, including SA-IInail afferents, are tailored to encode rather slow viscoelastic and quasi-static events occurring in dermal and subdermal tissues. Ongoing activity in the absence of externally applied stimulation is probably attributable to the inherent mechanical tension in the tissues where the receptors are located (Johansson, 1978). Importantly, the spatial low-pass filtering properties of the link between the skin surface and the nerve endings prevents an accurate representation of “fine-form” geometric features, such as Braille-like patterns in SA-II afferents (Phillips et al., 1990, 1992).
The abundance of SA-IInail afferents in the fingertips suggests that they may have important sensory functions. First, the population of SA-IInail afferents apparently transmits vectorial information about fingertip forces with similar directional properties as shown for SA-I, FA-I, and SA-II afferents terminating in volar aspects of the fingertips (see Results) (Birznieks et al., 2001). However, the SA-IInail afferents would provide “cleaner” force-related signals because fine-form and textural features of the contacted object would less influence force-related signals in SA-IInail afferents. Such clean signals might not only simplify computations of fingertip forces by the CNS but also help to resolve interaction effects between fingertip forces and other stimulation parameters (e.g., shape and orientation of contacted surfaces) on responses in other afferent populations (Jenmalm et al., 2003; Goodwin and Wheat, 2004).
Second, by constantly transmitting information related to the stress distribution in the fingertips, the SA-IInail afferents could keep neural control processes updated about the current mechanical state of the tissues linking the skin to the distal phalanx on which the muscles operate. In addition to application of contact forces on objects, several factors may change this state, e.g., the temperature of the fingertip, circulatory and metabolic factors, skin hydration, and, most importantly, factors associated with use of the digits—changes in angles of interphalangeal joints and changes in the mechanical properties of the fingertips related to previous interactions with objects. Interactions with objects transform the fingertip because of its viscoelastic properties and, depending on the stimulation history, seconds to minutes of inactivity are required for recovery to the resting state (Pubols, 1982; Pawluk and Howe, 1999). Importantly, such state changes not only influence the encoding of fingertip events by tactile afferents (Pubols, 1982; Birznieks et al., 2001) but also affect the motor commands required for desirable outcomes. That is, for dexterous performance, the CNS would need information about the current mechanical state of the soft tissues both for computing accurate motor commands and for predicting and evaluating their sensory consequences (Johansson and Flanagan, 2008, 2009). Rather than being problematic to deal with by the CNS, interaction effects between the position of the distal interphalangeal joint and fingertip forces on responses of SA-IInail afferents (cf. Knibestöl, 1975) might reflect peripheral integration in the sensory information used in motor control. That is, the muscle commands to achieve a certain force depend on the interphalangeal joint angles and vice versa.
Various lines of evidence suggest that the SA-IInail afferents may play roles in neural processes that lay outside the perceptual domain. For example, in contrast to all other types of tactile afferents innervating the human glabrous skin, selective intraneural stimulation of single SA-II afferents does not evoke a percept (Torebjörk et al., 1987; Macefield et al., 1990). Likewise, impulses in SA-II afferents, including SA-IInail afferents, can influence automatically ongoing EMG in muscles acting on the digits through spinal pathways (McNulty et al., 1999; McNulty and Macefield, 2001). It is also possible that the tonic impulse activity in SA-IInail afferents, which is not consciously perceived, contribute to upholding digit representations in the central somatosensory system, which apparently requires continuous peripheral input (Kelahan and Doetsch, 1984; Calford and Tweedale, 1988, 1991). The brain needs afferent input to maintain its body image (Melzack and Bromage, 1973), where tonic input from fingertips would define distinctly the endpoint of the upper extremity.
It is clear that the nails are important for performing fine manipulation and haptic tasks (Ashbell et al., 1967; Russell and Casas 1989; Drake et al., 1998; Salazard et al., 2004). For example, a finger without a nail will compromise a musician's career if the finger involved is necessary to play a note (strings, keyboards) or hold a position (winds) (Dumontier, 2003). However, since little has been known until now about functional properties of SA-IInail afferents, the sensory impairment after nail-related injury has not been sufficiently considered in attempts to understand the pathophysiology. We believe that our findings will trigger novel clinical and experimental studies striving to unravel the roles of the SA-IInail afferents for the functions of the hands.
Footnotes
The Swedish Research Council (Project 08667) and the Sixth Framework Program of the European Union (Project IST-028056) supported this work. The Sunderland Award from the Ian Potter Foundation of Australia supported V.G.M. in Sweden, and the Australian National Health and Medical Research Council (NHMRC) supported him in Australia (#957750). I.B. was also supported by the NHMRC/Australian Research Council Grant TS0669860 in Australia. We are grateful for the excellent technical assistance provided by Anders and Lars Bäckström in Sweden.
References
- Ashbell TS, Kleinert HE, Putcha SM, Kutz JE. The deformed finger nail, a frequent result of failure to repair nail bed injuries. J Trauma. 1967;7:177–190. doi: 10.1097/00005373-196703000-00001. [DOI] [PubMed] [Google Scholar]
- Birznieks I, Jenmalm P, Goodwin AW, Johansson RS. Encoding of direction of fingertip forces by human tactile afferents. J Neurosci. 2001;21:8222–8237. doi: 10.1523/JNEUROSCI.21-20-08222.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bisley JW, Goodwin AW, Wheat HE. Slowly adapting type I afferents from the sides and end of the finger respond to stimuli on the centre of the fingerpad. J Neurophysiol. 2000;84:57–64. doi: 10.1152/jn.2000.84.1.57. [DOI] [PubMed] [Google Scholar]
- Burgess PR, Perl ER. Cutaneous mechanoreceptors and nociceptors. In: Iggo A, editor. Handbook of sensory physiology. Berlin: Springer; 1973. pp. 30–78. [Google Scholar]
- Calford MB, Tweedale R. Immediate and chronic changes in responses of somatosensory cortex in adult flying-fox after digit amputation. Nature. 1988;332:446–448. doi: 10.1038/332446a0. [DOI] [PubMed] [Google Scholar]
- Calford MB, Tweedale R. Immediate expansion of receptive fields of neurons in area 3b of macaque monkeys after digit denervation. Somatosens Mot Res. 1991;8:249–260. doi: 10.3109/08990229109144748. [DOI] [PubMed] [Google Scholar]
- Chambers MR, Andres KH, von Duering M, Iggo A. The structure and function of the slowly adapting type II mechanoreceptor in hairy skin. Q J Exp Physiol Cogn Med Sci. 1972;57:417–445. doi: 10.1113/expphysiol.1972.sp002177. [DOI] [PubMed] [Google Scholar]
- Christel M. Grasping techniques and hand preferences in hominoidea. In: Preuschoft H, Chivers DJ, editors. Hands of primates. New York: Springer; 1993. pp. 91–108. [Google Scholar]
- Darian-Smith I. The sense of touch: performance and peripheral neural processes. In: Brookhart JM, Mountcastle VB, Darian-Smith I, Geiger SR, editors. Handbook of physiology. Bethesda, MD: American Physiological Society; 1984. pp. 739–788. [Google Scholar]
- Drake LA, Scher RK, Smith EB, Faich GA, Smith SL, Hong JJ, Stiller MJ. Effect of onychomycosis on quality of life. J Am Acad Dermatol. 1998;38:702–704. doi: 10.1016/s0190-9622(98)70199-9. [DOI] [PubMed] [Google Scholar]
- Dumontier C. Distal replantation, nail bed, and nail problems in musicians. Hand Clin. 2003;19:259–272. vi. doi: 10.1016/s0749-0712(02)00135-x. [DOI] [PubMed] [Google Scholar]
- Edin BB, Bäckström PA, Bäckström LO. Single unit retrieval in microneurography: a microprocessor-based device controlled by an operator. J Neurosci Methods. 1988;24:137–144. doi: 10.1016/0165-0270(88)90057-x. [DOI] [PubMed] [Google Scholar]
- Fuller MS, Grigg P, Hoffman AH. Response of joint capsule neurons to axial stress and strain during dynamic loading in the cat. J Neurophysiol. 1991;65:1321–1328. doi: 10.1152/jn.1991.65.6.1321. [DOI] [PubMed] [Google Scholar]
- Goodwin AW, Wheat HE. Sensory signals in neural populations underlying tactile perception and manipulation. Ann Rev Neurosci. 2004;27:53–77. doi: 10.1146/annurev.neuro.26.041002.131032. [DOI] [PubMed] [Google Scholar]
- Grigg P. Stretch sensitivity of mechanoreceptor neurons in rat hairy skin. J Neurophysiol. 1996;76:2886–2895. doi: 10.1152/jn.1996.76.5.2886. [DOI] [PubMed] [Google Scholar]
- Jenmalm P, Birznieks I, Goodwin AW, Johansson RS. Influence of object shape on responses of human tactile afferents under conditions characteristic of manipulation. Eur J Neurosci. 2003;18:164–176. doi: 10.1046/j.1460-9568.2003.02721.x. [DOI] [PubMed] [Google Scholar]
- Johansson RS. Tactile sensibility in the human hand: receptive field characteristics of mechanoreceptive units in the glabrous skin area. J Physiol. 1978;281:101–125. doi: 10.1113/jphysiol.1978.sp012411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson RS, Birznieks I. First spikes in ensembles of human tactile afferents code complex spatial fingertip events. Nat Neurosci. 2004;7:170–1177. doi: 10.1038/nn1177. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Flanagan JR. Tactile sensory control of object manipulation in humans. In: Gardner E, Kaas JH, editors. The senses: a comprehensive reference. Volume 6. San Diego: Academic; 2008. pp. 67–86. Somatosensation. [Google Scholar]
- Johansson RS, Flanagan JR. Coding and use of tactile signals from the fingertips in object manipulation tasks. Nat Rev Neurosci. 2009;10:345–359. doi: 10.1038/nrn2621. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Vallbo ÅB. Tactile sensibility in the human hand: relative and absolute densities of four types of mechanoreceptive units related to psychophysical thresholds in the human hand. J Physiol. 1979;297:405–422. doi: 10.1113/jphysiol.1979.sp012619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson RS, Vallbo ÅB. Tactile sensory coding in the glabrous skin of the human hand. Trends Neurosci. 1983;6:27–31. [Google Scholar]
- Kelahan AM, Doetsch GS. Time-dependent changes in the functional organization of somatosensory cerebral cortex following digit amputation in adult raccoons. Somatosens Res. 1984;2:49–81. [PubMed] [Google Scholar]
- Khalsa PS, Hoffman AH, Grigg P. Mechanical states encoded by stretch-sensitive neurons in feline joint capsule. J Neurophysiol. 1996;76:175–187. doi: 10.1152/jn.1996.76.1.175. [DOI] [PubMed] [Google Scholar]
- Knibestöl M. Stimulus-response functions of slowly adapting mechanoreceptors in the human glabrous skin area. J Physiol. 1975;245:63–80. doi: 10.1113/jphysiol.1975.sp010835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knibestöl M, Vallbo AB. Single unit analysis of mechanoreceptor activity from the human glabrous skin. Acta Physiol Scand. 1970;80:178–195. doi: 10.1111/j.1748-1716.1970.tb04783.x. [DOI] [PubMed] [Google Scholar]
- Macefield G, Gandevia SC, Burke D. Perceptual responses to microstimulation of single afferents innervating joints, muscles and skin of the human hand. J Physiol. 1990;429:113–129. doi: 10.1113/jphysiol.1990.sp018247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNulty PA, Macefield VG. Modulation of ongoing EMG by different classes of low threshold mechanoreceptors in the human hand. J Physiol. 2001;537:1021–1032. doi: 10.1111/j.1469-7793.2001.01021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNulty PA, Türker KS, Macefield VG. Evidence for strong synaptic coupling between single tactile afferents and motoneurones supplying the human hand. J Physiol. 1999;518:883–893. doi: 10.1111/j.1469-7793.1999.0883p.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melzack R, Bromage PR. Experimental phantom limbs. Exp Neurol. 1973;39:261–269. doi: 10.1016/0014-4886(73)90228-8. [DOI] [PubMed] [Google Scholar]
- Paré M, Behets C, Cornu O. Paucity of presumptive Ruffini corpuscles in the index finger pad of humans. J Comp Neurol. 2003;456:260–266. doi: 10.1002/cne.10519. [DOI] [PubMed] [Google Scholar]
- Pawluk DT, Howe RD. Dynamic contact of the human fingerpad against a flat surface. J Biomech Eng. 1999;121:605–611. doi: 10.1115/1.2800860. [DOI] [PubMed] [Google Scholar]
- Phillips JR, Johansson RS, Johnson KO. Representation of braille characters in human nerve fibres. Exp Brain Res. 1990;81:589–592. doi: 10.1007/BF02423508. [DOI] [PubMed] [Google Scholar]
- Phillips JR, Johansson RS, Johnson KO. Responses of human mechanoreceptive afferents to embossed dot arrays scanned across fingerpad skin. J Neurosci. 1992;12:827–839. doi: 10.1523/JNEUROSCI.12-03-00827.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pubols BH., Jr Factors affecting cutaneous mechanoreceptor response: II. Changes in mechanical properties of skin with repeated stimulation. J Neurophysiol. 1982;47:530–542. doi: 10.1152/jn.1982.47.3.530. [DOI] [PubMed] [Google Scholar]
- Robles-De-La-Torre G, Hayward V. Force can overcome object geometry in the perception of shape through active touch. Nature. 2001;412:445–448. doi: 10.1038/35086588. [DOI] [PubMed] [Google Scholar]
- Russell RC, Casas LA. Management of fingertip injuries. Clin Plast Surg. 1989;16:405–425. [PubMed] [Google Scholar]
- Salazard B, Launay F, Desouches C, Samson P, Jouve JL, Magalon G. Fingertip injuries in children: 81 cases with at least one year follow-up. Rev Chir Orthop Reparatrice Appar Mot. 2004;90:621–627. doi: 10.1016/s0035-1040(04)70722-9. [DOI] [PubMed] [Google Scholar]
- Sangiorgi S, Manelli A, Protasoni M, Ronga M, Raspanti M. The collagenic structure of human digital skin seen by scanning electron microscopy after Ohtani maceration technique. Ann Anat. 2005;187:13–22. doi: 10.1016/j.aanat.2004.06.001. [DOI] [PubMed] [Google Scholar]
- Schmidt HM, Lanz U. Surgical anatomy of the hand. Stuttgart: Thieme; 2004. [Google Scholar]
- Shimawaki S, Sakai N. Quasi-static deformation analysis of a human finger using a three-dimensional finite element model constructed from CT images. J Env Eng. 2007;2:56–63. [Google Scholar]
- Torebjörk HE, Vallbo ÅB, Ochoa JL. Intraneural microstimulation in man. Its relation to specificity of tactile sensations. Brain. 1987;110:1509–1529. doi: 10.1093/brain/110.6.1509. [DOI] [PubMed] [Google Scholar]
- Vallbo AB, Hagbarth KE. Activity from skin mechanoreceptors recorded percutaneously in awake human subjects. Exp Neurol. 1968;21:270–289. doi: 10.1016/0014-4886(68)90041-1. [DOI] [PubMed] [Google Scholar]
- Vallbo AB, Johansson RS. Properties of cutaneous mechanoreceptors in the human hand related to touch sensation. Hum Neurobiol. 1984;3:3–14. [PubMed] [Google Scholar]
- Westling G, Johansson RS. Responses in glabrous skin mechanoreceptors during precision grip in humans. Exp Brain Res. 1987;66:128–140. doi: 10.1007/BF00236209. [DOI] [PubMed] [Google Scholar]
- Zar JH. Biostatistical analyses. Englewood Cliffs, NJ: Prentice-Hall; 1996. [Google Scholar]
- Zook EG. Anatomy and physiology of the perionychium. Clin Anat. 2003;16:1–8. doi: 10.1002/ca.10078. [DOI] [PubMed] [Google Scholar]