Abstract
Irregular ongoing activity in cortical networks is often modeled as arising from recurrent connectivity. Yet it remains unclear to what extent its presence corrupts sensory signal transmission and network computational capabilities. In a recurrent cortical-like network, we have determined the activity patterns that are better transmitted and self-sustained by the network. We show that reproducible spiking and subthreshold dynamics can be triggered if the statistics of the imposed external drive are consistent with patterns previously seen in the ongoing activity. A subset of neurons in the network, constrained to replay temporal pattern segments extracted from the recorded ongoing activity of the same network, reliably drives the remaining, free-running neurons to call the rest of the pattern. Comparison with surrogate Poisson patterns indicates that the efficiency of the recall and completion process depends on the similarity between the statistical properties of the input with previous ongoing activity The reliability of evoked dynamics in recurrent networks is thus dependent on the stimulus used, and we propose that the similarity between spontaneous and evoked activity in sensory cortical areas could be a signature of efficient transmission and propagation across cortical networks.
Introduction
When injecting fluctuating current inputs into the soma of a neuron recorded in vitro, the spiking response is highly reliable (Mainen and Sejnowski, 1995). Such results, however, have been difficult to reproduce in vivo (Holt et al., 1996). The reason for this discrepancy is that much of the response variability observed in vivo seems to originate from the background activity (Arieli et al., 1996; DeWeese et al., 2005). Even in the absence of external drive, this ongoing neuronal activity is highly irregular (Timofeev et al., 2000), although the discharge statistics are still a matter of debate (Kenet et al., 2003; Fiser et al., 2004; Goldberg et al., 2004). Generic recurrent networks are a good model for understanding the possible interactions between ongoing and evoked activity in neocortical networks. Characterized by large, sparsely connected, excitatory and inhibitory populations, they can display a stable, self-generated regime called asynchronous irregular (AI) (van Vreeswijk and Sompolinsky, 1996; Brunel, 2000; Vogels et al., 2005; El Boustani and Destexhe, 2009a), which resembles the spontaneous activity observed in vivo. The central functional issue, as yet unsolved, is to characterize the sensitivity of these networks to external inputs (Destexhe and Contreras, 2006; Banerjee et al., 2008).
These recurrent AI networks are highly sensitive to small perturbations. As a consequence, propagation of either an increase in firing rate (Vogels et al., 2005) or a pulse of synchronized activity (Aviel et al., 2003; Mehring et al., 2003) is severely impaired by the ongoing activity, and in general this high variability and instability presents a severe challenge to information transmission or processing in recurrent networks. To achieve reliable signal propagation, these earlier studies introduced specific constraints in the network structure, either by selectively and substantially increasing synaptic weights (Vogels et al., 2005) or by adding connections (Mehring et al., 2003; Kumar et al., 2008) along a predetermined propagation path. Even in this latter case, the synfire chain stimulation can induce “synfire explosions,” which can subsequently silence the network activity.
While previous studies adapted the network connectivity to improve the transmission of the chosen (a priori) input patterns, we explored the converse approach: leave the network structure unchanged and find the activity patterns that are better transmitted and sustained by the network. Several experimental studies have shown a similarity between spontaneous and evoked cortical activity (Tsodyks et al., 1999; Kenet et al., 2003; Fiser et al., 2004). From the theoretical point of view, the irregular and sustained patterns found in ongoing activity are by definition highly compatible with the recurrent architecture of the neocortical network. We have designed a new stimulation paradigm, in which we drive part of the network with temporal pattern segments extracted from the recorded ongoing activity of the exact same network. This gives inputs which mimic the spontaneous activity of the network model. We refer to this as the “frozen paradigm.” In this article, we show using simulations that our paradigm produces efficient transmission, which is preserved over a broad range of parameters. To investigate the factors affecting transmission efficiency in the network, we performed further simulations with control, surrogate stimuli. Finally, we discuss the biological relevance of this paradigm.
Materials and Methods
Spiking network model
Neuron model.
Networks are composed of 10,000 leaky integrate-and-fire neurons. Each neuron has membrane time constant τm = 20 ms, and resting membrane potential Vm = −60 mV. When Vm reaches the spiking threshold Vthresh = −50 mV, a spike is generated and the membrane potential is held at the resting potential for a refractory period of duration τref = 5 ms. Synaptic connections are modeled as conductance changes, resulting in a model similar to the Conductance-Based, Integrate and Fire models case in the study by Vogels et al. (2005):
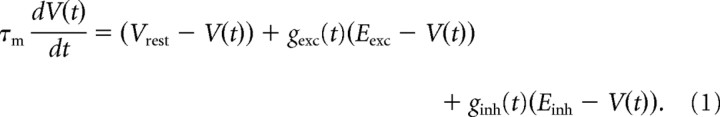 |
Reversal potentials are Eexc = 0 mV and Einh = −80 mV, and synaptic activation is modeled as a conductance step g → g + δg followed by exponential decay with time constants τexc = 5 ms and τinh = 10 ms. The integration time step of our simulations is 0.1 ms (reducing the time step to 0.01 ms was found to produce no qualitative change in the network behavior), and synaptic delays are set to 0.1 ms.
Network connectivity.
The network is composed of 8000 excitatory and 2000 inhibitory neurons, sparsely and randomly connected, with a connection probability of 2% (Vogels et al., 2005), independent of the identity of the target. While this connectivity ratio is at odds with anatomical data on neocortical connectivity [which shows a connectivity ratio of around 10%, and a dependence on the target cell type (Binzegger et al., 2004)], it allows a realistic pattern of activity to be generated and sustained, while higher connectivity ratios fail to do so (Vogels et al., 2005). We also note that for models with dynamic synapses (Markram and Tsodyks, 1996), due to the depression of synaptic strength of intracortical excitatory synapses which is dominantly reported in vitro (Thomson and West, 1993), there are fewer effective synapses than in the anatomical data, making the effective connectivity closer to that used in our simulations.
Synaptic parameters and network regime.
Network global states are defined as either synchronous or asynchronous (population viewpoint) and as either regular or irregular (neuron viewpoint). For Figures 1–4, the network is set to an asynchronous irregular state (Brunel, 2000) at 13 Hz with a mean interspike interval (ISI) coefficient of variation (CV) of 1.57. Synaptic parameters are as follows: δgexc = 6 nS and δginh = 61 nS. Weights are drawn from Gaussian distributions N(gexc, gexc/3) and N(ginh, ginh/3), with negative values discarded and then redrawn. To initiate the self-sustained activity, 5% of the cells receive an initial 50 ms burst of activity at 100 Hz.
Figure 1.
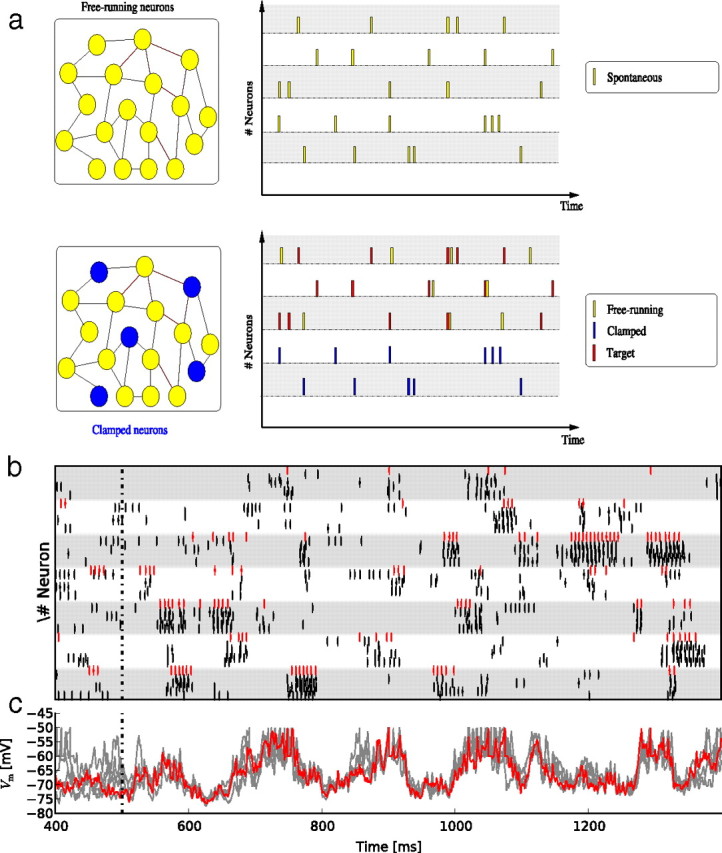
a, Conceptual schema of the “frozen paradigm.” A spontaneous pattern is recorded (top panel), and then a subset of neurons (labeled “frozen”; blue neurons and blue spikes) is forced to replay part of the pattern. We then examined whether the remaining, free-running neurons (yellow spikes) reliably reproduce the other part of the spontaneous pattern, which we label the “target” pattern (red spikes) (see Results for details). b, Raster plot of responses of free-running neurons to the frozen stimulation. Each white or gray band represents the activity of one free-running neuron. Short vertical lines represent spikes. The red spikes are from the target pattern, and each row of black spikes represents a different trial with the same stimulation pattern but a different initial state of the network. c, Superimposed Vm traces of responses to the same frozen stimulation, for one free-running neuron. The red trace indicates the target activity.
Figure 2.
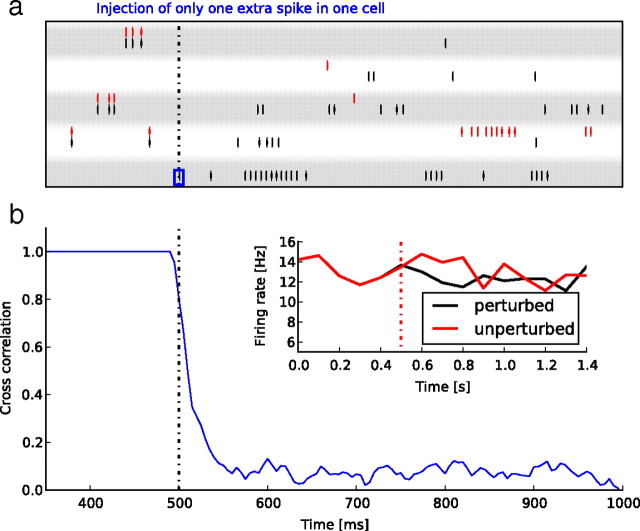
a, Raster plot of five neurons during two runs of activity (red and black) in the same network, starting with the same initial condition. The black run is perturbed by the addition of one extra spike in one neuron at 500 ms (dotted line, blue inset in the bottom row). b, Time course of the normalized cross-correlation between the two runs of activity. Correlation is computed with a time bin equal to the refractory period of the neurons, and measured on a sliding window. Note that this induces a smoothing of the estimated correlation. The vertical dotted lines indicate the time at which a perturbation (one extra spike) was artificially added to one of the neurons in one of the runs, inducing a fast drop of the correlation. The inset shows the mean firing rate for the two conditions as a function of time.
Figure 3.
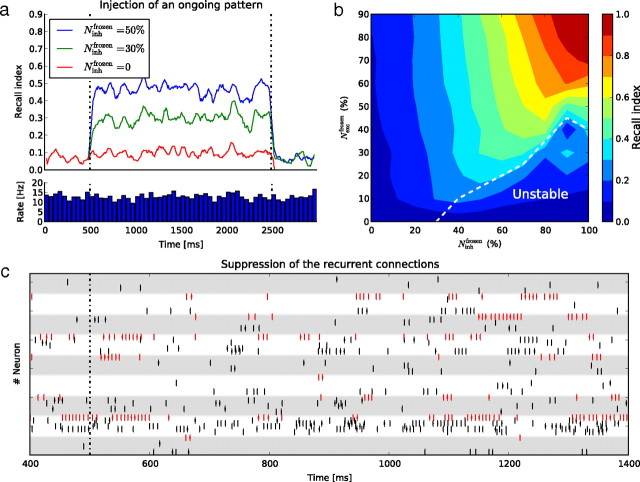
a, Kinetics of the recall index (the normalized cross-correlation between the target activity and the response) as a function of time, before, during, and after the frozen stimulation. b, Steady-state recall index color coded, as a function of the proportion of excitatory and inhibitory neurons that are frozen. The white dotted line delineates a zone of instability of the network in which the AI regime is not sustained. c, Raster plot of responses, as in Figure 1b, when recurrent connections between free-running neurons are cut and replaced by independent Poisson spike trains producing an equivalent mean level of input to the cells.
Figure 4.
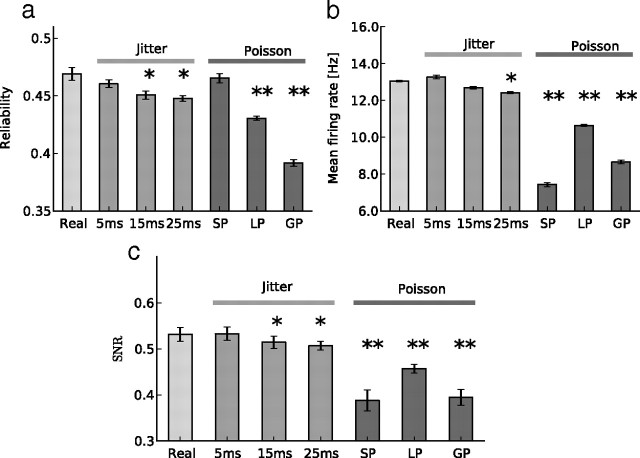
a, b, Comparison of the reliability (a) and mean firing rate (b) values obtained in response to different stimulation patterns, for 50% of excitatory and inhibitory frozen neurons. Stimulation patterns are, from left to right: a “real” pattern (Real) taken from the spontaneous activity, jittered versions of this pattern (5, 15, and 25 ms of jitter; see Materials and Methods), a Poisson stimulation (SP) reproducing the rate and the synchrony level observed in the real pattern, a Poisson stimulation in which each neuron has the same mean firing rate as in the spontaneous pattern (LP), and a Poisson stimulation in which all the neurons have the same firing rate, which is the global mean firing rate of the spontaneous activity (GP). c, Same comparison for the SNR (see Materials and Methods) across all the surrogates.
Measures.
To quantify the similarity between the “free-running” and “target” activity patterns, we calculated the recall index defined as the normalized cross-correlation of the target and actual spike trains (Aertsen et al., 1989) for a random sample of 500 cells, for zero phase delay and a time bin of 5 ms. We consider two spike trains of N = 500 neurons, binned with a time bin δt equal to the refractory period of the neuron (here, δt = 5 ms), obtained during two different trials. S1 and S2 are two matrices of size N × Nbins, with Nbins = T/δt, T being the length of the spike trains. Note that S are binary matrices: for each (i, j) ∈ N × Nbins, Sij ∈ {0, 1}. The recall index ρ12 is given by the following formula:
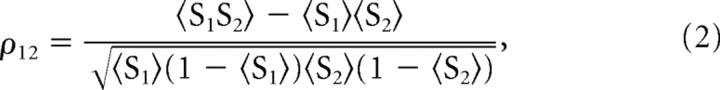 |
where < denotes the average number of filled bins per matrix. Since S is a binary matrix, we are sure that <S
denotes the average number of filled bins per matrix. Since S is a binary matrix, we are sure that <S < 1.
< 1.
To estimate the reliability (reproducibility) of the neural responses for different kinds of stimuli, we computed the mean of the paired normalized cross-correlations between the trials (n = 10) (Schreiber et al., 2003), with the same time bin. Error bars were computed by using different stimulation patterns (n = 10).
Signal-to-noise ratio for the binned spiking activity.
We chose a measure which can be directly related to the reliability and mean firing rates previously estimated. The signal S was given by the mean firing rate m multiplied by the time bin Δt: S = mΔt. The noise N was given by the standard deviation of the responses to the same stimulation. These values were estimated with the same time bin as the reliability to ensure a straightforward relationship between the two. If Xit ∈ {0; 1} represents the binned response at time t, for the ith trial, the noise N is such that the following is true:
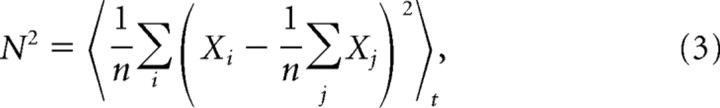 |
where n is the number of trials. Remarking that, since the bin size is small, Xi = Xi2, and that <Xi t = S, we obtain the following:
t = S, we obtain the following:
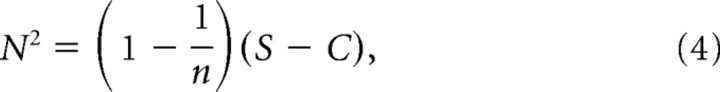 |
where C = <XiXj t. According to Palm et al. (1988), C = rS(1 − S) + S2, where r is the reliability estimated above as the normalized cross-correlation between trials. The signal-to-noise ratio (SNR) is then the mean over the standard deviation, such that the following is true:
t. According to Palm et al. (1988), C = rS(1 − S) + S2, where r is the reliability estimated above as the normalized cross-correlation between trials. The signal-to-noise ratio (SNR) is then the mean over the standard deviation, such that the following is true:
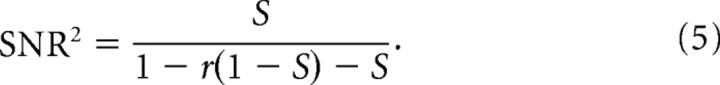 |
Note that we drop the (1 − 1/n) factor, which will affect all the estimations in the same manner, and will reach one for an infinite number of trials. This is not problematic for our comparative study.
Distance between spike trains.
to test the noise resistance, we used the Victor–Purpura distance (Victor and Purpura, 1996), which has the advantage of avoiding any binning artifact. Briefly, costs are assigned to three elementary operations over spike trains: changing the timing of a spike from ta to tb (cost = q‖ta − tb‖), adding a spike (cost = 1), and deleting a spike (cost = 1). The distance between two spike trains SA and SB is then defined as the least costly way of combining these three elementary operations to change spike train SA into spike train SB. This distance is dependent only on q, and this parameter is the cost for shifting the spikes when matching two spike trains. If q = 0, shifting spikes has no effect on the measure, so only the number of spikes will influence the distance between the two spike trains. Increasing q gives more importance to the precise spike times relative to their number. In our study, we estimated the distance between the two spike trains emitted by a same cell in response two different stimuli (the real pattern vs the jittered version of it), and averaged this estimation over n = 500 cells.
Simulator.
All simulations were performed using the NEST simulator (Diesmann and Gewaltig, 2001) version 1.9 (http://www.nest-initiative.uni-freiburg.de), using the PyNN interface (Davison et al., 2008) (http://neuralensemble.org/PyNN). The code for the model is freely available from ModelDB (http://senselab.med.yale.edu/ModelDB/) and on the UNIC website (http://www.unic.cnrs-gif.fr).
Neural field model
The model consists of N local “neural fields” defined by inputs hi and outputs Si = tanh(ghi). Their dynamics are given by Equation 1, above. All results given in this paper used N = 2000 neural fields. The frozen paradigm was applied by imposing the values of the hi of a subset of neural fields.
Results
Convergence of the network activity to a target activity pattern
The frozen paradigm is implemented as follows: We divide our recurrent network into two populations. The selection of which neuron belongs to which population is made at random and the connectivity of two neurons is independent of which populations they belong to. We first record a spontaneous pattern across the whole network (both populations) and then, while the spontaneous activity is ongoing, we force the neurons of one population to replay the sequence of spontaneous activity previously recorded (see Fig. 1a). We then measure the extent to which these clamped, or frozen, cells influences the free-running neurons to replay the spontaneous pattern previously recorded (see Fig. 1a). Replay of the recorded pattern by the free-running neurons is then equivalent to the recall of that pattern in the network.
We applied our paradigm to a sparsely connected, recurrent network of 8000 excitatory and 2000 inhibitory integrate and fire neurons (see Materials and Methods). The set of parameter values was that used by Vogels et al. (2005), except that the weights are drawn from Gaussian distributions instead of being all equal. The network settles in an asynchronous irregular regime in which it generates self-sustained activity with a mean rate of 13 Hz and a mean ISI CV of 1.57. It has been shown that, although the activity of this network appears very irregular on small time scales, where it cannot be distinguished from stochastic behavior, it can exhibit more coherent behavior at large time scales, where the dimensionality of the attractor can be reduced (El Boustani and Destexhe, 2009b). Figure 2 shows an example of the dependency on initial conditions in this network model: two initially identical trajectories quickly diverge after a perturbation as small as a single spike elicited in the same neuron. This divergence is characteristic of a chaotic network, and has already been observed and studied in several recurrent network models [see also Sompolinsky et al. (1988) and van Vreeswijk and Sompolinsky (1998, 2005)].
When 50% of the neurons are forced to replay a spontaneous pattern recorded previously (Fig. 1a, blue), the spiking activity of the free-running neurons (yellow) converges reliably to the target activity (red): repetitions of the same stimulation elicit temporally precise and reproducible spikes characterized by their temporal alignment across repetitions (Fig. 1b). The subthreshold membrane potentials Vm (Fig. 1c) of the free-running neurons closely follow the target activity waveforms (red) as soon as the input-recipient population is frozen. Note also the immediate reduction in the stimulus-locked variance following the “freeze” onset.
We quantified these observations with two measures. The recall index is a measure of how closely the free-running neurons of the network reproduce the target pattern (the previously recorded segment of spontaneous activity). It is defined as the cross-correlation between the target activity pattern and the response of the free-running neurons. The reliability is a measure of the variability of responses during frozen stimulation: the lower the variability the higher the reliability. It is defined as the mean cross-correlation between pairs of responses to the same frozen stimulus (see Materials and Methods for full details). Following the onset of stimulation, the recall index increases, within a time of ∼50 ms that is independent of the proportion of frozen neurons, to a steady-state value (Fig. 3), reflecting a rapid convergence of the free-running activity to the target pattern. The recall index decays equally rapidly following the end of the stimulation. The firing rate averaged over the neuronal population (Fig. 3a, bottom panel) remains constant over time. The frozen stimulation thus preserves the statistics of the ongoing activity while eliciting a reproducible and faithful replay, extended over the full network, of the target pattern.
The steady-state value of the recall index measure is dependent on the proportion of frozen neurons (see Fig. 3b). As expected, the recall index increases when the proportion of frozen neurons increases, whether these are excitatory or inhibitory, except in a region where the low proportion of inhibitory free-running neurons evokes a transition to a “synchronous regular” regime or a quasisilent state, which are insensitive to the stimulus. The proportion of frozen inhibitory neurons affects the recall index more than does that of frozen excitatory neurons, which is probably related to the higher weights of inhibitory synapses in this model (δgexc = 6 nS, δginh = 61 nS; see Materials and Methods). The recall index is insensitive to the particular pattern chosen for stimulation and to the initial conditions (ANOVA, p > 0.5 for both pattern and initial condition dependencies), with a standard deviation approximately constant over the whole bidimensional plot shown in Figure 3b (0.006 on average). This absence of sensitivity to the timing of the stimulation relative to the ongoing activity is probably a consequence of the irregularity of the network activity: there is no clear oscillatory behavior which could induce a phase dependency, and our stimulation is not related to a particular frequency to which the response would lock.
To check whether the frozen stimulation always makes the network converge to the target pattern, we compared the values of the recall index and of the reliability for the same stimulation repeated several times. Convergence to a different pattern would lead to a reliability significantly higher than recall index, but we did not find any significant difference (p > 0.4, t test, n = 10), proving that the activity converges in all cases to the target pattern. Our results thus demonstrate that the frozen stimulation induces robust convergence for a large enough frozen population.
The importance of the recurrent architecture in this behavior was confirmed by a control experiment in which the connections between free-running neurons were cut and a stochastic current of equivalent mean amplitude injected into the neurons (Fig. 3c). The injected current is independent over all neurons. The mean firing rate received by each neuron is thus preserved, while the interactions between stimulation and recurrent architecture are suppressed. For a frozen proportion of 50%, the reliability drops from 0.47 ± 0.007 (SD) to 0.09 ± 0.005, indicating that the free-running activity in the intact network during frozen stimulation is not dominated by the frozen drive, but results from a dynamic cooperation between the frozen units and the recurrent connections.
Influence of input temporal structure on reliability
It could be argued that the reliability of the responses could have been obtained with any other imposed stimulation, whatever its statistics. We thus compared the frozen stimulation with surrogate stimulations having the same number of spikes, but a shuffled temporal structure. Several different surrogates were compared: a first series consisting of temporally “jittered” patterns with standard deviation of the jitter ranging from 5 to 25 ms; and a second series consisting of Poisson spike trains. In “local Poisson” (LP) stimulation, the mean firing rate of each neuron equals that of the same neuron during the reference, frozen pattern (equivalent to an infinite jitter). In “synchronous Poisson” (SP) stimulation, all neurons have the same firing rate, equal to the mean rate of the spontaneous activity, but the spike trains are correlated (Kuhn et al., 2003), to match the synchrony level of spontaneous activity. Finally, “global Poisson” (GP) stimulation matches only the mean firing rate of the spontaneous activity, but not the synchrony. Note that all these controls have approximately the same number of spikes as the reference spontaneous pattern. These different surrogate patterns represent a progressively increasing deviation from spontaneous activity statistics, while keeping first-order statistics unchanged.
For this comparison we chose a level of frozen neurons (50%) at which each free neuron receives equal numbers of connections from frozen and free neurons. As shown in Figure 4a, the more the stimulation statistics deviate from those of spontaneous activity the lower is the reliability. This difference is significant for jitter of 15 ms and greater (p < 0.001) and for LP and GP (p < 0.0001), being largest for the global Poisson process. For the global Poisson, the reliability drops by 17%. However, the level of reliability is the same for synchronous Poisson as for the frozen stimulation. The reliability modulation is accompanied by a modulation of the mean evoked firing rate in the free running network, as can be seen in Figure 4b: the mean firing rate drops significantly (p < 0.0001) for local (18%), synchronous (43%), and global (34%) Poisson surrogate patterns.
To synthesize these results, we measured the SNR of the spiking responses, defined as the mean firing rate divided by the standard deviation of the firing rate responses over trials (see Materials and Methods). This takes into account both the reliability and the mean firing rate of the output. This SNR is significantly higher for the spontaneous stimulation than for the surrogate Poisson stimulations (see Fig. 4c) [decrease of 27% (SP), 14% (LP), and 26% (GP)]. In the case of the local and global Poisson stimulations, the difference in SNR is produced by both the reliability and the mean firing rate drops. But in the case of the synchronous Poisson stimulation, the reliability is comparable to that of the spontaneous pattern, and the lower, but still significant, difference originates in the lower firing rate. Together, these measures imply a larger degradation in signal transmission, the more the input statistics deviate from the spontaneous statistics. Thus, for the same number of spikes, the forced replay of spontaneous ongoing patterns seems to induce a better signal transmission and recall.
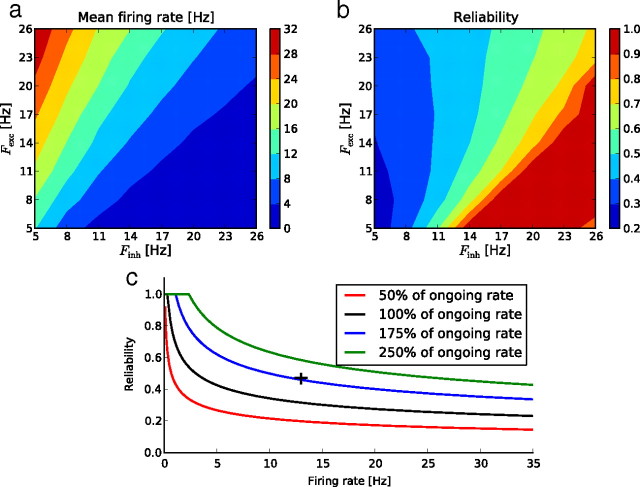
We have explored how the input structure influences the output reliability and mean firing rate. To compare this influence to that of the mean input firing rate, we explored the effects on mean activity (Fig. 5a) and reliability (Fig. 5b) of independently varying the mean excitatory and inhibitory firing rates of the global Poisson stimulation. The combination of high excitatory and low inhibitory stimulation rates produces a high mean firing rate in the free-running units, but a low trial-to-trial reliability. In contrast, low excitatory but high inhibitory stimulation rates induce a highly reliable response, but with a very low mean firing rate. We empirically fitted this inverse relationship between reliability and mean activity of the free running units by the following power law:
(r2 = 0.95), where the spike count is the total number of spikes in the imposed stimulation pattern, summed over all the frozen neurons, and K is a constant (α = 0.46, β = 1.48, K = 11.59).
Figure 5.
a, b, Mean firing rate (a) and reliability (b), color coded, in response to global Poisson stimulation, for different excitatory and inhibitory firing rates. c, Reliability versus mean firing rate for different total spike counts. Each “iso-spike count” curve corresponds to the stimulations of a and b with the same total number of spikes as in the Poisson stimulation, but differently partitioned between excitatory and inhibitory populations. The black cross indicates the reliability and mean firing rate for the spontaneous pattern.
Figure 5c represents the “iso-spike count” curves obtained when plotting reliability against mean firing rate. When compared with the Poisson surrogate stimulations, the particular structure of the imposed spontaneous pattern seems to be better adapted to the network connectivity: to reach similar levels of both reliability and response strength as observed for spontaneous statistics (Fig. 5c, black cross), the use of global Poisson stimulation would require a large increase in the spike frequency imposed on the frozen neurons (175% of the spontaneous rate, given in Fig. 5c by the iso-spike count curve intercepting the reference cross).
Together, these results indicate that, although the first determinant of the response reliability is the mean input firing rate, the structure of ongoing activity enables a more efficient signal transmission than uncorrelated stimulation. The input firing rate and synchrony levels explain a major part of this increase, but are not sufficient to reach similar levels of SNR.
Noise resistance
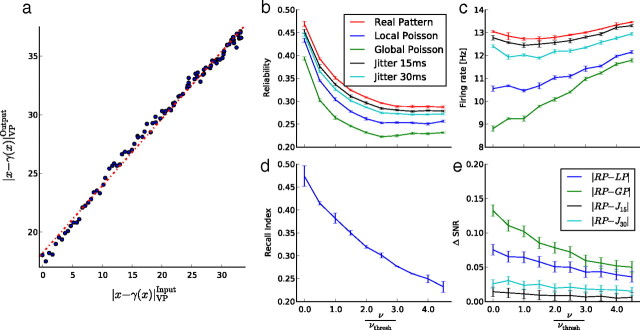
Our simulations allow us to replay precisely each time the same pattern in the frozen population. In more realistic situations, however, the frozen units, even if deterministic, could be corrupted by independent noise sources, which could interfere with signal transmission to the free-running units. To test the noise resistance of the pattern recall, we generated a set of degraded patterns from an original spontaneous pattern by randomly jittering each spike by a time drawn from a Gaussian distribution. The standard deviation of the distribution was varied from 1 to 50 ms. Each resulting pattern was then used to clamp the frozen units, and we compared the distance [measured as by Victor and Purpura (1996)] (see also Materials and Methods) between the spontaneous input and each jittered input against the distance between their corresponding outputs. We found that the modulus of the output distance increases linearly with input distance (Fig. 6a), showing that the response to our stimulation is robust to noise. The slope of the input–output relationship is 0.57. This sensitivity to noise well below 1 shows that our stimulation paradigm is compatible with a transmission of more “biological” (i.e., noisy) inputs.
Figure 6.
Noise resistance of the paradigm. a, The coordinates of each point are the Victor–Purpura (VP) distance ‖x − γ(x)‖VP between an input pattern x and the jittered version of it γ(x) (horizontal axis), and the VP distance between the corresponding output patterns (vertical axis). b, c, Evolution of the reliability (b) and the firing rate (c) in the free-running neurons for several level of external noise (relatively to νthresh). Errors bars are obtained on 10 run per surrogate. d, e, Linear decrease of the reproducibility for one particular pattern (d), and difference between the SNRs obtained with a real pattern and those obtained for surrogates (e), as a function of the external noise.
Noise could also be added in the model as external inputs that will perturb the recurrent activity of the free-running neurons. To check how robust is the preference for the ongoing statistics, while the network was asked to replay a particular pattern, all the free cells received, in addition to the pattern played by the frozen population, noisy inputs composed of uncorrelated excitatory and inhibitory Poisson spike trains at a certain frequency. This frequency is expressed relatively to νthresh, the input rate needed to reach the threshold in our particular neuron model with conductance-based synapses, in the absence of recurrent inputs:
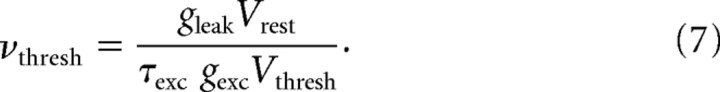 |
As can be seen in Figure 6, b and c, the reliability and the recall index both decrease to a steady-state value when noise is increased. However, the important point is that the relative differences between stimulation types, observed in the purely deterministic case (see Fig. 4), are unchanged in the presence of noise (Fig. 6b). This result cannot be explained by a change in the firing rates, which remain approximately constant despite the external noise applied (Fig. 6c): since this external noise is balanced (excitatory and inhibitory), it has only a small impact on the resulting firing rates. Figure 6e shows the differences in the SNR according to the noise levels and for several surrogates. A linear decrease can be observed, but even for high noise levels (ν up to 3νthresh), the SNR remains significantly (p < 0.001 for LP and GP) higher for the frozen stimulation with real patterns. These results confirm the robustness to noise of the paradigm.
Effect of network parameters
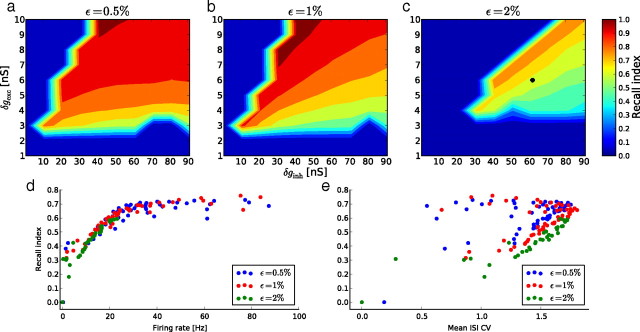
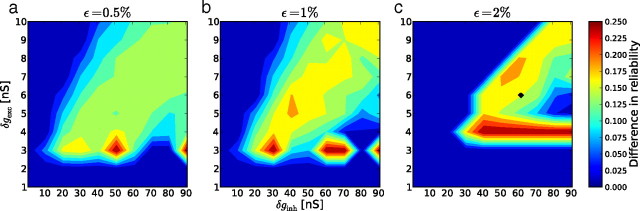
To further test the generality of our observations, we varied the excitatory synaptic weights δgexc between 1 and 10 nS and the inhibitory weights δginh between 1 and 91 nS, and used three different connection probabilities ϵ: 0.5%, 1%, and 2%. Over all the regions in which the network can generate an asynchronous irregular regime, the frozen paradigm with 50% frozen neurons produces qualitatively similar recall performance (Fig. 7a–c) (see also Vogels and Abbott, 2005). Surprisingly, the recall index is not directly related to the strength of the synaptic weights: an increase in synaptic weight does not necessarily increase the recall index. Over all conditions of connectivity and synaptic weights, the recall index increases with both the mean firing rate (Fig. 7d) and the ISI CV of the corresponding spontaneous activity. The structure of spontaneous activity, as characterized by the mean rate and ISI CV values, appears to be a better predictor of the convergence performance than is the connectivity structure of the network. This illustrates that our paradigm avoids focusing on the nonlinear relationship between the network structure and the way activity is transmitted inside this network by directly using those activity statistics that are proven to be sustained by the network. We also examined the level of reliability obtained with the GP stimulation over the same range of parameters. Figure 8 shows the normalized difference between the levels of reliability obtained for the spontaneous and GP stimulations. This difference could reach up to 25%. We did not find any clear correlation between the amount of synchrony in the spontaneous activity and this normalized difference (data not shown).
Figure 7.
a–c, Recall index for 50% of neurons frozen as a function of the excitatory and inhibitory synaptic weights, and for different connection probabilities ϵ: 0.5% (a), 1% (b), and 2% (c). The dark blue zones indicates regions in which the network either cannot sustain spontaneous activity or enters a synchronous regular state. d, e, Recall index values obtained in a–c plotted against the mean firing rate (d) and ISI CV (e) of the spontaneous activity of the same network.
Figure 8.
Normalized difference between the reliability obtained with global Poisson stimulation and that obtained with a real pattern, as a function of the synaptic weights, for different connectivities, ϵ.
Frozen paradigm in a chaotic neural field model
Although it generates an irregular activity pattern and exhibits rapidly diverging responses to small perturbations, the recurrent model has not been proven mathematically to be chaotic. To have a better understanding of the effect of stimulation statistics in a well defined chaotic system, we apply the frozen paradigm to a neural field model (Sompolinsky et al., 1988) (see Material and Methods), defined by the following:
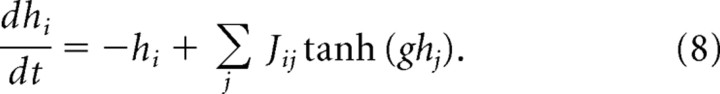 |
The network is composed of N units, each characterized by its activity hi. The synaptic weights Jij are drawn from a Gaussian distribution with mean 0 and variance J2/N. It has been shown for large N that when gJ < 1, the only stable state is the silent state. When gJ > 1, the network enters a chaotic regime (Sompolinsky et al., 1988).
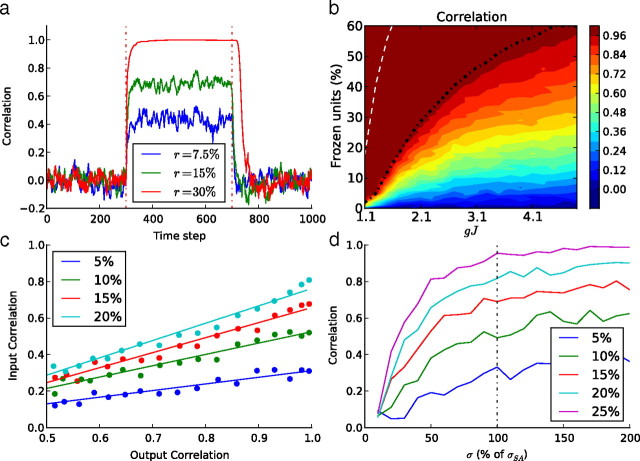
Using the same strategy as for the spiking network, we froze the chaotic system by clamping part of the network to a previously recorded trajectory. During this frozen stimulation, we measured the convergence by the normalized cross-correlation between the free-running activity (values of hi) and the target activity, equivalent to the previously defined recall index. As for the spiking network simulations, the cross-correlation (CC) rapidly increases to a plateau (Fig. 9a), whose value depends on the proportion of frozen units and on the network parameter gJ (Fig. 9b). Full convergence (CC > 0.99) occurs if the proportion of frozen units is greater than a threshold value (Fig. 9b, dotted black line), which increases with gJ.
Figure 9.
a, Kinetics of the normalized cross-correlation between the target activity and the response of neural fields as a function of time, before, during, and after the frozen stimulation, for three different ratios of frozen neural fields. In this example, gJ = 2.1. b, Steady-state values of the cross-correlation between target and free-running activities measured as a function of the ratio of frozen neural fields (vertical axis) and the network parameter gJ (horizontal axis). The black dotted line is the full convergence limit (CC > 0.99) and the white dotted line the limit under which the free subnetwork, without any stimulation, is still chaotic. c, Normalized cross-correlation for several percentages of frozen units and for several amounts of noise added (in percentage of σSA) to an ongoing pattern. d, Normalized cross-correlation when a surrogate Gaussian noise with a standard deviation expressed in percentage of σSA is used as a stimulation instead of a real pattern. In both cases, the network parameter was gJ = 2.1.
To test the resistance to noise of this convergence, we also injected random noise in addition to the frozen pattern. The convergence performance decreased linearly when the amplitude of this noise increased, the slope depending on the percentage of frozen units (see Fig. 9c). The noise resistance is thus similar to what we found for the spiking network.
To test the origin of this reliability, we again used a surrogate stimulation. We stimulated the subnetwork with random noise, of mean 0 and standard deviation σ equal to the spontaneous activity standard deviation σSA. The level of reliability was similar to that obtained with the real pattern. We then varied this standard deviation σ relative to σSA (see Fig. 9d). When σ decreased below σSA, the reliability decreased almost linearly. This confirms that the standard deviation of the activity is the main factor in explaining the reliability. Interestingly, when we increased σ above σSA, the reliability barely increased, whatever the absolute value of σSA. This result holds when the network parameters g and J and the ratio of frozen units do not give rise to full convergence (i.e., below the black line in Fig. 9). For a higher frozen fraction, stimulation with lower standard deviation can also lead to a saturated full convergence (data not shown). Thus, over a broad region of the network parameter space, σSA appears as a reference point in the relationship between σ and the output reliability.
Discussion
In this paper, we analyzed the response of recurrent network models to a stimulation which mimics episodes of spontaneous activity. Our main findings are as follows: (1) Stimulating with spontaneous patterns of activity induces a predictable and noise-resistant recall of the full ongoing pattern, despite the highly irregular background activity and the context sensitivity of the network. (2) Despite the fact that the network is deterministic, the response reliability is modulated by the stimulus type, and is higher (up to 25%) for the spontaneous stimulation than for uncorrelated Poisson stimulation. (3) This reliability increase is mainly explained by the higher synchrony of the input. However, mimicking the input firing rate and synchrony is not sufficient to fully reproduce the signal-to-noise ratio obtained with the spontaneous stimulation.
On the basis of these findings, we make two main experimental predictions: first, the reliability of the cortical responses should be modulated by the stimulus statistics in vivo; second, evoked sensory responses with a structure similar to the spontaneous activity could be the signature of an efficient transmission of information.
Reliable response/completion despite irregular background activity
Our model demonstrates the feasibility of a reliable encoding of stimuli within irregular background activity. Several studies have shown that a chaotic dynamical system can be reliably driven by appropriate stimulation, a phenomenon termed “chaos control” (Garfinkel et al., 1992). Our frozen paradigm could be seen as a high-dimensional application of “chaos synchronization” (Pecora and Carroll, 1990). While these previous studies did not explore the effect of the input statistics, we are able to demonstrate that choosing a driving stimulation that respects the statistics of spontaneous activity has the advantage of allowing a prediction of the responses of the free-running neurons. Our investigation extends these earlier studies by applying these concepts to large-scale neuronal networks. It is important to note that we do not focus on any global fixed point reached by the system under the stimulation, but rather on the evoked “succession of transients,” which are reliable and noise resistant. This concept has already been the subject of several studies (Rabinovich et al., 2008), and our results are a possible example of this concept in large-scale network models.
The neural field study illustrates the dual role of the stimulation. In this case, it has to be noted that the free subnetwork alone, without any stimulation, is chaotic (below the white line of Fig. 9b). Nevertheless, the stimulation due to the frozen population makes a reliable and noise-resistant propagation possible. The stimulation has two roles. First, it transmits the pattern, and second, it changes the context (background activity), so that the transmission is possible, and resistant to noise. These two complementary roles of the stimulation are due to the nature of recurrent networks, where the stimulation and the background activity interact with each other.
Origin and stimulus dependence of the reliability
Our reliability study uncovers two findings. First, even if the network model used in this study is entirely deterministic, we observed a large trial to trial variability in response to the repetitions of the same stimulus. All the observed variability must originate in the surrounding network activity. As a consequence, experimentally, a large part of the trial to trial variability may come from the context sensitivity of a cortical network, and could thus be predicted by the preceding ongoing activity. This is in line with previous experimental reports where the preceding ongoing activity was a major source of variability (Arieli et al., 1996; Azouz and Gray, 1999; Deweese and Zador, 2004).
Second, our study also demonstrates that the response reliability can be modulated by the stimulus statistics in a nontrivial manner. Although the first determinant of the reliability level is the mean firing of the input, the higher-order structure of the stimulation has also a non-negligible effect (up to 25%), and this over the whole range of model parameters explored. Previous theoretical results could be reinterpreted in light of this result. Vogels et al. (2005) noted that their modified network, which enhanced firing rate but not synfire chain propagation, occasionally transmitted “ghost signals.” We interpret this reminiscence of the reliably evoked activity in spontaneous dynamics as another example of a network model that better transmits signals whose statistics match those of the spontaneous activity.
Beyond rate and synchrony
Our surrogate stimulation mimicking both the level of input firing rate and synchrony reached the same output reliability as the spontaneous stimulation. Nevertheless, since the output firing rate is lower, the resulting SNR is still lower than for the spontaneous stimulation. Previous studies have focused on the impact of rate (Vogels and Abbott, 2005) and synchrony (Mehring et al., 2003; Kumar et al., 2008) on the propagation of activity in recurrent networks. Our study showed that these two factors, though important, are not entirely sufficient to explain the SNR of the response to the spontaneous stimulation. Further studies will aim at identifying additional contributions to this SNR modulation. Among others, using a stimulation with heterogeneous firing rates could be one of these factors (see the difference between local and global Poisson stimulation).
Relation to experimental data
In light of our results, we can propose an explanation for the discrepancy mentioned in the Introduction between the reliable spiking activity observed in vitro (Mainen and Sejnowski, 1995) and the variability often observed in vivo. Our study indeed predicts that the reliability should be modulated by the stimulus statistics, and this has been observed experimentally: intracellular studies demonstrate that the reliability of subthreshold activity is increased during natural scene viewing (Baudot et al., 2004; Frégnac et al., 2005) or when the stimulus evokes strong shunting inhibition (Monier et al., 2008).
Some reports point out that the reliability of responses could depend on the interaction between internally generated and sensory-evoked activities (see above). In particular, the precision of the spiking responses may depend on the global reverberation rhythm generated by the recurrent network connectivity, which could preserve or destroy the sensory information, depending on the relative phase and the amplitude of the fast oscillations (for review, see Tiesinga et al., 2008). We propose to extend this prediction for nonoscillatory, irregular stimuli and background activity. Reliability should be increased when a cooperative mode (Heidmann et al., 1984) between the structure of the input and the recurrent connectivity of the network is uncovered. The frozen stimulation might be an example of such a mode.
If our stimulation, mimicking the spontaneous statistics, is indeed relevant in an experimental context, a similarity between the structure of spontaneous and evoked activities should be observed, and would correspond to an increased reliability of cortical responses. Similar levels of activity during spontaneous and sensory evoked regimes have been reported in primary auditory cortex, area A1 (deCharms and Merzenich, 1996), but the relationship between the structures of spontaneous and sensory-evoked activities is still a matter of debate in primary sensory areas. In the visual cortex, voltage-sensitive dye imaging in the anesthetized cat has shown similar cortical activity maps for spontaneous and grating-evoked responses (Tsodyks et al., 1999; Kenet et al., 2003). Additionally, in awake ferrets, multiunit recordings have shown that the temporal correlations of the activity remain unchanged when switching from ongoing activity to natural stimulation (Fiser et al., 2004). Finally, Han et al. (2008) have shown that a repeated stimulation modifies the structure of the spontaneous activity over several minutes, such this latter becomes more similar to the previously imposed evoked activity. In A1, it seems that the sets of responses to different types of stimuli are all included in the phase space delimited by the spontaneous activity (Luczak et al., 2009). It would be interesting to compare the reliability of these responses to other types of stimuli. Our results make us hypothesize that the reliability will be higher when the spontaneous and evoked activities are similar.
Conclusion
We have shown that, even in a deterministic network, the reliability of the responses can be modulated by the type of stimuli. As a consequence, to a given recurrent network would correspond a set of stimuli which are more efficiently transmitted than others. According to our results, the spontaneous activity could be a reference point in this set. This supports the hypothesis that similarity between evoked and spontaneous activities is the signature of an efficient mode of transmission across recurrent networks. However, further research will need to delimit this set by searching for other types of stimuli that are as efficiently transmitted.
Having stated that a match between spontaneous activity and input statistics evokes a better recall, we can hypothesize that the connectivity could have been shaped by a learning process so that the spontaneous activity matches the natural input statistics. In the case of a Boltzmann machine with binary neurons, where the inputs are also transmitted by “freezing” some neurons, the learning of the input statistics does induce such a match (Ackley et al., 1985). However, an equivalent learning process for a network of integrate and fire neurons is currently unknown. Nevertheless, the connectivity in our network model can be viewed as the result of an unseen learning process, where the network has learned to transmit more efficiently a particular set of inputs. We can hypothesize that at least part of these inputs are replayed by spontaneous activity. Experimentally, a possible consequence could be that the spontaneous ongoing activity replays the learned “neuronal songs” (Han et al., 2008). A complete implementation of this hypothesis would require a better knowledge of unsupervised plasticity mechanisms during the learning phase. According to our interpretation, the cortical network would efficiently transmit learned, i.e., predicted, patterns, without departing from ongoing activity. This would allow a robust mapping for some features selected by the spontaneous activity.
A more speculative extrapolation is to view the spontaneous activity as what the cortical network “expects” to transmit efficiently. The dynamic changes in the temporal structure of the spontaneous activity could be interpreted as transient switches between different sets of “expectations” or hypotheses made on the basis of the continuously updated incoming sensory flow. More extensive experimental research on the conditions under which ongoing activity in recurrent networks recapitulates fragments of previously learned memories (or “songs”) (Louie and Wilson, 2001; Ikegaya et al., 2004) (but see Mokeichev et al., 2007) is needed to consolidate this view.
Footnotes
This work was supported by Centre National de la Recherche Scientifique, Agence Nationale de la Recherche (Natstats), and European Commission-funded (Bio-I3: Facets FP6-2004-IST-FETPI 15879) grants to Y.F. O.M. was supported by bursaries from the French Ministry of Defence and the Fondation pour la Recherche Médicale. P.Y. was supported by a Ministère de l'Education Nationale de la Recherche et de la Technologie bursary from the University of Paris XI. We thank Sami El Boustani and Drs. Alain Destexhe, Olivier Faugeras, and Cyril Monier for helpful discussions and critical comments on the manuscript.
References
- Ackley DH, Hinton GE, Sejnowski TJ. A learning algorithm for Boltzmann machines. Cogn Sci. 1985;9:147–169. [Google Scholar]
- Aertsen AM, Gerstein GL, Habib MK, Palm G. Dynamics of neuronal firing correlation: modulation of “effective connectivity.”. J Neurophysiol. 1989;61:900–917. doi: 10.1152/jn.1989.61.5.900. [DOI] [PubMed] [Google Scholar]
- Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. 1996;273:1868–1871. doi: 10.1126/science.273.5283.1868. [DOI] [PubMed] [Google Scholar]
- Aviel Y, Mehring C, Abeles M, Horn D. On embedding synfire chains in a balanced network. Neural Comput. 2003;15:1321–1340. doi: 10.1162/089976603321780290. [DOI] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neurosci. 1999;19:2209–2223. doi: 10.1523/JNEUROSCI.19-06-02209.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banerjee A, Seriès P, Pouget A. Dynamical constraints on using precise spike timing to compute in recurrent cortical networks. Neural Comput. 2008;20:974–993. doi: 10.1162/neco.2008.05-06-206. [DOI] [PubMed] [Google Scholar]
- Baudot P, Levy M, Monier C, Chavane F, Renè A, Huguet N, Marre O, Pananceau M, Kopysova I, Frégnac Y. Time-coding, low noise Vm attractors, and trial-to-trial spiking reproducibility during natural scene viewing in V1 cortex. Soc Neurosci Abstr. 2004;30:948–12. [Google Scholar]
- Binzegger T, Douglas RJ, Martin KA. A quantitative map of the circuit of cat primary visual cortex. J Neurosci. 2004;24:8441–8453. doi: 10.1523/JNEUROSCI.1400-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comput Neurosci. 2000;8:183–208. doi: 10.1023/a:1008925309027. [DOI] [PubMed] [Google Scholar]
- Davison AP, Brüderle D, Eppler J, Kremkow J, Muller E, Pecevski D, Perrinet L, Yger P. PyNN: a common interface for neuronal network simulators. Front Neuroinformatics. 2008;2:11. doi: 10.3389/neuro.11.011.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- deCharms RC, Merzenich MM. Primary cortical representation of sounds by the coordination of action-potential timing. Nature. 1996;381:610–613. doi: 10.1038/381610a0. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Contreras D. Neuronal computations with stochastic network states. Science. 2006;314:85–90. doi: 10.1126/science.1127241. [DOI] [PubMed] [Google Scholar]
- Deweese MR, Zador AM. Shared and private variability in the auditory cortex. J Neurophysiol. 2004;92:1840–1855. doi: 10.1152/jn.00197.2004. [DOI] [PubMed] [Google Scholar]
- DeWeese MR, Hromádka T, Zador AM. Reliability and representational bandwidth in the auditory cortex. Neuron. 2005;48:479–488. doi: 10.1016/j.neuron.2005.10.016. [DOI] [PubMed] [Google Scholar]
- Diesmann M, Gewaltig M. NEST: an environment for neural systems simulations. Forschung und wisschenschaftliches Rechnen, Beitrage zum Heinz-Biling-Preis. 2001;58:43–70. [Google Scholar]
- El Boustani S, Destexhe A. A master equation formalism for macroscopic modeling of asynchronous irregular activity states. Neural Comput. 2009a;21:46–100. doi: 10.1162/neco.2009.02-08-710. [DOI] [PubMed] [Google Scholar]
- El Boustani S, Destexhe A. Does brain activity stem from high-dimensional chaotic dynamics? Evidence from the human electroencephalogram, cat cerebral cortex and artificial neuronal networks. Int J Bifurcat Chaos. 2009b in press. [Google Scholar]
- Fiser J, Chiu C, Weliky M. Small modulation of ongoing cortical dynamics by sensory input during natural vision. Nature. 2004;431:573–578. doi: 10.1038/nature02907. [DOI] [PubMed] [Google Scholar]
- Frégnac Y, Baudot P, Levy M, Marre O. An intracellular view of time coding and sparseness in V1 during virtual oculomotor exploration of natural scenes. Paper presented at the 2nd International Cosyne Conference in Computational and Systems Neuroscience; March; Salt Lake City, Utah. 2005. [Google Scholar]
- Garfinkel A, Spano ML, Ditto WL, Weiss JN. Controlling cardiac chaos. Science. 1992;257:1230–1235. doi: 10.1126/science.1519060. [DOI] [PubMed] [Google Scholar]
- Goldberg JA, Rokni U, Sompolinsky H. Patterns of ongoing activity and the functional architecture of the primary visual cortex. Neuron. 2004;42:489–500. doi: 10.1016/s0896-6273(04)00197-7. [DOI] [PubMed] [Google Scholar]
- Han F, Caporale N, Dan Y. Reverberation of recent visual experience in spontaneous cortical waves. Neuron. 2008;60:321–327. doi: 10.1016/j.neuron.2008.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heidmann A, Heidmann T, Changeux JP. Selective stabilization of neuronal representations by resonance between spontaneous prerepresentations of the cerebral network and percepts evoked by interaction with the outside world. C R Acad Sci III. 1984;299:839–844. [PubMed] [Google Scholar]
- Holt GR, Softky WR, Koch C, Douglas RJ. Comparison of discharge variability in vitro and in vivo in cat visual cortex neurons. J Neurophysiol. 1996;75:1806–1814. doi: 10.1152/jn.1996.75.5.1806. [DOI] [PubMed] [Google Scholar]
- Ikegaya Y, Aaron G, Cossart R, Aronov D, Lampl I, Ferster D, Yuste R. Synfire chains and cortical songs: temporal modules of cortical activity. Science. 2004;304:559–564. doi: 10.1126/science.1093173. [DOI] [PubMed] [Google Scholar]
- Kenet T, Bibitchkov D, Tsodyks M, Grinvald A, Arieli A. Spontaneously emerging cortical representations of visual attributes. Nature. 2003;425:954–956. doi: 10.1038/nature02078. [DOI] [PubMed] [Google Scholar]
- Kuhn A, Aertsen A, Rotter S. Higher-order statistics of input ensembles and the response of simple model neurons. Neural Comput. 2003;15:67–101. doi: 10.1162/089976603321043702. [DOI] [PubMed] [Google Scholar]
- Kumar A, Rotter S, Aertsen A. Conditions for propagating synchronous spiking and asynchronous firing rates in a cortical network model. J Neurosci. 2008;28:5268–5280. doi: 10.1523/JNEUROSCI.2542-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louie K, Wilson MA. Temporally structured replay of awake hippocampal ensemble activity during rapid eye movement sleep. Neuron. 2001;29:145–156. doi: 10.1016/s0896-6273(01)00186-6. [DOI] [PubMed] [Google Scholar]
- Luczak A, Barthó P, Harris KD. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron. 2009;62:413–425. doi: 10.1016/j.neuron.2009.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science. 1995;268:1503–1506. doi: 10.1126/science.7770778. [DOI] [PubMed] [Google Scholar]
- Markram H, Tsodyks M. Redistribution of synaptic efficacy between neocortical pyramidal neurons. Nature. 1996;382:807–810. doi: 10.1038/382807a0. [DOI] [PubMed] [Google Scholar]
- Mehring C, Hehl U, Kubo M, Diesmann M, Aertsen A. Activity dynamics and propagation of synchronous spiking in locally connected random networks. Biol Cybern. 2003;88:395–408. doi: 10.1007/s00422-002-0384-4. [DOI] [PubMed] [Google Scholar]
- Mokeichev A, Okun M, Barak O, Katz Y, Ben-Shahar O, Lampl I. Stochastic emergence of repeating cortical motifs in spontaneous membrane potential fluctuations in vivo. Neuron. 2007;53:413–425. doi: 10.1016/j.neuron.2007.01.017. [DOI] [PubMed] [Google Scholar]
- Monier C, Fournier J, Frégnac Y. In vitro and in vivo measures of evoked excitatory and inhibitory conductance dynamics in sensory cortices. J Neurosci Methods. 2008;169:323–365. doi: 10.1016/j.jneumeth.2007.11.008. [DOI] [PubMed] [Google Scholar]
- Palm G, Aertsen AM, Gerstein GL. On the significance of correlations among neuronal spike trains. Biol Cybern. 1988;59:1–11. doi: 10.1007/BF00336885. [DOI] [PubMed] [Google Scholar]
- Pecora LM, Carroll TL. Synchronization in chaotic systems. Phys Rev Lett. 1990;64:821–824. doi: 10.1103/PhysRevLett.64.821. [DOI] [PubMed] [Google Scholar]
- Rabinovich M, Huerta R, Laurent G. Neuroscience. Transient dynamics for neural processing. Science. 2008;321:48–50. doi: 10.1126/science.1155564. [DOI] [PubMed] [Google Scholar]
- Schreiber S, Fellous J, Whitmera D, Tiesinga P, Sejnowski T. A new correlation-based measure of spike timing reliability. Neurocomputing. 2003;52–54:925–931. doi: 10.1016/S0925-2312(02)00838-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sompolinsky H, Crisanti A, Sommers HJ. Chaos in random neural networks. Phys Rev Lett. 1988;61:259–262. doi: 10.1103/PhysRevLett.61.259. [DOI] [PubMed] [Google Scholar]
- Thomson AM, West DC. Fluctuations in pyramid-pyramid excitatory postsynaptic potentials modified by presynaptic firing pattern and postsynaptic membrane potential using paired intracellular recordings in rat neocortex. Neuroscience. 1993;54:329–346. doi: 10.1016/0306-4522(93)90256-f. [DOI] [PubMed] [Google Scholar]
- Tiesinga P, Fellous JM, Sejnowski TJ. Regulation of spike timing in visual cortical circuits. Nat Rev Neurosci. 2008;9:97–107. doi: 10.1038/nrn2315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timofeev I, Grenier F, Bazhenov M, Sejnowski TJ, Steriade M. Origin of slow cortical oscillations in deafferented cortical slabs. Cereb Cortex. 2000;10:1185–1199. doi: 10.1093/cercor/10.12.1185. [DOI] [PubMed] [Google Scholar]
- Tsodyks M, Kenet T, Grinvald A, Arieli A. Linking spontaneous activity of single cortical neurons and the underlying functional architecture. Science. 1999;286:1943–1946. doi: 10.1126/science.286.5446.1943. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H. Chaos in neuronal networks with balanced excitatory inhibitory activity. Science. 1996;274:1724–1726. doi: 10.1126/science.274.5293.1724. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H. Chaotic balanced state in a model of cortical circuits. Neural Comput. 1998;10:1321–1371. doi: 10.1162/089976698300017214. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H. Irregular activity in large networks of neurons. In: Chow C, Gutkin B, Hansel D, Meunier C, Dalibard J, editors. “Les Houches Lectures LXXX” on methods and models in neurophysics, Chap 9. London: Elsevier; 2005. pp. 341–402. [Google Scholar]
- Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol. 1996;76:1310–1326. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]
- Vogels TP, Abbott LF. Signal propagation and logic gating in networks of integrate-and-fire neurons. J Neurosci. 2005;25:10786–10795. doi: 10.1523/JNEUROSCI.3508-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogels TP, Rajan K, Abbott LF. Neural network dynamics. Annu Rev Neurosci. 2005;28:357–376. doi: 10.1146/annurev.neuro.28.061604.135637. [DOI] [PubMed] [Google Scholar]