Abstract
In many species, motion-sensitive neurons responding to optic flow at higher processing stages are well characterized; however, less is known how this representation of ego-motion is further transformed into an appropriate motor response. Here, we analyzed in the blowfly Calliphora vicina the visuomotor transformation from motion-sensitive neurons in the lobula plate [V2 and vertical system (VS) cells] onto premotor descending neurons [descending neurons of the ocellar and vertical system (DNOVS) cells] feeding into the motor circuit of the fly thoracic ganglion. We found that each of these cells is tuned to rotation of the fly around a particular body axis. Comparing the responses of presynaptic and postsynaptic cells revealed that DNOVS cells have approximately the same tuning widths as V2 and VS cells. However, DNOVS signals cells are less corrupted by fluctuations arising from the spatial structure of the visual input than their presynaptic elements. This leads to a more robust representation of ego-motion at the level of descending neurons. Thus, when moving from lobula plate cells to descending neurons, the selectivity for a particular optic flow remains unaltered, but the robustness of the representation increases.
Introduction
Optic flow is an important source of information for an animal about its ego-motion (Gibson, 1974). Accordingly, it is used to control walking (Warren et al., 2001), or to trigger landing (Davies and Green, 1990) and to estimate travel distance (Collett et al., 2006). Motion-sensitive neurons analyzing this optic flow often have large receptive fields and are selective for particular flow fields. Well known examples are neurons in the lobula plate, the third optic lobe of flies (Krapp and Hengstenberg, 1996; Joesch et al., 2008; Nordström et al., 2008). In blowflies, a set of ∼60 large-field motion-sensitive neurons in the lobula plate are involved in the processing of optic flow. These lobula plate tangential cells can be identified due to their invariant anatomy and characteristic visual response properties (Pierantoni, 1976; Hausen, 1982; Hengstenberg et al., 1982; Borst and Haag, 2002). As one subgroup, the 10 vertical system (VS) cells have large and complex receptive fields matching the optic flow that occurs during rotations of the fly around different body axes (Krapp et al., 1998). Both the directionally selective input from an array of local motion detectors (Haag et al., 1992; Single and Borst, 1998; Haag et al., 2004) and their coupling among them and with other lobula plate tangential cells (Haag and Borst, 2003, 2004, 2007) are responsible for the VS cells' tuning to specific flow fields (Farrow et al., 2005; Elyada et al., 2009). The 10 VS cells are major output elements of the brain and synapse onto premotor descending neurons feeding into the motor circuit of the fly thoracic ganglion (Strausfeld and Bassemir, 1985a). The physiology and connectivity of two descending neurons of the ocellar and vertical system (DNOVS1 and DNOVS2) were described recently (Haag et al., 2007; Wertz et al., 2008). Whereas DNOVS1 responds with a graded shift of the membrane potential, DNOVS2 responds with action potentials to motion stimuli. Both DNOVS cells are electrically coupled to different subsets of VS cells. DNOVS1 is most strongly coupled to VS6 and VS7 while DNOVS2 is most strongly coupled to VS5 and VS6. Neighboring VS cells are coupled more weakly to the descending neurons. DNOVS2 integrates additional motion information from the contralateral eye, probably via the V2 cell (Wertz et al., 2008). Although the specific wiring was already described, it is not yet clear why DNOVS cells integrate motion information from more than one VS cell.
Here we analyze the consequences of this connectivity pattern by a precise comparison of the ego-motion representation in presynaptic (VS and V2 cells) and postsynaptic elements (DNOVS1 and DNOVS2). Stimulating the cells by large-field motion patterns presented on a custom-built arena of light-emitting diode (LED arena) subtending 240° × 95° of the visual field of a fly, we first determine the preferred axis of rotation of a cell. We then ask two major questions: Are DNOVS cells tuned to an axis of rotation more specifically than their presynaptic cells? In what other respect does the representation of ego-motion in DNOVS cells differ from the one in lobula plate tangential cells?
Materials and Methods
Electrophysiology.
Female blowflies (Calliphora vicina, 2–10 d old, laboratory stock) were prepared as previously described (Wertz et al., 2008) and were mounted on a heavy recording table facing the LED arena (Fig. 1C). DNOVS1 and VS cells were recorded intracellularly with sharp glass electrodes (Flaming/Brown micropipette puller, P-97; Sutter Instrument) using glass capillaries with an outer diameter of 1 mm (GC100F-10; Science Products). Electrodes had resistances between 25 and 50 MΩ. Tip solutions contained either 10 mm Alexa 488 or 10 mm Alexa 594 (both Invitrogen), allowing us to identify more than one cell at a time. The shaft of the electrode was filled with 2 m potassium acetate plus 0.5 m potassium chloride. For data analysis, the output signals of the amplifiers were fed to a PC via an analog-to-digital converter (PCI-DAS6025, Measurement Computing) with a sampling rate of 10 kHz for intracellular recordings. For recordings from DNOVS1, a VS cell was filled with Alexa and visualized under fluorescence light. The VS cell then served as a landmark for finding the DNOVS1 neuron (see Haag et al., 2007). DNOVS1 was recorded from the dendrite and VS cells from their axons. For the experiments shown in Figure 4, VS cells were also recorded from their dendrites. After the recording, several images of each Alexa-filled VS cell were taken by a CCD camera (Leica DC 320). These images allowed anatomical identification of the recorded cell on the basis of their characteristic branching patterns and the relative position of their ventral dendrite within the lobula plate. The V2 cell was recorded intracellularly and extracellularly from its axonal arborization and could be identified due to its invariant anatomy (Hausen and Egelhaaf, 1989) and its sensitivity for vertical motion along the azimuth (Wertz et al., 2008). Data analysis was performed offline using custom-built software written in Matlab (MathWorks).
Figure 1.
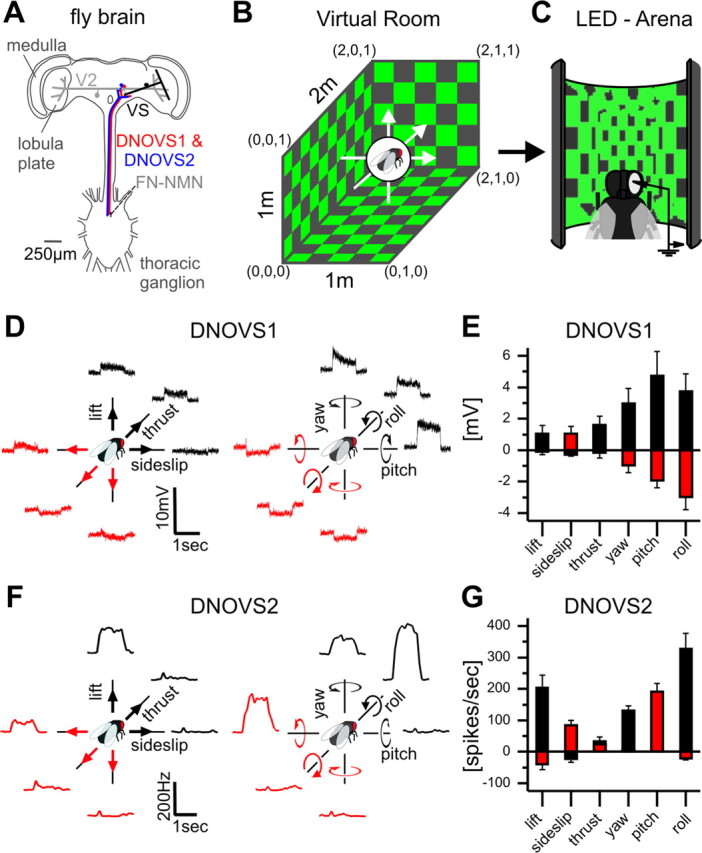
Ego-motion tuning of DNOVS cells. A, Schematic drawing of the investigated neural network. DNOVS cells receive motion information from lobula plate tangential cells (VS and V2) in the fly brain and convey the information among others onto neck motor neurons in the thoracic ganglion. B, Stimulus movies were generated by moving a virtual fly along or around the X-, Y-, or Z-axes in a virtual room. The virtual room was wallpapered with equally distributed squares. C, Movies were presented on the LED arena to a real fly while cells were recorded. D, DNOVS1 example responses to the three translations (lift, sideslip, and thrust) and to the three rotations (yaw, pitch, and roll). The movies were shown forward and backward corresponding to opposite movement directions of the fly, indicated by the black and red color. E, Mean responses ± SEM of DNOVS1 from n = 6 flies. F, Average peristimulus time histogram of the firing frequency of a DNOVS2 cell to the different movements (10 trials, bin size: 100 ms). G, Mean response ± SEM of DNOVS2 from n = 5 flies.
Figure 4.
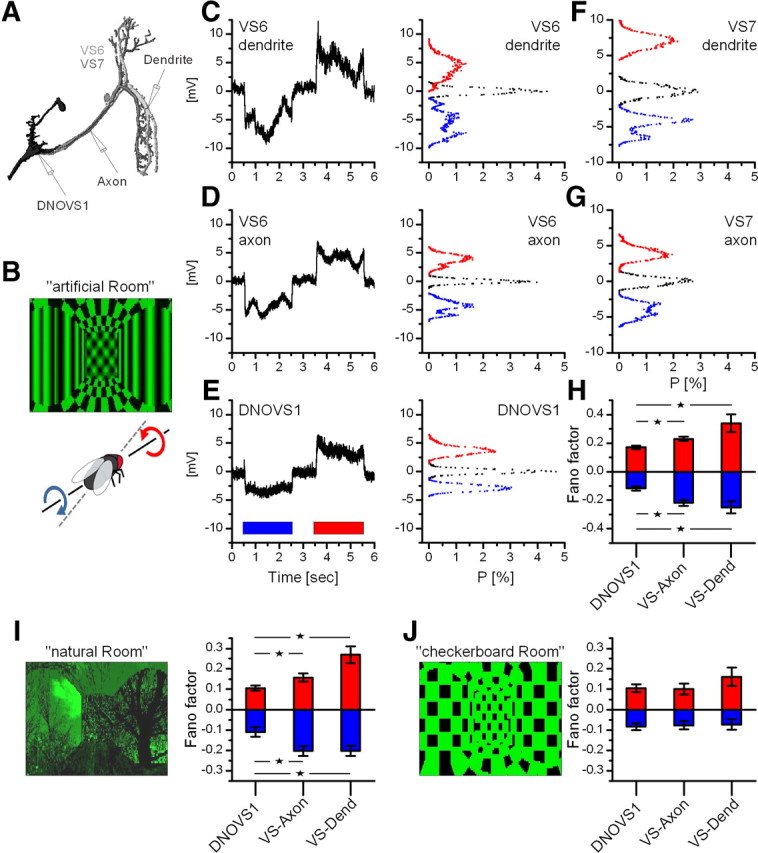
Robust coding of the axis of rotation in DNOVS1. A, Schematic drawing of the intracellular recording sites. VS6 and VS7 were recorded in the dendrite as well as in the axon, DNOVS1 in the dendrite. B, Picture of the stimulus movie called “artificial room” (movie can be seen in the supplemental material, available at www.jneurosci.org) representing a rotation around an axis at 30° azimuth. C–E, Average responses and membrane potential distributions of a VS6 dendrite, a VS6 axon, and a DNOVS1 cell to clockwise (blue) and counterclockwise rotation (red). Black distributions represent the variation of the resting membrane potential. F, G, Example membrane potential distributions of a VS7 dendrite and a VS7 axon. H, Mean Fano factors of DNOVS1, VS axon, and VS dendrite (pooled data from VS6 and VS7) for clockwise (blue) and counterclockwise (red) rotation. The mean values for DNOVS1 and VS axon/VS dendrite differed significantly. Data are from n = 7 DNOVS1, n = 7 VS axon (4 VS6, 3 VS7), and n = 12 VS dendrite (8 VS6, 4 VS7). I, Picture of the stimulus movie “natural room.” The Fano factors of DNOVS1 and VS axon/dendrite to rotations of the natural room differed significantly. Data are from n = 8 DNOVS1, n = 5 VS axon (2 VS6, 3 VS7), and n = 9 VS dendrite (5 VS6, 4 VS7). J, Stimulation with the “checkerboard room” elicited no observable difference in the responses of DNOVS1 and VS axon/dendrite. Data are from n = 5 DNOVS1, n = 3 VS axon (2 VS6, 1 VS7), and n = 8 VS dendrite (5 VS6, 3 VS7). Statistical tests were done between DNOVS1, VS axon, and VS dendrite (*p < 0.05, Wilcoxon rank sum test).
Stimulus device.
For visual stimulation an LED arena was custom built based on the open-source information of the Dickinson Laboratory (Reiser and Dickinson, 2008) (and see http://www.dickinson.caltech.edu/PanelsPage). Our arena consists of 30-by-16 TA08-81GWA dot matrix displays (Kingbright), each harboring 8-by-8 individual green (568 nm) LEDs, covering 240° in azimuth and 95° in elevation of the fly's visual field with an angular resolution better than 1° between adjacent LEDs. This angular resolution is sufficient since, in Calliphora, the highest spatial resolution was found in the frontal visual field and amounts to 1.2° (Land and Eckert, 1985). The luminance range of the stimuli was 0–80 cd/m2.
The arena is capable of frame rates of >600 frames per second (fps) with 16 intensity levels. Each dot matrix display is controlled by an ATmega644 microcontroller (Atmel) that obtains pattern information from one central ATmega128-based main controller board, which in turn reads in pattern information from a compact flash memory card. For achieving high frame rates with a system of this size, each panel controller was equipped with an external AT45DB041B flash memory chip for local pattern buffering. Matlab was used for programming and generation of the patterns as well as for sending the serial command sequences via RS-232 to the main controller board and local buffering.
Visual stimulation.
To measure the global motion responses of a cell, we programmed a virtual room (Fig. 1B) in which a virtual fly was translated and rotated along the X-, Y-, and Z-axes. In addition the fly was rotated around 36 axes within the horizontal plane. At every point in time, we projected the environment onto the virtual fly's eye and used the resulting movies subsequently as stimuli displayed to a real fly in the LED arena while recording from the neurons (Fig. 1C). The virtual room had the following dimensions: 2 m length, 1 m width, and 1 m height. The left corner in the front at the bottom was defined as origin with coordinates (0, 0, 0), and the right corner in the back on the top was defined as endpoint with coordinates (2, 1, 1) (Fig. 1B). To generate the translational movies, the virtual fly was moved for 1 s as follows: from (1, 0.5, 0.14) to (1, 0.5, 0.74) for upward lift, from (1, 0.14, 0.5) to (1, 0.74, 0.5) for rightward sideslip, and from (0.5, 0.5, 0.5) to (1.33, 0.5, 0.5) for forward thrust. For the opposite movements, the fly was moved mirror inversely, e.g., from (1, 0.5, 0.86) to (1, 0.5, 0.26) for downward lift. This results in speeds of 0.6 m/s for lift and sideslip and 0.833 m/s for thrust. For rotations, the virtual fly was positioned at (1, 0.5, 0.5) and was rotated around the X-, Y-, and Z-axes at a speed of 300°/s.
For the first set of experiments (Fig. 1), we wallpapered the virtual room with a regularly tiled checkerboard pattern with one square having a side length of 0.2 m. In the following we refer to this stimulus as the “checkerboard room.” An example movie for a roll rotation is shown in the supplemental material (available at www.jneurosci.org as supplemental material). All movies were presented for one second at a speed of 300 fps. In the following, we define the preferred ego-motion as the movement that elicits the maximal response in the investigated cell. To measure the preferred movement along or around the X-, Y-, and Z-axes, we presented the movies in the following sequence: upward and downward lift, rightward and leftward sideslip, forward and backward thrust, leftward and rightward yaw, downward and upward pitch, and clockwise and counterclockwise roll (indicated by black and red colors in Fig. 1D,F).
As the spatial frequency content and local speeds differ for translational and rotational movements, we quantified the movies of the checkerboard room by feeding them into an array of motion detectors of the Reichardt type (Reichardt, 1987). The array consisted of a pair of detectors at each location in space, one being oriented along the azimuth, the other being oriented along the elevation. Each detector consisted of two mirror-symmetric subunits. Within each subunit, the luminance value derived from one image pixel was low-pass filtered and subsequently multiplied with the high-pass filtered luminance value from the neighboring pixel. Both filters were of first order and had time constants of 20 ms (low-pass) and 50 ms (high-pass), respectively (Haag et al., 1999; Borst et al., 2005). The final output signal of each detector was obtained by subtracting the results of the multipliers from each subunit. These signals were then treated as the x- and y-components of the local motion vector. The spatial resolution of the input image was 2°, as was the sampling base of the Reichardt detectors. The temporal resolution was 2 ms. We defined the motion strength as the spatiotemporal average of the vector length of the motion detectors output. For the velocities we used to determine the preferred ego-motion (Fig. 1), the motion strength for translation was ∼1.3 times higher than for rotations. Thus, despite different local speeds and spatial frequency distributions, the overall stimulus strength was in the same range for both kinds of movement. This allowed us to compare the responses of a cell to rotational movements with the ones to translational movements.
To measure the preferred axis of rotation, we generated 18 movies in the “checkerboard room” showing rotations around 18 different axes within the horizontal plane. The axes had an interval of 10° and were played forward and backward resulting in 36 counterclockwise rotations. In the following, a rotation around an axis at 0° represents a counterclockwise rotation around the fly's longitudinal axis (roll movement). Nose-down pitch was assigned as 90° and nose-up pitch as −90°.
To investigate the pattern dependence of the response of a cell, we wallpapered the virtual room with two further patterns. The first pattern consisted of a checkerboard ceiling and floor, stripes on the side walls, and a plaid on the front wall. The room is called “artificial room” (see Fig. 4B). The second pattern consisted of a more naturalistic scene (“natural room”) with images of trees on the walls (see Fig. 4I) taken from Hans van Hateren's collection of natural images (van Hateren and van der Schaaf, 1998). Both rooms are characterized by their rather irregular texture and inhomogeneous contrast distribution. To generate the movies, the virtual fly was rotated around approximately the preferred axis of DNOVS1 (see Fig. 4) as well as the pitch and roll axis (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). The resulting movies were then displayed on the arena while we recorded from VS cells in the dendrite as well as in the axon, and from the dendrite of DNOVS1. Movies were displayed forward and backward for 2 s at 150 fps with 1 s of rest in between.
To quantify the differences between a movie showing a roll rotation in the “artificial room” and a movie showing a roll rotation in the “checkerboard room,” we analyzed the luminance variance and the motion variance. The luminance variance was calculated from the mean gray value in a 5° × 5° patch as a function of time. The luminance variance for the “artificial room” was 5.6 (in arbitrary units) and 6.1 for the “checkerboard room.” To calculate the motion variance, both movies were fed into a two-dimensional array of local motion detectors of the Reichardt type (Reichardt, 1987) (for details, see above). The motion variance was then calculated from the responses of local motion detectors oriented along the elevation axis and integrated within a stripe with extensions of 20° in azimuth and 100° in elevation as a function of time. The resulting values for motion variance were, again in arbitrary units, 127 for the “artificial room” and 34 for the “checkerboard room.” Thus, while both rooms produce a similar local luminance variance, the “artificial room” leads to an approximately four times higher motion variance than the “checkerboard room.”
Data analysis.
Graded neural responses were calculated by taking an average of the membrane potential during the stimulus starting 100 ms after stimulus onset minus the mean membrane potential within 200 ms before stimulus onset. The spiking response of DNOVS2 or V2 was calculated by counting the average number of spikes minus resting firing frequency for the same time intervals as indicated above. The exact axis of rotation was determined by fitting a sine function to the responses of a cell to the different axis of rotation (Fig. 2B) (see also Karmeier et al., 2005). The fits were based on the following free parameters: phase shift (y0), amplitude (w), and offset (A). From the fits we obtained the preferred axis of rotation by determining the azimuth position at which the fitted tuning curve had its maximum. In addition, we defined the width of the tuning curve by its width at half-maximum height of the fit. For DNOVS2 we fitted a truncated sine function to the responses to account for the fact that the cell's firing frequency cannot become negative.
Figure 2.
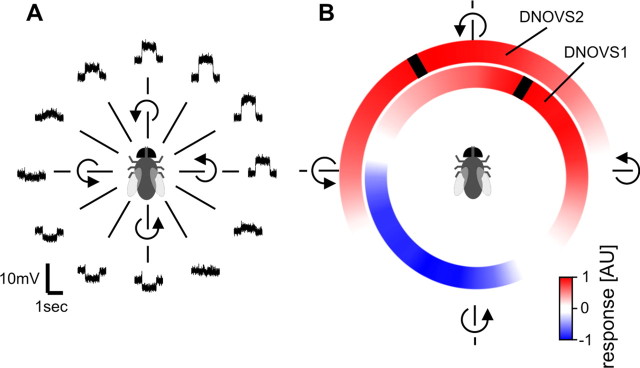
Preferred axis of rotation of DNOVS1 and DNOVS2. A, Example responses of DNOVS1 to 12 different axes of rotation. B, Mean responses to 36 axes of rotation of DNOVS1 (n = 4 flies) and DNOVS2 (n = 3 flies), shown in color code. Red represents a depolarization of DNOVS1 or an increase of the firing rate of DNOVS2, blue a hyperpolarization. Black bar indicates the preferred axis of rotation.
To analyze the stimulus dependency of the responses in DNOVS1, VS dendrite, and VS axon, we calculated the distributions from the average membrane potential. We averaged the membrane potential of three to five trials per recording site to avoid intrinsic noise fluctuations. Membrane potential distributions were calculated for 1800 ms starting 200 ms after stimulus onset and were normalized by the number of events (18,000 for a sample rate of 10 kHz). The normalized potential distribution for membrane potential in rest was calculated for 1200 ms (400 ms before movie was played forward and 800 ms before movie was played backward). To quantify the responses, we calculated the Fano factor of each cell by first averaging the trials, and then calculating the variance of the average beginning 200 ms after stimulus onset for 1800 ms and then normalizing it with the mean value of the average. Statistics were done with the statistics toolbox of Matlab.
Results
Preferred ego-motion of DNOVS cells
To determine the preferred type of ego-motion of DNOVS cells as well as their presynaptic cells (Fig. 1A), we programmed a virtual room with regularly tiled checkerboard walls, ceiling, and floor, in which a virtual fly could be translated along and rotated around the X-, Y-, and Z-axes, respectively (Fig. 1B). At every point in time, we projected the environment onto the virtual fly's eye and used the resulting movies subsequently as stimuli displayed to a real fly in the LED arena (Fig. 1C). All 12 movies were shown consecutively, with the movements first in one direction (Fig. 1D, black arrows) followed by the opposite direction (red arrows), while we recorded from the neuron of interest. In the following, all responses are shown as if the fly was performing this movement. To all three translational and rotational movements, DNOVS1 depolarized in one direction and hyperpolarized in the opposite direction (Fig. 1D). On average, the three rotational movements elicited a stronger response in DNOVS1 than the translational movements (Fig. 1E). DNOVS1 responded maximally to nose-down pitch. Counterclockwise roll movements or leftward yaw movements elicited a weaker response. Interestingly, a transient response of DNOVS1 was only observed for yaw movements. Whereas DNOVS1 responds with a graded shift of the membrane potential, DNOVS2 responds with action potentials to motion stimuli. The peristimulus time histograms of one DNOVS2 cell (Fig. 1F) and the mean responses to all kind of movements (Fig. 1G) show that the spike frequency in DNOVS2 was maximally increased for counterclockwise roll movements. Nose-up pitch and yaw elicited a weaker response. Whereas DNOVS2 responded only with a slight increase to sideslip and thrust, the cell responded strongly to an upward lift.
To exactly determine the preferred axis of rotation of DNOVS1 and DNOVS2, we rotated the virtual fly around 36 different axes of rotation within the horizontal plane. In Figure 2A an example response of DNOVS1 to 12 rotations in the horizontal plane, separated by 30°, is shown. Here again, the cell depolarized for rotation in one direction and hyperpolarized for rotation in the opposite direction. As the tuning curve of DNOVS1 to the different axes of rotation showed a sinusoidal response characteristic, we fitted a sine function to the tuning curve. For DNOVS2 we fitted a truncated sine function to the tuning curve as the hyperpolarization of the cell is limited by the non-negative firing frequency. These functions allowed for determining the response maxima, which represent the preferred axis of rotation. The mean responses of DNOVS1 and DNOVS2 to all 36 rotations together with the maxima are shown in Figure 2B in a color-coded way. Red represents a depolarization of DNOVS1 or an increase of the firing rate of DNOVS2, blue a hyperpolarization of DNOVS1. The maxima are marked by black stripes. In the following the counterclockwise roll movement around the longitudinal body axis is defined as a rotation with a pole at 0°, nose-down pitch with a pole at +90°, and nose-up pitch with a pole at −90°. DNOVS1 depolarized to counterclockwise rotations around poles from +100° to −20°. The opposite movements elicited a hyperpolarization in DNOVS1. DNOVS1 responded maximally to a counterclockwise rotation around an axis at azimuth position of 32° ± 3°. DNOVS2 increased its firing rate for counterclockwise roll movements around poles from −90° to 50°, and its preferred axis of rotation was at an azimuth position of −30° ± 3°.
Are DNOVS cells more specifically tuned to an axis of rotation than VS cells?
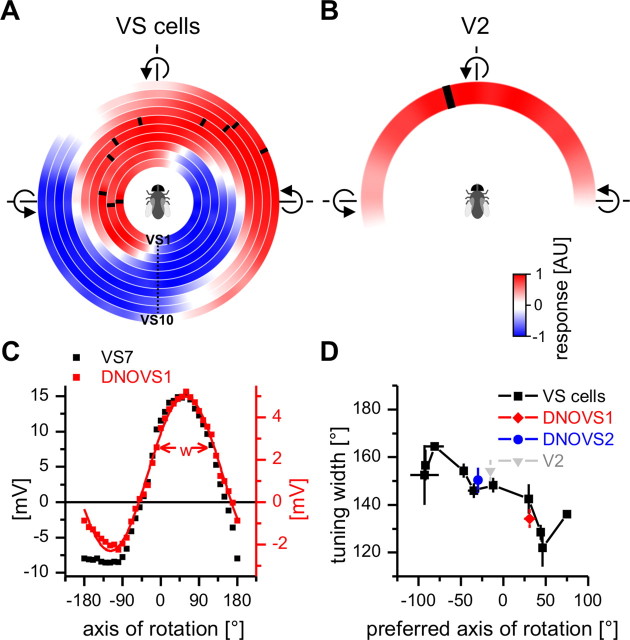
To compare the global motion preferences of DNOVS cells with those of VS cells, we measured the response of VS cells to movements along (translation) and around (rotation) the X-, Y-, and Z-axes (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). As expected from their receptive fields (Krapp et al., 1998) and previous global motion stimulations (Karmeier et al., 2005), rotations in the horizontal plane elicited the strongest response in VS cells. To determine the preferred axis of rotation, we measured the responses of all VS cells to 36 rotations within the horizontal plane as described above for DNOVS cells. In Figure 3A, the mean response of all 10 VS cells to the 36 rotations is shown beginning with VS1 plotted in the innermost circle and VS10 in the outermost one. Again, red represents a depolarization and blue a hyperpolarization of a cell. From VS1 to VS10, the preferred axes of rotation leading to maximum depolarization of a cell shifted along the azimuth from −93° to +75°. Compared with DNOVS1, VS cells responded with larger graded potential changes up to 20 mV. VS1 depolarized to nose-up pitch and nearby axes of rotation. VS6, instead, responded with a depolarization to counterclockwise rotation around the longitudinal body axis with a pole of rotation approximately at 0° (roll movement of the fly). VS10 was most sensitive to rotations related to nose-down pitch. With the same set of stimuli, we measured the responses of V2 to different rotations (Fig. 3B). Here, red represents an increase of the spike frequency. V2 responded to rotations from nose-down pitch to nose-up pitch with the strongest response approximately for counterclockwise roll. The preferred axis of rotation at −7° is indicated by a black bar and was calculated by fitting a truncated sine function to the tuning curve of V2.
Figure 3.
Preferred axis of rotation and tuning width of lobula plate tangential cells and DNOVS cells. A, Mean responses to 36 axes of rotation for 10 VS cells are shown color coded with red representing a depolarization and blue a hyperpolarization. The preferred axis of rotation (black ticks) shifts along the azimuth with increasing VS cell number. Data represents the mean of n number of flies for VS1 (n = 5), VS2 (n = 3), VS3 (n = 4), VS4 (n = 6), VS5 (n = 3), VS6 (n = 5), VS7 (n = 5), VS8 (n = 4), VS9 (n = 2), and VS10 (n = 1). B, Mean responses to 36 axes of rotation of n = 3 V2 cells. C, Tuning curve measured in a DNOVS1 and a VS7 neuron. The line drawn through the measured data of DNOVS1 indicates the fitted sinusoidal function. w indicates the tuning width defined as the part of the response tuning curve eliciting >50% of the maximum response. D, Tuning widths of DNOVS, VS, and V2.
To investigate whether DNOVS cells are more specifically tuned to their preferred axis of rotation than their presynaptic cells, we calculated the tuning width for VS, V2, and DNOVS cells. As tuning width we defined the part of the response curve eliciting >50% of the maximum response of a cell (Fig. 3C). DNOVS1 was found to be strongest coupled to VS6 and VS7 (Haag et al., 2007), and its tuning width was similar to the tuning width of VS7 (Fig. 3D). The tuning widths of VS cells decreased slightly from VS1 to VS10. For DNOVS2, the tuning width was also similar to the tuning width of VS5 and VS6, strongest coupled to DNOVS2 (Wertz et al., 2008). In addition, the tuning width of V2 and DNOVS2 were nearly the same. Thus, DNOVS cells are neither broader nor more specifically tuned to an axis of rotation than are VS cells or V2, which provide input to them.
Robust coding in DNOVS1
Modeling studies (Cuntz et al., 2007; Weber et al., 2008) suggested that the electrical coupling between VS cell axon terminals should smooth out response fluctuations during rotation that arise from spatial inhomogeneities of the visual surround. Thus, at the output of the VS cells, the representation of the axis of rotation should be robust even in the presence of textureless patches of the visual surround. To investigate whether this robust coding is indeed observed in DNOVS cells postsynaptic to VS cells, we recorded the responses of the DNOVS1 cell and compared the results with the recordings obtained from VS6 and VS7 in the dendrite as well as in the axon (Fig. 4A). In the first experiment, we used as a stimulus a visual environment that consisted of a virtual room with different patterns on the walls, floor, and ceiling (Fig. 4B). Stimulus movies were generated in the same way as described above (Fig. 1B). The stimulus corresponded to the fly rotating around an axis of 30° in azimuth, which represents approximately the preferred axis of rotation of DNOVS1. The movie was presented forward and backward representing a clockwise and counterclockwise movement of the fly. To quantify the response fluctuations over time, we calculated the membrane potential distributions of the responses recorded in a VS6 dendrite, a VS6 axon, and the DNOVS1 cell (Fig. 4C–E). Blue and red histograms represent membrane distributions occurring during clockwise and counterclockwise rotation, respectively. The black histogram represents the membrane potential distribution when no stimulus was applied. The potential distribution indicates the time-dependent fluctuation of the membrane potential. The more narrow the distribution, the less fluctuation in the membrane potential and the more robust the stimulus representation. We found that the fluctuations of the membrane potential were strongest in the VS6 dendrite and decreased continuously via the VS6 axon to the DNOVS cell (compare responses in Fig. 4C–E). The same phenomenon is observed in the potential distributions of the VS7 dendrite (Fig. 4F) and VS7 axon (Fig. 4G). Here, we focused on VS6 and VS7, which are strongest coupled to DNOVS1 (Haag et al., 2007), but similar results were found in the neighboring VS cells (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). To parameterize the potential distributions from the different recording sites, we calculated the variance divided by the mean, i.e., the Fano factor, for both stimulus situations (Fig. 4H). For VS axon and VS dendrite, we pooled the data of VS6 and VS7. The Fano factor of DNOVS1 for both stimulus situations differed significantly from the Fano factors of the VS axon or the VS dendrite. Thus, we found less variation in the response of DNOVS1 to these stimuli. In other words, the axis of rotation is represented more robustly in the time-dependent membrane potential of DNOVS1 than in VS cells. To test this robustness, we used a second stimulus the “natural room” containing a more naturalistic scene characterized also by its rather irregular texture and inhomogeneous contrast distribution (Fig. 4I). Here again, the Fano factor of DNOVS1 differed significantly from the Fano factors of VS axon and VS dendrite, supporting the robust representation of axis of rotation in DNOVS1. As a control, we used the checkerboard stimulus described before (Fig. 1) with equally distributed squares on the walls, ceiling, and floor of the room (“checkerboard room”). Compared with the “artificial room,” the “checkerboard room” has approximately the same mean luminance but a four times lower motion variance (see Material and Methods). For this stimulus, we found no difference of Fano factors between DNOVS1, VS axon, and VS dendrite. Thus, DNOVS1 responses are more invariant to the spatial structure of the environment than are VS cell responses. We found similar results for pitch and roll movements (supplemental Fig. 3, available at www.jneurosci.org as supplemental material), indicating furthermore a robust coding of ego-motion parameters in DNOVS1.
Discussion
In this study, we characterized the ego-motion tuning of two descending neurons in the fly called DNOVS1 and DNOVS2, as well as of their presynaptic cells in the lobula plate. Both DNOVS cells turned out to be tuned to rotations around different body axes (Fig. 2). DNOVS cells are tuned neither more broadly nor more selectively to an axis of rotation than their presynaptic cells (Fig. 3). However, we found that DNOVS1 responses fluctuated less during rotation of spatially inhomogeneous patterns than did VS cells (Fig. 4; supplemental Fig. 3, available at www.jneurosci.org as supplemental material). We conclude that, at the level of DNOVS cells, a robust representation of ego-motion is obtained.
Given the linear integration found in DNOVS1 (Haag et al., 2007), one expects no increase in response selectivity at this level compared with the presynaptic neurons. As shown in Figure 3, this is what indeed is found: The tuning width of DNOVS1 is in the range of the VS cells. However the responses of VS cells and DNOVS1 differed when using artificial or naturalistic stimuli with irregular contrast distributions, instead of patterns with homogeneous contrast distribution (Fig. 4). Compared with the axonal or dendritic recordings of VS6 or VS7 or neighboring VS cells (supplemental Fig. 2, available at www.jneurosci.org as supplemental material), DNOVS1 responded more invariantly to these stimuli. This suggests that the linear interpolation of VS cell output signals leads to a robust representation of the axis of rotation. The electrical coupling between VS cells (Haag and Borst, 2004) and the electrical coupling between DNOVS1 and VS cells (Haag et al., 2007) is the most likely explanation for this robust coding. In a simulation study, Cuntz et al. (2007) showed that a robust coding could be achieved by the electrical axo-axonal coupling between VS cells. This finding was confirmed recently by calcium-imaging experiments showing that the axon terminal responses of VS cells are linear interpolations of the dendritic responses of neighboring VS cells (Elyada et al., 2009). As we could not measure the membrane potential in the axonal terminal of VS cells for technical reasons, it is hard to determine whether the linear interpolation occurs exclusively in VS cells. However, DNOVS1 is electrically coupled to at least VS6 and VS7, suggesting that they form a functional syncytium that collectively is responsible for the robust coding. To avoid a comparison of graded potential responses with action potential responses of DNOVS2, we focused our analysis on DNOVS1. However, as DNOVS2 is electrically coupled to VS5 and VS6 (Wertz et al., 2008), we would expect a similar result for DNOVS2. Thus, at the level of descending neurons, not the selectivity but the robustness is increased compared with VS cells.
DNOVS1 and DNOVS2 cells receive synaptic input from lobula plate tangential cells as well as from the ocelli via ocellar interneurons (Haag et al., 2007; Wertz et al., 2008). The three ocelli are light-sensitive organs and form a triangle on the dorsal surface of the head [for an overview, see Krapp (2009)]. Stimulating the ocelli with an LED elicited a short on and off response in DNOVS1 (Haag et al., 2007) as well as in DNOVS2 (Wertz et al., 2008). Directional selective responses to UV gratings were recently described in ocellar interneurons of dragonflies (van Kleef et al., 2008). In dragonflies (Stange, 1981) as well as in locusts (Taylor, 1981), the ocelli are effective rotation detectors, crucial to proper gaze and flight stabilization. Recently it was found for blowflies that the ocellar component of V1's response appears to be tuned to rotation (Parsons et al., 2006). Whether these rotation-specific ocellar signals are transmitted to DNOVS cells or the ocellar component of DNOVS responses itself is tuned to rotation is not yet clear. In addition to visual motion and stimulation of the ocelli, DNOVS cells also respond to air currents delivered to the antennae (Gronenberg et al., 1995). Thus, at the level of descending neurons like DNOVS cells, at least three sensory modalities are integrated. How the different modalities are integrated and whether they lead to a higher selectivity in DNOVS cells are still open questions and require the systematical analysis of the combination of the modalities.
Functional relevance
DNOVS1 and DNOVS2 project to the thoracic ganglion and there inter alia onto frontal nerve–neck motor neurons (FN-NMNs) (Strausfeld and Bassemir, 1985a; Gronenberg et al., 1995). Twenty-one pairs of neck motor neurons were identified, which are organized on each side into four neck muscle nerves innervating 21 neck muscles (Strausfeld et al., 1987) involved in the fly gaze stabilization system. FN-NMNs innervate a variety of different neck muscles that, based on their anatomy (Strausfeld et al., 1987), could potentially be involved in nose-up pitch, nose-down pitch, yaw, and roll of the head. In addition, FN-NMNs are motion sensitive (Milde et al., 1987), and have receptive fields reminiscent of specific optic flow fields generated during pitch, a combination of pitch and roll and almost pure roll rotation (Huston and Krapp, 2008). DNOVS1 is tuned to a combination of pitch and roll and DNOVS2 is tuned to an almost pure roll rotation. Thus, the synaptic connection between lobula plate tangential cells and descending neurons might be regarded as a coordinate transformation where, from the full set of preferred axes of rotations represented within the lobula plate, those ones become transmitted to the motor centers that are appropriate for the muscles they finally innervate.
In contrast to the primary receptive field of lobula plate tangential cells, most neck motor neurons have binocular receptive fields and are therefore more selective to rotation over translation than lobula plate tangential cells (Huston and Krapp, 2008). Although DNOVS2 is sensitive to contralateral motion in the presence of ipsilateral downward motion (Wertz et al., 2008), contralateral motion alone elicited no response, neither in DNOVS2 (Wertz et al., 2008) nor in DNOVS1 (Haag et al., 2007). Thus, to achieve binocular receptive fields found for FN-NMNs (Huston and Krapp, 2008), different descending neurons should converge onto FN-NMNs. The integration of binocular visual motion information at the level of descending neurons, as was found for DNOVS2 (Wertz et al., 2008) or at the level of neck motor neurons, are at least two possibilities to achieve a higher binocularity and thus a higher selectivity in FN-NMNs.
In addition, VS cells encode multiple preferred axes of rotation (Krapp et al., 1998) (Fig. 3A). Recently it was shown that the joint responses of different subpopulations of VS cells can provide unambiguous information about lift, roll, or pitch components of an animal's ego-motion (Karmeier et al., 2006). Karmeier et al. (2006) proposed that the specificity to self-rotation is enhanced by subtracting the responses of two sets of VS cells from opposite sides of the visual sphere having the same preferred axes of rotation but with opposite directions. Whether postsynaptic descending neurons make use of this population code is not yet clear, as DNOVS1 integrates only ipsilateral motion. DNOVS2 increases its selectivity for roll movements by integrating motion information from the contralateral eye and could be the key player to encode the roll axis. Thus, to understand the transformation of the population code from lobula plate tangential cells onto descending neurons, further descending neurons, such as, e.g., DNOVS3 or DNColHS (Strausfeld and Bassemir, 1985a,b), need to be analyzed.
Flies rely heavily on optic flow to initiate landing when collisions are impending (Borst and Bahde, 1988a,b) and to control course stability during flight (Frye and Dickinson, 2001; Srinivasan and Zhang, 2004; Mronz and Lehmann, 2008). Therefore, head rotations of blowflies are effectively compensating part of the thorax rotations, which results in improved conditions for vision (Schilstra and van Hateren, 1998; van Hateren and Schilstra, 1999). Between saccades, the head is kept stable to maximize the information of translational optic flow about the three-dimensional structure of the visual environment. During saccades, the head compensates most of the thorax rotation (van Hateren and Schilstra, 1999). By minimizing the duration of head rotations, rotational optic flow is kept to a minimum, and the optic flow due to translation dominates. To achieve this, the fly gaze stabilization system consists of at least two visuomotor transformations: first, the integration of binocular visual motion information, which increases the rotation selectivity of neck motor neurons (Huston and Krapp, 2008); and second, the interpolation of VS cell output signals, which leads to a robust coding of ego-motion parameters in DNOVS cells. Both mechanisms are necessary to achieve an appropriate motor response.
Footnotes
This work was supported by the Max Planck Society, a grant of the Deutsche Forschungsgemeinschaft (GRK 1091), and a grant of the Bundesministerium für Bildung und Forschung to the Bernstein Center for Computational Neuroscience Munich. We are grateful to Renate Gleich for excellent technical assistance.
References
- Borst A, Bahde S. Spatio-temporal integration of motion—a simple strategy for safe landing in flies. Naturwiss. 1988a;75:265–267. [Google Scholar]
- Borst A, Bahde S. Visual information processing in the fly's landing system. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1988b;163:167–173. [Google Scholar]
- Borst A, Haag J. Neural networks in the cockpit of the fly. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2002;188:419–437. doi: 10.1007/s00359-002-0316-8. [DOI] [PubMed] [Google Scholar]
- Borst A, Flanagin VL, Sompolinsky H. Adaptation without parameter change: dynamic gain control in motion detection. Proc Natl Acad Sci U S A. 2005;102:6172–6176. doi: 10.1073/pnas.0500491102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collett M, Collett TS, Srinivasan MV. Insect navigation: measuring travel distance across ground and through air. Curr Biol. 2006;16:R887–R890. doi: 10.1016/j.cub.2006.09.027. [DOI] [PubMed] [Google Scholar]
- Cuntz H, Haag J, Forstner F, Segev I, Borst A. Robust coding of flow-field parameters by axo-axonal gap junctions between fly visual interneurons. Proc Natl Acad Sci U S A. 2007;104:10229–10233. doi: 10.1073/pnas.0703697104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies MNO, Green PR. Optic flow-field variables trigger landing in hawk but not in pigeons. Naturwiss. 1990;77:142–144. doi: 10.1007/BF01134481. [DOI] [PubMed] [Google Scholar]
- Elyada YM, Haag J, Borst A. Different receptive fields in axons and dendrites underlie robust coding in motion-sensitive neurons. Nat Neurosci. 2009;12:327–332. doi: 10.1038/nn.2269. [DOI] [PubMed] [Google Scholar]
- Farrow K, Borst A, Haag J. Sharing receptive fields with your neighbors: tuning the vertical system cells to wide field motion. J Neurosci. 2005;25:3985–3993. doi: 10.1523/JNEUROSCI.0168-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frye MA, Dickinson MH. Fly flight: a model for the neural control of complex behavior. Neuron. 2001;32:385–388. doi: 10.1016/s0896-6273(01)00490-1. [DOI] [PubMed] [Google Scholar]
- Gibson JJ. Perception of the visual world. Westport, CT: Greenwood; 1974. [Google Scholar]
- Gronenberg W, Milde JJ, Strausfeld NJ. Oculomotor control in calliphorid flies—organization of descending neurons to neck motor-neurons responding to visual-stimuli. J Comp Neurol. 1995;361:267–284. doi: 10.1002/cne.903610206. [DOI] [PubMed] [Google Scholar]
- Haag J, Borst A. Orientation tuning of motion-sensitive neurons shaped by vertical-horizontal network interactions. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2003;189:363–370. doi: 10.1007/s00359-003-0410-6. [DOI] [PubMed] [Google Scholar]
- Haag J, Borst A. Neural mechanism underlying complex receptive field properties of motion-sensitive interneurons. Nat Neurosci. 2004;7:628–634. doi: 10.1038/nn1245. [DOI] [PubMed] [Google Scholar]
- Haag J, Borst A. Reciprocal inhibitory connections within a neural network for rotational optic-flow processing. Front Neurosci. 2007;1:111–121. doi: 10.3389/neuro.01.1.1.008.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haag J, Egelhaaf M, Borst A. Dendritic integration of motion information in visual interneurons of the blowfly. Neurosci Lett. 1992;140:173–176. doi: 10.1016/0304-3940(92)90095-o. [DOI] [PubMed] [Google Scholar]
- Haag J, Vermeulen A, Borst A. The intrinsic electrophysiological characteristics of fly lobula plate tangential cells. III. Visual response properties. J Computat Neurosci. 1999;7:213–234. doi: 10.1023/a:1008950515719. [DOI] [PubMed] [Google Scholar]
- Haag J, Denk W, Borst A. Fly motion vision is based on Reichardt detectors regardless of the signal-to-noise ratio. Proc Natl Acad Sci U S A. 2004;101:16333–16338. doi: 10.1073/pnas.0407368101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haag J, Wertz A, Borst A. Integration of lobula plate output signals by DNOVS1, an identified premotor descending neuron. J Neurosci. 2007;27:1992–2000. doi: 10.1523/JNEUROSCI.4393-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hausen K. Motion sensitive interneurons in the optomotor system of the fly. I. The horizontal cells: structure and signals. Biol Cybern. 1982;45:143–156. [Google Scholar]
- Hausen K, Egelhaaf M. Neural mechanisms of visual course control in insects. In: Stavenga DG, Hardie RC, editors. Facets of vision. Berlin: Springer; 1989. pp. 391–424. [Google Scholar]
- Hengstenberg R, Hausen K, Hengstenberg B. The number and structure of giant vertical cells (VS) in the lobula plate of the blowfly Calliphora erythrocephala. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1982;149:163–177. [Google Scholar]
- Huston SJ, Krapp HG. Visuomotor transformation in the fly gaze stabilization system. PLoS Biology. 2008;6:e173. doi: 10.1371/journal.pbio.0060173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joesch M, Plett J, Borst A, Reiff DF. Response properties of motion-sensitive visual interneurons in the lobula plate of Drosophila melanogaster. Curr Biol. 2008;18:368–374. doi: 10.1016/j.cub.2008.02.022. [DOI] [PubMed] [Google Scholar]
- Karmeier K, Krapp HG, Egelhaaf M. Population coding of self-motion: applying Bayesian analysis to a population of visual interneurons in the fly. J Neurophysiol. 2005;94:2182–2194. doi: 10.1152/jn.00278.2005. [DOI] [PubMed] [Google Scholar]
- Karmeier K, van Hateren JH, Kern R, Egelhaaf M. Encoding of naturalistic optic flow by a population of blowfly motion-sensitive neurons. J Neurophysiol. 2006;96:1602–1614. doi: 10.1152/jn.00023.2006. [DOI] [PubMed] [Google Scholar]
- Krapp HG. Ocelli. Curr Biol. 2009;19:R435–R437. doi: 10.1016/j.cub.2009.03.034. [DOI] [PubMed] [Google Scholar]
- Krapp HG, Hengstenberg R. Estimation of self-motion by optic flow processing in single visual interneurons. Nature. 1996;384:463–466. doi: 10.1038/384463a0. [DOI] [PubMed] [Google Scholar]
- Krapp HG, Hengstenberg B, Hengstenberg R. Dendritic structure and receptive-field organization of optic flow processing interneurons in the fly. J Neurophysiol. 1998;79:1902–1917. doi: 10.1152/jn.1998.79.4.1902. [DOI] [PubMed] [Google Scholar]
- Land MF, Eckert H. Maps of the acute zones of fly eyes. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1985;156:525–538. [Google Scholar]
- Milde JJ, Seyan HS, Strausfeld NJ. The neck motor system of the fly Calliphora erythrocephala. 2. Sensory organization. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1987;160:225–238. [Google Scholar]
- Mronz M, Lehmann FO. The free-flight response of Drosophila to motion of the visual environment. J Exp Biol. 2008;211:2026–2045. doi: 10.1242/jeb.008268. [DOI] [PubMed] [Google Scholar]
- Nordström K, Barnett PD, Moyer de Miguel IM, Brinkworth RSA, O'Carroll DC. Sexual dimorphism in the hoverfly motion vision pathway. Curr Biol. 2008;18:661–667. doi: 10.1016/j.cub.2008.03.061. [DOI] [PubMed] [Google Scholar]
- Parsons MM, Krapp HG, Laughlin SB. A motion-sensitive neuron responds to signals from the two visual systems of the blowfly, the compound eyes and ocelli. J Exp Biol. 2006;209:4464–4474. doi: 10.1242/jeb.02560. [DOI] [PubMed] [Google Scholar]
- Pierantoni R. A look into the cock-pit of the fly. Cell Tissue Res. 1976;171:101–122. doi: 10.1007/BF00219703. [DOI] [PubMed] [Google Scholar]
- Reichardt W. Evaluation of optical motion information by movement detectors. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1987;161:533–547. doi: 10.1007/BF00603660. [DOI] [PubMed] [Google Scholar]
- Reiser MB, Dickinson MH. A modular display system for insect behavioral neuroscience. J Neurosci Methods. 2008;167:127–139. doi: 10.1016/j.jneumeth.2007.07.019. [DOI] [PubMed] [Google Scholar]
- Schilstra C, van Hateren JH. Stabilizing gaze in flying blowflies. Nature. 1998;395:654. doi: 10.1038/27114. [DOI] [PubMed] [Google Scholar]
- Single S, Borst A. Dendritic integration and its role in computing image velocity. Science. 1998;281:1848–1850. doi: 10.1126/science.281.5384.1848. [DOI] [PubMed] [Google Scholar]
- Srinivasan MV, Zhang S. Visual motor computations in insects. Annu Rev Neurosci. 2004;27:679–696. doi: 10.1146/annurev.neuro.27.070203.144343. [DOI] [PubMed] [Google Scholar]
- Stange G. The ocellar component of flight equilibrium control in dragonflies. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1981;141:335–347. [Google Scholar]
- Strausfeld NJ, Bassemir UK. Lobula plate and ocellar interneurons converge onto a cluster of descending neurons leading to neck and leg motor neuropil in Calliphora erythrocephala. Cell Tissue Res. 1985a;240:617–640. [Google Scholar]
- Strausfeld NJ, Bassemir UK. The organisation of giant horizontal-motion-sensitive neurons and their synaptic relationships in the lateral deutocerebrum of Calliphora erythrocephala and Musca domestica. Cell Tissue Res. 1985b;242:531–550. [Google Scholar]
- Strausfeld NJ, Seyan HS, Milde JJ. The neck motor system of the fly Calliphora erythrocephala. 1. Muscles and motor neurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1987;160:205–224. [Google Scholar]
- Taylor CP. Contribution of compound eyes and ocelli to steering of locusts in flight: I. Behavioural analysis. J Exp Biol. 1981;93:1–18. [Google Scholar]
- van Hateren JH, Schilstra C. Blowfly flight and optic flow. II. Head movements during flight. J Exp Biol. 1999;202:1491–1500. doi: 10.1242/jeb.202.11.1491. [DOI] [PubMed] [Google Scholar]
- van Hateren JH, van der Schaaf A. Independent component filters of natural images compared with simple cells in primary visual cortex. Proc Biol Sci. 1998;265:359–366. doi: 10.1098/rspb.1998.0303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Kleef J, Berry R, Stange G. Directional selectivity in the simple eye of an insect. J Neurosci. 2008;28:2845–2855. doi: 10.1523/JNEUROSCI.5556-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren WH, Jr, Kay BA, Zosh WD, Duchon AP, Sahuc S. Optic flow is used to control human walking. Nat Neurosci. 2001;4:213–216. doi: 10.1038/84054. [DOI] [PubMed] [Google Scholar]
- Weber F, Eichner H, Cuntz H, Borst A. Eigenanalysis of a neural network for optic flow processing. New J Phys. 2008;10 015013. [Google Scholar]
- Wertz A, Borst A, Haag J. Nonlinear integration of binocular optic flow by DNOVS2, a descending neuron of the fly. J Neurosci. 2008;28:3131–3140. doi: 10.1523/JNEUROSCI.5460-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]