Abstract
Although information in tactile afferent neurons represented by firing rates has been studied extensively over nearly a century, recent studies suggest that precise spike timing might be more important than firing rates. Here, we used information theory to compare the information content in the discharges of 92 tactile afferents distributed over the entire terminal segment of the fingertip when it was contacted by surfaces with different curvatures and force directions representative of everyday manipulations. Estimates of the information content with regard to curvature and force direction based on the precise timing of spikes were at least 2.2 times and 1.6 times, respectively, larger than that of spike counts during a 125 ms period of force increase. Moreover, the information regarding force direction based on the timing of the very first elicited spike was comparable with that provided by spike counts and more than twice as large with respect to object shape. For all encoding schemes, afferents terminating close to the stimulation site tended to convey more information about surface curvature than more remote afferents that tended to convey more information about force direction. Finally, coding schemes based on spike timing and spike counts overall contributed mostly independent information. We conclude that information about tactile stimuli in timing of spikes in primary afferents, even if limited to the first spikes, surpasses that contained in firing rates and that these measures of afferents' responses might capture different aspects of the stimulus.
Introduction
Following Adrian's discoveries in the 1920s (Adrian, 1928), most studies concerning encoding of information in sensory systems have assumed that neurons transmit information by their firing rates. Research in the past decade, however, has convincingly demonstrated that information in the precise timing of individual spikes in sensory pathways can carry more information than firing rates alone (Heil, 2004; VanRullen et al., 2005). The significance of first spikes, in particular, has been emphasized for central processes in auditory (Furukawa et al., 2000), visual (Gawne et al., 1996; Reich et al., 2001, Gollisch and Meister, 2008), and somatosensory (Panzeri et al., 2001; Petersen et al., 2001, 2002) systems. Despite this, most studies on the encoding of information in peripheral tactile afferents have focused on firing rates in individual neurons estimated from spike counts within a defined period (for review, see Darian-Smith, 1984; Torebjörk et al., 1987; Sathian et al., 1989; Johnson and Hsiao, 1992; Craig and Rollman, 1999; Johnson et al., 2000; Goodwin and Wheat, 2004). Recent findings in humans suggest, however, that information about complex mechanical fingertip events are conveyed by the relative timing of impulses in individual members of ensembles of afferents and that this code can operate fast enough to account for the use of tactile signals in natural manipulation tasks (Johansson and Birznieks, 2004). Specifically, the relative timing of the first spikes elicited when objects are contacted provides information about the shape of the contacted surface as well as force direction. That is, changes in either stimulus parameter can differentially alter the latency of the first spike of individual afferents with little systematic effects on the distribution of first-spike latencies within the population as a whole.
Although information about curvature of objects contacted by the human fingertip and the direction of the contact force can be conveyed both by firing rates assessed by spike counts (Goodwin et al., 1997; Birznieks et al., 2001; Jenmalm et al., 2003), and precise timing of spikes in populations of tactile afferents (Johansson and Birznieks, 2004), it is unclear how these two coding schemes compare regarding the amount of information conveyed. A related question is whether spike counts and spike timing transmit the same (redundant) or complementary (independent) information and whether additional information is carried jointly by both codes (synergistic information) (Mikula and Niebur, 2005; Nelken et al., 2005). Finally, little is known about whether information about fingertip stimuli conveyed by different coding schemes depends on the position where the afferent terminates in the fingertip in relation to the stimulation site. In the present study, we addressed these issues by using information-theoretic measures to compare information transmitted in individual afferents by spike counts and spike timing, with emphasis on first spikes.
Materials and Methods
Neural data were recorded from 33 healthy human volunteers (19–30 years of age) following written informed consent in accordance with the Declaration of Helsinki. Previous reports describe in detail the experimental procedure and the apparatus (Birznieks et al., 2001; Jenmalm et al., 2003). Briefly, impulses in single tactile afferents that terminated in the distal segment of the index, long or ring finger were recorded with tungsten needle electrodes (Vallbo and Hagbarth, 1968) inserted into the median nerve ∼10 cm proximal to the elbow (Fig. 1A, right). For each afferent, we used calibrated nylon filaments (“von Frey hairs”) to delineate its cutaneous receptive field from which a response could be elicited by a force four times the afferent's threshold force (Johansson and Vallbo, 1980). To represent the location where the afferent terminated in the skin, we used the center of the receptive field defined as the intersection of its minor and major axes. To pool data from different digits in different subjects, all data related to the location of the stimulation site and the locations of the afferents' receptive fields were overlaid on a generic distal phalanx as described previously (Birznieks et al., 2001).
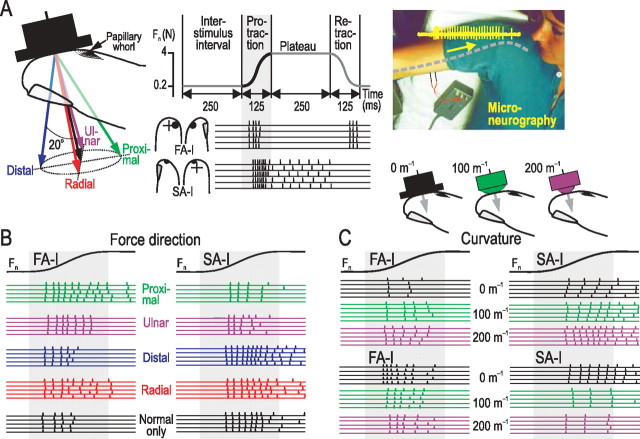
Figure 1.
Responses to fingertip force direction and contact surface shape by human tactile afferents under conditions representative for object manipulation tasks. A, The fingertip was stimulated with objects of different surface curvature (bottom right) in five different directions (left). The time course of force application, illustrated with the normal force component, is shown in the middle panel. Responses from an FA-I and an SA-I afferent to repeated stimuli with normal force only (n = 5) are displayed below. Microneurographic recordings were obtained from the median nerve (right). B, Impulse ensembles in an FA-I and an SA-I afferent to repeated force stimuli (n = 5) applied in different directions (color coded). C, Impulse ensembles in two FA-I and two SA-I afferents to repeated stimuli (n = 5) with normal forces applied with a flat surface and with two spherically curved surfaces (5 and 10 mm radius).
The afferents were classified as fast-adapting type I (FA-I), fast-adapting type II (FA-II), slowly adapting type I (SA-I), and slowly adapting type II (SA-II), according to criteria described previously (Johansson and Vallbo, 1983; Vallbo and Johansson, 1984). Briefly, FA afferents respond only to changes in skin deformation, whereas the SA afferents show an ongoing response during periods of static skin deformation (Fig. 1A, middle). The type I afferents (FA-I and SA-I), which the present study focuses on (see below), possess small and well delineated receptive fields if defined by light pointed skin indentations, whereas the receptive fields of the type II afferents (FA-II and SA-II) are often large and poorly defined (for further details, see Vallbo and Johansson, 1984).
Stimulation protocol.
Regardless of the termination of the afferents in the fingertip, the primary site of contact between the stimulation surface and the receptor-bearing finger was the midpoint of a line extending in the proximal–distal direction from the whorl of the papillary ridges to the distal end of the fingertip (Fig. 1A, left). Using a custom-built computer-controlled manipulator (Birznieks et al., 2001), force stimuli were superimposed on 0.2 Newton (N) background force normal to the skin at this site and consisted of a force protraction phase (125 ms), a plateau phase at 4 N normal force (250 ms), and a force retraction phase (125 ms) (Fig. 1A, middle). The time courses of the force changes followed a half-sinusoid. The interval between successive stimuli was 250 ms. Four of the five force directions included a tangential force component orthogonal to the normal axis in the radial, distal, ulnar, and proximal direction, respectively, and resulted in a force angle of 20° relative to the normal (Fig. 1A, left).
Thus, in trials with a tangential force component, the tangential force (equivalent to the load force in object manipulation task) was 1.4 N at the end of the force protraction phase, and the normal force (equivalent to the grip force) was 4 N. The magnitudes, directions, and time courses of the fingertip forces were similar to those used by subjects using a precision grip to lift an object weighing ∼280 g (Johansson and Westling, 1984; Westling and Johansson, 1984). A stimulation sequence consisted of 50 force stimuli, 10 in each of the five force directions, and stimuli with different force directions followed each other both in a fixed order and in a pseudorandom order [for details, see the “regular” and the “irregular” sequences in Birznieks et al. (2001)]. Such sequences were applied with each of three different stimulus surfaces (Fig. 1A, bottom right). One was flat (curvature 0 m−1), and the other two were spherically convex with radii of 10 and 5 mm (corresponding to curvatures of 100 and 200 m−1), respectively. These curvatures were considered representative for most objects that we grasp, lift, and further manipulate in natural tasks, i.e., objects with curvatures of the same order of magnitude as those of the fingertips (Jenmalm et al., 2003). A single stimulation sequence containing trials in the different force directions as described above was delivered with a fixed surface curvature, whereas the curvature was exchanged between sequences (for details, see Jenmalm et al., 2003). Depending on the stability of the recording, 1–3 stimulation sequences were executed with each surface curvature.
Afferent sample.
We analyzed 43 FA-I and 49 SA-I afferents that were included in a sample containing a total of 196 tactile afferents with receptive fields distributed over the entire distal segment of the finger (Birznieks et al., 2001). The density of FA-I and SA-I afferents in the glabrous skin on the inside of the hand on the very tips of the digits is estimated at ∼140 FA-I afferents and ∼70 SA-I afferents per cm2 skin area, whereas that of the SA-II and FA-II afferents is estimated at ∼12 and ∼22 afferents per cm2 skin area, respectively (Johansson and Vallbo, 1979). We focused, however, on the SA-I and FA-I afferents, because they likely provide overall richer information about object shape and direction of contact forces than the SA-II and FA-II afferents, partly attributable to the much higher innervation density in the fingertips (Birznieks et al., 2001; Jenmalm et al., 2003).
To minimize potential bias effects introduced by a low number of stimulations, we required that afferents had been exposed to at least 150 stimulations (corresponding to three stimulation sequences, one with each surface curvature), and we pooled data from trials with all curvatures when we examined information about force direction and from all force directions when information about curvature was examined. Thus, between 30 and 90 trials were available for each force direction and between 50 and 150 for each curvature. We also analyzed the subset of afferents for which >300 trials in total were available (≥2 stimulation sequences × 3 curvatures) to calculate interaction effects (see Results).
Analysis of information content in single afferents.
All our analyses focused on the protraction phase of the force stimuli, i.e., the first 125 ms after the onset of the force increase. This time window included most spikes of the FA-I afferents elicited by the stimuli, since the FA-I afferents principally responded to the deformation changes of the fingertip (see FA-I in middle panel of Fig. 1A). Because of their sensitivity to static skin deformations, the SA-I afferents could also fire during the plateau phase of the force stimulations but at lower rates than during the force protraction phase (see SA-I in middle panel of Fig. 1A). Figure 1B shows examples of responses in one FA-I and SA-I afferent to stimuli in the five force directions with the flat contact surface, whereas Figure 1C shows examples of responses in two FA-I and two SA-I afferent to normal force stimuli with the each of the three surface shapes. As previously shown, the number of impulses elicited during the protraction phase was related to both shape and force direction (Birznieks et al., 2001; Jenmalm et al., 2003). Moreover, the timing of spikes in ensembles of afferents of each type also changed depending on both shape and force direction (Johansson and Birznieks, 2004). Changes in either of these parameters could differentially influence both the spike counts and the spike timing among afferents without having significant effects on the distribution of these response measures within the afferents populations as a whole (Johansson and Birznieks, 2004). The first spikes elicited by the force stimuli could pass the recording electrode as soon as ∼35 ms after stimulus onset, but many afferents responded later; the overall mean of first-spike latencies across afferents and stimulation conditions was 55 ms [for distributions of latencies of the first and second spike, see Johansson and Birznieks (2004), their Figs. 3 and 4]. Several factors contributed to the delay between the onset of the stimulation and the appearance of the action potentials at the recording electrode and to the variation of the first-spike latencies between afferents. These include nerve conduction delays, which vary across afferents (Johansson and Vallbo, 1983; Kakuda, 1992) and the afferents' threshold sensitivity to the force stimulation, which also varies across afferents, combined with the fact that the force initially increased very slowly because of the sinusoidal waveform of the stimulus.
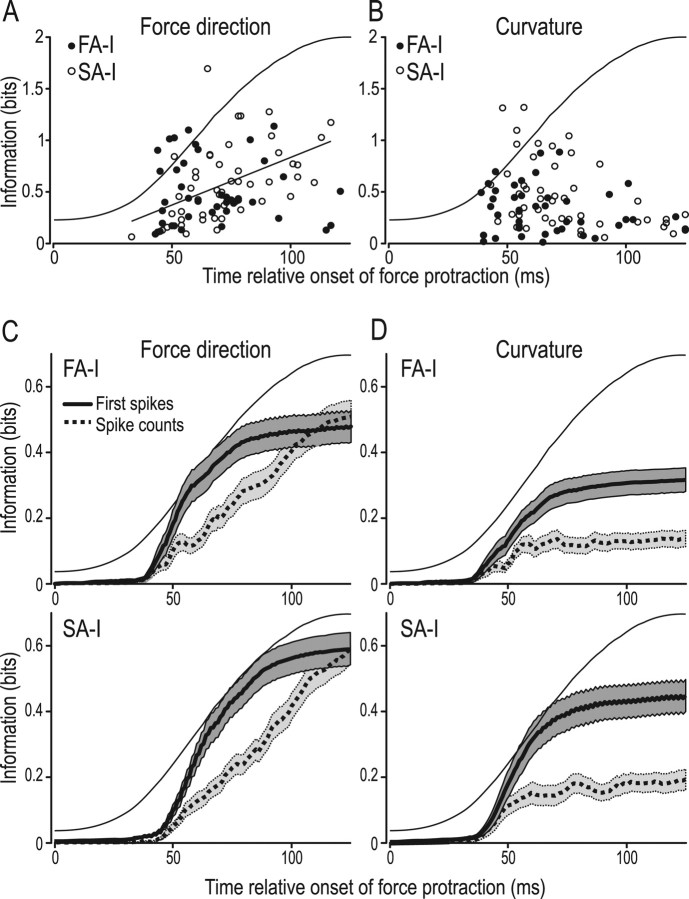
Figure 3.
Information (bits) in FA-I and SA-I afferents about force direction and curvature provided by spike counts and by timing of individual spikes. A, B, Information in timing of first spikes of individual FA-I and SA-I afferents about force direction and surface curvature plotted against the time when maximum information was reached during the protraction phase. As such, this time does not reflect the latency of the very first spike, as this varied with stimulation condition, but rather the amount of time necessary for an afferent to achieve optimal discrimination between different stimulation conditions. Each symbol refers to data from an individual afferent, and the linear regression line in A indicates a significant correlation for SA-I afferents. C, D, Increase in information about force direction and surface curvature, respectively, as a function of time during the force protraction phase estimated from spike counts and from timing of first spikes. Data averaged across all afferents of each type. Shaded areas correspond to ±1 SEM value given by the solid line. A–D, Thin solid line denotes the profile of the normal force increase during the force protraction phase.
Figure 4.
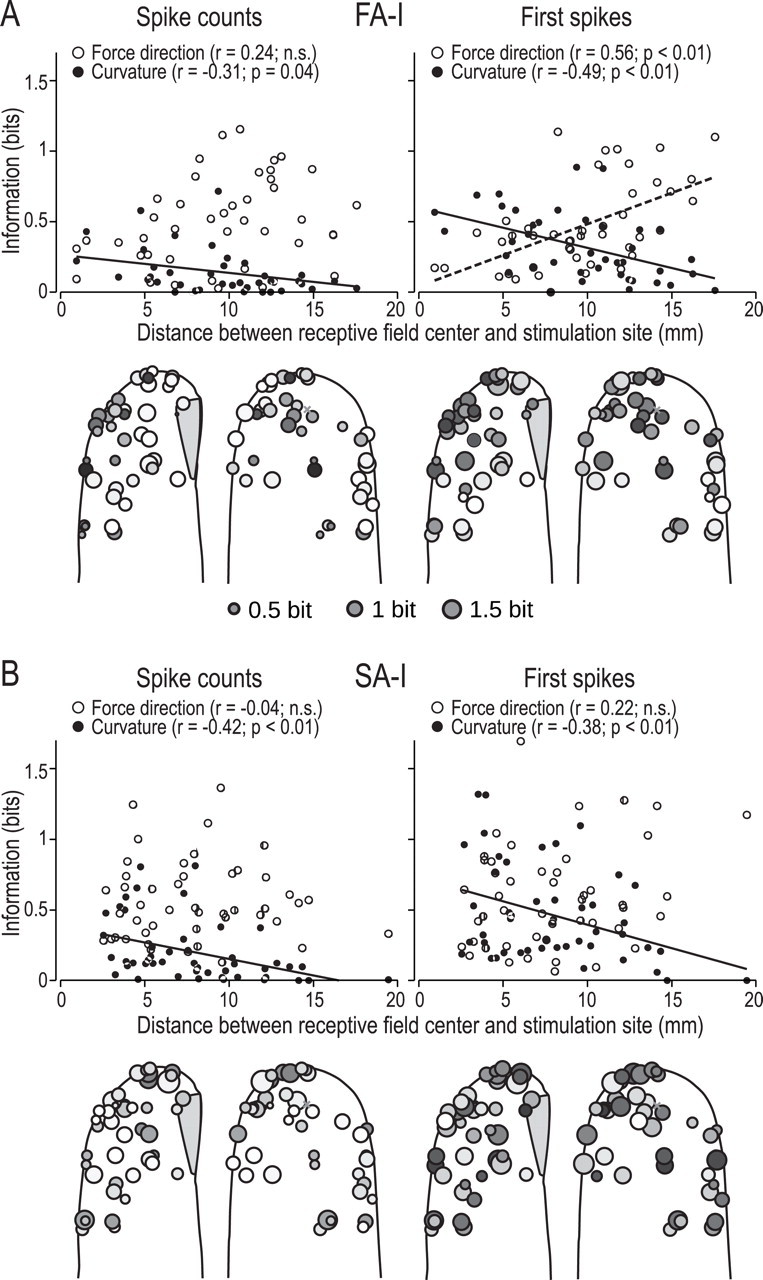
Information (bits) about force direction and surface curvature for individual FA-I afferents (A) and SA-I afferents (B) plotted as a function of distance from the stimulation site. The scatter diagrams show for each afferent the amount of information conveyed as a function of the distance between the center of the afferent's receptive field and the primary site contact. White and black dots represent information about force direction and curvature, respectively. Significant correlations are indicated by dashed (direction) or solid (curvature) regression lines. Each circle on the contours of the generic fingertip represents a single afferent, and the center of the circle corresponds to the position of the center of the afferent's cutaneous receptive field. The side view of the fingertip includes afferents located on either side of the finger. The area of a circle is proportional to the amount of information that is transmitted by the afferent, and the color reflects the stimulus parameter this information relates to, with black standing for only curvature, white for only force direction. Gray values arise when the afferent transmits information about both features with the exact level depending on the contribution of each tactile feature to the overall information. Note that in general, afferents closer to the stimulation site tend to contain more information about curvature, whereas afferents farther away might contain more information about force direction. However, the overall amount of information transmitted does not depend much on the distance of the afferent from the stimulation site. The gray cross on the contour of the generic fingertip indicates the location of the volar point where the stimulus first contacted averaged over all trials.
Mutual information is a measure of how much information one random variable contains about another random variable. In the present study, we asked how much mutual information I(R; S) about the stimulus (either curvature of the contact surface or the force direction) was contained in the responses of single tactile afferents. We calculated the mutual information I(R; S) in the afferent responses as follows (Panzeri et al., 2007):
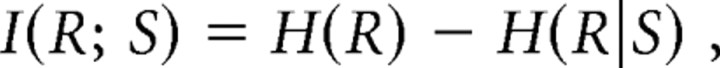 |
where H(R) is the entropy of the response as assessed from the response variability across all stimuli and represents the overall information contained in the neural response. H(R|S) is the conditional entropy of the response given the stimulus and represents in this context entropy attributable to noise in the system, i.e., information in the afferent signal that is not about the nominal stimulus parameter but may include information about the stimulus not accounted for by the model used (see Discussion). The entropy terms were calculated as follows:
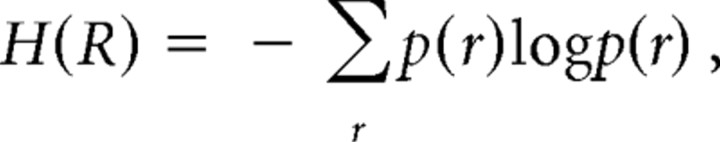 |
where p(r) is the probability that a given response r is recorded from the afferent, and
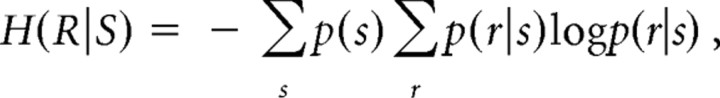 |
where p(r|s) is the conditional probability that the stimulus s elicits the response r, and p(s) is the probability that stimulus s occurs. The latter probability was defined by the stimulation protocol, where p(s) followed a uniform distribution. The probability distribution of the response given the data p(r|s) and the marginal probability of the data p(r) was estimated from the data. Binning procedures were used to discretize continuous response measures. As detailed further below, throughout our analyses we estimated and corrected for bias in our estimates of mutual information potentially resulting from limited amount of data, and we used techniques to calculate lower bounds on the information.
Information in spike counts.
We assessed mutual information about the stimulus parameters (force direction and surface curvature) by counting the number of spikes recorded from a single afferent during the force protraction phases (125 ms fixed window). Because this number ranged from 0 to 12 (mean, 2.2; median, 2) and from 0 to 13 (2.6; 2) among stimulation for the FA-I and SA-I afferents, respectively, the corresponding sizes of the response space was 13 and 14. Since sparse data can lead to an upward bias of estimates of mutual information, this estimate was corrected by subtracting the bias, B, estimated as follows (Panzeri and Treves, 1996):
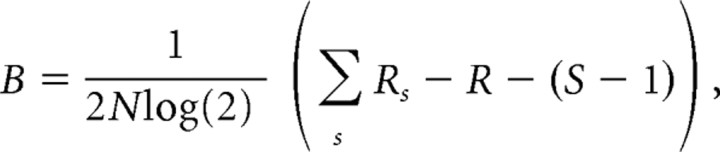 |
where N is the sample size (all stimuli delivered), R is the size of the response space that was not empty, Rs is the number of response bins that were not empty conditioned on the stimulus, and S is the number of different stimuli. This estimate of bias is considered correct provided that the number of trials for each stimulus condition is larger than the number of possible distinct responses, i.e., the size of the response space (Panzeri and Schultz, 2001). This condition was fulfilled in the present study. In addition, we assessed the validity of our bias-compensation methods by estimating the parameters of a Markov model of spike generation (cf. Montemurro et al., 2007) applied to signals in 10 FA-I and 12 SA-I afferents for which >300 trials were available. Generation of spike trains from these models and calculations of the remaining bias for sample sizes representative for afferents with the least data indicated negligible differences (<0.01 bit for both afferent types and for both stimulus parameters).
Information in precise timing of spikes.
We used the metric-space method (Victor and Purpura, 1996, 1997) to estimate mutual information contained in the precise timing of all spikes elicited during the force protraction phase. Because of the potentially large response space, use of the “direct method” used for spike counts might have resulted in large biases (Panzeri et al., 2007). The metric-space method calculates a lower bound of the mutual information and permits assessment of the temporal precision by which spike timing can contribute to stimulus classification. The method provides a measure of difference, or distance, between spike trains that reflects the minimal cost associated with transforming one spike train into the other. Single spikes are inserted and deleted at a cost of unity, and shifting a spike in time incurs a certain cost q per unit of time.
For each afferent, we first computed the distance between each spike train recorded and every other spike train. We then computed the average distances between every given spike train r and all other spike trains r′ belonging to a certain stimulus condition s (i.e., surface curvature or force direction) as follows:
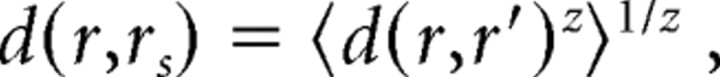 |
where d(r, r′) indicates the distance between spike trains r and r′, angle brackets denote the average with respect to all r observed under condition s, and z, set to −2 in this study, refers to the contribution of outliers to the average distance. A lower bound of the mutual information was then computed from a confusion matrix that indicated the condition from which a spike train originated and the condition it was most similar to, assessed by the average distance computed as described above. To estimate the bias of the estimate of the mutual information, we reassigned spike trains to random conditions and computed the mutual information with the metric space method. The bias term used was the average of the outcome of 20 such operations.
By varying the cost parameter q, we assessed the temporal resolution required for obtaining maximum mutual information for each afferent and stimulation condition. We used eight different q values that ranged from 8 to 1024, derived from powers of 2. This corresponds to a temporal precision ranging from a 125 ms window up to a 1 ms window. In Results, we report on mutual information obtained using an optimum temporal resolution for each afferent. To cross-validate the outcomes of the metric space method and direct method used with spike counts, we also computed mutual information at q = 0, where the cost of moving spikes in time is zero and the distance between two spike trains is just the difference in spike counts. It was found that both methods provided consistent results: Of the 43 FA-I afferents analyzed, the information about force direction and curvature estimated by the metric-space analysis exceeded that computed from spike counting in only two and four afferents, respectively. The corresponding numbers for the 49 SA-I analyzed were one afferent and three afferents, respectively.
Information in first spikes.
To assess the mutual information contained in the timing of the first spikes in individual afferents, we divided the force protraction phase into 2 ms consecutive bins and allocated the first spike elicited by each stimulus into the appropriate bin. From these data, we calculated the mutual information using the direct method as with spike counts. We chose 2 ms bins, because this bin size approximately matched the temporal resolution for maximal information as estimated by the metric space method when applied to the first spikes only. Furthermore, for nearly all afferents, the variability in the timing of first spikes across all stimulus conditions was contained within a 30 ms window (Johansson and Birznieks, 2004), which resulted in similar sizes of the response space as used with spike counts. Indeed, control analyses showed that the mutual information computed with an appropriately positioned 30 ms window matched that obtained with the procedure we used. That is, the remaining bias, computed as described for spike counts, was negligible (<0.02 bit for FA-I afferents and <0.01 bits for SA-I afferents).
Redundant and synergistic information contained in spike counts and first-spike latencies.
To assess if information transmitted by firing rates and spike timing is redundant, independent, or synergistic, we compared information available when both decoding schemes were used simultaneously with that contained in timing of first spikes and in spike counts independently according to the following equation:
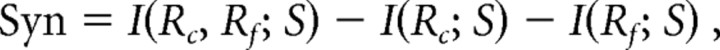 |
where I(Rc, Rf; S) represents the joint mutual information between the stimulus and both coding schemes [spike counts (c) and first-spike latencies (f)], and I(Rc; S) and I(Rf; S) stand for the mutual information about the stimulus with spike counts and first-spike latencies, respectively. Positive values of Syn indicate presence of synergistic information, where information contained in the two coding schemes jointly exceeds the sum of the information contained in each coding scheme if considered independently. Accordingly, negative values of Syn indicate that the two coding schemes provide redundant information. A value of zero means that both coding schemes contribute information independently. To minimize potential bias in the estimates of Syn related to the small sample sizes, we computed the joint information by using the recently introduced shuffling method (Montemurro et al., 2007; Panzeri et al., 2007). In addition, to correct for confounding effects attributable to the low number of different stimuli used, we also compared the distribution of Syn based on the original data with a distribution generated under the assumption of independence between spike counts and latencies, where spike counts and latencies were randomly reassigned across afferents.
Results
The Results are divided into four sections: First, we compare the mutual information between stimulus and response estimated from the number of spikes elicited during the protraction phase of the force stimuli and from the precise timing of all spikes elicited during the same 125 ms epoch. Second, we compare information in spike counts with that contained in the timing of the first spikes elicited by the force stimuli. Next, for each coding scheme, we examine how information about the direction of contact force and the curvature of the contact surface in single afferents might depend on where they terminate in the fingertip skin relative to the site of stimulation. Finally, we analyze to which degree first spikes and spike counts may convey redundant, independent, or synergistic information about the stimuli.
Information provided by spike times versus spike counts
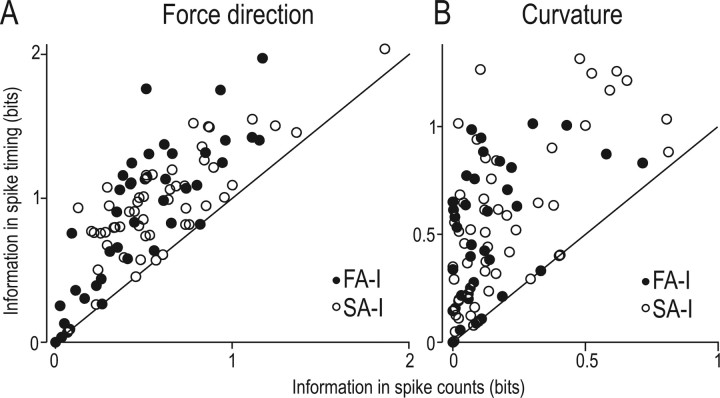
As expected, the information obtained from the timing of all spikes appeared substantially greater than that obtained from spike counts. This applied to both FA-I and SA-I afferents and to information about both force direction (Fig. 2A) and surface curvature (Fig. 2B). In order not to introduce any bias attributable to low sample sizes into our estimates of the mutual information, we calculated a lower bound on the information in spike timing and compared this lower bound with a direct estimate of the information in spike counts. On average, the estimated information content for individual FA-I afferents was 0.51 ± 0.33 bits (mean ± 1 SD) for force direction as assessed by spike counts and 0.92 ± 0.52 bits (lower bound) if spike timing was taken into account. The corresponding data for the SA-I afferents were 0.60 ± 0.33 bits for spike counts and 0.96 ± 0.32 bits as the lower bound for spike timing. Thus, considering spike timing provided an average information gain of at least 0.41 bits (80%) for the FA-I afferents and 0.36 bits (60%) for the SA-I afferents compared with spike counts. For surface curvature, spike timing conveyed information of on average 0.33 bits and 0.38 bits (lower bounds) for the FA-Is and the SA-Is, respectively, which corresponded to 236% and 200% of the information about curvature in spike counts (0.14 ± 0.16 bits for the FA-I and 0.19 ± 0.22 bits for the SA-I afferents). According to a two-way ANOVA, there was a significant effect of spike count versus temporal coding (F(1,181) >47.04; p < 0.001 in both cases) but not between different afferent types (F(1,181) <3.73; p > 0.05).
Figure 2.
Information provided in the responses of FA-I (filled) and SA-I (open circles) afferents about force direction (A) and curvature of surface contacting the fingertip (B). Information (bits) in spike counts plotted against maximal information in spike timing, and each symbol refers to data from an individual afferent. Points on the diagonal line indicate that spike count information and temporal information are equal.
We were also interested in the temporal resolution at which information was encoded in tactile afferents. We found that the median temporal resolution at which afferents transmitted maximal information was 16 ms, and a two-way mixed design ANOVA failed to indicate an effect on this for both afferent type (FA-I, SA-I; p = 0.53) and stimulus feature (curvature and force direction; p = 0.24; treated as repeated measures). However, we noted a marked variability among afferents; the lower and upper quartiles for the FA-Is were 32 and 8 ms and those of the SA-Is were 64 and 8 ms. Analytically imposed changes in temporal resolution from the optimum value generally resulted in fairly small effects on the information estimates. Different spikes within single spike trains may, however, contain information at different temporal resolutions (see analysis of first spikes, below).
Based on a lower bound on the mutual information for spike timing, we conclude that the tactile afferents examined (FA-I and SA-I), on average, convey at least 60% more information about force direction and 100% more information about surface curvature than spike counts do.
Information content in the timing of first spikes versus spike counts
The information about force direction provided by timing of the first spikes, regardless of when they occurred during the force protraction period, was 0.48 ± 0.32 bits (mean ± 1 SD) for the FA-Is and 0.59 ± 0.36 bits for the SA-Is. The corresponding numbers for surface curvature were 0.32 ± 0.23 bits and 0.45 ± 0.34 bits. The estimate of the information conveyed by the first spikes in the two types of afferents did not differ significantly regarding force direction (p = 0.13; two-sample Kolmogorov–Smirnov test) but did so for surface curvature (p = 0.04). We observed no simple relationship between the time during the protraction phase when an individual afferent reached maximum information and the information conveyed by the first spike (Fig. 3A,B). Tests of correlations between the amount of information in the first spikes and this time indicated significance only for force direction in the SA-I afferents (r = 0.48; p < 0.001). The amount of information was smaller for afferents reaching maximum information early compared with late (Fig. 3A). Afferents that transmitted a large amount of information in their first spikes also tended to transmit high information in their firing rates. In other words, with each stimulation parameter (force direction and curvature) and for both afferent types (FA-I and SA-I), there was a significant positive correlation across afferents between information contained in spike counts and in first-spike latencies (p < 0.002 in all four instances). For the FA-I afferents, the correlation coefficient was 0.50 for force direction and 0.58 for curvature. The corresponding values were 0.55 and 0.45 for the SA-I afferents.
We analyzed when information about force direction and curvature gradually became available in spike counts and in the timing of the first spike during the progression of the force protraction phase: we computed the information contained in the two encoding schemes during a series of time windows that all begun at the onset of the force protraction phase and had durations that increased stepwise by 1 ms from zero to 125 ms. For each window, we averaged information across all afferents in our sample regardless of whether they had responded or not. Before an afferent responded (in any of the trials recorded), the transmitted information was considered to be zero. Figure 3, C and D, plots information about force direction and curvature provided up to the time of the end of each window (abscissa value). Overall, the timing of the first spikes conveyed more information than spike counts during the force protraction phase. For surface curvature (Fig. 3D), the first spike contained about twice as much information as spike counts even at the end of the protraction phase for both the FA-I afferents (229%; p < 0.001) and the SA-I afferents (237%; p < 0.001). With force direction, the information contained in spike counts matched that in the first spikes at the end of the protraction phase (Fig. 3C) (p = 0.55 and p = 0.90 for FA-I and SA-I afferents, respectively; paired t test). From Figure 3, C and D, it can be seen that the initial increase of information in first-spike latencies and spike counts happens at around the same time. This early information is based on whether an afferent has already fired or not, which was available from both coding schemes.
All analyses concerning afferent information about force direction were based on data pooled across surface curvatures and the analyses concerning surface curvature on data pooled across force directions. To check for interaction effects between force direction and curvature, we compared mutual information calculated with and without pooling data across conditions for a subset of afferents for which a sufficient number of trials was available. We found that pooling decreased the information available for both spike counts and first-spike latencies by approximately the same amount, suggesting that the influence of interaction effects was similar for both coding schemes. For force direction and FA-I afferents (n = 10), on average, the mutual information decreased by 0.13 and 0.18 for spike counts and first-spike latencies (p = 0.38; Wilcoxon signed rank test), respectively. With SA-I afferents (n = 12), the corresponding decreases were 0.24 bits and 0.18 bits (p = 0.42). For curvature and FA-I afferents (n = 14), the information loss was 0.14 bits and 0.22 bits for spike counts and first-spike latencies, respectively (p = 0.09), and for SA-I afferents (n = 15), the loss was 0.24 bits for both coding schemes (p = 0.76).
We conclude that the first spikes provide significant information about our tactile stimuli earlier than spike counts do. Moreover, they appear to provide more than twice the information about curvature present in spike counts over the entire force protraction phase and similar amount of information about force direction as present in spike counts over the entire protraction phase.
Relationship between the termination of the afferent in the fingertip and information contained about the stimulus parameters
It has been suggested that afferents terminating at different locations with reference to the primary site of stimulation on the fingertip might preferentially contribute information about different aspects of tactile stimuli (Bisley et al., 2000; Birznieks et al., 2001; Jenmalm et al., 2003). We examined this issue by looking at the information transmitted about curvature and force direction in timing of first spikes and in spike counts over the entire protraction period. Afferents terminating closer to the primary site of stimulation tended to convey more information about curvature than afferents terminating more remotely. This applied to either coding scheme and to both the FA-I and the SA-I afferents (Fig. 4A,B). Concerning force direction, we found no correlation with distance except in first-spikes latencies of FA-I afferents, which tended to convey more information with greater distance (Fig. 4A). The color of the circles on the contours of the fingertips in Figure 4 illustrates the relative contribution by each afferents to information about surface curvature and force direction, i.e., the circles are filled in grayscale in proportion to the information estimated for curvature (black) and force direction (white), respectively. The area of the circles is proportional to the total information transmitted, computed as the sum of the information about curvature and force direction.
Redundancy/synergy between different coding schemes
We finally addressed the question of whether individual afferents transmit the same (i.e., redundant) or complementary (i.e., independent) information or whether both coding schemes might even jointly carry information (synergistic information which would only be available from both coding schemes together). We did this by calculating a measure of shared information between the two decoding schemes (see Materials and Methods). Positive values of this measure indicate that the two coding schemes contain more information if operating jointly compared with independently, whereas negative values indicate that the coding schemes would provide redundant information. For force direction, this measure was on average −0.07 ± 0.23 and −0.13 ± 0.38 bits for the FA-I and SA-I afferents, respectively (Fig. 5A). The corresponding values for curvature were −0.06 ± 0.16 and −0.09 ± 0.18 bits (Fig. 5A). This means that for FA-I and SA-I afferents, on average, just 8 and 10% of the information about force direction, respectively, represented redundant information. The corresponding values for curvature were 22 and 15%.
Figure 5.
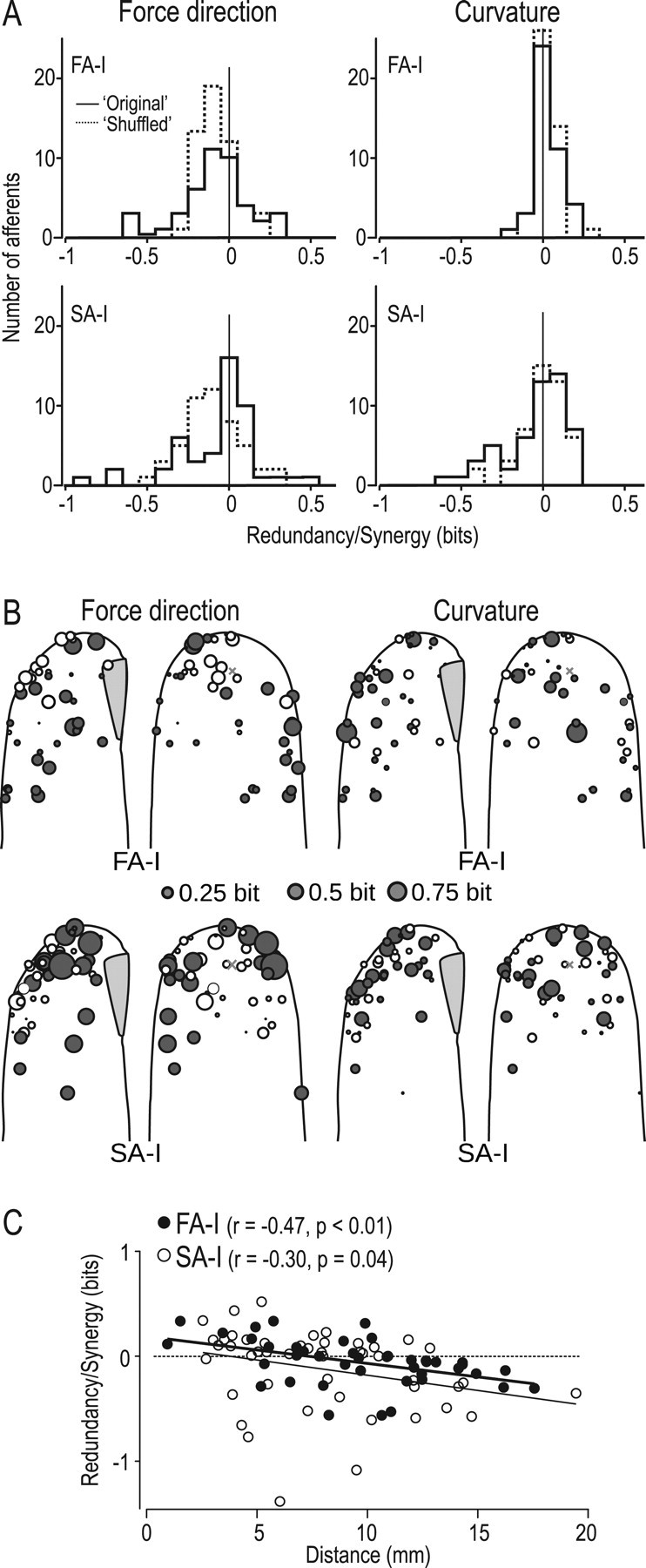
Synergistic versus redundant information between spike counts and first-spike latencies. A, Synergy/redundancy distributions for the original data (solid line) and shuffled data (dotted line) for FA-I (top) and SA-I (bottom) afferents and for force direction (left) and curvature (right). B, Synergy (white circles) and redundancy (gray circles) in individual FA-I (top) and SA-I (bottom) afferents for force direction and surface curvature, respectively, plotted on the contours of the generic fingertip, where the area of the circles corresponds to the total amount of synergy or redundancy. A gray cross denotes stimulus contact point averaged over all trials. C, Synergy/redundancy in the two coding schemes for force direction as a function of distance between the centers of the afferents cutaneous receptive field and the primary site of contact. Each symbol represents data from a single afferent. Positive and negative values imply synergistic and redundant information, respectively, normalized to the information jointly contained in both coding schemes.
Most of the slight redundancy observed above can be explained by noticing that both coding schemes carry information about whether an afferent had fired during a given trial or not. Accounting for this information which necessarily shows up as redundant reduced the observed redundancy by 0.01–0.06 bits, thereby bringing both coding schemes very close to independence.
The synergy measure showed considerable variance across afferents, where the signals in some afferents contained redundant information, whereas others contained synergistic information (Fig. 5A, solid line histograms). For both afferents types, redundancy was more common for force direction than surface curvature. The distances between the afferents' termination in the fingertip and the primary stimulation site explained a small amount of the variance in the synergy measure that concerned force direction. Afferents that terminated close to the stimulation site showed positive synergistic effects between the two encoding schemes, whereas afferents terminating farther away showed a gradual increase in redundancy (Fig. 5B,C). For curvature, there were no reliable relationships in this respect.
Last, we examined whether the variance of the synergy measure might be explained by the fact that the small stimulus sets used (five force detections and three surface curvatures) might have introduced spurious synergy estimates between coding schemes. We compared the synergy measures computed from the recorded neural data with measures computed from a shuffled distribution generated under the assumption that both coding schemes acted independently (see Materials and Methods) (solid and dashed line histograms in Fig. 5A). Two-sample t tests failed to indicate significant differences in the mean values of the synergy measures computed for original and shuffled data (p > 0.36 for force direction and curvature with both afferent types). Moreover, Kolmogorov–Smirnov tests did not find any significant differences between the original and the shuffled distributions (p > 0.40) apart from those for force direction in the SA-I afferents (p = 0.03).
Together, our results suggest that coding of surface curvature and force direction by tactile afferents by spike timing and spike counts contributes principally complementary information.
Discussion
To our knowledge, the present study is the first to employ information theory for assessing information represented in tactile afferents supplying glabrous skin, i.e., body areas that actively contact objects. We found that the information contained in spike timing about the shape of the surfaces contacting the fingertip was at least 2.2 times that conveyed by firing rates, and for fingertip forces, it was ≥1.6 times larger. Moreover, the timing of only the first spikes elicited in tactile afferents by our stimuli appeared to transmit the same amount of information about force direction as was transmitted by firing rates and transmitted considerably more information about object curvature. Furthermore, our results indicate that coding of surface curvature and force direction in tactile afferents by means of spike timing and spike counts overall contribute complementary information. Given that multiple parallel pathways use tactile afferent information, it is possible that different processes and tasks use different codes. For example, relative spike timing may primarily support fast stimulus classification in the control of action. Firing rates, in contrast, might preferentially support perceptual mechanisms that operate under less time pressure.
There are two main concerns which generally arise in information-theoretic studies: First, the selection of an adequate stimulus set, and second, the elimination of bias introduced by small sample sizes. Stimulus parameters were chosen such that they reflected fingertip stimuli that commonly arise during natural object manipulation tasks, but we used only three curvatures and five force directions. We argue, however, that we made a reasonable trade-off between the size of the stimulus set and the number of trials that we could obtain with each type of stimulation given the time limitation for recording signals in single human afferents. We used three methods to ensure that low sample sizes did not affect the validity of our results: First, we used established bias-reduction methods, and we confirmed the effectiveness of these methods in simulation and by cross-validating with alternative methods. This ensured that any potential remaining bias would be considerably smaller than the effect sizes we report. Second, we calculated a reliable lower bound on the mutual information in spike timing and compared this bound with a direct estimation of the information in spike counts. This resulted in a robust lower bound on the effect size. Third, to increase the effective sample size, we pooled data from trials with all curvatures when analyzing information about force direction and vice versa. We verified that pooling did not affect the comparison between different coding schemes (see Results).
Werner and Mountcastle (1965) quantified information about amplitude of skin indentations in spike counts in slowly adapting afferents innervating the hairy skin of the hind legs of cats and monkeys. Both the spike counts and the information transmitted (up to 2 bits) during the initial 100 ms of the stimulation were higher than what we report. This study was, however, designed to maximize the number of spikes elicited per stimulus. To that end, the skin was shaved, and for each afferent, the spot of maximum sensitivity was subjected to pointed skin indentations. In contrast, our approach was to obtain a representative picture of information conveyed in the population of afferents by analyzing information in all responsive afferents while stimuli were delivered to the same site regardless of the location of the afferents' terminals in the skin. Hence, many of the afferents analyzed were just weakly excited. Furthermore, we assessed information about more complex stimulus features that should be harder to discriminate than stimulus intensity (which was kept about constant). Despite that, we found that some afferents could be highly informative (up to 1.4 bits; see Results).
Complementary information in spike counts and first-spike latencies
Although we found a significant positive correlation between information transmitted by precise spike timing and firing rates for both curvature and force direction, the two coding schemes primarily conveyed independent information about both force direction and curvature. As such, these results agree with previous analyses indicating a lack of simple and consistent relationship between spike latencies and firing rate in tactile afferents (Johansson and Birznieks, 2004). Indeed, the complex nonlinear viscoelastic deformation properties of the fingertip caused by its geometry and composite material properties makes the afferent encoding of mechanical fingertip events highly intricate (Birznieks et al., 2001; Jenmalm et al., 2003; Goodwin and Wheat, 2004). Researchers have attempted to model the fingertip mechanically while incorporating its composite material properties with the goal of predicting responses of populations of tactile afferents to arbitrary fingertip stimuli (Srinivasan and Dandekar, 1996; Maeno and Kobayashi, 1998; Maeno et al., 1998, 2004; Serina et al., 1998; Nakazawa et al., 2000; Dandekar et al., 2003; Wu et al., 2003, 2006). However, no model yet possesses the level of realism that satisfies this goal.
The mechanics of the fingertip presumably also accounted for the relationship between information conveyed about object curvature and the distance from the site of stimulation on the fingertip and afferents' termination in the skin. In agreement with observations in monkeys suggesting that SA-I afferents terminating at the sides of the fingertip are less affected by changes in curvature than afferents terminating close to the stimulation site (Bisley et al., 2000), we observed that afferents located close to the primary stimulation site transmitted higher information about object curvature than afferents located farther away in both firing rates and first spikes. Interestingly, we found the opposite relationship for information about force direction conveyed by the first spikes in FA-I afferents, where afferents terminating on the sides and end of the fingertip tended to convey more information about force direction than afferents located close to the stimulation site.
The intricacy of the mechanical properties of the fingertip might also have accounted for the apparent difference between force direction and curvature concerning information contained in spike counts versus first spikes. In addition to the fact that the first spikes conveyed significant information about both stimulus parameters considerably faster than firing rates, the information about force direction in spike counts increased throughout the force protraction period, whereas the amount of information about surface curvature in spike counts saturated comparatively early during the force protraction period. Hence, later spikes appeared to contribute little information about curvature.
The SA-I and FA-I afferents showed overall similar properties regarding information content across the coding schemes. One likely explanation for this similarity is that the force stimulus during the protraction phase followed a time course that could excite both types of afferents with similar efficiency: its frequency content was 4 Hz. A major difference between the FA-I and SA-I systems is their sensitivity, with the FA-Is being most sensitive to relatively high frequencies (∼5–50 Hz) and the SA-Is to lower frequencies content (less than ∼5 Hz) (Johansson et al., 1982).
Relative spike timing in ensembles of afferents offers fast information
Neural mechanisms that support fast reception and processing of sensory information are critical for control of actions. In object manipulation tasks, information about discrete mechanical fingertip events is typically expressed in the control of fingertip actions within ∼100 ms or less (for review, see Johansson and Flanagan, 2008). This requires that significant information is transmitted even when most afferents recruited have only had time to fire one spike; this, in turn, implies that the precise timing of the first impulses elicited in the afferent population convey information, which we conclude to be the case. Since it is improbable that the CNS can predict contact events with millisecond precision in manipulation tasks for decoding of information conveyed in timing of spikes in individual afferents, the relative timing of impulses in ensembles of afferents most probably convey the relevant information (Johansson and Birznieks, 2004). How the CNS can decode such information is not known, but various mechanisms have been proposed (Johansson and Flanagan, 2009).
Neural codes operating on latency differences between pairs of neurons might convey substantially more information than codes focusing on latencies in single neurons alone, if noise is correlated across neurons (Gollisch and Meister, 2008). We could not specifically address this possibility, as our experimental technique was limited to single-cell recordings. However, this assumption seems a very plausible one, as a substantial intertrial variability in tactile afferent responses to the same stimulus is accounted for by nonstationary physiological conditions that globally affect the responsiveness of afferent populations. This includes volume changes of the fingertip with the pulse pressure wave and the respiratory cycle (Westling et al., 1976) and, in particular, changes in viscoelastic properties of the fingertip related to previous tactile stimuli (Pubols, 1982; Birznieks et al., 2001). Because of such correlations, the relative timing of spikes in pairs of tactile afferents is likely to fluctuate less than expected from the noise in individual afferent latencies and, thereby, leading to higher information rates. Thus, based on our analyses and these considerations, it seems suggestive that codes based on the timing of first spikes may provide an explanation for the rapid use of tactile information, as, for example, shown in object-manipulation tasks.
Footnotes
This work was supported by the Sixth Framework Program of the European Union (project IST-028056) and the Swedish Research Council (project 08667). H.P.S. is supported by an Engineering and Physical Sciences Research Council/Medical Research Council scholarship from the Neuroinformatics and Computational Neuroscience Doctoral Training Centre at the University of Edinburgh. S.V. is supported through a Microsoft Research–Royal Academy of Engineering senior research fellowship. We thank G. Westling and L. Bäckström for technical support, A.W. Goodwin, I. Birznieks, and P. Jenmalm for their participation in the original neural experiments, and P. Series for comments on this manuscript.
References
- Adrian ED. New York: W. W. Norton; 1928. The basis of sensation. [Google Scholar]
- Birznieks I, Jenmalm P, Goodwin AW, Johansson RS. Encoding of direction of fingertip forces by human tactile afferents. J Neurosci. 2001;21:8222–8237. doi: 10.1523/JNEUROSCI.21-20-08222.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bisley JW, Goodwin AW, Wheat HE. Slowly adapting type I afferents from the sides and end of the finger respond to stimuli on the center of the fingerpad. J Neurophysiol. 2000;84:57–64. doi: 10.1152/jn.2000.84.1.57. [DOI] [PubMed] [Google Scholar]
- Craig JC, Rollman GB. Somesthesis. Annu Rev Psychol. 1999;50:305–331. doi: 10.1146/annurev.psych.50.1.305. [DOI] [PubMed] [Google Scholar]
- Dandekar K, Raju BI, Srinivasan MA. 3-D finite-element models of human and monkey fingertips to investigate the mechanics of tactile sense. J Biomech Eng. 2003;125:682–691. doi: 10.1115/1.1613673. [DOI] [PubMed] [Google Scholar]
- Darian-Smith I. The sense of touch: performance and peripheral neural processes. In: Brookhart JM, Mountcastle VB, Darian-Smith I, Geiger SR, editors. Handbook of Physiology. Bethesda, MD: American Physiological Society; 1984. pp. 739–788. [Google Scholar]
- Furukawa S, Xu L, Middlebrooks JC. Coding of sound-source location by ensembles of cortical neurons. J Neurosci. 2000;20:1216–1228. doi: 10.1523/JNEUROSCI.20-03-01216.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gawne TJ, Kjaer TW, Richmond BJ. Latency: another potential code for feature binding in striate cortex. J Neurophysiol. 1996;76:1356–1360. doi: 10.1152/jn.1996.76.2.1356. [DOI] [PubMed] [Google Scholar]
- Gollisch T, Meister M. Rapid neural coding in the retina with relative spike latencies. Science. 2008;319:1108–1111. doi: 10.1126/science.1149639. [DOI] [PubMed] [Google Scholar]
- Goodwin AW, Wheat HE. Sensory signals in neural populations underlying tactile perception and manipulation. Annu Rev Neurosci. 2004;27:53–77. doi: 10.1146/annurev.neuro.26.041002.131032. [DOI] [PubMed] [Google Scholar]
- Goodwin AW, Macefield VG, Bisley JW. Encoding of object curvature by tactile afferents from human fingers. J Neurophysiol. 1997;78:2881–2888. doi: 10.1152/jn.1997.78.6.2881. [DOI] [PubMed] [Google Scholar]
- Heil P. First-spike latency of auditory neurons revisited. Curr Opin Neurobiol. 2004;14:461–467. doi: 10.1016/j.conb.2004.07.002. [DOI] [PubMed] [Google Scholar]
- Jenmalm P, Birznieks I, Goodwin AW, Johansson RS. Influences of object shape on responses in human tactile afferents under conditions characteristic for manipulation. Eur J Neurosci. 2003;18:164–176. doi: 10.1046/j.1460-9568.2003.02721.x. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Birznieks I. First spikes in ensembles of human tactile afferents code complex spatial fingertip events. Nat Neurosci. 2004;7:170–1177. doi: 10.1038/nn1177. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Flanagan JR. Tactile sensory control of object manipulation in humans. In: Gardner E, Kaas JH, editors. The senses: a comprehensive reference. Vol 6. San Diego: Academic; 2008. pp. 67–86. Somatosensation. [Google Scholar]
- Johansson RS, Flanagan JR. Coding and use of tactile signals from the fingertips in object manipulation tasks. Nat Rev Neurosci. 2009;10:345–359. doi: 10.1038/nrn2621. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Vallbo AB. Tactile sensibility in the human hand: relative and absolute densities of four types of mechanoreceptive units in glabrous skin. J Physiol. 1979;286:283–300. doi: 10.1113/jphysiol.1979.sp012619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson RS, Landström U, Lundström R. Sensitivity to edges of mechanoreceptive afferent units innervating the glabrous skin of the human hand. Brain Res. 1982;244:27–35. doi: 10.1016/0006-8993(82)90900-3. [DOI] [PubMed] [Google Scholar]
- Johnson KO, Hsiao SS. Neural mechanisms of tactual form and texture perception. Annu Rev Neurosci. 1992;15:227–250. doi: 10.1146/annurev.ne.15.030192.001303. [DOI] [PubMed] [Google Scholar]
- Johnson KO, Yoshioka T, Vega-Bermudez F. Tactile functions of mechanoreceptive afferents innervating the hand. J Clin Neurophysiol. 2000;17:539–558. doi: 10.1097/00004691-200011000-00002. [DOI] [PubMed] [Google Scholar]
- Kakuda N. Conduction velocity of low-threshold mechanoreceptive afferent fibers in the glabrous and hairy skin of human hands measured with microneurography and spike-triggered averaging. Neurosci Res. 1992;15:179–188. doi: 10.1016/0168-0102(92)90003-u. [DOI] [PubMed] [Google Scholar]
- Maeno T, Kobayashi K. FE analysis of the dynamic characteristics of the human finger pad in contact with objects with/without surface roughness. ASME Int Mech Eng Congr Expo. 1998;64:279–286. [Google Scholar]
- Maeno T, Kobayashi K, Yamazaki N. Relationship between the structure of human finger tissue and the location of tactile receptors. JSME Int J. 1998;41:94–100. [Google Scholar]
- Maeno T, Kawamura T, Cheng SC. Friction estimation by pressing an elastic finger-shaped sensor against a surface. IEEE Trans Rob Autom. 2004;20:222–2228. [Google Scholar]
- Mikula S, Niebur E. Rate and synchrony in feedforward networks of coincidence detectors: analytical solution. Neural Comput. 2005;17:881–902. doi: 10.1162/0899766053429408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montemurro MA, Senatore R, Panzeri S. Tight data-robust bounds to mutual information combining shuffling and model selection techniques. Neural Comput. 2007;19:2913–2957. doi: 10.1162/neco.2007.19.11.2913. [DOI] [PubMed] [Google Scholar]
- Nakazawa N, Ikeura R, Inooka H. Characteristics of human fingertips in the shearing direction. Biol Cybern. 2000;82:207–214. doi: 10.1007/s004220050020. [DOI] [PubMed] [Google Scholar]
- Nelken I, Chechik G, Mrsic-Flogel TD, King AJ, Schnupp JW. Encoding stimulus information by spike numbers and mean response time in primary auditory cortex. J Comput Neurosci. 2005;19:199–221. doi: 10.1007/s10827-005-1739-3. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Schultz SR. A unified approach to the study of temporal, correlational, and rate coding. Neural Comput. 2001;13:1311–1349. doi: 10.1162/08997660152002870. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Treves A. Analytical estimates of limited sampling bias in different information measures. Network: Comput Neural Syst. 1996;7:87–107. doi: 10.1080/0954898X.1996.11978656. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Petersen RS, Schultz SR, Lebedev M, Diamond ME. The role of spike timing in the coding of stimulus location in rat somatosensory cortex. Neuron. 2001;29:769–777. doi: 10.1016/s0896-6273(01)00251-3. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Senatore R, Montemurro MA, Petersen RS. Correcting for the sampling bias in spike train information measures. J Neurophysiol. 2007;98:1064–1072. doi: 10.1152/jn.00559.2007. [DOI] [PubMed] [Google Scholar]
- Petersen RS, Panzeri S, Diamond ME. Population coding of stimulus location in rat somatosensory cortex. Neuron. 2001;32:503–514. doi: 10.1016/s0896-6273(01)00481-0. [DOI] [PubMed] [Google Scholar]
- Petersen RS, Panzeri S, Diamond ME. The role of individual spikes and spike patterns in population coding of stimulus location in rat somatosensory cortex. Biosystems. 2002;67:187–193. doi: 10.1016/s0303-2647(02)00076-x. [DOI] [PubMed] [Google Scholar]
- Pubols BH., Jr Factors affecting cutaneous mechanoreceptor response. II. Changes in mechanical properties of skin with repeated stimulation. J Neurophysiol. 1982;47:530–542. doi: 10.1152/jn.1982.47.3.530. [DOI] [PubMed] [Google Scholar]
- Reich DS, Mechler F, Victor JD. Temporal coding of contrast in primary visual cortex: when, what, and why. J Neurophysiol. 2001;85:1039–1050. doi: 10.1152/jn.2001.85.3.1039. [DOI] [PubMed] [Google Scholar]
- Sathian K, Goodwin AW, John KT, Darian-Smith I. Perceived roughness of a grating: correlation with responses of mechanoreceptive afferents innervating the monkey's fingerpad. J Neurosci. 1989;9:1273–1279. doi: 10.1523/JNEUROSCI.09-04-01273.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serina ER, Mockensturm E, Mote CD, Jr, Rempel D. A structural model of the forced compression of the fingertip pulp. J Biomech. 1998;31:639–646. doi: 10.1016/s0021-9290(98)00067-0. [DOI] [PubMed] [Google Scholar]
- Srinivasan MA, Dandekar K. An investigation of the mechanics of tactile sense using two-dimensional models of the primate fingertip. J Biomech Eng. 1996;118:48–55. doi: 10.1115/1.2795945. [DOI] [PubMed] [Google Scholar]
- Torebjörk HE, Vallbo AB, Ochoa JL. Intraneural microstimulation in man. Its relation to specificity of tactile sensations. Brain. 1987;110:1509–1529. doi: 10.1093/brain/110.6.1509. [DOI] [PubMed] [Google Scholar]
- Vallbo AB, Hagbarth KE. Activity from skin mechanoreceptors recorded percutaneously in awake human subjects. Exp Neurol. 1968;21:270–289. doi: 10.1016/0014-4886(68)90041-1. [DOI] [PubMed] [Google Scholar]
- Vallbo AB, Johansson RS. Properties of cutaneous mechanoreceptors in the human hand related to touch sensation. Hum Neurobiol. 1984;3:3–14. [PubMed] [Google Scholar]
- VanRullen R, Guyonneau R, Thorpe SJ. Spike times make sense. Trends Neurosci. 2005;28:1–4. doi: 10.1016/j.tins.2004.10.010. [DOI] [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol. 1996;76:1310–1326. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Metric-space analysis of spike trains: theory, algorithms and application. Network: Comput Neural Syst. 1997;8:127–164. [Google Scholar]
- Werner G, Mountcastle VB. Neural activity in mechanoreceptive cutaneous afferents: stimulus-response relations, Weber functions, and information transmission. J Neurophysiol. 1965;28:359–397. doi: 10.1152/jn.1965.28.2.359. [DOI] [PubMed] [Google Scholar]
- Westling G, Johansson RS. Factors influencing the force control during precision grip. Exp Brain Res. 1984;53:277–284. doi: 10.1007/BF00238156. [DOI] [PubMed] [Google Scholar]
- Westling G, Johansson RS, Vallbo ÅB. A method for mechanical stimulation of skin receptors. In: Zotterman Y, editor. Sensory functions of the skin in primates, with special reference to man. Oxford: Pergamon; 1976. pp. 151–158. [Google Scholar]
- Wu JZ, Dong RG, Smutz WP, Schopper AW. Modeling of time-dependent force response of fingertip to dynamic loading. J Biomech. 2003;36:383–392. doi: 10.1016/s0021-9290(02)00427-x. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Welcome DE, Dong RG. Three-dimensional finite element simulations of the mechanical response of the fingertip to static and dynamic compressions. Comput Methods Biomech Biomed Engin. 2006;9:55–63. doi: 10.1080/10255840600603641. [DOI] [PubMed] [Google Scholar]