The Sparseness of Neuronal Responses in Ferret Primary Visual Cortex

Abstract

Various arguments suggest that neuronal coding of natural sensory stimuli should be sparse (i.e., individual neurons should respond rarely but should respond reliably). We examined sparseness of visual cortical neurons in anesthetized ferret to flashed natural scenes. Response behavior differed widely between neurons. The median firing rate of 4.1 impulses per second was slightly higher than predicted from consideration of metabolic load. Thirteen percent of neurons (12 of 89) responded to <5% of the images, but one-half responded to >25% of images. Multivariate analysis of the range of sparseness values showed that 67% of the variance was accounted for by differing response patterns to moving gratings. Repeat presentation of images showed that response variance for natural images exaggerated sparseness measures; variance was scaled with mean response, but with a lower Fano factor than for the responses to moving gratings. This response variability and the “soft” sparse responses (Rehn and Sommer, 2007) raise the question of what constitutes a reliable neuronal response and imply parallel signaling by multiple neurons. We investigated whether the temporal structure of responses might be reliable enough to give additional information about natural scenes. Poststimulus time histogram shape was similar for “strong” and “weak” stimuli, with no systematic change in first-spike latency with stimulus strength. The variance of first-spike latency for repeat presentations of the same image was greater than the latency variance between images. In general, responses to flashed natural scenes do not seem compatible with a sparse encoding in which neurons fire rarely but reliably.

Introduction

It is debated how visual systems encode natural stimuli (Simoncelli and Olshausen, 2001). Should we study neurons with naturalistic rather than simple stimuli (Theunissen et al., 2001; Felsen and Dan, 2005; Rust and Movshon, 2005)? Are rate codes sufficient or do temporal codes give greater insights (Thorpe et al., 2001; Butts et al., 2007)? Are spatiotemporal receptive fields designed for efficient encoding of natural scenes (Srinivasan et al., 1982; Atick and Redlich, 1992)? Discussion mostly stems from the proposal by Barlow (1972) of “cardinal” cells as a strategy for redundancy reduction, intermediate between the two extremes of Sherrington (1941) of a “pontificate” (Lettvin's “grandmother cell”) or a “million-fold democracy” (a parallel distributed system). Barlow proposed that only a small fraction of the neuronal population need be active to reliably signal higher-order structure in each natural stimulus; different subsets of neurons being activated by different stimuli.

This leads to the concept of “sparse encoding” (Treves and Rolls, 1991; Field, 1994; Rolls and Tovee, 1995; Rolls and Treves, 1997; Weliky et al., 2003). Computational models of efficient encoding for natural visual scenes generate filters resembling the receptive fields of V1 neurons only when constrained to exhibit sparse encoding (Bell and Sejnowski, 1997; Olshausen and Field, 1997; van Hateren and van der Schaaf, 1998; Rehn and Sommer, 2007). Furthermore, because relatively few cortical neurons can have high firing rates at any one time (Attwell and Laughlin, 2001; Lennie, 2003), sparse encoding may minimize the metabolic costs of neuronal encoding (but see Tolhurst et al., 2004). Although the concept of sparse encoding seems straightforward, we have no quantitative predictions to test and sparseness can be defined in two ways that are surprisingly poorly correlated in simulations of natural scene encoding. Most studies of visual cortex (Baddeley et al., 1997) have focused on the response of individual neurons to large stimulus sets: “lifetime sparseness” measures how often each cell responds (Willmore and Tolhurst, 2001). Fewer studies (Weliky et al., 2003; Lin et al., 2006; Yen et al., 2007) have tried to investigate “population sparseness”: the proportion of neurons activated by a given stimulus. But what constitutes a response, which timescales are important for neural computation, and are all spikes equal (Butts et al., 2007)?

Here, we investigate factors that might determine lifetime sparseness values for the responses of individual V1 neurons to natural images. The most commonly used measure of sparseness (Treves and Rolls, 1991) was introduced to measure the storage capacity of associative neuronal networks, whether response is binary or continuous. We examine this and other measures, and investigate the impact of response variability (Tolhurst et al., 1981, 1983) and of the different tuning bandwidths found for “classical” stimuli such as sinusoidal gratings (Tolhurst and Thompson, 1981). Finally, we examine the temporal characteristics of neuronal responses to flashed natural scenes; in particular, whether first-spike latencies might encode information about natural scenes (Thorpe et al., 2001), as in the coding of contrast (Gawne et al., 1996; Mechler et al., 1998; Reich et al., 2001; Geisler et al., 2007).

Materials and Methods

Animal preparation and recording methods.

Our experimental methods have been described in detail (Baker et al., 1998; Smyth et al., 2003), and some of the results reported here involve evaluation of data also examined by Smyth et al. (2003). Briefly, extracellular recordings of action potential timings were made with tungsten-in-glass microelectrodes from units in primary visual cortex of adult pigmented ferrets (bred in Oxford, UK, or imported from Marshalls Farms). During recordings, the ferrets were anesthetized by artificial ventilation with 0.5–1.5% halothane in a mixture of 75% N₂O and 25% O₂. The animals were paralyzed by intravenous infusion of gallamine triethiodide (10 mg · kg⁻¹ · h⁻¹), and the adequacy of anesthesia was assessed from monitoring the heart rate and the waveform of the EEG. At the end of the experiments, the ferrets were injected with a lethal dose of barbiturate while still under anesthesia. All procedures were approved under license from the United Kingdom Home Office.

Visual stimulation.

Visual stimuli were presented monocularly (the eye ipsilateral to the recorded cerebral hemisphere was covered). Pupils were dilated and accommodation was paralyzed by topical application of 1% w/v homatropine. Clear zero-power contact lenses protected the corneas; auxiliary lenses were not used because the small ferret eye has large depth of focus (Green et al., 1980; Price and Morgan, 1987; Baker et al., 1998). Visual stimuli were presented in shades of gray on cathode ray tube (CRT) computer monitors under control of a Cambridge Research Systems VSG 2/4 graphics card. This card has pseudo 15 bit analog output (Pelli and Zhang, 1991), allowing precise control of the luminance of each pixel; natural-scene stimuli could be presented with 256 equally spaced gray levels, and low-contrast grating stimuli could be presented with the same precision and the same number of gray levels as high-contrast ones. Two different CRT monitors were used in these experiments. Some units were studied with an Eizo Flexscan T562-T monitor with a viewable area of 28.5 × 21.5 cm, frame rate of 100 Hz, and mean luminance of 36 cd · m⁻². Later units were studied with a Sony GDM-500PST monitor with 39.6 × 29.7 cm area, frame rate of 160 Hz, and mean luminance of 54 cd · m⁻² [the latter display was used for the experiment described in the supplemental material (available at www.jneurosci.org)]; we moved to a higher frame rate because the responses of some neurons seemed to be entrained to the lower frame rate (Williams et al., 2004). The monitors were placed 57 or 28.5 cm from the ferret's eye so that they subtended from 28.5 × 21.5° of visual angle up to 79.2 × 59.4° of visual angle. The displays had 800 × 600 pixels, and were approximately centered on the receptive field of each unit, which occupied 15–60% of the display, allowing scope for the natural images stimuli to activate the surrounds to the classical receptive fields (Vinje and Gallant, 2000, 2002; Guo et al., 2005).

Classification of units.

We report experiments on 89 units. Their receptive fields were usually mapped with hand-held stimuli so that they could be provisionally classed as simple or complex according to the qualitative definitions of Hubel and Wiesel (1959, 1962). Classification could be quantified to greater extent by measuring the “relative modulation” of response to a moving sinusoidal grating of optimal spatial frequency and orientation (Maffei and Fiorentini, 1973; Movshon et al., 1978a,b). In the response poststimulus time histogram (PSTH), we calculated the amplitude of the Fourier component at the same frequency as the moving grating, divided by the average firing rate (we did not subtract the spontaneous level of activity from this average firing rate). Often, neurons are classified as “simple” if relative modulation is >1.0 and as “complex” if the value is <1.0 (Skottun et al., 1991). Although this dividing line is exactly midway between the extreme possible values of 0.0 and 2.0, it is entirely arbitrary and any dip in the distribution of relative modulation at the midway value of 1.0 may be an artifact of the measure (Mechler and Ringach, 2002; Priebe et al., 2004). The distinction between the simple and complex classes may not be abrupt (Dean and Tolhurst, 1983; Mata and Ringach, 2005); relative modulation may not be a perfect measure for making a distinction (Mechler and Ringach, 2002; Priebe et al., 2004), and, even for a given neuron, relative modulation can be affected considerably by stimulus configuration (Bardy et al., 2006). Thus, the relative modulation range of 0.8–1.2 should certainly be regarded as ambiguous. The distinction in the relative modulation measure is further blurred if, say, some simple cells have significant spontaneous activity, which lowers the relative modulation measure. Even within the simple cell “class,” a range of relative modulation values is seen, reflecting significant differences between cells in their receptive-field construction (Tolhurst and Dean, 1987, 1990). Here, we shall assume that a relative modulation above ∼1.2 is reasonably associated with simple cells (39 units), although some might be “nonlinear simple cells” (Movshon et al., 1978a), whereas a relative modulation of <0.8 is associated with complex cells (42 cells); this leaves 8 “ambiguous” units.

Experimental design.

We used moving high-contrast sinusoidal gratings to determine the bandwidths (width at half-height) of the orientation and spatial-frequency tuning curves of each unit (for details, see Baker et al., 1998). These curves were generally measured with gratings with contrast 0.7 (70%) and were based on averaging the responses to 30 cycles of gratings moving at 1–2 Hz. These experiments also provided estimates of “responsivity” [firing rate in impulses per second (i.p.s.) to a high-contrast grating of optimal spatial frequency and orientation] and of the relationship between response variance and mean response magnitude (cf. Tolhurst et al., 1981, 1983). We generally presented only enough grating orientations and spatial frequencies to clearly define the half-width bandwidth; we did not study the full range of orientations, and so we are unable to comment on global measures of orientation tuning (Chapman and Stryker, 1993; Xing et al., 2004). In most of our neurons, we made sufficient measurements of the low spatial frequency tuning that we can calculate the “low spatial frequency variance” (LSFV) (Xing et al., 2004), which is arguably a better overall measure of tuning for comparison with the responses to natural images.

Then, the responses of each unit were recorded for a long sequence of briefly flashed fragments of monochrome photographs of natural scenes that had been digitized to >1000 distinct gray levels and that were corrected for the nonlinear “gamma” of the photographic process (Tolhurst et al., 1992). The corrected photographs were rescaled so that the darkest pixel in each became zero (nominally, absolutely black on the display). There were 256 equally spaced gray levels with the brightest being twice the mean luminance of the display. No attempt was made to equate the space-averaged mean luminance of the photographs to the mean luminance of the display, either across the whole photograph or across the smaller central portion that might fall within the receptive field of a neuron. Some photographs (Tolhurst et al., 1992) were of plants, people, landscapes, and man-made objects, but others (photographed by D. Smyth) were of ferrets or of “ferret's-eye” views of terrain. Each image fragment measured 150 × 150 pixels and was cut at random from a set of 128 whole digitized and linearized photographs, each measuring 256 × 256 pixels. When displayed on the CRTs, the fragments were “zoomed” so that each fragment pixel was expanded to occupy 4 × 4 hardware display pixels, thereby exactly filling the 600 pixel height of the display (i.e., from 21.5 deg² up to 59.4 deg², depending on display). The effective pixel size was, therefore, 0.14–0.4° of visual angle, depending on the model of CRT and the viewing distance. For most ferret neurons, even the larger effective pixel size would be smaller than their resolution limit (Price and Morgan, 1987; Baker et al., 1998).

In a typical experiment, 5000 photograph fragments were presented to each neuron. These might be 5000 independent random selections (150 × 150 pixels) cropped from the parent set of 128 photographs (256 × 256 pixels). Or 500 fragments might be chosen from the set of 128 photographs, and then these 500 fragments would be presented up to 10 times each (24 neurons); the 500 stimuli would be presented once, and then the order of presentation would be randomized before they were all presented once again, and so on.

Each image fragment was presented statically for 100 ms (10 or 16 frames, depending on the display CRT frame rate). Between the sudden offset of one image fragment and the sudden onset of the next, the screen was held at a uniform gray: the mean luminance (i.e., 36 or 54 cd · m⁻² depending on the display). The interval between image fragments, during which the display was held a uniform gray, was usually 150–170 ms (occasionally 100 ms), long enough for any “OFF” response to one fragment to be distinct from the “ON” response to the next. This procedure allowed clear decisions as to which action potentials were generated by which images and, to an extent, stylizes natural viewing in which the fixations between saccades to new targets might last 250 ms or more (Stryker and Blakemore, 1972; Vinje and Gallant, 2000, 2002; Moeller et al., 2004; Maldonado and Babul, 2007; Foulsham and Underwood, 2008). Furthermore, a 100 ms presentation is generally sufficient to allow detection or discrimination in simple (Tolhurst, 1975) or complex visual stimuli (Buracas et al., 1998; Müller et al., 2001; Thorpe et al., 2001). Each block of 500 image fragment presentations was preceded by a 5 or 10 s episode in which the level of spontaneous activity was measured. Figure 1A shows a schematic of the stimulus presentation protocol.

Figure 1.

A, A schematic illustration of the protocol for presenting 150 × 150 pixel fragments of photographs of natural scenes. Each fragment was turned on suddenly for 100 ms and then removed suddenly; between fragments, the display CRT was held at a uniform midgray for 100–170 ms. B–E, Poststimulus time histograms for four neurons, showing the most likely times of action potential generation with respect to the presentation time of the natural scene fragments. The histograms are averaged across all the image fragments presented to each neuron.

We measured the response of each recorded unit to each 100 ms presentation of each image fragment. First, we constructed PSTHs to show the average timing of action potentials with respect to the onset and offset of the image fragments; responses were pooled across fragments, regardless of whether they were the same fragment or not. Figure 1B–E shows some examples of these PSTHs. Typically, image fragments would increase the action potential generation of a neuron during their presentation (ON response) and/or would evoke a burst of activity on their removal (OFF responses). In complex cells, a single image fragment might evoke both an ON and an OFF response; in a well behaved simple cell, a single image fragment would generate either an ON response or an OFF response (Smyth et al., 2003). Responses typically began ∼20–70 ms after the stimulus onset or offset and were often transient (cf. Maldonado and Babul, 2007). For most of the additional analysis, we chose a 100 ms period that best included the responses of the neuron. Generally, a period such as 30–130 ms after stimulus onset typified the response of a neuron, although we used a period such as 100–200 ms for 13 neurons, which gave much bigger OFF than ON responses (see Fig. 1E); nine of these were simple cells, and we imagine that their OFF responses might have been identical with the ON responses of unrecorded simple cells with complementary receptive field organization.

Quantification of “sparseness.”

A “sparse” lifetime response distribution (Willmore et al., 2000; Willmore and Tolhurst, 2001; Weliky et al., 2003; Yen et al., 2007) is one in which a neuron gives a low (zero) response to most stimuli, but high-magnitude responses to relatively few stimuli (Field, 1994). For most analyses, the response of a neuron to each image fragment was simplified and summarized as the number of action potentials generated within the chosen 100 ms period. Because we are interested in how neurons and populations of neurons encode the information in a scene while it is actually present, we have not included both the ON and OFF responses of any cells in our analyses. If we had pooled ON and OFF responses, the sparseness of many neurons would have seemed to be less. A good measure of sparseness should reflect the form of the response distribution; however, most of the proposed sparseness measures have weaknesses [discussed by Willmore et al. (2000), Willmore and Tolhurst (2001), and Lehky et al. (2005)]. The different measures highlight different aspects of a response distribution, but, if all response distributions did have the same form, then the measures would be proportional to each other. We consider four different measures.

First, we start with a measure first proposed by Treves and Rolls (1991), but we use the slight modifications of Vinje and Gallant (2000, 2002) and Willmore and Tolhurst (2001) as follows:

Our version simply ensures first that a sparser response distribution gives a larger value (unlike the original definition by Treves and Rolls). Furthermore, the original measure was designed for use in situations in which neurons have no spontaneous activity; this is particularly appropriate to primary visual cortex in which most neurons do have little spontaneous activity, but we want also to apply the measure to hypothetical distributions with mean of zero (hence the taking of absolute values). For zero mean, the original Treves–Rolls formulation would give a value of zero whatever the shape of the response distribution.

Second, we parameterize sparseness of a response distribution by simply counting the proportion of image presentations that evoked zero response (P₀). Sparse response behavior would generally be expected to be accompanied by a high proportion of zero responses.

Third, we calculate the kurtosis of a response distribution (Olshausen and Field, 1997) as follows:

where r_i is the response to a particular image fragment, r̄ is the average response to all the fragments, n is the number of responses under consideration, and σ² is the variance of the responses. This measures how different the shape of a symmetrical distribution is from that of a normal, Gaussian distribution (which has kurtosis of zero). A distribution more concave (more leptokurtic) than a Gaussian (see Fig. 3E) has a kurtosis greater than zero. The fourth power in Equation 2 means that the kurtosis measure gives particularly exaggerated measures of sparseness (Willmore and Tolhurst, 2001).

Figure 3.

Sparseness measures for eight hypothetical response distributions. A, A Gaussian distribution with mean response of zero should have kurtosis and entropy of zero, by definition. B, The same distribution as in A, but with all negative values set to zero; such “half-wave rectification” is a stylized model of the responses of simple cells with no spontaneous activity. C, The same distribution as in A, but with all negative values made positive and reflected through zero; such “full-wave rectification” is a stylized model of the responses of complex cells with no spontaneous activity. D, A stylized model of the response distribution of a simple cell with spontaneous level of activity equivalent to a response of “5 units”: 5 is added to the Gaussian distribution of A and all negative values are then set to zero. E, A leptokurtic distribution (exponential) with the same mean (zero) and variance as in A. F, G, Half-wave rectified and full-wave rectified versions of the exponential distribution in E. H, A stylized model of the responses of a simple cell with no spontaneous activity and with a response threshold equivalent to a response of “5 units”: 5 is subtracted from the Gaussian distribution of A, and all negative values are then set to zero.

Last, an “entropy” measure of sparseness has been proposed by Lehky et al. (2005), which not only quantifies the shape of a response distribution but also carries implications about coding efficiency. The response distribution is first normalized to have a variance of 1 and is then converted to a probability density function p(r), with bin width of Δr as follows:

where k is the number of bins into which the n normalized responses have been grouped. A Gaussian distribution has S_E of zero; a sparser distribution has greater entropy. For a given distribution, the calculated value of S_E depends on k, which is supposed to be set to be √n (Lehky et al., 2005). However, in most of our examples, √n (usually √5000) was considerably larger than the number of discrete (integer) response levels (generally <20); then we had to reduce k to match the number of discrete response levels actually found. In the experiments in which we were able to average the responses to 10 repetitions of each image fragment, √n is reduced to √500 while the number of possible response levels increases dramatically (rather than integers, the averaged responses are now spaced at an interval of 0.1). Such capricious differences in n and k make it difficult to compare the entropy of the response distributions before and after averaging the responses to repetitions of image fragments.

For 24 neurons, we examined how the form of the response distribution was affected by the inherent response variability of V1 neurons. In that context, we summarized the form of the distribution of responses to 5000 image presentations as the ratio of the overall variance to the overall mean (i.e.,

).

Mutual information.

For those 24 neurons in which we had presented the same image set repeatedly, we were able to estimate the mutual information between the responses of a neuron and the image presented. The uncertainty in the 500-strong stimulus set, H(S), is given by log₂(500), the probability that you could guess correctly which of the stimuli had just been presented before examining the responses of the neuron. The mutual information is given by H(S) − H(S|R) in bits, where H(S|R) is the residual uncertainty that remains even with knowledge of the responses of the neuron.

where P(r) is the probability of occurrence of a given response level across the whole experiment, whereas P(s,r) is the joint probability that the given response level is evoked and that a given stimulus is presented.

Results

The overall pattern of responses to natural scene stimuli

Figure 1B–E shows PSTHs of the responses of four neurons to 100 ms flashed presentations of fragments of black-and-white photographs of natural scenes. Between successive image fragments, the display was held at a spatially uniform midgray for 100 ms (E) or 150–170 ms (B–D). For the four neurons of Figure 1, there were 500 different image fragments in the experimental set, and the set of 500 was presented 10 times (in different random order each time) to each neuron. The PSTHs combine the action potential timings for all 5000 image presentations, to show an “averaged form of response” to the natural scene stimuli. The form of the PSTH varied widely between neurons. Some neurons (Fig. 1B) responded primarily during the presence of the fragments (ON response), whereas others (e.g., E) responded more to stimulus offset than to onset. In some neurons (e.g., B and, to some extent, C), the response was sustained for a full 100 ms, which, accounting for a response latency, represents a sustained response for the full duration of the stimulus. Not surprisingly, OFF responses were usually relatively brief (30–50 ms) (Fig. 1C–E), but ON responses could also be brief (D, E). Complex cells often gave both ON and OFF responses to individual image fragments, whereas simple cells would usually give either an ON response or an OFF response to any one fragment (Smyth et al., 2003), as would be expected from the way that simple and complex cells respond to the flashed presentation of simpler grating or spot stimuli (Movshon et al., 1978a,b).

Although the PSTHs can reach peak firing rates of up to 30–40 i.p.s., these peak rates are achieved only transiently so that the firing rate averaged over the full 100 ms after response onset is only between ∼5 (Fig. 1B) and 13 (Fig. 1C) i.p.s. in the illustrated examples. Many other neurons had smaller averaged firing rates; one gave a total of only 255 action potentials during the whole experiment. This represented an average firing rate of only 0.34 i.p.s. during the 100 ms after response onset; yet, this small response was consistent enough to allow us to reconstruct the receptive field of the neuron [cell f32203 in the study by Smyth et al. (2003)]. For the 89 neurons in our sample, the firing rate averaged over all the 100 ms counting epochs of an experiment ranged widely from 0.28 to 45.94 i.p.s.; the largest values were recorded from neurons with substantial levels of spontaneous activity. The heterogeneity of neuronal responses to natural stimuli has also been emphasized by Yen et al. (2007). In our sample, the median response was 4.10 i.p.s. (25 and 75 percentiles: 1.49 and 8.95 i.p.s.). These low firing rates are consistent with other work on responses of single V1 neurons to natural-scene stimuli in anesthetized and, importantly, in awake animals (Legéndy and Salcman, 1985; Baddeley et al., 1997; Gallant et al., 1998; Ringach et al., 2002; Guo et al., 2005; Maldonado and Babul, 2007; Yen et al., 2007).

It can be seen in Figure 1, B–E, that the latency of response onset could vary quite considerably from neuron to neuron, and Figure 2 shows the latencies of response of 86 of the neurons, estimated from their PSTH averaged over all stimuli. The onset latencies (Fig. 2A) ranged from 17 to 67 ms, with a mean of 33.5 ms. The offset latencies (Fig. 2B), when they occurred, covered a similar range: from 15 to 61 ms, with a mean of 33.2 ms. Figure 2C confirms the impression given by the example PSTHs in Figure 1 that, when cells give both onset and offset responses, the latencies are similar (r = 0.769; n = 52). Most of the neurons had PSTHs like Figure 1C–E, in which the onset response began abruptly. However, 14 neurons had a more gradual response onset that developed relatively slowly toward a peak response (Fig. 1B); all of these “slow cells” had response latencies exceeding 35 ms. We could not identify any differences between the slow-onset and abrupt-onset neurons in terms of, say, whether they were simple or complex or whether they were sharply tuned or narrowly tuned for orientation or spatial frequency.

Figure 2.

A, The histogram shows the latency of response of 86 neurons to the onset of the flashed natural scene stimuli. Latency is estimated from the PSTH averaged across all stimuli (like those in Fig. 1). This includes the latency of the small ON response for most of the neurons in which we have analyzed the sparseness of their larger OFF responses. Three neurons of the 89 are not included because either they gave only OFF responses or their responses were so weak that a clear “turn-up” in the PSTH at response onset was difficult to discern. B, The latency of the offset response for those 52 neurons with a clearly defined offset response. C, The latency of the offset response is plotted against the latency of the onset response. The symbols on the axes show the many cases (x-axis) in which a clear offset response was not discernible and a single case (y-axis) in which no onset response was obvious.

The PSTHs of Figure 1 are averaged across 500 different natural scene stimuli, and it is possible that the form of the response might vary from stimulus to stimulus. This turned out not to be the case (as we shall show in Fig. 11), so it seems reasonable to provisionally summarize the response of a neuron to a given stimulus presentation simply as the total number of action potentials evoked in a fixed time. In subsequent analyses, we shall initially look at a time window of 100 ms from response onset, the same duration as the stimulus (for 13 neurons we look at a 100 ms window from stimulus offset). This is actually longer than the transient burst responses of some neurons, so that a shorter time window would make no difference. Furthermore, a 100 ms time window fully covers the difference in response latencies of different neurons, a factor we should consider in questioning how populations of neurons encode information in flashed images or movies (see Discussion).

Figure 11.

For three neurons (A–C, respectively), the figure shows three PSTHs summarizing the responses to three different image sets. Neuron B is the same as in Figure 1C; neuron C is the same as in Figure 1E. For each neuron, the 500 stimulus images were ranked according to the number of action potentials evoked over the whole stimulus interval including the blank between images. The top row of histograms shows PSTHs summed only across the 20 most powerful stimuli for each neuron; the middle rows sums the responses to stimuli ranked 41–70 for each neuron; whereas the bottom row sums the responses to stimuli ranked 101–150 for each neuron. The response bins are 4 ms. Note the expansion in the y-axis scale as one proceeds down the rows.

Different measures of sparseness

The PSTHs in Figure 1 show the average response to natural-scene stimuli; it is an important question to ask whether the forms of response to different scenes are the same or different for a given neuron. For instance, for the neuron in Figure 1B, the single most effective image in the experiment evoked 14 action potentials in the 100 ms image flash; for the neuron of Figure 1E [illustrated in detail by Smyth et al. (2003), their Fig. 9], a different “best image” evoked 16 action potentials at offset. Averaged over 100 ms (the flash duration), therefore, the firing rates for these highly favored stimuli were 140 and 160 i.p.s., respectively, much higher than the firing rates averaged across all images. Moreover, given the transience of its OFF response (some 30 ms), the neuron in Figure 1E will have attained an instantaneous firing rate to its favored stimulus of >500 i.p.s. We will quantify the “nonuniformity” of response with measures of sparseness and entropy (see Materials and Methods).

Figure 9.

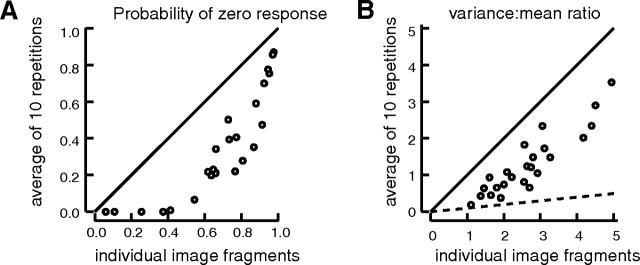
For 24 neurons, 500 image fragments were presented 10 times each. The graphs show the effects on the response distributions of averaging the responses to the 10 repetitions of each fragment. The abscissas show measures of the distributions of the 5000 individual responses; the ordinates show the equivalent measures of the distributions of the 500 averaged responses. The solid lines are the lines of equality. A, P₀, the probability of obtaining a zero response either to individual stimulus presentations (abscissa) or on average to particular image fragments (ordinate). B, The variance of the distribution of responses divided by the mean response. The overall variance of the distribution is lowered by averaging responses to stimulus repetitions, but the mean response is, of course, unchanged. The dashed line has a slope of 1/10 and shows how much the variance of the response distribution could have been reduced by averaging 10 repetitions, if the whole variety of responses to natural images was attributable to response variability.

Figure 3 shows some stylized response distributions to illustrate how various measures of sparseness (see Materials and Methods) reflect changes in the shapes of response distributions. Figure 3A shows a Gaussian distribution with a mean of zero. The kurtosis and entropy (S_E) are, by definition, near zero. Figure 3E shows a distribution that is obviously more concave (more leptokurtic) than a Gaussian; it has the same variance and the same mean (zero) as that in Figure 3A. The modified TR measure, the kurtosis, and entropy are all higher (0.489, 1.88, and 0.17, respectively) than for a Gaussian (0.363, −0.085, and 0.079). The probability of obtaining a zero response (P₀) is obviously higher for the leptokurtic distribution of Figure 3E.

The number of action potentials generated by a neuron within our 100 ms sampling period cannot, of course, be negative, and so we should consider stylized distributions only of non-negative response values. Figure 3, B and F, shows a simplified expectation of the forms of simple-cell response distributions. The measured responses of simple cells are hypothesized to be half-wave rectified versions of the expected underlying linear responses (Movshon et al., 1978a; Tolhurst and Dean, 1987; Heeger, 1992). Half-wave rectification of the parent distributions (Fig. 3A,E) obviously causes a massive increase in the proportion of zero responses (note the breaks in the y-axes): over one-half of the response values are now zero, which necessarily causes an increase in the Treves–Rolls, kurtosis, and entropy measures. All measures indicate that half-wave rectification causes a big increase in response sparseness (presuming that we can ignore, say, OFF responses in neurons in which we analyze only the ON responses); they also agree that the distribution in Figure 3F is sparser than that in Figure 3B.

Figure 3, C and G, shows potential response distributions for complex cells; we have simply taken the absolute values of the responses in the distributions of Figure 3, A and E, as if the responses of complex cells might be full-wave rectification of their summed inputs (Movshon et al., 1978b). Full-wave rectification affects the kurtosis and entropy measures to suggest an increase in response sparseness; however, the TR measure and the probability of obtaining a zero response (P₀) are unchanged (note the difference in y-axis scales between Fig. 3C,G, and A,E). All four measures (including TR) agree that the distribution in Figure 3G is sparser than that in Figure 3C. However, it is important to note that the response distributions for model complex cells are less sparse than those for model simple cells (Fig. 3, compare B with C, and F with G), mostly because of the many zero responses given by simple cells.

Figure 3D shows the hypothetical response distribution for a simple cell with spontaneous activity equal to five response units. Starting with the distribution of Figure 3A but shifted five response units to the right, we have made all negative responses become zero. The proportion of zero responses necessarily falls when we shift the parent distribution to the right. The presence of spontaneous activity (Fig. 3D) reduces the amount of sparseness on all four measures, compared with the more usual situation in which simple cells have little spontaneous activity (Fig. 3, compare B, D). Figure 3H models the more likely case (Movshon et al., 1978a; Schumer and Movshon, 1984; Tolhurst and Dean, 1987; Robson et al., 1988) that simple cells have a response threshold and that their responses are, therefore, overrectified. We have started with the Gaussian distribution of Figure 3A, have shifted it five response units to the left, and have made all negative values become zero. Compared with the original (Fig. 3A) and the half-wave rectified model (Fig. 3B), thresholding has caused a big increase in sparseness given by all four measures, especially kurtosis and the proportion of zero responses. A complex cell with no spontaneous activity might also produce a response distribution of this form if its responses were also subject to a threshold.

In the examples of Figure 3, the four measures of sparseness mostly go in the same direction. However, in detail, the four measures describe different aspects of a response distribution shape, and sometimes they do not agree as to which of two distributions is the “sparser” (for example, see the measures in Fig. 3D). The kurtosis measure generally exaggerates the differences between different distribution forms. However, these detailed differences in the behavior of the different metrics will not affect the conclusions of this study.

Distribution of responses to different natural scene stimuli

Figure 4 shows the responses of three neurons to 100 natural-scene stimuli. Each stimulus was presented 10 times for these three neurons, and so Figure 4 shows the responses to 1000 of the 5000 stimulus presentations for each neuron. The area of each square symbol is proportional to the number of action potentials evoked in the 100 ms counting period associated with each repetition of each natural-scene stimulus. Figure 4, A and B, shows the response patterns of two simple cells with no spontaneous activity (relative modulation to gratings of 1.63 and 1.59). There are clear “columns” in the response rasters showing that the neurons tended to respond reliably to the particular subsets of stimuli when these were repeated, and that some stimuli evoked strong responses, whereas others evoked weak (but nonzero) responses. It is obvious that the neuron of Figure 4A responded more sparsely to the stimulus presentations than did the neuron of Figure 4B. It is also very clear that the responses of the neurons to repeated presentations of the same stimuli were not identical: there is variance in the responses to natural scene stimuli, as there is for moving sinusoidal gratings (Dean, 1981; Tolhurst et al., 1981, 1983; Vogels et al., 1989; Wiener et al., 2001). Response variability makes it difficult to be certain whether the generation of, say, one action potential is a response to a stimulus or is, in fact, a very rare spontaneous event. Comparing the responses to repetitions of the same stimuli greatly increases the experimentalist's confidence at deciding whether the neuron has responded to stimuli, but, in a very sparsely responding neuron (like Fig. 4A), there may still be some doubt (see, e.g., its responses to fragments 25–70).

Figure 4.

The numbers of action potentials generated by three neurons during 100 ms counting periods for 100 image fragments; these are part of the records of experiments in which 500 fragments were presented 10 times each to each neuron. The abscissas give an arbitrary i.d. code for which of the image fragments was presented (the responses to different fragments are shown for the 3 neurons). The ordinate shows the 10 repetitions of each stimulus. The square symbols show the number of action potentials generated in 100 ms for each repetition of each fragment; the area of the square is proportional to the number of action potentials evoked in the illustrated sequences (maximum responses: A, 9; B, 12; C, 12). The neuron of C had substantial spontaneous activity, and, to avoid clutter, only the responses to odd-numbered image fragments are shown.

The neuron of Figure 4C had spontaneous activity of ∼16 Hz; it was probably a simple cell, but the high spontaneous activity gave it a low relative modulation for gratings (0.78). During each 100 ms natural-scene presentation, we would expect 1.6 action potentials to be evoked on average, and to avoid clutter only the responses to odd-numbered stimuli are shown in Figure 4C. Indeed, action potentials were evoked during the presentation of most repetitions of most stimuli. Much of this may be regarded as spontaneous activity, but it is clear that a few stimuli evoked more activity than the average (e.g., fragments 249 and 251), whereas others seem to have suppressed the spontaneous activity (e.g., fragments 215 and 239) as would be expected of a simple cell. Given the response variability, it is not possible to subtract the spontaneous activity from the firing pattern to leave the true evoked responses to the stimuli.

Figure 5A–D shows how often responses of different magnitude were evoked by natural-image presentations. Three of the neurons (Fig. 5A–C) are the same as those illustrated in Figure 4. Each histogram shows the proportion of times (of 5000 total presentations) that particular responses were evoked; the present analysis considers the 10 repetitions of each image fragment as 10 independent data (plots in Fig. 5E,F, describing averaged data, will be discussed later). The figure shows the four sparseness measures (see Materials and Methods) that describe the form of each histogram. Figure 4, A and B, implied that, of the two simple cells, the responses of A were sparser: it gave responses to very few of the 100 image fragments. This is mostly confirmed by the four sparseness measures shown in Figure 5, A and B: the modified Treves–Rolls measures, the probability of a zero response and the kurtosis are all higher for neuron A. Curiously, the entropy measure is lower for A. Spontaneous activity (Fig. 5C) causes a substantial reduction in all four sparseness measures (compare with Fig. 3B,D).

Figure 5.

A–D, The distribution of response magnitudes for experiments on four neurons. A–C are the distributions for the three neurons whose rasters are shown in Figure 4A–C, respectively. The histograms show the proportion of image presentations of the total 5000 in which a particular action potential count was obtained. No account is taken at this stage that the 5000 presentations may have consisted of 10 repetitions of only 500 different images. The arrows point to largest response evoked for any one image presentation (9, 16, 17, and 44); the ordinate scales are such that the histogram bins for the most infrequent response magnitudes are difficult to discern from the abscissa lines. Four sparseness measures are shown for each histogram. For histograms A, B, and D, the full height of the bin is not shown at a response magnitude of zero; the proportion of zero responses is given by the P₀ sparseness metric. E, F, Distribution of the averaged response magnitudes for neurons A and B after the responses to the 10 repetitions of each image fragment are averaged together. Note the magnified x and y scales compared with histograms A and B. Note also that averaged responses are no longer integers but can be binned in steps of 0.1. The change in bin size has large effects on the calculation of distribution entropy.

The forms of distributions in Figure 5A–C are typical of those that we have measured. The Treves–Rolls measure is the one most often adapted and used (Vinje and Gallant, 2000, 2002; Weliky et al., 2003; Yen et al., 2007), and our range of values (Fig. 6A) is compatible with previous studies. For neurons with little or no spontaneous activity, the most frequent response was generally zero: P₀ was 0.804 (SD, 0.161) on average for the 66 neurons with little or no spontaneous activity. Of these 66, 33 could be classed unambiguously (see Materials and Methods) as simple and their average P₀ was 0.854 (SD, 0.125), whereas unambiguously defined complex cells (27) had lower P₀ of 0.724 (SD, 0.181). This difference between simple and complex cells is consistent with the argument given by Figure 3, and was significant on a Kolmogorov–Smirnov two-sample test and a Student's t test (t = 3.28). For 23 neurons with substantial spontaneous activity (Figs. 4C, 5C), P₀ was understandably lower: average, 0.384 (SD, 0.232; 23 neurons). The difference between neurons with and without spontaneous activity was highly significant (t = 9.56).

Figure 6.

For the 89 neurons under study, the graphs in A–C plot the Treves–Rolls sparseness measure (TR) (A), kurtosis (k₄) (B), and entropy (S_E) (C) against the probability of obtaining a zero response (P₀). The gross outlier in C with entropy >3.0 is for the response distribution shown in Figure 5D. The correlation coefficients for these plots are given in Table 1. D, A histogram to show how many neurons were found with each level of sparseness; the filled blocks are for neurons with spontaneous activity >3 i.p.s.

Thus, the most frequent response was zero for most neurons, although for neurons with substantial spontaneous activity, the most frequent responses might have been one or two action potentials in the 100 ms counting period. For response magnitudes greater than the most frequent magnitude, the frequency of occurrence declined approximately exponentially with increasing response magnitude (Baddeley et al., 1997), as is shown in Figure 5A–C. Almost all the neurons exhibited “soft sparseness” of this kind (Rehn and Sommer, 2007). Often there was a tail to the distribution, in which only one or two stimulus presentations might have evoked a relatively large response. The arrows in Figure 5 show the largest response evoked in each experiment. An exponential response distribution has been argued to be the most efficient (Baddeley et al., 1997).

The distribution shown in Figure 5D was unique in our study, being the only one showing “hard sparseness” (Rehn and Sommer, 2007). The most frequent response is again zero, but there is a very obvious distinct mode centered on a response of ∼15 action potentials in 100 ms; some 25% of responses are in that mode (responses, >8). This neuron fired in bursts of 4–15 action potentials with interspike intervals of 1.5–4.5 ms. The P₀ and Treves–Rolls sparseness measures are quite similar for the distributions in Figure 5, B and D, but the kurtosis in Figure 5D is surprisingly low, whereas the entropy is the highest that we measured. The high entropy may partly arise from the larger number of response bins in Figure 5D (44 compared with 17 or less in the other cases) (see Materials and Methods). In general, the highest response evoked by a single stimulus rarely exceeded 20 spikes in a 100 ms window for our population of neurons, and was often as low as 6.

If the response distributions of the 89 neurons had the same basic form, we should expect the four sparseness measures to be highly correlated. Figure 6A–C shows plots of the Treves–Rolls measure [modified so that the greater the sparseness, the greater the measure (Eq. 1)], kurtosis and entropy against P₀, the probability of a zero response. Table 1 lists parametric correlation coefficients for all pairwise comparisons between the four measures. P₀ is highly correlated with Treves–Rolls (TR) (Fig. 6A) (r = 0.992). The correlation between kurtosis and P₀ (Fig. 6B) is not as high, but this results mostly from the fourth-power aspect of the calculation of kurtosis (Eq. 1), which leads to the rapid acceleration in the graph at high values of P₀. Nonparametric (rank order) correlations (Table 1, values in brackets) show that kurtosis is highly correlated with TR and P₀. However, the entropy measure of Lehky et al. (2005) is only weakly correlated with the other three measures (Table 1), as is confirmed by the scatter in the plot of P₀ against entropy in Figure 6C, in which the gross outlier belongs to the unique distribution shown in Figure 5D. Entropy is measuring a different aspect of response distributions compared with the other three measures. Given these correlations, we will use only the P₀ measure in the next section of this study, although TR would give identical conclusions.

Table 1.

The correlations between the four measures of the sparseness of response distributions such as those in Figure 3

	Probability of zero response (P0)	Kurtosis (k4)	Treves–Rolls measure
Kurtosis	0.607 (0.949)
Treves–Rolls	0.992	0.603 (0.971)
Entropy (SE)	0.434	0.073 (0.471)	0.474

The table shows Pearson's r with 87 df for each pairwise comparison between the measures. The numbers in brackets show Spearman's ρ based on rank orders for those comparisons involving kurtosis, which obviously varies monotonically but nonlinearly with the other measures.

Figure 6D shows how many neurons exhibited each level of sparseness. The range is considerable, with the least sparse neurons being ones that exhibited appreciable spontaneous activity (>3 i.p.s., filled blocks). Theoretical studies of sparse coding unfortunately do not predict what values we should expect.

Image sparseness and the responses to sinusoidal gratings

The graphs of Figure 6 show clearly that the sparseness of response to natural-image stimuli varies greatly from neuron to neuron, and the question arises whether differences in response sparseness are associated with differences in the ways that neurons respond to simpler stimuli such as sinusoidal gratings (cf. Vinje and Gallant, 2000, 2002). We have already argued (Fig. 3) that simple cells should show sparser responses than complex cells, and that the presence of significant spontaneous activity would reduce sparseness, both predictions borne out in our data (Figs. 5, 6D). Now, the distinction between simple and complex cells is not absolute (Dean and Tolhurst, 1983; Mechler and Ringach, 2002; Priebe et al., 2004; Mata and Ringach, 2005); instead, there is a continuous range of response behaviors than can be described parametrically by the “relative modulation” of response to moving sinusoidal gratings (Movshon et al., 1978a; Dean and Tolhurst, 1983). Figure 7A plots sparseness of response to natural images (P₀) against relative modulation for sinusoidal gratings; there is a weak but very significant correlation (r = 0.52; n = 89) (Table 2). The presence of spontaneous activity is also not all-or-none, but is graded from one neuron to the next. Figure 7B plots sparseness of response to natural images (P₀) against spontaneous activity; although there is a stronger, inverse correlation (r = −0.68; n = 89) (Table 2), it is still the case that sparseness also varies among neurons with little spontaneous activity. A regression of P₀ against both relative modulation and spontaneous activity gives a multivariate correlation coefficient of 0.748 (Table 2).

Figure 7.

Plots to show the associations between the sparseness of response to natural image stimuli and other response properties. A, Relative modulation in the responses to moving sinusoidal gratings of optimal orientation and spatial frequency. B, Spontaneous activity. C, The bandwidth of the orientation tuning curve measured with moving sinusoidal gratings of optimal spatial frequency (see Baker et al., 1998). D, The bandwidth of the spatial-frequency tuning curve measured with moving sinusoidal gratings of optimal orientation. Bandwidths were measured as full width at half-amplitude. The correlation coefficients for these plots are given in Table 2. Filled symbols, Relative modulation, <1.0; open symbols, relative modulation, >1.0, the arbitrary dividing line by which some separate complex cells from simple cells (Skottun et al., 1991).

Table 2.

The correlations between the sparseness of response to natural image stimuli (P₀) and five different aspects of the responses of the neurons to moving sinusoidal gratings

Factor in the response to sinusoidal gratings					Multivariate r coefficient	n
Relative modulation	Spontaneous activity	Peak response	Orientation bandwidth	Frequency bandwidth
✓					0.520	89
	✓				−0.680	89
		✓			−0.569	89
			✓		−0.474	85
				✓	−0.482	86
✓	✓				0.748	89
✓	✓	✓			0.781	89
			✓	✓	0.584	83
✓	✓	✓	✓	✓	0.818	83
✓	—	✓	✓	✓	0.681	63

The single-factor correlations (first five rows) are given by Pearson's r with 83–87 df. The multivariate correlation coefficient is always positive whatever the direction of the regression. The bottom row (with low n) excludes those neurons with spontaneous activity >3 i.p.s. All correlation coefficients are highly statistically significant.

A third factor of interest in the responses to sinusoidal gratings is the responsivity of the neuron. We would expect that a neuron that responds weakly to gratings will also respond weakly to natural images, and that “weak responsiveness” would imply frequent responses of zero, especially if the low response magnitudes were caused by a high response threshold (compare Fig. 3H). We would expect, therefore, sparseness to natural images to be inversely related to the maximal response to a high-contrast sinusoidal grating of optimal spatial frequency and orientation. Indeed, Table 2 shows that P₀ and peak response had a correlation coefficient of −0.57, whereas the multivariate regression coefficient for P₀ against relative modulation, spontaneous activity, and peak grating response was 0.781. Relative modulation, spontaneous activity, and peak response are not, however, independent variables (see Discussion).

If a neuron responds sparsely to natural images, it might be that it would also respond sparsely to sinusoidal gratings (Vinje and Gallant, 2000, 2002) (i.e., neurons with the narrowest tuning curves for grating parameters might respond most sparsely to natural images). Figure 7 plots P₀ against orientation bandwidth (C) and spatial-frequency bandwidth (D) calculated as width at half-height. As predicted, the negative correlation coefficients are extremely statistically significant (Table 2), although they are low (−0.47, −0.48). The multivariate correlation on the two bandwidths is stronger (r = 0.58), but orientation and spatial frequency bandwidth are not fully independent factors (Tolhurst and Thompson, 1981; Baker et al., 1998; Xing et al., 2004). For 71 of the neurons, we were also able to calculate a more global measure of spatial-frequency tuning, LSFV (Xing et al., 2004). The correlation between P₀ and LSFV was −0.53, compared with a correlation of −0.51 against bandwidth at half-height for the same 71 neurons. Table 2 shows the multivariate correlation coefficient for P₀ against all five of the “grating” factors that we have discussed: the coefficient is 0.818, representing 67% of the variance in the widespread values of sparseness in our population.

The effects of response variability

Figure 4 shows clearly that the responses of V1 neurons to natural image stimuli are subject to response variability or “noise”; the form of the noise distribution is likely to have contributed to the form of the response distributions and, therefore, to the measures of sparseness reported above. For instance, if a particular image were to evoke a response of 1–2 on average, it would quite likely evoke responses of zero on individual trials, thereby increasing P₀. Furthermore, those few images that evoke large responses on average will sometimes evoke particularly large responses by chance, exaggerating the distribution tail that so contributes to the kurtosis measure in particular. The increase in P₀ and the lengthening of the response distribution tail would be expected to increase the various sparseness measures. Figure 8 shows schematically how “clean” response distributions (redrawn from Fig. 3B,H) might be affected by the kinds of response noise seen with moving sinusoidal gratings, in which the response variance is approximately equal to twice the response mean (Dean, 1981; Tolhurst et al., 1981, 1983; Vogels et al., 1989; Snowden et al., 1992; Geisler and Albrecht, 1997; Wiener et al., 2001) (but see Gur et al., 1997; Kara et al., 2000). The distributions of Figure 8, A and B, are considered as the distributions of the mean responses to individual images; the values in Figure 8, C and D, are given by sampling from noisy distributions with those means and with variances twice the means. All four sparseness measures are increased by the response variability.

Figure 8.

Schematics to how the potential effects of response variability on the forms of simple cell response distributions for natural image stimuli. A and B show “clean” thresholded Gaussian distributions (replotted from Fig. 3B,H, respectively). Each of these occurrences is considered to be the mean value in a Poisson-like distribution, the underlying noise-free response to an image. Each occurrence in A and B is replaced in C and D by noise-corrupted values: each “clean” occurrence is first replaced from a randomly chosen sample from a Poisson distribution with parameter equal to the “clean” response; then, that sample is in turn replaced with a randomly chosen sample from a second Poisson distribution with parameter equal to the interim “noisy” value. This gives variance approximately equal to twice the mean response level for any particular stimulus. Note that response noise increases the number of zero responses and also the length of the distribution tail at high response magnitudes.

To determine the actual effect of response variance on response sparseness, we measured the responses of 24 neurons to 10 repeated presentations of a set of 500 natural image stimuli. For each neuron, we could consider the 5000 image presentations as independent events (as in Fig. 5A–D), or we could average the 10 evoked responses for each stimulus before plotting the distributions and measuring their sparseness. Figure 5, E and F, shows the distributions of the averaged responses to the 10 repetitions of each of 500 image fragments for the same two neurons whose individual responses to the 5000 image presentations are shown in Figure 5, A and B. The Treves–Rolls, P₀, and kurtosis measures are all reduced by the averaging as predicted (Fig. 8). Averaging the responses to stimulus repetitions seems to have caused an increase in response entropy, but this is attributable more to the ∼10 times increase in the number of response bins than to any change in the form of the response distribution (see Materials and Methods); because of differences in bin sizes, it is not possible to describe the effect of response averaging on the entropy of the distributions (see Materials and Methods)!

For the 24 neurons in which we presented the same image fragments 10 times, Figure 9A plots P₀ after averaging the 10 repetitions of each of the 500 stimuli against P₀ calculated from the overall distribution of 5000 responses. The results all lie below the line of equality showing that response noise had, indeed, increased the measured response sparseness over that expected from clean responsiveness. The same was found with the Treves–Rolls and kurtosis measures of response sparseness. In Discussion, we will consider how these observations might make population coding of stimulus features less sparse than is implied by the sparseness of response of single neurons.

To determine the magnitude of the effects of response noise, we characterized the forms of response distributions as the ratio of the overall variance of the response distribution divided by the mean response magnitude. If there were no response variability, then averaging of the responses to 10 repetitions of each stimulus would have no effect on the variance/mean ratio of the response distribution. However, if the variety of responses to individual stimulus presentations is attributable entirely to the form of the noise distribution (such that the averaged response to all stimuli was actually the same), then averaging the responses to 10 repetitions should lead to a 10 times reduction in the variance/mean ratio. Figure 9B plots the variance/mean ratio of the response distributions after averaging stimulus repetitions against the variance/mean ratio of the individual, unaveraged responses. The results do lie below the line of equality confirming that response variability has contributed to the form of the response distribution, but the variance/mean ratio is not nearly reduced by a full factor of 10 by averaging the responses to 10 stimulus repetitions; thus, response variability contributes no more than ∼20–50% of the variance in the distribution of the responses to individual stimuli.

The nature of the response variability

Figure 10, A and B, further examines the nature of the response variability for the two neurons illustrated in Figures 4, A and B, and 5, A and B, and E and F. For the 500 image fragments, the graphs plot the variance of the responses to the 10 repetitions of each fragment against the mean response to that fragment (zero values are omitted from the log–log graphs). The graphs have an obvious positive slope showing that response variance for natural image fragments is proportional to the mean response (is “multiplicative”), just as it is for moving sinusoidal gratings (Tolhurst et al., 1981, 1983). The graphs show the lines of equality and it can be seen that response variance is only slightly greater than (Fig. 10A) or lower than (Fig. 10B) the mean response level. Given only 10 repetitions, mean responses below ∼0.2–0.4 tell us little interesting about the detailed form of response variability. Thus, we have analyzed only those data for which the mean response is 0.4 action potentials per presentation and above. Generally, the slopes of regression lines on log–log axes were close to unity (Fig. 10, legend), and, on average, the variance was 1.502 times the response mean. The slope close to unity is similar to that often reported for experiments on moving sinusoidal gratings (Dean, 1981; Tolhurst et al., 1981, 1983). However, the ratio of variance to response is lower than has generally been reported for moving gratings. Figure 10C confirms that, in the present experiments, response variance for 100 ms flashed presentations of natural image fragments was lower than the response variance for gratings moving at 1–2 Hz. The figure plots the ratio of response variance/mean for the natural image stimuli against the variance/mean ratio of the same neurons for moving sinusoidal gratings. The data mostly lie well below the line of equality. In the present experiments on ferrets, the variance of response to gratings was 2.79 times the mean response on average, comparable with our first reports on response variance in cat V1 (Tolhurst et al., 1981).

Figure 10.

A, B, The variance of response to 10 repetitions of each natural image fragment is plotted against the mean response to that fragment for the two neurons illustrated in Figures 4, A and B, and 5, A and B, and E and F. Data with mean response of zero cannot be plotted on the log–log axes; there are fewer data plotted in A because the responses of this neuron were sparser than the responses of B (Figs. 4A,B, 5A,B). The lines are the lines of equality. Regression lines fitted to those points with abscissa value 0.4 and above had slope and intercept: 0.951, 1.238 (A), and 0.707, 0.783 (B). The intercept is the average ratio of variance to mean response for that neuron. C, For 24 neurons, the average variance/mean-response ratio was calculated for those flashed natural image stimuli giving a mean response of at least 0.4 action potentials per presentation and is plotted as ordinate against the variance/mean-response ratio for moving high contrast sinusoidal gratings. The ratio for natural image stimuli was calculated from 10 repetitions of up to 500 stimuli; the ratio for gratings was calculated for 30 cycles of up to 12 stimuli, varying in spatial frequency or orientation. The line is the line of equality.

Information transfer

We can summarize many aspects of the responses to natural stimuli by calculating the mutual information between response and stimulus (Eq. 4). For the 24 neurons for which we examined response reliability by presenting 500 different stimuli repeatedly, the information conveyed in their responses about which image was presented ranged from only 0.130 to 1.247 bits (mean, 0.551 bits). Three factors contribute to these low values. First, we have characterized the response to each stimulus presentation as a single integer number, and few neurons generated >20 different response states to distribute across 500 or more different stimuli, whereas many neurons produced <10 states. Second, there is inherent response variability so that a given image does not generate a unique response, and the few response states are not a reliable measure of which image is presented. Last, in many neurons, the high sparseness of response means that a large number of different images give the same, nonvariable response (i.e., zero spikes).

Temporal factors

It may be too simplistic to characterize neuronal response only as an integer spike count in, say, a 100 ms interval. In particular, we asked whether the responses to the most powerful stimuli are of the same form as responses to weaker stimuli. Figure 11 shows some examples. For each neuron, we averaged its responses to the 10 repetitions of each natural scene stimulus and then ranked the 500 images in order of averaged response. The upper row shows, for each neuron, the PSTH generated by summing the responses for the 20 most powerful stimuli; the second row shows the summed responses to stimuli ranked 41–70; whereas the bottom row shows the summed responses to 50 much weaker stimuli. The overall form of the response PSTH is little affected by the changes in response magnitude, apart from the change in balance between the ON and OFF responses of the simple cell in Figure 11B, which is the same as Figure 1C. Here, the strongest responses were ON responses to some stimuli, whereas the OFF responses to other stimuli were generally weaker. It is interesting that the obvious shoulder in the overall PSTH (Fig. 1C) at ∼40 ms after stimulus onset is evident in all three PSTHs of Figure 11B; it is not that, say, the more powerful and the weaker stimuli differ in latency to cause the shoulder. The histograms of Figure 11C all show pure OFF responses; this is the same simple cell as in Figure 1E, in which the ON/OFF overall PSTH is derived from pure ON responses given to some stimuli, but pure OFF responses given to other stimuli.

Although there is no systematic change in response form with the overall strength of response, it may still be that the exact timings of spikes may vary in a consistent manner between stimuli so that, say, a response of “eight spikes” to one stimulus could be treated as a different code from a response of eight spikes to a different stimulus. Figure 12 shows spike–time rasters for four of the neurons for which we made 10 or more repeated presentations of stimuli. The rasters are arranged so that the 10 responses to a given stimulus are closely grouped together, with those stimuli giving the most powerful responses (on average) being listed at the top of the panels. The lower halves of the panels show the repeated responses to stimuli that were so weak that they evoked spikes on only ∼50% of presentations. The black and red dots show the times of action potentials, the red dots showing the timing of the first spike in each response (i.e., the latency of the response). The green symbols show trials in which the neurons failed to respond at all. Because response latency to flashed gratings varies with contrast or stimulus strength (Gawne et al., 1996; Reich et al., 2001; Geisler et al., 2007) and because it has been argued that first-spike latency could be important in encoding stimulus information (Thorpe et al., 2001; Van Rullen et al., 2005), we particularly investigated the consistency of first-spike latency (red symbols).

Figure 12.

The rasters show the times of action potentials of four neurons in response to repetitions of different subsets of the 500 images. For each neuron, the responses are shown for the 20 images that evoked the greatest response on average from the respective neuron and a further 20+ images that evoked weak responses. The rows of the rasters are grouped in 10 s (A, C, D) (or 11 s; B), the number of repeats, with gaps to separate the responses to the different images. The black and red symbols show the times of action potentials after stimulus onset (B–D) or offset (A); the red symbols show the first spike after the stimulus transition in each raster row. The green symbols show those stimulus presentations that elicited no action potentials at all.

It is very clear that, for the most powerful stimuli (in the top one-half of the figure), there are small differences in response latency between stimuli (up to 15 ms in Fig. 12A; up to 30 ms in Fig. 12B), and that the tonic or phasic nature of the response may also vary. This is most obvious for neurons A and B. Indeed, for these two neurons, among the responses to the 20 most powerful images, the variance of the latencies within the repeated presentations of single stimuli was less than the variance between the latencies to different stimuli (A, interstimulus variance, 25.6 ms²; intrastimulus variance, 15.1 ms²; B, 24.31 vs 37.2 ms²). Although neuron C (and perhaps D) shows some evidence that response timings differ between stimuli, the intrastimulus variance is more than double the interstimulus variance (C, interstimulus variance, 74.4 ms²; intrastimulus variance, 153.7 ms²; D, 35.9 vs 101.4 ms²). Although there may be small differences in response latency between stimuli that are evident from repeated presentations, these are overshadowed on any single trial by the large variability of latency and spike count in the responses to any single stimulus image (note the wide dispersal of the red symbols within each block of 10 raster lines in C and D). Apart from neurons A and B, all the other neurons in our sample with repeated presentations of stimuli behaved like neurons C and D: either there was no evidence that response timings differed between stimuli, or the differences between stimuli on average were smaller than the inherent response variability to the same stimulus.

The bottom one-half of Figure 12 shows the repeated responses of the four neurons to stimuli that were so weak that they rarely evoked more than one spike (note how few black symbols are present) and sometimes no spikes at all (green symbols). The variability of first spike latency is clearly greater for the weak responses, but the earliest spikes still have much the same latency as the more regular first-spikes for stronger stimuli. Confirming the implications of Figure 11, there is no systematic change in response form as the stimuli get weaker; any change in average latency is artifactual and is accompanied by a great drop in reliability. There may still be evidence of small timing differences between stimuli on average, but, trial by trial, spike timing in a single neuron would be a poor code for stimulus identity, given the variability of latency and the frequent failure to fire at all. At these low response levels, the great variability is such that temporal cues are unlikely to be useable for determining whether a response has occurred or not, unlike the situation in auditory cortex (DeWeese et al., 2003, 2005).

If we consider response as a simple spike count in 100 ms, neuron A in Figure 12 gave 17 different integer response levels (0–16). The mutual information between response and stimulus was only 0.796 bits. However, this neuron clearly showed different response timing to different stimuli, and so this must be an underestimate of the amount of information that could be conveyed in the responses of this neuron. Although the response to a given stimulus may not be the same on each presentation, it might still be that those different response patterns are unique to that stimulus. If we take the extreme and unrealistic view that every nonzero response is unique in its exact timing details, neuron A gave 1357 “different” nonzero responses. The mutual information increased to 2.62 bits (500 stimuli needs 8.97 bits). This extreme upper limit on information transmitted presumes an immense level of precision in the interpretation of spike timings (e.g., the neuron gave only one spike on 576 of the 100 ms presentations). If these really were to be treated as 576 different responses, we would have to presume that the code is precise to 0.2 ms or less.

Discussion

We have examined responses of ferret striate cortex neurons to flashed natural scenes, using a stimulation protocol mimicking, in a stylized way, the static fixations interspersed with sudden saccades of “natural” vision. The supplemental material (available at www.jneurosci.org) describes preliminary analysis of experiments with, arguably, more naturalistic stimulus movies (Smyth et al., 2002): single scenes presented for 5.6 s and panned in irregular steps as if the animal was moving its gaze around one scene. The basic results are the same in the two kinds of experiment. Are the forms of response to either kind of stimulus compatible with theories of sparse encoding, argued to be advantageous on various grounds (Field, 1994; Attwell and Laughlin, 2001)?

We initially made simple spike counts as blunt measures of response, and we measured response variability by presenting the same stimuli several times. Variability for flashed natural scenes was less than for moving sinusoidal gratings, perhaps because flashed stimuli have well defined sudden temporal discontinuities (cf. Gur et al., 1997; Kara et al., 2000) and not because of special adaptations for coding natural images. The firing rates averaged across all stimulus presentations ranged widely (0.28–45.94 i.p.s.; median, 4.10 i.p.s.). Such low average firing rates are similar to other natural-image studies in anesthetized and, importantly, in awake animals (Legéndy and Salcman, 1985; Baddeley et al., 1997; Gallant et al., 1998; Ringach et al., 2002; Guo et al., 2005; Maldonado and Babul, 2007; Yen et al., 2007), and with firing rates measured in other sensory areas in alert, behaving animals (e.g., Griffith and Horn, 1966; Burns and Webb, 1976; Fanselow and Nicolelis, 1999; Schoenbaum et al., 1999; DiCarlo and Maunsell, 2000). Our range is slightly higher than estimated rates (0.25–1.5 i.p.s.) that would be compatible with the overall energy consumption of cerebral cortex (Attwell and Laughlin, 2001; Lennie, 2003). Arguably, this might reflect undersampling, with extracellular recordings, of neurons with very low spontaneous activity (cf. Margrie et al., 2002). However, the spontaneous firing rate in our study (median, 0.64 i.p.s) is close to that found in a two-photon comparison of spontaneous activity in awake versus anesthetized rat visual cortex (Greenberg et al., 2008)

Sparse responses

We characterized the lifetime sparseness of each neuron (Willmore and Tolhurst, 2001). In a sparse code, each neuron should fail to respond to most stimulus images but should respond distinctly and reliably to just a few. Indeed, 12 of 89 of our neurons responded to <5% of flashed images (Fig. 6D); one-half responded to <25% of flashed images, but this seems a higher proportion of nonzero responses than is implied by theories of sparse coding.

We used the measure of response sparseness of Treves and Rolls (1991), as well as other measures. Sparseness varied considerably between neurons, but the averages (mean TR sparseness, 0.783; SD, 0.19) were similar to other studies (Vinje and Gallant, 2000; Yen et al., 2007). Some 20% of the neurons in our sample had appreciable spontaneous activity (above ∼3 i.p.s.) so that spikes were generated during the presentation of most stimuli, and our sparseness measures implied that their responses were not sparse. Superficially, the decrease in spontaneous activity seen in anesthetized animals (Greenberg et al., 2008) should increase sparseness, but this may be offset by decreases in burst firing (Greenberg et al., 2008).

In a sparse code, a neuron should respond to few stimulus images, but we expect those few responses to be reliably different from the baseline response of zero (hard sparseness) (Rehn and Sommer, 2007). However, the responses of all but one of our ferret V1 neurons were compatible only with soft sparseness: although the most common response of the neuron to images might indeed be zero spikes, the second most common was one spike, the next most common was two spikes, and so on. Response distributions tailed away like the exponential distributions of Baddeley et al. (1997).

When the same images were presented repeatedly, the responses of a neuron were not identical, exaggerating the measures of response sparseness: images that (on average) evoke a small response often evoke zero spikes, whereas the rare images which evoke big responses will sometimes evoke extra large ones. Because response variability is multiplicative, larger responses will be most distorted; however, this may not be a consideration if the sparse code is one in which response magnitude is irrelevant, provided that it is distinctly nonzero. Response variability lessens the impact of the proposal that a few nonzero responses of a neuron convey significant information about a few images. However, this might be overcome by averaging the responses of multiple neurons signaling in parallel. The sparseness of the overall population would be less than measured for any one neuron, but having multiple neurons with replicated firing patterns rather contradicts metabolic arguments for sparse codes.

Neurons differ markedly in sparseness

Multivariate analysis revealed that response sparseness for flashed natural images was strongly correlated with the response pattern of the neurons for moving sinusoidal gratings. Sparseness varied inversely with orientation and spatial-frequency tuning bandwidth, and with the peak firing rate to gratings; the fewer gratings that activated a neuron and the lower the firing rates, the fewer the responses to natural images too. Sparseness was inversely related to the amount of spontaneous activity, but was positively correlated with the degree of modulation (F1/F0) in the responses to sinusoids. These five factors are themselves partly correlated, of course: high spontaneous activity was more commonly found in complex cells with low F1/F0 and, unfortunately, such activity also lowers the calculated value of F1/F0 in other neurons. Neurons with low responsivity (high threshold, perhaps) would tend to have higher F1/F0 (Mechler and Ringach, 2002). Overall, the multivariate correlations imply that response sparseness for flashed natural images does not depend on any special mechanisms above those for grating responses. Is a comparison between responses to drifting gratings and flashed natural scenes appropriate? The supplemental material (available at www.jneurosci.org) shows responses to moving natural stimuli and, crucially, the correlation of sparseness for movies with F1/F0 closely resembles that for flashed stimuli (supplemental Fig. 3, available at www.jneurosci.org as supplemental material).

Sparseness was greater for neurons with higher F1/F0, implying that simple cells (Hubel and Wiesel, 1959, 1962) give sparser responses than complex cells. However, we expect complex cells to respond to twice as many images as simple cells, because responses of “classical” simple cells are effectively half-wave rectified, whereas complex cells give full-wave rectified responses (Movshon et al., 1978a,b). Each simple cell only codes for one-half the natural scenes; complete coding requires a pair of simple cells, whose receptive fields are complementary, making the population code less sparse.

Temporal response structure

Summarizing neuronal responses as total spike counts neglects any stimulus-dependent differences in the temporal structure of responses. Changes in latency or response form are expected of spatiotemporal inseparable simple cells (Maffei and Fiorentini, 1973; Movshon et al., 1978a; Dean and Tolhurst, 1986; McLean and Palmer, 1989; Reid et al., 1991; DeAngelis et al. 1993). Thorpe et al. (2001) propose that the latency of the first spike gives enough information for rapid behavioral decisions about scene content and, indeed, some of our neurons showed different response latencies for different natural stimuli.

“Integrate-and-fire” models imply that latency is shortest for strong stimuli, becoming systematically longer as stimuli become less favored. However, we found no systematic changes in overall PSTH shape, even as total spike count fell. Because the PSTH represents the probability of spike occurrence against time, and because PSTH shape remained constant despite falling overall response probability, this necessarily means that the first-spike latency became much more variable for weak stimuli (often no spikes would be generated on some trials). The average first-spike latency did increase as stimuli became weak, but the variance of the latency also increased so dramatically that it is difficult to envisage latency as a useful code.

For some neurons, we could compare the intrastimulus latency variance with the interstimulus latency variance. Although, on average, some stimuli evoked shorter latency responses than others, the inherent trial-by-trial response variability to identical stimuli mostly outweighed any subtle differences between stimuli. Thus, first-spike latency was not reliable trial-by-trial, unlike in the auditory cortex (DeWeese et al., 2003, 2005). It is difficult to see how first-spike latency could be a reliable encoder, unless many neurons of like spatiotemporal character signal in parallel. Furthermore, when considering how our whole disparate population of neurons might encode natural scenes, the response latency of different neurons varied widely (by 30 ms or more), as found for other visual stimuli (Troy and Lennie, 1987; Maunsell et al., 1999; Saul and Feidler, 2002; Weng et al., 2005). Differences between neurons were far greater than any subtle intrastimulus differences within the responses of a single neuron. It would be curious if coding relied on small differences in response latency of the quickest neurons, whereas many neurons were unable to contribute because they always responded too late!

In conclusion, the responses of ferret V1 neurons are difficult to reconcile with our expectations of the needs of sparse coding. The soft sparseness and the unreliability of spike counts and of spike timing suggest that reliable coding must rely on the simultaneous activity of many neurons conveying redundant information in the noise.