Timescale-Invariant Representation of Acoustic Communication Signals by a Bursting Neuron

Abstract

Acoustic communication often involves complex sound motifs in which the relative durations of individual elements, but not their absolute durations, convey meaning. Decoding such signals requires an explicit or implicit calculation of the ratios between time intervals. Using grasshopper communication as a model, we demonstrate how this seemingly difficult computation can be solved in real time by a small set of auditory neurons. One of these cells, an ascending interneuron, generates bursts of action potentials in response to the rhythmic syllable–pause structure of grasshopper calls. Our data show that these bursts are preferentially triggered at syllable onset; the number of spikes within the burst is linearly correlated with the duration of the preceding pause. Integrating the number of spikes over a fixed time window therefore leads to a total spike count that reflects the characteristic syllable-to-pause ratio of the species while being invariant to playing back the call faster or slower. Such a timescale-invariant recognition is essential under natural conditions, because grasshoppers do not thermoregulate; the call of a sender sitting in the shade will be slower than that of a grasshopper in the sun. Our results show that timescale-invariant stimulus recognition can be implemented at the single-cell level without directly calculating the ratio between pulse and interpulse durations.

Introduction

Object recognition relies on the extraction of stimulus attributes that are invariant under natural variations of the sensory input. Such stimulus variations include the size, orientation, or position of a visual object (Sáry et al., 1993; Ito et al., 1995; Rolls, 2000), the strength of an odor (Stopfer et al., 2003), and the intensity, frequency composition, or duration of a sound signal (Shannon et al., 1995; Moore, 1997; Bendor and Wang, 2005; Benda and Hennig, 2008). A particular challenge arises when timescale-invariant features of an acoustic signal are to be extracted because this computation generally involves ratios of temporal quantities. For example, to calculate the relative duration of two sound patterns, the respective durations of both components need to be measured and their ratio calculated.

Many animals use acoustic communication signals to find conspecific mates and judge their reproductive fitness (Gerhardt and Huber, 2002). Temporal parameters of songs are species-specific and decisive for song recognition in most insects that use acoustic signals (Hennig et al., 2004). For ectothermic species, such as grasshoppers, this poses a severe problem because their calling songs are faster or slower depending on the ambient temperature. Sound signals that are rhythmically structured into syllables and pauses (see Fig. 1A) offer a solution if the receiver uses the temperature-independent syllable-to-pause ratio for species identification, as suggested by behavioral experiments with artificial stimuli (see Fig. 1B). Indeed, the syllable-to-pause ratio varies greatly between different species, facilitating the recognition of conspecific songs (von Helversen and von Helversen, 1994). However, to compute this quantity, durations of syllables and pauses need to be measured and compared with each other. The present study reveals that even a relatively small neural network such as the grasshopper auditory system (Stumpner and Ronacher, 1991; Stumpner et al., 1991) can achieve this task. The underlying computational strategy is surprisingly simple and applicable to a wide range of sensory systems that need to extract timescale-invariant stimulus features in real time.

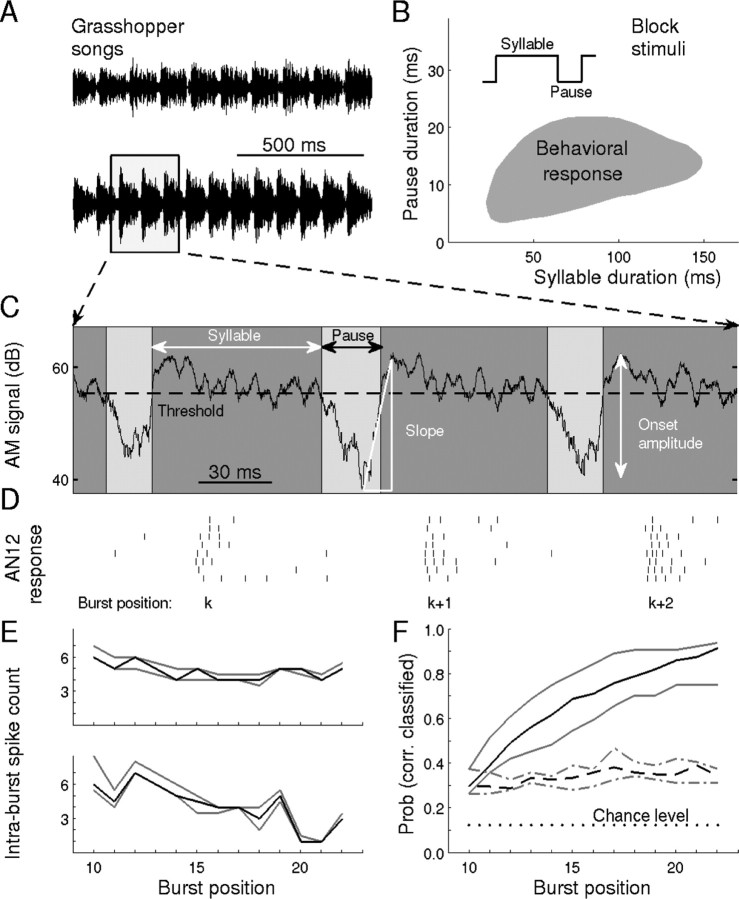
Figure 1.

Bursts of action potentials contain stimulus-specific information. A, Acridid grasshoppers produce species-specific acoustic communication signals by rasping their hindlegs across their forewings. This generates an amplitude-modulated broadband noise signal (AM signal). Shown are two such “songs” from males of the species C. biguttulus. Each song consists of many repetitions of a pair of basic patterns, called “syllable” and “pause,” episodes of high and low amplitude, respectively. B, Conspecific female grasshoppers respond to a certain range of syllable and pause durations, as tested with artificial block stimuli. Within the gray area, a female responded positively in at least 20% of all trials [data were taken from von Helversen and von Helversen (1994) with permission]. C, Enlarged AM signal with song parameters analyzed in the present study. The calculated amplitude threshold for this cell was 55.4 dB SPL. For illustrative purposes, pauses are only marked for threshold crossings that are followed by, on average, at least one spike per trial. Smaller amplitude modulations are neglected; they are also not perceived as pauses by the animal, as shown by behavioral experiments (Wohlgemuth, 2008 A. Einhäupl and B. Ronacher, unpublished results). D, Spike trains of a particular ascending auditory interneuron, the AN12. Syllable onsets trigger burst responses. The response latency of ∼12ms is attributable to acoustic delays, response latencies of the receptor neurons, axonal and synaptic delays, and the intrinsic AN12dynamics. E, IBSC as a function of the burst index (i.e., the position of the burst within the particular calling song). For the two songs in A, the black lines denote the median IBSC, and the gray lines indicate upper and lower quartiles. F, Probability of correctly classifying one of eight songs by IBSC only (chance level, 1/8). Dotted line, Classification using IBSCs from one burst index; solid line, classification by cumulating the information contained in IBSCs from the 10th burst up to the indicated burst. These data demonstrate that songs can be classified successfully in >90% of all trials if IBSCs from 12 or more bursts are used. Hence, the spike count within bursts is sufficient for conspecific song discrimination. Data shown in D–F are from one sample cell.

Materials and Methods

Experimental paradigms, animals, and electrophysiology.

For this study, two different sets of experiments were performed. In the first set, grasshopper mating songs (see Fig. 1A,C) were presented to six females, three Chorthippus biguttulus, and, for comparison, three Locusta migratoria. Homologous auditory receptor neurons and interneurons have been identified in the auditory systems of both species (Römer and Marquart, 1984; Stumpner and Ronacher, 1991). In the second set of experiments, responses to artificial stimuli that mimic the basic syllable–pause structure of the natural songs (see Fig. 1B) were studied in nine C. biguttulus females. The experimental procedures for both paradigms were similar and are described in detail by Wohlgemuth and Ronacher (2007) and Stumpner and Ronacher (1991), respectively. Briefly, legs, wings, head, and gut were removed, and the animals were fixed with wax, dorsal side up, onto a free-standing holder. The thorax was opened to expose the auditory pathway in the metathoracic ganglion. The whole torso was filled with locust Ringer (Pearson and Robertson, 1981). Neurons were recorded intracellularly; responses were amplified and recorded with a sampling rate of 20 kHz. The microelectrode tips were filled with a 3–5% solution of Lucifer yellow in 0.5 m LiCl. After completion of the stimulation protocols, the dye was injected into the recorded cell by applying hyperpolarizing current. After an experiment, the thoracic ganglia were removed, fixed in 4% paraformaldehyde, dehydrated, and cleared in methylsalicylate. Stained cells were identified under a fluorescent microscope according to their characteristic morphology. The experimental protocols complied with German laws governing animal care.

Acoustic stimulation.

For both experimental paradigms, the stimulus–response curve of each AN12 cell was determined using 100-ms-long sound pulses whose intensity was varied from 30 to 90 dB sound pressure level (SPL) in steps of 10 dB. For the core experiments, maximum stimulus intensities were then chosen to lie approximately halfway on the rising slope of the stimulus–response curve. For the natural-song paradigm, songs from eight different males were used: two examples are shown in Figure 1A. The artificial songs consisted of six syllables with constant sound intensity, separated by silent pauses (see also Fig. 1B). The durations of syllables (40, 85, or 110 ms) and pauses (3.2, 8.8, 16.3, 24.0, 33.0, and 42.5 ms) were constant for each artificial song and varied in a pseudorandom manner within the experiments. The sound envelopes were filled with a white noise carrier, band passed between 2.5 and 40 kHz. Both types of stimuli are known to evoke positive responses in behavioral experiments with female grasshoppers (von Helversen and von Helversen, 1994). Each stimulus set was repeated eight times. Note that stimulus–response curves of AN12 cells have a dynamic range of ∼40 dB (Stumpner and Ronacher, 1991), so that the songs presented (mean SD of the amplitude fluctuations of each song, 10 dB) do not extend into the saturated region of the stimulus–response functions.

Data analysis.

From the digitized recordings, spike times were determined using a voltage-threshold criterion. To account for neural fatigue, bursts were defined by a recursive formula: a spike belongs to a burst if it follows the preceding, nth, spike of that burst by no more than (3 + n) ms. The first interspike interval (ISI) within a burst is thus at most 4 ms, the second at most 5 ms, and so on. This definition reflects the observation that interspike intervals within an AN12 burst typically increase from spike to spike. Accordingly, ISI distributions do not show a clear gap. Using a fixed ISI criterion would therefore either miss the later spikes within a long burst (for short ISI cutoffs) or misclassify isolated spikes as belonging to a multispike burst (for longer ISI cutoffs). Note also that, unlike in other systems (for review, see Krahe and Gabbiani, 2004), the biophysical mechanism underlying AN12 bursting is unknown. For notational simplicity, isolated spikes were treated as bursts with one spike. Throughout this study, we ignored any information in the temporal fine structure within bursts and concentrated on intraburst spike counts (IBSCs). In natural grasshopper songs, each syllable onset is preceded by a period of relative quietness (see Fig. 1A,C). As for the artificial songs, this period of relative quietness will be called a “pause.” It is defined as the interval between the times at which the sound signal, normalized with respect to its mean and SD, passes a certain amplitude threshold from above and again from below. For each cell, the threshold was determined by maximizing the correlation between pause and spike count within the subsequent burst. This procedure leads to a robust threshold estimate (see Fig. 2C). The relative onset amplitude of a specific song syllable is defined as the difference between the maximal amplitude of that syllable and the minimal amplitude in the preceding pause. The total syllable period is calculated as the time interval between the first spikes of two subsequent bursts. Finally, the onset slope is given by the onset amplitude divided by the time interval between maximal and minimal amplitude values. These definitions are illustrated in Figure 1C. To obtain the correlation between spike count and signal features, the R² value (explained variance, Pearson's correlation) was calculated. It was tested for multicollinearity by computing the semipartial R value for each independent variable. The mutual information between pause duration and IBSC was calculated using the adaptive method (Nelken et al., 2005).

Figure 2.

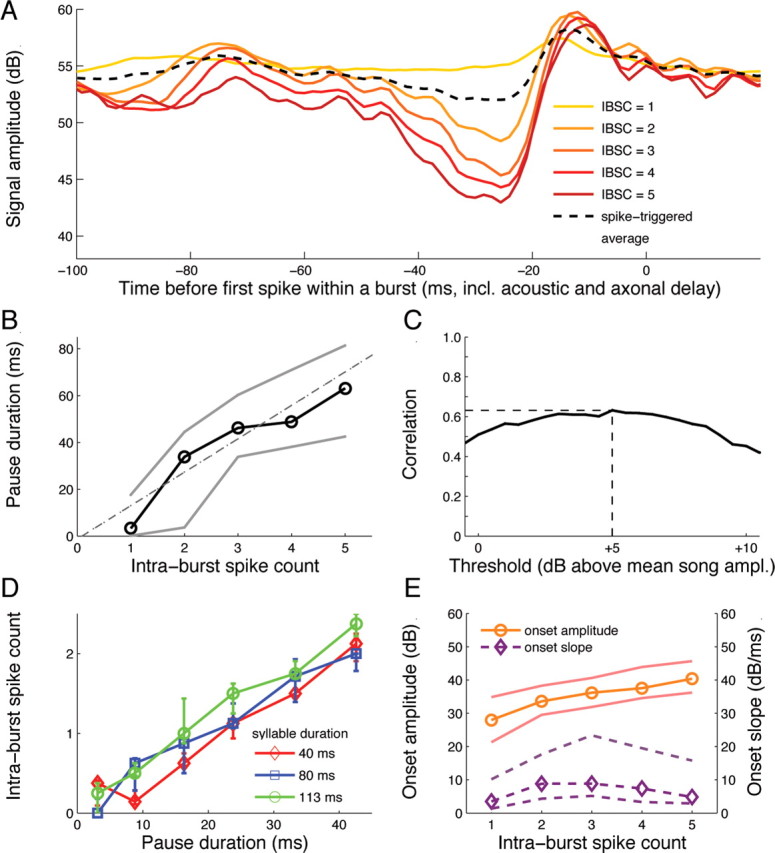
IBSC encodes preceding pause duration. A, Burst-triggered average (i.e., mean stimulus before a burst with given IBSC); for comparison, the spike-triggered average over all action potentials is depicted too. As shown by these data, bursts with large IBSC occur preferentially after long phases of low sound intensity. B, Pause duration is linearly correlated with the IBSC of the following burst [R² = 0.69 ± 0.15 (SD); p < 10⁻⁵; Pearson's]; the gray lines indicate upper and lower quartiles. With a y-intercept of only −1.1 ± 2.1 ms, the best fit agrees with a direct proportionality of pause duration and IBSC. The pause duration was defined individually for each cell by setting a threshold for the sound amplitude level of all songs (Fig. 1C); to account for global amplitude differences between the songs, amplitudes were first normalized with respect to mean and SD. C, Correlation coefficient between pause duration and intraburst spike count, as a function of the amplitude threshold used for defining pauses. The smooth maximum demonstrates that the definition in B is robust against variations of the threshold, here shown relative to the mean song amplitude. D, For artificial block stimuli, IBSC is again linearly correlated with pause duration (R² = 0.76 ± 0.15; p < 10⁻⁵). Different colors correspond to stimuli with different syllable durations. E, For natural songs, the onset amplitude, but not onset slope, is partially correlated with IBSC (R² = 0.27 ± 0.08; p < 10⁻⁵) because of covariations of pause duration and onset amplitude in natural songs. The ordinate depicts amplitude (in decibels) for the solid curve, and amplitude/time (in decibels/millisecond) for the dashed curve. Data in A–C and E are from one sample cell; D refers to a second neuron. The statistics refer to all cells tested.

Song classification.

AN12 responses were classified according to their IBSCs without relying on explicit temporal information: First, the IBSC of each burst was assigned to the time bin t (bin width, 2 ms) of the first spike within the burst. Second, for each bin t and song j, the mean IBSC value over all repetitions i of the song was calculated. If this mean, IBSC(j, t),exceeded unity, the burst was given a burst position k (1, 2, 3, … ), in ascending order. This procedure was performed for all songs. Third, for every burst position k and repetition i, each IBSC(i, j, k) was assigned to the song j̃ with closest IBSC(j, k), i.e., j̃ = arg(min_ĵ (diff(i, j, ĵ, k))) where diff(i, j, ĵ, k) = |IBSC(i, j, k) − IBSC(ĵ, k)|. To avoid a bias, for each IBSC(i, j, k), the corresponding IBSC(j, k) was calculated without taking IBSC(i, j, k) into account. Finally, for the cumulative classification, we calculated diff_cum(i, j, ĵ, k*) = $\underset{k=1}{\overset{k*}{\Sigma }}$diff(i, j, ĵ, k) and assigned each IBSC (i, j, k*) = $\underset{k=1}{\overset{k*}{\Sigma }}$IBSC(i, j, k) to song j̃ = arg(min_ĵ,(diff_cum(i, j, ĵ, k*))). Here, k* denotes the burst position up to which information is used for cumulative song classification.

Let us emphasize that this analysis of responses to natural grasshopper songs is based on the stationary part of the calling songs, discarding the first nine syllable-and-pause segments of each song. We do so because, during the transient song phase, stimulus amplitudes increase slowly in time. Adaptation processes partially counteract this increase (Machens et al., 2001), leading to approximately equal burst responses on the AN12 level. However, because the duration of transients differs between songs, IBSCs calculated during the initial song phase carry additional information about song identity that reflects the large-scale structure of the song. To focus on the local syllable–pause structure, we analyze only responses to the stationary part of the songs.

Results

The response properties of a particular neuron (AN12) from the metathoracic ganglion, the first major relay station for auditory signal processing in grasshoppers, may provide an answer to the problem of timescale-invariant sound pattern representation. This neuron belongs to the ∼50 auditory interneurons in the metathoracic ganglion, many of which have been morphologically and physiologically classified (Stumpner and Ronacher, 1994; Stumpner et al., 1991). Ascending neurons (ANs) project into the head ganglion. Some of them (AN1, AN2) encode directional information, whereas others (e.g., AN3, AN4, AN6, AN11, AN12) are presumably involved in pattern recognition (Stumpner and Ronacher, 1994; Krahe et al., 2002). AN12 has a large dynamic range (Stumpner and Ronacher, 1991) of ∼40 dB and generates burst-like discharge patterns when stimulated by the amplitude-modulated sound patterns of grasshopper calling songs (Fig. 1C,D). Its anatomical and stimulus–response characteristics are almost identical in different grasshopper species (Stumpner and Ronacher, 1991; Stumpner et al., 1991; Neuhofer et al., 2008), indicating a highly conserved functional role. For the first part of our study, we recorded from C. biguttulus (n = 3) and L. migratoria (n = 3), as described in Materials and Methods. Unless stated otherwise, data from C. biguttulus are shown. Under stimulation with natural songs, 67% of all spikes were contained in bursts with two or more spikes.

Such bursts are mainly generated in response to syllable onsets (Fig. 1D). The IBSC (i.e., number of spikes within a burst) is highly reproducible from trial to trial but varies from syllable to syllable (Fig. 1E). Reflecting the different time courses of different songs (Fig. 1A), each song thus results in a particular IBSC sequence (Fig. 1E). This signature can be used to discriminate among songs. For example, for a sample with eight songs from one species, each burst carries enough information to assign ∼30% of the responses to the correct song, using the IBSC only (Fig. 1F, dashed line). Accumulated over time, a 90% hit rate is reached after 12 bursts (i.e., ∼1 s) (Fig. 1F, solid line). This astounding discrimination performance is similar to that of grasshopper receptor neurons (Machens et al., 2003), although AN12 neurons have a far lower overall firing rate and their exact spike timing is neglected within the present analysis. Because IBSCs suffice to discriminate songs even from the same species, this measure must contain useful information about the detailed song structure and thus also help discriminate songs from different species.

Which song features elicit burst activity? To address this question, we constructed burst-triggered stimulus averages (i.e., the mean sound wave preceding a burst with given IBSC). As illustrated in Figure 2A, large IBSC values typically occur after extended and deep stimulus excursions, long pauses followed by strong syllable onsets. To identify the song feature that is most important for burst generation, we disentangled the effects of various song parameters (Fig. 1C), such as pause duration, onset amplitude, onset slope, total duration of the preceding song element (syllable plus pause), and minimal pause amplitude. This analysis revealed that pause duration covaries with IBSC (Fig. 2B). The correlation depends on the amplitude level used to define the pause duration, but over a wide range of amplitude levels, it is rather insensitive to parameter variations (Fig. 2C).

To ascertain that pause duration correlates with IBSC under various stimulus conditions, a second set of experiments was performed (C. biguttulus, n = 9). Here, the duration of artificial song units (Fig. 1B, inset) was systematically varied (see Materials and Methods) and IBSC increased linearly with pause duration (Fig. 2D). These data also demonstrate that IBSC does not depend on syllable duration. However, IBSC increases with the onset amplitude for natural songs, but with low R² value (Fig. 2E, top trace). This effect is attributable to covariations of pause duration and onset amplitude in the grasshopper songs. Finally, IBSC is not systematically influenced by onset slope (Fig. 2E, bottom trace) and all other song features tested. Together, these findings support the hypothesis that the AN12 intraburst spike count is well suited to encode the duration of pauses in grasshopper communication signals.

Could the intraburst spike count be used to reliably transmit information about specific structures of the natural calling songs, such as the pause durations, or does the trial-to-trial variability blur the IBSC signal too strongly? To investigate this behaviorally relevant question, we calculated the mutual information between IBSC and preceding pause duration, using the adaptive method (Nelken et al., 2005). On average, the IBSC transmitted 0.49 ± 0.24 bits per burst about the pause duration. Hence, a single burst would not convey enough information for a binary classification of pause durations. However, grasshoppers can integrate over several subsequent bursts, as shown when they evaluate longer song segments to estimate song quality (von Helversen and von Helversen, 1994). This is useful because trial-to-trial IBSC fluctuations are not significantly correlated from burst to burst in individual cells [p > 0.05, turning point test (Kendall and Stuart, 1966)]. Consequently, groups of subsequent bursts could be used to encode average pause durations.

Successful auditory discrimination between songs of different species requires the readout of the syllable-to-pause ratio to be independent of the sender's temperature and thus be timescale invariant. Can this task be accomplished with a neural code based on IBSCs? The following consideration helps to answer this question: Any global speed up of a mating song by some factor X increases the number of syllables per second and, hence, the burst frequency by X. However, because intraburst spike counts are proportional to the preceding pause durations (Fig. 2B,D), the IBSC decreases by the same factor X. As a result, the total spike count per second stays constant and does not reflect the absolute syllable duration but rather the syllable-to-pause ratio (i.e., the relevant feature for time warp-invariant song pattern recognition) (Fig. 3A). This prediction is supported by experimental data, as shown by responses from a sample cell to two conspecific grasshopper songs that differ strongly in syllable duration but have almost identical syllable-to-pause ratio (Fig. 3B). Population data from all cells investigated confirm this finding: there is no correlation between the individual timescale of each of the eight songs, given by the duration of one syllable plus one pause, and the elicited total spike count for a given cell (Fig. 3C). Note that the lower spike count values at ∼80 ms correspond to one specific song. This particular song had a less pronounced syllable–pause structure, which resulted in a lower overall spike count. Integrating the AN12 response over a time window of ∼500 ms or longer thus suffices to reliably estimate the timescale-invariant syllable-to-pause ratio.

Figure 3.

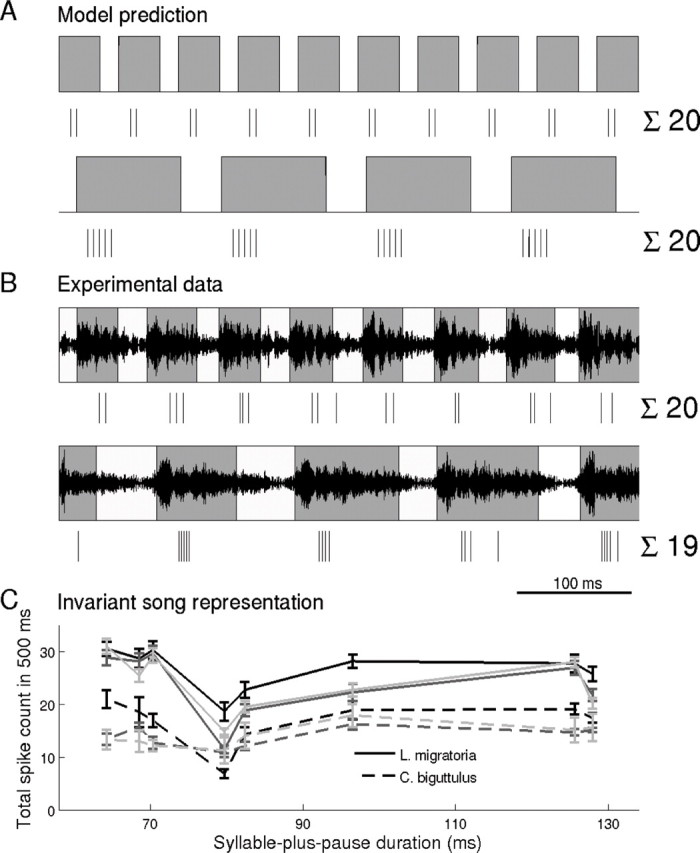
Total spike count is invariant to temporal stimulus rescaling. A, Sketch of two simple auditory sound signals. The lower stimulus is obtained by stretching the upper stimulus by a factor of 2.5. Assuming that the IBSC scales linearly with the preceding pause duration, this rescaling results in 4 instead of 10 bursts, but each burst has now 5 instead of only 2 spikes. Both effects compensate each other so that the total spike count stays constant. B, Measured AN12 responses to two conspecific grasshopper songs. Although the songs differ strongly in their pause durations, the total spike count is approximately equal because the syllable-to-pause ratios of both songs are approximately the same (1.41 for the upper and 1.40 for lower song, respectively), in agreement with the model prediction. C, Total spike count (window length, 500 ms) of responses to the eight tested songs, as a function of the duration of one syllable plus one pause. The duration of this basic song element differs for each song, resulting in the eight different values on the abscissa. Each of the six curves represents data from one neuron, with the species indicated by line type. Error bars indicate upper and lower quartiles of total spike count across eight repetitions. The total spike count varies from cell to cell but without overall correlation to the syllable-plus-pause duration (R² = 0.00 ± 0.14). Downstream neurons thus have access to the behaviorally relevant syllable-to-pause ratio in a timescale-invariant manner.

Discussion

Recognition of timescale-invariant stimulus features is a general challenge for sensory systems and seems to imply that ratios are computed in the temporal domain. Here, we showed that this computationally difficult problem can be solved on the single-cell level by a bursting neuron whose output is integrated over a few hundred milliseconds. Temporal integration over such time scales is well known from various neural systems, such as the auditory cortex (Nelken et al., 2003) or the electromotor system of weakly electric fish (Oestreich et al., 2006). The counting mechanism proposed for readout is similar to that of frogs that also communicate with rhythmic patterns of sound pulses and quiet intervals. Specific neurons in the frog's auditory midbrain integrate the number of acoustic pulses and respond only if a minimal number of appropriate pulses and interpulse intervals arrive (Alder and Rose, 1998; Edwards et al., 2002, 2007). Combined excitation and inhibition determine the dependence of the responses on the duration of the acoustic elements (Edwards et al., 2008; Leary et al., 2008). Together with these results, our findings suggest that the recognition of temporally extended acoustic objects is supported by neural integration over multiple timescales. This hierarchical integration is reminiscent of current models for invariant object recognition in vision that suggest that high-level invariances are detected by successive spatial integration over lower-level stimulus features (Riesenhuber and Poggio, 1999).

It has been suggested that bursts can represent signal slope (Kepecs et al., 2002). In fact, IBSC codes the relative slope of skin displacement in leech (Arganda et al., 2007) and the integral of rate of change in peak pressure in the auditory cortex (Heil, 1997). In contrast to these findings, our data show that the IBSCs of the AN12 neuron do not encode the slope of a stimulus transient but rather the duration of a quiescent stimulus segment. In addition, this time interval is recoded in that a pause of 40 ms may be represented by a burst that lasts for 4 ms only. The temporal compression makes it possible that this new burst code can multiplex information about the time of occurrence and behavioral relevance of a particular sound pattern. Using pause duration instead of syllable duration may be beneficial because this strategy lowers the overall dependency on sound intensity. Although the timescale-invariant readout mechanism proposed by this study depends in principle on the existence of “pauses” in an atonal noise signal, this mechanism can be easily extended to stimuli with rich tonal structure if the raw signal is first split into multiple frequency bands. For rhythmic stimuli in acoustic environments with background noise, separately analyzing specific frequency components using the mechanism proposed in this study will help improve the signal-to-noise ratio in frequency bands with low noise content. Likewise, in mixtures of stimuli with different rhythms and carrier frequencies, a frequency-resolved analysis may reveal otherwise hidden signal components. Computationally demanding divisions in the time domain are thus not required to extract timescale-invariant information from sensory stimuli.