Abstract
Introduction
To evaluate the public health benefit of yearly influenza vaccinations, CDC estimates the number of influenza cases and hospitalizations averted by vaccine. Available input data on cases and vaccinations is aggregated by month and the estimation model is intentionally simple, raising concerns about the accuracy of estimates.
Methods
We created a synthetic dataset with daily counts of influenza cases and vaccinations, calculated “true” averted cases using a reference model applied to the daily data, aggregated the data by month to simulate data that would actually be available, and evaluated the month-level data with seven test methods (including the current method). Methods with averted case estimates closest to the reference model were considered most accurate. To examine their performance under varying conditions, we re-evaluated the test methods when synthetic data parameters (timing of vaccination relative to cases, vaccination coverage, infection rate, and vaccine effectiveness) were varied over wide ranges. Finally, we analyzed real (i.e., collected by surveillance) data from 2010 to 2017 comparing the current method used by CDC with the best-performing test methods.
Results
In the synthetic dataset (population 1 million persons, vaccination uptake 55%, seasonal infection risk without vaccination 12%, vaccine effectiveness 48%) the reference model estimated 28,768 averted cases. The current method underestimated averted cases by 9%. The two best test methods estimated averted cases with <1% error. These two methods also worked well when synthetic data parameters were varied over wide ranges (≤6.2% error). With the real data, these two methods estimated numbers of averted cases that are a median 8% higher than the currently-used method.
Conclusions
We identified two methods for estimating numbers of influenza cases averted by vaccine that are more accurate than the currently-used algorithm. These methods will help us to better assess the benefits of influenza vaccination.
Keywords: Influenza vaccine, Influenza epidemiology, Prevented cases, Compartment model, Vaccine effectiveness
1. Introduction
Each year in the United States, there are an estimated 9–35 million illnesses and 139,000–707,000 hospitalizations due to influenza [1]. Because of the high frequency and potential severity of this illness, CDC recommends an influenza vaccination for everyone 6 months or older each year [2]. Yearly surveillance and identification of circulating influenza viruses as well as vaccine formulation, manufacture, and distribution require considerable effort and expense. Therefore, it is useful to assess the public health benefit that influenza vaccination provides.
Each season, CDC performs surveys to estimate the numbers of persons receiving influenza vaccine, observational studies to estimate the effectiveness of the season’s vaccine, and surveillance for influenza-associated hospitalizations [3–6]. In addition, since 2010, CDC has used these figures in a model to estimate the numbers of influenza cases and hospitalizations averted by vaccination [1,7,8]. However, the estimates may have inaccuracies. Vaccination and influenza cases occur continuously over the course of a season, and the use of available data aggregated by month may introduce error. The current model for calculating averted cases is intentionally simple, creating transparency but possibly sacrificing accuracy. Additionally, self-reported vaccine coverage estimates reported annually by CDC may exceed actual vaccine receipt as determined by immunization records [3]. We undertook this project to assess the accuracy of the current method for estimating influenza cases averted by vaccination, as well as several alternate test methods. We identify improved estimation methods and make updated estimates of the numbers and fraction of total influenza cases averted by vaccination.
2. Methods
2.1. Data inputs
We evaluated routinely available U.S. data on influenza cases, influenza vaccination coverage, and vaccine effectiveness from 2010–11 to 2016–17 by age group (6 months-4 years, 5–17 years, 18–49 years, 50–64 years, and ≥65 years). The number of influenza cases (including both medically-attended and non-attended) occurring each month was estimated from the Influenza Hospitalization Surveillance Network (FluSurv-NET) [5,9,10]. In brief, influenza hospitalization rates from 9% of U.S. hospitals are adjusted for testing frequency, converted to counts and multiplied by a previously-estimated ratio of cases to hospitalizations to derive the total number of influenza cases. For each age group, the number of cases is a constant multiple of the number of hospitalizations, and so in this manuscript we will refer only to cases. We obtained the prevalent proportion of the total population vaccinated at the end of each month from survey data [3], and used this figure to determine the incident number vaccinated during each month. We obtained vaccine effectiveness estimates from the U.S. Influenza Vaccine Effectiveness Network [11] and age-group specific population data from U.S. census estimates [12].
2.2. Reference model
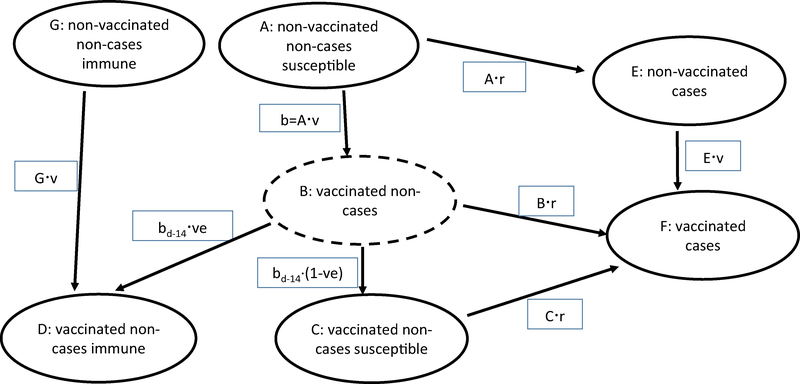
We built a reference model with seven compartments defined by combinations of persons that were ill or well, vaccinated or non-vaccinated, and immune or susceptible (Fig. 1 and Supplemental Table 1). We found that accounting for persons with pre-existing immunity at the start of the season (Fig. 1, G) had a minimal effect when the probability of vaccination did not differ by prior immunity status (data not shown); therefore, all calculations presented here assume no pre-existing immunity. Accordingly, all population members are susceptible, non-vaccinated, non-cases at the beginning of each season (Fig. 1, A). When vaccinated, persons move to compartment B for the immune lag period (generally 14 days), during which they are susceptible to infection and after which they either remain susceptible (C) or become immune (D). We assumed no indirect protection (i.e., herd immunity) and an all-or-none vaccination effect: vaccinated persons either developed complete immunity or remained fully susceptible. We assumed that vaccine would be given with equal frequency to both previously uninfected persons and those who had been infected earlier in the season. Susceptible persons (Fig. 1, A–C) could become infected and move to compartment E or F, after which they would be immune to further infection.
Fig. 1.
Reference model for calculation of numbers of cases averted by influenza vaccination. Solid-line ovals are prevalent counts for a given time period. Rectangles are incident counts during the time period. Persons stay in the dotted-line oval (B) for an immune lag period (generally 14 days), during which they are susceptible to infection and at the end of which they become either susceptible (C) or immune (D). Lower-case “b” indicates those vaccinated on individual days; bd-14 denotes the number vaccinated 14 days before. Abbreviations: ve, vaccine effectiveness; r, infection risk; v, vaccination rate (see Supplemental Table 1).
If the daily number of cases in the absence of vaccination is specified, calculations can be made for infection risk (=cases/number at risk without vaccination) and cases with vaccination (=infection risk · number at risk with vaccination; Supplemental Table 1). In contrast to some infectious disease models, in our model infection risk did not depend on the number of cases on prior days. Conversely, the number of cases with vaccination can be specified and cases without vaccination calculated (Supplemental Table 2, Method 7). The number of averted cases is the difference between the numbers of cases without vs. with vaccination. The number of averted cases estimated by the reference model was the “gold standard” to which we compared each test method.
2.3. Creation of synthetic data and evaluation of test methods
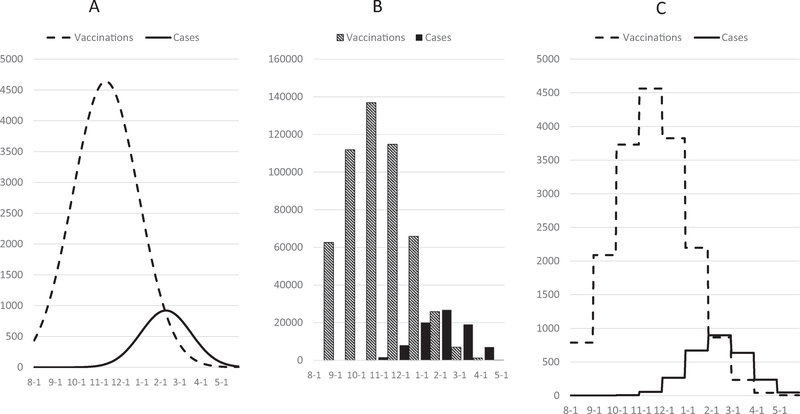
Using information from a descriptive analysis on available monthly-aggregated influenza cases and vaccinations observed during the 2010–11 to 2016–17 seasons stratified by age group, we created a synthetic dataset. The dataset had a population of 1,0, 000 and rates of vaccination and illness typical of the real (i.e., collected by surveillance/observational studies) data, including: 55% vaccination coverage, 48% vaccine effectiveness, and 12% infection rate in the absence of vaccination (Supplemental Table 3). Daily counts of vaccinations and influenza cases were simulated using the normal distribution probability density function (Fig. 2A). We applied the reference model (Fig. 1, Supplemental Table 1) to this synthetic daily data to determine the true numbers of cases that would have occurred with vaccination and the cases averted by vaccination. We then aggregated the synthetic daily counts by month to simulate the format of real data (Fig. 2B), analyzed this aggregated data by seven test methods (see below), and compared the numbers of calculated averted cases between the reference model and the test methods. We considered test methods with the smallest differences in averted case estimates relative to the reference model to be the most accurate.
Fig. 2.
Simulated data used to test estimation methods. A, incident daily counts of vaccinations and cases simulated using the normal probability density distribution. B, daily data aggregated into months was used for test methods 1–6. C, monthly aggregated data was divided by number of days per month to create a proxy for daily data, forming a step function, and used for test method 7.
Next, we performed more detailed evaluations of the two most accurate test methods across a variety of potential influenza seasons. We created several additional synthetic datasets with normal-distribution daily case and vaccination counts but with variation of the following characteristics: proportion of vaccine given before cases (or “vaccination timing”; 5–98%), vaccine effectiveness (10–70%), vaccine coverage (10–80%) and infection risk (2%–50%). We also evaluated the test methods in skewed distributions and datasets with distributions similar to real data (Supplemental Table 4); because results were similar, we do not show these additional results.
We wanted to determine how the methods performed with less separation between months of vaccine administration and case occurrence. To measure this, we defined “vaccination timing” as the proportion of vaccinations occurring before case accrual. Vaccination timing could vary from 0% (no vaccine given before cases occurred) to 100% (all vaccine given before cases) and was defined as the sum over all months of vcm (1-case_cumm), where vcm is the proportion of total vaccine given in month m and case_cumm is the proportion of total cases that occurred by the end of month m.
2.4. Specifications of test methods
We evaluated the following seven test methods (Supplemental Table 2):
Method 1. Current method: uses a month time-scale, incorporates a 14-day immune lag by averaging the current and prior month’s vaccination coverage, and applies vaccine coverage and effectiveness to the susceptible (i.e., non-cases not effectively vaccinated) population.
Method 2. Similar to method 1, uses a month time-scale, but does not incorporate an immune lag and applies vaccine coverage and effectiveness to the non-case population (Supplemental Table 5).
Method 3. Simplified version of reference model, uses a month time-scale, does not include an immune lag, and calculates proportions infected and vaccinated by applying current-month case and vaccination counts to prior-month compartment values.
Method 4. Similar to method 3 but uses the average of the prior- and current-month compartment values.
Method 5. Uses a month time-scale and calculates the number of cases without vaccination by dividing cases with vaccination by one minus the product of vaccine coverage and vaccine effectiveness.
Method 6. Similar to method 5 but calculations done using data aggregated over an entire season.
Method 7. Similar to reference model but uses a proxy for daily values of cases and vaccinations created by dividing monthly values by the number of days per month. The resulting daily values form a step-function as shown in Fig. 2C and thus simulate the effect of converting real monthly-aggregated data to daily data.
2.5. Analysis of real data with best test methods
We analyzed real month-level data from 2010–11 to 2016–17 by age-group and season to compare the numbers of averted cases estimated by method 1 (the current method) and the two best-performing test methods. We created all-age estimates by umming age-group-specific estimates. Finally, we performed a sensitivity analysis to examine the effect on estimates if true vaccine coverage were 10–20% lower than estimated by CDC using self-reported vaccination status [3].
Data for this analysis came from publicly available sources, preexisting research projects with human subjects approval, and public health surveillance systems that have been determined to not require human subjects review. Calculations were done using SAS version 9.4 (Cary, N.C.) and R [13].
3. Results
Among seven seasons and five age groups, median vaccine effectiveness was 48%, vaccine coverage 55% and 9% of the total population became infected (Table 1). Median month of vaccination was mid-October and median month of illness was late January. The median percentage of vaccine given before cases occurred was 90%. Observed data on vaccinations were skewed to the right (skewness = 1.1) and cases to the left (skewness = −0.4).
Table 1.
Data characteristics, 2010–11 to 2016–17 influenza seasons.
| Characteristic | Median | Minimum | Maximum |
|---|---|---|---|
| Vaccination measures | |||
| Vaccine effectiveness, %* | 47.6 | 15.2 | 67.0 |
| Vaccine coverage, % | 55.0 | 28.4 | 70.1 |
| Vaccination timing, %† | 89.9 | 79.0 | 96.7 |
| Month of vaccination, mean‡ | 3.5 | 3.4 | 4.0 |
| Month of vaccination, SD | 1.6 | 1.3 | 1.8 |
| Skewness | 1.1 | 0.8 | 1.7 |
| Kurtosis | 1.3 | 0.2 | 3.7 |
| Illness measures | |||
| Infected, % | 9.2 | 2.3 | 14.5 |
| Month of onset, mean‡ | 6.7 | 5.8 | 7.9 |
| Month of onset, SD | 1.2 | 1.0 | 1.4 |
| Skewness | −0.4 | −1.7 | 0.9 |
| Kurtosis | 0.3 | −0.6 | 3.9 |
Values were calculated from 35 data subsets defined by seven seasons and five age groups (6-months-4 years, 5–17 years, 18–49 years, 50–64 years, ≥65 years). Values were not weighted by population size.
Abbreviations: SD, standard deviation.
For most seasons, vaccine effectiveness was the same throughout the season for a given age group. However, in 2012–13 and 2014–15, vaccine effectiveness varied, being lower during August-February when A/H3N2 viruses predominated and higher in March-April when influenza B viruses predominated.
Percent of vaccine given before cases occurred (see Methods).
Months were counted from August of each season (e.g., month 3 was October and month 6 was January of the following year).
3.1. Assessment of test methods using simulated data
In the initial synthetic dataset, there were 120,000 cases in the absence of vaccination and 55% of the population was vaccinated. The reference model estimated 91,232 cases with vaccination and 28,768 cases averted by vaccination (Table 2). Compared with the reference model, the test methods varied from a 9% underestimate (method 1) to a 14% overestimate (method 6) of averted cases. Estimates from methods 2 and 3 were most accurate (<1% error).
Table 2.
Accuracy of test methods in determining averted cases in simulated data*.
| Method † | No. of cases without vaccination | Averted cases | Proportion averted, % | Errors: % difference in averted cases compared with reference model |
|---|---|---|---|---|
| Reference model | 120,000 | 28,768 | 24.0 | NA |
| Test method 1 | 117,408 | 26,176 | 22.3 | −9.01 |
| Test method 2 | 120,043 | 28,811 | 24.0 | 0.15 |
| Test method 3 | 120,014 | 28,782 | 24.0 | 0.05 |
| Test method 4 | 121,064 | 29,832 | 24.6 | 3.70 |
| Test method 5 | 122,386 | 31,153 | 25.5 | 8.29 |
| Test method 6 | 123,957 | 32,725 | 26.4 | 13.76 |
| Test method 7 | 119,598 | 28,365 | 23.7 | −1.40 |
| * Simulated input data characteristics | ||||
| Beginning population | 1,000,000 | |||
| Vaccinated, % of population | 55% | |||
| Vaccination month (mean, ±standard deviation) | 3.6 ± 1.5 | |||
| Vaccine effectiveness, % | 48% | |||
| No. of cases with vaccination | 91,232 | |||
| Cases month (mean ± standard deviation) | 6.5 ± 1.2 | |||
| Vaccination timing, % | 90% | |||
Notes: months counted from August, month 3 indicates October and month 6 indicates January; vaccination timing indicates proportion of vaccine doses given before cases occurred (see Methods).
See Methods and Supplemental Table 2 for details of test methods. The current method is method 1.
We next compared the current method (method 1) and the two best-performing test methods (methods 2 and 3) in simulated datasets with widely varying characteristics (Table 3). As vaccination timing (the proportion vaccinated before cases) increased from 5% to 98%, true averted cases increased from 1630 to 31,159, and method 1 errors varied from an 90% overestimate to an 12% underestimate. In contrast, relative errors for methods 2 and 3 were much lower; of note, the maximum errors of 6.0–6.2% for methods 2 and 3 corresponded to absolute differences of <100 averted cases. When we varied vaccine effectiveness, vaccine coverage, and infection risk one at a time, we observed that method 1 errors varied but methods 2 and 3 repeatedly performed well, with maximum relative errors of 3.1% and 2.6%, respectively. However, when multiple factors were varied to produce high numbers of averted cases (vaccine effectiveness 70%, vaccine coverage 80%, and infection rate 50%), methods 2 and 3 produced overestimates of up to 26% and 24%, respectively.
Table 3.
Effect of varying synthetic data parameters on accuracy of test methods 1–3 in estimating averted cases*
| Factor(s) varied† | Vaccination timing, %‡ |
Vaccine effectiveness, % |
Vaccine coverage, % |
Infection risk without vaccination, % | Infection risk with vaccination, % | Immune lag, days§ |
True averted cases per reference model |
Errors: % difference in averted cases compared with reference model |
|||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of averted cases | Averted % | Method 1 (current) | Method 2 | Method 3 | |||||||
| Vaccination timing‡ | |||||||||||
| 5 | 48 | 55 | 12 | 11.8 | 14 | 1630 | 1.4 | 89.8 | 6.2 | 6.0 | |
| 25 | 48 | 55 | 12 | 11.2 | 14 | 8346 | 7.0 | 32.4 | 3.5 | 3.2 | |
| 50 | 48 | 55 | 12 | 10.3 | 14 | 16,616 | 13.8 | 10.8 | 1.9 | 1.5 | |
| 75 | 48 | 55 | 12 | 9.6 | 14 | 24,336 | 20.3 | −2.5 | 0.7 | 0.5 | |
| 90 | 48 | 55 | 12 | 9.1 | 14 | 28,768 | 24.0 | −9.0 | 0.2 | 0.0 | |
| 98 | 48 | 55 | 12 | 8.9 | 14 | 31,159 | 26.0 | −12.0 | 0.0 | 0.0 | |
| Vaccine effectiveness | |||||||||||
| 90 | 10 | 55 | 12 | 11.4 | 14 | 5993 | 5.0 | 0.8 | 0.0 | 0.0 | |
| 90 | 20 | 55 | 12 | 10.8 | 14 | 11,986 | 10.0 | −1.5 | 0.1 | 0.0 | |
| 90 | 30 | 55 | 12 | 10.2 | 14 | 17,980 | 15.0 | −4.0 | 0.1 | 0.0 | |
| 90 | 50 | 55 | 12 | 9.0 | 14 | 29,966 | 25.0 | −9.6 | 0.2 | 0.1 | |
| 90 | 60 | 55 | 12 | 8.4 | 14 | 35,959 | 30.0 | −12.8 | 0.2 | 0.1 | |
| 90 | 70 | 55 | 12 | 7.8 | 14 | 42,075 | 35.1 | −16.4 | 0.2 | 0.1 | |
| Vaccine coverage | |||||||||||
| 90 | 48 | 10 | 12 | 11.5 | 14 | 5231 | 4.4 | 1.1 | 0.0 | 0.0 | |
| 90 | 48 | 20 | 12 | 11.0 | 14 | 10,461 | 8.7 | −0.9 | 0.1 | 0.0 | |
| 90 | 48 | 30 | 12 | 10.4 | 14 | 15,692 | 13.1 | −3.0 | 0.1 | 0.0 | |
| 90 | 48 | 50 | 12 | 9.4 | 14 | 26,152 | 21.8 | −7.7 | 0.1 | 0.0 | |
| 90 | 48 | 70 | 12 | 8.3 | 14 | 36,613 | 30.5 | −13.2 | 0.2 | 0.0 | |
| 89 | 48 | 80 | 12 | 7.8 | 14 | 41,843 | 34.9 | −16.2 | 0.3 | 0.0 | |
| Infection risk | |||||||||||
| 90 | 48 | 55 | 2 | 1.5 | 14 | 4794 | 24.0 | −9.0 | −0.5 | −0.5 | |
| 90 | 48 | 55 | 6 | 4.6 | 14 | 14,383 | 24.0 | −9.0 | −0.2 | −0.3 | |
| 90 | 48 | 55 | 12 | 9.1 | 14 | 28,768 | 24.0 | −9.0 | 0.2 | 0.0 | |
| 90 | 48 | 55 | 25 | 19.0 | 14 | 59,943 | 24.0 | −9.0 | 1.1 | 0.8 | |
| 90 | 48 | 55 | 40 | 30.4 | 14 | 95,929 | 24.0 | −9.1 | 2.2 | 1.8 | |
| 90 | 48 | 55 | 50 | 38.0 | 14 | 119,930 | 24.0 | −9.1 | 3.1 | 2.6 | |
| Multiple, low averted | |||||||||||
| 5 | 10 | 10 | 2 | 2.0 | 14 | 10 | 0.1 | 88.4 | 2.9 | 2.9 | |
| 50 | 10 | 10 | 2 | 2.0 | 14 | 101 | 0.5 | 18.2 | −0.4 | −0.4 | |
| 98 | 10 | 10 | 2 | 2.0 | 14 | 196 | 1.0 | 0.3 | −0.2 | −0.2 | |
| Multiple, high averted | |||||||||||
| 5 | 70 | 80 | 50 | 48.6 | 14 | 14,470 | 2.9 | 90.5 | 25.7 | 23.6 | |
| 50 | 70 | 80 | 50 | 34.5 | 14 | 154,568 | 30.9 | −2.8 | 21.8 | 13.8 | |
| 98 | 70 | 80 | 50 | 22.5 | 14 | 275,427 | 55.1 | −34.2 | 1.2 | 0.9 | |
| Immune lag§ | |||||||||||
| 90 | 48 | 55 | 12 | 9.0 | 1 | 29,763 | 24.8 | −12.9 | −4.1 | −4.2 | |
| 90 | 48 | 55 | 12 | 9.1 | 7 | 29,343 | 24.5 | −11.3 | −2.4 | −2.5 | |
| 90 | 48 | 55 | 12 | 9.1 | 14 | 28,768 | 24.0 | −9.0 | 0.2 | 0.0 | |
| 90 | 48 | 55 | 12 | 9.2 | 21 | 28,094 | 23.4 | −6.2 | 3.2 | 3.1 | |
| 90 | 48 | 55 | 12 | 9.3 | 28 | 27,315 | 22.8 | −2.7 | 7.0 | 6.9 | |
Method 1 is currently used; methods 2 and 3 are the best performing test methods (see text Methods section and Supplemental Table 2).
Factors varied are indicated with bold type.
Proportion of vaccinations given before cases, see Methods section.
Days from vaccine receipt to immune protection.
We also evaluated the effect of varying the immune lag (i.e., days from vaccination to protective immunity) from 1 to 28 days in the simulated data (Table 3). For a lag of 14 days, methods 2 and 3 performed well with errors of 0.2% or less. However these methods produced underestimates of up to 4% when lag was <14 days and overestimates of up to 7% when lag was >14 days.
3.2. Analysis of real data
We analyzed the real data from 2010–11 to 2016–17 seasons, comparing averted cases among methods 1–3 (Table 4). For all ages combined, methods 2 and 3 produced estimates that were a median 8% higher than method 1; only in 2014–15 did methods 2 and 3 produce estimates that were lower than method 1 (median 3% lower). Among the age groups, median differences were highest for those 6 months-4 years (methods 2 and 3 were both 17% higher than method 1) and lowest for those 18–49 years (methods 2 and 3 were both 2% higher than method 1).
Table 4.
Comparison of averted cases determined by test methods 1–3*, by age group and season, 2010–11 to 2016–17.
| Age | Season | Method 1 (currently used method) |
Method 2 |
Method 3 |
Difference in averted cases compared with method 1, % |
||||
|---|---|---|---|---|---|---|---|---|---|
| No. of averted cases | Averted % | No. of averted cases | Averted % | No. of averted cases | Averted % | Method 2 vs. Method 1 | Method 3 vs. Method 1 | ||
| All | 2010–11 | 5,039,277 | 20.0 | 5,593,760 | 21.7 | 5,588,717 | 21.7 | 11.0 | 10.9 |
| 2011–12 | 1,981,571 | 18.2 | 2,179,701 | 19.7 | 2,179,404 | 19.7 | 10.0 | 10.0 | |
| 2012–13 | 5,628,332 | 14.0 | 5,838,328 | 14.5 | 5,831,551 | 14.5 | 3.7 | 3.6 | |
| 2013–14 | 6,683,929 | 19.5 | 7,199,195 | 20.6 | 7,192,944 | 20.6 | 7.7 | 7.6 | |
| 2014–15 | 1,607,848 | 4.6 | 1,560,287 | 4.5 | 1,559,520 | 4.5 | −3.0 | −3.0 | |
| 2015–16 | 5,083,498 | 17.2 | 5,645,614 | 18.8 | 5,642,695 | 18.8 | 11.1 | 11.0 | |
| 2016–17 | 5,288,312 | 14.8 | 5,713,451 | 15.8 | 5,709,538 | 15.8 | 8.0 | 8.0 | |
| Median | 17.2 | 18.8 | 18.8 | 8.0 | 8.0 | ||||
| 6 m-4 y | 2010–11 | 965,327 | 33.7 | 1,203,220 | 38.8 | 1,200,195 | 38.7 | 24.6 | 24.3 |
| 2011–12 | 241,406 | 27.7 | 282,620 | 30.9 | 282,496 | 30.9 | 17.1 | 17.0 | |
| 2012–13 | 799,295 | 23.4 | 883,121 | 25.3 | 880,887 | 25.2 | 10.5 | 10.2 | |
| 2013–14 | 741,609 | 30.6 | 875,027 | 34.2 | 873,252 | 34.2 | 18.0 | 17.8 | |
| 2014–15 | 134,300 | 6.1 | 130,283 | 6.0 | 130,173 | 6.0 | −3.0 | −3.1 | |
| 2015–16 | 980,052 | 32.3 | 1,212,842 | 37.1 | 1,211,129 | 37.1 | 23.8 | 23.6 | |
| 2016–17 | 602,072 | 23.8 | 678,393 | 26.1 | 677,793 | 26.0 | 12.7 | 12.6 | |
| Median | 27.7 | 30.9 | 30.9 | 17.1 | 17.0 | ||||
| 5–17 y | 2010–11 | 1,350,617 | 23.0 | 1,500,044 | 24.9 | 1,498,908 | 24.9 | 11.1 | 11.0 |
| 2011–12 | 490,865 | 20.0 | 540,115 | 21.6 | 540,075 | 21.6 | 10.0 | 10.0 | |
| 2012–13 | 1,506,488 | 18.1 | 1,595,647 | 19.0 | 1,593,335 | 19.0 | 5.9 | 5.8 | |
| 2013–14 | 1,081,574 | 21.9 | 1,179,996 | 23.4 | 1,179,153 | 23.4 | 9.1 | 9.0 | |
| 2014–15 | 356,330 | 5.0 | 345,777 | 4.8 | 345,565 | 4.8 | −3.0 | −3.0 | |
| 2015–16 | 1,281,134 | 24.3 | 1,454,669 | 26.7 | 1,454,025 | 26.7 | 13.5 | 13.5 | |
| 2016–17 | 1,920,214 | 23.8 | 2,165,577 | 26.1 | 2,163,846 | 26.0 | 12.8 | 12.7 | |
| Median | 21.9 | 23.4 | 23.4 | 10.0 | 10.0 | ||||
| 18–49 y | 2010–11 | 1,093,537 | 13.2 | 1,125,819 | 13.5 | 1,125,608 | 13.5 | 3.0 | 2.9 |
| 2011–12 | 445,893 | 11.5 | 462,906 | 11.9 | 462,877 | 11.9 | 3.8 | 3.8 | |
| 2012–13 | 1,397,741 | 10.4 | 1,381,399 | 10.3 | 1,380,769 | 10.3 | −1.2 | −1.2 | |
| 2013–14 | 2,174,882 | 14.8 | 2,220,864 | 15.0 | 2,219,686 | 15.0 | 2.1 | 2.1 | |
| 2014–15 | 322,419 | 2.9 | 305,897 | 2.8 | 305,825 | 2.8 | −5.1 | −5.1 | |
| 2015–16 | 1,591,114 | 14.1 | 1,671,719 | 14.7 | 1,671,462 | 14.7 | 5.1 | 5.0 | |
| 2016–17 | 526,812 | 5.6 | 523,433 | 5.6 | 523,348 | 5.6 | −0.6 | −0.7 | |
| Median | 11.5 | 11.9 | 11.9 | 2.1 | 2.1 | ||||
| 50–64 y | 2010–11 | 1,169,470 | 19.7 | 1,261,901 | 20.9 | 1,261,355 | 20.9 | 7.9 | 7.9 |
| 2011–12 | 488,982 | 20.5 | 537,764 | 22.1 | 537,698 | 22.1 | 10.0 | 10.0 | |
| 2012–13 | 1,631,408 | 15.7 | 1,687,342 | 16.2 | 1,685,819 | 16.2 | 3.4 | 3.3 | |
| 2013–14 | 2,213,864 | 21.6 | 2,400,974 | 23.0 | 2,398,707 | 23.0 | 8.5 | 8.3 | |
| 2014–15 | 355,391 | 4.2 | 344,114 | 4.1 | 343,946 | 4.1 | −3.2 | −3.2 | |
| 2015–16 | 743,725 | 9.6 | 765,353 | 9.9 | 765,189 | 9.9 | 2.9 | 2.9 | |
| 2016–17 | 1,635,009 | 15.6 | 1,723,831 | 16.3 | 1,722,608 | 16.3 | 5.4 | 5.4 | |
| Median | 15.7 | 16.3 | 16.3 | 5.4 | 5.4 | ||||
| ≥65 y | 2010–11 | 460,327 | 20.9 | 502,777 | 22.4 | 502,651 | 22.4 | 9.2 | 9.2 |
| 2011–12 | 314,425 | 24.5 | 356,296 | 26.9 | 356,258 | 26.9 | 13.3 | 13.3 | |
| 2012–13 | 293,400 | 6.4 | 290,819 | 6.4 | 290,741 | 6.4 | −0.9 | −0.9 | |
| 2013–14 | 472,000 | 23.6 | 522,334 | 25.5 | 522,146 | 25.5 | 10.7 | 10.6 | |
| 2014–15 | 439,408 | 7.1 | 434,215 | 7.0 | 434,011 | 7.0 | −1.2 | −1.2 | |
| 2015–16 | 487,473 | 22.4 | 541,031 | 24.3 | 540,890 | 24.3 | 11.0 | 11.0 | |
| 2016–17 | 604,205 | 11.5 | 622,218 | 11.8 | 621,943 | 11.8 | 3.0 | 2.9 | |
| Median | 20.9 | 22.4 | 22.4 | 9.2 | 9.2 | ||||
Abbreviations: m, months; y, years.
Methods 1–3 are defined in Supplemental Tables 1–2 and the Methods section of text.
Using method 3 (method 2 gave nearly identical results), we determined the effect on our estimates if true vaccine coverage was lower than reported by CDC based on self-reported vaccination status. Among the 35 data subsets defined by season and age group, if true coverage were 10% lower on a relative scale (e.g., a change from 50% to 45%), averted cases would be a median 12% (range 10–15%) lower (also on a relative scale) than originally estimated; if true coverage was 20% lower, averted cases would be a median 24% (range 20–29%) lower than originally estimated.
4. Discussion
Influenza epidemics occur each year, causing symptomatic disease in 3–11% of the U.S. population [9]. CDC supplements routine surveillance data with models to estimate the total burden of influenza as well as how much illness was prevented by vaccination [1,7,8,14]. We report our evaluation of the accuracy of our current modeled estimates of influenza vaccination impact using simulated data and present alternative methods. We identified two test methods that performed better than our current method compared with a reference model. Under scenarios similar to recent influenza seasons, these two methods estimate averted cases with <1% error. Method 3 was marginally more accurate under some extreme circumstances, but method 2 involves fewer derived variables and could be preferred for simplicity. Use of either of these methods will improve the accuracy of calculations of averted cases made for future influenza seasons.
The reference model, considered the “gold standard”, uses daily vaccination and case counts and can incorporate immune lags (days from vaccination to immune protection) of any length. The change in counts in each model compartment depends on simultaneous processes, e.g., as the numbers unvaccinated in oval A of Fig. 1 decrease due to vaccination, the numbers at risk for infection also decrease. Calculations therefore must be made over short intervals (e.g., 1 day) or inaccuracies will occur.
Because it requires daily data, the reference model can be used to calculate averted cases on real data (which are aggregated by month) only if the data are converted to proxy daily data, as we did by dividing by the number of days per month (Fig. 2C). We tested this procedure (Table 2, test method 7) but it was less accurate than methods 2 and 3, which use aggregate data. We could evaluate more sophisticated methods to create proxy daily data or make efforts to obtain data aggregated at shorter intervals (e.g., 1- or 2-week blocks). However, our simulations indicate that this is unnecessary, as methods 2 and 3 work well to estimate averted cases with month-level data.
Neither method 2 nor 3 explicitly include an immune lag, which we thought would be important to consider and therefore included in the current method. The lag between vaccination and immunity is commonly cited as 10–14 days [4,15] but longer or shorter intervals are possible [16–18]. Both methods 2 and 3 are most accurate when a 14-day lag is incorporated into synthetic data, and so empirically do account for a 14-day lag. If effective immunity occurs before 14 days, our test methods will underestimate averted cases, and vice versa.
As expected, higher values of vaccine effectiveness, vaccine coverage and infection risk produced higher averted case estimates. Method 1 (current method) produced larger underestimates as vaccine effectiveness and vaccine coverage increased. In contrast, methods 2 and 3 were stable across the varied parameter values that we tested. Only when multiple parameters were set to produce high numbers of averted cases did these two methods show >6% error; however, levels this extreme (vaccine effectiveness 70%, vaccine coverage 80%, and infection rate 50%) are unlikely during U.S. influenza seasons.
Averted cases are strongly influenced by the timing of vaccination relative to cases. When we varied vaccination timing (the proportion of vaccinations given before cases) from 5% to 98%, the proportion of cases averted by vaccine increased from 1% to 26%. In recent seasons, about 90% of vaccine was given before cases occurred. However, during the 2009 H1N1 pandemic, the monovalent vaccination campaign started as the second wave of cases was peaking in October 2009 [19]. Our simulations suggest that methods 2 and 3 would perform better than the current method under such circumstances.
Using the best-performing test methods on observed data, we estimate that averted cases were a median 8% higher over seven recent seasons than previously reported. However, the number of vaccinations estimated from self- or parent- reports can be higher than the number of manufacturer-distributed doses [3] and the number documented in medical records or immunization registries [20–22]. Using methods 2 or 3, averted case estimates would be 12% lower if true vaccine coverage were 10% lower than the figures we used in our calculations.
Limitations of this study include that the number of cases averted by vaccination is a counterfactual concept without any “true” value. Input values for vaccine effectiveness were not stratified by influenza virus type or subtype nor by vaccine preparation (e.g., high dose vaccine for those ≥65 years) [1]. We do not account for possible waning of vaccine-induced immune response [23] or for potential indirect effects of vaccination (“herd immunity”) [24,25]. Input values for the number of cases, which are estimated from hospitalizations, also have recognized limitations [9,10]. Finally, we also assume that influenza infection induces immunity for the remainder of the season, ignoring the possibility of a second infection with a virus of a different type, subtype, or lineage.
Influenza is a unique infectious disease in that it is vaccine-preventable but remains very common. The impact of influenza vaccine may be underappreciated because the disease is generally mild in previously healthy people and vaccine effectiveness is typically lower than that of other vaccines. Therefore, it is helpful to view influenza immunization from a population perspective by estimating national numbers of cases and hospitalizations likely averted by vaccine. While these calculations have been made for several years, our current evaluation has identified methods that materially improve the accuracy of our estimates of the benefits of the seasonal influenza vaccination campaign in the United States.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge personnel for the following groups that collected data used in this project: Influenza Hospitalization Surveillance Network, Flu Vax View, and the U.S. Influenza Vaccine Effectiveness Network.
Footnotes
None of the authors have a potential conflict of interest or a funding source.
Appendix A. Supplementary material
Supplementary data to this article can be found online at https://doi.org/10.1016/j.vaccine.2018.10.026.
The findings and conclusions in this report are those of the authors and do not necessarily represent the official position of the Centers for Disease Control and Prevention.
References
- [1].Rolfes MA, Foppa IM, Garg S, Flannery B, Brammer L, Singleton JA, et al. Estimated influenza illnesses, medical visits, hospitalizations, and deaths averted by vaccination in the United States. Available at <https://www.cdc.gov/flu/about/disease/2016-17.htm2018> [Accessed April 2, 2018].
- [2].Grohskopf LA, Sokolow Lz , Broder KR, Walter EB, Bresee JS, Fry AM, et al. Prevention and control of seasonal influenza with vaccines: recommendations of the advisory committee on immunization practices - United States, 2017–18 influenza season. MMWR Recomm Rep 2017;66:1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Santibanez TA, Zhai Y, O’Halloran A, Kahn K, Srivastav AL, L, Ormson E, et al. Santibanez TA, Zhai Y, O’Halloran A, Kahn K, Srivastav A, Liu L, Ormson E, Lu P, Williams WW, Greby SM. FluVaxView.
- [4].Flannery B, Chung JR, Belongia EA, McLean HQ, Gaglani M, Murthy K, et al. Interim estimates of 2017–18 seasonal influenza vaccine effectiveness - United States, February 2018. MMWR Morb Mortal Wkly Rep 2018;67:180–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Centers for Disease Control and Prevention. Overview of influenza surveillance in the United States. Available at <https://www.cdc.gov/flu/weekly/overview.htm> [Accessed April 11, 2017].
- [6].Centers for Disease Control and Prevention. Seasonal influenza vaccine effectiveness, 2004–2018. Available at https://www.cdc.gov/flu/professionals/vaccination/effectiveness-studies.htm[Accessed April 25, 2018.]
- [7].Kostova D, Reed C, Finelli L, Cheng PY, Gargiullo PM, Shay DK, et al. Influenza illness and hospitalizations averted by influenza vaccination in the United States, 2005–2011. PLoS ONE 2013;8:e66312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Reed C, Kim IK, Singleton JA, Chaves SS, Flannery B, Finelli L, et al. Estimated influenza illnesses and hospitalizations averted by vaccination-United States, 2013–14 influenza season. MMWR Morb Mortal Wkly Rep 2014;63:1151–4. [PMC free article] [PubMed] [Google Scholar]
- [9].Tokars JI, Olsen SJ, Reed C. The seasonal incidence of symptomatic influenza in the United States. Clin Infect Dis 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Reed C, Chaves SS, Daily Kirley P, Emerson R, Aragon D, Hancock EB, et al. Estimating influenza disease burden from population-based surveillance data in the United States. PLoS ONE 2015;10:e0118369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Flannery B, Chung JR, Thaker SN, Monto AS, Martin ET, Belongia EA, et al. Interim estimates of 2016–17 seasonal influenza vaccine effectiveness - United States, February 2017. MMWR Morb Mortal Wkly Rep 2017;66: 167–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].National Center for Health Statistics. Bridged-race population estimates. Available at <https://www.cdc.gov/nchs/nvss/bridged_race/data_documentation.htm> [Accessed June 7, 2018].
- [13].R Development Core Team. R: A language and environment for statistical computing. Vienna: ARFfSC. [Google Scholar]
- [14].Rolfes MA, Foppa IM, Garg S, Flannery B, Brammer L, Singleton JA, et al. Annual estimates of the burden of seasonal influenza in the United States: a tool for strengthening influenza surveillance and preparedness. Influenza Other Respir Viruses 2018;12:132–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].European Centre for Disease Prevention and Control. Seasonal influenza vaccines. Available at <https://ecdc.europa.eu/en/seasonal-influenza/prevention-and-control/seasonal-influenza-vaccines> [Accessed April 15, 2018].
- [16].BreseeJ FryA, Sambhara S, Cox N. Inactivated influenza vaccines In: Plotkin S, Orenstein WA, Offit P, Edwards K, editors. Vaccines. Philadelphia (PA): Elsevier; 2017. [Google Scholar]
- [17].Gross PA, Russo C, Dran S, Cataruozolo P, Munk G, Lancey SC. Time to earliest peak serum antibody response to influenza vaccine in the elderly. Clin Diagn Lab Immunol 1997;4:491–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Kunzel W, Engelmann H, D’Hondt E. Immune response to influenza vaccination. Lancet 1994;343:173. [DOI] [PubMed] [Google Scholar]
- [19].Borse RH, Shrestha SS, Fiore AE, Atkins CY, Singleton JA, Furlow C, et al. Effects of vaccine program against pandemic influenza A(H1N1) virus, United States, 2009–2010. Emerg Infect Dis 2013;19:439–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Irving SA, Donahue JG, Shay DK, Ellis-Coyle TL, Belongia EA. Evaluation of self-reported and registry-based influenza vaccination status in a Wisconsin cohort. Vaccine 2009;27:6546–9. [DOI] [PubMed] [Google Scholar]
- [21].Mac Donald R, Baken L, Nelson A, Nichol KL. Validation of self-report of influenza and pneumococcal vaccination status in elderly outpatients. Am J Prev Med 1999;16:173–7. [DOI] [PubMed] [Google Scholar]
- [22].Brown C, Clayton-Boswell H, Chaves SS, Prill MM, Iwane MK, Szilagyi PG, et al. Validity of parental report of influenza vaccination in young children seeking medical care. Vaccine 2011;29:9488–92. [DOI] [PubMed] [Google Scholar]
- [23].Ferdinands JM, Fry AM, Reynolds S, Petrie J, Flannery B, Jackson ML, et al. Intraseason waning of influenza vaccine protection: evidence from the US influenza vaccine effectiveness network, 2011–12 through 2014–15. Clin Infect Dis 2017;64:544–50. [DOI] [PubMed] [Google Scholar]
- [24].Arinaminpathy N, Kim IK, Gargiullo P, Haber M, Foppa IM, Gambhir M, et al. Estimating direct and indirect protective effect of influenza vaccination in the United States. Am J Epidemiol 2017;186:92–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Yin JK, Heywood AE, Georgousakis M, King C, Chiu C, Isaacs D, et al. Systematic review and meta-analysis of indirect protection afforded by vaccinating children against seasonal influenza: implications for policy. Clin Infect Dis 2017;65:719–28. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.