Abstract
Objective:
To parameterize and validate two existing algorithms for identifying out-of-bed time using 24-hour hip-worn accelerometer data from older adults.
Approach:
Overall, 628 women (80±6 years old) wore ActiGraph GT3X+ accelerometers 24 hours/day for up to 7 days and concurrently completed sleep-logs. Trained staff used a validated visual analysis protocol to measure in-bed periods (criterion). The Tracy and McVeigh algorithms were adapted for optimal use in older adults. A training set of 314 women was used to choose two key thresholds by maximizing the sum of sensitivity and specificity for each algorithm and data (vertical axis, VA, and vector magnitude, VM) combination. Data from the remaining 314 women were then used to test agreement in waking wear time (i.e., out-of-bed time while wearing the accelerometer) by computing sensitivity, specificity, and kappa. Waking wear time-adjusted means of sedentary time, light-intensity physical activity (light PA) and moderate-to-vigorous-intensity physical activity (MVPA) were then estimated and compared.
Main results:
Waking wear time agreement with the criterion was high for Tracy_VA, Tracy_VM, McVeigh_VA, and highest for McVeigh_VM. Compared to the criterion, McVeigh_VM had mean sensitivity=0.92, specificity=0.87, kappa=0.80, and overall mean difference±SD=−0.04±2.5 hours/day. Minutes of sedentary time, light PA, and MVPA adjusted for waking wear time using the criterion measure and McVeigh_VM were not meaningfully different (p >0.43 | all).
Significance:
The McVeigh algorithm with optimal parameters using VM performed best compared to sleep-log assisted visual analysis and is suitable for automatic identification of waking wear time in older women when visual analysis is not feasible.
INTRODUCTION
Accelerometers have been used to measure human movement beginning in 1983 (Montoye et al 1983) and have since become the most used sensor in physical activity research (Chen et al 2012). Early research protocols required accelerometers be worn only while awake, often requiring participants remove devices when they were likely to get wet (e.g., during showers or while swimming) and while sleeping [eg, (Diaz et al 2017)]. One problem with this waking-wear protocol is that taking devices off before bed and putting them on after waking presents opportunities for participants to forget to wear devices while awake (Troiano et al 2014). This non-wear results in missing data (Tudor-Locke et al 2015) that is more likely to occur just before and just after sleep—a pattern that is not missing at random. Furthermore, systematically requiring device removal creates missed opportunities to assess sleep duration and several other dimensions of sleep that can be measured using hip-worn or wrist-worn accelerometers, though accuracy of some sleep dimensions measured with hip-worn accelerometry remains debatable (Zinkhan et al 2014, Weiss et al 2010).
For the assessment of time spent in physical activity, accelerometers are commonly worn on the hip to measure whole-body acceleration in three dimensions 30 to 100 times per second (Migueles et al 2017). Raw acceleration data are summarized to manageable epochs (commonly 1 minute) using proprietary algorithms built into manufacturer-provided software, resulting in activity measures known as “counts per minute” (cpm). The resulting cpm data can be used to classify each minute of the day into one of four categories: sedentary behavior; physical activity (light, moderate, vigorous); sleep; or non-wear.
Data processing techniques for classifying sedentary behavior and physical activity that rely solely on cpm data are widely used (Freedson et al 1998, Troiano et al 2008, Matthews et al 2008). These techniques use cpm thresholds, also called “cutpoints”, that are established often in laboratory studies that calibrate cpm data to energy expenditure while participants perform various tasks such as walking on a treadmill, folding laundry, moping, and watching TV (Evenson et al 2015). Automated algorithms to classify non-wear time (Choi et al 2011) are also pervasively used. The identification of in-bed time (sometimes a proxy for sleep duration) using automated algorithms is common when accelerometers are worn on the wrist (Ancoli-Israel et al 2003). Identifying in-bed time using data from hip-worn accelerometers is more challenging because differences in whole-body movement patterns between sedentary behavior and sleep are not as clearly distinct as those observed on wrist-worn accelerometers. Despite the added difficulty, several automated in-bed detection algorithms for hip-worn accelerometer data have been developed and validated against whole-room calorimetry (Tracy et al 2014), parent-reported sleep logs (Barreira et al 2015) and expert visual analysis of cpm data (Tudor-locke et al 2014, McVeigh et al 2016). Two of the algorithms—Tracy et al.’s bed-rest algorithm (referred to as the “Tracy algorithm”) and McVeigh et al.’s waking wear time algorithm (referred to as the “McVeigh algorithm)—rely solely on cpm output from ActiGraph accelerometers (McVeigh et al 2016, Tracy et al 2014). The simplicity of the cpm algorithms makes their application in large epidemiologic studies more feasible than other time intensive approaches.
Algorithms designed to categorize out-of-bed time from hip-worn accelerometry rely on temporal patterns of whole-body activity while out of bed or in bed/asleep. The algorithms are heavily influenced by activity profiles during the waking period. For example, a person who is consistently active throughout their out-of-bed period will have cpm readings that are distinctly different than the cpm readings during their in-bed period, making the distinction between the two periods clear. For someone who spends the vast majority of their out-of-bed periods sedentary (e.g., watching television), distinctions between in-bed and out-of-bed periods would be more difficult to make. The Tracy and McVeigh algorithms were developed and validated using data from youth aged 10–18 and young adults aged ~22 years, respectively. Since sleep patterns (Yoon et al 2003) and activity intensity profiles (Troiano et al 2008) are highly variable by age, there is good reason to believe that the algorithms developed for adolescents and young adults are not directly generalizable to older adults (McVeigh et al 2016). However, both the Tracy and McVeigh algorithms were originally designed with parameters that could be modified to fit different population subgroups.
The first objective of this study was to identify parameter values that optimized the Tracy and McVeigh algorithms for identifying waking wear time for older women. Waking wear time was defined as the daily out-of-bed time during accelerometer wear, and is the key variable used for adjustment in studies of physical activity and sedentary behavior that collect data over the 24-hour day. The second objective was to validate both algorithms in a separate sample of older women using the newly-identified optimal parameters. An algorithm parameterized for older adults, if sufficiently valid, could measurably reduce the resource burden of data processing, making it more feasible for large epidemiologic studies to include 24-hour accelerometry measures.
METHODS
Sample
Accelerometer and sleep log data from a subsample of Women’s Health Initiative (WHI) participants that enrolled in the ancillary Objective Physical Activity and Cardiovascular Health Study (OPACH) were used (LaCroix et al 2017). OPACH participants were recruited from 40 clinical centers around the US that were originally used for WHI recruitment. Participants were between 63 and 99 years old (average age 79 ± 7 years), community-living, ambulatory, and cognitively able to provide consent. About half (49.4%) were non-Hispanic white, 33.7% were non-Hispanic black, and 16.9% were Hispanic/Latina. ActiGraph GT3X+ accelerometers were worn over the right hip for 24 hours per day (removed only when showering or swimming) over a 7-day measurement period. Sleep logs were concurrently distributed to collect in-bed and out-of-bed times during accelerometer wear; the sleep logs were published elsewhere (Rillamas-Sun et al 2015). Of the 6489 women who wore accelerometers for at least one day, 6114 (94%) also completed sleep logs for at least one day.
The first 628 participants whose accelerometer data went through a validated sleep log-assisted visual inspection (described below) were included in the present study. Participants were randomly assigned to either a “parameterization subsample” that was used to determine optimal parameters or a “validation subsample” that was a separate sample used only to evaluate the optimal parameters.
Parameters for the Tracy and the McVeigh algorithms were largely dependent on in-bed and out-of-bed body movement. Sleep duration (short <7 hr/night, average 7–9 hr/night, and long >9 hr/night) and total physical activity (high and low, determined by a median split to accelerometer cpm) were used as proxies for this movement. To ensure sufficient variation in sleep and physical activity patterns in the parameterization and validation subsamples, the 628 women were stratified into the 6 mutually exclusive categories based on sleep duration and total physical activity. Then 50% of women from each category were randomly sampled without replacement for the parameterization subsample; the remaining women formed the validation subsample. The parameterization and validation subsamples each had 18 high activity short sleepers, 119 high activity average sleepers, 21 high activity long sleepers, 15 low activity average sleepers, 96 low activity average sleepers, and 45 low activity long sleepers.
Accelerometer data processing
ActiGraph GT3X+ accelerometers measured acceleration at 30 Hz. Raw acceleration data were converted into counts per 15-second epoch using the low frequency filter in ActiLife v6.11. This filter was used by McVeigh and colleagues and is designed so that activity at the lower end of the activity intensity spectrum can be detected with similar consistency as older ActiGraph accelerometer models such as those used by Tracy and colleagues (Tracy et al 2014, McVeigh et al 2016, ActiGraphcorp.com 2015). Data were then aggregated to 1-minute epochs to represent cpm. Vector magnitude counts for each 1-minute epoch was computed as the square root of the sum of the vertical axis cpm squared, the horizontal axis cpm squared, and the perpendicular axis cpm squared. Non-wear time was identified by a commonly used automated algorithm which identified periods with ≥ 90 minutes of consecutive vector magnitude cpm of zero, allowing for up to 2 consecutive minutes of nonzero counts (to account for movement of the unworn device) conditional on there being 30 minute windows of zero cpm before and after the device was moved (Choi et al 2011, 2012).
Sleep log-assisted visual analysis
Similar to the procedures used by McVeigh et al., two raters were trained to visually identify in-bed periods by systematically observing cpm data in the context of self-reported in-bed periods. Using ActiLife V6.11.8, raters created 60-sec condensed AGD files and scored each participant’s 24-hour accelerometer data using the software’s sleep analysis tab. Raters identified in-bed periods by inputting self-reported in-bed and out-of-bed times from completed sleep logs into the software and visually inspecting the accelerometer tracings (in cpm) for changes in activity levels that would indicate that the participant transitioned from in-bed to out-of-bed or vice versa. If the visually identified transition was different from the self-reported time by ≥ 15 minutes, then the self-reported sleep period was adjusted based on the observed accelerometer data. The 15-minute requirement was determined by raters and investigators during the protocol development process in part to give the self-reported times priority when raters’ and reporters’ times were ‘close’ and as pragmatic step to reduce coder burden. Raters identified the start of the in-bed period as the first zero count following a significant and persistent reduction in activity (<100 cpm) and defined the end of the in-bed period as a significant and persistent increase in activity (>100 cpm). The resulting in-bed periods were used as the criterion for algorithm parameterization and for validation. This protocol was developed based on a method used by sleep researchers shown previously to have high inter-rater reliability with mean absolute differences between raters and experts of 3.4±5.4 minutes and interclass correlations ranging from 0.84 to 0.99 (Blackwell et al 2005).
For 20 participants, a second rater coded data for the same days. The double-coded data were used to assess the degree to which the criterion data was reliable by computing % agreement allowing for in-bed and out-of-bed times to differ by ±5 minutes. The inter-rater agreement was 88.2%.
The Tracy and McVeigh algorithms
Generally, both the Tracy and McVeigh algorithms work by first identifying long periods of relatively low intensity activity, to operationalize an in-bed period. The algorithms then search the beginning and end of each period for a more precise in-bed and out-of-bed time. Both steps rely on cpm cutpoints that were applied to data from the vertical axis only. Our study extends this by also using data from all three axes, summarized as the vector magnitude.
The Tracy and McVeigh algorithms were designed with modifiable parameters enabling them to be tuned to work in samples different from those used in their development and validation. Both algorithms are described in detail elsewhere (McVeigh et al 2016, Tracy et al 2014). The Tracy algorithm has three modifiable parameters (CP0, CP1, and CP2), with CP1 and CP2 having the largest influence on the accuracy of the algorithm. CP1 is the cpm cutpoint that differentiates high from low intensity activity and is used to identify what the authors call “bedtime rest periods”. CP2 is the cpm cutpoint used to find a more precise end time for the bed rest period. The validated cpm cutpoints supplied by the authors—determined by examining receiver operation curves for different options and optimizing for sensitivity and specificity—for CP1 and CP2 were 20 cpm and 500 cpm, respectively (Tracy et al 2014). CP0 – a parameter to identify precise start times for the bedtime rest period – was fixed at 50 cpm. The McVeigh algorithm had five modifiable parameters (slthres, prslthresh1, prslthresh2, prwkthresh1, and prwkthresh2), with slthres and prwkthresh2 being central to its functioning. Slthres was used to define period of prolonged low activity that indicated participants were either in bed or the device was not being worn (called in-bed/non-wear [BNW] periods); McVeigh et al. set this equal to 88 cpm. Prslthresh1 and prslthresh2 are parameters used to identify the precise beginning time for a BNW, while prwkthresh1 and prwkthresh2 are parameters used to identify the precise ending time of a BNW. Parameter values were determined by repeatedly changing values, graphing the results, then visually inspecting the results in relation to their criterion. McVeigh et al. set the parameters as follows: prslthresh1=89, prslthresh2=50, prwkthresh1=91, prwkthresh2=200 (McVeigh et al 2016).
Selecting optimal parameters for each algorithm
For the Tracy and McVeigh algorithms, optimal parameters were selected separately using both the vertical axis (VA) and the vector magnitude (VM) data. A range of possible cpm cutpoints was prespecified for the two key modifiable parameters for each algorithm. We then choose 10 to 50 grid points within the plausible range for each parameter. The ranges of plausible values [low:high, by gridpoint] were [VA=10:120, by 10; VM=90:300, by 10] for CP1, [VA=60:200, by 20; VM=200:700, by 50] for CP2, [VA=50:150, by 10; VM=150:300, by 10] for slthres, and [VA=120:400, by 40; VM=300:700, by 50] for prwkthresh2, based on the literature (Evenson et al 2015, Tracy et al 2014) and our practical experiences.
Each combination of parameters was applied to data from participants in the parameterization subsample, one participant at a time, to implement the Tracy and McVeigh algorithms. One-minute epochs were classified as either out-of-bed or in-bed and/or non-wear time. After each implementation, the newly classified minutes were compared with minutes classified using the criterion sleep-log guided visual inspection method by computing sensitivity and specificity. Sensitivity was defined as the proportion of algorithm-identified out-of-bed minutes in agreement with out-of-bed minutes classified using the criterion method. Specificity was defined as the proportion of algorithm-identified in-bed minutes in agreement with in-bed minutes classified using the criterion method. The above procedures were repeated for all unique combinations of modifiable parameters. Sensitivity and specificity were computed for each participant first, and then the medians across all participants were calculated. The parameter combination with the highest median sensitivity plus specificity was selected.
To reduce the computational resources needed for the parameterization process, the following parameters, which based on our experience from systematically deconstructing both algorithms and on results from early exploratory sensitivity analyses we determined would be less influential for algorithm accuracy than the varied parameters, were fixed for all analytic steps: CP0=50 cpm; prslthresh2=50 cpm; prslthresh1=slthresh+1; and prwkthresh1=slthresh+10.
Validation
The parameterization process resulted in 4 optimal cpm cutpoint combinations: Tracy_VA; Tracy_VM; McVeigh_VA; and McVeigh_VM. The Tracy and McVeigh algorithms were then implemented on data from the validation sample using the 4 optimal cutpoint combinations and the two originally validated cutpoint combinations supplied by the authors (Tracy_original and McVeigh_original). Agreement in daily out-of-bed time between the criterion measure and all 6 implementations of the algorithms was assessed using sensitivity, specificity, and Cohen’s kappa.
For each participant and each algorithm implementation, waking wear time was computed as the average number of out-of-bed minutes per day. Agreement in waking wear time was assessed by computing mean bias (i.e., the overall mean difference) and 95% limits of agreement. Bland-Altman plots displayed differences in waking wear time between the algorithm-identified measures and the criterion measure.
Each epoch of waking wear time was separated into “activity measure” categories identified as sedentary behavior, light intensity physical activity (light PA), and moderate-to-vigorous intensity physical activity (MVPA) using vector magnitude cutpoints previously established in the OPACH Calibration Study (sedentary time <39 counts/15-seconds, light PA 40–573 counts/15-seconds, MVPA > 573 counts/15-seconds) (Evenson et al 2015). A confusion matrix comparing activity measures for data processed using the criterion method to data processed using all 6 algorithm implementations was then tabulated to identify where misclassification occurred.
Estimates of sedentary time, light PA, and MVPA were computed for the validation sample after adjusting for waking wear time, which is consistent with the analytic method used by many studies of accelerometer-measured physical activity and sedentary behavior. The residuals method was used to adjust the activity measures (Willett and Stampfer 1986) and differences were analyzed using generalized estimating equations.
Simple linear regression was used to assess how the waking wear time computation method influenced associations between waking wear time-adjusted activity measures and health-related characteristics. The health-related characteristics at the time of accelerometry included age and measured body mass index (BMI), physical functioning assessed using the short physical performance battery (SPPB), and blood pressure. The SPPB is a series of three timed tests—balance in three standing position, one 4-meter usual gait speed test, and 5 unassisted chair stands—that are each given a score from 0 to 4 based on previously validated thresholds and are summarized to a score ranging from 0 to 12 with 12 being highly functioning (Guralnik et al 1994). Beta coefficients from regression models were compared using the Horton method (Horton and Fitzmaurice 2004) with and without Bonforoni correction for multiple tests.
All analyses were conducted in R (R Foundation for Statistical Computing; Vienna, Austria) using two-tailed statistical tests with p<0.05 considered statistically significant.
RESULTS
The parameterization and validation subsamples had similar ages (mean=80±6 years; p=0.75) and similar racial-ethnic variation with the majority of each sample being White (60% and 57%; p=0.71). BMI was slightly higher in the parameterization subsample (29 vs 27 kg/m2; p=0.01), while SPPB and blood pressure were slightly higher in the validation subsample (Table 1; p-values all > 0.05).
Table 1.
Participant characteristics by subsample
| Parameterization subsample (n=314) | Validation Subsample (n=314) | p-value | |
|---|---|---|---|
| Age (years) | 80 ± 6 | 80 ± 6 | 0.75 |
| Race-ethnicity, % | 0.71 | ||
| White | 60% | 57% | |
| Black | 23% | 24% | |
| Hispanic | 17% | 19% | |
| BMI (kg/m2) | 29 ± 6 | 27 ± 6 | 0.01 |
| SPPB | 8.0 ± 2.6 | 8.2 ± 2.5 | 0.37 |
| Diastolic BP (mmHg) | 71 ± 8 | 72 ± 9 | 0.38 |
| Systolic BP (mmHg) | 125 ± 14 | 127 ± 15 | 0.10 |
Abbreviations: BMI = body mass index; SPPB = short physical performance battery; BP = blood pressure
Data are mean ± sd for continuous variables, percentarges for categorical variables
For all analyses, only days with complete accelerometer data and self-reported sleep logs were used, resulting in 314 women with 1436 days in the parameterization subsample and 307 women with 1402 days in the validation subsample. The ROC curves show joint distributions of sensitivity and (1-specificity) for each combination of algorithm parameters (Supplemental Figure 1). Optimal (CP1, CP2) cutpoints (cpm) maximizing the sum of sensitivity and specificity were (60, 100) for Tracy_VA and (210, 350) for Tracy_VM, and optimal McVeigh (slthres, prwkthresh2) cutpoints were (90, 280) for McVeigh_VA and (210, 600) for McVeigh_VM.
Agreement in waking wear time comparing the criterion method to the Tracy and McVeigh algorithms implemented using the original, optimal VA and optimal VM thresholds for each calendar day in the validation subsample are in Table 2. In general, agreement was high with day-level agreements across all algorithm implementations ranging from 84 to 91 for percent agreement, 85 to 92 for sensitivity, 81 to 89 for specificity, and 67 to 80 for kappa. Between 87 and 94 percent of all calendar days, on average, had moderate to excellent kappa values.
Table 2:
Agreement in awake wear time relative to sleep log-assisted visual analysis; validation subsample (1402 days from 307 women)
| Tracy original | Tracy VA | Tracy VM | McVeigh original | McVeigh VA | McVeigh VM | |
|---|---|---|---|---|---|---|
| Day-level agreement | ||||||
| Percent agreement, mean (sd) | 84.8 (11.7) | 85.3 (12.2) | 87.0 (11.5) | 86.3 (14.9) | 86.0 (15.0) | 90.5 (11.1) |
| Sensitivity, mean (sd) | 0.87 (0.2) | 0.85 (0.2) | 0.86 (0.2) | 0.86 (0.2) | 0.85 (0.2) | 0.92 (0.2) |
| Specificity, mean (sd) | 0.81 (0.2) | 0.86 (0.2) | 0.89 (0.1) | 0.87 (0.2) | 0.87 (0.2) | 0.87 (0.2) |
| Kappa, mean (sd) | 0.67 (0.2) | 0.69 (0.2) | 0.73 (0.2) | 0.72 (0.3) | 0.71 (0.3) | 0.80 (0.2) |
| Kappa category | ||||||
| Poor (<0.4), n (%) | 184 (13%) | 169 (12%) | 110 (8%) | 179 (13%) | 186 (13%) | 86 (6%) |
| Moderate (0.4–0.75), n (%) | 590 (42%) | 560 (40%) | 517 (37%) | 403 (29%) | 400 (29%) | 310 (22%) |
| Excellent (>0.75), n (%) | 626 (45%) | 671 (48%) | 773 (55%) | 818 (58%) | 814 (58%) | 1004 (72%) |
| Person-level agreement | ||||||
| Mean bias (hr/day), mean (sd) | −0.28 (2.5) | −1.06 (2.6) | −1.28 (2.5) | −1.00 (3.3) | −1.20 (3.4) | −0.04 (2.5) |
| 95% Limits of agreement | −4.9, 4.8 | −5.2, 5.1 | −5.0, 4.9 | −6.5, 6.5 | −6.6, 6.5 | −5.0, 4.9 |
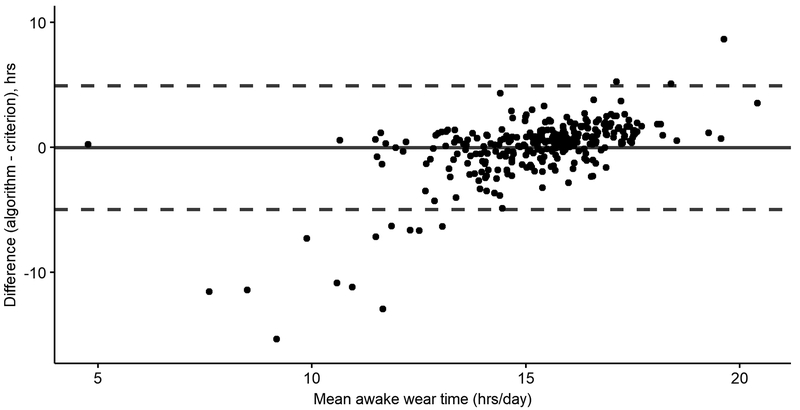
For nearly all agreement metrics, the McVeigh_VM performed best. Seventy-two percent of days had excellent kappa values. When average waking wear times were computed, the mean bias was near zero (−0.04 hours/day) with 95% levels of agreement ranging from −5.0 hours/day to 4.9 hours/day. The Bland-Altman plot of waking wear time agreement between the McVeigh_VM and the visual analysis approach is show in Figure 1. Bland-Altman plots for all algorithm implementations are in Supplemental Figure 2.
Figure 1.
Agreement in average daily waking wear time for each participant in the validation subsample. The mean difference (solid line) was computed by subtracting the average daily waking wear time measured by criterion method from the average daily waking wear time measured by the McVeigh algorithm using the optimal vector magnitude (VM) cutpoints; upper and lower limits of agreement are shown with dotted lines. The x-axis is the average waking wear time between criterion method and McVeigh_VM.
The confusion matrix in Table 3 shows minute-level epoch classifications for the McVeigh_VM implementation and the criterion method. Matrices for all other algorithm implementations are in the Supplemental Tables 1–5. Cells on the downward-sloping diagonal indicate perfect agreement for 90.5% of all 1-minute epochs in the validation subsample. Nearly all misclassification occurs between the in-bed/non-wear classifications and sedentary time. For 4.3% of the 1-minute epochs, sedentary time was classified as in-bed/non-wear by the McVeigh_VM. Similarly, 4.1% of the 1-minute epochs that were classified as in-bed/non-wear by the criterion method were classified as sedentary time by the McVeigh_VM. Few light intensity or moderate to vigorous intensity physical activity 1-minute epochs were differentially classified, less than 2% of all epochs in total.
Table 3.
Confusion matrix for the McVeigh algorithm implemented using the optimal vector magnitude cutpoints showing activity measures and in-bed/non wear. Data are the number of 1-minute epochs (percentages) in the Validation subsample.
| Sleep-log-assisted visual inspection (criterion method) | ||||
|---|---|---|---|---|
| In-bed / non wear time | Sedentary time | Light PA | MVPA | |
| In-bed / non wear time | 635540 (31.6) | 85865 (4.3) | 10738 (0.5) | 967 (0.0) |
| Sedentary time | 81812 (4.1) | 716989 (35.6) | 0 (0.0) | 0 (0.0) |
| Light PA | 10009 (0.5) | 0 (0.0) | 390413 (19.4) | 0 (0.0) |
| MVPA | 1754 (0.1) | 0 (0.0) | 0 (0.0) | 77830 (3.9) |
Abbreviations: PA = Physical activity, MVPA = Moderate-to-vigorous intensity physical activity
The average number of minutes per day spent in sedentary time, light PA, and MVPA were adjusted for waking wear time, as is typically done in studies of sedentary time and physical activity (Table 4). Women in the validation sample were sedentary for 574 minutes/day, in light PA for 286 minutes/day, and were in MVPA for 56 minutes/day. Across the 6 algorithm implementations, the magnitude of mean differences was highest for sedentary time and lowest for MVPA. Activity time estimates were most similar between the McVeigh_VM and the criterion method, with no significant differences for sedentary time (p=0.43), light PA (p=0.82), or MVPA (p=0.51). MVPA estimates adjusted for awake wear time computed using all 6 algorithms were not significantly different from MVPA adjusted using the criterion method (p >0.27 | all).
Table 4:
Average minutes per day spent in sedentary time, light physical activity (PA), and moderate to vigorous physical activity (PA) after adjustment for awake wear time. Validation subsample (n=307).
| Criterion method | Tracy original | Tracy VA | Tracy VM | McVeigh original | McVeigh VA | McVeigh VM | |
|---|---|---|---|---|---|---|---|
| Sedentary timea | 574 (99) | 559 (86) | 513 (79) | 499 (71) | 529 (82) | 519 (81) | 572 (82) |
| mean difference | - | −15.1 | −61.2 | −75.2 | −45.6 | −54.7 | −2.3 |
| 95% CI | - | (−20.5, −9.7) | (−67.3, −55.0) | (−82.5, −67.9) | (−51.5, −39.7) | (−60.8, −48.7) | (−8.1, 3.4) |
| p-value | - | <.001 | <.001 | <.001 | <.001 | <.001 | 0.428 |
| light PAa | 286 (75) | 283 (66) | 282 (62) | 283 (56) | 271 (65) | 269 (64) | 285 (64) |
| mean difference | - | −2.7 | −3.2 | −2.4 | −14.2 | −16.6 | −0.5 |
| 95% CI | - | (−6.6, 1.1) | (−7.5, 1.1) | (−7.7, 2.8) | (−18.2, −10.3) | (−20.7, −12.6) | (−4.6, 3.6) |
| p-value | - | 0.162 | 0.140 | 0.361 | <.001 | <.001 | 0.820 |
| MVPAa | 56 (41) | 56 (38) | 57 (37) | 56 (36) | 55 (36) | 55 (36) | 56 (38) |
| mean difference | - | 0.8 | 1.1 | 0.5 | −0.3 | −0.5 | 0.6 |
| 95% CI | - | (−0.8, 2.4) | (−0.8, 3.0) | (−1.6, 2.6) | (−2.3, 1.8) | (−2.6, 1.6) | (−1.1, 2.3) |
| p-value | - | 0.347 | 0.275 | 0.612 | 0.808 | 0.638 | 0.508 |
Data are mean (sd)
Inferences about the statistical significance and, when significant, the direction of associations between sedentary time and age, BMI, SPPB, and diastolic blood pressure were similar when sedentary time was adjusted for waking wear time using the criterion method and all 6 implementations of the Tracy and McVeigh algorithms (Table 5). Qualitatively, the magnitude of associations with health-related characteristics were generally most similar when sedentary time was adjusted for the waking wear time computed using the criterion method and McVeigh_VM. Quantitatively, the beta coefficients for age estimated using all algorithm-derived waking wear times were different from the beta coefficients adjusted for waking wear time computed using the criterion method (p<0.05 | all) with and without Bonforoni correction. When using the Bonforoni method to correct for possible Type 1 error due to multiple testing, the beta coefficients for BMI, SPPB, and diastolic blood pressure estimated using all algorithm-derived waking wear times were not significantly different from the beta coefficients estimated using the criterion method (except Tracy_VM and BMI). Similar patterns were observed for associations with light PA and with MVPA (Supplemental Tables 6 and 7). Analyses were also run for systolic blood pressure and results were similar to those for diastolic blood pressure (data not shown).
Table 5:
Simple linear regression results for associations between 1 hour of sedentary time (adjusted for awake wear time) and health-related characteristics. Validation subsample (n=307).
| Criterion method (1) | Tracy Original (2) | Tracy VA (3) | Tracy VM (4) | McVeigh original (5) | McVeigh VA (6) | McVeigh VM (7) | |
|---|---|---|---|---|---|---|---|
| Age (years) | |||||||
| beta | 0.86 | 0.57 | 0.52 | 0.55 | 0.64 | 0.65 | 0.76 |
| 95% CI | (0.48,1.24) | (0.12,1.02) | (0.03,1.01) | (0.00,1.10) | (0.17,1.11) | (0.18,1.13) | (0.29,1.23) |
| p-value | <.001 | 0.013 | 0.037 | 0.050 | 0.008 | 0.007 | 0.002 |
| Δ betaa | 2,3,4,5,6,7 | 1 | 1,7 | 1,7 | 1 | 1 | 1,3,4 |
| Δ beta (corrected)b | 2,3,4,5,6,7 | 1 | 1,7 | 1,7 | 1 | 1 | 1,3,4 |
| BMI (kg/m2) | |||||||
| beta | 1.10 | 1.36 | 1.47 | 1.26 | 1.54 | 1.53 | 1.21 |
| 95% CI | (0.75,1.46) | (0.95,1.76) | (1.03,1.91) | (0.75,1.76) | (1.12,1.97) | (1.10,1.96) | (0.77,1.65) |
| p-value | <.001 | <.001 | <.001 | <.001 | <.001 | <.001 | <.001 |
| Δ betaa | 4,7 | 4,7 | 4 | 1,2,3,5,6,7 | 4,6,7 | 4,5,7 | 1,2,4,5,6 |
| Δ beta (corrected)b | 4 | 4 | 4 | 1,2,3,5,6,7 | 4,6,7 | 4,5,7 | 4,5,6 |
| SPPB | |||||||
| beta | −0.35 | −0.41 | −0.35 | −0.33 | −0.30 | −0.30 | −0.30 |
| 95% CI | (−0.54,−0.17) | (−0.63,−0.20) | (−0.58,−0.12) | (−0.60,−0.07) | (−0.53,−0.08) | (−0.53,−0.07) | (−0.52,−0.07) |
| p-value | <.001 | <.001 | 0.003 | 0.013 | 0.009 | 0.012 | 0.010 |
| Δ betaa | 4,5,6,7 | 3,4,5,6,7 | 2,4 | 1,2,3 | 1,2 | 1,2 | 1,2 |
| Δ beta (corrected)b | - | 3,4,6 | 2 | 2 | - | 2 | - |
| Diastolic BP (mmHg) | |||||||
| beta | −0.10 | 0.05 | −0.15 | 0.08 | −0.10 | −0.10 | −0.10 |
| 95% CI | (−0.70,0.50) | (−0.64,0.74) | (−0.90,0.59) | (−0.75,0.92) | (−0.81,0.62) | (−0.82,0.62) | (−0.83,0.62) |
| p-value | 0.740 | 0.882 | 0.683 | 0.848 | 0.788 | 0.792 | 0.777 |
| Δ betaa | - | - | - | - | - | - | - |
| Δ beta (corrected)b | - | - | - | - | - | - | - |
Abbreviations: CI = confidence interval; BMI = body mass index; SPPB = short physical performance battery; BP = blood pressure
Differences between betas tested using the Horton method with p<0.05 considered significant.
Differences between betas tested using the Horton method with p-values corrected for multiple tests using the Bonforoni method (i.e., p<0.05/7 considered significant).
DISCUSSION
This project intended to parameterize and validate two existing algorithms to identify in-bed time to accurately measure waking wear time using data from hip-worn accelerometers worn 24 hours/day by older adults. Automation reduces errors from human visual inspection and drastically reduces the resources needed to process accelerometer data collected using a 24-hour wear protocol, making these approaches more scalable. Our results showed an overall high agreement between the criterion method and all 6 implementations of the Tracy and McVeigh algorithms, with the highest agreement achieved by the McVeigh_VM with optimized parameters. The McVeigh_VM implementation provided unbiased estimates of average waking wear time though with high variation around the mean (±5 hours). Other implementations had mean biases ranging from −0.28 to −1.28 hours. Most often, sedentary time was the activity misclassified by the algorithms, with some instances of light PA and relatively little MVPA misclassification. After adjusting sedentary time, light PA, and MVPA for waking wear time, there were no differences in average estimates between the criterion method and McVeigh_VM, but other implementations including the McVeigh_original significantly underestimated sedentary time and in some instances light PA as well. Generally, similar overall inferences were made between health-related characteristics and sedentary time, light PA, and MVPA regardless of the method used to quantify awake wear time. In most tests, estimates based on McVeigh_VM were closest to those based on the criterion method than all other implementations, although there were few significant differences between algorithm implementations. Of particular note, the direction of associations were similar between the criterion method and McVeigh_VM for all health-related variables, and there was statistically significant differences in the magnitude of associations of sedentary time, light PA, and MVPA only with age.
Similar to McVeigh and colleagues, our study objective was to advance methods to accurately and efficiently identify waking wear time. The objective of Tracy and colleagues was to identify bedrest time which they measured using both energy expenditure using a whole-room calorimeter and movement-related mechanical work measured using a force plate in the floor of the whole room calorimeter. This focus on bedrest, which the authors note has also been referred to as sleep or sleep-period, could account for why the McVeigh algorithm outperformed the Tracy algorithm when compared to our criterion measure. Tracy et al. reported bedrest time sensitivity and specificity in their adolescent validation sample (n=40) of 0.97 and 0.97, respectively. The authors subsequently adapted their algorithm to function using data from adults (using a sample of 141 men and women aged 40±14) and achieved bedrest time sensitivity and specificity of 0.82 and 0.97, respectively (Tracy et al 2018). McVeigh et al. reported waking wear time sensitivity and specificity in their validation sample (n=97) of 0.97 and 0.96, respectively. The mean bias and 95% limits of agreement reported in their study was (3.6 min/day and −2.3 to 2.5 h/day). The waking wear time sensitivity and specificity observed in our study for the best performing algorithm implementation (McVeigh_VM) was comparable, although lower, at 0.92 and 0.87, respectively, and McVeigh_VM mean bias and 95% limits of agreement were (0 min/day and −5 to 4.9 h/day). It is noteworthy that McVeigh_VM outperformed the McVeigh_original demonstrating that parameterizing for older adults and/or using signals from the vector magnitude instead of the vertical axis only was an improvement.
Our criterion method was similar to the one used to develop and validate the McVeigh algorithm and is the approach commonly used by researchers when processing sleep-related actigraphy data from wrist-worn devices. The protocol used was originally developed for systematic visual inspection of raw data from wrist-worn accelerometers to determine in-bed periods (Blackwell et al 2005) and was modified for use on hip-worn accelerometers; the full protocol is available upon request. While visual inspection is the standard method in the field of sleep research, it is resource intensive, taking approximately 15 minutes per participant in the present study, and can lead to error. In our analysis, the error was small with inter-rater agreement of 88%. Furthermore, in our sleep-log assisted visual analysis, when the in-bed and out-of-bed time appeared to be within 15 minutes of the participants’ self-reported in-bed or out-of-bed time, the in-bed period was defined by self-report. This protocol decision was made to reduce rater burden. The 15-minute buffer combined with the inter-rater error could account for some of the observed differences in waking wear time observed between the criterion method and all 6 algorithm implementations.
The use of automated algorithms can greatly reduce the resources needed to accomplish repetitive tasks in a large scale study setting, especially when set-up time, which sometimes can be long, is reduced by the availability of ready-to-use software. When working with intensive longitudinal data, it is always good practice to visually inspect how algorithms perform (Bolger and Laurenceau 2013). This can be accomplished for a randomly chosen subset of data and/or for the days with unusually long and unusually short waking wear times. In some instances, manually correcting the data following algorithm implementation may be needed. In the present study, we did not manually correct any data. However, we strongly recommend that all researchers implementing this algorithm visually inspect the results. In practice, an example workflow would be to implement the Choi algorithm, then McVeigh_VM, plot the results of both overlaid on the VM cpm data for each valid day, then make modifications to the McVeigh_VM results as needed. The McVeigh_VM algorithm can also be used to perform sensitivity analyses when other in-bed period imputation methods are used such as mean imputation [eg, (Bellettiere et al 2019)]. If desired, the McVeigh_VM parameters can be further changed to improve the algorithms’ accuracy for different samples.
This study is not without limitations. Our focus was on identifying waking wear time and not sleep, primarily because sleep is a construct characterized by physiologic states that is difficult to proxy using only accelerometer data from hip-worn devices. In-bed time (a proxy for sleep duration) is output by the McVeigh algorithm, but this was not the focus of our parameterization or validation. The algorithms were originally designed then newly optimized and validated using data from ActiGraph accelerometers; caution should be taken when applying them to accelerometer data from other devices. New algorithms were published after the design and implementation of our study protocol and were therefore not evaluated [eg, (Tracy et al 2018)]. Our study was conducted among older community-living, ambulatory women and we are not sure whether the results can be generalized to the entire older adult population. Finally, we modified only two parameters for each algorithm to conserve computational resources. It is unlikely that this had an appreciable negative effect on parameterization, considering the overall waking wear time agreement was relatively high and that some optimal parameters (specifically the McVeigh_VM) tended to outperform the original parameters.
Strengths of our study include the sample size that was more than twice the size of other comparative studies. We had sufficient numbers to parameterize and validate the optimal parameters on two separate datasets, each with over 300 participants. We also parameterized and compared algorithm performance to data from a sleep-log assisted visualization process that is thought to be better than using un-augmented self-reported bed times (Lockley et al 1999).
Using only hip-worn accelerometer data collected 24-hours/day from older women, the McVeigh algorithm with the optimal VM parameters provided unbiased estimates of waking wear time. Adjustment for waking wear time computed using McVeigh_VM can introduce error into measures of sedentary time, light PA, and MVPA, which could lead to biased associations with health indicators or other factors of interest. However, most of the associations tested in the validation subsample were not qualitatively different when adjusting for waking wear time computed using the criterion method or McVeigh_VM. We also observed unbiased estimates of wear time-adjusted sedentary time, light PA, and MVPA when the McVeigh_VM implementation was used. We therefore conclude that the McVeigh_VM implementation is suitable for identifying awake wear time among older adults. Caution should be used when implementing automated algorithms on intensive longitudinal data, and users of this algorithm should take appropriate precautions, such as visually inspecting the results as needed and manually making changes where appropriate.
Supplementary Material
ACKNOWLEDGEMENTS
The following is a short list of WHI Investigators, the full list can be found at the following site: www.whi.org/researchers/Documents%20%20Write%20a%20Paper/WHI%20Investigator%20Long%20List.pdf
Program Office: (National Heart, Lung, and Blood Institute, Bethesda, Maryland) Jacques Rossouw, Shari Ludlam, Dale Burwen, Joan McGowan, Leslie Ford, and Nancy Geller; Clinical Coordinating Center: Clinical Coordinating Center: (Fred Hutchinson Cancer Research Center, Seattle, WA) Garnet Anderson, Ross Prentice, Andrea LaCroix, and Charles Kooperberg; Investigators and Academic Centers: (Brigham and Women’s Hospital, Harvard Medical School, Boston, MA) JoAnn E. Manson; (MedStar Health Research Institute/Howard University, Washington, DC) Barbara V. Howard; (Stanford Prevention Research Center, Stanford, CA) Marcia L. Stefanick; (The Ohio State University, Columbus, OH) Rebecca Jackson; (University of Arizona, Tucson/Phoenix, AZ) Cynthia A. Thomson; (University at Buffalo, Buffalo, NY) Jean Wactawski-Wende; (University of Florida, Gainesville/Jacksonville, FL) Marian Limacher; (University of Iowa, Iowa City/Davenport, IA) Robert Wallace; (University of Pittsburgh, Pittsburgh, PA) Lewis Kuller; (Wake Forest University School of Medicine, Winston-Salem, NC) Sally Shumaker Women’s Health Initiative Memory Study: (Wake Forest University School of Medicine, Winston-Salem, NC) Sally Shumaker.
FUNDING SOURCES
The National Heart, Lung, and Blood Institute provided funding for the OPACH study (grant number RO1 HL105065 to AZL). Funding also came from training grants provided by the National Institutes of Health (grant numbers T32HL079891–11 to JB). The Women’s Health Initiative program was funded by the National Heart, Lung, and Blood Institute, National Institutes of Health, U.S. Department of Health and Human Services (contract numbers HHSN268201600018C, HHSN268201600001C, HHSN268201600002C, HHSN268201600003C, and HHSN268201600004C).
REFERENCES
- ActiGraphcorp.com. White Paper Low Frequency Extension Filter. 2015. ActiGraph. Online: http://actigraphcorp.com/wp-content/uploads/2015/06/Low-Frequency-Extension-Filter.pdf. [Google Scholar]
- Ancoli-Israel S, Cole R, Alessi C, Chambers M, Moorcroft W and Pollak CP 2003. The role of actigraphy in the study of sleep and circadian rhythms. Sleep 26 342–92 [DOI] [PubMed] [Google Scholar]
- Barreira TV, Schuna JM, Mire EF, Katzmarzyk PT, Chaput JP, Leduc G and Tudor-Locke C 2015. Identifying children’s nocturnal sleep using 24-h waist accelerometry Med. Sci. Sports Exerc 47 937–43 [DOI] [PubMed] [Google Scholar]
- Bellettiere J, LaMonte MJ, Evenson KR, Rillamas-Sun E, Kerr J, Lee I-M, Di C, Rosenberg DE, Stefanick ML, Buchner DM, Hovell MF, LaCroix AZ, Rossouw J, Ludlam S, Burwen D, McGowan J, Ford L, Geller N, Anderson G, Prentice R, Kooperberg C, Manson JE, Howard BV., Jackson R, Thomson CA, Wactawski-Wende J, Limacher M, Wallace R, Kuller L, Shumaker S and Shumaker S 2019. Sedentary Behavior and Cardiovascular Disease in Older Women Circulation 139 1036–46 Online: https://www.ahajournals.org/doi/10.1161/CIRCULATIONAHA.118.035312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackwell T, Ancoli-Israel S, Gehrman PR, Schneider JL, Pedula KL and Stone KL 2005. Actigraphy scoring reliability in the study of osteoporotic fractures Sleep 28 1599–605 [DOI] [PubMed] [Google Scholar]
- Bolger N and Laurenceau J-P 2013. Intensive longitudinal methods: an introduction to diary and experience sampling research ed Kenny DA (Guilford Press; ) [Google Scholar]
- Chen KY, Janz KF, Zhu W and Brychta RJ 2012. Redefining the roles of sensors in objective physical activity monitoring Med. Sci. Sport Exerc 44 13–23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi L, Liu Z, Matthews CE and Buchowski MS 2011. Validation of accelerometer wear and nonwear time classification algorithm Med. Sci. Sports Exerc 43 357–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi L, Ward SC, Schnelle JF and Buchowski MS 2012. Assessment of wear/nonwear time classification algorithms for triaxial accelerometer Med. Sci. Sports Exerc 44 2009–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaz KM, Goldsmith J, Greenlee H, Strizich G, Qi Q, Mossavar-Rahmani Y, Vidot DC, Buelna C, Brintz CE, Elfassy T, Gallo LC, Daviglus ML, Sotres-Alvarez D and Kaplan R 2017. Prolonged, uninterrupted sedentary behavior and glycemic biomarkers among US Hispanic/Latino adults : The Hispanic Community Health Study/Study of Latinos (HCHS/SOL) Circulation 136 1362–73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evenson KR, Wen F, Herring AH, Di C, LaMonte MJ, Tinker LF, Lee IM, Rillamas-Sun E, LaCroix AZ and Buchner DM 2015. Calibrating physical activity intensity for hip-worn accelerometry in women age 60 to 91years: The Women’s Health Initiative OPACH Calibration Study Prev. Med. Reports 2 750–6 Online: 10.1016/j.pmedr.2015.08.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedson PS, Melanson E and Sirard J 1998. Calibration of the Computer Science and Applications, Inc. accelerometer. Med. Sci. Sports Exerc 30 777–81 [DOI] [PubMed] [Google Scholar]
- Guralnik JM, Simonsick EM, Ferrucci L, Glynn RJ, Berkman LF, Blazer DG, Scherr P a. and Wallace RB 1994. A short physical performance battery assessing lower extremi J. Gerontol 49 85–94 [DOI] [PubMed] [Google Scholar]
- Horton NJ and Fitzmaurice GM 2004. TUTORIAL IN BIOSTATISTICS Regression analysis of multiple source and multiple informant data from complex survey samples 2933 2911–33 [DOI] [PubMed] [Google Scholar]
- LaCroix AZAZ, Rillamas-Sun E, Buchner D, Evenson KRKR, Di C, Lee I-MI-M, Marshall S, LaMonte MJMJ, Hunt J, Tinker LFLF, Stefanick M, Lewis CECE, Bellettiere J and Herring AHAH 2017. The Objective Physical Activity and Cardiovascular Disease Health in Older Women (OPACH) Study BMC Public Health 17 Online: http://bmcpublichealth.biomedcentral.com/articles/10.1186/s12889-017-4065-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lockley SW, Skene DJ and Arendt J 1999. Comparison between subjective and actigraphic measurement of sleep and sleep rhythms J. Sleep Res 8 175–83 [DOI] [PubMed] [Google Scholar]
- Matthews CE, Chen KY, Freedson PS, Buchowski MS, Beech BM, Pate RR and Troiano RP 2008. Amount of time spent in sedentary behaviors in the United States, 2003–2004. Am. J. Epidemiol 167 875–81 Online: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3527832&tool=pmcentrez&rendertype=abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVeigh JA, Winkler EAH, Healy GN, Slater J, Eastwood PR and Straker LM 2016. Validity of an automated algorithm to identify waking and in-bed wear time in hip-worn accelerometer data collected with a 24-hour wear protocol in young adults Physiol. Meas 37 1636–52 [DOI] [PubMed] [Google Scholar]
- Migueles JH, Cadenas-Sanchez C, Ekelund U, Delisle Nystrom C, Mora-Gonzalez J, Lof M, Labayen I, Ruiz JR and Ortega FB 2017. Accelerometer Data Collection and Processing Criteria to Assess Physical Activity and Other Outcomes: A Systematic Review and Practical Considerations Sport. Med 47 1821–45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montoye HJ, Washburn R, Servias S, Ertl A, Webster JG and Nagle FJ 1983. Estimation of energy expenditure by a portable accelerometer Med. Sci. Sport Exerc 15 403–7 [PubMed] [Google Scholar]
- Rillamas-Sun E, Buchner DM, Di C, Evenson KR and LaCroix AZ 2015. Development and application of an automated algorithm to identify a window of consecutive days of accelerometer wear for large-scale studies BMC Res Notes 8 270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tracy DJ, Xu Z, Choi L, Acra S, Chen KY and Buchowski MS 2014. Separating bedtime rest from activity using waist or wrist-worn accelerometers in youth PLoS One 9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tracy JD, Acra S, Chen KY and Buchowski MS 2018. Identifying bedrest using 24-h waist or wrist accelerometry in adults PLoS One 13 1–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troiano RP, McClain JJ, Brychta RJ and Chen KY 2014. Evolution of accelerometer methods for physical activity research Br J Sport. Med 48 1019–23 Online: http://www.ncbi.nlm.nih.gov/pubmed/24782483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troiano RRP, Berrigan D, Dodd KWK, Masse L, Tilert T, McDowell M, Mâsse LC, Tilert T and McDowell M 2008. Physical activity in the United States measured by accelerometer. Med. Sci. Sports Exerc 40 181–8 Online: http://www.researchgate.net/publication/5757920_Physical_activity_in_the_United_States_measured_by_accelerometer/file/9fcfd50a2830d51ac9.pdf [DOI] [PubMed] [Google Scholar]
- Tudor-Locke C, Barreira TV, Schuna JM, Mire EF, Chaput J-P, Fogelholm M, Hu G, Kuriyan R, Kurpad A, Lambert EV, Maher C, Maia J, Matsudo V, Olds T, Onywera V, Sarmiento OL, Standage M, Tremblay MS, Zhao P, Church TS, Katzmarzyk PT and ISCOLE Research Group 2015. Improving wear time compliance with a 24-hour waist-worn accelerometer protocol in the International Study of Childhood Obesity, Lifestyle and the Environment (ISCOLE). Int. J. Behav. Nutr. Phys. Act 12 11 Online: http://www.scopus.com/inward/record.url?eid=2-s2.0-84924584808&partnerID=tZOtx3y1%5Cnhttp://www.ncbi.nlm.nih.gov/pubmed/25881074%5Cnhttp://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC4328595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tudor-locke C, Barreira TV, Schuna JM, Mire E and Katzmarzyk PT 2014. Fully automated waist - worn accelerometer algorithm for detecting children ‘ s sleep period time separate from 24 - hour physical activity or sedentary behaviors Appl. Physiol. Nutr. Metab 39 53–7 [DOI] [PubMed] [Google Scholar]
- Weiss AR, Johnson NL, Berger NA and Redline S 2010. Validity of activity-based devices to estimate sleep J. Clin. Sleep Med 6 336–42 [PMC free article] [PubMed] [Google Scholar]
- Willett W and Stampfer MJ 1986. Total energy intake: implications for epidemiologic analyses. Am. J. Epidemiol 124 17–27 [DOI] [PubMed] [Google Scholar]
- Yoon IY, Kripke DF, Youngstedt SD and Elliott JA 2003. Actigraphy suggests age-related differences in napping and nocturnal sleep J. Sleep Res 12 87–93 [DOI] [PubMed] [Google Scholar]
- Zinkhan M, Berger K, Hense S, Nagel M, Obst A, Koch B, Penzel T, Fietze I, Ahrens W, Young P, Happe S, Kantelhardt JW, Kluttig A, Schmidt-Pokrzywniak A, Pillmann F and Stang A 2014. Agreement of different methods for assessing sleep characteristics: A comparison of two actigraphs, wrist and hip placement, and self-report with polysomnography Sleep Med. 15 1107–14 Online: 10.1016/j.sleep.2014.04.015 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.