Radiomics and Artificial Intelligence for Biomarker and Prediction Model Development in Oncology

Graphical abstract

1. Introduction

Advanced cross-sectional and functional imaging techniques enable non-invasive visualization of tumor extent and functional metabolic activity and play a central role in the diagnostic work-up and surveillance of oncology patients. However, the criteria used for tumor staging and surveillance are largely based on anatomic criteria at this time. From a quantitative standpoint, the evaluation in the clinical setting remains very basic in many instances, largely relying on measurement of size on initial assessment and for the evaluation of response to treatment, supplemented with qualitative assessment of other tumor characteristics such as homogeneity and shape [1,2]. This is not without basis, since size measurements are easy to make and these criteria can be universally implemented and used using basic platforms for image display and analysis, without the need for more complicated infrastructure or analytic platforms that may not be widely available. However, the downside is that there is potential for under-utilization, or wasting, of substantial information that could potentially be used for improvement in tumor evaluation and treatment planning for oncology patients.

Broadly, texture analysis and radiomics approaches aim to fill this gap, extracting and analyzing the higher dimensional and quantitative data with the aim of more accurate, tumor specific evaluation and characterization [3,4]. Coupled with artificial intelligence (AI), these can serve as biomarkers and can be used to construct prediction models that have the potential to provide an evaluation far beyond what is achieved using the largely qualitative approaches to image evaluation currently performed in the clinical setting. Increasing evidence suggests that these approaches can be used to enhance non-invasive tumor characterization, including prediction of certain tumor molecular features, association with tumor spread, better prediction of treatment response and prognosis [[5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20]], and this constitutes one area of great interest and significant research among the broader potential medical applications of AI that extend far beyond oncology or evaluation of medical images alone. In this article, we will provide an overview of radiomics and AI applications for medical image analysis, focusing on oncologic applications. The article will review the fundamentals of these approaches and commonly used techniques, followed by a review of selected examples to illustrate how these techniques can be applied for oncologic evaluation. Lastly, the article will briefly review the potential challenges and pitfalls of these techniques and the long-term potential for oncologic care and personalized medicine.

2. Texture Analysis and Radiomics

2.1. Overview

Texture analysis refers to computerized analysis and quantification of the local spatial variations in image brightness that in turn are related to properties such as coarseness and regularity of the voxel densities or intensities [21]. For example, on computed tomography (CT), texture analysis can be used to analyze the distribution and relationship of pixel or voxel grey levels on an image, quantifying the coarseness and regularity that results from local spatial variations in image brightness [4,22]. This in turn can be used to capture and quantify tumor heterogeneity and other quantitative patterns with predictive importance, with the potential to perform tumor characterization beyond what is possible by qualitative visual analysis alone. Interest in image texture analysis is not new, dating back to early days of development of advanced cross-sectional imaging techniques and computerized image analysis for the evaluation of the images produced using these advanced imaging modalities [21,23,24]. This interest emerges at least in part from early studies of human perception demonstrating that despite the impressive performance of the human visual system in evaluating different phenotypic characteristics of an object, the visual system may have difficulty in effortlessly discriminating certain textural characteristics, such as those related to higher order statistical features of an object or image [21,25].

In the last decade, there has been renewed interest in the potential of this approach for oncologic evaluation, further fueled by interest and advances in AI that make future wide-scale application achievable. In oncology, texture analysis can be used to provide an objective and quantitative evaluation of a tumor, including tumor heterogeneity, that complements the visual assessment by expert radiologists and has the potential to predict various characteristics and clinical endpoints of interest. Different approaches can be used for performing texture analysis that include statistical-based methods, model-based methods, and transform-based methods [4]. It should be noted that there is variation in the definitions used for the term texture in this context and confusion regarding what texture analysis entails. In the fields of computer science and computer vision, texture analysis frequently refers specifically to second order determinants of spatial inter-relationships of pixel grey-level values. However, in the medical literature, including the Radiology literature, some have used the term texture analysis more broadly to include other features, including primary statistical features [4]. For the purposes of this article, we will use the term texture to specifically refer to second order determinants of spatial inter-relationships or texture matrix-based features [26]. It should also be noted that although texture analysis and radiomics have been used to refer to similar analytic processes, it is generally accepted that radiomics is broader, and includes but is not limited to texture analysis alone.

The first published occurrence of the term radiomics dates back to 2012 [27,28]. Radiomics was defined as the high-throughput extraction of large amounts of image features from radiographic images [27]. In a review published in 2016, the definition was extended to include the conversion of images to higher dimensional data and the subsequent mining of these data for improved clinical decision support [26]. There is disagreement among researchers whether feature extraction needs to be restricted to imaging modalities that are routine in clinical practice, or if it is acceptable to include emerging techniques such as molecular imaging [26,27]. In terms of published research, radiomics has been performed on CT, magnetic resonance imaging (MRI), positron-emission tomography (PET), and ultrasound images. Later in this section, we will briefly discuss the pros and cons of these techniques with respect to radiomic model building. From a pure research perspective, there is no reason to limit the possibilities regarding how the images are acquired or the types of scans that are used for radiomic analysis as long as a valid research or clinical question is being addressed. The application of similar feature extraction techniques to images of histological slides can be referred to as pathomics [29].

In the traditional practice of radiology, images are used as pictures meant solely for human visual interpretation. The emergence of radiomics is tied to two major changes [27]. The first change is multi-factorial and concerns the improvement in the quality of the image. This was brought about by the emergence of new hardware like combined modality machines (CT/PET) and dual-energy CT (DECT), innovations with respect to imaging contrast agents (e.g. dynamic contrast enhanced MRI), and the gradual introduction of standardized imaging protocols and sequences. The other change is tied to how images are processed and analyzed. This was facilitated by improvement in hardware (higher CPU processing power at a lower cost, GPUs becoming ubiquitous) as well as availability of free feature extraction software packages that make it easier to quantify features in a standardized way. Although radiomics can be applied to any clinical problem where imaging plays a role, most publications are tied to oncology. Gillies et al. [26] suggest that this is because of support from the National Cancer Institute (NCI) Quantitative Imaging Network (QIN) and other initiatives from the NCI Cancer Imaging Program.

The guiding philosophy behind radiomics is that images contain interchangeable as well as complementary information to other sources of patient data, e.g., demographic information, liquid biopsies, and core biopsies. A related hypothesis is that information reflecting genomic and proteomic patterns is present and can be identified by analysis of macroscopic patient images [27]. If true, prognostically meaningful phenotypes or gene-protein signatures can be derived from the quantitative analysis of medical image data. It is not expected that non-invasive radiomic analysis can replace or reflect in granular detail tumor molecular profiling. However, it is hypothesized that sufficiently important tumor characteristics, including certain molecular features, can be predicted using this approach in a way that would be important for patient management. In this sense, one of the primary benefits of an image-based biomarker is its non-invasiveness. However, the scope of radiomics is grander. Most clinically relevant solid tumors are highly heterogeneous at the phenotypic, physiologic, and genomic levels and evolve over time [26]. Genomic heterogeneity within tumors and across metastatic tumor sites in the same patient is one major reason targeted therapies may fail and therapy resistance develops. Precision medicine therefore requires in vivo biomarkers that are spatially and temporally resolved. Radiomics enables quantitative measurement of intra- and intertumoral heterogeneity, including the possibility of use in treatment monitoring and optimization or in active surveillance. Importantly, radiomics enables analysis of the entire tumor volume, eliminating challenges related to sampling bias, which is a potentially significant advantage of this approach.

2.2. Radiomic Workflow

In order to understand radiomics and its applications, it is important to be familiar with the typical radiomic workflow, which starts with image acquisition. The imaging workhorse of oncology is CT. With respect to the repeatability and robustness of radiomic features, CT scans are by far the best studied (e.g., “test-retest” studies, meaning scans repeated on the same patient cohort after a short break; phantom studies to understand effect of different acquisition parameters offered by major vendors; examining the usefulness of cone beam CT derived features) [30]. The greatest strengths of CT are its widespread availability, rapid scan acquisition times, the existing normalization of image brightness or densities, and the relative straightforwardness of agreeing to a standard imaging protocol. The stability of PET features has also been well-studied. Unfortunately, various researchers found that PET radiomic features can be susceptible to differences in reconstruction parameters as well as to respiratory motion, indicating a need for greater harmonization efforts [30]. MRI is another exciting imaging modality for radiomics evaluation because of the exquisite soft tissue contrast provided (which is superior to CT) and the ability to perform functional imaging at a high resolution. Early studies also demonstrate technique related variations in features extracted from MRI images that will have to be remedied for generalized implementation of radiomic analysis using that modality [31]. Ultrasound is perhaps the least studied modality so far. One major challenge with radiomics analysis of sonographic images is the high inter-operator variability that may represent a barrier to reliable and reproducible radiomics applications using current technology [30]. Possible approaches for improving quality and reproducibility of radiomic features extracted from medical images are discussed at the end of this section, following the discussion of different features.

The next step in the workflow is image segmentation (i.e. tumor contouring or annotation). Before we discuss segmentation, it needs to be noted that in the ideal setting, or if this is ever seamlessly integrated into the clinical workflow, this would be done in the same viewing environment as image interpretation takes place, either using the same software or through other software integrated with the viewer. However, this is currently not the case, at least in most instances, for radiomics research investigations where the data need to be transferred to another program for analysis. The image sets also need to be de-identified or anonymized for purposes of research. If one is analyzing large datasets, these seemingly simple steps can be very time consuming and creation of robust, secure pipelines that automate this part of the process is a key component for successfully conducting large scale radiomics research in the future.

Going back to segmentation, this can be done in 2D or 3D. If done in 2D, the delineation is referred to as the region of interest (ROI). If translated into 3D (by segmenting multiple image slices covering the entire tumor volume), it may be referred to as a volume of interest (VOI), although ROI is used as well. Manual segmentation by clinicians or trained personnel is often treated as ground truth. However, one needs to be aware that depending on the problem at hand and expertise level, there can be high inter-operator variability. Furthermore, manual contouring is very time-consuming and therefore impractical for curating large data sets (>~100) or implementation in the clinical setting for routine use. To this end, automatic or semi-automatic segmentation methods are being investigated to minimize manual input and increase consistency and reproducibility [26,30]. There is ongoing debate over whether reproducibility trumps ground truth. A crude but consistent method of segmenting a dataset (e.g., by using an edge detection algorithm or using fixed threshold segmentation or growing a region from a user-defined seed) has to be weighed against manual segmentation performed by multiple people. Depending on the application, more advanced methods such as the fuzzy c-means, fuzzy hidden Markov chains or fuzzy locally adaptive Bayesian segmentation algorithms may be employed [30]. The introduction of deep learning via U-Net has begun to tip the scales towards automation [32]. Segmentation of normal tissue can now be achieved with full automation. However, diseased tissue often requires some human input because of inter- and intra-subject morphologic and contrast heterogeneity. Ultimately, the success of any given algorithm as a biomarker would have to be judged based on the reliability for predicting the outcome of interest, i.e. a given molecular or clinical endpoint, rather than the “ground truth” as it pertains to the matching of segmentation with expert annotations.

Once the image has been segmented, the next step is feature extraction. One review separates features into two main groups: semantic and agnostic [26]. Semantic features refer to computer-aided quantification of characteristics or terms commonly used in the radiology lexicon to describe ROIs (for example size, shape, location, presence of necrosis, etc.). Since it is known that such descriptors have prognostic value, there is an inherent justification for this approach. By (semi-)automating semantic data generation, there would be higher inter-observer agreement, faster throughput, and lower variance. Nonetheless, there has been relatively few radiomic research done towards this goal. For practical purposes, and in the rest of this paper, when discussing radiomic features, agnostic features are implied.

Agnostic features arose from the field of computer vision. In general, they are not explicitly engineered for the field of medicine. There is no biological justification for why such features should prove to be prognostic, and many agnostic features are hard to mentally visualize and interpret. Hence, any observed correlations are purely empirical, and difficult to gain intuition for. Nonetheless, they still offer the possibility of hypothesis generation, and the hypothesis can subsequently be tested on an independent dataset (either retrospective or preferably, prospectively). The greatest advantage of agnostic features is the absence of subjectivity and the speed of feature extraction. Another advantage is the large number (hundreds or even in the thousands) of features that can be derived by changing extraction parameters. An associated downside is the prospect of a false discovery arising purely out of statistical fluctuation, and careful reduction of the feature set size is essential to avoid such scenarios [33].

In many ways, feature extraction is the easiest part of the workflow to standardize, since it is entirely software-based and requires no human input. The pre-eminent effort in this direction is called the “Image biomarker standardisation initiative” (IBSI) [34]. The discussion presented in the rest of this section regarding feature extraction is summarized from the IBSI reference manual. IBSI groups features as follows: intensity-based statistical features, intensity histogram-based features, intensity-volume histogram-based features, morphological features, local intensity features, and texture matrix-based features. The first five of these groups can jointly be referred to as non-texture features, using the definition discussed earlier. All texture matrices are rotationally and translationally invariant. None of the texture matrices are scale invariant, a property which can be useful for scale optimization. Features are calculated on the original image, as well as images obtained using transformation filters (e.g., wavelet).

Intensity-based statistical features describe how grey levels within the ROI are distributed. The features in this set do not require discretization and are not meaningful if the intensity scale is arbitrary. An intensity histogram is generated by discretizing the original set of grey levels. The (cumulative) intensity-volume histogram describes the relationship between discretized grey level i and the fraction of the ROI volume containing at least grey level i. The implementation depends on whether the intensity units are definite or arbitrary. Morphological features describe geometric aspects of the ROI, such as area and volume. Local intensity features are calculated using voxel intensities within a defined neighborhood around a center voxel. While only voxels within the ROI are used as a center voxel, the corresponding local neighborhood need not be restricted within the ROI.

Texture features were originally designed to assess surface texture in 2D images, but texture analysis has been extended to 3D objects. Texture features are calculated from different types of matrices. The grey level co-occurrence matrix (GLCM) expresses how combinations of discretized grey levels of neighboring voxels are distributed along one of the image directions. Generally, the neighborhood for GLCM is 26-connected in 3D and 8-connected in 2D. Thus, there are 13 or 4 (3D or 2D) unique direction vectors within the neighborhood for Chebyshev distance of 1. The grey level run length matrix (GLRLM) assesses the distribution of discretized grey levels in terms of run lengths. A run length is defined as the length of a consecutive sequence of voxels with the same grey level along a fixed image direction. The GLRLM contains the occurrences of runs with length j for a discretized grey level i. The grey level size zone matrix (GLSZM) counts the number of groups (or zones) of linked voxels. Voxels are linked if the neighboring voxel has an identical discretized grey level. Whether a voxel classifies as a neighbor depends on its connectedness (26-connectedness in 3D and 8-connectedness in 2D).

The grey level distance zone matrix (GLDZM) counts the number of groups (or zones) of linked voxels which share a specific discretized grey level value and possess the same distance to ROI edge. Two maps are required to calculate the GLDZM: a grey level zone map (identical to the map needed to calculate GLSZM) and a distance map. Distance is defined according to 6 and 4-connectedness for 3D and 2D, respectively. The distance of a voxel to the ROI edge is equal to the minimum number edges of neighboring voxels that need to be crossed to reach the ROI edge. The distance for a linked group of voxels with the same grey value is the minimum distance for the respective voxels in the distance map. The neighborhood grey tone difference matrix (NGTDM) contains the sum of grey level differences of voxels with discretized grey level i and the average discretized grey level of neighboring voxels within a fixed Chebyshev distance. Neighboring grey level dependence matrix (NGLDM) aims to capture the coarseness of the overall texture. It is computed from the grey tone relationship between every voxel in the ROI and all of its neighboring voxels within a fixed Chebyshev distance [34,35].

Image features are only as good as the images they are extracted from. Hence, images may be pre-processed to enhance image quality. Possible image pre-processing includes image smoothing by averaging, applying Gaussian filters to reduce image noise, and image enhancement using histogram equalization, deblurring and resampling. Texture feature calculations require interpolation to isotropic voxel spacing to be rotationally invariant, and to allow comparison between different datasets. Many features are sensitive to voxel size. Hence, maintaining consistent isotropic voxel spacing is important for reproducibility. Interpolation via down-sampling requires inference and introduces artificial information. Upsampling, on the other hand, results in information loss and may introduce image aliasing artifacts. Neither technique is a clear winner. Discretization of image intensities inside the ROI is often required to make calculation of texture features tractable. It may also aid noise-suppression. Two approaches to discretization are commonly used. One uses a fixed number of bins, and the other uses bins of a fixed bin width. Both methods have particular characteristics that may make them preferable for specific purposes. Once these steps have been performed, feature calculations can begin. Image normalization may also be performed using convolutional neural networks (CNN; see below in section on machine learning) [36]. Various image processing approaches that can improve quality and importantly help standardize or normalize quantitative features are likely to represent an important step for reliable radiomic evaluation of images that can overcome variations related to technique, an essential step for more widespread implementation in the clinical setting.

3. Overview Machine Learning Approaches

Artificial Intelligence (AI) is the development of computer systems that process data and attempt to simulate human-like reasoning, i.e. algorithms that not only analyze but learn from experience. From its establishment in the 1950's, AI has been implemented or evaluated in a range of applications ranging from games, automobiles, economy, aviation industry, and health care, among others. AI continues to grow and pushes the boundaries of many traditional industries. Early implementation of AI revolved around systems, known as agents, interacting intelligently with an environment. Sensors interpret the environment and the most reasonable decision is determined and performed [37]. As the field evolved, so did these intelligent agents and with the inclusion of stored data, Machine Learning (ML) was introduced to AI. ML is one of the major subfields in AI and plays a central role in image analysis and radiomic or predictive model construction. Therefore, for purposes of this article, we will focus mainly on ML approaches.

ML may be defined as algorithms that build classifiers based on analysis of training data, infer a hypothesis (or function), and predict the labels of unseen observations (e.g. patient outcome or tumor phenotype) [35]. Training can be subdivided in two major learning methods: supervised and unsupervised learning. Supervised Learning utilizes the training data with associated labels (classes) to learn the relationship between the training data and labels. Unsupervised Learning corresponds to learning the training data without labels by exploiting the intrinsic relationship within the data to cluster the data. Typically, supervised learning offers better performance, especially for smaller datasets. However, acquiring labelled data is laborious and can be expensive. On the other hand, unsupervised learning benefit from an abundance of unlabelled data since the labelling process is not required. Furthermore, unsupervised learning has the potential to identify previously unknown associations and in oncology, cancer subtypes that may be of prognostic value. When discussing ML algorithms, one should also be familiar with the concept of overfitting. Overfitting refers to a modeling error where the algorithm “memorizes” or reflects the training data too closely, using noise or random fluctuations in the training data as concepts that may not be applicable to new datasets and consequently negatively impact algorithm performance in new datasets (or generalization of the model). Simply put, overfitting provides an overtly optimistic or exaggerated measure of algorithm performance.

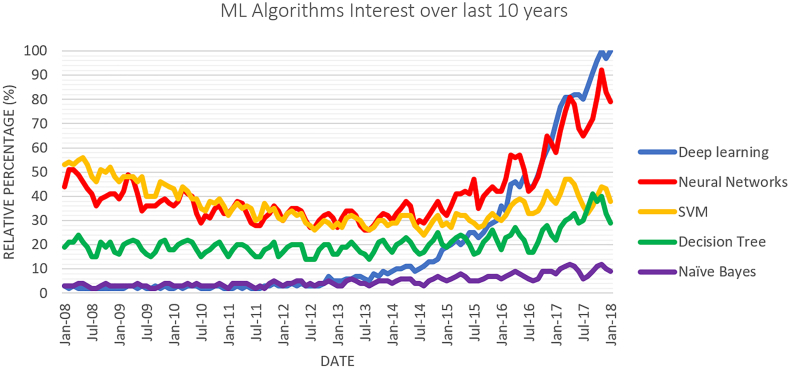
There are many types of ML classifiers available including Decision Trees and Support Vector Machine classifiers, however Deep Learning (DL) has garnished the most attention in recent years, as illustrated in Fig. 1 depicting the most popular Google search trends. This section will give an overview of some Classic ML and DL classifiers.

Fig. 1.

Google trends data for machine learning algorithms between 2008 and 2018.

3.1. Logistic Regression

Logistic Regression is a classical machine learning algorithm typically used for binary classification. The model attempts to estimate the probability, P(y = 1| x), that is the probability of a positive outcome (class y = 1) given data x. Using Bayes rule, P(y = 1| x) can be expressed in the form of a logistic function:

$$P\left(y=1|x\right)=\frac{1}{1+e^{-\alpha }}$$

where α is the log-odds ratio (the odds of a positive classification relative to the odds of a negative classification), which can be expressed as a linear function:

$$\alpha =\mathit{ln}\frac{P\left(x|y=1\right)P\left(y=1\right)}{P\left(x|y=0\right)P\left(y=0\right)}={\beta }_0+{\beta }_1^T\mathit{x}$$

The weights (β₀, β₁) can be calculated using the maximum likelihood approach [38]. The log-likelihood expression serves as an error function and using gradient descent, the optimal weights can be iteratively solved for to minimize error.

The advantage of logistic regression is that it is fast to train and can use discrete and continuous variables as inputs. The disadvantages include that it is a linear model. Therefore, complex data problems may pose difficulties. Nevertheless, the logistic regression model can work well on many datasets and can serve as a useful benchmark due to its ease of implementation.

3.2. Naïve Bayes

Similar to logistic regression, the Naïve Bayes algorithm attempts to model the probability of an outcome based on the data, P(y | x). However, it uses a generative learning approach instead. Generative learning is the indirect estimation of the probability of an outcome using the joint probability. This is achievable due to Bayes' Theorem:

$$P\left(y|x\right)=\frac{P\left(x|y\right)P\left(y\right)}{P\left(x\right)}$$

where, P(x | y) is the likelihood of the data, P(y) is the prior probability of the class before observing data, and P(x) is the probability of observing a data sample x. The term P(x) is treated as a weighing term and can be disregarded. To estimate the outcome for a given data sample x, with independent discrete features f₁, f₂, …, f_n, the probability of the positive class occurring and the probability of the negative class occurring are compared as follows:

$$P\left(y=1|x\right)\propto P\left(f_1|y=1\right)P\left(f_2|y=1\right)\dots P\left(f_n|y=1\right)P\left(y=1\right)=P_{\mathit{US}}\left(y=1|x\right)$$

$$P\left(y=0|x\right)\propto P\left(f_1|y=0\right)P\left(f_2|y=0\right)\dots P\left(f_n|y=0\right)P\left(y=0\right)=P_{\mathit{US}}\left(y=0|x\right)$$

These calculated probabilities are unscaled and denoted as P_US. The probability of each class can be scaled and calculated as:

$$P\left(y=1|x\right)=\frac{P_{\mathit{US}}\left(y=1|x\right)}{P_{\mathit{US}}\left(y=1|x\right)+P_{\mathit{US}}\left(y=0|x\right)}$$

$$P\left(y=0|x\right)=\frac{P_{\mathit{US}}\left(y=0|x\right)}{P_{\mathit{US}}\left(y=1|x\right)+P_{\mathit{US}}\left(y=0|x\right)}$$

For continuous features, under the linear discriminate analysis assumption, the likelihood of the data is assumed to be a multivariate gaussian with class specific means and a common covariance.

The advantages and disadvantages of the Naïve Bayes classifier are the same as Logistic Regression. Both are faster to train and are simple, and both have difficulties with complex datasets due to being linear classifiers. The Naïve Bayes classifier has generally shown to have superior performance in comparison to the Logistic Regression classifier on smaller datasets and inferior performance on larger datasets [39].

3.3. Support Vector Machine

The Support Vector Machine (SVM) algorithm is a classical machine learning algorithm. The premise of the algorithm is to compute the decision boundary that separate two classes with the maximum marginal distance to provide a robust decision boundary that can tolerate noisy test data. Thus, the SVM algorithm optimizes between maximum margin and training error to solve the ideal decision boundary [40]. By setting the margin, m, to be inversely proportional to decision boundary parameters, $m=\frac{1}{\mid \left|\mathit{\beta }\right|\mid }$, the soft margin SVM classifier can be formulated as the following minimization problem, where x is the training data, y is the label, β₀ and β are decision boundary parameters, N is the number of training data, ε is a slack variable to measure misclassification overlap and C is a penalization cost for misclassification:

$$\underset{{\beta }_0,\mathit{\beta }}{minimize}\frac{1}{2}{‖\mathit{\beta }‖}^2+\mathrm{C}\sum _{i=1}^N{\epsilon }_i\text{subject to}{\mathrm{y}}_i\left({\beta }_0+\mathit{\beta }\mathit{\bullet }{\mathit{x}}_{\mathit{i}}^{\mathit{T}}\right)\mathit{\ge }\mathbf{1}\mathit{-}{\epsilon }_{\mathit{i}\mathit{.}}{\epsilon }_{\mathit{i}}\ge \mathbf{0},\mathbf{i}=\mathbf{1},\dots ,\mathbf{N}$$

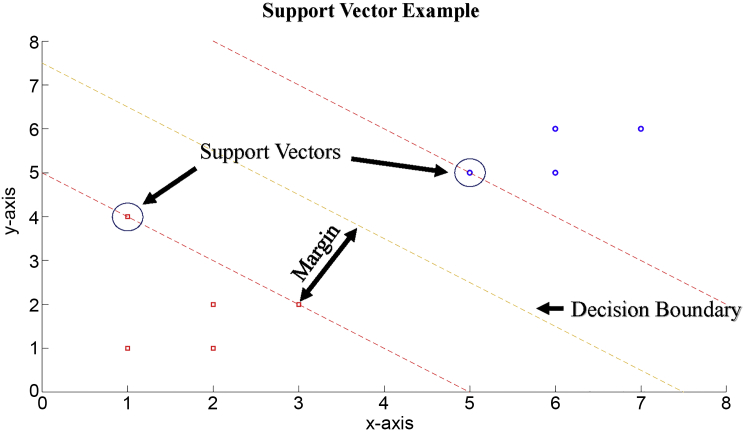
The minimization problem is solved by computing the Lagrange Dual and performing quadratic optimization. Fig. 2 demonstrates a graphical example of SVM. The two classes to be separated are represented by the blue circles and red squares, the decision boundary is represented by the yellow dotted line, the margins between the class and the decision boundary is represented by the red dotted lines and the Support Vectors (SVs), the data closest to the decision boundary and lying on the margins, are circled data. This decision boundary is then used to evaluate new data based on the position of the data with respect to the decision boundary.

Fig. 2.

Support vector machine example.

In the case of non-linearly separable data, SVM uses kernel functions to transform the data into a higher dimension, in which the data can be linearly separated [38] (Fig. 3).

Fig. 3.

Non-linearly separable data transformed to higher dimension.

The advantage of SVM is the simple mathematics behind the decision boundary and its application in higher dimensions. However, since SVM is essentially an optimization problem attempting to balance between errors in the training set with a larger margin decision boundary, it may be slow for large datasets, especially where the class separation is small.

3.4. Decision Tree

Decision Tree (DT) is another example of a classical machine learning algorithm. The DT divides the data based on features to determine the appropriate class. The features used to split the data are determined using the Information Gain provided by individual features [41]. To determine information gain, first the entropy of a dataset is computed. For a dataset (S) with two classes, the entropy would be:

$$\mathit{Entropy}\left(S\right)=\sum _{i=1}^2-p_i{log}_2{p}_i$$

Individual feature specific information gain is calculated by the difference between entropy of the training set and entropy of the feature [42]. The information gain for a feature A would be as follows:

$$\mathit{Information\; Gain}=\mathit{Entropy}\left(S\right)-\sum _{\mathit{vϵ}\mathit{Values}\left(A\right)}\frac{\mid S_v\mid }{\mid S\mid }\mathit{Entropy}\left(S_v\right)$$

where Values(A) is the set of all possible values for a feature A and S_v corresponds to the subset of S where feature A has a value v.

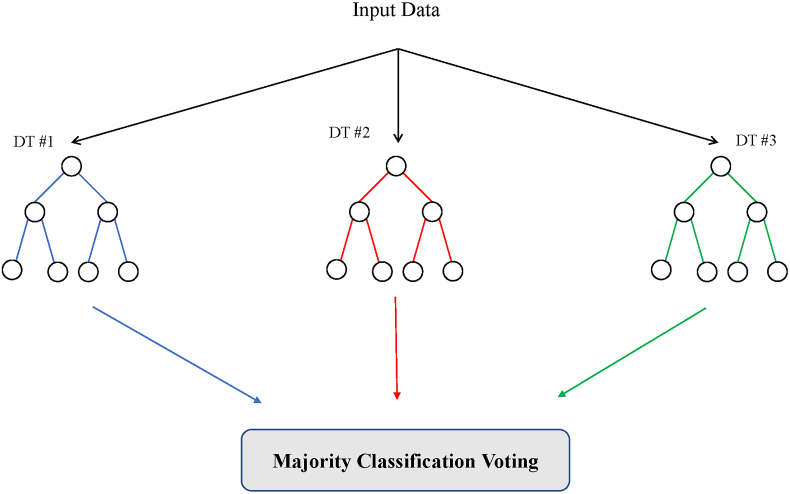
Features that provide relevant and valuable information to divide the classes are then selected and used in the DT. Features that provide the highest information gain split the data earlier in the tree, and features that provide less information gain are at lower stages in the DT. This hierarchy also allows for pruning (removing lower feature separation) to avoid overfitting. Furthermore, to ensure overfitting will not happen, other steps can be taken, depending on the approach used. For example, Random Forests (RF; one example of a decision tree-based ML) use multiple small decision trees built from a random subset of features to vote on the classification. Fig. 4 illustrates an example of Random Forests.

Fig. 4.

Random Forests example of decision tree ML classification.

The advantage of Decision Trees is that they are both easy to visualize and understand. The disadvantage is that feature selection plays a dominant role in the accuracy of the algorithm. One set of features can provide drastically different performance than a different set of features. A large Random Forests can be used to alleviate this problem.

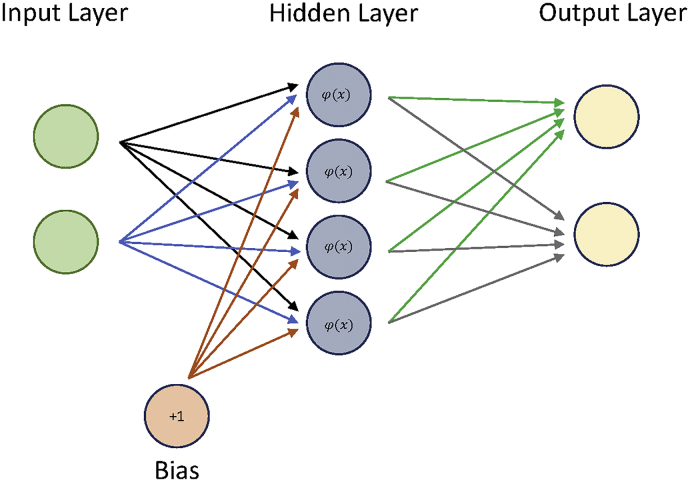
3.5. Neural Networks

Neural Networks (NN) are modelled after the human brain and function by combining multiple perceptron models (neurons) into a network, to perform complex calculations (Fig. 5). Each NN is composed of an input layer, hidden layers, and an output layer, with each layer composed of individual nodes [43]. Nodes in different layers are connected by weights, depicted by arrows in Fig. 5. The values from each node in the previous layer are multiplied by the corresponding weights and are summed at nodes in the next layer. Furthermore, a bias node and activation functions are included in the hidden layer to introduce non-linearity into the NN. Outputs at a hidden layer node (o_i) can be represented as:

$$o_i=\phi \left(\sum _i{w}_i{x}_i+b\right)$$

where, w_i corresponds with weights connecting to inputs from the previous layer denoted as x_i, b is the bias and φ is the activation function. The most popular activation for NN is the sigmoid function $\phi \left(z\right)=\frac{1}{1+e^{-z}}$ because it outputs values between the range of 0 and 1 and has the simple derivative form:

$${\phi }^1\left(z\right)=\phi \left(z\right)\left(1-\phi \left(z\right)\right)$$

Fig. 5.

Neural network example.

After the values from the input layer are traversed forward through the hidden layer(s), at the output layer a SoftMax function is applied to calculate the NN's confidence percentage in each class. During training, the error between the calculated class and the expected class is determined (typically using the sum-squared error function) and the error is backpropagated through the network to update the values of the weights. Backpropagation uses the derivative of the error to update the weights, which is why simple to derive activation functions, like the sigmoid function, are favorable. The algorithm iterates through all training data until the error of the network falls below a certain threshold to avoid overfitting.

An advantage of NN is that although the mathematics behind the algorithm are simple, the non-linearities and weights allow the NN to solve complex problems. Disadvantages of NN include the training time required for numerous iterations over the training data, tendency to easily overfit (i.e. provide a falsely optimistic or elevated estimate of performance) on training data, and numerous additional tuning hyperparameters including # of hidden layers/hidden nodes are required for determining optimal performance.

3.6. Deep Learning

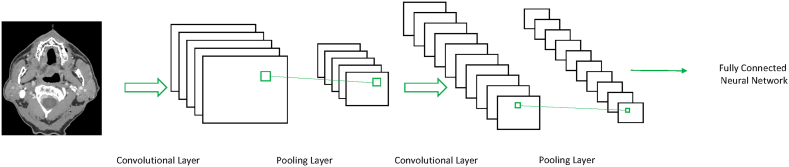
Deep Learning (DL) is based on NN but is composed of many additional layers with the purpose of adding complexity to the algorithm to learn features and representations automatically. Networks with three or more layers are generally considered deep, however there are some debates on the matter [44]. An example of DL is the Convolution Neural Network (CNN) model. As illustrated in Fig. 6, CNNs are composed of multiple convolutional and pooling layers with fully-connected layers for classification [45]. In the convolutional layers, filters are convolved with the input to create a stack of filtered images. In the pooling layer, the stack of filtered images is simplified by reducing the size. At lower levels of the CNN, the CNN learns simple features such as edges and corners [46]. These simple features are then used to learn more complex features at higher layers of the CNN. As in NN, all weights in the CNN are randomly initialized and are updated throughout training and backpropagation until the error of the training set falls below a specified threshold.

Fig. 6.

Example of a convolutional neural network.

One advantage of DL approaches such as the CNN is that they can be used to perform both image analysis (deep feature extraction) and construction of a prediction algorithm, precluding the need for separate steps of extracting hand-crafted radiomic features and using that as an input for a ML algorithm to construct a prediction model. Another main advantage of CNN is the ability to learn complex datasets and achieve high performance without prior feature extraction. The disadvantage is the additional hyper-parameters required to tune the CNN for better performance including the number of convolution filters, the size of the filters, and parameters involved in the pooling. Furthermore, due to the numerous weights in CNN, more data is required to determine the optimal values for the weights involved. Therefore, this approach may not be the optimal approach for pilot studies with small datasets.

4. Application of Machine Learning for Biomarker Development and Construction of Prediction Models

4.1. Radiomic Models for Prediction and Prognosis

The ultimate goal of the radiomics approach is to build predictive models for treatment outcome and for risk assessment, based on quantitative phenotypic characteristics of the tumor computed from radiological images and other clinically available information [30,47]. In essence, radiomics consists of converting images into a high-dimensional feature space that can be studied via statistical and machine learning methods. It should be noted that extraction of texture or radiomic features by itself does not necessarily require AI. However, AI (ML) is used to construct prediction models that can learn from existing datasets and analyze and perform predictions on related but new datasets. Therefore, a radiomic pipeline may be constructed by combining a computerized image analysis software (for image analysis and feature extraction) and a ML approach (either classic ML or deep learning) for constructing prediction models. Alternatively, DL may be used to perform both tasks (i.e. image analysis and construction of prediction models). This is a clear advantage of DL and highlights the great interest in this technology for applications in medical imaging. However, the relative disadvantage are the larger datasets required for constructing reliable algorithms that may be a disadvantage for early studies and pilot investigations, especially on uncommon disease entities or disease entities requiring significant sub-stratification resulting in small patient numbers, as has been alluded to earlier.

Once a predictive model is built from a training set of images (assumed to be representative of the overall disease population), it then becomes possible to classify a new patient into a particular risk category, or to predict that patient's response to a particular therapy. Ideally, the classification performance of the model needs to be validated on a dataset that is independent from the initial training set of images, for instance acquired at a different institution and/or on different scanning machines. When truly independent validation datasets are not available, another option is to divide the initial training set into several subsets, train the model on some of the subsets and validate it on the others, a method known as cross-validation [38].

If the initial training set contains time-to-event data, for instance patient survival information, then, in addition to treatment outcome prediction, it also becomes possible to perform prognostic time-to-event analyses (e.g., [18]). The prognostic performance of radiomic models is evaluated using metrics different from the ones used to assess prediction performance. While the latter can be evaluated using Receiver Operating Characteristic (ROC) curve metrics, prognostic performance can be assessed for instance with Kaplan-Meier analysis, using the log-rank test between risk groups, or via an index of rank correlation between predicted and observed outcomes. This index is known as the concordance index [48,49] and is a popular measure of model performance in survival studies. It measures the concordance between the rankings of the survival times and the model output. In other words, it measures the ability of a model to discriminate between groups of patients based on survival times.

4.2. Model Building

4.2.1. Feature Selection

Regardless of the final application, the radiomics model building pipeline begins with an analysis of the individual features computed from the input images. Given the large number of such features involved in a typical radiomics study, a feature pruning step is required prior to moving on to the actual classification task. This is because the computation of a large number of features from a few matrices can result in many features that are redundant and/or highly correlated, which increases dramatically the dimensionality of the problem without adding useful information. Furthermore, the discriminatory power of features depends on the task. Thus, many of the computed features may be irrelevant for a given task. Because of this, reducing the number of features by selecting the most relevant features for a particular application can significantly increase classification performance [50], though this is not always the case [51]. We note that feature selection is not a task specific to radiomics, but rather is common to many, if not all, large scale data-mining problems. Furthermore, it is important to be aware that feature selection may results in biased performance with small finite datasets and imbalanced datasets [52,53]. A more detailed discussion of feature selection is beyond the scope of this article but can be found elsewhere [35,52,53].

Three main strategies for feature selection have been proposed in the literature. Wrapper methods use a given classification algorithm to score different subsets of features, based on their classification performance [54]. Filter methods select features in a pre-processing step, independently of any classification method. In essence, wrapper methods measure the “usefulness” of features in a practical classification task, while filter methods focus on the ‘intrinsic’ value of each feature. The third category is that of Embedded methods. They are similar to wrapper methods, in that features are selected as to optimize the performance of a learning algorithm. However, unlike wrapper methods which use the classification method as an external black box to rank features, here the variable selection is an inherent part of the learning algorithm itself [50].

Some of the simplest methods in the filter category consist in the ranking of features based on their individual discriminatory power, which can be measured, for instance, with correlation criteria, or information-theoretic criteria [50], or with tests for statistical significance such as the Mann-Whitney U test [55]. The features are then ranked and a pre-determined number of features with the highest rankings are selected. One example is the minimum redundancy maximum relevance (mRMR) method which computes and ranks features based on the mutual information between the features and an outcome [35]. Another popular method within the Filter category makes use of Fisher's linear discriminant, which is defined based on the ratio of between-class variance to within-class variance (e.g., [56,57]).

While feature ranking is a simple and computationally-efficient approach, it also comes with several problems. One obvious problem is that features are considered independently of each other, and any interactions between them are ignored. It can be shown that a better approach consists in selecting subsets of features that together have a good predictive power, as opposed to focusing on the predictive power of individual features. On the other hand, searching for optimal groups of features is much more computationally expensive than searching for individual features. In fact, an exhaustive search of all possible feature combinations becomes quickly intractable.

Because of that, methods within the Wrapper category need to devise search strategies over the feature space which keep the search tractable while also optimizing performance and reducing the risk of overfitting. Greedy search strategies have been shown to be particularly advantageous, examples of such strategies including e.g. Forward- and Backward Stepwise Selection [38], or Recursive Feature Elimination algorithms [58]. More advanced search algorithms include, for instance, genetic algorithms [59].

The advantage of wrapper methods is that they can be used with any classification algorithm to evaluate the prediction performance of a subset of features, which makes them, in essence, universal. Embedded methods do not have this advantage of universality, as by definition they are specific to the particular classification method they are embedded with. At the same time, they are more efficient in several aspects. For instance, they do not need to re-train the classifier from scratch for every new feature subset under investigation, as the selection is intrinsic to the model training. A prominent example of an embedded method is the Least Absolute Shrinkage and Selection Operator (LASSO) [60], which alters standard regression methods by selecting only a subset of the available covariates.

4.2.2. Predictive Modeling

A range of algorithms for predictive modeling have been proposed and investigated over time, falling within two broad categories. Classification methods aim to predict two or more distinct class labels, for instance, benign vs malignant, or a particular tumor grade, or good vs bad response to treatment. Regression algorithms typically aim at predicting continuous variables, for instance, survival time, although regression can also be adapted to predicting discrete outcome variables as well, as in the case of logistic regression. In either case, the algorithms learn a mapping from the input feature space to an output variable, whether a class label or a continuous value [38].

Classical machine learning methods, such as those reviewed in the earlier sections, have proven very useful in a variety of applications and produce classifiers that are relatively easy to train and use. However, heterogeneous datasets of ever-increasing size and complexity have become more and more common, and oftentimes exceed the capabilities of individual classifiers. This insight has led to the development of two strategies based on ensembles of classifiers: bagging and boosting [38]. Both make use of a large number of “weak learners”, which are relatively simple classifiers, each trained only on part of the data. The estimate produced by each weak learner is then aggregated into an overall decision using mechanisms such as voting. In this manner, a large number of weak learners are combined to produce one strong learner.

In the case of boosting, a sequential training process creates a cascade of weak learners, such that at each subsequent step, weak learners focus on data that was the most difficult to classify at the previous step. A prominent example of the boosting strategy is the AdaBoost algorithm [61]. As for bagging, it is based on the idea of generating random subsamples of training data and features to train the weak learners. The predictions obtained on each random subsample are then combined to reach an overall decision. One of the most popular algorithms that follows the bagging strategy is the Random Forests method discussed earlier, based on the Decision Tree algorithm as a weak learner [62].

As radiomics is still a young and emerging discipline, it seeks to borrow the best tools that the machine learning field has to offer. However, it is not yet clear whether one particular choice of modeling algorithm is better than another, or whether one particular feature selection strategy outperforms another. To address these questions, recent research has begun to look into comparing different feature selection and classification methods in terms of their performance in the radiomics context [11].

As discussed earlier, more recently, DL has emerged into the mainstream and has rapidly become very popular in a wide variety of technological domains [63]. Such learning models are implemented with multi-layer artificial neural networks, and are able to perform simultaneously feature construction, feature selection and prediction modeling, essentially performing an end-to-end analysis from input data to prediction. As such, they are very powerful learning algorithms, however, just as any other tool, they come with their own strengths and limitations. Because of the inherent model complexity, they require much larger datasets than classical machine learning algorithms. In some domains, such as online photo classification or social network analyses, online data is abundant and lends itself well to deep learning analyses. In the specific context of radiology, on the other hand, datasets are often limited due to practical, legal and ethical constraints, and deep learning algorithms need to be adapted to overcome the limitations of small radiological datasets. A thorough review of deep learning and its applications to radiology is outside the scope of the present paper, but extensive literature has been published on this topic [[64], [65], [66], [67], [68], [69], [70], [71], [72], [73]].

5. Selected Examples of Radiomics and ML for Oncologic Evaluation

In this section, we will provide a few examples of radiomics and ML applications for tumor evaluation to familiarize the reader with applications of these techniques. These were selected by the authors to demonstrate applications for the evaluation of different pathologies and provide an example of how this technology may be used, using a combination of work from other groups and the author's groups. It should be noted that this is not meant in any way to constitute an exhaustive or representative review of the various applications published in the literature. In reviewing these examples, the reader should keep in mind that given the large number of feature selection, classification and prediction modeling algorithms available, it is not a priori clear which particular method (or a combination of methods) would perform best in a given study. This is why several radiomics studies have been carried out with the dual objective of (a) learning a model to predict outcome, or response to treatment, or to classify tumor histological type and (b) compare the performance of different feature selection and classification methods.

5.1. Example 1

An example is a study by Wu et al. [74], which investigates the association between radiomics features and two histological subtypes of non-small cell lung cancer (NSCLC): adenocarcinoma and squamous carcinoma. The study worked with two independent cohorts of patients, one training cohort consisting of 198 patients, and a testing cohort consisting of 152 patients. In all cases, the histological type of cancer was confirmed using histopathology.

The image processing pipeline involved 440 3D radiomic features, described in Aerts et al. [10] and extracted from manually delineated tumor regions from each patient's pre-treatment CT images. Then, feature selection was performed in a two-step procedure. First, a correlation matrix representing the correlation coefficients between all pairs of features was computed, and those features exceeding a certain correlation threshold were removed, resulting in a smaller set of non-redundant features. In the second step, 24 different univariate filter-based feature selection methods were applied to the smaller subset of non-redundant features. These univariate feature selection methods rank individual features based on their discriminating abilities between classes. The top-ranking features were then selected, and classification into two classes (adenocarcinoma or squamous carcinoma) was performed using one of three different algorithms: Random Forests, Naïve Bayes, and K-nearest neighbors.

To compare performance across these three different classifiers, a representative AUC for each classifier was defined as the median AUC across the 24 feature selection methods used in conjunction with this classifier. In this manner, Naive Bayes was found to give the best performance (AUC = 0.72), while K-Nearest Neighbor showed the worst performance (AUC = 0.64). Random Forests was the least sensitive to feature selection methods as it showed very little standard deviation in AUC. This is not surprising, since Random Forests is an ensemble method with embedded feature selection, as discussed earlier, and therefore is expected to be more robust to variations in external feature selection methods. As for the feature selection methods, one particular method was found to give the highest performance with all three classifiers (RELIEF feature selection; [75]).

5.2. Example 2

While more recent radiomics studies use an ever-increasing number of radiomic features, usually in the hundreds or even in the thousands, earlier methods usually referred to as ‘texture analysis’ use a much smaller number of features, as well as simpler statistical analysis methods. An example of such an approach is found in the study by Lubner et al. [76], where 77 patients with liver metastases of colorectal cancer were studied to determine whether features computed on CT images relate to pathology and clinical outcomes. Single hepatic metastatic lesions on pre-treatment contrast-enhanced CT scans were manually contoured, the histogram of pixel intensity values in the contoured region was constructed, and six features were computed from this histogram: its mean, standard deviation, entropy, kurtosis, skewness, and mean of positive pixels. The original CT images were then smoothed at six different smoothing levels, using a Laplacian-of-Gaussian filter, in order to enhance structures at different spatial scales, ranging from coarse to fine. The six features were computed at each of the six different smoothing levels. This processing was carried out with the commercial software TexRAD (TexRAD Ltd., Somerset, UK), and is typical for studies falling into the ‘Texture analysis’ category.

Given the small number of features involved, the statistical analysis is relatively simple. The association of image features with numerical and ordinal variables (e.g., tumor grade) was tested with least squares or linear regression analysis, respectively. This analysis was performed for each of the six features at each level of image smoothing. Logistic regression was used for binary variables, e.g. KRAS mutation status. For survival and time-to-event analyses, Cox proportional hazards regressions were performed. Based on their results, the authors concluded that there is an association of CT image features with pathologic characteristics and clinical outcomes. Given that the histogram features used in this study can be broadly related to image heterogeneity, the authors suggest that tumors that are more homogeneous (less entropy, smaller standard deviation and higher in attenuation) are potentially more aggressive, with higher tumor grade and poorer overall survival.

5.3. Example 3

Another example of a texture analysis approach with TexRAD software on breast cancer imaging can be found in the study by Chamming's et al. [77]. In this study, the goal was to test whether the same histogram-based image features described above, computed on pre-treatment MRI images, can be associated with pathologic complete response (pCR) after neoadjuvant chemotherapy in breast cancer. In addition to response, this study also explores the association between image features and tumor subtypes on pre-treatment MRIs. Manual contouring of lesions was applied on T2-weighted MR imaging and contrast material–enhanced T1-weighted MR imaging on 85 patients with breast cancer.

Univariate analysis discovered two features that underscored a significant difference between triple-negative breast cancer and non–triple-negative breast cancer. Another feature was found to show a significant difference between pCR and non-pCR. In addition, multivariate logistic regression found one feature (kurtosis) that was independently associated with pCR in non– triple-negative breast cancer (P = .033). A multivariate model incorporating kurtosis in both T2-weighted and contrast-enhanced T1-weighted imaging had a good performance for predicting triple-negative status for breast cancer (AUC = 0.834).

5.4. Example 4

Another example is application of radiomics for the evaluation of glioblastomas performed in the study by Kickingereder et al. [78]. In this study, a total of 119 patients with newly diagnosed glioblastoma were evaluated. 12,190 radiomic features were extracted from the multiparametric (contrast material–enhanced T1-weighted and fluid-attenuated inversion-recovery imaging sequences) and multiregional (contrast-enhanced and unenhanced) tumor volumes. The MR images were treated with both discrete and stationary or undecimated wavelet transformations sequentially along the three spatial dimensions to generate eight additional transformed images each. Discrete and undecimated wavelet transformations enabled a multiscale representation of imaging data while decomposing edges and uniform image regions into low– and high–spatial frequency regions. Supervised principal component (SPC) analysis was performed on radiomic features of patients in the training set to predict progression-free survival (PFS) and overall survival (OS). The performance of a Cox proportional hazards model with the SPC analysis predictor was assessed with C index and integrated Brier scores (IBS, lower scores indicating higher accuracy) and compared with Cox models based on clinical (age and Karnofsky performance score) and radiologic (Gaussian normalized relative cerebral blood volume and apparent diffusion coefficient) parameters. SPC analysis allowed stratification based on 11 features of patients in the training set into a low- or high-risk group for PFS. The results were verified in the validation set for PFS. The performance of the SPC analysis was higher compared with that of the radiologic and clinical risk models. The performance of the SPC analysis model was further improved when combined with clinical data. In summary, the authors identified an 11-feature radiomic signature derived from MRI for prediction of survival and stratification of patients with newly diagnosed glioblastomas. The signature showed improved performance compared with that of established clinical and radiologic risk models.

5.5. Example 5

In this example, we discuss a study using CT and PET imaging data from 300 head and neck cancer patients from four institutions by Vallières et al. [18]. The outcomes studied were risk of locoregional recurrences (LR), distant metastases (DM), and overall survival (OS). The ROI was the gross tumor volume, from which 1615 radiomic features were extracted. Clinical variables (age, T-Stage, N-Stage, TNM-Stage and human papillomavirus status) were also available for analysis. Initially, only radiomic features were used. Feature set reduction, feature selection, prediction performance estimation, choice of model complexity and final model computation processes were carried out using logistic regression, imbalance adjustment, and bootstrap resampling. Then, radiomic models (CT-only, PET-only, PET-CT) were combined with clinical variables using Random Forests. The highest performance for LR prediction was obtained using the model combining the PET-CT radiomic model with clinical variables, with an AUC of 0.69. For DM prediction, the highest performance was obtained using the CT radiomic model, with an AUC of 0.86. The highest performance for OS prediction was obtained by combining the PET radiomic model with clinical variables, with an AUC of 0.74. Thus, only for prediction of DM were images able to supplant the need for clinical variables. In a follow-up study [79], the CT images alone were used to predict the same outcomes using deep learning. The hypothesis was that CNNs could enhance the performance of traditional radiomics by detecting image patterns that may not be covered by a traditional radiomic framework. Instead of relying on transfer learning, the network was trained de novo. This approach resulted in an AUC of 0.88 in predicting DM. When the CNN output score was combined with the previous model, the AUC improved to 0.92. This shows the complementarity of the two approaches of feature-extraction-based radiomics and deep learning. Certain layers of the CNN were shown to explicitly recognize the radiomic features that the original study found to be predictive.

5.6. Example 6

In this final example, we will review applications of radiomics and ML for evaluating head and neck pathology by using large multi-energy datasets derived from dual-energy CT (DECT) scans. DECT is an advanced type of CT where attenuation data acquisition is performed at two instead of one peak energy [[80], [81], [82]]. This enables multi-energy or spectral tissue characterization and reconstruction of image sets far beyond what is possible with a conventional single energy CT. One type of image that can be reconstructed using DECT is the virtual monochromatic or virtual monoenergetic image (VMI). These images are created using sophisticated computer algorithms and simulate what an image would look like if acquired at a pre-determined energy level. The energy range for VMIs that can be created varies based on the scanner used but typically includes at least energies between 40 and 140 keV. There are currently few investigations applying texture analysis or radiomics to DECT datasets and no standard accepted approach for radiomic analysis of DECT scan data. However, one proposed approach is to analyze multiple energy VMIs, ranging from low energy VMIs that accentuate enhancement characteristics of tumors and other lesions to high energy VMIs that approach what an uninfused CT scan would look like [19,20,83]. The idea is to capture the energy-dependent properties of tissues which can be different between normal tissues and pathology. This can then potentially be leveraged to improve prediction model performance.

In a study by Al Ajmi et al. [19], texture analysis was performed on multi-energy VMI datasets ranging between 40 and 140 keV, in steps of 5 keV, resulting in 21 VMI datasets. These were then compared to the 65 keV VMIs, typically considered equivalent to a standard single energy CT acquisition [[84], [85], [86]]. 40 patients were evaluated and the study used a basic testing paradigm: distinction and histologic classification of the two most common benign parotid neoplasms as either pleomorphic adenoma or Warthin tumor. Texture analysis was performed using the commercial software TexRAD, and prediction models were constructed using Random Forests. The ML part included internal cross-validation and randomly selected independent training and testing sets. For single-energy datasets, the accuracy for correct tumor classification was 75%. This accuracy is not very high, considering a straightforward classification paradigm, but this is not surprising given the small patient numbers. The design was also done on purpose as part of the design to enable an evaluation of the potential for multi-energy analysis, meaning that the potential could be masked if the reference standard had a very high accuracy to begin with that would not allow much room for improvement. When the 21 multi-energy VMI set on the same cases was evaluated, the accuracy increased to 92%. This suggests that the additional quantitative information in DECT datasets has the potential to improve prediction in radiomic studies.

The potential value of multi-energy radiomic analysis was confirmed in a subsequent study by Forghani et al. [20] using DECT scans of 87 patients with head and neck squamous cell carcinoma (HNSCC). In the latter study, the texture or radiomic features of the primary tumor were used to predict associated lymph node metastases. This is important clinically because detection of early nodal micrometastases remains a challenge using current imaging methods [87,88], which in turn can result in over-treatment of some head and neck cancer patients with unnecessary neck dissections [[89], [90], [91], [92]]. This study also used Random Forests as ML method, with internal cross-validation and randomly selected independent training and testing sets. Using data extracted from the 65 keV VMIs typically considered equivalent to a conventional single energy CT, the prediction accuracy in the subgroup of patients that had no prior treatment (n = 64) was 60%. However, using multi-energy analysis, the accuracy increased to 88%. This study again demonstrates the potential added value of the additional quantitative spectral information in DECT scans for radiomic studies. It also demonstrates the potential for a clinical assistant tool that can be combined with expert radiologist evaluation to increase accuracy for accurate identification and exclusion of early nodal metastases.

6. Beyond Image Analytics: Big Data Integration for Oncology Using AI

In this article, we have focused on radiomics and applications of AI on analysis of medical images for improving diagnostic tumor evaluation. This is a very exciting area of research and application of AI with great potential for improving oncologic care. However, it is worth emphasizing that medical image analysis is one of many potential applications of AI in oncology. In the future, AI is likely to assist technologists and enhance the scan acquisition process, including patient positioning and tailoring image dose optimally to an individual patient. AI is already being tested at the time of image acquisition for improving image quality. As an extension of image evaluation, AI may be used to generate preliminary reports that can then be modified by the supervising physician, one step among various potential steps in increasing efficiency. Lastly, combined with natural language processing, AI can be used to analyze the entire electronic medical record, providing chart summaries and combining different clinical information with that obtained from the patient's imaging studies and laboratory work up to improve the diagnosis of challenging cases or rare syndromes, follow up on results, etc. There is also the entire field of applications of AI for analysis of digital pathology slides, similar to what is being done with medical images. These are just a few examples of the potential of this technology to change and revolutionize the way we practice medicine, if correctly and successfully implemented.

7. Challenges and Barriers

Despite the great potential of the radiomics and ML approaches discussed so far, significant challenges remain, and major barriers have to be overcome if this technology is ever to gain widespread use and be applied routinely in the clinical setting. We will begin by a discussion of technical challenges. Some of these were briefly alluded to in the earlier section on radiomics workflow but will be discussed more in-depth here. One of the main challenges pertains to the replicability of radiomic studies, a pre-requisite for widespread clinical implementation. The first major source of variation to be considered are those related to the image acquisition and reconstruction process. Major sources of variation include (1) various scan acquisition parameters, (2) the degree of enhancement achieved on a given scan which in turn depends on timing of a contrast agent, an individual patient's circulatory dynamics, and the specific anatomical location of the area or lesion of interest, (3) wear and tear of a given scanner, (4) differences in manufacturer or model type of a scanner, and (5) differences in reconstruction parameters, including but not limited to application (and degree) of iterative or other image reconstruction algorithms. There is a trend for technique standardization that may help but is unlikely to be sufficient by itself for completely addressing all of the potential sources of variations described. Application or pre-processing with different image normalization or style transfer methods is one potential solution for overcoming these technical barriers.

The next step, image segmentation, also represents a significant source of variability. When done by a human, the two main reasons for discrepancies are differences in education and training (e.g., between a radiologist, a radiation oncologist, or other specialist involved in the care of an oncology patient) and differences in experience level. Even though in principle, both of these sources can be addressed by having an unambiguous delineation protocol, in practice, studies show that this may not work [93]. Semi-automated approaches can help reduce this variability but are still reliant on human input [30]. Fully automatic segmentation may be achieved through deep learning; in this case, the choice of training set is crucial, as the algorithm will learn to faithfully reproduce the contouring practice of the humans who annotated the training data. At the core of this uncertainty is the question whether there is such a thing as the objective “ground truth”. Current clinical gold standards are not absolute, although in that regard the consistency of an algorithm may actually be an advantage, as long as one focuses on the specific clinical endpoint of interest. Therefore, the ideal way to eliminate this problem is to avoid segmentation altogether and have the deep learning algorithm establish the relevant parts of the image without the need for a ROI. However, while this is theoretically possible given enough training data, there are no publications to date that have shown a convincing proof of principle.

As mentioned previously, the third step of the workflow, feature extraction, is the easiest to standardize. However, there is the possibility that instead of a consensus in the form of a single software platform that is used globally, there emerge several competing platforms. Nonetheless, even this turn of events would be sufficient for replicability, since by adhering to a certain standard, it would make the task of feature traceability (exact definition and method of computation) trivial. Contrast this with the status quo of using in-house software and providing insufficient detail in resulting publications.

The final step, which includes feature set reduction, model building, and validation, is unlikely to be standardized. This is because this step is critical in terms of achieving high model performance (e.g., accuracy), and researchers (and companies providing radiomic models) are going to use their ingenuity to push performance to its limit. For researchers, a requirement of sharing the code used for a published study is the best way to enhance replicability. For companies, they may not agree to share code, in order to avoid losing their competitive edge and to protect their intellectual property. In this case, it would be useful if the company made the model available to researchers free of cost for widespread testing. A mandatory component for any clinically implemented algorithm would be periodic independent testing to ensure proper functioning of the algorithms and ensure that the algorithm has not been corrupted, as part of an active quality assurance process. Lastly, it is important to emphasize the need for basic fundamentals, including readily mineable systems and records and robust information technology health infrastructure with systems that can readily exchange data. As simple as this may sound, this may be the biggest immediate challenge to taking advantage of the full potential of AI.

Beyond the technical considerations that have been discussed in detail, there are also ethical and regulatory considerations that must be addressed. By default, successful implementation of any big data project will likely require access to large datasets. This brings up important issues pertaining to informed consent, protection of patient privacy, and the principle of “the right to benefit from science”. For example, is it acceptable to imply consent unless explicitly withdrawn or do patients have to explicitly consent to have their data used anonymously for research and algorithm construction? This requires a risk benefit analysis for the patient and society as a whole. The practicality of access to large datasets will also vary based on the health care system organization. For example, one may argue that access to data would be easier in a single payer system covering large territories (assuming there is interest and buy in from the decision makers) compared to more fragmented health systems, although the latter may have the advantage of more efficient (presumably) decision making and implementation compared to larger government run systems. Regardless of which approach is taken, i.e. implied versus explicit consent, strong protection of patient privacy and systems that would prevent misuse of patient protected information are mandatory.

There are also important regulatory and legal considerations. The first is a certification process that is reliable and robust. This can be a challenge given that some of ML approaches at least in part include a “black box” component, but it is not insurmountable. The use of independent testing platforms and periodic monitoring and quality assurance will be helpful in this regard for ensuring proper performance and increasing public confidence. The other major issue that arises is who is to blame, or liable, when things go wrong? So far, the approach has been to use different software as supporting tools, and the supervising physician is ultimately responsible, and by extension liable, for the final decision made. However, with increasing complexity and sophistication of the clinical assistant AI tools, there will likely be a component of liability for the companies providing these algorithms, just like any other medical device. The liability will further be shifted towards software developers if certain routine tasks are ever completely automated without human supervision, or certain types of studies, for example certain types of normal studies (for example a mammogram that is normal – i.e. does not demonstrate any pathology), are evaluated solely by a software without human intervention. These are challenges that will likely require inter-disciplinary engagement by medial professionals, legal professionals, ethicists, and society as a whole for optimal resolution and decision making.

8. Conclusions

In this article, we have provided an overview of radiomics and AI/ML, focusing on radiomic analysis and prediction model construction in oncology. We have provided an overview of the fundamentals of these approaches, their potential, as well as barriers for widespread implementation. Although there are clearly significant challenges that need to be overcome, there is undoubtedly great potential for the use of radiomics for improving diagnostic evaluation and care of oncology patients. By enabling extraction of higher-level data that is currently largely under-utilized in routine clinical practice, the field of radiomics and AI has the potential to revolutionize oncology, providing a platform for more personalized, higher quality, and cost-effective care for oncology patients. The multiple challenges highlighted in this article represent exciting areas for future research and development.

Funding information

R.F. is a clinical research scholar (chercheur-boursier clinicien) supported by the FRQS (Fonds de recherche en santé du Québec), Montreal, Quebec, Canada.

Declaration Competing of Interest

R.F. has acted as consultant and speaker for GE Healthcare and is a founding partner and stockholder of 4Intel Inc.

The other authors have no conflicts of interest to declare.