Use of self-reported vaccination status can bias vaccine effectiveness estimates from test-negative studies

Abstract

Introduction

A number of national/multi-national networks provide annual estimates of influenza vaccine effectiveness (VE) based on the test-negative design. Most of these networks use subject self-reports to define influenza vaccination history. In this study, we used simulations to estimate the degree to which self-reported vaccination status can bias test-negative VE estimates.

Methods

We simulated a population whose members are at risk for acute respiratory illness (ARI) due to influenza and for ARI due to other respiratory pathogens. Vaccination was assumed to reduce the risk of influenza but not of non-influenza ARI. We simulated a range of possible values for VE and for vaccine coverage. Across simulations, we varied the sensitivity and specificity of self-reported vaccination status relative to true vaccination. We estimated bias as the percent difference in VE in the presence of misclassification relative to true simulated VE.

Results

Assuming self-report has sensitivity of 95% and specificity of 90%, estimated VE underestimated true VE by 16% (95% confidence interval, 4–30%). Decreasing specificity of self-reports resulted in greater bias than decreasing sensitivity of self-reports. Bias also increased as vaccine coverage decreased.

Conclusions

The use of self-reported influenza vaccination history can meaningfully bias influenza VE in test-negative studies. Researchers using test-negative designs should attempt to supplement or validate self-reported vaccination history using additional data sources.

1. Introduction

Over the past decade or so, the test-negative design has become the global standard for observational studies of influenza vaccine effectiveness (VE) [1], [2], [3]. As use of the test-negative design has increased, researchers have paid increasing attention to the assumptions of this design and the biases that may result from violating these assumptions [4], [5], [6], [7], [8]. Less work has been done to explore the consequences of information bias on test-negative VE estimates.

Information bias arises when subjects’ outcomes, exposures, or covariates are ascertained with error [9]. For test-negative influenza VE studies, outcome misclassification can occur due to the imperfect sensitivity and specificity of laboratory tests for influenza. We have previously explored the effects of outcome misclassification in this context [10]. Another potential source of misclassification occurs in the ascertainment of subjects’ vaccination history. Most major influenza VE study networks define subjects’ exposure to the current season’s influenza vaccine either wholly [2], [3] or partially [1], [11] from subjects’ self-reports. Of concern, self-reported influenza vaccination tends toward false positives, in which unvaccinated individuals incorrectly report have received influenza vaccine [12], [13], [14], [15]. Notably, the reported specificity of self-reported vaccination has rarely exceeded 90%, and with at least one reported value as low as 38%. The present study uses simulations to explore the effects of exposure misclassification on test-negative VE estimates.

2. Methods

We previously developed a simulation model to explore the effects of misclassification in test-negative studies [10]. In this model, we simulate a population whose members are at risk for acute respiratory illness (ARI) due to influenza and for ARI due to other respiratory pathogens. We assumed that risk of influenza ARI was independent from risk of non-influenza ARI, and that subjects could be infected with influenza only once but could be have multiple non-influenza ARI infections. To focus on the effects of exposure misclassification, we assumed that other sources of bias are absent. In particular, we assume no outcome misclassification, no confounding by age or other factors, and no selection bias by differential healthcare seeking between vaccinated and unvaccinated subjects [7]. Our simulation model involves six parameters (Table 1):

• •VE = influenza vaccine effectiveness against medically attended influenza
• •IP_flu = incidence proportion (risk) of medically attended ARI due to influenza
• •IP_other = incidence proportion of medically attended ARI due to non-influenza pathogens
• •Sens = sensitivity of self-reported influenza vaccination history
• •Spec = specificity of self-reported influenza vaccination history
• •P_v = probability of vaccination (i.e. vaccine coverage).

Table 1.

Parameters used in the simulation model.

Parameter	Value in base case	Range in sensitivity analyses
Vaccine effectiveness (VE)	50%	10–50%
Incidence proportion of influenza ARI (IPflu)	5%	N/A
Incidence proportion of non-influenza ARI (IPother)	15%	N/A
Sensitivity of self-reported vaccination history (Sens)	0.95	0.4–1.0 (in 0.01 increments)
Specificity of self-reported vaccination history (Spec)	0.90	0.4–1.0 (in 0.01 increments)
Probability of vaccination (Pv)	40%	10–70% (in 1% increments)

We assumed that IP_flu was 5% over the course of the influenza season and that IP_other was 15% (Table 1) [7], [10]. We also assumed the simulated population contained 50,000 individuals, which results in test-negative study sizes that are consistent with those in observational VE studies [1], [2], [3]. We assumed VE of 50% as a base case, with VE of 10% in sensitivity analyses to simulate a year in which the vaccine is antigenically mismatched to the dominant circulating virus type/subtype [16]. We simulated a range of scenarios with different values for the assumed sensitivity (Sens) and specificity (Spec) of self-reported vaccination history. Based on prior observational studies, sensitivity of self-reports has ranged from 0.93 to 0.98 (median, 0.95) relative to documented vaccination, while specificity has ranged from 0.38 to 0.94 (median, 0.78) [12], [13], [14], [15]. We also varied vaccine coverage (P_v) across scenarios, from 10% to 70%.

For each combination of parameters, we ran 100 iterations of the simulation model. In each simulation we estimated $\widehat{\mathit{VE}}$ as (1-OR), where OR is the odds ratio for vaccination in persons with influenza ARI vs. non-influenza ARI from a test-negative study. We calculated the mean $\widehat{\mathit{VE}}$ and 95% confidence limits across the 100 simulation iterations. We also calculated the mean bias proportion in each scenario as $\left(\frac{\widehat{\mathit{VE}}}{\mathit{VE}}-1\right)$. For example, $\widehat{\mathit{VE}}$ of 40% when true VE is 50% would have a bias proportion of 0.2. Analyses were conducted using SAS Version 9.4 (SAS Institute, Cary NC) and R Version 3.3.3 (The R Foundation for Statistical Computing, Vienna, Austria).

3. Results

Under the base case, self-report was assumed to be 95% sensitive and 90% specific, with 40% vaccine coverage, and true VE to be 50%. In this base case, the mean estimated VE across simulations was 42% (95% CI, 35–48%). This represents a bias proportion of −0.16 (95% CI, −0.04 to −0.3) relative to the true simulation VE. With true VE set to 10%, the relative bias in the base case was similar, with estimated VE of 8.3% (95% CI, −1.1–17%), a bias proportion of −0.17.

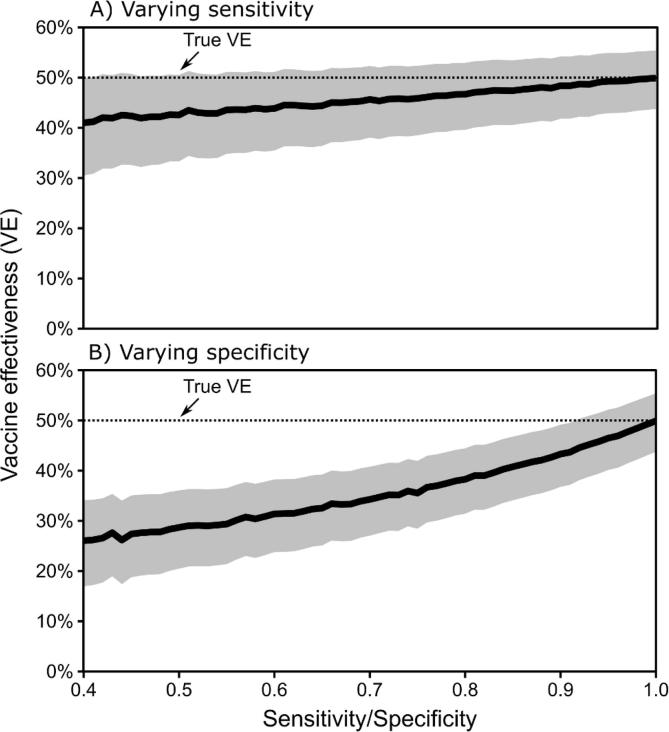
Imperfect sensitivity of self-report had a modest impact of estimated VE (Fig. 1A). When holding specificity constant at 1.0 and varying specificity from 0.4 to 1.0, the lowest estimated VE was 41% (95% CI, 30–50%), a bias proportion of −0.18 (Fig. 1). In contrast, imperfect specificity had a much larger impact on estimated VE (Fig. 1B). With sensitivity of 1.0, specificity of 0.4 resulted in estimated VE of 26% (95% CI, 17–34%), a bias proportion of −0.48.

Fig. 1.

Estimated vaccine effectiveness (VE) from test-negative studies with imperfect self-reported vaccination, when (A) specificity of self-report is fixed at 1.0 and sensitivity varies, and (B) sensitivity is fixed at 1.0 and specificity varies.

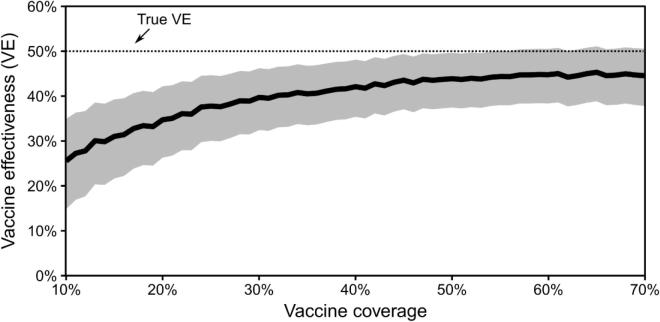
Across simulations, bias in estimated VE also depended on vaccine coverage (Fig. 2). In the base case, estimated VE was 45% (95% CI, 38–51%) when vaccine coverage was 70%. If vaccine coverage was as low as 10%, estimated VE was 26% (95% CI, 15–35%), a bias proportion of −0.48.

Fig. 2.

Estimated vaccine effectiveness (VE) from test-negative studies with varying levels of vaccine coverage in the source population, assuming self-reported vaccination status has sensitivity of 0.95 and specificity of 0.9.

4. Discussion

Misclassifying subjects’ exposure status will bias the results from any epidemiologic study, but the magnitude of bias will depend on the frequency of the exposure and the degree of misclassification. Self-reported influenza vaccination, relative to vaccination records from electronic health records or registries, has typically shown high sensitivity across various populations [12], [13], [14], [15]. Specificity of self-reports has been lower and more variable, particularly in some sub-populations such as older adults. Observational studies of influenza VE have generally been conducted among populations with vaccine coverage ranging from 15–40% [17], [18], [19], [20]. At this level of coverage, our simulations suggest that the use of self-reported vaccination history can meaningfully bias influenza VE estimates in test-negative studies. In our base case scenario, which may be a “best case” scenario in practice, use of self-reported vaccination history could lead to underestimating VE by 16%.

This finding contrasts with our prior work on information bias, which suggested that misclassification of outcomes was unlikely to cause significant bias in test-negative influenza VE estimates [10]. This is due to the high sensitivity and specificity of polymerase chain reaction tests for influenza, which are the de facto standard for test-negative studies. In the case of exposure misclassification, low specificity of self-reports increases the likely information bias. Self-reported vaccination may lack specificity for several reasons, such as the fact that it is easier to recall the occurrence of an event (i.e. receiving a vaccine) than non-occurrence, and the potential for false positive reports from subjects who may wish to appear compliant with vaccine recommendations [15]. Although extremely low values for specificity of self-reported vaccination(<40%) may be unlikely in most situations, even specificities in the upper reported range can cause bias. A recent simulation study by De Smedt and colleagues reached a similar conclusion, as they found that exposure misclassification was likely to result in greater bias than outcome misclassification in test-negative studies [21].

This study had several limitations that should be considered. First, we assumed that misclassification of self-reported vaccination did not differ based on disease status (i.e. whether ARI was due to influenza or a non-influenza pathogen). This assumption seems likely to hold in test-negative studies where vaccination is assessed prior to influenza testing. However, if test-negative studies are conducted among patients after influenza test results are made available, subjects’ knowledge of test results may bias exposure reporting. Second, we did not consider other sources of bias, including confounding, selection bias, or misclassification of disease status, which may complicate the effects of exposure misclassification on VE estimates.

Test-negative VE studies have occasionally relied solely on self-reported influenza vaccination history to define subjects’ vaccine exposure. The present study suggests that this could lead to meaningful bias in estimated VE. Researchers should endeavor to validate self-reported using sources such as vaccination history through registries, electronic health records, and detailed questions to improve recall.

Funding

This work was supported by the Centers for Disease Control and Prevention through a cooperative agreement with Kaiser Permanente Washington Health Research Institute (5U01 IP001037).

Conflict of interest

The author reports no conflicts of interest.