Estimation of Area Under the ROC Curve under nonignorable verification bias

Abstract

The Area Under the Receiving Operating Characteristic Curve (AUC) is frequently used for assessing the overall accuracy of a diagnostic marker. However, estimation of AUC relies on knowledge of the true outcomes of subjects: diseased or non-diseased. Because disease verification based on a gold standard is often expensive and/or invasive, only a limited number of patients are sent to verification at doctors’ discretion. Estimation of AUC is generally biased if only small verified samples are used and it is thus necessary to make corrections for such lack of information. However, correction based on the ignorable missingness assumption (or missing at random) is also biased if the missing mechanism indeed depends on the unknown disease outcome, which is called nonignorable missing. In this paper, we propose a propensity-score-adjustment method for estimating AUC based on the instrumental variable assumption when the missingness of disease status is nonignorable. The new method makes parametric assumptions on the verification probability, and the probability of being diseased for verified samples rather than for the whole sample. The proposed parametric assumption on the observed sample is easier to be verified than the parametric assumption on the full sample. We establish the asymptotic properties of the proposed estimators. A simulation study is performed to compare the proposed method with existing methods. The proposed method is also applied to an Alzheimer’s disease data collected by National Alzheimer’s Coordinating Center.

1. Introduction

The Receiving Operating Characteristic (ROC) curve is one of the most commonly used statistical tools for evaluating the accuracy of a diagnostic marker. The area under the curve (AUC) is a popular summary index for evaluating a method’s power of discriminating diseased from non-diseased subjects; it is the probability that the score of a randomly chosen diseased individual exceeds that of a randomly chosen non-diseased subjects (Bamber, 1975). Estimation of AUC relies on knowledge of the true status of subjects, which can usually be verified through a gold standard. However, such verification is not applicable for all subjects because it is expensive, invasive or both. On the other hand, the estimation based on verified sub-samples only is generally biased (Begg and Greenes, 1983).

A common assumption of adjusting verification bias is that the verification mechanism is ignorable, also known as missing at random (MAR), which means that the selection of a subject for verification is independent of the subject’s disease status, conditional on the score of the marker and other covariates. Several approaches based on the MAR assumption have been proposed by, for example, Begg and Greenes (1983), Zhou (1996), Zhou (1998), Rodenberg and Zhou (2000), Alonzo and Pepe (2005), He, Lyness and McDermott (2009) and He and McDermott (2011). See Zhou, Obuchowski and McClish (2011) for a comprehensive overview of these works.

The MAR assumption can be unrealistic when the doctors’ decision to send a subject to verification is based on his or her detailed information on that subject, which may depend on some un-measured covariates related to disease status (Rotnitzky, Faraggi and Schisterman, 2006); such case is known as nonignorable verification bias. The earlier existing works under nonignorable verification bias are limited to dichotomous or ordinal markers, including Baker (1995), Zhou and Rodenberg (1998), Kosinski and Barnhart (2003), Zhou and Castelluccio (2003) and Zhou and Castelluccio (2004). Two recent methods proposed by Rotnitzky, Faraggi and Schisterman (2006) and Liu and Zhou (2010) under nonignorable verification bias can efficiently estimate AUC for markers that are measured in any quantitative scale, i.e., continuous, ordinal or dichotomous. In particular, Rotnitzky, Faraggi and Schisterman (2006) proposed a doubly robust estimator of AUC, with the validity of the estimator only requiring either the disease model (the probability of being diseased given covariates) or the verification model (the probability of being verified given some covariates and the true disease outcome) to be correctly specified. The nonignorabilty parameter (the coefficient of the disease outcome) in their verification model was not identifiable, and thus a sensitivity analysis was suggested. On the other hand, Liu and Zhou (2010) suggested a parametric model to estimate the nonignorability parameter; they assumed a parametric disease regression model of the responses for the whole sample and jointly estimated the verification probability and the disease probability. However, such a parametric assumption is hard to be verified in practice, because of assumptions on the unobserved responses.

In this paper, instead of applying rather subjective sensitivity analysis for the nonignorability parameter, we consider a way of estimating the nonignorability parameter based on the maximum likelihood method under identifiability assumption based on an instrumental variable (Wang, Shao and Kim, 2014). We use a similar idea as the propensity-score-adjustment method proposed by Sverchkov (2008) and Riddles, Kim and Im (2016), which were originally developed in the context of survey sampling, to correct nonignorable verification bias in AUC estimators. It is based on parametric assumption of the disease model for observed subjects, and parametric assumption of the verification model. An instrumental variable can be used to construct a reduced verification model and result in a high efficient estimation.

The rest of this paper is organized as follows: In Section 2, we present our proposed estimator, and its asymptotic properties are discussed in Section 3, then the simulation studies and real data analysis are provided in Section 4. We end our paper with a brief discussion and conclusion in Section 5.

2. Methods

2.1. Basic Setup

Consider a sample of size n, which is assumed to be a random sample. Suppose Y_i = 1 if the sample i is from diseased group, and Y_i = 0 otherwise, and X_i and V_i are the marker of interest and the covariates, respectively. Let R_i = 1 if Y_i is observed and R_i = 0 otherwise, i = 1,..., n. Based on the result of Bamber (1975), the AUC of marker X is equal to

$$AUC=\frac{E\left\{Y_1\left(1-Y_2\right)I_{12}\right\}}{E\left\{Y_1\left(1-Y_2\right)\right\}},$$ (2.1)

where I₁₂ = I (X₁ > X₂) + 0.5I(X₁ = X₂) and I(·) is the indicator function. If there is no missing value, AUC can be estimated by:

$$\widehat{A}=\frac{{\sum }_{i=1}^n{\sum }_{j\ne i}{Y}_i\left(1-Y_j\right)I_{ij}}{{\sum }_{i=1}^n{\sum }_{j\ne i}{Y}_i\left(1-Y_j\right)},$$ (2.2)

where I_ij = I(X_i > X_j) + 0.5I(X_i = X_j).

2.2. Estimator of AUC with adjustment of verification bias

Since some Ys in (2.2) are unobserved, we need to model the distribution of the disease status Y based on the information of X and covariates V. Assume that the covariates can be decomposed into V = (V₁, V₂) and the dimension of V₂ is greater than or equal to one. We assume that V₂ is conditionally independent of R given (X, Y, V₁). The variable V₂ is called a (nonresponse or) instrument variable (IV) and it helps to make the model identifiable (Wang, Shao and Kim, 2014). We then define the verification model as

$${\pi }_i=pr\left(R_i=1|X_i,{\mathit{V}}_i,Y_i\right)=\pi \left(X_i,{\mathit{V}}_{1i},Y_i;\varphi \right),$$ (2.3)

where π(·) is a known function and ϕ is the unknown parameter. The IV assumption (2.3) is a way of making a reduced model for π_i. Roughly speaking, IV can reduce the number of parameters to be estimated and ensure the identifiability of the reduced model. In practice, the IV assumption is hard to be verified; however, as confirmed in the simulation study in Section 4, the proposed method shows reasonable performance even when the IV assumption is weakly violated.

We write $\varphi =\left({\psi }_1,{\psi }_2,{\mathit{\psi }}_3,\beta \right)$ and assume

$$\pi \left(X_i,{\mathit{V}}_{1i},Y_i;\varphi \right)=\frac{1}{1+\exp \left({\psi }_1+{\psi }_2{X}_i+{\psi }_3{\mathit{V}}_{1i}+\beta Y_i\right)}.$$ (2.4)

The above verification model is a logistic regression model using (X, V₁, Y) as explanatory variables. Parameter β is the nonignorability parameter; if β = 0, then the response mechanism is MAR. Note that

$$\frac{E\left\{R_1{\pi }_1^{-1}{R}_2{\pi }_2^{-1}{Y}_1\left(1-Y_2\right)I_{12}\right\}}{E\left\{R_1{\pi }_1^{-1}{R}_2{\pi }_2^{-1}{Y}_1\left(1-Y_2\right)\right\}}=\frac{E\left\{Y_1\left(1-Y_2\right)I_{12}\right\}}{E\left\{Y_1\left(1-Y_2\right)\right\}}.$$ (2.5)

Thus, if a consistent estimator ${\hat{\pi }}_i$ of π_i is available, we can estimate AUC by an inverse weighted type of estimator

$${\widehat{A}}_{iv}=\frac{{\sum }_{i=1}^n{\sum }_{j\ne i}{R}_i{\widehat{\pi }}_i^{-1}{R}_j{\widehat{\pi }}_j^{-1}{Y}_i\left(1-Y_j\right)I_{ij}}{{\sum }_{i=1}^n{\sum }_{j\ne i}{R}_i{\widehat{\pi }}_i^{-1}{R}_j{\widehat{\pi }}_j^{-1}{Y}_i\left(1-Y_j\right)},$$ (2.6)

We will discuss how to estimate π_i, or equivalently, to estimate ϕ in the verification model (2.3).

2.3. Parameter Estimation

To estimate ϕ in the verification model (2.3), note that the likelihood of ϕ with full response is

$$L=\prod _{i=1}^n\left[\pi {\left(X_i,{\mathit{V}}_{1i},Y_i;\varphi \right)}^{R_i}{\left\{1-\pi \left(X_i,{\mathit{V}}_{1i},Y_i;\varphi \right)\right\}}^{1-R_i}\right],$$ (2.7)

and under some regularity conditions the maximum likelihood estimator (MLE) of ϕ can be obtained by solving the score equation

$$\begin{gathered} S(\varphi )=\sum _{i=1}^n\left\{R_i-\pi \left(X_i,V_{1i},Y_i;\varphi \right)\right\}\frac{\partial logit\left({\pi }_i\right)}{\partial \varphi } \\ \equiv \sum _{i=1}^{n}s\left(X_i,R_i,{\mathit{V}}_{1i},Y_i;\varphi \right)=0, \end{gathered}$$ (2.8)

where $\mathit{logit}\left({\pi }_i\right)=log\left({\pi }_i/\left(1-{\pi }_i\right)\right)$. Since some Y_i is missing, the score function (2.8) is not applicable. Alternatively, the MLE of ϕ can be obtained by solving the following mean score equation

$$\begin{gathered} \overline{\mathit{S}}(\varphi )\equiv \sum _{i=1}^{n}E\left\{s\left(X,R,{\mathit{V}}_1,Y;\varphi \right)|{\mathit{O}}_i\right\} \\ =\sum _{i=1}^n\left[R_{i}s\left(X_i,1,{\mathit{V}}_{1i},Y_i;\varphi \right)+\left(1-R_i\right)E_0\left\{s\left(X_i,0,{\mathit{V}}_{1i},Y;\varphi \right)|X_i,{\mathit{V}}_i\right\}\right] \\ =0, \end{gathered}$$ (2.9)

where $E_0\left(\cdot |X_i,{\mathit{V}}_i\right)=E\left(\cdot |X_i,{\mathit{V}}_i,R_i=0\right)$ and O_i is the observed information for sample i, that is,

$${\mathit{O}}_i=\{\begin{array}{ll}\left(X_i,R_i,{\mathit{V}}_i,Y_i\right)\hfill & \text{if}{R}_i=1,\hfill \\ \left(X_i,R_i,{\mathit{V}}_i\right)\hfill & \text{otherwise}.\hfill \end{array}$$

Using the mean score equation for estimating the MLE has been discussed by, for example, Louis (1982), Riddles, Kim and Im (2016).

We then need to estimate the conditional distribution of unobserved Y given the marker X and covariant V, or equivalently, the second term in (2.9). A simple choice is applying a parametrical disease model for all samples, like Liu and Zhou (2010) did. Instead of using a full parametric model, we consider an alternative approach based on the following Bayes formula

$$Pr\left(Y_i=1|X_i,{\mathit{V}}_i,R_i=0\right)=\frac{Pr\left(Y_i=1|X_i,{\mathit{V}}_i,R_i=1\right)O\left(1,X_i,{\mathit{V}}_i\right)}{{\sum }_{y=0}^{1}Pr\left(Y_i=y|X_i,{\mathit{V}}_i,R_i=1\right)O\left(y,X_i,{\mathit{V}}_i\right)}$$ (2.10)

where

$$O(Y,X,\mathit{V})=\frac{Pr\left(R_i=0|Y,X,\mathit{V}\right)}{Pr\left(R_i=1|Y,X,\mathit{V}\right)}=\frac{1-\pi \left(X,{\mathit{V}}_1,Y;\varphi \right)}{\pi \left(X,{\mathit{V}}_1,Y;\varphi \right)}.$$

Thus, in addition to the verification model (2.3), we only need a model for the distribution of the conditional distribution of Y in the verified samples, i.e., the disease model for verified samples Pr(Y_i|X_i, V_i, R_i = 1). Rotnitzky, Faraggi and Schisterman (2006) also considered (2.10), but they did not discuss the estimation of the nonignorability parameter β. Instead, they considered a sensitivity analysis for β. Kim and Yu (2011) used (2.10) to obtain a semiparametric estimation of the population mean under nonignorable nonresponse assuming a followup sample.

Here we specify a parametric model for Pr(Y_i = y|X_i, V_i, R_i = 1) and derive Pr(Y_i = y|X_i, V_i, R_i = 0) based on (2.10). We denote Pr(Y_i = y|X_i, V_i, R_i = 1) ≡ P₁(y, X_i, V_i; μ), where P₁(·) is a known function and μ is an unknown parameter, and denote Pr(Y_i = y|X_i, V_i, R_i = 0) ≡ P₀(y, X_i, V_i; μ, ϕ), y = 1, 0. Using (2.10), the conditional distribution of the unobserved Y reduces to

$$\begin{gathered} Pr\left(Y_i=1|X_i,{\mathit{V}}_i,R_i=0\right)=\frac{P_1\left(1,X_i,{\mathit{V}}_i;\mu \right)e^{\beta }}{1-P_1\left(1,X_i,{\mathit{V}}_i;\mu \right)\left(1-e^{\beta }\right)} \\ \equiv P_0\left(1,X_i,{\mathit{V}}_i;\varphi ,\mu \right). \end{gathered}$$

Here, μ₀ can be simply estimated by solving

$$\begin{gathered} {\mathit{S}}_1(\mu )=\sum _{i=1}^n{R}_i\left[Y_i\frac{\partial \mathit{log}\left\{P_1\left(Y_i,X_i,{\mathit{V}}_i;\mu \right)\right\}}{\partial \mu }+\left(1-Y_i\right)\frac{\partial \mathit{log}\left\{P_1\left(1-Y_i,X_i,{\mathit{V}}_i;\mu \right)\right\}}{\partial \mu }\right] \\ \equiv \sum _{i=1}^n{R}_i{s}_1\left(X_i,{\mathit{V}}_i,Y_i;\mu \right)=0. \end{gathered}$$ (2.11)

That is, parameter μ is estimated by maximizing the likelihood among the respondents. Once we get a ML estimator $\hat{\mu }$ from (2.11), we plug $\hat{\mu }$ into (2.9) to solve for ϕ. We write (2.9) as

$$\begin{gathered} {\mathit{S}}_2(\varphi ,\mu )=\sum _{i=1}^n\left\{R_{i}s\left(X_i,1,{\mathit{V}}_{1i},Y_i;\varphi \right)+\left(1-R_i\right)\sum _{y=0}^{1}s\left(X_i,0,{\mathit{V}}_{1i},y;\varphi \right)P_0\left(y,X_i,{\mathit{V}}_i;\varphi ,\mu \right)\right\} \\ =\sum _{i=1}^n{s}_2\left(X_i,R_i,{\mathit{V}}_i,Y_i;\varphi ,\mu \right)=\mathbf{0}, \end{gathered}$$ (2.12)

where P₀(0, X_i, V_i; ϕ, μ) = 1 − P₀(1, X_i, V_i; ϕ, μ).

The actual computation for obtaining $\hat{\varphi }$ from (2.12) can be implemented by the following EM algorithm:

1. Specify the initial value $\hat{\varphi }$⁽⁰⁾.

2. For each t = 0, 1, 2,..., let $\hat{\varphi }$^(t+1) be the solution of

   $\sum _{i=1}^n\left\{R_{i}s\left(X_i,1,{\mathit{V}}_{1i},Y_i;\varphi \right)+\left(1-R_i\right)\sum _{y=0}^1{w}_{iy}^{(t)}s\left(X_i,0,{\mathit{V}}_{1i},y;\varphi \right)\right\}=0,$

   where $w_{iy}^{(t)}=P_0\left(y,X_i,{\mathit{V}}_i;{\widehat{\varphi }}^{(t)},\widehat{\mu }\right)$.

3. Set t = t + 1 and go to step (2) until ‖$\hat{\varphi }$^(t+1) − $\hat{\varphi }$^(t)‖₁ < ϵ, where ϵ is a very small arbitrary number, such as ϵ = 10⁻⁵.

3. Asymptotic Properties

In this section, we establish some asymptotic properties of the proposed propensity-score-adjustment AUC estimator $\hat{A}$_iv. The regularity conditions and the proofs are shown in the Supplementary material.

Define

$$D_{ij}(A,\varphi )=R_i{\pi }_i^{-1}(\varphi )R_j{\pi }_j^{-1}(\varphi )Y_i\left(1-Y_j\right)\left(I_{ij}-A\right),$$

and A₀ to be the true AUC, and the following theorem presents the asymptotic properties of the proposed estimator of A.

Theorem 1.

Suppose the regularity conditions (r1-r10) given in the Supplementary material hold. We have

$$\sqrt{n}\left({\widehat{A}}_{iv}-A_0\right)\stackrel{d}{\to }N\left(0,{\sigma }^2\right),$$ (3.1)

where ${\sigma }^2=Var\left(Q_i\right)/{[Pr(Y=0)Pr(Y=1)]}^2$, and

$$\begin{array}{l}{Q}_i=E\left(D_{ij}+D_{ji}|{\mathit{O}}_i\right)-{\mathrm{\Gamma }}^{\prime }{E}^{-1}\left\{\frac{\partial s_2(X,R,V,Y;\varphi )}{\partial \varphi }\right\}[s_2\left(X_i,R_i,V_i,Y_i;\varphi ,\mu \right)\\ +E\left\{\frac{s_2(X,R,\mathit{V},Y;\varphi ,\mu )}{\partial \mu }\right\}{E}^{-1}\left\{\frac{\partial s_1(X,\mathit{V},Y;\mu )}{\partial \mu }\right\}{R}_i{s}_1\left(X_i,{\mathit{V}}_i,Y_i;\mu \right)],\end{array}$$ (3.2)

Γ = ∂E(D_ij)/∂ϕ and s₂(·) was defined in (2.12).

A sketched proof of Theorem 1 is given in the supplementary material. Pr(Y = 1), Pr(Y = 0) and Var(Q_i) can be consistently estimated by ${\sum }_{i=1}^n{R}_i{\widehat{\pi }}_i^{-1}{Y}_i/n$, ${\sum }_{i=1}^n{R}_i{\widehat{\pi }}_i^{-1}\left(1-Y_i\right)/n$ and $\widehat{V}ar\left(Q_i\right)={\sum }_{i=1}^n{\left({\widehat{Q}}_i-{\overline{Q}}_n\right)}^2/(n-1)$, respectively, with

$$\begin{gathered} {\widehat{Q}}_i=\sum _{j=1}^n\left\{D_{ij}\left({\widehat{A}}_{iv},\widehat{\varphi }\right)+D_{ji}\left({\widehat{A}}_{iv},\widehat{\varphi }\right)\right\}/n-{\widehat{\mathrm{\Gamma }}}_k^{\prime }{\widehat{E}}^{-1}\left\{\partial s_2(X,R,V,Y;\widehat{\varphi },\widehat{\mu })/\partial \varphi \right\}[s_2\left(X_i,R_i,V_i,Y_i;\widehat{\varphi },\widehat{\mu }\right)+ \\ \widehat{E}\left\{\partial s_2(x,R,\mathit{V},Y;\widehat{\varphi },\widehat{\mu })/\partial \mu \right\}{\widehat{E}}^{-1}\left\{\partial s_1(X,\mathit{V},Y;\widehat{\mu })/\partial \mu \right\}{R}_i{s}_1\left(X_i,{\mathit{V}}_i,Y_i;\widehat{\mu }\right)], \end{gathered}$$

$$\begin{gathered} {\overline{Q}}_n={\sum }_{i=1}^n{\widehat{Q}}_i/n,{\widehat{E}}^{-1}\left\{\partial s_2(X,R,V,Y;\widehat{\varphi },\widehat{\mu })/\partial \varphi \right\}=n{\left\{{\sum }_{i=1}^n\partial s_2\left(X_i,R_i,V_i,Y_i;\widehat{\varphi },\widehat{\mu }\right)/\partial \varphi \right\}}^{-1}, \\ \begin{array}{l}{\widehat{E}}^{-1}\left\{\partial s_1(X,V,Y,\widehat{\mu };\widehat{\mu })/\partial \mu \right\}=n{\left\{{\sum }_{i=1}^n\partial s_1\left(X_i,V_i,Y_i;\widehat{\mu }\right)/\partial \mu \right\}}^{-1},\widehat{E}\left\{\partial s_2(X,R,V,Y;\widehat{\varphi },\widehat{\mu })/\partial \mu \right\}=\\ {\sum }_{i=1}^n{n}^{-1}\partial s_2\left(X_i,R_i,V_i,Y_i;\widehat{\varphi },\widehat{\mu }\right)/\partial \mu \text{and}\widehat{\mathrm{\Gamma }}=n^{-2}{\sum }_{i=1}^n{\sum }_{i=1}^n\partial D_{ij}/\partial \varphi .\end{array} \end{gathered}$$

Remark:

To have a better understanding of the asymptotic variances in (3.1), we can further decompose Var(Q_i) in (3.2). Denote the first and second terms of the right side of (3.2) as Q_i1 and Q_i2, respectively, so that Q_i = Q_i1 + Q_i2. Rewrite (3.2) as

$$Var\left(Q_i\right)=Var\left(Q_{i1}\right)+Var\left(Q_{i2}\right)+2Cov\left(Q_{i1},Q_{i2}\right).$$

Here,

$$Var\left(Q_{i1}\right)=Var\left({\widehat{A}}_f\right){\{Pr(Y=0)Pr(Y=1)\}}^2+E\left\{g^2\left(X_i,Y_i,{\mathit{V}}_i\right)\left({\pi }_i^{-1}-1\right)\right\},$$ (3.3)

$$Var\left(Q_{i2}\right)={\mathrm{\Gamma }}^{\prime }{T}_{22}^{-1}\mathrm{\Gamma },$$ (3.4)

and

$$Cov\left(Q_{i1},Q_{i2}\right)={\mathrm{\Gamma }}^{\prime }{T}_{22}^{-1}E\left[\left(D_{ij}+D_{ji}\right)\left\{s_{2i}+T_{21}{T}_{11}^{-1}{R}_i{s}_{1i}\right\}\right]=2{\mathrm{\Gamma }}^{\prime }{T}_{22}^{-1}Cov\left(D_{ij},s_{2i}+T_{21}{T}_{11}^{-1}{R}_i{s}_{1i}\right),$$ (3.5)

where $\widehat{A}$_f is the AUC estimator defined in (2.2) when there is no missing data, $g\left(X_i,Y_i,{\mathit{V}}_i\right)=Y_{i}Pr(Y=0)\left\{F_0\left(X_i\right)-A_0\right\}+\left(1-Y_i\right)Pr(Y=1)\left\{1-F_1\left(X_i\right)-A_0\right\}$, with F₀(·) and F₁(·) being the cumulative distribution function of X conditional on Y = 0 and Y = 1, respectively. The derivation of variance decomposition (3.3) and (3.5) are also given in the supplementary document.

In summary, the asymptotic variance of the proposed estimators can be decomposed into three terms:

$$\begin{gathered} Var\left(Q_i\right)=Var\left({\widehat{A}}_f\right){\{\mathit{Pr}(Y=0)\mathit{Pr}(Y=1)\}}^2+E\left\{g^2\left(Y_i,X_i,{\mathit{V}}_i\right)\left({\pi }_i^{-1}-1\right)\right\} \\ +{\mathrm{\Gamma }}^{\prime }{T}_{22}^{-1}\left\{\mathrm{\Gamma }+4Cov\left(D_{ij},s_{2i}+T_{21}{T}_{11}^{-1}{R}_i{s}_{1i}\right)\right\}. \end{gathered}$$ (3.6)

The first term is the variance of $\widehat{A}$_f, where no missing data is assumed; the second one $E\left\{g^2\left(X_i,Y_i,{\mathit{V}}_i\right)\left({\pi }_i^{-1}-1\right)\right\}$ is due to the fact only partial samples are verified (i.e., π_i smaller than 1); the third term ${\mathrm{\Gamma }}^{\prime }{T}_{22}^{-1}\mathrm{\Gamma }$ is the variance generated from estimating ϕ—the unknown parameter in the verification model π(·) and the connection between the statistic of interest (here AUC) and the likelihood of ϕ and μ. It’s easy to see that the second and third terms become zero when no data is missing. These terms can be treated as variances produced by the missing mechanism. Note that g(X_i, Y_i, V_i) do not depend on R_i and π_i. Compared to the estimator $\widehat{A}$_f using the full data, the increased variance of our estimators are due to the estimation of unknown parameter ϕ and partial verification; smaller verification probability would lead to a larger variance.

4. Numerical studies

4.1. Simulation studies

To test our theory, we generate synthetic data similarly as Liu and Zhou (2010): first generate the marker X ~ unif (−1, 1) and the covariate V under different scenarios, and then generate the outcome variable Y through the disease model on the full sample:

$$Pr\left(Y_i=1|X_i,V_i\right)=\frac{1}{1+\mathit{exp}\left({\mu }_1+{\mu }_2{X}_i+{\mu }_3{V}_i\right)},$$

and generate the missing indicator R though

$${\pi }_i=Pr\left(R_i=1|X_i,V_i,Y_i\right)=\frac{1}{1+exp\left({\psi }_1+{\psi }_2{X}_i+{\psi }_3{V}_i+\beta Y_i\right)}.$$

Note that under the above setting, the disease model on verified samples that we will fit, takes the following form:

$$Pr\left(Y_i=1|X_i,V_i,R_i=1\right)=\frac{1}{1+U\left(X_i,V_i\right)exp\left({\mu }_1+{\mu }_2{X}_i+{\mu }_3{V}_i\right)},$$

where $U\left(X_i,V_i\right)=\left(1+exp\left({\psi }_1+{\psi }_2{X}_i+{\psi }_3{V}_i+\beta \right)\right)/(1+exp\left({\psi }_1+{\psi }_2{X}_i+{\psi }_3{V}_i\right)$, which is not equal to 1 when missingness is nonignorable, in other words, Pr(Y_i = 1|X_i, V_i, R_i = 1) does not follow a logistic distribution. However, in the simulation study, the logistic form is always tapped because of its prevalence in practice. In this sense, we at least weakly misspecified the disease model on the verified sample for nonignorable cases.

We have six different scenarios:

1. V ~ Bernoulli(0.5), (μ₁, μ₂, μ₃) = (2, −2.5, −1), (ψ₁, ψ₂, ψ₃) = (1.2, −1, 0) and β = −1.5. We fit the disease model on verified samples in a logistic form with explanatory variables X and V, while the working verification model is another logistic model with V as the IV. Under this setting, the verification model is correctly specified, with Y and V being weakly correlated (the correlation coefficient between them is 0.16).

2. Similar to scenario I, but with (μ₁, μ₂, μ₃) = (2, −2.5, −1), (ψ₁, ψ₂, ψ₃) = (2, −1, −1) and β = 0. Under this setting, the verification model is incorrectly specified since ψ₃ ≠ 0, with the correlation coefficient 0.16 between Y and V, and 0.19 between R and V.

3. V ~ N(0, 1), (μ₁, μ₂, μ₃) = (2, −2.5, −1), (ψ₁, ψ₂, ψ₃) = (1, −1, 0) and β = −1.5. We fit the model similarly as in Scenario I except that the working disease model with sign(V)|V|^1/3 instead of V. Under this setting, the working disease model is incorrectly specified, with Y and V being moderately correlated (the correlation coefficient between them is 0.28).

4. V ~ N(0, 1), (μ₁, μ₂, μ₃) = (0.5, −2.5, −1.5), (ψ₁, ψ₂, ψ₃) = (2, −1, −0.8) and β = −2. We fit the model similarly as in Scenario I. Under this setting, the working verification model is incorrectly specified, with Y and V being weakly correlated.

5. V ~ N(0, 1), (μ₁, μ₂, μ₃) = (0.5, −2.5, −1), (ψ₁, ψ₂, ψ₃) = (2, −1, 0.8) and β = −2. We fit the model similarly as in Scenario I except that the working disease model with sign(V)|V|^1/3 instead of V. Under this setting, both the working disease model and the verification model are incorrectly specified, with Y and V being moderately correlated (the correlation coefficient between them is 0.32).

6. Here we generate more covariates: V₁ ~ Bernoulli(0.5), V₂ ~ N(0, 1) and V₃ ~ unif(0, 1). (μ₁, μ₂, μ₃, μ₄, μ₅) = (0.6, −1.5, 0.5, −0.5, 0.5), (ψ₁, ψ₂, ψ₃, ψ₄, ψ₅) = (1, −1, 0.5, −0.5, 0.5) and β = −2. We fit the working verification model using V₃ as IV since it is less correlated with R than other covariates.

Table 1 summarizes some design statistics for each scenario, including whether the working models are correctly specified, verification proportion, disease prevalence and the true AUC.

Table 1:

Summary statistics for the simulation design. Notation: for working disease model, W—weak misspecification, i.e., disease model is misspecified as having a logistic form, IC—incorrect specification, not only disease model is misspecified as having a logistic form but also the covariates effect misspecified, for working verification model, C—correct specification, the selected instrument variable (IV) is indeed an IV, IC— incorrect specification, indicates that the selected IV is not an IV, I—ignorable scenario, and NI — nonignorable scenario

Scenario	I	II	III	IV	V	VI
Working disease model	W	W	IC	W	IC	W
Working verification model	C	IC	C	IC	IC	IC
Ignorable/Nonignorable	NI	I	NI	NI	NI	NI
Verification proportion	0.33	0.21	0.37	0.30	0.30	0.33
Prevalence	0.26	0.26	0.21	0.42	0.42	0.29
AUC	0.81	0.81	0.79	0.79	0.79	0.71

We consider 200 and 2,000 samples for each scenario and generate 500 data sets for each case. Four additional estimators are compared to the proposed estimator: $\widehat{A}$_ig, $\widehat{A}$_f, $\widehat{A}$_v and $\widehat{A}$_fp, which stand for the AUC estimators using the ignorable assumption (β = 0 and without using IV), using full data, using verified data only and using a full parametric disease model (Liu and Zhou, 2010), respectively. Note that we calculate $\widehat{A}$_ig and $\widehat{A}$_fp in the same way as $\widehat{A}$_iv, therefore, these estimators are only different in the way of estimating parameters ϕ and/or μ.

The estimator $\widehat{A}$_f is treated as the gold standard. A summary of the simulation results is presented in Tables 2, where the bias (defined as the mean difference with $\widehat{A}$_f), standardized sample variance (Svar) and standardized mean square error (SMSE) are displayed for the six estimators considered. In Table 2, SVar (SMSE) of an estimator is defined as its variance (MSE) divided by the variance (MSE) of $\widehat{A}$_f. Note that SMSE is also known as relative efficiency. The median value of the estimated asymptotic variances for the proposed estimators are compared with the Monte Carlo sample variances in Table 3. The following conclusions can be made from the simulation results.

Table 2:

Monte Carlo bias, standardized variance (SVAR), standardized mean squared error (SMSE) and 95% coverage probability (CP) of AUC estimators in simulation study. $\widehat{A}$_f, $\widehat{A}$_iv, $\widehat{A}$_ig, $\widehat{A}$_v and $\widehat{A}$_fp stand for the AUC estimators using full data, using IV method, using ignorable assumption (missing at random), using verified data only and using a full parametric disease model (Liu and Zhou, 2010), respectively. SVar and SMSE stand for the standardized variance, and standardized MSE, respectively. SVar (SMSE) of an estimator is defined as its variance (MSE) divided by the variance (MSE) of $\widehat{A}$_f. Note that SMSE is also known as relative efficiency and CP for each AUC estimator was calculated using the median of the sample estimators of the corresponding asymptotic variances.

		n=200				n=2000
Scenario	Estimators	Bias	SVar	SMSE	CP	Bias	SVar	SMSE	CP
I	$\widehat{A}$f	0.000	1.000	1.000	0.95	0.000	1.000	1.000	0.95
	$\widehat{A}$iv	−0.006	2.997	3.046	0.93	−0.009	3.167	3.973	0.92
	$\widehat{A}$fp	−0.064	11.949	15.276	0.74	−0.067	63.574	104.644	0.51
	$\widehat{A}$ig	−0.027	5.138	5.712	0.85	−0.018	4.132	6.997	0.80
	$\widehat{A}$v	−0.062	3.449	6.615	0.80	−0.059	3.080	34.647	0.10
II	$\widehat{A}$f	0.000	1.000	1.000	0.95	0.000	1.000	1.000	0.95
	$\widehat{A}$iv	−0.003	4.551	4.557	0.92	−0.017	3.833	6.588	0.88
	$\widehat{A}$fp	−0.007	8.766	8.811	0.84	−0.010	14.601	15.585	0.82
	$\widehat{A}$ig	0.006	5.748	5.776	0.91	0.001	5.773	5.778	0.91
	$\widehat{A}$v	−0.029	4.632	5.293	0.89	−0.032	4.871	13.968	0.69
III	$\widehat{A}$f	0.000	1.000	1.000	0.95	0.000	1.000	1.000	0.96
	$\widehat{A}$iv	−0.004	2.307	2.317	0.95	−0.009	2.292	2.970	0.93
	$\widehat{A}$fp	−0.059	9.031	11.478	0.72	−0.058	45.982	71.221	0.80
	$\widehat{A}$ig	−0.015	3.589	3.757	0.88	−0.019	3.424	6.148	0.80
	$\widehat{A}$v	−0.062	2.907	5.657	0.79	−0.063	2.525	31.856	0.10
IV	$\widehat{A}$f	0.000	1.000	0.95	1.000	0.000	1.000	1.00	0.95
	$\widehat{A}$iv	0.020	6.065	6.434	0.93	0.035	6.196	18.72	0.72
	$\widehat{A}$fp	−0.038	11.557	12.972	0.82	−0.022	32.353	37.08	0.77
	$\widehat{A}$ig	−0.044	9.874	11.714	0.82	−0.040	8.482	24.95	0.63
	$\widehat{A}$v	−0.055	5.837	8.788	0.86	−0.056	4.992	36.91	0.34
V	$\widehat{A}$f	0.000	1.000	1.000	0.95	0.000	1.000	1.00	0.95
	$\widehat{A}$iv	0.016	6.520	6.760	0.91	0.034	7.604	19.44	0.70
	$\widehat{A}$fp	−0.034	11.368	12.486	0.83	−0.039	47.822	63.30	0.62
	$\widehat{A}$ig	−0.041	9.568	11.203	0.83	−0.037	7.928	22.08	0.67
	$\widehat{A}$v	−0.055	5.837	8.788	0.86	−0.056	4.992	36.91	0.37
VI	$\widehat{A}$f	0.000	1.000	1.000	0.95	0.000	1.000	1.00	0.96
	$\widehat{A}$iv	−0.049	5.109	6.756	0.89	−0.041	4.875	16.24	0.79
	$\widehat{A}$fp	−0.049	6.659	8.313	0.83	−0.044	10.281	23.87	0.75
	$\widehat{A}$ig	−0.053	6.777	8.741	0.83	−0.044	5.807	18.93	0.82
	$\widehat{A}$v	−0.079	3.712	8.070	0.83	−0.069	3.671	36.08	0.52

Table 3:

Variance comparison. SV, AV stand for sample variance and the median of estimated asymptotic variance for $\widehat{A}$_iv.

Scenario	n	1000 × SV	1000 × AV
I	200	3.7	3.5
	2000	0.4	0.3
II	200	5.6	5.3
	2000	0.4	0.5
III	200	3.2	3.1
	2000	0.3	0.3
IV	200	6.2	5.0
	2000	0.6	0.6
V	200	6.7	5.0
	2000	0.7	0.6
VI	200	7.3	7.9
	2000	0.7	0.9

1. When the verification model is correctly specified (Scenarios I and III), the proposed $\widehat{A}$_iv estimator achieves the best or almost the best performance. Specifically, for nonignorable cases, $\widehat{A}$_iv has the smallest bias and smallest variance. Also, $\widehat{A}$_iv achieved a closer coverage probability to the nominal level than $\widehat{A}$_v, $\widehat{A}$_ig and $\widehat{A}$_fp.

2. $\widehat{A}$_iv is robust to the disease model (Scenario III). Note that in the disease model, the true covariate’s effect is cubic while we fit a linear covariate’s effect. $\widehat{A}$_iv is superior than $\widehat{A}$_v, $\widehat{A}$_ig and $\widehat{A}$_fp.

3. When the verification model is incorrectly specified (Scenarios II, IV, V and VI), in the sense of bias or variance $\widehat{A}$_iv does not always outperform other estimators, but in the sense of MSE and coverage probability, it outperforms others. Moreover, the proposed estimator generally has similar bias as $\widehat{A}$_fp but is more efficient than $\widehat{A}$_fp.

4. Further extensive simulation has been shown in the supplementary document, including scenarios similar to Scenario III but with different verification proportion and different disease prevalence. The proposed estimator $\widehat{A}$_iv is superior in these studies too.

The asymptotic variance of $\widehat{A}$_iv is compared with its sample variance in Table 3. When the verification model is correct (scenario I and III), the asymptotic variance is very close to the sample variance: When the verification model is incorrectly specified, the asymptotic variance biased slightly. It indicates that the variance estimation is slightly sensitive to the specification of the verification model.

4.2. Example

We use the Alzheimer’s Disease (AD) data set collected by the National Alzheimer’s Coordinating Center (NACC) to illustrate the proposed method. Liu and Zhou (2010) have analysed an earlier version of this data; the current data includes the Uniform Data Set (UDS) data up through the September 2014 freeze. Here we want to study the diagnostic ability of a medical test Mini Mental State Examination (MMSE) in detecting AD. MMSE ranges from 0 to 30, with lower score corresponding to a larger risk of having cognitive impairment. The gold standard for AD is based on a primary neuropathological diagnostic test (NPTH), which requires brain autopsy; only dead people can have disease verification. Also, some patients or their family would not like to accept brain autopsy. These are the main reasons for missing disease status; only about 10% patients have been verified. Originally, there are several values of NPTH, for example, “Normal”, “definitely AD”, “probably AD”, “possible AD”, etc; we define AD as “definitely AD” (Y =1) and treat others as control sample (Y = 0). Five covariants, AGE, SEX, marriage status (MRGS), Depression (DEP) and Parkinson’s disease (PD) are considered, which are known to be related to AD or the disease verification. After removing missing values in MMSE and covariants, 52,673 samples remains, in which 5,707 samples were verified by autopsy. In the verified sample, 55% are AD. We also categorize MRGS into two groups; coding “never married” as 1 and the others as 0. The boxplots for MMSE are shown in Figure 1, which shows that lower MMSE scores are more likely to be associated with AD.

Figure 1:

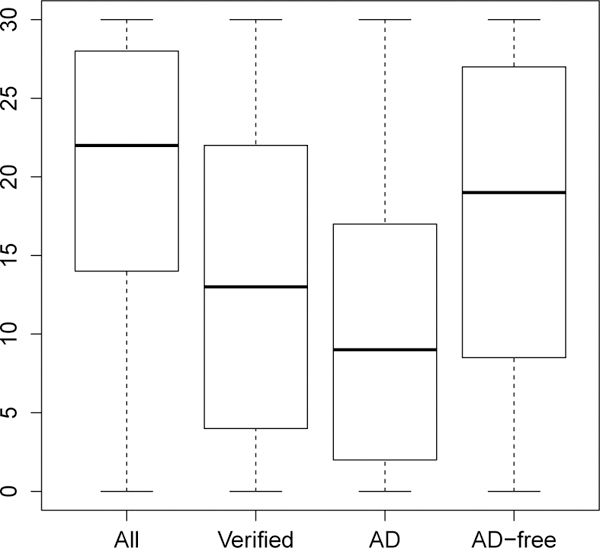
Boxplots for MMSE. “All” — using all samples, “Verified” — using all verified samples, “AD” — using verified AD samples, and “AD-free” — using verified AD-free samples.

We fit the following logistic regression model as the disease model for verified samples:

$$Pr\left(Y_i=1|X_i,{\mathit{V}}_i,R_i=1\right)=\frac{1}{1+exp\left({\mu }_1+{\mu }_2{X}_i+{\mu }_3^{\prime }{\mathit{V}}_i\right)},$$ (4.1)

where V represents the vector of covariates (AGE, SEX, MRGS, PD, DEP), R indicates whether X is observed, and Y and X stand for MMSE and true disease status, respectively. The verification model is also a logistic regression model:

$${\pi }_i=Pr\left(R_i=1|X_i,{\mathit{V}}_i,Y_i\right)=\frac{1}{1+exp\left({\psi }_1+{\psi }_2{X}_i+{\mathit{\psi }}_3^{\prime }{\mathit{V}}_{1i}+\beta Y_i\right)},$$ (4.2)

where V₁ are the covariates without the selected IV. For demonstration purpose, we simply select AGE as the instrument variable. Therefore, V₁ stands for the reduced covariate vector (MRGS, SEX, PD, DEP). In the supplementary material, we also extended out study by using different variable as IV. Most of those studies lead to nonsignificant β or non-convergence, which indicates that there might be no good IV existing for some studies in practice.

The estimated parameters, standard errors and their p-values are listed in Table 4; the p-value is decided by a Wald-statistic and the asymptotic variances calculated according to Lemma 1.1 in the supplementary material. All parameters except DEP in the diseased model are significant. The nonignorable parameter β is estimated to be −3.777 (two-side p-value is about 0.10), which indicates that the missing mechanism may be nonignorable. β = −3.777 indicates that the odds of verification for diseased individuals is about exp(3.78) = 43 units larger than it for non-diseased individuals with the same values of (MRGS, SEX, PD, DEP).

Table 4:

Coefficients, Standard error (SE) and p-values.

	Disease model			Verification model
	coefficient	SE	P-value	coefficient	SE	P-value
Intercept	1.068	0.244	<0.001	2.358	0.222	<0.001
MMSE (X)	−0.079	0.003	<0.001	0.043	0.008	<0.001
MRGS	−0.125	0.068	0.065	0.203	0.054	<0.001
PD	−0.994	0.107	<0.001	−0.994	0.107	<0.001
SEX	−0.309	0.064	<0.001	−0.755	0.036	<0.001
AGE	0.005	0.003	0.085	—
DEP	−0.076	0.086	0.375	0.195	0.053	<0.001
AD (Y)	—			−3.777	2.306	0.104

The AUC value calculated using only verified samples is 0.699 (95% Confidence Interval (CI): 0.686, 0.713), and the proposed estimators $\widehat{A}$_iv = 0.786 (95% CI: 0.754, 0.818). The 95% CI was constructed using normal distribution. There is a significant difference between our AUC estimators and the AUC calculated only using verified samples (Wald test, p-value < 0.001). Note that, the full parametric model in this example is not converged and based on our study, using AGE as IV is just for an illustrative example, there might not be good choices of IV in this data example.

5. Concluding Remarks

We propose a new parametric approach using an instrumental variable to estimate AUC in the context of nonignorable verification bias. We make parametric assumptions on the verificaiton model and on the disease model for the observed samples only, which is easier to verify in practice than the disease model for the whole sample. The nonignorability parameter is estimated through mean score equations and joint estimation of disease probability and verification probability is avoided. An inverse probability weighting estimator of AUC is considered and its asymptotic properties are established.

Simulation studies show that the proposed method is efficient and rather robust to the incorrect specifications of the disease model, but not to the incorrect specification of the verification model. Even when the verification model is misspecified, the suggested estimator is comparable to existing estimators for nonignorable cases in the sense of similar bias, but outperforms the existing method in the sense of efficiency. In practice, because it is hard to specify verification model correctly, sensitivity analyses suggested by Rotnitzky, Faraggi and Schisterman (2006) can be used to complement the non-robustness. An alternative choice involves the treatment of nonparametric techniques such as kernel regression models for the disease model. Also, Bayesian modeling coupled with sensitivity analyses in the context of missing data (Daniels and Hogan, 2008) can also be considered for further analyses. Such extension can be a topic of future study.

The proposed method is based on the instrumental variable (IV) assumption. We use the variable which has the lowest marginal correlation with R (the verification status) as the IV in our simulation study, it leads to good performance. This method is not ideal but is simple. Selecting IV is never a easy job in practice. A good practicable example of IV choice was introduced by Wang, Shao and Kim (2014), for a study of a data set from the Korean Labor and Income Panel Survey (KLIPS), in which the monthly income of 2506 regular wage earners in 2006 was of interest, and gender, age, level of education and the monthly income in 2005 were the covariates. About 35% missing values of the interested variable and all covariate values are observed. In such study, the monthly income in 2005 is a good choice of IV because it is highly correlated with the income in 2006 but it seems to be independent of the missingness given the other covariates. We note that if an IV is inappropriately chosen, the bias in AUC estimation could be substantial and the model could have nonconvergence problems (shown in the data example). We need more future studies on choosing IV.

After estimating the verification probability and disease probability for each individual, other types of AUC estimators can also be used, for example, the other AUC estimators introduced in Alonzo and Pepe (2005) or Liu and Zhou (2010), such as using full imputation (FI) method or mean score imputation (MSI) method instead of inverse probability weighting (IPW) method. The proposed Instrumental Variable method can also be used for FL and MSI. Liu and Zhou (2010) noticed that FI and MSI method generally performed better than IPW method. One probable reason may be that for IPW method, there are 1/$\widehat{\pi }$_i terms, which may produce very extreme values for the AUC estimator and its corresponding asymptotic variance estimator if the $\widehat{\pi }$_i is very small. In addition to AUC, the proposed method can be easily extended to the estimation of the other indexes related to ROC curve, such as sensitivity, specificity, and the partial area under the curve (McClish, 1989) as well as the modified area under the Curve (Yu, Chang and Park, 2014).