Abstract
Rationale and Objectives:
Breast segmentation using the U-net architecture was implemented and tested in independent validation datasets to quantify fibroglandular tissue volume in breast MRI.
Materials and Methods:
Two datasets were used. The training set was MRI of 286 patients with unilateral breast cancer. The segmentation was done on the contralateral normal breasts. The ground truth for the breast and fibroglandular tissue (FGT) was obtained by using a template-based segmentation method. The U-net deep learning algorithm was implemented to analyze the training set, and the final model was obtained using 10-fold cross-validation. The independent validation set was MRI of 28 normal volunteers acquired using four different MR scanners. Dice Similarity Coefficient (DSC), voxel-based accuracy and Pearson’s correlation were used to evaluate the performance.
Results:
For the 10-fold cross-validation in the initial training set of 286 patients, the DSC range was 0.83-0.98 (mean 0.95±0.02) for breast and 0.73-0.97 (mean 0.91±0.03) for FGT; and the accuracy range was 0.92-0.99 (mean 0.98±0.01) for breast and 0.87-0.99 (mean 0.97±0.01) for FGT. For the entire 224 testing breasts of the 28 normal volunteers in the validation datasets, the mean DSC was 0.86±0.05 for breast, 0.83±0.06 for FGT; and the mean accuracy was 0.94±0.03 for breast and 0.93±0.04 for FGT. The testing results for MRI acquired using 4 different scanners were comparable.
Conclusions:
Deep learning based on the U-net algorithm can achieve accurate segmentation results for the breast and FGT on MRI. It may provide a reliable and efficient method to process large number of MR images for quantitative analysis of breast density.
1. INTRODUCTION
Breast density is an established risk factor for the development of breast cancer. Measurement of breast density is mostly performed on two-dimensional (2D) mammography. While two quantitative volumetric analysis tools (Volpara and Quantra) are commercially available to measure dense tissue volume, studies have found that they tend to underestimate the percent breast density in women with dense breast (1, 2). Furthermore, differences between Volpara and Quantra alone have been found to be as high as 14% (1). A fundamental limiting factor of all mammography-based density quantification methods is the characteristic 2D overlapping tissues on mammography.
Breast MRI is an established clinical imaging modality for high-risk screening, diagnosis, preoperative staging and neoadjuvant therapy response evaluation. The most common clinical indication was diagnostic evaluation (40.3%), followed by screening (31.7%) (2). Passage of the breast density notification law has had a major impact on MRI utilization, showing increases from 8.5% to 21.1% in non-high-risk women after the law in California went into effect (3). Furthermore, as early results of the abbreviated MRI protocols are promising, this may reduce the cost of MRI for patients allowing for wider use in women with dense breasts and women with mild to moderate cancer risk for screening (4).
The increasing popularity of breast MRIs have led to the fast accumulation of large breast MRI database. This offers a great opportunity to address some clinical questions regarding the use of breast density, e.g. whether the volumetric density can be incorporated into risk models to improve the prediction accuracy (5), or be used as a surrogate biomarker to predict hormonal treatment efficacy (6, 7). Since MRI is a three-dimensional (3D) imaging modality with distinctive tissue contrast, it can be used to measure the fibroglandular tissue (FGT) volume. However, because many imaging slices are acquired in one MRI, an efficient, objective, and reliable segmentation method is needed. Various semi-automatic (8) and automatic (9-11) breast MRI segmentation methods have been developed in T1 weighted (12) or Dixon-based images (12, 13). Although the results are promising, errors due to blurred contrast and bias-field are common and manual inspection and correction is often needed to ensure accuracy.
In recent years, deep learning algorithms have been widely applied for classification applications, and they also provided an efficient method for organ and tissue segmentation, including the brain (14, 15), head and neck (16), chest and heart (17, 18), abdomen and pelvis (19-21), breast (22-24), and bone and joint (25). Since most medical images have high resolutions, patch-based approach is commonly employed for segmentation, where images are divided into small patches with a specified size as the input of the neural network (24, 26, 27). This method can fully utilize the local information of the focused area. However, for large structures like the entire organ, a large receptive field for pixel classification is required (28). The Fully-Convolutional Residual Neural Network (FC-RNN), commonly noted as U-net, is another algorithm that can search a large area (16, 22, 23, 25). and has been shown suitable for segmenting the whole breast and FGT (22, 23).
The purpose of this study was to develop and validate a deep-learning segmentation method based on the U-net architecture, first for breast segmentation within whole image, and then for FGT segmentation within the breast. The developed model using a training dataset was tested in independent validation datasets acquired using four different MR systems.
2. MATERIALS AND METHODS
2A. Training dataset
The initial dataset used for training included 286 patients with unilateral estrogen receptor positive, HER2-negative, lymph node-negative invasive breast cancer (median age, 49 years; range, 30–80 years), as reported in a recent publication (29). In this study only the contralateral normal breast was analyzed. MRI was performed on a 3T Siemens Trio-Tim scanner (Erlangen, Germany), and the pre-contrast T1-weighted images without fat suppression were used for segmentation. The Institutional Review Board approved this retrospective study and requirement for informed consent was waived.
2B. Independent validation datasets
The validation dataset included 28 healthy volunteers (age 20–64, mean 35 years old), as described in a previous paper (30). These women were recruited to participate in a non-contrast breast density study. Each subject was scanned using four different MR scanners in two institutions, including GE Signa-HDx 1.5T, GE Signa-HDx 3T (GE Healthcare, Milwaukee, WI), Philips Achieva 3.0T TX (Philips Medical Systems, Eindhoven, Netherlands) and Siemens Symphony 1.5T TIM (Siemens, Erlangen, Germany). Non-contrast T1-weighted images without fat suppression were used for segmentation. Since both left and right breasts were normal, they were analyzed separately, so there was a total of 56 breasts. The validation was done using the 56 breasts acquired by each scanner first, and then using all 224 breasts acquired by all 4 scanners together. With a cases number of more than 200, it should be sufficient to do independent validation.
2C. Ground truth segmentation
The ground truth was generated using a template-based automatic breast segmentation method (9). In most breast MR scans, while breasts presented very different shapes and sizes, the chest region including the lung and the heart could be detected at similar locations with similar shape and intensity. These features were used to locate and segment out the chest region to isolate the breast. After the breast was segmented, the next step was to differentiate FGT from fat. A correction method combined Nonparametric Nonuniformity Normalization (N3) and Fuzzy C-means (FCM) algorithms was used to correct the field inhomogeneity (bias-field) within the imaging region (31). After the bias-field correction, K-means clustering was used to separate FGT from fatty tissues on pixel levels, with the number of clusters determined by the operator (KTC) who was a research physician and had one year of experience in performing breast segmentation. Since our group has been devoting to the development of breast MRI segmentation methods since 2008 (32) and many papers have been published, the operator knew the most likely clusters number to be used to accurately segment the fibroglandular tissue. In some cases, due to issues of tissue contrast, the mostly applied clusters number might need to be modified to produce the most accurate segmentation results. The segmentation results were then inspected by a radiologist, who had 12 years of experience in interpreting breast MR images, and if necessary, manually corrected. The manual correction, if needed, usually happened in the upper and lower margin of the breast tissue and in the breast areas showing inhomogeneous signal intensity. Not all subjects needed the correction. For those studies which needed correction, the number of slices ranged from 1 to 5 in each subject. This template-based segmentation has a very good reproducibility. The average interreader variability of breast and FGT were 3.7% and 3.9%, respectively (32).
The results were used as the ground truth for neural network training and independent validation.
2D. Deep learning using U-net architecture
The goal was to use U-net to separate three-class labels on each MR image, including (1) fat tissue and (2) FGT inside the breast, and (3) all non-breast tissues outside the breast. The first U-net was used to segment the breast from the entire image. Then, within the obtained breast mask, the second U-net was used to differentiate fat and FGT. The left and right breasts were separated using the centerline, and a square matrix containing one breast was cropped and used as the input. The pixel intensity on the cropped image was normalized to z-score maps (mean=0, and standard deviation = 1).
The U-net is a fully connected convolutional residual network (Figure 1) (28), which consists of convolution and max-pooling layers at the descending part (the left component of U), and convolution and up-sampling layers at ascending part (the right component of U). In the down-sampling stage, the input image size is divided by the size of the max-pooling kernel size at each max-pooling layer. In the up-sampling stage, the input image size is increased by the operations, which are performed and implemented by convolutions, where kernel weights are learned during training. The arrows between the two components of the U show the incorporation of the information available at the down-sampling stage into the up-sampling stage, by copying the outputs of convolution layers from descending components to the corresponding ascending components. In this way, fine-detailed information captured in descending part of the network is used at the ascending part. The output images share the same size of the input images.
Figure 1.
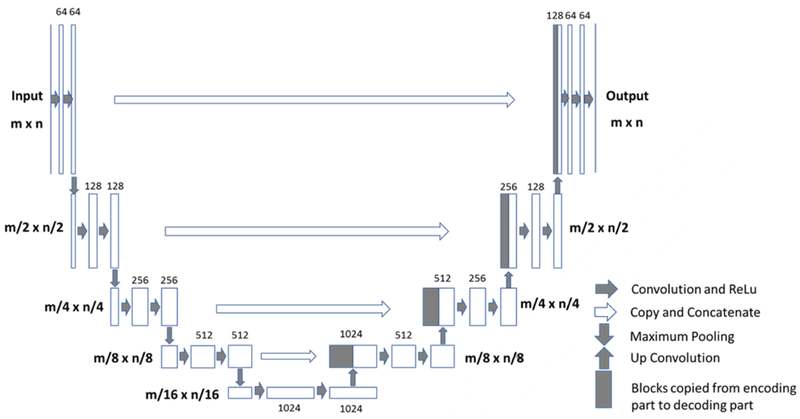
Architecture of the Fully-Convolutional Residual Neural Network “U-net”. The input of the network is the normalized image and the output is the probability map of the segmentation result. The U-net consists of convolution and max-pooling layers at the descending phase (the initial part of the U), as down-sampling stage. At the ascending part of the U network, up-sampling operations are performed. The arrows between the two parts show the incorporation of the information available at the down-sampling steps into the up-sampling operations performed in the ascending part of the network.
In this study, there were four down-sampling and four up-sampling blocks. In each downsampling block, two convolutional layers with a kernel size of 3 × 3 were each followed by a rectified-linear unit (ReLu) for nonlinearity (33), and then followed by a max-pooling layer with 2 × 2 kernel size. In the up-sampling blocks, the image was up-convolved by a factor of two using nearest neighbor interpolation, followed by a convolution layer with a kernel size of 2 × 2. The output of the corresponding down-sampling layer was concatenated. Then, two convolutional layers, each followed by a ReLu, was applied to this concatenated image. During the training process, the He initialization method was used to initialize the weights of the network and the optimizer was Adam with a learning rate = 0.001 (34). Finally, a convolutional and a sigmoid unit layer was added to produce probability maps for each class which correspond to the input image size. A threshold of 0.5 was utilized to determine the final segmented mask. The training processes included a total of 60,000 iterations before convergence. L2 regularization was used to prevent overfitting. Also, some background noise was added into the original images to do the image augmentation. Software code for this study was written in Python 3.5 using the open-source TensorFlow 1.0 library (Apache 2.0 license). Experiments were performed on a GPU-optimized workstation with a single NVIDIA GeForce GTX Titan X (12GB, Maxwell architecture).
2E. Evaluation
In the initial training set of 286 patients, a 10-fold cross-validation was used to evaluate the performance of the U-net model. The final model was developed by training the 286 patient dataset with the hyperparameters which were optimized from the 10-fold cross-validation. The obtained model was then applied to segment the MRI of 28 healthy volunteers in the independent validation datasets. The ground truth for each case was available for comparison, and the segmentation performance was evaluated using the Dice Similarity Coefficient (DSC) and the overall accuracy based on all pixels(35). For example, the pixel accuracy of FGT segmentation was the correct classified pixel number over all pixel number of FGT. The algorithm was tested using 10-fold cross validation, so 10 accuracies could be calculated. The mean accuracy was the mean value of these 10 values. In addition, the Pearson’s correlation was applied to evaluate the correlation between the U-net prediction output and the ground truth volume.
3. Results
In the 10-fold cross-validation performed in the training dataset, the DSC range for breast segmentation was 0.83-0.98 (mean 0.95±0.02) and accuracy range was 0.92-0.99 (mean 0.98±0.01). For the FGT segmentation, the DSC range was 0.73-0.97 (mean 0.91±0.03) and accuracy range was 0.87-0.99 (mean 0.97±0.01). Figures 2 and 3 show the segmentation results from two women with different breast morphology and density. The correlation between the U-net prediction output and ground truth for breast volume and FGT volume are shown in Figure 4.
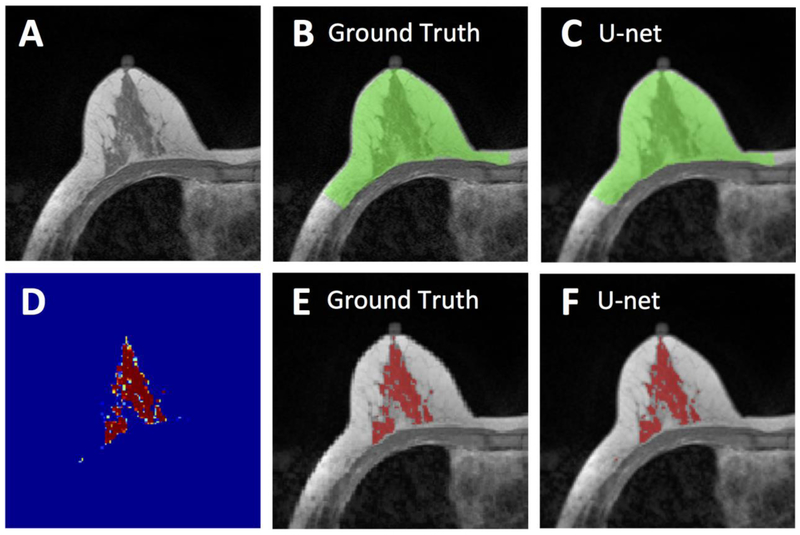
Figure 2.
Segmentation results from a 62-year-old woman with moderate breast density. A: The original non-fat-suppressed T1-weighted image. B: The ground truth breast segmentation result obtained by using template-based method, shown in green. C: The breast segmentation result generated by U-net (green). D: The generated FGT probability map by the U-net. E: The ground truth FGT segmentation result within the breast obtained by using K-means clustering after bias-field correction (shown in red). F: The FGT segmentation result generated by U-net (red). For breast segmentation, DSC is 0.99 and accuracy is 0.99. For FGT segmentation, DSC is 0.97 and accuracy is 0.99.
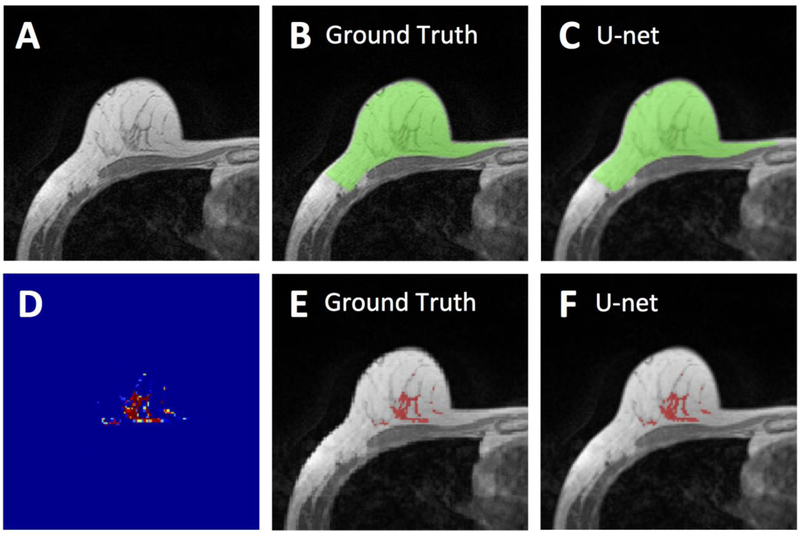
Figure 3.
Segmentation results from a 55-year-old woman with fatty breast. A: The original non-fat-suppressed T1-weighted image. B: The ground truth breast segmentation result obtained by using template-based method, shown in green. C: The breast segmentation result generated by U-net (green). D: The generated FGT probability map by the U-net. E: The ground truth FGT segmentation result within the breast obtained by using K-means clustering after bias-field correction (shown in red). F: The FGT segmentation result generated by U-net (red). For breast segmentation, DSC is 0.99 and accuracy is 0.99. For FGT segmentation, DSC is 0.94 and accuracy is 0.98.
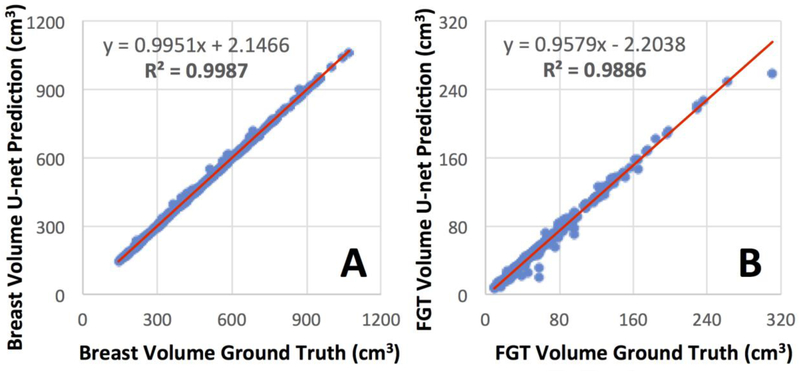
Figure 4.
Correlation of breast volume (A) and FGT volume (B) between the ground truth obtained by using the template-based segmentation and the U-net prediction.
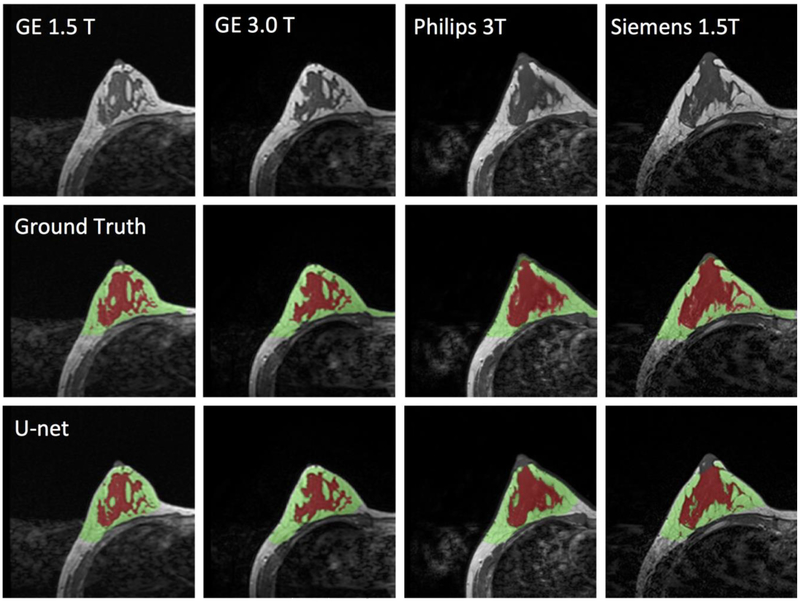
The final model obtained from the training set was applied to the independent datasets acquired from the 28 healthy women using 4 different scanners. The processing time for one case was within 10s. The DSC and accuracy for each scanner was calculated separately, and then combined for all 4 scanners together. The results are shown in Table 1. Figures 5 and 6 illustrate the segmentation results of two women with different breast morphology. The correlation between the U-net prediction output and ground truth for breast volume is shown in Figure 7. The obtained results for four different scanners were similar. The correlation coefficient r was high, in the range of 0.96-0.98. In each figure, the fitted line was very close to the unity line, and the slope was close to 1. The segmentation result for FGT volume is shown in Figure 8. The FGT segmentation results for MRI acquired using 4 different scanners were similar. The correlation coefficient r was very high, in the range of 0.97-0.99. However, using the unity line as reference, the U-net segmented FGT volume was lower compared to the ground truth, as in the two case examples demonstrated in Figures 5 and 6.
Table 1.
The dice similarity coefficient (DSC) and the accuracy for the segmentation of breast and FGT in different MR scanners.
| GE 1.5T | GE 3T | Philips 3T | Siemens 1.5T | All MRI | ||
|---|---|---|---|---|---|---|
| Dice Similarity Coefficient | ||||||
| Breast | Mean ± stdev | 0.86 ± 0.06 | 0.87 ± 0.04 | 0.86 ± 0.05 | 0.87 ± 0.06 | 0.86 ± 0.05 |
| Range | 0.56 – 0.95 | 0.54 – 0.95 | 0.50 – 0.95 | 0.58 – 0.97 | 0.50 – 0.97 | |
| FGT | Mean ± stdev | 0.84 ± 0.05 | 0.81 ± 0.07 | 0.86 ± 0.05 | 0.84 ± 0.07 | 0.83 ± 0.06 |
| Range | 0.61 – 0.96 | 0.53 – 0.94 | 0.64 – 0.94 | 0.61 – 0.94 | 0.53 – 0.96 | |
| Accuracy | ||||||
| Breast | Mean ± stdev | 0.95 ± 0.03 | 0.92 ± 0.03 | 0.92 ± 0.03 | 0.96 ± 0.04 | 0.94 ± 0.03 |
| Range | 0.73 – 0.98 | 0.72 – 0.98 | 0.69 – 0.98 | 0.73 – 0.99 | 0.69 – 0.90 | |
| FGT | Mean ± stdev | 0.92 ± 0.03 | 0.93 ± 0.03 | 0.93 ± 0.04 | 0.93 ± 0.04 | 0.93 ± 0.04 |
| Range | 0.74 – 0.98 | 0.71 – 0.97 | 0.75 – 0.97 | 0.74 – 0.97 | 0.71 – 0.98 | |
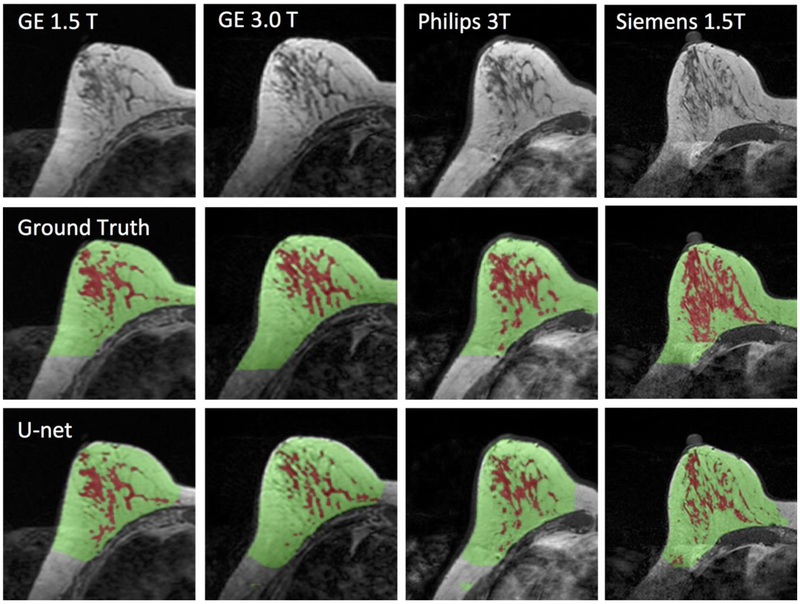
Figure 5.
Images of a 43-year-old woman with heterogeneous breast morphology acquired using the GE 1.5T, GE 3.0T, Philips 3.0T, and Siemens 1.5T systems. The top row shows the original images. The center row shows the ground truth obtained by using the template-based segmentation method. The bottom row shows the U-net prediction results. The FGT volume segmented by U-net is smaller compared to the ground truth.
Figure 6.
Images of a 29-year-old woman with dense breast acquired using the GE 1.5T, GE 3.0T, Philips 3.0T, and Siemens 1.5T systems. The top row shows the original images. The center row shows the ground truth obtained by using the template-based segmentation method. The bottom row shows the U-net prediction results.
Figure 7.
Correlation of breast volume between the ground truth obtained from the template-based segmentation method and the U-net prediction. (A) GE 1.5 T, (B) GE 3T, (C) Philips 3T, (D) Siemens 1.5T. The red line is the trend line, and the dashed black line is the unity line as reference.
Figure 8.
Correlation of FGT volume between the ground truth obtained from the template-based segmentation method and the U-net prediction. (A) GE 1.5 T, (B) GE 3T, (C) Philips 3T, (D) Siemens 1.5T. The red line is the trend line, and the dashed black line is the unity line as reference. The volume segmented by U-net is smaller compared to the ground truth.
4. Discussion
In this study, a deep-learning method based on the U-net architecture (28), for breast and FGT segmentation on MRI was implemented. To objectively test the performance of the developed method, we used independent validation datasets from MRI acquired using four scanners at two different institutions. The results showed that for both the breast and the fibroglandular tissue segmentation, high accuracy was achieved (0.98±0.01 and 0.97±0.01, respectively). When the model was applied to independent datasets for validation, the performance was also very good (accuracy >0.92). The results suggest that deep learning segmentation using U-net is feasible to perform fully automatic segmentation for the breast and FGT and yield reasonable accuracy compared to the ground truth segmented by using a template-based method verified by a radiologist.
Over the last decade, segmentation of the breast and FGT on MRI has been studied using semiautomatic (9, 32), to automatic approaches with some operator inputs (31). Recently, fully automatic breast segmentation methods have been reported and shown feasible (36-38). but still with unsatisfactory FGT segmentation (39). The processing time for these methods varies from minutes to more than half an hour, which is partially due to the need for the post-segmentation correction. In the present study, the results were compared against the ground truth for each case. Furthermore, testing independent validation datasets allows us to evaluate whether the developed segmentation method can be applied widely to other MRI datasets acquired using different imaging protocols on different MR scanners.
Unlike 2D mammography, 3D MRI provides genuine volumetric assessment of the FGT for quantification of breast density, thus it may be used to assess small changes in density over time following hormonal or chemotherapy (7, 40). Three-dimensional MR density can also be used to study breast symmetry (41), and peritumoral environment (42). Additionally, 3D MR breast and FGT segmentation method is necessary for the quantitative measurement of background parenchymal enhancement (BPE) (43, 44), which has shown to be related to the aggressiveness of the tumor, treatment response, prognosis, and breast cancer risk (45). Quantitative measurement of dense tissue volume may also be incorporated into risk prediction models to improve the accuracy of breast cancer risk predicted for each individual woman. Currently, some models have already included mammographic density as a risk factor. The value of MR density has also been proven in two large scale studies (46, 47). King et al (46) specifically states an association of increased FGT on MRI and breast cancer risk. Because of accurate fully automatic FGT segmentation in T1-weighted imaging, the quantified assessment of BPE is possible, and both King and Dontchos' work (46, 47) shows that increased quantified BPE is associated with increased breast cancer risk. With more and more large MRI datasets gradually becoming available, this will allow studies to investigate whether the inclusion of MR volumetric density into the risk models outperforms other models. Since a very large dataset needs to be analyzed, an efficient segmentation tool that can provide precise information about breast density is required.
Different deep learning approaches have been applied for automatic segmentation of normal tissues or organs (14, 15). A patch-based approach is commonly employed for segmentation, where images are divided into small patches with specified size as the input of neural network (24, 26, 27). This method can fully utilize the local information of the focused area. When an unsupervised approach was used for mammographic density segmentation, the DSC for dense tissue and fatty tissue was 0.63 and 0.95, respectively (24). However, for large structures like the entire organ, a large receptive field for pixel classification is required (28). The U-net can search a large area. Several studies have utilized U-net for medical image applications and obtained satisfactory results (22, 23). Two studies using U-net to segment FGT on sagittal and axial view MR images obtained an accuracy of 0.813, (22) and 0.85 (23), respectively.
In this present study, 286 cases were used as the initial training dataset, and ten-fold cross-validation was used to adjust the hyperparameters of the neural networks. One noticeable problem, generally seen in this study, showed that the FGT was under-segmented by the U-net (Figure 8). From other literature, the issue of the underestimation in FGT segmentation has not been addressed. Hence, this should not be the flaw of U-net. As this trend was consistent for all 4 scanners, this appeared to be a systematic bias problem, and not due to sporadic variations. The ground truth in FGT segmentation was performed by the operator, who had to select the cluster numbers to differentiate FGT from fat based on their image intensities. For example, when using a total cluster number of 6 with 3 for FGT, the segmentation appeared reasonable. However, when using a total cluster number of 5 with 2 for FGT, the segmentation quality was very likely to be reasonable as well, but this would result in a lower FGT volume. As shown in the two case examples illustrated in Figures 5 and 6, the U-net segmented FGT volume was lower; however, when visually inspecting the segmentation results separately, both appeared reasonable. Therefore, although U-net FGT volume was lower than manually segmented volume, this did not mean that there was an error. In fact, we believe that the fully automatic method using deep learning can provide an objective method not affected by the operator’s judgment, and it has a potential to replace the semi-automatic method and eliminate the operator’s input.
Another strength of deep learning was the ability to handle field inhomogeneity, or bias-field. Intensity inhomogeneity often presented as a smooth intensity variation across the image is mainly due to poor radio frequency (RF) coil uniformity, gradient-driven eddy currents, and patient’s anatomy inside and outside the field of view (48). For conventional segmentation algorithms, retrospective correction methods including filtering (39), or bias field estimation (31), were commonly used. However, for medical images with high noise level or severe intensity inhomogeneity, this problem could not be completely eliminated. In our experience, the images at caudal and cranial ends of an MRI volume often had a low signal intensity, and the bias-field correction was very important for segmentation on these slices. Our results showed that U-net methods were minimally affected by the bias field, although no specific bias-field correction was applied as a prior step. This indicated that U-net was able to learn the bias field and make corrections. However, other studies (22) found that bias field correction would improve the segmentation results and had shown specific examples. Ha et al. (22) used smaller dataset and different modality. Thus the importance of the bias field correction cannot be evaluated based on different datasets. We believe if the inhomogeneity is very high or higher than the mean intensity, bias field correction will definitely improve the results.
Some limitations existed in our study. First, we only analyzed the non-fat-suppressed T1-weighted MR images, and the developed segmentation method cannot be directly applied to images acquired using other sequences, such as Dixon-based images (12, 13). Second, all datasets in this study were from Asian women who were known to have denser breast with different morphological features compared to Western women. To increase the model robustness, datasets from Caucasian and other ethnic groups of women need to be tested. The current U-net model was for 2D segmentation using each individual slices as inputs. In the future, the architecture can be extended for 3D segmentation which will involve more trainable parameters, but more subjects are required.
5. CONCLUSION
In summary, we presented deep-learning approaches based on the U-net architecture for breast and FGT segmentation on MRI. This method showed good segmentation accuracy, and there was no need to do the post-processing correction. With further refinement of the methodology and validation, this deep learning-based segmentation method may provide an accurate and efficient means to quantify FGT volume for evaluation of breast density.
ACKNOWLEDGEMENT
This study is supported in part by NIH R01 CA127927, R21 CA170955, R21 CA208938, and R03 CA136071, and a Basic Science Research Program through the National Research Foundation of Korea (NRF, Korea) funded by the Ministry of Education (NRF-2017R1D1A1B03035995).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Brandt KR, Scott CG, Ma L, Mahmoudzadeh AP, Jensen MR, Whaley DH, Wu FF, Malkov S, Hruska CB, Norman AD. Comparison of clinical and automated breast density measurements: implications for risk prediction and supplemental screening. Radiology 2015;279(3):710–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wernli KJ, DeMartini WB, Ichikawa L, Lehman CD, Onega T, Kerlikowske K, Henderson LM, Geller BM, Hofmann M, Yankaskas BC. Patterns of breast magnetic resonance imaging use in community practice. JAMA internal medicine 2014;174(1):125–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ram S, Sarma N, López JE, Liu Y, Li C-S, Aminololama-Shakeri S. Impact of the California Breast Density Law on Screening Breast MR Utilization, Provider Ordering Practices, and Patient Demographics. Journal of the American College of Radiology 2018;15(4):594–600. [DOI] [PubMed] [Google Scholar]
- 4.Kuhl CK, Schrading S, Strobel K, Schild HH, Hilgers R-D, Bieling HB. Abbreviated breast magnetic resonance imaging (MRI): first postcontrast subtracted images and maximum-intensity projection—a novel approach to breast cancer screening with MRI. Journal of Clinical Oncology 2014;32(22):2304–2310. [DOI] [PubMed] [Google Scholar]
- 5.Kerlikowske K, Ma L, Scott CG, Mahmoudzadeh AP, Jensen MR, Sprague BL, Henderson LM, Pankratz VS, Cummings SR, Miglioretti DL. Combining quantitative and qualitative breast density measures to assess breast cancer risk. Breast Cancer Research 2017;19(1):97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lundberg FE, Johansson AL, Rodriguez-Wallberg K, Brand JS, Czene K, Hall P, Iliadou AN. Association of infertility and fertility treatment with mammographic density in a large screening-based cohort of women: a cross-sectional study. Breast Cancer Research 2016;18(1):36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chen J-H, Chang Y-C, Chang D, Wang Y-T, Nie K, Chang R-F, Nalcioglu O, Huang C-S, Su M-Y. Reduction of breast density following tamoxifen treatment evaluated by 3-D MRI: preliminary study. Magnetic resonance imaging 2011;29(1):91–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nie K, Chen J-H, Hon JY, Chu Y, Nalcioglu O, Su M-Y. Quantitative analysis of lesion morphology and texture features for diagnostic prediction in breast MRI. Academic radiology 2008;15(12):1513–1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lin M, Chen JH, Wang X, Chan S, Chen S, Su MY. Template-based automatic breast segmentation on MRI by excluding the chest region. Medical physics 2013;40(12). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Petridou E, Kibiro M, Gladwell C, Malcolm P, Toms A, Juette A, Borga M, Leinhard OD, Romu T, Kasmai B. Breast fat volume measurement using wide-bore 3 T MRI: comparison of traditional mammographic density evaluation with MRI density measurements using automatic segmentation. Clinical radiology 2017;72(7):565–572. [DOI] [PubMed] [Google Scholar]
- 11.Ribes S, Didierlaurent D, Decoster N, Gonneau E, Risser L, Feillel V, Caselles O. Automatic segmentation of breast MR images through a Markov random field statistical model. IEEE transactions on medical imaging 2014;33(10):1986–1996. [DOI] [PubMed] [Google Scholar]
- 12.Clendenen TV, Zeleniuch-Jacquotte A, Moy L, Pike MC, Rusinek H, Kim S. Comparison of 3-point dixon imaging and fuzzy C-means clustering methods for breast density measurement. Journal of Magnetic Resonance Imaging 2013;38(2):474–481. [DOI] [PubMed] [Google Scholar]
- 13.Doran SJ, Hipwell JH, Denholm R, Eiben B, Busana M, Hawkes DJ, Leach MO, Silva IdS. Breast MRI segmentation for density estimation: Do different methods give the same results and how much do differences matter? Medical physics 2017;44(9):4573–4592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen H, Dou Q, Yu L, Qin J, Heng P-A. VoxResNet: Deep voxelwise residual networks for brain segmentation from 3D MR images. Neuroimage 2017. [DOI] [PubMed] [Google Scholar]
- 15.Moeskops P, de Bresser J, Kuijf HJ, Mendrik AM, Biessels GJ, Pluim JP, Išgum I. Evaluation of a deep learning approach for the segmentation of brain tissues and white matter hyperintensities of presumed vascular origin in MRI. Neuroimage: Clinical 2018;17:251–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tong N, Gou S, Yang S, Ruan D, Sheng K. Fully Automatic Multi-Organ Segmentation for Head and Neck Cancer Radiotherapy Using Shape Representation Model Constrained Fully Convolutional Neural Networks. Medical physics 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Commandeur F, Goeller M, Betancur J, Cadet S, Doris M, Chen X, Berman DS, Slomka PJ, Tamarappoo BK, Dey D. Deep learning for quantification of epicardial and thoracic adipose tissue from non-contrast CT. IEEE Transactions on Medical Imaging 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Oktay O, Ferrante E, Kamnitsas K, Heinrich M, Bai W, Caballero J, Cook SA, de Marvao A, Dawes T, O‘Regan DP. Anatomically constrained neural networks (ACNNs): application to cardiac image enhancement and segmentation. IEEE transactions on medical imaging 2018;37(2):384–395. [DOI] [PubMed] [Google Scholar]
- 19.He K, Cao X, Shi Y, Nie D, Gao Y, Shen D. Pelvic Organ Segmentation Using Distinctive Curve Guided Fully Convolutional Networks. IEEE transactions on medical imaging 2018. [DOI] [PubMed] [Google Scholar]
- 20.Gibson E, Giganti F, Hu Y, Bonmati E, Bandula S, Gurusamy K, Davidson B, Pereira SP, Clarkson MJ, Barratt DC. Automatic multi-organ segmentation on abdominal CT with dense v-networks. IEEE Transactions on Medical Imaging 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lu F, Wu F, Hu P, Peng Z, Kong D. Automatic 3D liver location and segmentation via convolutional neural network and graph cut. International journal of computer assisted radiology and surgery 2017;12(2):171–182. [DOI] [PubMed] [Google Scholar]
- 22.Ha R, Chang P, Mema E, Mutasa S, Karcich J, Wynn RT, Liu MZ, Jambawalikar S. Fully Automated convolutional neural network method for quantification of breast MRI fibroglandular tissue and background parenchymal enhancement. Journal of digital imaging 2018:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dalmiş MU, Litjens G, Holland K, Setio A, Mann R, Karssemeijer N, Gubern-Mérida A. Using deep learning to segment breast and fibroglandular tissue in MRI volumes. Medical physics 2017;44(2):533–546. [DOI] [PubMed] [Google Scholar]
- 24.Kallenberg M, Petersen K, Nielsen M, Ng AY, Diao P, Igel C, Vachon CM, Holland K, Winkel RR, Karssemeijer N. Unsupervised deep learning applied to breast density segmentation and mammographic risk scoring. IEEE transactions on medical imaging 2016;35(5):1322–1331. [DOI] [PubMed] [Google Scholar]
- 25.Zhou Z, Zhao G, Kijowski R, Liu F. Deep convolutional neural network for segmentation of knee joint anatomy. Magnetic resonance in medicine 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang J, Fang Z, Lang N, Yuan H, Su M-Y, Baldi P. A multi-resolution approach for spinal metastasis detection using deep Siamese neural networks. Computers in Biology and Medicine 2017;84:137–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Trebeschi S, van Griethuysen JJ, Lambregts DM, Lahaye MJ, Parmer C, Bakers FC, Peters NH, Beets-Tan RG, Aerts HJ. Deep learning for fully-automated localization and segmentation of rectal cancer on multiparametric MR. Scientific reports 2017;7(1):5301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention: Springer, 2015; p. 234–241. [Google Scholar]
- 29.Shin GW, Zhang Y, Kim MJ, Su MY, Kim EK, Moon HJ, Yoon JH, Park VY. Role of dynamic contrast-enhanced MRI in evaluating the association between contralateral parenchymal enhancement and survival outcome in ER-positive, HER2-negative, node-negative invasive breast cancer. Journal of Magnetic Resonance Imaging 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen JH, Chan S, Liu YJ, Yeh DC, Chang CK, Chen LK, Pan WF, Kuo CC, Lin M, Chang DH. Consistency of breast density measured from the same women in four different MR scanners. Medical physics 2012;39(8):4886–4895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lin M, Chan S, Chen JH, Chang D, Nie K, Chen ST, Lin CJ, Shih TC, Nalcioglu O, Su MY. A new bias field correction method combining N3 and FCM for improved segmentation of breast density on MRI. Medical physics 2011;38(1):5–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nie K, Chen JH, Chan S, Chau MKI, Yu HJ, Bahn S, Tseng T, Nalcioglu O, Su MY. Development of a quantitative method for analysis of breast density based on three-dimensional breast MRI. Medical physics 2008;35(12):5253–5262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nair V, Hinton GE. Rectified linear units improve restricted boltzmann machines. Proceedings of the 27th international conference on machine learning (ICML-10)2010; p. 807–814. [Google Scholar]
- 34.Kingma D, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv: 14126980 2014. [Google Scholar]
- 35.Zou KH, Warfield SK, Bharatha A, Tempany CM, Kaus MR, Haker SJ Wells WM III, Jolesz FA, Kikinis R. Statistical validation of image segmentation quality based on a spatial overlap index1: scientific reports. Academic radiology 2004;11(2):178–1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ertas G, Doran SJ, Leach MO. A computerized volumetric segmentation method applicable to multi-centre MRI data to support computer-aided breast tissue analysis, density assessment and lesion localization. Medical & biological engineering & computing 2017;55(1):57–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jiang L, Hu X, Xiao Q, Gu Y, Li Q. Fully automated segmentation of whole breast using dynamic programming in dynamic contrast enhanced MR images. Medical physics 2017;44(6):2400–2414. [DOI] [PubMed] [Google Scholar]
- 38.Wu S, Weinstein SP, Conant EF, Kontos D. Automated fibroglandular tissue segmentation and volumetric density estimation in breast MRI using an atlas-aided fuzzy C-means method. Medical physics 2013;40(12). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhou L, Zhu Y, Bergot C, Laval-Jeantet A-M, Bousson V, Laredo J-D, Laval-Jeantet M. A method of radio-frequency inhomogeneity correction for brain tissue segmentation in MRI. Computerized Medical Imaging and Graphics 2001;25(5):379–389. [DOI] [PubMed] [Google Scholar]
- 40.Chen J-H, Nie K, Bahri S, Hsu C-C, Hsu F-T, Shih H-N, Lin M, Nalcioglu O, Su M-Y. Decrease in breast density in the contralateral normal breast of patients receiving neoadjuvant chemotherapy: MR imaging evaluation 1. Radiology 2010;255(1):44–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hennessey S, Huszti E, Gunasekura A, Salleh A, Martin L, Minkin S, Chavez S, Boyd N. Bilateral symmetry of breast tissue composition by magnetic resonance in young women and adults. Cancer Causes & Control 2014;25(4):491–497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chen J-H, Zhang Y, Chan S, Chang R-F, Su M-Y. Quantitative analysis of peri-tumor fat in different molecular subtypes of breast cancer. Magnetic resonance imaging 2018;53:34–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pujara AC, Mikheev A, Rusinek H, Gao Y, Chhor C, Pysarenko K, Rallapalli H, Walczyk J, Moccaldi M, Babb JS. Comparison between qualitative and quantitative assessment of background parenchymal enhancement on breast MRI. Journal of Magnetic Resonance Imaging 2018;47(6):1685–1691. [DOI] [PubMed] [Google Scholar]
- 44.Jung Y, Jeong SK, Kang DK, Moon Y, Kim TH. Quantitative analysis of background parenchymal enhancement in whole breast on MRI: Influence of menstrual cycle and comparison with a qualitative analysis. European journal of radiology 2018;103:84–89. [DOI] [PubMed] [Google Scholar]
- 45.Hu X, Jiang L, Li Q, Gu Y. Quantitative assessment of background parenchymal enhancement in breast magnetic resonance images predicts the risk of breast cancer. Oncotarget 2017;8(6):10620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.King V, Brooks JD, Bernstein JL, Reiner AS, Pike MC, Morris EA. Background parenchymal enhancement at breast MR imaging and breast cancer risk. Radiology 2011;260(1):50–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dontchos BN, Rahbar H, Partridge SC, Korde LA, Lam DL, Scheel JR, Peacock S, Lehman CD. Are qualitative assessments of background parenchymal enhancement, amount of fibroglandular tissue on MR images, and mammographic density associated with breast cancer risk? Radiology 2015;276(2):371–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Vovk U, Pernus F, Likar B. A review of methods for correction of intensity inhomogeneity in MRI. IEEE transactions on medical imaging 2007;26(3):405–421. [DOI] [PubMed] [Google Scholar]