Flexible Modeling of the Association Between Cumulative Exposure to Low-Dose Ionizing Radiation From Cardiac Procedures and Risk of Cancer in Adults With Congenital Heart Disease

Abstract

Adults with congenital heart disease are increasingly being exposed to low-dose ionizing radiation (LDIR) from cardiac procedures. In a recent study, Cohen et al. (Circulation. 2018;137(13):1334–1345) reported an association between increased LDIR exposure and cancer incidence but did not explore temporal relationships. Yet, the impact of past exposures probably accumulates over years, and its strength may depend on the amount of time elapsed since exposure. Furthermore, LDIR procedures performed shortly before a cancer diagnosis may have been ordered because of early symptoms of cancer, raising concerns about reversal causality bias. To address these challenges, we combined flexible modeling of cumulative exposures with competing-risks methodology to estimate separate associations of time-varying LDIR exposure with cancer incidence and all-cause mortality. Among 24,833 patients from the Quebec Congenital Heart Disease Database, 602 had incident cancer and 500 died during a follow-up period of up to 15 years (1995–2010). Initial results suggested a strong association of cancer incidence with very recent LDIR exposures, likely reflecting reverse causality bias. When exposure was lagged by 2 years, an increased cumulative LDIR dose from the previous 2–6 years was associated with increased cancer incidence, with a stronger association for women. These results illustrate the importance of accurate modeling of temporal relationships between time-varying exposures and health outcomes.

Epidemiologic studies increasingly assess exposures and treatments that vary not only between subjects but also within-subject over time. Such studies have to explore possibly complex temporal relationships between past values of time-varying exposures and the occurrence of the clinical event(s) of interest, which requires addressing several analytical and conceptual challenges (1–3).

First, many exposures may affect the outcome only after some time lag, but its duration is seldom known a priori (4, 5), and lag estimation requires specialized methods (1, 6–10). Failure to accurately model a lagged association may dilute its estimated strength and lead to incorrect conclusions (11). When the exposure itself varies considerably during follow-up of individual subjects, specification of a time-varying exposure metric, which aggregates information on past exposures, may materially affect the validity of conclusions and the statistical power to detect a true association (4, 12). Moreover, because the relative importance of past exposures probably varies with time since exposure (1, 13), sophisticated, flexible methods are required in order to accurately model the exposure weighting function (1, 14–16). Furthermore, exposures related to (for example) therapeutic or diagnostic procedures ordered by health professionals raise concerns about potential reverse causality, due to protopathic bias. This occurs whenever exposure is induced by a treatment or procedure administered because of early symptoms of the health condition considered the “outcome” (17). In addition, time-to-event analyses of cohort studies that assess outcomes other than all-cause mortality have to account for competing risks of events that may preclude observation of the outcome of interest (18, 19). Finally, whereas for any association it is important to explore the roles of possible effect modifiers (e.g., sex or gender) (20, 21), it may be less obvious how to assess such interactions in flexible modeling of time-varying exposures.

Several approaches have been proposed for addressing the challenges related to the latency periods and varying impacts of exposures received at different times in the past. Earlier methods have included time window models (6–8), parametric exposure weighting functions (1), and different methods for estimating lags (9, 10, 22, 23). In the past 2 decades, parallel progress in both flexible modeling techniques and computational resources has led to the development of flexible weighted cumulative exposure (WCE) methodology, which models the joint association of past exposures with the hazard using splines to avoid the need to specify the form of the exposure weighting function. The spline-based WCE modeling approach was initiated in the case-control setting by Hauptmann et al. (14) and extended to generalized linear models by Berhane et al. (15). More recently, building on earlier parametric WCE extensions of the Cox model (4, 24), spline-based WCE modeling was adapted to time-to-event analyses (16, 25), where the time-varying cumulative exposure metric is continuously updated during follow-up. This approach has been extended to marginal structural models with time-varying confounders/mediators (26) and to competing-risks analyses (27). All of these flexible models have been validated in extensive simulations, and most have started to show their advantages in real-life epidemiologic studies (28–31). In contrast, to date we are not aware of any application of WCE modeling accounting for competing risks.

One challenging and timely clinical question concerns the potential association between time-varying exposure to low-dose ionizing radiation (LDIR) and the risk of cancer among patients with congenital heart disease (CHD) (32). The increasingly longer survival of CHD patients, due to improved care and therapy, makes it important to assess nonfatal health outcomes in this growing population (33, 34). In particular, the recently reported increased prevalence of cancer in adults with CHD, compared with the general population (35), raises concerns about the potential impact of LDIR procedures, to which CHD patients are frequently exposed at relatively young ages (32). Indeed, similar associations between radiation and cancer have been reported in other clinical populations (1, 21, 36–39).

In particular, in a recent large population-based study, Cohen et al. (40) reported that CHD patients with a higher number of LDIR-emitting cardiac imaging procedures during follow-up had a higher cancer incidence than those who had only 1 procedure or no procedures. However, as the authors recognized, the analyses did not employ time-varying exposure metrics (12, 40), which would be necessary to explore how LDIR exposures received at different times in the past may affect the hazard (12).

In this paper, we reanalyze the same database using a flexible, recently developed and validated approach (27) to model the separate associations of cumulative dose of past LDIR exposures with the competing risks of cancer incidence and all-cause mortality. Our main objective is to illustrate how such flexible modeling may yield new insights into the complex temporal relationships between a time-varying exposure and the hazards of competing events in a large population-based cohort.

METHODS

Data sources

The cohort was derived from the Quebec Congenital Heart Disease Database, which merged Quebec, Canada’s, medical claims database (Régie de l’Assurance Maladie du Québec) with its hospital discharge database (Med-Echo) and death registry (33). The Quebec Congenital Heart Disease Database contains longitudinal information on diagnoses, demographic factors, hospitalizations, and inpatient and outpatient diagnostic and therapeutic procedures for all patients diagnosed with CHD who used the Quebec provincial health-care system between January 1, 1983, and March 31, 2010 (33). After exclusion of prevalent cancer cases and patients with unspecified CHD lesions or genetic disorders (40), the final cohort included 24,833 CHD patients who were aged 18–64 years between January 1, 1995, and December 31, 2009, and free of cancer on January 1, 1995.

Exposures

Exposure to LDIR-related cardiac procedures was identified from physicians’ billing codes during a 27-year period from 1983 to 2009 (40, 41). The 118 procedure codes included catheterizations (diagnostic procedures, structural heart interventions, and coronary interventions), computed tomography scans of the chest, nuclear imaging, and cardiac rhythm procedures (41). Three alternative time-varying exposures, updated every 6 months during follow-up, were defined: 1) the total number of LDIR procedures in a given 6-month period, 2) the total dose of radiation incurred from those procedures, and 3) the logarithm of the total dose, which was considered to account for a possible nonlinear dose-response relationship (4, 16) and the potential inaccuracy of imputed doses (40) (details are provided in Web Appendix 1, available at https://academic.oup.com/aje).

Outcomes

The outcome of primary interest was incident cancer, defined as the first outpatient diagnosis of primary specified cancer during the 15-year period from January 1, 1995, to December 31, 2009, confirmed by inpatient data (40). Primary specified cancers were ascertained by means of International Classification of Diseases, Ninth Revision, codes (before 2006) and International Classification of Diseases, Tenth Revision, codes (beginning in 2006), which were used in the Quebec Congenital Heart Disease Database, and were categorized on the basis of cancer site (35, 40). Web Appendix 2 outlines data manipulations implemented to avoid potential immortal time bias, and Web Appendix 3 provides details on the outcome ascertainment.

Covariates

LDIR exposures were adjusted for the following a priori-selected potential confounders (40): age at diagnosis, represented by linear and squared terms to account for its possibly nonlinear association with the logarithm of the hazard; sex; year of birth; specific types of lesions (severe defects, shunts, and valvular lesions), to account for disease severity; chronic coronary artery disease, a major comorbid condition for CHD patients (42); and time-varying transplantation status, which was recently shown to be an important confounder of the radiation-cancer association (43).

Statistical analyses

The main analyses relied on flexible extensions of the Cox proportional hazards model to competing risks, with a time-varying exposure. Cohort entry was defined as the latest of January 1, 1995, or the patient’s 18th birthday. The event time was defined as the time to the earlier of 2 competing events: 1) cancer diagnosis (k = 1) or 2) death from any cause (k = 2). Subjects who had no event during follow-up were censored at the earliest of either December 31, 2009, or their 65th birthday (40).

The joint association of past LDIR exposures with the hazard of event k at time u was represented by the time-varying weighted cumulative exposure (WCE_k(u)) metric (24), defined as the weighted sum of exposures received during different 6-month intervals in the past (27):

$${\mathrm{WCE}}_{i,k}(u)=\sum _t^u{w}_k(u-t)X_i(t),$$ (1)

where X_i(t), t ≤ u, represents the exposure received by subject i in the 6-month interval t (e.g., the number of LDIR procedures or the total dose of radiation incurred), and the event-specific weight function w_k(u − t) assigns weights to past exposures, depending on the time elapsed since exposure (u − t).

The weight functions were estimated using flexible cubic regression splines, which avoided a priori assumptions regarding their shape (14, 25). The weight functions are defined over a user-specified time window [0, a], where a represents the maximum width of the exposure time window over which past exposures may affect the current hazard (27), and can be constrained to smoothly decay to 0 at the right end of this window (25). A likelihood ratio statistic with 2 degrees of freedom (df) was used to assess the statistical significance of the improvement in the deviance of the unconstrained model relative to the constrained model, which would indicate that the selected support interval a should be increased (25).

We relied on full maximum likelihood estimation to fit a single flexible competing-risks WCE model (27), which simultaneously estimates the hazards of the two competing events, cancer incidence and noncancer death (27), by adapting the data augmentation approach (44):

$$\begin{array}{c}{\mathrm{\lambda }}_{i,k}\left(u|\left\{X_i\left(u\right),{\mathit{Z}}_i\left(u\right)\right\}\right)\hfill \\ ={\mathrm{\lambda }}_{0,k}\left(u\right)\exp \left[\sum _{k=1}^2\left[\sum _t^u{w}_k\left(u-t\right)X_i\left(t\right)+\sum _{s=1}^p{\mathrm{\mu }}_{ks}{Z}_{i,s}\left(u\right)\right]\right],\hfill \end{array}$$ (2)

where the event-specific baseline hazard λ_0,k(u) is modeled by cubic regression B-splines with 1 interior knot at the median of the uncensored event times (45) and ${\mathrm{\mu }}_{ks}$ represents the corresponding adjusted log hazard ratio for the (time-varying or time-fixed) covariate $Z_s(u)$. Finally, ${\mathrm{WCE}}_{i,k}\left(u\right)=\sum _t^u{w}_k\left(u-t\right)X_i\left(t\right)$ represents the estimated weighted cumulative exposure metric for event k at time interval u for subject i. Web Appendix 4 provides further details of the estimation and explains how the hazard ratios for different exposure patterns are calculated.

To minimize the risk of reverse causality bias, we lagged the LDIR exposure by 2 years. We then assessed the improvement in the deviance of the lagged WCE model (2) relative to a simpler 1-df model that represented the lagged cumulative exposure with the unweighted sum of past exposures X(t) over the same time window [0, a] (27). We performed several sensitivity analyses to compare the goodness of fit, in terms of the Akaike information criterion (AIC) (46), of alternative models and to inform the choices regarding 1) the flexibility (number of knots) of splines, 2) use of either the number of procedures or their (possibly log-transformed) dose as the exposure measure, and 3) the time window (parameter a) during which past LDIR exposures might be associated with the hazard (more details are provided in the Results section). Then we assessed whether, in the resulting final WCE model, the associations of cumulative LDIR exposure with the outcomes differed between a priori-selected subgroups of 1) women versus men and 2) subjects aged <40 years at cohort entry versus subjects aged ≥40 years at cohort entry, by comparing the deviances of 2 nested WCE models (2). For example, when exploring possible interaction with sex, the first model included a single WCE metric for each event, common to men and women, adjusted for the main effect of sex. The second, more complex model included, for each event, 2 separate WCE metrics, one for each sex. The statistical significance of the difference between the two models was tested at α = 0.05, using the likelihood ratio statistic with 2m df, where m corresponded to the degrees of freedom required to fit each of the two event-specific weight functions (27).

We estimated 95% pointwise confidence intervals around the weight functions using the Monte Carlo procedure (27). All WCE analyses were performed using a customized R program (R Foundation for Statistical Computing, Vienna, Austria) (27).

RESULTS

During a follow-up period of up to 15 years, there were 602 incident cancer diagnoses and 500 deaths from all causes among cancer-free patients, with incidence rates of 1.09/1,000 person-years for cancer and 0.90/1,000 person-years for mortality. Table 1 summarizes the distributions of baseline characteristics and the frequency of LDIR procedures during follow-up. Table 2 presents sex-specific distributions of cancer sites.

Table 1.

Baseline and Clinical Characteristics of a Cohort of Patients With Congenital Heart Disease (n = 24,833), Quebec, Canada, 1995–2010

Characteristic	Categorical Covariates		Continuous Covariates
	No. of Persons	%	Mean (SD)	Median (IQR)
Covariates
Age at entry, years			28 (13.4)	19.7 (18–36)
Age group, years
18–39	19,802	79.7
40–64	5,031	20.3
Sex
Male	11,020	44.4
Female	13,813	55.6
Year of birth			1970.5 (16.8)	1975 (1959–1985)
Type of lesion
Severe defect	3,495	14.1
Shunt	15,498	62.4
Valvular lesion	5,840	23.5
Chronic coronary artery disease
Yes	1,588	6.4
No	23,245	93.6
Exposure
Total amount of LDIR received during follow-up, mSva
From catheterizations			13.5 (14.5)	7 (7–15)
From computed tomography scans			24.3 (20.4)	15 (15–30)
From nuclear medicine			17.3 (16.2)	15.6 (7.8–15.6)
From cardiac rhythm procedures			15.9 (16.4)	15 (3–16.5)
Average no. of procedures performed during follow-upa
From catheterizations			1.5 (1.8)	1 (1–2)
From computed tomography scans			1.6 (1.4)	1 (1–2)
From nuclear medicine			2.1 (1.9)	1 (1–2)
From cardiac rhythm procedures			1.9 (1.5)	1 (1–2)
Outcome (During ≤15 Years of Follow-up)
Incident cancer	602	2.4
All-cause mortality	500	2.0

Abbreviations: IQR, interquartile range; LDIR, low-dose ionizing radiation; SD, standard deviation.

^a When there was at least 1 procedure.

Table 2.

Distribution of Cancer Sites^a Among Men and Women With Congenital Heart Disease Who Developed Cancer During ≤15 Years of Follow-up, Quebec, Canada, 1995–2010

Sex and Cancer Site	No. of Cases	%
Male	263	100.0
Genitourinary organs	81	30.8
Digestive organs	61	23.2
Lymphatic and hematopoietic tissue	50	19.0
Respiratory organs	39	14.8
Bone, connective tissue, and skin	20	7.6
Thyroid and other endocrine glands	5	1.9
Brain and nervous system	4	1.5
Lip, oral cavity, and pharynx	3	1.1
Breast	0	0.0
Female	339	100.0
Breast	117	34.5
Respiratory organs	48	14.2
Genitourinary organs	45	13.3
Digestive organs	39	11.5
Lymphatic and hematopoietic tissue	37	10.9
Bone, connective tissue, and skin	24	7.1
Thyroid and other endocrine glands	18	5.3
Brain and nervous system	10	2.9
Lip, oral cavity, and pharynx	1	0.3

^a Primary specified cancers were ascertained by means of International Classification of Diseases, Ninth Revision, codes (before 2006) or International Classification of Diseases, Tenth Revision, codes (during and after 2006).

Full cohort analyses

Web Appendix 5 and Web Figure 1 illustrate how flexible WCE modeling can help in detecting the reverse causality bias (47, 48). To avoid such biases, in all analyses discussed below, the LDIR exposure was lagged by 2 years.

In preliminary WCE analyses, we addressed the choice of the number of knots with exposures cumulated over the longest possible time window of 27 years (a = 27), where potential benefits of added flexibility in modeling the weight function should be most evident (27, 49, 50). However, even in that case, the parsimonious 1-knot model yielded a better fit (lower AIC) (46) than the more complex 2- or 3-knot models (data not shown). Thus, all further analyses were limited to 1-knot models, implying 3 df for each event-specific constrained weight function (27).

Next, we compared 3 alternative ways of measuring time-varying LDIR exposure X(t) in consecutive 6-month intervals: 1) the total number of LDIR procedures, 2) the total radiation dose from all corresponding procedures, and 3) the logarithm of the total dose. Because use of the log-transformed dose systematically improved the WCE model’s fit to data relative to the other two exposure measures (as illustrated in Web Appendix 6 and Web Table 1), all results presented below rely on the log dose.

Then, because of the uncertainty regarding how long past LDIR exposures may be associated with the current hazard of incident cancer (1), we fitted alternative unlagged 1-knot unconstrained WCE models for time windows of 3, 5, 9, 12, and 18 years (very short time windows being considered, these analyses did not employ the 2-year lag). The 9-year model yielded the lowest AIC. Furthermore, the estimates based on shorter windows suggested that the LDIR doses received 5 or more years prior were still associated with the current hazard, whereas the 12- and 18-year estimates did not show any risk increases associated with LDIR doses received more than 7–8 years prior (see Web Appendix 7 and Web Figure 2 for the comparison of AICs and weight function estimates). Finally, the 9-year unconstrained model did not improve the fit in comparison with the more parsimonious right-constrained model (P = 0.25). Given the above results, the main analyses relied on the lagged 1-knot right-constrained WCE model, with cumulative exposure defined as the weighted sum of log LDIR doses received in the past 9 years. This model fitted better (AIC = 15,769.3) than the unweighted sum of past doses (AIC = 15,776.3) from the same time window (P = 0.0047).

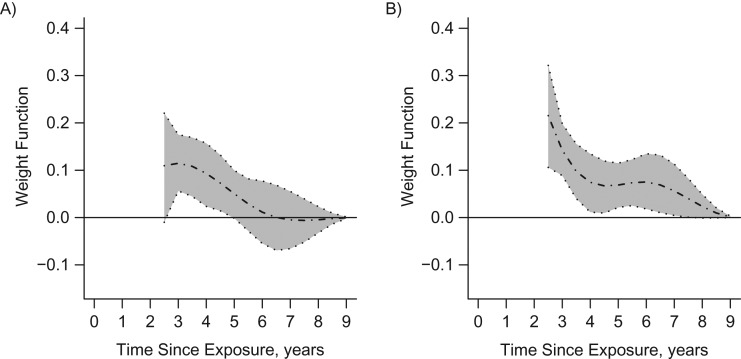
Figure 1 shows the corresponding weight functions for the two events, estimated in the full cohort, with their 95% confidence intervals. Because of the 2-year lag, the curves show the relative importance of LDIR exposures received 2–9 years before. Figure 1A indicates that LDIR doses from the past 2–5 years were associated with statistically significant increases in the hazard of incident cancer, but those received more than 6 years ago did not seem to matter, as reflected by weights close to 0. In contrast, for all-cause mortality, the most recent LDIR exposures seemed to play a dominant role, probably reflecting the reverse causality bias (Figure 1B). Table 3 shows event-specific hazard ratios for covariates from the final WCE model.

Figure 1.

Estimated weight functions (dotted-dashed lines) and pointwise 95% bootstrap confidence intervals (shaded areas) for associations between the logarithms of past doses of low-dose ionizing radiation exposure and cancer incidence (A) and all-cause mortality (B) among persons with congenital heart disease (2-year-lagged analysis), Quebec, Canada, 1995–2010.

Table 3.

Adjusted Event-Specific Hazard Ratios for Cancer and All-Cause Mortality Among Men and Women With Congenital Heart Disease According to Covariates Included in the Final Weighted Cumulative Exposure Competing-Risks Model, Quebec, Canada, 1995–2010

Covariate	Cancer		All-Cause Mortality
	HR	95% CI	HR	95% CI
Age (per year)	1.06	0.99, 1.14	0.97	0.91, 1.02
Age2 (per year2)	1.00	1.00, 1.00	1.00	1.00, 1.00
Sex (female vs. male)	1.16	0.99, 1.37	0.67	0.57, 0.80
Year of birth (per year)	0.97	0.92, 1.03	0.94	0.90, 0.98
Type of lesion
Severe defect	1.00	Referent	1.00	Referent
Shunt	1.24	0.92, 1.61	0.52	0.41, 0.65
Valvular lesion	1.02	0.75, 1.37	0.45	0.34, 0.57
Chronic coronary artery disease	1.48	1.14, 1.93	4.52	3.49, 6.01
Previous transplantationa status (yes/no)	5.09	2.45, 11.49	4.48	2.49, 7.80

Abbreviations: CI, confidence interval; HR, hazard ratio.

^a Binary time-varying covariate.

Subgroup analyses

Sex

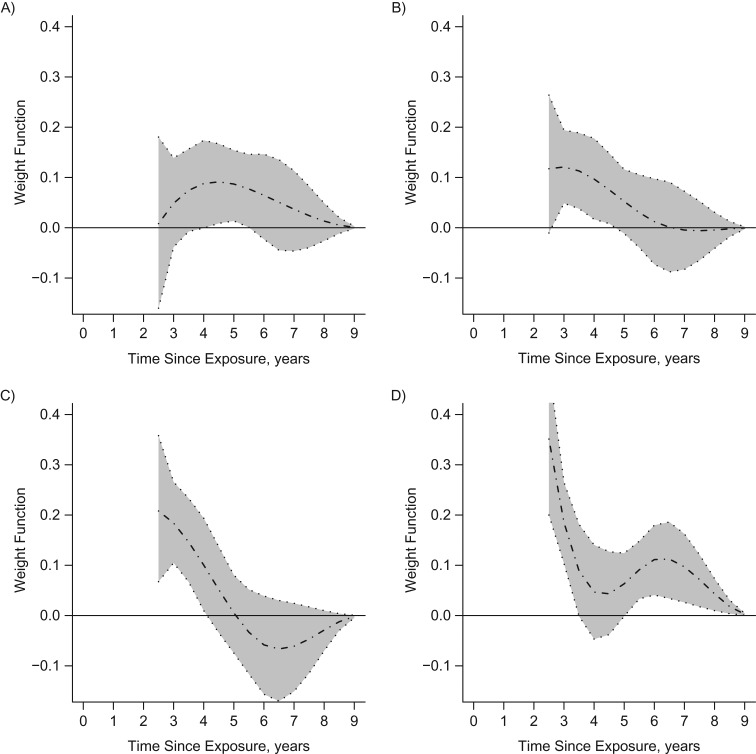
The extended competing-risks WCE model that estimated separate weight functions for women and men fitted the data significantly better than the model that assumed the same association for both sexes (P = 0.0057 for the likelihood ratio statistic with 6 df).

For men, only LDIR exposures from 3 years before to about 6 years before were associated with increased cancer incidence (Figure 2A), whereas all-cause mortality was mostly associated with recent LDIR exposures (Figure 2B). For women, the short-term associations of LDIR exposures with cancer incidence were stronger than those for men, as reflected by higher values of the corresponding weight functions, but were limited to doses received less than 5 years before (Figure 2C). For women, all-cause mortality was mostly associated with recent LDIR exposures (Figure 2D).

Figure 2.

Estimated weight functions (dotted-dashed lines) and pointwise 95% bootstrap confidence intervals (shaded areas) for associations between the logarithms of past doses of low-dose ionizing radiation exposure and cancer incidence (left panels) and all-cause mortality (right panels) for men (A and B) and women (C and D) with congenital heart disease (2-year-lagged analysis), Quebec, Canada, 1995–2010.

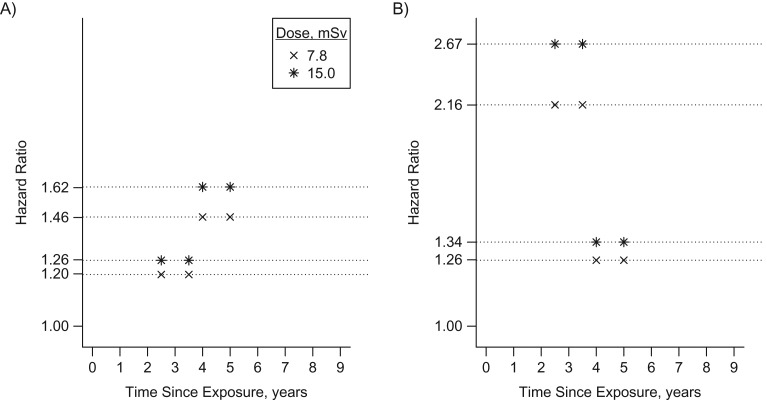
To assess the strength of the estimated associations between LDIR and incident cancer (Figure 3), we evaluated adjusted sex-specific hazard ratios (vertical axis) for selected hypothetical patterns of LDIR doses received at different times in the past (horizontal axis), relative to patients with no LDIR procedures in the past 9 years. Comparison of different patterns illustrates the impact of 1) more recent exposures (for men, hazard ratio (HR) = 1.46 (4–5 years before) vs. HR = 1.20 (2.5–3.5 years before) for a dose of 7.8 mSv and HR = 1.62 (4–5 years before) vs. HR = 1.26 (2.5–3.5 years before) for a dose of 15.0 mSv; for women, HR = 2.16 (2.5–3.5 years before) vs. HR = 1.26 (4–5 years before) for a dose of 7.8 mSv and HR = 2.67 (2.5–3.5 years before) vs. HR = 1.34 (4–5 years before) for a dose of 15.0 mSv) and 2) higher doses (for men, HR = 1.26 (15.0 mSv) vs. HR = 1.20 (7.8 mSv) 2.5–3.5 years before and HR = 1.62 (15.0 mSv) vs. HR = 1.46 (7.8 mSv) 4–5 years before; for women, HR = 1.34 (15.0 mSv) vs. HR = 1.26 (7.8 mSv) 4–5 years before and HR = 2.67 (15.0 mSv) vs. HR = 2.16 (7.8 mSv) 2.5–3.5 years before). Comparison of hazard ratios for equivalent patterns in Figures 3A and 3B indicates that the impact of recent LDIR exposures was stronger for women than for men. We also estimated hazard ratios associated with selected dose histories actually observed in our cohort. For women and men, across all patients and all periods when they were exposed, the median hazard ratios were 1.06 and 1.17, respectively, as compared with no LDIR procedures in the past 9 years, with 90th percentiles of 1.70 and 1.46 (Web Appendix 8 provides more details, and Web Table 2 shows examples of exposure patterns corresponding to median and 90th percentile hazard ratios). Even if the exposure-cancer association was stronger in women (Figure 3), their median hazard ratio was slightly lower because they were less frequently exposed.

Figure 3.

Adjusted hazard ratios from the final model (2-year-lagged analysis of associations between the logarithms of past doses of low-dose ionizing radiation (LDIR) exposure and cancer incidence) for selected hypothetical patterns of LDIR received at 2 different times in the past 9 years, relative to patients with no LDIR procedures in the past 9 years, among men (A) and women (B) with congenital heart disease, 1995–2010.

Age

Similar analyses yielded a marginally nonsignificant interaction with age (P = 0.13) and suggested that the association with LDIR doses from the past 2–6 years may have been somewhat stronger for younger adults than for persons aged 40–64 years at cohort entry (results are shown in Web Appendix 9 and Web Figure 3).

DISCUSSION

Our analyses shed light on the findings of the first study that found an association between LDIR exposure from cardiac procedures and cancer risk in adults with CHD (40), which may have important public health implications (32). Our analyses offer new insights into this complex association, help estimate its approximate latency, account for the time-varying nature of radiation exposures, and address analytical challenges related to modeling of cumulative exposures, competing risks, and effect modification by sex. Specifically, flexible WCE modeling indicated that increased cumulative LDIR dose from the previous 2–6 years was associated with increased cancer incidence, with a stronger association for women, and permitted estimation of how hazard ratios varied depending on the past exposure pattern.

Preliminary unlagged analyses illustrated how WCE modeling may help detect reverse causality bias, which occurs because some recent LDIR procedures, especially computer tomography chest scans, were probably performed because of early precancer symptoms (51). A combination of reverse causality and confounding bias probably also explains the association of higher cumulative LDIR dose with the competing risks of all-cause mortality, for which biological plausibility may be difficult to establish. Indeed, patients with more severe CHD and/or life-threatening comorbidity both 1) require more diagnostic procedures and 2) have higher mortality. In contrast, our finding that cumulative LDIR dose is associated with cancer incidence is in line with results of previous large epidemiologic studies (1, 52).

However, our consistent findings that the increased cancer risks are associated with only those LDIR exposures—whether represented by cumulative measures of log dose, dose, or the number of procedures—that occurred in the past 2–6 years raises 2 important interrelated questions. 1) Can such a short latency represent a biologically plausible cause-effect relationship? 2) If not, what are possible alternative explanations for an association specific to LDIR exposures from the past 2–6 years? We recognize that the latency suggested by our analyses is shorter than that reported in the Life Span Studies (53) and studies of cancer incidence after a major nuclear accident (54). Yet, the impact of a single massive radiation dose may be different from the cumulative impact of several low-dose exposures, where there seems to be some uncertainty regarding the latency period for their association with cancer incidence (55, 56). For example, Richardson and Ashmore (1) found that among nuclear industry workers, the lags varied substantially across cancer sites, and might be as short as 5 years for all cancers but lung cancer. Furthermore, even exposures that occurred only 2–3 years earlier contributed substantially to the cumulative risk of cancer death (1). Finally, in their study, the outcome was cancer mortality (1), which can partly explain why our analyses of cancer incidence suggested somewhat shorter latencies. Indeed, in a recent large study of computed tomography scans received in childhood and adolescence, exposures from the past 2–5 years had the strongest association with cancer incidence (52).

Regarding alternative mechanisms that might have produced “evidence” of a statistically significant association, found in our analyses with the 2-year lag, a simple reverse causality bias can arguably be ruled out. It is unlikely that LDIR procedures performed more than 2 years before the diagnosis of most cancers, with the possible exception of brain cancers, were ordered because of early precancer symptoms (52), and brain cancers were too rare in our population (2.3%) to materially affect the results. Furthermore, the main source of LDIR exposure in our study was cardiac imaging tests, which are seldom ordered as a diagnostic work-up for cancer. One reason why our analyses suggested a shorter latency period could be “detection bias.” Because our CHD population is followed more closely than the general population (57), it is possible that cancers are detected at earlier stages. Indeed, in a large population-based Taiwanese study, the median time from CHD diagnosis to cancer diagnosis was only 3 years (58). Our database does not include information on cancer stage at diagnosis, but future research should explore this issue. Finally, even if we excluded patients with known genetic abnormalities (40), we cannot exclude the possibility that some unknown abnormalities could both 1) require more frequent LDIR procedures and 2) increase the risk of cancer, inducing unmeasured confounding bias. If our results were largely driven by a small subpopulation of highly susceptible patients (59, 60) who developed cancers soon after exposure, the resulting depletion of susceptible persons could also explain an absence of an association with LDIR exposures received more than 6 years before (52).

Our finding that CHD patients who had received relatively high LDIR doses in the past 2–6 years were at increased risk of incident cancer suggests that these patients should be monitored more closely. Whereas hazard ratios associated with typical LDIR exposures were modest, patients with cumulative doses in the top percentiles of the distribution observed in our cohort had relative risk increases above 60% (Figure 3), which are clinically meaningful.

The weight functions differed significantly by sex: The association between LDIR exposures and cancer incidence was stronger, and the latency shorter, for women than for men. These findings, which emphasize the need to explore the role of sex as a potential effect modifier in epidemiologic studies (20, 61), are in line with those of other large studies (52, 55) confirming the concerns about higher radiosensitivity and vulnerability in women (21, 39), which may be attributable to their smaller body sizes and to the presence of radiosensitive breast and lung tissues in the radiated field (21, 39). Indeed, cancers of the breast and respiratory organs together represent approximately 50% of all cancers diagnosed among women in our cohort (40). This difference may also partly reflect sex-related differences in the distributions of cancer sites (Table 2), which may be differentially affected by LDIR exposures (1). Because our sample size was not sufficient for analyses of particular cancer sites, these questions should be explored in future studies.

Similar to other database studies of time-varying exposures, our study had limitations related to 1) exposure measurement errors, 2) unmeasured confounding, 3) heterogeneity in exposure across calendar time, and 4) uncertain external validity (62, 63). With regard to the first limitation, procedure-specific data on doses delivered, which were not available in our database, were imputed (40), similarly to other studies (52), based on the typical effective dose reported in the literature (36, 64–67). Yet, the actual LDIR dose received may vary by sex, age, radiation type, and the exposed organ (68). However, we found similar latencies in sensitivity analyses based on the number of LDIR procedures, which avoided measurement errors in dosage. Second, smoking status, which is not recorded in the Quebec Congenital Heart Disease Database, may be an important unmeasured confounder for the association between LDIR exposure and cancer incidence (1). However, in the same database, exclusion of smoking-related cancers did not materially change the results (40). Third, in future research, investigators should also explore the potential impact of secular trends in exposure intensity, reflecting progress in radiation technology (69). Finally, our results were limited to adults with CHD and should not be generalized to other adult populations or to children with CHD, who require further, dedicated studies.

In conclusion, we recognize that a single observational study cannot establish a causal relationship. However, the ultimate goal of statistical analyses is to best reflect what the empirical data tell us about the complex processes underlying disease occurrence, progression, and outcomes. From this perspective, our flexible WCE modeling helped establish the temporal relationship between LDIR exposures and cancer incidence, raising intriguing questions about the underlying mechanisms and the plausibility of the causal effect. Similar analytical challenges arise while studying many other time-varying exposures/treatments where, depending on the study design and data structure, researchers may apply flexible exposure weighting methods developed for (nested) case-control studies (1, 14), time-to-event analyses (16, 25), marginal structural models (26), generalized linear models (15), or competing risks (27). Extrapolating from our findings, such flexible methods may yield interesting new insights and help generate new hypotheses.

Abbreviations

AIC

Akaike information criterion

CHD

congenital heart disease

df

degrees of freedom

HR

hazard ratio

LDIR

low-dose ionizing radiation

WCE

weighted cumulative exposure