Cortical Cell Diameter Is Key To Energy Costs of Root Growth in Wheat^,

Genotypic diversity and phenotypic plasticity in root cortical cell diameter play key roles in reducing energy costs of root growth under high soil penetration resistance.

Abstract

Root growth requires substantial amounts of energy and thus carbohydrates. The energy costs of root growth are particularly high in both dry and compacted soil, due to high soil penetration resistance. Consequently, more carbon must be allocated from aboveground plant tissue to roots, which limits crop productivity. In this study, we tested the utility of root cortical cell diameter as a potential selection target to reduce the energy costs of root growth. Isothermal calorimetry was adopted for in situ quantification of the energy costs of root growth of 16 wheat (Triticum aestivum) genotypes under three levels of penetration resistance. We show that cortical cell diameter is a pivotal and heritable trait, which is strongly related to the energy costs of root growth. Genotypic diversity was found for cortical cell diameter and the energy costs of root growth. A large root cortical cell diameter correlated with reduced energy costs of root growth, particularly under high soil penetration resistance. Moreover, significant correlations were found between the ability to radially enlarge cortical cells upon greater penetration resistance (i.e. phenotypic plasticity) and the responsiveness in the energy costs of root growth. A higher degree of phenotypic plasticity in cortical cell diameter was associated with reduced energy costs of root growth as soil penetration resistance increased. We therefore suggest that genotypic diversity and phenotypic plasticity in cortical cell diameter should be harnessed to adapt crops to dry and compacted soils.

Plant roots need to grow through soil to gain access to water and nutrients, which are vital resources for plant growth and therefore crop productivity. Root growth, as such, requires substantial amounts of energy and thus photosynthate (Lynch, 2015). The energy costs of root growth are particularly high in dry and compacted soil because soil penetration resistance and therefore root penetration stress increase with drying and with increasing soil bulk density (Atwell, 1990a; Bengough and Mullins, 1991; Bengough et al., 2006, 2011; Bengough, 2012; Jin et al., 2013; Ruiz et al., 2015, 2016; Colombi et al., 2017). As a result, more photosynthate is needed for root system expansion, leaving less carbon available for aboveground plant growth (Atwell, 1990a). Furthermore, root growth rates decrease with increasing penetration resistance, resulting in limited and delayed access to soil resources (Araki and Iijima, 2005; Bengough et al., 2011; Valentine et al., 2012; Colombi et al., 2018). High energy costs of root growth and low resource accessibility both reduce shoot growth and eventually lead to yield losses. The problem of low crop yields due to high soil penetration resistance will aggravate in the future. Droughts are expected to become more frequent and severe with climate change (Bates et al., 2008), and agricultural mechanization involving heavy machinery will increase the acreage of compacted arable land (Schjønning et al., 2015; Stolte et al., 2016). Novel crop varieties that are adapted to high soil penetration resistance are therefore urgently needed to mitigate the effects of drought and compaction on global food security (Bengough et al., 2011).

Optimizing plant root systems is crucial in adapting crops to soil-borne abiotic stress (Bengough et al., 2011; White et al., 2013; Bishopp and Lynch, 2015; Lynch, 2015; Lynch and Wojciechowski, 2015). To achieve this through plant breeding, genotypic diversity of target traits within a single crop species and trait heritability are needed. In addition, phenotypic plasticity and thus the ability of plants to adjust their root phenotypes upon exposure to stress may be harnessed to improve crop performance under unfavorable soil conditions (York et al., 2013; Bishopp and Lynch, 2015; Lobet et al., 2018). Recent research indicates that elemental traits such as root cell size and cell number are more promising selection targets than aggregate traits such as root diameter, which are composed of several elemental traits. In comparison with aggregate traits, elemental traits are suggested having a more direct influence on plant physiological processes and being under simpler genetic control (York et al., 2013; Chimungu et al., 2015; Lynch, 2015; Rao et al., 2016). Adaptation to high soil penetration resistance must focus on traits that decrease the energy costs of root growth and facilitate root elongation, as these are the main physiological processes affected (Atwell, 1990a; Bengough et al., 2006, 2011; Jin et al., 2013; Ruiz et al., 2015). Recently, a number of root traits that are related to improved resource accessibility in soil with high penetration resistance were identified. In maize (Zea mays), root hairs were found to increase soil penetrability by anchoring the root to the soil (Haling et al., 2013; Bengough et al., 2016). Another study on maize showed that root cortical thickness is related to root buckling and therefore to the penetrability of soil with high penetration resistance (Chimungu et al., 2015). A sharp root tip opening angle was found to reduce the penetration stress at the root tip in wheat (Triticum aestivum), which facilitates root elongation in soil with high penetration resistance (Colombi et al., 2017). However, traits reducing the energy costs of root growth in soil with increased penetration resistance have yet to be identified.

Root cortical cell diameter was shown to be associated with the energy costs of root maintenance due to its influence on cell surface–volume and cytoplasm–vacuole ratio (Lynch, 2013, 2015). Previous studies reported considerable genotypic diversity in root cortical cell diameter in maize and wheat (Chimungu et al., 2014a, 2015; Colombi et al., 2017). Measuring respiration rates in excised pieces of mature roots showed that cortical cell diameter is related to genotypic root respiration rates in maize (Chimungu et al., 2014a). Moreover, cortical cell diameter can be quantified at relatively high throughput from root cross sections, which is needed to screen large diversity panels to link plant phenomics with genomics (Furbank and Tester, 2011; White et al., 2013). A recent study reported that >1,000 root cross sections can be cut and imaged per week (Atkinson and Wells, 2017), which highlights the potential of cortical cell diameter as a selection target in plant breeding programs. However, respiration rates of mature roots relate to the energy costs of root maintenance and do not reflect the presumably much higher costs of root growth (Szaniawski and Kietkiewicz, 1982; Atwell, 1990a; Wullschleger et al., 1992). To identify root traits that reduce the energy costs of root growth, in situ measurements of energy turnover by growing roots are required (Atwell, 1990a).

We sought to quantify the energy costs of root growth by isothermal calorimetry, with which heat dissipation is recorded nondestructively at microwatt precision (Braissant et al., 2010). The method allows quantification of energy turnover by soil organisms to show how bioenergetics define biogeochemical processes (Rong et al., 2007). Recently, calorimetry has been used to explore the functional importance of soil biota, including their composition, in various land use systems and across different temperature regimes (Sparling, 1983; Harris et al., 2012; Herrmann et al., 2014; Bölscher et al., 2016, 2017). Embedding calorimetry into a phenomics framework (i.e. combining calorimetry with the assessment of other root phenotypic traits; Furbank and Tester, 2011; York et al., 2013), carries great potential to identify root traits that reduce the energy costs of root growth under high soil penetration resistance.

In this study, we investigated whether (1) genotypic diversity and (2) phenotypic plasticity in root cortical cell diameter can be used to reduce the energy costs of root growth in soils with increased penetration resistance. A total of 16 wheat genotypes were grown under three different levels of soil penetration resistance for 1 d. Heat dissipation was recorded continuously during the entire growth period using isothermal calorimetry. The energy costs of root growth were then expressed as the ratio between daily heat dissipation (representing the energy turnover of growing roots) and daily root elongation. From this, we assessed the genotypic diversity in the energy costs of root growth as well as the genotypic diversity of the responsiveness in the energy costs of root growth to higher penetration resistance. Genotypic diversity in root cortical cell diameter and its phenotypic plasticity in response to greater penetration resistance was quantified from root cross sections with brightfield microscopy. Combining heat dissipation measurements with root anatomical data finally allowed us to relate the energy costs of root growth to genotypic diversity and phenotypic plasticity in root cortical cell diameter.

RESULTS

Energy Turnover of Root Growth

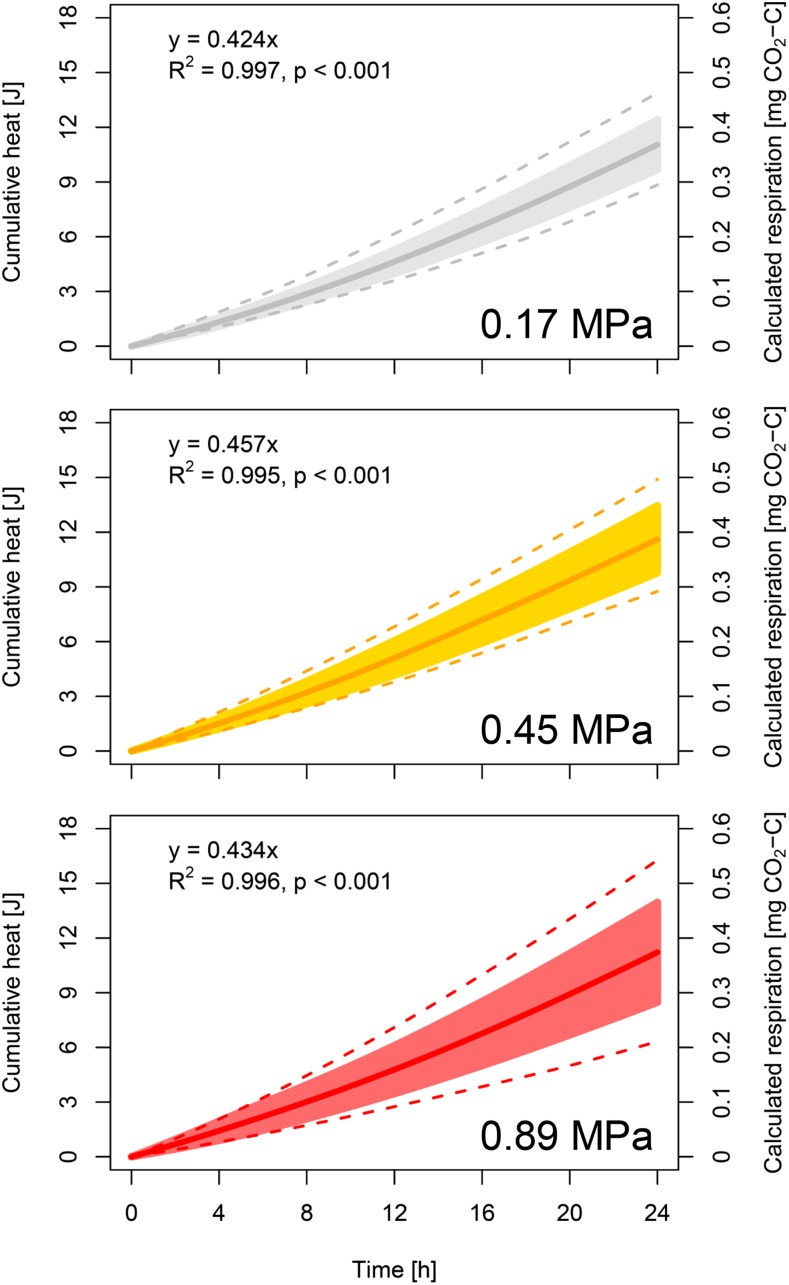
To measure the energy turnover of root growth, heat dissipation of newly emerged roots was measured for 24 h using isothermal calorimetry. Wheat was grown in 23.5-mL ampoules under low (0.17 MPa; se = 0.013), moderate (0.45 MPa; se = 0.029) and high (0.89 MPa; se = 0.081) soil penetration resistance, which was quantified by cone penetrometer measurements (n = 5; Supplemental Table S1). Heat dissipation rates were nearly constant over the measurement period, resulting in a linear increase in cumulative heat output under all levels of soil penetration resistance (R² > 0.99, P < 0.001). Average daily heat output (Eq. 1) across the different levels of soil penetration resistance was 11.3 J d⁻¹. Assuming a calorespirometric ratio of 30 kJ g⁻¹ CO₂-C (Sparling, 1983; Hansen et al., 2004; Wadsö et al., 2004; Barros et al., 2010; Herrmann and Bölscher, 2015), cumulative heat output of 11.3 J d⁻¹ corresponds to mean daily respiration of 376 μg CO₂-C d⁻¹ (Fig. 1). Daily heat output was not significantly affected (P = 0.39) by soil penetration resistance but differed significantly (P < 0.001) among the 16 wheat genotypes (Table 1). Genotypic diversity increased with increasing penetration resistance (Fig. 1).

Figure 1.

Cumulative heat output, quantified using isothermal calorimetry, during 24 h of wheat root growth. Continuous line and shaded area represent mean value and sd of 16 genotypes, respectively, at low (0.17 MPa), moderate (0.45 MPa), and high (0.89 MPa) soil penetration resistance. Dashed lines represent genotypes with the lowest and highest cumulative heat output. Cumulative respiration was calculated assuming a calorespirometric ratio of 30 kJ g⁻¹ CO₂-C. Presented data are based on genotype mean values (n = 5).

Table 1. Effects of soil penetration resistance, genotype, and their interaction on wheat root traits after 24 h of growth.

Effects were obtained from ANOVA (n = 5). A complete ANOVA table including degrees of freedom and exact F and P values is provided in Supplemental Table S2. PR, soil penetration resistance; GT, genotype; PR:GT, interaction of PR and GT.

Root Trait	PR	GT	PR:GT
Cumulative heat [J d−1]	P = 0.390	P < 0.001	P = 0.180
Root system elongation [mm d−1]	P < 0.001	P < 0.001	P < 0.05
Energy costs per unit increment in length [J mm−1]	P < 0.001	P < 0.001	P < 0.01
Root diameter [mm]	P < 0.001	P < 0.001	P < 0.05
Root cortical cell diameter [µm]	P < 0.001	P < 0.001	P < 0.001
Root cortical cell file number [#]	P < 0.001	P < 0.001	P = 0.072
Root stele diameter [µm]	P < 0.001	P < 0.001	P = 0.338
Root system volume growth [mm3 d−1]	P < 0.001	P < 0.001	P = 0.170
Energy costs per unit increment in volume [J mm−3]	P < 0.001	P < 0.001	P < 0.05

Effects of Soil Penetration Resistance and Genotype on Energy Costs of Root Elongation

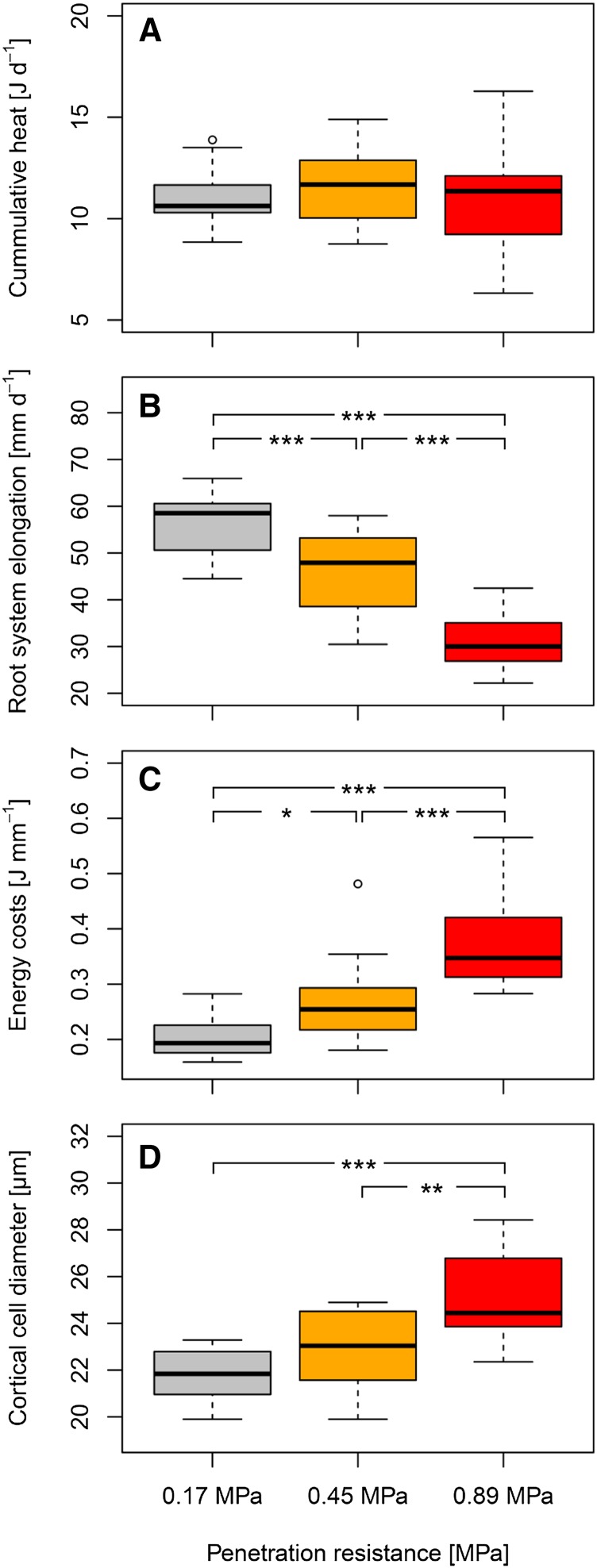
The energy costs of root growth were determined as the ratio of daily heat output to daily root system elongation, obtained from flatbed scans of excavated wheat seedlings. Because root system expansion and resource accessibility depend primarily on root length rather than root volume, we express the energy costs of root growth per unit increment in root length. Higher soil penetration resistance resulted in significantly (P < 0.001) decreased root system elongation (Table 1). Root elongation under moderate and high penetration resistance was reduced by 18% and 45%, respectively, in comparison to low penetration resistance (Fig. 2). Due to this reduction, the energy costs of root elongation increased significantly (P < 0.001) with increasing penetration resistance (Table 1). The mean energy costs of root elongation across all 16 wheat genotypes were 0.20 J mm⁻¹ under low soil penetration resistance. The costs increased to 0.27 J mm⁻¹ and 0.38 J mm⁻¹ in soil with moderate and high penetration resistance, respectively (Fig. 2). Significant (P < 0.001) responses to penetration resistance were also observed for volumetric root system growth and energy costs per unit increment in root volume (Table 1). However, due to root thickening upon greater penetration resistance, these effects were less pronounced (Supplemental Fig. S1).

Figure 2.

Effects of soil penetration resistance on wheat root traits after 24 h of growth. A–D, Boxplots for cumulative heat output (A), daily root system elongation (B), energy costs of root elongation (C), and root cortical cell diameter (D) are based on mean values (n = 5) of 16 genotypes. ***, **, and * denote significant differences between soil penetration resistance levels using Tukey´s honest significance test at P < 0.001, P < 0.01, and P < 0.05.

Highly significant genotype effects (P < 0.001) were obtained for daily root system elongation. Moreover, the energy costs of root elongation differed significantly (P < 0.001) among wheat genotypes (Table 1). The genotypic diversity in the energy costs of root elongation was higher at higher soil penetration resistance (Fig. 2). Genotype mean values were between 0.28 J mm⁻¹ and 0.57 J mm⁻¹ under high penetration resistance. In soil with moderate and low penetration resistance, energy costs of root elongation ranged from 0.18 J mm⁻¹ to 0.48 J mm⁻¹ and from 0.16 J mm⁻¹ to 0.28 J mm⁻¹, respectively (Fig. 2). Significant genotype effects (P < 0.001) also occurred for volumetric root growth and the energy costs of root volume growth (Table 1). Energy costs of root volume growth were between 1.01 J mm⁻³ and 1.86 J mm⁻³ under high soil penetration resistance. Under moderate and low penetration resistance, genotype mean values ranged from 0.81 J mm⁻³ to 1.77 J mm⁻³ and from 0.78 J mm⁻³ to 1.19 J mm⁻³, respectively (Supplemental Fig. S1). We converted the energy costs of volumetric root growth into specific root respiration rates assuming a fresh weight density of 0.001 g mm⁻³, a root dry matter content of 10% (Atwell, 1990a; Ennos et al., 1993; Shipley and Vu, 2002), and, as above, a calorespirometric ratio of 30 kJ g⁻¹ CO₂-C (Sparling, 1983; Hansen et al., 2004; Wadsö et al., 2004; Barros et al., 2010; Herrmann and Bölscher, 2015; Eqs. 6–10). Across all levels of penetration resistance and wheat genotypes, calculated genotype mean respiration rates ranged from 21.6 to 51.7 mmol CO₂-C g⁻¹ root dry weight d⁻¹ (Supplemental Tables S3 and S4).

Effects of Soil Penetration Resistance and Genotype on Cortical Cell Diameter

The diameter of root cortical cells was quantified from root cross sections taken in the middle between the apex and the base of the roots using bright field microscopy. Cortical cell diameter increased significantly (P < 0.001) in response to higher soil penetration resistance (Table 1). On average, cortical cell diameter of roots grown under high soil penetration resistance was 10% and 15% larger than that of roots exposed to moderate and low penetration resistance, respectively (Fig. 2). Root cortical cell file number, stele diameter, and root diameter were significantly (P < 0.001) affected by soil penetration resistance (Table 1) and increased with greater penetration resistance (Supplemental Fig. S1).

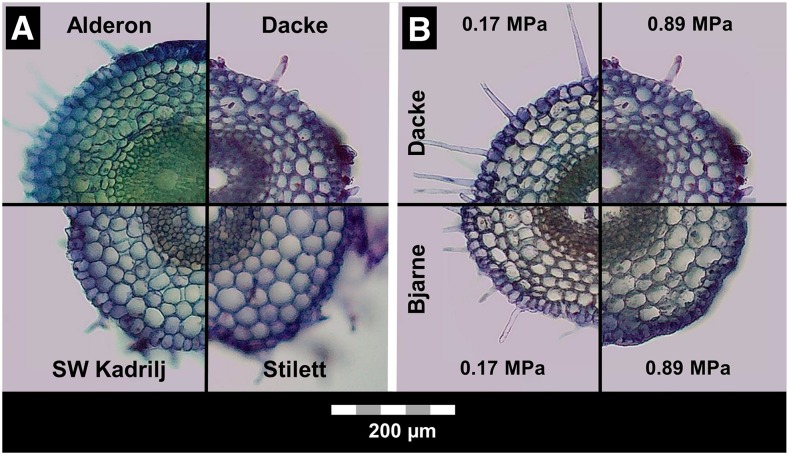
The 16 wheat genotypes assessed differed significantly (P < 0.001) in root cortical cell diameter (Table 1), as illustrated by the genotypes ‘Alderon’, ‘Dacke’, ‘SW Kadrilj’, and ‘Stilett’ (Fig. 3). Genotypic diversity in cortical cell diameter increased with increasing soil penetration resistance. Under high and moderate penetration resistance, genotype mean diameter of cortical cells varied from 22 μm to 28 μm and from 20 μm to 25 μm, respectively. In roots exposed to low soil penetration resistance, genotype mean cortical cell diameter ranged from 20 μm to 23 μm (Fig. 2). Cortical cell file number, stele diameter, and root diameter also differed significantly (P < 0.001) among wheat genotypes (Table 1). However, under moderate and high penetration resistance, the genotypic diversity of these three traits was considerably lower than the diversity in cortical cell diameter. In soil with low penetration resistance, similar genotypic diversity was observed for cortical cell diameter, cortical cell file number, stele diameter, and root diameter (Fig. 2; Supplemental Fig. S1).

Figure 3.

Typical wheat root cross sections that were taken from the middle of primary roots between the apex and the base and stained for 1 min with 0.1% (m/v) Toluidine blue. A, Genotypic diversity in cortical cell diameter at high soil penetration resistance (0.89 MPa). B, Phenotypic plasticity in cortical cell diameter in response to an increase of soil penetration resistance from 0.17 MPa to 0.89 MPa.

Responsiveness in Energy Costs of Root Growth and Phenotypic Plasticity in Cortical Cell Diameter upon Increased Soil Penetration Resistance

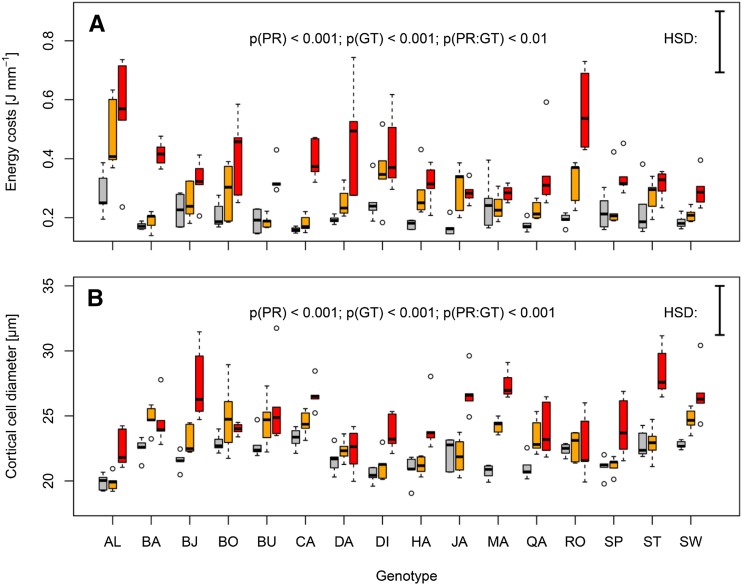
The degree to which the energy costs of root elongation increased in response to higher soil penetration resistance varied among wheat genotypes, as indicated by significant penetration resistance-genotype interactions (P < 0.01; Table 1). Hence, the responsiveness in the energy costs of root elongation to increased soil penetration resistance differed among genotypes. In certain genotypes, the energy costs of root elongation increased by >80% and >150% when soil penetration resistance increased from 0.17 MPa to 0.45 MPa and 0.89 MPa, respectively (Fig. 4). In other genotypes, however, the energy costs of root elongation remained constant or increased by only a small percentage upon increased penetration resistance (Fig. 4). Similar findings were obtained for the energy costs of root volume growth (Table 1; Supplemental Fig. S2).

Figure 4.

Interaction effects of soil penetration resistance and genotype on wheat root traits after 24 h of growth. A and B, Boxplots show energy costs of root elongation (A) and root cortical cell diameter (B) under low (0.17 MPa, gray), moderate (0.45 MPa, orange), and high (0.89 MPa, red) soil penetration resistance in 16 genotypes. P values refer to ANOVA with penetration resistance (PR), genotype (GT), and their interaction (PR:GT) as explanatory factors. Vertical bars represent Tukey’s honest significant difference at P < 0.05 (n = 5). Genotype abbreviations and names are provided in Supplemental Table S6.

Strong penetration resistance-genotype interactions (P < 0.001) were also found for root cortical cell diameter (Table 1). Thus, the degree of phenotypic plasticity in cortical cell diameter varied significantly among wheat genotypes. The comparison between ‘Dacke’ and ‘Bjarne’ illustrates how wheat genotypes differed in their ability to enlarge cortical cell diameter in response to increased soil penetration resistance (Fig. 3). Upon increasing soil penetration resistance from 0.17 MPa to 0.45 MPa, cortical cell diameter was increased by 10% to 20% in certain genotypes, while in others it remained nearly unchanged. When soil penetration resistance increased from 0.17 MPa to 0.89 MPa, some genotypes enlarged their root cortical cell diameter by >25%, whereas other genotypes showed almost no adjustment of cortical cell diameter (Fig. 4). Hence, phenotypic plasticity in cortical cell diameter showed higher genotypic diversity upon severely increased soil penetration resistance than upon a moderate increase in penetration resistance. Significant effects of penetration resistance-genotype interactions also occurred for root diameter (P < 0.05, Table 1), but the genotypic diversity was relatively low (Supplemental Fig. S2). No significant effects of penetration resistance-genotype interactions were obtained for root cortical cell file number (P = 0.07) and stele diameter (P = 0.34; Table 1).

Root Cortical Cell Diameter and Energy Costs of Root Growth

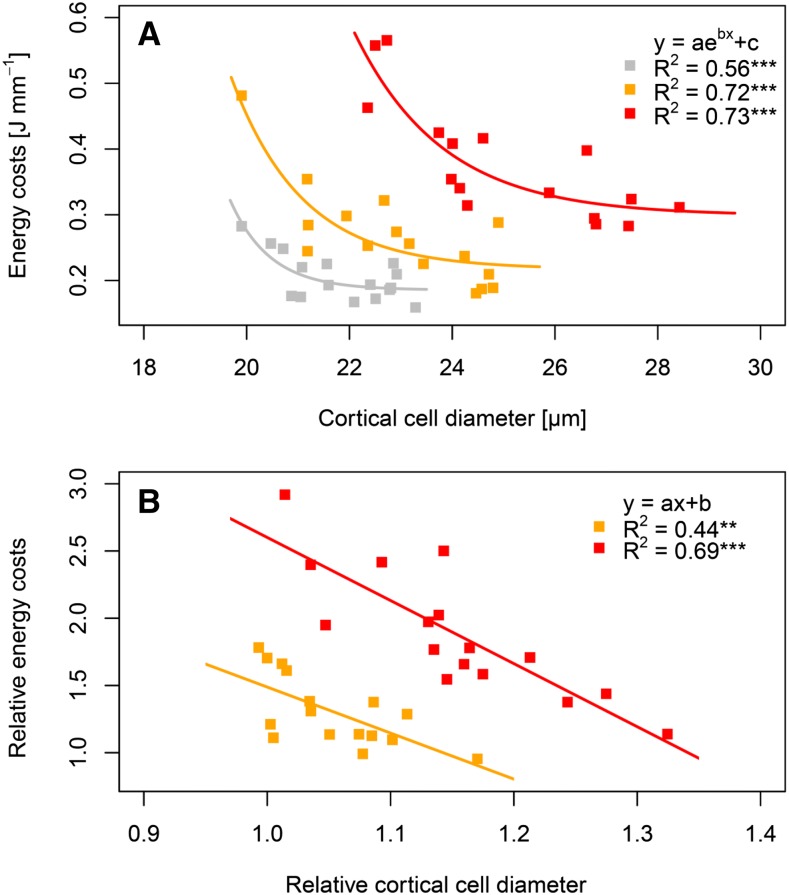
The energy costs of root elongation decreased exponentially with increasing root cortical cell diameter and asymptotically approached a lower energy cost limit (Fig. 5). Under moderate and high soil penetration resistance, the regressions yielded multiple R² values > 0.70 (P < 0.001). The coefficient of determination was 0.56 under low penetration resistance, but the regression remained highly significant (P < 0.001; Fig. 5). Furthermore, the energy costs of root volume growth decreased linearly with increasing cortical cell diameter in soil with low (R² = 0.36, P < 0.05), moderate (R² = 0.56, P < 0.001), and high (R² = 0.53, P < 0.01) penetration resistance (Supplemental Fig. S3). These regressions show that wheat genotypes with larger cortical cell diameter require less energy for root growth than genotypes with smaller cortical cell diameter. Seed dry weight, representing initial energy reserves, was not related to the energy costs of root elongation and root volume growth (R² < 0.03; Supplemental Table S5).

Figure 5.

A and B, Influence of root cortical cell diameter on energy costs of root elongation. Regressions are based on genotype mean values (n = 5) of 16 wheat genotypes under low (0.17 MPa, gray), moderate (0.45 MPa, orange), and high (0.89 MPa, red) soil penetration resistance. Regressions are shown for absolute (A) and relative values referring to the ratio of genotype mean values under increased (i.e. moderate or high) to low penetration resistance (B). R² represents multiple r-squared; *** and ** denote significant regression at P < 0.001 and < 0.01, respectively.

Moreover, we found significant relationships between phenotypic plasticity in root cortical diameter and the responsiveness in the energy costs of root growth to increased soil penetration resistance. Relative values for cell diameter and energy costs of root growth were determined to relate phenotypic plasticity in cortical cell diameter to the responsiveness in energy costs of root growth upon higher penetration resistance. These relative values were calculated as the ratio of genotype mean values under elevated (0.45 MPa and 0.89 MPa) to low (0.17 MPa) soil penetration resistance. The relative energy costs of root elongation decreased linearly with increasing relative cortical cell diameter upon severely (R² = 0.69, P < 0.001) and moderately increased soil penetration resistance (R² = 0.44, P < 0.01; Fig. 5). Similar results were obtained for the relative energy costs of root volume growth, which also decreased with increasing relative root cortical cell size (0.49 < R² < 0.63, P < 0.01; Supplemental Fig. S3).

Root elongation and root volume growth did not decrease with increasing root cortical diameter. In soil with low and high penetration resistance, no significant relationships between cortical cell diameter and root growth were found (R² < 0.12). Under moderate soil penetration resistance, genotypes with larger cortical cell diameter showed improved root elongation (R² = 0.52, P < 0.01) and root volume growth (R² = 0.38, P < 0.05). Phenotypic plasticity in root cortical diameter was positively related to the responsiveness in root elongation (R² = 0.39, P < 0.05) and volumetric root growth (R² = 0.40, P < 0.01) upon moderately increased soil penetration resistance. No such relationship was observed when soil penetration resistance was increased from 0.17 MPa to 0.89 MPa (Supplemental Fig. S4).

Under high soil penetration resistance, the energy costs of root elongation (R² = 0.53, P < 0.01; Supplemental Fig. S5) and root volume growth (R² = 0.38, P < 0.05; Supplemental Fig. S6) increased with higher number of root cortical cell files. In soil with low and moderate penetration resistance, no such correlations were found. Phenotypic plasticity in cortical cell file number was not related to the responsiveness in the energy costs of root elongation (Supplemental Fig. S5) or root volume growth (Supplemental Fig. S6) upon increased penetration resistance. Furthermore, stele diameter was not related to the energy costs of root elongation (Supplemental Fig. S5) or root volume growth (Supplemental Fig. S6). Positive correlations were found between root diameter and the energy costs of root elongation under moderate and high penetration resistance, and between phenotypic plasticity in root diameter and the relative costs of root elongation (0.28 < R² < 0.48; Supplemental Fig. S5). Root diameter was not related to the energy costs of root volume growth (Supplemental Fig. S6).

Heritability Estimations

Broad-sense heritability of wheat root traits was estimated using variance components obtained from linear mixed models (Hallauer and Miranda, 1981; Falconer and Mackay, 1996). Overall trait heritability was assessed across all levels of soil penetration resistance (Eqs. 2 and 4). Root cortical cell diameter showed heritability >0.7. To assess the stability of trait inheritance in response to changed soil penetration resistance, heritability values were also calculated separately for each level of penetration resistance (Eqs. 3 and 5). The heritability for cortical cell diameter decreased slightly with increasing soil penetration resistance. Nevertheless, it was >0.7 even under high soil penetration resistance, indicating high stability of trait inheritance in response to increased soil penetration resistance (Table 2). These heritability values were comparable to, or even higher, than those obtained for all other wheat root traits, including daily root system elongation, the costs of root elongation, root and stele diameter, and cortical cell file number (Table 2).

Table 2. Broad-sense heritability of wheat root traits after 24 h of growth.

Heritability was calculated for all levels of soil penetration together (overall, Eqs. 2 and 4) and separately (LPR, MPR, HPR; Eqs. 3 and 5), using variance components obtained from linear mixed models (n = 5) LPR, low penetration resistance (0.17 MPa); MPR, moderate penetration resistance (0.45 MPa); HPR, high penetration resistance (0.89 MPa).

Root Trait	Heritability
	Overall	LPR	MPR	HPR
Cumulative heat [J d−1]	0.81	0.61	0.44	0.78
Root system elongation [mm d−1]	0.76	0.47	0.85	0.53
Energy costs per increment of length [J mm−1]	0.70	0.57	0.80	0.71
Root diameter [mm]	0.81	0.78	0.79	0.70
Root cortical cell diameter [μm]	0.72	0.88	0.87	0.77
Root cortical cell file number [#]	0.84	0.76	0.72	0.76
Root stele diameter [μm]	0.80	0.71	0.52	0.58
Root system volume growth [mm3 d−1]	0.81	0.49	0.80	0.58
Energy costs per increment of volume [J mm−3]	0.67	0.56	0.69	0.58

DISCUSSION

In this study, we demonstrate that isothermal calorimetry is a suitable approach for in situ quantification of heat dissipation and therefore energy turnover of root growth (Fig. 1). The use of experiments with three different levels of soil penetration resistance and 16 wheat genotypes showed that both stress responses and genotypic differences in the energy costs of root growth can be assessed with calorimetry (Table 1). Ultimately, the combined assessment of the energy costs of root growth and root anatomy revealed that root cortical cell diameter is key to the amount of energy that plants need to invest into root system expansion.

As found in previous studies (Atwell, 1990b; Bengough and Mullins, 1991; Jin et al., 2013; Colombi et al., 2017), higher soil penetration resistance resulted in decreased daily root elongation (Fig. 2) and root volume growth (Supplemental Fig. S1). The energy costs of root growth, expressed here as the ratio between daily heat dissipation and daily root elongation, increased with increasing soil penetration resistance. On average, the energy costs of root growth increased by 35% and 90% when soil penetration resistance increased from 0.17 MPa to 0.45 MPa and 0.89 MPa, respectively (Fig. 2). Similar findings were reported by Atwell (1990a) showing that higher amounts of photosynthate were required for root growth when soil penetration increases. Converting the energy cost of root growth into specific respiration rates (Eqs. 6–10) enabled us to compare our results with previous studies. The energy costs of root growth measured here were comparable with respiration rates of intact roots and leaves (Supplemental Table S4; Bloom et al., 1992; Wullschleger et al., 1992; Fan et al., 2003; Zhu et al., 2005). However, the energy costs of root growth obtained in this study (Supplemental Table S3) were at least one order-of-magnitude higher than respiration rates measured from excised mature roots (Atwell, 1990a; Bouma et al., 1997; Theertham Pradyumna and Osamu, 1998; Nielsen et al., 2001; Fan et al., 2003; Schneider et al., 2017). In line with other studies comparing respiration rates of growing and mature plant tissues (Szaniawski and Kietkiewicz, 1982; Atwell, 1990a; Wullschleger et al., 1992), this shows that root growth requires much more energy than root maintenance. Because soil penetration resistance primarily affects root growth (Bengough et al., 2006, 2011; Valentine et al., 2012; Jin et al., 2013; Colombi et al., 2018), the development of new crop varieties needs to focus on traits that reduce the energy costs of root growth rather than root maintenance. Therefore, target traits that are related to the costs of root growth have to be identified to adapt germplasm to soil with high penetration resistance.

Genotypic diversity, heritability, and physiological implications of target traits are necessary prerequisites for the development of crop varieties with superior performance under unfavorable soil conditions (Furbank and Tester, 2011; Passioura, 2012; White et al., 2013; Lynch, 2015). Here, we found significant genotypic differences in root cortical cell diameter (Table 1; Fig. 4), which has been reported previously for wheat (Colombi et al., 2017) and maize (Chimungu et al., 2014a, 2015). Other studies on both mono- and dicotyledonous crops showed that genotypic differences in root number and root biomass increase upon higher soil penetration resistance (Bushamuka and Zobel, 1998; Grzesiak et al., 2014; Colombi and Walter, 2017). In agreement with these results, we found that genotypic diversity in root cortical cell diameter was greater at high soil penetration resistance (Fig. 3). Furthermore, high heritability was obtained for root cortical cell diameter (Table 2). The heritability for cortical cell diameter obtained for wheat in this study is comparable to that of root number, and root and shoot growth rates in wheat (Colombi et al., 2017; Colombi and Walter, 2017) and other crops (Li et al., 2015; Richard et al., 2015; Burridge et al., 2016; Le Marié et al., 2016). The significant correlation between root cortical cell diameter and the energy costs of root growth shows that root cortical cell diameter is related to root physiological processes. Genotypes with large cortical cell diameter required significantly less energy to access a given soil volume than those with rather small cortical cell diameter, particularly under increased soil penetration resistance (Fig. 5). This corresponds to other studies, which found that large cortical cell diameter reduces respiration rates of excised roots, as it leads to decreased cell surface–volume and cytoplasm–vacuole ratios (Lynch, 2013, 2015; Chimungu et al., 2014a). Atwell (1990b) reported that cortical cells become shorter upon increased soil penetration resistance, suggesting that there might be a tradeoff between cortical cell diameter and root growth rate. In this study, we did not find such a tradeoff, because increased root cortical cell diameter was not related to decreased root growth rates (Supplemental Fig. S4). Root growth is crucial for plants to access soil resources (Colombi et al., 2018) and is not limited to the seedling stage (Rasse and Smucker, 1998; Perkons et al., 2014). Hence, substantial amounts of energy are required for root growth even at later developmental stages. Increased cortical cell diameter was also found to reduce the costs of root maintenance (Lynch, 2013, 2015; Chimungu et al., 2014a), which eventually exceed the costs of the root growth as plant development progresses (van der Werf et al., 1988). We therefore propose that large cortical cell diameter decreases not only the energy costs of root growth but reduces the energy costs of soil exploration under high penetration resistance in general.

Because environmental conditions in soils vary in space and time, it has been emphasized that phenotypic plasticity in root traits should be harnessed when optimizing plants to soil-borne abiotic stress (York et al., 2013; Lobet et al., 2018). High phenotypic plasticity allows plants to adjust their root phenotype at small spatiotemporal scales to efficiently cope with environmental stress. Due to spatiotemporal fluctuations in soil moisture and spatial heterogeneity in bulk density, roots of a single plant are exposed to variable and changing soil penetration resistance (Bengough et al., 2011; Colombi et al., 2018). Here, we found significant relationships between phenotypic plasticity in root cortical cell diameter and the responsiveness in energy costs of root growth to increased soil penetration resistance. Genotypes showed different degrees of responsiveness in the energy costs of root growth. While energy costs of root growth remained almost constant upon increased penetration resistance in certain genotypes, these costs increased tremendously in others (Fig. 4). Radial enlargement of cortical cell diameter upon greater penetration resistance and thus phenotypic plasticity was found here (Fig. 2), corroborating results from other studies on wheat (Atwell, 1990b; Colombi et al., 2017). More importantly, the degree of phenotypic plasticity differed among wheat genotypes (Fig. 4) and was related to the responsiveness in the energy costs of root growth. Genotypes with high plasticity in cortical cell diameter showed only marginal increases in the energy costs of root elongation upon higher penetration resistance. In contrast, the energy costs of root elongation increased strongly with increasing penetration resistance when cortical cell diameter was static (Fig. 5). Hence, high phenotypic plasticity in root cortical cell diameter enabled plants to minimize the amount of extra energy needed to grow through soil with higher penetration resistance.

In a previous study in maize, root cortical cell file number was shown to be related to the costs of root maintenance (Chimungu et al., 2014b). As shown here (Supplemental Fig. S1) and previously (Colombi et al., 2017), wheat shows lower genotypic diversity in cortical cell file number than maize (Chimungu et al., 2014b). This low genotypic diversity most likely explains why cortical cell file number was less suitable to explain the energy costs of root growth in wheat than cortical cell diameter in this study (Fig. 5; Supplemental Fig. S5). Besides highlighting the potential of root cortical cell diameter as a selection target, our findings emphasize the necessity to focus on elemental traits in adapting germplasm to high soil penetration resistance. Root diameter, which is an aggregate trait composed of different elemental traits such as cell file number and cell diameter, was a weaker predictor (Supplemental Figs. S5 and S6) for the energy costs of root growth than cortical cell diameter (Fig. 5). As highlighted by others (York et al., 2013; Chimungu et al., 2015; Lynch, 2015; Rao et al., 2016), this shows that elemental traits such as cortical cell diameter are more directly related to physiological processes than aggregate traits such as root diameter. We therefore conclude that selection efforts to adapt wheat to high soil penetration resistance should focus on elemental root traits such as root cortical cell diameter.

CONCLUSION

Embedding isothermal calorimetry into a phenomics framework enabled us to show that root cortical cell diameter is key to the energy costs of root growth under high soil penetration resistance. Our results demonstrate that genotypic diversity and phenotypic plasticity in cortical cell diameter can be harnessed to reduce the energy costs of root growth in wheat—one of the world’s most important crops. The high heritability and the possibility for high throughput quantification of root cortical cell diameter underscores the potential to integrate this trait into breeding programs. Selecting for large root cortical cell diameter and high plasticity in cortical cell diameter will therefore be key in the development of varieties with improved performance on both dry and compacted soil.

MATERIALS AND METHODS

Soil Preparation

The soil was excavated from the top 20-cm of a plowed field near Uppsala, Sweden (59.83° N; 17.71°E; 15 m above sea level). It is classified as a silt loam soil (United States Department of Agriculture, 2018) with a textural composition of 25% clay, 56% silt, and 19% sand, an organic carbon content of 14.4 g C kg⁻¹ dry soil, and a pH (water) of 5.9 (Supplemental Table S1). After excavation, the soil was homogenized and dried to ∼17% gravimetric soil water content. Plant and animal debris were removed before passing the soil through a sieve with a mesh width of 2 mm and mixing it again. To avoid water loss, the soil was stored in darkness at 4°C until further processing.

The soil was autoclaved twice at 121°C and 100 kPa above atmospheric pressure for 20 min (Benchtop Sterilizer 3150 EL; Tuttnauer Europe) to ensure that soil microbial activity did not interfere with heat dissipation measurements. Autoclaving was performed in glass jars filled with the equivalent of 400-g dry soil. Easily available carbon may be released during the first autoclaving cycle. To remove any residual available carbon, the soil was amended with fresh soil at a rate of 1 g of fresh soil kg⁻¹ after the first autoclaving, and the soil was then incubated in darkness at 21°C for two weeks before a second autoclave cycle. Filter-sterilized water (DMSO-Safe Acrodisc Syringe Filter, 0.2-μm Nylon Membrane, 25 mm; Pall) was added after both autoclaving cycles to keep soil moisture at 17%.

Soil Physical Conditions

The soil was filled into sterilized (70% [v/v] ethanol) high density polyethylene ampoules (TA Instruments, Sollentuna, Sweden) of 23.5-mL volume and 24-mm i.d. To achieve different levels of soil penetration resistance, the soil was packed to three different dry bulk densities. In total, 19 mL of soil were added in five layers to the ampoules at low (1.1 g cm⁻³), moderate (1.4 g cm⁻³), and high (1.55 g cm⁻³) bulk density. Hence, an air-filled headspace of 4.5 mL remained. To ensure homogeneous packing, each layer was slightly abraded on the surface before adding the next layer of soil. Filter-sterilized water (0.2-μm Nylon Membrane, 25 mm) was added to the packed soil to reach 22% gravimetric soil water content.

Soil penetration resistance in the ampoules was determined by cone penetrometer measurements using the setup described by Ruiz et al. (2015). The cone had a recessed shaft, a base radius of 2.5 mm, and a full opening angle of 30°. The penetration force was measured with a force transducer (LC 703; OMEGA Engineering) connected to the cone shaft. The penetration speed was 4 mm min⁻¹. Penetration force was recorded from the point the cone was fully inserted into the soil until 15-mm penetration depth, resulting in ∼200 force measurements per insertion. Soil penetration resistance was calculated by dividing the mean penetration force by the cone base area. Cone penetrometer measurements were conducted in five separate ampoules (n = 5) for each level of soil penetration resistance (Supplemental Table S1).

Plant Material

The following 16 spring wheat (Triticum aestivum) genotypes of northern and central European origin were included in the study: Alderon (abbreviation: AL; country of origin: Germany), Bamse (BA; Sweden), Bjarne (BJ; Sweden), Boett (BO; Sweden), Bumble (BU; Sweden), Caress (CA; Sweden), Dacke (DA; Sweden), Diskett (DI; Sweden), Happy (HA; Sweden), Jack (JA; Sweden), Maggie (MA; Sweden), Quarna (QA; Switzerland), Rohan (RO; Sweden), Sport (SP; Sweden), Stilett (ST; Sweden), and SW Kadrilj (SW; Sweden). All these genotypes are commercially available varieties. Mean seed dry weight was determined by drying 200 seeds per genotype for 72 h at 60°C and varied from 28.3 mg to 43.2 mg (Supplemental Table S6).

Growth Conditions

For each genotype, 150 individual seeds were selected based on weight (average genotype seed fresh weight ± 10%) for pregermination in darkness at 21°C for 72 h. Pregerminated seeds in which embryonic roots had just emerged (root length < 2 mm), were selected for the experiment. The seeds were placed with the roots facing downward in a small conical pit (diameter = 3 mm, height = 4 mm) that was pinched out from the soil surface. To avoid root pull-out artifacts, the soil was smeared gently around the top of the seed. Immediately after seed placement, the ampoules were closed and placed in isothermal calorimeters (TAM Air Calorimeter; TA Instruments). Roots grew for 28.5 h at 21°C in the calorimeters. This short growth period minimized effects of leaf growth on heat dissipation measurements, as the coleoptile had just emerged from the seed at the end of the 28.5-h growth period. Each treatment level was replicated five times (n = 5).

Heat Output Measurements Using Isothermal Calorimetry

Three calorimeter devices with eight measurement channels each were used so that 24 measurements could be carried out at the same time (Herrmann and Bölscher, 2015). It was ensured that the five replicates of each treatment level were allocated across the three devices. After an equilibration period of 4.5 h, heat dissipation was recorded continuously for 24 h, representing a full diurnal cycle. High density polyethylene ampoules filled with filter-sterilized water (0.2-μm nylon membrane, 25 mm) served as the inert reference for heat dissipation measurements. Daily cumulative heat production (Q_tot [J d⁻¹]) was obtained by integrating heat dissipation measurements over the entire measurement period of 24 h. To account for background noise, heat dissipation was measured for 24 h in ampoules filled with autoclaved soil into which no seed was placed. Background noise measurements were carried out in seven separate ampoules for each level of penetration resistance (n = 7). The replicates of the background noise measurements were distributed over the entire duration of the experiment and across the three calorimeters. On average, the background noise signal ranged between 17 μW and 25 μW, which corresponded to ∼15% of the total heat dissipation (Supplemental Fig. S7). As described above, cumulative heat production due to background noise (Q_noise [J d⁻¹]) was calculated by integrating the respective heat dissipation measurements over 24 h. The net daily heat production resulting from root growth (Q_root [J d⁻¹]) was then calculated as

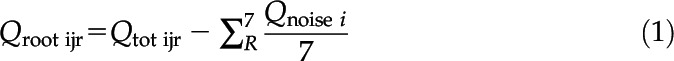where i denotes the level of soil penetration resistance (i = 0.17, 0.45, 0.89 mPa), j represents the different wheat genotypes (j = 1, 2,…, 16), r denotes the replicates of each treatment level (r = 1, 2,…, 5), and R represents the replicates of the background noise measurements (R = 1, 2,…, 7).

Root Phenomics

Upon completion of heat dissipation measurements, i.e. after 28.5 h of growth, roots were washed out from the soil. The washed roots were preserved in 70% (v/v) ethanol and stored at 4°C in darkness until further processing. Of the 240 plants sampled, 232 developed three embryonic roots, while the remaining eight plants developed two embryonic roots.

Root length and diameter were measured manually from high-resolution flatbed scans with a pixel edge length of 8 μm (3,200 dpi, Epson Perfection V800; Seiko Epson), using the software ImageJ v1.51r (U.S. National Institutes of Health). Root length was measured separately for all individual roots of one plant. Root diameter was determined for each individual root by three diameter measurements along the root axis. Average root diameter per plant was calculated as the mean diameter of all individual roots per plant. Root volume was calculated from root diameter and length, assuming a cylindrical root shape. Root system length and root system volume were calculated for each plant as the sum of each individual root length and root volume, respectively. As the growth period was 28.5 h, total root system length and root system volume were first converted into mm d⁻¹ and mm³ d⁻¹ to obtain daily root system elongation and daily root system volume growth. Cumulative heat output (Q_root [J d⁻¹]) was then divided by daily root system elongation and volumetric root system growth to calculate the energy costs per unit increment in root length [J mm⁻¹] and volume [J mm⁻³], respectively.

Cortical cell diameter was quantified using brightfield microscopy (Kern Optics OBF 122; Kern & Sohn. Objective: 10× magnification, 0.25 numerical aperture). Root cross sections of ∼150-μm thickness were taken manually from each individual root, using a razor blade. To get root tissue of similar age (∼12 h), the cross sections were taken in the middle of the root, between the base and the apex. The cross sections were stained for 1 min with Toluidine Blue (0.1% [w/v] in distilled water). Pictures were taken at a resolution of eight megapixels at 100× magnification with a digital microscope camera (Mirazoom MZ808; Oowl Tech), resulting in a pixel edge length of 0.7 µm. In each cross section, the radial diameter of 15 cortical cells was measured manually in ImageJ. Because embryonic roots in wheat typically have <5 cortical cell files (Colombi et al., 2017), a separation into different cortical regions is not possible. Therefore, measurements were taken across all cortical cell files excluding epidermal and endodermal cells to represent the typical cortical cell diameter of each root. Average root cortical cell diameter per plant was calculated as the mean cortical cell diameter of all sampled embryonic roots per plant. In addition, root cortical cell file number and stele diameter were determined manually in each root cross section.

Data Analysis and Statistics

Data processing, statistical evaluation, and data visualization were performed in “R” v3.4.1 (R Core Team, 2017). Two-way ANOVA was applied to evaluate the effects of soil penetration resistance, genotype, and their interaction on the different root traits assessed. Treatment means were compared using Tukey’s honest significance test at P < 0.001, P < 0.01, and P < 0.05, as implemented in the “agricolae” package (Mendiburu, 2015). Broad-sense heritability was estimated using variance components obtained from linear mixed models for all levels of soil penetration resistance together (Eq. 2) and for each level separately (Eq. 3). The following linear mixed models were evaluated with the “lme4” package (Bates et al., 2015)

and

where Y represents the measured root trait in the ith penetration resistance level (i = 0.17, 0.45, 0.89 MPa), the jth genotype (j = 1, 2,…, 16), and rth replicate (r = 1, 2,…, 5); α denotes the effect of soil penetration resistance, β denotes the genotype effect, αβ denotes the effect of the interaction between penetration resistance and genotype, and γ denotes the replicate effect. Here, α and γ were treated as fixed factors and αβ and β were set as random factors. Broad-sense heritability (H²) across all levels of penetration resistance (Hallauer and Miranda, 1981; Eq. 4) and for each level of penetration resistance (Falconer and Mackay, 1996; Eq. 5) was then calculated as

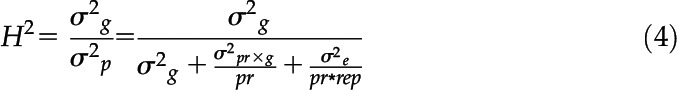and

where σ²_g and σ²_p denote genotypic and phenotypic variance, respectively; σ²_g×pr and σ²_e denote the variance covered by the penetration-resistance–genotype interaction and the residual variance, respectively; pr represents the number of penetration resistance levels (pr = 3); and rep is the number of replications (rep = 5).

Linear and nonlinear regression models were used to explain the costs of root elongation and volumetric root growth as a function of root cortical cell diameter and root diameter. The regressions were performed separately for each level of soil penetration resistance and were based on genotype mean values. Linear and nonlinear regressions were evaluated using the linear and nonlinear least-squares methods, respectively, which are both implemented in the “stats” package for “R.”

To compare the costs of root growth obtained here with measured root maintenance costs reported in previous studies (Atwell, 1990a; Bouma et al., 1997; Theertham Pradyumna and Osamu, 1998; Nielsen et al., 2001; Fan et al., 2003; Schneider et al., 2017), daily heat output was converted into mmol CO₂-C g⁻¹ root fresh and dry weight d⁻¹. Root fresh (FW_root [g]) and dry weight (DW_root [g]) were calculated based on root volume after 24 h of growth (V_root [mm³]) as

and

where ρ_f and DMC_root denote the density of fresh root tissue in g mm⁻³ and root dry matter content in g g⁻¹, respectively. We assumed a density of root fresh weight of 0.001 g mm⁻³ and a root dry matter content of 0.1 g dry weight g⁻¹ fresh weight (Atwell, 1990a; Ennos et al., 1993; Shipley and Vu, 2002). Total root respiration (R_{root tot}) in mmol CO₂-C d⁻¹ was then calculated using the cumulative heat output of root growth (Q_root [J d⁻¹]) and the molar mass of carbon (M_C [g mol⁻¹]) as

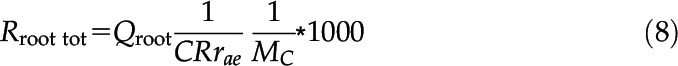where CRr_ae [kJ g⁻¹ CO₂-C] denotes the aerobic calorespirometric ratio, which we assumed to be 30 kJ g⁻¹ CO₂-C (Sparling, 1983; Hansen et al., 2004; Wadsö et al., 2004; Barros et al., 2010; Herrmann and Bölscher, 2015). Finally, specific root respiration per root fresh weight (R_{root sp-fw}) and root dry weight (R_{root sp-dw}) in mmol CO₂-C g⁻¹ d⁻¹ were obtained as

and

To compare root respiration rates obtained in previous studies with those calculated here, data from previous studies were converted into mmol CO₂-C g⁻¹ root fresh weight d⁻¹ or into mmol CO₂-C g^-1 root dry weight d⁻¹.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Effects of soil penetration resistance on root diameter, daily volumetric root system growth, energy costs of root volume growth, cortical cell file number, and stele diameter in wheat.

• Supplemental Figure S2. Interaction effects of soil penetration resistance and genotype on energy costs of root volume growth and root diameter in wheat.

• Supplemental Figure S3. Influence of root cortical cell diameter on energy costs of root volume growth in 16 wheat genotypes under low, moderate, and high soil penetration resistance.

• Supplemental Figure S4. Influence of root cortical cell diameter on daily root system elongation and daily volumetric root system growth in 16 wheat genotypes under low, moderate, and high soil penetration resistance.

• Supplemental Figure S5. Influence of root cortical cell file number, stele diameter, and root diameter on energy costs of root elongation in 16 wheat genotypes under low, moderate, and high soil penetration resistance.

• Supplemental Figure S6. Influence of root cortical cell file number, stele diameter, and root diameter on energy costs of root volume growth in 16 wheat genotypes under low, moderate, and high soil penetration resistance.

• Supplemental Figure S7. Influence of background noise on total heat dissipation measured during 24 h using isothermal calorimetry at low, moderate, and high soil penetration resistance.

• Supplemental Table S1. Basic soil properties in low, moderate, and high penetration resistance treatment.

• Supplemental Table S2. Complete ANOVA table on the effects of soil penetration resistance, genotype, and their interaction on wheat root traits after 24 h of growth.

• Supplemental Table S3. Comparison of calculated in situ root respiration rates from current study and measured respiration rates of excavated roots reported in the literature.

• Supplemental Table S4. Comparison of calculated in situ root respiration rates from current study and measured respiration rates of intact roots and leaves reported in the literature.

• Supplemental Table S5. Influence of seed dry weight on wheat root traits after 24 h of growth obtained from linear correlations.

• Supplemental Table S6. Names, abbreviations, country of origin, and average seed dry weight of the different wheat genotypes used in the study.