Abstract
Causal/formative indicators directly affect their corresponding latent variable. They run counter to the predominant view that indicators depend on latent variables and are thus often controversial. If present, causal/formative indicators have serious implications for factor analysis, reliability theory, item response theory, structural equation models, and most measurement approaches that are based on reflective or effect indicators. Psychological Methods has published a number of influential papers on causal/formative indicators as well as launching the first major backlash against them. This paper examines seven common criticisms of these indicators distilled from the literature: (1) A construct measured with “formative” indicators does not exist independently of its indicators, (2) Such indicators are causes rather than measures, (3) They imply multiple dimensions to a construct and this is a liability, (4) They are assumed to be error-free which is unrealistic, (5) They are inherently subject to interpretational confounding, (6) They fail proportionality constraints, and (7) Their coefficients should be set in advance and not estimated. We summarize each of these criticisms and point out the flaws in the logic and evidence marshaled in their support. The most common problems are not distinguishing between causal-formative and composite-formative indicators, tautological fallacies, and highlighting issues that are common to all indicators but presenting them as special problems of causal-formative indicators. We conclude that measurement theory needs to incorporate these types of indicators and to better understand their similarities to and differences from traditional indicators.
Keywords: causal indicators, formative indicators, composites, measurement models, factor analysis, structural equation models
“…formative indicators are not measures at all…” (Lee, Cadogan, & Chamberlain, 2013, p. 12)
“…disciplines such as IS should consider avoiding formative measurement … editors should question and perhaps even temporarily discourage the use of formative measurement” (Hardin & Marcoulides, 2011, p. 761)
“The shortcomings of formative measurement lead to the inexorable conclusion that formative measurement models should be abandoned.” (Edwards, 2011, p. 383)
New and unconventional ideas typically elicit backlash. The idea that indicators sometimes affect rather than are affected by the latent variable that they measure has historic roots (Blalock, 1963, 1964, 1968, 1971), but is relatively new to a large group of researchers. The above quotes are part of the backlash stimulated by the increased attention to causal/formative indicators. Such papers not only highlight allegedly insurmountable problems associated with the use of causal/formative indicators in measurement models but often go so far as to explicitly call for a ban on their use. In doing so, they often praise the allegedly superior virtues of reflective (effect) indicators which for some authors even constitute “the only defensible measurement model” (Iacobucci, 2010, p. 94, added emphasis). The recent attack on causal/formative indicators commenced with Howell, Breivik, and Wilcox’s (2007a, 2007b) and Bagozzi’s (2007) articles in Psychological Methods, was followed by Franke, Preacher, and Rigdon’s (2008) and Wilcox, Howell, and Breivik’s (2008) contributions to a Special Issue of Journal of Business Research and culminated in a series of increasingly hostile articles in a variety of disciplines including organizational behavior (e.g., Edwards 2011), consumer psychology (e.g., Iacobucci, 2010), marketing (e.g., Lee & Cadogan, 2013; Lee, Cadogan, & Chamberlain, 2013, 2014; Howell, 2013) and information systems (e.g., Hardin, Chang, & Fuller, 2008; Hardin & Marcoulides, 2011; Howell, Breivik, & Wilcox, 2013; Kim, Shin, & Grover, 2010).
While some of the above articles have attracted individual responses from scholars more open to causal/formative indicators (e.g., see Bainter & Bollen, 2014; Bollen, 2007; Diamantopoulos, 2013; Diamantopoulos & Temme, 2013), to date there has been no systematic and comprehensive attempt to answer the critics. Such lack of defense could be misinterpreted as an admission that such indicators are indeed fatally flawed - eventually leading to the abandonment of causal/formative indicators. This would be unfortunate, not least because “it could encourage researchers to use only latent variables that are measured with effect (reflective) indicators even though these might not be the latent variables best suited to a theory” (Bollen, 2007, p. 227–228). Bearing in mind that misspecification of measurement models adversely affects theory development (MacKenzie, 2003; Petter, Rai, & Straub, 2012) and given that such misspecification has been found to be widespread across disciplines (Eggert & Fassot, 2003; Fassot, 2006; Jarvis, MacKenzie, & Podsakoff, 2003; MacKenzie, Podsakoff, & Jarvis, 2005; Petter, Straub, & Rai, 2007; Podsakoff, Shen, & Podsakoff, 2006; Roy, Tarafdar, Ragu-Nathan, & Marsillac, 2012), a decision to abandon these nontraditional indicators should not be taken lightly.
Against this background, the purpose of the present paper is to (a) review the primary criticisms leveled against causal/formative indicators and highlight their underlying bases, (b) address each criticism by offering arguments that either render it invalid or show that it is a problem shared by reflective (effect) indicators, and (c) reassure researchers that opting for indicators that affect the latent variable is neither inherently problematic nor necessarily inferior to using reflective (effect) indicators. Our ultimate aim is to advance our understanding of models with causal/formative indicators as a viable measurement option and to reinforce their relevance in empirical research endeavors.1
Why Distinguish between Reflective (Effect) and Causal/Formative Indicators?
The issue of causal/formative indicators extends well beyond structural equation models involving latent variables. Summated rating scale construction is based on reflective (effect) indicators (Spector, 1992). Item-response theory (IRT) implicitly assumes reflective (effect) indicators (Meade & Lautenschlager, 2004). Exploratory factor analysis has room only for reflective (effect) indicators (Harman, 1976). Cronbach’s alpha is based on reflective (effect) indicators (Bollen & Lennox, 1991). In other words, nearly all of the approaches and tools to measurement in the social and behavioral sciences implicitly (if not explicitly) assume that the indicators depend on the latent variable and do not take account of the possibility of causal/formative indicators.
Is this important? We believe that it is crucial to correctly specify indicators as causal/formative or as reflective (effect) for several reasons. First, suppose that a researcher has a set of indicators, some or all of which are really causal/formative indicators. Because of this, they might not exhibit internal consistency; they might have a low Cronbach’s alpha; or a factor analysis might not reveal clear separation of factors. This, in turn, could lead the researcher to remove or discard indicators based on these traditional measure development diagnostics. In other words, perfectly valid measures might be discarded if the researcher fails to realize that they are causal/formative (Bollen & Lennox, 1991; Diamantopoulos & Winklhofer, 2001).
Another important reason the choice of causal/formative versus reflective (effect) indicators matters is that mixing these up can bias the coefficients in at least some parts of a model. Suppose that we had two variables, say Y1 and Y2 and that the true relation was that Y1 determines Y2. If a researcher mistakenly estimates a model with Y2 affecting Y1, both the coefficient for this relationship and the coefficients for other relationships in the overall model could be biased. The same is true when the relationship between an indicator and its latent variable is misspecified. Treating a causal-formative indicator as reflective (effect) would bias the indicator-latent variable relation and might bias other coefficients in the model (Jarvis et al., 2003; MacKenzie et al., 2005; Petter et al., 2007). It could be that the bias would be concentrated in that part of the model that contains the indicator to latent variable relation or the bias might spread more widely depending on the specific model and estimator. Because, for theory testing purposes, researchers seek accurate estimates of the effects of one variable on another, the misspecification of the type of indicator can undermine this goal.
Third, the effectiveness and understanding of the consequences of interventions could also be harmed when the direction of the relationship between the indicator and a latent variable is improperly specified. For instance, suppose that we are interested in how a latent variable, exposure to stress, affects cortisol levels. To keep the situation simple, consider two indicators of exposure to stress, whether a person lost a job in the last six months and whether (s)he changed residency. These are likely causal/formative indicators of the latent variable of exposure to stress. Interventions that affect whether a person loses a job or moves have direct effects on exposure to stress and indirect effects on cortisol levels. However, if the researcher treats losing a job or moving as reflective (effect) indicators of exposure to stress, then interventions that change these indicators have no effect on cortisol levels. In other words, understanding how and whether an intervention works will depend on the correct specification of causal/formative or reflective (effect) indicators.
In sum, there are several theoretical and practical reasons why researchers should care whether causal-formative or reflective (effect) indicators are used to operationalize latent variables in research models and this choice has wide-reaching implications for measurement practice. Indeed, as Table 1 shows, researchers are urged to apply both conceptual and empirical tests to determine the correct specification of indicators.
Table 1.
Conceptual Checks and Empirical Test for Determining Whether Indicators Are Causal-formative or Reflective (Effect)
| Conceptual Check | |
| Mental Experiment (see Bollen, 1989; Bollen & Lennox, 1991) | 1. Reflective (effect) Indicators: Imagine a change in latent variable net of other indicator influences. Will this lead to a change in the indicators? |
| 2. Causal-formative Indicators: Imagine a change in the indicator net of other latent variable influences. Will this lead to a change in the latent variable? | |
| Empirical Test | |
| Vanishing Tetrad Test (see Bollen & Ting, 2000) | 1. Based on hypotheses and mental experiments, formulate one or more measurement models with causal-formative indicators, reflective (effect) indicators, or some combination. |
| 2. Calculate chi-square test for each model and assess fit. | |
| 3. Compare any of the competing models that are nested in their vanishing tetrads. | |
| 4. Choose the hypothesized model with the best fit. | |
Mental experiments are one conceptual tool for determining the nature of an indicator. A researcher should imagine a change in the indicator and ask whether this change is likely to change the value of the latent variable. If so, this is theoretical evidence supporting causal/formative indicators. Alternatively, the researcher should imagine changing the latent variable and ask whether this is likely to change the value of the indicator(s). If so, this favors reflective (effect) indicators. Such mental experiments can provide conceptual support for one type of indicator over the other.
There is also an empirical test proposed by Bollen and Ting (2000) that is particularly useful when theory and substantive knowledge leave the researcher uncertain about the nature of the indicators. This Vanishing Tetrad Test for Causal indicators is available in a SAS macro (Bollen, Lennox, & Dahly, 2009; Hipp, Bauer, & Bollen, 2005) and in a Stata procedure (Bauldry & Bollen, 2015). These provide a way to empirically compare one or more specifications for the indicator-latent variable relationship.
Clarifying Terminology: What Are “Formative” Indicators?
Most definitions of latent variables (or true scores) are based on assuming that measures are reflective (effect) indicators. For instance, classical true score theory2 (Lord & Novick, 1968), factor analysis (Spearman, 1904), and IRT (Binet & Simon, 1916) are all built on the basic idea that the latent variable determines the measure. As such, these approaches are not suitable for causal/formative indicators. We thus rely on Bollen’s (2002, p. 612) definition according to which “a latent random (or nonrandom) variable is a random (or nonrandom) variable for which there is no sample realization for at least some observations in a given sample” (see also Bollen & Hoyle, 2012).3 Bollen’s (2002) definition is more general and consistent with both reflective (effect) and causal/formative indicators. Typically the latent variable is a random variable and the sample realizations are missing for all cases. Under these common conditions, the latent random variable is formally defined as a random variable without any observed values. In other words, we can use the statistical definition of random variables to provide a formal foundation for latent variables. In a less formal sense, a latent variable is a variable that is postulated because it is substantively important even though the researcher has no observed (or “realized”) values of it. As such, the latent variable is sometimes a function of its measures, sometimes a determinant of its measures, and sometimes we have measures of both types as in a MIMIC model (Joreskog & Goldberger, 1975).
Turning now to indicators, the term “formative” has not been interpreted consistently in the literature and this seems to have been a source of great confusion among many supporters and opponents alike. Our review of the relevant methodological literature has revealed several distinct types of variables that have all been labelled as “formative” by various authors. Table 2 offers a classification of the different “formative” specifications according to two key criteria, namely (a) whether there is conceptual unity among the indicators (i.e., whether the indicators all correspond to the same concept or concept dimension), and (b) whether the indicator weights are empirically estimated or pre-specified by the researcher. The meanings of estimated or pre-specified are self-evident, but conceptual unity requires some elaboration. A concept or construct must be given meaning through a definition of its intended content (Bollen, 1989; MacKenzie, 2003). This definition then guides the researcher as to which indicators fall under its umbrella and which do not (Bisbe, Batista-Foguet, & Chenhall, 2007). Indicators that correspond to the concept’s meaning exhibit conceptual unity. Those that fall outside of it, do not.
Table 2.
Alternative “Formative ” Specifications Found in the Literature
| Conceptual Unity | |||||
|---|---|---|---|---|---|
| Yes | No | ||||
| Indicator Weights | Estimated | (A) | (D) | ||
| (B) | |||||
| Pre specified | (C) | (E) | |||
In Table 2, specification A refers to what Bollen and Bauldry (2011) term “causal” indicators (see also Bollen, 2007, 2011; Bollen & Davis, 2009; Bollen & Lennox, 1991) whereby (a) the indicators (x’s) are assumed to have conceptual unity and (b) act as measures of a latent variable (η). Furthermore, though not essential to the idea of causal indicators, it is typical to assume (c) that the latent variable is influenced by a disturbance term (ζ) so that the causal indicators do not completely determine the latent variable, and (d) that the indicator coefficients (γ’s) are estimated empirically. In what follows, we use the term “causal-formative” to refer to this type of indicator where conditions (a) and (b) must hold, while (c) and (d) typically hold.
Specification B is a special case of specification A and arises when ζ=0. Here, the latent variable is completely determined by its causal-formative indicators. This can happen under certain special circumstances (see Diamantopoulos, 2006) which, however, are “extremely unlikely” in practice (Bollen & Bauldry, 2011, p. 271). Note that, formally speaking, the two specifications A and B are nested and thus it is possible to formally test whether the hypothesis of a zero disturbance term is tenable or not.4
Specification C is also a special case of specification A where ζ=0 and the indicator weights (γ*’s) are fixed to pre-specified values rather than being empirically estimated.5 Again, the plausibility of this specification can be tested against specifications A and B since all three models are nested (see Diamantopoulos & Temme, 2013 for an illustrative example).6
Specification D refers to what Bollen and Bauldry (2011) denote as “composite” indicators (see also Bollen, 2011; Grace & Bollen, 2008) whereby a set of observed variables (x’s) which are not assumed to have conceptual unity, (b) form an exact weighted linear composite (C), with (c) weights (w’s) that are typically estimated empirically. We use the term “composite-formative” to refer to this type of indicator.
Finally, specification E is a special case of Specification D, the only difference being that indicators weights (w*’s) are now pre-specified rather than empirically estimated.7
Unfortunately, references to - as well as criticisms of - “formative” indicators in the literature often fail to distinguish among the various specifications in Table 2, with confusion being the inevitable result. For example, Diamantopoulos and Winklhofer (2001) use the term “formative” to refer to specifications A and B in Table 2; Fornell and Bookstein (1982) use the same term to refer to specifications D and E; Bagozzi’s (1994) definition is so broad as to be consistent with specifications B, C, D and E; for Lee and Cadogan (2013) only specification C is legitimate but they do not see it as a special case of either A or B; Lee et al. (2013) consider specification D as a special case of specification A (and thus implicitly equate B with D); one could go on, but the reader surely gets the point. To confuse matters more, when PLS (under Mode B) is used to estimate models with “formative” indicators, it is not possible to distinguish between specification B (which involves causal-formative indicators) and C (which involves composite-formative indicators); the reason for this is that it is not possible to estimate specification A in PLS (Cenfetelli & Bassellier, 2009; Hardin, Chang, Fuller, & Torkzadeh, 2011) of which B is a special case (see Table 2).8
Careful inspection of Table 2 reveals that only causal-formative indicators (i.e. specifications A-C in Table 2) can be legitimately considered as being measures of a concept (or a dimension of a concept) because only causal-formative indicators have conceptual unity and thus “it is sensible to view the indicator as matching the idea embodied by the concept” (Bollen, 2011, p. 361). With composite-formative indicators, conceptual unity is not a requirement and, therefore, “with composite indicators and a composite variable, the goal might not be to measure a scientific concept, but more to have a summary of the effects of several variables” (Bollen, 2011, p. 366; see also Bollen & Bauldry, 2011; Grace & Bollen, 2008; Heise, 1972). Thus the x’s in Table 2 do not have the same meaning in all specifications. This is an extremely important point which, however, is lost or ignored in critical discussions of “formative” indicators. For example, Howell et al. (2013, p. 47) argue that “the distinction between causal indicators, causes, covariates, and predictors is semantic; they are mathematically identical”. This position sharply differs from ours because it implies that it is the mathematical specification that determines the underlying conceptual model rather than the other way round.9 For example, according to Howell and colleagues, the interpretation of specifications B and D should be identical despite the fact that, in the former specification, all indicators must have conceptual unity whereas in the latter the x’s “can be an arbitrary combination of variables” (Bollen & Bauldry, 2011, p. 268). In our view, theoretical considerations are critical and “a particularly important consideration applicable to both reflective and formative indicators has to do with the content adequacy of a measure” (Diamantopoulos & Siguaw, 2006, p. 276, original emphasis). We also believe that theoretical considerations should be the starting point in model building and it is with this in mind that we proceed to address the various criticisms of “formative” indicators in the literature.
Are Criticisms of “Formative” Indicators Valid?
Table 3 provides a summary of the key criticisms that have been leveled to “formative” indicators at various times, along with illustrative quotes and literature sources relating to each criticism.
Table 3.
Common Criticisms of “Formative” Indicators
| 1. | A construct measured with “formative” indicators does not exist independently of its indicators. |
| Constructs with “formative” indicators do not exist independently; are not real entities; the indicators are the construct; the construct does not exist independently of its measurement. | |
| Quotes to illustrate: | |
| “This lack of distinction between the indicators and the construct is explicit in the conceptual definition of formative measurement” (Lee et al., 2013, p. 7). | |
| “The formative model is not a measurement model, precisely because the notion of measurement presupposes that the measured attribute plays a causal role in the generation of test sources. Thus, the distinction between formative modeling and formative measurement is important” (Markus & Borsboom, 2013, p. 120). | |
| Examples of criticism:1 Borsboom et al. (2003); Edwards (2011); Lee et al. (2013, 2014); Cadogan et al. (2013); Bagozzi (2007, 2011); Edwards and Bagozzi (2000); Hardin et al. (2011); Howell et al. (2007a, 2007b); Treiblmaier, Bentler, andMair (2011); Markus and Borsboom (2013) | |
| 2. | “Formative ” indicators are causes rather than measures. |
| “Formative” indicators are observed variables that are causes, antecedents, or drivers of the latent variable. This is different than being measures of it. | |
| Quotes to illustrate: | |
| “One wonders whether it is appropriate to view formative models as measurement models in the first place. They might be better conceptualized as models for indexing or summarizing the indicators or as causal” (Borsboom et al., 2004, p. 1069). | |
| “Early literature conceptualizes causal indicators as causes of unmeasured constructs rather than as measures of latent constructs as is their common interpretation by formative measurement proponents today” (Hardin & Marcoulides, 2011, p. 759). | |
| “As long as (1) the latent variable is interpreted only in terms of the content of its reflective indicators; (2) the Xs are interpreted as causes, predictors, or covariates (call them what you wish), but not as measures; and (3) the error term is interpreted as all sources of variation in the reflectively measured latent variable not included in the model, then all is well. There is no “formative measurement” issue to discuss” (Howell, 2013, p. 20). | |
| Examples of criticism: Borsboom et al. (2004); Hardin et al. (2011); Hardin and Marcoulides (2011); Howell et al. (2007a, 2007b); Howell (2013, 2014); Markus and Borsboom (2013); Markus (2014) | |
| 3. | “Formative” indicators imply multiple dimensions to a construct and this is a liability. |
| “Formative” indicators capture multiple facets of a construct which complicates its interpretation. It is illogical to simultaneously have causal-formative and reflective indicators of the same construct. | |
| Quotes to illustrate: | |
| “When conceptually distinct measures are channeled into a single construct, the resulting construct is conceptually ambiguous” (Edwards, 2011, p. 373). | |
| “A single variable cannot have both formative and reflective content valid indicators” (Cadogan et al., 2013, p. 44). | |
| Examples of criticism: Edwards (2011); Cadogan et al. (2013); Lee et al. (2013) | |
| 4. | “Formative” indicators are assumed to be error-free which is unrealistic. |
| Measurement error is likely present in most “formative” indicators, but this error is implicitly assumed absent | |
| Quotes to illustrate: | |
| “In the formative approach, the observed variables are all thought to be measured without error, and the measurement error contributes instead to the factor itself, along with the factor’s prediction error” (Iacobucci, 2010, p. 94). | |
| “The assumption that formative measures contain no error is difficult to reconcile with the basic premise that measures are nothing more than scores collected using methods such as self-report, interview, or observation” (Edwards, 2011, p. 377). | |
| “No measure error is designated for the formative measurement model” (Bagozzi, 2011, p. 270). | |
| Examples of criticism: Edwards (2011); Iacobucci (2010); Bagozzi (2011); Edwards and Bagozzi (2000); Markus and Borsboom (2013) | |
| 5. | “Formative” indicators are inherently subject to interpretational confounding. |
| Models with “formative” indicators are not independently identified; introduction of outcomes (whether constructs or observed variables) can result in unstable indicators weights and interpretational confounding; indicator weights and disturbance term depend on external variables introduced to achieve identification; meaning of construct not stable. | |
| Quotes to illustrate: | |
| “For a formatively measured latent variable, the parameters relating the latent construct to its indicants, as well as the error term in the model, will always be a function of the observed relationships between the formative indicators and the outcome variables, whether interpretational confounding occurs or not. This makes formative measurement ambiguous, at best” (Howell et al., 2007b, p. 245). | |
| “The parameters relating the observed variables to their purported formative latent variable are functions of the number and nature of endogenous latent variables and their measures. This means that the measurement of latent formative variables depends seemingly on the consequences of these variables, as well as their presumed measures” (Bagozzi, 2007, p. 236). | |
| “Regardless of correct or incorrect specification, all formative models revealed problems associated with interpretational confounding and weakened external consistency” (Kim et al., 2010, p. 357). | |
| Examples of criticism: Edwards (2011); Kim et al. (2010); Hardin et al. (2008); Franke et al. (2008); Hardin et al. (2011); Lee et al. (2013); Howell (2013); Lee and Cadogan (2013); Bagozzi (2007, 2011); Howell et al. (2007a, 2007b); Wilcox et al. (2008); Treiblmaier et al. (2011); Howell et al. (2013); Markus and Borsboom (2013); Markus (2014); Widaman (2014) | |
| 6. | “Formative” indicators fail proportionality constraints. |
| Latent variables with “formative” indicators fail to function as point variables; (some) indicators may not have proportional effects on outcome variables; fit might be good even when external consistency is poor. | |
| Quotes to illustrate: | |
| “Internal consistency among formative indicators is not applicable, however, so external consistency becomes the sole condition for assessing the degree to which a formatively measured construct functions as a unitary entity” (Wilcox et al., 2008, p. 1226). | |
| “The degree to which a reflective measure operates as a point variable can and should be assessed through an examination of model fit. The same is true for formative measures, but there is greater reason to believe that this may be a problem for indicators that, by definition, need not have the same antecedents and consequences” (Howell et al., 2007a, p. 216). | |
| “If the formative indicators could have direct as well as mediated effects on the outcome variables, then the proportionality constraint would not necessarily hold and would not be a consideration in conceptualizing or testing formative models. However, in this case, the formative construct no longer captures the effects of the components on other variables, raising questions about the meaning and value of the formative conceptualization” (Franke et al., 2008, p. 1235). | |
| Examples of criticism: Howell et al. (2007a); Franke et al. (2008); Kim et al. (2010); Wilcox et al. (2008); Markus and Borsboom (2013) | |
| 7. | The coefficients for “formative” indicators should be set in advance. |
| Indicators weights should be apriori chosen/fixed and not empirically estimated; indicator weighting should be part of the latent variable definition (indirectly also implies that the disturbance term of the latent variable with causal-formative indicators is zero). | |
| Quotes to illustrate: | |
| “It is the job of the researcher to define the relative weightings of the formative dimensions at the time that the researcher decides to create a formative variable. There is no single ‘true’ weighting profile to be discovered by empirical research - weighting allocation is something the researcher is responsible for” (Lee & Cadogan, 2013, p. 244). | |
| “Components in formed measures (abstract formed objects or formed attributes) should not be empirically weighted” (Rossiter, 2002, p. 325). | |
| “Using an optimum set of predetermined weights in either components- or covariance-based SEM allows researchers to employ a fixed-weight composite whose weights are now included in the construct definition. This renders conceptual definitions stable across contexts” (Hardin et al., 2011, p. 301). | |
| Examples of criticism: Rossiter (2002, 2008), Hardin et al. (2011); Lee et al. (2013, 2014); Howell (2013, 2014); Cadogan et al. (2013); Cadogan and Lee (2013); Lee and Cadogan (2013); Howell et al. (2007a, 2013) | |
Two important points are worth noting in relation to Table 3. First, as already noted, different authors have different implicit conceptions of “formative” indicators in mind which they then proceed to criticize (see Table 2); thus it is not always clear whether such criticisms are intended to apply to causal-formative indicators, composite-formative indicators or both. Second, a large number of the critics develop their theoretical arguments relying - almost exclusively - on the work of scholars (e.g., Borsboom, Mellenbergh, & van Heerden, 2003, 2004) who by definition exclude causal-formative indicators from their notion of measurement; for them, “the notion of measurement presupposes that the measured attribute plays a causal role in the generation of test scores” (Markus & Borsboom, 2013, p. 120, added emphasis). As we will see shortly, the adoption of such a restrictive perspective on measurement has resulted in arguments of a tautological nature which lessens their scientific value. With these points in mind, we now proceed to address, one at a time, the various criticisms summarized in Table 3.
1. A Construct Measured with “Formative” Indicators Does Not Exist Independently of its Indicators
Concepts or constructs are the starting point in measurement where these are defined as “an idea that unites phenomena (e.g. attitudes, behaviors, traits) under a single term” (Bollen 1989, p.180). In this context, the first criticism in Table 3 suggests that constructs measured with “formative” indicators are derivable from the indicators and have no standing beyond those indicators. By implication, if you change the indicators, you will change the construct.
While it is difficult to trace the origin of this criticism, we suspect that it has emerged as a result of descriptions of the relationship between constructs and causal-formative indicators included in some highly influential papers on the topic. For example, in their widely-cited Journal of Consumer Research article, Jarvis et al. (2003, p. 201) state that “the indicators, as a group, jointly determine the conceptual and empirical meaning of the construct” and repeat the point in their Journal of Applied Psychology paper when they state that “the full meaning of the composite latent construct is derived from its measures” (MacKenzie et al., 2005, p. 712). Thus the alleged “inseparability” of the construct and its indicators has appeared in some writings on “formative” indicators. Having said that, we see several fundamental problems with this criticism including, (a) a failure to distinguish between the different meanings of “formative” indicators (see Table 2 earlier), (b) a somewhat unusual perspective on the nature of constructs, latent variables, and indicators, and (c) not realizing the analogies to effect (reflective) indicators. We elaborate on these issues below.
Part of the problem originates from not clearly distinguishing between the different meanings of “formative” indicators. If “formative” refers to what we called composite-formative (see specifications D and E in Table 2), then the composite, which is a weighted sum of the composite-formative indicators, is equated to the construct. This “construct”, however, is nothing more than the weighted sum of the observed indicators from which it is formed and we are, therefore, hesitant to give composites a theoretical standing that suggests some degree of abstraction. Indeed, if we were to engage in hypothesis testing involving abstract constructs it would be highly unusual to use composite-formative indicators.10
Causal-formative indicators, on the other hand, are much more in tune with hypothesis testing involving abstract constructs. Usually hypotheses contain ideas about the relationship between constructs and these constructs are abstract and not capable of exact measurement (Bollen, 2002). Latent variables are the “stand-ins” for the construct in a model and we use indicators as a way of gauging the degree to which a latent variable (and thus a construct) is present. Our theoretical definition of the construct provides guidance in selecting the indicators that correspond to the construct and the latent variable represents the construct in the formal model. This line of argument directly contradicts the claim that the construct does not exist independent of the indicators. To develop or select indicators of a construct requires that we know what the construct consists of; indeed, “failure to clearly define the focal construct makes it difficult to correctly specify how the construct should relate to its measures” (MacKenzie, 2003, p. 324). As such, the construct always precedes the indicators be them causal-formative or reflective (effect) indicators. Given a construct’s temporal priority, it does not make sense to claim that the indicators “create” the construct.11
Perhaps another interpretation of this criticism is that the “empirical meaning” might differ from the “intended meaning” of the construct depending on the indicators chosen. So in this sense it is the empirical meaning of the concept that is “created” by the causal-formative indicators. The chance that the indicators of a latent variable depart from the meaning assigned to a construct always exists and this is certainly possible for causal-formative indicators. But this same possibility also exists for reflective (effect) indicators and is tied to the issue of whether indicators are valid; importantly, this notion of validity originated with reflective (effect) indicators (Burt, 1976). Thus the critics are right in suggesting that causal-formative indicators might lead to unintended empirical meaning, but the same is true for reflective (effect) indicators. In brief, both causal-formative and reflective (effect) indicators might not be valid and could lead to a change in the empirical meaning of a construct. However, we see no reason to expect causal- formative indicators as being more susceptible to this problem.
In sum, the criticism that the construct does not exist independent of the selected causal-formative indicators can be rejected on multiple counts. First is that the critics often fail to distinguish composite-formative indicators from causal-formative indicators and to realize the differences in their properties; second is that the construct always precedes the selection or development of causal-formative indicators and that it is the construct that justifies the indicators and not the other way round; third is that the potential for the empirical meaning of the construct to change depending on the indicators is present for all types of indicators, not just for causal-formative indicators.
2. “Formative” Indicators Are Causes Rather Than Measures
The fundamental claim that, “formative” indicators are not measures suffers from three major problems: (a) not distinguishing the different meanings of “formative” indicators, (b) a tautological argument grounded in a definition of measurement that automatically rules out causal-formative indicators, and (c) failing to distinguish the mathematics of an equation from its substantive justification. We consider each of these issues in turn.
First, consider the confusing and mixed use of the term “formative” indicators. When “formative” is used to refer to situations (D) and (E) in Table 2, that is, when the meaning of “formative” is equivalent to what we call composite-formative indicators, then we would agree that these are not measures. Furthermore, they might not be causes either. We say this because a composite variable is a weighted sum of the composite-formative indicators and this relation is generally not seen as causal but simply as a convenient way to form a summary composite variable. For instance, we could be interested in comparing the combined effects of race, gender, and age on income to that of education. A sheaf coefficient (Heise, 1972) combines the estimated effects of race, gender and age into a single standardized coefficient that can be contrasted with a standardized coefficient of education. In so doing, it forms a composite of race, gender, and age without assuming that these are measures of a single theoretically-defined construct. In general, we see composite-formative indicators as neither measures nor causes (antecedents) of the composite variable that they create, but rather as a way to summarize several variables in a single variable.
Alternatively, if the term “formative” is used to refer to situations (A) - (C) in Table 2, that is, if we are dealing with causal-formative indicators, then we do view these as being measures. But what about those critics who argue that even causal-formative indicators are not measures? This brings us to the second major problem, namely the definitions of measurement relied on by these critics. These definitions require that to be a measure, a variable must depend on the latent variable. For instance, “the only thing that all measurement procedures have in common is … that there is an attribute out there that, somewhere in the long and complicated chain of events leading up to the measurement outcome, is playing a causal role in determining what values the measurements will take” (Borsboom et al., 2004, p. 1063). If you define measures as observed variables that depend on the latent variable, then causal-formative indicators are (obviously) not measures. But this is essentially a tautological argument that is true by definition. And as we explain below, it is not necessary to define measurement so that it only applies to reflective (effect) indicators.
Before stating the definition of measurement that we use, some background is useful (see also Bollen, 1989, chapter 6). We see concepts or constructs as theoretical ideas that suggest that a series of phenomena have something in common (Barki, 2008). For instance, we might observe individuals who exhibit negative affect, have unhappy facial expressions, and say that they are sad. Depressed affect is a construct that we might use to summarize this collection of observations (Bainter & Bollen, 2014). A term such as depressed affect is thus a name or label assigned to a construct, but to explain the meaning that we give to the construct requires a theoretical definition. The theoretical definition assigns meaning to the term as used by a researcher. It should be sufficiently clear so as to communicate the denotation of the construct and its dimensions or distinct components. Each dimension of a construct is represented by a latent variable in a formal model.12 To know whether an indicator is a measure of the latent variable requires that we assess whether the indicator corresponds to the definition of the construct in question (DeVellis, 2003). Without the construct and its definition, we cannot evaluate whether an indicator is a measure.
With this background summary, we are now ready to define measurement as “the process by which a concept is linked to one or more latent variables, and these are linked to observed variables” (Bollen, 1989, p. 180). Once we have the latent variable that represents the construct in a model, we need to ask how the indicator is related to the latent variable. The dominant assumption is that the latent variable affects the indicator so that the latter is an effect or reflective measure. But another possibility is that the indicator affects the latent variable as with causal-formative indicators. In either case, the indicator is a measure of the latent variable, even though the nature of their relationships is different. Now, if you define measurement as only involving indicators depending on a latent variable, then this excludes causal-formative indicators based on tautological logic. But other definitions that do not define away this possibility readily accommodate causal-formative indicators.
A third flaw in the critique of causal-formative indicators as measures is that some critics have focused on the mathematical expression for causal-formative indicators rather than the substantive justification that led to the equation. The quotes from Table 3 illustrate how some critics use the similarity in equations to equate the meaning of the x’s without giving any weight to the justifications for the x’s. Consider the following equation:
| (1) |
Without giving the rationale for this equation, the x’s could have several meanings. For instance, one researcher might use this equation in a model that predicts the latent η variable from three distinct variables that have little in common other than that they influence η. In another analysis, the x’s might be three measures of η that correspond to the definition of the latent variable that represents the focal construct. In yet another application, two of the x’s might be causal-formative indicators and while a third is a distinct causal variable. A researcher cannot distinguish between these cases by only having the mathematical expression in equation (1). It is the justification that underlies the equation that distinguishes one meaning of the x’s from the others. If a researcher intends these to be measures and if they correspond to the theoretical definition of the construct, then these three x’s are causal-formative indicators. Alternatively, if these are three determinants or covariates of n that lack conceptual unity, then we should treat them as distinct causes or covariates of n. The equation stays the same and it is the context that determines its meaning.
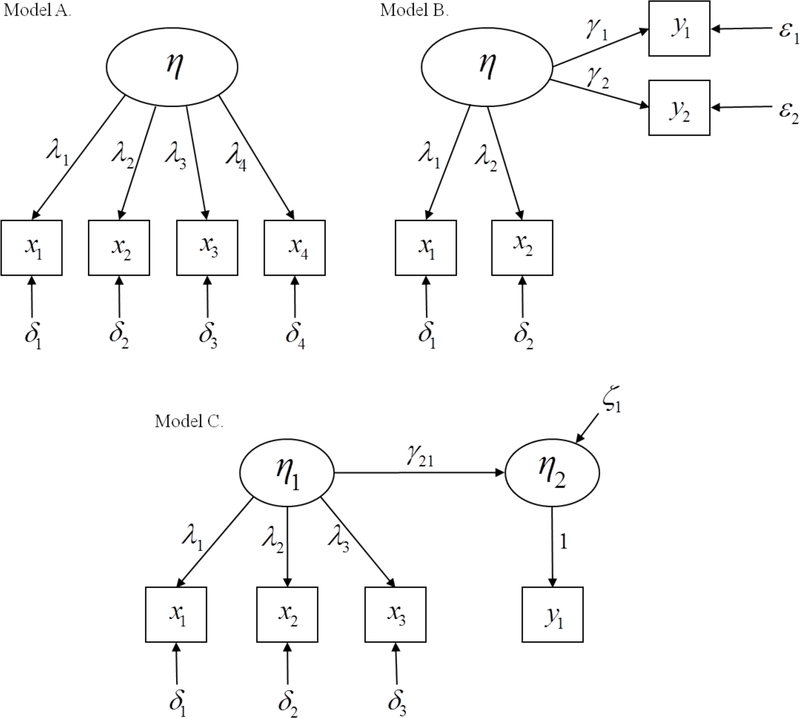
The issue can also be illustrated by reference to reflective (effect) indicators. Just as causal-formative indicators can be labeled as causes instead of measures, reflective (effect) indicators can be labeled as outcomes rather than measures or as measures of different outcomes. Consider for example the three models shown in Figure 1. Model A would be invariably interpreted as a single latent variable (η) measured by four reflective (effect) indicators (x1-x4). Model B, on the other hand, shows a reflectively-measured latent variable (η) with two indicators (x1 and x2) impacting two observed outcomes (y1 and y2); finally, Model C shows a reflectively-measured latent variable (η1) with three indicators (x1-x3) influencing another latent variable (η2) measured by a single indicator (y1). What is common about all three models (and several others that could easily be created) is that they are statistically indistinguishable and will all produce identical fit. It is not possible to distinguish between them solely on the basis of their formal (mathematical) specification; as Wang, Engelhard, and Lu (2014, p. 158) aptly put it “it is not possible to classify indicators solely by using empirical analyses or simulations without careful attention to the variables that the indicators are designed to measure”.
Figure 1.
Three equivalent models that illustrate that indicators might be measures, outcomes, or indicators of different outcomes
Determining whether we have causal-formative indicators or distinct causes of a latent variable or if we have reflective (effect) indicators or distinct outcomes of the latent variable is not something that can be done just by looking at an equation. To be causal-formative indicators or reflective (effect) indicators requires that the variables concerned are measures that correspond to the theoretical definition of the concept; “if they do not, then this is sufficient grounds to eliminate an indicator” (Bollen, 2011, p. 363).
In sum, the claim that causal-formative indicators are not measures is incorrect. It is based on failing to separate the different uses of the term “formative”, on tautological definitions of measurement, and on equating the (very) different meanings that a single equation might represent.
3. “Formative” Indicators Imply Multiple Dimensions to a Construct and This Is a Liability
The core argument underlying this criticism is that “formative” indicators are by nature multidimensional: “There is little dispute that formative measures typically describe multiple dimensions…” (Edwards, 2011, p. 373). We dispute this.
To explain why, we need to clarify what we mean by dimensionality and distinguish between conceptual and empirical dimensionality. Conceptual dimensionality refers to the number of distinct constituent parts (i.e. dimensions or components) of a construct that appear in its theoretical definition. Each distinct part is represented by a separate latent variable (Bollen, 1989). Empirical dimensionality, on the other hand, is the actual number of distinct parts (latent variables) present in the data. In general, we expect the number of conceptual dimensions to be the same as the number of empirical dimensions, though it is possible for two theoretically distinct dimensions to have a single empirical dimension (e.g., Bollen & Grandjean, 1981). Focusing on the common situation rather than on the exception, both conceptual and empirical dimensionalities are relevant to reflective (effect) and causal-formative indicators.
The first point to emphasize is that the dimensionality of a construct resides at the theoretical level. The construct definition should reveal whether there are one or more constituent parts to it. Indeed, a mark of a useful theoretical definition is whether it clearly communicates the number of conceptual dimensions (MacKenzie, 2003).
Note also that it is the concept that has dimensions, not the indicators. The meaning of the dimension of indicators is unclear. Reflective (effect) indicators might depend on more than one latent variable and causal indicators might affect more than one latent variable. But this is different than saying that either type of indicator is multidimensional.13 For reflective (effect) indicators, the term “factor complexity” is used to refer to the number of latent variables that influence it (e.g. Netemeyer, Bearden, & Sharma, 2003). There is no analogous expression for causal-formative indicators.
Virtually all of the work on empirical dimensionality assumes reflective (effect) indicators. For example, in his classic article, McDonald (1981, p. 101, original emphasis) states that “a set of n tests is considered of dimension r if the residuals of the n variables … about their regression on r further (hypothetical) variables, the common factors, are uncorrelated, i.e. if the partial correlations of the test scores are all zero if the common factors are partialled out”. Similarly, Kumar and Dillon (1987, p. 440) consider a set of items to be unidimensional “if and only if their covariation is accounted for by a common factor model (possibly non-linear) with just one common factor”, while Netemeyer et al. (2003, p. 20) state that “a set of items is considered to be unidimensional if the correlations among them can be accounted for by a single common factor”. Thus discussions of empirical dimensionality assume reflective (effect) indicators as based on the common factor model. As such, the rationale for criticizing causal-formative indicators as multidimensional is not well-founded.
As a general guideline we suggest that if, according to its theoretical definition, the focal construct is unidimensional and if the indicators correspond to that definition, then on the face of it the indicators are tied to a single dimension. This face validity check is true for causal-formative or reflective (effect) indicators. The empirical checks for reflective (effect) indicators (based on factor analysis) were mentioned in the last paragraph. Empirical checks for causal-formative indicators are not developed, but we briefly suggest an idea. If we have an identified model with causal indicators such as the MIMIC model (Jöreskog & Goldberger, 1975) and the overall fit of the model is poor, then one possible explanation is that there are two latent variables rather than one which mediate the effects of the causal-formative indicators on the outcome variables. A second latent variable could be introduced and those causal-formative indicators that influence it included and the fit of the new model tested. Of course, this new latent variable must affect at least two outcome variables in order to identify the model. And we must keep in mind that another possible reason for poor model fit in a MIMIC model is that, rather than one latent variable, there is none.
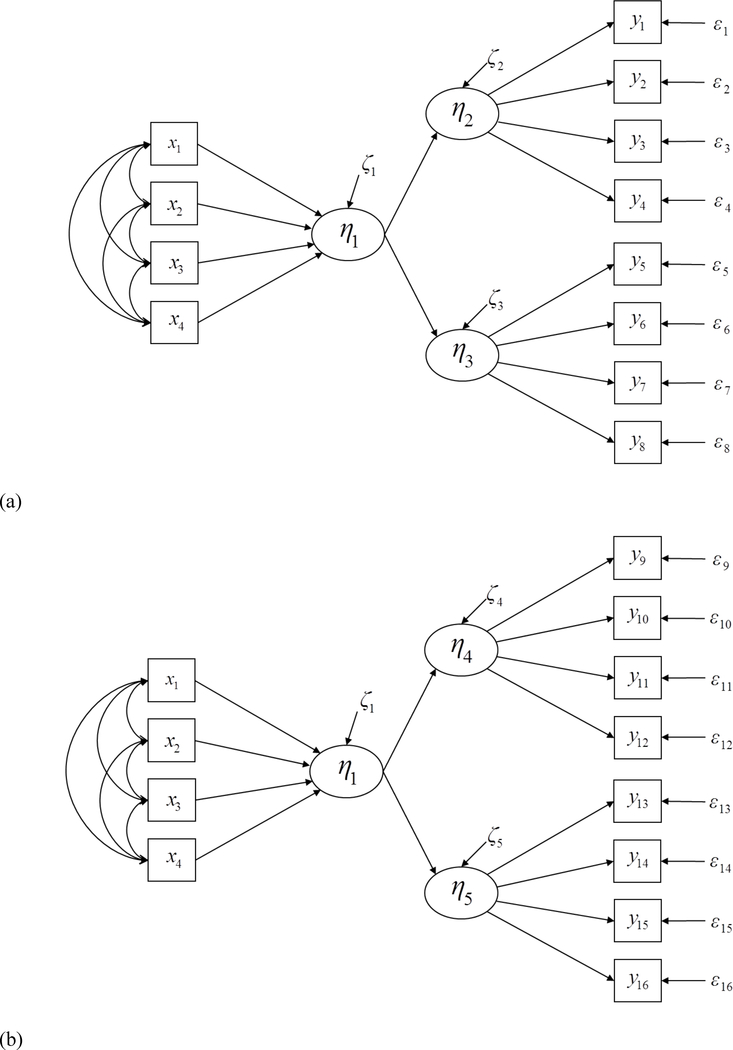
To further illustrate this testing strategy with causal-formative indicators, consider Figure 2. Figure 2a shows a MIMIC model with four causal-formative indicators and four reflective (effect) indicators with a single intervening latent variable, η1. In Figure 2b, on the other hand, the causal-formative indicators measure two latent variables rather than one; whereby x1 and x2 measure η1, x4 measures η2, and x3 is a causal-formative indicator for both η1 and η2; in this sense x3 is analogous to an effect indicator that is influenced by two latent variables. Similarly, the reflective (effect) indicators either measure a single latent variable, (η1 − see Figure 2a) or break into measures of two latent variables (η1 and η2 - see Figure 2b). If the model in Figure 2b were true, we would expect an inadequate fit for Figure 2a provided that the data and structure have sufficient statistical power to detect the problem; conversely, we would expect a good fit for the model in Figure 2b. Furthermore, if the latter model were true, we would expect that the coefficients from the causal-formative indicators to their respective latent variables and from the latent variables to their effect indicators would be of sufficient statistical and substantive significance. In this fashion, we could test a single-versus two-dimensional model for the causal-formative indicators. It is even possible that all the causal-formative indicators influence both latent variables; however, if this were true we would expect a poor fit also for the model in Figure 2b. These are just a couple of examples of numerous possibilities, but they illustrate how causal-formative indicators might influence more than one latent variable.
Figure 2.
Illustration of dimensionality test for causal-formative indicators
To sum up, concepts or constructs have dimensions; indicators do not. Causal-formative or reflective (effect) indicators ideally measure a single dimension of a construct, though it sometimes happens that they measure more than one latent variable. There is nothing inherent about causal-formative indicators to lead them to always measure more than one dimension and therefore the conclusion that “the multidimensionality of formative measures should be considered a liability” (Edwards, 2011, p. 374) does not stand up to scrutiny.
4. “Formative” Indicators Are Assumed to be Error-free Which Is Unrealistic
A potentially confusing aspect of a model with causal-formative indicators is the role of the error term. In the “classic” causal-formative indicator model (see Specification A in Table 2), the error term directly influences the latent variable and not the indicator. The error consists of all influences on the latent variable besides the included causal-formative indicators (see e.g., Diamantopoulos, 2006). This error should be uncorrelated with the included causal-formative indicators in the same way that the disturbance of a regression equation is uncorrelated with the exogenous variables in the equation. In other words, the causal-formative indicators directly affect the latent variable and the error of the latent variable is uncorrelated with the indicators. Contrast this with the error terms in an effect (reflective) indicator measurement model. Here the errors include all other variables that influence the indicator besides its latent variable. The error affects the indicator rather than the error affecting the latent variable.
The causal-formative indicators are chosen because they correspond to the theoretical definition of the target concept. But what happens if the causal-formative indicators themselves contain unwanted error? If our standard is perfect measurement with zero error, then virtually all observed variables (including causal-formative indicators) would come up short. But practically speaking, if a causal-formative indicator has negligible measurement error, then directly linking it to the focal latent variable is probably doing little harm. However, as Bollen and Ting (2000, p. 11) observe, “in some situations the causal indicators are flawed measures” and uncorrected error in the causal-formative indicator will bias the estimate of the coefficient from the indicator to the latent variable. Thus if there is significant error, then it makes sense to explicitly model this by creating a separate latent variable that underlies each indicator with a corresponding measurement error. The resulting model will then have the latent counterparts of the original formative indicators impacting the focal latent variable. These new variables are still causal-formative variables but they are latent rather than observed. Thus the presence of measurement error does not change the situation for the focal latent variable (for further details on this modified model, see Edwards and Bagozzi (2000, Figure 5B), Diamantopoulos (2006, Figure 2), Diamantopoulos, Riefler, and Roth (2008, Figure 3) and Edwards (2011, Figure 5)).
Figure 5.
A simple MIMIC model
Figure 3.
A three-indicator model
In brief, any model with explanatory variables with non-negligible measurement errors should take account of the error or run the risk of inaccurate estimates. On this count, there is no reason to single out causal-formative indicators. The same standards apply to them as to any other type of explanatory variables.
5. “Formative” Indicators Are Inherently Subject to Interpretational Confounding
Interpretational confounding is “…the assignment of empirical meaning to an unobserved variable which is other than the meaning assigned to it by an individual a priori to estimating unknown parameters. Inferences based on the unobserved variable then become ambiguous and need not be consistent across separate models.” (Burt, 1976, p. 4). As the quotes in Table 3 show, this critique suggests that interpretational confounding is a particular problem for causal-formative indicators.14
There are at least two points of agreement between most critics and defenders of causal-formative indicators. First is that both causal-formative indicators and reflective (effect) indicators are potentially subject to interpretational confounding.15 Second is that if the coefficients between indicators and latent variables significantly shift depending on the other endogenous variables in the model, then this is evidence of interpretational confounding (see e.g., Bollen, 2007; Howell et al., 2007a, 2007b). The disagreement comes over the critics’ claim that interpretational confounding is essentially a side effect of using causal-formative indicators whereas the same is not true for effect (reflective) indicators. In other words, causal-formative indicators are particularly prone to interpretational confounding.
What is the basis for this claim? The primary evidence offered to support it is the shift in the coefficient estimates for the causal-formative indicators in a MIMIC model when the critic changes the magnitude of the covariances either between the causal-formative and reflective indicators or just the covariances among the latter. Bagozzi (2007) uses a simulation example where he changes only the covariances of the causal-formative indicators with the effect indicators and he points to the resulting shift in the coefficients of the causal-formative indicators as a limitation of them. His conclusion is that the coefficients of the causal-formative indicators depend on the magnitude of the covariances of the causal-formative and effect indicators and hence there is an inherent instability leading to interpretational confounding. Howell et al. (2007a) take a similar approach. Using Bollen’s (2007) Figure 1A model and data, they modify the covariance of the reflective items and nothing else and use the change in the estimate of the error variance for the latent variable as evidence of a problem with causal-formative indicators.
There are several problems with the above analyses that undermine the critics. First is that the latter seem to believe that it is the SEM parameters that depend on covariances of observed variables rather than that the covariances of observed variables depend on the SEM parameters which is the view that underlies structural modeling. In SEM, the model is constructed first. Based on the model, we derive the model-implied covariance matrix. The model-implied covariance matrix states each covariance and variance as an exact function of the parameters in the hypothesized model. A shift in a population covariance occurs in one of two ways.16 Either the magnitude of the parameters involved in the covariance shift or the specification of the model changes, and the changes lead to a new implied covariance. Shifts in the values of the implied covariances of the observed variables do not occur without one of these events. If an analyst changes a covariance, then it can only occur for one of these two reasons. Assuming that the model keeps the same set of relationships (same structure), then the change in the covariance must be accommodated by a change in the values of some parameters. So it is logical (and hardly surprising) that by changing certain covariances we can change the values of the coefficients of the causal-formative indicators.
To make these points more clear, we construct a simple model with a single latent variable (η1) and with one causal-formative indicator (x1) and two effect (reflective) indicators (y1, y2). The relevant path diagram is given in Figure 3.
The model equations are:
| (2) |
| (3) |
| (4) |
with the usual assumptions that the errors and disturbances have means of zeros and are uncorrelated with the exogenous variables and with each other. The three observed variables (x1, y1, y2) means that we have three variances and three covariances. The implied covariances are:
| (5) |
| (6) |
| (7) |
From these model implied covariances, we see that the coefficient for the causal-formative indicator equals:
| (8) |
If we keep the model the same, but change the numerical value of the covariance of y1 and x1, then of course the coefficient of the causal-formative indicator must change given equation (8) above. For instance, if COV(y1, x1) is 2 to begin with and the VAR( x1) is 1, then the coefficient is 2; if we switch the covariance to be 1 while keeping the variance at 1, then the new coefficient becomes 1. The critics suggest that this property is somehow a flaw of causal-formative indicators when in reality it is just a property of model-implied covariances. If the values of covariances or variances differ, this must result from one or more parameters in the model taking different values, because it is the model parameters that determine the variances and covariances.
Another flaw of the argument that interpretational confounding is inherent with causal-formative indicators is that the same logic would lead us to conclude that effect (reflective) indicators are also inherently subject to interpretational confounding. Staying with the same model, we can solve for λ21 from the implied covariance equations leading to:
| (9) |
If only the COV(y2, x1) differs, this is enough to change the factor loading of the effect (reflective) indicators for y2. Following the same logic as the critics, this would be evidence that effect (reflective) indicators are inherently subject to interpretational confounding because they can take different values when only the covariances of two variables differ.
But we reject this logic. As we illustrate above, the covariances of observed variables are a function of one or more model parameters. If the covariance is made to take a different value for the same model structure, then this could only result from different numerical values of one or more parameters as long as we stay with the assumption that the model is valid. We could make the factor loadings differ if we kept the same model, but changed the values of covariances of variables that include the factor loadings. This follows from an understanding of the implied covariance matrix and it has little to do with interpretational confounding.
In short, neither causal-formative nor reflective (effect) indicators are inherently subject to interpretational confounding. Instead, if we see the coefficient for the same causal-formative or effect (reflective) indicator differing when variables are added or dropped from a model, then this is evidence of structural misspecification as argued in Bollen (2007). If the same variable’s coefficient differs across studies, it is either evidence of a different population with different parameters or even a different structure, or of structural misspecification.
Another line of empirical attack estimates two models with the same causal-formative indicators, but a different set of effect (reflective) indicators or latent endogenous variables that depend on the latent variable measured by the causal-formative indicators. Wilcox et al. (2008) and Kim et al. (2010) have models with causal-formative indicators influencing a latent variable which then influences two other latent variables as in Figure 4a. In a second model, one or both of these outcome latent variables are exchanged for another as in Figure 4b. It is then claimed that these models with different sets of outcome latent variables each have a good fit, but that the coefficients for the causal-formative indicators change.
Figure 4.
Two models with same predictors but different outcomes
A major limitation of Wilcox et al. (2008) and Kim et al. (2010) is that neither article tests whether all outcome latent variables are indeed effects of the same latent variable as would be required if the model were correctly specified. That is, these authors run separate models with just two outcome latent variables at a time. Bainter and Bollen (2014) use the data reported in Wilcox et al. (2008) to estimate whether all outcome latent variables are indeed effects of the same latent variable as is implicit in their argument. They find that when all outcome variables are considered, the fit of the model is poor and the evidence of structural misspecification is strong.17
In sum, the arguments that causal-formative indicators are inherently subject to interpretational confounding do not stand up to closer scrutiny. One problem is that the critics treat the parameters of a SEM as dependent on the covariances of the observed variables rather than the model parameters determining the covariances. A second problem is that the empirical tests that purport to show that causal-formative indicators differ by outcome, do not include all outcomes simultaneously so as to see whether such a model fits the data. In the one case when this is checked (Bainter & Bollen, 2014), the model is inadequate suggesting model misspecification as the source of shifts in coefficients.
6. “Formative” Indicators Fail Proportionality Constraints
To explain the meaning of proportionality constraints, consider a simple MIMIC model with two causal indicators and two effect (reflective) indicators as in Figure 5. The equations of the model are:
| (10) |
| (11) |
| (12) |
where the usual assumptions of errors with means of zero and errors that are uncorrelated with each other and with the exogenous variables hold. Substituting the right hand side of the equation for η in the first two equations leads to:
| (13) |
| (14) |
Notice that the ratio of the coefficients for x1 in the y2 and y1 equations is . The ratio of the coefficients for x2 in the y2 and y1 equations is . If there were more causal-formative indicators, the ratio of the coefficients would continue to equal λ2 and this is the proportionality constraint that follows when the influence of the causal-formative indicators on the effect (reflective) indicators are fully mediated through a single latent variable. If a causal-formative indicator also has a direct effect on one or more reflective indicators, then the proportionality constraint need not hold.18
Franke et al. (2008, p. 1235) question the value of a mediating latent variable if a number of the causal-formative indicators have direct effects on the outcome variables. In general, we agree with this point. However, if one or two of a group of causal-formative indicators have direct effects on the reflective indicators for well-justified reasons, it can still be useful to specify a latent variable that totally mediates the influences of all the others. Although not an identical situation, this would be analogous to having an association between two effect indicators that persists even after controlling for their common latent variable. Correlated measurement errors are a common example of this. Method factors would be another. Or consider differential item functioning (DIF) with effect indicators. A covariate might influence both the latent variable and the indicator when a group (e.g., males) responds differently to an item even net of the value of the latent variable. But if we had too many correlated errors or too many DIF indicators, we would rightly question the overall model. Similarly, if too many of the causal-formative indicators had unmediated impacts on the effect indicators or outcome variables, we would question the utility of the measurement model and its indicators.
In conclusion, proportionality constraints offer a test for assessing the quality of causal-formative indicators rather than constitute a flaw of the latter. Just as with reflective (effect) indicators the possibility exists that they may depend on multiple latent variables and/or method factors, causal-formative indicators may sometimes fail to satisfy proportionality constraints. If too many indicators fail, we rightly would question their validity.
7. The Coefficients for “Formative” Indicators Should be Set in Advance
As put forward by the critics, the essence of this argument is grounded in criticisms #1 and #2 in Table 3. Given that the construct supposedly does not exist independently of its “formative” indicators (i.e., there is no latent variable involved) and given the latter are not measures of a (non-existent) construct, it makes no sense to estimate any parameters because “the idea of estimation is meaningful only if there is something to be estimated” (Borsboom et al., 2003, p. 209). In other words, “the formative model is not a measurement model … although it might satisfy a conditioned response, a desire to undertake testing of hypotheses about formative indicators and their relationships with the formative variable, the fact remains that these relationships should not be estimated; rather the relationships should be part of the construct definition, and so cannot be inferred by statistical approaches or MIMIC models” (Cadogan et al., 2013, p. 43). Thus, allegedly, the correct approach is to pre-set the indicator weights because “the only true scores for formative weightings are those defined by the researcher” (Lee & Cadogan, 2013, p. 244).
Our previous responses to the first two criticisms in Table 2 have shown that a construct can very well be distinguished from its causal-formative indicators and that the latter can be legitimately viewed as measures of the latent variable representing the focal construct in the model. Our responses have also shown that there is a world of difference between causal-formative indicators and composite-formative indicators although this is too frequently ignored.19 Finally, our responses have demonstrated that a lot of the problems specifically attributed to causal-formative indicators also apply to reflective (effect) indicators. Thus there is no compelling reason to suggest that models with causal-formative indicators should not in principle be subjected to estimation.
Note that we are not advocating that (specific) parameter estimates should never be fixed by the researcher. Indeed, we fully agree with Rigdon (2013, p. 26) that “specifying models with parameters mostly fixed - minimizing the number of free parameters - enhances rigor (Mulaik, 2009, pp. 342–345) and increases statistical power (MacCallum, Browne, Sugawara, & Hazuki, 1996, p. 142)”. However, this applies equally to models with causal-formative indicators and to those with reflective (effect) indicators. Moreover, the fact that one decides to fix certain parameters in a given model based on theory or prior evidence does not mean that one should not test whether these fixed parameters (and the resulting model as a whole) are indeed consistent with the empirical data. As already pointed out in connection with Table 2, models with fixed parameters are special cases of a more general model specification and nested model tests can readily be employed for comparison purposes (e.g., see Diamantopoulos & Temme, 2013; Hardin et al., 2011). It is therefore difficult to see why some critics take the position of strongly advocating that the values of predefined weights should be based on theory but at the same time recommending that no testing should be undertaken to empirically confirm (or otherwise) the choice of weights (see in particular Cadogan & Lee, 2013; Cadogan et al., 2013; Lee et al., 2014). Our own position on this issue is simple: irrespective of whether one is dealing with causal- formative or reflective (effect) indicators, “the relationships between the constructs and the measures should … be thought of as hypotheses that need to be evaluated” (Petter et al., 2007, p. 624). This holds regardless of whether or not some (all) indicator coefficients are fixed a priori by the researcher.
As a final point it is worth noting that some critics suggest that fixing weights to pre-specified values overcomes the problem of interpretational confounding (see criticism #5 in Table 3).20 For example, according to Howell (2013, p. 20), “when the weights used to form the composite are part of the composite variable’s definition, interpretational confounding is avoided”. However, other critics argue exactly the opposite. Thus Hardin et al. (2008, p. 531) argue that “at least when retention is based upon the significance of formative indicator weights, researchers have at their disposal an empirical tool that can be used to evaluate the validity of formative indicators. If this metric is abandoned, and instead, researchers’ subjective perceptions of indicator contribution are utilized, capturing the conceptual meaning of latent constructs in a consistent manner becomes even less likely”. While it is not our intention to resolve differences of opinion between the critics, suffice it to say that interpretational confounding is not solved by fixing the indicator weights; if this was the case, then this solution would have long been adopted with reflective (effect) indicator models as it is in such models that the notion of interpretational confounding was first introduced (Burt, 1976).
To conclude, neither the rationale offered by the critics for fixing the coefficients of causal-formative indicators to pre-specified values nor the alleged benefit of such a practice in terms of eliminating interpretational confounding seems to be justified.
Concluding Remarks
Science does not operate by shutting doors. Censorship of ideas - however novel or controversial - is a dangerous thing and runs against the very nature of academic discourse. We have noticed that recent critical writings on causal-formative indicators have adopted an increasingly aggressive and/or dismissive tone even to the point of openly calling for a moratorium on causal indicators (e.g., see Hardin & Marcoulides, 2011).
But why such hostility towards causal/formative indicators despite their increased diffusion in diverse literatures? We suspect that one reason is that the very idea of causal/formative indicators runs against conventional wisdom in measurement. The reflective (effect) indicator model has dominated measurement thinking for more than a century. Nearly all of the treatments of measurement in contemporary psychology and related disciplines are based on the implicit assumption of indicators depending on latent variables. The same applies to the measurement diagnostics (e.g., Cronbach’s alpha and factor analysis) that are typically used to assess psychometric properties of measurement scales. Entrenched positions change slowly.
Another reason is perhaps the widespread confusion that exists in the literature among the several types of nontraditional indicators (see Table 2 in the paper). Even today, authors simply refer to “formative” indicators with no further qualification and readers cannot tell which type of formative indicator is of interest. So the confusion among indicator types has hindered broader/faster acceptance of what we call causal-formative indicators.
Furthermore, misunderstandings about the properties of causal-formative indicators might have also slowed progress with the adoption of the latter. For instance, as we note in the paper, the (false) claim that causal-formative indicators are inherently subject to interpretational confounding has most probably scared some potential users away. Similar misunderstandings apply to dimensionality and measurement error issues in relation to causal-formative indicators.
Finally, identification issues are also more complex with causal-formative indicators and this might have also discouraged some researchers from using them. Nowadays, there is (much) more guidance on this issue (e.g., Bollen & Davis, 2009; Diamantopoulos, 2011), but is perhaps diffusing through the field somewhat slowly.
We never have and still do not recommend replacing reflective (effect) indicators with causal-formative indicators unless there are sound reasons for doing so. We also do not believe that causal-formative indicators are inherently superior to reflective (effect) indicators or vice-versa. But - as our responses to the critics have hopefully shown - we do not accept the argument that causal-formative indicators are inherently inferior to reflective (effect) indicators. Indeed, we see little scientific value in placing causal-formative indicators against reflective (effect) indicators in a tug of war. There is no reason why both types of indicators cannot happily coexist even within the same model. And there is certainly no reason why different approaches cannot be used to assess the validity of measures depending on whether these are specified as reflective (effect) indicators versus causal-formative indicators (Bollen, 2011; Diamantopoulos & Siguaw, 2006). What we do argue is that researchers define their concept, choose corresponding indicators, and that they consider whether the indicators depend on or influence the latent variable that they measure.
In conclusion, contrary to a moratorium, we look forward to further constructive exchanges regarding the specification and validation of models with different types of indicators. Our door is open.
Acknowledgments
The authors would like to thank the editor and three anonymous reviewers for helpful comments on previous drafts of this paper.
Footnotes
One reviewer suggested that a formal mathematical theory of measurement be developed for causal-formative indicators. Though we agree with this goal, it is also premature as it presupposes broad acceptance of the idea of causal-formative indicators as measures. Our paper is more focused toward making the case that such indicators are indeed measures.
Steyer, Mayer, Geiser, and Cole (2015) provide a recent review and revision of measurement in the true score tradition.
Bollen (2002) contrasts his definition of latent variables with other ones including the true score definition. We refer readers to this source to see the differences in these formal definitions.
This is only possible with covariance structure analysis (CSA) methods but not with partial least squares (PLS) estimation (for details, see Diamantopoulos, 2011).
For different approaches to pre-specifying weights, see Rossiter (2002), Hardin, Chang, Fuller, and Torkzadeh (2011) and Lee et al. (2013).
In principle, it is also possible to have a nonzero disturbance with weights set in advance; however, we have not come across such a situation in literature and therefore do not discuss it further.
This is the case of “fixed-weight composites” noted by Grace and Bollen (2008).
This is an important but little understood shortcoming of PLS and one of the reasons why “relying on PLS for measure development purposes is not generally recommended” (Diamantopoulos, 2011, p. 354).
As an aside, note that a corresponding claim can also easily be made for reflective indicators, i.e. “the distinction between reflective indicators, effects, and outcomes is semantic; they are mathematically identical”.
As will become evident when discussing criticism #2, composite-formative indicators are not measures of constructs and, therefore, cannot be used to operationalize the latter for theory-testing purposes.
This temporal priority is made very clear by Diamantopoulos and Winklhofer (2001, p. 271, added emphasis) who state, in no uncertain terms, that “the items used as indicators must cover the scope of the latent variables as described under the content specification”.
To simplify our discussion, we restrict ourselves to unidimensional constructs represented in the model by a single latent variable.
Failure to appreciate this point has led some critics to conclude that causal-formative indicators cannot logically coexist with effect (reflective) indicators within the same model. For example, in discussing a MIMIC model (Jöreskog & Goldberger, 1975), Cadogan, Lee, and Chamberlain (2013, pp. 34–44, added emphasis) state that “if the MIMIC model’s reflective items are unidimensional (as reflective items should be), and if its formative items are multidimensional (as formative items should be), and if … η is a valid representation of the formative items, and the reflective items are valid representations of η, then the single entity, η, is simultaneously unidimensional and multidimensional. Such a state of affairs is a logical impossibility, and so we conclude that a single variable cannot have both formative and reflective content valid indicators”.
Note that if criticisms #1 and #2 in Table 3 were to simultaneously hold, then interpretational confounding cannot be a deficiency of causal-formative indicators; if the construct does not exist independently and if the indicators are not measures then how can Burt’s (1976) definition possibly apply?
After all, Burt’s (1976) original paper that introduced interpretational confounding focused exclusively on reflective indicators.
Here we refer to the population covariances to avoid changes that can occur just due to sampling fluctuations.
Bainter and Bollen (2014) also requested but were denied the data for Kim et al. (2010) so that their example could not be subjected to the same type of test.
Bollen and Davis (2009 [1994]) suggested that the proportionality constraints in a model with causal-formative indicators is sometimes testable even when all parameters of the model are not identified.
Consider, for example, the following statement by Lee et al. (2013, p. 14, original emphasis): “when constructing a formative variable, the researcher is making a statement that ‘these components form this composite in this manner’”.
This seems to be a tautological argument given the definition of interpretational confounding offered by Burt (1976) and embraced by the critics (see our response to criticism #5 earlier). If there is no “estimating of unknown parameters” (Burt, 1976, p. 4) - because the latter are fixed - the notion of interpretational confounding becomes irrelevant.
Contributor Information
Kenneth A. Bollen, University of North Carolina at Chapel Hill
Adamantios Diamantopoulos, University of Vienna.
References
- Bagozzi RP (1994). Structural equation models in marketing research: Basic principles In Bagozzi RP (Ed.), Principles of marketing research. Oxford: Blackwell Publishing. [Google Scholar]
- Bagozzi RP (2007). On the meaning of formative measurement and how it differs from reflective measurement: Comment on Howell, Breivik, and Wilcox (2007). Psychological Methods, 12(2), 229–237. doi: 10.1037/1082-989X.12.2.229 [DOI] [PubMed] [Google Scholar]
- Bagozzi RP (2011). Measurement and meaning in information systems and organizational research: Methodological and philosophical foundations. MIS Quarterly, 35(2), 261–292. [Google Scholar]
- Bainter S, & Bollen KA (2014). Interpretational confounding or confounded interpretations of causal indicators? Measurement: Interdisciplinary Research and Perspectives, 12(4), 125–140. doi: 10.1080/15366367.2014.968503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barki H (2008). Thar’s gold in them thar constructs. The Data Base for Advances in Information Systems, 39(3), 9–20. doi: 10.1145/1390673.1390677 [DOI] [Google Scholar]
- Bauldry S & Bollen KA (2015). Tetrad: A set of tetrad commands for confirmatory tetrad analysis. Unpublished manuscript. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binet A, & Simon Th. (1916). The development of intelligence in children: The Binet-Simon Scale Publications of the Training School at Vineland New Jersey Department of Research, 11. E. S. Kite (Trans.). Baltimore: Williams & Wilkins. [Google Scholar]
- Bisbe J, Batista-Foguet J-M, & Chenhall R (2007). Defining management accounting constructs: A methodological note on the risks of conceptual misspecification. Accounting, Organizations and Society, 32(7–8), 789–820. doi: 10.1016/j.aos.2006.09.010 [DOI] [Google Scholar]
- Blalock HM Jr. (1963). Correlated independent variables: The problem of multicollinearity. Social Forces, 42(2), 233–237. doi: 10.1093/sf/42.2.233 [DOI] [Google Scholar]
- Blalock HM Jr. (1964). Causal inferences in nonexperimental research. Chapel Hill, NC: University of North Carolina Press. [Google Scholar]
- Blalock HM Jr. (1968). The measurement problem: A gap between the languages of theory and research In Blalock HM & Blalock AB (Eds.), Methodology in social research. New York: McGraw-Hill. [Google Scholar]
- Blalock HM Jr. (1971). Causal models involving unmeasured variables in stimulus-response situations In Blalock HM Jr. (Ed.), Causal models in the social sciences (pp. 335–347). Chicago, IL: Aldine Press. [Google Scholar]
- Bollen KA (1989). Structural equations with latent variables. New York: John Wiley & Sons. [Google Scholar]
- Bollen KA (2002). Latent variables in psychology and the social sciences. Annual Review of Psychology, 53, 605–634. doi: 10.1146/annurev.psych.53.100901.135239 [DOI] [PubMed] [Google Scholar]
- Bollen KA (2007). Interpretational confounding is due to misspecification, not to type of indicator: Comment on Howell, Breivik, and Wilcox. Psychological Methods, 12(2), 219–228. doi: 10.1037/1082-989X.12.2.219 [DOI] [PubMed] [Google Scholar]
- Bollen KA (2011). Evaluating effect, composite, and causal indicators in structural equation models. MIS Quarterly, 35(2), 359–372. [Google Scholar]
- Bollen KA, & Bauldry S (2011). Three cs in measurement models: Causal indicators, composite indicators, and covariates. Psychological Methods, 16(3), 265–284. doi: 10.1037/a0024448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollen KA, & Davis WR (2009 [1994]). Causal indicator models: Identification, estimation, and testing. Structural Equation Modeling, 16(3), 498–522. doi: 10.1080/10705510903008253 [DOI] [Google Scholar]
- Bollen KA, & Grandjean BD (1981). The dimension(s) of democracy: Further issues in the measurement and effects of political democracy. American Sociological Review, 46(5), 651–659. http://www.jstor.org/stable/2094946 [Google Scholar]
- Bollen KA, & Hoyle RH (2012). Latent variables in structural equation models In Hoyle RH (Ed.), Handbook of structural equation modeling (pp. 56–67). New York: Guilford Publications. [Google Scholar]
- Bollen KA, & Lennox R (1991). Conventional wisdom on measurement: A structural equation perspective. Psychological Bulletin, 110(2), 305–314. doi: 10.1037/0033-2909.110.2.305 [DOI] [Google Scholar]
- Bollen KA, Lennox R & Dahly DL (2009). Practical application of the vanishing tetrad test for causal indicator measurement models: An example from health- related quality of life. Statistics in Medicine 28, 1524–36. [DOI] [PubMed] [Google Scholar]
- Bollen KA, & Ting K-F (2000). A tetrad test for causal indicators. Psychological Methods, 5(1), 3–22. doi: 10.1037/1082-989X.5.1.3 [DOI] [PubMed] [Google Scholar]
- Borsboom D, Mellenbergh GJ, & van Heerden J (2003). The Theoretical Status of Latent Variables. Psychological Review, 110(2), 203–219. doi: 10.1037/0033-295X.110.2.203 [DOI] [PubMed] [Google Scholar]
- Borsboom D, Mellenbergh GJ, & van Heerden J (2004). The concept of validity. Psychological Review, 111(4), 1061–1071. doi: 10.1037/0033-295X.111.4.1061 [DOI] [PubMed] [Google Scholar]
- Burt RS (1976). Interpretational confounding of unobserved variables in structural equation models. Sociological Methods Research, 5(1), 3–52. doi: 10.1177/004912417600500101 [DOI] [Google Scholar]
- Cadogan JW, & Lee N (2013). Improper use of endogenous formative variables. Journal of Business Research, 66(2), 233–241. doi: 10.1016/j.jbusres.2012.08.006 [DOI] [Google Scholar]
- Cadogan JW, Lee N, & Chamberlain L (2013). Formative variables are unreal variables: Why the formative MIMIC model is invalid. Academy of Marketing Science Review, 3, 38–49. doi: 10.1007/s13162-013-0038-9 [DOI] [Google Scholar]
- Cenfetelli RT, & Bassellier G (2009). Interpretation of formative measurement in information systems research. MIS Quarterly, 33(4), 689–707. [Google Scholar]
- DeVellis RF (2003). Scale development: Theory and applications. (2nd ed.). Newbury Park, CA: Sage Publications. [Google Scholar]
- Diamantopoulos A (2006). The error term in formative measurement models: Interpretation and modeling implications. Journal of Modelling in Management, 1(1), 7–17. doi: 10.1108/17465660610667775 [DOI] [Google Scholar]
- Diamantopoulos A (2011). Incorporating formative measures into covariance-based structural equation models. MIS Quarterly, 35(2), 335–358. [Google Scholar]
- Diamantopoulos A (2013). MIMIC models and formative measurement: Some thoughts on Lee, Cadogan & Chamberlain. Academy of Marketing Science Review, 3(1), 30–37. doi: 10.1007/s13162-013-0035-z [DOI] [Google Scholar]
- Diamantopoulos A, Riefler P, & Roth KP (2008). Advancing formative measurement models. Journal of Business Research, 61(12), 1203–1218. doi: 10.1016/j.jbusres.2008.01.009 [DOI] [Google Scholar]
- Diamantopoulos A, & Siguaw JA (2006). Formative versus reflective indicators in organizational measure development: A Comparison and Empirical Illustration. British Journal of Management, 17, 263–282. doi: 10.1111/j.1467-8551.2006.00500.x [DOI] [Google Scholar]
- Diamantopoulos A, & Temme D (2013). MIMIC models, formative indicators and the joys of research. Academy of Marketing Science Review, 3(3), 160–170. doi: 10.1007/s13162-013-0050-0 [DOI] [Google Scholar]
- Diamantopoulos A, & Winklhofer HM (2001). Index construction with formative indicators: An alternative to scale development. Journal of Marketing Research, 38(2), 269–277. 10.1509/jmkr.38.2.269.18845 [DOI] [Google Scholar]
- Edwards JR (2011). The fallacy of formative measurement. Organizational Research Methods, 14(2), 370–388. doi: 10.1177/1094428110378369 [DOI] [Google Scholar]
- Edwards JR, & Bagozzi RP (2000). On the nature and direction of relationships between constructs and measures. Psychological Methods, 5(2), 155–174. doi: 10.1037/1082-989X.5.2.155 [DOI] [PubMed] [Google Scholar]
- Eggert A, & Fassott G (2003). Zur Verwendung formativer und reflektiver Indikatoren in Strukturgleichungsmodellen: Ergebnisse einer Metaanalyse und Anwendungsempfehlungen. Kaiserslauterner Schriftenreihe Marketing, 20, Kaiserslautern. [Google Scholar]
- Fassott G (2006). Operationalisierung latenter Variablen in Strukturgleichungsmodellen: Eine Standortbestimmung. Zeitschrift für betriebswirtschaftliche Forschung, 58(Februar), 67–88. [Google Scholar]
- Fornell C, & Bookstein FL (1982). A comparative analysis of two structural equation models: LISREL and PLS applied to market data In Fornell C (Ed.), A Second Generation of Multivariate Analysis (pp. 289–324). New York: Praeger. [Google Scholar]
- Franke GR, Preacher KJ, & Rigdon EE (2008). Proportional structural effects of formative indicators. Journal of Business Research, 61(12), 1229–1237. doi: 10.1016/j.jbusres.2008.01.011 [DOI] [Google Scholar]
- Grace JB, & Bollen KA (2008). Representing general theoretical concepts in structural equation models: The role of composite variables. Environmental and Ecological Statistics, 15(2), 191–213. doi: 10.1007/s10651-007-0047-7 [DOI] [Google Scholar]
- Hardin AM, Chang JC-J, & Fuller MA (2008). Formative vs. reflective measurement: Comment on Marakas, Johnson, and Clay (2007). Journal of the Association for Information Systems, 9(9), 519–534. http://digitalscholarship.unlv.edu/met_fac_articles/6 [Google Scholar]
- Hardin A, Chang J, Fuller M, & Torkzadeh G (2011). Formative measurement and academic research: In search of measurement theory. Educational and Psychological Measurement, 71(2), 281–305. doi: 10.1177/0013164410370208 [DOI] [Google Scholar]
- Hardin A, & Marcoulides GA (2011). A commentary on the use of formative measurement. Educational and Psychological Measurement, 71(5), 753–764. doi: 10.1177/0013164411414270 [DOI] [Google Scholar]
- Harman HH (1976). Modern factor analysis (3rd Ed.). Chicago, IL: The University Press of Chicago. [Google Scholar]
- Heise DR (1972). Employing nominal variables, induced variables, and block variables in path analyses. Sociological Methods & Research, 1(2), 147–173. doi : 10.1177/004912417200100201 [DOI] [Google Scholar]
- Hipp J, Bauer DJ, & Bollen KA (2005). Conducting tetrad tests of model fit and contrasts of tetrad-nested models: A new SAS macro. Structural Equation Modeling, 12, 76–93. [Google Scholar]
- Howell RD (2013). Conceptual clarity in measurement - constructs, composites, and causes: A commentary on Lee, Cagogan and Chamberlain. AMS Review, 3(1), 18–23. doi: 10.1007/s13162-013-0036-y [DOI] [Google Scholar]
- Howell RD (2014).What is the latent variable in causal indicator models? Measurement: Interdisciplinary Research and Perspectives, 12(4), 141–145. doi: 10.1080/15366367.2014.980105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell RD, Breivik E, & Wilcox JB (2007a). Reconsidering formative measurement. Psychological Methods, 12(2), 205–218. doi: 10.1037/1082-989X.12.2.205 [DOI] [PubMed] [Google Scholar]
- Howell RD, Breivik E, & Wilcox JB (2007b). Is formative measurement really measurement? Reply to Bollen (2007) and Bagozzi (2007). Psychological Methods, 12(2), 238–245. doi: 10.1037/1082-989X.12.2.238 [DOI] [PubMed] [Google Scholar]
- Howell RD, Breivik E, & Wilcox JB (2013). Formative measurement: A critical perspective. The DATA BASE for Advances in Information Systems, 44(4), 44–55. doi: 10.1145/2544415.2544418 [DOI] [Google Scholar]
- Iacobucci D (2010). Structural equations modeling: Fit indices, sample size, and advanced topics. Journal of Consumer Psychology, 20(1), 90–98. doi: 10.1016/jjcps.2009.09.003 [DOI] [Google Scholar]
- Jarvis CB, MacKenzie SB, & Podsakoff PM (2003). A critical review of construct indicators and measurement model misspecification in marketing and consumer research. Journal of Consumer Research, 30(2), 199–218. doi: 10.1086/376806 [DOI] [Google Scholar]
- Joreskog KG, & Goldberger AS (1975). Estimation of a model with multiple indicators and multiple causes of a single latent variable. Journal of the American Statistical Association, 10, 631–639. doi: 10.1080/01621459.1975.10482485 [DOI] [Google Scholar]
- Kim G, Shin B, & Grover V (2010). Investigating two contradictory views of formative measurement in information systems research. MIS Quarterly, 34(2), 345–365. [Google Scholar]
- Kumar A, & Dillon WR (1987). Some further remarks on measurement-structure interaction and the unidimensionality of constructs. Journal of Marketing Research, 24(4), 438–444. [Google Scholar]
- Lee N, & Cadogan JW (2013). Problems with formative and higher order reflective variables. Journal of Business Research, 66(2), 242–247. doi: 10.1016/j.jbusres.2012.08.004 [DOI] [Google Scholar]
- Lee N, Cadogan JW, & Chamberlain L (2013). The MIMIC model and formative variables: Problems and solutions. Academy of Marketing Science Review, 3(1), 3–17. doi: 10.1007/s13162-013-0033-1 [DOI] [Google Scholar]
- Lee N, Cadogan JW, & Chamberlain L (2014). Material and efficient cause interpretations of the formative model: resolving misunderstandings and clarifying conceptual language. Academy of Marketing Science Review, 4(1–2), 32–43. doi: 10.1007/s13162-013-0058-5 [DOI] [Google Scholar]
- Lord FM, & Novick MR (1968). Statistical theories of mental test scores. Reading MA: Addison-Wesley Publishing Company. [Google Scholar]
- MacCallum RC, Browne M, Sugawara W, & Hazuki M (1996). Power analysis and determination of sample size for covariance structure modeling. Psychological Methods, 1(2), 130–149. doi: 10.1037/1082-989X.1.2.130 [DOI] [Google Scholar]
- MacKenzie SB (2003). The dangers of poor construct conceptualization. Journal of the Academy of Marketing Science, 31(3), 323–326. doi: 10.1177/0092070303254130 [DOI] [Google Scholar]
- MacKenzie SB, Podsakoff PM, & Jarvis CB (2005). The problem of measurement model misspecification in behavioral and organizational research and some recommended solutions. Journal of Applied Psychology, 90(4), 710–730. doi: 10.1037/0021-9010.90.4.710 [DOI] [PubMed] [Google Scholar]
- Markus KA (2014). Unfished business in clarifying causal measurement: Commentary on Bainter and Bollen. Measurement: Interdisciplinary Research and Perspectives, 12(4), 146–150. doi: 10.1080/15366367.2014.980106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markus KA, & Borsboom D (2013). Frontiers of test validity theory: Measurement, causation, and meaning. New York, NY: Routledge. [Google Scholar]
- McDonald RP 1981. The dimensionality of tests and items. British Journal of Mathematical and Statistical Psychology, 34(1), 100–7. doi: 10.1111/j.2044-8317.1981.tb00621.x [DOI] [Google Scholar]
- Meade AW, & Lautenschlager GJ (2004). A comparison of item response theory and confirmatory factor analytic methodologies for establishing measurement equivalence/invariance. Organizational Research Methods, 7(4), 361–388. doi : 10.1177/1094428104268027 [DOI] [Google Scholar]
- Mulaik SA (2009). Linear causal modeling with structural equations. Boca Raton, FL: CRC Press. [Google Scholar]
- Netemeyer RG, Bearden WO, & Sharma S (2003). Scaling procedures: Issues and applications. London: Sage Publications. [Google Scholar]
- Petter S, Rai A, & Straub D (2012). The critical importance of construct measurement specification: a response to Aguirre-Urreta and Marakas. MIS Quarterly, 36(1), 147–155. [Google Scholar]
- Petter S, Straub D, & Rai A (2007). Specifying formative constructs in information systems research. MIS Quarterly, 31(4), 623–656. [Google Scholar]
- Podsakoff NP, Shen W, & Podsakoff PM (2006). The role of formative measurement models in strategic management research: Review, critique, and implications for future research. Research Methodology in Strategy and Management, 3, 197–252. doi: 10.1016/S1479-8387(06)03008-6 [DOI] [Google Scholar]
- Rigdon EW (2013). Lee, Cadogan, and Chamberlain: An excellent point … but what about that iceberg? AMS Review, 3(1), 24–29. doi: 10.1007/s13162-013-0034-0 [DOI] [Google Scholar]
- Rossiter JR (2002). The C-OAR-SE procedure for scale development in marketing. International Journal of Research in Marketing, 19(4), 305–335. doi: 10.1016/S0167-8116(02)00097-6 [DOI] [Google Scholar]
- Rossiter JR (2008). Content validity of measures of abstract constructs in management and organizational research. British Journal of Management, 19(4), 380–388. doi: 10.1111/j.1467-8551.2008.00587.x [DOI] [Google Scholar]
- Roy S, Tarafdar M, Ragu-Nathan TS, & Marsillac E (2012). The effect of misspecification of reflective and formative constructs in operations and manufacturing management research. The Electronic Journal of Business Research Methods, 10(1), 34–52. [Google Scholar]
- Spearman C (1904). “General Intelligence,” objectively determined and measured. The American Journal of Psychology, 15(2), 201–292. http://www.jstor.org/stable/1412107 [Google Scholar]
- Spector PE (1992). Summatedrating scale construction: An introduction. Newbury Park, CA: Sage Publications. [Google Scholar]
- Steyer R, Mayer A, Geiser C, & Cole DA (2015). A theory of states and traits-revised. Annual Review of Clinical Psychology, 11, 71–98. doi: 10.1146/annurev-clinpsy-032813-153719. [DOI] [PubMed] [Google Scholar]
- Treiblmaier H, Bentler PM, & Mair P (2011). Formative constructs implemented via common factors. Structural Equation Modeling: A Multidisciplinary Journal, 18(1), 1–17. doi: 10.1080/10705511.2011.532693 [DOI] [Google Scholar]
- Wang J, Engelhard G Jr., & Lu Z (2014). Clarifying the conceptualization of indicators within different models. Measurement: Interdisciplinary Research and Perspectives, 12(4), 155–159. doi: 10.1080/15366367.2014.981124 [DOI] [Google Scholar]
- Widaman KF (2014). Much ado about nothing-or at best, very little. Measurement: Interdisciplinary Research and Perspectives, 12(4), 165–168. doi: 10.1080/15366367.2014.980109 [DOI] [Google Scholar]
- Wilcox JB, Howell RD, & Breivik E (2008). Questions about formative measurement. Journal of Business Research, 61(12), 1219–1228. doi: 10.1016/j.jbusres.2008.01.010 [DOI] [Google Scholar]