Abstract
Rhythmic oscillations of up to 600 Hz in grouped neurons frequently occur in the brains of animals. These high-frequency oscillations can be sustained in calcium-free conditions and may be blocked by gap junction blockers, implying a key role for electrical synapses in oscillation generation. Mathematical theories have been developed to demonstrate oscillations mediated by electrical synapses without chemical modulation; however, these models have not been verified in animals. Here we report that oscillations of up to 686 Hz are induced by paired spikes of short spike intervals (SIs) in a junction-coupled network. To initiate oscillations, it was essential that the second spike was elicited during the relative refractory period. The second spike suffered from slow propagation speed and failure to transmit through a low-conductance junction. Thus, at the spike initiation site, paired spikes of short SIs triggered one transjunctional spike in the postsynaptic neuron. At distant synaptic sites, two transjunctional spikes were produced as the SI increased during spike propagation. Consequently, spike collision of these asymmetrical transjunctional spikes occurred in the interconnected network. The remaining single spike reverberated in a network serving as an oscillator center. Paired-spike-induced oscillations were modeled by computer simulation and verified electrophysiologically in a network that mediates the tail-flip escape response of crayfish.
Keywords: high-frequency oscillation, reverberation, electrical synapse, gap junction, spike propagation, rhythm
Introduction
Oscillatory behaviors such as locomotion and respiration are a result of rhythmic excitations of the corresponding neural systems. Synchronized rhythmic oscillations of neurons in brain regions have been observed. Such oscillations occur at various frequencies of up to 600 Hz (Watanabe and Grundfest, 1961; Buzsáki et al., 1992; Jones and Barth, 1999; Marin et al., 2005; Spampanato and Mody, 2007). For example, fast ripples in the frequency range of 200–500 Hz have also been observed in the epileptogenic regions of patients (Bragin et al., 1999; Urrestarazu et al., 2007). Studies of the mechanisms underlying oscillations in animals suggest that high-frequency discharge is much easier to obtain from networks with special geometric architectures than from single bursting neurons, because of limitations imposed by ion channel dynamics (Mann-Metzer and Yarom, 1999). In a special geometric architecture, synaptic modulations purportedly play important roles in oscillation induction.
In terms of synaptic modulations, it is proposed that chemical inhibitory synapses restrict the direction of the spike propagation that is essential for oscillation initiation, whereas electrical synapses assist in phase synchronization (Dzhala and Staley, 2004). However, a variety of studies have shown that oscillations in the CA1 and CA3 regions of the hippocampus can be induced in the presence of GABAA-, AMPA-, or NMDA-receptor antagonists, or in calcium-free conditions, which rules out a role for chemical synapses in oscillation induction (Jefferys and Haas, 1982; Taylor and Dudek, 1982; Draguhn et al., 1998; Jones and Barth, 2002). In addition, very fast electroencephalography in human hippocampal slices (Perez-Velazquez et al., 1994; Traub et al., 2001) as well as oscillations in rat hippocampal slices are blocked by the application of gap junction blockers, implying that electrical synapses play important roles in oscillation generation (Jefferys and Haas, 1982; Perez-Velazquez et al., 1994; Draguhn et al., 1998; Traub et al., 2001; Jones and Barth, 2002). Various neural network theoretical models have been developed to explain these electrical synapse-dependent oscillations (Abbott and van Vreeswijk, 1993; Skinner et al., 1997; Lewis and Rinzel, 2000; Tegnér et al., 2002; Traub et al., 2005). Unfortunately, these models cannot be verified in animals. In this study, we found that a spike elicited during the relative refractory period suffers from slow propagation speed and failure of transmission through a low-conductance junction. Thus, paired spikes of short spike interval (SI) would trigger one transjunctional spike. The SI of a spike pair increases during spike propagation in axon. Consequently, two transjunctional spikes are produced at distant synaptic sites. These transmitted spikes collide in the junction-coupled network and leave a remaining spike reverberating in the neurons that form a closed-looped network. Thus, asymmetrical transmission of a paired spike through a low-conductance electrical synapse induces high-frequency oscillations in a junction-coupled network. Here we studied self-sustained oscillations by computer simulations and electrophysiological experiments in a network responsible for the tail-flip escape behavior of crayfish.
Materials and Methods
Animal preparations.
Both male and female juvenile crayfish (Procambarus clarkii, 2.5–4 cm) used in this study were raised in the laboratory. After animal anesthetization by placement in a 4°C water bath for 20–30 min, the nerve cord was dissected and pinned dorsal side up on Sylgard 184 (Dow Corning) in a 4.5-cm-diameter Petri dish. The preparation was kept at 22–24°C in crayfish saline (210 mm NaCl, 15 mm CaCl2, 5.4 mm KCl, 2.6 mm MgCl2, and 5 mm HEPES, pH 7.4) throughout the experiment. All chemicals were from Sigma-Aldrich.
Electrophysiology.
A pair of bipolar electrodes made from Teflon-coated silver wires (70 μm in diameter; A-M Systems) was placed on the lateral giant (LG) axon to elicit spikes with a stimulating strength of 1.5–3 V and a duration of 0.1 ms. Intracellular microelectrodes used to record LG spikes were filled with 3 m KCl and had resistances ranging from 10 to 15 MΩ. The electrode holders were encapsulated with copper foils whose potentials were driven by the output of preamplifiers to reduce cross talk between electrodes. Electrophysiological recording experiments were performed according to the procedures described previously (Tsai et al., 2005). After capacitance neutralization by negative capacitance compensation (Guld, 1962), spike signals on all electrodes were recorded and digitized at 160 kHz by a PCI-6251 data-acquisition card (National Instrument) and saved on a PC for later numerical analyses.
Computer simulation.
Standard Hodgkin–Huxley axons (gNabar = 0.12 S/cm2; gKbar = 0.036 S/cm2; gleak = 0.3 mS/cm2; ENa = 50 mV; EK = −77 mV; EL = −53.4 mV) were used to simulate the properties of spike propagations with NEURON software (Hines et al., 2007). The gap junction used for simulation followed Ohm's law: the current passing through a gap junction was directly proportional to the potential difference between cells and the conductivity of the gap junction. Other simulation parameters included the following: cell length (L), 25 μm; diameter, 25 μm; membrane capacitance, 1 μF/cm2; temperature, 25°C; and cytoplasm volume resistance, 35.4 Ω · cm. The cell length L was replaced by 50 mm for simulating spike propagation delay along the long axon. In the three-cell model, L was replaced by 5 mm for network oscillation, and gap junction conductivities of 1.05 μS were used.
Results
Spike interval increases during spike propagation
For computer simulation, an active Hodgkin–Huxley axon cable was constructed to generate spikes (Hodgkin and Huxley, 1952). Spike generation is associated with an increase in Na+ channel conductance followed by an increase in K+ channel conductance. Activation of the Na+ channels allows Na+ ions to enter the cell, depolarizing the membrane, which activates K+ channels and allows the membrane to repolarize. The activation of K+ channels also generates an afterhyperpolarization (AHP), which makes the firing of an additional spike impossible regardless of the stimulation intensity. After the AHP, more current influx is required to elicit additional spikes, because of the remaining activation of K+ channels. In our simulation studies, up to a 640% increase of injected current was needed when we attempted spike initiation soon after AHP (supplemental Fig. 1, available at www.jneurosci.org as supplemental material).
The activation of K+ channels not only makes a spike hard to fire but also affects the spike propagation speed in a long axon. To study the propagation speed of spikes elicited during the refractory period, paired spikes were generated in which the second spike of the pair (designated the “second spike”) was obtained at various times after AHP. In pairs with a short SI, the SI at the spike initiation site increased from 1.38 to 2.42 ms after 40 mm of axonal propagation (Fig. 1A). SI values of paired spikes dramatically increased at the onset of spike propagation and eventually plateaued after propagation (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). This increase arose from the lower propagation velocity of the second spike, because the propagation time for the first spike of the pair (designated the “leading spike”) was the same as that of an isolated single spike. In contrast, a longer initial SI (2.63 ms) of paired spikes remained unchanged after the same distance of spike propagation (Fig. 1A).
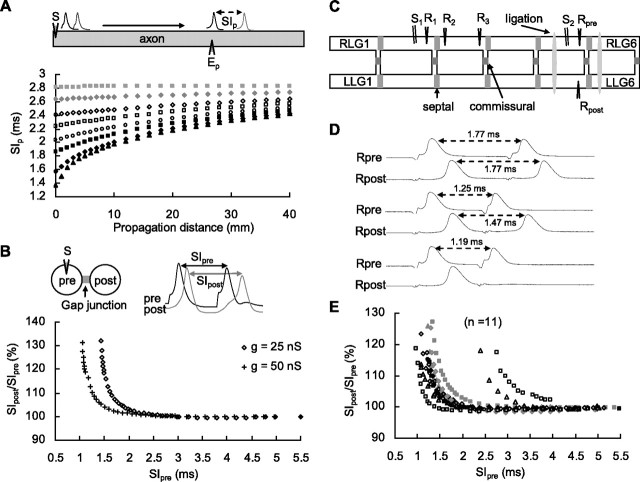
Figure 1.
A–E, Spike propagation delay in simulation (A, B) and in the LG network (C–E). A, Current pulses of 20 nA/100 μs were injected (S) to initiate a paired spike that was recorded at various propagation distances (Ep). B, Paired current injection (S) into a presynaptic neuron connected to a postsynaptic neuron with gap junctions of either 50 or 25 nS in conductance. The SIs of paired spikes in presynaptic and postsynaptic axons (SIpre and SIpost) were measured. C, The LG neurons on the left side of ganglia (from LLG1 to LLG6) couple with septal junctions. Six pairs of LG neurons (from LLG1, RLG1 to LLG6, RLG6) are each connected with commissural junctions. Two biphasic pulses (0.8–3 V, 0.1 ms of duration) on an LG axon (S1 or S2) initiated the paired spikes. Recordings were made by microelectrodes (R1, R2, R3, Rpre, and Rpost) located near each side of septum. Ligations were made on the connectives of LG neurons in the fifth ganglia (RLG5, LLG5) and the sixth ganglia (RLG6, LLG6) for the measurements of commissural transmission. D, Paired spikes recorded in precommissural and postcommissural axons (Rpre and Rpost) for SI measurements. E, The ratio of SIpost/SIpre is plotted against SIpre to illustrate the change in SIs after commissural transmissions.
The conductance of the gap junction also affected the spike traveling speed. The spike transmission delay across a gap junction was calculated from the ratio of SI values of a paired spike before (SIpre) and after (SIpost) electrical synapse transmission (Fig. 1B, top). When the second spike was evoked after a relative refractory period (RRP) of 2 ms, the SIpost/SIpre ratio remained unchanged; this indicated that propagation of the second spike was normal unless it was evoked during the RRP. Similar to the propagation delay in the axon, paired spikes of shorter SIpre in which the second spike was elicited very soon after the AHP during the RRP had a greater increase in SIpost/SIpre (Fig. 1B). The change in SIpost/SIpre occurred more readily when the paired spikes were transmitted through a weaker conductance junction (Fig. 1B, 25 nS vs 50 nS).
To investigate whether the spike propagation delay observed in our computer simulations also occurred in real axons, we used an electrically coupled LG network that mediates the tail-flip escape behavior of crayfish. This LG network consists of six pairs of LG neurons that receive excitatory inputs from the sensory afferents innervating the abdominal exoskeleton surface hairs. In each abdominal ganglion, two small axonal branches from the LG neuron cord axons connect to each other through a commissural junction, creating an “H” shape. The cord LG axons of the adjacent ganglia are also coupled with the septal junction; thus, six H-shaped axons form a ladder-like network in the abdomen (Fig. 1C). Both the septal and commissural junctions of the LG network are nonrectifying (Watanabe and Grundfest, 1961). Therefore, once an LG spike is elicited, it produces both transseptal and transcommissural spikes with a very short transmission delay. Consequently, the paired spikes that propagate caudally collide and disappear in the last abdominal ganglion. The paired spikes that propagate rostrally excite the motor neurons that innervate the abdominal flexor muscles, allowing the animal to escape from predators (Furshpan and Potter, 1959; Ye et al., 2004).
To study the spike propagation speed, two direct electrical shocks of various stimulus intervals were applied to the LG axon to produce paired spikes of varying initial SIs. The propagation or transmission delays of paired spikes along the axon and across the junctions, respectively, were measured by recording electrodes at various recording sites (Fig. 1C, R1, R2, R3, Rpre, and Rpost). The LG spike elicited during the refractory period suffered from a slow transmitting speed across the commissural junction, consistent with simulation results (Fig. 1B). After commissural transmission, in the fifth abdominal ganglion the SI values of the paired spikes increased from 1.25 to 1.47 ms (Fig. 1D, middle paired traces), whereas the SI of the presynaptic axon (1.77 ms) remained unchanged (Fig. 1D, top paired traces). Paired spikes in the presynaptic neuron with shorter SI values were associated with longer SI time lags in the postsynaptic neuron (Fig. 1E). Similar SI time lags after axonal propagation and septal transmission were also observed in all 17 preparations investigated (data not shown).
The SIpost/SIpre ratio increased when the second spike was elicited within 1.5 ms, because the refractory period of the LG spike was ∼1.5 ms (Fig. 1E). The maximal increase in the SIpost/SIpre ratio varied from animal to animal, with greater ratio increases being consistently associated with a shorter SIpre (Fig. 1E). However, the true maximal SIpost/SIpre ratio could not be measured for two reasons. First, when the SIpre became very short, the second spike failed to transmit through the junction. Second, attempts to evoke the second spike very soon after the leading spike sometimes failed, making measurement of SIpre impossible.
Although the RRP of the LG spike was quite constant, the onset of the increase in SIpost/SIpre varied from animal to animal (Fig. 1E). Our simulation results indicated that this increase occurred more readily when the spike was transmitted across a weaker conductance junction (Fig. 1B). However, the correlation between the onset of the ratio increase and the junctional conductance was studied indirectly; the extreme volume of the LG axons made direct measurement of commissural conductance between the LG neurons impossible. Thus, we estimated the conductance of junctions by measuring the transcommissural delay of a single spike in the 11 preparations in which we measured the SIpost/SIpre ratio in Figure 1E. The transcommissural delays for a single spike ranged from 0.4 to 1.2 ms (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). A longer transmitting delay reflects a lower junctional conductance between these two junction-coupled LG neurons. In the two preparations with 0.8 and 1.1 ms of transcommissural delays for a single spike, SIs of 2.4 and 2.8 ms were needed for the second spike to transmit through commissural junctions successfully (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). Consistent with the simulation results in Figure 1B, the increase in the SIpost/SIpre ratio in two preparations was obtained with a longer SIpre when paired spike transmitted through a junction of lower conductance (Fig. 1E). For the other nine preparations, the shorter transmitting time for a single spike (∼0.5 ms) (supplemental Fig. 2A, available at www.jneurosci.org as supplemental material) reflected stronger junction coupling that allowed paired spikes of short SI (1–1.5 ms) (supplemental Fig. 2, available at www.jneurosci.org as supplemental material) to transmit successfully. In agreement with these observations, the increases in the SIpost/SIpre ratio were observed in nine preparations with shorter SIpre. In addition to spike transmission through commissural junctions, similar SI time lags after axonal propagation and septal transmission were observed in another 17 preparations investigated (data not shown).
The increase in SIpost after spike transmission might be due in part to the faster transmission speed of the leading spike or the lower transmission velocity of the second spike. Therefore, a single LG spike was evoked, and the spike transmission time across a junction was measured and compared. Both the spike propagation time and transmission time delay of the leading spike were the same as that of an isolated single spike. Thus, increases in the SIpost/SIpre ratio arose from the lower propagation velocity of the second spike. The second spike, but not the leading spike, failed to trigger a corresponding transcommissural spike when the SI of a paired spike was short. For example, paired spikes with an SI of 1.19 ms were evoked successfully in the RLG5 neuron. Under this condition, the second spike failed to transmit through the commissural junction, and the SIpost was unable to measure (Fig. 1D, bottom paired traces). This is because the SI of the paired spike in the presynaptic neuron approached the absolute refractory period of the leading spike. Thus, the maximal SIpost/SIpre ratio was plotted from the shortest SIpre evoked in the presynaptic neuron against the successful SIpost measured in the postsynaptic neuron in each animal (Fig. 1E).
Transmission failures through gap junctions were also observed in our simulation studies (Fig. 1B). An SI of 1.05 ms was the shortest SI value that would allow the paired spikes to successfully transmit through a gap junction of 50 nS in conductance; an SI of 1.44 ms was the shortest SI value for transmission through a gap junction of 25 nS in conductance (Fig. 1B). These results suggest that both the spike interval of paired spikes and the conductance of a junction are major limiting factors for successful spike transmission through a gap junction. In summary, spike transmission across weaker conductance junctions failed more readily, suggesting that a gap junction provides “gating” to filter out spikes elicited during the refractory period.
Induction of high-frequency oscillations
It has been documented that asymmetrical spike transmission is required for oscillation induction in an electrically coupled network. Our simulation studies indicate that a single spike in a neuron of an electrically coupled network would transmit bidirectionally. However, the gap junction conductance determines the success of spike transmission but not the direction of spike propagation; inhibitory modulation is needed to restrict the direction of spike propagation for oscillation induction. Therefore, mechanisms other than chemical modulation are needed to induce oscillations in a pure electrically coupled network. We propose that “gating” by the gap junction in an electrically coupled network restricts the propagation direction of a spike. We used computer simulations to study this phenomenon with paired spikes of short SI.
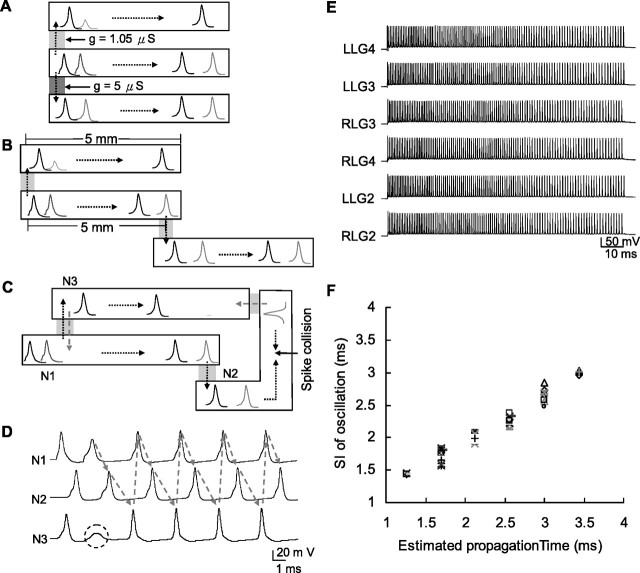
As expected, a spike elicited during the RRP (SI of 2.5 ms) was filtered by low-conductance (1.05 μS), but not by high-conductance (5 μS), gap junctions (Fig. 2A). The same paired spikes elicited only one spike in the postsynaptic neuron when the gap junction was close to the site of spike initiation. The SIs of these paired spikes increased after spike propagation. Therefore, two transjunctional spikes were produced when the junction was located some distance (i.e., 5 mm in Fig. 2B) away from the spike initiation zone. Such asymmetrical spike transmission leads to spike collision when the two spikes are propagated in a three-cell loop (Fig. 2C, N1, N2, and N3). Spike collision occurred in a loop and left the remaining spike reverberating in this closed-loop network (Fig. 2C). An oscillation of 297 Hz was induced by evoking paired spikes of 2.53 ms SI in the N1 neuron of this three-cell loop (Fig. 2D).
Figure 2.
Spike reverberates in a junction-coupled network. A, Evoked paired spikes (middle axon) transmitted through high- (g = 5 μS) but not low- (g = 1.05 μS) conductance gap junctions. B, The second spike of evoked paired spikes transmitted through a synapse 5 mm away from initiation site, but not through the synapse at the spike initiation site. C, Asymmetric paired spike transmission and spike collision led to spike reverberation in a three-cell loop (N1, N2, and N3). D, Transmission failure of paired spikes (indicated by dashed circle) initiated spike oscillation. Directions of spike propagation are indicated by arrows. E, Recordings of oscillatory LG spikes in the second, third, and fourth abdominal ganglia induced by paired-pulse stimuli. LLG4 represents the LG neuron on the left side of the fourth ganglion. F, The SIs of paired-spike-induced oscillations plotted against the estimated time for an isolated spike to propagate through a network consisting of 2, 4, 6, 8, 10, 12, and 14 neurons.
This spike reverberating model was verified in the LG network by impaling recording microelectrodes to monitor the propagation of spikes in the 6 LG neurons in the second, third, and fourth abdominal ganglia (Fig. 2E, LLG2, RLG2, LLG3, RLG3, LLG4, and LLG4). An oscillation of 686 Hz was induced by a pair of LG spikes with an SI of 1.03 ms (Fig. 2E). Similar oscillations with varying frequencies were induced by paired spikes of 1.0–1.9 ms SI in 19 preparations. The frequencies of these paired-spike-induced oscillations ranged from 425 to 686 Hz, and their durations ranged from 15 to 179 ms (data not shown).
Oscillating frequency determined by spike propagation time
In the LG network, a single spike was found to take 0.41 ± 0.05 ms (n = 12) to transmit through a commissural junction (Fig. 1C, Rpre to Rpost) and 0.22 ± 0.05 ms (n = 10) to travel through the connective between two ganglia (Fig. 1C, R1 to R3). According to our spike reverberation model, the SI of oscillation was the same as the spike's traveling time throughout the network (Fig. 2C). In the 19 preparations studied, paired-spike-induced oscillations with SIs of 1.44, 1.70, 2.0, 2.26, 2.65, and 2.99 ms were obtained. These SI values correlated linearly with the estimated time for a single spike to run through an oscillating loop of 4, 6, 8, 10, 12, or 14 neurons, respectively (Fig. 2F).
Analysis of spike reverberation in the network
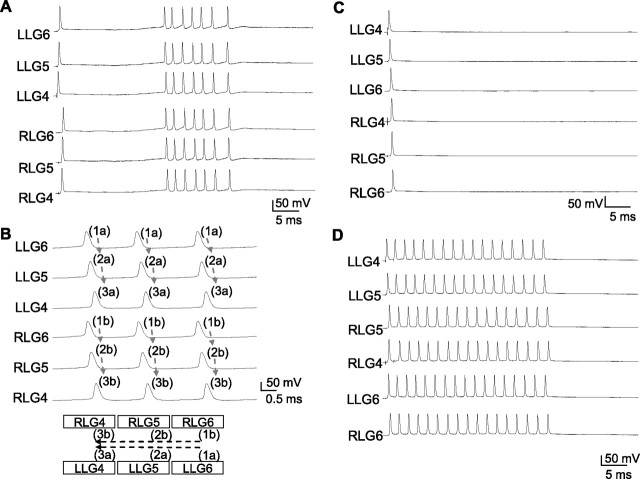
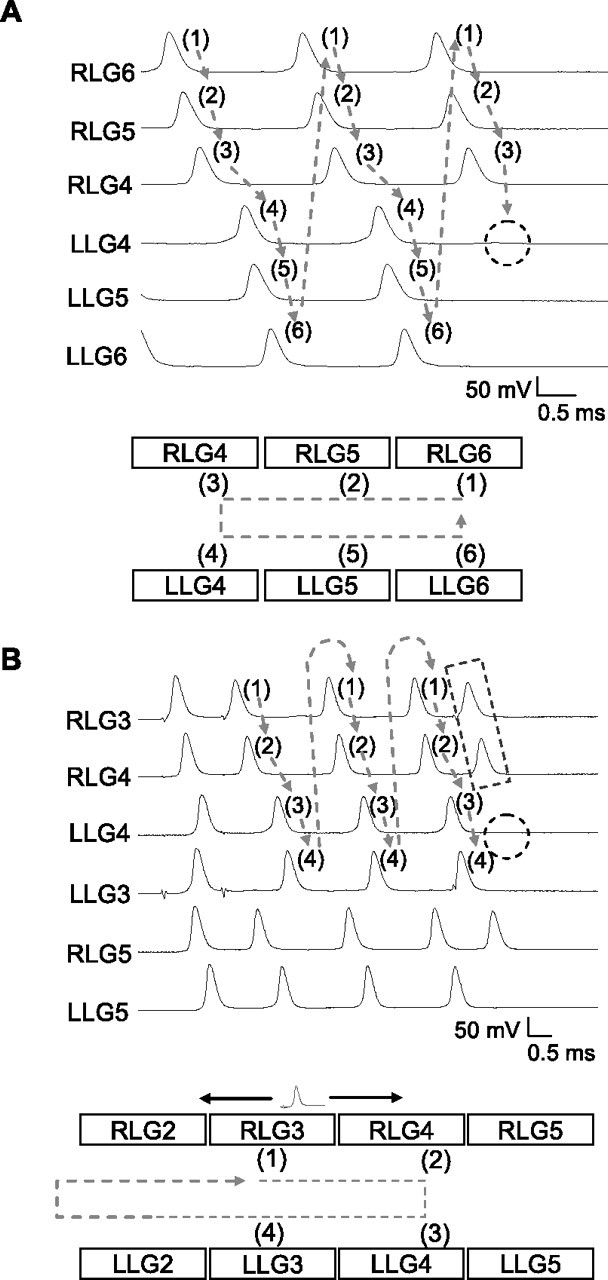
The evoked paired spikes in the left LG axon of the fourth ganglion (LLG4) produced two transseptal spikes in the LG neurons on the left side of the third ganglion (LLG3) (Fig. 3A). In contrast, the second spike failed to transmit across the commissural junction, and only one transjunctional spike was triggered in RLG4. This single spike was 0.38 ms behind the leading spike and 0.65 ms ahead of the second spike in LLG4 (the spikes of the first and fourth traces in the dashed polygon). The short SI value of the second spike (0.65 ms) meant it was unable to transmit across the commissural junction. A single spike in RLG3 led the second spike in LLG3 by 0.87 ms, because of propagation delay of the second spike in LLG4. The second spike in LLG3 transmitted through the commissural junction to trigger a new action potential in RLG3 (Fig. 3B). As a result, this transcommissural spike backpropagated to RLG4 and then reverberated in a closed loop consisting of the RLG3, RLG4, LLG4, and LLG3 (Fig. 3C, dashed circle). Although both the single transcommissural spike in RLG5 and the transseptal paired spikes in LLG5 propagated toward the LG neurons in the sixth ganglion and collided there, the remaining spike in RLG5 failed to reexcite RLG4, because oscillating spikes were already induced in RLG4. Under this condition, the oscillating spike in RLG4 prevented spike transmission from RLG5 to RLG4. Once an oscillator loop had formed, the oscillatory spikes produced by this loop transmitted through septal junctions and contributed to the oscillating spikes recorded in LLG2 and RLG2 (Fig. 3A,C).
Figure 3.
Initiation of paired-spike-induced oscillations in the LG network. A, Illustration of the initially evoked paired spikes (indicated by dashed polygon), the direction of spike reverberation (indicated by arrows), and the sequence of propagation (marked by numbers) during the early phase of oscillation. Failure of spike transmission is indicated by the dashed circle. B, Summary of the propagation delay and failure of spike transmission of paired spikes of short SI. Propagation delay of the second spike led to spike transmission from LLG3 to RLG3 (indicated by dashed arrow). C, The spike reverberated in the oscillator center formed by LLG3, RLG3, RLG4, and LLG4 (indicated by dashed arrows). Multiple spikes generated by the oscillator center were transmitted via septal junctions to the LG neurons outside this center (indicated by solid arrows).
Figure 3C summarizes how spikes reverberate in the oscillator center formed by four LG neurons and how these oscillating spikes transmit to the neurons outside the oscillator loop. In contrast, a pair of spikes with a SI of 2.5 ms evoked in the same neuron (LLG4) failed to induce oscillatory spikes, as symmetrical spikes were successfully transmitted through both the septal and commissural gap junctions in the fourth ganglion (data not shown). These results confirm the prediction that the asymmetrical transmission of paired spikes through electrical synapses leads to the generation of high-frequency oscillations in a junction-coupled network.
The paired-spike-induced oscillations terminated naturally at the low-conductance commissural junction, where the initial second spike was filtered out (Fig. 4A). In some preparations, although spike transmission through the initial low-conductance commissural junction failed, lower frequency oscillations remained. We found that spikes transmitted through a new commissural junction in a neighboring ganglion contributed to the sustaining of oscillation, usually with a longer SI (Fig. 2E). This phenomenon was observed in most preparations examined, and occurred during the late phase of oscillation.
Figure 4.
Termination of paired-spike-induced oscillations in the LG network. A, Spike failed to transmit (dashed circle) through the junction during the late phase of oscillation. B, An inserted extra spike (indicated by dashed rectangle) causing the failure of spike transmission (dashed circle) terminated oscillation. Bottom panels summarize the directions of spike propagation in the oscillator centers (indicated by gray dashed arrows) before the termination of oscillations. The propagations of the inserted spike are indicated by a solid black arrow.
Oscillations could also be terminated by introducing an extra spike between two oscillating spikes. Figure 4B illustrates how an inserted spike in RLG3 propagated bidirectionally through septal junctions to RLG2 and RLG4 (and then to RLG5). The transjunctional spikes in RLG2 collided with the transcommissural spike coming from LLG2. The transseptal spike in RLG4 failed to excite an extra spike in LLG4 because of the very short SI that resulted from the inserted spike (Fig. 4B). Figure 4B (bottom) summarizes how an extra spike between oscillating spikes leads to a spike collision and nontransmission through the commissural junction, thereby terminating the oscillation.
Chemical synapse-independent oscillations
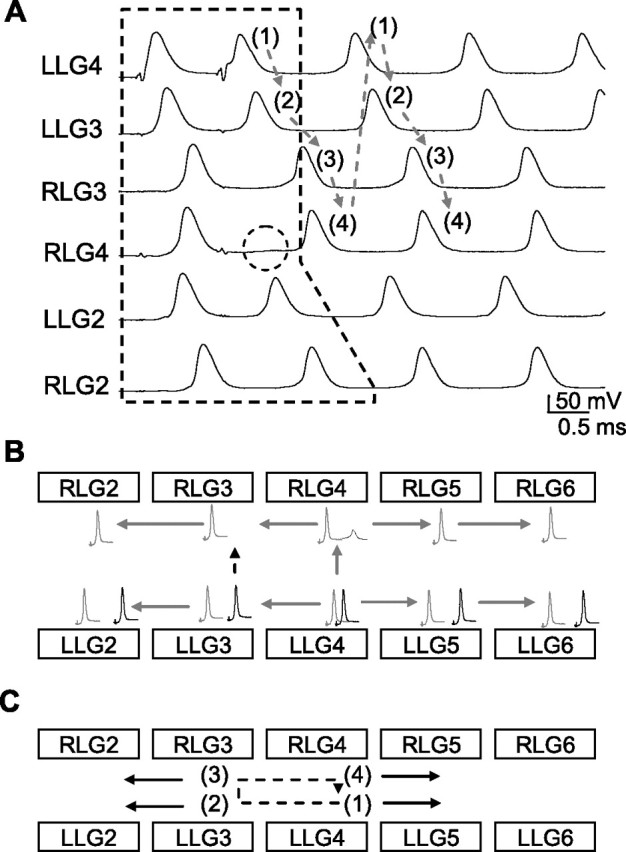
The tail-flip response mediated by LG spike would lead to the reexcitation of the sensory afferents that innervate the abdominal exoskeleton surface hairs. The GABAergic tonic and recurrent inhibitions on sensory afferents and interneurons have been found to prevent the reexcitation of LG by LG spike itself (Edwards et al., 1999). A long delay multiple spikes of irregular SIs generally would obtain after the activation of interneurons in the sixth abdominal ganglion by LG spike. In the presence of picrotoxin, which blocks GABAergic inhibitions in LG network, multiple spikes of irregular SIs were induced by a single spike evoked in LLG4 (Fig. 5A, the first spike of the third trace). These multiple spikes in LLG6 transmitted through septal junction to LLG5 and then to LLG4 with ∼0.15 ms of septal delay in each ganglion (Fig. 5B, labeled as 1a, 2a, and 3a). The first spike in LLG6 was 0.3 ms behind that in RLG6 because of transcommissural delay (Fig. 5A, the first spike of the fourth trace); however, the multiple spikes in RLG6 were <60 μs behind that in LLG6, because they both were induced by the interneurons in the sixth abdominal ganglion. From RLG6, the spikes transmitted through septal junction to RLG5 and then to RLG4 with ∼0.15 ms of junctional delay in each ganglion (Fig. 5B, labeled 1b, 2b, and 3b). Figure 5B (bottom) summarizes that, after the application of picrotoxin, the multiple spikes induced by a single spike were not a result of spike reverberation in a closed-loop network.
Figure 5.
Irregular multiple spikes by the blockade of GABAergic inhibition. A, Multiple spikes in RLG6 and LLG6 were produced by the repetitive excitatory inputs from the interneurons in the sixth ganglion that are excited by the initial single shock on LLG4 in the presence of picrotoxin (100 μm). B, The directions of spike propagation are indicated by arrows, and propagation sequences are marked by numbers. C, In Ca2+-free crayfish saline containing picrotoxin (100 μm), only a single spike without multiple spikes was evoked. D, Typical paired-spike-induced spike reverberation is obtained in Ca2+-free crayfish saline without picrotoxin.
Additionally, in the presence of picrotoxin, the multiple spikes induced by a single spike evoked in LLG4 were abolished when the LG network was incubated in calcium-free crayfish buffer (Fig. 5C). This result confirmed that the generation of multiple spikes by a single LG spike was a result of escape from the inhibitions, which were mediated by GABAergic modulations. In addition to the blockade of GABAergic inhibition, most chemical transmissions in the LG network were also abolished under the calcium-free condition (Miller et al., 1992; Araki and Nagayama, 2003) (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). However, under calcium-free conditions, paired spikes of short SI still induced rhythmic oscillation (Fig. 5D). These results exclude the role of chemical modulation in paired-spike-induced oscillations, because the removal of chemical inhibition is not likely the underlying mechanism for these oscillations.
Discussion
In this study, we reported that high-frequency oscillations were induced by paired spikes of short SIs in a junction-coupled network. Asymmetrical transmission of paired spikes through a low-conductance gap junction leads to a spike reverberation in a junction-coupled network. This underlying mechanism for oscillation was modeled by computer simulation and verified electrophysiologically in a network that mediates the tail-flip escape response of crayfish.
Oscillation induction in an electrically coupled network
High-frequency multiple spiking has been observed in various electrically coupled neurons, such as the median giant neurons of the earthworm and the LG neurons of crayfish (Kao and Grundfest, 1957; Kao, 1960). It has been proposed that both chemical and electrical synapses play key roles in oscillation generation (Kandler and Katz, 1995; Palva et al., 2000). However, oscillations can be induced when chemical synapses are blocked in some brain areas, ruling out a role for chemical synapses in certain types of oscillations (Jefferys and Haas, 1982; Taylor and Dudek, 1982; Draguhn et al., 1998). Nonsynaptic brain oscillations during early brain development suggest that gap junction communication alone can lead to oscillations (Kandler and Katz, 1995; Perez Velazquez and Carlen, 2000; Corlew et al., 2004; Minlebaev et al., 2007). Our results also suggest that chemical synapse modulation is unlikely to be the underlying mechanism for oscillation induction in the LG network. Without modulations of chemical synapses, theoretical models of electrically coupled networks have been developed to demonstrate how oscillations are induced (Abbott and van Vreeswijk, 1993; Skinner et al., 1997; Traub et al., 1999; Lewis and Rinzel, 2000; Tegnér et al., 2002). Unfortunately, the mechanism by which the direction of spike propagation in a network is restricted without inhibitory neuromodulation remains unclear. In this study, the second spike in paired spikes of short SI, filtered by a low-conductance gap junction that results in asymmetrical spike transmission, was proven to play a key role in oscillation induction in the LG network.
Asymmetrical transmission leads to spike reverberation
Gap junctions interconnect neurons and allow the exchange of small molecules, ions, and electrical potentials between cells (Bennett and Zukin, 2004; Söhl et al., 2005). High-conductance gap junctions guarantee the propagation of an action potential, whereas junctions of lower conductance might act as a filter to gate spike transmission across a junction. Thus, gating by low-conductance gap junctions provides asymmetrical spike transmission without chemical synaptic modification. In addition to the junctional conductance, the SI between spikes plays an important role in spike transmission across a junction. Therefore, a pair of spikes with very short SI evoked in one neuron might produce one spike in one postsynaptic neuron, whereas two transjunctional spikes might be produced in another strongly coupled neuron or in a neuron that makes a synapse at some distance away from the spike initiation site.
When a pair of spikes is evoked in a junction-coupled network, asymmetrical transmission can lead to spike collision, leaving repeated propagation of the remaining single spike if a closed-loop network is formed. This closed loop can serve as an oscillator to produce a self-sustained oscillation in the absence of chemical modulations. Because spikes reverberate in a closed-loop network, the number of neurons forming this closed loop determines the spike traveling time and therefore the oscillation interval. The oscillation frequency could be very high in an oscillator loop formed by only a few neurons. Additionally, the lack of a chemical synaptic delay in a junction-coupled network also contributes to the high frequency of the oscillations.
According to the spike reverberation model, the frequency of oscillations is determined by the traveling time of a spike running through the oscillator loop. Based on measurements of spike propagation time, an LG spike takes ∼1.26 ms to travel through an oscillating loop of four LG neurons (Fig. 2F). However, this estimated traveling time only fits the SIs of the first few oscillation spikes, and not those of the successive spikes. This is because the successive oscillatory spikes are elicited during the refractory periods of the previous spikes. Thus, the initial spike interval of oscillation increases gradually during oscillation, because spikes elicited during the refractory period all suffer from propagation delay. Here, the mean spike interval for the entire oscillation in an oscillator consisting of four LG neurons was 1.43 ms instead of 1.26 ms (Fig. 2F). This measured SI value of oscillation is better correlated with the estimated spike traveling time through an oscillating loop consisting of a larger number of neurons, because the successive spikes are even further away from the absolute period of the leading spike (Fig. 2F).
Physiological significance of high-frequency oscillations
In the LG network, spikes always transmit successfully through septal junctions because of their high conductance. Spike transmission is more likely to fail across commissural junctions because of their lower conductance. Because the conductance of the septal junction is stronger than that of the commissural junction in LG network, a key factor for oscillation induction is the coupling strength of the junction, because both septal and commissural junctions are known to be nonrectifying (Watanabe and Grundfest, 1961). A rectifying junction would determine the direction of spike transmission. Asymmetrical transmission through a rectifying junction might occur and thus induce oscillation. However, the oscillation induced by the asymmetrical transmission through a rectifying junction would be unidirectional rather than bidirectional. In this study, oscillations in LG network were induced by spike in any neurons of this electrically coupled network. Additionally, the direction of oscillations could be either clockwise or counterclockwise, ruling out the involvement of rectifying junctions in oscillation induction.
Based on our model, asymmetrical spike transmission is required for oscillation induction in an electrically coupled network. Paired spikes of short SI traveling through weaker coupling junctions readily trigger oscillation. A single spike evoked in a presynaptic neuron fails to fire an action potential during the period in which the excitability of postsynaptic neuron is inhibited by the actions of inhibitory neurotransmitters or by a negative current injection (Watanabe and Grundfest, 1961; Traub and Bibbig, 2000). A self-sustained oscillation could be induced if such asymmetrical spike transmissions occur in an electrically coupled network. As expected, high-frequency oscillations in the LG network, similar to paired-spike-induced oscillations, were obtained by evoking a single spike accompanied by a negative current injection to prevent the generation of a transcommissural spike (Watanabe and Grundfest, 1961).
In some preparations with low coupling in commissural junction, we found that the asymmetrical transmission of a single spike also led to the induction of high-frequency oscillations in the LG network. Two to six spikes of high-frequency oscillation were induced by a single LG spike in LG network. These high-frequency oscillatory spikes might be physiologically significant, because repetitive LG spikes give rise to the synaptic bombardment that produces effective summation of the excitatory junctional potentials in the flexor muscle neuromuscular junctions (our unpublished data). This synaptic bombardment produced by LG repetitive spikes is purportedly needed for the vigorous contraction of the abdominal muscle during molting (our unpublished observations). These observations suggest that high-frequency oscillations occur under physiological conditions.
Here, we demonstrate that a ladder-like network responsible for the tail-flip escape behavior in crayfish forms a ring-like network by changing the neurons' interconnecting couplings. This ring-like network could generate repetitive spikes with a very high frequency. The simple mechanism for high-frequency oscillation induction demonstrated in this study may be widely applicable during early brain development or in the adult brain under physiological or pathological conditions.
Footnotes
We thank Margaret Dah-Tsyr Chang, Hsin Chen, and Ping-Chang Lin for discussions and manuscript suggestions.
References
- Abbott LF, van Vreeswijk C. Asynchronous states in networks of pulse-coupled oscillators. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1993;48:1483–1490. doi: 10.1103/physreve.48.1483. [DOI] [PubMed] [Google Scholar]
- Araki M, Nagayama T. Direct chemically mediated synaptic transmission from mechanosensory afferents contributes to habituation of crayfish lateral giant escape reaction. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2003;189:731–739. doi: 10.1007/s00359-003-0456-5. [DOI] [PubMed] [Google Scholar]
- Bennett MV, Zukin RS. Electrical coupling and neuronal synchronization in the mammalian brain. Neuron. 2004;41:495–511. doi: 10.1016/s0896-6273(04)00043-1. [DOI] [PubMed] [Google Scholar]
- Bragin A, Engel J, Jr, Wilson CL, Fried I, Buzsáki G. High-frequency oscillations in human brain. Hippocampus. 1999;9:137–142. doi: 10.1002/(SICI)1098-1063(1999)9:2<137::AID-HIPO5>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Horváth Z, Urioste R, Hetke J, Wise K. High-frequency network oscillation in the hippocampus. Science. 1992;256:1025–1027. doi: 10.1126/science.1589772. [DOI] [PubMed] [Google Scholar]
- Corlew R, Bosma MM, Moody WJ. Spontaneous, synchronous electrical activity in neonatal mouse cortical neurones. J Physiol. 2004;560:377–390. doi: 10.1113/jphysiol.2004.071621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Draguhn A, Traub RD, Schmitz D, Jefferys JG. Electrical coupling underlies high-frequency oscillations in the hippocampus in vitro. Nature. 1998;394:189–192. doi: 10.1038/28184. [DOI] [PubMed] [Google Scholar]
- Dzhala VI, Staley KJ. Mechanisms of fast ripples in the hippocampus. J Neurosci. 2004;24:8896–8906. doi: 10.1523/JNEUROSCI.3112-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards DH, Heitler WJ, Krasne FB. Fifty years of a command neuron: the neurobiology of escape behavior in the crayfish. Trends Neurosci. 1999;22:153–161. doi: 10.1016/s0166-2236(98)01340-x. [DOI] [PubMed] [Google Scholar]
- Furshpan EJ, Potter DD. Transmission at the giant motor synapses of the crayfish. J Physiol. 1959;145:289–325. doi: 10.1113/jphysiol.1959.sp006143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guld C. Cathode follower and negative capacitance as high input impedance circuits. Proc IRE. 1962;50:1912–1927. [Google Scholar]
- Hines M, Moore JW, Carnevale T. NEURON. 2007. [accessed 19 June 2008]. from http://www.neuron.yale.edu/neuron/
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jefferys JG, Haas HL. Synchronized bursting of CA1 hippocampal pyramidal cells in the absence of synaptic transmission. Nature. 1982;300:448–450. doi: 10.1038/300448a0. [DOI] [PubMed] [Google Scholar]
- Jones MS, Barth DS. Spatiotemporal organization of fast (>200 Hz) electrical oscillations in rat vibrissa/barrel cortex. J Neurophysiol. 1999;82:1599–1609. doi: 10.1152/jn.1999.82.3.1599. [DOI] [PubMed] [Google Scholar]
- Jones MS, Barth DS. Effects of bicuculline methiodide on fast (>200 Hz) electrical oscillations in rat somatosensory cortex. J Neurophysiol. 2002;88:1016–1025. doi: 10.1152/jn.2002.88.2.1016. [DOI] [PubMed] [Google Scholar]
- Kandler K, Katz LC. Neuronal coupling and uncoupling in the developing nervous system. Curr Opin Neurobiol. 1995;5:98–105. doi: 10.1016/0959-4388(95)80093-x. [DOI] [PubMed] [Google Scholar]
- Kao CY. Postsynaptic electrogenesis in septate giant axons. II. Comparison of medial and lateral giant axons of crayfish. J Neurophysiol. 1960;23:618–635. doi: 10.1152/jn.1960.23.6.618. [DOI] [PubMed] [Google Scholar]
- Kao CY, Grundfest H. Postsynaptic electrogenesis in septate giant axons. I. Earthworm median giant axon. J Neurophysiol. 1957;20:553–573. doi: 10.1152/jn.1957.20.6.553. [DOI] [PubMed] [Google Scholar]
- Lewis TJ, Rinzel J. Self-organized synchronous oscillations in a network of excitable cells coupled by gap junctions. Network. 2000;11:299–320. [PubMed] [Google Scholar]
- Mann-Metzer P, Yarom Y. Electrotonic coupling interacts with intrinsic properties to generate synchronized activity in cerebellar networks of inhibitory interneurons. J Neurosci. 1999;19:3298–3306. doi: 10.1523/JNEUROSCI.19-09-03298.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marín G, Mpodozis J, Sentis E, Ossandón T, Letelier JC. Oscillatory bursts in the optic tectum of birds represent re-entrant signals from the nucleus isthmi pars parvocellularis. J Neurosci. 2005;25:7081–7089. doi: 10.1523/JNEUROSCI.1379-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MW, Vu ET, Krasne FB. Cholinergic transmission at the first synapse of the circuit mediating the crayfish lateral giant escape reaction. J Neurophysiol. 1992;68:2174–2184. doi: 10.1152/jn.1992.68.6.2174. [DOI] [PubMed] [Google Scholar]
- Minlebaev M, Ben-Ari Y, Khazipov R. Network mechanisms of spindle-burst oscillations in the neonatal rat barrel cortex in vivo. J Neurophysiol. 2007;97:692–700. doi: 10.1152/jn.00759.2006. [DOI] [PubMed] [Google Scholar]
- Palva JM, Lamsa K, Lauri SE, Rauvala H, Kaila K, Taira T. Fast network oscillations in the newborn rat hippocampus in vitro. J Neurosci. 2000;20:1170–1178. doi: 10.1523/JNEUROSCI.20-03-01170.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez Velazquez JL, Carlen PL. Gap junctions, synchrony and seizures. Trends Neurosci. 2000;23:68–74. doi: 10.1016/s0166-2236(99)01497-6. [DOI] [PubMed] [Google Scholar]
- Perez-Velazquez JL, Valiante TA, Carlen PL. Modulation of gap junctional mechanisms during calcium-free induced field burst activity: a possible role for electrotonic coupling in epileptogenesis. J Neurosci. 1994;14:4308–4317. doi: 10.1523/JNEUROSCI.14-07-04308.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skinner FK, Kopell N, Mulloney B. How does the crayfish swimmeret system work? Insights from nearest-neighbor coupled oscillator models. J Comput Neurosci. 1997;4:151–160. doi: 10.1023/a:1008891328882. [DOI] [PubMed] [Google Scholar]
- Söhl G, Maxeiner S, Willecke K. Expression and functions of neuronal gap junctions. Nat Rev Neurosci. 2005;6:191–200. doi: 10.1038/nrn1627. [DOI] [PubMed] [Google Scholar]
- Spampanato J, Mody I. Spike timing of lacunosom-moleculare targeting interneurons and CA3 pyramidal cells during high-frequency network oscillations in vitro. J Neurophysiol. 2007;98:96–104. doi: 10.1152/jn.00188.2007. [DOI] [PubMed] [Google Scholar]
- Taylor CP, Dudek FE. Synchronous neural afterdischarges in rat hippocampal slices without active chemical synapses. Science. 1982;218:810–812. doi: 10.1126/science.7134978. [DOI] [PubMed] [Google Scholar]
- Tegnér J, Compte A, Wang XJ. The dynamical stability of reverberatory neural circuits. Biol Cybern. 2002;87:471–481. doi: 10.1007/s00422-002-0363-9. [DOI] [PubMed] [Google Scholar]
- Traub RD, Bibbig A. A model of high-frequency ripples in the hippocampus based on synaptic coupling plus axon–axon gap junctions between pyramidal neurons. J Neurosci. 2000;20:2086–2093. doi: 10.1523/JNEUROSCI.20-06-02086.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traub RD, Schmitz D, Jefferys JG, Draguhn A. High-frequency population oscillations are predicted to occur in hippocampal pyramidal neuronal networks interconnected by axoaxonal gap junctions. Neuroscience. 1999;92:407–426. doi: 10.1016/s0306-4522(98)00755-6. [DOI] [PubMed] [Google Scholar]
- Traub RD, Whittington MA, Buhl EH, LeBeau FE, Bibbig A, Boyd S, Cross H, Baldeweg T. A possible role for gap junctions in generation of very fast EEG oscillations preceding the onset of, and perhaps initiating, seizures. Epilepsia. 2001;42:153–170. doi: 10.1046/j.1528-1157.2001.26900.x. [DOI] [PubMed] [Google Scholar]
- Traub RD, Contreras D, Cunningham MO, Murray H, LeBeau FEN, Roopun A, Bibbig A, Wilent WB, Higley MJ, Whittington MA. Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts. J Neurophysiol. 2005;93:2194–2232. doi: 10.1152/jn.00983.2004. [DOI] [PubMed] [Google Scholar]
- Tsai LY, Tseng SH, Yeh SR. Long-lasting potentiation of excitatory synaptic signaling to the crayfish lateral giant neuron. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2005;191:347–354. doi: 10.1007/s00359-004-0589-1. [DOI] [PubMed] [Google Scholar]
- Urrestarazu E, Chander R, Dubeau F, Gotman J. Interictal high-frequency oscillations (100 500 Hz) in the intracerebral EEG of epileptic patients. Brain. 2007;130:2354–2366. doi: 10.1093/brain/awm149. [DOI] [PubMed] [Google Scholar]
- Watanabe A, Grundfest H. Impulse propagation at the septal and commissural junctions of crayfish lateral giant axons. J Gen Physiol. 1961;45:267–308. doi: 10.1085/jgp.45.2.267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye SR, Yang JW, Chen CM. Effect of static magnetic fields on the amplitude of action potential in the lateral giant neuron of crayfish. Int J Radiat Biol. 2004;80:699–708. doi: 10.1080/09553000400017424. [DOI] [PubMed] [Google Scholar]