Biomechanics of the Vibrissa Motor Plant in Rat: Rhythmic Whisking Consists of Triphasic Neuromuscular Activity

Abstract

The biomechanics of a motor plant constrain the behavioral strategies that an animal has available to extract information from its environment. We used the rat vibrissa system as a model for active sensing and determined the pattern of muscle activity that drives rhythmic exploratory whisking. Our approach made use of electromyography to measure the activation of all relevant muscles in both head-fixed and unrestrained rats and two-dimensional imaging to monitor the position of the vibrissae in head-fixed rats. Our essential finding is that the periodic motion of the vibrissae and mystacial pad during whisking results from three phases of muscle activity. First, the vibrissae are thrust forward as the rostral extrinsic muscle, musculus (m.) nasalis, contracts to pull the pad and initiate protraction. Second, late in protraction, the intrinsic muscles pivot the vibrissae farther forward. Third, retraction involves the cessation of m. nasalis and intrinsic muscle activity and the contraction of the caudal extrinsic muscles m. nasolabialis and m. maxillolabialis to pull the pad and the vibrissae backward. We developed a biomechanical model of the whisking motor plant that incorporates the measured muscular mechanics along with movement vectors observed from direct muscle stimulation in anesthetized rats. The results of simulations of the model quantify how the combination of extrinsic and intrinsic muscle activity leads to an enhanced range of vibrissa motion than would be available from the intrinsic muscles alone.

Introduction

A ubiquitous feature of perception is that the movement of biological sensors is subject to active control. Sensory receptors are often embedded in a specialized mechanical apparatus, referred to as a motor plant, that affords the animal precise control over their position and orientation. Within mammalian vision, the eyes are controlled by extraocular muscles that allow for a wide range of motor behaviors that include saccades, pursuit, accommodation, and vergence (Haslwanter, 2002). Within human haptic perception, the highest density of tactile receptors are found on the hands, arguably our most complex motor apparatus (An et al., 1989). In rodent somatosensation, the vibrissae of the animal's snout are moved by a complex network of muscle fibers that comprise >50 individual muscles (Dorfl, 1982; Wineski, 1985).

The vibrissa system in rat provides an ideal model for the investigation of a motor plant that is central to active sensing (Kleinfeld et al., 1999, 2006). In a form of whisking called exploratory whisking, rats rhythmically sweep their vibrissae at 4–12 Hz (Vincent, 1912; Welker, 1964). Trained animals typically whisk for bouts of 1 s or more during which the vibrissae move predominantly in the horizontal plane (Bermejo et al., 2002) with great temporal regularity (Berg and Kleinfeld, 2003). Rhythmic whisking exhibits bilateral symmetry (Gao et al., 2001) in the absence of head movements (Towal and Hartmann, 2006) or contact with an object (Sachdev et al., 2003; Mitchinson et al., 2007). Thus, whisking may be described by a small number of possibly interdependent control parameters, which include frequency of whisking as well as amplitude and anteroposterior set point of both vibrissa and pad motion.

The motor plant that underlies exploratory whisking consists of the vibrissae, the mystacial pad, and a network of intrinsic and extrinsic musculature (Dorfl, 1982; Wineski, 1985). The vibrissae form an ordered grid of tactile hairs, each held by a follicle that is embedded in the mystacial pad. The musculature of the pad can be divided into two groups (Dorfl, 1982; Wineski, 1985): (1) the intrinsic muscles, which are small sling-like muscles that wrap around the base of each follicle and attach to the superficial part of the next caudal vibrissa, and (2) the extrinsic muscles, which have bony attachment points external to the pad and send fibers throughout the extent of the pad without associating with individual vibrissae (see Fig. 1). Electromyography has shown previously that intrinsic muscles activate rhythmically during vibrissa protraction (Carvell et al., 1991) and that one of the extrinsic muscles, musculus (m.) nasolabialis, activates during retraction (Berg and Kleinfeld, 2003). Yet we currently lack a composite understanding of the complete muscular control of vibrissa motion, including passive contributions and geometric constraints.

Figure 1.

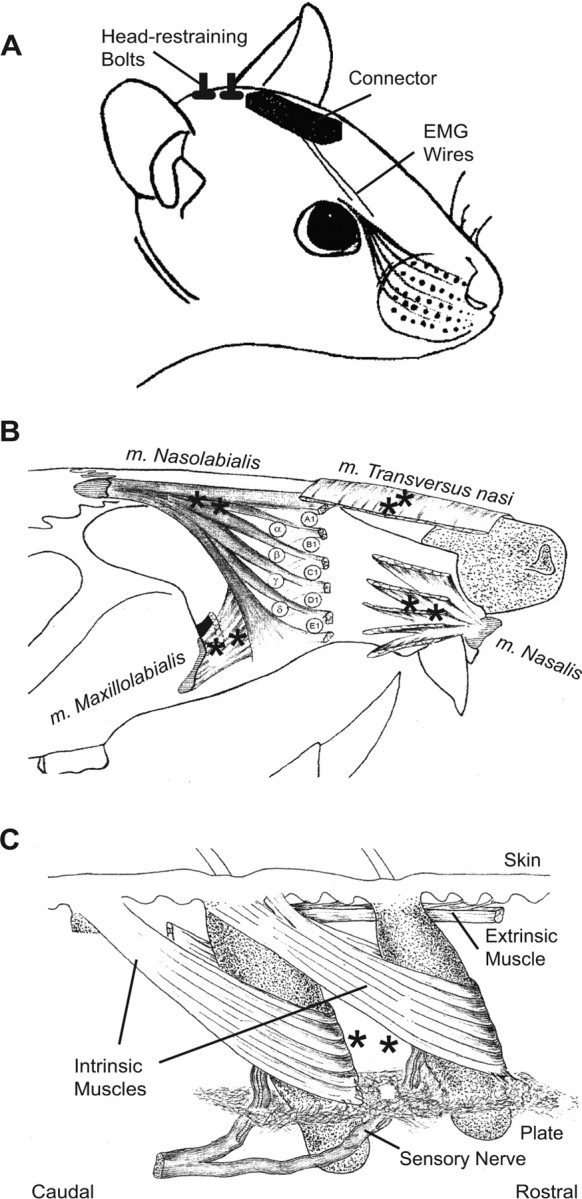
Intrinsic and extrinsic musculature of the mystacial pad. A, Drawing of the surgical preparation. Rats were implanted with EMG microwires and head-restraining bolts. EMG electrodes exited the skin through a catheter placed just caudal to the eyes at the midline and were soldered to a custom-made connector board. Head-restraining bolts were placed caudal to the connector at the midline. B, Drawing of extrinsic musculature. Four extrinsic muscles invade the mystacial pad while maintaining external attachment points. M. nasolabialis attaches dorsocaudal to the pad and runs superficially below the skin. M. maxillolabialis attaches ventrocaudal to the pad and fuses with the fibers of m. nasolabialis as they invade the pad. M. nasalis attaches rostral to the pad at the nasal septum and runs deep to the follicles as it extends caudally. M. transversus nasi lies transverse to the snout and runs superficially through the pad. The recording sites for each muscle are indicated by asterisks. C, Drawing of intrinsic musculature and follicular anatomy. The intrinsic muscles join adjacent follicles of a single row. Each muscle attaches medially and laterally to the superior part of the caudal follicle while forming a sling around the lower third of the rostral follicle. The skin and other connective tissue, e.g., the fibrous plate, provide a passive visco-elastic restoring force. Superficial extrinsic muscles run just below the skin. Asterisks indicate the approximate locations of the exposed tips of a pair of EMG microwires. The drawings in B and C were adapted from Figures 1 and 3 of Dorfl (1982, 1985); m. nasolabialis is also referred to as m. levator labii superioris. Note that, in the convention of Wineski (1985), m. transversus nasi corresponds to m. nasolabialis superficialis, m. nasalis corresponds to m. nasolabialis profundus, and the intrinsic muscles are referred to as vibrissal capsular muscles.

Here we ask the following. (1) What is the complete pattern of muscle activity that underlies rhythmic vibrissa movement in rats? (2) What are the detailed mechanical properties of the motor plant? (3) Can we summarize the biomechanical properties in terms of an anatomically based model of the whisking motor plant? (4) What are the functional roles of the various physical components of the vibrissa system?

Materials and Methods

Subjects.

We report data from 17 Long–Evans adult female rats, 250–350 g in mass. In 10 of these rats, pairs of microwires were implanted in the musculature of the mystacial pad to record the electromyogram (EMG), as described previously (Berg and Kleinfeld, 2003) and appended as described below. Head-restraining bolts were embedded in the head-mount along the midline of the skull (Fig. 1A) as described previously (Bermejo et al., 1996). After recovery, these rats were trained to whisk while head-fixed for a chocolate drink reward using an operant conditioning paradigm designed to elicit large-amplitude whisks (Gao et al., 2003a). A subset of these rats were also trained to whisk unrestrained on a platform (Ganguly and Kleinfeld, 2004). Four additional rats were used for muscle stimulation experiments that were performed under anesthesia. A final set of three rats was used for histological studies. The care and all aspects of experimental manipulation of our animals were in strict accord with Guide for the Care and Use of Laboratory Animals (National Institutes of Health publication 85-23) and have been approved by Institutional Animal Care and Use Committees at Hunter College, City University of New York, and University of California, San Diego.

EMG surgery.

All surgeries were performed under ketamine (90 mg/kg rat mass) and xylazine (10 mg/kg rat mass) anesthesia. Injections were made intraperitoneally with supplemental injections of ketamine (20 mg/kg rat mass) given every 2 h as needed. Bupivicaine, a local anesthetic, was administered at the surgical incision to minimize postoperative pain.

Electrodes for muscle implantation were constructed from Teflon-coated tungsten microwire (0.002 inch diameter; California Fine Wire, Grover Beach, CA). Microwires were stripped of 1 mm of insulation and implanted in pairs. The tips were separated by ∼1 mm and oriented along the muscle fibers to obtain the maximum signal (Kamen and Caldwell, 1996). Two incisions were made to expose the musculature for implantation of EMG electrodes: (1) a midline incision extending from the back of the skull to the end of the snout; and (2) a lateral incision just caudal to the mystacial pad extending from the midline to the most ventral vibrissa row. The skin was deflected to reveal the two extrinsic muscles m. nasolabialis and m. maxillolabialis (Fig. 1B). The exposed tip of each electrode was pressed into the muscle tissue and secured at its entry point using nylon sutures (6-0, Ethicon; Johnson and Johnson, Piscataway, NJ). It was not practical to directly expose the intrinsic muscles because of their small size or m. nasalis because of its deep location within the pad (Fig. 1B,C). These muscles were implanted by threading the microwires through a 26-gauge needle and shuttling the needle beneath the skin to its target (Berg and Kleinfeld, 2003). Wire tips were bent back at the needle tip to anchor the wires to the surrounding tissue. These wires were sutured in place at the point at which they exited the pad. Finally, a pair of reference wires were stripped of 4 mm of insulation and implanted in the dermis at the tip of the snout, beyond the extent of m. transversus nasi.

Electrodes to monitor activation of the intrinsic muscles were implanted in all rats, whereas electrodes to monitor up to three extrinsic muscles were implanted in specific rats (Table 1). Electrode positions were verified at the conclusion of surgery by passing current through the implanted microwires to stimulate the muscles and confirm the site of implantation. Each muscle has a specific direction of action and produces a characteristic ratio of pad movement to vibrissa deflection as determined in a separate set of stimulation experiments (see Fig. 7). These data were used to confirm that the movement stimulated via the microwires was typical for the implanted muscle. In the case of an intrinsic muscles implantation, the EMG electrodes were unlikely to be inside a specific intrinsic muscle. We determined an implantation to be successful if minimal stimulation deflected a localized group of one to three vibrissae without larger pad movement.

Table 1.

Slope of phase lag versus whisking frequency

Animal		Slope, Δφ/Δf (mean ± 2 SE) in π radians/Hz
Number	Condition	NL	NA	ML
1	Freely exploring	−0.04 ± 0.03	0.04 ± 0.05*
2	Freely exploring	−0.04 ± 0.03	0.03 ± 0.03*
3	Freely exploring	−0.10 ± 0.08	−0.20 ± 0.08	−0.04 ± 0.04
4	Freely exploring	−0.00 ± 0.03*
5	Freely exploring	0.02 ± 0.02*
6	Head-fixed	−0.09 ± 0.02	0.01 ± 0.01*
7	Head-fixed	−0.03 ± 0.04*	0.01 ± 0.06*	0.07 ± 0.03
8	Head-fixed	−0.04 ± 0.08*	−0.09 ± 0.09*	−0.07 ± 0.09*
9	Head-fixed		−0.02 ± 0.06*
10	Head-fixed	−0.05 ± 0.04	−0.06 ± 0.04	−0.08 ± 0.04
Population average		−0.04 ± 0.02	−0.02 ± 0.01	−0.01 ± 0.04*

*The null hypothesis of zero slope is satisfied (p ≤ 0.05). NA, m. nasalis; NL, m. nasolabialis; ML, m. maxillolabialis.

Figure 7.

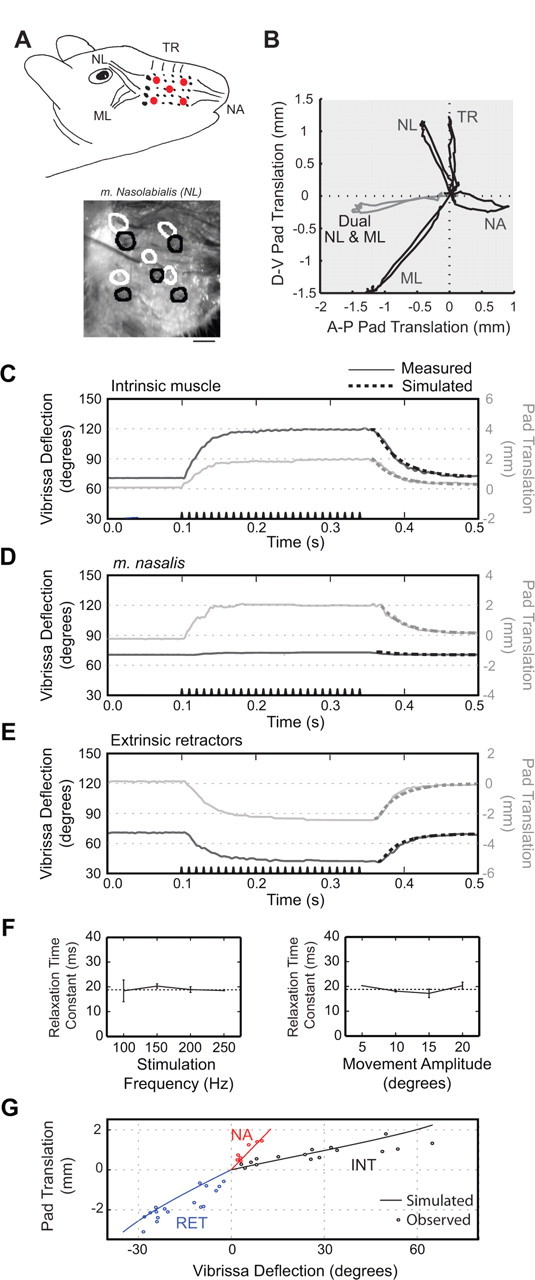
Trajectories of movement elicited by current stimulation of facial muscles in an anesthetized rat. Motion is typical of results obtained from four rats. A, Top, Diagram of extrinsic muscles indicating location of markers on pad (red dots). NL, m. nasolabialis; ML, m. maxillolabialis; NA, m. nasalis; TR, m. transversus nasi. Bottom, Image of mystacial pad with circles indicating location of the markers before stimulation (black) and during (white). B, Pad motion during muscle stimulation. Each trace represents the path of the central marker on the mystacial pad during extrinsic muscle stimulation. Dual stimulation of m. nasolabialis and m. maxillolabialis in gray demonstrates the reduced D-V translation of the pad during simultaneous contraction of these muscles. C–E, A-P vibrissa deflection and pad translation during muscle stimulation. The stimulus train is shown along the time axis. The dashed curve at the offset of stimulation is the estimated relaxation time course from the biomechanical model. F, Relaxation time constant as a function of stimulus parameters. Both panels are from data obtained from intrinsic muscle stimulation in a single rat. Error bars are 1 SE. Lack of error bar indicates only one data point was obtained. For movement amplitudes, trials were binned at the indicated value ±5°. G, Pad translation versus vibrissa deflection at peak movement during stimulus. Points represent all trials across three rats. Solid lines are estimated pad translation and vibrissa deflection from biomechanical model when only the indicated muscle is active.

The raw EMG signals were processed as described previously (Fee et al., 1997; Ganguly and Kleinfeld, 2004). In brief, the electrical signals were bandpass filtered with a 16 Hz first-order high-pass filter and a 10 kHz, sixth-order Bessel low-pass filter and digitized at 25 kHz. We then numerically calculated the differential EMG signal across the pair of wires in each muscle, filtered these signals between 400 Hz and 3 kHz with a seventh-order Butterworth bandpass filter run sequentially in the forward and reverse directions, rectified the signals by taking their absolute value, and then smoothed the signals with a fourth-order Chebyshev low-pass filter run sequentially in the forward and reverse directions. The cutoff frequency of the final filter was varied for different analyses. The final rectified and smoothed differential EMG signals are denoted |∇EMG|.

Behavioral training.

Animals were initially handled and gentled for 5 d, followed by at least 1 week of body-restraint training, during which the rat's body was enclosed in a snug cloth sack that left its head free. The animal was then either placed into its home cage or the rat holder of the behavioral apparatus (Fig. 2A, left) for 20 min each day until the animal acclimated to body restraint. Animals were then implanted with EMG microwires and given a minimum of 2 d to recover.

Figure 2.

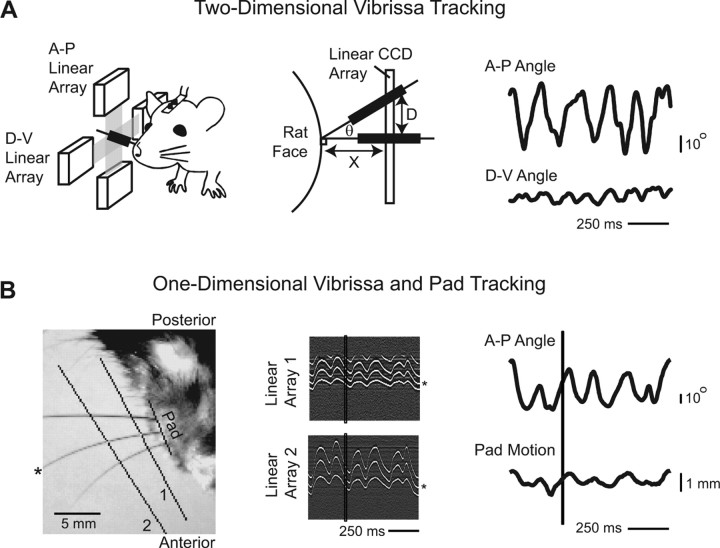
Tracking methods for vibrissa and pad movement in head-restrained rats. A, Left, Drawing of apparatus used for A-P and D-V vibrissa tracking. Vibrissa C3 was marked with an adhesive strip of foam to enlarge its shadow on two perpendicularly mounted linear CCD arrays. Middle, Schematic of the method used to calculate the A-P and D-V angle of the marked vibrissa. A calibration point was chosen along the linear array by taking a line normal to the face at the base of the vibrissa and finding its intersection with the linear array. This position was defined as 90°. Given the distance between the calibration point and the face, X, and the distance between the calibration point and the shadow of the vibrissa, D, the angle of the vibrissa, θ, was determined from the formula tanθ = D/X. Right, Trace of vibrissa motion over time. Increases in angle correspond to anterior or dorsal movement of the vibrissae, whereas decreases correspond to posterior or ventral movement. B, Left, Image taken from setup used to track A-P angle of vibrissa and A-P translation of mystacial pad. A two-dimensional CCD camera was mounted above the rat's head. Linear arrays were manually chosen from the image to track the vibrissa at multiple points. The pad was marked manually to determine the vibrissa angle and to find the point of intersection between the vibrissa and the face. For this method, vibrissae were clipped except for C1, C2, and C3. The vibrissa tracked in this example is marked with an asterisk. Middle, Output of the linear arrays as a function of time. The image has been filtered as described in Materials and Methods with intensity flipped so that the vibrissae appear white. The black vertical line marks the frame shown at left, and the asterisk marks the tracked vibrissa. Right, Trace of vibrissa and pad motion over time. Pad position was calculated by finding the intersection between the pad line and the line formed by the points tracked along the vibrissa. An increase in pad position corresponds to anterior translation. The vertical black bar represents the slice in time when the image at left was taken.

Electromyographic signals and vibrissa position were tracked during behavioral sessions that consisted of 30 trials, each of 60 s in duration. The animal was placed in a cloth sack and held in the head-fixing apparatus with its head bolts locked into place. Stable periods of whisking in air were generated using a Go/No-Go task in which the Go condition had a variable interval for reward and the No-Go condition was unrewarded (Gao et al., 2003a). On Go trials, the availability of reinforcement was signaled by the onset of a light and tone combination. Vibrissa movements were monitored in real time, and rats were reinforced for protractions that were >40° in amplitude and no more than once every 5 s.

Data in the head-fixed condition were compared with the whisking responses obtained from unrestrained rats tested on whisking in air while on a raised platform. To elicit whisking, the rat was repeatedly shown its home cage, and, after several whisking bouts, the animal was allowed to spend a few seconds in the cage before being returned to the platform (Ganguly and Kleinfeld, 2004). These sessions typically lasted 20 min. Finally, we note that neither the head-fixed nor unrestrained animals in this study performed foveal whisking behavior, i.e., whisk frequency >15 Hz.

Vibrissa tracking.

Vibrissae C1–C3 move primarily in the horizontal plane when the animal's head is restrained. Two complementary systems were used to track different aspects of this motion in head-fixed sessions. In the first, a pair of perpendicularly mounted optoelectronic devices were used to track vibrissa movement along the anteroposterior (A-P) and dorsoventral (D-V) axes (Fig. 2A, left). Each device consisted of a linear CCD array opposite an infrared laser emitter (Alpha X07; Metralight, Santa Clara, CA). The system has a temporal resolution of 1 ms, a spatial resolution of 7 μm, and a spatial range of 28 mm. All vibrissae were intact, and a foam marker of diameter 1 mm was attached to a single vibrissa to enlarge its shadow on the array. The angle of the vibrissa was calculated using the measured distance of the devices from the pad, typically 10 mm, and a calibration point taken to be normal to the face (Fig. 2A, middle). This system allowed us to identify the action of extrinsic muscles that do not pull solely along the A-P axis.

A second system made use of a high-speed video camera (A602f; Basler Vision Technologies, Exton, PA), with temporal resolution of 2 ms at our frame size and spatial resolution of 100–200 μm, to simultaneously monitor translation of the mystacial pad and motion of the vibrissae (Fig. 2B), along the A-P axis only. Only vibrissae along row C were left intact to avoid images with overlapping vibrissae. Software was developed in Matlab (MathWorks, Natick, MA) to track movement in the high-speed video. In brief, two or three linear arrays were selected from the video window, and the associated pixels were extracted from each frame (Fig. 2B). Each array was processed by a bandpass spatial filter with a bandwidth matched to the vibrissa. The center-of-mass about the point of maximum intensity was taken as the location of the vibrissa. An estimate of the current velocity of the vibrissa was used to narrow the range of pixels that were searched in the subsequent frame. To track the insertion point of the vibrissa into the pad, multiple points were tracked along the length of the vibrissa and were fit with a line. The intersection of this line and a stationary line manually chosen along the pad was taken to be the location of the insertion point.

Analysis and simulations.

All spectral power densities and phase differences were calculated using the multi-taper spectral estimation techniques of Thomson (Thomson, 1982; Percival and Walden, 1993) as implemented in the “Chronux” toolbox for Matlab (www.chronux.org). Simulations were performed in Matlab using Runge–Kutta integration techniques (Press et al., 1988).

Stimulation experiments.

Direct stimulation of the facial musculature was used in anesthetized rats to determine the magnitude and direction of the action of each muscle on the pad and vibrissae. The surgical procedure was performed as described for EMG implantation, except that the animal was transferred to the vibrissa-tracking apparatus while still anesthetized. India ink was used to mark locations on the pad to aid tracking. Muscles were excited with a concentric bipolar stimulation electrode (FHC, Bowdoin, ME). A train of biphasic current pulses, 200 μs in duration, was passed through the electrodes with the current varied between 50 and 500 μA in amplitude and the frequency varied between 100 and 250 Hz. Animals were killed at the end of the experiment.

Histology.

Sagittal sections of the mystacial pad were obtained from three rats. Animals were anesthetized with ketamine/xylazine, as above, and the fur around the vibrissae was removed using a chemical depilatory (Nair; Church & Dwight, Madera, CA). The vibrissae were positioned in either a protracted or retracted posture and glued into place with a cyanoacrylate. The rat was then deeply anesthetized with pentobarbital and perfused with PBS (Sigma, St. Louis, MO), followed by 4% (w/v) paraformaldehyde in PBS. The left and right mystacial pads were removed and postfixed in 4% paraformaldehyde. A 2-mm-wide section about the C row of the vibrissae was blocked and embedded in paraffin wax, and blocks were sectioned at a thickness of 5 μm (Pacific Pathology, San Diego, CA). Selected sections were processed with a trichrome stain (Masson; Sigma) to contrast muscle fibers and connective tissue for microphotography under bright-field illumination at low magnification.

Results

We first present the |∇EMG| recorded from the facial muscles of 10 rats during awake, behaving exploratory whisking. In five of these animals, measurements were taken in the freely exploring condition in which animals whisked while confined to a raised platform. In a separate set of five rats, data were taken in the head-fixed condition; this paradigm allowed us to perform automated vibrissa tracking. The spectral characteristics of head-fixed whisking are analyzed to identify the potential effect of this manipulation on behavior. Our focus then shifts to direct muscle stimulation in an anesthetized preparation. The combined data from these experiments are used to inform a biomechanical model of the whisking motor plant that provides the link between motor neuron signals and vibrissa movement.

Intrinsic and extrinsic |∇EMG| in relation to vibrissa motion

We recorded |∇EMG| activity from the intrinsic and extrinsic muscles of freely exploring animals that were trained to whisk in air for their home cage. Our most striking observation is that all of the recorded muscles are rhythmically active through each whisking bout. In general, we observe that each muscle produces a burst of activity on each whisking cycle. Although there is some overlap in the timing and duration of these bursts, they occur in a stereotypical sequence with the caudal extrinsic muscles m. maxillolabialis and m. nasolabialis contracting simultaneously, followed by the rostral extrinsic muscle m. nasalis, and finally the intrinsic muscles. Qualitative aspects of these observations are seen in the two example of Figure 3A. This pattern is consistent with previous reports that the intrinsic muscles and m. nasolabialis contract in anti-phase (Berg and Kleinfeld, 2003), but now we show that m. nasalis and m. maxillolabialis also contract rhythmically during exploratory whisking.

Figure 3.

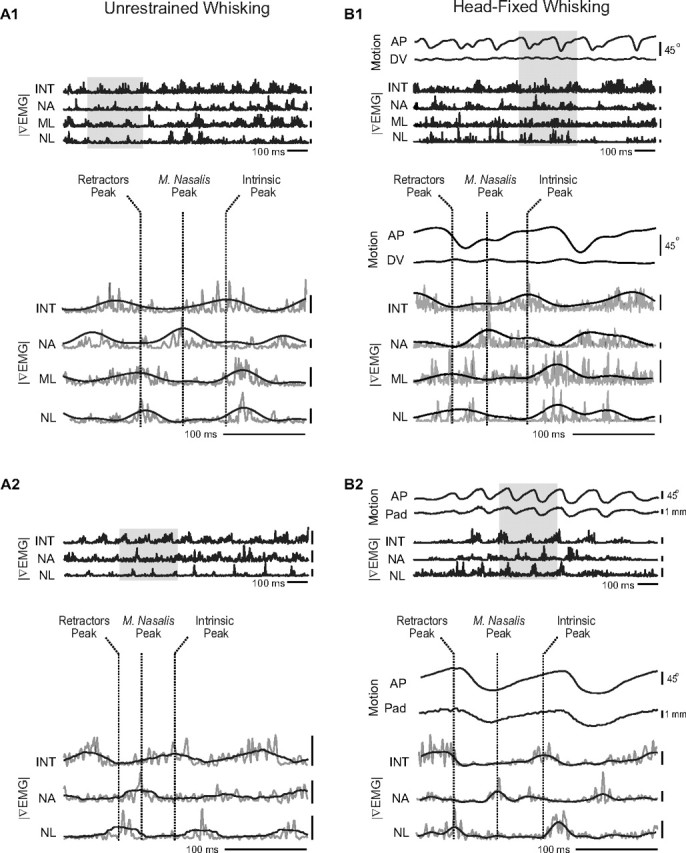
Muscle activity and vibrissa motion from head-restrained and unrestrained rats. |∇EMG| signals are abbreviated as INT (intrinsic muscles), NA (m. nasalis), NL (m. nasolabialis), and ML (m. maxillolabialis). Note that m. maxillolabialis was not recorded in every animal. Shaded area in the top panel is shown in detail in the bottom panel along with dashed vertical lines to indicate the three phases of muscle activity. |∇EMG| traces are low-pass filtered at 250 Hz except for black |∇EMG| traces in the bottom panel, which were low-pass filtered at 20 Hz. All voltage calibration bars are 100 μV. A1, A2, Examples of triphasic whisking from two unrestrained animals. B1, Example of triphasic whisking from a head-fixed animal showing A-P and D-V vibrissa motion. B2, Example of triphasic whisking from a second head-restrained animal in which A-P pad movement was tracked.

Vibrissa motion and muscle activity during head-fixed whisking

Examination of whisking bouts from head-fixed animals confirms that intrinsic and extrinsic muscle activity maintains rhythmic contraction with a three-phase sequence under head restraint. Comparing the |∇EMG| with motion of the shaft along the A-P axis, we observe that the caudal extrinsic muscles m. nasolabialis and m. maxillolabialis reach their maximum activation during retraction, consistent with previous recordings of m. nasolabialis and shaft motion (Berg and Kleinfeld, 2003). Maximal activation of the rostral extrinsic muscle m. nasalis occurs early during protraction, whereas activity in the intrinsic muscles peaks near the end of protraction. Qualitative aspects of these observations are seen in the two examples of Figure 3B.

Quantification of whisking

We calculated the average |∇EMG| and vibrissa trajectory during all whisking bouts as a means to quantify the sequence of muscle activation across whisking cycles. Direct averaging of whisk cycles was prohibited by the large variability in whisking frequency, ranging from 4 to 12 Hz. To compare cycles of different duration, we averaged across phase. Individual whisk cycles, with amplitude of 20° or more, were taken to last a period of 2π radians and then the complete set of traces was averaged by phase. The result of averaging 1750 cycles in one head-fixed animal illustrates the essential relative phase relationships (Fig. 4). First, the average |∇EMG| activity confirms the three-phase nature of rhythmic whisking. The peak activities of m. nasolabialis and m. maxillolabialis nearly coincide and are distinct from the peak activity of m. nasalis and the intrinsic muscles. Second, the extreme positions of vibrissa motion are slightly preceded by the maximum activation of specific muscles. In particular, the caudal extrinsic muscles exhibit maximum activation just before the end of retraction, and the intrinsic muscles peak just before the end of protraction. The activity of m. nasalis rises before retraction ends but reaches a peak after the onset of protraction. The relative phase relationship between maximum muscle activation and vibrissa motion were similar in all head-fixed animals.

Figure 4.

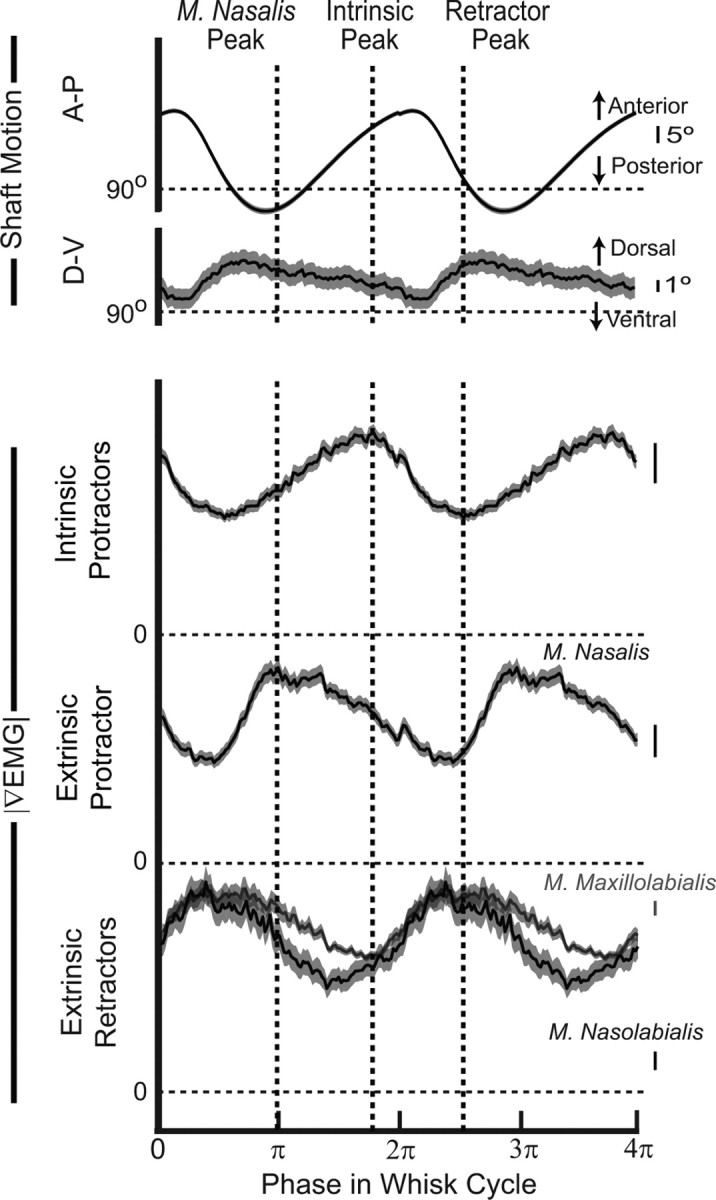
Average vibrissa motion and muscle activity from a head-restrained rat. Each whisk was linearly mapped from time onto the range of 0–2π radians so that the average is taken across phase. Average traces (1750 whisks) are repeated to display two cycles. SEs are shown as a gray boundary to each trace. |∇EMG| values were normalized by their maximum voltage. All voltage calibration bars are 2 μV. The dashed vertical lines indicate the peaks of the three phases of average muscle activity. The peak for the extrinsic retractors was set midway between the individual peaks.

Although the dominant motion is along the A-P axis, the average shaft motion along the D-V axis exhibits a distinct albeit small peak during retraction (Bermejo et al., 2002). This suggests that whisking on average takes a highly eccentric “backstroke” path, seen as a counterclockwise loop motion when viewing the right side of the face. By examining the shape of the trajectory of individual whisks, we confirmed that, in >80% of whisks, the shaft moved in a distinctly counterclockwise direction (data not shown).

Phase lag of extrinsic muscle activity

The previous analysis rests on the assumption that individual whisks of different duration are comparable when rescaled in time. Moreover, the effect of whisking frequency on the pattern of muscle activity is of critical importance for characterizing the hypothetical central pattern generator(s) that underlie whisking (Welker, 1964; Semba and Komisaruk, 1984; Gao et al., 2001; Berg and Kleinfeld, 2003; Hattox et al., 2003; Cramer and Keller, 2006). Previously, m. nasolabialis was shown to activate at a constant phase lag with respect to the intrinsic muscles even as the frequency of whisking varied (Berg and Kleinfeld, 2003). This is opposed to the hypothesis that muscle activity occurs at a constant time delay, which would result in a phase lag that increases with whisking frequency.

We test the hypothesis that the phase lag between all of the extrinsic muscles and the intrinsic muscles is constant as a function of whisking frequency, as illustrated across 200 bouts from a typical freely exploring animal (Fig. 5A). The peak of the activation of intrinsic muscles is defined as phase 0. First, we examine the consistency of the average phase lags across animals (Fig. 5 B–D). The phase lags of m. nasolabialis (0.83 ± 0.06 π radians, mean ± SE) and m. maxillolabialis (0.81 ± 0.04 π radians) were not significantly different, which supports the conclusion that these muscles operate concurrently. M. nasalis activated at a relative phase of −0.71 ± 0.06 π radians. For all three muscles, there was no significant difference for the mean phase of activation between freely exploring and head-fixed animals (p > 0.05). These data indicate that the relative phase shifts among muscle groups are preserved across animals and that the three phases of whisking are approximately evenly spaced within the whisking cycle. Next we examined the phase lag of muscles of individual animals as a function of whisking frequency. In all three extrinsic muscles, the phase lag remained essentially constant throughout the range of whisking frequencies (4–12 Hz across all animals). We quantified this observation by the slope of a line fit to the phase versus frequency plot for each animal (Table 1). For two of the three extrinsic muscles, the mean slope was significantly different from zero albeit weakly, so the change in phase lag over a range of 8 Hz would be <0.33 π radians compared with the separation of individual muscle phases of ∼0.66 π radians.

Figure 5.

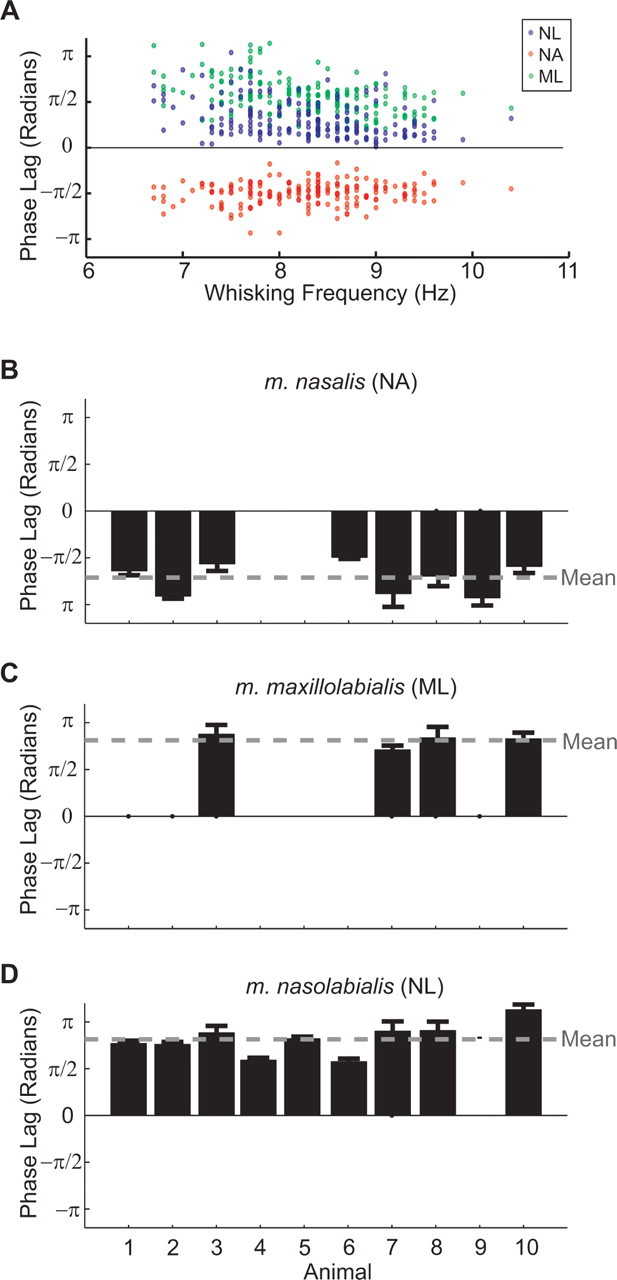
The phase relationship between intrinsic and extrinsic muscle |∇EMG| activity. The phase was calculated with respect to the intrinsic muscles, which were defined as activating at phase zero. Positive phase values correspond to a phase lag relative to the intrinsic muscles, whereas negative values correspond to a phase advance. A, Phase lag of extrinsic muscles relative to the intrinsic muscles for a representative animal (n = 198 bouts). Each dot represents the phase lag of an individual extrinsic muscle for a single bout. The frequency of whisking was determined by the location of the peak in the power spectrum of the |∇EMG| of the intrinsic muscle. Note the constant phase relationship of each muscle as a function of whisking frequency. B–D, Summary of the mean phase lags for all muscles and animals used in this study. The number of whisking bouts is 250, 200, 198, 83, 125, 110, 125, 200, 180, and 351 for animals 1 through 10, respectively. Error bars indicate 2 SEs, i.e., 95% confidence intervals. Columns with no bars correspond to animals in which the particular extrinsic muscle was not implanted with EMG electrodes. The gray horizontal line is the mean phase across all animals. NL, m. nasolabialis; ML, m. maxillolabialis; NA, m. nasalis.

Spectral properties of whisking

Previous studies have found that freely exploring rats whisk at a wide range of frequencies, but that the frequency of whisking during a single bout is exceedingly stable (O'Connor et al., 2002; Berg and Kleinfeld, 2003). In our study, we observed that individual whisking bouts of both restrained and unrestrained animals vary in frequency and rhythmicity (Fig. 6A,B). We now quantify the differences in the spectral characteristics of whisking behavior between freely exploring and head-fixed animals to determine the behavioral effect of restraint.

Figure 6.

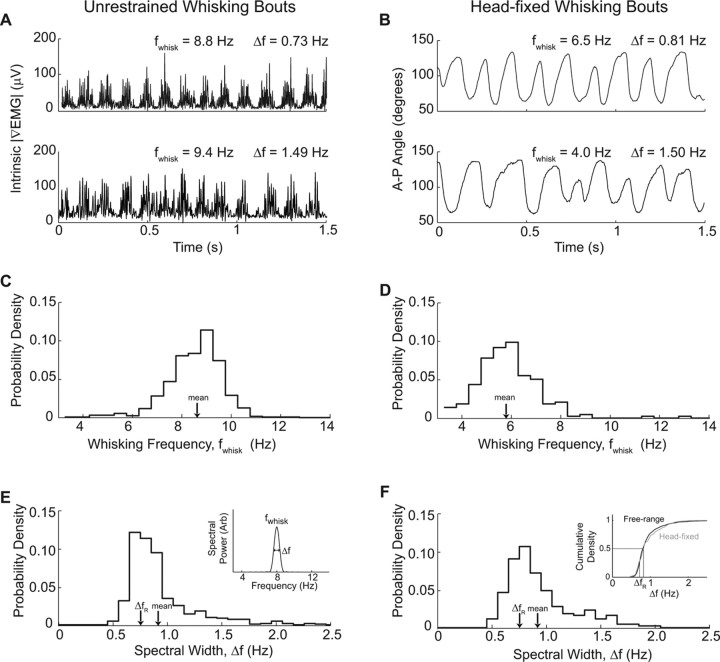
Spectral characteristics of freely exploring and head-fixed whisking. A, B, Examples of unrestrained (A) and head-fixed (B) whisking. |∇EMG| is shown for freely exploring animals, whereas vibrissa angle along the A-P axis is shown for head-fixed animals. These bouts were chosen to demonstrate the variability in both frequency and regularity of whisking for animals in both conditions. C, D, Probability distribution of whisking frequencies, f_whisk, calculated from freely exploring (C; n = 566 bouts across 5 rats) and head-fixed (D; n = 195 bouts across 3 rats) animals. The frequency was calculated from the intrinsic |∇EMG| signal recorded during 1.5-s-long whisking bouts and was defined as the frequency between 3 and 15 Hz with the greatest spectral power (inset in E). Bin size is 0.5 Hz. E, F, Probability distribution of spectral width of whisking bouts calculated from freely exploring and head-fixed animals; data as in C and E. The spectral bandwidth Δf is defined as the full-width at half-maximal amplitude of the spectral peak at f_whisk; this may be compared with the bandwidth of a pure sine wave, denoted by Δf_R = 0.73 Hz (inset in E). Bin size is 0.1 Hz. The mean spectral width was Δf = 0.93 Hz for freely exploring rats and Δf = 0.94 Hz for head-fixed rats. The cumulative probability distribution functions of the two widths are compared in the inset.

We determined the central frequency of whisking bouts from the peak of the power spectral density, f_whisk (Fig. 6E, inset) computed over the central 1.5 s interval from each bout. We then pooled the results for all rats in the same condition, either freely exploring or head-fixed, to find the probability distribution of whisking frequencies (Fig. 6C,D). Consistent with previous studies (Berg and Kleinfeld, 2003), the frequency of whisking in unrestrained animals ranges between 6 and 12 Hz, with a mode at 9.3 Hz. In contrast, the histogram of head-fixed whisking bouts showed a distinct shift toward lower frequencies. Whisking ranged from 4 to 8 Hz, with a mode at 6.1 Hz. This difference in frequency did not result from our behavioral training paradigm because this lower frequency persisted in a rat that was not rewarded for large-amplitude whisks (mean f_whisk = 6.3 Hz; n = 125 bouts). Thus, whisking in head-fixed animals was typically one-third slower than in freely exploring animals.

The regularity, or spectral purity, of a periodic signal is quantified by its spectral width Δf (Fig. 6E, inset). Highly regular, periodic behavior has a power spectrum with a narrow peak at the whisking frequency. The average width of this peak has a theoretical lower limit, called the Rayleigh limit, of Δf_R ∼ (duration of bout)⁻¹. For our specific analysis, this limit is given by the full-width at half-maximal amplitude of the power spectrum of a sine wave that is 1.5 s in duration, i.e., Δf_R = 0.73 Hz. We found that the spectral width of the intrinsic muscle |∇EMG| was typically near Δf_R in both freely exploring and head-fixed animals (Fig. 6E,F), which indicates that whisking was highly regular. Although the probability distributions of Δf appear to be similar in these two conditions, a statistical test on the cumulative probability density of spectral width shows that whisking in head-fixed animals is slightly less regular than that in freely exploring animals (p = 0.04, Kolmogorov–Smirnov test) (Fig. 6F, inset).

Movement vectors from direct stimulation of facial muscles

The highly rhythmic nature of whisking makes correlation-based techniques, as used above, ill-suited to disentangle the relationship between specific muscle activation and different aspects of vibrissa motion. To eliminate this confound, we directly stimulated intrinsic and extrinsic muscles in the anesthetized rat to determine the range of vibrissa motion each muscle can elicit, along with its direction of action and the time course of relaxation (Fig. 7). Because every muscle may both deflect vibrissae and translate the mystacial pad, we used frame-based imaging to simultaneously monitor both aspects of the motion.

We observed that each extrinsic muscle pulls the mystacial pad toward its respective attachment point (Fig. 7A,B). M. nasalis pulls the pad anterior, m. maxillolabialis pulls posteroventral, and m. nasolabialis pulls posterodorsal. Additionally, the muscle m. transversus nasi effects a strictly dorsal translation of the pad.

The concomitant activation of m. nasolabialis and m. maxillolabialis seen in the |∇EMG| activity of awake animals (Figs. 4, 5) suggests a cooperative role. In support of this, we found that a simultaneous and balanced stimulation of these two muscles produces a strictly posterior motion of the mystacial pad (Fig. 7B), although the individual muscles have a strong D-V component. We conclude that active retraction along the A-P axis requires the simultaneous excitation of the two extrinsic retractor muscles.

We determined a time constant for relaxation of the intrinsic muscles, m. nasalis, and the extrinsic retractors when stimulated together, after the offset of stimulation (Fig. 7 C–E). The observed angular motion was fit with a decaying exponential, i.e., θ = θ_rest + Δθ_maxexp(−t/τ), where θ_rest is the position of the vibrissa in the absence of stimulation and Δθ_max is the steady-state amplitude of the stimulus-induced motion. The time constant for relaxation, τ, was found to lie between 18 and 26 ms (n = 4 for each muscle) across all muscle groups. As expected for a passive process, the relaxation time was independent of stimulus parameters (Fig. 7F). These results suggest that the relaxation force is a bulk property of the mystacial pad rather than a property of a specific muscle. Last, we note that the rise time of vibrissa movement at the onset of stimulation varied with stimulus parameters. We did not fully investigate this phenomenon because extracellular stimulation of muscles recruits large rather than small individual fibers first, the reverse order of endogenous recruitment (Dorgan and O'Malley, 1997).

Finally, we determined the range of vibrissa and mystacial pad motion that can be elicited by each muscle (Fig. 7G). We use vibrissa C2 as a reference to compare our stimulation results with our behavioral data, although the range of motion may vary in different vibrissae. The range of vibrissa deflection about its rest angle is ∼35° of retraction and ∼65° of protraction, or a total range of ∼100°. In our behavioral experiments, the full range of observed vibrissa angles was 108°. The total range of pad translation in stimulation experiments is ∼5 mm in the A-P direction and 3 mm in the D-V direction. We note that each muscle exhibits a characteristic ratio of angular deflection to pad movement, with the intrinsic muscles producing the largest deflections for a given amplitude of pad movement (Fig. 7G).

Electromechanical model of vibrissa and mystacial pad motion

We now use the joint EMG and behavioral data (Fig. 4), with the stimulated movement data (Fig. 7), to develop an anatomically based model of the motor plant (Fig. 8). The model serves to summarize, in a self-consistent manner, the relationship between muscle activation and the movement of the vibrissae and mystacial pad. It consists of the equations of motion for the vibrissae as a function of the forces generated by the facial muscles, i.e., intrinsics, m. nasalis, and the retractors taken together, and the visco-elastic properties of the mystacial pad. This yields a set of first-order nonlinear differential equations that we use to numerically simulate the A-P translation and rotation of the vibrissae. The full equations and initial conditions are given in Appendix and Tables 4–7. Parameter values are given in Table 2. Our software implementation is included as supplemental information (available at www.jneurosci.org as supplemental material).

Figure 8.

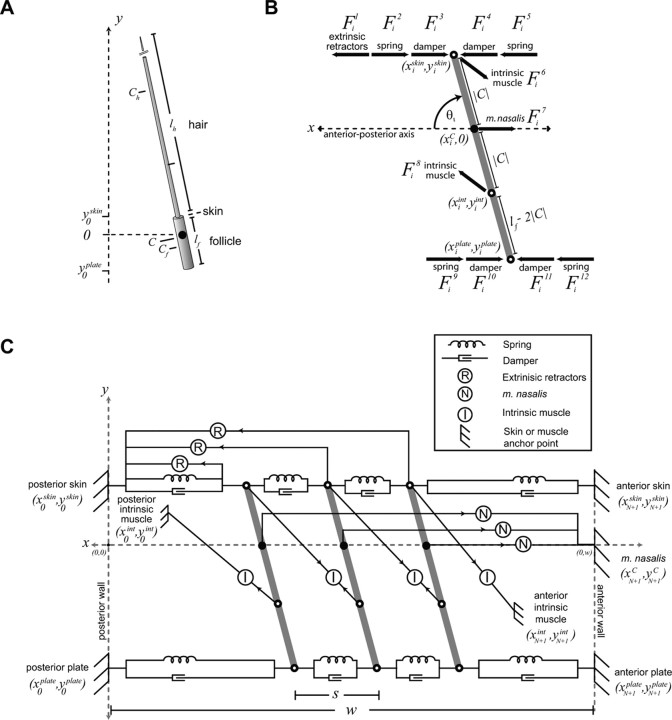
Biomechanical model of motor plant. A, Rigid body model of a vibrissa unit. The follicle is a rod of length l_f embedded below the skin, with center of mass located at C_f. The hair protrudes from the follicle as a cone of length l_h, with center of mass at C_h; the hair is displayed truncated. The composite center of mass is at C and defines the location y = 0. B, Diagram of forces (Table 6) and attachment points (Table 4) along the ith follicle/vibrissa unit. Circles indicate the location of a muscle attachment point, with the filled circle corresponding to the center of mass. The arrows indicate the approximate direction of the labeled force. The distances between attachment points are given in terms of the depth from the center of mass, i.e., y = 0, and the length of the follicle, l_f. The angle of the follicle/vibrissa unit, θ_i, is taken with respect to the A-P axis. C, Schematic of the full mechanical model of a row of three vibrissae (Appendix and Tables 2–7), shown in the rest state. The attachment points are illustrated for the springs, dampers, and muscles that correspond to the forces labeled in B. The approximate relationship between attachment points is conserved, but the figure is not drawn to scale. Arrows indicate the direction of muscle forces, which point away from the attachment points.

Table 2.

Parameters used in biomechanical simulations

Parameter	Value	Description
N	3	Number of vibrissae
lh	40 mm	Length of hair
lf	4 mm	Length of follicle
s	2 mm	Distance between vibrissae at rest
w	20 mm	Extent of mystacial pad
θ rest	80°	Resting angle of vibrissae
Mh	0.5 mg	Mass of hair
Mf	10 mg	Mass of follicle
C	−1.43 mm	Center of mass of vibrissa as measured from base of hair
I	112 mg mm2	Moment of inertia of vibrissa unit about center of mass
τ relaxation	27 ms	Relaxation time-constant of the mystacial pad

Each value represents the mean from across three rats except for τ^relaxation.

We consider a row of three rigid follicle/vibrissa units acted on by muscles and visco-elastic elements that represent the elasticity of the mystacial pad. We model the visco-elastic elements as overdamped springs (Eqs. 8, 11) that connect the vibrissae to each other and to the ends of the pad. The intrinsic and extrinsic muscles are represented by force actuators whose output is proportional to their |∇EMG| activity with a length-dependent scaling term (Eqs. 17–19). We note that the relatively minor D-V component of whisking is ignored, and so we exclude m. transversus nasi from the model and take m. nasolabialis and m. maxillolabialis to act as a single force in the A-P direction. The direction of all force vectors is determined by the geometry of the mystacial pad, i.e., how the various muscles, springs, and dampers are attached, which varies dynamically with the motion of the vibrissae.

Geometric parameters

Parameters related to the morphology of the mystacial pad were measured from dissections performed on three rats (Table 2). We obtained sagittal sections of the mystacial pad that reveal the spacing and orientation of the follicles (Fig. 9). The caudal vibrissae, i.e., C1–C3, have follicles of approximately l_f = 4 mm in length with a spacing of s = 2 mm. We note that the space between the capsules of adjacent follicles was as little as 200 μm. This suggests that vibrissae along a single row are sterically constrained to move primarily in unison during whisking.

Figure 9.

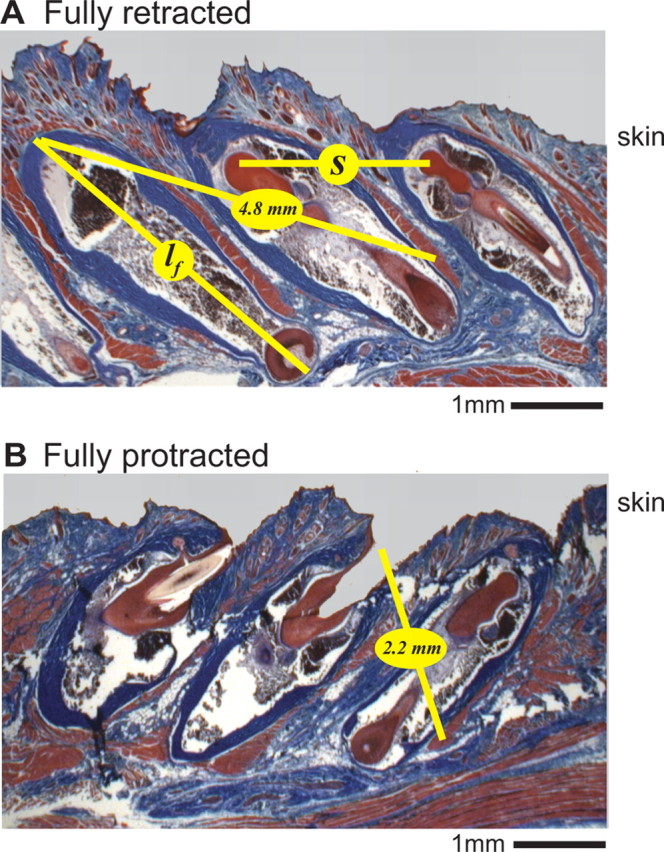
Sagittal sections of the follicles for vibrissae C1 through C3. A, Section with follicles fixated in a retracted position. Image is posterior to anterior from left to right. The trichrome stain highlights connective tissue in blue and muscle fibers in red. The length of the follicle is denoted l_f and the horizontal spacing of the follicles is denoted s. The 4.8 mm yellow line indicates the estimated path of an intrinsic muscle fiber in the fully retracted state. B, Same as in A but with the follicles fixated in a protracted position. The 2.2 mm yellow line indicates the estimated path of an intrinsic muscle fiber in the fully protracted states.

The force generated by a muscle is a function of the deviation from its rest length. This change is expected to be greatest for the relatively short intrinsic muscles. We inferred the fractional change in length of these muscles from histological sections with the vibrissae in either a protracted or retracted position (Fig. 9). Note that the protracted and retracted vibrissae are positioned at 135° and 40°, respectively, which closely matches the physiological range of vibrissa motion (Fig. 7G). The length of the intrinsic muscle is estimated as twice the distance from the apex of the caudal follicle to ∼70% of the depth on the outer capsule of the rostral follicle, plus ∼1.0 mm for the muscle to wrap around the follicle (Fig. 1C). We estimate a length of 10.5 mm in the retracted position and 5.5 mm in the protracted position (n = 3 rats), with a rest length given by the mean, or 8.0 mm. Therefore, an intrinsic muscle may contract or elongate by ±30%. We account for this change with a length-dependent scaling factor applied to all muscle forces (Eq. 18).

Validation of geometry

We observed in our stimulation experiments that each muscle produces a characteristic ratio of pad movement to vibrissa deflection (Fig. 7G). We used our biomechanical model to estimate these ratios by exciting individual simulated muscles over a range of inputs. A constant input was passed into one muscle at a time, and the total vibrissa deflection and pad translation was recorded at steady state. The amplitude of the input was increased until movement exceeded the physiological range; this yielded the full curve of pad translation versus vibrissa deflection (Fig. 7G). For each muscle, the theoretical curve passes through the cloud of data points obtained from stimulation experiments. This result is determined solely by the geometry of the pad and therefore serves as validation of our geometric parameters.

Relaxation time constant

Passive relaxation of the model vibrissae is determined by the time constant of a set of damped springs (Eqs. 8, 11, 16). To determine this constant, we fit its value to the observed relaxation time course of each muscle from a rat used in the stimulation experiments (Fig. 7 C–E). The model was initialized to the deflected vibrissa position from individual muscle stimulations. The model vibrissae were then allowed to passively relax back to their rest position, θ_rest, that was set to the observed angle of the vibrissa when unstimulated. The simulated motion of the middle vibrissa was compared with the measured movement of C2 to compute the root mean square (RMS) error (Eq. 27) for particular values of the time constant that yielded an optimal value of 27 ms that compares favorably with the range of 18–26 ms for exponential fits of the relaxation time course (Fig. 7 C–E).

Simulated vibrissa movement from EMG data

We validated the model on data from head-fixed experiments, for which we used the measured triphasic |∇EMG| data as input to the model. A set of 20 bouts of 1 s in duration were selected. Protraction of the vibrissae is essentially synchronous (Sachdev et al., 2002), so the intrinsic |∇EMG| signal is interpreted as representative of the contraction of individual intrinsic muscles. The geometric parameters and spring time constants were fixed (Table 2). The rest position of the vibrissae were determined from epochs when the vibrissae were still. The free parameters were three gain factors, one for each type of muscle, that relate the force produced by a given muscle to the value of the respective |∇EMG| signal (Eq. 19). These constants were fit to each bout to minimize the RMS error of the estimated vibrissa and pad motion, as illustrated by the three examples of Figure 10. Only one set of parameters was found to minimize the error. The lack of systematic error in the estimated motion suggests that no other muscles play a significant role in driving the motion. Our model achieved an average RMS error of 8.1° for A-P angle and 0.31 mm for pad translation across all 20 bouts, compared with an average range of movement 61° and 1.6 mm for each bout.

Figure 10.

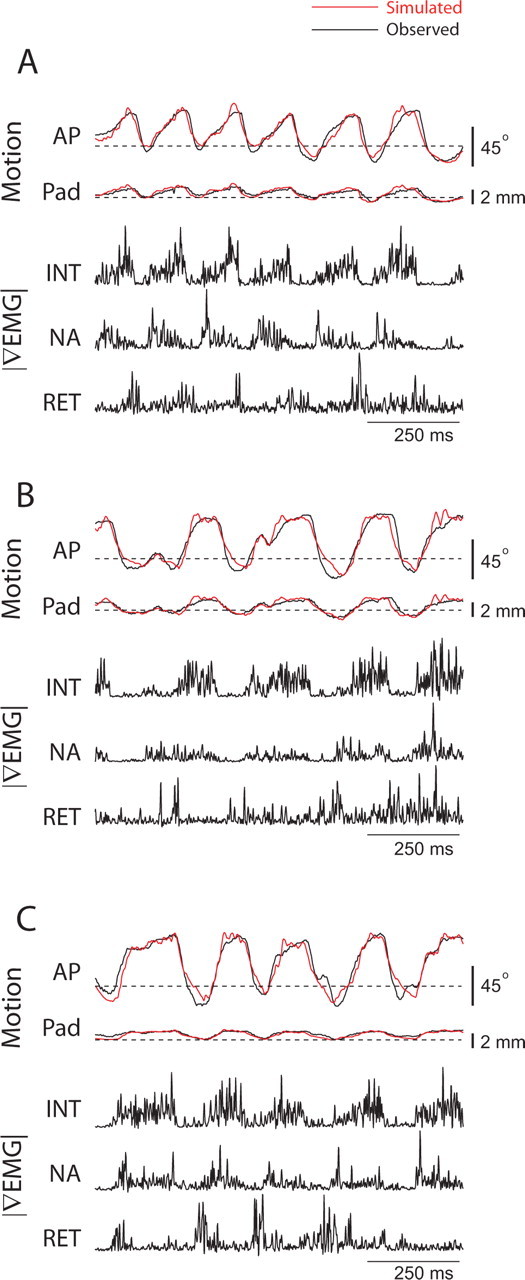
Estimation of vibrissa motion from |∇EMG| during head-fixed whisking. A–C, |∇EMG| signals were used as input to the biomechanical model to generate the estimated motion shown in red. The |∇EMG| activity of m. nasolabialis was used as the extrinsic retractor signal. All parameters were taken from Table 2 except for the muscle gain factors, which were fit to the motion data. INT, Intrinsic muscles; RET, retractor muscles; NA, m. nasalis.

We estimated the relative significance of each muscle in driving the vibrissae by rerunning each simulation with the optimal parameters but one of the muscles inactivated. We then recorded how much the amplitude of each whisk in the dataset (n = 102) was reduced by the absence of this muscle (Table 3). We find that the intrinsic muscles contribute 71% of the amplitude of the whisk with the extrinsic retractors contributing 25% and m. nasalis 4%. We note that this variability is large compared with the variation of average force output for each muscle, which only varied by a factor of 3 (Table 3). The fact that m. nasalis makes a negligible contribution to whisking amplitude is consistent with our stimulation data showing that this muscle produces a relatively small whisker deflection for a given amount of pad movement. Furthermore, by activating early in protraction, m. nasalis may have less control over the maximum angle that occurs at the end of protraction. A video demonstration of the model's prediction of vibrissa position is available at www.jneurosci.org as supplemental material.

Table 3.

Sensitivity analysis of free parameters in biomechanical simulations

Parameter	Mean value	Mean output	Relative angle sensitivitya	Relative pad sensitivitya	Mean A-P angle contributionb	Mean A-P pad translation contributionb
gINT	32.6 N/V	2.7 × 10−4 N	2.6	2.1	26.1°	1.0 mm
gNA	4.5 N/V	0.9 × 10−4 N	0.2	0.9	1.4°	0.3 mm
gRET	18.6 N/V	2.1 × 10−4 N	1.0	1.6	9.1°	0.6 mm

^aSensitivity is defined by Equations 28 and 29.

^bMean reduction in amplitude when muscle force is set to 0.

Sensitivity analysis

We determined the sensitivity of motion of the vibrissae and mystacial pad to changes in the gain parameters g^INT, g^NA, and g^RET (Table 3). Our analysis used a measure that compares the normalized RMS error between the calculated and measured motion of the vibrissae and the mystacial pad (Eqs. 28 and 29). The sensitivity may be interpreted as the relative impact of a given muscle group on the motion. We find that the intrinsic muscles have the greatest impact on both motion of the vibrissae and the pad, whereas the retractor muscles have less effect on vibrissa motion but near equal effect on motion of the pad. The protractor m. nasalis has little impact on motion of the vibrissae but significant impact on motion of the pad.

Application of the model: constraints on whisking kinematics

Motivated by evidence that the range of whisking amplitudes is diminished for large offset angles and high values of whisking frequency (Carvell and Simons, 1995; Berg and Kleinfeld, 2003; Knutsen et al., 2006), we analyzed the available range of whisk amplitudes and set points, defined here as the point of maximal retraction, within the context of our model. Our strategy was to use all possible realistic patterns of muscle activity as input for the model to determine the bounds on its range of motion. The waveforms for the simulated neuromuscular input were derived from the average waveform of the |∇EMG| data for individual muscles used in Figure 4. We recomputed the average waveform with each |∇EMG| signal aligned on its own peak rather than the peak of protraction. The latter method can overestimate the overlap in timing of different muscles. These waveforms were then scaled and given a baseline offset (Fig. 11A). All possible amplitudes and offsets were tested up to a bound set by the observed physiological movements (Fig. 7G), i.e., a maximum of 40° for retraction, 140° for protraction, and 3.0 mm for anterior translation of the mystacial pad. The peaks of the waveforms for the different muscles were staggered to match the phase delay observed in behavior (Fig. 5). Different frequencies of input were tested by rescaling the input signals in time. Simulations were run for 1 s, and the range of motion was assessed from the final whisk cycle of each trial.

Figure 11.

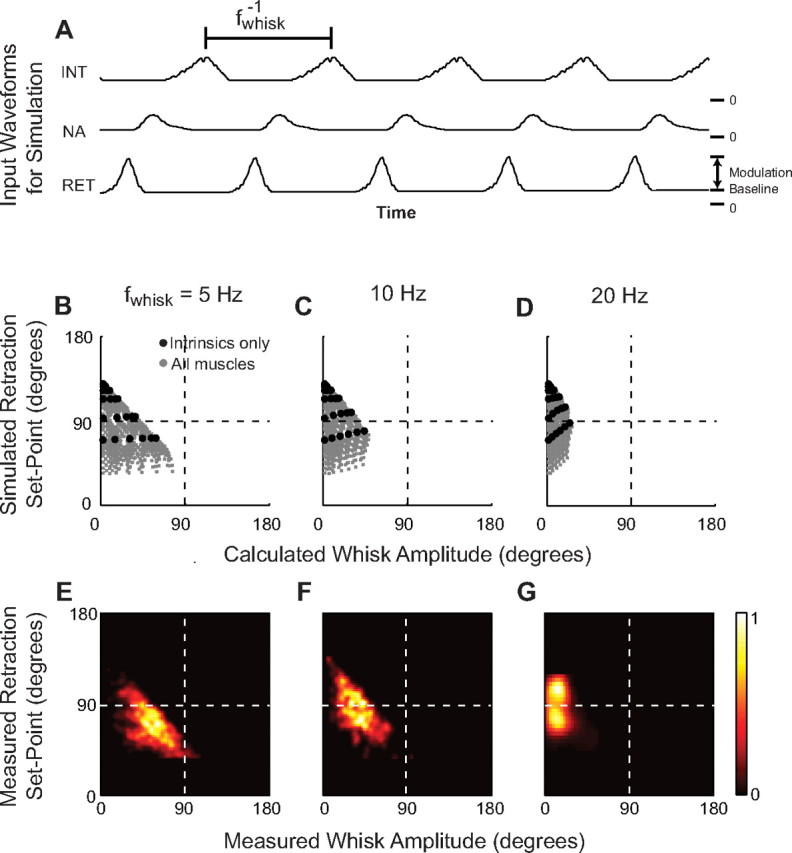
Biomechanical constraints on whisking kinematics compared with behavioral repertoire. A, Illustration of input signals. The modulation and constant offset of each muscle as well as the overall whisking frequency, f_whisk, were varied to determine the bounds on vibrissa motion. B–D, Scatter plot of kinematic parameters produced when each muscle received input at the indicated frequency. Black dots indicate runs in which only the intrinsic muscles were active. E–G, Map of kinematic parameters obtained from awake, behaving animals. The color bar represents the density of events. The dashed line in B–G represents the rest angle. INT, Intrinsic muscles; RET, retractor muscles; NA, m. nasalis.

Our results show that the range of set points available to the animal diminishes as the whisking amplitude increases (Fig. 11 B–D). Furthermore, the largest available amplitudes decrease and the available set points become more protracted as whisking frequency increases. Whisking at a protracted angle produces a stronger relaxation force and allows the intrinsic muscle to contract closer to their angle of maximum torque (Fig. 11B), so that only protracted set points can produce large-amplitude whisks at high frequencies.

The calculated range of kinematic parameters was compared with that found in behaving animals (Fig. 11, compare E,G with B,D). We used data from a single head-fixed rat to plot the histogram of amplitude and set points for whisk cycles with instantaneous frequencies near 5 Hz (n = 761) and 10 Hz (n = 326). Our head-fixed animals did not whisk in the foveal range (15–20 Hz), so additional data points were obtained from two separate studies. The first dataset involved unrestrained rats whisking in air (n = 20) (Berg and Kleinfeld, 2003), and the second used unrestrained rats whisking in air during an object localization task (n = 150) (P. M. Knutsen, M. Pietr, and E. Ahissar, unpublished observations) (for methods, see Knutsen et al. 2005, 2006). The behavioral data have comparable boundaries with the estimated behavioral limits at all frequencies and exhibit the same trend toward smaller, protracted whisks at higher frequencies. These results support the hypothesis that whisking behavior is limited by mechanical constraints rather than behavioral choice.

An analysis of simulations of the model with the extrinsic muscles inactive shows that the range of set points and amplitudes is more limited. For example, we predict that a rat without extrinsic muscles can no longer whisk at retracted positions. Furthermore, the increase in whisk amplitude gained by using extrinsic muscle diminishes at higher whisking frequencies (Fig. 11D).

Discussion

We report the full pattern of rhythmic muscle activity that drives the A-P motion of the vibrissae and the mystacial pad during exploratory whisking by rat. Four separate muscle groups are observed to activate at three distinct phases during the whisking cycle (Fig. 3). M. nasolabialis and m. maxillolabialis activate during retraction, m. nasalis during the early part of protraction, and the intrinsic muscles during late protraction (Fig. 4). The precise phase relationship is essentially independent of whisking frequency (Fig. 5). We further characterized the elastic properties of each muscle group via direct stimulation (Fig. 7), as well as the extension of the intrinsic muscle by anatomy (Fig. 9). These mechanical properties and the previously described geometry of the follicle and mystacial pad complex (Dorfl, 1982; Wineski, 1985) (Fig. 1) informed a mechanical model of the motor plant (Fig. 8). The calculated transformation of motor input into mechanical output, i.e., transformation of |∇EMG| input to motion of the vibrissae and mystacial pad, compares favorably with the measured output. In particular, the model accounts for the amplitude and time course of vibrissa motion during direct muscle stimulation (Fig. 7) and behavior (Fig. 10) and explains the lack of extrinsic retractor muscle activity during high-frequency foveal whisking (Fig. 11). Our measurements and model link neuronal motor commands to sensor motion (Fig. 10). They emphasize that the biomechanical properties of an active sensory apparatus provide the ultimate constraints on sensory behaviors and thus underlie the interpretation of studies on sensorimotor control.

Whisking in head-fixed versus freely exploring animals

Head restraint is a useful tool to facilitate vibrissa tracking and to create a controlled behavioral paradigm (Bermejo et al., 1996). As such, this procedure has enabled other difficult behavioral tasks (Gao et al., 2001; Bermejo et al., 2002; Gao et al., 2003b; Friedman et al., 2006) and intracellular (Crochet and Petersen, 2006) and extracellular (Sachdev et al., 2000; Kleinfeld et al., 2002; Melzer et al., 2006) recording studies. Yet it has been heretofore undocumented how head restraint may alter whisking behavior. We find that exploratory whisking for head-fixed versus freely exploring animals involves the same pattern of muscle activation (Fig. 3, compare A, B). However, the probability densities of whisking frequency for head-fixed versus freely exploring animals have little overlap (Fig. 6C,D). The mean frequency for whisking decreases from 9 Hz for the unrestrained case to 6 Hz for head-fixed animals. In both cases, whisking was spectrally pure, i.e., it is characterized by a sharp peak at the whisking frequency in the power spectrum of the |∇EMG| (Fig. 6E,F). It remains unclear whether the decrease in whisking frequency results from a change in whisking strategy or from the lack of head movements.

Biomechanical constraints on the behavioral repertoire of whisking

The intrinsic muscles are sufficient to produce rhythmic vibrissa motion. The contraction of these muscles, which form a sling around the base of each follicle (Fig. 1B), provide the major protraction of the vibrissae (Fig. 11 A–D). In the absence of the extrinsic muscles, the concomitant retraction can be effected through passive relaxation of the elastic facial tissue (Fig. 11 A–D). Of practical relevance, this form of retraction can be generated by electrically stimulating the facial nerve to induce protraction in anesthetized animals and is referred to as “artificial whisking” (Zucker and Welker, 1969; Brown and Waite, 1974; Szwed et al., 2003, 2006; Arabzadeh et al., 2005).

Our biomechanical model sheds light on the limitations of whisking by intrinsic muscles alone. First, the visco-elasticity in the mystacial pad is overdamped, so the vibrissae cannot passively retract beyond their rest angle. This is manifest as a region of parameter space for whisking kinematics that lies behind the rest angle that is accessible only when the model includes extrinsic muscles (Fig. 11 B–D). Active retraction by m. nasolabialis and m. maxillolabialis enables larger-amplitude whisks to occur. Second, passive relaxation sets an upper bound on the velocity of retraction. With only activation of the intrinsic muscles, the vibrissae must shift their set point farther forward to increase the elastic tension on the vibrissae. This may explain why high-frequency foveal whisking, which does not involve active retraction (Berg and Kleinfeld, 2003), has a protracted set point.

Extrinsic retractor muscles cooperate to control dorsoventral motion

The extrinsic retractor muscles are ideally situated to counterbalance each other in the control of the D-V component of vibrissae and mystatial pad motion, with the fibers of m. nasolabialis running superficially and ventrally as they invade the pad and those of m. maxillolabialis entering deep and dorsally. Anatomically, the fibers intermingle and fuse as they run superficially between the vibrissae (Dorfl, 1982). Direct excitation of these muscles demonstrates that neither one is sufficient to produce a strictly posterior movement (Fig. 7B). Only a balanced stimulation, resulting in a linear summation of their action, results in a purely posterior retraction. The concomitant activation of both muscles during whisking (Fig. 3–5) suggests that the animal uses such a summation.

Relationship of the model of the motor plant to sensation

Our model considers motion of the follicle and vibrissa as a single unit. In fact, the vibrissa can move within the follicle, as will occur during contact of a vibrissa with an object (Rice et al., 1986). Such movement leads to activation of pressure sensitive-trigeminal ganglion neurons that innervate the apical (skin) and the distal (plate) ends of the follicle (Fig. 1) (Zucker and Welker, 1969; Lichtenstein et al., 1990; Waite and Jacquin, 1992; Szwed et al., 2003; Leiser and Moxon, 2006). In principle, differential activation of these two groups of receptors provides a means to code both the angle (Curtis and Kleinfeld, 2006) and radial distance (Solomon and Hartmann, 2006; Szwed et al., 2006) of the contact point. A second form of sensory signaling concerns the angular position of the follicle in the absence of vibrissa contact (Fee et al., 1997; Szwed et al., 2003; Ganguly and Kleinfeld, 2004). This proprioceptive-like reference signal was shown to result from peripheral reafference (Fee et al., 1997). It may, in principle, be generated by periodic compression and distortion of the follicles during the whisk cycle. The model of the motor plant presented here provides the substrate for a full model that incorporates the dynamics of the follicle/vibrissa complex (Mitchinson et al., 2004) and bending properties of the vibrissae (Hartmann et al., 2003; Andermann et al., 2004; Ritt et al., 2008).

Motor control of exploratory whisking

The results of this study bear on the neural circuitry for pattern generation of whisking. Lesion studies have shown that whisking persists after sensory nerve transection (Welker, 1964; Gao et al., 2001; Berg and Kleinfeld, 2003; Berg et al., 2006), contralateral motor cortex ablation (Gao et al., 2003b), and extensive decerebration (Welker, 1964). These results argue for a brainstem central pattern generator to drive rhythmic whisking. It was proposed previously that this central pattern generator consists of two coupled oscillators, consistent with a constant phase relationship between the intrinsic muscles and m. nasolabialis across frequencies (Berg and Kleinfeld, 2003). We now find that such a constant phase relationship holds for all of the muscles involved in whisking (Fig. 5) and thus revise the original hypothesis to include three coupled oscillators that correspond to the three phases of muscle activity.

Many rhythmic behaviors in rat have been reported to alternately couple and decouple to whisking. These include sniffing and head movements (Welker, 1964), breathing (Welzl and Bures, 1977), and mastication (Travers et al., 1997). This suggests that the brainstem contains multiple pattern generators, each for a different motor action. These oscillators may phase lock or decouple in a dynamic manner that depends on their synaptic interactions (Kopell and Ermentrout, 1986) and on the overall oral-facial task of the animal.

The present results further highlight the need to understand motor control in terms of the activation of individual muscle groups. In principle, retraction of the vibrissae may involve any combination of activation of m. nasolabialis and m. maxillolabialis along with passive relaxation of the mystacial pad. This confound is removed by recording the |∇EMG| for each muscle. This approach is also crucial for interpreting the results of studies that make use of intracortical microstimulation of vibrissa motor cortex (vM1), which may evoke a nonbehavioral pattern of muscle activation. Rhythmic stimulation of vM1 simultaneously activates m. nasolabialis and the intrinsic muscles, which normally activate in anti-phase, with the retractor muscle dominating the evoked movement (Berg and Kleinfeld, 2003). Furthermore, it remains to be shown whether rhythmic vibrissa motion produced by tonic stimulation of vM1 in anesthetized rats (Cramer and Keller, 2006) or induced rhythmic activity in vM1 (Castro-Alamancos, 2006) produces the three-phase pattern of muscle activation observed in awake, behaving rats (Figs. 3, 4). A myotopic map of vM1 would clarify how the control of whisking is segregated in cortex, e.g., how do “rhythmic whisking” versus “retraction-facial” areas correspond to different patterns of intrinsic and extrinsic muscle activation (Haiss and Schwarz, 2005)?

Appendix

Here we define the equations that describe translation and rotation of the vibrissa along the A-P axis (Fig. 8). The D-V component of whisking, as well as movement along the length of the shaft, are ignored.

Follicle/vibrissa unit

A follicle/vibrissa unit consists of a hair that protrudes from a follicle. We take both components to be straight, rigid bodies (Fig. 8A). The tips of real vibrissae are curved and flexible, but our approximation is valid for motion at the base of the shaft. The follicle is modeled as a rod of length l_f and mass M_f that is embedded below the skin. The hair is modeled as a cone of length l_h and mass M_h with its base at the surface of the skin. We approximate a follicle/vibrissa unit as infinitely thin, so we consider its moment of inertia about the A-P axis only. The unit has a center of mass, C, and moment of inertia with respect to the center of mass, I, that is derived from the corresponding values for the hair and follicle alone, denoted by the subscripts h and f, respectively (Fig. 8A):

The center of mass of the entire unit is the weighted average of C_h and C_f, i.e.,

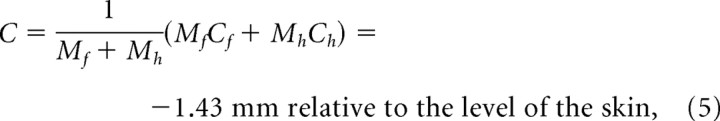where we substituted values from Table 2. By the parallel axis theorem, we can write the moment of inertia of the follicle/vibrissa unit as follows:

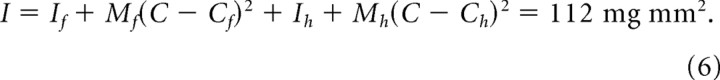The hair contributes negligibly to the mass of the vibrissa/follicle unit, but its length dominates the moment of inertia. With the hair removed, the moment of inertia of the follicle alone is 13.3 mg mm².

Vibrissa and pad

Enumeration of forces that act on each vibrissa

The vibrissae are driven actively by the contraction of facial muscles and passively by the visco-elastic properties of the mystacial pad. We enumerate these forces and specify their attachment points along the follicle. The calculation of the magnitude and direction of each force requires a model for the geometry of the pad as a whole, so we defer these equations to a later section. In the discussion below, we denote the jth force on the ith follicle/vibrissa as F_i^j.

First, we consider the visco-elastic properties of the mystacial pad. We observe that a deflected vibrissa passively returns to a rest position and rest angle without oscillation (Fig. 7 C–E). The simplest model that generates this behavior consists of two sets of overdamped springs that return the top and bottom of the follicle to different A-P rest positions. At the level of the skin, there are two springs, with forces F_i² and F_i⁵, and two dampers, with forces F_i³ and F_i⁴, that act on the point (x_i^skin and y_i^skin) (Fig. 8B). At the plate, there are two springs, with forces F_i⁹ and F_i¹², and two dampers, with forces F_i¹⁰ and F_i¹¹, that act on the point (x_i^skin and y_i^skin).

We include four muscles that directly manipulate each vibrissa unit. First, we combine the retractor muscles m. nasolabialis and m. maxillolabialis into a single force, denoted F_i¹. This is motivated by the observations that the two muscles activate concurrently (Figs. 4, 5) and that only a balanced excitation leads to motion strictly along the A-P axis (Fig. 7B). The extrinsic retractor muscles run just below the skin. Their fibers do not necessarily attach directly to the follicle, but the force they produce on the vibrissae is directed at the level of the skin. We therefore place the attachment point for this muscle at the top of the follicle, at the point (x_i^skin and y_i^skin).

The fibers of m. nasalis, the caudal extrinsic muscle, run deep to the follicle, yet the muscle produces a minimal angular deflection of the vibrissae when stimulated (Fig. 7G), which is consistent with the net force of m. nasalis, denoted F_i⁷, acting at the center of mass of the follicle/vibrissa unit. We thus attach m. nasalis to the center of mass of the unit (Fig. 8C).

Each vibrissa is also actively driven by two intrinsic muscles that correspond to forces F_i⁶ and F_i⁸. Each intrinsic muscle spans two adjacent vibrissae, so the direction of force is expected to be oblique to the A-P axis (Fig. 1B). The more superficial attachment point is at the level of the skin (x_i^skin and y_i^skin). We set the other attachment point to twice the depth of the center of mass, at the point (x_i^int and y_i^int). This is consistent with the anatomical location and implies that the intrinsic muscles exert an equal torque on the follicle.

In total, the 12 forces act on each follicle at four unique attachment points. Additionally, we constrain the center of mass of each vibrissa to move along the A-P axis so that y_i^c = 0 ∀ i. The location, x_i^c, and speed, ẋ_i^c, of the centers of mass of each vibrissa and the angle, θ_i, and angular velocity, θ̇_i, of each vibrissa about its center of mass comprise the state of the model (Fig. 8B). The position and velocity of each of the four attachment points can be derived from these state variables (Table 4).

Table 4.

Equations for position and velocity of follicle attachment points

Attachment	Position		Velocity
	A-P axis	Depth	A-P axis	Depth
(xskin, yskin)	xC + Ccos(θ)	−Csin(θ)	ẋC − Csin(θ)(θ̇)	−Ccos(θ)(θ̇)
(xint, yint)	xC − Ccos(θ)	Csin(θ)	ẋC + Csin(θ)(θ̇)	Ccos(θ)(θ̇)
(xplate, yplate)	xC + (lf + C)cos(θ)	−(lf + C)sin(θ)	ẋC − (lf + C)sin(θ)(θ̇)	−(lf + C)cos(θ)(θ̇)

Geometry of the vibrissae in the mystacial pad

Each of the forces acts between two attachment points, whose locations determine the direction and scale the magnitude of the associated force. We define the attachment points associated with each force by considering a row of N identical vibrissae (Fig. 8C) (Table 5), where the vibrissae are numbered from 1 (posterior) to N (anterior) and are separated by a distance s at rest. We illustrate the case when N = 3 because this is the minimum case that includes a vibrissa that is coupled to two neighboring vibrissae by connective tissue and intrinsic muscles along with two vibrissae that are coupled to anchors by connective tissue and intrinsic muscles. The attachment points A^i,j and B^i,j associated with the force f_i^j are listed in Table 6; the coordinates of the attachment point are denoted by (A_i,j^x, A_i,j^y) and (B_i,j^x, B_i,j^y), and the force is directed toward the point A^i,j.

Table 5.

Equations for position of anchor points

Anchor point	A-P axis	Depth axis
(x0skin, y0skin)	0	−Csin(θ rest)
(x0int, y0int)	x1rest + Ccos(θ rest) − 2s	−Csin(θ rest)
(x0plate, y0plate)	0	−(C + lf)sin(θ rest)
(xN+1skin, yN+1skin)	w	−Csin(θ rest)
(xN + 1C, yN + 1C)	w	0
(xN + 1int, yN + 1int)	xNrest + (lf + C)cos(θ rest) + 2s	−(C + lf)sin(θ rest)
(xN + 1plate, yN + 1plate)	w	−(C + lf)sin(θ rest)

Table 6.

Forces and attachment point for each force on the ith vibrissa

Force	Description	To (Ai,j)	From (Bi,j)
Fi1	Extrinsic retractor muscles	(xiskin, yiskin)	(x0skin, y0skin)
Fi2	Posterior skin spring	(xiskin, yiskin)	(xi − 1skin, yi − 1skin)
Fi3	Posterior skin damper	(xiskin, yiskin)	(xi − 1skin, yi − 1skin)
Fi4	Anterior skin damper	(xiskin, yiskin)	(xi + 1skin, yi + 1skin)
Fi5	Anterior skin spring	(xiskin, yiskin)	(xi + 1skin, yi + 1skin)
Fi6	Superficial intrinsic muscle	(xiskin, yiskin)a	(xi + 1int, yi + 1int)
Fi7	M. nasalis	(xiC, yiC)	(xi + 1C, yi + 1C)
Fi8	Deep intrinsic muscle	(xiint, yiint)	(xi − 1skin, yi − 1skin)
Fi9	Posterior plate spring	(xiplate, yiplate)	(xi − 1plate, yi − 1plate)
Fi10	Posterior plate damper	(xiplate, yiplate)	(xi − 1plate, yi − 1plate)
Fi11	Anterior plate damper	(xiplate, yiplate)	(xi + 1plate, yi + 1plate)
Fi12	Anterior plate spring	(xiplate, yiplate)	(xi + 1plate, yi + 1plate)

^aIf i = 1, this attachment point is the anchor (x₀^int, y₀^int).

Several components in our model attach to immobile anchor points. We use the subscripts 0 and N + 1 to designate anchors that lie posterior or anterior to the row of vibrissae, respectively. The extrinsic muscles and the elastic tissue at either end of the row of vibrissae have attachment points external to the pad, represented by posterior and anterior walls. The separation of these walls is the measured length of the face, w. The depth of these attachment points is set so that the attached components lie horizontally when the vibrissae are at their rest angle, θ_i^rest. Additionally, the intrinsic muscles at either end of a row of vibrissae are taken to have an attachment point embedded within the pad (Figs. 1C, 8C). We placed the caudal intrinsic muscle anchor, (x_i^int, y_i^int), at the level of the skin and the anterior intrinsic muscle anchor, (x_{N + 1}^int, y_{N + 1}^int), at the level of the plate. Horizontally, the intrinsic muscle anchor points are positioned a distance of 2s from the rest position of their respective follicle attachment points.

Specification of visco-elastic forces

Damped restoring forces are generated by a parallel combination of a spring with a damper (Fig. 8C).

A spring (F_i², F_i⁵, F_i⁹, and F_i¹²) produces a force proportional to its displacement from its rest position. The distance between the two attachment points associated with spring force F_i^j is

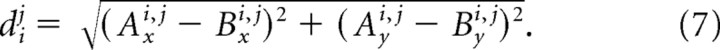Therefore, the magnitude of the force generated by a spring is

where κ_i^j is a proportionality constant and d_i^j,rest is the rest length of the spring. The sign of the force opposes displacement from rest. The constants κ_i^j were determined from the results of muscle stimulation experiments (Fig. 7 C–E). The rest length of each spring was set so that the springs have no tension when the vibrissa/follicle units are in their rest state. This corresponds to (1) all of the vibrissae are at the angle θ_i^rest, (2) adjacent vibrissae are separated by the distance s, and (3) the entire row of vibrissae is centered between the anterior and posterior walls. The rest position of the center of mass for the ith vibrissa is therefore

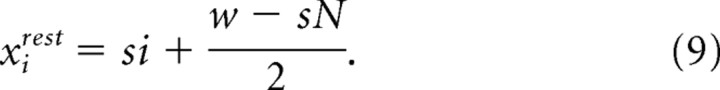The springs lie horizontally when the vibrissae are at their rest angle, so that the rest length of a spring that connects two follicles is s. Springs that have an attachment point on an anchor have a rest length chosen to center the row of vibrissae between the two walls (Table 7).

Table 7.

Rest lengths of model springs

Attachment points	Symbol	Rest length
Two follicles at skin	di2,rest; di −15,rest for 2 ≤ i ≤ N	s
Two follicles at plate	di9,rest; di −112,rest for 2 ≤ i ≤ N	s
Follicle to posterior skin anchor	di2,rest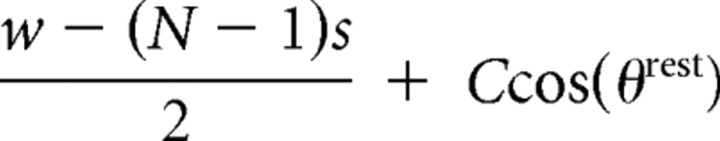
Follicle to anterior plate anchor	di12,rest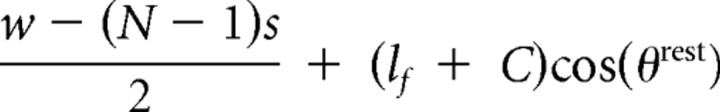
Follicle to posterior plate anchor	di9,rest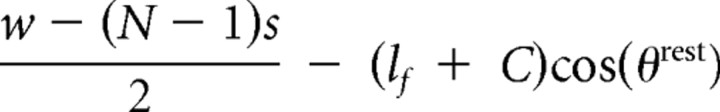
Follicle to anterior skin anchor	di5,rest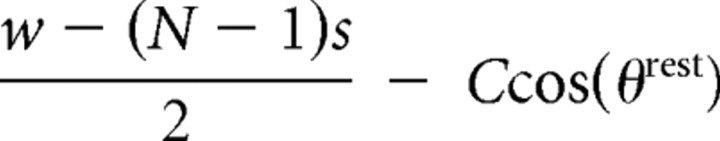

A damper (F_i³, F_i⁴, F_i¹⁰, and F_i¹¹) produces a force proportional to the velocity at which it changes length. The speed at which the attachment points associated with damper force F_i^j are moving with respect to each other is

These derivatives are calculated for follicle attachment points and are zero for anchor points (Table 4). The force generated by a damper is then

where ζ_i^j is a proportionality constant associated with this damper, and the sign is chosen to oppose motion.

We assume that the visco-elastic properties of the mystacial pad are homogeneous. The individual spring and damper constants are normalized by rest length, i.e.,

As a result, the relatively short springs and dampers between follicles are much stiffer than the relatively long springs and dampers between the follicles and the ends of the pad. The overall scale factors, i.e., κ for the spring constants and ζ for the damper constants, are fit to muscle stimulation experiments (Fig. 7 C–E). The results from these measurements imply that the mystacial pad is overdamped, so that

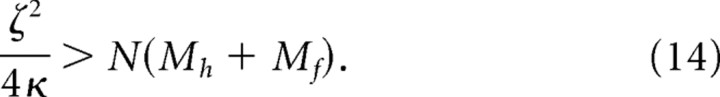A linear overdamped system is not greatly sensitive to the exact value of this ratio, so we arbitrarily chose

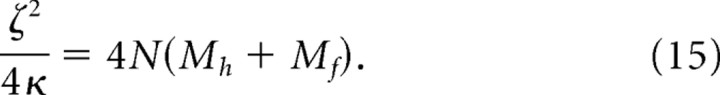This leaves only a single free parameter, τ^relaxation, which is the time constant of the exponential decay to rest. Its value is given by

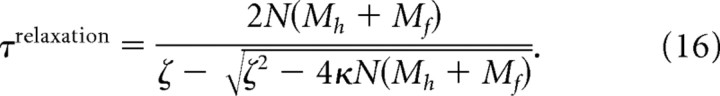Specification of muscle forces

The force output of the muscles (F_i¹, F_i⁶, F_i⁷, and F_i⁸) is a function of its electrical activation. We denote the electrical activity of a particular muscle as |∇EMG^γ| (t), where γ identifies the muscle type, and we assume that each muscle of the same type activates identically.

Each muscle is at its rest length when the vibrissae are in their rest position. We calculate the length-dependent variation in force in terms of the length of the muscle as a fraction of its rest length:

We scale the force of the muscle by a function, f(z_i^j), which is a simplified piece-wise linear function for the length dependence in type 2B fibers in rats (Galler et al., 1996), the fiber type that predominates in the mystacial pad (Jin et al., 2004). Thus,

The force output of a given muscle is

where the scale factor, g^γ, is chosen to fit to the vibrissa motion data from the concurrently recorded |∇EMG| data (Fig. 11). Note that we ignored the velocity dependence of the muscle force.

Equations of motion

The dynamics are expressed in terms of the A-P translation of each center of mass, x_i^c, and the angle of each vibrissa, θ_i. Translation is found from summing the horizontal component of each of the 12 individual forces that act on the ith follicle at each time step. The direction of a force F_i^j is along the line connecting its two attachment points. This angle with respect to the A-P axis is

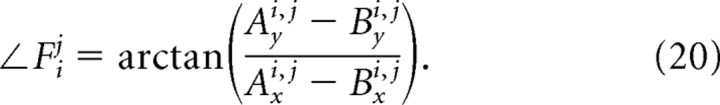The center of mass for each vibrissa responds to the component of each force along the A-P axis (Fig. 8B), i.e.,

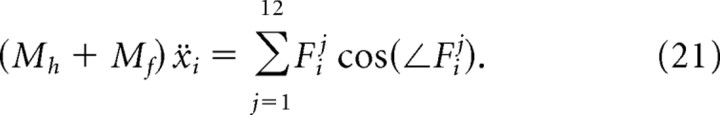Angular motion is determined by the net torque about the center of mass of the follicle/vibrissa unit (Fig. 8A,C). The torque is the product of the moment arm and the component of the force that lies perpendicularly to the follicle (Figs. 8B, 11A), i.e.,

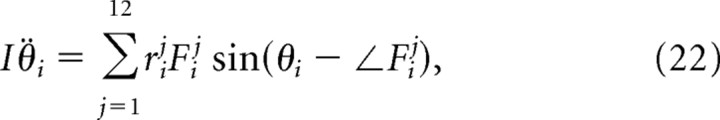where r_i^j is the distance between center of mass (x_i^c, 0) and the point where F_i^j acts on the vibrissa, A_i^j. The attachment points move with the vibrissae and are recalculated at each time step (Table 4). This movement, in turn, determines the magnitude and direction of each force at the next time step.

Initial conditions

The vibrissae start from rest, with initial displacements and velocities given by

Recall that the y position of the center of mass is fixed at 0.

Parameter estimation and sensitivity analysis

The time constant τ^relaxation and muscle gain parameters g^γ were optimized to fit motion data from stimulation experiments and head-fixed whisking as described in Results. The optimal values were chosen to minimize the normalized sum of the RMS error of the simulated angle E^θ₂ and the RMS error of the simulated pad translation E^x₂

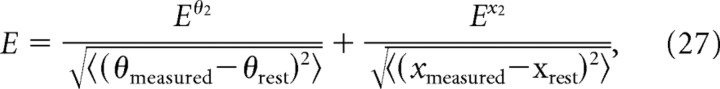where θ_measured and x_measured are the observed vibrissa angle and pad translation, respectively, and 〈·〉 denotes an average over the entire whisking bout. A global numerical search of parameter space verified that there was only one minimum in the error (Eq. 27) for each bout, which was found exactly through gradient descent. A detailed inspection of the parameter space suggests that increases in error subsequent to a change in one gain parameter can be partially offset by a change in another. For example, an increase in g^INT is partially offset by an increase in g^RET.

To assess the sensitivity of the model to a change in a single gain parameter g^γ, we estimated the quantities

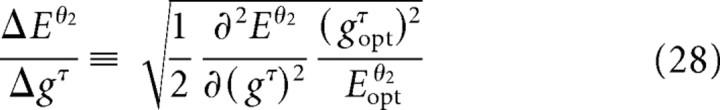and

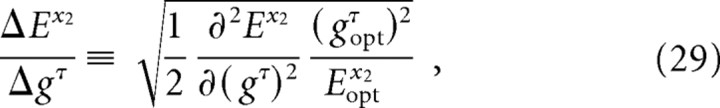where the subscripted variables are the values found during optimization. The expressions on the right are the square root of the normalized second-order term of the Taylor expansion of the error function. The first-order term is zero because the parameters are optimal. Values for Equations 28 and 29 were estimated by first varying the optimal parameters by ±10% and ±20% and then using a spline to estimate the second derivative of E^θ₂ and E^x₂ as a function of g^γ (Table 3).

Comparison with observed pad translation

Our experimental measurement of translation of the mystacial pad refers to points at which the vibrissa exits the skin. Therefore, we report the estimated translation at a height, h, above the center of mass (Fig. 8C):

The value of h is approximately the height of the skin anchor points but was adjusted by up to 0.25 mm to fit the measured translation.