Adaptation across the Cortical Hierarchy: Low-Level Curve Adaptation Affects High-Level Facial-Expression Judgments

Abstract

Adaptation is ubiquitous in sensory processing. Although sensory processing is hierarchical, with neurons at higher levels exhibiting greater degrees of tuning complexity and invariance than those at lower levels, few experimental or theoretical studies address how adaptation at one hierarchical level affects processing at others. Nevertheless, this issue is critical for understanding cortical coding and computation. Therefore, we examined whether perception of high-level facial expressions can be affected by adaptation to low-level curves (i.e., the shape of a mouth). After adapting to a concave curve, subjects more frequently perceived faces as happy, and after adapting to a convex curve, subjects more frequently perceived faces as sad. We observed this multilevel aftereffect with both cartoon and real test faces when the adapting curve and the mouths of the test faces had the same location. However, when we placed the adapting curve 0.2° below the test faces, the effect disappeared. Surprisingly, this positional specificity held even when real faces, instead of curves, were the adapting stimuli, suggesting that it is a general property for facial-expression aftereffects. We also studied the converse question of whether face adaptation affects curvature judgments, and found such effects after adapting to a cartoon face, but not a real face. Our results suggest that there is a local component in facial-expression representation, in addition to holistic representations emphasized in previous studies. By showing that adaptation can propagate up the cortical hierarchy, our findings also challenge existing functional accounts of adaptation.

Introduction

Adaptation is a basic phenomenon associated with sensory processing (Gibson, 1933; Barlow, 1990; Webster and MacLin, 1999; Dragoi et al., 2000; Felsen et al., 2002; Clifford and Rhodes, 2005; Krekelberg et al., 2006; Kohn, 2007). Psychologically, showing a stimulus such as a concave curve or a happy face leads at least to normalization: the adapting stimulus appears less extreme in its character (less curved or less smiling); aftereffects: new neutral test stimuli appear to have opposite characteristics (convex or sad); and discriminability: discrimination thresholds near to the adapting stimulus are frequently reduced. Neurally, there are complex changes to receptive fields of neurons coding for the adapting stimulus and its fellow travelers. Adaptation's centrality has made it the target of substantial modeling, with mechanistic approaches attempting to integrate the neural and psychological findings (Bednar and Miikkulainen, 2000; Clifford et al., 2000; Teich and Qian, 2003; Jin et al., 2005; Schwartz et al., 2007) and functional approaches suggesting informational or probabilistic underlying principles (Barlow and Foldiak, 1989; Barlow, 1990; Atick, 1992; Wainwright, 1999; Clifford et al., 2000; Stocker and Simoncelli, 2006; Zhaoping, 2006; Schwartz et al., 2007).

Cortical sensory processing is hierarchical (Felleman and Van Essen, 1991), with neurons in lower areas (like V1) having spatially smaller receptive fields and responding to simpler features of the stimulus than those in higher areas such as inferotemporal cortex. However, existing studies mostly use adapting and test stimuli coded at the same level of the hierarchy, with orientation tilt aftereffects measured after orientation adaptation and facial identity or expression aftereffect assessed after face adaptation. Thus, after viewing a curve, straight lines appear to be bent in the opposite direction (Gibson, 1933). This can be viewed as a generalization of the orientation tilt aftereffect (Gibson and Radner, 1937). Neurons tuned to curvature, like those tuned to orientation, have been found as early as V1 (Hubel and Wiesel, 1965; Dobbins et al., 1987). Similarly, after viewing a sad face, a neutral face appears happy (Hsu and Young, 2004; Webster et al., 2004). However, brain regions involved in face representation are much higher level than V1. They include various areas in the temporal lobe of monkeys (Gross et al., 1972; Desimone, 1991; Afraz et al., 2006; Leopold et al., 2006; Tsao et al., 2006) and humans (Kanwisher et al., 1997; Haxby et al., 2000; Winston et al., 2004).

We investigated cross-level adaptation, with adapting and test stimuli coded at opposite ends of the hierarchy (simple curves vs cartoon and real faces) to illuminate the structure of hierarchical processing and the possibility that adaptive changes to a code (at lower levels) are precisely tracked by higher levels, eliminating corruption from low-level adaptation. We showed that there is a substantial, although not complete, transfer of curvature adaptation to create a facial-expression aftereffect; that cartoon, but not real, faces, transfer to create a curvature aftereffect; and that these effects are retinally quite local. Our findings have physiological, psychophysical, and computational implications. Preliminary results have been reported in abstract form (Xu et al., 2007).

Materials and Methods

Subjects

A total of 10 subjects consented to participate in the four experiments of this study. Among them, two were experimenters, and the rest were naive to the purpose of the study. All subjects had normal or corrected-to-normal vision. Each experiment had four subjects. In experiment 1, one subject was an experimenter, and the other three were naive. In experiments 2–4, two subjects were experimenters, and the other two were naive. The study was approved by the Institutional Review Board of the New York State Psychiatric Institute.

Apparatus

The visual stimuli were presented on a 21 inch ViewSonic (Walnut, CA) P225f monitor controlled by a Macintosh G4 computer. The vertical refresh rate was 100 Hz, and the spatial resolution was 1024 × 768 pixels. In a dimly lit room, subjects viewed the monitor from a distance of 75 cm, using a chin rest to stabilize head position. Each pixel subtended 0.029° at this distance. The luminance values below were measured with a Minolta LS-110 photometer. All experiments were run in Matlab with Psychophysics Toolbox extensions (Brainard, 1997; Pelli, 1997).

Visual stimuli

A black (0.23 cd/m²) fixation cross was always shown at the center of the white (56.2 cd/m²) screen. It consisted of two line segments, each 0.41° in length and 0.06° in width. All stimuli were grayscale. They included computer-generated cartoon faces and curves, and real faces derived from images from the Ekman Pictures of Facial Affect (PoFA) database (Ekman and Friesen, 1976) and the M&M Initiative (MMI) facial espression database (Pantic et al., 2005). The stimuli were shown on the right side of the fixation for eight subjects, and on the left side for the other two subjects, who preferred the left visual field.

Cartoon faces and curves.

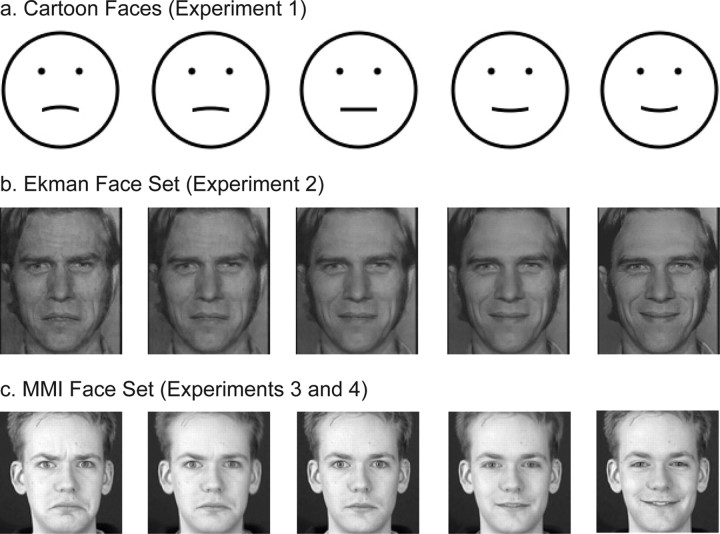
For experiment 1, we generated a set of black cartoon faces on a white background. Each face was made of a circle for the face contour, two dots for the eyes, and a curve for the mouth. The Michelson contrast was 0.99. The face contour had a diameter of 3°. The eye and mouth levels were at one-third and two-thirds of the face diameter, respectively. The center-to-center distance between the eyes was one-third of the face diameter. The widths of the face contour and the mouth curve, and the radius of the eye dots, were 0.09°. The curvature of the mouth varied from concave to convex (−0.69, −0.46, −0.23, 0, 0.23, 0.46, and 0.69 in units of 1/°) so that the facial expressions varied gradually from sad to happy. All mouths had the same arc length of 0.9°. We also generated a set of curves that were identical to the mouths of the faces. Because rugged edges of stimuli could provide potential cues to curvature or facial expression, we created our stimuli with an anti-aliasing method (Matthews et al., 2003). All stimuli appeared smooth at the viewing distance and eccentricity (see below). Examples of the cartoon faces are shown in Figure 1 a.

Figure 1.

Examples of the face stimuli used in this study. a, Cartoon faces used in experiment 1, generated with our anti-aliasing program. The mouth curvature varied from concave to convex to produce sad to happy expressions. b, Ekman faces used in experiment 2. The first (sad) and last (happy) images were taken from the Ekman PoFA database, and the intermediate ones were generated with MorphMan 4.0. c, MMI faces used in experiments 3 and 4. The first (sad), middle (neutral), and last (happy) images were taken from the MMI face database, and the other images were generated with MorphMan 4.0. See Materials and Methods for details.

Real face images.

For experiment 2, we selected a sad face and a happy face of the same person from the Ekman database. Because pilot data showed that the sad face was less sad than the happy face was happy, we used MorphMan 4.0 (STOIK Imaging, Moscow, Russia) to pull down the ends of the mouth of the sad face slightly to make it a little sadder. We cropped the two images to a size of 3 × 3.6° to remove most of the hair and neck areas. We then equated the Fourier amplitude spectra of the images by performing a Fourier transform on them and using the average of the two amplitude spectra and the original phase spectra to do the inverse transform. Finally, we used MorphMan 4.0 to generate intermediate facial expressions by morphing the two source images. We selected 36 markers (5 along the forehead hair line, 8 along the eyebrows, 6 along the eyes, 5 around the nose, 2 on the cheeks, and 10 around the mouth) on each source image to align important features between the images. The small number of markers was sufficient because the source images were taken from the same person under the same setting. We generated 21 images with the proportion of happiness from 0 (saddest) to 1 (happiest) in steps of 0.05. Those with the proportions equal to 0, 0.1, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.6, and 0.7 were used in experiment 2. Example images are shown in Figure 1 b. The images were presented at a relatively low contrast. We sampled the luminance at 10 locations along the mouth and at 10 locations surrounding the mouth of the saddest image. Based on the two mean luminance values, the Michelson contrast of the mouth in the face was 0.25.

Experiment 2 involved a condition in which the adapting stimulus was the mouth of the saddest face (the m-c condition below) instead of the whole face. We first used Photoshop to carve out the mouth from the image manually, and then assigned the rest of the image a uniform luminance equal to the mean luminance of the whole face excluding the mouth. This way, the contrast of the isolated mouth was identical to that of the mouth in the face.

In experiments 3 and 4, we selected a neutral face as well as a sad and a happy face, all of the same person, from the MMI database. Because the sad face also looked surprised, we used MorphMan 4.0 to reduce the eye opening slightly. Each color image was converted to grayscale and cropped to a size of 3 × 3°. Because equating Fourier amplitude spectra makes images look somewhat “cloudy,” and because the original images appear well matched in luminance already, we did not equate the amplitude spectra for the MMI faces.

When a sad face and a happy face are directly morphed, as we did for the Ekman faces above, there is a possibility that an intermediate face may have a mixture of sad and happy features in different parts of the face. To avoid this potential problem, for the MMI faces we morphed the sad face with the neutral face to generate 11 images with proportion of happiness from 0 (saddest) to 0.5 (neutral) and morphed the neutral face with the happy face to generate another 11 images with proportion of happiness from 0.5 (neutral) to 1 (happiest). In the experiments, we used the proportions of happiness equal to 0.2, 0.3, 0.4, 0.45, 0.5, 0.55, 0.6, 0.7, and 0.8. Example images are shown in Figure 1 c. These images were presented at a higher contrast than those in experiment 2. The mean Michelson contrast of the mouth in the saddest face was 0.78.

Adapting curves.

For experiment 1, the adapting curve was identical to the mouth curve of the saddest cartoon face. For the other experiments with real faces, we used the adapting curve that matched the mouth of the saddest or the happiest face in both curvature and length. The curve overlapped the narrow region where the two lips meet.

Experiment 2 included a condition in which both the adapting and the test stimuli were curves, but we wanted to match the contrast of the adapting curve to the mouth of the saddest face (the c′-c condition below). To do so, we chose the luminance of the adapting curve so that its contrast against the screen background was equal to the mouth contrast in the face (0.25).

Procedure

We used the method of constant stimuli and the two-alternative forced-choice paradigm in all experiments.

Experiment 1.

This experiment measured cross-level aftereffects between the curves and the cartoon faces described above. The adapting stimulus was either the most concave curve or the saddest face, and the test stimuli were either the sets of curves or faces that we generated. Subjects were run on all four possible combinations of the adapting and test stimuli. These conditions are termed c-f, f-f, f-c, and c-c, where the first letter indicates whether the adapting stimulus was the saddest face (f) or the most concave curve (c), and the second letter indicates whether the test stimuli were the face set (f) or the curve set (c). For example, c-f means the adapting stimulus was the most concave curve and the test stimuli were the face set. Subjects were also run on the baseline conditions for the face and curve sets without adaptation (0-f and 0-c conditions). When the test stimuli were the curve set (f-c, c-c, and 0-c conditions), subjects were asked to judge the curvature (convex or concave) in each trial. When the test stimuli were the face set (c-f, f-f, and 0-f conditions), subjects were asked to judge the facial expression (happy or sad). We randomly interleaved catch trials using the inversion of the saddest face as the test stimulus to ensure that subjects really judged the facial expression instead of the mouth curvature of the faces (see Results). We also ran a seventh condition in which the adapting stimulus was the inversion of the saddest face and the test stimuli were the (upright) face set (if-f condition).

The face stimuli were horizontally aligned with the fixation cross, with a center-to-center distance of 3.8°. The curves and the mouths of the faces had the same location on the screen. Whenever the inverted saddest face was used, whether as the test stimulus in the catch trials or as the adapting stimulus in the if-f condition, the mouth of the inverted face was at the same position as the mouths of the upright faces.

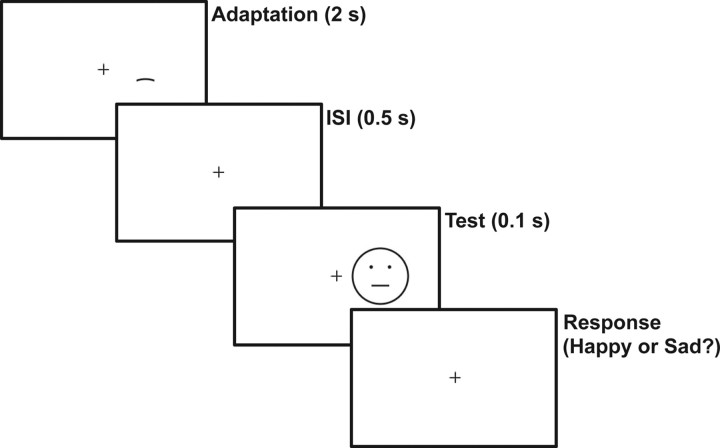
Subjects started each block of trials by fixating the central cross and then pressing the space bar. After 500 ms, for each adaptation block the adapting stimulus appeared for 30 s in the first trial (initial adaptation) and for 2 s in all subsequent trials (top-up adaptation) (Fig. 2). After a 500 ms interstimulus interval, a test stimulus appeared for 100 ms. The short test stimulus duration was selected to enhance aftereffects (Wolfe, 1984). For the baseline blocks without adaptation, only a test stimulus was shown in each trial for 100 ms. A 50 ms beep was then played to remind subjects to report their perception of the test stimulus. For facial-expression judgments, subjects had to press the “A” or “S” key to report happy or sad. For curvature judgments, subjects had to press the “E” or “D” key based on whether the center of the test curve appeared to point up (concave) or down (convex). After a 1 s intertrial interval, the next trial began. Subjects received no feedback on their performances at any time.

Figure 2.

Trial sequence for the c-f condition in experiment 1. Subjects fixated on the cross and pressed the space bar to initiate a trial. After 500 ms, the adapting curve appeared for 30 s in the first trial of a block (initial adaptation) and for 2 s (shown here) in all subsequent trials (top-up adaptation). After a 500 ms interstimulus interval (ISI), a test face appeared for 100 ms. The screen position of the adapting curve was identical to that of the mouth curves in the test faces. A beep was then played to remind the subjects to report the perceived expression of the test face. Subjects had to press either the “A” or the “S” key to indicate a perception of a happy or sad expression. Experimental parameters for all conditions and experiments are detailed in Materials and Methods.

The seven conditions were run in separate blocks with two blocks per condition. Different random orders of the total 14 blocks were used for different subjects. Over the two blocks for each condition, each test stimulus was repeated 20 times. The trials for different test stimuli in a block were also randomized. There was a 10 min break after each adaptation block to avoid carryover of the aftereffects to the next block. Data collection for each block started after subjects had sufficient practice trials (typically 10–20) to feel comfortable with the task.

Experiment 2.

This experiment tested whether the results obtained with the cartoon faces in experiment 1 were applicable to real faces. The procedure was identical to that of experiment 1 with the following exceptions. First, morphed real-face images derived from two Ekman faces, instead of the cartoon faces, were used. Second, the center-to-center distance between the faces and the fixation cross was 2.9°, instead of 3.8°. Third, we did not use any inverted face and there was no if-f condition. Finally, the c-c condition in experiment 1 was replaced by the c′-c and m-c conditions. As mentioned above, in the c′-c condition, the adapting curve had a contrast equal to that of the mouth in the saddest face. In the m-c condition, the adapting stimulus was the mouth isolated from the saddest face. There were a total of seven conditions (c-f, f-f, 0-f, f-c, c′-c, m-c, and 0-c).

Experiment 3.

This experiment further established the effect of curve adaptation on the perceived expression of real faces and tested positional specificity of the effect. The procedure was identical to experiment 2 with the following exceptions. First, the morphed real-face set was derived from three MMI faces, instead of two Ekman faces. Second, only the c-f and 0-f conditions were run. However, the c-f condition was split into four separate conditions, using either a concave or a convex curve as the adapting stimulus, and placed either at the same location as the mouth in the test faces or 0.9° below the mouth (0.2° below the lower edge of the test faces). The total of five conditions are termed cv-f-same, cx-f-same, cv-f-diff, cx-f-diff, and 0-f, where “cv” and “cx” stand for concave and convex adapting curves, respectively, “f” stands for the test faces, and “same” and “diff” indicate whether the adapting curve was at the same location as the mouth of the test faces or was below the test faces. For example, cv-f-same means the adapting stimulus was a concave curve placed at the same location as the mouth of the test faces. The block and trial randomizations were done as in experiments 1 and 2. Third, the initial adaptation time and the top-up adaptation time were both 4 s. This modification was made because subjects of experiments 1 and 2 indicated that the long 30 s initial adaptation sometimes made them miss the first trial of a block. Because the top-up adaptation time was increased to 4 s, the total adaptation time of a block (6 min) was actually longer than that of experiment 2 (4 min). We therefore ran a pilot study on two experimenters and confirmed that a 10 min break after an adaptation block was long enough for the aftereffect to decay. Fourth, the face images were smaller (3° instead of 3.6° in height) and were presented more eccentrically (3.8° instead of 2.9°) than those in experiment 2 (the image height and eccentricity were identical to those in experiment 1). Finally, we increased the presentation time of the test stimuli from 100 to 200 ms because subjects for this experiment found 100 ms too short to enable good performance.

Experiment 4.

This experiment was identical to experiment 3 except that the adapting stimuli were the saddest and the happiest faces in the MMI face set we used, instead of the concave and convex curves. The five conditions were termed sf-f-same, hf-f-same, sf-f-diff, hf-f-diff, and 0-f, where, for example, sf-f-same means that the adapting stimulus was the saddest face, the test stimuli were the MMI face set, and the adapting and test faces had the same location. When the adapting faces and the test faces were at different locations (sf-f-diff and hf-f-diff conditions), the top edge of the adapting faces were 0.2° below the bottom edge of the test faces (the center-to-center distance between the adapting and test faces was 3.2°).

Data analysis

For each condition of each completed experiment, the data were sorted into fraction of happy or convex responses to each test stimulus. The test stimuli were parameterized according to the curvature of curves, the mouth curvature in the cartoon faces, or the proportion of happiness in the morphed real-face images. The fraction of happy or convex responses was then plotted against the test stimulus, and the resulting psychometric curve was fitted with a sigmoidal function of the form ƒ(x) = 1/[1 + e ^−a(x−b)], where a determines the slope and b gives the test-stimulus parameter corresponding to the 50% point of the psychometric function [the point of subjective equality (PSE)]. We used two-tailed paired t test to compare subjects' PSEs for different conditions in an experiment.

Results

We first investigated whether there are cross-level adaptation aftereffects between the low-level curvature of curves and the high-level facial expression of cartoon faces. For experiment 1, we generated a set of cartoon faces whose mouth curvatures varied from concave to convex so that the facial expressions varied gradually from sad to happy. We also generated a set of curves that were identical to the mouths of the cartoon faces. The adapting stimulus was either the most concave curve or the saddest face, and the test stimuli came from either the face set or the curve set. The curves and the mouths of the faces had the same locations on the screen. Subjects were run on all four possible combinations of the adapting and test stimuli. Subjects were also run on the baseline conditions for the face and curve sets without adaptation. Because all subjects showed the same trend in this and the other experiments, in the following we will first describe the results from a naive subject and then present a summary of all subjects' data.

Curve adaptation biased perceived facial expression in cartoon faces

The results from a naive subject judging the facial expression of the cartoon faces under various conditions are shown in Figure 3 a. We plotted the fraction of happy responses as a function of the mouth curvature of the test faces. The blue psychometric curve is the baseline condition without adaptation (0-f). After adapting to the saddest face, the subject saw happy expression more frequently, and the psychometric curve (green, f-f) shifted to the left. This is the standard facial-expression aftereffect (Hsu and Young, 2004; Webster et al., 2004) reproduced here with the cartoon faces. The new finding is that after adapting to the most concave curve, which is neither happy nor sad by itself, the subject also perceived happy expressions more frequently (red curve, c-f).

Figure 3.

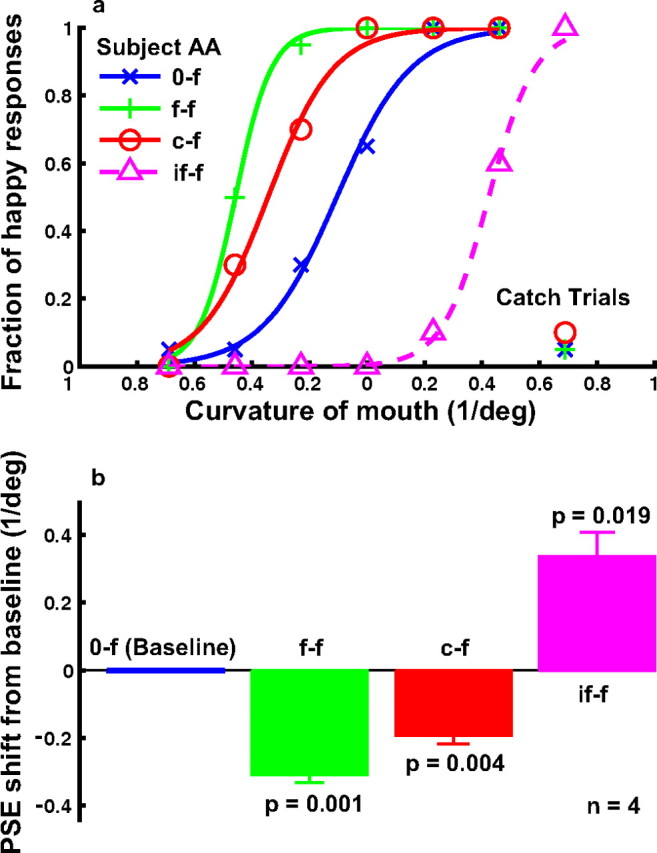
The effect of curve adaptation on the perceived expression of the cartoon faces (experiment 1). a, Psychometric functions from a naive subject under the following conditions. 0-f, No adaptation baseline (blue); f-f, adaptation to the saddest face (green); c-f, adaptation to the most concave curve, which was identical to the mouth of the saddest face (red); if-f, adaptation to the inverted saddest face (magenta dashed). For each condition, the fraction of happy responses was plotted as a function of the mouth curvature of the test faces. The catch-trial results for the 0-f, f-f, and c-f conditions are also shown. b, Summary of all four subjects' data. For each condition, the average PSE relative to the baseline condition and the SEM were plotted. The p value shown for each condition in the figure was calculated against the baseline condition using the two-tailed paired t test.

As we will show below, adaptation to the most concave curve made the other curves appear more convex (Fig. 4, c-c condition). This curvature aftereffect (Gibson, 1933) must also make the mouth of the cartoon faces more convex, and in this sense, it is not surprising that the curve adaptation biased the perceived facial expression. However, the curvature aftereffect is a low-level phenomenon whose physiological substrate is thought to start as early as V1, where curvature-tuned cells are found (Hubel and Wiesel, 1965; Dobbins et al., 1987). In contrast, the representation of facial expression has been found in high-level areas but never in V1 (Hasselmo et al., 1989; Haxby et al., 2000; Winston et al., 2004). Therefore, the important new insight provided by our results is that the curvature-adaptation effects in V1 must propagate all the way to the high-level areas that encode facial expression. Furthermore, although previous psychophysical studies emphasized the nonlocal, holistic nature of faces (Tanaka and Farah, 1993; Leopold et al., 2001; Zhao and Chubb, 2001; Rhodes et al., 2003; Watson and Clifford, 2003; Hsu and Young, 2004; Yamashita et al., 2005), our results suggest that there is also a strong local component in facial-expression representation, because adaptation to a local feature (the adapting curve) biased the perceived facial expression. This is consistent with a recent study by Harris and Nakayama (2008), who found that face parts can adapt a face-selective EMG signal.

Figure 4.

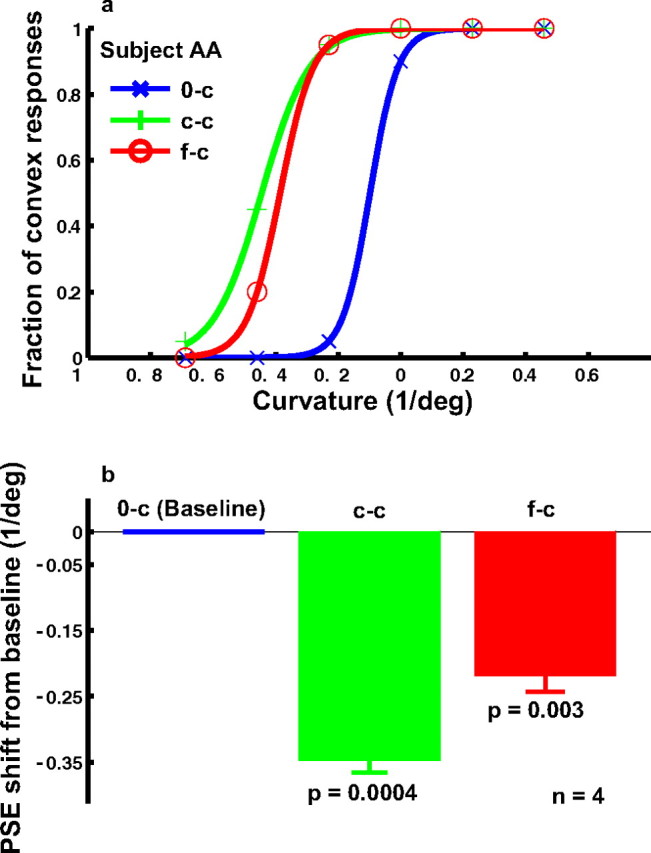
The effect of cartoon-face adaptation on curvature judgment (experiment 1). a, Psychometric functions from a naive subject under the following conditions. 0-c, No adaptation baseline (blue); c-c, adaptation to the most concave curve (green); f-c, adaptation to the saddest face, whose mouth was identical to the most concave curve (red). For each condition, the fraction of convex responses was plotted as a function of the curvature of the test curves. b, Summary of all four subjects' data. For each condition, the average PSE relative to the baseline condition and the SEM were plotted. The p value shown for each condition in the figure was calculated against the baseline condition using the two-tailed paired t test.

To ensure that the subjects did judge the high-level facial expression, instead of the low-level mouth curvature, we randomly interleaved catch trials in the 0-f, f-f, and the c-f conditions. In these trials, the test stimulus was the upside-down version of the saddest face, so that its mouth curvature was identical to that of the happiest face. If the subjects judged the mouth curvature, then the fraction of “happy” responses for the catch trials would be close to 1. On the other hand, if they judged facial expressions, then because the inverted saddest faces still appeared sad, the fraction of happy response would be close to 0. The actual data for the naive subject, at the bottom right corner of Figure 3 a, indicate that he indeed judged the facial expression as instructed.

Local and nonlocal components in facial-expression representation

Another relevant point in Figure 1 a is that the facial-expression aftereffect generated by the curve adaptation (c-f) is not as large as that generated by the face adaptation (f-f). Somehow, the presence of the face contour and the eye dots made the aftereffect stronger even though these parts were identical in all faces and therefore could not produce any facial-expression aftereffects by themselves. It is difficult to provide a low-level explanation of this difference because the face contour and the eye dots were not collinear or cocircular with the mouth curve to facilitate it, and the suppressive surround outside the classical receptive fields of V1 cells should, if anything, make the mouth less effective than an isolated curve as an adaptor (Gilbert and Wiesel, 1990). The finding thus provides additional evidence for a nonlocal component in facial-expression representation, likely in a high-level area.

In the light of this result, we also ran an additional condition that pitted local and nonlocal components of facial expression against each other. In this condition (termed if-f), the adapting stimulus was the inverted saddest face, and the test stimuli were the upright faces. The mouth position of all faces was the same. Because the mouth curvature of the inverted face was identical to that of the happiest face, this local feature alone predicts that subjects should perceive happy expression less frequently. However, the overall expression of the inverted face was sad (see catch trials in Fig. 1 a), so the adapting stimulus as a whole predicts that subjects should perceive happy expression more frequently. The result is shown in Figure 1 a as the dashed magenta curve (if-f). The subject perceived happy expressions less frequently, suggesting that the local component dominated over the nonlocal component in this task.

To quantify the aftereffects and summarize the results from all four subjects, we determined the PSE (the mouth curvature corresponding to 50% happy responses) for each psychometric curve of each subject. Figure 1 b shows the mean PSEs relative to the baseline condition. A negative value means a leftward shift of the psychometric curve, or more happy responses, relative to the baseline. The error bars indicate SEMs. The p value for each adaptation condition in the figure was obtained by comparing the four PSEs of that condition against those of the baseline condition via a two-tailed paired t test. All aftereffects were significant. We also compared the c-f and f-f conditions and found that the difference between them was significant (p = 0.011). Finally, for the catch trials in the 0-f, f-f, and c-f conditions, no subject reported a fraction of happy responses larger than 0.15 in any condition, and the mean was 0.046.

Cartoon-face adaptation biased perceived curvature of curves

We also addressed the converse question of whether cartoon-face adaptation affects curvature perception. The results from a naive subject judging the curvature of the test curves under various conditions are shown in Figure 4 a. We plotted the fraction of convex responses as a function of the curvature of the test curves. The blue psychometric curve is the baseline condition without adaptation (0-c). After adapting to the most concave curve, the subject perceived convex curvature more frequently and the psychometric curve (green, c-c) shifts to the left. This is the standard curvature aftereffect (Gibson, 1933). A shift in the same direction was found when the subject was adapted to the saddest cartoon face (red curve, f-c condition). Once again, the shift for the f-c condition was smaller than that for the c-c condition even though the adapting curve in the c-c condition was identical to the mouth curve of the adapting face in the f-c condition.

The data from the four subjects are summarized in Figure 4 b. Relative to the baseline condition, the aftereffects in the c-c and f-c conditions were both significant. The difference between the c-c and f-c conditions was also significant (p = 0.027).

Curve adaptation biased perceived facial expression in real faces

Experiment 1 demonstrated that curve adaptation generated a facial-expression aftereffect in the cartoon test faces (Fig. 3). The facial expression of the cartoon faces we used was completely determined by the mouth curvature. This is not true for the real faces, whose expressions depend on many features over and above the mouth. We therefore wondered whether the same cross-level aftereffects could be found when real faces were used as the test stimuli. In experiment 2, we generated a set of real faces with expressions from sad to happy by morphing a sad and a happy face of the same person from the Ekman database, and ran the 0-f, f-f, and c-f conditions as we did in experiment 1. The psychometric curves for a naive subject (Fig. 5 a) and the summary of four subjects' data (Fig. 5 b) show that curve adaptation also biased the perceived facial expression in the real faces. The effect was smaller than for the cartoon faces, but still significant (p = 0.02) (Fig. 5 b).

Figure 5.

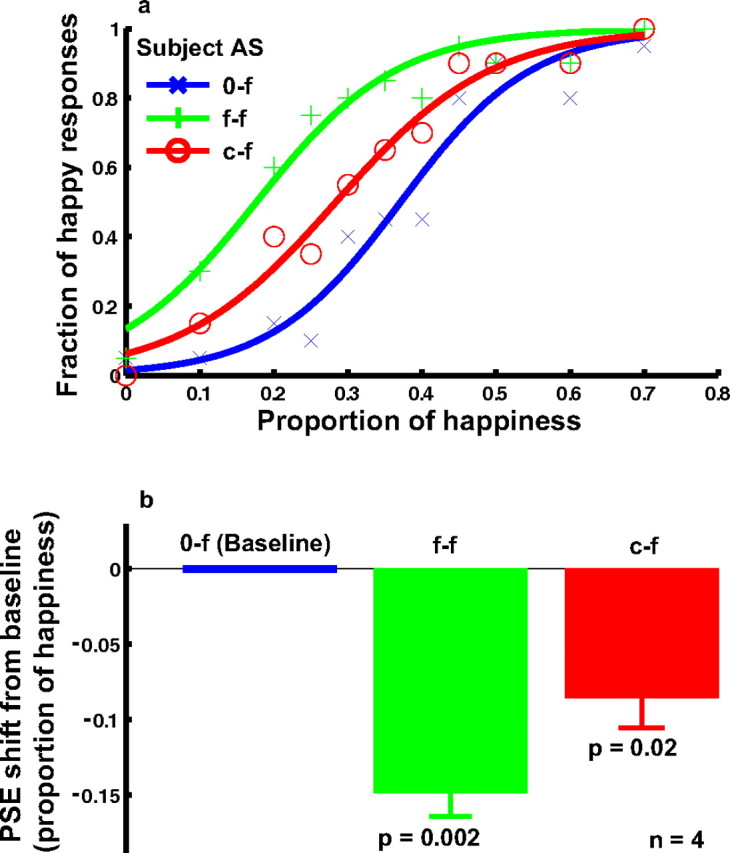
The effect of curve adaptation on the perceived expression of the real-face set derived from two Ekman faces (experiment 2). a, Psychometric functions from a naive subject under the following conditions. 0-f, No adaptation baseline (blue); f-f, adaptation to the saddest face (green); c-f, adaptation to the concave curve, whose curvature and length matched those of the saddest face (red). For each condition, the fraction of happy responses was plotted as a function of the proportion of happiness in the morphed test faces. A proportion of 0 or 1 corresponded to the original sad or happy image taken from the Ekman database. b, Summary of all four subjects' data. For each condition, the average PSE relative to the baseline condition and the SEM were shown. The p value for each condition in the figure was calculated against the baseline condition using the two-tailed paired t test.

Real-face adaptation did not bias perceived curvature of curves

We reported above that cartoon-face adaptation produced a curvature aftereffect. Surprisingly, real-face adaptation did not affect curvature perception in experiment 2. We used the saddest face in our Ekman face set as the adapting stimulus. As shown in Figure 6, there was no significant shift between the psychometric curve for the adaptation condition (f-c) and that for the baseline condition (0-c).

Figure 6.

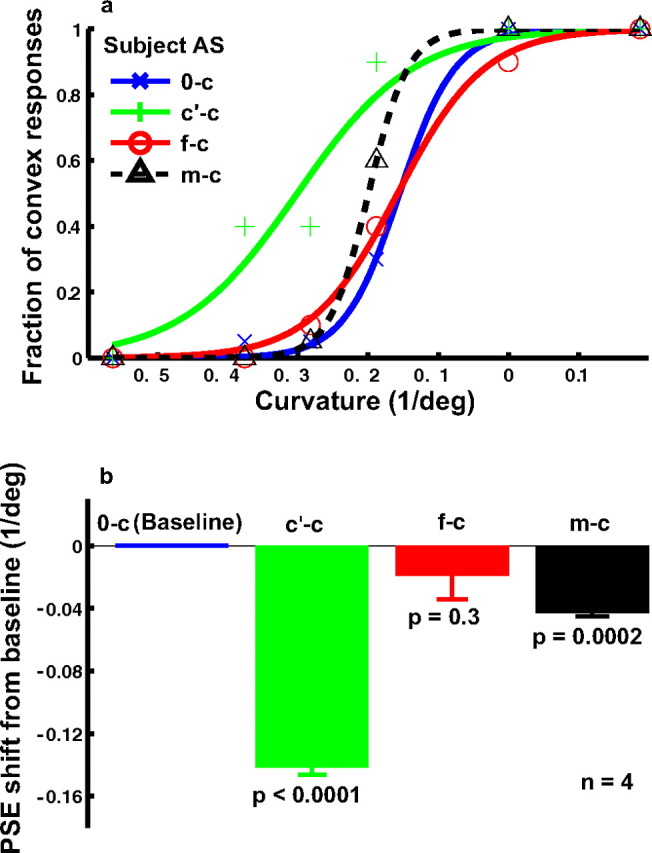
The (null) effect of real-face adaptation on curvature judgment (experiment 2). a, Psychometric functions from a naive subject under the following conditions. 0-c, No adaptation baseline (blue); c′-c, adaptation to the concave curve, whose curvature, length, and contrast matched those of the saddest face (green); f-c, adaptation to the saddest face (red); m-c, adaptation to the mouth isolated from the saddest face (black). For each condition, the fraction of convex responses was plotted as a function of the curvature of the test curves. b, Summary of all four subjects' data. For each condition, the average PSE relative to the baseline condition and the SEM were plotted. The p value shown for each condition in the figure was calculated against the baseline condition using the two-tailed paired t test. Unlike the corresponding cartoon-face result in Figure 4, the f-c condition did not generate a significant shift of the PSE from the baseline.

The contrast of the mouth in the real face was obviously lower than that in the cartoon face. Was the contrast too low to generate an aftereffect? To answer this question, we measured the mean mouth contrast in the adapting face by sampling 10 points on the mouth and 10 points around the mouth. We then created a curve that matched the mouth in contrast as well as in curvature and length. Using this curve as the adapting stimulus, we found a large shift of the psychometric curve (Fig. 6, c′-c condition) with respect to the baseline (0-c). This ruled out the low-contrast explanation.

Alternatively, the difference between the face adaptation (f-c) and the curve adaptation (c′-c) conditions might be attributable to the fact that the face had complex features surrounding the mouth. Perhaps the rest of the face somehow diminished the potency of the mouth in generating a curvature aftereffect. To test this possibility, we isolated the mouth from the face and placed it in a rectangle whose size and position were identical to those of the face stimulus. The rectangle had a uniform luminance identical to the mean luminance of the face so that the contrast of the isolated mouth was identical to that of the mouth in the face. We found that the isolated mouth generated a small but significant aftereffect (Fig. 6, m-c condition), suggesting that the rest of the face reduced the curvature aftereffect slightly in the f-c condition. In contrast, there was a large difference between the isolated mouth adaptation and the curve adaptation. Although the isolated mouth and the curve had the same mean contrast, curvature, and length, they were still very different in terms of width and local luminance distribution, and it is perhaps these differences that are critical.

Concave and convex adapting curves generated opposite facial-expression aftereffects

Experiment 2 above showed that after viewing a concave curve, subjects perceived happy expressions more frequently in real faces. We interpreted this as a facial-expression aftereffect generated by curve adaptation. However, there is a possible alternative explanation. In experiment 2, we morphed a happy face and a sad face of the same person to generate a set of test faces. It is possible that some of the intermediate faces contained a mixture of happy and sad features on different parts of the faces. Therefore, the perceived facial expression could depend on where on the faces subjects paid attention to. In the c-f condition, the adapting curve always appeared at the mouth location of the faces and thus could draw subjects' attention to the mouth area. This attentional focus might not occur in the baseline condition (0-f). If the mouth region appeared happier than the rest of the faces, then that could cause a shift between the c-f and the 0-c psychometric curves. In other words, the observed shift could be caused by different attentional focuses and might have nothing to do with adaptation aftereffects. Of course, this explanation cannot account for the aftereffects associated with cartoon faces, which lack extra features.

We performed experiment 3 to rule out this possibility. If the attention explanation were correct, then a concave and a convex adapting curve would generate the same shift of the psychometric function, because either curve would draw subjects' attention to the mouth area. On the other hand, if the change in perception was caused by the adaptation aftereffect, then concave and convex adapting curves would produce opposite shifts in perceived facial expressions. For experiment 3, we also used a different set of morphed faces from those in experiment 2. We picked a sad face, a neutral face, and a happy face of the same person from the MMI database. We then morphed the sad face with the neutral face, and the neutral face with the happy face. By not morphing the sad and the happy face directly, we eliminated the possibility of an intermediate face containing a mixture of sad and happy features in different parts of the face, the premise of the attention explanation above.

The results from one naive subject are shown in Figure 7 a. The solid red and the green psychometric functions are for the concave (cv-f-same) and convex (cx-f-same) adapting curves, respectively. They shifted in opposite directions with respect to the baseline condition (0-f). The summary of four subjects' data are shown in Figure 7 b. These results ruled out the attention explanation.

Figure 7.

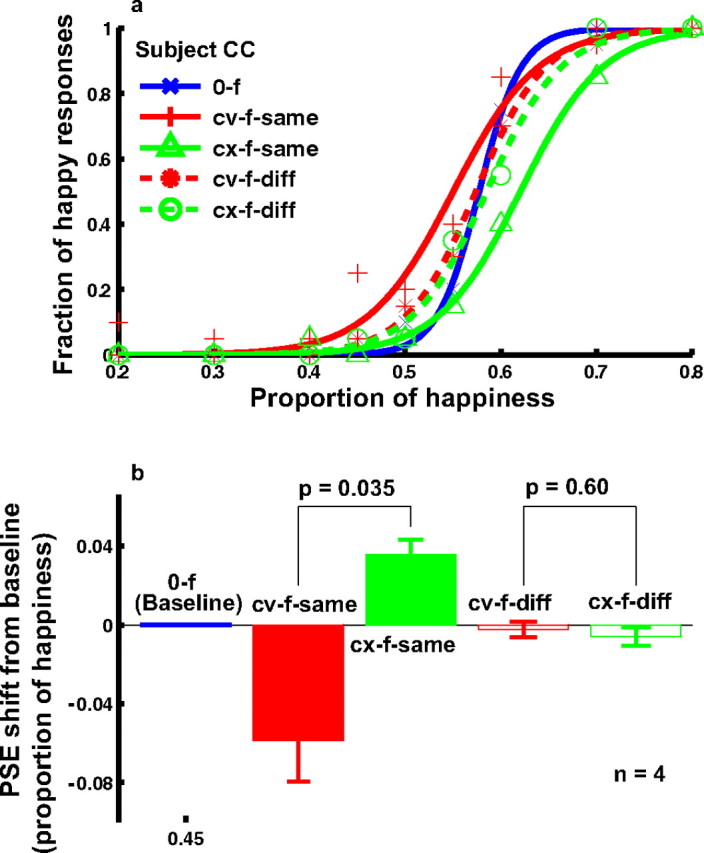
The effect of concave and convex curve adaptation on the perceived expression of the real-face set derived from three MMI faces and the positional specificity of the effect (experiment 3). a, Psychometric functions from a naive subject under the following conditions. 0-f, no adaptation baseline (blue); cv-f-same, adaptation to the concave curve placed at the same location as the mouth position in the test faces (red solid); cx-f-same, adaptation to a convex curve placed at the same location as the mouth position in the test faces (green solid); cv-f-diff, adaptation to the concave curve placed 0.2° below the bottom edge of the test faces (or 0.9° below the mouth position) (red dashed); cx-f-diff, adaptation to the convex curve placed 0.2° below the bottom edge of the test faces (or 0.9° below the mouth position) (green dashed). b, Summary of all four subjects' data. The cv-f-same and cx-f-same conditions were compared, and the cv-f-diff and cx-f-diff conditions were compared, using the two-tailed paired t test.

Positional specificity of facial-expression aftereffects

Another goal of experiment 3 was to investigate the positional specificity of the facial-expression aftereffect generated by curve adaptation. In addition to placing the adapting curves at the mouth location, we also moved them downward by 0.9° so that the adapting curves were 0.2° below the lower edge of the test faces. The results for the concave (cv-f-diff) and convex (cx-f-diff) adapting curves are shown as dashed red and green curves in Figure 7. The aftereffects largely disappeared in these conditions, indicating a high degree of positional specificity. The lack of transfer of the aftereffect to locations away from the adapting curve further supports the notion of a strong local component in facial-expression representation. It is also consistent with Gibson's finding that the curvature aftereffect induced by curve adaptation is very local and disappears at a distance of ∼0.3° (Gibson, 1933).

However, the implications of this result depend on a control experiment investigating whether the positional specificity revealed in experiment 3 is a general property of facial-expression aftereffects or whether it is a consequence of using local curves as the adapting stimuli. It is known that adaptation to certain characteristics of faces is somewhat local, with, for instance, the bias in judging the masculinity of a face after adaptation to a female face being significantly less when adapting and test faces are nonoverlapping (Kovacs et al., 2005). To test locality in our case, we conducted experiment 4, which was identical to experiment 3 except that the adapting stimulus was either the saddest or happiest face in the MMI face set we used. The results are shown in Figure 8. When the adapting and test faces were at the same location (sf-f-same and hf-f-same conditions), significant aftereffects were observed (solid red and green curves). When the top edge of the adapting faces was 0.2° below the bottom edge of the test faces (sf-f-diff and hf-f-diff conditions), the aftereffect disappeared (dashed red and green curves), suggesting that positional specificity is a general property of the facial-expression aftereffect.

Figure 8.

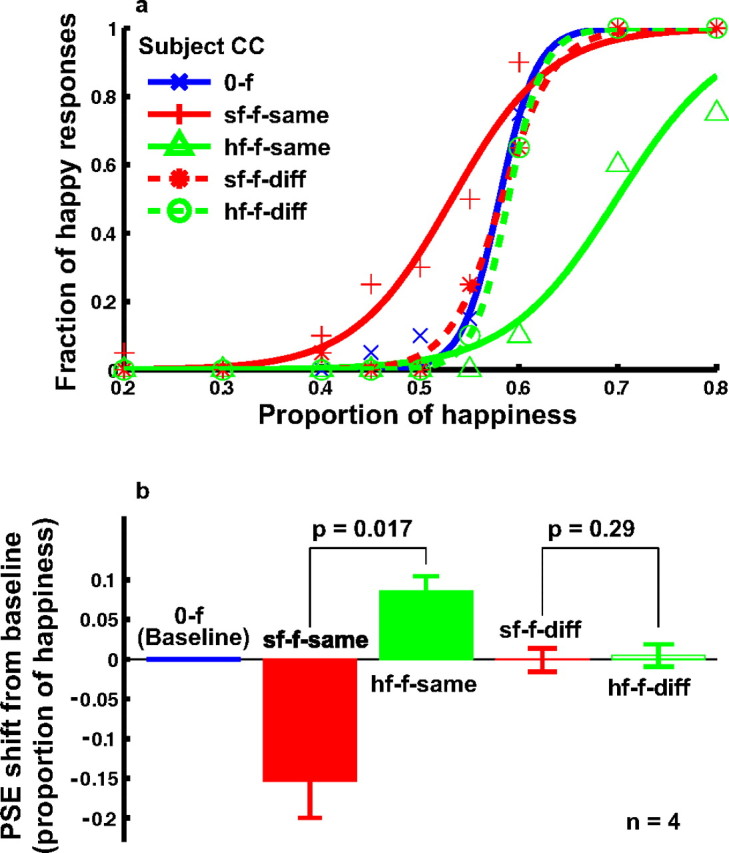
Positional specificity of the facial-expression aftereffect after adaptation to real faces from the MMI face set (experiment 4). a, Psychometric functions from a naive subject under the following conditions. 0-f, No adaptation baseline (blue); sf-f-same, adaptation to the saddest face placed at the same location as the test faces (red solid); hf-f-same, adaptation to the happiest face placed at the same location as the test faces (green solid); sf-f-diff, adaptation to the saddest face, whose top edge was 0.2° below the bottom edge of the test faces (red dashed); hf-f-diff, adaptation to the happiest face, whose top edge was 0.2° below the bottom edge of the test faces (green dashed). b, Summary of all four subjects' data. The sf-f-same and hf-f-same conditions were compared, and the sf-f-diff and hf-f-diff conditions were compared, using the two-tailed paired t test.

Discussion

Summary of key findings

We conducted a set of experiments to investigate multilevel adaptation aftereffects. Experiment 1 showed that curve adaptation affected not only curvature judgments but also facial-expression judgments with cartoon faces, and conversely, cartoon-face adaptation biased the perception of not only facial expression but also curvature. Catch trials with an inverted face ensured that subjects indeed judged facial expression when instructed to do so. The facial-expression aftereffect generated by the curve adaptation was smaller than that generated by the face adaptation. A further condition using the inverted face as the adapting stimulus indicated that the mouth curvature dominated over the overall facial expression in generating the facial-expression aftereffect. Experiment 2 demonstrated that curve adaptation also produced a facial-expression aftereffect in real faces. However, real-face adaptation failed to bias curvature perception. This was not a result of the lower contrast of the real face, because a contrast-matched curve produced a large curvature aftereffect. Experiment 3 showed that adaptation to concave and convex curves produced opposite facial-expression aftereffects. This ruled out an attentional explanation of the results in experiment 2 and further established the facial-expression aftereffect in real faces generated by curve adaptation. Experiments 3 and 4 together demonstrated that the facial-expression aftereffect, whether induced by an adapting curve or an adapting face, was local to the adapted region and did not transfer to nonoverlapping regions.

In terms of the issues we intended the study to illuminate, we found significant interactions between different levels of the hierarchy, with adaptations at one level not being nullified by between-level processing. This has psychophysical, physiological, and computational implications.

Psychophysical implications

Complex stimuli such as faces could be represented holistically, as a collection of properly arranged local features, or both. Numerous studies argue for a holistic representation of faces. The main finding is that after adapting to a face of a given size and orientation, aftereffects are found on test faces of different sizes and orientations (Leopold et al., 2001; Zhao and Chubb, 2001; Rhodes et al., 2003; Watson and Clifford, 2003; Hsu and Young, 2004; Yamashita et al., 2005). Because the adapting and test faces have different local features as a result of the size and orientation differences, this finding provides evidence against a purely local representation of face. However, in these studies the adapting and test faces generally overlapped spatially, and the possibility that they shared some common local features cannot be ruled out. Aftereffects, although typically present, are reduced either when adapting and test faces are explicitly nonoverlapping (Kovacs et al., 2005) at least for the sort of long adaptation durations we used (Kovacs et al., 2007), or have different sizes or orientations.

Because the adapting curve used in our experiments was a simple, local feature, our finding that curve adaptation generated a facial-expression aftereffect suggests that there is a strong local component in facial-expression representation. However, the facial-expression aftereffect induced by a face was larger than that induced by a curve. This was true even in experiment 1, in which the adapting curve was identical to the mouth curve in the adapting cartoon face and the expressions of all the cartoon faces were completely specified by the mouth curve, with no additional distinguishing features. As we mentioned in Results, this difference in aftereffect strength cannot be easily explained by a local mechanism. Therefore, there are both local and nonlocal contributions to face representation. When we pitted the local and nonlocal factors against each other by using the inversion of the saddest cartoon face as the adapting stimulus, we found that the local component dominated over the nonlocal component in this condition.

A related question is whether face aftereffects generalize to locations away from the adapting face. On the one hand, because visual areas encoding faces such as IT have large receptive fields that often cover both sides of fixation point (Gross et al., 1972; Desimone et al., 1984), one expects such generalization. On the other hand, IT receptive fields are not uniform, and sharp decreases of responses over small distances have been reported (DiCarlo and Maunsell, 2003), opening up the possibility of retinotopic specificity. Recently, Afraz and Cavanagh (2007) systematically investigated the issue in the context of the face-identity aftereffect. They found that the aftereffect decreases quickly with increasing distance from the adapting face, indicating strong specificity. However, even at the mirror location across the fixation point, a small but significant aftereffect was found, analogous to Meng et al. (2006)'s previous finding of the cross-fixation transfer of expansion-motion aftereffect. In a related result, Kovacs et al. (2005, 2007) found that masculinity aftereffects consequent on adapting to a female face are invariant to the hemifield of presentation of the latter given very short adaptation durations (500 ms), but are substantially weaker in the opposite hemifield given the sort of durations that we used.

In this study, we found that the facial-expression aftereffect induced by either an adapting curve or an adapting face disappeared when the adapting stimuli were only 0.2° below the test faces. Therefore, compared with the face-identity aftereffects studied by Afraz and Cavanagh (2007), the facial-expression aftereffect appears much more local. It is possible that people rely more on the overall face for the identity task but more on a few local features for the expression task (Gosselin and Schyns, 2001). In addition, a recent functional magnetic resonance imaging (fMRI) study showed that different brain areas are involved in processing face identity and facial expression (Winston et al., 2004). These differences might be responsible for the different degrees of specificity.

Physiological implications

Our finding that curve adaptation generated a facial-expression aftereffect strongly suggests that adaptation-induced biases in early stages of cortical visual processing such as V1 propagate to later stages such as temporal lobe. A physiological prediction is that curve adaptation will not only depress or otherwise affect responses of V1 cells tuned to curvature but also responses in high-level areas encoding facial expressions. This prediction could be tested with single-unit recording in monkeys and fMRI experiments with humans. Such studies should also help reveal whether the neurons tuned to facial expression are directly activated by the adapting curves, thereby potentially supporting their own adaptation, or inherit adaptation from lower levels, or both. Another physiological prediction based on our specificity results is that facial-expression areas should show less positional invariance than face identity areas.

Computational implications

One of the goals of our study was to gather evidence about the normative status of communication between lower and higher levels in the sensory processing hierarchy (Fairhall et al., 2001; Dayan et al., 2003; Schwartz et al., 2007). Studies using adapting and test stimuli that are similar have been used to suggest that adaptation is highly normatively sophisticated (Barlow and Foldiak, 1989; Barlow, 1990; Wainwright, 1999; Clifford et al., 2000, 2007; Dayan et al., 2003; Stocker and Simoncelli, 2006), for instance, accepting perceptual bias as a cost of maximizing coding efficiency or information transmission or to enable optimal Bayesian inference, according to complex temporal natural scene statistics. However, because most curves in the visual world do not arise from anything remotely face-like, such an account is hard to sustain in the light of the cross-level adaptations that we observed.

One functional account that survives is normalization (Gibson and Radner, 1937; Andrews, 1964; Over, 1971; Webster et al., 2004, 2005), i.e., the attribution of the biased output of the low-level systems during adaptation to some retinal or thalamic flaw that should itself be cancelled so as not erroneously to affect downstream processing and to enable shared esthetic experiences. However, this itself runs into other problems, such as being silent about the marked similarity between the effects of temporal context (as in the tilt aftereffect) and spatial context (as in the tilt illusion) (Felsen et al., 2005; Schwartz et al., 2007). Of course, the latter has yet to be shown to operate across levels.

Conclusions

We have demonstrated a multilevel adaptation aftereffect: adaptation to a curve not only generates a low-level curvature aftereffect but also a high-level facial-expression aftereffect. We further showed that the facial-expression aftereffect is position specific. These results, together with other findings, suggest that there are both local and nonlocal components in facial-expression representation. They further suggest that physiological substrates of adaptation in early visual areas propagate to high-level areas. Finally, they challenge theories that rationalize aftereffects as the inevitable consequence of information maximization.

In the light of our results, there are various important lines of future inquiry. For instance, one is to understand the consequences of adapting to distributions of curves or faces rather than single instances. This will help address issues associated with the functional models. Another is to create a spatial analog of our exclusively temporal adaptation. A third is to use a similar multilevel paradigm but to focus on the recognition of identity rather than expression (Leopold et al., 2001). The latter is of particular interest given the greater spatial specificity of our facial-expression aftereffect compared with the face identity aftereffect (Afraz and Cavanagh, 2007).

It should also be possible to adopt our paradigm to investigate potential multilevel adaptation aftereffects in other visual submodalities, such as motion, depth, and color. For example, does a local translational motion adaptation near the focus of expansion in optic flow patterns affect our direction-of-heading judgment? It may also be interesting to investigate multilevel adaptation aftereffects in other sensory modalities or even in motor control systems. Indeed, one could ask the question of whether adaptation of the shoulder joint movement has an aftereffect at the levels of elbow and wrist. By looking for aftereffects beyond a single level, we may significantly enhance the power of adaptation as a tool to dissect neural mechanisms of perception and action.