Abstract
Auditory neurons must represent accurately a wide range of sound levels using firing rates that vary over a far narrower range of levels. Recently, we demonstrated that this “dynamic range problem” is lessened by neural adaptation, whereby neurons adjust their input–output functions for sound level according to the prevailing distribution of levels. These adjustments in input–output functions increase the accuracy with which levels around those occurring most commonly are coded by the neural population. Here, we examine how quickly this adaptation occurs. We recorded from single neurons in the auditory midbrain during a stimulus that switched repeatedly between two distributions of sound levels differing in mean level. The high-resolution analysis afforded by this stimulus showed that a prominent component of the adaptation occurs rapidly, with an average time constant across neurons of 160 ms after an increase in mean level, much faster than our previous experiments were able to assess. This time course appears to be independent of both the timescale over which sound levels varied and that over which sound level distributions varied, but is related to neural characteristic frequency. We find that adaptation to an increase in mean level occurs more rapidly than to a decrease. Finally, we observe an additional, slow adaptation in some neurons, which occurs over a timescale of tens of seconds. Our findings provide constraints in the search for mechanisms underlying adaptation to sound level. They also have functional implications for the role of adaptation in the representation of natural sounds.
Keywords: adaptation, auditory neuron, time course, sound level, rate level function, inferior colliculus
Introduction
First described by Adrian (1928), adaptation is a widespread property of sensory neurons in which the neural response, or firing rate, declines during sustained stimulation. Much recent research has focused on elucidating the functional effects of adaptation. In several cases, adaptation enables neurons whose output varies over only a narrow range of inputs (the neural “dynamic range”) to represent the far greater range of inputs with which the environment presents the observer. Thus, in visual cortex, adaptation adjusts the neuronal contrast sensitivity to match the current context or distribution of contrasts in the visual scene (Ohzawa et al., 1982, 1985). Such adjustment of responses according to stimulus statistics has been reported for adaptation to other visual parameters (Brenner et al., 2000; Fairhall et al., 2001) and in other sensory systems (e.g., somatosensory) (Maravall et al., 2007).
Recently, we reported that the responses of neurons in the inferior colliculus (IC), the major midbrain nucleus of the auditory pathway, adapt to the statistics of the prevailing distribution of sound levels (Dean et al., 2005). This adaptation causes a shift in the relationship between firing rate and sound level, which increases the accuracy with which the most probable levels are coded by the neural population. These adjustments enable the auditory system to achieve high coding accuracy over a wide range of sound levels, by altering the position of the neural dynamic range according to the statistics of the current acoustic environment.
It is not known which mechanisms drive the adaptation in sound level coding. Adaptation may arise through changes in the balance of excitatory and inhibitory inputs to an adapting neuron, or through changes in the intrinsic excitability of the neuron itself. The IC lies at least three synaptic stages beyond the auditory transducers, the cochlear hair cells, and is a site of extensive excitatory and inhibitory synaptic convergence. Some IC neurons also display intrinsic conductances that lead to adaptive responses in vitro (Sivaramakrishnan and Oliver, 2001; Bal et al., 2002). Finally, the IC, and its inputs, are subject to centrifugal influences (Zhang et al., 1997; Winer, 2006; Bajo et al., 2007; Lim and Anderson, 2007). Such processes operate over widely varying timescales; it remains unclear which of them contribute to adaptation observed in the IC in vivo, and at what stage in the auditory pathway the adaptation first arises.
Here, we characterize the time course of neural adaptation to sound level in the IC. We were motivated by two main aims. First, the stimuli which revealed the adaptive changes in neural coding (Dean et al., 2005) precluded high-resolution analysis of the time course of this adaptation. However, it is important to examine in detail the dynamics of the adaptation, because the timescale over which the adaptation operates will constrain the usefulness of the adaptive neural code. We find that the adaptation is rapid, occurring over hundreds of milliseconds, and propose that it is fast enough to take account of changes in sound level that occur naturally. Second, by assessing the time course of the adaptation, we lend insight into which mechanisms are likely to be involved, guiding future research examining the bases of the adaptation.
Materials and Methods
Surgery.
All experiments were performed in accordance with the United Kingdom Animals (Scientific Procedures) Act of 1986. Experiments were performed in a sound-shielded booth (IAC). Pigmented guinea pigs were anesthetized with urethane (1.0 g/kg; 20% solution), and administered with atropine sulfate (0.06 mg) to reduce bronchial secretions. Analgesia was induced, and supplemented as necessary throughout experiments, with 0.1 cc of intramuscular Hypnorm (fentanyl citrate/fluanisone). Body temperature, breathing rate, and pedal withdrawal reflexes were monitored to ensure a sufficient and stable level of analgesia. At all sites of incision, 0.1 ml of local anesthetic (lignocaine) was also given subcutaneously. Body temperature was maintained at 37°C by means of a rectal probe and thermostatically controlled heating blanket. A tracheal cannula was inserted, and the animal was held in a modified stereotaxic frame, on which hollow ear speculas allowed the insertion of tubes for delivery and sampling of sound (see below). Middle ear pressure was equalized by sealing a high acoustic-impedance cannula into each bulla. A craniotomy was performed, and the dura removed, to allow electrode access to the right IC through the overlying intact cerebral cortex.
Physiological recordings.
Extracellular recordings were made from single IC neurons. Glass-coated tungsten electrodes (impedance range, 0.9–1.0 MΩ) were advanced stereotaxically into the IC in a dorsoventral direction, using a piezoelectric stepper motor (Inchworm IW-700/710; Burleigh Instruments) or a motorized manipulator (LN Junior; Luigs and Neumann). The potential between the electrode and a reference clip on the neck muscles was digitized (25 kHz), filtered (600–3000 Hz), amplified, and recorded using Tucker-Davis Technologies System 3 hardware (RA16 Medusa or RX5 Pentusa; TDT) and software (Brainware v 8.11; TDT), and stored for subsequent analysis.
Sound generation.
Stimuli were generated digitally, converted to analog signals (RP2.1 at 50 kHz sampling rate; TDT), attenuated (PA5; TDT), and amplified (Blueprint A75; Beyerdynamic) before being presented to the ears via loudspeaker units (Beyerdynamic DT48) fit to custom-made brass tubes that were sealed into the hollow ear speculas. Calibration of the sound system was performed in situ with a probe tube microphone (modified Knowles FG3452; Knowles Electronics), which had been precalibrated against a Brüel and Kjær microphone (Type 4136; Brüel and Kjær); the probe tube was inserted into each ear speculum to within a few millimeters of the tympanic membrane.
Stimulus design and presentation.
All stimuli were presented diotically. Single neurons were isolated using bursts of white noise or pure tones at variable sound levels. After isolation, two characterizations of the neuron were usually performed. A “baseline” rate level function was obtained by presenting 50 ms bursts of white (<25 kHz) noise, separated by 300 ms intervals, at integer sound levels every 5 dB from 21 to 85 or 90 dB sound pressure level (SPL); levels were presented in random order and each was repeated 10 times. Another familiar measure of the sound level of noise, the spectrum level, which gives the sound level within a 1 Hz band, was 44 dB lower than the total noise level [calculated as 10 × log(1 Hz/25,000 Hz)]. Second, for all neurons, the characteristic frequency (CF) (the frequency at which the lowest sound level evokes a response) of the neuron was determined by manually varying the level and frequency of 50 ms pure tones, separated by 300 ms intervals, until the frequency was found at which spike rate increased with the lowest threshold, as determined audiovisually. For 23 of 45 (51%) of neurons, CF was also assessed by obtaining a response area (spike rate as a function of frequency and level), extending 2 octaves above and 4 octaves below the manually determined CF at a spacing of 1/10th of an octave over an 80 dB range of levels at 5 dB intervals. Here, the CF was again determined as the frequency with the lowest threshold to increase spike rate.
For the remainder of the experiment, a broadband noise stimulus, designed to elicit adaptation, was presented. For this stimulus, white (<25 kHz) noise was presented in 40 s segments, separated by <0.5 s, for ∼10 min (range, 4–27 min, depending on the duration for which a given neuron could be held). In the standard protocol, the sound level was set every 50 ms (the “epoch” duration) to a new value chosen randomly from a defined distribution. Only integer decibel values of sound level, spaced every 2 dB between 21 and 85 dB SPL (for 23 of 45 neurons) or 90 dB SPL (for 22 of 45 neurons), were used. For three neurons, sound levels were spaced by 1 dB (see Fig. 4A). The sound level distribution consisted of a region of highly probable levels (the stimulus “high-probability region”) over either 51 ± 6 or 75 ± 6 dB SPL, from which levels were selected with an overall probability of 0.8. Sound levels from the rest of the distribution were selected with an overall probability of 0.2 (see Fig. 1A). The two sound level distributions were alternated in time, such that sound levels were chosen from one distribution for 5 s before switching to the other (giving a 10 s “switch period”) (see Fig. 1B). Thus, in a 40 s stimulus segment, four switch periods were presented, and over the course of a 10 min recording, ∼60 switch periods (range, 24–162 switch periods) were presented. For each of the two sound level distributions, ∼40 repeats of every low-probability sound level, and 690 repeats of every high-probability sound level, were presented over the course of a 10 min recording. The level sequence and noise token were the same for all neurons. For a given sound level distribution, the level sequence differed in each switch period.
Figure 4.
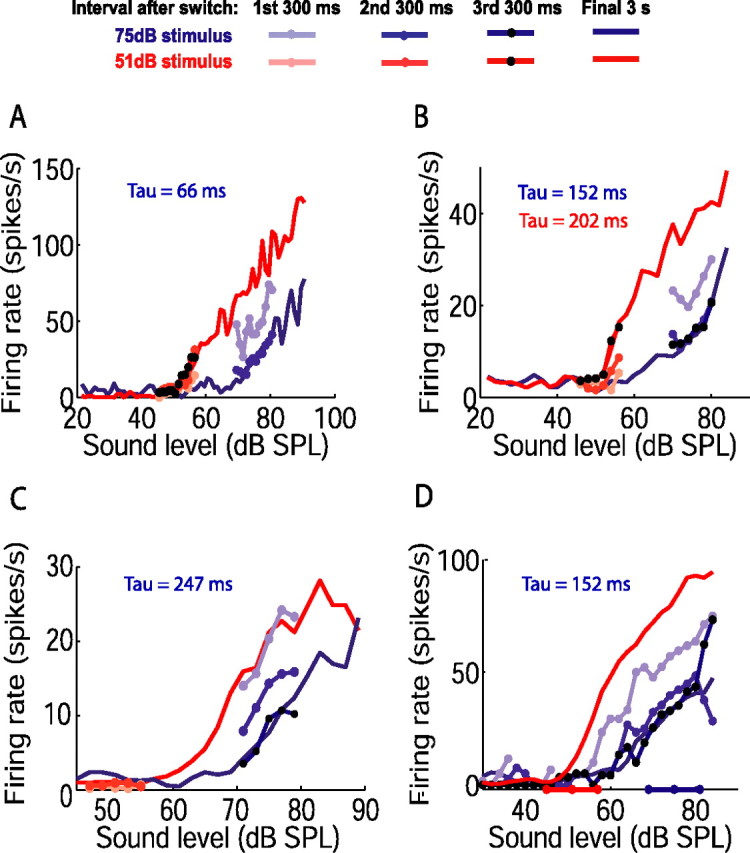
Time course of adjustment of rate level functions between two adapted states. A–D, Each panel shows rate level functions of one neuron obtained during the final 3 s of the 51 dB (red solid line) and 75 dB (blue solid line) half-periods of the switching stimulus. The numbers of switch periods presented were as follows: 38 (A); 160 (B); 68 (C); 84 (D). Rate level functions are also shown for the first (pale lines and symbols), second (dark lines and symbols), and third (black symbols) 300 ms time bins after the switch between sound level distributions. In several cases, the points for these 300 ms functions closely overlie each other. For most neurons, 300 ms functions were plotted for the stimulus high-probability regions only, because less probable levels were presented too few times. For the neuron in D, which showed little spike-rate variability, a sufficient number of switch periods was presented to plot responses over the full range of levels; for clarity, only adaptation to the 75 dB stimulus is shown (stimulus high-probability regions indicated on abscissa). Time constants from single exponential fits to mean firing rate are shown (blue: 75 dB stimulus; red: 51 dB stimulus, where fit).
Figure 1.
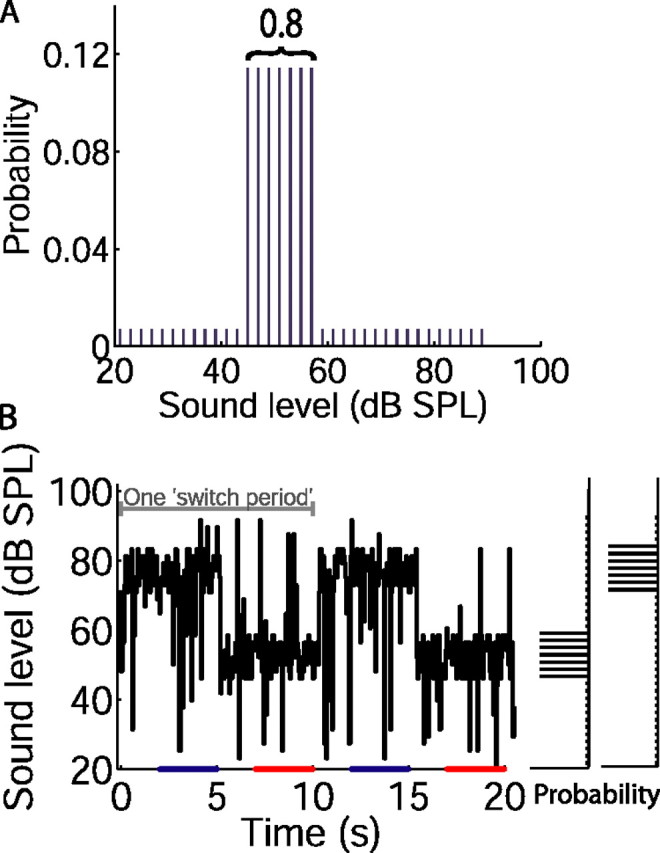
Design of switching stimuli. A, Distribution of sound levels with high-probability region centered at 51 dB SPL (referred to as the “51 dB stimulus”). The value 0.8 refers to the probability of a sound level being drawn from the high probability region. B, Sound level over two 10 s switch periods, drawn from distributions shown to the right. Mean level changed every 5 s when the distribution switched between the 75 and 51 dB stimuli; the total range of levels presented remained the same. The bars on abscissa indicate sampling periods (repeated throughout stimulus) for plotting rate level functions from the final 3 s of each sound level distribution (as plotted in Figs. 2 and 4).
Data analysis.
All analyses were performed in MATLAB (The MathWorks). For each of the two sound level distributions, rate level functions were plotted by calculating the mean spike count of the neuron during the 50 ms epochs corresponding to a given level, taking into account neural latency. Latencies were taken from the responses to the 50 ms noise bursts used in the collection of the baseline rate level functions. For measurement of the time course of adaptation of mean firing rate, spikes were binned into 50 ms epochs and the spike count in each epoch was averaged over all switch cycles. A single exponential decay was then fit to the mean firing rate over the first 2.5 s after each switch in sound level distribution, giving a time constant of the change in firing rate (see Fig. 3, gray curves). For measurement of the time course of the change in rate level functions, functions were plotted from responses in successive, 300 ms duration intervals over the first 3 s after the switch to the 75 dB stimulus. This analysis was performed for sound levels in the high-probability region of the stimulus only. The root-mean-squared (rms) difference between each of these 300 ms functions and the average function from the final 2 s of the 75 dB half-period was then calculated. A single exponential decay was fit to the rms data for each neuron, giving a time constant of the change in the rate level function. Responses during the first switch period of each 40 s segment of the switching stimulus were excluded from the above analyses. Finally, long-term changes in neural response were analyzed by counting the total number of spikes in every 10 s switch period, and fitting a single exponential decay to the spike counts over the full duration of the recording. Exponentials in all analyses were accepted if they provided a better fit than a flat line (F test, p < 0.05 to accept exponential), and passed visual inspection for the goodness of fit.
Figure 3.
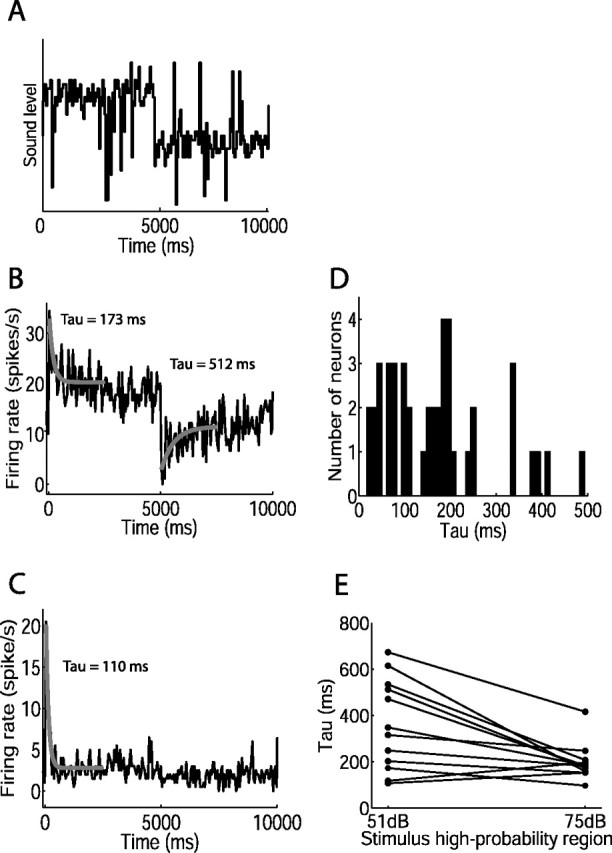
Time course of adaptation of mean firing rate during switching stimulus. A, Representation of sound levels over one switch period, switching from 75 to 51 dB stimulus after 5 s. B, C, Mean firing rate against time, averaged over many cycles of the switching stimulus indicated in A, for two neurons. The gray curves show single exponential fits to firing rate after switch in sound level distribution; time constants are shown. Exponential curves could not be fit after the switch to the 51 dB stimulus for most cells (see, for example, C). The numbers of switch periods presented were as follows: 72 (B); 160 (C). D, Distribution of time constants of adaptation to the 75 dB stimulus, for all adapting neurons (n = 44). E, Time constants of adaptation to the 51 and 75 dB stimuli. The lines connect time constants from individual neurons.
The firing rate of all but one neuron could be fit in this manner to either the 75 or 51 dB stimuli or both. One neuron showed no adaptation in mean firing rate during each 5 s stimulus half-period; this was also the only neuron that showed no change between rate level functions for the two sound level distributions (data not shown). This neuron had a high baseline threshold, and the high-probability regions of the stimuli lay below (51 dB SPL) or at (75 dB SPL) threshold. The lack of adaptive behavior in this neuron accords with our previous observation that adaptation does not shift rate level functions below the lowest, or baseline, threshold of the neuron (Dean et al., 2005).
Recording and analysis of environmental sounds.
Sounds were recorded in seven urban or rural environments (urban: open area in Regent's Park, close to fountains, café, heavy traffic; rural: Peak District caves, open fields, hills), each over several (2–15) minutes, using a 24 bit linear PCM recorder (R-09; Edirol) at a sampling rate of 44.1 or 48 kHz. Sound levels were calculated from these recordings in 10 ms time bins.
Illustrative model.
To illustrate how the time course of adaptation may influence the neural response, an illustrative, linear model was constructed in which the sound level driving the response (rt) at the current time step (t) was taken to be the current sound level (st) minus a “memory” of previous sound levels (mt): rt = st − mt. mt is a low-pass-filtered version of preceding sound levels. In detail, the memory mt was defined as the exponentially weighted average of previous levels over the course of the sound level sequence as follows:
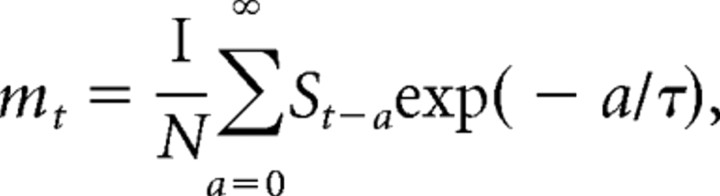 |
where τ was the time constant of the memory; τ was varied to model different time courses of adaptation. N was the normalizing constant as follows:
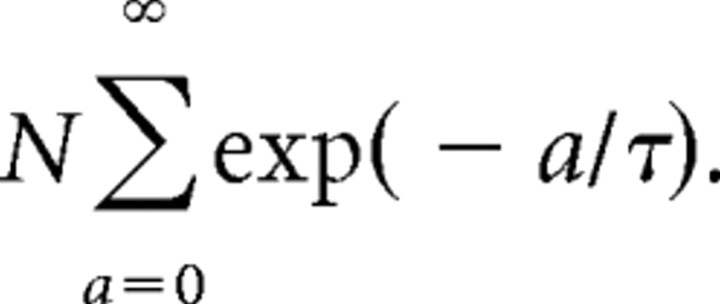 |
In Figure 7, the black traces show s, the blue traces show m, and the red traces show r.
Figure 7.
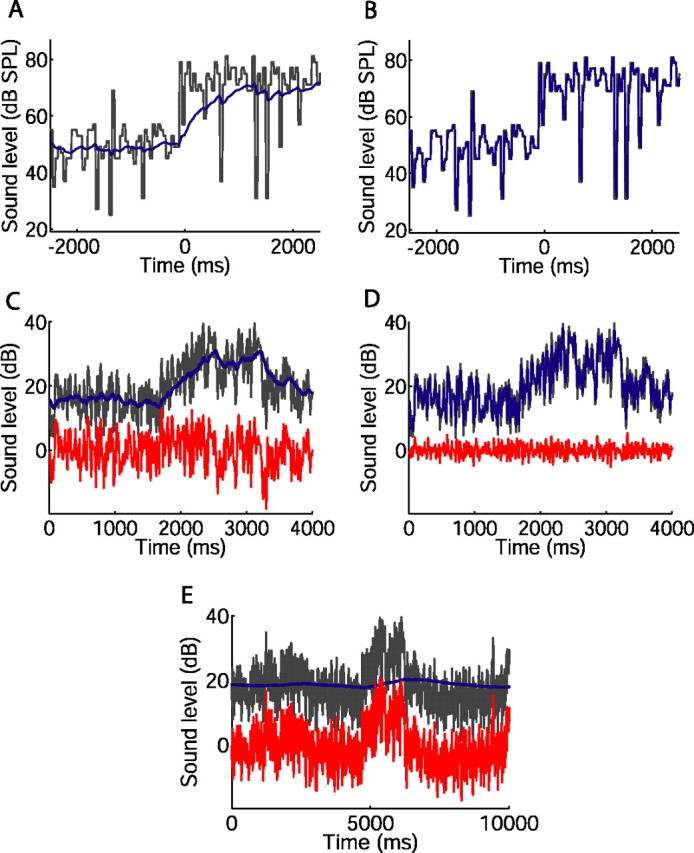
Implications of adaptation time course, examined using an illustrative, linear model of neural memory. A, B, Sound level during a portion of the switching stimulus (black), with sound level distribution switching from 51 to 75 dB stimulus at t = 0 s. Blue, Sound levels averaged over the preceding, exponentially weighted memory window, with a time constant of 493 ms (A) or 17 ms (B). C–E, Variations in sound level in a rural environment (black), and sound levels averaged over memory window (blue). The red traces show the difference between the black and blue traces, representing, in this model, the input driving the neuron that remains after adaptation. C, Four second section of recording; 160 ms memory time constant. D, Same section of recording as in C; 15 ms memory time constant. E, Ten second section of recording; 5000 ms memory time constant.
Results
Responses were recorded from 45 IC neurons in 18 guinea pigs, to ∼10 min of diotic, broadband noise. During the course of this stimulus, sound level was set every 50 ms to a new value chosen randomly from a defined distribution. The sound level distribution consisted of a region of highly probable levels (referred to as the stimulus high-probability region) at either 51 ± 6 or 75 ± 6 dB SPL, from which levels were selected with an overall probability of 0.8. Sound levels from the rest of the distribution were selected with an overall probability of 0.2 (Fig. 1A). These two distributions are henceforward referred to as the 51 or 75 dB stimuli. The 51 and 75 dB stimuli were alternated in time, such that sound levels were chosen from one distribution for 5 s (a stimulus “half-period”) before switching to the other (Fig. 1B). Thus, every 5 s, the mean of the high-probability region was changed, thereby changing the mean sound level with which the animal was presented. This allowed us to examine the dynamics of adaptation to the mean sound level, and the resultant changes in neural stimulus–response relationships, over this time course.
Figure 2 shows baseline, or unadapted, firing rates of two IC neurons as a function of sound level (gray). These functions were obtained by presenting bursts of broadband noise separated by intervals of 300 ms, where sound levels were selected with equal probability (see Materials and Methods). Rate level functions obtained from the “switching” stimulus are also shown for both neurons, for the 51 dB (red) and 75 dB (blue) stimuli. These functions were constructed from responses to the final 3 s of each sound level distribution (i.e., the interval 2–5 s after each switch in distribution) (Fig. 1B). As described previously (Dean et al., 2005), neural responses adapted to the current distribution of sound levels. This adaptation was characterized by a shift in the rate level function along the abscissa, such that neural threshold approached the most commonly occurring sound levels, and by a change in the slope of the rate level function.
Figure 2.
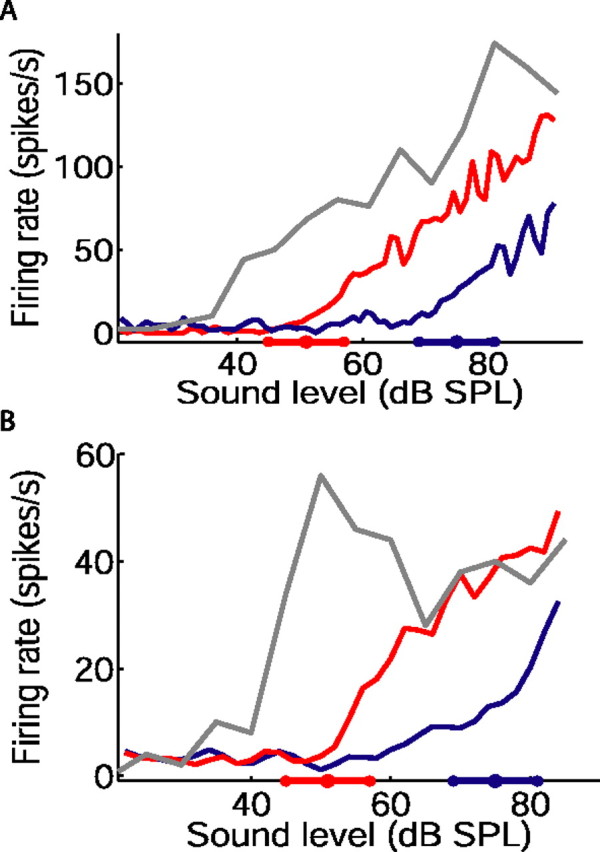
Adjustment of inferior colliculus rate level functions to mean sound level. A, B, Each panel shows the unadapted, baseline rate level function of one neuron (gray), and the adapted rate level functions obtained from the same neuron during the final 3 s of the 51 dB (red) and 75 dB (blue) half-periods of the switching stimulus. The position of the high-probability region of each stimulus is indicated on the abscissas. The numbers of switch periods presented were as follows: 38 (A); 160 (B).
The switching stimulus reveals rapid, and asymmetrical, adaptation of mean firing rate
Do IC neurons adapt to sound level statistics rapidly, over a faster timescale than could previously be assessed? Previous work used a stimulus that allowed only a low-resolution measure of the adaptation time course (Dean et al., 2005). Here, by switching repeatedly between sound level distributions, we were able to assess in detail the time course over which neural responses adapt from one level distribution to another.
Adaptation of the neural response over the 5 s half-period was apparent when the firing rate of each neuron was averaged over multiple cycles of the switching stimulus (Fig. 3A–C). On switching to the 75 dB stimulus, firing rate increased sharply, and then gradually decreased to reach an approximately steady state for the remainder of the 75 dB stimulus. Switching to the 51 dB stimulus usually elicited a sudden reduction in firing rate; in some cases, the rate partially recovered to reach a steady state during the course of the 51 dB stimulus. Only 1 of the 45 neurons recorded showed neither of these adaptive effects; this neuron showed a sharp increase in firing rate after the switch to the 75 dB stimulus, and a sharp decrease after switching to the 51 dB stimulus, but no adaptation of firing rate during either 5 s half-period (data not shown) (see Materials and Methods). Across all adapting neurons, the adaptation occurring during the 75 dB stimulus led to a mean reduction in firing rate of 58 ± 17% (mean ± SD, n = 44 neurons; firing rate in first 50 ms of 75 dB half-period compared with that in final 1 s).
To quantify the time course of adaptation, we fit single exponentials to the mean firing rate after the switch between sound level distributions (Fig. 3B,C). For the 75 dB stimulus, the fit was significant for 98% (44 of 45) of neurons (see Materials and Methods). The median time constant of adaptation to the 75 dB stimulus across these adapting neurons was 159.7 ms (25–75% quartiles, 73.7–203.9 ms; n = 44) (Fig. 3D). The time constant of adaptation during the 75 dB stimulus was negatively correlated with the depth of adaptation (Spearman's rank correlation coefficient rs = −0.48; p = 0.001; n = 44), indicating that rapidly adapting neurons underwent larger changes in their firing rates than more slowly adapting neurons.
Adaptation of mean firing rate to the 51 dB stimulus is evident in Figure 3B. However, although rate level functions adapted to the 51 dB stimulus, as shown in Figure 2, many neurons did not show obvious adaptation of mean firing rate after the switch to this stimulus (Fig. 3C). This is not surprising and does not reflect the baseline thresholds of the neurons, but is related to the effect of adaptation on rate level functions. The mean firing rate is, through averaging over many periods of the stimulus, the mean rate across all levels presented. This rate is dominated by the responses to the most commonly occurring levels; that is, the contribution of each response to the mean firing rate is weighted by the sound level distribution. In the IC, one effect of the adaptation is to shift the neural threshold toward the most commonly occurring levels; thus, sound levels within the high-probability region of the 51 dB stimulus usually lay at or below threshold in both states of adaptation. Thus, both immediately after the switch to this stimulus, and a few seconds later, the most probable levels evoked few spikes. This results in little change in average rate over time, despite the adjustment that occurs of the rate level function over less probable levels. Single exponentials could be fit to mean firing rates for 12 of 45 neurons during the 51 dB half-period. The median time constant of adaptation to the 51 dB stimulus was 331.8 ms (25–75% quartiles, 187.3–523.1 ms; n = 12). There was an asymmetry in time course of adaptation between the two sound level distributions: adaptation to the 51 dB stimulus was significantly slower than that to the 75 dB stimulus (p < 0.01, paired t test; mean increase in time constant, 88%) (Fig. 3E).
Adjustments of rate level functions over time
How does adaptation of the mean firing rate of a neuron correspond to changes in its representation of sound level? To examine this, rate level functions were constructed from responses during successive, 300-ms-duration intervals after the switch between sound level distributions. By comparing these 300 ms rate level functions to the functions constructed from responses immediately preceding the switch (calculated over the final 3 s of each stimulus), the transformation in the representation of sound level could be visualized as adaptation proceeded (Fig. 4). In a 10 min recording, over the 300 ms there were ∼40 repeats of every sound level in the high-probability region, but only 3 repeats in the low-probability regions. Thus, accurate construction of rate level functions over 300 ms intervals could only be performed for sound levels drawn from the high-probability region of each stimulus, except for a few neurons with low intrinsic spiking variability and long recording durations.
The time course of adaptation of mean firing rate was reflected in the evolution of rate level functions over successive 300 ms intervals. Figure 4 illustrates that neuronal rate level functions reached their final form rapidly after the switch to the 75 dB stimulus. The time constants of the change in mean firing rate for the neurons in Figure 4, A, B, and D, were 66, 152, and 152 ms, respectively, and their rate level functions had completely (Fig. 4A) or mostly (Fig. 4B,D) reached their final form by the end of the second interval (i.e., within 600 ms of the switch). In contrast, the rate level function of the neuron in Figure 4C, whose time constant of adaptation was 247 ms, did not settle to its final position until the third 300 ms interval (i.e., within 900 ms of the switch). Although it is more difficult to visualize changes in rate level functions over the most probable levels of the 51 dB stimulus, for the neuron shown in Figure 4B (time constant during 51 dB stimulus, 202 ms) this function reached its final position within the third 300 ms interval after the switch. Finally, for some neurons that were recorded for long durations, rate level functions could be constructed over both high- and low-probability regions, as illustrated in Figure 4D; adaptation over the full range of levels occurred in register with adaptation over the stimulus high-probability region.
To confirm that the change in mean firing rate was related to the change in rate level functions, a single exponential was fit to the rms differences between each of the 300 ms functions and the function from the final portion of the half-period (see Materials and Methods). This fit was significant for 28 of 44 neurons. The resulting time constants of change in rate level functions were highly correlated with the time constants of adaptation of mean firing rate measured above (Spearman's rank correlation coefficient rs = 0.8; p < 0.0001; n = 28). Unless otherwise specified, time constants henceforth refer to those measured for the adaptation of mean firing rate.
The time course of adaptation does not depend on timescales in the stimulus
The results above indicate that adaptation time course differs between the two directions of change in mean level. To examine whether adaptation time course also depends on timescales in the stimulus, the period of the switch between sound level distributions was varied between 5 and 20 s. This did not significantly affect the time course of adaptation to the 75 dB stimulus across the population of neurons tested (two-way ANOVA, p < 0.0005 for effect of neuron, p = 0.2 for effect of switch period; n = 16 neurons). Furthermore, varying the length of time for which sound remained at any given level (the epoch), between 25 and 200 ms, also had no effect on adaptation time course across the neural population (two-way ANOVA, p < 0.005 for effect of neuron, p = 0.1 for effect of epoch; n = 14 neurons). These results indicate that the time course of adaptation to the sound level statistics of our stimulus is not dependent on the two timescales within it.
Adaptation time constants vary with neural CF
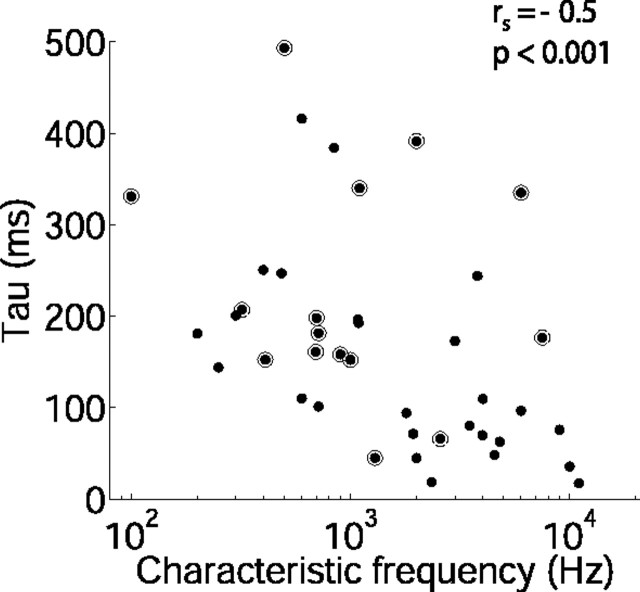
Previous studies have demonstrated that the time course of spike rate adaptation of auditory nerve fibers (ANFs) during pure tone bursts is related to neural CF (Westerman and Smith, 1985; Crumling and Saunders, 2007). A similar relationship was observed in the adaptation to sound level statistics examined in the current study. Figure 5 shows adaptation time constants for the 75 dB stimulus as a function of CF. The median CF was 1198 Hz (range, 100–11,000 Hz; n = 40). Adaptation time constants were negatively correlated with CF (Spearman's rank correlation coefficient rs = −0.5, p < 0.001, n = 40; using only the densely sampled data, at CF < 5000 Hz, rs = −0.53, p < 0.01, n = 34). Thus, neurons with higher CFs tend to adapt to the new level distribution more rapidly than those with lower CFs.
Figure 5.
Time course of adaptation is related to neural CF. Time constant of adaptation of mean firing rate during the 75 dB stimulus is shown as a function of neural CF (n = 40). The circled points indicate neurons for which a slow component of adaptation could also be measured. rs, Spearman's rank correlation coefficient.
Although our stimulus was broadband noise and not pure tones, the neurons in our experiments are likely to have been driven most strongly by frequencies at or near CF. The faster adaptation at high CFs in ANFs appears to be partly attributable to a dependence of adaptation time course on tone frequency (Crumling and Saunders, 2007), whereby phase-locking at the hair cell–ANF synapse may result in more rapid transmitter depletion at high stimulating frequencies. To assess whether the relationship between CF and adaptation time course in the IC was similarly attributable to effective stimulating frequency, adaptation profiles were examined in response to tones which were amplitude-modulated at frequencies to which responses are phase-locked. Responses were recorded to these “transposed” tones (Griffin et al., 2005), with the carrier frequency set to CF (median CF, 4522 Hz; 25–75% quartiles, 3854–6550 Hz; n = 22 neurons) and the modulation frequency varied between 10 and 640 Hz. If phase-locking is responsible for the relationship observed between adaptation time course and CF, the time course of adaptation during transposed tones would be expected to change with modulation frequency. Note that the modulation depth was 100% across all transposed tones. The filtering of broadband noise by the wide bandwidth of high CF neurons may result in smaller modulations than at lower CFs (Hartmann, 1998). In addition, some properties of auditory neurons are known to be sensitive to the depth and variance of amplitude modulation (Kvale and Schreiner, 2004; Nagel and Doupe, 2006). Thus, the use of the transposed tones did not examine the possibility that the relationship between CF and adaptation time course arises through a dependency on modulation depth. However, changing modulation frequency did not affect the time course of adaptation during the transposed tone (two-way ANOVA, p < 0.001 for effect of neuron, p = 0.6 for effect of modulation frequency; n = 22 neurons). This suggests that a change in the frequency to which neural responses are locked is not sufficient to account for the relationship observed between adaptation time course and CF in the IC.
A slow component of adaptation is apparent in some neurons
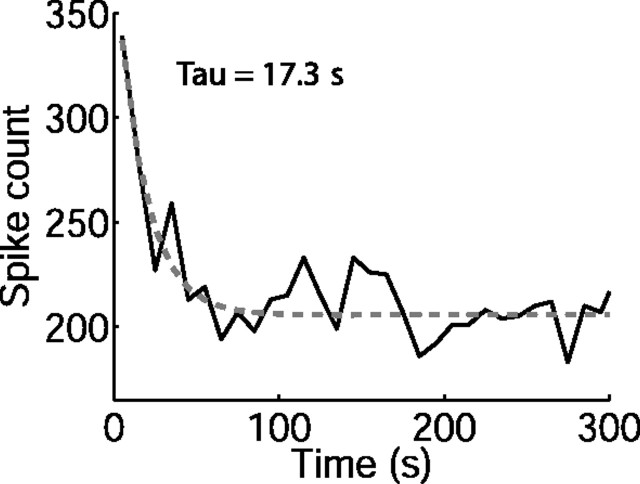
In addition to the adaptation occurring during each cycle of the switching stimulus, the responses of some neurons also displayed a far slower adaptation, occurring over the course of many switching cycles (Fig. 6). We analyzed this long-term adaptation for all neurons from responses recorded to the standard switching stimulus (i.e., 10 s switch period, 50 ms epoch). The slow adaptation was apparent in 36% (16 of 45) of neurons (those circled on Fig. 5). Fit with a single exponential, the median time constant of the slow adaptation was 12.3 s (25–75% quartiles, 8.0–26.6 s; n = 16 neurons). There was no significant relationship between the time course of the slow adaptation and that of the rapid adaptation (Spearman's rank correlation coefficient rs = −0.17; p = 0.5) or neural CF (rs = −0.03; p = 0.9). This slow adaptation resulted in a median decrease in average firing rate of 37% (25–75% quartiles, 26–40%; n = 16) over the first 5 min of recording (comparing rates at 0–10 s with those at 270–300 s of recording). The depth of the slow adaptation was not correlated with that of the fast adaptation (rs = −0.06; p = 0.83).
Figure 6.
Long-term adaptation. Spike count over each 10 s switch period from one neuron during the first 5 min of recording. The dashed gray curve shows single exponential fit to spike counts (time constant, 17.3 s).
Interpretation of time course of adaptation
The adaptation time constant clearly has implications for “real-world” listening conditions, in that adaptation to a given distribution of sound levels will only be complete if that distribution persists severalfold longer than the time constant. In addition, the adaptation time constant is also a measure of the duration of the window into the past during which sound levels exert an influence over responses to the current level (the “integration window”) (Theunissen and Miller, 1995). The time course of the adaptation therefore reflects the duration of the memory of a neuron for previous sounds. The exponential time course of the adaptation suggests that this window into the past is exponentially weighted, whereby the most recent sounds have a greater influence on current neural response than sounds in the more distant past.
The concept of an integration window affecting current neural responses is illustrated in Figure 7. The black traces in Figure 7, A and B, indicate the sound level of the switching stimulus over time. Adaptation can be seen as resulting in a high-pass version of the stimulus by subtracting away a low-pass “neural memory.” We represent the neural memory as a linear low-pass filter: each point on the blue traces indicates the sound level averaged over the preceding, exponentially weighted memory window, with time constants of 493 ms (Fig. 7A) or 17 ms (Fig. 7B), the maximum and minimum, respectively, recorded for the rapid adaptation during the 75 dB stimulus. In this simple, illustrative model only a single time constant is used, and it therefore does not take account of nonlinearities, such as the difference in time constants for the 51 and 75 dB stimuli. Whereas the sound level distributions themselves switch instantaneously, the blue trace in Figure 7A indicates that the levels affecting the neural response change over the first few hundred milliseconds after the switch, and approximate the new mean level only later during the 5 s half-period. The faster time constant in Figure 7B, however, results in a faster approach to the new mean level after the switch, at the cost of the mean being less consistently approximated. It is such changes in the levels captured by the memory window of a neuron that, when averaged over many cycles of the switching stimulus in our analysis, result in the adaptive changes in responses described above.
We also applied the exponentially weighted memory window to sound levels recorded in several urban and rural environments. Across all the recordings, sound level varied over 90 dB, illustrating the dynamic range problem faced by the auditory system. Changes in level occurred over several timescales in all environments, ranging from rapid, transient increases or decreases that lasted a few tens of milliseconds, to slower fluctuations lasting several seconds. Figure 7C shows the exponentially weighted average sound levels over a 4 s period in a rural environment (blue trace), using the median time constant of the rapid adaptation (160 ms). As in Figure 7, A and B, the weighted average describes a low-pass-filtered version of the variation in actual (black) sound level. In this model, the blue traces represent the sound levels that drive adaptation, reducing the response to current levels. By selectively reducing responses to slow changes in level, adaptation renders neural output into a high-pass-filtered version of the stimulus (Benda and Herz, 2003; Benda et al., 2005). The red trace in Figure 7C shows the difference between the actual (black) levels and the levels to which the neuron is adapted (blue) (i.e., the sound levels remaining after subtraction of the exponentially weighted average) and suggests that the neural response remaining after adaptation will not follow the slow variations in level. Faster adaptation increases the corner frequency of the filter (Fig. 7D, with a time constant of 15 ms). Now, the blue trace follows not only the slow fluctuations, but also captures more rapid changes in level. Finally, with a longer neural memory adaptation can follow only the slowest fluctuations in level, so that some of the slow fluctuations, removed from neural output in Figure 7, C and D, now appear in the red trace (Fig. 7E, with a time constant of 5000 ms).
Discussion
We demonstrated previously that adaptation to the statistics of sound level distributions leads to increased accuracy of coding around the most probable levels (Dean et al., 2005). The aim of the current study was to assess in detail how quickly this adaptation occurs. Several timescales of adaptation were evident, with adaptation to an increase in mean sound level occurring within a fraction of a second, more rapidly than we had previously been able to measure. Adaptation to a reduction in mean level tended to occur more slowly. Finally, in some neurons, we also observed a slow adaptation, occurring over tens of seconds.
Adaptation to an increase in mean sound level
By using a stimulus that switched repeatedly between two sound level distributions, we showed a rapid component of adaptation to sound level statistics: adaptation to an increase in mean level occurred with an average time constant, across neurons, of 160 ms.
We assessed the time course of adaptation by fitting curves to the change in mean firing rate after a switch in sound level distribution. Although it is possible that adaptation of the input–output relationship of a neuron and changes in its mean rate are not associated (Fairhall et al., 2001; Baccus and Meister, 2002), the rate adaptation that we observe after a change in mean level corresponds closely to the adaptive changes in rate level functions. Our results are therefore comparable with those reported for somatosensory cortex, in which adaptation of mean firing rate is associated with adaptation of stimulus–response relationships (Maravall et al., 2007).
Adaptation of mean firing rate to the variance and kurtosis of pure-tone levels has been examined in cat IC using a stimulus switching paradigm, although adaptation of rate level functions, or any CF dependence of the adaptation, were not examined (Kvale and Schreiner, 2004). Adaptation to increased variance or kurtosis occurred with a time constant of 140 or 260 ms, respectively. Although we assessed adaptation to the mean, using noise rather than pure tones, and changed sound level over longer timescales, the similarity in time course between the two studies suggests that adaptation over hundreds of milliseconds is characteristic of the adjustment of IC responses to stimulus statistics.
Relationship of adaptation time course to neural CF
The time course of adaptation to an increase in mean level was negatively correlated with neural CF. We showed that this relationship is unlikely to result from a dependency of adaptation time course on stimulus modulation frequency. Remaining possible mechanisms include a dependency on stimulus modulation depth or tonotopically organized factors intrinsic to the neurons. An additional question is whether the relationship to CF is functionally relevant, linked, for example, to the representation of natural sound environments salient to the guinea pig.
Adaptation to a decrease in mean level
For those neurons in which it could be measured, adaptation to a reduction in mean level also occurred over hundreds of milliseconds. However, neurons tended to adapt more rapidly to an increase than to a decrease in mean level. Such time course asymmetry has been shown for other forms of adaptation; for example, visual responses adapt more quickly to an increase in stimulus variance than to a decrease (Smirnakis et al., 1997; Fairhall et al., 2001). More generally, it seems that adaptive reduction in firing rate after an increased response is faster than adaptive recovery after a decreased response. Such asymmetry is observed in ANF responses to isolated tones (Harris and Dallos, 1979), and for adaptive processes arising after binaural integration in the brainstem (Ingham and McAlpine, 2004). Thus, the asymmetry we report appears to reflect a general property of adaptation and, interestingly, is predicted by a relatively simple model of adaptation based on synaptic plasticity (Hosoya et al., 2005).
Multiple timescales of adaptation in the IC
Neither the timescale over which sound level varied, nor that over which sound level distributions varied, affected the time course of the rapid component of adaptation. In contrast, adaptation time course in fly visual neurons scales with stimulus switch period (Fairhall et al., 2001). Previously, we demonstrated a slow component of IC adaptation, occurring over seconds (Dean et al., 2005). We also observed a slow adaptation in the present study, with an average time constant of 12 s. Because the current experiments were not designed to examine this timescale in detail, additional characterization is required to assess its function; it may reflect transient adaptation to slow timescales in natural stimuli, or a form of longer term plasticity. Although rapid adaptation in the IC appears to be invariant to changes in stimulus timescales, the range of adaptation time courses we report indicates that IC neural responses can adapt over several timescales, as has been found in auditory cortex (Ulanovsky et al., 2004).
Mechanisms of adaptation
The adaptive effects we describe may arise not within the IC itself, but may partly or wholly result from mechanisms occurring lower in the auditory pathway. Indeed, forms of adaptation are displayed at lower sites, including the auditory nerve (Westerman and Smith, 1984) and the CN (Bleeck et al., 2006); mechanisms underlying these effects may contribute to the adaptation we observe. Such mechanisms may act at the cellular level, such as synaptic depression or channel-based adaptation, or involve network interactions, including those arising through efferents to all stages in the pathway. The present study will assist future work in identifying the basis of the adaptation, by constraining the possibilities to mechanisms operating over comparable timescales.
The rapid adaptive effects shown here occur over a similar timescale to adaptation resulting from synaptic depression, for example in somatosensory cortex (Chung et al., 2002; Higley and Contreras, 2006) (but see also Best and Wilson, 2004). Furthermore, synaptic depression in the IC in vitro occurs over hundreds of milliseconds (Wu et al., 2004); therefore, adaptation of synaptic strength within the IC itself may contribute to the rapid effects we describe. Alternatively, the rapid adaptation of IC responses after an increase in mean level is suggestive of medial olivocochlear (MOC) efferent effects, which modulate outer hair cell activity over a similar time course (Boyev et al., 2002; Backus and Guinan, 2006; Guinan, 2006) and indeed adjust ANF rate level functions (Guinan and Stankovic, 1996).
MOC effects additionally occur over tens of seconds (Backus and Guinan, 2006), raising the possibility that these efferents also contribute to the slow adaptation we describe. In addition, slow effects can result from intrinsic, channel-based adaptation, arising through activity-dependent potassium conductances [e.g., in visual cortical neurons (Carandini and Ferster, 1997; Sanchez-Vives et al., 2000a,b)]. Such conductances are intrinsic to some IC neurons (Sivaramakrishnan and Oliver, 2001). Interestingly, the proportion of IC neurons displaying slow adaptation (36%) is similar to the proportion expressing these conductances and showing adapting firing patterns in vitro (29%) (Sivaramakrishnan and Oliver, 2001). In contrast to the above mechanisms, lateral olivocochlear (LOC) efferents operate over minutes (Guinan, 2006). Therefore, we discount the LOC pathway, which directly modulates ANF activity, from causing the adaptive effects we report.
Potential mechanisms must also be able to explain the particular features of the adaptation, such as the relationship to CF. Although this relationship may result from a variation of modulation depth with CF, it is also possible that the CF dependence arises from an adaptive mechanism that varies in time course along the tonotopic axis. A second feature is the time course asymmetry between increases and decreases in mean level. For example, although MOC effects show an opposite asymmetry (Backus and Guinan, 2006), and therefore are unable to account fully for the IC adaptation, synaptic depression has a complementary time course asymmetry to that shown here (Dobrunz et al., 1997; Chung et al., 2002).
Time course of adaptation: relevance to environmental sounds
We suggest two general, conflicting constraints on the speed with which adaptation occurs. First, if adaptation is too slow, then for rapidly changing sound level distributions, the neural responses would not adjust in time to achieve the improvement in coding of the most commonly occurring levels demonstrated by Dean et al., 2005). Second, overly rapid adaptation might be disadvantageous in that a continuously fluctuating adaptive state (as in Fig. 7D) might exacerbate coding ambiguity, whereby the representation of sound level in the IC reconfigures too rapidly for higher centers to decode. In addition, adaptation improves coding accuracy over a restricted range of sound levels near to and just above the mean level (Dean et al., 2005), and the width of this dynamic range has limited flexibility. On this basis, to use the full dynamic range of the adapted rate level function so that current levels cover this range, it might be advantageous for the adaptation state not to adjust instantaneously to levels varying from instant to instant, but rather to track more generally the background level. Excessively rapid adaptation might prevent the neuron from using the full extent of its dynamic range, by always adapting out responses to those sound levels currently being encountered (note narrow range of fluctuations remaining in red trace of Fig. 7D). We speculate that the time course of adaptation that we found in this study, occurring over a few hundred milliseconds, represents a compromise between these opposing demands on neural coding.
Footnotes
This work was supported by a Royal Society Dorothy Hodgkin Fellowship (I.D.) and the Medical Research Council (United Kingdom). We thank J. Linden and J. Ashmore for critical reading of this manuscript and J. Agapiou for the design of the model used for Figure 7.
References
- Adrian ED. The basis of sensation. London, UK: Christophers; 1928. [Google Scholar]
- Baccus SA, Meister M. Fast and slow contrast adaptation in retinal circuitry. Neuron. 2002;36:909–919. doi: 10.1016/s0896-6273(02)01050-4. [DOI] [PubMed] [Google Scholar]
- Backus BC, Guinan JJ., Jr Time-course of the human medial olivocochlear reflex. J Acoust Soc Am. 2006;119:2889–2904. doi: 10.1121/1.2169918. [DOI] [PubMed] [Google Scholar]
- Bajo VM, Nodal FR, Bizley JK, Moore DR, King AJ. The ferret auditory cortex: descending projections to the inferior colliculus. Cereb Cortex. 2007;17:475–491. doi: 10.1093/cercor/bhj164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bal R, Green GG, Rees A, Sanders DJ. Firing patterns of inferior colliculus neurons—histology and mechanism to change firing patterns in rat brain slices. Neurosci Lett. 2002;317:42–46. doi: 10.1016/s0304-3940(01)02425-9. [DOI] [PubMed] [Google Scholar]
- Benda J, Herz AV. A universal model for spike-frequency adaptation. Neural Comput. 2003;15:2523–2564. doi: 10.1162/089976603322385063. [DOI] [PubMed] [Google Scholar]
- Benda J, Longtin A, Maler L. Spike-frequency adaptation separates transient communication signals from background oscillations. J Neurosci. 2005;25:2312–2321. doi: 10.1523/JNEUROSCI.4795-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best AR, Wilson DA. Coordinate synaptic mechanisms contributing to olfactory cortical adaptation. J Neurosci. 2004;24:652–660. doi: 10.1523/JNEUROSCI.4220-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bleeck S, Sayles M, Ingham NJ, Winter IM. The time course of recovery from suppression and facilitation from single units in the mammalian cochlear nucleus. Hear Res. 2006;12:176–184. doi: 10.1016/j.heares.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Boyev KP, Liberman MC, Brown MC. Effects of anesthesia on efferent-mediated adaptation of the DPOAE. J Assoc Res Otolaryngol. 2002;3:362–373. doi: 10.1007/s101620020044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner N, Bialek W, de Ruyter van Steveninck R. Adaptive rescaling maximizes information transmission. Neuron. 2000;26:695–702. doi: 10.1016/s0896-6273(00)81205-2. [DOI] [PubMed] [Google Scholar]
- Carandini M, Ferster D. A tonic hyperpolarization underlying contrast adaptation in cat visual cortex. Science. 1997;276:949–952. doi: 10.1126/science.276.5314.949. [DOI] [PubMed] [Google Scholar]
- Chung S, Li X, Nelson SB. Short-term depression at thalamocortical synapses contributes to rapid adaptation of cortical sensory responses in vivo. Neuron. 2002;34:437–446. doi: 10.1016/s0896-6273(02)00659-1. [DOI] [PubMed] [Google Scholar]
- Crumling MA, Saunders JC. Tonotopic distribution of short-term adaptation properties in the cochlear nerve of normal and acoustically overexposed chicks. J Assoc Res Otolaryngol. 2007;8:54–68. doi: 10.1007/s10162-006-0061-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat Neurosci. 2005;8:1684–1689. doi: 10.1038/nn1541. [DOI] [PubMed] [Google Scholar]
- Dobrunz LE, Huang EP, Stevens CF. Very short-term plasticity in hippocampal synapses. Proc Natl Acad Sci USA. 1997;94:14843–14847. doi: 10.1073/pnas.94.26.14843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fairhall AL, Lewen GD, Bialek W, de Ruyter Van Steveninck RR. Efficiency and ambiguity in an adaptive neural code. Nature. 2001;412:787–792. doi: 10.1038/35090500. [DOI] [PubMed] [Google Scholar]
- Griffin SJ, Bernstein LR, Ingham NJ, McAlpine D. Neural sensitivity to interaural envelope delays in the inferior colliculus of the guinea pig. J Neurophysiol. 2005;93:3463–3478. doi: 10.1152/jn.00794.2004. [DOI] [PubMed] [Google Scholar]
- Guinan JJ., Jr Olivocochlear efferents: anatomy, physiology, function, and the measurement of efferent effects in humans. Ear Hear. 2006;27:589–607. doi: 10.1097/01.aud.0000240507.83072.e7. [DOI] [PubMed] [Google Scholar]
- Guinan JJ, Jr, Stankovic KM. Medial efferent inhibition produces the largest equivalent attenuations at moderate to high sound levels in cat auditory-nerve fibers. J Acoust Soc Am. 1996;100:1680–1690. doi: 10.1121/1.416066. [DOI] [PubMed] [Google Scholar]
- Harris DM, Dallos P. Forward masking of auditory nerve fiber responses. J Neurophysiol. 1979;42:1083–1107. doi: 10.1152/jn.1979.42.4.1083. [DOI] [PubMed] [Google Scholar]
- Hartmann WM. Signals, sound and sensation. New York: Springer; 1998. Noise; pp. 522–540. [Google Scholar]
- Higley MJ, Contreras D. Balanced excitation and inhibition determine spike timing during frequency adaptation. J Neurosci. 2006;26:448–457. doi: 10.1523/JNEUROSCI.3506-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosoya T, Baccus SA, Meister M. Dynamic predictive coding by the retina. Nature. 2005;436:71–77. doi: 10.1038/nature03689. [DOI] [PubMed] [Google Scholar]
- Ingham NJ, McAlpine D. Spike-frequency adaptation in the inferior colliculus. J Neurophysiol. 2004;91:632–645. doi: 10.1152/jn.00779.2003. [DOI] [PubMed] [Google Scholar]
- Kvale MN, Schreiner CE. Short-term adaptation of auditory receptive fields to dynamic stimuli. J Neurophysiol. 2004;9:604–612. doi: 10.1152/jn.00484.2003. [DOI] [PubMed] [Google Scholar]
- Lim HH, Anderson DJ. Antidromic activation reveals tonotopically organized projections from primary auditory cortex to the central nucleus of the inferior colliculus in guinea pig. J Neurophysiol. 2007;97:1413–1427. doi: 10.1152/jn.00384.2006. [DOI] [PubMed] [Google Scholar]
- Maravall M, Petersen RS, Fairhall AL, Arabzadeh E, Diamond ME. Shifts in coding properties and maintenance of information transmission during adaptation in barrel cortex. PLoS Biol. 2007;5:e19. doi: 10.1371/journal.pbio.0050019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagel KI, Doupe AJ. Temporal processing and adaptation in the songbird auditory forebrain. Neuron. 2006;51:845–859. doi: 10.1016/j.neuron.2006.08.030. [DOI] [PubMed] [Google Scholar]
- Ohzawa I, Sclar G, Freeman RD. Contrast gain control in the cat visual cortex. Nature. 1982;298:266–268. doi: 10.1038/298266a0. [DOI] [PubMed] [Google Scholar]
- Ohzawa I, Sclar G, Freeman RD. Contrast gain control in the cat's visual system. J Neurophysiol. 1985;54:651–667. doi: 10.1152/jn.1985.54.3.651. [DOI] [PubMed] [Google Scholar]
- Sanchez-Vives MV, Nowak LG, McCormick DA. Membrane mechanisms underlying contrast adaptation in cat area 17 in vivo. J Neurosci. 2000a;20:4267–4285. doi: 10.1523/JNEUROSCI.20-11-04267.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Vives MV, Nowak LG, McCormick DA. Cellular mechanisms of long-lasting adaptation in visual cortical neurons in vitro. J Neurosci. 2000b;20:4286–4299. doi: 10.1523/JNEUROSCI.20-11-04286.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivaramakrishnan S, Oliver DL. Distinct K currents result in physiologically distinct cell types in the inferior colliculus of the rat. J Neurosci. 2001;21:2861–2877. doi: 10.1523/JNEUROSCI.21-08-02861.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smirnakis SM, Berry MJ, Warland DK, Bialek W, Meister M. Adaptation of retinal processing to image contrast and spatial scale. Nature. 1997;386:69–73. doi: 10.1038/386069a0. [DOI] [PubMed] [Google Scholar]
- Theunissen F, Miller JP. Temporal encoding in nervous systems: a rigorous definition. J Comput Neurosci. 1995;2:149–162. doi: 10.1007/BF00961885. [DOI] [PubMed] [Google Scholar]
- Ulanovsky N, Las L, Farkas D, Nelken I. Multiple time scales of adaptation in auditory cortex neurons. J Neurosci. 2004;24:10440–10453. doi: 10.1523/JNEUROSCI.1905-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerman LA, Smith RL. Rapid and short term adaptation of auditory nerve responses. Hear Res. 1984;15:249–260. doi: 10.1016/0378-5955(84)90032-7. [DOI] [PubMed] [Google Scholar]
- Westerman LA, Smith RL. Rapid adaptation depends on the characteristic frequency of auditory nerve fibers. Hear Res. 1985;17:197–198. doi: 10.1016/0378-5955(85)90022-x. [DOI] [PubMed] [Google Scholar]
- Winer JA. Decoding the auditory corticofugal systems. Hear Res. 2006;212:1–8. doi: 10.1016/j.heares.2005.06.014. [DOI] [PubMed] [Google Scholar]
- Wu SH, Ma CL, Kelly JB. Contribution of AMPA, NMDA, and GABAA receptors to temporal pattern of postsynaptic responses in the inferior colliculus of the rat. J Neurosci. 2004;24:4625–4634. doi: 10.1523/JNEUROSCI.0318-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Suga N, Yan J. Corticofugal modulation of frequency processing in bat auditory system. Nature. 1997;387:900–903. doi: 10.1038/43180. [DOI] [PubMed] [Google Scholar]