Deformation Field Morphometry Reveals Age-Related Structural Differences between the Brains of Adults up to 51 Years

Abstract

Age-related differences in the anatomical structure of the brains from 51 healthy male subjects (age: 18–51 years) were analyzed by deformation field morphometry in a cross-sectional study. The magnetic resonance images of the brains were nonlinearly registered onto the image of a reference brain: the registration algorithm simulated an elastic deformation of each brain (source brain) so that the voxelwise intensity differences with the reference brain were minimized. A three-dimensional deformation field was calculated for each source brain that encoded the anatomical differences between the source brain and the reference brain. Maps of voxelwise volume differences between each subject's brain and the reference brain were analyzed. They showed age-related differences in anatomically defined regions of interest. Major volume decreases were found in the white matter and nuclei of the cerebellum, as well as in the ventral thalamic nuclei and the somatosensory and motor cortices, including the underlying white matter. These findings suggest that aging between the second and sixth decade predominantly affects subcortical nuclei and cortical areas of the sensorimotor system, forming the cortico-rubro-cerebello-thalamo-cortical pathway. Additionally, a pronounced age-related decline in volume was observed in the rostral anterior cingulate, orbitofrontal, and lateral prefrontal cortices. Almost no differences were observed in the occipital and temporal lobes. The ventricles showed a pronounced widening. Remarkably, these volume differences occur at a relatively early period of the human life span. It may be speculated that these structural differences accompany or precede differences in sensorimotor functions and behavior.

Introduction

Deformation field morphometry (DFM) is a highly automatized technique based on the nonlinear transformation (i.e., registration) of individual three-dimensional (3D) magnetic resonance (MR) images to a reference image. Each “source” MR image is warped to a reference image such that the differences between them are minimized, yielding a deformation field. The analysis of deformation fields enables quantification of the shape of human brains at the voxel level. Thus, this technique has the potential to detect local structural differences between brains.

Various algorithms based on substantially different mathematical approaches have been proposed for DFM. The accuracy of the registrations may differ significantly between currently used algorithms (Crivello et al., 2002). In the present study, we applied an algorithm that is based on an elastic, nonlinear deformation of the source MR images (Hömke, 2006). DFM techniques were applied that enabled us to derive from the deformation fields both voxelwise volume measures and volume measurements of atlas-based regions of interest (ROIs).

DFM was used to detect relationships between age and brain structure. Several previous studies reported age-related declines of the volume of the whole brain, gray matter, or macroanatomical regions (Courchesne et al., 2000; Jernigan et al., 2001; Resnick et al., 2003; Sowell et al., 2003; Raz et al., 2004; Allen et al., 2005; Walhovd et al., 2005). Some studies found such volume declines even for young and middle-aged adults (Gur et al., 2002; Fotenos et al., 2005). Gray matter volume declines in the frontal lobe were found to be stronger than in any other lobe. Concerning the parietal lobe, however, these studies differ in neurobiologically important aspects: some authors (Resnick et al., 2003, Sowell et al., 2003; Allen et al., 2005) reported a significant age-related decline in the volume of the parietal cortex, whereas Jernigan et al. (2001) found such a relationship for the parietal white but not for the gray matter. Raz et al. (2004) found no cross-sectional age–volume relationship for either the inferior parietal lobe (IPL) or for the parietal white matter, whereas in a longitudinal study a significant decline of the IPL was found (Raz et al., 2005). Measurements of the thalamus also showed some conflicting results: Van Der Werf et al. (2001), Sullivan et al. (2004), and Walhovd et al. (2005) reported a significant decrease in volume with age, whereas Resnick et al. (2003) and Jernigan et al. (2001) did not find such a relationship. Finally, Good et al. (2001) and Grieve et al. (2005) reported a “relative preservation” of the thalamus using voxel-based morphometry.

The MR images of the brains of young to middle-aged healthy adults (18–51 years) were analyzed in the present study. Age-related volume declines in circumscribed brain regions are detected, which are part of functionally defined systems, i.e., the sensorimotor system, encompassing the cerebellum, thalamus, somatosensory and motor cortices, and the prefrontal system, encompassing the anterior cingulate as well as the lateral and basomedial frontal cortices. Regions belonging to other functional systems, such as the auditory system or the visual system, did not show such age–volume relationships.

Materials and Methods

Subjects

MR images of 51 healthy male subjects with a mean age of 32.8 ± 8.6 years (range, 18–51) and an education period of 12.1 ± 3.8 years (range, 9–18) were analyzed. Volunteers were assessed for being healthy (no lifetime DSM IV diagnosis, no first-degree relatives with psychiatric diseases). The following exclusion criteria were applied: neurological or psychiatric diseases, disorders that affect cerebral metabolism, age <18. All subjects were right handed as assessed by the Edinburgh Inventory (Oldfield, 1971). After a complete description of the study, written informed consent was obtained from each subject in accordance with the guidelines of the ethical committee of the University of Düsseldorf.

MRI

The anatomical MR images were acquired in the Institute of Neurosciences and Biophysics–Medicine (INB-3) of the Research Center Jülich using a Siemens Magnetom Vision 1.5 tesla scanner (Siemens, Erlangen, Germany). A 3D magnetization-prepared rapid-acquisition gradient echo sequence with the following parameters was used: TR (repetition time) = 11.4 ms, TE (echo time) = 4.4 ms, flip angle = 15°, matrix = 256 × 256, field of view = 230 mm, and slice thickness = 1.25 mm, or field of view = 256 mm and slice thickness = 1 mm, respectively. The distribution of the subjects' age was nearly identical (33.0 ± 8.8 and 32.7 ± 8.5 years) within both groups of MR images, which were defined by the different MR parameters sets.

Image registration

An MR image is considered as a 3D set of grid points, with each grid point having an intensity value. The grid points are discrete; i.e., neighboring grid points have a nonzero distance from each other (according to the voxel size). A voxel is a volume element, which is assigned to each grid point.

All structural MR images (source images) were segmented by setting to zero the intensity value of all grid points containing skull, meninges, any other nonbrain tissue, or background. The automatic segmentation of SPM2 (Ashburner and Friston, 2000) was used for the presegmentation of the MR images, yielding masks of the tissue classes gray matter (GM) and white matter (WM) for each MR image. The latter were collapsed into one segmentation mask for the brain, because our method does not require a distinction between the tissue classes GM and WM. After this, the segmentation of each MR image was visually inspected and manually corrected: each MR image was visualized with the borders of the segmentation mask superimposed to it. Thus the location of the segmentation mask border was compared with the brain border. If necessary, the segmentation mask was edited manually. These corrections were performed by trained raters and supervised by one of the authors (P.P.), so that they were as consistent as possible. The reliability of this procedure was assured as described below (see Caveats and validation).

The MR images were registered to the T1-weighted, single-subject template of the Montreal Neurological Institute (MNI) (see Reference brain and anatomical atlas). The image registration consisted of an affine and a nonlinear step (Fig. 1A–H). The affine registration adjusted the position and alignment of each source image with the reference image. Additionally, the overall size and shape were adjusted by a global scaling and skewing. These transformations were summarized in a 12-parameter transformation matrix. The program FLIRT, which is part of the FSL package (http://www.fmrib.ox.ac.uk/fsl/index.html), was used for the calculation of the affine transformation. In calculating the registration, the spatial correlation between the intensity values of the transformed and the reference image was maximized (Jenkinson et al., 2002).

Figure 1.

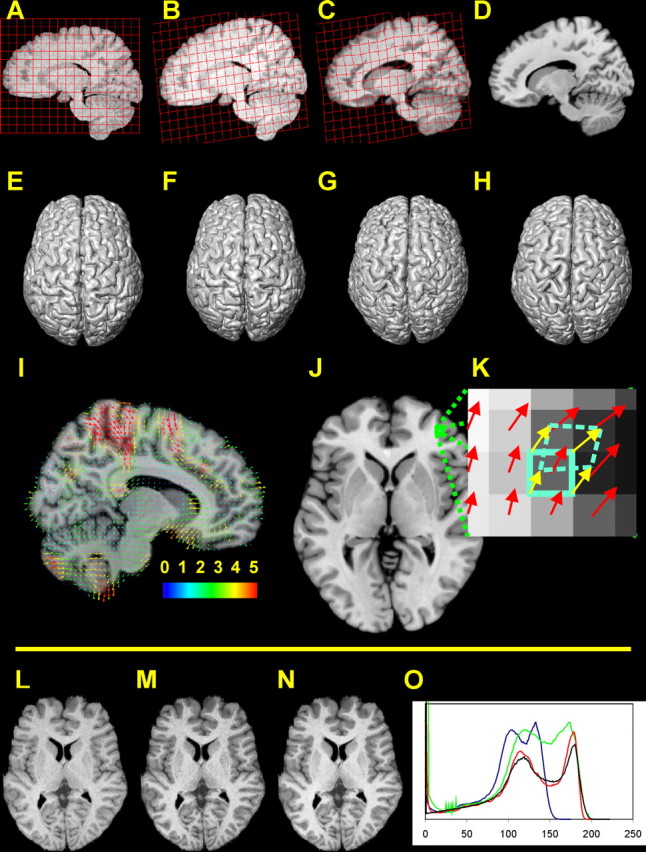
A–H, Registration of a brain image (sagittal sections and dorsal view of a 3D reconstruction); a regular grid is overlaid on the sagittal sections of the source MR image and is transformed in the same way as the brain image. A, E, Segmented brain image before registration. B, F, Result of the affine transformation. C, G, Result of the nonlinear registration. D, H, Reference image. I, Deformation field. Only a subset of the deformation vectors is presented (for the sake of visualization). The starting point of each vector is related to the reference image. The endpoint of each vector marks the corresponding point in the individual source image (after the affine transformation). The colors of the vectors indicate their length in millimeters. J, K, Calculation of local volume ratios on the voxel scale (in two dimensions). J, Horizontal section of the reference brain. K, Magnified part of the section in J. The starting point of a deformation vector (red arrows) is located in the center of each voxel of the reference image. Consider the voxel within the cyan frame (solid line): the deformation vectors of the corner points of this voxel (yellow arrows) are calculated by interpolating the original deformation vectors. The endpoints of the interpolated deformation vectors define the positions of the corner points within the source image (after the affine transformation). Thus the volume of the distorted voxel (dashed cyan line) within the space of the source image can be calculated. To calculate 3D volumes, this procedure is applied to the eight corner points of a cubical voxel. L–O, Matching of intensity values and edge-preserving filtering. L, MR image with original intensity values. M, MR image after having matched its histogram with the histogram of the reference image. N, Result of applying the edge-preserving SUSAN filter (Smith et al., 2001). O, Intensity histograms of the MR images in L–N and of the reference image. Blue, Original histogram (L); green, matched histogram (M); red, histogram of the filtered image (N); black, histogram of the reference image. A transformation of the voxel values regardless of the voxel positions leads from L to M. The gray and white matter peaks in the histograms of M and the reference image (green and black line) match quite well (O). However, the contrast is low. Therefore, the edge-preserving filtering is applied, creating an image with visibly enhanced contrast-to-noise ratio (N). It should be noted that the intensity values in the SUSAN-filtered and the reference image are more densely distributed than in the original and histogram-matched images, leading to generally lower frequencies in the histograms of the former two images. Thus the deepening of the valley between the GM and WM peak in the histogram of the SUSAN-filtered image is in part attributable to the stretching and redistribution of the intensity values in-between these peaks.

Because the following nonlinear registration is driven by intensity differences between the source image and the reference image, the cumulative histograms of the intensity values of both images were matched (Gonzales and Woods, 2002):

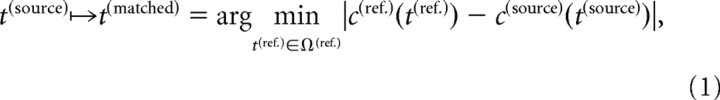where t^(source), t^(ref.) represents the intensity value of a grid point in the source and reference image; t^(matched) represents the matched intensity value; c^(source)(t^(source)), c^(ref.)(t^(ref.)) represents the cumulative frequencies of the intensities in the source and reference image; and Ω^(ref.) represents the set of all intensity values of the grid points in the reference image.

Noise in the source images was reduced by applying the filter program SUSAN (smallest univalue segment assimilating nucleus), which is part of FSL (Smith and Brady, 1997). This program applies an adaptive filter, which enables reduction of the noise in an MR image while preserving intensity value edges. The effect of the histogram matching and the SUSAN filtering on an MR image and its histogram are shown in Figure 1L–O: matching histograms transforms the intensity values independently of a given voxel's position or neighborhood. On the other hand, the SUSAN filter enhances clearly the contrast-to-noise ratio of the MR image (Fig. 1N).

The nonlinear registration achieved a highly accurate matching between brain MR images. It benefited from the complete anatomical information that the MR images contained, because neither was an “averaged” template applied as a reference image, nor were the MR images of the examined subjects smoothed before the registration. Software that was developed in our institute (Hömke, 2006) was applied for the nonlinear registration. It determines for each grid point of the reference image a “deformation vector” that points to a corresponding position in the source image. The computation is based on a mathematical optimization procedure, which aims to minimize the sum of the voxelwise squared differences of the intensity values between the reference and the deformed source image. High-resolution registrations as in the present study require that extremely many degrees of freedom are incorporated into the optimization procedure: these equal the coordinates of all deformation vectors; i.e., there are several millions. The deformation vectors are not independent from each other, but are coupled by a regularization term, thereby avoiding extreme local distortions. The coupling is implemented by means of modeling the image, which is to be registered, as an elastic body undergoing a nonlinear deformation. Furthermore, the deformations are calculated on several levels of resolution. The behavior of the registration algorithm can be characterized as follows: local mismatches between the reference image and the source image give rise to “forces,” which drive the deformations. By means of the regularization (and the multiresolution procedure), however, these deformations are also “propagated” into the neighborhood. Thus distinct structural elements of the reference and source image can be matched while keeping the transformation “smooth” (Fig. 1I). A further description of the mathematics underlying this algorithm is in Appendix A.

Deformation field morphometry

The computation of the nonlinear registration results in a deformation field (DF), i.e., a vector field, defining in each grid point x^(ref.) of the reference image a three-dimensional shift vector u(x^(ref.)), which points to the corresponding position x^{(aff. source)} in the source image (after the affine transformation). Applying to the shifted point x^{(aff. source)} the inverse affine transformation, which was calculated during the registration, yields the corresponding point x^{(nat. source)} in the original (native) source image. In general, the shifted points x^{(aff. source)} and x^{(nat. source)} are not located exactly on the grid points of the source image, but in between them.

where T represents the affine transformation of the native source image to the reference image.

Thus, a DF in combination with the affine transformation matrix encodes the structural differences between the MR image of one individual brain (source image) and the reference image (Fig. 1I).

The DFs were filtered by a binomial filter (size, 3 × 3 × 3 voxels) to reduce noise, which can be caused by potential local inaccuracies in the registration. This filtering is the only smoothing step in the whole image processing. Afterward, the DFs were resampled to a voxel size of 2 mm in each direction.

In the next step, local volume differences between the reference image and each source image were calculated as follows (Fig. 1J,K): the start points of the deformation vectors of a DF are located at the grid points of the reference image. Each voxel of the reference image is centered at the grid points. The volume element in the source image, which corresponds to a given voxel in the reference image, can be defined by adding to the eight corner points of the voxel in the reference image their deformation vectors. However, because the corner points of this voxel are located in between the grid points, the deformation vectors have to be interpolated. Thus, the shifted corner points of the voxel in the reference image define the corresponding, distorted voxel in the space of the source image (Fig. 1K). The “local volume ratio” (LVR) is defined as the ratio of the volume of this distorted voxel to the original voxel in the reference image:

where V_voxel^(ref.) represents the volume of a voxel in the reference image, V_{distorted voxel}^(source) represents the volume of a distorted voxel in the space of the source image, x^(ref.) represents a grid point in the reference image, and x_i^(source) represents the shifted corner point (in the source image) of the voxel that is centered at x^(ref.) in the reference image (i = 1, …, 8)

An LVR map of a given source image comprises the LVRs of all voxels. Because the LVRs are related to the grid points of the reference space, LVR maps of different source images can be compared voxel by voxel, thus enabling analysis of them by voxelwise statistics.

Previous DFM studies used the Jacobian determinant of the transformation in Equation 2 to calculate a volume measure similar to the LVR (Gaser et al., 1999; Thompson et al., 2000; Chung et al., 2001). The Jacobian determinant is defined in calculus for differentiable functions. However, because a DF is defined on a discrete grid, the Jacobian determinant is only an approximation for a volume measure. On the other hand, the calculation of the LVRs of a given source image is based on a unique relation between all points (not just the grid points) of the reference image and the source image space. Thus, under the assumption that a given deformation field is exact, the LVR defines a precise volumetric relation between two image spaces. This gain of precision is particularly important, if the nonlinear registration achieves a highly accurate matching between two images, because such a matching can require comparatively strong local distortions.

The LVR maps of the MR images of a study were analyzed by two different methods. (1) Voxelwise statistics: these statistics benefit from the power of the DFs to quantify the local structure of the source images. Statistical maps can be calculated, which are related to the reference image. (2) ROI-based statistics: summing the LVR values in one subject's LVR map over an ROI within the reference image yields the volume of the corresponding region in the source image:

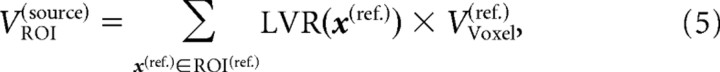where ROI^(ref.) represents the set of all grid points that belong to a given ROI in the reference space. In contrast to conventional ROI-based morphometry, here the ROI has to be defined only in the reference image, but not in each of the source images. An anatomical atlas, which is related to the reference image, can be used to define the ROIs.

Reference brain and anatomical atlas

The single-subject template of the MNI was used as reference image (Holmes et al., 1998; Evans et al., 1993; Collins et al., 1994; http://www.loni.ucla.edu/ICBM). It was created from 27 T1-weighted MR scans of the same subject aligned with each other and averaged, yielding an MR image with excellent signal-to-noise ratio. The template that was used in the present study had an isotropic voxel size of 1 mm. The reference image was segmented in the same way as the source MR images. All coordinates of the results will refer to the MNI single-subject template space.

Probabilistic maps of several cytoarchitectonic areas, subcortical nuclei, and fiber tracts have been registered to this template (http://www.fz-juelich.de/inb/inb-3/Brainmapping/eng). Among them are maps of the motor and premotor areas 4a, 4p, and 6 (Zilles et al., 1995; Geyer et al., 1994; Geyer, 2004); somatosensory areas 1, 3a, 3b (Geyer et al., 1999, 2000), and 2 (Grefkes et al., 2001); areas 44 and 45 of Broca's region (Amunts et al., 1999, 2004); the amygdala and hippocampus (Amunts et al., 2005); and the corticospinal tract (Rademacher et al., 2001; Buergel et al., 2006). Macroanatomical labels of the MNI single-subject template (http://www.loni.ucla.edu/ICBM) were also applied, because cytoarchitectonic maps are not yet available for the complete human brain. Furthermore, labels of the ventricles, as well as lobes and white matter compartments of the cerebellum, were added in this template. Supplemental Table 2 (available at www.jneurosci.org as supplemental material) contains a complete list of all anatomical ROIs that were examined, as well as references of their origin. Note that some of the macroanatomical ROIs and maps of cytoarchitectonically defined areas partially overlap.

Statistical analysis

For the voxelwise statistical analysis of age–volume relationships, a linear regression was calculated in each voxel of the LVR maps, taking the LVR as the observed variable and the subjects' age as predictor. The null hypothesis of no linear relationship was tested against the hypothesis of a linear volume decrease or increase by a two-sided Student's t test. The significance level was set at p < 0.01. SPM2 (http://www.fil.ion.ucl.ac.uk/spm/software/spm2) (Friston et al., 1995) was used for the estimation of the regression coefficients and the calculation of the t-value maps.

The ROI volume data were analyzed similarly: for each ROI, a linear regression was calculated with the ROI volume as observed variable, and again with the subjects' age as predictor. In this procedure, the significance level of the two-sided t test was set at p < 0.05 (see also Discussion, Methodical considerations). Calculations were performed with SAS 9.1 (SAS Institute, Cary, NC).

Thus, the regression model for the LVRs and the ROI volumes was as follows:

The expression V^(.) represents either an ROI volume or an LVR. From the analysis of this model, two quantities could be deduced for each voxel or ROI: (1) The estimated slope β gives the annualized age-related difference of V^(.). (2) The t value of the hypothesis test gives the “strength” of the linear relationship between V^(.) and the subjects' age.

For the ROI volume data, the following measures were additionally calculated for each region: (1) The probabilities that correspond to the actually observed t values. (2) The region volume for the age 20 years (V₂₀ = μ + β × 20, because the parameter μ in the regression model corresponds to the extrapolated region volume at age 0 years). (3) The relative annualized volume difference β_rel = β/V₂₀ × 100 (percentage). (4) The coefficient of correlation.

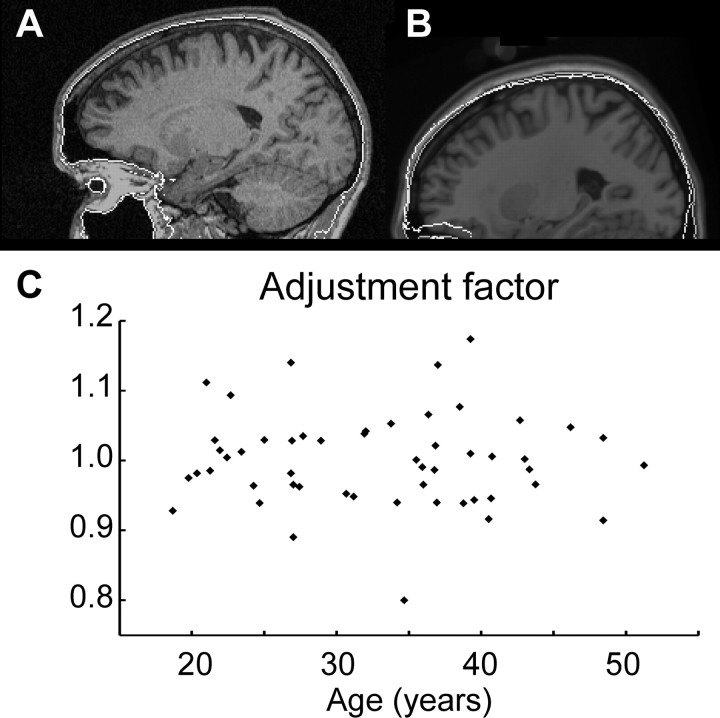
To control for the interindividual variability in premorbid size of the brain, i.e., before this is influenced by age or other factors, an adjustment factor was estimated, which is based on the global size of the exterior surface of the skull. The intracranial volume (ICV) would be preferable, but measuring the ICV is difficult without T2-weighted MR images. To measure the size of the skull, the skull surface was extracted from the MR images of all subjects, as well as the reference image, yielding binary skull surface images. These images were smoothed by applying a Gauss filter (width = 5 mm). Then the subjects' smoothed skull surface images were affinely registered with the reference's smoothed skull surface by applying the affine registration program FLIRT (Jenkinson et al., 2002). The previous smoothing of the skull surface images improved the robustness of the affine registration. A volume scaling factor was extracted from each affine transformation matrix and divided by the sample mean of all scaling factors, yielding for each subject the adjustment factor. Further details of this procedure are described in Appendix B. Similar techniques were described previously by Smith et al. (2001) and Buckner et al. (2004).

The following statistical analyses report the results for the adjusted data. Corresponding results for the nonadjusted data are available as supplemental material.

Because in the present study cross-sectional data are analyzed, the results of the regression analysis cannot predict expected changes for individual subjects. Consequently, terms like “volume increase” or “decline” refer to the relationship between volumes and ages of different subjects. Age-related volume changes observed in longitudinal studies often exceed those that are derived from a cross-sectional analysis (Raz et al., 2003).

Caveats and validation

Segmentation.

In our experience, the manual corrections of the whole-brain segmentations required particular care at the medial temporal lobes and the tentorium between cerebellum and occipital lobes. Therefore the reliability of the manual corrections and possible effects on the measurement of ROI volumes were examined in two steps.

(1) Each of eight brains (from a different but equivalent series) was segmented by two different raters for determining the interrater reliability. In addition, each of six brains was segmented two times by the same rater for determining the intrarater reliability. The time interval between segmentations of the same brain was always approximately several months. The agreement of two segmentation masks belonging to the same brain was defined as follows:

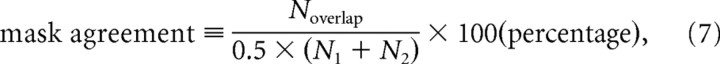where N_overlap represents the number of overlapping voxels of both segmentation masks, and N₁ and N₂ represent the number of voxels of the segmentation masks 1 and 2, respectively. The interrater agreement was always >97.5%, and the intrarater agreement was >98.2%.

(2) Possible effects of segmentation errors on the measurement of ROI volumes were examined by registering the eight brain MR images, for each of which two segmentation masks were created by different raters (see above), two times with a reference brain image, each time using one of the different segmentation masks. Next, volumes of anatomical ROIs were calculated based on the resulting deformation fields in the same way as in the present study of age-related volume differences. Intraclass correlations (ICCs) (Shrout and Fleiss, 1979) of volumes between the segmentations were calculated for each ROI separately. These calculations were based on the assumptions that raters were sampled randomly, and each rater had segmented all brains (i.e., ICC[2,1]) (Shrout and Fleiss, 1979), resulting in a two-way random effects model for each ROI:

where V_r,s is the volume estimate of a given ROI, as it results (by means of the deformation field analysis) from the segmentation of the brain of subject s by rater r; a_r and b_s are the effects of rater r and subject s, respectively, which are assumed to be normally distributed with a mean of zero; a × b_r,s is the interaction between rater r and subject s; ε_r,s means normally distributed random error. The formula for the ICC[2,1] can be found in Shrout and Fleiss (1979).

Only the following ROIs had an ICC ≤0.95: right flocculonodular lobe (0.66), left corpus mamillare (0.83), left and right lateral dorsal nucleus (0.89 and 0.95), and left amygdala (0.91). Seventy-nine percent of all examined ROIs had an ICC >0.98. These findings suggest that registration errors had only a minor influence on most of the volume measurements.

Image registration.

The registration of MR images of the human brain has to cope with two difficulties: (1) The registration of an image usually is computed by means of a mathematical optimization procedure, minimizing the “distance” between the registered and the reference image. Such an optimization, however, can be trapped in “local,” nonoptimal minima. In such cases, visible differences may remain between the registered and the reference image. Sophisticated techniques were developed for limiting such effects, but a perfect solution does not exist. (2) At the lowest scale (i.e., voxel-resolution of the images), it may be impossible to define a precise correspondence between the source and reference image, because of the macroanatomical and microanatomical variability of human brains (e.g., the presence of various sulci varies between brains). This difficulty concerns mainly the registration of structurally highly variable brain regions, like the prefrontal and parietal cortex. Such ambiguities are clearly not dependent on the registration algorithm that is used. Rather, they are caused by the limited resolution of whole-brain MR images.

A further possible source of error of intensity-driven registration methods are local intensity shifts in MR images. For example, when a region that contains spots with changed intensity is matched with a homogenous region in the reference image, these spots could be compressed, thus leading to an artificial deformation or local volume difference between the source and the reference image. Such artifacts are particularly relevant when they have a consistent relationship with the interesting effect. Spots of white matter hyperintensity in T2 MR images were described in the brains of patients of Alzheimer's disease but also healthy elderly subjects (Lee et al., 2003). Such hyperintensities were compared with changes of the vascular structure (Moody et al., 2004; Matsusue et al., 2006). Local T2 hypointensities occurring in neurodegenerative diseases like multiple sclerosis or Parkinson's disease are explained by the deposition of iron (Tjoa et al., 2005). Analyses of MR images gave indications for a relationship between age and iron content in certain parts of the brains of healthy subjects, including in particular the basal ganglia, nucleus (Ncl.) ruber, substantia nigra, and Ncl. dentatus (Milton et al., 1991; Martin et al., 1998). Thus it cannot be ruled out that similar local intensity shifts occurred in the T1-weighted MR images that were analyzed in the present study, leading potentially to artificial deformations. If there were in certain parts of the brain a consistent relation between age and such artifacts, then a similar relationship between age and the quality of the nonlinear registration had to be expected, because the mismatches caused by the intensity shifts should remain even after the nonlinear registration. Therefore, maps of voxelwise residual differences between the nonlinearly registered MR images and the reference image were calculated, and a linear relationship of these maps with the subjects' age was tested. Furthermore, influences of the choice of the reference image on the results of the analysis were qualitatively examined.

A further potential source of artificial findings is a possible influence of the subjects' age on the quality of the affine registration. Because of the widening of the sulci and ventricles, the affinely registered images of older subjects' brains might be systematically larger or smaller than those of younger subjects. Therefore, possible relations between age and the quality of the affine registration were examined.

The details of these examinations are described in Appendix C. Here we anticipate the result that no indications were found for relevant relationships between the subjects' age and the quality of the registrations, arguing against the assumption that the age-related volume differences that were found in the present study could be caused by systematically age-related registration errors.

Nevertheless, errors in measurement of the local volume ratio can occur for several reasons, as described above, compromising the analysis of age-related volume differences even if they might not have a systematic relation with age: (1) The sensitivity of voxelwise statistical tests for the detection of “real” age-related volume differences can be diminished. (2) The subjects' local volume ratios in a given voxel can simulate an artificial relationship with the subjects' age by chance only, leading to “false-positive” voxels. In neuroimaging, such problems occur often when statistical maps covering the whole brain are evaluated. Statistical maps may contain even extended clusters consisting of false-positive voxels (i.e., voxels that have t values above the threshold given by the significance level of the applied t test). However, it is difficult to discern reliably between true-positive and false-positive clusters: age-related changes that affect only small, anatomically defined structures as, e.g., certain subcortical nuclei might also lead only to small clusters in the statistical maps. Thus the size of the clusters may not serve as a suitable criterion. The volume measure of a spatially extended ROI might be less sensitive against measurement errors, because the ROI volume will be impaired only by misregistrations of voxels near the surface of the ROI, whereas registration errors inside the ROI cancel out each other.

Results

Voxelwise statistics

The voxelwise analysis indicated large clusters of voxels with significant decrease of the LVR in the cerebellum, covering primarily the WM and the deep cerebellar nuclei (DCNs) (Figs. 2, 3). These clusters preponderate in the left compared with the right hemisphere. The vermis showed comparatively little age-related decline.

Figure 2.

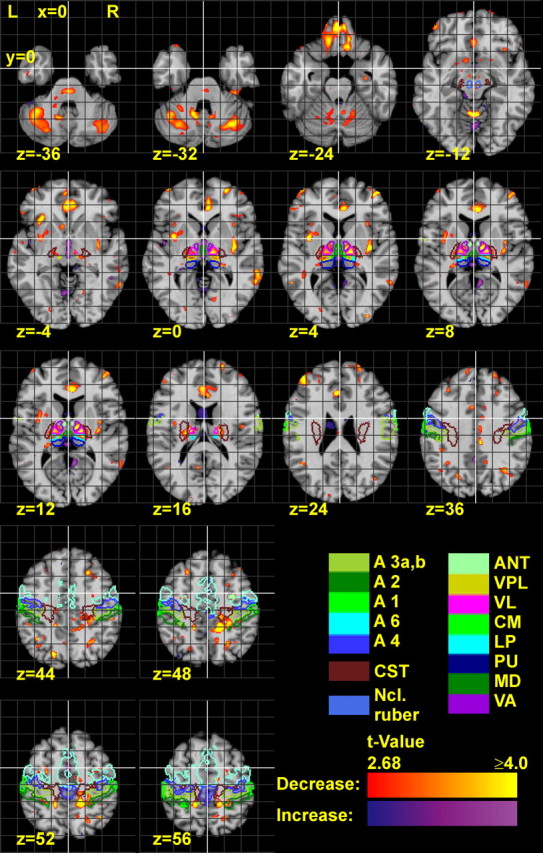
Horizontal sections of the reference brain with statistical maps, showing the t values of age-related volume decline and increase. t values were calculated by a two-sided t test for a linear regression in the voxels of the LVR maps, depending on age. The statistical map is thresholded according to a significance level of p < 0.01. The contours of several anatomical regions are also delineated. A1–A6, Areas of the somatosensory and motor/premotor cortex; CST, corticospinal tract.

Figure 3.

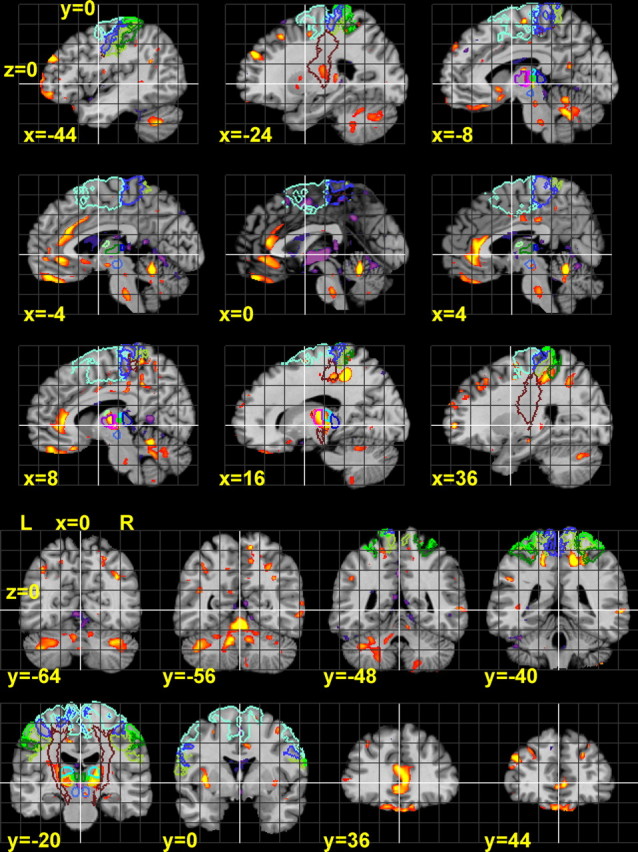
Sagittal and coronal sections of statistical maps, showing the t values of age-related volume decrease and increase. These were calculated by a two-sided t test for a linear regression in the voxels of the LVR maps, depending on age. The statistical map is thresholded according to a significance level of p < 0.01. The contours of several anatomical regions are also delineated (for legend, see Fig. 2).

The thalamus also revealed a strong decline of the LVR, predominantly in the ventral and lateral nuclei (right slightly more pronounced than left) (Fig. 2, z = 0–12). These clusters of volume decline extended into the posterior portion of the internal capsule. Large clusters of volume decline were located in the anterior cingulate cortex (ACC) and the olfactory sulcus, i.e., in the banks of the gyrus rectus and gyrus frontoorbitalis medius. The latter did not show pronounced interhemispheric differences. Clusters of volume decline were also present in the left gyrus frontalis medius and superior (Fig. 2). Further clusters of volume decline were spread over the frontal, prefrontal, motor, premotor, and sensory cortices and the insula. With respect to the size of the clusters, the volume decline in the somatosensory and motor cortices and underlying WM of the right hemisphere appeared to exceed that of the left hemisphere. The occipital and temporal lobes showed almost no volume decline. The right hippocampus showed only little age-related volume differences. A small cluster of volume decline was found in the right Ncl. ruber (Fig. 3, y = −20) (supplemental Table 1, available at www.jneurosci.org as supplemental material).

The ventricles showed a volume increase, which was strongest in the third ventricle (Fig. 3). In addition, volume increases were found in the cisterns between the forebrain and the cerebellum, and in a few small clusters in the prefrontal WM.

ROI-based statistics

The estimated annualized volume declines of the left and right hemispheres of the brain were 1086 and 1134 mm³, respectively, and those of the cerebral white matter were 254 mm³ and 252 mm³, respectively. The declines of both structures were not significant (Figs. 4, 5, Table 1) (Note that this table reports the results of the whole brain and only of those ROIs that showed a significant age–volume relationship at least in one hemisphere. The complete table is available as supplemental Table 2, available at www.jneurosci.org as supplemental material). The annualized volume decline of the cerebellum was 255 mm³ (left) and 203 mm³ (right), but only the decline in the left cerebellum was significant. The cerebellar white matter had a significant volume decline in both hemispheres, which was more pronounced in the left than in the right hemisphere.

Figure 4.

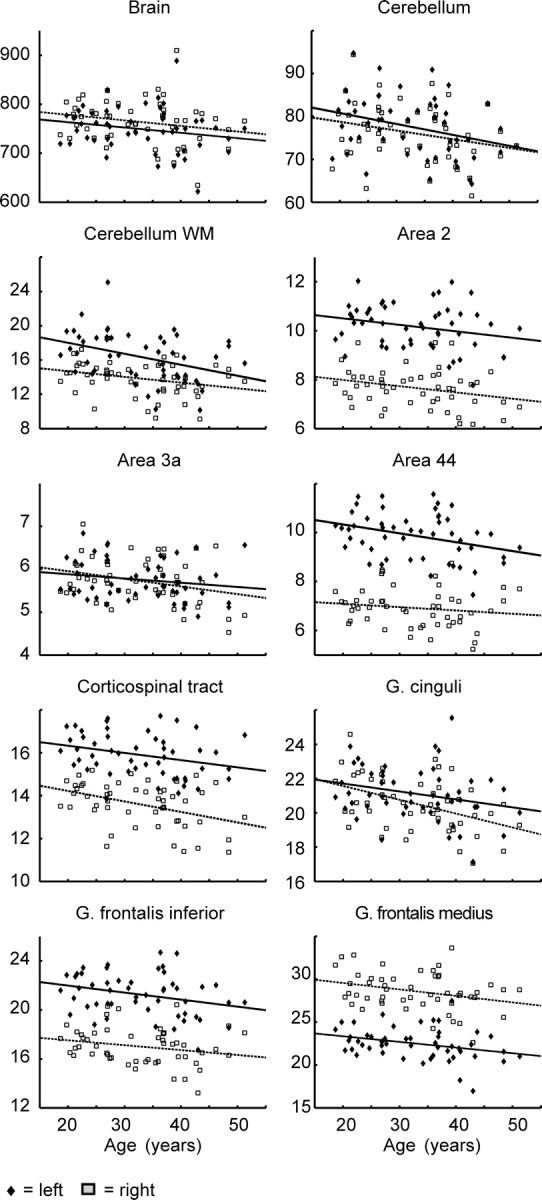
Scatterplots showing individual ROI volume data (in cm³), as well as regression lines (separately for each hemisphere) against age. Diamonds/rectangles, ROI volume in left/right hemisphere; solid/dashed lines, regression lines of left/right hemisphere.

Figure 5.

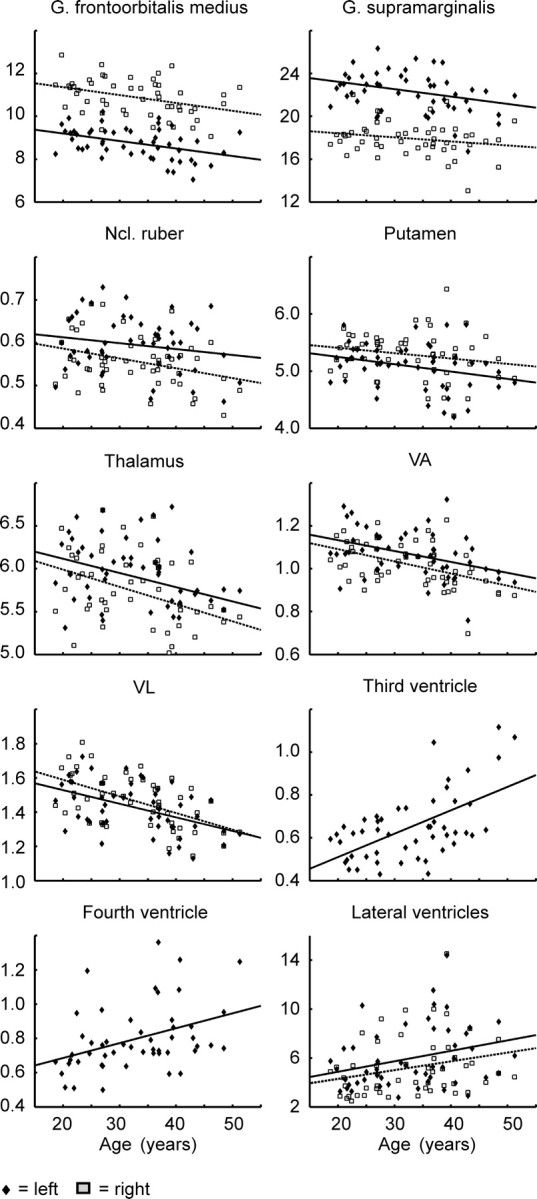
Scatterplots showing individual ROI volume data (in cm³), as well as regression lines (separately for each hemisphere) against age. Diamonds/rectangles, ROI volume in left/right hemisphere; solid/dashed lines, regression lines of left/right hemisphere.

Table 1.

Results of the linear regression of anatomical ROI volumes (adjusted by skull size), depending on age

Region	Side	Volume offset (20 years) (mm3)	Volume slope (mm3/year)	Relative volume slope (%/year)	t value	p	r
Total brain	Botd	1520071.5	−2251.5311	−0.1481	−1.553	0.1269	0.217
	Left	763316.5	−1086.0298	−0.1423	−1.494	0.1415	0.209
	Right	778468.2	−1133.9542	−0.1457	−1.518	0.1354	0.212
Area 2e	Left	10501.7	−26.3437	−0.2509	−1.776	0.0819	0.246
	Right	7987.4	−25.5443	−0.3198	−2.026	0.0483	0.278
Area 3ac	Left	5886.3	−9.9074	−0.1683	−1.289	0.2034	0.181
	Right	5956.5	−17.936	−0.3011	−2.14	0.0374	0.292
Area 44a	Left	10332.6	−36.2104	−0.3504	−2.444	0.0182	0.33
	Right	7094.0	−13.6849	−0.1929	−1.055	0.2965	0.149
Cerebellumf	Left	80800.1	−255.2249	−0.3159	−2.281	0.0269	0.31
	Right	78758.2	−203.4446	−0.2583	−1.878	0.0664	0.259
Corticospinal tractd	Left	16332.6	−33.5228	−0.2053	−2.095	0.0413	0.287
	Right	14225.1	−49.0162	−0.3446	−3.143	0.0028	0.41
Cerebellum WM	Left	18012.4	−128.2004	−0.7117	−2.918	0.0053	0.385
	Right	14700.6	−66.7117	−0.4538	−2.092	0.0417	0.286
Cerebrum WMf	Left	176436.5	−253.4979	−0.1437	−1.417	0.1629	0.198
	Right	178777.7	−252.274	−0.1411	−1.111	0.2721	0.157
Fascia dentatab	Left	3763.1	−2.7513	−0.7310	−0.559	0.5786	0.08
	Right	4150.6	−7.8443	−0.1890	−2.081	0.0427	0.285
G. cingulif	Left	21704.1	−46.1828	−0.2128	−1.825	0.074	0.252
	Right	21569.2	−80.7096	−0.3742	−3.477	0.0011	0.445
G. frontalis inf.f	Left	21983.1	−57.2715	−0.2605	−2.095	0.0414	0.287
	Right	17518.8	−39.9141	−0.2278	−1.655	0.1044	0.23
G. frontalis med.f	Left	23349.7	−66.1401	−0.2833	−2.271	0.0276	0.309
	Right	29572.4	−75.2546	−0.2545	−2.147	0.0368	0.293
G. frontoorbitalis lat.f	Left	7599.4	−26.317	−0.3463	−2.399	0.0203	0.324
	Right	8841.2	−24.0131	−0.2716	−1.914	0.0615	0.264
G. frontoorbitalis med.f	Left	9202.0	−35.3023	−0.3836	−3.29	0.0019	0.425
	Right	11359.8	−36.6049	−0.3222	−2.769	0.0079	0.368
G. rectusf	Left	5620.9	−20.3736	−0.3625	−2.065	0.0442	0.283
	Right	5686.9	−22.0824	−0.3883	−2.866	0.0061	0.379
G. supramarginalisf	Left	23239.9	−69.0177	−0.2970	−2.11	0.0400	0.289
	Right	18431.3	−38.0395	−0.2064	−1.494	0.1417	0.209
LPf	Left	629.5	−1.5142	−0.2405	−1.456	0.1517	0.204
	Right	720.4	−2.6443	−0.3671	−2.512	0.0153	0.338
Ncl. ruberf	Left	612.5	−1.3807	−0.2254	−1.32	0.1929	0.185
	Right	585.9	−2.3012	−0.3927	−2.468	0.0171	0.333
Putamenf	Left	5249.6	−12.8529	−0.2448	−2.088	0.0420	0.286
	Right	5409.5	−9.3655	−0.1731	−1.394	0.1696	0.195
Subcallosal areaf	Left	939.1	−4.5841	−0.4881	−2.929	0.0052	0.386
	Right	913.2	−2.7391	−0.3000	−1.656	0.1041	0.23
Thalamusf	Left	6118.3	−16.6095	−0.2715	−2.372	0.0217	0.321
	Right	5991.4	−20.152	−0.3363	−2.904	0.0055	0.383
VAf	Left	1134.1	−5.0852	−0.4484	−2.999	0.0042	0.394
	Right	1092.0	−5.698	−0.5218	−3.736	0.0005	0.471
Ventricle 3f	mid	510.2	10.9448	2.1450	5.041	0.0000	0.584
Ventricle 4f	mid	685.3	8.718	1.2722	2.969	0.0046	0.39
Ventricle lat.	Left	4874.1	85.5122	1.7544	2.146	0.0368	0.293
	Right	4291.5	71.724	1.6713	1.839	0.0719	0.254
Ventricle total	Left	8113.7	112.341	1.3846	2.339	0.0234	0.317
	Right	8057.2	110.5764	1.3724	2.19	0.0333	0.299
VLf	Left	1529.1	−7.9648	−0.5209	−3.777	0.0004	0.475
	Right	1589.0	−9.7043	−0.6107	−4.608	0.0000	0.55
VPLf	Left	710.9	−3.0441	−0.4282	−2.834	0.0067	0.375
	Right	440.4	−2.2247	−0.5052	−3.553	0.0009	0.453

Volume offset, ROI volume at age 20 years in cubic millimeters; volume slope, volume change in cubic millimeters per year; relative volume slope, volume slope/volume offset × 100 (percentage); p, p value, corresponding to the measured t value; r, correlation coefficient. The table contains the data of those ROIs where the regression was significant at least in one hemisphere (as well as the data for the complete brain and cerebral white matter). The complete table of all examined ROIs is available as supplemental Table 2 (available at www.jneurosci.org as supplemental material). Abbreviations are explained in Appendix D. Note that macroanatomical and cytoarchitectonic areas in part overlap with each other. Cytoarchitectonically defined areas and fiber tracks are discussed by the following: ^aAmunts et al. (1999); ^bAmunts et al. (2005); ^cGeyer et al. (1999); ^dRademacher et al. (2001); ^eGrefkes et al. (2001); ^fMacronanatomical labeling of the MNI single-subject template can be found at http://www.loni.ucla.edu/ICBM.

The ROI-based statistics indicated a significant bilateral volume decrease in the thalamus, orbitofrontal cortex, gyrus frontalis medius, and left gyrus frontalis inferior (Table 1). The latter overlaps with the cytoarchitectonically defined areas 44 and 45 (Amunts et al., 1999). The relative annualized volume decline of the nuclei ventral anterior nucleus (VA), ventral lateral complex (VL), ventral posterolateral nucleus (VPL), and lateral posterior nucleus (LP) of the thalamus was larger on the right than on the left side.

The volumes of the gyrus frontalis superior, gyrus precentralis, gyrus postcentralis, and lobulus parietalis superior and inferior did not show a significant volume decline. The third and fourth ventricle showed a strong volume increase. The t values of the latter exceeded clearly the t values for the increase of the lateral ventricles.

Interhemispheric differences in the annualized volume differences were not statistically significant for any of the examined ROIs.

Discussion

Methodical considerations

LVR maps were analyzed by two different approaches, a voxelwise and an ROI-based method. Both analysis techniques provided complementary results. However, the results are not independent, because both analyses are based on the same data. Each method has certain advantages and disadvantages: voxelwise analyses of local volume changes have the potential to detect and localize the effects under study comprehensively (i.e., capturing the complete brain) as well as with high sensitivity. These methods work independently of an anatomical parcellation of the brain. On the other hand, they are sensitive against registration inaccuracies (as described above). These might lead to enhanced “noise,” possibly obscuring true differences, but also to clusters of false-positive voxels by chance.

ROI-based analyses are expected to be more robust for reasons given above (see also Raz et al., 2004). Furthermore, ROI volumes facilitate the analysis of hypotheses that focus on, e.g., the correlations between the volumes of different regions. Thus, more complex designs can be analyzed than is feasible with standard voxelwise analysis techniques. On the other hand, ROI-based analyses might be less sensitive if a given ROI covers a much larger volume than is affected by the effect under study. Macroanatomical ROI definitions, in particular, may be too coarse in certain brain regions, because postmortem studies had demonstrated that aging can affect specifically microanatomical areas, neurons of a certain size or type, or certain cortical layers (Haug et al., 1984; Terry et al., 1987; West, 1993; Uylings and de Brabander, 2002). Hence probabilistic maps of cytoarchitectonic areas and fiber tracts are more appropriate for the definition of ROIs, because they reflect the microanatomical and functional organization of the brain (Zilles, 2004; Zilles et al., 2002).

Relationships between age and structure

The significance of the observed age-related differences is limited to young to middle-aged male adults (age <52 years). In old age, however, additional changes of brain structure might occur, and the strength of regional volume changes might be shifted compared with the age-related differences, which we observed. Furthermore, the decline of the whole brain volume as well as of certain regions was found to be accelerated in subjects beyond 50 years of age (Jernigan et al., 2001; Liu et al., 2003). A possible confound could result from cerebrovascular diseases, which were shown to be common in subjects after 50 years of age, and which could be associated with changed brain morphology (DeCarli et al., 2005; Raz et al., 2007). Because the subjects of the present study were not examined for cerebrovascular diseases, such influences cannot be ruled out.

The estimate of the age-related decline of the whole brain volume (−0.14%/year) is comparable with the findings of previous studies (Kruggel, 2006; Fotenos et al., 2005, and references therein). However, it is somewhat lower and it is not significant, in contrast to the latter studies, presumably because of the limited age range in the present study (see above). However, the prominent findings of the present study were significant age–volume relationships in two functional systems, which are known to be affected in older subjects, but which had not been identified before by imaging techniques in subjects between 18 and 51 years of age.

Sensorimotor system

Significant volume declines were found in the DCNs, Ncl. ruber, and several nuclei of the thalamus. Furthermore, several clusters of volume decline were demonstrated in the GM of the motor, premotor, and somatosensory cortices and in the underlying WM. These structures are components of the motor system, interconnected by the cortico-rubro-cerebello-thalamo-cortical (CRCTC) circuit (Jones, 1985; Percheron, 2004; Voogd, 2004).

The DCNs are localized in the WM of the medial part of the cerebellum, where a significant volume decline was found in the present observations (Figs. 2, 3). In the thalamus, the volume decline mainly involved its ventral part, with the VA, VL, and VPL nuclei. The posterior part of VL relays input from (among other sources) the DCNs to the motor cortex. VPL acts as a relay station of sensory input to the somatosensory cortex (Jones, 1985). To a minor degree, differences were also found in the LP. Interestingly, the lateralization of the volume decline in the cerebellum (left > right), Ncl. ruber (right > left), VL, VP (slightly right > left), and WM underlying somatosensory and motor cortices (right > left) appears to reflect the course of the CRCTC pathway, which crosses the midline between the cerebellum and Ncl. ruber. The volume decrease, which was detected in the posterior portion of the internal capsule, suggests that also the corticospinal tract and the superior and posterior thalamic peduncles are spots of age-related volume decline.

The cerebellum is assumed to be functionally involved in movement control (Horne and Butler, 1995) but also in higher cognitive functions (Schmahmann and Sherman, 1998). fMRI experiments revealed age-related differences during the processing of motor tasks in the anterior and posterior lobes of the cerebellum, premotor, parietal, left prefrontal, and anterior cingulate cortices, supplementary motor area, Ncl. caudatus, and thalamus (Hutchinson et al., 2002; Mattay et al., 2002; Heuninckx et al., 2005; Wu and Hallett, 2005). The age of the subjects in the latter studies ranged between 20 and 80 years. Such age-related differences in the functional activations coincide well with the locations of structural differences found in the present study.

The present study's estimates of the age-related volume decline of the left and right cerebellar hemispheres (−0.32 and −0.26%/year, respectively) agree well with the findings of previous morphometry studies: Andersen et al. (2003) examined the cerebellum of 19 postmortem brains (age, 19–84 years). They measured a volume reduction of 25.9% for the WM, whereas the GM volume was not significantly reduced. In vivo morphometry studies found a cross-sectional decline of 0.249 and 0.264%/year (left and right hemisphere) (Kruggel, 2006). Raz et al. (2003, 2005) measured a cross-sectional decline of 0.22%/year and a longitudinal decline of 0.61%/year. Associations between age, volumes of cerebellar hemispheres, and motor performance were demonstrated by Raz et al. (2000).

Recent in vivo morphometry studies (Van Der Werf et al., 2001; Sullivan et al., 2004; Walhovd et al., 2005) reported an age-related decline for the whole thalamus, which is also similar to the present study.

Prefrontal cortex and limbic system

The prefrontal cortex (PFC) has a central role in the perception–action cycle (Fuster, 2001). In this concept, the lateral PFC incorporates the temporal organization of goal-directed actions, behavior, speech and reasoning, as well as the integration of various forms of information. Subordinate functions are working memory, the preparation of actions contingent on the sensory input, inhibition, and attention selection. The latter two are assumed to be localized in the medial region of the PFC and rostral ACC (Fuster, 2001, 2002), i.e., the cytoarchitectonic areas 24 and 32 (Vogt et al., 2004). The ACC is also described as being involved in the regulation of the autonomic nervous system, processing of emotions, behavioral control, and several other functions (Paus et al., 1993; Whalen et al., 1998; Paus, 2001; Vogt et al., 1995, 2004). Hof et al. (1995) described the orbitofrontal cortex (OFC) as being involved in the integration of memory, motivation, emotion, and sensory processes.

The recruitment of a network encompassing the ventrolateral and dorsolateral PFC and ACC in response to different cognitive demands has been demonstrated by numerous imaging studies (for review, see Duncan and Owen, 2000). The results of the present analysis suggest a pattern of age-related volume decline that is strikingly similar to the aforementioned network, because it consists of the rostral ACC (bilateral), the cytoarchitectonic area 44 (left), the gyrus frontalis inferior (left), gyrus frontalis medius (left and right; presumably area 46), and the banks of the olfactory sulcus (bilateral; in the OFC, anterior to the piriform cortex). The left-dominant volume decrease in area 44 resembles the underrecruitment of this region by older compared with younger subjects during verbal encoding tasks, as detected by fMRI (Logan et al., 2002). It could also indicate causes for the age-related changes in the lateralization of the processing of verbal and spatial memory tasks found in positron emission tomography studies (Reuter-Lorenz et al., 2000).

The comparatively strong volume decline of the PFC and OFC, which was found in the present study, agrees well with the findings of previous in vivo MR morphometry studies (Raz et al., 1997, 2004; Sowell et al., 2003). Previous measurements of the hippocampus volume yielded partially conflicting results: Sullivan et al. (1995) found no volume decline; Pruessner et al. (2001) found a volume decline in male subjects; Jernigan et al. (2001) reported a rapidly increased volume decline after age 50 years. This could explain why the hippocampal volumes of our relatively young subjects did not reveal a significant decline.

Conclusions

The present observations based on cross-sectional data suggest that age-related volume decline occurs in circumscribed brain regions. The regional distribution pattern of our anatomical findings matches the regional representation of defined complex neural systems as demonstrated in previous fMRI studies. This highlights the potential functional relevance of the localized volume differences.

Appendix A: Mathematical description of the image registration algorithm

Given are a source image T and a reference image R. It is assumed that a transformation Φ exists that spatially relates T and R with each other (x is a coordinate triplet of a point in the reference image):

The transformation Φ can be represented by a three-dimensional vector field u (deformation field), which assigns a shift vector (deformation vector) u(x) to each grid point x of the reference image:

That is, each deformation vector u(x) contains the coordinate difference between a grid point in the space of the reference image R and the corresponding point in the space of the source image T. The goal of the nonlinear registration is to compute the unknown deformation field u. To this end, the squared difference D between the intensity values of T and R has to be minimized:

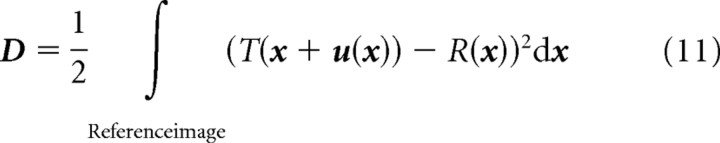Linearization of this expression, which is interpreted as a nonlinear energy functional, defines an iteration (outer iteration):

where v is the solution to a linear subproblem. Because such subproblems are generally ill posed, a regularization term borrowed from the theory of linear elasticity is added. It measures the elastic energy necessary to perform an equivalent deformation with a mechanical body, thus punishing nonsmooth transformations.

A necessary condition for a minimum of the resulting energy functional is derived using the calculus of variation, leading to a boundary value problem composed of the Euler–Lagrange equations from the variational calculus and the boundary conditions. The regularization term yields the elliptic differential Navier-Lamé operator L, where

with the Navier-Lame constants μ and λ. Discretization on a grid given by the image points yields a system of partial differential equations. Because of the size of the system, a direct solution of this system is not feasible. Although the system is large, it is sparse. Hence, fast iterative solvers can be used to compute approximate solutions to the necessary precision. Here a multigrid solver is used. Multigrid solvers are extremely efficient because they compute solutions in asymptotic linear time. Because of the iterative nature of the solvers, this part is also called inner iteration.

Additionally, the outer iteration is embedded into a multiresolution approach. Solutions are first computed on coarser image scales and serve as start approximations for finer resolutions. This multiresolution technique facilitates the computation of large deformations and aids robustness (Hömke, 2006; Henn and Witsch, 2001).

Appendix B: Adjustment of volume data

Local volume data were adjusted using the size of the skull as a reference. The extraction of the exterior skull surface and the calculation of the adjustment factor consisted of the following steps: (1) A mask of the image background (outside the head) was generated. (2) Beginning at the border of the background mask, the nearest voxels inside the head (i.e., nonbackground) were searched that had an intensity value below a certain threshold (which was extracted from the image histogram). These voxels defined the binary skull surface mask. All masks were checked by superimposing them with the original MR image. (3) The binary skull surface masks were smoothed by a Gauss filter (width, 5 mm) to facilitate the following affine registration. (4) The subjects' smoothed skull surface masks were affinely registered with the reference's smoothed skull surface mask. Only the skull surface mask above the orbits was taken into account, because below the orbits the consistent definition of the skull was not sufficiently robust. The volume scaling factor was extracted from the transformation matrix. Dividing each volume scaling factor by the sample mean value of all scaling factors yielded the volume adjustment factors. ROI volumes and local volume ratios of a given subject are adjusted by multiplying them with the subject's volume adjustment factor:

Figure 6 shows an example of a skull mask and its registration with the reference skull mask. No significant linear relationship between the adjustment factors and the subjects' age was found (p = 0.814). The statistical analysis of relationships between age and local volumes was calculated for the adjusted as well as the nonadjusted volume data. However, the analysis of the adjusted data yielded stronger effects in almost all regions of the brain.

Figure 6.

A volume adjustment factor is determined based on the exterior surface of the skull. This surface is automatically extracted from the T1-weighted MR image of each subject. A given subject's skull surface image is affinely matched with the skull surface image of the reference. The volume scaling that is defined by the affine transformation yields the adjustment factor. A, Example of a skull surface superimposed to an original MR image. The skull surface around the forebrain is found quite robustly. However, below the orbits and tentorium of the cerebellum, it becomes more difficult to define the skull reliably. For this reason, only the skull above the orbits is used for calculation of the adjustment factor. B, Image of a reference brain, onto which the extracted surface of its skull is superimposed (gray contour), and the affinely matched skull image of a subject (white contour). C, The scatterplot of all subjects' volume adjustment factors against their age shows no significant linear relationship (a linear regression yielded p = 0.814).

Appendix C: Validation experiments

Test 1: relation between age and affine registrations

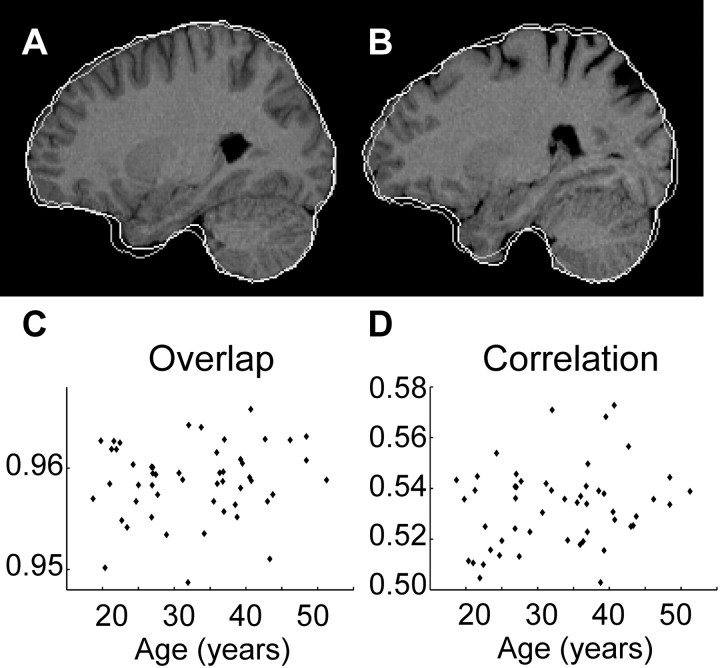
Because in general a given brain's sulci and ventricles become wider during aging (Kemper, 1994), the question arises whether this could influence the quality of the affine registration and the results of the nonlinear registration (see also Buckner et al., 2004). Therefore, the following measures were tested for a linear relation with age by computing a linear regression (predictor = age). (1) The spatial correlation between the reference image and each affinely transformed source image, because the correlation function between both images was to be maximized by the affine registration. (2) The relative overlap of the closed (see below) mask of the brains in the reference image and the affinely transformed source image.

The closed mask of a given brain was calculated by applying a morphological closing operation on that brain's segmentation mask. A sphere having a diameter of 11 mm was used as the structuring element of this operation (e.g., Gonzales and Woods, 2002). Thus in a brain's closed mask, the sulci and ventricles were “filled” without expanding the brain's “outer hull,” as demonstrated in Figure 7, A and B (white contour). The segmentation mask of the reference image underwent the same morphological closing operation. The overlap of a subject's closed brain mask with the closed reference mask corresponds to the matching of the global dimensions of the source image with the reference image. Therefore, a significant correlation between age and the overlap of the closed masks could indicate a systematic incorrect global enlargement or reduction of the affinely transformed images relative to the reference image.

Figure 7.

The quality of the affine registrations was tested for a linear relation with age. Therefore, a “closed” mask of each brain, which covers the brain but also “fills” the sulci and ventricles, was generated for each brain. A, B, MR images of a 20- and a 48-year-old subject. Both images are affinely registered with a reference image. The contour of their own “closed” mask (white) and the contour of the reference's closed mask (gray) are superimposed to the MR images. The relative overlap of each subject's closed mask with the reference's closed mask is calculated, as well as the spatial correlation of each affinely matched MR image with the reference MR image. C, D, Scatter plots of relative overlap and correlation of each subject's affinely matched image with the reference image, against age. Neither of these measures indicates a significant linear relationship (linear regressions yielded p = 0.113 and p = 0.408).

The linear regression showed that neither the spatial correlation between each affinely transformed source image and the reference image nor the overlappings of the affinely transformed closed brain masks had a significant linear relation with age (p = 0.113 and p = 0.408) (Fig. 7C,D). Thus these tests did not indicate an influence of age on the quality of the affine registration. In particular, they did not indicate any age-related incorrect enlargement or reduction by the affine transformation.

In contrast to the previous results, the overlaps of the original brain masks with the reference brain mask did indeed reveal a significant relation with age. However, the sizes of the affinely matched original brain masks also declined significantly with the subjects' age, in contrast to the size of the closed affinely matched brain masks. This decline of the mask size presumably reflects the widening of the sulci and ventricles. Considering also the negative result of the test for a relationship between age and the overlaps of the closed brain masks, we conclude that the relationship between age and the overlap of the original masks does not necessarily imply an impairment of the affine registration.

Test 2: relation between age and residual differences after the nonlinear registration

For each nonlinear registration, 3D images of the voxelwise (signed and absolute) differences between the nonlinearly transformed MR image and the reference image were calculated, yielding for each subject an image of the voxelwise residual differences. Next, these residual difference images were analyzed by voxelwise regression against age, yielding statistical maps of the relation between age and the voxelwise registration quality. Statistical maps showing the F value of these voxelwise linear regressions are presented in Figure 8A: voxels having an F value >7.18 (corresponding to p < 0.01) form only very small clusters, compared with the statistical maps of the volume differences (Figs. 2, 3). The statistical maps of the residual absolute differences have the same appearance. Thus these findings suggest that the relation between age and the quality of the nonlinear registration is, if any, much weaker than the relation between age and the observed volume differences.

Figure 8.

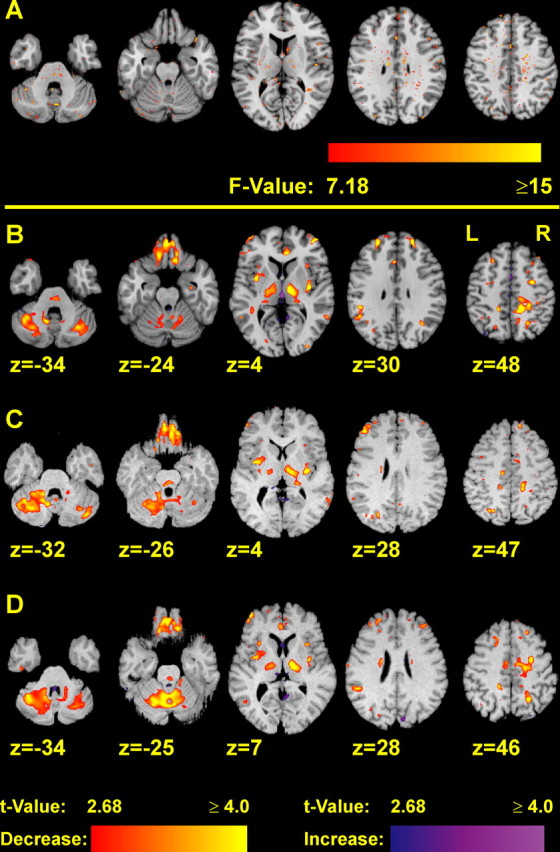
A, Statistical maps showing spots where the residual differences have a significant relation with the subjects' age. The residual differences are the differences between each subject's nonlinearly transformed MR image and the reference MR image. Thus they give estimates of the local accuracy of the registration. Color-coded F values exceeding 7.18 (corresponding to p ≤ 0.01) are superimposed to the reference image. Voxels having F values above this threshold form much smaller cluster than those voxels where an age–volume relation was detected at the same significance level (B, Figs. 2, 3). B–D, The complete deformation field analysis was calculated separately for each of three different reference images: the MNI single-subject template (B) and the MR images of an 18- (C) and a 51- (D) year-old subject. The latter two MR images were acquired on the same MR scanner as the examined MR images. Locations of major age-related structural differences in the cerebellum and thalamus are very similar between the different reference images. Only for the purpose of visualization, the latter two reference images were affinely registered with the MNI single-subject template.

Test 3: application of different reference images

All source MR images of the present study were registered with three different reference images: the MNI single-subject template and one MR image of an 18-year-old and a 51-year-old male subject. None of the reference images belongs to the examined source MR images. The latter two reference images were acquired on the same MR scanner and with the same MR sequence as the source MR images. The complete deformation field analysis and following statistical analysis was calculated for each of these reference MR images separately, enabling examination of possible influences of the reference MR images on the results of the analysis, which could be caused, e.g., by differences in brain structure or tissue contrast. Furthermore, the MNI single-subject template was nonlinearly matched with the other two reference images: thus, the anatomical atlases, which are related to the MNI single-subject template, were nonlinearly transformed onto the other two reference images. This enabled to compute the ROI-based analysis for each of the reference images.

Statistical maps of the linear regressions of age-related volume increases or declines are presented in Figure 8B–D: the locations of volume declines are apparently similar in the analyses belonging to the different reference images. The ROI-based analyses suggest the same finding (data are available as supplemental Tables 5, 6, available at www.jneurosci.org as supplemental material): major volume declines were consistently found in the cerebellum, thalamus, orbitofrontal cortex, and lateral frontal cortex. Only the volume decline in the anterior cingulate cortex was reduced and shifted somewhat in anterior direction when the brain of the 18-year-old subject was used as a reference (Fig. 8C).

The three reference images differed in image quality, noise content, tissue contrast, but also the brain structure. It should be noted that the results of the deformation field morphometry were largely robust against these differences.

Conclusions

The results of these tests showed that possible relations between the subjects' age and the quality of the registrations can be neglected for the examined sample of subjects. The existence of spots of changed intensity (hyperintensities or hypointensities, as described in Materials and Methods, Image registration) cannot be ruled out for individual brains. However, in the light of these findings, it is improbable that they had a significant influence on the observed age-related differences for two reasons: (1) if such spots were located consistently in certain parts of the brain and were related with age, then they should be visible also in the statistical map of the age relationship of the residual differences (test 2), because the nonlinear registration could compress such spots, but it could not make them vanish. However, these maps did not indicate such spots. Furthermore, the statistical maps of the age-related volume differences and the residual differences did not show any similarity. (2) If the observed volume differences were caused by mismatches between such spots in the source images and the reference images, then these seeming age–volume relations should be influenced by the choice of the reference image. However, although the three reference images of the present study differed in the age of the subject, brain structure, noise, and tissue contrast, the results of the deformation field analyses were essentially similar.

Therefore these tests argue against the assumption that systematic, age-related artifacts or disturbances influenced the observed structural differences. It should be noted that these results are valid only for a sample of subjects with an age range, as in the present study. The processing of MR images of subjects being older than those of the present study might lead to stronger disturbances or artifacts (because of larger macroanatomical differences compared with younger subjects, as well as MR contrast changes), which possibly have a stronger influence on the analysis.

Appendix D: Abbreviations

A, Microanatomical area; Crbll., cerebellum/cerebellar; Crbr., cerebrum/cerebral; G., gyrus; HATA, Hippocampus–amygdala transition area; Lobul., Lobulus; SII_Op1, …, SII_Op4, opercular areas of secondary somatosensory cortex (Eickhoff et al., 2006). Thalamic nuclei: ANT, Anterior nuclei; CGL, corpus geniculatum laterale; CGM, corpus geniculatum mediale; CM, centromedian nucleus; IML, internal medullary lamina; LD, lateral dorsal nucleus; MD, mediodorsal nucleus; PU, pulvinar complex; VA, ventral anterior nucleus; VPM, ventral posteromedial nucleus.