CNS Learns Stable, Accurate, and Efficient Movements Using a Simple Algorithm

Abstract

We propose a new model of motor learning to explain the exceptional dexterity and rapid adaptation to change, which characterize human motor control. It is based on the brain simultaneously optimizing stability, accuracy and efficiency. Formulated as a V-shaped learning function, it stipulates precisely how feedforward commands to individual muscles are adjusted based on error. Changes in muscle activation patterns recorded in experiments provide direct support for this control scheme. In simulated motor learning of novel environmental interactions, muscle activation, force and impedance evolved in a manner similar to humans, demonstrating its efficiency and plausibility. This model of motor learning offers new insights as to how the brain controls the complex musculoskeletal system and iteratively adjusts motor commands to improve motor skills with practice.

Introduction

Most daily activities require that we learn to apply forces and stabilize our limbs to move and interact with objects in our environment (Hogan, 1985; Rancourt and Hogan, 2001). The learning process appears to involve the gradual formation of an internal representation of the relationship between motor commands and motion enabling the CNS to adapt the dynamics of the limb to its physical environment. This internal representation appears to be used for both feedforward (anticipatory) (Lackner and Dizio, 1994; Shadmehr and Mussa-Ivaldi, 1994; Flanagan and Wing, 1997; Krakauer et al., 1999; McIntyre et al., 2001; Singh and Scott, 2003) and feedback (Todorov and Jordan, 2002; Franklin et al., 2007; Kurtzer et al., 2008) control. Although there is some controversy as to whether the internal representation comprises inverse and/or forward models of the task dynamics (Ostry and Feldman, 2003; Pasalar et al., 2006; Yamamoto et al., 2007), it is clear that to ensure stable control when the environmental forces arise from unpredictability or mechanical instability it must also have the capacity to regulate mechanical impedance (Hogan, 1984; Burdet et al., 2001; Franklin et al., 2004, 2007). Feedforward control of mechanical impedance is necessary in biological systems because neural delays preclude the use of feedback to compensate for instability in the environment (Mehta and Schaal, 2002).

Although it is recognized that the internal representation can be rapidly modified to adapt to changes in environmental forces, the mechanisms used by the CNS are still unknown. By investigating iterative changes in muscle activation during adaptation we identified several principles which we used as the basis for a simple algorithm in a new computational model. Our novel algorithm learns the time-varying motor commands to individual muscles that produce the same force and mechanical impedance observed when humans adapt to changes in environmental forces, including those arising from instability in the environment. It departs significantly from algorithms based on optimization (Burdet and Milner, 1998; Harris and Wolpert, 1998; Stroeve, 1999; Todorov, 2000; Todorov and Jordan, 2002; Guigon et al., 2007; Trainin et al., 2007; Izawa et al., 2008) as it predicts the transients of learning, as well as from existing supervised learning schemes (Kawato et al., 1987; Slotine and Li, 1991; Katayama and Kawato, 1993; Burdet et al., 1998; Gribble and Ostry, 2000; Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Emken et al., 2007) because they have no mechanism to counteract mechanical instability.

Materials and Methods

Principles of our motor dynamics adaptation mechanism.

Motor learning uses sensory feedback to modify feedforward commands and improve performance (Johansson and Cole, 1994). Existing learning schemes from neuroscience or robotics based on iterative learning or adaptive control change the feedforward command based on a monotonic function of the kinematic error in joint or muscle space (Kawato et al., 1987; Slotine and Li, 1991; Katayama and Kawato, 1993; Burdet et al., 1998; Gribble and Ostry, 2000; Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Emken et al., 2007) (see Fig. 1A). Positive error leads to an increase in the feedforward motor command on the next trial, and negative error to a decrease. This mechanism can learn joint torques to counteract predictable environmental forces. However, environmental forces are sometimes not predictable. In particular, when a task involves unstable interaction with the environment the same central motor command can produce very different movements if the mechanical output varies because of perturbations, neural noise, or history and state-dependent features of muscle force. Therefore, the corrective action needed to compensate for disturbances experienced when a movement is attempted on one occasion cannot be used to predict the appropriate feedforward command for subsequent movements, unlike stable systems. Under these conditions existing learning schemes fail because they do not provide a means for adapting limb impedance (Osu et al., 2003; Burdet et al., 2006).

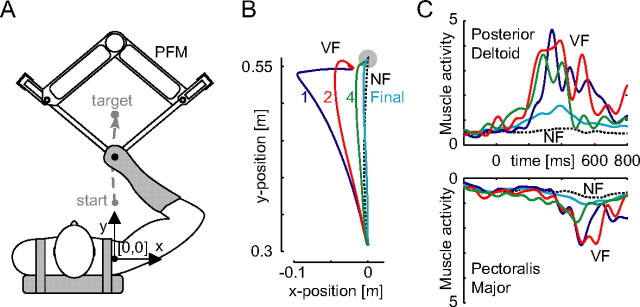
Figure 1.

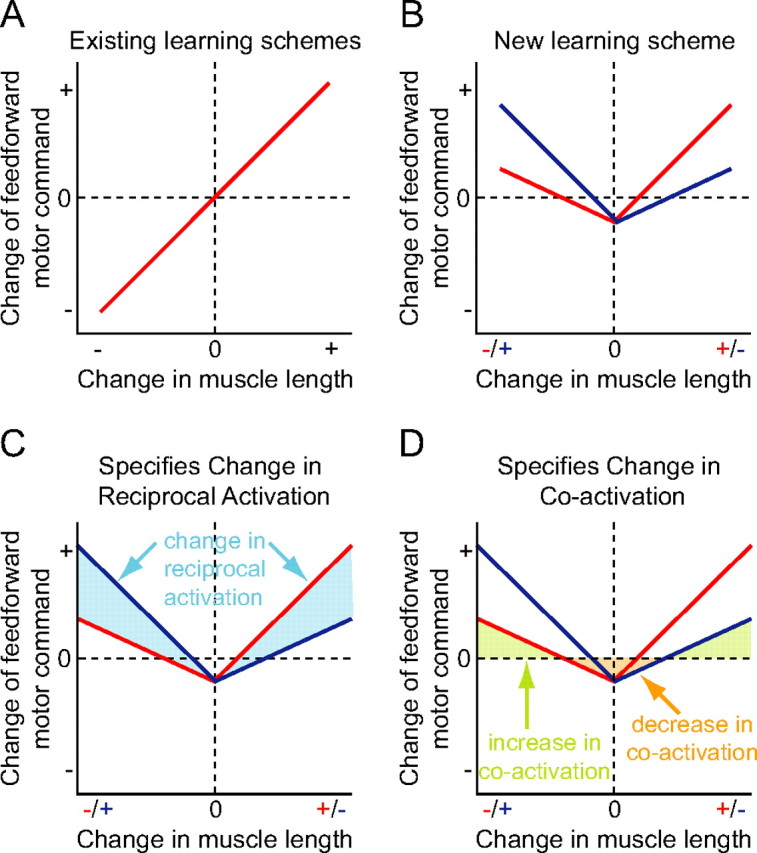
Comparison of models for motor learning. A, In previous motor learning schemes, update of the motor command (joint torque or muscle activation) corresponds to a monotonic antisymmetric (in most cases, linear) function of the joint angle error or muscle length error. B, In our new model there is a proportional increase in the feedforward command in response to muscle lengthening, a proportional increase in response to muscle shortening with a slightly lower gain, and a decrease when the error is near zero. This is shown for both muscles of an agonist–antagonist pair. C, When a disturbance occurs, this model produces a scaled response by modifying the reciprocal activation by the amount indicated in the shaded region to generate an opposing force. D, When a large disturbance occurs, this model will produce an increase in coactivation (green area) to stiffen the joint. When no disturbance is present, the motor command is reduced (orange area) to decrease metabolic cost.

The principles for a general model of motor learning emerged from detailed examination of trial-by-trial changes in temporal patterns of muscle activation in studies where subjects performed a reaching task in the presence of a perturbing force field (Franklin et al., 2003a; Milner and Franklin, 2005). We identified common features in the evolution of muscle activation whether the force field elicited a stable or unstable interaction with the arm, which are captured in the three principles described below. If a muscle was stretched relative to its normal trajectory during unperturbed movements, its activity increased later in the same trial (online feedback). It also increased in the following trial with an advance in the temporal profile, leading to a reduction in the perturbing effect of the force field. This is evident from a comparison of the blue and red curves for posterior deltoid, corresponding to the first and second trials (see Fig. 2B). As our first principle, the feedforward muscle activity increases in response to positive error (unexpected muscle lengthening) on the previous trial. This is similar to the learning function of most previous motor learning models when restricted to the positive error domain (see Fig. 1A).

Figure 2.

Changes in posterior deltoid and pectoralis major muscle activity during learning of a novel skill. A, The PFM exerts forces on the hand during horizontal point-to-point reaching movements. B, Initial movements in the VF color coded by trial number (left). C, Hand trajectories (right) (mean of five subjects). The NF muscle activity is shown in black (solid: mean of 20 movements; dashed: SD). The activity in the first movement (blue) contains large feedback responses delayed ∼200 ms from the start of movement in the lengthened posterior deltoid and slightly later in pectoralis major, which is shortened. On the second movement (red), there is a large early increase in the activity of both muscles suggesting a feedforward pathway. This feedforward muscle activity is increased again by the fourth trial (green). As the feedforward command compensates for the external dynamics, there is a reduction of the muscle activity to a final level (cyan) (mean of the final 10 trials). Approximately 60 ms phase advance in muscle activity was observed only between the first and second trials, and this suggests that only the feedback component of the motor command is phase advanced by 60 ms and becomes a part of the feedforward command of the next trial. EMG signals from five subjects were rectified, averaged and then filtered (fifth-order Butterworth 10 Hz low pass) for display purposes.

However, if a muscle was shortened by the perturbation, its activity also increased, both later in the same trial and with a temporal advance on the following trial (see Fig. 2B, blue and red curves for pectoralis major). As our second principle, negative error (muscle shortening) also results in an increase in feedforward activity on subsequent trials. Given these two principles, an additional condition for learning is that the increase in activation of lengthened muscles produces a greater change in joint torque than that of shortened muscles, as in Figure 1B. This is not necessarily a straightforward task for the control system as the joint torque produced by a given muscle is a function of muscle length and moment arm, which can both vary with the joint angle. Finally, we noted that the activation of all muscles gradually decreased during training (see Fig. 2B, light blue curves). As our third principle, the CNS reduces the feedforward activation of a muscle if the error is below some threshold. This will reduce feedforward muscle activity as performance improves (Franklin et al., 2003a). We propose that the CNS combines these three principles to learn movements that are stable, accurate, and energy efficient.

The feedforward motor command can be conceptually divided into reciprocal activation of antagonistic muscle groups (to control net joint torque) and coactivation (to control joint stiffness) (Feldman, 1980). The difference between changes in feedforward activity of lengthened and shortened muscles produces the necessary reciprocal activation to compensate perturbing forces (Fig. 1C, shaded region). In contrast, the common change in feedforward activity of all muscles produces changes in coactivation to optimize the mechanical impedance (Fig. 1D, shaded regions), given that muscle stiffness and damping are monotonic functions of muscle activation (Hunter and Kearney, 1982; Weiss et al., 1988). Models of motor learning which fail to take into account this aspect of the muscular system will be unable to learn to compensate for unstable environmental dynamics. In the proposed scheme, limb endpoint force and impedance are learned simultaneously through trial-by-trial iteration without distinctly or explicitly representing dynamics and impedance (or reciprocal and coactivation commands). This unique feature is not found in previous models (Kawato et al., 1987; Slotine and Li, 1991; Katayama and Kawato, 1993; Burdet et al., 1998; Gribble and Ostry, 2000; Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Emken et al., 2007).

Apparatus.

Subjects sat in a chair and moved the parallel-link direct drive air-magnet floating manipulandum (PFM) in a series of forward reaching movements performed in the horizontal plane (Fig. 2A). Their shoulders were held against the back of the chair by means of a shoulder harness. The right forearm was securely coupled to the PFM using a rigid custom molded thermoplastic cuff. The cuff immobilized the wrist joint, permitting movement of only the shoulder and elbow joints. The subjects' right forearm rested on a support beam projecting from the handle of the PFM. Motion was, therefore, limited to a single degree of freedom at the shoulder and at the elbow. The manipulandum and setup were described in detail previously (Gomi and Kawato, 1997).

Experimental protocol.

A total of 10 healthy right-handed individuals participated in this study (20–34 years of age; four females and six males). The institutional ethics committee approved the experiments and subjects gave informed consent. Subjects were required to make 0.25 m long reaching movements in 600 ± 100 ms in the forward direction. All subjects practiced making movements in the null force field (NF) with the apparatus on at least 1 d before the experiment. These training trials were used to accustom the subjects to the equipment and to the movement speed and accuracy requirements. Subjects were presented with different force fields separated by intervals of more than 3 d. There were three force fields, although some subjects were not tested on all three. These included a velocity-dependent force field (VF) and two different divergent force fields (DFs), which exerted forces (F_x, F_y) on the hand described respectively by

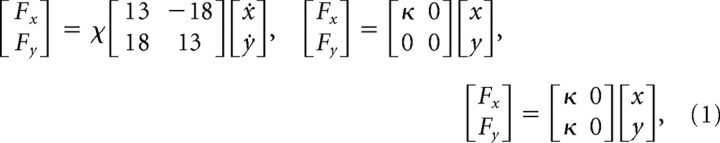where (2/3 < χ < 1) and (300 < κ < 500) were adjusted to the strength of each subject. The DFs were inactivated when |x| exceeded 5 cm for safety reasons. Subjects began by performing 50 successful movements in an NF which was unexpectedly switched to one of the force fields to initiate the learning session. No information was given to the subjects as to when the force field trials would begin. Subjects then continued to perform reaches in that force field until 75 successful trials had been completed. Successful trials were those which ended inside a 2.5 cm diameter target window within the prescribed time (0.6 ± 0.1 s). All movements were recorded whether successful or not. Movements were self-paced so subjects were able to rest between movements if they wished.

Electromyography.

Surface electromyographic (EMG) activity of six arm muscles was recorded using pairs of silver-silver chloride surface electrodes during the learning sessions. The electrode locations were chosen to maximize the signal from a particular muscle while avoiding cross talk from other muscles. The skin was cleansed with alcohol and prepared by rubbing in electrode paste. This was removed with a dry cloth and pregelled electrodes were then attached to the skin with tape. The spacing between the electrodes of each pair was ∼2 cm. The impedance of each electrode pair was tested to ensure that it was <10 kΩ. The activity of six arm muscles [pectoralis major (sternocostal head), posterior deltoid, biceps brachii (short head), triceps longus, brachioradialis, triceps lateralis] were recorded. The EMG signals were analog filtered at 25 Hz (high pass) and 1.0 kHz (low pass) using a Nihon Kohden amplifier (MME-3132) and then sampled at 2.0 kHz.

Data analysis.

Integrated, rectified EMG was calculated over the interval [-100–100 ms] relative to the time of movement onset. The EMG recorded during this time interval, which we will refer to as EMG_FF, was assumed to be representative of feedforward muscle activity with zero contribution from the feedback mechanisms that respond to perturbations induced by the force fields (see section below entitled “timing of feedback activity”). The signed handpath error (Franklin et al., 2003a) was used as a measure of position error on a given trial, which corresponds to the integral of the lateral error between the handpath on a given trial and the mean handpath in the null field. The signed handpath error of a force field trial was estimated as:

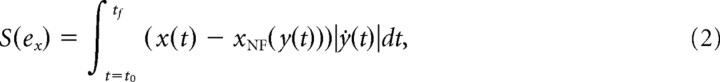where x_NF(y(t)) is the x position of the mean NF trajectory at the current y position of the force field trial and x(t) and y(t) represent the trajectory during the force field trial. Hand-path errors were calculated from the start time, t₀ (75 ms before crossing a hand-velocity threshold of 0.05 m/s), to the termination time, t_f (when curvature exceeded 0.07 mm⁻¹) (Schaal and Sternad, 2001). The mean NF trajectory was estimated using the last 10 trials in the NF for each subject before the onset of the force field. Because movements both in the null field and force fields tend to be slightly curved after learning, this measure should more closely represent an error sensed by the somatosensory system than a measure relative to a straight-line trajectory. The error was related to the incremental changes in feedforward muscle activity by computing the difference in EMG_FF between consecutive trials and plotting it against the signed handpath error of the previous trial. Only data from the first 40 trials in each force field were used in the analysis so as to maximize the signal-to-noise ratio of changes in the EMG, which are largest during the initial stages of learning. The change in EMG_FF was expressed as a percentage of the NF muscle activity before force field onset. The 840 values of change in the feedforward command, compiled from 10 subjects adapting to the different force fields, was separated into eight equally sized (n = 105) groups according to the size of the signed handpath error on the previous trial and tested for a significant difference from zero using a two-sided t test. We focus on the shoulder muscles because the shoulder angle changes much more than the elbow angle as a result of lateral deviation from the unperturbed handpath. Changes in elbow angle are negligible compared with changes in shoulder angle (more than an order of magnitude less) for lateral deviation from the unperturbed handpath. Therefore, for the shoulder muscles a closer relationship between our kinematic error estimate and the actual stretch of the muscle would be expected than for the single joint elbow muscles. Because of the high trial-to-trial variability in the EMG caused by its stochastic nature, the signal-to-noise ratio is low. Therefore, of the two antagonistic muscle pairs acting at the shoulder, the pair undergoing the greatest change in activation in response to the perturbing effect of a force field would provide the more suitable data for analysis of the relationship between error and change in activation. Because the change in activity of pectoralis major and posterior deltoid was greater than that of biceps brachii and triceps longus the analysis focused on the former rather than the latter.

Force.

The force measured at the hand during movements is a function of two components: the force produced by the subject by feedforward or feedback mechanisms and the force produced by the robot. The mean change in force from one trial to the next was quantified over two intervals. The first was before the movement onset (−100 to −10 ms relative to movement onset) and the second included the early part of the movement (−10–130 ms relative to movement onset). Whereas the second interval will be highly representative of the effects of the force field, the early interval before any movement can only result from a change in the feedforward control. The change in force was examined as a function of the signed handpath error on either the current trial or the previous trial. Linear regression on the data were performed to determine if the slope was significantly different from zero. Statistical significance was determined at the p < 0.05 level.

Timing of feedback activity.

After a short break and a washout of the learning (50 NF trials), subjects performed additional reaching movements in the NF. On randomly selected trials the NF was replaced by a force field. The force field perturbed the trajectory which elicited reflex and voluntary changes in muscle activity to correct the error. A total of 80 NF and 20 force field trials were recorded for each force field. These randomly applied force field trials are referred to as before effect (BE) trials. Because the subjects assume that they will normally be moving in the NF the feedforward command can be presumed to represent that in the NF.

The rectified, integrated NF EMG was subtracted from the corresponding BE EMG to determine the onset and magnitude of the corrective (feedback) responses. The data from the BE trials for all force fields and subjects were combined. The onset of the feedback response was determined by testing if the BE EMG was significantly greater than the NF EMG in successive 10 ms windows from 100 ms before the start of the movement. This was then related to the signed handpath error. An ANOVA with main effects of force field (BE or NF) and signed handpath error and subjects as a random effect was used to test if the BE activity was different from the NF activity in each window. A difference in activity was assumed to be significant at the p < 0.05 (uncorrected for multiple comparisons) level only if during the next interval the difference was significant at p < 0.01 (uncorrected), i.e., the change in activity was both sustained and became less variable. The responses of individual subjects in each field were also examined [ANOVA with main effect of force field (BE or NF)] to confirm the earliest onset time for each subject. To determine the onset of the perturbing effect of the force field movement in the x-direction was compared (BE versus NF) using the same technique to identify the point in time where the position traces began to diverge.

The perturbations produced by the force fields were characterized by a gradual increase in force as the trajectory progressed. The trajectory did not start to deviate noticeably from the unperturbed trajectory until some time after the movement onset and did so gradually. A comparison of the perturbed trajectories with NF movements shows that the force field did not create a significant deviation in the trajectory until 50 ms after the start of movement (Fig. 3A). The earliest significant differences in position were found at 52 and 86 ms after the onset of the movement in the VF and DF, respectively. The first significant change in muscle activation on BE trials relative to NF movements occurred after this time (Fig. 3B).

Figure 3.

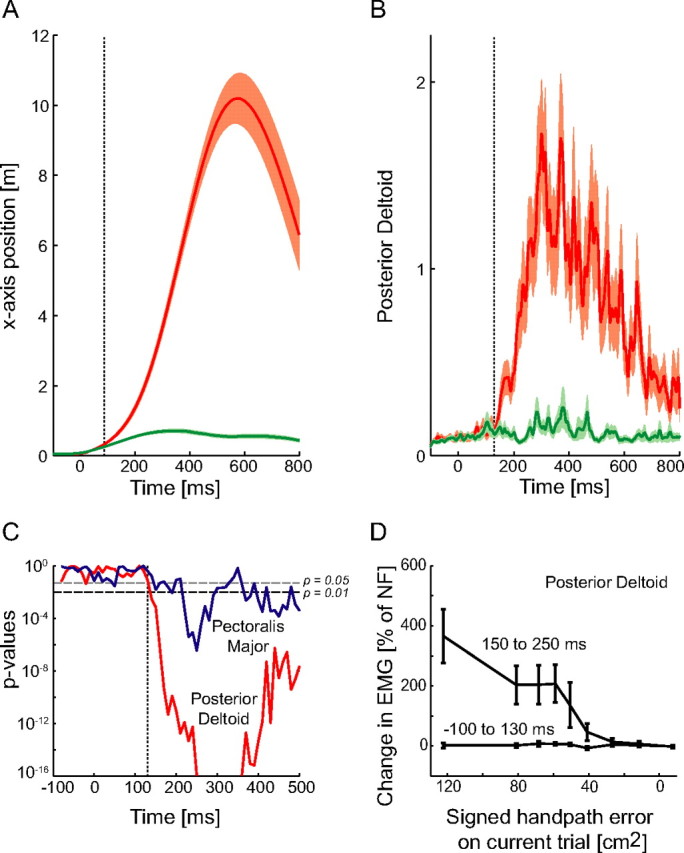
Onset of feedback during perturbed trials. A, Position (x-axis) in the BE trials (red) compared with that in the NF trials (green) as a function of the time. Shaded regions represent the SEM of the position. The dotted line indicates the time at which the position in the BE trials was significantly (p < 0.05) different from that in the NF trial. Data is shown for one subject. B, Posterior deltoid muscle activity in the BE trials (red) compared with that in the NF trials (green). C, Muscle activity in BE trials was compared with that in NF movements. The p values of these comparisons are plotted on a log scale against time interval to determine the onset of the feedback response. No significant differences were seen before 130 ms (dotted vertical line) after movement onset. The horizontal line is located at p = 0.01. The earliest feedback responses occurred in the posterior deltoid muscle (shown). D, Responses in the posterior deltoid for two different time intervals (−100 to 130 ms) and (150–250 ms) relative to the onset of the movement. For each interval the integrated muscle activity was determined and grouped according to the signed handpath error. The mean values ± SEM are shown as a percentage increase in the muscle activity relative to the muscle activity in the NF movements for the same time interval. An ANOVA was used to compare differences with a main effect of signed handpath error and random effect of subjects. As expected, there was no significant difference in the muscle activity in the early interval (p = 0.28), i.e., before 130 ms after the onset of movement, whereas a clear response is seen in the later interval (p < 0.00001).

For none of the six muscles was the BE activity significantly different from that of the NF trials before 130 ms after the start of the movement (Fig. 3C). The earliest significant difference was found in the posterior deltoid muscle ∼130 ms after movement onset. For individual subjects, the earliest significant difference in muscle activation was determined to occur 140 ms after the onset of the movement. It was only later than 130 ms that the size of the feedback response began to increase with the kinematic error (Fig. 3D). Based on these results, the earliest detectable onset time of the feedback component produced by the smooth perturbations induced by the force fields was estimated as 130 ms after the start of the movement. The feedback latency relative to movement onset (130 ms) is still considerably less than that found in similar force field perturbation studies investigating the elbow joint (200 ms) (Shapiro et al., 2002, 2004). Because the force fields used in our study produced no significant changes in muscle activity earlier than 130 ms, before this time it can be assumed that reflex responses produced by the force fields are zero. This does not mean that reflex activity cannot occur before 130 ms after the onset of a movement, but for the slow perturbations induced by the smooth displacements of the force fields used in this study no detectable change in muscle activity that could be attributed to feedback occurred before 130 ms. A conservative approach was taken in the analysis of changes in the feedforward control by assuming that the interval of purely feedforward activity ended 100 ms after the onset of the movement.

Simulations.

Simulations were performed using a 2-joint 6-muscle arm model with shoulder and elbow joints and agonist–antagonist pairs of shoulder, elbow and double-joint muscles. The force produced by each muscle was the sum of a feedforward control signal, signal-dependent noise, muscle elasticity and a feedback signal. Noise was modeled as Brownian motion multiplying a linear function of the total muscle activation (i.e., the sum of feedforward and feedback signals), with parameters set to produce variance similar to experimental data for NF movements. Muscle elasticity and feedback were modeled as linear functions of the stretch and its derivative, with the feedback signal delayed by 60 ms, and muscle impedance increasing with activation. Model parameters were set such that muscle elastic force depended primarily on muscle length whereas force produced by feedback depended primarily on muscle velocity. These values were set so that feedback contributed 20–35% of the total restoring force in NF movements.

Although extensive work has shown that a linear muscle model is not accurate enough to reproduce the actual mechanical behavior of muscles, this does not invalidate our use of a simple muscle model for investigating the learning algorithm. Whereas the model is linear in terms of the length–tension relationship, it is nonlinear with respect to its input-output relationships between command and tension. In particular, in our model muscle, impedance increases with activation (one of the main properties of nonlinear muscle models, critical for impedance control). Because the muscle activation level depends both on the feedforward and feedback motor commands, the tension does not depend linearly on the command. We selected a simple muscle model with activation dependent impedance for clarity in understanding how the learning algorithm works. Although we believe that incorporating a nonlinear muscle model would not invalidate our learning algorithm, it would make the simulations more complex and could obscure some features of the learning algorithm.

The feedforward waveform was updated iteratively after each trial before executing the next trial. The change in the feedforward waveform was determined using the three principles of motor learning related to the V-shaped learning function (supplemental Fig. S1, available at www.jneurosci.org as supplemental material) where the error measure was a function of the muscle length and its derivative. The feedforward activation for each muscle is updated from one trial u_FF^k to the next u_FF^{k + 1} by (considering that it must remain positive):

where the change in activation from one trial to the next is governed by

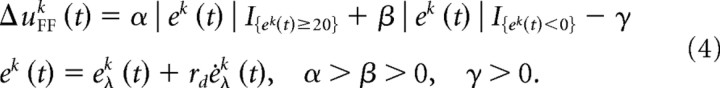The superscript k denotes the trial number, α, β are the learning parameters and γ a constant deactivation parameter (supplemental Fig. S1, available at www.jneurosci.org as supplemental material). The Kronecker function I_S = 1 for the set S and 0 outside it. We phase advance the feedforward update by ψ equal to the feedback delay to compensate for this delay. In our implementation the length error e_λ(t) was evaluated relative to a reference trajectory, as described in the supplemental material (available at www.jneurosci.org) and the term r_d indicates the relative level of velocity error to length error. The term α|e|I_{{e ≥ 0}} causes an increase in feedforward command in response to stretching of the muscle, β|e|I_{{e < 0}} causes an increase in the feedforward command in response to shortening of the muscle, and −γ a decrease of activation when the stretch or shortening is below some threshold. Changes in the kinematics, endpoint stiffness and muscle activity during and after the learning process were compared with experimental data. The endpoint stiffness was estimated using the same procedure as in human experiments (Burdet et al., 2000; Franklin et al., 2003b). A detailed description of the algorithm and of how physiological parameters were identified is provided in the supplemental material (available at www.jneurosci.org as supplemental material).

Results

Adaptation mechanism is supported by experimental results

The principles of our adaptation mechanism were examined by quantifying changes in feedforward muscle activity during learning of novel dynamics. Electromyographic activity was recorded during adaptation of horizontal point-to-point movements, away from the body, subjected to force fields exerted on the hand by a robotic interface. Activity was recorded from shoulder and elbow muscles. We focus on the shoulder muscles as their length changes were most closely linked with the hand position error. Subjects initially performed movements in an NF which was unexpectedly changed to one of three perturbing force fields after fifty to sixty trials. A measure of feedforward muscle activity was obtained by considering only the early part of the movement. To relate position error to changes in the feedforward command, trials were sorted into eight groups of equal size according to signed handpath error. The signed handpath error for each trial (Eq. 2) was paired with the change in the feedforward activity of the following trial and the relationship was tested for significance. The feedforward activity of the posterior deltoid or pectoralis major muscle increased significantly on the subsequent trial if the muscle had been stretched. However, its feedforward activity also increased if it had been shortened on the previous trial (Fig. 4A,B). In contrast, if the signed handpath error was small, then the subsequent feedforward activity decreased. This provides quantitative evidence for the three principles of our new model for motor learning.

Figure 4.

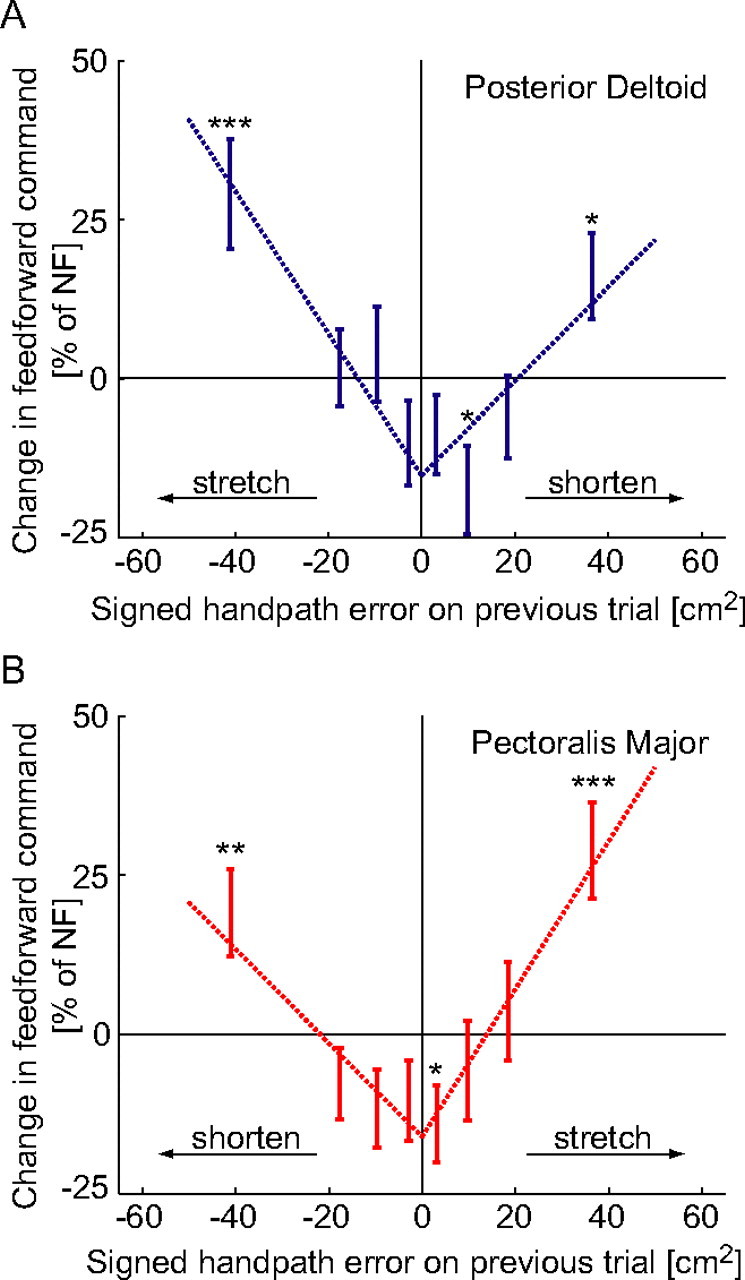
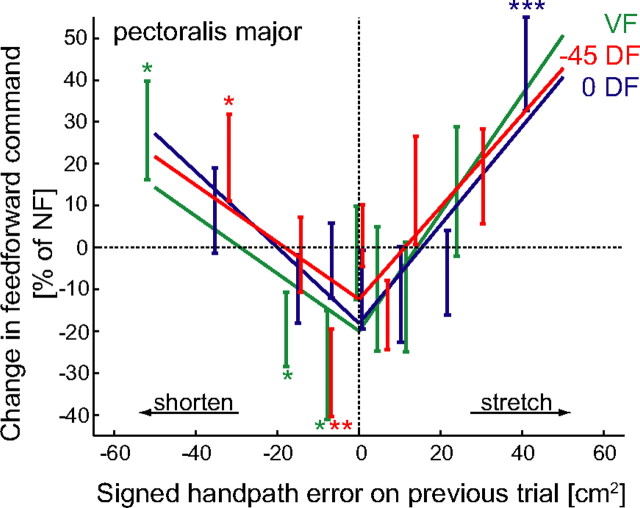
Changes in the feedforward components of the motor command. A, Change in feedforward activity of the posterior deltoid (mean ± SEM) plotted against the signed handpath error from the previous trial. The change in the feedforward activity was binned into equally sized groups depending on the signed handpath error and plotted against the mean signed handpath error of each group. *p < 0.05, **p < 0.01), ***p < 0.005, changes in feedforward activity significantly different from zero. B, Change in the feedforward activation of the pectoralis major. Both muscles showed similar responses: if the muscle either lengthened or shortened on the previous trial the feedforward command increased on the subsequent trial. However, if the signed handpath error was close to zero on the previous trial, then the feedforward command of both muscles was reduced. The dotted lines are the least squares linear fit to the positive and negative error regions of the data with a common intercept for both regions.

To confirm that the V-shaped curve is representative of the data for all three force fields and is not simply the result of combining three different adaptation patterns; we also examined each force field separately. The changes in feedforward muscle activity in each force field are well fit by the V-shaped function supporting the idea that the CNS utilizes such an algorithm for motor adaptation under a variety of environmental conditions (Fig. 5).

Figure 5.

Changes in the feedforward components of the motor command for the pectoralis major muscle in each of the three force fields. The change in feedforward activity of the muscle (mean ± SEM) plotted against the signed handpath error from the previous trial. *p < 0.05), **p < 0.01), ***p < 0.005, changes in feedforward activity significantly different from zero. The solid lines are the least squares linear fit to the positive and negative error regions of the data with a common intercept for both regions.

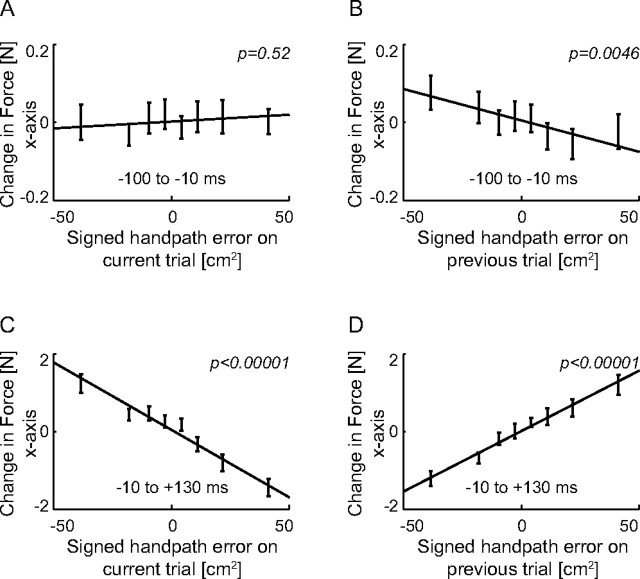
The adaptation mechanism predicts that for a given kinematic error on a trial, there will be both a change in the coactivation level (impedance) and reciprocal activation level (force). The previous results clearly support the higher coactivation levels for larger errors. To confirm the second prediction, a change in the net force, we examined the changes in the lateral force produced at early times during movements in the unstable force fields (Fig. 6). The change in the endpoint force was quantified over two intervals: before the start of the movement (−100 to −10 ms relative to the onset of the movement) and during the early portion of the movement (−10 to 130 ms relative to the onset of the movement). When we examine the forces during the movements, the forces are mainly produced by the force fields themselves. By constraining the timing to before the start of the movement, no forces from the field are present allowing us to examine the changes produced by the subject's feedforward change in motor command. According to our hypothesis we would expect to see a monotonic relationship between the change in the force on the current trial and the kinematic error on the previous trial. If the early change in endpoint force is examined as a function of the error on the same trial (Fig. 6A), it is clear that the slope is not significantly different from zero (p = 0.52), demonstrating that there is no effect of the force field on the force experienced at the handle during this interval. In contrast, if we examine the force during the early portion of the movement (Fig. 6C), a significant negative slope is found (p < 0.00001), purely indicative of the subject's resistance to the PFM which produces a force related to the position of the hand. When the early change in force (before movement start) is examined as a function of the kinematic error on the previous trial (Fig. 6B), we also see a significant negative slope (p = 0.0046). However, this no longer represents resistance to the PFM, which produces no force before movement onset. Instead, it represents the change in the force applied by the subject which would act opposite to the error experienced on the previous trial as predicted by our model of adaptation. The force experienced later in the movement as a function of the error on the previous trial (Fig. 6D) has a positive slope (p < 0.00001) because subjects compensate for errors in the unstable DF field by producing a small movement in the opposite direction, causing the hand to be pushed in that direction by the force field. These results show that the appropriate change in the direction of the force is seen as predicted by our model of adaptation, supporting the theory that there are different slopes in the V-shaped function for stretched and shortened muscles of each muscle pair.

Figure 6.

Changes in endpoint force (x-axis) from one trial to the next as a function of the kinematic error. A, The change in force from the last trial to the current trial before the start of the movement expressed as a function of the signed handpath error on the current trial. The mean change in the force was determined from −100 to −10 ms relative to the onset of the movement. The p value indicates whether the slope of the linear regression is significantly different from zero. B, The trial-by-trial change in the force before the start of movement expressed as a function of the signed handpath error on the previous trial. The mean change in the force was determined from −100 to −10 ms relative to the onset of the movement. C, The trial-by-trial change in the force during an early time in the movement plotted as a function of the error on the current trial. The change in force was determined from −10 to 130 ms relative to the onset of movement. D, The trial-by-trial change in the force during an early time in the movement plotted as a function of the error on the previous trial. The change in force was determined from −10 to 130 ms relative to the onset of movement.

Simulations confirm that our algorithm is a viable mechanism for adaptation

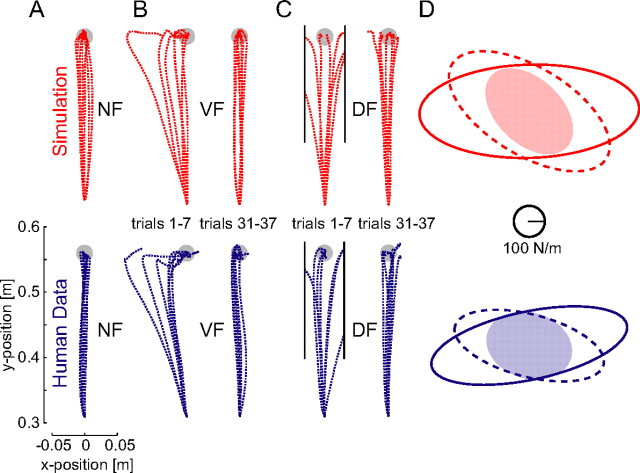
To verify that the new model represents a viable mechanism for adaptation to novel dynamics, particularly when interactions are initially unstable, we simulated the control of arm movements under conditions equivalent to those of our experiments using a computational model based on our three principles (Materials and Methods and supplemental material, available at www.jneurosci.org as supplemental material). The simulation produced NF movements similar in terms of mean trajectory and variability to those of human subjects (Fig. 7A). When a VF was introduced, the arm was clearly perturbed from its normal trajectory (Fig. 7B). On subsequent trials, the feedforward command gradually adapted, converging monotonically to the NF trajectory. In a DF, the initial trials were perturbed either to the right or the left because of the instability just as for human subjects (Fig. 7C). However, as control improved with training, movements became stable and successfully reached the target. For both the VF (dashed) and DF (solid), the stiffness (comprising both intrinsic and reflexive stiffness) changed during learning, resulting in the same characteristics as found experimentally (Burdet et al., 2001; Franklin et al., 2003b) (Fig. 7D). This increased endpoint stiffness was produced by the combined action of a larger intrinsic stiffness and larger reflexive force, arising from changes to the feedforward command. The mechanism also correctly predicted the trial-by-trial changes in the muscle activity during learning (Fig. 8). The magnitude and time course of changes in the simulated muscle activity paralleled that observed during human adaptation (Franklin et al., 2003a).

Figure 7.

Simulation (red) shows that our new model adapts to both stable and unstable interactions and reproduces experimental data (blue). A, NF trajectories. B, Adaptation to the VF. C, Adaptation to the DF. D, Changes in endpoint stiffness after adaptation. Top, Stiffness ellipses in the NF (filled) and after adaptation to the VF (dashed) and DF (solid) estimated from simulated perturbations after completion of model learning. Bottom, Stiffness ellipses for the same conditions from experimental measurements on human subjects (mean of 6 subjects shown) (Franklin et al., 2003b).

Figure 8.

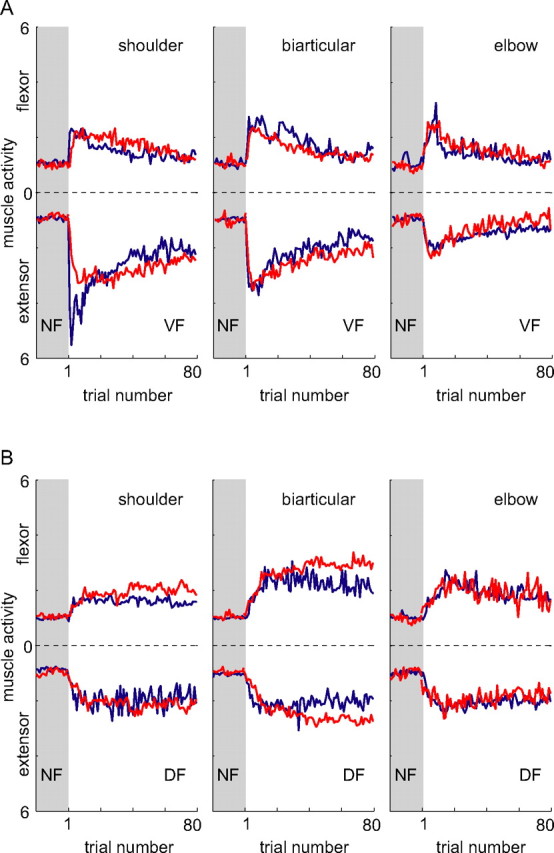
Changes in integrated muscle activity as a function of trial number during learning. Results are shown for both the simulation (red) and the mean of five subjects (Franklin et al., 2003a) (blue). A, Learning in the VF. Movements were initially performed in the NF (shaded region). Once the force field was turned on, the muscle activity increased dramatically. As learning progressed, the activity leveled off and was gradually reduced to a steady state value. Similar trends in muscle activity are seen in the simulated and experimental data. Initially, coactivation is seen in all muscle pairs, but this is reduced and effectively eliminated by the end of learning, leaving significant activity only in the muscles producing shoulder extensor torque. B, Learning in the DF. Again similar patterns of changing muscle activation were seen in both the experimental and simulated data. In response to the initial perturbing effects of the force field, coactivation was seen in all muscle groups, with more occurring in the biarticular muscles. As learning progressed, muscle activation was reduced to a steady state value. Like the experimental data, the greatest steady-state activity was found in the biarticular muscles.

Discussion

This new computational model of motor learning is general because it provides mechanisms for adapting to interactions that can be either stable or unstable, in the presence of inherent motor noise, and comprehensive because it predicts trial-by-trial changes in kinematics and temporal profiles of muscle activation. Our algorithm corresponds to concurrent optimization of stability, error, and activation, at the muscle level. It extends algorithms based on the gradient descent of an error function, which have been used to show how the state space representation of a feedforward model can be generalized to different movement directions (Thoroughman and Shadmehr, 2000). Current neurophysiological models able to predict trial to trial modifications of force or torque (Kawato et al., 1987; Katayama and Kawato, 1993; Gribble and Ostry, 2000; Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Emken et al., 2007) and corresponding nonlinear adaptive controllers for robots (Slotine and Li, 1991; Burdet et al., 1998), which use a monotonic antisymmetric (in most cases, linear) update of the feedforward command, have no explicit mechanism to alter the limb impedance independently from joint torque (or limb posture), and, therefore, cannot learn to compensate for unstable dynamics (Osu et al., 2003). Models based exclusively on optimization of cost functions such as minimization of end-point variance and/or muscle activation (Burdet and Milner, 1998; Harris and Wolpert, 1998; Stroeve, 1999; Todorov, 2000; Todorov and Jordan, 2002; Guigon et al., 2007; Trainin et al., 2007; Izawa et al., 2008) can only predict final learning outcomes, whereas our model can account for the complete progression of experimentally observed changes in force and impedance throughout learning. This algorithm, when combined with a method for generalization (Donchin et al., 2003), and a method for storing and accessing multiple internal representations (Haruno et al., 2001) could provide a powerful description of motor adaptation.

The new model has different implications for reaching in force fields which produce a stable interaction versus those which produce an unstable interaction with the arm. In both cases, the initial error results in muscle coactivation on the subsequent trial because both lengthened and shortened muscles increase their feedforward activity. The effect on shortened muscles is evident in Figure 2B where activation of pectoralis major increased for the first five trials. This coactivation increases the impedance of the limb and makes it more resistant to the disturbance of the force field. When the interaction is stable, the directional error is consistent from trial to trial so the greater change in feedforward activity of lengthened muscles compared with shortened muscles favors a gradual increase in reciprocal muscle activation (Franklin et al., 2003a) producing a net force in the direction compensating for the perturbation (Milner and Franklin, 2005). When the interaction is unstable, consecutive movements may be perturbed in opposite directions (Osu et al., 2003) such that antagonistic muscles undergo lengthening on alternate trials. Consequently, coactivation increases to a much greater extent than reciprocal activation. When the error is sufficiently small there is a gradual reduction of superfluous coactivation (Thoroughman and Shadmehr, 1999; Franklin et al., 2003a). This allows reciprocal activation to develop when stability prevails or tuning of mechanical impedance when instability is encountered.

Another unique feature of our model is a mechanism for trade-off between performance (e.g., accuracy) and metabolic cost of muscle activation. This is determined by the location of the zero crossing in Figure 1D, which represents a threshold that separates increasing and decreasing coactivation. The learning scheme does not attempt to further reduce errors once they fall below the threshold; rather it reduces energy consumption in this region by reducing feedforward commands. Supporting evidence for this reduction in feedforward commands has been shown during walking studies examining motor adaptation (Emken et al., 2007). Assuming that the error threshold of the learning function (Fig. 1C) is reduced as performance improves this algorithm could also accurately predict the slow decrease in learned lateral force when a subject is unaware that a lateral perturbing force has been replaced by a virtual channel (Scheidt et al., 2000).

This learning scheme resembles feedback error learning (Kawato et al., 1987), in the sense that the movement error in the last trial determines the appropriate change in the feedforward command for the next trial. However, there are a number of important differences: learning takes place in muscle space, disturbance of any one muscle produces activation of the antagonist (cocontraction) and there is a gradual reduction in activation when the error is small. The error information determines the change to the feedforward command by means of a V-shaped learning function. This error information needs to be phase advanced before being incorporated into the feedforward command for the following trial such that the new motor command acts to prevent the disturbance that produced this feedback in the first place. Such a phase advance can be implemented computationally (Katayama and Kawato, 1993; Schweighofer et al., 1998) and may be produced through spike-timing-dependent plasticity (Chen and Thompson, 1995; Doi et al., 2005). The data presented here also show that the learning, the change in feedforward motor command, is guided by the error, and in particular by the size of the error which indicates that a type of supervised learning is used by the brain. Fine and Thoroughman (2006, 2007) have suggested that there are situations where categorical rather than proportional responses to error are observed, which would not be expected with supervised learning. Although categorical responses are not predicted by our model, it is possible that proportional responses could be masked and appear to be categorical if the responses were quantified in terms of changes in kinematics, as in the cited studies. Our model predicts that the change in feedforward compensation for a disturbance will include both an increase in the impedance of the limb and a change in the applied force. If the disturbance is particularly difficult to counteract, such as a brief force pulse (Fine and Thoroughman, 2006) or if its strength is unpredictable (Fine and Thoroughman, 2007) then the CNS might reduce the difference in the slope of the V-shaped learning function (Fig. 1B) between the agonist and antagonist muscles. This would bias the strategy for reducing the kinematic error toward increased limb impedance through coactivation as opposed to enerating a counteracting force. Although such changes in coactivation would be proportional to error, they would not be manifest as proportional aftereffects and would, therefore, be classified as categorical using the measures used by Fine and Thoroughman (2006).

With a simple control mechanism that incorporates the muscle length error experienced in one movement as a learning signal, the CNS can quickly adapt to changes in the environmental dynamics. Unlike many proposed schemes for the control of redundant muscle systems, muscle forces and limb impedance can be appropriately modified, using a single adaptive process, without explicit calculation of inverse dynamics or impedance. When both the perturbed muscle and its antagonists change their feedforward activity in response to the perturbation, joint torques and limb impedance are modified to progressively improve performance. This mechanism provides powerful capabilities for adaptation, as demonstrated in our simulation.