Persistent Na⁺ and K⁺-Dominated Leak Currents Contribute to Respiratory Rhythm Generation in the Pre-Bötzinger Complex In Vitro

Abstract

A central problem in analyzing neural circuit function is establishing how intrinsic neuronal conductances contribute to the generation of network activity. We used real-time calcium activity imaging combined with whole-cell patch-clamp recording to analyze contributions of subthreshold conductances in the excitatory rhythm-generating network in the respiratory pre-Bötzinger complex (pre-BötC) of neonatal rat in vitro brainstem slice preparations. Voltage-clamp ramp recordings from imaged pre-BötC neurons revealed that persistent sodium (NaP) and K⁺-dominated leak currents primarily contribute to subthreshold I–V relations. We quantified NaP and leak conductance densities (g/C_m) in intrinsic oscillatory bursters and intrinsically nonbursters, the two main electrophysiological phenotypes of inspiratory neurons within the pre-BötC. Densities of g_NaP were significantly higher for intrinsic bursters, whereas leak conductance densities were not significantly different between intrinsic bursters and nonbursters. By pharmacologically manipulating g_NaP and/or g_Leak directly within the pre-BötC, we could modulate network oscillation frequency over a wide dynamic range and cause transitions between oscillatory and quiescent states. These results were consistent with models of the pre-BötC excitatory network consisting of heterogeneous mixtures of intrinsic bursters and nonintrinsic bursters incorporating g_NaP and g_Leak with parameter values found experimentally. We propose a paradigm whereby NaP and Leak represent a functional set of subthreshold conductances that endow the pre-BötC with rhythmogenic properties and represent targets for modulatory control of inspiratory rhythm generation.

Introduction

Neural network activity results from intrinsic neuronal conductances generating cellular electrophysiological behavior and from synaptic connections that give rise to collective network dynamics (Llinas, 1988; Grillner et al., 2005). In vertebrate rhythmic motor pattern generation networks, such as brainstem circuits generating respiratory movements, a major problem is to establish how intrinsic neuronal conductances are functionally specialized within different populations of circuit neurons for generation of network activity. In the present study, we have investigated how rhythmic activity is generated and controlled in the pre-Bötzinger complex (pre-BötC) (Smith et al., 1991; Gray et al., 1999, 2001), a spatially localized and functionally specialized region of the medulla containing a heterogeneous excitatory network with autorhythmic properties (Koshiya and Smith, 1999; Johnson et al., 2001). The pre-BötC network is the substrate for inspiratory rhythm generation and the source of rhythmic excitatory drive to premotor transmission circuits in the brainstem respiratory network.

Despite intensive investigation, the biophysical mechanisms underlying rhythm generation in the pre-BötC have not been resolved (Smith et al., 1991, 2000; Rekling and Feldman, 1998; Richter and Spyer, 2001; Ramirez et al., 2004; Feldman and Del Negro, 2006). We focused our analysis on the roles of two specific neuronal subthreshold conductances that we show are prevalent in pre-BötC neurons: a subthreshold voltage-activated persistent sodium current (NaP) and a K⁺-dominated leak current (Leak). We have hypothesized that these conductances play a fundamental role in rhythmogenesis in combination with excitatory synaptic interactions (Butera et al., 1999a,b; Smith et al., 2000) (see also Rybak et al., 2003). Previous experimental studies investigating contributions of NaP, however, have suggested that rhythm generation in the pre-BötC in slice preparations in vitro normally does not depend on NaP, despite observations establishing that this conductance is a ubiquitous property of pre-BötC neurons and endows a subset of these cells with intrinsic oscillatory bursting properties (Del Negro et al., 2002a, 2005; Pena et al., 2004; Feldman and Del Negro, 2006; Pace et al., 2007). Furthermore, regulation of pre-BötC network activity by Leak has not been thoroughly analyzed experimentally. Particular types of K⁺-dominated leak or background conductances play fundamental roles in neuronal excitability control (North, 2000; Bayliss et al., 2003; Lesage, 2003), and our previous computational modeling and experimental studies point to a potential major role (Butera et al., 1999a,b; Del Negro et al., 2001). We therefore reexamined the contributions of NaP with novel experimental approaches and extended our analysis of contributions of Leak.

In contrast to previous studies (Del Negro et al., 2002a, 2005; Pena et al., 2004; Pace et al., 2007), we find that NaP can be pharmacologically manipulated within the pre-BötC in vitro to change network activity state and regulate oscillation frequency over a wide dynamic range. Furthermore, we find that Leak can regulate cellular and network oscillatory activity, either independently or coordinately with NaP. These results support our hypothesis that NaP and Leak represent a functional set of subthreshold conductances that endow the pre-BötC network with rhythmogenic properties and represent potential targets for neuromodulatory control of inspiratory rhythm generation.

Materials and Methods

Thin slice and pre-BötC island preparations.

Transverse slices (250–350 μm thick) of medulla oblongata were cut from Sprague Dawley neonatal [postnatal day 0 (P0)–P3] rats to contain the pre-BötC and rostral end of the hypoglossal (XII) motor nucleus including XII nerve rootlets as previously described (Smith et al., 1991; Koshiya and Smith, 1999). The caudal end was cut through the caudal pre-BötC for imaging and recording neuronal activity. Pre-BötC island preparations, which enabled us to study activity of part of the pre-BötC network isolated from the slice, were obtained by excising the pre-BötC and immediately surrounding tissue from one side of the slice as previously described (Johnson et al., 2001). The slices or pre-BötC islands were mounted in a recording chamber (0.2 ml) on a microscope stage and superfused (4 ml/min) with artificial CSF (ACSF) containing (in mm) 124 NaCl, 25 NaHCO₃, 3 KCl, 1.5 CaCl₂, 1.0 MgSO₄, 0.5 NaH₂PO₄, 30 d-glucose, and antibiotics (500 U/L penicillin, 0.5 mg/L streptomycin, and 1 mg/L neomycin), equilibrated with 95% O₂ and 5% CO₂ (pH 7.35–7.40 at 27°C). Rhythmic respiratory network activity recorded from XII nerves in slices, or directly from the pre-BötC in island preparations, was maintained by elevating the superfusate K⁺ concentration (7–9 mm).

Pharmacological procedures.

Pharmacological agents [tetrodotoxin (TTX; Sigma, St. Louis, MO), substance P (SP; Sigma), and sodium cyanide (NaCN; Sigma)] were dissolved in the standard perfusion solution with elevated K⁺ concentration. The NaP blocker riluzole [Sigma or Tocris (Ellisville, MO)] (Urbani and Belluzzi, 2000; Del Negro et al., 2002a; Spadoni et al., 2002; Ptak et al., 2005) was dissolved in this solution at ≤100 μm concentrations. For microinfusion experiments, the drug-containing solution was continuously infused into the pre-BötC with a glass pipette (∼10 μm tip diameter) inserted into the center of the imaged pre-BötC (125–175 μm below the slice surface depending on slice thickness). Low pressure (∼10–20 mmHg) was continuously applied to the pipette during infusion with a precision pressure control and valve system [picospritzer-IID (General Valve, Fairfield, NJ); 2PK+ pressure controller (ALA Scientific Instruments, Westbury, NY)]. This system allowed us to precisely control convective microdelivery of pharmacological probes locally within the imaged locus (below) of pre-BötC network activity.

Electrophysiological recording and data analysis.

Voltage- and current-clamp data obtained from whole-cell patch-clamp recording was recorded with a HEKA EPC-9 amplifier (HEKA, Lambrecht/Pfalz, Germany) or an Axopatch-1D amplifier (Molecular Devices, Union City, CA) controlled by Pulse software (HEKA; 2.9 kHz low-pass filter). Recording electrodes (4–6 MΩ), positioned with microdrives [Narishige (Tokyo, Japan) or Siskiyou (Grants Pass, OR)], contained (in mm) 130.0 K-gluconate, 10.0 Na-gluconate, 4.0 NaCl, 10.0 HEPES, 4.0 Mg-ATP, 0.3 Na-GTP, and 4.0 sodium phosphocreatine, pH 7.3. Measured potentials were corrected for the liquid junction potential (−10 mV). To identify intrinsic oscillatory bursting neurons, excitatory synaptic transmission was blocked with 20 μm 6-cyano-7-nitroquinoxaline-2-dione disodium (CNQX; Sigma) and in some experiments by the calcium channel blocker Cd²⁺ (200 μm). XII motoneuron population activity (used to monitor inspiratory network activity in slices and pre-BötC network population activity in island preparations) were recorded with fire-polished glass suction electrodes (100–120 μm diameter); for direct pre-BötC activity recording, the electrodes were applied to the surface of the island preparations. Signals were amplified (50,000×; CyberAmp 380; Molecular Devices), bandpass filtered (0.3–2 kHz), digitized (10 kHz), and then rectified and integrated (∫XII or ∫pre-BötC) either by analog integrator or digitally with Chart software (ADInstruments, Castle Hill, New South Wales, Australia).

Measurements of parameters of cellular and network population activity (inspiratory population and neuronal burst frequency and population burst amplitude) were made off-line with automated algorithms [PowerLab with Chart software (ADInstruments) and Igor Pro (Wavemetrics, Lake Oswego, OR)] and hand-checked for accuracy. All data presented as burst frequency were first analyzed by computing burst period, defined as the interval from onset to onset of consecutive bursts. Voltage dependence of whole-cell currents was analyzed from voltage-clamp data using Pulsefit (HEKA), Chart (ADInstruments), and Igor Pro (Wavemetrics) software. Voltage-ramp data were fitted to first-order Boltzmann functions: g/g_max = [1 + exp([V_m − V_1/2max]/k)]⁻¹, where g and g_max represent whole-cell conductance at V_m and the maximal conductance, respectively, V_m is membrane potential, V_1/2max is half-maximal activation voltage, and k is a slope factor. Linear regression analysis applied to the linear region of the quasi-steady-state voltage-clamp ramp I–V relations was used to determine g_Leak. Cell capacitance (C_m) was determined from the integral of the transient capacity current (I_C, leak subtracted) evoked by 15 ms hyperpolarizing voltage-step commands applied within −10 mV of resting potential, using ∫I_Cdt = − Q_m at each command potential (V_m). C_m was determined from the slope of the plot of Q_m versus ΔV_m for the series of step commands. Series resistance (R_S) was calculated from the decay-timeconstant of I_C. Neurons failing to meet the criterion R_m > 10R_S necessary to achieve space clamp were excluded from voltage-clamp analysis. Furthermore, neurons with clear evidence of poor space clamp such as unclamped action potential currents during the slow voltage-clamp ramps were excluded from the analysis. Statistical significance was determined by a Student's paired t test on mean data. Data are presented as means ±SD unless indicated otherwise.

Calcium activity and infrared differential interference contrast imaging.

We imaged Ca²⁺ fluorescence activity of rhythmic inspiratory neurons to identify the location of the pre-BötC and individual neurons for whole-cell recording. Methods for pre-BötC neuronal labeling with Ca²⁺-sensitive dye and imaging were as previously described (Koshiya and Smith, 1999; Johnson et al., 2001). Briefly, membrane-permeant Ca²⁺-sensitive dye, Calcium Green-1 AM (CaG; Invitrogen, Carlsbad, CA; 50 μg), dissolved in 5 μl of DMSO containing 25 μg of pluronic F-127 (BASF, Florham Park, NJ) and dispersed in 10 μl of ACSF, was microinjected with a glass pipette (∼10 μm tip diameter) into the slice near the midline to retrogradely label bilaterally pre-BötC neurons overnight (8–12 h). CaG-labeled inspiratory neurons were visualized with a fixed-stage upright videomicroscope (Axioskop-FS1; Zeiss, Thornwood, NY) with a 75 W xenon epi-illuminator, optical filters (excitation 485 nm, emission 530 and 505 nm beam splitter; Omega Optical, Brattleboro, VT), and water-immersion objectives (Zeiss Achroplan). Fluorescence images were captured with a CCD camera fiber-optically coupled to a fluorescence image-intensifying camera (ICCD-1000F; VideoScope International, Sterling, VA) and recorded on videotape together with electrophysiological signals. Changes in fluorescence intensity (ΔF/F) were detected in real time with an image processor (ARGUS 20; Hamamatsu Photonics, Hamamatsu, Japan) and quantified off-line after digitizing images using an audio–video board (Sony, Tokyo, Japan). Inspiratory population and single-neuron “flash” images were obtained by subtracting baseline CaG fluorescent images from images acquired during peak inspiratory activity with an image processor in real time and displayed in pseudocolor. Simultaneous videomicroscopic infrared differential interference contrast (IR-DIC) imaging was done with an extended IR Newvicon camera (Hamamatsu Photonics) and enhanced with the ARGUS 20 in real time. Infrared (900 nm) transmission was optimized with a polarizer (wide spectrum; Melles Griot, Irvine, CA) and analyzer (850–950 nm; Polarcor; Corning, Midland, MI). For dual imaging, the Newvicon and ICCD cameras were mounted on a dual-port imaging head incorporating a dichroic beam splitter (700 nm; Zeiss), and images were aligned by reverse scanning and scan range shifting of the Newvicon camera.

Modeling methods.

We modeled the pre-BötC excitatory network by 50 synaptically coupled (Butera et al., 1999b; Purvis et al., 2007), heterogeneous, single-compartment neurons incorporating a fast-activating, slowly inactivating NaP and a K⁺-dominated ohmic leak conductance for the two subthreshold currents, as well as Hodgkin-Huxley-like transient Na⁺ current (NaT) and delayed-rectifier-like K⁺ current for action potential generation, as previously described in detail [Model 1 (Butera et al., 1999a; Del Negro et al., 2001)]. Except for NaP activation properties, neuron capacitance values, and E_K, all other Model 1 current parameters, as well as parameters for phasic excitatory synaptic currents, were identical to those used previously (Butera et al., 1999a,b). Steady-state activation properties for NaP were based on Boltzmann function data obtained in the present study (V_1/2max = −47 mV; k = 5.0); similarly data-based C_m (28 pF) and E_K (−73 mV) values were used. Because of the adjustments to the NaP half-maximum activation voltage (hyperpolarized by 7 mV relative to the original Model 1), the NaP steady-state half-maximum inactivation voltage was hyperpolarized by 7 mV, similar to the adjustments described by Purvis et al. (2007). The networks also incorporated a constant background tonic synaptic excitatory conductance as previously described (Butera et al., 1999b; Purvis et al., 2007), which was set to 0.1 nS. All simulations used all-to-all synaptic coupling for the 50 cells [the smallest population that preserves the dynamics observed for populations an order of magnitude larger (Butera et al., 1999b)]. To incorporate parameter heterogeneity, maximum conductances of NaP and Leak within the heterogeneous population and phasic excitatory synaptic conductance (g_syn) (Purvis et al., 2007) were randomly assigned from normal distributions with ±30% SD for each parameter to mimic our experimental data as described in detail in Purvis et al. (2007). The heterogeneity of NaP and Leak resulted in networks composed of variable numbers of intrinsically bursting and nonintrinsically bursting neurons [depending on the population mean values of NaP maximum conductance (G_NaP) and maximum Leak conductance (G_Leak)], when excitatory synaptic transmission was eliminated (g_syn = 0). Total Leak was partitioned into a dominant K⁺ component (e.g., population G_LeakK in Fig. 13) and a small fixed Na⁺ leak component as previously described (Del Negro et al., 2001). To model perturbations of network activity with changes in neuronal g_NaP or g_Leak, we varied G_NaP and/or G_Leak for the heterogeneous population of bursters and nonbursters with the SD for parameters fixed at ±30%. Numerical methods were identical to those described previously (Butera et al., 1999b; Purvis et al., 2007). The initial 20 s of simulated time (90 s total) was discarded. Network activity was displayed and analyzed from running histograms (adjustable bin size, 10–100 ms) of average spike times computed across the population. Raster plots of neuron spiking were used to assess neuronal burst synchronization and analyze the composition of intrinsic burster and nonburster neurons within the heterogeneous network.

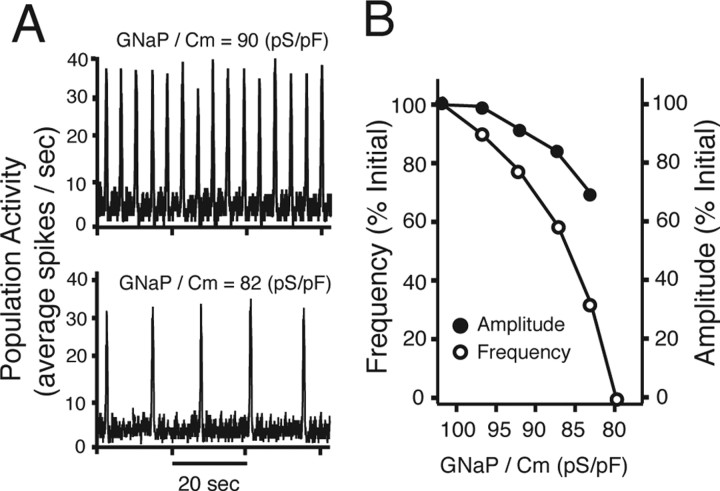
Figure 13.

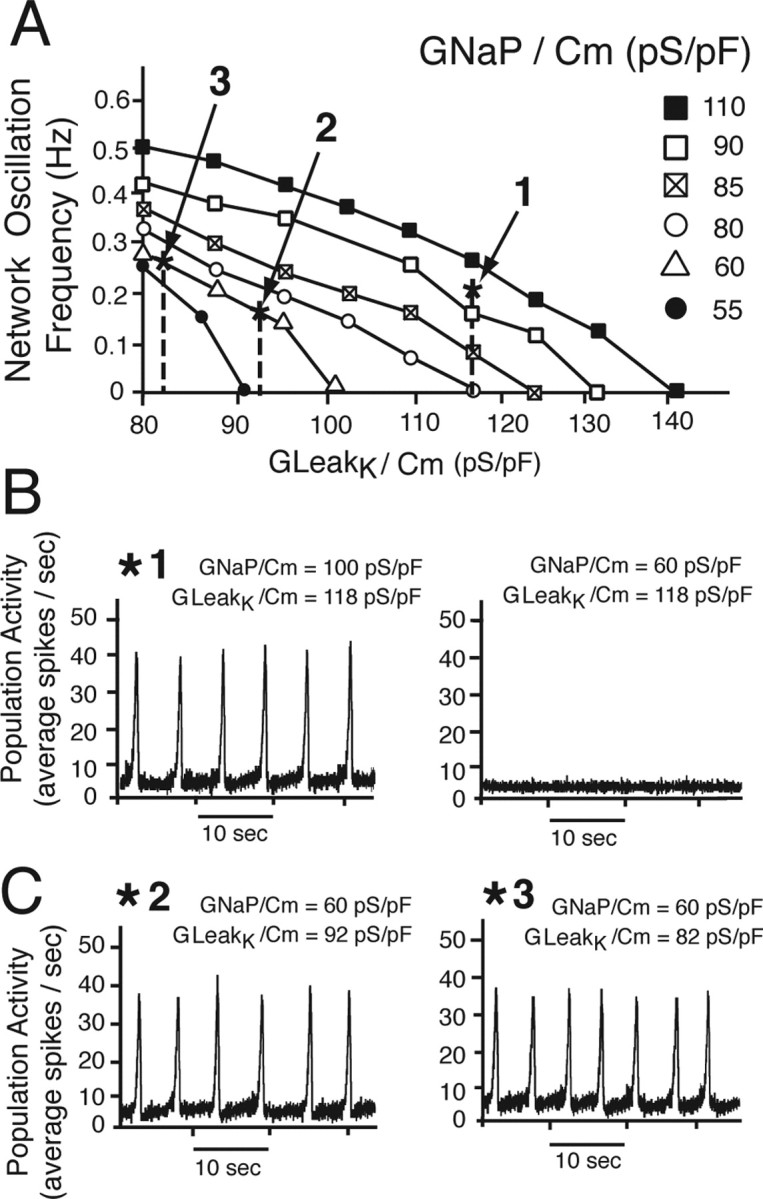
Network simulations examining regulation of oscillation frequency by Leak and interactions of NaP and Leak in control of activity in a heterogeneous excitatory network of intrinsic burster and nonburster neurons. A, Reduction of G_Leak monotonically increases oscillation frequency at various fixed values of G_NaP. B, Reduction of G_NaP/C_m from an initial value (*1; G_NaP/C_m = 100 pS/pF, representing an upper bound estimate for the heterogeneous population) by a percentage (∼40% to 60 pS/pF) similar to that found experimentally for the average reduction by 5 nm TTX [estimated from single-neuron-level data (Fig. 3)] stops network oscillations at initial value of G_Leak/C_m (118 pS/pF; vertical dashed line, which represents a lower bound estimate for the combined population of bursters and nonbursters). Network oscillations in general stop for any initial conditions when G_NaP/G_Leak < 0.6. C, Reduction of G_Leak/C_m over the range found experimentally with SP (20–30%), corresponding in the model network to a change from 118 pS/pF initially to 92 pS/pF (*2) and 82 pS/pF (*3), respectively, restores network oscillations. Oscillations cannot be reactivated with any reductions in G_Leak under conditions in which G_NaP is reduced below ∼50% of initial value.

Results

NaP and Leak in pre-BötC neurons in vitro

We imaged pre-BötC neuronal Ca²⁺ activity at population and single-neuron levels (Fig. 1) to identify inspiratory neurons for whole-cell voltage- and current-clamp recording. Our objective was to characterize electrophysiological phenotypes, determine subthreshold conductance properties, and determine whether these properties were functionally correlated with phenotypic differences.

Figure 1.

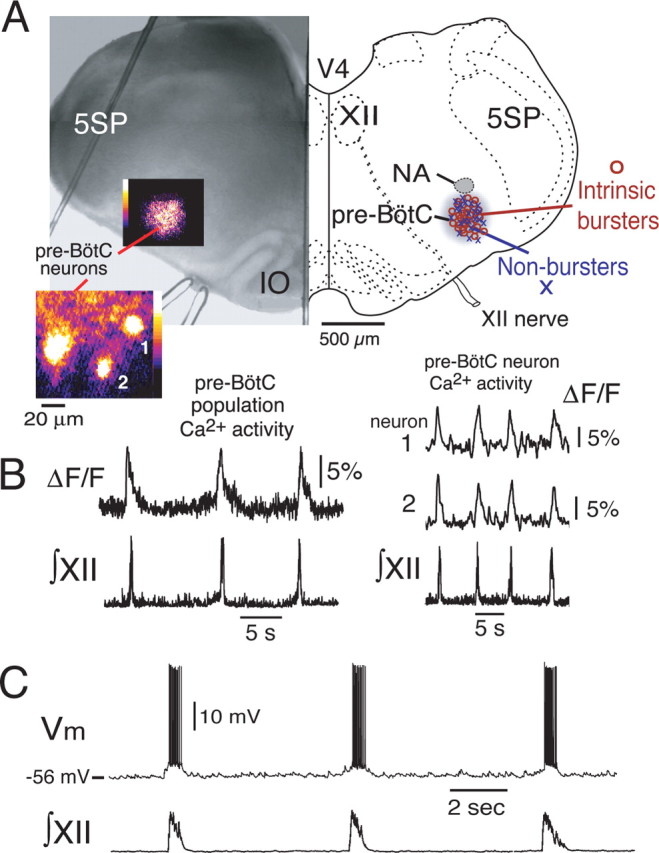
Functional imaging and spatial reconstruction of pre-BötC neurons studied electrophysiologically in vitro. A, Hemisection IR-DIC image of thin slice preparation (left) shows examples of pre-BötC inspiratory population (20× magnification) and single-neuron (63×) activity (pseudocolored, background fluorescence subtracted, “flash” images) obtained with Ca²⁺-sensitive dye (Calcium Green-1 AM) after retrograde labeling of pre-BötC neurons. Composite maps (2-dimensional projection) of 50 pre-BötC inspiratory neurons (30 intrinsic bursters and 20 nonbursters) used for the electrophysiological analysis are shown at right in reconstruction of hemimedullary section at the level of the slice. B, Examples of inspiratory Ca²⁺ fluorescence transients (ΔF/F) for the pre-BötC population (population Ca²⁺ activity; left) and two neurons (1, 2; right) from the flash image are shown. Fluorescence transients are synchronous with inspiratory motor population discharge (∫XII) recorded from hypoglossal motor nerve roots. C, Example of whole-cell current-clamp recording of imaged inspiratory neuron (nonintrinsic burster) with spike discharge in synchrony with motoneuronal population bursts. V4, Fourth ventricle; NA, semicompact division of nucleus ambiguus; 5SP, spinal trigeminal nucleus; IO, inferior olivary nucleus.

All neurons analyzed electrophysiologically exhibited Ca²⁺ transients during the inspiratory phase of network activity, as monitored by nerve recordings of the XII population discharge. We confirmed by current-clamp recording that these cells exhibited spike discharge in synchrony with inspiratory network activity (Fig. 1C). Consistent with our previous observations (Koshiya and Smith, 1999; Del Negro et al., 2002), these inspiratory neurons (Fig. 1) had two distinct electrophysiological profiles. Approximately 60% of the labeled neurons exhibited intrinsic voltage-dependent oscillatory bursting (intrinsic bursters; n = 30) after blocking excitatory synaptic transmission by either bath applying the non-NMDA glutamate receptor antagonist CNQX (20 μm) (Koshiya and Smith, 1999) or the Ca²⁺ channel blocker Cd²⁺ (200 μm; n = 8). The other cells (intrinsically nonbursters; n = 20) exhibited only tonic spiking when the baseline potential was depolarized (Koshiya and Smith, 1999; Del Negro et al., 2002). Spatial reconstruction of the location of individual cells used in our analysis (n = 50 total) (Fig. 1), which were located in superficial layers of the slices at depths up to limits of optical resolution (∼70 μm deep), indicated that these two cell types were interspersed within the main locus of imaged pre-BötC population activity.

Subthreshold currents in the two types of inspiratory neurons were analyzed by applying slow voltage ramps (30 mV/s; −100 to +10 mV) under voltage-clamp conditions. All neurons exhibited N-shaped I–V relationships (Fig. 2A,B) that could be decomposed into two primary subthreshold conductances (Fig. 2A): an ohmic-like conductance, evident by the essentially linear region of the I–V curve below −65 mV (with little if any rectification at hyperpolarized voltages), and a voltage-activated, riluzole- and TTX-sensitive NaP, generating the negative slope region in the approximately −65 mV to −40 mV membrane voltage range. The linear region defining the total Leak conductance had a 0 current intercept (i.e., E_Leak) near −65 mV (−65.1 ± 2 mV; n = 30 bursters; −64.7 ± 2.6 mV; n = 20 nonbursters), which was ∼8 mV depolarized from the calculated Nernst K⁺ equilibrium potential (E_K = −73 mV) for the extracellular and intracellular recording solutions used. Thus Leak was dominated by a K⁺ current with a small contribution from an inward cationic current (Na⁺ and/or Ca²⁺) that caused the depolarized shift in E_Leak from E_K.

Figure 2.

Decomposition of neuronal I–V relations into NaP and Leak current/conductance components. A, B, Representative I–V relations obtained by slow (30 mV/s) voltage-clamp ramp for intrinsically bursting (A) and nonburster (B) pre-BötC neuron types, illustrating pharmacological attenuation of NaP (inward, negative slope-generating current) by either TTX (20 nm; A) or riluzole (20 μm; B). Linear region of I–V relations at hyperpolarized voltages (dashed lines) indicates g_Leak, which is computed by linear regression. E_Leak is indicated. g_NaP is computed from difference current [subtraction of I–V relations before and after one of the NaP blockers, TTX (A) or riluzole (B)]. C, D, Quasi-steady-state activation properties of g_NaP are described by identical Boltzmann functions for both intrinsic bursters (C) and nonbursters (D), whether obtained from difference currents after TTX (left) or riluzole (right); V_1/2max and k parameters for the Boltzmann functions are indicated.

NaP was completely blocked in burster and intrinsically nonburster pre-BötC neurons by bath-applied riluzole (20 μm) or TTX at concentrations as low as 20 nm (Figs. 2A, 3B); lower concentrations of these blockers attenuated peak NaP amplitude in a concentration-dependent manner (Fig. 3) (EC₅₀ = 5.1 μm for riluzole; n = 22 neurons; EC₅₀ = 6.2 nm for TTX; n = 12). To characterize voltage dependence of quasi-steady-state NaP activation, we fit a first-order Boltzmann function to the computed NaP conductance versus voltage data derived from difference curves before and after block of NaP by riluzole (n = 12 bursters; n = 10 nonbursters) or TTX (n = 18 bursters; n = 10 nonbursters) (Fig. 2C,D). Essentially superimposable Boltzmann functions were obtained for intrinsically bursting versus nonbursting cell types, whether the NaP activation characteristics were obtained by the TTX or riluzole NaP-blocking protocols (compare Fig. 2C,D); the pooled group mean V_1/2max = −46.6 ±2.3 mV versus −46.9 ±2.1 mV, and k = 5.0 ± 0.2 versus 5.0 ±0.3, for bursters and nonbursters, respectively; values of V_1/2max or k were not statistically different. Thus, the NaP identified from our voltage-clamp measurements was identical for all neurons. The half-maximum activation voltages obtained from this analysis were hyperpolarized by ∼7 mV from values that we have previously reported (Del Negro et al., 2002b) for a small sample of intrinsic burster and nonburster neurons; these new values were used in our modeling studies (below).

Figure 3.

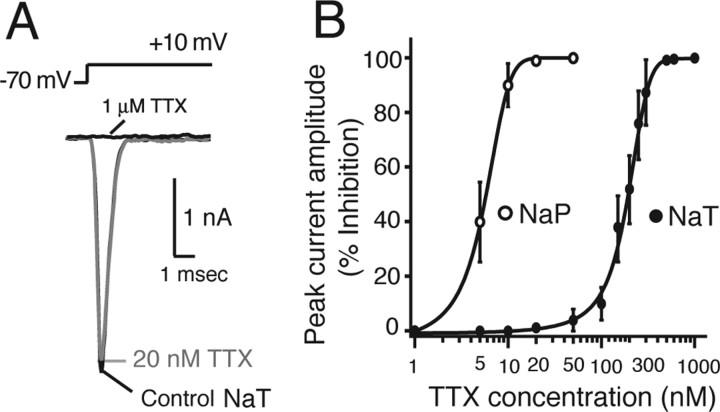
Pharmacological profile of effects of TTX on NaP and NaT. A, Effect of 20 nm TTX on NaT from a representative nonburster neuron. Peak amplitude of NaT measured by voltage-clamp step (−70 to +10 mV; 10 ms duration) is only slightly affected by 20 nm TTX. NaT is completely blocked in this neuron by 1 μm TTX. B, Peak NaP and NaT amplitude versus TTX concentration, indicating relatively selective NaP attenuation at ≤20 nm TTX (n = 12; pooled intrinsic burster and nonburster pre-BötC neurons) with EC₅₀ = 6.2 nm TTX concentration for NaP and 112 nm for NaT.

In characterizing blocking actions of TTX on NaP, we also compared actions on the NaT in bursting (n = 7) and nonbursting (n = 5) neurons; this analysis was critical for our studies (below) evaluating the role of NaP in cellular and network bursting, which required specificity of low TTX for NaP. Effects on NaT were determined from voltage-clamp steps (−70 to +10 mV, 10 ms duration) (Fig. 3A). Whereas NaP was completely blocked by bath application of 20 nm TTX within 3.2 ± 1.2 min in all neurons (Fig. 4C), the peak amplitude of NaT (2.4 ± 0.6 nA, pooled data; n = 12) was only slightly reduced (by 4.4 ± 1.0%; n = 12) (Fig. 3A). The rise time, median width, and duration of NaT were not affected (Fig. 3A). Concentration–response curves (Fig. 3B) indicated a broad separation of EC₅₀ values (6.4 nm for peak NaP current amplitude measured at −40 mV vs 112 nm for NaT) (Fig. 3B).

Figure 4.

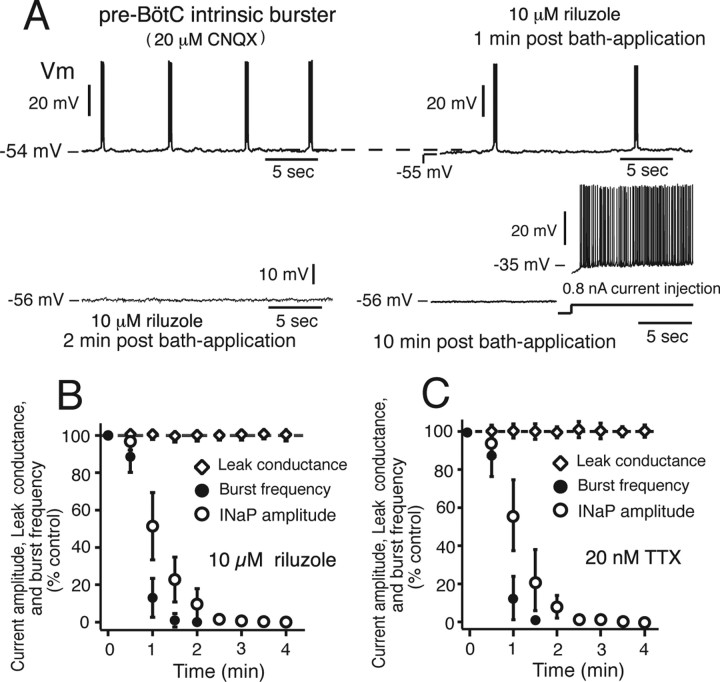
Perturbations of single-cell oscillatory bursting activity by attenuation of NaP. A, Example of current-clamp recording of pre-BötC oscillatory bursting neuron (isolated from excitatory synaptic input by bath-applied 20 μm CNQX). Bath-applied riluzole (10 μm) progressively slows and stops neuron oscillatory bursting, but does not block action potential generation (right bottom trace) during sustained current injection. B, C, Time course of reduction in burst frequency and NaP amplitude (measured at −40 mV from voltage-clamp ramp I–V curve) for a group of intrinsic oscillatory burster neurons by bath-applied riluzole (B; n = 12) or low concentration of TTX (C; 20 nm; n = 12). Neurons stop endogenous bursting after ∼70–80% reduction in NaP amplitude. Complete block of NaP occurs within 3 min; g_Leak is unaffected by riluzole or TTX.

Conductance densities in intrinsically bursting versus nonbursting neurons

NaP conductance densities (g_NaP/C_m) were significantly higher in intrinsically bursting neurons (92.6 ± 33 pS/pF; n = 30; p < 0.01, one-way factorial parametric ANOVA) compared with nonbursting neurons (42.1 ± 11.9; n = 20), whereas g_Leak densities of the same bursting neurons (119.3 ± 44.1 pS/pF) and nonbursting neurons (134.3 ± 45.4 pS/pF) were not significantly different (p > 0.05). Thus, a higher g_NaP density relative to g_Leak density distinguishes the subpopulation of intrinsic bursters from all other circuit neurons within the pre-BötC, as we have previously suggested from modeling (Butera et al., 1999a; Purvis et al., 2007) and measurements in a small set of pre-BötC neurons (Del Negro et al., 2002b). According to our models, the intrinsic activity state (i.e., silence, bursting, or tonic spiking) for neurons with a subthreshold I–V profile similar to that found here is described by a g_NaP versus g_Leak parameter space [for detailed analysis of the data set obtained in this study, see Purvis et al., (2007)], where specific combinations of g_NaP and g_Leak yield intrinsic oscillatory bursting, nonbursting, or tonically spiking behavior. In our modeling studies (below), we take advantage of this to construct heterogeneous networks of intrinsic bursters and nonintrinsic bursters. Our data exhibited considerable heterogeneity for conductance densities (± ∼30% SD; CV = 0.41 and 0.38 of g_NaP and g_Leak, respectively, for intrinsic bursters; 0.27 and 0.34, respectively, for nonintrinsic burster populations), which we also mimic in our models.

NaP-dependent intrinsic bursting behavior of pre-BötC neurons

To assess contributions of NaP to intrinsic neuronal bursting in our cell population with high g_NaP densities, we blocked excitatory synaptic transmission and bath-applied riluzole or low concentrations of TTX while recording bursting behavior and ramp I–V curves from imaged cells. Intrinsic bursting under current clamp was completely disrupted by riluzole (10–20 μm; n = 12) or TTX (10–20 nm; n = 12), both of which caused slight hyperpolarization (≤3 mV) and slowed and then stopped (within ∼3 min) intrinsic oscillations (Fig. 4A). Bursting activity could not be restored by depolarizing shifts of baseline voltage with constant current injection. In contrast, action potential generation above spike threshold and action potential amplitudes during steady depolarizing current (Fig. 4A) were essentially unaffected, consistent with the voltage-clamp data. The time courses for the slow down and elimination of intrinsic rhythmic bursting were similar to the attenuation of NaP amplitude, assessed by voltage clamp; Leak conductance was unaffected in all cases (Fig. 4B,C). This elimination of voltage-dependent oscillatory bursting behavior by reductions in NaP at a constant Leak is predicted by our models (Butera et al., 1999a; Purvis et al., 2007).

Perturbations and termination of network oscillations by attenuating NaP

We analyzed perturbations of inspiratory rhythm caused by attenuating NaP pharmacologically at the network level in slice and pre-BötC island preparations. In slices, we microinfused riluzole or low concentrations of TTX directly into the core of the pre-BötC bilaterally. The tips of the microinfusion pipettes were inserted into the tissue at a depth midway through the slice thickness (see Materials and Methods), in the center of the active pre-BötC populations as determined in the plane of the slice by activity imaging (Fig. 5A). This approach of convective microdelivery of NaP blockers assured that perturbations of network activity could be attributed to local attenuation of NaP within the pre-BötC network, in contrast to bath application of NaP blockers as used in previous studies (Del Negro et al., 2002a; Pena et al., 2004; Del Negro et al., 2005), where there is the possibility that any observed disturbances of respiratory network activity could result from perturbations of neuron activity in populations outside of the pre-BötC [e.g., midline raphe neurons (Pace et al., 2007)] that provide inputs controlling excitability of the pre-BötC network. Experiments in the pre-BötC island preparations also allowed us to analyze activity disturbances of an isolated pre-BötC network for comparison. Furthermore, to check for consistency of results, we also tested the two different blockers of NaP (riluzole and TTX), whose pharmacology we have characterized in detail at the cellular level in our preparations.

Figure 5.

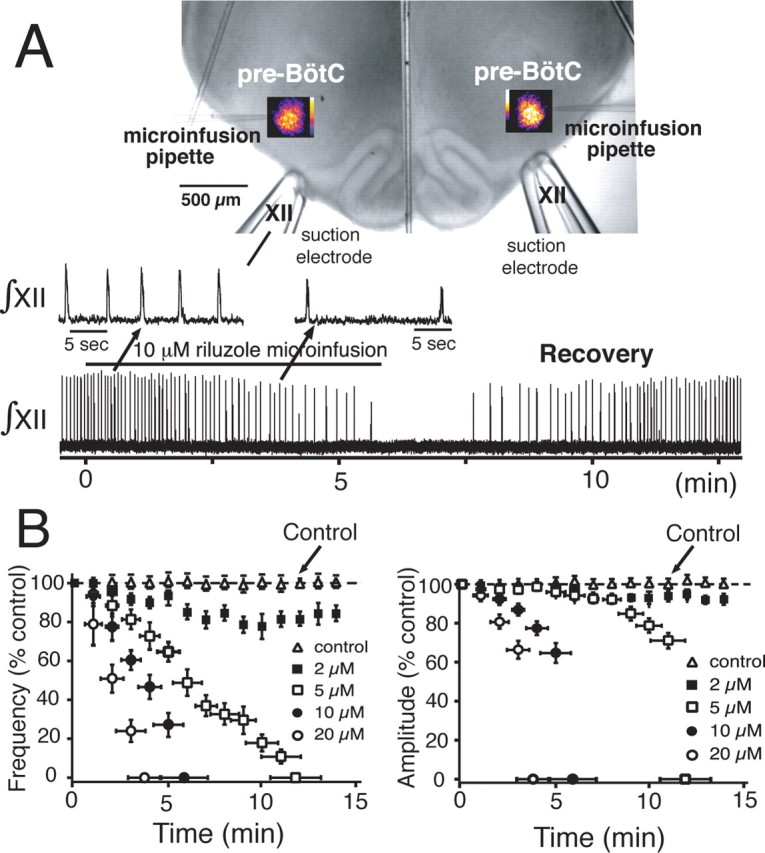
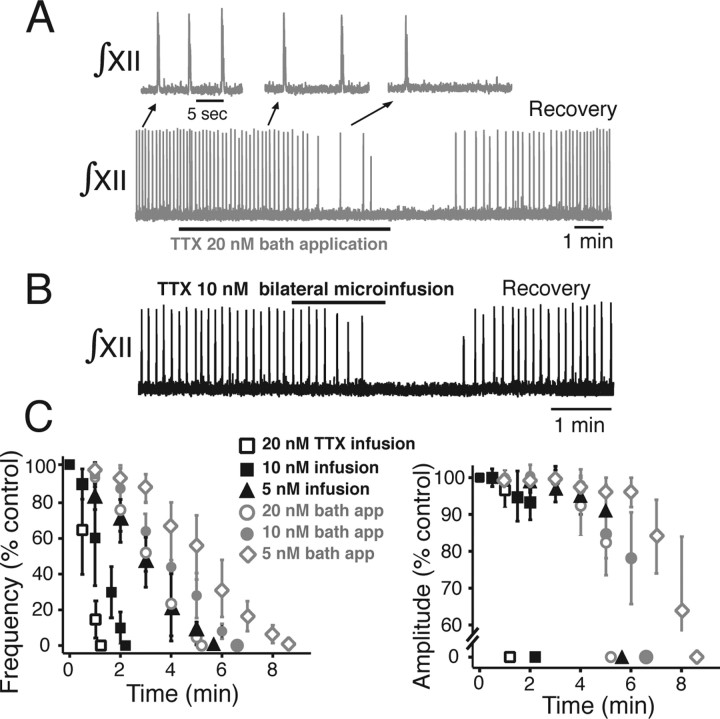
Perturbations of network oscillatory activity accompanying attenuation of NaP. A, Continuous bilateral microinfusion of riluzole into the pre-BötC imaged by Ca²⁺-sensitive dye (population flash images during inspiratory activity shown) slows and then stops network inspiratory oscillations (monitored by ∫XII). Spontaneous recovery always occurred with 5 min after terminating infusion. B, Time course of perturbation of network activity is dependent on infusate riluzole concentration. Both frequency (left) and amplitude (right) of activity are reduced, with frequency predominately affected (n = 26 slices). Microinfusion of control solution (slice bathing medium) does not disturb network activity.

Continuous microinfusion of riluzole (2–20 μm) reduced network oscillation frequency in a concentration-dependent manner with a monotonic time-dependent decrease of inspiratory burst frequency monitored by XII motoneuron discharge (n = 26 slices total: n = 6 at 2 μm, n = 6 at 5 μm, n = 6 at 10 μm, and n = 8 at 20 μm riluzole) (Fig. 5B). Riluzole concentrations as low as 5 μm reduced oscillation frequency and then completely blocked inspiratory rhythm generation (Fig. 5B). Lower concentrations (2 μm) consistently slowed (by 18.2 ± 6.8%), but did not eliminate network oscillations. The pharmacological profile for attenuation of network oscillations (Fig. 5B) with riluzole microinfusion resembled the profile for attenuation of NaP in individual pre-BötC neurons located in superficial layers of the slice (compare with Fig. 4B). Population burst amplitude and duration were also reduced in a concentration-dependent manner (33.8 ± 6.9% decrease in amplitude at 5–20 μm; 8.6 ± 3.9% decrease at 2 μm), before network activity stopped (Fig. 5C). All perturbations were rapidly reversible when microinfusion was terminated (Fig. 5A). We also verified site specificity of these disturbances of network activity with our microinfusion approach. Microinfusion of 20 μm riluzole (or 20 nm TTX below) after repositioning the pipette tips bilaterally at the same depth in the tissue, but 75–100 μm outside of the region of imaged pre-BötC activity (i.e., ∼175–200 μm from the center of imaged activity) failed to cause perturbations of network activity. We also confirmed that at the pipette tip locations that caused perturbations of inspiratory rhythm with the NaP blockers, microinfusion of control solution (standard slice perfusion solution) did not perturb network activity (Fig. 5B) with the microinfusion pressures applied (see Materials and Methods); higher perfusion pressures (≥30 mmHg) caused a depression of network activity, however. This site specificity was also confirmed for experiments with microinfusions of neuromodulators that caused network excitation (NaCN and SP, below) only when the microinfusion pipettes were positioned in the core of the pre-BötC as guided by the activity imaging.

Perturbations of frequency and inspiratory burst amplitude similar to those caused by riluzole were obtained during bilateral microinfusion of TTX (5–20 nm) (Fig. 6B,C) (n = 12 slices for each TTX concentration shown in Fig. 6C). Microinfused TTX rapidly and reversibly slowed network oscillations with a concentration- and time-dependent decrease in frequency (Fig. 6B), resulting in termination of network oscillations. The oscillations were rapidly and completely stopped by concentrations of TTX as low as 5 nm. There were comparatively small perturbations of the XII inspiratory burst amplitude (Fig. 6B,C). For comparison, we also analyzed perturbations of network activity by low concentrations of bath-applied TTX; these experiments also provided a basis for the studies (below) using pre-BötC island preparations as well as studies in slices where both bath-applied TTX and local manipulations of NaP or Leak in the pre-BötC were used. Bath-applied TTX also reversibly slowed and blocked network oscillations with relatively small changes in activity amplitude (n = 10 slices) (Fig. 6A,C), but the average time to attenuate/block rhythmic activity (at a given concentration) was slightly longer (e.g., 3 min vs 1.0 min for 50% reduction in burst frequency at 20 nm TTX) (Fig. 6C). Imaging of pre-BötC population activity verified complete loss of cellular activity (data not shown) when network activity stopped. The differences in time courses for disturbances of the inspiratory activity reflects the time differences for drug penetration into the tissue by diffusion with bath application (despite the thin slices used) versus convective delivery into the core of the pre-BötC, which appears to be more efficacious for rapidly establishing relatively uniform local drug concentrations in the tissue close to those in the microinfusion pipettes [e.g., see Lonser et al. (1999) and references therein for general convective microinfusion theory]. The end result of termination of rhythmic activity at steady state is the same for both approaches, however.

Figure 6.

Perturbations of network oscillations by low concentrations of TTX. A, B, Bath application of low concentrations of TTX (A) (n = 10), or continuous bilateral microinfusion (n = 12 slices) of low concentrations of TTX into the core of the imaged pre-BötC (B), slows and then stops network oscillations with time course dependent on TTX concentration. Immediate recovery occurs on bath washout or discontinuation of local microinfusion. C, Frequency (left) and amplitude (right) of network activity are both reduced, but frequency is predominately affected by local microinfusion or bath application of TTX.

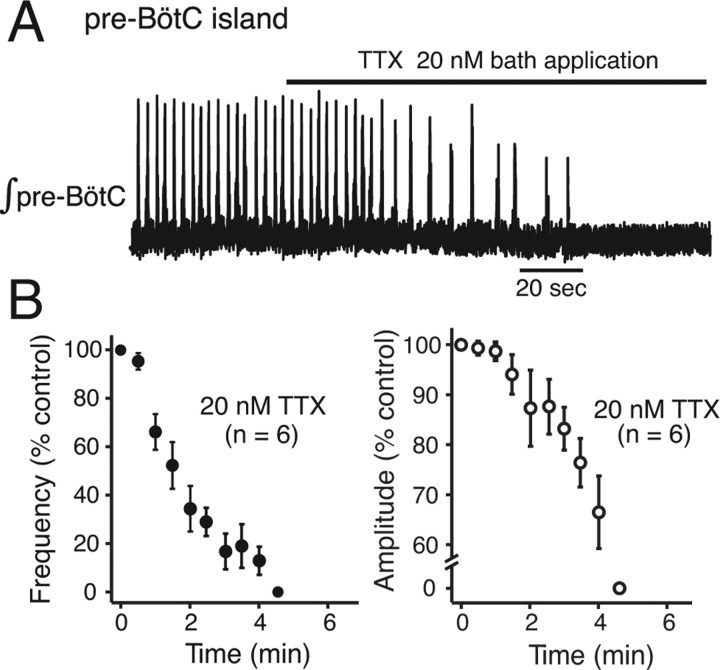
In pre-BötC island preparations (n = 6), bath-applied TTX (20 nm) also slowed and then stopped pre-BötC network oscillations as monitored by direct electrophysiological recordings of pre-BötC network activity (Fig. 7A). The time courses of the reductions in oscillation frequency and amplitude of population activity (Fig. 7B) were on average faster than with bath application in the intact slices [e.g., 1.5 min vs 3 min for 50% reduction in frequency (compare Figs. 6C, 7B)].

Figure 7.

Perturbations of network oscillations in isolated pre-BötC island preparations by low concentrations of TTX. A, Bath-applied TTX (20 nm) rapidly reduces the frequency and then stops network oscillations as recorded electrophysiologically from the pre-BötC population. Integrated pre-BötC population activity (∫pre-BötC) is shown from a representative island preparation. B, Frequency (left) and amplitude (right) of network activity are both reduced in the group of islands studied, but frequency is predominately affected by bath-applied TTX, similar to perturbations of inspiratory network activity in the intact slices (compare with Fig. 6).

For comparison with experimental results, we modeled effects of progressive, uniform attenuation of G_NaP in a heterogeneous excitatory network, consisting of both intrinsic bursters and nonintrinsically bursting neurons, both with NaP and Leak and subthreshold I–V relationships closely matching those found here experimentally (see Materials and Methods, Modeling methods). As G_NaP was reduced, the model network exhibited reductions in oscillation frequency, with relatively small perturbations of population activity amplitude, and ultimately termination of network oscillations (Fig. 8). Thus, our modeling results indicated that a hallmark of a heterogeneous excitatory network incorporating NaP and Leak is that reductions in population mean NaP conductance result predominately in large perturbations of frequency with smaller amplitude perturbations, as displayed by the in vitro network.

Figure 8.

Model pre-BötC network simulations examining effects of uniform reductions in G_NaP within the network. A, Examples of simulated network activity represented by population spike frequency histograms (average spikes per second; 30 ms bin size) at values of G_NaP density indicated; maximum conductance density of Leak was set at 118 pS/pF (refer also to point *1 in Fig. 13). B, Reducing G_NaP monotonically reduces and blocks primarily network oscillation frequency; amplitude of population activity is less sensitive to G_NaP attenuation. Simulations were performed with a heterogeneous population of excitatory neurons (n = 50), with I–V relationships and G_Leak and G_NaP distributions (see Materials and Methods, Modeling methods) within ranges found experimentally (see Results).

Augmentation of network oscillations by augmenting NaP

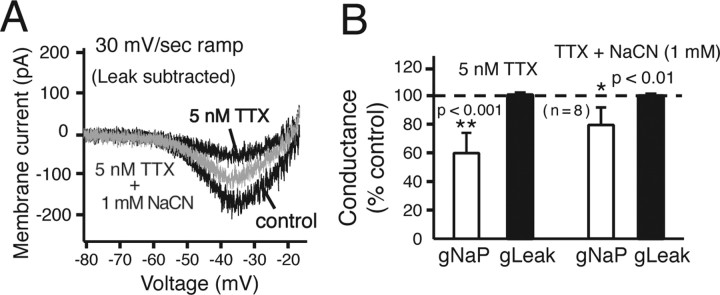
The modeling results (Fig. 8) indicated that augmenting NaP conductance independently of Leak conductance should increase oscillation frequency. We tested this prediction. From studies in other CNS neurons, cellular hypoxia is known to augment NaP (Hammarstrom and Gage, 1998, 2002; Horn and Waldrop, 2000). We therefore postulated that cellular hypoxia induced by NaCN (1 mm) would augment NaP. We examined this at the level of individual pre-BötC intrinsically bursting and nonintrinsically bursting inspiratory neurons. In bursting neurons, NaCN caused a small but statistically insignificant increase of peak NaP conductance (mean increase of 14.3 ± 8.8%; p > 0.05; n = 4) without affecting g_Leak as measured from ramp I–V curves, whereas there was a statistically significant increase (mean increase of 19 ± 3.5%; p < 0.05) in a group (n = 4) of nonbursting neurons. In another group of intrinsically bursting neurons (n = 8), we found that NaCN (1 mm) could significantly augment g_NaP after partial block of NaP by 5 nm TTX (34 ± 12.6% increase of g_NaP after NaCN) (Fig. 9A,B). This also occurred without affecting g_Leak (Fig. 9B).

Figure 9.

Augmentation of NaP at single pre-BötC neuron level by cellular hypoxia induced with NaCN. A, Ramp I–V relations (Leak subtracted) of a pre-BötC intrinsically bursting neuron showing partial block of NaP by 5 nm bath-applied TTX and subsequent NaP augmentation by bath-applied NaCN (1 mm). B, Histograms summarizing g_NaP and g_Leak values after partial NaP block with TTX (left histograms) and subsequent augmentation of NaP by NaCN (right); g_NaP could be almost restored (average of 80% of control values; n = 8 neurons) by NaCN, whereas g_Leak was unaffected.

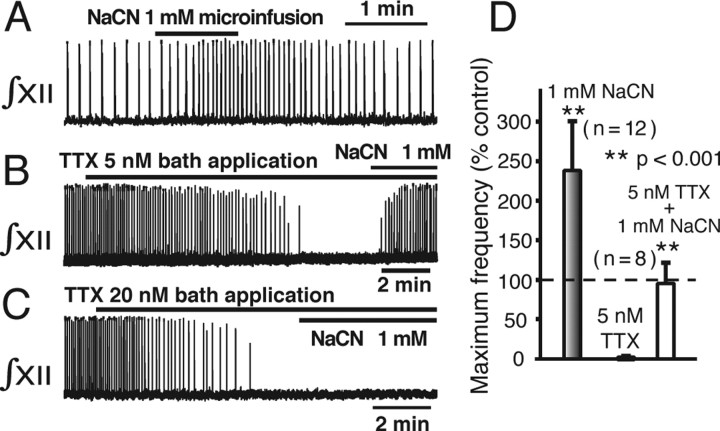
To test for a corresponding augmentation of network activity, we bilaterally microinfused NaCN into the pre-BötC at the concentration (1 mm) found to augment neuronal NaP, which reversibly increased network oscillation frequency (n = 8 slices) (Fig. 10A). We next continuously superfused the slices with TTX at concentrations (5 nm) sufficient to stop network oscillations (Fig. 10B,D), which were then rapidly reactivated by NaCN microinfused directly into the pre-BötC. However, at higher concentrations of TTX (20 nm), at which neuronal NaP should be completely blocked (Fig. 3), network oscillations could not be reactivated (n = 6) (Fig. 10C).

Figure 10.

Augmentation of pre-BötC network inspiratory oscillations by NaCN. A, Augmentation of network oscillations with bilateral microinfusion of NaCN (1 mm) into pre-BötC. B, Restoration of oscillations by microinfusion of NaCN after network activity was stopped by bath-applied 5 nm TTX. C, Failure to restore network activity by microinfusion of NaCN after elimination of network activity by 20 nm TTX. D, Histograms summarizing maximum oscillation frequency obtained with microinfusion of 1 mm NaCN under control conditions (left), reduction in frequency after 5 nm TTX (middle), and subsequent reactivation of activity with NaCN (right; n = 8 slices), which restores frequency to near control levels.

Independent and cooperative modulatory actions of Leak on network rhythm

Our modeling results also suggest that g_Leak can regulate pre-BötC network oscillatory activity either independently or cooperatively with NaP (see Fig. 13). We tested these predictions experimentally by (1) analyzing how altering g_Leak modulates pre-BötC neuronal and network oscillation frequency; and (2) determining whether reducing g_Leak (relative to g_NaP) after attenuating g_NaP can cooperatively restore network activity. This latter type of network reactivation experiment has been previously attempted with variable results (Del Negro et al., 2005), and has not been analyzed from the viewpoint of g_Leak–g_NaP (or any other set of membrane current) interactions.

Modulation of rhythm by Leak

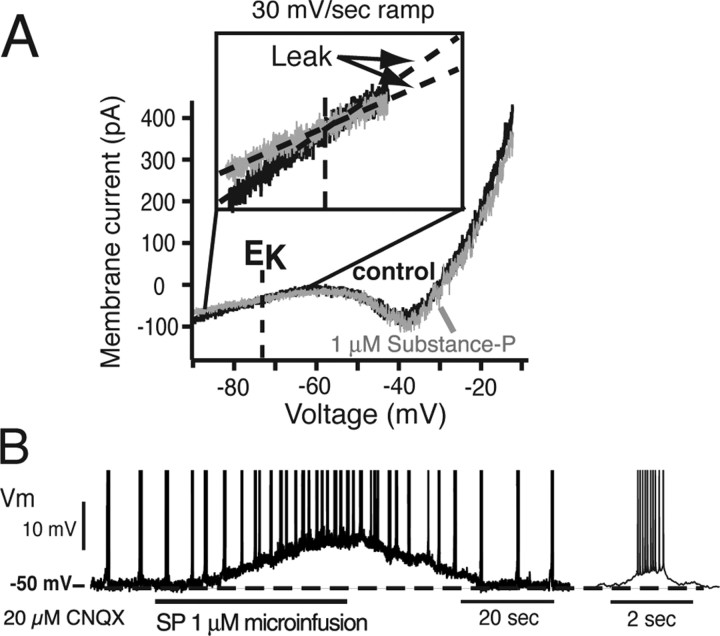
To alter g_Leak, we used SP, which is known to potently augment inspiratory oscillation frequency in slices (Johnson et al., 1996; Gray et al., 1999; Pena and Ramirez, 2004), and has been shown to modulate a K⁺ leak in other CNS neurons (Lepre et al., 1996; Ptak et al., 2000; Talley et al., 2000). We verified for a group of pre-BötC intrinsically bursting (n = 6) and nonbursting neurons (n = 6) that a K⁺ Leak conductance is reduced by SP (Fig. 11). Local application of SP (1 μm), via a pipette positioned just above the slice surface over the imaged pre-BötC and recorded neuron, significantly reduced g_Leak (by 15–30% range; mean decrease of 21 ± 6.4%, p < 0.01, for intrinsic bursters, and 19 ± 5.7%, p < 0.01, for nonbursters) without significantly affecting g_NaP (Fig. 11A). Ramp I–V relations obtained with SP intersected pre-SP I–V curves at −72.5 ± 2 mV (n = 12) (Fig. 11A), close to the calculated E_K (−73 mV) for our recording conditions. Consistent with these results, SP depolarized nonbursters (5.5 ± 2.4 mV; n = 6) and NaP-dependent intrinsic bursters (6.8 ± 4.1 mV; n = 6) and increased bursting frequency (by maximally a factor of three) (Fig. 11B) of intrinsic bursters after blocking synaptic transmission (see also Pena and Ramirez, 2004). We also confirmed that bilateral microinfusion of SP (1 μm) into the pre-BötC increased network oscillation frequency (Fig. 12A), consistent with previous observations (Johnson et al., 1996; Gray et al., 1999).

Figure 11.

Reduction in g_Leak and augmentation of intrinsic neuronal bursting by SP. A, Ramp I–V relations of pre-BötC intrinsic burster neuron showing reduction in g_Leak (see inset) by 1 μm SP continuously applied locally to cell by microinfusion pipette positioned just above slice surface. I–V curves before and after SP intersect at E_K (−73 mV). B, Membrane depolarization and augmentation of intrinsic bursting frequency (<20 μm CNQX) of a neuron (from A) during local SP application (current-clamp recording; action potentials have been artificially truncated).

Figure 12.

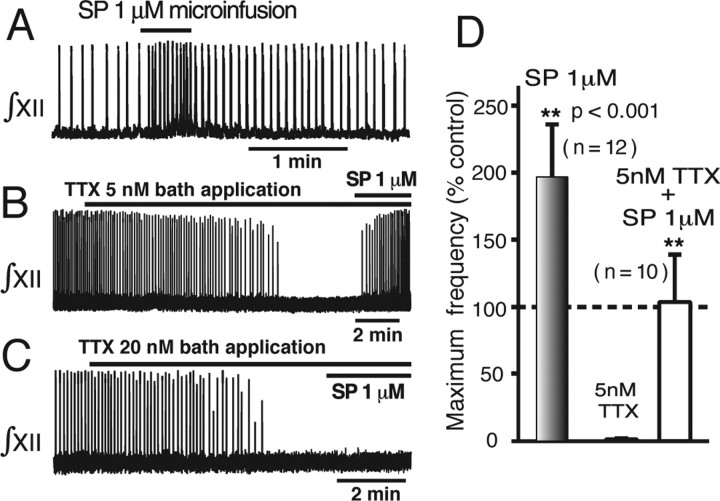
Augmentation of pre-BötC network activity by SP. A, Augmented network inspiratory oscillation frequency by microinfusion of SP (1 μm) bilaterally into pre-BötC. B, Restoration of network oscillations by microinfusion of SP after network activity was terminated by bath application of 5 nm TTX. C, Failure to restore network oscillations by SP microinfusion bilaterally into the pre-BötC after elimination of network activity by bath-applied 20 nm TTX. D, Histograms summarizing augmentation of oscillation frequency by SP under control conditions (left; n = 12) and after restoration of activity (n = 10 slices), when frequency returns to near control values.

Interactions of g_Leak and g_NaP in controlling network and cellular oscillations

We first superfused the slice with 5 nm TTX, which terminated network oscillations, and subsequently microinfused SP (1 μm) into the pre-BötC, which restored network oscillations in all cases (n = 10) (Fig. 12B,D). Our previous modeling studies have demonstrated the interplay between NaP and Leak in controlling intrinsic oscillatory bursting activity at the single-neuron level (Butera et al., 1999a; Purvis et al., 2007); furthermore, network simulations for a heterogeneous excitatory network consisting of a mixture of intrinsic bursters and nonintrinsic bursters (Fig. 13) show that relatively small reductions of the population mean Leak conductance, similar to those found experimentally with SP for individual neurons, should be sufficient to restore network oscillations after partial attenuation of population mean NaP conductance. However, network oscillations should theoretically not occur after complete block of NaP (Fig. 13). To test this, we continuously superfused the slice with TTX at concentrations (20 nm) found to completely block neuronal NaP (Fig. 3B). Under these conditions, SP microinfusion (1 μm) into the pre-BötC did not restore network activity in any experiment (n = 7 experiments) (Fig. 12C).

Our modeling results also indicated that with reductions in Leak conductance at a fixed G_NaP, as during reactivation experiments, the composition of intrinsic burster and nonburster neurons within the network changes. Some intrinsic bursters are converted to tonically spiking neurons, whereas a small fraction (e.g., 8/46 in supplemental Fig. 1C, available at www.jneurosci.org as supplemental material) of nonintrinsic bursters are converted to intrinsic bursters, depending on the magnitude of the reduction in g_Leak relative to g_NaP and the initial conditions of a given neuron [i.e., whether or not the neuron has a high enough g_NaP to support intrinsic bursting under any conditions (Butera et al., 1999a)]. This shift in network composition may explain network reactivation by SP under our experimental conditions. The concept that the extent of intrinsic bursting activity in the pre-BötC network can be regulated by neuromodulators such as SP has been described (Pena and Ramirez, 2004), and changes in network dynamics by the fractional composition of intrinsic NaP-dependent bursters and nonintrinsic bursters have been explored theoretically in detail (Purvis et al., 2007). We therefore examined a group of intrinsic and nonintrinsic burster neurons to determine whether a change in electrophysiological phenotype occurs as g_Leak was reduced by SP (1 μm) under conditions in which synaptic transmission was blocked. A few intrinsic bursters (2 of 8 tested) were converted to tonically spiking neurons, whereas we could not convert nonintrinsically bursting cells (n = 10) to intrinsic bursting behavior with the small SP-induced reduction in g_Leak (18.4–23.7% range). This was likely a result of the low initial values of g_NaP density in these nonbursters (41.1 ± 9.5 pS/pF) relative to g_Leak densities (131.0 ± 43.2 pS/pF); indeed, the majority of the nonbursters that we have analyzed in the present study have values of g_NaP relative to g_Leak densities that are too low to support intrinsic bursting even with much larger changes in g_Leak, as indicated by plots of g_NaP versus g_Leak for this data as presented in Purvis et al. (2007). This question of the possible conversion of electrophysiological phenotypes by neuromodulators requires more extensive experimental investigation.

Discussion

Our results indicate that generation and control of inspiratory rhythm in the pre-BötC in vitro can to an important extent be understood from contributions of NaP and Leak operating within a heterogeneous excitatory network (Butera et al., 1999b). Subthreshold I–V relations are dominated by g_NaP and g_Leak, where g_NaP conductance densities distinguish intrinsic bursters from nonintrinsic bursters, as we previously postulated (Del Negro et al., 2002b) but now demonstrate for a large sample of neurons (see also Purvis et al., 2007). Manipulations of g_NaP and/or g_Leak within the pre-BötC upregulated or downregulated network oscillations over a wide dynamic range. Importantly, attenuating NaP reduced oscillation frequency and could terminate rhythmogenesis. These results are the first direct evidence for the concept (Butera et al., 1999a,b; Smith et al., 2000) that NaP and Leak are fundamental for generation and control of rhythmogenesis in the pre-BötC in vitro.

Pre-BötC neurons have voltage- and calcium-activated currents (Smith et al., 2000; Richter and Spyer, 2001; Ramirez et al., 2004) contributing to repetitive spiking properties and inspiratory burst generation. Specifically, h-current (Mironov et al., 2000; Thoby-Brisson et al., 2000) and Ca²⁺-activated nonselective cationic current (CAN) (Pena et al., 2004; Del Negro et al., 2005) have been proposed to contribute to burst generation in some inspiratory neurons. NaP and Leak have the largest subthreshold conductance densities in the neurons studied here. We did not find pronounced rectification of I–V relations at hyperpolarized voltages that would indicate a major h-current contribution. We also did not find residual subthreshold inward currents after block of Na⁺ currents, consistent with observations that pre-BötC neuron Ca²⁺ currents are primarily high-voltage activated (Elsen and Ramirez, 2005). NaP-dependent intrinsic bursting is also not substantially affected by attenuating Ca²⁺ currents (Del Negro et al., 2001, 2005; Pena et al., 2004). The neuron models used here are biophysically minimal models. Sorting out how these other cationic currents may operate dynamically with NaP and Leak, including CAN, which has not yet been biophysically characterized in pre-BötC neurons, remains an important problem.

NaP as a ubiquitous pre-BötC neuronal property contributing to rhythm generation

Many CNS neurons have NaP that underlies spontaneous persistent spiking (Taddese and Bean, 2002; Do and Bean, 2003) and oscillatory activity (Llinas, 1988; Agrawal et al., 2001; Darbon et al., 2004; Wu et al., 2004). The contribution to respiratory network oscillations, however, has not been clearly resolved. In contrast to our results and an earlier report (Rybak et al., 2003), it has been suggested (Del Negro et al., 2005; Pace et al., 2007) that NaP does not play a role in generating inspiratory oscillations in neonatal mouse slices, whereas others (Pena et al., 2004) propose that NaP-dependent and CAN current-dependent bursting mechanisms collectively contribute to rhythm generation (but not NaP mechanisms alone) in mouse slices.

We suggest several explanations for these discrepancies. First, large perturbations of oscillation frequency would theoretically occur only when a uniform attenuation of NaP is achieved throughout the pre-BötC network. Perturbations of network activity amplitude without frequency perturbations (Del Negro et al., 2002a, 2005) can result from spatially and/or temporally nonuniform pharmacological attenuation of NaP (see supplemental Fig. 2, available at www.jneurosci.org as supplemental material); this may occur with bath-applied blockers in thick (500–600 μm) mouse slices used in these previous studies. We have convectively delivered NaP blockers by microinfusion into the pre-BötC to minimize local tissue concentration gradients. This approach has also been used recently in neonatal mouse slices [but without activity imaging for placement of pipette tips in the pre-BötC (Pace et al., 2007)], in which no disturbances of rhythm generation were found with NaP blockers. These results differ from ours in neonatal rat slices and isolated pre-BötC islands. Possibly rhythmogenic mechanisms operating in mice are different from rats; this issue needs to be resolved.

Second, contributions of NaP and rhythm generation mechanisms depend on network state. We have shown that, in a more intact brainstem network, only small perturbations of inspiratory rhythm occur after NaP block (Paton et al., 2006; Smith et al., 2007). We postulate that this insensitivity results from network mechanisms (tonic excitation and phasic inhibition) operating in the pre-BötC (Smith et al., 2007), which are reduced or absent in our isolated slice and island preparations (Smith et al., 2000; Richter and Spyer, 2001). The thick mouse slices used previously contain not only the pre-BötC but also flanking network components, which may introduce such additional mechanisms. Thus, only when the network is isolated/reduced (Smith et al., 2007) as in our thin slice or pre-BötC island preparations, unmasking the pre-BötC's autorhythmic properties (Koshiya and Smith, 1999; Johnson et al., 2001), or in other states such as during CNS anoxia in the more intact network when “gasping” inspiratory oscillations occur, does rhythm generation depend critically on NaP (Paton et al., 2006).

What rhythmogenic properties does NaP confer to the pre-BötC network? This issue has been framed around a debate (Del Negro et al., 2002; Rybak et al., 2003; Pena et al., 2004; Ramirez et al., 2004) about whether “pacemaker” neurons (i.e., NaP-dependent intrinsic bursters as well as CAN-dependent bursters) versus “emergent” network properties underlie inspiratory oscillations (Feldman and Del Negro, 2006).

NaP-dependent bursters clearly exist in the pre-BötC in vitro and also in a more intact, mature respiratory network (Paton et al., 2006). However, heterogeneous networks with various g_NaP and g_Leak distributions have a continuum of dynamic states that give rise to oscillations, even in the absence of bursting “pacemaker” neurons (Purvis et al., 2007). Network oscillations can emerge from interactions between excitatory synaptic currents, NaP, and Leak, in which subthreshold activation of NaP promotes network-wide synchronized bursting. Slow inactivation of NaP (Butera et al., 1999a; Magistretti and Alonso, 1999), driven by excitatory synaptic currents and bursting, leads to synchronized population-level burst termination, whereas slow recovery from inactivation promotes regenerative activation of network bursting (Butera et al., 1999a,b). NaP can therefore dynamically organize oscillations at not only the single-cell level, but also the network level.

Thus regardless of whether or not rhythm generation in vitro can be attributed to cellular “pacemaker” properties per se, it is clear from our results that NaP, as a common conductance in pre-BötC neurons, contributes to rhythm generation, at least in the isolated neonatal rat pre-BötC network in vitro and in certain states in the more intact, rat respiratory network (Paton et al., 2006). This conclusion is supported by our results that once g_NaP is reduced to low enough levels, network oscillations cannot be generated in reactivation experiments. The augmentation of NaP and network oscillations by cellular hypoxia shows that NaP can be modulated, consistent with a homeostatic role of NaP in maintaining network activity during CNS hypoxia (Pena et al., 2004; Paton et al., 2006).

Nature of Leak currents

Leak is a K⁺-dominated conductance that can both promote and terminate oscillatory activity at cellular and network levels. We show that an excitatory neuromodulator (SP) implicated in rhythm generation control (Gray et al., 1999) operates through g_Leak. We have other evidence (S. Smerin, H. Koizumi, and J. C. Smith, unpublished observations) that TASK channels (North, 2000; Bayliss et al., 2003) mediate a major K⁺ current component of Leak in pre-BötC neurons. TASK channels, as background conductances, are modulated in other neurons (Bayliss et al., 2003) by a variety of neurochemical signals (Talley et al., 2000), including SP and H⁺. A Na⁺-dependent leak current has been implicated in SP-induced depolarization of mouse inspiratory neurons (Pena and Ramirez, 2004). Our data indicate that there is a relatively small Na⁺ or mixed cationic inward current that opposes the outward K⁺ current in establishing E_Leak. Our voltage-clamp analysis indicates that SP reduces the dominant K⁺ current component in some pre-BötC neurons. In recent work (T. Yamanishi, K. Ptak, and J. C. Smith, unpublished observations), however, we found that SP also altered g_Leak in a group of pre-BötC neurons, but caused a several millivolt depolarized shift of neuronal I–V relations, causing a more depolarized value of E_Leak than can be accounted for by reduction of a K⁺ current alone. This suggests that SP may also simultaneously augment the inward cationic component of Leak in some neurons (Shen and North, 1992) (see discussions in Pena and Ramirez, 2004). The nonselective, Na⁺ leak channel [NALCN (Lu et al., 2007)] is a possible candidate for this component. Furthermore, additional G-protein coupled K⁺ channels (e.g., GIRK channels) may also contribute to Leak and neuromodulatory control of pre-BötC neurons (Johnson et al., 1996). Our model predicts that regardless of the how total g_Leak is changed, the general trends shown for modulation of inspiratory rhythm in Figure 13 (in that case for changes in the K⁺ component) would apply. Dissection of Leak into discrete channel components remains an important problem.

In general, our experimental and modeling results suggest that Leak and NaP are key conductances that can be targeted for modulation of inspiratory rhythm, either independently or coordinately, by neurochemical signals that control generation of pre-BötC oscillatory activity.