A Biologically Realistic Model of Contrast Invariant Orientation Tuning by Thalamocortical Synaptic Depression

Abstract

Simple cells in layer 4 of the primary visual cortex of the cat show contrast-invariant orientation tuning, in which the amplitude of the peak response is proportional to the stimulus contrast but the width of the tuning curve hardly changes with contrast. This study uses a detailed model of spiny stellate cells (SSCs) from cat area 17 to explain this property. The model integrates our experimental data, including morphological and intrinsic membrane properties and the number and spatial distribution of four major synaptic input sources of the SSC: the dorsal lateral geniculate nucleus (dLGN) and three cortical sources. The model also includes synaptic properties of these inputs. The cortical input served as sources of background activity, and visual stimuli was modeled as sinusoidal grating. For all contrasts, strong synaptic depression of the dLGN feedforward afferents compresses the firing rates in response to orthogonal stimuli, keeping these rates at practically the same low level. However, at preferred orientations, despite synaptic depression, firing rate changes as a function of contrast. Thus, when embedded in an active network, strong synaptic depression can explain contrast-invariant orientation tuning of simple cells. This is true also when the dLGN inputs are partially depressed as a result of their spontaneous activity and to some extent also when parameters were fitted to a more moderate level of synaptic depression. The model response is in close agreement with experimental results, in terms of both output spikes and membrane voltage (amplitude and fluctuations), with reasonable exceptions given that recurrent connections were not incorporated.

Introduction

The connection between the dorsal lateral geniculate nucleus (dLGN) of the thalamus and layer 4 of the primary visual cortex in cat is one of the most studied connections in the CNS, yet there is still no universally accepted theory of the role of this connection in generating the “simple” cortical receptive fields (RFs) from the center-surround RFs of the dLGN. The feedforward model of cortical processing suggested by Hubel and Wiesel (1962) retains its appeal because of its text-book simplicity and because it has garnered experimental support and refutation in almost equal measure (Sillito, 1975; Sillito et al., 1980; Burr et al., 1981; Sclar and Freeman, 1982; Ferster et al., 1996; Reid and Alonso, 1996) (for review, see Martin, 1988; Sompolinsky and Shapley, 1997). The fundamental flaw in this model is its failure to explain why the amplitude of the response of dLGN and cortical cells varies according to the contrast of the stimulus but the tuning width of the orientation response of simple cells does not: it is contrast invariant (Sclar and Freeman, 1982). An additional problem with this model is that it predicts that increases in contrast of orthogonal stimuli will elevate both the subthreshold membrane voltage and the firing rate; this is rarely found in simple cells.

Contrast invariance, which can be viewed as a gain-control mechanism, is not present at the level of the dLGN. Most modeling studies assume that this gain-control mechanism must arise from local cortical interactions, e.g., from a divisive inhibitory mechanism (Rose, 1977; Morrone et al., 1982; Worgotter and Koch, 1991; Carandini and Heeger, 1994; Ben-Yishai et al., 1995; Sompolinsky and Shapley, 1997; Troyer et al., 1998; Teich and Qian, 2006). Direct experimental evidence for any of the proposed mechanisms is lacking.

With the discovery that the geniculocortical synapse in the cat depresses with repeated stimulation (Stratford et al., 1996; Boudreau and Ferster, 2005), modeling studies have shown that nonlinear frequency-dependent synaptic transmission may contribute to response properties of cells in primary visual cortex (V1), including contrast-dependent phase advance, change in shape of the temporal frequency, contrast adaptation, etc. (Abbott et al., 1997; O'Donovan and Rinzel, 1997; Chance et al., 1998; Senn et al., 1998; Kayser et al., 2001; Carandini et al., 2002). Could the feedforward thalamocortical depressing synapses, on their own, provide the mechanism required for generating contrast invariance? Different experimental works show diverse levels of thalamocortical synaptic depression (Stratford et al., 1996; Boudreau and Ferster, 2005). The degree of depression will have a significant effect on the response properties of cells in V1, including contrast invariance.

To explore these issues, we developed a biologically realistic model of the L4 spiny stellate cells (SSC) with simple RF. Such detailed compartmental models are very rare because comprehensive biophysical, morphological, and synaptic data are lacking for most neuron types. However, exploring the responses of a biophysically realistic neuron embedded in an active network provides an important tool for studying whether the specific computation in question (e.g., contrast-invariant orientation tuning) can emerge directly from the experimental data.

Materials and Methods

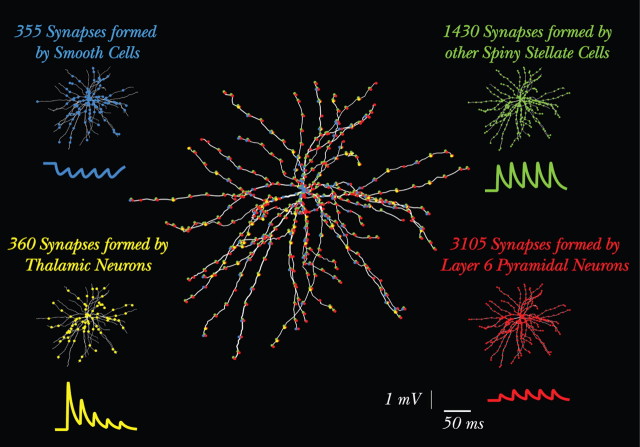
A layer 4 SSC of cat V1, recorded in vivo, was reconstructed and physiologically characterized and served as a basis for modeling of the present study (Fig. 1). The cell is one of the six SSCs characterized in detail by Anderson et al. (1994a,b); it had a simple RF with two subfields and showed directional selectivity.

Figure 1.

Model overview: morphology of the modeled SSC and its synaptic input. The modeled L4 SSC is shown in the center with all ∼5500 synapses depicted in circles (many synapses overlap because of the segmentation in NEURON). In each of the four corners, the circles depicting the synapses from only one input source are superimposed on the SSC model, using the same color for a given input source (blue, inhibition; green, SSCs; yellow, dLGN; red, L6 input). For each input source, there is also a somatic voltage trace showing the short-term synaptic dynamics of this specific synapse. These traces were computed after the activation of a single axon from the corresponding input source. In this case, for all four input sources, the synapses belonging to a single axon contacted the dendritic tree at a distance of ∼50 μm from the soma and were activated at 40 Hz. Note the different number of synapses, amplitudes, and the short-term plasticity of each of the inputs. In the present study, all cortical input sources are activated for the purpose of generating realistic background activity for the modeled SSC, but there are no intracortical interactions.

Model.

Dendritic spines were incorporated globally into the membrane of the modeled cell by modifying the length and diameter of the parent dendrites while keeping their original electrotonic length (Stratford et al., 1989). A total of 2000 dendritic spines was assumed (Anderson et al., 1994a,b), each having an area of 1 μm²; density of spines on the dendritic tree was 0.35 spine/μm. The initial segment of the modeled axon was taken from Mainen and Sejnowski (1996). It was 15 μm long and had a diameter of 0.78 μm.

Passive parameters.

Membrane resistivity and capacitance were set to R_m = 12 kΩcm² and C_m = 1 μF/cm², respectively. Axial resistivity was R_i = 200 Ωcm and resting potential was V_rest = −65 mV. The resulting model input resistance was R_in = 76 MΩ with membrane time constant, τ_m = 12 ms. All measures are well within the range of experimental results (Stratford et al., 1996; Tarczy-Hornoch et al., 1998; Anderson et al., 2000; Bannister et al., 2002).

Active channels.

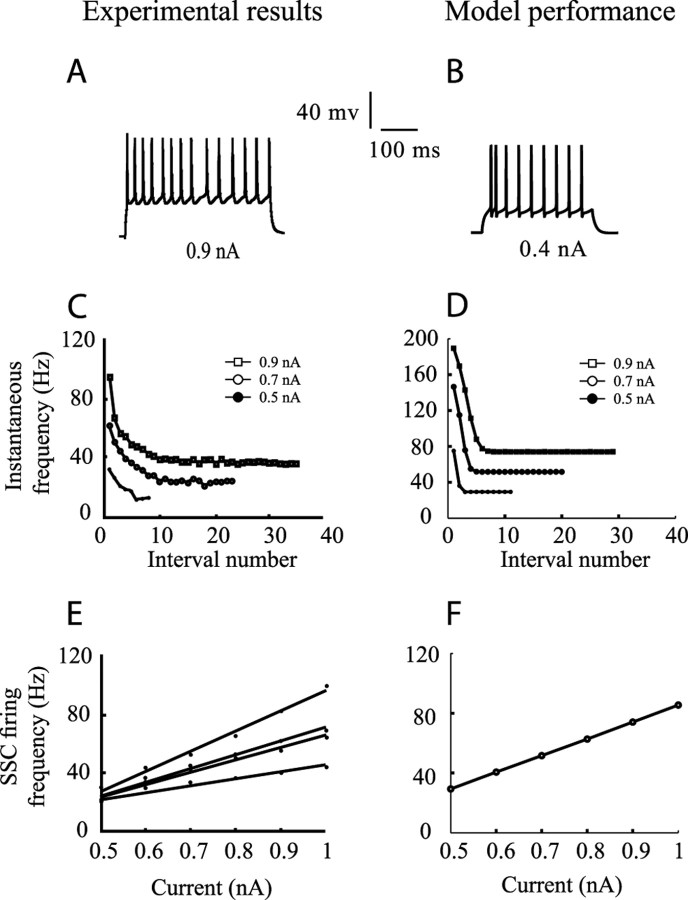
Individual ion channel properties in these cells were not measured experimentally. We therefore incorporated active membrane conductances that provide the model with similar firing characteristics as recorded in vitro (Stratford et al., 1996; Ahmed et al., 1998; Bannister et al., 2002). We assumed fast sodium and potassium currents underlying the spike mechanism based on Bernander et al. (1994), calcium and calcium-dependent potassium currents for the adaptation of the firing frequency based on Bernander et al. (1994), and an A-current to linearize the current/frequency (I/f) curve based on Huguenard and McCormick (1992). Excitable currents were inserted to the soma, and the axon and the dendrites were assumed to be passive. Figure 2 compares a typical firing characteristic of V1 SSC in vitro (left column) with the performance of our model (right column). We also tried other sets of parameters that, for example, yield a lower firing threshold. These modifications had little effect on the results.

Figure 2.

Comparison between in vitro recordings of SSCs (left column) and model response (right column). A, Response of an SSC to step current depolarization; B, response of the modeled SSC to step current injection. C, D, Adaptation of firing frequency in experiments versus model, correspondingly. Measured instantaneous firing frequencies are marked for three corresponding current injections denoted in insets. E, I/f curves at steady state for four different SSCs in experiments; F, model I/f curve at steady state. Data in A, C, and E are taken from the laboratory of Stratford et al. (unpublished results).

Modeling synapses.

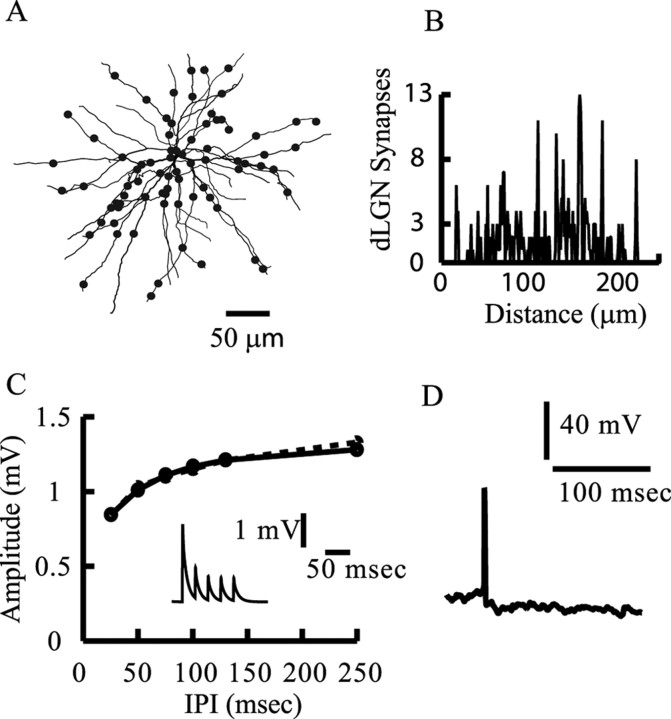
dLGN synapses were distributed on the model dendritic tree (Figs. 1, 3), according to the detailed synaptic maps (Ahmed et al., 1994; Anderson et al., 1994a,b; Binzegger et al., 2004). The distribution of dLGN synapses was divided to proximal synapses (below 50 μm from the soma) and distal synapses (above 50 μm from the soma). A total of 360 dLGN synaptic contacts (36 proximal and 324 distal) (Figs. 1, bottom left, 3B) were estimated (Ahmed et al., 1994; Anderson et al., 1994a,b; Binzegger et al., 2004).

Figure 3.

Modeling the thalamic input. A, The modeled SSC with 360 synaptic contacts (90 axons) arising from the dLGN (each filled circle represents 4 dLGN contacts). B, Distribution of dLGN synaptic contacts as a function of distance from the soma. C, Strong short-term synaptic depression of the dLGN-to-SSC input. The amplitude of the second EPSP is shown as a function of the interpulse intervals (IPI) in a paired-pulse protocol. Model, Dashed line; experiment, continuous line (taken from Stratford et al., 1996). For large interpulse intervals, the second EPSP recovers from depression and attained the amplitude of the first EPSP of 1.35 mV. The inset shows the modeled short-term depression for a single dLGN input at interpulse intervals of 25 ms (40 Hz). D, Model firing output in response to random and asynchronous activation of all 90 dLGN afferents converging onto the modeled SSC; each dLGN afferent fires randomly at 20 Hz. Because there are only 360 dLGN synapses with a strong synaptic depression, only one spike is elicited in this case.

We next calibrated the strength of a single thalamic synapse as follows. (1) We assumed four synaptic contacts per axon (Freund et al., 1985a,b), implying that 90 axons from dLGN converge onto a single SSC. This number is similar to that assumed by Troyer et al. (1998); see also similar estimation in the case of the rat barrel cortex (Bruno and Sakmann, 2006). All contacts belonging to one axon were activated synchronously. (2) We fit the EPSP amplitude and shape indices generated by the modeled dLGN synapse to the experimentally measured average EPSP. The activation of a single dLGN axon generates, on average, a somatic EPSP with amplitude of 2 mV (Stratford et al., 1996; Bannister et al., 2002); To fit the EPSP amplitude and shape indices to experimental results, we activated each of the 90 dLGN axons individually, measured the resultant EPSPs, and averaged over all EPSPs. We then used the NEURON automatic fitting tool to repeat the process and set parameters to obtain an optimal fit. We found that, to obtain an average peak EPSP of 2 mV, we had to assume that the peak conductance at each dLGN contact is 1.5 nS; the kinetic parameters for this input are given below.

The LGN–V1 connection also exhibits short-term depression. In our model, the level of depression varies from strong depression as found in vitro (Stratford et al., 1996) and for polysynaptic input in vivo (Boudreau and Ferster, 2005), through moderate depression as found for monosynaptic input in vivo (Boudreau and Ferster, 2005), to a case of no depression at all as a reference. We modeled short-term synaptic plasticity based on Varela et al. (1997). We used the NEURON automatic fitting tool to adjust the parameters that control synaptic depression (D1; τ_D1 in the model synapse) and to fit the model response to the experimental data.

Synaptic conductance change was modeled as a sum of two exponents (rise and decay time constants, τ₁ and τ₂, respectively) and a peak conductance change, g_max. Parameters were uniform across all dLGN synapses. For a single dLGN contact, g_max = 1.5 nS, τ₁ = 0.4 ms, and τ₂ = 0.5 ms. For the strong depression, modeled fit yielded D1 = 0.17, and τ_D1 = 121.3 ms. For the moderate depression, D1 = 0.34, τ_D1 = 69.5 ms, F = 0.75, and τ_F = 21.46 ms. In the case of no depression, D1 = 1 and F = 0. The summary of the model fit to experiments is provided in Figures 3C and 6.

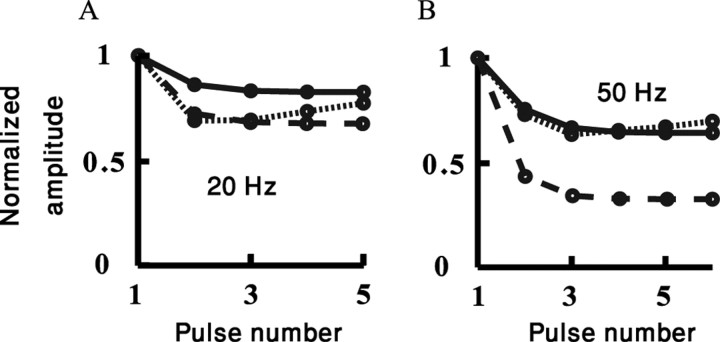
Figure 6.

Fit of modeled dLGN-to-SSC depressing synapses to a train of stimuli. The amplitude of the nth EPSP in a train is shown as a function of the pulse number in the train at 20 Hz (A) and 50 Hz (B). Responses are normalized to the first EPSP amplitude. Dotted line, In vivo recordings, monosynaptic input (Boudreau and Ferster, 2005); continuous line, model with moderate depression; dashed line, model with strong depression. Note the similarities in depression for the 20 Hz and the differences in depression for the 50 Hz dLGN stimulation.

We repeated this procedure for the rest of the input sources of the SSC (Fig. 1). Other SSCs from L4 contribute 1430 synapses onto our model SSC, with three synaptic contacts per axon (476 axons). Pyramidal neurons in layer 6 contribute 3105 synapses, with two synaptic contacts per axon (1552 axons). Inhibitory basket cells in L4 form 355 synapses with our SSC model, with five synaptic contacts per axon (71 axons only). These numbers and distributions of synapses are based on detailed experimental work (Martin et al., 1983; Martin and Whitteridge, 1984; Freund et al., 1985b; Ahmed et al., 1994, 1997; Anderson et al., 1994a,b; Stratford et al., 1996; Tarczy-Hornoch et al., 1998; Bannister et al., 2002; Binzegger et al., 2004).

The synapse model described by Varela et al. (1997) was also used for the other three input sources. The modeled synapses from other SSC in L4 had no short-term plasticity; for this input, the parameters for each individual synaptic contact were g_max = 0.8 nS, τ₁ = 0.59 ms, and τ₂ = 0.59 ms. For the L6 (facilitatory) input, g_max = 0.45 nS, τ₁ = 0.4 ms, τ₂ = 0.6 ms, D1 = 0.0017, τ_D1 = 11.3 ms, F = 2.67, and τ_F = 21.9 ms. For the inhibitory basket cell synapses (facilitatory at high frequency), g_max = 0.53 nS, τ₁ = 0.55 ms, τ₂ = 6.5 ms, D1 = 0.56, τ_D1 = 45.24 ms, F = 2.53, and τ_F = 6.6 ms. The battery for the inhibitory synapses was set to −75 mV (Tarczy-Hornoch et al., 1998) and 0 mV for the excitatory synapses. The quality of the fit for the synapses of the rest of the input sources was just as good as the fit of the dLGN shown in Figure 3 (data not shown). NEURON hoc file (Hines, 1989; Hines and Carnevale, 1997) of the model can be found at http://www.spike.ls.huji.ac.il/∼ybanitt/SSC_model/SSC_model.tar.gz.

Note that, for this study, the whole population of cortical synapses was activated only for serving as a background input impinging randomly at the modeled SSC. Thus, in the present study, there are no explicit recurrent connections. Unless otherwise mentioned, this baseline activity was implemented by the activation of L4 and L6 synapses at 2 Hz and the basket cells at 5 Hz. This background activity generated a spontaneous output firing of 2 Hz in the modeled SSC.

Modeling dLGN input to SSC after visual stimulation.

We used a standard model of sustained dLGN X cells that acts as a center-surround spatiotemporal filter convolved with the luminance of the drifting grating stimulus (Maex and Orban, 1996). This convolution produced a temporal waveform of firing frequency that depended on the contrast of the visual input (Fig. 4A); this temporal waveform was then used with a Poisson process to generate spike times (see below).

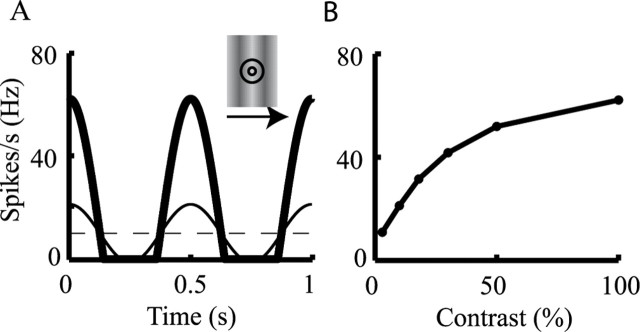
Figure 4.

Modeling dLGN response to visual input. A, Temporal waveform of firing rates of a dLGN afferent in response to drifting grating at 2 Hz at low contrast of 10% (thin line) and high contrast of 100% (thick line) (see Eq. 4 in Materials and Methods). Inset illustrates a grating stimulus, drifting at the indicated direction. Circles denote the center and surround RF of the dLGN afferent. Dashed line depicts the spontaneous firing rate of the dLGN axons (10 Hz). B, Contrast–response function, showing maximal dLGN response to six different contrasts (model was constructed to fit the results of Sclar, 1987) (see Materials and Methods).

The center and surround spatial filters of the RF were each modeled by two-dimensional Gaussians. The center and surround temporal filters were each modeled as a difference between two α functions. To compute the averaged firing rate, R, of a dLGN afferent at time t, the convolution of the surround spatiotemporal filter with the luminance of the stimulus, I, was subtracted from the convolution of the center spatiotemporal filter with the stimulus. The result was then multiplied by a nonlinear contrast–response function A(C) and added to a rate of spontaneous activity, R_b:

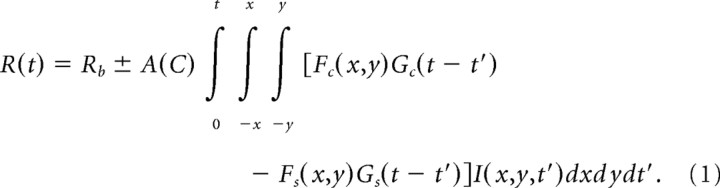+ and − signs are for ON-center or OFF-center afferents, respectively. Center, c, and surround, s, spatial filters, F(x,y), were as follows:

with σ_c = 0.3° and σ_s = 1.5°. Temporal filters, G(t), were as follows:

with α_c = 8 ms, α_s = 16 ms, and β = 32 ms (Maex and Orban, 1996). The luminance values of I ranged spatially in a sinusoidal manner from −1 (dark) to 1 (light), and the stimulus drifted at a rate of 2 Hz (we got similar results using 4 Hz; data not shown). The contrast–response function is shown in Figure 4B; it is similar to the contrast–response functions from Sclar (1987). We also used the contrast–response function from Cheng et al. (1995):

where C is the contrast, C₅₀ = 0.3, p = 1.7, and K = 3.7; both functions gave the same results. Spontaneous uncorrelated (background) activity of dLGN afferents was set to R_b = 10 Hz (Bullier and Norton, 1979; Mastronarde, 1992), implying that the dLGN input is already rather depressed before the visual input is presented (Boudreau and Ferster, 2005).

Finally, the averaged firing rate, R(t), was used as a probability for a Poisson spike generator to emit a spike at time (t) and activate a dLGN axon. If interspike intervals were shorter then a refractory period of 3 ms, spike times were reselected. A response R(t) of a single dLGN afferent to the drifting grating is shown in Figure 4A.

The RFs of dLGN afferents were spatially arranged in a lattice, whereby the RFs of every two adjacent afferents are spaced by a distance of a center RF radius [similar to retinal ganglion cells (Wassle et al., 1981)]. The 90 dLGN afferents were arranged in an OFF–ON–OFF spatial arrangement, corresponding to three subfields of V1 simple cells. The subfield aspect ratio (subfield length/subfield width) was 3.3 (for review, see Ferster and Miller, 2000), and each subfield contained 30 afferents (lattice of 10 × 3).

To explore the robustness of our results, we also tried other aspect ratios. In Figure 10B, we used an aspect ratio of 1.75, with 28 afferents per subfield (lattice of 7 × 4). Because that gives only 84 afferents (instead of 90), in this simulation, we multiplied g_max of each dLGN synapses by 90/84 (1.07).

Figure 10.

Membrane voltage fluctuations and aspect ratio for the strong depression parameters. A, Tuning curve of the peak-to-peak fluctuations of the averaged voltage for different contrasts (colors as in Figs. 5–9). B, Tuning curve of the spikes for a model with subfield aspect ratio of 1.75. The tuning curve is broader than for an aspect ratio of 3.3 (as was used throughout), but it remains contrast invariant.

The tuning curves (TCs) were normalized by subtracting the minimal value of the response from the response curve for each contrasts and then dividing by the maximal value. We then used Matlab (MathWorks, Natick, MA) to find the best Gaussian fit to the normalized data.

Last, it is typically assumed that a biologically realistic model such as the one described here is computationally unwieldy. However, the simulation time of our model is only fourfold slower than real time when using an AMD (Sunnyvale, CA) ATHLON 64 bits 2 GHz processor, running Linux, e.g., a simulation of 15 s lasts less than 1 min run time.

Results

We first tested the response of the modeled cell to random (asynchronous) input from the 90 dLGN axons each activated at 20 Hz using the strong depression (Fig. 3C), without the activation of the three cortical input sources. Only one spike (sometimes two spikes) was evoked at early times (when the dLGN depression is not yet at its steady state). At later times, because of the strong depression of the dLGN input, no additional spikes were initiated in the modeled L4 cell. In fact, for any input frequency, when the thalamocortical synapses were driven into a steady state, the dLGN input alone could no longer evoke spikes at all (data not shown). We therefore activated the other three modeled cortical input sources as a background input, so that the modeled SSC fires at an average rate of 2 Hz (see Materials and Methods) and to this was added the visual stimuli.

Suprathreshold response to visual stimuli

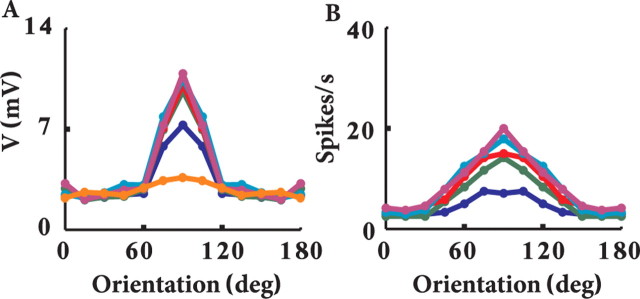
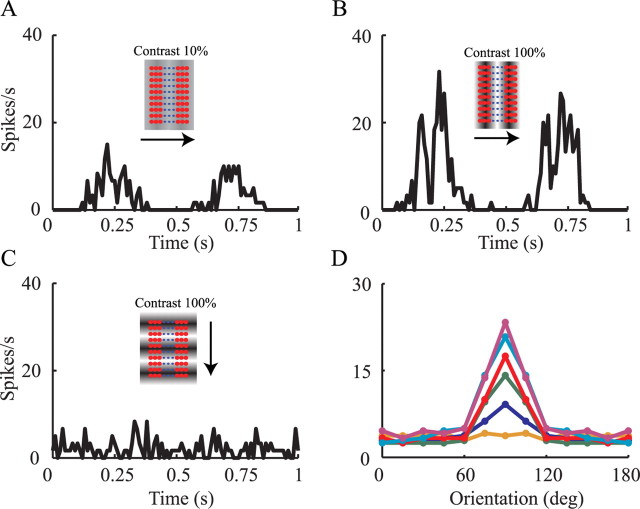
We first tested the model in which the dLGN input has strong synaptic depression. Figure 5A shows the firing rate of the model in response to a drifting grating at the preferred orientation and at a temporal frequency of 2 Hz and 10% contrast (Fig. 5A, inset). The peak averaged firing rate of the model is 16 Hz (Fig. 5A). When the same stimulus was presented at 100% contrast, the average peak firing rate was 36 Hz (Fig. 5B). In both cases, the maximal response is attained when the stimulus is in-phase with the corresponding model subfields, as illustrated by the insets in Figure 5, A and B, i.e., the grating (light/dark) are superimposed on the (ON/OFF) center afferents that form the (ON/OFF) subfields of the SSC model. In this position, the stimulus coactivates all thalamic afferents and generates enough depolarization (Fig. 5A) so that, despite the synaptic depression, the peak firing of the modeled cell is significantly enhanced. In this optimal degree of synchronization, even a slightly stronger input leads to a notable increase in output firing. The response of the cell to the preferred orientation is therefore contrast dependent. When the stimulus is out of phase, the dLGN neurons hardly fire and the cortical neuron falls silent (Fig. 5A,B). Thus, the phase dependence of the receptive field of the simple cell is essential for its response.

Figure 5.

Firing response of modeled SSC to visual input. Firing rates in A–C are calculated by binning the output spike train to 40 ms bins and averaging over 60 cycles of 1 s each. A, Response rate for preferred stimulus at 10% contrast; B, response rate for preferred stimulus at 100% contrast. C, Response rate for orthogonal stimulus at 100% contrast. Insets illustrate stimuli drifting at indicated direction (arrow). Small circles depict the center of the RFs of 90 dLGN afferents. Red circles are OFF center RFs, whereas blue circles are ON center RFs. D, Tuning curve of the peak of the average response, for each orientation and for different contrasts at bins of 40 ms (from lower to upper curves, contrast is 3, 10, 18, 30, 50, and 100%). Note the emergence of tuning width contrast invariance.

Figure 5C shows the model response to grating of 100% contrast drifting at the orthogonal (nonpreferred) orientation (Fig. 5C, inset). The model output is very much like the output obtained with background input alone. The same stimulus at 10% contrast generates a similar response (data not shown). The orthogonal orientation stimulus always coactivates approximately half of the dLGN afferents (Fig. 5C, inset), for both high and low contrasts. This reduced number of activated dLGN afferents, together with the sharp depression of the dLGN synapses with increased input frequency (Abbott et al., 1997) and the saturating contrast–response functions (Fig. 4B), produces hardly any change in the response to both low and high contrasts. Thus, in the orthogonal orientation, the response is contrast invariant (Fig. 5D). A more complete explanation of this result is discussed in the text corresponding to Figure 8.

Figure 8.

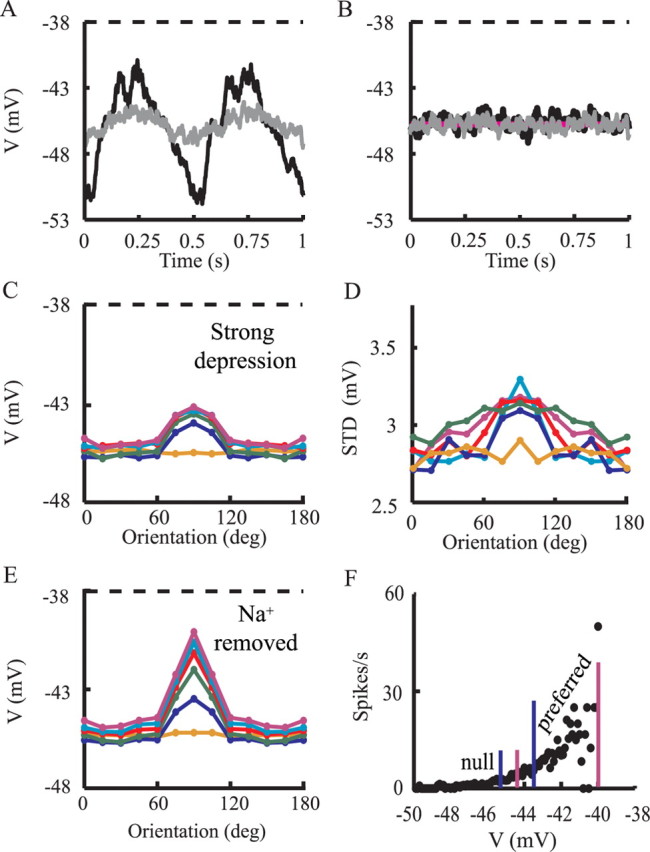
Membrane voltage responses to visual stimuli. A, Averaged voltage responses for preferred stimuli at contrast of 3% (gray line) and contrast of 100% (black line). Dashed line shows threshold for spike firing. B, Averaged voltage responses for orthogonal stimuli at contrast of 3% (gray) and contrast of 100% (black). Purple line shows average voltage without visual stimulus (background activity as described in Materials and Methods). C, Tuning curve for the peak averaged membrane potential for time bins of 40 ms. D, As in C but for the SD of the membrane potential. E, As in C but for a model without the sodium channels. F, V/f curve for the model. Blue lines (left and right) indicate the average membrane voltage for 10% contrast (at orthogonal and preferred orientations). Pink lines (left and right) indicate the average membrane voltage for 100% contrast (at orthogonal and preferred orientations, respectively).

The orientation TC for the maximal response to the drifting grating visual input is plotted for six different contrasts in Figure 5D. As can be seen, the width of the orientation tuning is contrast invariant, as found in vivo (Sclar and Freeman, 1982; Anderson et al., 2000). Again, this is a result of the combined effect of synaptic depression and the spatiotemporal organization of the feedforward model. In general, synaptic depression acts to reduce the differences in response to different contrasts. For orthogonal stimulus, in which only half of the dLGN axons are synchronized, the reduced total level of depolarization combined with the synaptic depression puts the neuron in a regime that is insensitive to slight differences in depolarization for different contrasts (contrast invariant). Conversely, with 100% coactivation, as occurs for the preferred orientation, the depolarization is sufficiently large so that the neuron becomes sensitive to small changes in depolarization induced by different contrasts. Thus, the effect of contrast on the tuning curves is strongest for the optimal orientation and falls off progressively toward the null orientations.

We next used two other sets of parameters for the dLGN synapses to test how different levels of depression affect our results. Figure 6 shows a comparison between the in vivo data for monosynaptic input with moderate depression [dotted line (taken from Boudreau and Ferster, 2005)], the model response with moderate depression (continuous line), and the model response with strong depression (dashed line). All amplitudes were normalized to the first EPSP in the train. At 20 Hz (Fig. 6A), responses for all three cases are essentially similar. At 50 Hz (Fig. 6B), the strong depression response is significantly more pronounced. This trend increases with input frequency (data not shown).

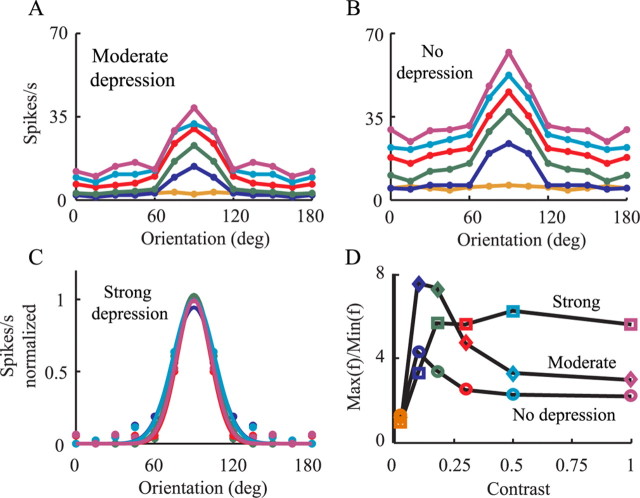
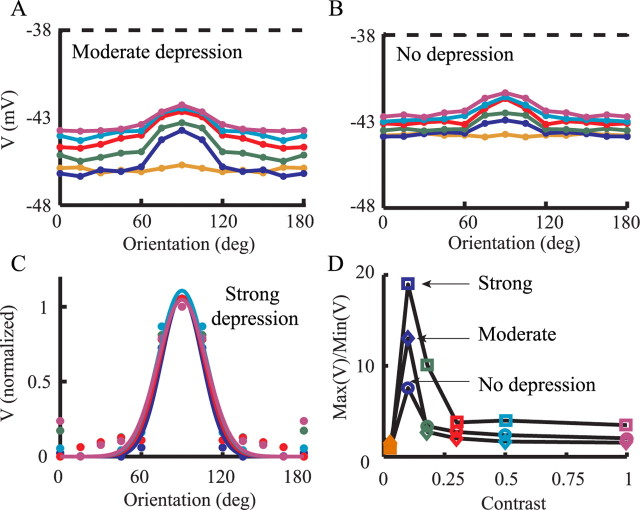
We then repeated the simulations shown in Figure 5 once with moderate depression (Fig. 7A) and again with no synaptic depression (Fig. 7B). Reduced depression leads to the elevation of responses to orthogonal orientations with increased stimulus contrast, as found in the original feedforward model (for review, see Ferster and Miller, 2000). Note that, when using the moderate level of depression (Fig. 7A), up to a contrast of 18% (green line) there is still no elevation in response to orthogonal stimuli.

Figure 7.

Quantification of tuning curves of firing response to visual input. A, B, Firing response of modeled SSC for different contrasts (colors as in Fig. 5D) for moderate depression (A) and for the case without depression (B). C, Best Gaussian fits (continuous lines) to model response (circles) for the strong depression (same data as in Fig. 5D). D, The ratio between the maximal firing rate (at the preferred orientation) and the averaged firing rates for the four nonpreferred orientations (0, 15, 30, and 45°) is plotted against contrast, for the strong depression (squares), for the moderate depression (diamonds), and for the case without depression (circles).

Figure 7C shows the normalized TC when using strong synaptic depression. The width of the Gaussian fit for the curves at half-maximum does not change appreciably over a wide range of contrast (for contrasts of 10, 18, 30, 50, and 100%, the widths are 53, 45, 42, 52, and 44°, respectively). In the case of the strong synaptic depression, there is essentially no contrast-dependent change in response for orthogonal orientations, but this is not the case for moderate and no depression, both of which show contrast-dependent increases in response to orthogonal orientations.

Figure 7D depicts the ratio between the response to the preferred orientation and that to the orthogonal at different contrasts and for different levels of depression. In the case of strong depression, the ratio increases with contrast and then saturates, and the response to orthogonal stimuli is contrast invariant (Fig. 5D). For the two other levels of depression, the curves rise for low contrasts and then decline with increased contrast, mostly attributable to the elevation of the response to orthogonal orientations. To summarize, Figure 7 shows that, as synaptic depression becomes more pronounced, the firing response becomes more contrast invariant (Sclar and Freeman, 1982).

Subthreshold response to visual input

Figure 8 depicts the voltage response for the strong depression case. Figure 8A shows the averaged membrane potential of the modeled cell in response to the preferred visual stimuli at low contrast (3%; gray line) and at high contrast (100%; dark line), with spikes truncated. Note that, for both contrasts, the average voltage is below threshold for spike firing (dashed line), implying that firing results from voltage fluctuations caused by the synaptic input, around the mean voltage (Anderson et al., 2000). When the stimulus is in-phase with the RF (Fig. 8A) (t = 0.25 s and t = 0.75 s), the peak-averaged membrane potential for the high contrast is 4 mV more depolarized than for the low-contrast case. Note that 3% contrast induces fluctuations at the stimulus frequency, but they are too small to induce spikes above baseline (Fig. 5D).

Unlike the case of the preferred orientation, the average membrane voltage for orthogonal orientation is essentially the same for all contrasts, and it is also similar to that of the background activity (Fig. 8B, spikes truncated). Consequently, the firing rate in the orthogonal case is similar to that of the baseline case in which no visual stimulus is presented. Next (Fig. 8C) we computed the TC for the average peak membrane voltage (spikes were truncated). For orthogonal orientations, the average peak voltage response for high contrast is slightly larger than for low contrast. A similar result is sometimes found experimentally (Anderson et al., 2000; Finn et al., 2007).

Membrane voltage fluctuations may sharpen the TC for spike response compared with that of the average peak voltage response (Anderson et al., 2000). We therefore examined the tuning of membrane voltage fluctuations for contrast and orientation. Figure 8D demonstrated that, for the preferred orientation, the fluctuations (measured as SD of the voltage; see figure legend) are coarsely tuned for contrast, and this results in sharpening of the spikes TC compared with the voltage TC (compare Figs. 5D, 8C). A similar result was obtained in the experiments of Anderson et al. (2000). The level of membrane voltage fluctuations that we have in the present work corresponds to experimental (Anderson et al., 2000) and theoretical (Hansel and van Vreeswijk, 2002) results, which show that fluctuations of ∼3 mV are optimal to maintain contrast invariance from membrane voltage to spike response.

However, we examined whether other factors may explain the difference between the TCs for spikes (Fig. 5D) and for the membrane voltage (Fig. 8C). We repeated the simulations but removed the sodium channels, so that there are no spikes. This makes it easier to assess the effect of the synaptic input separately from the effect of the spike mechanism and to understand better the connection between the TCs for spikes and for membrane voltage. Figure 8E shows the TC for the membrane voltage in the absence of the sodium channels. For the orthogonal stimuli, it is identical to the TCs for the membrane voltage when spikes were truncated (Fig. 8C). At a low contrast, the averaged peak response is approximately −45.5 mV, whereas for the highest contrast it is approximately −44.5 mV, a difference of only 1 mV.

However, for the preferred stimuli, the TCs for membrane voltage when spikes were truncated (Fig. 8C) still show ∼1 mV difference, whereas in the case in which Na channels were removed from the model (Fig. 8E), the TCs differ by ∼3.5 mV between 10% contrast (−43.5 mV) and the 100% contrast (−40.1 mV).

The reason is that the suprathreshold membrane voltage (EPSPs) is also truncated together with the spikes. These larger EPSPs are unmasked when Na channels are blocked and no spikes occur. The more spikes there are, the bigger the difference is. Indeed, care has to be taken when drawing conclusions on the underlying synaptic input when using truncated voltage response, as commonly done.

However, why is the difference in average peak voltage between high and low contrasts larger for the preferred orientation (3.5 mV) than it is for the orthogonal orientation (1 mV)? The simple reason for this is that, in the preferred orientation, all 90 thalamic afferents are coactivated (for all contrasts), whereas only half of them are coactivated for the orthogonal orientation at any time point (for all contrasts). This implies that, for any two contrasts, the voltage difference at the preferred orientation is approximately twice the difference in the orthogonal orientation. Because of nonlinearities, this difference may be larger than twofold. Note that by “coactivation” we mean in a time window of a few tens of milliseconds and not precisely at the same millisecond (see Materials and Methods).

We next examined why, for orthogonal orientations, there is a contrast-dependent shift (of ∼1 mV) for the TCs for the membrane voltage but not for the spikes. We therefore plotted the V/f curve of the model (Fig. 8F) to examine the correspondence between changes in voltage and changes in firing rates. The curve was calculated by binning all traces from all visual responses to 40 ms bins and, for each bin, calculating the firing frequency (f) and then the average voltage (V) with spikes truncated.

Figure 8F demonstrates that, for the nonpreferred (null) orientations, the change in voltage with increases in contrast lies in the relatively flat range on the V/f curve, in which small additional increases in membrane depolarization lead to a very small additional increase in firing rates (Fig. 8F, “null” range). Conversely, for the preferred orientations, the level of depolarization lies on a much steeper part of the V/f curve, in which small changes in depolarization result in significant increases in firing rates (Fig. 8F). The consequence of this is that the elevation of membrane depolarization attributable to increases in contrast hardly affects spike response in the orthogonal orientation, whereas for the preferred orientation, the changes in membrane voltage response are larger and so cause large changes in firing.

The sine-wave-like voltage response is the result of using spatial arrangement of three columns per subfield. Simpler RFs with only one column per subfield produce voltage response with a different shape (Chance et al., 1998; Kayser et al., 2001). Note also the three peaks during the rising phase of the membrane potential response (Fig. 8A), which are the result of the spatial arrangement of the dLGN thalamic afferents RFs (Fig. 5A,B, insets). In each subfield of the SSC model, there are 30 dLGN afferents, arranged in three columns of 10 afferents. A sine-wave stimulus at the preferred orientation and preferred spatial frequency synchronizes together the first, second, or third column in each of the three subfields, e.g., three first columns of afferents from all three subfields are activated at the same time, generating a voltage peak.

Figure 9 shows the model TCs for the membrane voltage using the values of the moderate depression (Fig. 9A) and without depression (Fig. 9B). As explained for Figure 8 above, the average membrane potential is below spike threshold (dashed line). The simulations shows that, as with the TCs for the spikes, the TCs for the membrane voltage are progressively less contrast invariant as synaptic depression is reduced (i.e., there is an increase in the baseline response for the nonpreferred orientations). The average voltage is higher for the case of no depression (Fig. 9B) than for the moderate depression (Fig. 9A) because the EPSPs are larger in the former case. Also, TCs are more compressed in Figure 9B compared with Figure 9A because the average voltage is closer to firing threshold and (with spikes truncated) it can never cross threshold. Figure 9C shows a Gaussian fit to the strong depression data in Figure 8C. The width of the Gaussian curves at half-maximum are 49, 58, 55, 57, and 59° for contrasts of 10, 18, 30, 50, and 100%, respectively. However, as mentioned above, for the voltage response [unlike the firing response (Fig. 5)], there is an elevation in the response for the orthogonal stimuli with increased contrast (but note that this elevation is masked by the Gaussian fit in Fig. 9C). This is summarized in Figure 9D that shows the ratio of the maximal response (at preferred orientation) to the minimal response, as in Figure 7D. Unlike for the TCs for the spikes (Fig. 7D), here all curves show first an increase then a decline; the latter is less steep and less deep in the case of strong depression (Fig. 9D, top curve).

Figure 9.

Quantification of tuning curves to visual input for the average membrane potential. A, B, Average voltage response of the modeled SSC for different contrasts, as in Figure 8C, but for moderate depression (A) and for the case without depression (B). The spike threshold is indicated by the dashed line. C, Best Gaussian fits (continuous lines) to average voltage response (open circles) for the strong depression (same data as in Fig. 8C). D, The ratio between the maximal firing rate (at the preferred orientation) and the averaged firing rates for the four nonpreferred orientations (0, 15, 30, and 45°) is plotted against contrast, for the strong depression (squares), for the moderate depression (diamonds), and for the case without depression (circles). For each level of depression, the ratios were calculated after shifting all voltage data points by the absolute value of the minimal voltage point obtained at the lowest contrast at the orthogonal orientation (such that for this point the value is now 0).

Contrast invariance, membrane voltage modulation, and aspect ratio

Figure 10A shows the TC of the modulations of the membrane potential, measured as peak depolarization minus peak hyperpolarization, in the case of the strong depression. The modulation frequency reflects the stimulus drift frequency of 2 Hz. In close agreement with Anderson et al. (2000), this modulation is tuned to orientation and is contrast invariant. Note that modulation saturates as the contrast increases. This is the direct consequence of the synaptic depression of the dLGN input and the saturating contrast–response function (Fig. 4B). Because of the contrast–response function, as the contrast increases, the additional increase in firing rate of the dLGN afferents is reduced and, in addition, the depression of the dLGN synapses is more severe.

The aspect ratio of the simple-cell subfields is believed to be indicative of whether simple cells shape their RF based on a feedforward or a feedback mechanism (Ferster and Miller, 2000). We wanted to test whether changing the aspect ratio affects the contrast invariance in our model. To do this, we repeated the simulations with strong depression and changed the aspect ratio from 3.3 to 1.75 (see Materials and Methods) (Fig. 10B). This change broadened the width of the tuning by ∼60° (compare Figs. 10B, 5D), but it still remained contrast invariant. The reason is that, with an elongated subfield (e.g., aspect ratio of 3.3), changing the stimulus orientation results very quickly with a dramatic decrease in the number of coactivated afferents. Indeed, for aspect ratio of 3.3, at 30° from the preferred orientation, coactivation is reduced to half the afferents. However, with a wider subfield (e.g., 1.75), loss of synchrony to approximately half the afferents occurs only at 60° away from the preferred orientation (Fig. 10B). In both cases, however, synchrony is lost and so the response is invariant to contrast. Thus, we show that, with strong synaptic depression, a feedforward model will result in contrast invariance for both high aspect ratio and also for aspect ratio as low as 1.75 (Pei et al., 1994).

Contrast invariance and the strength of the dLGN input

In feedforward models (Ferster and Miller, 2000), the excitatory drive to the neuron comes solely from the dLGN, whereas weak thalamic input with subsequent intracortical amplification is a feature of recurrent models (Douglas et al. 1989; Douglas and Martin, 1991; Worgotter and Koch, 1991; Ben-Yishai et al., 1995; Somers et al., 1995; Sompolinsky and Shapley, 1997; Troyer et al., 1998). The distribution of dLGN synapses in this model is based on Ahmed et al. (1994) who found that, in the cat, the dLGN contributes only ∼6% to the total excitatory synapses formed with SSCs. To examine how the strength of dLGN afferents affects our results, we repeated the simulations and either kept the number of dLGN afferents fixed while increasing the conductance of each dLGN synapse by a factor of 3–6 or fixed the strength of dLGN synapse and increased the number of dLGN afferents by this factor. In all cases, the TC for the spikes remained contrast invariant (data not shown). Again, the reason is that the spatial arrangement of the thalamic afferents, along with synaptic depression, lead to a very similar response to orthogonal stimuli at all contrasts, and this response is similar to the response without any stimulus (Figs. 5, 8 and corresponding text). However, for preferred stimuli, increasing contrast will lead to a stronger response that will saturate with increasing contrast. The change in the strength of the thalamic input only scales the TC up or down, but it does not change its basic shape.

Discussion

We used a biologically realistic model of an L4 spiny stellate cell to show that, under reasonable assumptions of the ongoing neuronal activity in vivo, the frequency-dependent synaptic depression of the thalamic input can contribute significantly to contrast invariance of the orientation tuning width of simple cells in V1. Moreover, the response to visual input gives a contrast-invariant tuning curve regardless of the size of the synaptic conductance change, the number of thalamic inputs, or the aspect ratio of the RF, so long as the thalamocortical synapse depresses with frequency. Our model can very well replicate the experimental finding demonstrating that simple cells remain contrast invariant (in both suprathreshold and subthreshold regimen) even when parts of the circuits were inactivated by cooling or electrical shock (Ferster et al., 1996; Chung and Ferster, 1998).

We showed that, in the feedforward model, when responses to all orientations and contrasts are above threshold so that there is no iceberg effect, there is also no widening of the TC with increased contrast. However, there is an elevation in the baseline response to nonpreferred stimuli. When synaptic depression is introduced, it can also compress the elevation of the baseline responses, especially for the TCs of the spikes (Figs. 7–9).

Why is our model so insensitive to change in contrast in the orthogonal orientation, whereas it is sensitive to contrast in the preferred orientation? The answer is threefold. The first is the initial depolarization. In the orthogonal case, only ∼50% of the dLGN afferents are activated synchronously (for any contrast, see insets in Fig. 5). This results with a smaller depolarization (for any given contrast) compared with the corresponding depolarization obtained in the preferred orientation. The second is the degree of change in depolarization with contrast. For the same reason, increase in contrast results in a smaller increase in depolarization for the orthogonal orientation compared with the preferred orientation. The third is the location of depolarization level on the V/f curve. Synaptic depression compresses all response amplitudes (in all cases) but it places the depolarization in the orthogonal case on the flat phase of the V/f curve (firing rate is insensitive to contrast), whereas in the preferred orientation, the depolarization (for all contrasts) lies at the more steep part of the V/f curve (firing rate is sensitive to contrast) (Fig. 8). Without depression, the depolarization for all orientations at sufficiently large contrasts reaches the steep part of the V/f curve and responses to orthogonal orientations are elevated (although the shape of the normalized TC is still contrast invariant).

The consensus of anatomical evidence is that the dLGN contributes a small fraction of the synapses in layer 4 in both cat and monkey. Estimates of the proportion of dLGN synapses formed with SSC give numbers of ∼5% (Ahmed et al., 1994; Latawiec et al., 2000; Binzegger et al., 2004). By integrating the anatomical and physiological data, our model suggests that only synchronized dLGN input (as occurs, for example, when the visual input arrives at the preferred orientation) may have a significant effect on the firing of the SSC (Bruno and Sakmann, 2006).

The thalamic input in our model is composed of only 90 afferents, each forming four synaptic contacts on the SSC. Each of these synapses can potentially generate, on average, a large EPSP of 2 mV, but it depresses sharply with consequent activations. Note that, if we assume, say, two synapses per thalamic axon (rather than four), we have 180 axons (there are 360 synaptic contacts). Because the model requires ∼6 nS per axon to generate an average 2 mV EPSP, in the case of two contacts per axon, a single dLGN contact would be twice as potent (3 nS per contact) and, thus, the total dLGN input strength would also be doubled. As mentioned above, this will not change the results of this study. Together with the feedforward spatial arrangement of the receptive fields of these dLGN afferents, it seems that the thalamic input is “designed” to deliver a precise and brief signal in the case in which a preferred stimulus is presented (and the thalamic afferents are well synchronized). Thus, because of their phase sensitivity, simple cells may be far more efficient at transmitting their input at this first stage of cortical processing than the phase-insensitive complex cells. This might be the reason why the dLGN contributes only ∼6% to the total synapses formed onto SSCs and why virtually all spiny stellate cells in layer 4 are simple (Hubel and Wiesel, 1962, Gilbert, 1977; Martin and Whitteridge, 1984).

Recently, Finn et al. (2007) suggested that contrast invariance in a feedforward model can be the result of other nonlinear mechanisms. They show that contrast-dependent trial-to-trial variability may lead to contrast-dependent changes in gain and thus enable the simple cell to fire in response to preferred stimuli at low contrast but not to orthogonal stimuli at high contrast, although the average voltage response in both cases is similar. It is important to note that synaptic depression (strong or moderate) could be one of the neural mechanisms that underlie this variability. When the drifting grating is out of phase with the simple-cell RF and, thus, the geniculate input is silent, the synapses recover from depression. When the grating drifts into phase, all synapses are activated synchronously and such synchronous input would lead to an enhanced voltage fluctuations. This is valid only for the simple cells that receive a dominant geniculate input (Finn et al., 2007). In our model, however, the voltage fluctuations are only slightly tuned (Fig. 8D) because most of the input in our model comes from background activity.

If, conversely, the recurrent connections are numerically and functionally dominant, the feedforward dLGN signal should be regarded as introducing a bias to the overall pattern of cortical activity (Sompolinsky and Shapley, 1997; Tsodyks et al., 1999; Kenet et al., 2003). If this is so, the central question is then, how does the dLGN input interact with the intracortical recurrent excitation and inhibition?

Previous models have suggested a possible role for the push–pull inhibition in generating contrast invariance (Troyer et al., 1998). This model was further elaborated to include synaptic depression of the thalamic input (Carandini et al., 2002) and shows that such depression can explain a number of other response properties of simple cells, such as mask stimuli (Carandini et al., 2002). It was also shown in this work that push–pull inhibition can explain contrast invariance even in the face of synaptic depression. Here we showed that actually synaptic depression could itself be the mechanism that gives rise to contrast invariance. It is therefore possible that, once contrast invariance is induced by the feedforward input, as shown in this study, the push–pull cortical inhibition acts to stabilize and refine the response.

With respect to inhibition, it is important to note that layer 4 basket cells also receive direct thalamic input (Martin et al., 1983; Kisvarday et al., 1985; Gabbott et al., 1988; Binzegger et al., 2004), and much of this input is located proximal to the soma and even on the soma itself (Ahmed et al., 1997). Basket cells are also smaller (larger input resistance) than SSC (Ahmed et al., 1997), and thus the thalamocortical input is relatively more dominant for these cells and they may respond earlier than the SSCs to a given dLGN input. Indeed, there is evidence from in vivo studies that the initial synaptic conductance change in L4 simple cells after visual stimulus is predominantly inhibitory (Borg-Graham et al., 1998; Monier et al., 2003). Unpublished evidence of Stratford et al. (personal communication) indicates that the thalamic input to the basket cells is depressing and thus the response of the basket cells to visual input will be quantitatively similar to that of the SSC model as shown here (tuning width contrast invariant). Moreover, the basket cells will respond faster and stronger to the thalamic input and may play a key role in shaping the RF of SSC and of the column as a whole (Cruikshank et al., 2007). This is presently under theoretical exploration using a detailed anatomical and physiological data of cortical inhibitory neurons.