The Cerebellar Interpositus Nucleus and the Dynamic Control of Learned Motor Responses

Abstract

The role played by the cerebellum in movement control requires knowledge of interdependent relationships between kinetic neural commands and the performance (kinematics) of learned motor responses. The eyelid motor system is an excellent model for studying how simple motor responses are elaborated and performed. Kinetic variables (n = 24) were determined here by recording the firing activities of orbicularis oculi motoneurons and cerebellar interpositus neurons in alert cats during classical conditioning, using a delay paradigm. Kinematic variables (n = 36) were selected from eyelid position, velocity, and acceleration traces recorded during the conditioned stimulus–unconditioned stimulus interval. Optimized experimental and analytical tools allowed us to determine the evolution of kinetic and kinematic variables, the dynamic correlation functions relating motoneuron and interpositus neuron firing to eyelid conditioning responses, the falling correlation property of the interpositus nucleus across the successive training sessions, the time and significance of the linear relationships between these variables, and finally, the phase-inversion property of interpositus neurons with respect to acquired conditioned responses. Whereas motoneurons encoded eyelid kinematics at every instant of the dynamic correlation range and generated the natural oscillatory properties of the neuromuscular elements involved in eyeblinks, interpositus neurons did not directly encode eyelid performance: namely, their contribution was only slightly significant in the dynamic correlation range, and this regularity caused the integrated neuronal activity to oscillate by progressively inverting phase information. Therefore, interpositus neurons seem to play a modulating role in the dynamic control of learned motor responses, i.e., they could be considered a neuronal phase-modulating device.

Introduction

The enigmatic role of cerebellar circuits in relation to the generation and control of spontaneous and acquired motor responses has been variously ascribed to a putative center for motor coordination and integration (Eccles et al., 1967; Thach et al., 1992), a neural center controlling motor timing of the different muscles involved in a given movement (Llinás and Welsh, 1993; Welsh and Llinás, 1997; Lang et al., 1999; Kitazawa and Wolpert, 2005), the place for motor learning and memory storage (Ito, 1984; Krupa et al., 1993; Mauk, 1997; Bracha et al., 2001; Christian and Thompson, 2003) and, in a more parsimonious way, that of a center designed for the reinforcement and/or proper performance of ongoing movements (Holmes, 1939; Welsh and Harvey, 1991; Llinás and Welsh, 1993; Gruart et al., 2000; Delgado-García and Gruart, 2002; Seidler et al., 2002; Jiménez-Díaz et al., 2004). Nevertheless, for a proper understanding of cerebellar functioning, it will be necessary to approach the neural activity of cerebellar circuits during the actual performance of spontaneous, reflex, and learned movements. Moreover, cerebellar unitary activity should be correlated with both the activity present in the final common pathway (i.e., that of the motoneurons participating in the generation of the selected motor responses) and the kinematics (position, velocity, and acceleration) of the motor system involved.

In this regard, the eyelid motor system appears a suitable model for the study of cerebellar function in the acquisition of new motor abilities, because the brainstem and cerebellar circuits involved have been described precisely (Krupa et al., 1993; Llinás and Welsh, 1993; Mauk, 1997; Bracha et al., 2001; Carey and Lisberger, 2002; Delgado-García and Gruart, 2002; Morcuende et al., 2002; Christian and Thompson, 2003), the inputs and outputs of the system can be presented and/or measured quantitatively (Evinger et al., 1991; Gruart et al., 1995), and the neuronal activity of the relevant centers can be recorded in vivo during the actual performance of associative learning tasks (Trigo et al., 1999; Gruart et al., 2000; Chen and Evinger, 2006). Moreover, this motor system can be easily trained using classical conditioning paradigms (Gormezano et al., 1983). Nevertheless, the kinetic (neurally generated) motor commands and the kinematic (i.e., physical mechanics of the eyelid, including muscle activity) characterization of learned motor responses requires exhaustive knowledge of interdependent relationships between physiological variables. For this, powerful analytical tools (such as cluster analysis, multiparametric evolution of involved variables, dynamic correlation functions, and oscillatory properties) need to be used to achieve a proper understanding of cerebellar functioning in the behaving animal during the very process of motor and/or associative learning (Belsley et al., 1980; Allen and Cady, 1982; Hair et al., 1998; Grafen and Hails, 2002).

In the present study, kinetic variables involved in the generation of eyelid conditioned responses (CRs) were determined by recording the firing activities of identified orbicularis oculi motoneurons (i.e., the final common pathway) and cerebellar interpositus neurons (the area under study) in alert behaving cats during classical conditioning, using a delay paradigm. For this, a tone was presented for 370 ms as a conditioned stimulus (CS), followed 270 ms from its start by an air puff (100 ms) directed at the left cornea as an unconditioned stimulus (US). The kinematic variables were collected from eyelid position, velocity, and acceleration traces recorded during the CS–US interval using the search-coil technique (Gruart et al., 1995), as well as from the electromyographic (EMG) activity of the orbicularis oculi muscle. The two types of variable were associated by means of multivariate cluster analysis and dynamic correlation analysis (Belsley et al., 1980; Allen and Cady, 1982; Banfield and Raftery, 1993; Hair et al., 1998). Results allow us to propose that orbicularis oculi motoneurons certainly encode eyelid kinematics directly at every instant of the dynamic correlation range, as well as generate the natural oscillatory properties of the neuromuscular elements involved in eyelid kinematics. In contrast, interpositus neurons do not directly encode eyelid kinematics but do play a modulating role in the dynamic control of learned motor responses, i.e., they could be considered a neuronal phase-modulating device.

Materials and Methods

Subjects.

Experiments were performed on seven adult cats (weighing 2.1–2.8 kg on arrival) obtained from an authorized supplier (Iffa-Credo, Arbresle, France). All experiments were performed in accordance with guidelines of the European Union (86/609/EU) for the use of laboratory animals in chronic experiments and were approved by the Institution Committee for animal care and handling.

Surgical procedures.

Animals were anesthetized with sodium pentobarbital (35 mg/kg, i.p.) after a protective injection of atropine sulfate (0.5 mg/kg, i.m.). As illustrated in Figure 1 A, animals were implanted with a search coil (five turns, 3 mm in diameter) in the center of the left upper eyelid, at 2 mm from the lid margin. The coil was made from Teflon-coated multistranded stainless steel wire, with an external diameter of 50 μm. Animals were also implanted with two hook electrodes, bared 1 mm at their tips, in the ipsilateral orbicularis oculi muscle, for EMG recordings. Recording electrodes were made of the same wire. Four of the animals were prepared for the chronic recording of antidromically identified posterior interpositus neurons. For this, a stimulating bipolar (200 μm enamel-coated silver wire) electrode was implanted in the magnocellular division of the contralateral (right) red nucleus following stereotaxic coordinates (Berman, 1968). For comparative purposes, three animals were prepared for the chronic recording of facial motoneurons projecting to the orbicularis oculi muscle. For this, a pair of stainless steel hook electrodes was aimed at the zygomatic subdivision of the facial nerve, 1–2 mm posterior to the external canthus. For each animal, a recording window (5 × 5 mm) was opened in the occipital bone to allow access to the ipsilateral (left) interpositus nucleus or facial nucleus. The dura mater was removed, and an acrylic chamber was constructed around the opening. The cerebellar surface was protected with a piece of silicone sheet and sterile gauze and hermetically closed using a plastic cover. At the end of the implantation procedure, a head-holding system was attached to the skull in stereotaxic coordinates. Wires were soldered to a socket fixed to the holding system. A more detailed description of these chronic preparations have been published previously (Trigo et al., 1999; Gruart et al., 2000; Jiménez-Díaz et al., 2004).

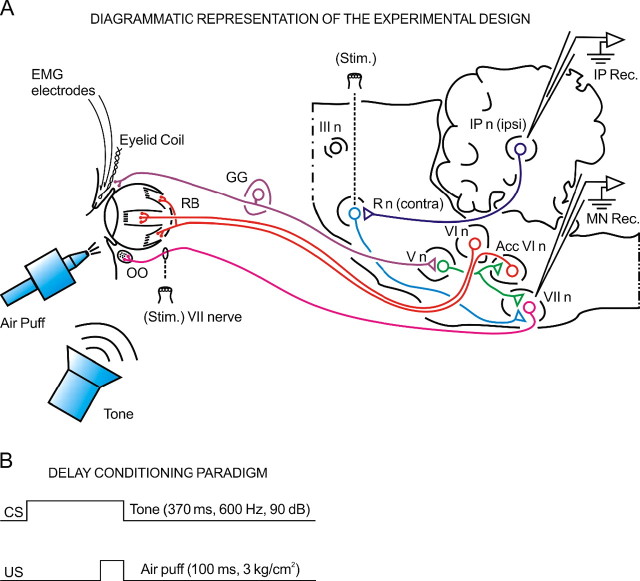
Figure 1.

Diagrammatic representation of the experimental design. A, The characterization of kinetic neural commands and of eyelid kinematics requires a precise measurement of exhaustive correlation indicators. The kinetic variables were determined here from the firing properties of antidromically identified orbicularis oculi (OO) motoneurons located in the facial nucleus (VII n) and interpositus neurons located in the cerebellar posterior interpositus nucleus (IP n). In turn, the kinematic variables were collected from eyelid position, velocity, and acceleration data. A complete list of kinetic and kinematic parameters measured in this study is included in Tables 1 and 2. The two types of variable were associated by means of dynamic correlation analysis. The diagram also illustrates the stimulating (Stim.) and recording (Rec.) sites, as well as the eyelid coil and EMG electrodes implanted in the upper eyelid. III n, Oculomotor complex; V n, trigeminal nucleus; VI, abducens nucleus; AccVI n, accessory abducens nucleus; GG, Gasser ganglion; R n, red nucleus. B, For classical conditioning of eyelid responses, we used a delay paradigm consisting of a tone (370 ms, 600 Hz, 90 dB) as a CS. The CS started 270 ms before and coterminated with an air puff (100 ms, 3 kg/cm²) used as an US.

Recordings and stimulating techniques.

Eyelid movements were recorded with the magnetic search-coil technique (Gruart et al., 1995). The EMG activity of the orbicularis oculi muscle was recorded with differential amplifiers at a bandwidth of 0.1 Hz to 10 kHz. Neural activity in both facial and interpositus nuclei was recorded with glass micropipettes filled with 2 m NaCl (3–6 MΩ of resistance) and with the help of an NEX-1 preamplifier (Biomedical Engineering, Thornwood, NY). For antidromic activation of selected neurons, we used single- or double- (interval of 1–2 ms) cathodal square pulses (50 μs) with current intensities <300 μA. Only antidromically identified interpositus neurons (n = 174) and orbicularis oculi motoneurons (n = 110) were stored and analyzed. Site location and identification procedures have been described in detail for both interpositus neurons (Gruart et al., 2000) and facial motoneurons (Trigo et al., 1999). Tones were applied from a loudspeaker located 80 cm below the animal';s head. Air puffs were applied through the opening of a plastic pipette (3 mm in diameter) located 2 cm from the left eye.

Classical conditioning.

Classical conditioning of eyelid responses was achieved by the use of a delay conditioning paradigm (Fig. 1 B). For this, a tone (370 ms, 600 Hz, 90 dB) was used as CS. The tone was followed 270 ms from its onset by an air puff (100 ms, 3 kg/cm²) directed at the left cornea as a US. Thus, the tone and the air puff terminated simultaneously. The experimental subjects underwent a sequence of two habituation, 10 conditioning sessions, and three extinction sessions. In all cases, the conditioning session consisted of 12 blocks separated by a variable (5 ± 1 min) interval. Each block consisted of 10 trials separated by intervals of 30 ± 10 s. The CS was presented alone in the first trial of each block. A complete conditioning session lasted for ∼2 h. The CS was presented alone during habituation and extinction sessions for the same number of blocks per session and trials per block and with similar random interblock and intertrial distribution (Gruart et al., 1995).

Histology.

At the end of the recording sessions, animals were deeply reanesthetized (50 mg/kg sodium pentobarbital, i.p.). Electrolytic marks were placed in selected recording sites with a tungsten electrode (1 mA for 30 s). Animals were perfused transcardially with saline and phosphate-buffered Formalin. Serial sections (50 μm) including the cerebellum and the brainstem were mounted on glass slides and stained with toluidine blue for confirmation of the recording sites.

Physiological parameter definitions.

A total of 60 parameters were determined in an automated way, taking into account physiological criteria based on a kinetic–kinematic characterization of the neuronal firing activities and the learned motor responses. For a quantitative determination of kinetic neural commands, a total of 24 kinetic parameters (Table 1) were quantified from the selected interpositus neurons and orbicularis oculi motoneurons. According to the performance of learned motor responses, 36 kinematic parameters (Table 2) were quantified from the selected eyelid position, velocity, and acceleration traces.

Table 1.

The 24 kinetic variables selected for this study

No.	Parameter
1	Number of action potentials of the interpositus neuron in the CS–US interval.
2	Latency of the maximum instantaneous frequency for the interpositus neuron in the CS–US interval, with respect to the reference zero (ms).
3	Amplitude of the maximum instantaneous frequency for the interpositus neuron in the CS–US interval (spikes/s).
4	Latency of the first action potential of the interpositus neuron after the CS (ms).
5	Latency of the maximum instantaneous frequency for the interpositus neuron, with respect to CS presentation (ms).
6	Time of occurrence of the maximum instantaneous frequency for the interpositus neuron, with respect to the start of the CR (ms).
7	Number of action potentials of the interpositus neuron in the interval between US presentation and the subsequent 100 ms.
8	Latency of the maximum instantaneous frequency for the interpositus neuron between US presentation and the subsequent 100 ms (ms).
9	Amplitude of the maximum instantaneous frequency for the interpositus neuron between US presentation and the subsequent 100 ms (spikes/s).
10	Latency of the first action potential of the interpositus neuron after the US (ms).
11	Latency of the maximum instantaneous frequency for the interpositus neuron, with respect to US presentation (ms).
12	Time of occurrence of the maximum instantaneous frequency for the interpositus neuron, with respect to the start of the UR (ms).
13	Number of action potentials of the orbicularis oculi motoneuron in the CS–US interval.
14	Latency of the maximum instantaneous frequency for the motoneuron in the CS–US interval, with respect to the reference zero (ms).
15	Amplitude of the maximum instantaneous frequency for the motoneuron in the CS–US interval (spikes/s).
16	Latency of the first action potential of the motoneuron after the CS (ms).
17	Latency of the maximum instantaneous frequency for the motoneuron, with respect to CS presentation (ms).
18	Time of occurrence of the maximum instantaneous frequency for the motoneuron, with respect to the start of the CR (ms).
19	Number of action potentials of the motoneuron in the interval between US presentation and the subsequent 100 ms.
20	Latency of the maximum instantaneous frequency for the motoneuron between US presentation and the subsequent 100 ms (ms).
21	Amplitude of the maximum instantaneous frequency for the motoneuron between US presentation and the subsequent 100 ms (spikes/s).
22	Latency of the first action potential of the motoneuron after the US (ms).
23	Latency of the maximum instantaneous frequency for the motoneuron, with respect to US presentation (ms).
24	Time of occurrence of the maximum instantaneous frequency for the motoneuron, with respect to the start of the UR (ms).

Table 2.

The 36 kinematic variables selected in this study

No.	Parameter
25	Latency between the CS and the start of the CR (ms).
26	Latency between the start of the CR and the US (ms).
27	Latency between the start of the CR and the minimum eyelid position value (ms).
28	Eyelid position amplitude at US presentation compared with the amplitude at the start of the CR (°).
29	Minimum eyelid position amplitude, as compared with the amplitude at the start of the CR (°).
30	Amplitude between the minimum and maximum eyelid velocity peaks (°/s).
31	Mean velocity (half the amplitude between the minimum and maximum eyelid velocity peaks) (°/s).
32	Latency between the minimum and maximum eyelid velocity peaks (ms).
33	Ratio between parameter 28 and the latency between the start of the CR and US presentation (°/s).
34	Ratio between parameters 29 and 27 (°/s).
35	Slope between US presentation and the minimum eyelid position points (°/s).
36	Slope between the minimum and maximum eyelid velocity peaks (°/s2).
37	Latency between the start of the CR and the start of the UR (ms).
38	Eyelid position amplitude at the start of the UR compared with the amplitude at the start of the CR (°).
39	Ratio between parameter 38 and the latency between the start of the CR and the start of the UR (°/s).
40	Slope between the start of the UR and the minimum eyelid position points (°/s).
41	Slope of the regression line that fits the eyelid position record between the start of the CR and US presentation (°/s).
42	Intercept of the regression line that fits the eyelid position record between the start of the CR and US presentation (°).
43	Slope of the regression line that fits the eyelid position record between the start of the CR and the start of the UR (°/s).
44	Intercept of the regression line that fits the eyelid position record between the start of the CR and the start of the UR (°).
45	Slope of the regression line that fits the eyelid position record between the start of the CR and the minimum eyelid position (°/s).
46	Intercept of the regression line that fits the eyelid position record between the start of the CR and the minimum eyelid position (°).
47	Slope of the regression line that fits the eyelid velocity record between the minimum and the maximum eyelid velocity (°/s2).
48	Intercept of the regression line that fits the eyelid velocity record between the minimum and the maximum eyelid velocity (°/s).
49	Latency at the start of the downward phase of the blink (ms).
50	Eyelid position amplitude at the start of the downward phase of the blink (°).
51	Latency at US presentation (ms).
52	Eyelid position amplitude at US presentation (°).
53	Latency at the start of the eyelid position UR (ms).
54	Eyelid position amplitude at the start of the CR (°).
55	Time of occurrence of the minimum eyelid position peak (ms).
56	Amplitude of the minimum eyelid position peak (°).
57	Time of occurrence of the minimum eyelid velocity peak (ms).
58	Amplitude of the minimum eyelid velocity peak (°/s).
59	Time of occurrence of the maximum eyelid velocity peak (ms).
60	Amplitude of the maximum eyelid velocity peak (°/s).

Data collection and analysis.

Eyelid position, EMG and neuronal activity, and rectangular pulses corresponding to CS and US presentations were stored digitally on a computer, using an analog-to-digital converter (CED 1401 Plus; Ceta Electronic Design, Cambridge, UK). Commercial computer programs (Spike 2 and SIGAVG; Ceta Electronic Design) were used for acquisition and on-line conventional analysis. The off-line analysis and quantification and representation programs used here were developed by one of the authors (R.S.-C.) with the help of Matlab routines (MathWorks, Natick, MA).

On the basis of direct records of neuronal activity from the cerebellar interpositus nucleus or the facial nucleus, the action potential pulses were quantified. In all cases, the quantification algorithm took into account the identification of the standard waveform of the action potential and the absolute refractory period (i.e., the mean duration of the action potential) and relative refractory period (minimum interspike time interval). The instantaneous firing rate was calculated as the inverse of the interspike intervals. Velocity and acceleration profiles were computed digitally as the first and second derivatives of eyelid position records after low-pass filtering of the data (−3 dB cutoff at 50 Hz and zero gain at is ≈100 Hz). The power spectra were calculated using the fast Fourier transform, and the significance of power spectral peaks was tested with the χ²-distributed test for spectral density functions.

Computed results were processed for statistical analysis using the Statistics Matlab Toolbox. Collected data were analyzed using a multivariate cluster technique. As statistical inference procedures, both ANOVA (estimate of variance both within groups and between groups, on the basis of one dependent measure) and multivariate ANOVA (MANOVA) (estimate of variance in multiple dependent parameters across groups) were used to assess the statistical significance of differences between groups. The corresponding statistical significance test (i.e., F_{[(m − 1), (m − 1) × (n − 1), (l − m)]} statistic) was performed, with kinetic and kinematic parameters and sessions as repeated measures, coupled with contrast analysis when appropriate (Hair et al., 1998; Grafen and Hails, 2002). The orders m (number of groups), n (number of cats), and l (number of multivariate observations) were reported accompanying the F statistic values. Wilk';s λ criterion, and its transformation to the χ² distribution used in Matlab, were used to extract significant differences from MANOVA results. Regression analysis and computational algorithms of dynamic correlation were used to study the relationship between kinetic and kinematic variables. The corresponding statistical significance tests (i.e., Student';s t test and F statistic) were performed for the three parameters of correlation coefficient (r), slope, and intercept of the regression line. These parameters were statistically significant if the resulting probability P, met the requirements of the hypothesis test: P < p, where p < 0.01 was the predetermined statistical significance level (Belsley et al., 1980). Identical intervals were chosen for both eyelid CRs and instantaneous frequencies of interpositus neurons and orbicularis oculi motoneurons. The mean length of the intervals was within the range of 187–261 points, which corresponded to 179.51–250.55 ms. The correlation coefficients >0.1238 were statistically significant, at least 95% (p < 0.05), according to the criterion $r>\frac{2}{\sqrt{Np}}$, where r is the Pearson';s product moment correlation coefficient, and Np is the total number of points of the correlated variables (Allen and Cady, 1982).

Additional details regarding off-line processing of collected physiological data for the construction of the hierarchical cluster tree are presented in supplemental Appendix S1 and Figure S1A–E (available at www.jneurosci.org as supplemental material). Details regarding the rationale underlying the dynamic correlation functions and the relationships between the falling correlation and phase-modulation properties of cerebellar interpositus neurons are presented in supplemental Appendices S2 and S3 (available at www.jneurosci.org as supplemental material), respectively.

Results

Firing properties of cerebellar interpositus neurons and orbicularis oculi motoneurons during classical conditioning of eyelid responses

In those animals (n = 4) prepared for recording the firing activity of identified interpositus neurons, deep cerebellar nuclei were systematically explored to find unitary activity related with eyelid responses. The unitary activity was recorded during the random presentation of puffs of air (10–100 ms, 1–3 kg/cm²) aimed at the ipsilateral cornea (Fig. 1A). This procedure took no more than five recording sessions. As confirmed later by the histological study, the dorsomedial part of the posterior interpositus nucleus was found to contain a high density of neurons related to reflexively evoked eyelid responses. Recorded neurons were identified by their antidromic activation (latency of 0.6–0.8 ms) from the contralateral red nucleus (Fig. 1A). Although other deep cerebellar nuclei (mainly anterior interpositus and dentate nuclei) also contain neurons related to eyelid movements, we consider here only those located in the indicated area of the posterior interpositus nucleus.

Once the recording area was located, animals were classically conditioned using a delay paradigm (see Materials and Methods). Posterior interpositus neurons were recorded in the four animals across two habituation, 10 conditioning, and three extinction sessions. The mean number of neurons recorded per session was 2.9 (i.e., a mean of 41.37 min of recording per neuron). Interpositus neurons fired during downward movements (either conditioned or unconditioned eyelid responses) of the upper eyelid (Fig. 2A–C). Tones presented during the two habituation sessions evoked rather few reflex eyelid responses that appeared mainly during the first blocks of the habituation H01 session. During habituation sessions, interpositus neuron firing lagged the beginning of evoked eyelid responses by 20–40 ms, but this lag decreased progressively across conditioning (see below). Their discharge rates were related to eyelid position (with a gain of 0.1–8.0 spikes/°; r < 0.7; p ≤ 0.05) and/or to eyelid velocity (0.05–0.25 spikes/° per second; r < 0.7; p ≤ 0.05). In accordance with previous reports (Van Kan et al., 1993; Gruart and Delgado-García, 1994; Chen and Evinger, 2006), the recorded neurons (n = 131) were classified as type A. Posterior interpositus type B neurons (n = 43) were also antidromically activated from the red nucleus (0.85–1.25 ms) but presented a noticeable inhibition in their firing coinciding exactly with the downward displacement of the upper eyelid during reflexively evoked blinks (Gruart and Delgado-García, 1994; Gruart et al., 2000). Only those neurons located in the posterior interpositus nucleus, antidromically activated from the red nucleus and classified as type A, were included in this study.

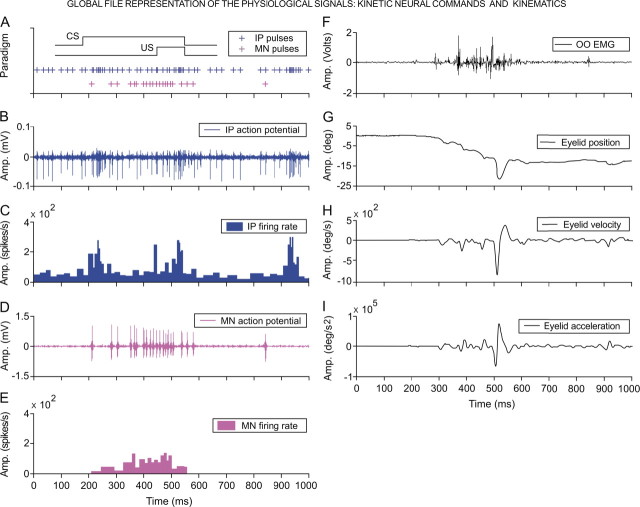
Figure 2.

Global file representation. A, A diagrammatic representation of the delay conditioning paradigm with indication of the time presentation for CS and US. Records illustrated in B–I were collected from the ninth conditioning session of two representative animals. The action potential pulses (IP pulses), marked with blue plus signs (A), correspond to the direct representation of the neuronal activity in the cerebellar interpositus nucleus (IP action potential, in B), and its respective instantaneous frequency (IP firing rate, in C). Action potential pulses (MN pulses) recorded from an orbicularis oculi motoneuron are indicated with magenta plus signs (A) and are the direct representation of the neuronal activity in the facial nucleus (MN action potential, in D) and its corresponding instantaneous frequency (MN firing rate, in E). The 24 kinetic parameters determined in this study (see Table 1) were collected from the firing activities of identified orbicularis oculi motoneurons (n = 110) and cerebellar interpositus (n = 174) neurons recorded across the successive habituation (n = 2), conditioning (n = 10), and extinction (n = 3) sessions from seven cats. F–I, These traces illustrate the electromyographic activity of the orbicularis oculi muscle (OO EMG, in F), the direct recording of the eyelid position by the magnetic field search-coil technique (G), and the estimated eyelid velocity (H) and acceleration (I) curves. The 36 kinematic parameters determined in this study (see Table 2) were collected from eyelid responses recorded across habituation, conditioning, and extinction sessions. For each of the physiological variables represented, the magnitude and the respective unit of measurement are indicated.

In the other group of animals (n = 3), the facial nucleus was systematically explored in the search for motoneurons antidromically activated from the electrode implanted in the zygomatic branch of the facial nerve. As described previously (Shaw and Baker, 1985; Gruart et al., 2003) and confirmed histologically, orbicularis oculi motoneurons were concentrated in the dorsal subdivision of the facial nucleus. These motoneurons (n = 110) were antidromically activated, with a mean latency of 2.25 ± 0.31 ms, and their firing started ≈10 ms before air-puff-evoked eyelid reflex responses. Once the recording area was located, animals were classically conditioned as indicated above. Orbicularis oculi motoneurons fired tonically during the performance of eyelid CRs (Fig. 2A,D,E). Thus, and as described previously (Trigo et al., 1999), their discharge was related to eyelid position (with a gain of 4.5–11.3 spikes/°; r ≥ 0.92; p ≤ 0.01) during CRs.

A total of 24 kinetic parameters (including latency, firing rate and profile, number of spikes during the CR, etc.) (Table 1) were systematically quantified from the selected interpositus neurons and orbicularis oculi motoneurons. For a quantitative determination of eyelid kinematics (Fig. 2F–I) during habituation, acquisition, and extinction, a total of 36 kinematic parameters were quantified from eyelid position, velocity, and acceleration profiles collected across the successive training sessions (for a complete relation of selected kinematic parameters, see Table 2).

Construction of a hierarchical cluster tree with kinetic neural commands and kinematic parameters collected during classical conditioning of eyelid responses

A piece of information still missing in learning studies relates to the coherence of recorded parameters regarding the actual learning process. It is expected that, during the acquisition of a new motor ability, both kinetic commands and kinematic parameters should present an intrinsic homogeneity. Cluster analysis is a powerful tool for the analysis of such data (Taganova and Silakov, 1980; Banfield and Raftery, 1993; Hair et al., 1998; Ma et al., 2006). This algorithm for the processing of physiological recordings provides more homogeneity in the experimental database for the subsequent dynamic correlation analysis. The global files including the 60 selected parameters were clustered in an automated way, taking into account physiological criteria based on a kinetic–kinematic characterization of the activity of orbicularis oculi motoneurons and interpositus neurons and of the types of eyelid response (Tables 1, 2) (supplemental Appendix S1, available at www.jneurosci.org as supplemental material). This characterization was performed trial by trial, block by block, and session by session for selected animals (n = 5) during the successive experimental sessions (Fig. 3A). As explained in detail in Materials and Methods, each experimental (two habituation, 10 conditioning, and three extinction) session consisted of 12 blocks, and each block consisted of 10 trials. The computer program arranged the data in a total of 180 conditioning blocks (15 conditioning sessions × 12 blocks) according to their significant homogeneity: namely, blocks within clusters were displayed close together when plotted geometrically, whereas different clusters were displayed far apart. Significant clusters (n = 15), illustrated by the bottom set of colored lines in Figure 3A, corresponded to blocks presenting significant coherent data (F_{(14, 56, 136)} > F_{(15, 60, 140)}, …, F_{(29, 116, 150)}, with Nr = 5; Wilk';s λ = 0.12, and F_{(14, 56, 136)} = 20.18; p < 0.01). These 15 significant clusters include 151 (i.e., 83.9%) of the averaged blocks, whereas the remaining nonsignificant clusters (n = 15, clusters indicated by black lines) included only 29 (i.e., 16.1%) of the averaged blocks. For the sake of clarity, the color code of significant clusters (n = 15, including 151 blocks) shown in Figure 3A is maintained for the colored bars shown in Figure 3B, the colored curves illustrated in Figure 4B, and the colored circles shown in Figure 5, A and B. Data corresponding to the nonsignificant clusters (n = 15) (Fig. 3A, black lines, including 29 blocks) were not further considered in this study.

Figure 3.

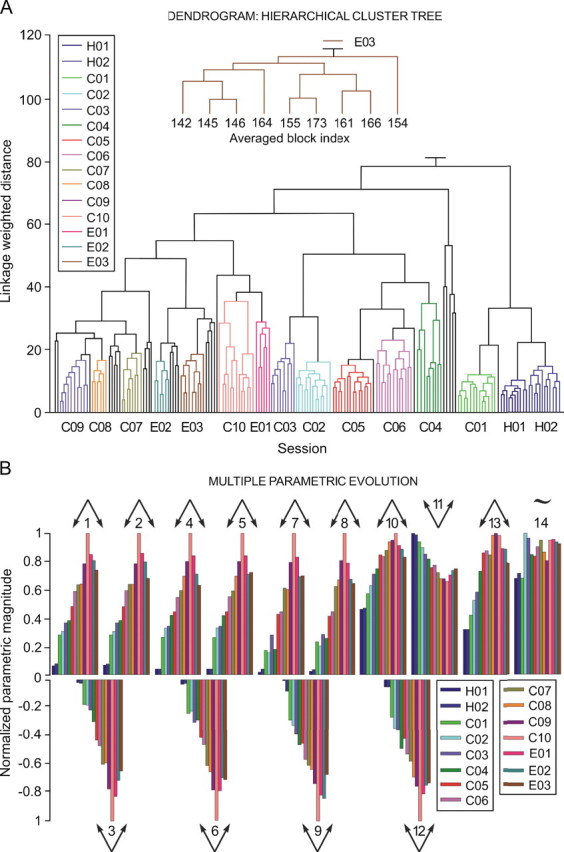
A representation of the hierarchical cluster tree and of multiparametric evolution of results collected across habituation, conditioning, and extinction sessions. A, This dendrogram illustrates the hierarchical cluster tree constructed from data collected from five animals for each experimental session. A total of 63 orbicularis oculi motoneurons and 71 interpositus neurons were included in the analysis. Quantified parameters are listed in Tables 1 and 2. Each bar at the bottom of the dendrogram represents an averaged conditioning block (see Materials and Methods). The linkage-weighted distance between the objects is represented on the y-axis in arbitrary units. According to the illustrated results, a total of 30 clusters were obtained. The comparison depth was of 16 levels to both sides of the objective level, and the clusters were formed without specifying the maximum number of clusters. The x-axis represents, in colored lines (not black lines), the 15 statistically significant (F_{(14, 56, 136)} > F_{(15, 60, 140)}, …, F_{(29, 116, 150)}, with Nr = 5; Wilk';s λ = 0.12; and F_{(14, 56, 136)} = 20.1821; p < 0.01) clusters (corresponding to the 2 habituation, 10 conditioning, and 3 extinction sessions), which add up to 151 averaged blocks distributed in the 15 experimental sessions during the delay conditioning paradigm (H01–H02, 22 blocks; C01–C10, 108 blocks; and E01–E03, 21 blocks). The black lines represent the 29 averaged blocks that fall into the remaining 15 statistically nonsignificant clusters. An enlargement of the third extinction session (E03) is presented in the inset, and the order number assigned to each averaged block is indicated. B, Multiple parametric evolution. A total of 14 parameters (4 kinetic and 10 kinematic, see Table 3) were included in this analysis. As illustrated in the inset, each color corresponds to a habituation, conditioning, or extinction session. Each set of color bars corresponds to the evolution of a given parameter (numbered from 1 to 14). Each color bar indicates the mean parametric value resulting from averaging all of the blocks (n = 12) of the same session, a procedure applied for each of the sessions. The Λ arrows indicate that the parameter increases across conditioning sessions (n = 10) and then decreases across extinction sessions (n = 3). The V arrows indicate the opposite. This parametric evolution is analogous to the one observed in typical learning curves using this classical conditioning paradigm. For this representation, the parameters have been normalized according to their maximum absolute values. Parameters 3, 6, 9, and 12 kept their negative values because of the reference system adopted: namely, the eyes of the experimental subject are open at 0° and totally closed at 25–30°.

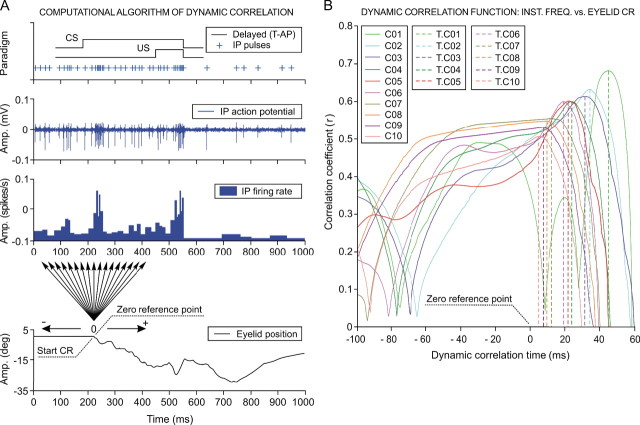
Figure 4.

The dynamic correlation function between interpositus neuron firing and eyelid conditioned responses. A, Computational algorithm of the dynamic correlation. The implementation of the dynamic correlation algorithm during the ninth conditioning session is illustrated. A delay [tone-air puff (T-AP)] conditioning paradigm was used. Note the correspondence, in terms of time and magnitude, between three different representations of neuronal activity recorded in the cerebellar interpositus (IP) nucleus: (1) the temporal localization of the action potential pulses marked with plus signs; (2) the direct representation of the action potentials in the interpositus nucleus; and (3) the resultant instantaneous frequency (in spikes per second). A direct eyelid position record obtained simultaneously with neuronal activity is also shown. The start of the eyelid CR is taken as the zero reference point of the dynamic correlation, and the arrows indicate the dynamic correlation range (±200 ms). The corresponding regression lines and correlation coefficients were determined in steps of 1 ms (i.e., 400 regression lines from each trial, like the one illustrated). B, Dynamic correlation functions. Ten dynamic correlation function curves are represented. Each representation corresponds to the average of all dynamic correlation curves obtained for the trials presenting CRs (n < 10) and collected from all of the blocks (n = 12) of the same conditioning session (C01–C10) for all of the experimental subjects (n = 4 cats). The dynamic correlation interval illustrated extends over the instantaneous frequency representation from −100 ms up to +60 ms to both sides of the zero reference point. There is a significant (F_{(9, 27, 98)} = 161.54, p < 0.01) decrease in the maximum correlation coefficient during conditioning sessions, in parallel with a decrease in the time of occurrence (T.K) of the maximum correlation. The broken lines indicate the T.K (K = C01, …, C10), which are always located to the right of the zero reference point, as indicated in A. Note that correlation coefficients obtained across the successive sessions were statistically significant (F_{(9, 27, 98)} = 37.56; p < 0.01), although their values show only a slight coupling (r coefficient < 0.7) between neuronal activity recorded at the interpositus nucleus and eyelid position during CRs.

Figure 5.

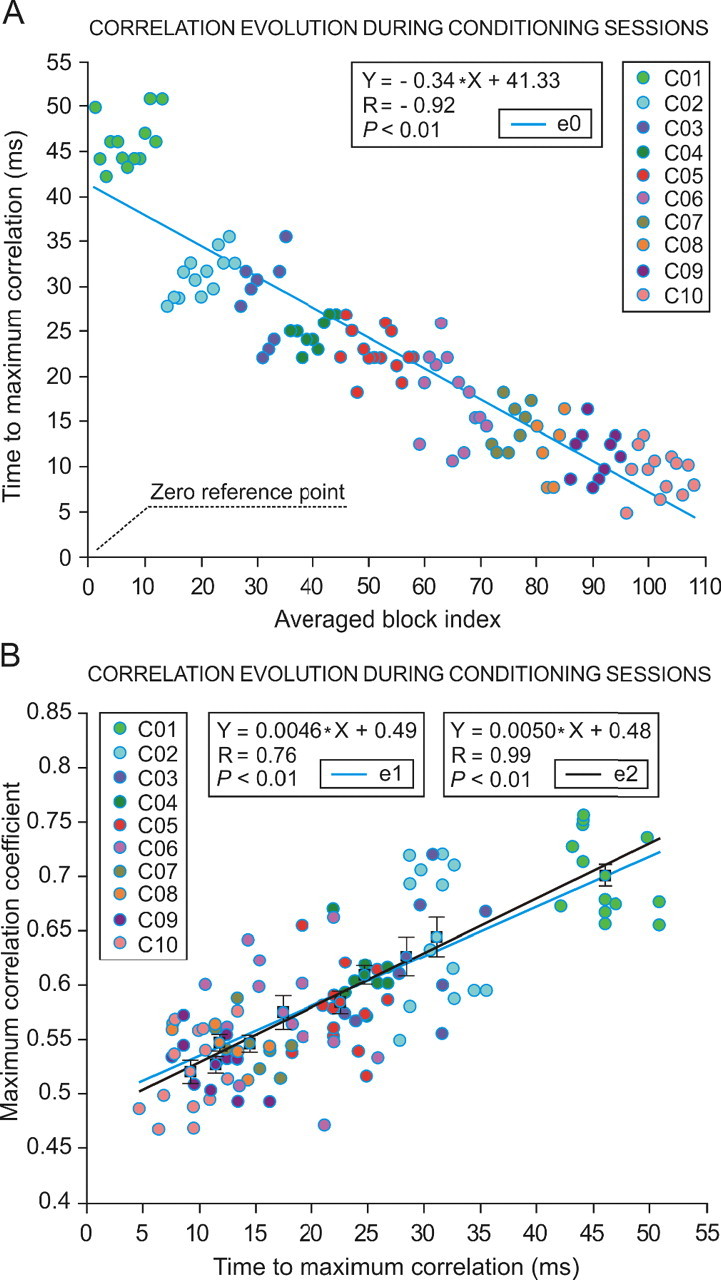
Evolution of the correlation coefficient of linear regression analysis between interpositus neuron firing and eyelid conditioned responses across conditioning sessions. A, Falling time to maximum correlation coefficient across sessions. On the x-axis are represented the successive blocks across conditioning sessions (C01–C10, 108 blocks) that presented significant (Wilk';s λ = 0.19; F_{(9, 36, 98)} = 15.24; p < 0.01) homogeneity values with their corresponding cluster. Blocks are arranged by their index number. The color code indicates the block session. The y-axis represents the latency (in milliseconds) to the maximum correlation time. Each colored circle corresponds to the mean time of occurrence of the maximum correlation associated to each averaged block. The averaged block indexes are sorted from 1 to 108 along the conditioning sessions: C01, 13; CO2, 13; C03, 9; C04, 9; C05, 14; C06, 13; C07, 8; C08, 6; C09, 10; C10, 13. The simple regression model used for this representation indicates a high correlation (r = −0.92; p < 0.01). Note the negative sign of both the regression coefficient (R) and the slope (−0.34) in the linear equation e0 (see inset). B, Relationships between the time to maximum correlation coefficient and maximum correlation coefficient. This plot represents the mean maximum correlation coefficients (y-axis) corresponding to each averaged block with respect to the mean time of occurrence of the maximum correlation coefficient (x-axis). The color code indicates the corresponding conditioning session (C01–C10). The linear equation e1 (see middle inset) is applied to the set of circles associated to the averaged blocks, whereas the linear equation e2 is applied to the 10-square/circle subset representing the mean values per session. For each mean value, the SE is indicated.

The main outcome of the analytical procedure was that the hierarchical cluster tree was significantly consistent (cophenetic correlation coefficient, 0.97; the closer this value is to 1, the better the clustering solution) with the actual conditioning sessions. For example, and given the similarity of the data collected in the corresponding trials and blocks, the two habituation sessions (H01, H02) were clustered close to the first conditioning session (C01). In addition, the first extinction session (E01) was clustered close to the 10th conditioning session (C10), whereas the following extinction sessions (E02, E03) were clustered close to the last four (7–10) conditioning sessions. Finally, middle experimental sessions (CO2–C06) formed by themselves a set of clusters.

Data organized in the matrix provided by cluster analysis allowed the selection of the most significant parameters representing the acquisition and extinction processes (Fig. 3B). A total of 14 representative parameters (4 kinetic and 10 kinematic) (Table 3) are depicted in Figure 3B. The evolution of these parameters across training was analogous to that observed in typical learning curves using this classical conditioning paradigm (Gruart et al., 1995). For example, parameter 1 in Figure 3B corresponded to the peak amplitude of the evoked CR. Note that this parameter increased steadily across conditioning and decreased progressively during the three extinction sessions (F_{(14, 56, 136)} = 123.68; p < 0.01). The mean peak firing rate of interpositus neurons (parameter 10) also increased across conditioning and decreased during extinction (F_{(14, 56, 136)} = 749.46; p < 0.01). Interestingly, the total number of spikes generated by facial motoneurons (parameter 13) during the CS–US interval increased across conditioning (F_{(14, 56, 136)} = 276.38; p < 0.01). In contrast, the mean number of spikes generated by interpositus neurons in the CS–US interval (parameter 14) did not change significantly across conditioning, suggesting that the increase in their firing rate after CS presentation represented a reorganizing (instead of a net increase) of their mean spontaneous firing. Finally, an inversed evolution was obtained for the latency of the maximum instantaneous frequency for the interpositus neurons in the CS–US interval (parameter 11; F_{(14, 56, 136)} = 297.99; p < 0.01).

Table 3.

The 14 physiological variables (10 kinematic and 4 kinetic) included in Figure 3B

No.	Parameter
1	Eyelid position amplitude at US presentation compared with the amplitude at the start of the CR (°).
2	Ratio between parameter 1 and the latency between the start of the CR and US presentation (°/s).
3	Slope of the regression line that fits the eyelid position record between the start of the CR and US presentation (°/s).
4	Eyelid position amplitude at the start of the UR compared with the amplitude at the start of the CR (°).
5	Ratio between parameter 4 and the latency between the start of the CR and the start of the UR (°/s).
6	Slope of the regression line that fits the eyelid position record between the start of the CR and the start of the UR (°/s).
7	Intercept of the regression line that fits the eyelid position record between the start of the CR and US presentation (°).
8	Intercept of the regression line that fits the eyelid position record between the start of the CR and the start of the UR (°).
9	Eyelid position amplitude at US presentation (°).
10	Amplitude of the maximum instantaneous frequency for the interpositus neuron in the CS–US interval (spikes/s).
11	Latency of the maximum instantaneous frequency for the interpositus neuron, with respect to CS presentation (ms).
12	Eyelid position amplitude at the start of the CR (°).
13	Number of action potentials of the motoneuron in the CS–US interval.
14	Number of action potentials of the interpositus neuron in the CS–US interval.

The dynamic correlation function between interpositus neuron firing and eyelid conditioned responses

Cluster analysis allowed us to homogenize the data collected during the different trials, blocks, and sessions with regard to the 60 selected parameters. One particular analysis that we performed after cluster analysis was to establish the dynamic correlation function between interpositus neuron firing and eyelid CRs. As illustrated in Figure 4A, the dynamic correlation analysis enabled us to determine the time of occurrence of the maximum correlation with respect to the zero reference point (i.e., the moment at which the CR started). The dynamic correlation analysis ranged, for each trial, from 200 ms before to 200 ms after the zero reference point (Fig. 4A, arrows). Details regarding the rationale underlying the dynamic correlation function are described in supplemental Appendix S2 (available at www.jneurosci.org as supplemental material).

For the curves represented in Figure 4B, the correlation functions corresponding to the trials taken from all of the blocks of the same session were averaged, session by session, for each animal across the successive conditioning sessions (C01–C10) (see color code in Fig. 4B). Dynamic correlation functions allowed describing how the correlation coefficients (r) evolved during the successive sessions. Thus, we were able to determine whether the maximum correlation between interpositus neurons firing and eyelid CRs took place before or after the zero reference point (i.e., the moment at which the CR started).

Peak firing rate of interpositus neurons in response to CS presentations increased across conditioning, with a mean slope of 0.14 spikes/s per trial (from 150 spikes/s during the first conditioning session to 322 spikes/s during conditioning session 10). Interestingly, the time of occurrence of interpositus neuron peak firing rate decreased with respect to the zero reference point from 49.1 ms during the first conditioning session to 13.4 ms during conditioning session 10. The increase in peak frequency, together with a decrease in its time of occurrence with respect to the zero reference point, caused a decrease in correlation coefficient values (r = 0.68 for C01 to r = 0.51 for C10, p < 0.01; see r values for each session from −100 to +60 ms with respect to the zero reference point in Fig. 4B). In Figure 5A is represented the evolution of the time to maximum correlation of the interpositus population with respect to the zero reference point for the 108 blocks that presented homogenous values according to the cluster analysis (slope, −0.34; R = −0.92; p < 0.01). In the same way, Figure 5B illustrates that the time to maximum correlation determined for interpositus neurons across the 10 conditioning sessions presented a linear relationship with the mean maximum correlation coefficient achieved during each block and conditioning session (slope, 0.0046; R = 0.76; p < 0.01). According to this analysis, both the time to maximum correlation and the maximum correlation coefficient of interpositus neuron firing decreased across conditioning but always lagged the zero reference point (i.e., the start of the CR). Thus, the developed statistical algorithm indicated that the contribution of interpositus neurons might be related more to the modulation of eyelid responses than to their generation. Additional analysis performed regarding the functional relationships between interpositus neuron firing and eyelid CRs are detailed in supplemental Figure S2, A and B, and Appendix S4 (available at www.jneurosci.org as supplemental material).

In contrast, the dynamic correlation function for orbicularis oculi motoneurons remained quasi-stationary and with high mean correlation coefficient values (r_max = 0.68 for C01 and r_max = 0.96 for C10; p < 0.01; data not illustrated) across conditioning sessions. According to these results, it can be proposed that orbicularis oculi motoneurons certainly encode eyelid kinematics at every instant of the dynamic correlation range. This inference is supported by the experimental fact that the discharge rate of orbicularis oculi motoneurons increased progressively across the learning process in relation to the increased amplitude of corresponding CRs. Thus, the discharge pattern for orbicularis oculi motoneurons correlates significantly (F_{(9, 27, 98)} = 42.46; p < 0.01) with eyelid position during CRs in all of the conditioning sessions.

Figure 6 further illustrates the different functional properties of interpositus neurons (Fig. 6A) and orbicularis oculi motoneurons (Fig. 6B) with regard to the maximum correlation coefficients they reached during habituation, conditioning, and extinction sessions, and the time these maximum values were achieved with respect to the zero reference point (indicated by the dashed line a). On the color raster display illustrated in Figure 6A, it can be observed that the maximum correlation coefficient evolved from relatively high coefficient values (r < 0.7) to intermediate coefficient values (r ≈ 0.5). This is clearly indicative of the progressive diminution of correlation across conditioning. At the same time, the dashed line b indicates that maximum r values were reached at decreasing (i.e., shorter) times with regard to the zero reference point. In contrast, the raster color display illustrated in Figure 6B indicates that orbicularis oculi motoneurons presented high correlation values (r = 0.68–0.96) during all of the conditioning sessions. Importantly, their dynamic correlation times were always set at ≈10 ms before the zero reference time (dashed line b).

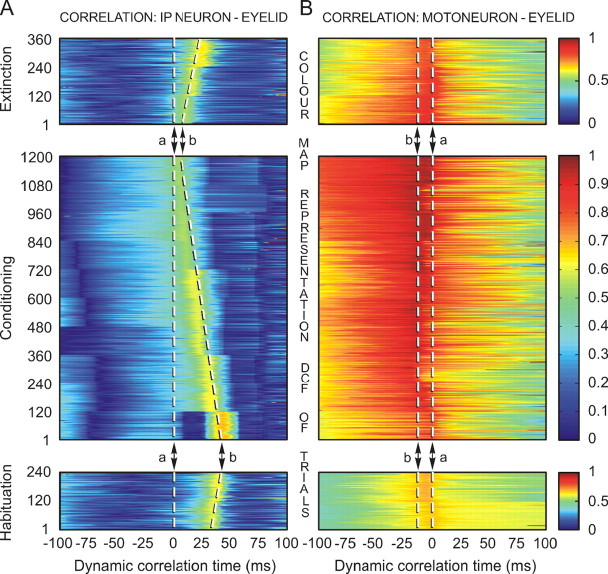
Figure 6.

A color map representation of the dynamic correlation evolution across habituation, conditioning, and extinction sessions for cerebellar interpositus neurons and orbicularis oculi motoneurons. A, A two-dimensional map resulting from dynamic correlation between eyelid position during CRs and the instantaneous firing rate of identified cerebellar interpositus neurons. The map represents the dynamic evolution of the correlation coefficients (0–1) across two habituation (2 neurons, 240 trials), 10 conditioning (17 neurons, 1200 trials), and three extinction (5 neurons, 360 trials) sessions, with respect to the dynamic correlation time which, in this case, is of 100 ms, on both sides of the start of the eyelid CR (0 time, dashed line a). Note a reduction in the time of occurrence of the maximum correlation in parallel with a slight decrease (shades of orange degrading to shades of green, going through yellow) in the maximum correlation coefficient across conditioning (indicated by the dashed line b). B, A two-dimensional map resulting from dynamic correlation between eyelid position during CRs and the instantaneous firing rate of identified orbicularis oculi motoneurons. The map represents the dynamic evolution of the correlation coefficients (0–1) across two habituation (5 neurons), 10 conditioning (21 neurons), and three extinction (7 neurons) sessions. The correlation coefficient values remained high during learning and were predominant around the 10.4 ± 4 ms (indicated by the dashed line b) before the start of the CR (0 time, dashed line a).

Oscillatory and phase inversion properties of interpositus neurons and orbicularis oculi motoneurons

Figure 7, A and B, illustrates the cumulative trapezoidal integral of three representative interpositus neurons (IP1–IP3) and a representative orbicularis oculi motoneuron during the first (C01) (Fig. 7A) and the 10th (C10) (Fig. 7B) conditioning sessions. It should be noticed that all of the neurons presented an increasing profile and that they showed some slight and relative variations around the local and global maximum instantaneous frequency values. We defined three equivalence times (L1–L3) at the points at which interpositus neuron type IP2 and motoneurons crossed their lines. The equivalence times meet the requirement L2(C01) > L2(C10) and L3(C01) > L3(C10) in the CS–US interval during the conditioning sessions, given the following experimental facts: (1) an increase in the amplitude of the maximum instantaneous frequency of interpositus neurons (C01, 151.5 spikes/s; C10, 322.6 spikes/s); (2) a decrease in the time of occurrence (C01, 49.1 ms; C10, 13.4 ms) of the maximum instantaneous frequency for interpositus neurons, and (3) a progressive increase in the discharge rate of orbicularis oculi motoneurons across the learning process (smaller in C01 and larger in C10).

Figure 7.

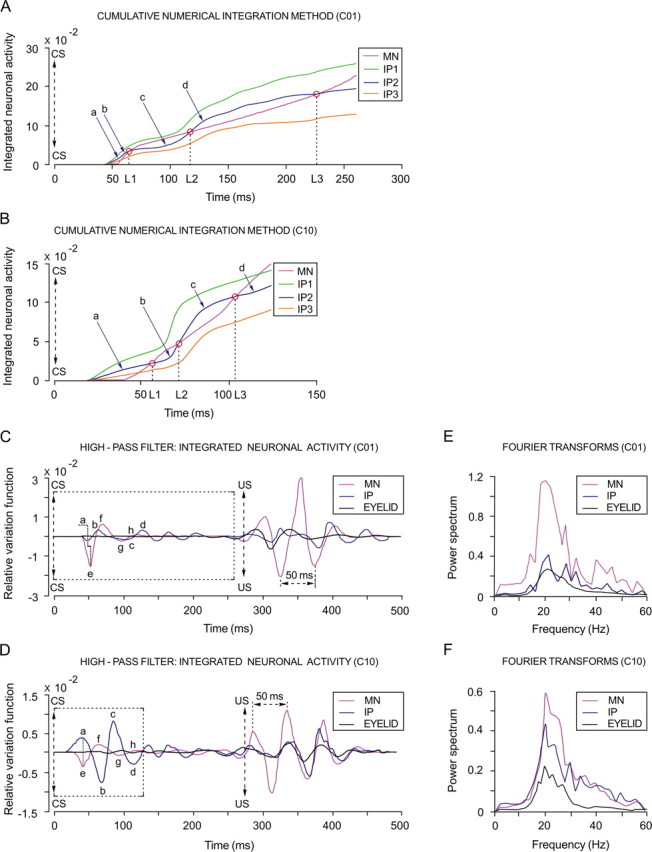
Oscillatory and phase-inversion properties of cerebellar interpositus neurons. A, B, A representation of the cumulative numerical integration method. Three of the illustrated traces correspond to the averaged integrated neuronal activity of identified cerebellar interpositus (IP; see color codes in the inset) neurons, and the fourth trace represents the integrated neuronal activity of a selected orbicularis oculi motoneuron (MN; see code in the inset). Data were collected from the first (A) and the 10th (B) conditioning session, respectively. In each case, CS presentation (time 0) and the equivalence times (L1, L2, and L3) of integrated neuronal activity are indicated. Note that, for IP2 traces, the equivalence times accord with L2.C01 > L2.C10 and L3.C01 > L3.C10. For session C01, the IP2 trace represents 63.7% of the analyzed data, and the IP1 and IP3 traces represent 24.1 and 12.2%, respectively. For session C10, the IP2 trace represents 68%, the IP1 trace 12.6%, and the IP3 trace 19.4%. C, D, High-pass filtering of the integrated neuronal activity. Oscillatory curves (relative variation functions) resulting from high-pass filtering (−3 dB cutoff at 5 Hz and zero gain at ≈15 Hz) of integrated neuronal firing activities illustrated in (A, B) and of eyelid position corresponding to the same set of records. In C, the motoneuron (magenta trace) and the interpositus neuron (blue trace) curves show a phase difference (≈π/2, as indicated by the crooked dashed line) during their oscillations in the CS–US interval, which remains during eyelid unconditioned responses to US presentation. Note that, in fact, components a–d (from interpositus neuron traces as shown in A–C) are partially out of phase with components e–h (from MN traces, as indicated in C), respectively. In D, motoneuron and interpositus neuron curves present a phase difference (≈π, as indicated by the straight dashed line) during their oscillations in the CS–US interval. Note that, in this case, components a–d are totally out of phase with components e–h, respectively. In contrast, during the occurrence of eyelid unconditioned responses, both motoneuron and interpositus neuron variation curves show oscillations with a similar phase. E, F, Fast Fourier transforms. Power spectra for the oscillating curves shown in C and D, respectively. Note that the three illustrated spectra, during both the first (E, C01) and 10th (F, C10) conditioning sessions, presented a significant predominance of spectral components at ≈20 Hz and significant differences between their power spectra for both interpositus neurons (interpositus neurons, F_{(9, 54, 98)} = 216.28; p < 0.01) and orbicularis oculi motoneurons (motoneurons, F_{(9, 54, 98)} = 225.48; p < 0.01).

The presence of an oscillatory behavior in the firing of interpositus neurons and orbicularis oculi motoneurons was evidenced by high-pass filtering the traces illustrated in Figure 7, A and B. The relative variation curves obtained after the high-pass filtering process (Fig. 7C,D) presented oscillatory and phase-inversion properties. By phase inversion, we mean the transition from a partial phase difference (≈π/2 for C01, i.e., a cosine-type curve for motoneurons and a sine-type curve for interpositus neurons) to a total phase difference (≈π for C10, i.e., a cosine-type curve for motoneurons and a minus cosine-type curve for interpositus neurons). These results allow proposing a modulatory role of interpositus neurons in the final common pathway for the eyelid system (i.e., the motoneuronal pool) that, by progressively inverting phase information, modulate or reinforce eyelid motor responses inversely (not opposed) to the contribution of orbicularis oculi motoneurons.

The relative power spectra illustrated in Figure 7, E and F, correspond to the curves shown in Figure 7, C and D, respectively. The predominance of spectral components observed ∼20 Hz was probably attributable to the 50 ms mean period characteristic of eyelid kinematics, as evidenced in the unconditioned responses (for both motoneuron firing and eyelid position) illustrated in Figure 7, C and D. In fact, an oscillation at the same (≈20 Hz) dominant frequency has been observed in eyelid acceleration traces and in the EMG activity of the orbicularis oculi muscle (Domingo et al., 1997). It should also be noticed that, during the first conditioning session (C01) (Fig. 7C), the oscillation amplitude of the motoneuron relative variation function was more significant (F_{(9, 54, 98)} = 170.26; p < 0.01), both in the CS–US interval and after US presentation, than that of interpositus neurons. In contrast, the oscillation amplitude of the interpositus neuron relative variation function increased progressively across the learning process, reaching significant values (F_{(9, 54, 98)} = 59.51; p < 0.01) during the 10th conditioning session (Fig. 7D) but only during the CS–US interval.

Discussion

Design of optimized experimental and analytical tools for the study of cerebellar functions

The multivariate cluster analysis is an optimal analytical tool to link the kinetic neural commands (i.e., motor and premotor neuronal activities computed from different quantitative parameters) and kinematic (i.e., motor activities computed from EMG and actual movement) parameters during motor learning and used here allows us to determine the intrinsic coherence of collected data. For this, we developed the necessary computer programs and algorithmic procedures to deal with such a huge amount of data (60 parameters quantified across 15 experimental sessions collected from 7 experimental animals). The main result indicated that up to 151 blocks could be correctly assigned to the corresponding experimental (habituation, conditioning, or extinction) session, and only data collected from 29 blocks were discarded because of their low homogeneity with the corresponding session. Importantly, these positive results indicated that neural firing properties recorded from different animals during the same conditioning paradigm can be correctly assigned to the corresponding experimental session (i.e., in agreement with the actual CR evoked during the CS–US interval). Although we have checked here the firing characteristics of only orbicularis oculi motoneurons and interpositus neurons, it can be proposed that the intrinsic coherence demonstrated between kinetic and kinematic properties strongly suggests the presence of a functional neuronal state involving many different cerebral centers evoked by the learning process (Delgado-García and Gruart, 2002). An additional advantage of this experimental approach is that, once collected data were properly arranged according to the hierarchical cluster tree (and that nonsignificant data were rejected), it was possible to determine analytically the multiple and coherent evolution of kinetic and kinematic parameters (Fig. 3B), the dynamic correlation function relating motoneurons and interpositus firing to eyelid CRs (Fig. 4B), the falling correlation property of the interpositus nucleus across the successive training sessions (Fig. 5), the time and significance of the linear relationships between these variables (Fig. 6), and, finally, the oscillatory and phase-inversion properties of orbicularis oculi motoneurons and interpositus neurons with regard to acquired CRs (Fig. 7). Thus, these novel (experimental and analytical) approaches to the study of actual neuronal mechanisms underlying the acquisition of new motor abilities will certainly contribute to the better understanding of brain functioning in alert behaving animals.

The posterior interpositus nucleus as an enhancer of acquired motor abilities

As already stated (Gruart and Delgado-García, 1994) and further confirmed here, the discharge rate of interpositus neurons seems to mirror the position and/or the velocity of eyelid CRs and increases during the CS–US interval in parallel with the amplitude of the CR. According to the present results, the maximum instantaneous frequency reached by type A (Gruart et al., 2000) interpositus neurons increased during the successive conditioning sessions, reaching mean amplitude values of ≈150 spikes/s during the first (C01) conditioning session and up to ≈320 spikes/s during the 10th (C10) session. The slope of this increase (0.14 spikes/s per trial) is similar to values reported for orbicularis oculi motoneurons (Trigo et al., 1999), interpositus neurons (Gruart et al., 2000), and hippocampal CA3 and CA1 pyramidal neurons (Múnera et al., 2001) during associative learning using both delay and trace conditioning procedures in alert behaving cats. This important finding reinforces the hypothesis that associative learning using classical conditioning procedures evokes a functional state in many different neuronal centers, characterized by a common increase in firing rate, and not necessarily related with the specific function fulfilled by each neural site (Delgado-García and Gruart, 2002).

The sustained increase in mean peak firing rate presented by the interpositus neuronal pool across conditioning was in parallel with a decrease in the mean time of its occurrence (≈49 ms for the first conditioning session to ≈13 ms by the 10th session) with respect to the start of the CR. The increase in firing rate, in association with the decrease in its mean time of occurrence, caused the maximum correlation coefficient between interpositus neuron activity and eyelid CR to decrease (r = 0.68 during the first conditioning session to r = 0.51 during the 10th). As a result, maximum correlation coefficient values between instantaneous interpositus firing and eyelid position during the CS–US interval always lagged (≈45 ms during the first conditioning session to ≈5 ms during the 10th) the zero reference point (i.e., the start of the CR). The foregoing allows us to affirm that interpositus neurons do not directly encode eyelid kinematics, i.e., their contribution is only weakly significant in the dynamic correlation range. Nevertheless, slight correlation (r < 0.7) values are not necessarily indicative of an absence of functional relationships between the involved variables. At the same time, a high correlation does not necessarily indicate a causal relationship (Granger, 1980; Baccala and Sameshima, 2001). In practice, the significance of the correlation coefficient is usually checked, at the desired level of statistical confidence, by calculating the residual cross-correlation. It must be mentioned here that the cross-correlation function at zero time lag is the linear correlation coefficient, an index frequently used to measure the linear interdependence between two variables (Belsley et al., 1980; Allen and Cady, 1982). According to the present results, it is important to indicate that the difference between occurrence of peak firing rate of interpositus neurons and that of maximum correlation coefficient was always positive (i.e., ≈4 ms for the first conditioning session and ≈8.5 ms for the 10th): namely, the time of occurrence of the maximum correlation coefficient was always shorter than the time of occurrence of the maximum instantaneous frequency, suggesting that interpositus firing does not encode directly CR kinematics.

Other experimental evidence, such as the increase in the maximum instantaneous frequency of cerebellar interpositus neurons and the decrease in the time of occurrence of the maximum frequency after the start of the CR across the 10 conditioning sessions, suggested a slightly significant covariance between the correlated variables. It should be noticed that the dynamic correlation curves (illustrated in Fig. 4B) were irregular under the same experimental conditions, indicating a limited, or at least an uncertain, influence of interpositus neurons on the generation of learned responses. The statistical algorithm developed here indicates that the contribution of this neuronal population can be interpreted better on the assumption that its members enhance eyelid responses. Thus, the role of interpositus neurons might be related more to the modulation of eyelid responses than to their generation.

In relation to eyelid responses, the interpositus area studied here corresponded to the dorsomedial part of the posterior division of the nucleus. This area coincides with previous mapping studies, performed with electrophysiological techniques in behaving cats (Gruart and Delgado-García, 1994; Gruart et al., 2000) and monkeys (Van Kan et al., 1993). The same area was labeled with retrograde transneuronal tracing of rabies virus injected in the upper eyelid of the rat (Morcuende et al., 2002). In contrast, the rabbit anterior interpositus nucleus has been assumed as the site in which this type of associative learning is acquired and stored (Christian and Thompson, 2003; Krupa et al., 1993). It is possible that lesion studies performed in the anterior interpositus (Yeo et al., 1985; Krupa et al., 2003) did affect axons originated in the posterior part of the nucleus. Moreover, as reported in previous studies (Gruart et al., 1995, 2000; Trigo et al., 1999; Jiménez-Díaz et al., 2004), there are important functional differences between rabbits and cats. The more important is that the retractor bulbi system seems not to be involved in the generation of CRs in cats (Trigo et al., 1999). Thus, minor differences in the location of eyelid-related neurons in the interpositus nuclei could be expected between species.

In contrast, and according to the present results, it can be stated that orbicularis oculi motoneurons certainly encode eyelid kinematics directly at every instant of the dynamic correlation range. This inference is supported by the experimental fact that the discharge rate of these facial motoneurons increased progressively across the learning process, with a relative refractory period (minimum interspike time interval) that decreased progressively in the CS–US interval and reached values slightly >3 ms immediately after US presentation (i.e., a peak firing rate of ≈330 spikes/s). Thus, an orbicularis oculi motoneuronal discharge pattern that correlated significantly with eyelid position during CRs in all of the conditioning sessions was obtained.

Phase-inversion properties and modulating role of posterior interpositus neurons in learned motor responses

The presence of oscillation in the relative variation functions of interpositus neurons is in evident concordance with reports regarding the wavy form CRs, formed in the cat by a succession of small waves (Domingo et al., 1997; Trigo et al., 1999). These waves are present not only in the position, velocity, and acceleration profiles of eyelid traces (Domingo et al., 1997) but have also been noticed in the EMG activity of the orbicularis oculi muscle (Domingo et al., 1997), in the firing activity of facial motoneurons innervating this muscle (Trigo et al., 1999), in the resting potential of facial motoneurons recorded both in vivo (Trigo et al., 1999) and in vitro (Magarinos-Ascone et al., 1999), and, finally, in the firing activities of motor cortex neurons during CRs evoked in behaving cats (Aou et al., 1992).

According to the high correlation coefficients between eyelid CRs and the instantaneous frequency of orbicularis oculi motoneurons, these small waves can be directly related to the motoneuron relative variation function components. They may, then, be partially (in session C01) or totally (in session C10) out of phase compared with relative variation function components of interpositus neurons. A sequential and out-of-phase release of the activity of interpositus neurons would certainly be helpful for a proper performance of consolidated eyelid CRs. Thus, we have to assume that interpositus neurons might play a role related more to phase modulation of the oscillation already observed in eyelid motor responses than to its generation. Accordingly, it could be necessary to have a neural site taking charge of compensating the oscillation of the lid, mostly during the acquisition of a new motor ability (Delgado-García and Gruart, 2002). In this sense, the increase in peak firing frequency and the decrease in its mean time of occurrence described here for interpositus neurons could contribute to its role as a neuronal phase-modulating device: namely, peak interpositus neuron firing should reach the orbicularis oculi motoneuron pool at the time when these motoneurons initiate their repolarization process, facilitating their repetitive firing in a decreasing time interval across conditioning sessions (Trigo et al., 1999; Delgado-García and Gruart, 2002) (Fig. 8). This phase-modulating device could play a damping role in eyelid performance, particularly during the process of acquiring new motor abilities (Jiménez-Díaz et al., 2004), a proposal already put forward by others (Thach et al., 1992). In this regard, it has been recently reported that disturbances in fast cerebellar oscillation in the cerebellar cortex could be related to cerebellar ataxia (Cheron et al., 2005). A mathematical demonstration of the relationships between falling correlation and phase-modulation properties of interpositus neurons is presented in supplemental Appendix S3 (available at www.jneurosci.org as supplemental material).

Figure 8.

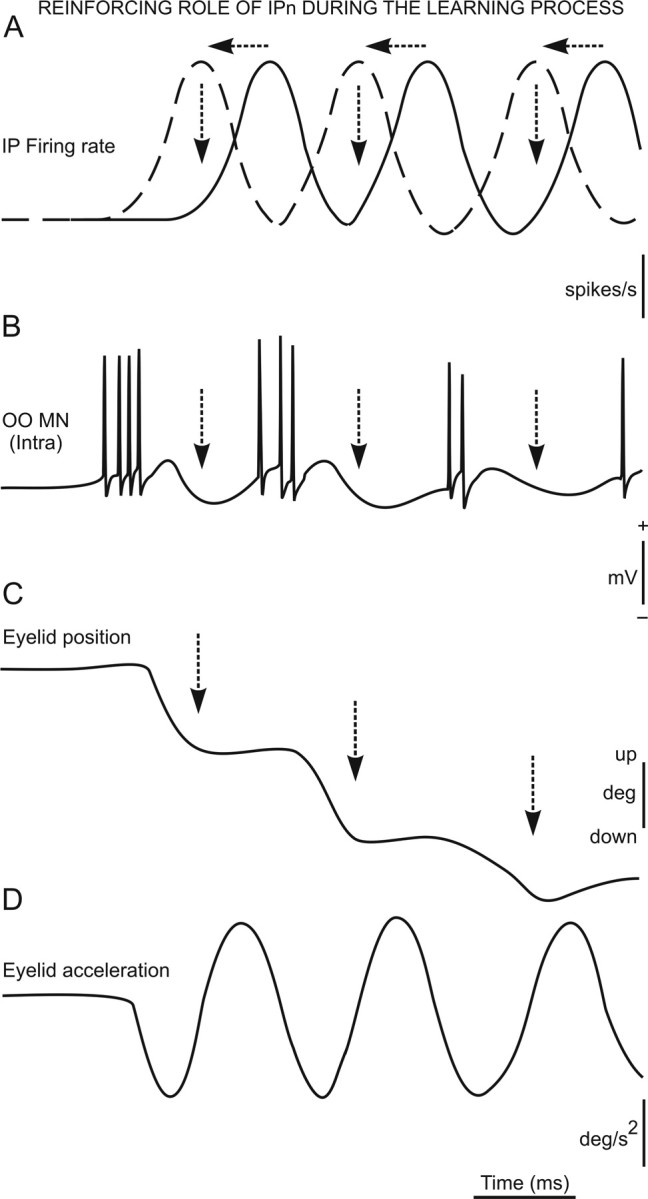
A functional representation of the reinforcing role of interpositus neurons during the learning (acquisition) process. A–D, From top to bottom are represented the firing rate (in spikes per second) of interpositus neurons (IP) (A), the typical firing of orbicularis oculi motoneurons (OO) (B; in millivolts) during the performance of an eyelid CR (see Trigo et al., 1999) and the corresponding eyelid position (C; in degrees) and acceleration (D; in degrees per squared second) traces. Note that the latency of peak interpositus firing decreases across conditioning and becomes out of phase with motoneuronal firing. Thus, at given a latency of 4 ms for interpositus action potentials to reach the motoneuron pool (Trigo et al., 1999), interpositus firing would facilitate a quick repolarization process of orbicularis oculi motoneurons, reinforcing their tonic firing during CR performance.

In summary, the double role of posterior interpositus neurons as an enhancer of facial motoneuron firing and as a damping device could help to explain cerebellar contribution to the proper performance of ongoing motor responses (mainly during the acquisition process) and to its proper timing (Welsh and Harvey, 1991; Delgado-García et al., 2002; Medina et al., 2002; Seidler et al., 2002; Koekkoek et al., 2003).