Modular Control of Limb Movements during Human Locomotion

Abstract

The idea that the CNS may control complex interactions by modular decomposition has received considerable attention. We explored this idea for human locomotion by examining limb kinematics. The coordination of limb segments during human locomotion has been shown to follow a planar law for walking at different speeds, directions, and levels of body unloading. We compared the coordination for different gaits. Eight subjects were asked to walk and run on a treadmill at different speeds or to walk, run, and hop over ground at a preferred speed. To explore various constraints on limb movements, we also recorded stepping over an obstacle, walking with the knees flexed, and air-stepping with body weight support. We found little difference among covariance planes that depended on speed, but there were differences that depended on gait. In each case, we could fit the planar trajectories with a weighted sum of the limb length and orientation trajectories. This suggested that limb length and orientation might provide independent predictors of limb coordination. We tested this further by having the subjects step, run, and hop in place, thereby varying only limb length and maintaining limb orientation fixed, and also by marching with knees locked to maintain limb length constant while varying orientation. The results were consistent with a modular control of limb kinematics where limb movements result from a superposition of separate length- and orientation-related angular covariance. The hypothesis finds support in the animal findings that limb proprioception may also be encoded in terms of these global limb parameters.

Introduction

It is generally accepted that the nervous system adopts strategies that reduce the complexity of controlling motor behavior. Controlling multijointed limbs, for example, presents the complexity of controlling redundant degrees of freedom, and it has been proposed that the nervous system may use global variables having fewer degrees of freedom (Bernstein, 1967; Lacquaniti et al., 1999, 2002; Latash, 1999; Orlovsky et al., 1999; Giszter et al., 2001; Hultborn, 2001; Bizzi et al., 2002; Flash and Hochner, 2005). Such controlled variables might pertain to the limb endpoint, which can be reduced to a direction or orientation component and a length component (Lacquaniti et al., 1995; Georgopoulos, 1996; Schwartz and Moran, 2000; Poppele et al., 2002; Roitman et al., 2005; Osaki et al.,2007).

Human locomotion control is an example of multijointed limb control that may be specific for different gaits of locomotion. A classic distinction between walking and running, for example, is in the behavior of a “telescopic limb” that acts as a rigid strut during the stance phase of walking and as a compressible spring in running. These behaviors can be predicted by modeling the limb axis as an inverted pendulum during stance in walking (Cavagna et al., 1976; Margaria, 1976) and a simple spring-mass system that is compressed and released during stance in running (McMahon and Cheng, 1990). The stiffness and compression of the limb axis can also be accounted for by the angular rotations of the limb segments in the sagittal plane (Lee and Farley, 1998). Therefore, a controlled pattern of covariation among segment rotations could also specify the limb endpoint motion as well as the resulting vertical motion of the center-of-mass.

The idea that limb segment angle covariation might relate to more global kinematics variables comes from animal studies (Lacquaniti et al., 1984, 1990; Lacquaniti and Maioli, 1994a,b; Shen and Poppele, 1995; Bosco et al., 1996). Limb segment rotations were also found to covary in human walking, so that the three-dimensional trajectory of temporal changes in the elevation angles lies close to a plane (Borghese et al., 1996; Lacquaniti et al., 1999; Courtine and Schieppati, 2004). This planar law of intersegmental coordination holds for walking at different speeds (Bianchi et al., 1998b), forward or backward directions (Grasso et al., 1998), erect or bent posture (Grasso et al., 2000), and different levels of body weight unloading (Ivanenko et al., 2002) and may therefore represent an invariance for locomotion.

This limb segment relationship in locomotion may result from more than one underlying mechanism (Bosco et al., 1996). Here, we explored the idea that the covariance might be related to limb endpoint control (i.e., control of the limb axis orientation and length). To test this hypothesis, we explored various human gaits with potentially different covariances and compared the resultant segment angle coordination with gait-specific limb length and limb orientation behavior. We found that the covariance can be accounted for by these two variables, and that differences between gaits may relate to a differential distribution of compliance among limb segments.

Materials and Methods

Subjects

Eight healthy subjects (six males and two females; between 26 and 44 years of age; 69 ± 10 kg, mean ± SD; 1.75 ± 0.07 m) volunteered for the experiments. All subjects were right leg dominant. The studies conformed to the Declaration of Helsinki, and informed consent was obtained from all participants according to the procedures of the Ethics Committee of the Santa Lucia Institute.

Experimental setup and tasks

Subjects (with shoes on) walked or ran either over ground at one speed (on average, 5.6 ± 1.1 and 9.6 ± 0.9 km/h, respectively) or on a treadmill (EN-MILL 3446.527; Bonte Zwolle BV, Zwolle, The Netherlands) at different speeds. In addition, the subjects hopped at a single speed over ground. In each case, they were asked to swing their arms normally and look straight ahead. Before the recording session on the treadmill, subjects practiced for a few minutes at the different speeds. In a treadmill protocol, subjects were asked to walk at 3, 5, 7, and 9 km/h and to run at 5, 7, 9, and 12 km/h so that we could compare walking and running at the same speeds (5, 7, and 9 km/h). During over-ground locomotion, they moved along an 8 m walkway with a force plate at the center by either walking, running, or hopping, all at natural freely chosen speeds. In addition, they were also asked to step, hop, and run in place at a similar cadence. Note that we found more kinematic variability among subjects in the hopping tasks than in walking and running, presumably because the subjects were more familiar with the latter. We also asked subjects to walk over ground using a “knee-locked” marching gait (at 2 km/h) to minimize leg joint rotations.

In addition to these basic three gaits, we explored other locomotion tasks that we also studied previously. These were stepping over an obstacle, walking in a crouched position with the knees flexed, and air-stepping. These conditions impose additional constrains either on the amplitude of foot motion (like in the obstacle task) or on the leg length and stiffness (crouched walking) or on the foot-support interactions (air-stepping). We showed previously that there is a planar covariation for each of these conditions (Grasso et al., 2000; Ivanenko et al., 2002, 2005a); however, we did not decompose the planar trajectories into limb length and orientation components. Details of the methods for these tasks are published, so we provide only a basic description here.

For the obstacle task, subjects were asked to walk at a preferred speed (on average, 5.0 ± 0.9 km/h) and step over an obstacle (30 cm height, made of foam rubber) with the right leg. We report only the data obtained for the step cycle in which the obstacle was cleared.

For the crouched walking, subjects were asked to walk knees and hips flexed (Grasso et al., 2000). Before this experiment, we asked our subjects to adopt knee-flexed static postures and then maintain approximately the same mean trunk orientation during walking. The mean trunk orientation was on average 25 ± 5° inclined forward, and the mean height of the hip marker was on average 13 ± 5 cm lower with respect to normal walking.

In air-stepping, subjects were supported in a harness pulled upwards by a force equal to the body weight (by means of a well-characterized pneumatic device) (Ivanenko et al., 2002) and stepped in the air. Their feet oscillated back and forth just above but never contacting the ground (to accomplish this, subjects' height above the treadmill was adjusted by operating on the harness-steel suspension). They were instructed to execute alternate stepping with both legs, as if they walked on ground, at a comfortable cadence. In the lack of ground contact, all subjects tended to step at a preferred speed of 2.7 ± 0.5 km/h (cadence was 63 ± 12 strides/min). To avoid trunk rotations in air-stepping, subjects maintained a light contact of their arms with the roll bars aside the body.

Before each experiment, subjects practiced for 1–2 min to perform the specific condition at a preferred speed. Immediately after each experiment, the subject was asked to perform the same movement in place [i.e., to step in place with a high vertical foot lift (∼30 cm) after the obstacle task] with knee-flexed vertical foot lift after crouched walking or vertical walking movement in the air after air stepping.

Data recording

We recorded kinematic data bilaterally at 100 Hz by means of the Vicon-612 system (Oxford Metrics, Oxford, UK) with nine television cameras spaced around the walkway. Infrared reflective markers (diameter, 1.4 cm) were attached on each side of the subject to the skin overlying the following landmarks: glenohumeral joint (GH), the midpoint between the anterior and the posterior superior iliac spine [ilium (IL)], greater trochanter (GT), lateral femur epicondyle (LE), lateral malleolus (LM), heel (HE), and fifth metatarsophalangeal joint (VM). The spatial accuracy of the system is better than 1 mm (root mean square).

During over-ground locomotion, the ground reaction forces (F _x, F _y, and F _z) under the right foot were recorded at 1000 Hz by a force platform (0.9 × 0.6 m; 9287B; Kistler, Zurich, Switzerland).

Data analysis

Biomechanical analysis.

The gait cycle was defined with respect to the right leg movement, beginning with right foot contact with the surface (touch-down). The body was modeled as an interconnected chain of rigid segments: IL-GT for the pelvis, GT-LE for the thigh, LE-LM for the shank, and LM-VM for the foot. For a schematic illustration of the instantaneous foot orientation and the corresponding center-of-pressure (COP) position during stance (see Appendix), we interconnected the LM-VM-HE markers. For walking and running, the gait cycle was defined as the time between two successive foot contacts of the right leg corresponding to the local minima of the HE marker. The timing of the lift-off was determined analogously (when the VM marker elevated by 3 cm). For hopping, we used the VM marker to evaluate the timing of both the touch-down and lift-off events. For air-stepping, the gait cycle was determined using the time between two successive maxima in the whole limb (GT-VM) elevation angle (Ivanenko et al., 2002). The touch-down and lift-off events were also verified from the force plate recordings (when the vertical ground reaction force exceeded 7% of the body weight), and we found that the kinematic criteria we used predicted the onset and end of stance phase with an error smaller than 2% of the gait cycle duration (Borghese et al., 1996). The data were time-interpolated over individual gait cycles on a time base with 200 points.

Limb axis definition

The limb axis may be formally defined as connecting the proximal joint with the point of contact with the ground. Thus, the anatomical correspondence may vary as a function of gait. For example, during walking, there is no contact with the ground during the swing phase and the contact moves from the heel to the ball of the foot as stance progresses from touch-down to lift-off. The operational definition we adopted is to approximate the endpoint with a virtual point that is defined for each gait (for details, see Appendix). To estimate the amount of the endpoint migration, the instantaneous center-of-pressure position with respect to the foot location on the force platform was calculated for over-ground trials from the force plate data and compared across conditions (walking, running, hopping). The mean position of the COP relative to the sole during stance was used as the first approximation of the virtual endpoint (VE) in different gaits. Accordingly, the limb axis was defined by GT-VE. For running and hopping, VE was close to the VM marker; for walking, it was located approximately at the midsole.

In addition, we estimated the virtual endpoint trajectory predicted from the two principal components of the segment angle covariance associated with limb length and limb orientation changes (see Appendix).

Intersegmental coordination

The intersegmental coordination was evaluated in position space as described previously using the principal component analysis (PCA) (Borghese et al., 1996; Bianchi et al., 1998a,b). The temporal changes of the elevation angles of lower limb segments do not evolve independently, but they are tightly coupled. When the elevation angles are plotted versus one another, they describe regular trajectory loops constrained close to a plane (Borghese et al., 1996). Thus, there are two principal components (that account for ∼99% of total variance), whereas there are three original angular waveforms. The specific orientation of the plane of angular covariance reflects the phase relationships between the elevation angles of the leg segments and therefore the timing of the intersegmental coordination.

To define the plane, we computed the covariance matrix of the ensemble of time-varying elevation angles (after subtraction of their mean value) over each gait cycle. The three eigenvectors u₁–u₃, rank ordered on the basis of the corresponding eigenvalues, correspond to the orthogonal directions of maximum variance in the sample scatter. The first two eigenvectors u₁–u₂ lie on the best-fitting plane of angular covariance. The third eigenvector (u₃) is the normal to the plane and defines the plane orientation. For each eigenvector (i), the parameters u_it, u_is, and u_if correspond to the direction cosines with the positive semiaxis of the thigh, shank, and foot angular coordinates, respectively. The planarity of the trajectories was quantified by the percentage of variance (PV) accounted for by the first two eigenvectors of the data covariance matrix (for ideal planarity the third eigenvalue is 0).

The first two eigenvectors also determine the axes of plane, and the data projected onto these axes correspond to the first and second principal components (PCs). We hypothesized that the PCs may reflect in some way the global characteristics of the limb motion, for instance, the endpoint motion in the sagittal plane.

To simulate the covariance planes (see Results, Conceptual model), we used a model of linear combinations of different angular covariances under the assumption of equal yielding at all joints and equal thigh and shank segment lengths:

where t, s, and f are time-varying thigh, shank, and foot elevation angles, respectively. A sensitivity analysis to different yielding patterns is also considered by using the same linear relationship but assuming different patterns of yielding:

where a and b are coefficients determined from the actual data. The underlying hypothesis across all simulations is that the “elementary” covariances are related to the specific control of relative yielding of all limb segments.

Statistics

Spherical statistics on directional data (Batschelet, 1981) were used to characterize the mean orientation of the normal to the covariation plane (see above) and its variability across subjects. To assess the variability directly, we calculated the angular SD (called spherical angular dispersion) of the normal to the plane. Statistics on correlation coefficients was performed on the normally distributed, Z-transformed values.

Results

We begin by comparing treadmill and over-ground locomotion with two different gaits, namely walking and running. We examined both walking and running on a treadmill at 5, 7, and 9 km/h and also walking alone at 3 km/h and running alone at 12 km/h. There are a number of clear differences between walking and running that do not simply depend on locomotion speed. For example, joint angle motion is larger during running compared with walking because of a greater flexion of hip and knee joints and an increased dorsiflexion at the ankle.

The main kinematics features of the leg during the gait cycle are captured by the average waveforms of the elevation angles of the leg segments (thigh, shank, and foot) (Fig. 1). We focus on the elevation angles, rather than on the relative angles (hip, knee, ankle flexion-extension), because they capture directly the limb configuration in space (i.e., the limb segment orientations relative to the vertical). The time course of the relative angles at the hip and ankle is variable not only across subjects but also from trial to trial in the same subject (Borghese et al., 1996). The segment orientation angles, in contrast, are much more stereotyped, possibly because of compensatory kinematic synergies (that would reduce segment angle variability) and/or complex joint motions not captured by simple joint angle measurements.

Figure 1.

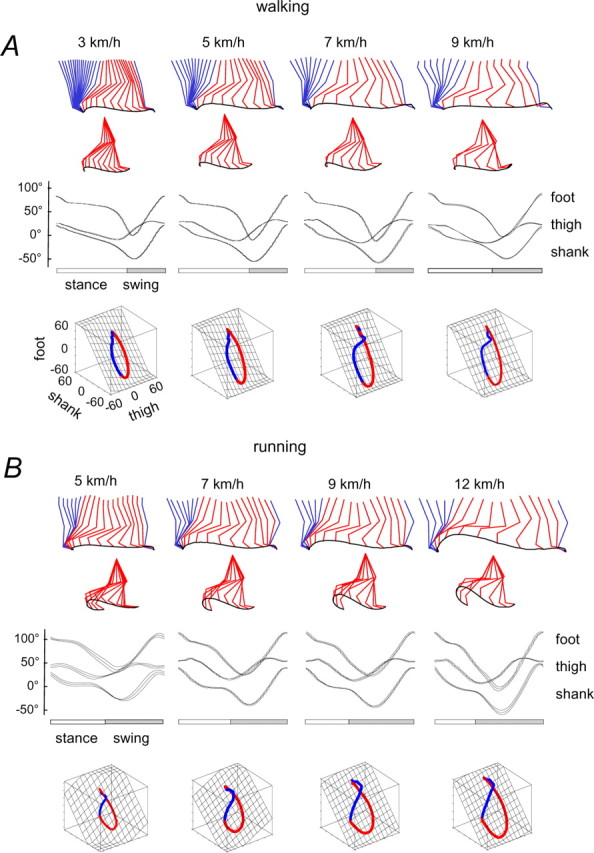
Kinematic patterns during walking (A) and running (B) on a treadmill at different speeds. Top to bottom, Stick diagrams for a single stride (blue during stance and red during swing; swing phase referenced to hip joint); ensemble averages (±SD; n = 8 subjects) of thigh, shank, and foot elevation angles of the right leg and corresponding trajectories in segment angle space (swing phase is red) along with the interpolated plane. Paths progress in time in the counterclockwise direction, touch down and lift-off corresponding approximately to the top and bottom of the loop, respectively.

It has been shown that the segment elevation angles covary during human walking so that their three-dimensional trajectories in the coordinates of the segment angles lie close to a plane (Borghese et al., 1996; Bianchi et al., 1998a,b; Courtine and Schieppati, 2004). This segment angle relationship is also not strongly dependent on speed (Fig. 1 A,B). The main effect of speed in general is to increase the amplitude of the segment angle trajectories without altering their waveform or the planar covariance. The planarity of the segment angle trajectories is considered below in detail.

The main features of the leg kinematics described above for walking and running on the treadmill were also observed during over-ground locomotion (Fig. 2 A, left panels) (Borghese et al., 1996; Ivanenko et al., 2005a; Cappellini et al., 2006). In particular, the average limb segment angle trajectories for over-ground locomotion were the same as those shown in Figure 1. There appear to be no major kinematics differences between treadmill and over-ground locomotion or differences in limb segment angle covariance that depend on speed.

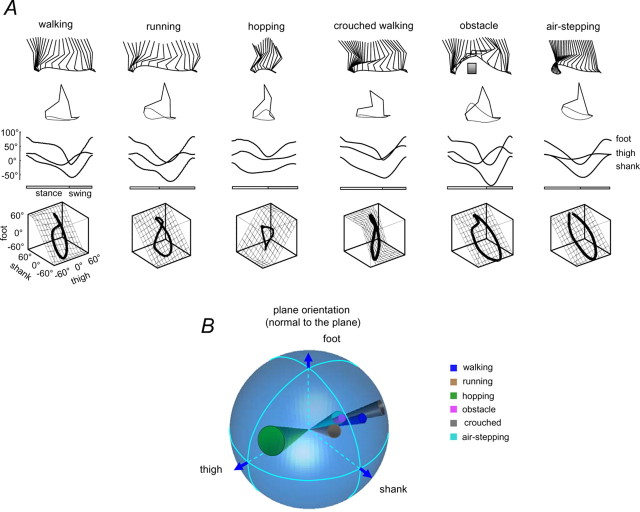
Figure 2.

Kinematic patterns during over-ground locomotor movements. A, Kinematic patterns of different gaits at a natural cadence in one representative subject. Top to bottom, Stick diagrams, thigh, shank, and foot elevation angles of the right leg, and corresponding trajectories in segment angle space along with the interpolated plane. For air-stepping, we simulated the speed of progression equivalent to the horizontal speed of foot motion during midstance, 3.1 km/h for this subject. The interpolation plane results from orthogonal planar regression: the first eigenvector (u ₁) is aligned with the long axis of the gait loop, the second eigenvector (u ₂) is aligned with the short axis, and the third eigenvector (u ₃) is the normal to the plane. B, Spatial distribution of the normal to the plane for each gait. Each circle on the sphere surface corresponds to the projection of the mean plane normal (the center of the circle) onto the unit sphere the axes of which are the direction cosines with the semiaxis of the thigh, shank, and foot. The radius of the circles correspond to the angular SD across subjects (n = 8). The angles of cones correspond to 2 SDs, accordingly. The foot semiaxis is positive, and the thigh and shank semiaxes are negative.

Leg kinematics for different gaits

Hopping has some features of both running and walking, but here the two legs move together in synchrony. Therefore, any “crossover” of leg motion to the opposite leg is different than in either walking or running. We found that the segment angles also covary during hopping; however, whereas the covariance planes for walking and running are similar, that for hopping is quite different (Fig. 2 A).

Crouched walking is basically normal walking in a crouched position. In this task, limb length is constrained by maintaining the knees in a flexed position. The covariance plane we obtained during this task is also rotated with respect to the planes for normal walking and running (Fig. 2 A).

Stepping over an obstacle also affects primarily the limb length during stepping by imposing a large excursion in length. The covariance plane we obtained in this task (for the step over the obstacle) is similar to that for normal walking, but the loop is opened up along the direction of the thigh angle axis (Fig. 2 A).

Air stepping occurs without foot contact in the “stance” phase. In this condition, any contribution to the limb kinematics from foot contact or weight support would be absent (Shen and Poppele, 1995). In this condition, we found that covariance plane was similar to that of normal walking (Fig. 2 A).

Planarity of the limb segment angle trajectories

The trajectories of the limb segment angles all appear to lie close to a plane (Fig. 2 A). Their planarity can be quantified by the PV accounted for by the first two eigenvectors of the data covariance matrix (Borghese et al., 1996). For ideal planarity, the third eigenvalue is 0. The planarity of the covariance is close to 100% for all the gaits (Table 1). There was more variability in the plane orientation among subjects in the hopping, air stepping, and crouched walking tasks (angular dispersion of the normal to the plane was 11.2, 7.1, and 6.3°, respectively) than in walking, obstacle, and running (3.8, 4.1, and 4.6°, respectively) (Fig. 2 B), presumably because each subject performed the former tasks slightly differently and was less familiar with them. In air stepping, the plane orientation depended significantly on how the subject moved the foot, because in the absence of foot contact, they were free to choose a preferred pattern. Nevertheless, it is worth stressing that the pattern of angular covariation tended to lie on a plane in all cases, although the plane orientation could differ.

Table 1.

Variance in limb segment angle trajectories

	Planarity (over ground)	Linearity (in place or marching)
Walking	99.1 ± 0.2%	99.0 ± 0.5%
Running	97.1 ± 1.1%	89.6 ± 3.7%
Hopping	98.0 ± 1.1%	98.5 ± 0.3%
Crouch	98.8 ± 0.3%	96.1 ± 3.0%
Obstacle	99.0 ± 0.4%	98.1 ± 1.2%
Air-stepping	99.8 ± 0.2%	89.1 ± 4.2%
Marching		95.7 ± 1.3%

Planarity, Percentage of total variance accounted for by PC₁ and PC₂ (ideal plane, 100%); linearity, percentage of total variance accounted for by PC₁ (ideal line, 100%).

Figure 2 B shows the spatial distribution statistics of the normal to the plane for each gait. Each circle on the sphere surface corresponds to the projection of the normal to the mean plane (the center of the circle) onto the unit sphere, the axes of which are the direction cosines with the semiaxis of the thigh, shank, and foot. The radius of the circles correspond to the angular SD across subjects (n = 8). The mean radius of the circles across all gaits was 5.6 ± 2.9° (range, 3.6–11.1°). There was a tendency for the normals to intersect the unit sphere along an arc and therefore to lie in a plane (p < 0.05) [test for coplanarity (Mardia 1972)]. For hopping and crouched walking, the planes rotated in the opposite directions with respect to the walking plane, and the orientations of the planes for running, obstacle, and air stepping were all quite similar. The mean angular deviation between each normal and the best fitting plane was only 3° (maximal deviation, −5.1°). Indeed, the normals spanned a pie-shaped wedge of 111° on this plane. The normal to the plane was defined by t = 0.27, s = 0.23f and corresponds to an axis of rotation of normals.

Thus, the full limb behavior in all gaits can be expressed as the two degrees of freedom (DOF) planar motion in each gait (Fig. 2 A), plus the rotation of the motion plane about a defined axis (1DOF). This extends the analysis to a full 3DOF spatial control of locomotion. Interestingly, the rotation of the motion planes in Figure 2 B mainly occurs about the same axis (u _3t) as we found previously for the effect of walking speed. Indeed, during walking at different speeds (Fig. 1), there is a slight rotation of the covariance plane quantified by small changes in the direction cosine of the normal with the thigh axis, u _3t (Bianchi et al., 1998b). In that case, the rotation was related to phase shifts between the shank and foot segment angles. Additional investigation is needed, however, to relate rotations of the covariance planes in different gaits with segment angle phase relationships.

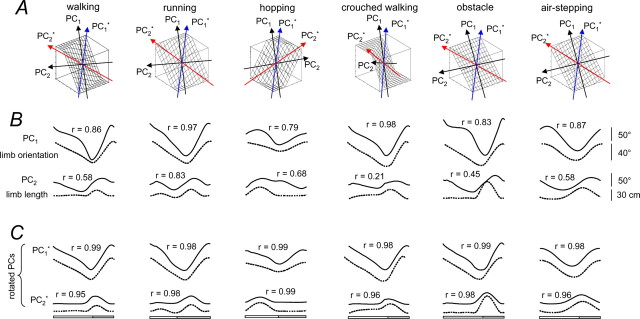
The eigenvector analysis illustrated in Figure 3 shows the waveforms of the two principal components (Fig. 3 B, PC₁ and PC₂) compared with the limb axis orientation and length trajectories, respectively. Although there was a correspondence between PCs and limb axis trajectories, it was somewhat weak in many cases. We found, however, that we could rotate the component axes such that they also lined up with the limb axes trajectories. For example, during running, PC₁ is highly correlated with limb axis rotation (r = 0.97), and PC₂ is well correlated with the limb length trajectory (r = 0.83). A minor rotation of the axes (data not shown) was able to increase the correlation for PC₂ to well over 0.9 without affecting much the correlation for PC₁. This simple rotation was not as effective for the other gaits and tasks, but it did suggest that the limb axis components could provide a basis to account for almost all the variance in the segment angle trajectories.

Figure 3.

PCA of elevation angles during over-ground locomotor movements. A, Covariance planes from Figure 2 with the directions of the PCs superimposed (black arrows). Directions of rotated PCs (PC*) (see Appendix and C) are shown in color (PC₁* in blue; PC₂* in red). B, Two principal components (PC₁ and PC₂; solid lines) and their correlations with limb length (GT-VE) and limb angle (dotted lines). C, Rotated PCs and their correlations with limb length and limb angle. PC₁* was approximated by projecting the data to the hypothetical limb orientation covariance line (t = s = f), and PC₂* was obtained by projecting the data to the in-place experimental covariance line (red). For air-stepping, subjects executed small horizontal foot excursions (∼15–20 cm) when stepping in-place in the air; accordingly, there was an ellipse rather than a line. In this case, we took the orientation of the long axis of the ellipse as an approximation of the direction of the limb length covariance.

Although there are no unique reference axes for the segment angle data set, a question we pose is whether length and orientation can provide a reference that is consistent across tasks. A more rigorous analysis presented in the Appendix shows a highly significant correspondence between rotated PCs and limb axis components for each case we examined (Fig. 3 C).

Limb length and orientation

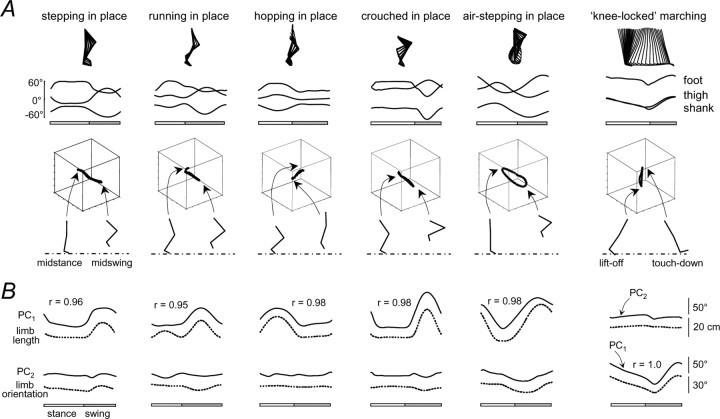
The PCA therefore suggests a way to dissociate the components of the two-dimensional covariance experimentally. If these two components can be controlled independently, the prediction would be that subjects should be able to produce movements confined to one component axis resulting in a linear rather than planar covariance of the limb segment angles. We tested this prediction by having subjects produce the locomotion movements in place, by producing the movements along the limb length axis with close to zero motion along the orientation axis (Fig. 4). We also had subjects walk over ground using a knee-locked marching gait (Fig. 4, right panel). In this case, the movements were along the limb orientation axis with nearly zero motion along the limb length axis.

Figure 4.

Kinematic patterns of in-place movements at a natural cadence and knee-locked marching by one representative subject. A, Kinematic patterns. During stepping, hopping, crouched in place, and knee-locked marching, the trajectory loop reduces to a line (see Results). During running, there is a small deviation from the line in stance, and during air-stepping, the trajectory is a loop, because subjects could not suppress some horizontal movement. B, Two principal components (PC₁ and PC₂; solid lines) and their correlations with limb length (GT-VE) and limb angle (dotted lines). During in-place movements, the limb angle was nearly constant, and the limb length varied as shown by the dotted line. During marching, the limb orientation varied, and the limb length was nearly constant. The first principal component of the linear trajectory is highly correlated with changes in the limb length for each in-place gait. The first principal component is correlated with the limb orientation for marching.

We did indeed find linear segment angle trajectories when the subjects tried to confine movements along the limb length direction (Table 1). During stepping in place (Fig. 4 A), the intersegmental coordination collapsed to a straight line, because the phase shift between adjacent segments was either 0 or 180°. The situation was similar during hopping in place, resulting also in linear trajectory. During running in place, the relationship was also linear for most of the trajectory, although there was a small segment during part of the stance that appears to deviate from a single line, and there was more intersubject variability (range, 85.2–93.3%). We also found a linear covariance of the limb segment angles for the obstacle task and crouched walking (Fig. 4 A).

All our subjects were unable to avoid making small horizontal foot excursions (∼15–20 cm) during the “in-place” air stepping. This resulted in an ellipse rather than a line (Fig. 4 A). In this case, we took the orientation of the long axis of the ellipse as an approximation of the direction of the limb length covariance.

During knee-locked marching, the trajectory also collapsed to a line, because there was little or no relative motion among the limb segments.

The linear trajectories observed in these experimental conditions strongly suggest that the limb axis coordinates may also be components of the planar trajectories observed during over-ground locomotion. The differences between these in-place movements and the over-ground locomotion seems to be mostly in the horizontal motion of the foot, which provides the propulsion for over-ground motion, and presumably adds the second dimension to the intersegmental covariance relationship. Thus, the data imply that the over-ground kinematics may result from the superposition of a limb axis length component and an orientation component.

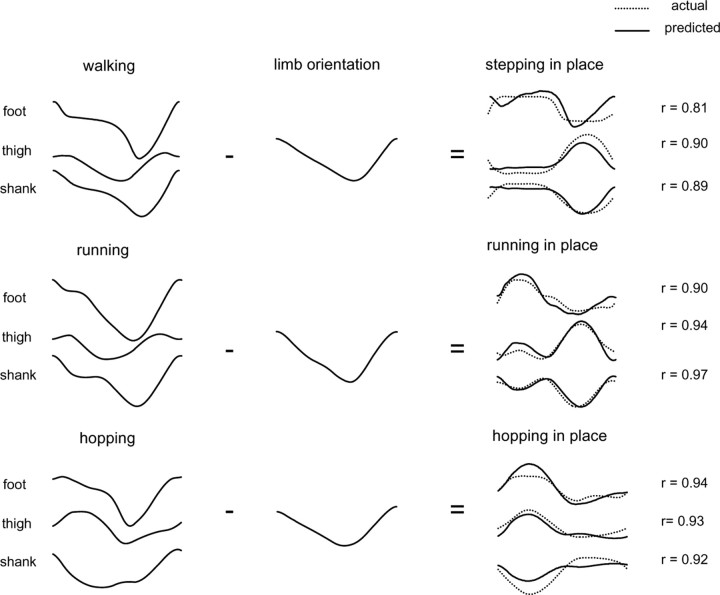
We tested this by subtracting the limb axis orientation from the over-ground segment angle trajectories to predict the in-place segment angle trajectories (Fig. 5). We found a high level of overall correspondence between the in-place data and the values predicted from the over-ground trajectories. The best predictions were for running and hopping (mean waveform correlation, r = 0.93 ± 0.02) and the poorest for walking (r = 0.86 ± 0.04). In the case of walking, foot rotation was actually different in the over-ground and in-place conditions, because the heel strike used over ground became a foot or toe strike in place. This difference seems to be reflected primarily in the relatively poor fit between actual and predicted foot orientation trajectories.

Figure 5.

Linear combination of segment angle covariance during in-place movements with limb orientation obtained during actual locomotor movements. Left column, Over-ground kinematic patterns during walking, running, and hopping in one representative subject. Middle column, Limb (GT-VE) orientation waveforms correspond to walking at 5 km/h, running at 9 km/h, and hopping at 4 km/h. Right column, Comparison of actual kinematic patterns during in-place stepping, running, and hopping with those predicted by subtracting the respective limb orientation from the over-ground trajectories. Waveform correlation coefficients (r) for each pair listed at the far right.

Overall, the data are in agreement with our hypothesis. For example, PC₂* amplitude was greater in the obstacle task (Fig. 3 C) corresponding to the high foot lift in this task, and somewhat smaller during crouched walking corresponding to a smaller excursion of the limb axis length in that task. The PC₁* amplitudes were also smaller during hopping and air-stepping corresponding to the relatively smaller leg swing in those tasks. Thus, we concluded that the planar covariation of limb segment angles likely results from discrete kinematic synergies predicted from a weighted combination of limb length and orientation angular covariance.

Conceptual model

A particular pattern of covariance is likely to reflect an underlying pattern of relative joint yielding or stiffness that governs how much each joint may rotate under load (Lee and Farley, 1998; Arampatzis et al., 1999). We explored this idea further with a simple model (Fig. 6) based on the experimental dissociation of components.

Figure 6.

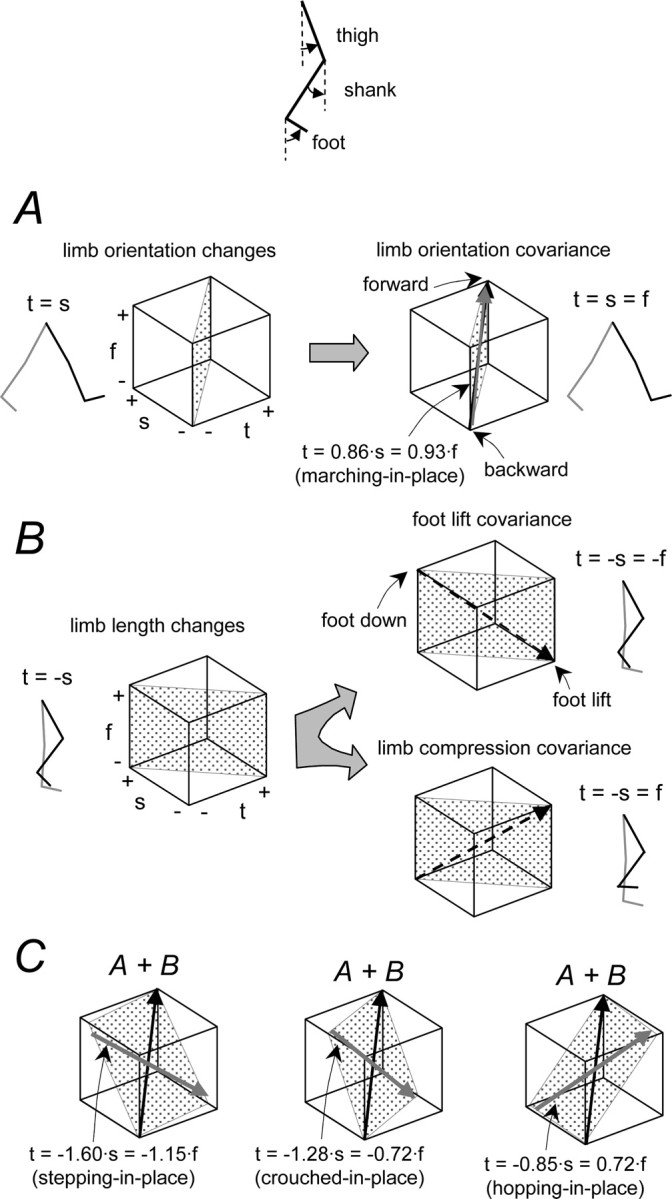
A simple model of additive limb segment angle covariances. A, Limb orientation basic covariance with t = s = f (black line) compared with the average linear trajectory for marching (t = 0.86 · s = 0.93 · f; brown). B, Limb length basic covariance (along the line t = −s) leading to a foot lift covariance with shank and foot segments in phase (t = −s = −f; dashed black line) and a limb compression covariance with shank and foot out of phase (t = −s = f; dashed black line). C, Examples of additive covariance. Linear combinations of elementary covariance vectors result in planar covariance patterns (gray planes) resembling those observed during walking, hopping, and crouched walking (compare with Fig. 2 A). The in-place linear trajectories averaged across subjects were: t = −1.60 · s = −1.15 · f for stepping in place (blue), t = −1.28 · s = −0.72  · f for crouched stepping in place (gray), and t = −0.85 · s = 0.72 · f for hopping in place (green). Elevation angles: t, thigh; s, shank; f, foot.

As a first approach to understanding these interactions, we looked at the two basic components of limb axis movement, namely changes in limb orientation and limb axis length, determined by only the relative trajectories of the thigh and shank segments in the absence of ankle rotation (Fig. 6 A,B, left panels). For simple limb axis rotation at constant limb length, the simplest case is when all limb segments rotate together (knee and ankle joints locked), so the thigh (t) and shank (s) rotations are equal (t = s). Limb length changes at a given limb orientation, however, depend on the relative lengths of the limb segments as well as on the relative yielding at the joints. Consider first the simple case in which thigh and shank lengths are equal and their rotations are equal in opposite directions (t = −s). These movement components, orientation and length, may be represented as orthogonal planes in the space of the thigh, shank, and foot elevation angles, where the motions of the foot segment determine specific linear trajectories on these planes (Fig. 6 A,B, right panels).

To examine the effects of the foot trajectories, we considered the two basic patterns of changes in segment angles (Fig. 6 B, right panels). In one, the ankle joint is relatively locked so that the foot and shank rotate in phase (s ∼ f) (Fig. 6 B, foot lift covariance). This is the pattern we observed during stepping in place (Fig. 3 A). The other pattern we observed had the foot and shank rotating out of phase (s ∼ −f) (Fig. 6 B, limb compression covariance). This pattern was observed during hopping (Fig. 3 A).

Although our simple model for a limb length covariance plane (Fig. 6 B) assumed equal yielding at all joints and equal thigh and shank segment lengths, the linear trajectories we observed during in-place trials were nevertheless close to the predictions, as seen by comparing the dashed trajectories in Figure 6 B with the respective colored trajectories in Figure 6 C. On average, the linear trajectories during in-place movements were fit by t = −1.60 · s = −1.15 · f for stepping, t = −0.97 · s = −0.78 · f for running, t = −0.85 · s = 0.72 · f for hopping, t = −1.28 · s = −0.72 · f for crouched stepping, and t = −1.46 · s = −1.32 · s for air stepping. Thus, deviations from the theoretical lines (Fig. 6 B, dashed trajectories) were accounted for by different magnitudes of relative limb segment rotation.

To extend this to the locomotion trials, we included the limb rotation (Fig. 6 C). If we consider only the limb axis rotation such that the segments all rotate together, the shank and foot will covary in phase: t = s = f (Fig. 6 A, limb orientation covariance). This theoretical limb orientation trajectory is also compared with the experimental trajectory obtained during knee-locked marching over ground (fit by t = 0.86 · s = 0.93 · f) (Fig. 6 A, brown arrow). The planes that include this orientation line and the lines defined above for the limb axis length changes should correspond to the covariance planes observed during over-ground locomotion.

In general, the correspondence was quite good. Each of the three gaits considered in Figure 6 resulted in a different plane orientation that was basically captured by the superposition of the linear trajectories. Although the predicted planes differed from the experimental planes on average by 15 ± 9° (for all gaits studied), the prediction showed that the crouched walking plane was rotated slightly with respect to normal walking and that the hopping plane was rotated significantly in the opposite direction. Thus, the yielding patterns expected from the limb segment rotations during in-place movements could also account for the segment covariance during the corresponding locomotion. It seems this might reflect a general property of the control system that could specify somehow the relative yielding across limb segments and thereby control the endpoint kinematics.

Discussion

We examined leg kinematics in human subjects for different locomotion gaits and found that they could each be reduced to two independent components. We presented evidence to show that these components may be equivalent to the limb axis length and orientation. These two whole-limb components can account for the trajectories of the limb segment angles in the sagittal plane for different gaits and speeds. The covariance of the limb segment angles showed gait-dependent differences that might be indicative of differences in the distribution of yielding across limb segments.

The full limb behavior in all gaits can be expressed as the 2DOF planar motion for each gait (Fig. 2 A), plus the rotation of the planes about a defined axis (1DOF) (Fig. 2 B). This extends the analysis to a full 3DOF spatial control of locomotion. This 3DOF control strategy may be consistent with an energetic optimization by the CNS based on the limb inertia, viscoelastic properties, and joint constraints. For example, it was shown previously that the amount of covariance plane rotation with increasing walking speed correlates with the net mechanical power output during the gait cycle (Bianchi et al., 1998a). Various other optimization criteria have been proposed and discussed (Collins, 1995; Zajac et al., 2002). Muscles, especially double joint spanning muscles, may further constrain limb kinematic motion and enable energy transfers in the limb (Bolhuis et al., 1998; Zajac et al., 2002). These optimizations might be reflected in both kinematics and kinetics covariance in the control of multijoint movements. For instance, Winter (1991) has demonstrated the existence of a law of kinetic covariance that involves a tradeoff between the hip and knee torques, such that the variability of their sum is less than the variability of each joint torque taken separately. In this study, we focused on the kinematics rules and the modular control of limb movements in human locomotion.

We conclude from these new findings that the planar rule of the intersegmental coordination found previously for human walking may underlie a basic control strategy for leg movements. The findings suggest a modular limb control and a hierarchical organization whereby appropriate coordination of the thigh and shank segments representing limb length and orientation could specify basic limb movements, whereas specific endpoint control might involve a further coordination with the foot segment (Fig. 6). In this way, a control of endpoint kinematics may be achieved by controlling the distribution of joint stiffness and thus the relative rotation of limb segments.

The planar covariance among limb segment angles has been recognized as a constraint that reduces the three degrees of freedom of the limb segments to two degrees of freedom (Lacquaniti et al., 1999, 2002). This was confirmed by the PCA showing that nearly all the segment angle variance can be accounted for by two principal components. Our hypotheses that these components correspond to the limb axis orientation and length trajectories predicted that leg movements that were confined along only one component axis, like limb length for example, would reduce the total degrees of freedom further to one.

This prediction was realized for in-place movements, where the motion cycle was made by varying only the limb axis length. The segment angle trajectories in this condition for a variety of gaits were described by a one-dimensional locus (Table 1). In fact, a linear trajectory was also found for over-ground marching movements where the limb axis length was nearly constant. We concluded from these results that limb axis length and orientation can be controlled separately and they can provide a basis to account for limb segment angle trajectories.

A possible interpretation of this is that the nervous system may also control limb movements by controlling separately the length and orientation of the limb (Maioli and Poppele, 1991; Lacquaniti and Maioli, 1994a,b; Bosco et al., 1996). A separate control of limb axis length might, for example, be associated with the control of limb loading, because this involves yielding along the limb axis and corresponding adjustments in limb axis length (Bosco et al., 2006). A similar separation of control has also been highlighted in animal studies of locomotion. Control of stride length or limb orientation (Grillner and Rossignol, 1978) may be separate from the control of limb loading (Prochazka et al., 1997), and both have been shown to comprise essential elements of limb control in locomotion (Pearson, 1995). Both theoretical and robotic models have also explored this type of modular organization for control (Nashner and McCollum, 1985; Raibert, 1986).

There is also some developmental evidence supporting this idea for human locomotion. Ivanenko et al. (2005b) showed that the toddler's first steps are kinematically similar to adult stepping in place, whereas the components associated with adult over-ground walking develop only later. Interestingly, toddlers also exhibit a particular kinematic pattern when their body weight is supported (Dominici et al., 2007); they move their legs stiffly in alternating swing or kicking-like movements, as if to produce predominantly limb orientation movements. Kicking (Thelen, 1981) and foot lift (“flexor-biased” locomotor component) (Forssberg, 1985) movements can also be considered as motor primitives or stereotypies in young infant behavior. These findings suggest that the control of limb axis length and orientation may also mature separately during the acquisition of adult locomotion.

Another indication of a separate control for limb axis length was observed recently using a statistical analysis of the electromyographic (EMG) data. When subjects were required to step over an obstacle while walking, as in the current study (Ivanenko et al., 2005a), the task was accomplished by using a muscle activation component equivalent to an activation synergy occurring during stepping in place. The effect of this on the limb segment angle trajectory was to widen the covariance loop along its minor axis (i.e., in the direction of the linear trajectory for in-place stepping) (Fig. 2 A). This activation component correlates with the foot lift in both healthy subjects (Ivanenko et al., 2005a) and patients (Ivanenko et al., 2003), suggesting that it may control the limb length. It was also relevant that specific activation components present during over-ground walking were missing during stepping in place, suggesting that they may be involved in the control of limb orientation instead.

The success of the simple covariance model described above (Fig. 6) emphasizes the role that biomechanical yielding across limb segments may play in determining the covariance relationship (Figs. 2, 3) (Shen and Poppele, 1995). The model also demonstrates that limb motion in locomotion can be considered to have two separate components, and a linear superposition of motion along these component axes can account for endpoint movement. This may reflect a more general “modular” property of the system to decompose and control complex interactions both at the neural and behavioral levels (Latash, 1999; Kargo and Giszter, 2000; Giszter et al., 2001; Hultborn, 2001; Stein and Daniels-McQueen, 2002; Tresch et al., 2002; Flash and Hochner, 2005; Lafreniere-Roula and McCrea, 2005; Ivanenko et al., 2006; Krouchev et al., 2006; Kelso, 2007). This is also consistent with the idea that neural elements in the central pattern generator may be shared with those for a different behavior or different forms of locomotion (Stein and Smith, 1997; Earhart and Bastian, 2000; d'Avella and Bizzi, 2005). For example, in our previous study of voluntary movements during locomotion (Ivanenko et al., 2005a), we found that specific EMG components associated with task elements were combined linearly in the combined task.

The model also emphasizes the role played by the differential stiffness across joints in the limb (Arampatzis et al., 1999; Gunther and Blickhan, 2002; Cavagna, 2006) in determining the segment angle covariance. Thus, the covariance may provide an indicator of the changes in relative interjoint compliance resulting from underlying control mechanisms. Joint stiffness is controlled primarily by muscle contraction, but contractions may interact differently with the resulting kinematics. Muscle contraction can either work against a load by moving the limb opposite to the load, or it may act as a brake, as in a lengthening or isometric contraction. Muscles may also contract in response to a load, as for example in the stretch reflex, and this can also serve to increase joint or limb stiffness (Houk, 1979). Ankle extensor reflexes have been assessed during locomotion using the H reflex in human subjects. The soleus H reflex was found to be lower during locomotion than during standing and it has been shown to be modulated differentially over the gait cycle (Capaday and Stein, 1986). During both walking and running, the soleus H reflex increases somewhat advanced in phase with respect to the peak activation of soleus (Simonsen and Dyhre-Poulsen, 1999). Such data show that reflex modulation occurs during locomotion and suggest that it might contribute to determining limb stiffness changes in the step cycle.

Our interpretation of the modular control of limb motion also finds some support in animal studies. For example, populations of spinocerebellar neurons that receive sensory input from proprioceptors and cutaneous receptors in the cat hindlimb encode these global parameters of the limb axis kinematics rather than specific local information about muscles or joints (Bosco and Poppele, 2000). Moreover, the sensory regulation of locomotion in cats has been shown to play an essential role in determining both the magnitude and onset of the swing, and the regulation of forces appropriate to limb loading (Pearson, 1995), relating to orientation and length control, respectively. Recent advances in the neural control of movement have led to a re-examination of the mechanisms of sensorimotor integration by means of which the functional units in the spinal circuitry might contribute to motor control in general (Hultborn, 2001; Poppele and Bosco, 2003).

Conclusion

The control strategy suggested by our observations is centered on whole-limb kinematics rather than on the underlying kinetics. Robust kinematics patterns revealed by segment angle covariance persist under conditions requiring quite diverse patterns of muscle activation (Bianchi et al., 1998b; Grasso et al., 1998, 2000; Ivanenko et al., 2002, 2005a; Courtine and Schieppati, 2004), implying that kinetics control may be adapted to produce the desired kinematics. Moreover, the separation of limb endpoint control into limb axis length and orientation components also finds support in the finding that limb proprioception may also be encoded in terms of limb length and orientation (Bosco and Poppele, 2000; Poppele et al., 2002; Stein et al., 2004). In fact, a similar control strategy has also been proposed for arm reaching (Lacquaniti et al., 1995; Schwartz and Moran, 2000; Roitman et al., 2005).

Appendix

Rotation of principal components and their association with limb length and orientation

To associate and correlate the limb length and orientation changes with specific segment angle covariances, it is necessary to consider the following two aspects: (1) to define the orientation of the reference axes on the plane and (2) to map these axes to the polar coordinates of the endpoint motion (Fig. 7 B, top panel). Below, we describe the procedures we used to accomplish this.

Figure 7.

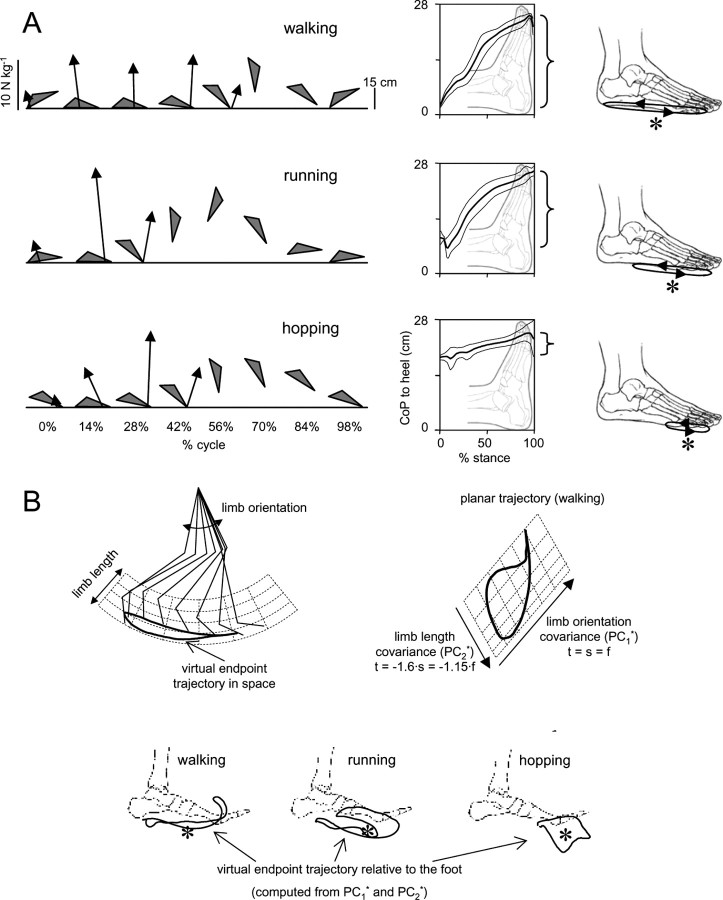
General foot placement characteristics and association of plane trajectories of the segment angles with endpoint motion. A, Left panel, Foot orientation (gray triangles formed by connecting LM-VM-HE markers) and ground reaction forces (upward pointing vectors) during over-ground walking, running, and hopping at a natural speed plotted every 14% of the gait cycle in one representative subject. Middle panel, Averaged (±SD; n = 8 subjects) time course of the instantaneous position of the COP relative to the foot during stance. Right panel, Excursion and mean position (asterisk) of the COP for each gait. B, Stick diagram, gait loop (for walking), and virtual endpoint trajectories obtained from PC₁* and PC₂* (see Appendix). Mapping of the polar coordinates of the limb axis (left) to the coordinates of the covariance plane (right) is shown for walking using the grid. Limb orientation (t = s = f) and limb length (stepping in-place) covariance directions are indicated. Note an oblique orientation of the two axes. In the bottom panel, virtual endpoint trajectories obtained from PC₁* and PC₂* and transformed to the foot frame are shown for walking, running, and hopping in one representative subject. Asterisks denote mean COP positions during stance in each gait.

The aim of PCA is to represent the original waveforms as a linear combination of a few PCs:

where angles are the set of limb segment angle trajectories, W is weighting coefficients (3 · 2 matrix), and PCs are principal components that explain the most variance in the limb angle space. The residual is the variance not accounted for by the PCs. The residual not accounted for by the first two PCs was typically <1–3% regardless of plane orientation. Thus, two PCs accounted for 97–99% or the total variance in the three angular waveforms.

Although PCA adequately captures the space spanned by the basic waveforms, there is no unique expansion for a set of waveforms (Glaser and Ruchkin, 1976). The reference axes can be oriented in any direction in the variable space, and they need not be orthogonal. It is only necessary that the number of separately oriented axes equal the dimensionality of the space spanned by the variables set of vectors. The choice may depend on the computational feasibility and the degree of insight the experimenter has in dealing with the data (Glaser and Ruchkin, 1976). One usually examines several solutions and chooses the one that makes the best “sense.” It is assumed that the data arise from a linear interaction of factors such that the model can be described by a linear expansion of the form of Equation 3.

Accordingly, in our model, we used the basic set of PCs associated with the limb length and orientation covariance. To this end, for the first PC, we chose the vector t = s = f (Fig. 6 A), and for the second one, we chose the vector corresponding to the in-place covariance line for each gait. For all conditions, these vectors lie close to the covariance plane (see Results), so that their directions projected on the plane formed the basic set of reference axes: limb orientation axis and limb length axis.

Finally, mapping of the polar coordinates of the endpoint motion to the coordinates of the covariance plane (Fig. 7 B) is monotonic but may not be necessarily isotropic along the limb length covariance line. Therefore, we corrected PC₂ (PC₂*) before correlating it with the limb length changes using the function approximated from in-place movements. To find this function, we computed the relationship between vertical foot displacements and the thigh angle under the assumption of the ideal limb length covariance t = −a · s = −b · f, where a and b were obtained from in-place movements (Fig. 3). This function resembled a cosine function. PC₁* and PC₂* in Figure 4 C were obtained using the above-described logic.

Our procedures were based on linear assumptions (e.g., limb orientation covariance could possibly also include some gait-dependent coefficients: t = a · s = b · f, rather than t = s = f). Nevertheless, the results strongly indicate that >97–99% of total variance can be accounted for by planar covariation in all locomotion conditions studied, and a large part of this variance can be decomposed into limb length and limb orientation reference axes specified for each gait (Figs. 3, 5).

Hypothetical virtual endpoint in different gaits

A control of the limb axis in locomotion may depend on the precise nature of the axis and that may in turn depend on gait. For example, the limb axis extends from the proximal joint (hip, GT marker) to the end of the foot (approximately the VM marker) when defined according to the anatomical endpoints of the limb segments. However, when it is defined instead by using the contact point of the limb as its distal point, it may become gait dependent. For example, during walking, the axis endpoint would correspond to the distal shank (LM marker) with heel strike at touch-down and it would correspond to the foot (VM marker) at lift-off.

Indeed, in walking, the foot strikes the ground with the rear part of the heel and with a marked plantarflexion in the ankle (Fig. 7 A). In running, in contrast, initial contact is generally made with a more anterior part of the foot. Individual differences exist in the way the foot is placed on the ground (Rodgers, 1988; Chan and Rudins, 1994). In hopping, the foot touches the ground with its distal (toe) part only (Fig. 7 A). As a result, the COP behavior during stance displays a clear shift of the mean position from midsole (walking) to toe (hopping). We also found previously (Ivanenko et al., 2002) that the variability of LM (marker located close to the heel) was lower than that of VM around heel touch-down. This agrees with the observation made by Winter (1992) that heel contact at the beginning of stance is controlled as precisely as is toe clearance at early and mid-swing.

An indirect argument in favor of potentially different virtual endpoints in different gaits comes from our results on the association of the PC₁ and PC₂ with limb orientation and limb length. The limb axis definition (e.g., GT-VE or GT-VM) did not affect appreciably the correlation between PC₁ and limb orientation, likely because of a similar forth and back horizontal motion of any fixed point on the foot. However, it did affect significantly the vertical component and thus the limb length changes. For instance, the time course of the vertical displacements of the heel and toe markers shows considerable differences (Winter, 1992; Osaki et al., 2007). During walking, the correlation of PC₂* with the limb length is higher for GT-VE (r = 0.95 ± 0.02) than for GT-VM limb axis (r = 0.87 ± 0.07). In contrast, for running and hopping, it is high both for GT-VE (0.96 ± 0.02) and GT-VM (0.95 ± 0.03), because the mean COP position lies close to VM (Fig. 7 A). This suggested that the contact point may be the relevant endpoint for determining the limb axis. Therefore, as discussed in Materials and Methods, we used the mean COP position as the first approximation of the endpoint (VE) in different gaits.

To determine this more precisely, we searched for a virtual endpoint that represented the contact of the foot with the ground during the progression. Indeed, the virtual endpoint of the foot may migrate during the gait cycle, as well as it may involve the vertical excursion. Using complex variables, the endpoint vector could be calculated in the polar coordinates, in which the angle of its rotation was approximated using PC₁ and the length using PC₂:

where L ₀ is the initial limb length at touchdown. An example is shown in Figure 7 B. Virtual endpoint trajectories obtained from PC₁* and PC₂* and transformed to the foot frame show some migration relative to the foot frame, although in a close vicinity to the mean COP position (asterisks). Some variability could likely be expected, because PC₁* and PC₂* explain only 97–99% of variance, and their mapping to the polar coordinates of limb motion requires additional assumptions (see above). Furthermore, force can even overcome object geometry in the perception of shape (Robles-De-La-Torre and Hayward, 2001) as well as a location of the rotation axis of the inverted pendulum of the stance limb lies below the ground surface (Lee and Farley, 1998). The issue of the nature and migration of the functional endpoint of the foot in different gaits requires additional investigation. However, the success in predicting the limb length and orientation from PCs using our simple model supports our hypothesis on the modular control of limb movements during human locomotion.