Recent History of Stimulus Speeds Affects the Speed Tuning of Neurons in Area MT

Abstract

Visual motion processing plays a key role in enabling primates' successful interaction with their dynamic environments. Although in natural environments the speed of visual stimuli continuously varies, speed tuning of neurons in the prototypical motion area MT has traditionally been assessed with stimuli that moved at constant speeds. We investigated whether the representation of speed in a continuously varying stimulus context differs from the representation of constant speeds. We recorded from individual MT neurons of fixating macaques while stimuli moved either at a constant speed or in a linearly accelerating or decelerating manner. We found clear speed tuning even when the stimulus consisted of visual motion with gradual speed changes. There were, however, important differences with the speed tuning as measured with constant stimuli: the stimulus context affected neuronal preferred speed as well as the associated tuning width of the speed tuning curves. These acceleration-dependent changes in response lead to an accurate representation of the acceleration of these stimuli in the MT cells. To elucidate the mechanistic basis of this signal, we constructed a stochastic firing rate model based on the constant speed response profiles. This model incorporated each cell's speed tuning and response adaptation dynamics and accurately predicted the response to constant speeds as well as accelerating and decelerating stimuli. Because the response of the model neurons had no explicit acceleration dependence, we conclude that speed-dependent adaptation creates a strong influence of temporal context on the MT response and thereby results in the representation of acceleration signals.

Introduction

Detection and analysis of visual motion are crucial for successful interaction with the visual environment. Consistent with this role, the visual motion system has been studied extensively in the primate brain. The middle temporal area (MT) of primate visual cortex is a key structure for the analysis of visual motion. This is shown, for instance, by the prevalence for direction- and speed-tuned neurons [for review, see Albright (1993) and Born and Bradley (2005)]. Using microstimulation, physiology, lesion studies, and a range of behavioral paradigms, researchers have shown that activity in monkey area MT plays a key role in the perception of speed (Maunsell and Van Essen, 1983; Newsome et al., 1985; Rodman and Albright, 1987; Pasternak and Merigan, 1994; Orban et al., 1995; Rudolph and Pasternak, 1999; Liu and Newsome, 2005; Krekelberg et al., 2006a,b).

Behavioral studies have suggested that temporal stimulus context can affect the perception of the direction and speed of motion (Williams et al., 1986). These results naturally lead to the question of how the temporal context of a moving stimulus influences the neuronal representation of stimulus speed. Most studies of MT, however, have focused on one aspect of visual motion (e.g., its direction or speed) and varied it parametrically across different stimulus conditions. Hence, within a trial, the motion stimuli were constant (e.g., they moved at a fixed speed for a given duration). Such studies provided important insight into the mechanisms of visual motion perception but disregarded the fact that natural object motion almost never remains constant. Only two previous studies have investigated responses in area MT to stimuli with changing speeds (Lisberger and Movshon, 1999; Price et al., 2005). We extend their studies to stimuli mimicking everyday object motion rather than brief accelerations to high stimulus speeds associated with eye movements (Lisberger and Movshon, 1999) in an effort to disentangle the roles of speed, acceleration, and adaptation.

By carefully controlling the tested speed range, the duration of the stimulus, and the adaptation state of the neurons, our design allowed us to attribute changes in the neuronal tuning width and preferred speed to the temporal context of the stimulus profile. Our data show consistent changes in the speed tuning of MT neurons that are dependent on the acceleration context. From these changes, it is possible to derive information regarding stimulus speed as well as acceleration from the spiking rate of the neurons.

These findings led us to question the source of the acceleration signals. To answer this question, we developed a stochastic model based on the response of MT neurons to stimuli moving at constant speeds. We found that this model, which was solely based on the speed tuning and adaptation dynamics for constant speeds, provided an accurate description of the responses to accelerating as well as decelerating stimuli. This suggests a new role for adaptation: speed-dependent adaptation provides a mechanism to establish acceleration (or, more generally, speed history) signals in area MT. Parts of these results have been published in abstract form (Schlack et al., 2004).

Materials and Methods

Subjects

Electrophysiological recordings were performed in two adult male rhesus monkeys (Macaca mulatta). Experimental protocols were approved by the Salk Institute Animal Care and Use Committee and conform to United States Department of Agriculture regulations and to the National Institutes of Health guidelines for humane care and use of laboratory animals.

Surgical procedures

Monkeys were implanted under sterile conditions using isoflurane anesthesia. The surgical procedures have been described in more detail previously (Dobkins and Albright, 1994). Briefly, a head post and a recording cylinder were affixed to the skull using stainless steel rails, screws, and dental acrylic in the first monkey and CILUX screws and dental acrylic in the second monkey. We determined the anatomical location from structural magnetic resonance (MR) scans and placed the MT chambers vertically centered above this area. The coordinates of the chambers were 5 mm posterior and 20 mm lateral in the first animal and 4 mm posterior and 19 mm lateral in the second animal. After recovery, a craniotomy was performed to allow for electrode penetrations into area MT.

Experimental setup

We used the CORTEX program (Laboratory of Neuropsychology, National Institute of Mental Health, Bethesda, MD; http://www.cortex.salk.edu/) to control the behavior of the monkeys and the stimulus presentation as well as data recording. Eye position was monitored at a 60 Hz sampling rate using an infrared video-based system (Iscan, Burlington, MA).

Visual stimuli were generated with in-house OpenGL software using a high-resolution graphics display controller (Quadro Pro Graphics card; 1024 × 768 pixels, 8 bits per pixel). Stimuli were displayed on a 21 inch monitor (75 Hz, noninterlaced, 1024 × 768 pixels; GDM-2000TC; Sony, Tokyo, Japan). Monkeys viewed stimuli from a distance of 57 cm in a dark room (<0.5 cd/m²). During experiments, our monkey subjects were seated in a standard primate chair (Crist Instrument, Germantown, MD). Head movements were constrained by a head post.

General procedures

Monkeys received liquid rewards (juice) for fixating a visual target (a red dot of 0.2° diameter) for brief durations (≤3100 ms). The stimuli used in our speed history paradigm (see below) were optimized according to the preferred motion direction and receptive field (RF) location of the cells. To determine these characteristics, we used automated methods (for details, see Krekelberg and Albright, 2005). In brief, we used whole-field circular motion in the frontoparallel plane (Schoppmann and Hoffmann, 1976) to determine the direction tuning of the neurons. RF locations were determined with patches (size, 5 × 5°) of random dot motion into the preferred direction of the neuron randomly positioned at nonoverlapping locations in a 6 × 6 square grid. This led to a mapping range of 30 × 30° centered on the center of gaze.

Visual stimuli

The basic visual stimulus used in all experiments consisted of white random dots that moved coherently in a single direction within a 10° diameter circular aperture. The direction of motion was always the preferred direction for the cell under study (see below). The dots had unlimited lifetimes and were randomly repositioned after leaving the aperture. Each dot had a diameter of 0.15° and was 70% more luminous than the gray background (5 cd/m²).

Assessment of speed sensitivity and effects of temporal context

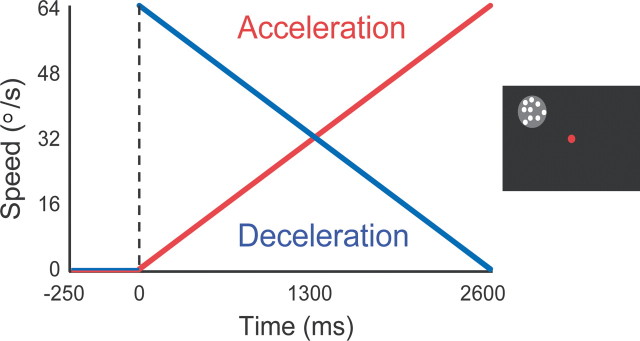
To measure effects of the speed history of smoothly changing moving patterns, we centered the random dot stimulus described above on the classical RF location of each recorded neuron. The motion direction was set to the preferred direction of the neuron rounded to the nearest multiple of 45°. Patterns appeared 250 ms after the monkey achieved central fixation, remained stationary for another 250 ms, and then started to move (Fig. 1). The duration of stimulus motion was 2600 ms. The trial was counted as correct if the monkey maintained central fixation (within a 2° tolerance window around the fixation dot) during the entire stimulus duration. Otherwise, the trial was aborted; these trials were not used in the analysis.

Figure 1.

Speed history stimulus. Left, Speed of the stimulus motion in the acceleration condition (red) and the deceleration condition (blue) over time. Right, The screen display. The gray shaded circle symbolizes the receptive field location of the neuron. The white dots represent the moving random dot field. The red dot at the center of the display represents the fixation target. For details, see Materials and Methods.

We used two “ramp” stimulus conditions, which were presented in randomized order. The first condition, which we termed “acceleration,” consisted of a stimulus that started moving at 1°/s and linearly accelerated by 24.2°/s² to 64°/s before being terminated. Similarly, in the “deceleration” condition the stimulus decelerated linearly from 64°/s to 1°/s. Each condition was repeated 15 times. The speed range used (1–64°/s) was centered on the optimal sensitivity range for human motion perception (De Bruyn and Orban, 1988) and covered the typical range of preferred speeds in area MT (Rodman and Albright, 1987).

Traditionally, the speed tuning of cells is assessed using stimuli that move at a constant rate (chosen from a predetermined set of speeds) for each presentation (Rodman and Albright, 1987). To enable a comparison of our data in the ramp conditions (acceleration and deceleration) with such traditional measures, we added control conditions in which stimuli moved at a constant rate during each presentation (1, 2, 4, 8, 16, 32, or 64°/s). In these control conditions, the stimulus remained stationary for 250 ms after its appearance and then moved for 2600 ms. We recorded these control conditions in addition to ramp conditions for a subset of 75 cells.

Electrodes and recording location

We used tungsten microelectrodes (3–5 MΩ base impedance; FHC, Bowdoinham, ME) to record the activity of single units in area MT. In each experiment, electrodes were positioned using a hydraulic micropositioner (model 650; David Kopf, Tujunga, CA). We used the Plexon (Dallas, TX) system to filter, store, and sort the neurophysiological signals. We identified recordings as being from area MT neurons by means of physiological criteria (i.e., strong directionally selective responses, RFs that were relatively small compared with those of neighboring area MST) and recording locations on the posterior bank of the superior temporal sulcus. The coordinates and depths of the neurons so identified were consistent with the expected location of area MT derived from MR scans.

Data analysis

We analyzed neuronal responses with our own software, written in Matlab (The Mathworks, Natick, MA). For each neuron, we computed the spike density function before and during the stimulus presentation as a measure of the neuronal response. The spike density function in each condition was corrected for latency (see below) and aligned relative to the respective stimulus speeds presented.

Latency.

Our stimulus set consisted primarily of smoothly changing stimuli. It is inherently difficult to determine neuronal response latency of the neurons under these conditions, because the “onset” of the stimulus (the point in time when the stimulus enters the spatiotemporal sensitivity range of the cell) can only be inferred from the neuronal response profile. We thus fixed the latency estimate for all analyses to 70 ms (i.e., the mean response latency to the abrupt onset of visual motion stimuli). However, we also performed the same analyses using a 0 ms latency estimate, which led to qualitatively similar results. Additionally, for the subset of cells (n = 75) tested with the “constant speed” control, we determined response latency as the point in time at which the neuronal response exceeded a threshold of three times the SD above the baseline activity rate (i.e., the activity rate during passive fixation period before stimulus onset). This procedure also yielded results that were qualitatively similar to those obtained using the fixed latency. We thus show below only the results of analyses performed using the fixed latency estimate of 70 ms.

Speed sensitivity.

Many MT neurons show an onset transient in response to stimulation with visual motion, which typically lasts for 20–80 ms (Priebe et al., 2002). To eliminate these onset transients from analysis and to equate the speed range analyzed in the acceleration and deceleration conditions, we discarded the first and last 150 ms of the response. We then binned the response into 40 ms bins and performed an ANOVA on ranks over those bins. For the constant speed conditions, we used the mean response per trial per speed (seven response vectors per trial) and performed the ANOVA on ranks over those. Cells were considered significantly speed sensitive to our stimuli if the resulting p value was <0.05. Note that this definition of speed sensitivity includes neurons that have a so-called low- or high-pass speed tuning curve, as well as those that are tuned to a particular speed (bandpass tuning curve). For each speed-sensitive neuron, a preferred speed and tuning width can be defined. It should be kept in mind, however, that these definitions will necessarily be affected by the range of tested stimulus speeds (i.e., it is possible that another speed, outside the tested range, could be the true preferred speed).

Fitting.

We used a nonlinear least-squares method to fit gamma functions of the following form to the following speed spike density function: r = γ × (s/β)^(α/β)exp(−s/β), where r is the firing rate, s is the speed in degrees per second, and α, β, and γ are fitted parameters. The speed tuning curves of 98% of our neurons were well fitted with this function (Kolmogorov–Smirnov test for goodness of fit, α = 0.05).

Preferred speed and tuning width analyses.

Using the gamma function, we determined the preferred speed for acceleration and deceleration conditions and compared the parameter estimates over the population of neurons with a Wilcoxon signed-rank test.

We defined the speed tuning width of the neurons as the speed range at 75% of the response maximum. We used these estimates to compare the speed tuning widths of the two speed history conditions at the population level using a Wilcoxon signed-rank test.

Speed and acceleration decoding.

To determine whether a population of MT cells carries a reliable representation of speed as well as acceleration, we used a linear support vector machine (SVM; as implemented in libsvm; http://www.csie.ntu.edu.tw/∼cjlin/libsvm). This linear classifier provided a lower bound to the accuracy of stimulus speed and acceleration categorization that can be achieved on the basis of our population of MT cells (n = 75). The data used for classification were the MT responses in 50 ms time bins from stimulus onset, for each cell, and for each condition. The perceived speed labels (i.e., the categories to be learned by the classifier) were determined for each time bin; for the constant speeds, the same speed label was assigned for the whole trial, and for the accelerating/decelerating stimuli, the instantaneous stimulus speed in the preceding bin was used (to correct for the neural transmission latency). The acceleration labels assigned to the bins were +1 for acceleration, 0 for constant speeds, and −1 for deceleration.

All training was done with fivefold cross-validation; the input data were divided into five equal sets, the classifier was trained on four of the sets, and the performance was tested on the remaining set. This was then repeated such that each set was used to test the model once. This cross-validation approach avoids overfitting while ensuring that the generalization performance of the classifier is tested on all input data.

Results

We recorded from 195 neurons in two awake, fixating macaque monkeys (M. mulatta). Receptive field eccentricities ranged from 3 to 15°, with a median eccentricity of 8°. We analyzed the speed tuning properties of these neurons in the two speed history conditions (acceleration ramp and deceleration ramp). Previous studies using stimuli that moved at constant speeds found that the majority of MT neurons are speed sensitive (Rodman and Albright, 1987). In agreement with those findings, the majority of neurons in our sample (67%; 130 of 195) were significantly speed sensitive in both the acceleration and deceleration condition. The distribution of preferred speeds in area MT is broad (Rodman and Albright, 1987; Duhamel et al., 1998; Churchland and Lisberger, 2001; Palanca and DeAngelis, 2003). We obtained a qualitatively similar result with the smoothly changing stimulus in our study; the quartile range of preferred speeds across the ramp conditions extended from 12°/s to 35°/s with a median of 24°/s.

Effects of speed history on responses of single neurons

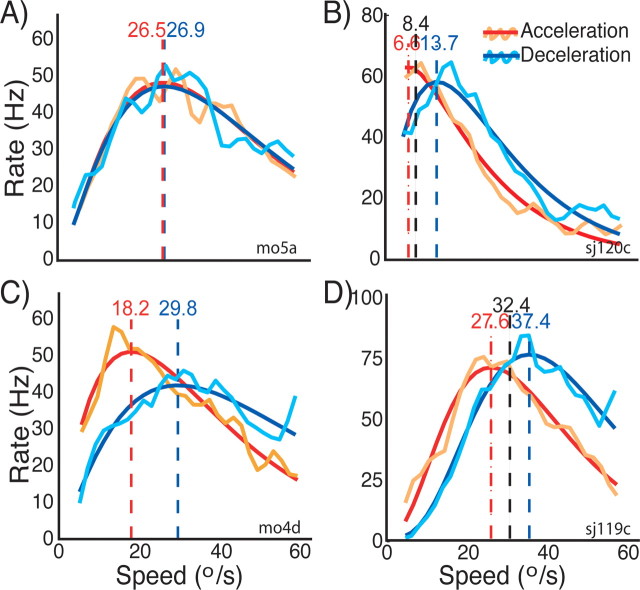
To assess how stimulus history affects the speed tuning of single neurons, we compared the speed tuning curves obtained under acceleration and deceleration stimulation as shown in Figure 2. The orange and turquoise curves represent the spike density functions obtained with acceleration and deceleration stimulation, respectively. To derive the preferred speed, we fitted these data with gamma functions. The so derived speed tuning curves are represented by the red lines (acceleration speed tuning curves) and blue lines (deceleration tuning curves). The vertical dashed lines indicate the preferred speed in the two conditions. B and D show neurons that we also recorded from during constant speed stimulation. The preferred speed determined during constant speed stimulation is represented by the black vertical dashed line. The neuron depicted in A did not show any differences in tuning between the two conditions: all curves largely overlap.

Figure 2.

Speed tuning of single neurons to stimuli with acceleration history compared with stimuli with deceleration history. Each of the four panels shows the tuning curves for one neuron. The orange and turquoise lines correspond to the spike density functions of the neurons during acceleration and deceleration stimulation, respectively. The red and blue lines are the corresponding fits to these spike densities. The vertical dashed red and blue lines with the numbers on top indicate the preferred speed estimates for the two conditions that we extracted from the fits (see Materials and Methods). In B and D, the two dashed black lines with numbers on top indicate the preferred speed determined with constant speed stimuli (see Materials and Methods). The neuron in A does not show any differences between the two conditions. However, there are obvious differences in the tuning curves in the other three neurons. The main effects of stimulus history that these neurons show are as follows: differences in the response strength (peak height); differences in the preferred speed; and differences in tuning width (for details, see Results).

The other three neurons in Figure 2B–D exhibited striking differences between the two conditions. First, there was a difference in the peak height of the tuning curves: the peak was higher for two of the neurons in the acceleration condition and lower in the deceleration condition. For the neuron in C, the opposite was true. Second, the neuron in C exhibited different tuning widths for the two conditions: the tuning curve in the acceleration case was narrower than in the deceleration case. Third, the preferred speeds differed for acceleration versus deceleration for all three neurons (B–D): in each case, the peak response in the acceleration condition occurred at lower speeds than in the deceleration condition. In the two example neurons for which we also measured the speed tuning during constant speed stimulation (B, D), the preferred speed in this control condition (vertical black dashed line) was in between the preferred speed estimates of the acceleration and deceleration conditions.

Population effects of stimulus speed history

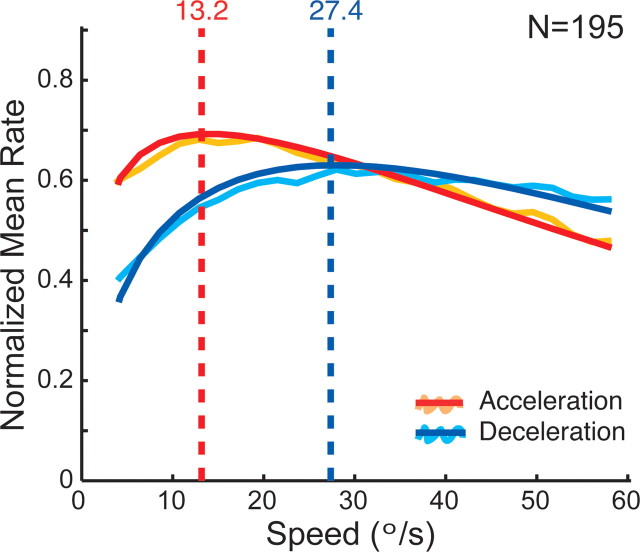
To determine the mean population response, we normalized the response functions (spike densities) of each cell to the maximum response of the individual neuron and then computed the average response over all cells for both acceleration and deceleration conditions (Fig. 3, orange and turquoise curves). These were then fitted with gamma functions to assess speed tuning parameters as in the single neurons (Fig. 3, red and blue curves). The main effects present in the single-cell examples of Figure 2 can also be observed here: the mean preferred speed is lower and the tuning width is narrower in the acceleration condition compared with the deceleration condition.

Figure 3.

Mean speed tuning for acceleration versus deceleration speed history (n = 195). Orange and turquoise lines represent the mean of the normalized spike density functions of all neurons for acceleration and deceleration history, respectively. Red and blue lines are the corresponding fits. The vertical dashed lines indicate the preferred speeds of the population responses. The peak of the population response is higher, the preferred speed is lower, and the tuning width is narrower in the acceleration case compared with the deceleration condition (for details, see Results).

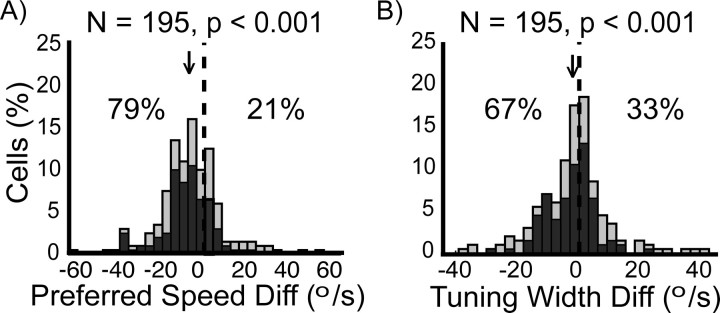
Because the previous analysis averaged over heterogeneous neurons, we also determined the acceleration versus deceleration differences in preferred speed (Fig. 4A) and tuning width (Fig. 4B) for each individual neuron. Figure 4 shows the distribution of these measures for our sample of 195 MT neurons. The analyses revealed that the effects observed at the single cells and in the mean population response shown in Figure 3 were significant at the population level (p ≤ 0.001). For 79% of the neurons, the preferred speed during acceleration speed history was lower than during deceleration history (Fig. 4B). The median absolute preferred speed difference was −7.15°/s. Finally, the tuning width of 67% of the neurons was narrower for accelerating visual stimuli than for decelerating visual stimuli with a median absolute tuning width difference of −2.5°/s (Fig. 4C). The results for the subpopulation of 108 neurons with, according to our definition, significantly speed-sensitive neurons are qualitatively similar (Fig. 4, dark bars). From the significantly speed-sensitive neurons, 93 (86%) had a slower preferred speed, and 76 (70%) had a narrower tuning width in the acceleration as opposed to the deceleration condition.

Figure 4.

Effects of speed history on preferred speed (A) and tuning width (B) (n = 195). Shown are histograms of the differences (Diff; acceleration condition − deceleration condition) in normalized preferred speed and tuning width between the two conditions. Light bars refer to the whole dataset, whereas the dark bars depict the subset of significantly speed-sensitive neurons (n = 108). (Numbers in this figure refer to the whole dataset (n = 195); for information on the significantly speed-sensitive subset, see Results.) The vertical dashed line indicates the level of no difference between the two conditions. The percentage numbers indicate the percentage of values to the left or to the right of the origin, respectively. The arrow indicates the location of the median of the distribution. All distributions are significantly shifted (p value above each panel shows the result of a Wilcoxon signed-rank test). The preferred speeds during acceleration tended to be lower than during deceleration (A) as indicated by the shift of the distribution to the left (median, −7.15°/s). The tuning width tended to be narrower in the acceleration compared with the deceleration history conditions (B; distribution shifted toward the left; median, −2.5°/s).

Previous studies have shown that MT speed tuning curves are not bell shaped in linear coordinates but are more homogeneous when presented in log-normal speed coordinates (Nover et al., 2005). If a neuron's tuning width is constant in logarithmic speed coordinates, it necessarily has a smaller tuning in linear speed coordinates when its preferred speed is reduced. This suggests that the (linear) tuning width change that we observed between acceleration and deceleration conditions might also be described as a consequence of the observed change in preferred speed together with a naturally logarithmic scale of speed encoding. To address this possibility, we reanalyzed the tuning changes on a log-normal scale: for 86% of the speed-sensitive neurons (93 of 108), the acceleration preferred speed was lower than the preferred speed in the deceleration condition (p < 0.001). However, in this analysis, there was no longer a consistent relationship between tuning width and speed history conditions: approximately one-half (56 of 108) of the neurons had a narrower tuning curve in log-normal speed coordinates for the acceleration condition. This suggests that an alternative interpretation of the reduction in preferred linear speed and linear tuning width is that preferred speed on logarithmic axes is reduced for accelerating stimuli but that the logarithmic tuning width of the cell has a fixed relationship with the preferred speed.

Speed tuning for changing versus constant speeds

The finding that speed tuning properties in area MT depend on stimulus history leads one to ask how the tuning properties observed using acceleration and deceleration conditions compare with speed tuning assessed by more traditional means. To answer this question, we recorded from a subset of cells (n = 75) using acceleration and deceleration stimuli as well as stimuli with constant stimulus speeds (for details, see Materials and Methods).

When tested with constant speeds, 92% of these neurons were significantly speed sensitive (69 of 75). In the acceleration condition, this percentage was reduced to 63% (47 of 75), and in the deceleration condition, 80% were speed sensitive. It should be noted, however, that these percentages are based on slightly different statistical tests; hence, a direct comparison should be done only with caution.

The differences between acceleration and deceleration conditions reported for the overall population were similar in this subset of neurons. We compared the tuning widths and preferred speeds under the speed history conditions (acceleration and deceleration) with those obtained under constant speed stimulation. For the majority of neurons (85%), the tuning width was broader during constant speed stimulation than during the speed ramps. We then compared the preferred speed determined in the three conditions. Figure 5 shows the distribution of acceleration and deceleration preferred speeds relative to the preferred speed determined during constant speed stimulation. For most neurons [65% of neurons tested (49 of 75) and 76% of significantly speed-tuned neurons (35 of 46)], the constant preferred speed was greater than that for acceleration and less than that for deceleration conditions. There was no difference in the magnitude of the difference between acceleration and the constant preferred speed on the one side and the deceleration preferred speed and constant preferred speed on the other side (Wilcoxon signed-rank test, p > 0.05). The preferred speed in the constant speed condition thus tended to be centered between the two history conditions.

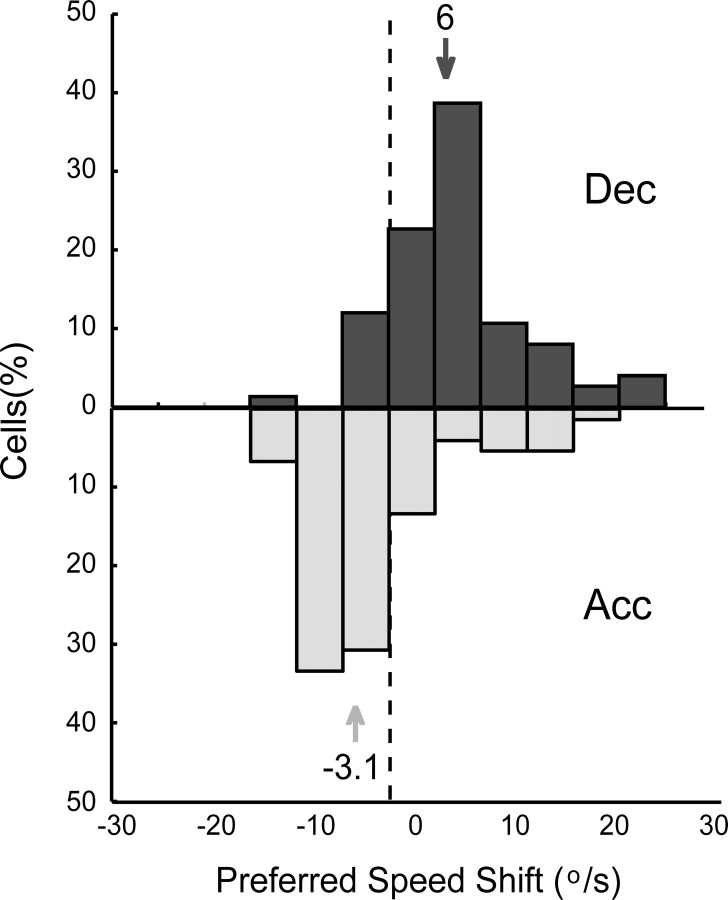
Figure 5.

Distribution of preferred speeds during acceleration (Acc) versus deceleration (Dec) stimulation relative to the speed preference during constant speed stimulation (n = 75). The top (dark gray bars) represents the distribution of distances of the deceleration preferred speed from the preferred speed determined during constant speed stimulation (indicated by the dashed vertical line). The bottom part of the figure (light gray bars) shows the distribution for the acceleration condition. The arrows indicate the medians of the two distributions. The median of the acceleration preferred speed distribution was −3.1°/s; the preferred speed during acceleration tended to be lower than the preferred speed during constant speed stimulation. The preferred speeds during deceleration stimulation, in contrast, were generally larger than the constant preferred speed (median, 6°/s).

Acceleration signals in MT

The data presented in the previous section clearly demonstrate that speed history of a stimulus affects the response of MT neurons in a consistent manner. This implies that, at least for the stimuli presented in these experiments, it should be possible to extract information on speed as well as acceleration from this population of MT cells.

To quantify the fidelity of the speed and acceleration representation in the population of MT cells, we used a linear classification method. We trained a linear SVM to categorize the stimulus speed on the basis of the response of 75 MT cells in 50 ms time bins. This should not be interpreted as a claim that speed perception makes use of a support vector machine to read out MT cells; the SVM is merely a convenient way to read out information from a high-dimensional input. We argue that if a simple linear classifier can attain a certain performance, then surely a more complicated neural readout mechanism can. In other words, we interpret the performance of the linear classifier as a lower bound to what can be extracted from this population of MT cells.

First, we used the linear classifier to extract speed information from the MT population. The classifier scored a 95% correct performance (see Materials and Methods) on the categorization of the seven constant speeds. Using the same classifier (based only on the constant speeds) to classify the instantaneous speed in the sweep stimuli led to 85% correct performance. This shows that the information available in the average firing in 50 ms time bins of only 75 MT neurons is enough to support accurate (≥85% correct) speed perception for constant, accelerating, and decelerating speeds.

Second, we tested whether the classifier could determine whether a response was evoked by an accelerating or decelerating stimulus (while ignoring speed). Using the same MT responses, this classification could be done at a 90% correct performance level.

Finally, we tested whether acceleration and speed information could be extracted from the MT responses at the same time. We trained a linear classifier to report both the instantaneous speed and the acceleration of a stimulus on the basis of the response of the MT cells during the sweeps. The cross-validation performance of this classifier reached 68% correct. In other words, a readout mechanism that relies on 75 MT cells can correctly identify the speed as well as the acceleration in an ongoing sweep stimulus 68% of the time.

The performance on speed and acceleration decoding by the linear classifier shows that speed and acceleration information is available in the population response of MT cells. Strictly speaking, this has only been shown for the particular stimuli used in our experiments, and we make no claims with respect to the generalization to other stimuli, or with respect to the invariance of this speed and acceleration representation (see Discussion). Nevertheless, this finding is in line with the view that the perception of acceleration can be based on MT responses.

The origin of acceleration signals

The next step in our understanding of the representation of acceleration in MT is to gain insight into how acceleration becomes represented in MT. It is well known that the responses of many MT neurons diminish after prolonged stimulation (Petersen et al., 1985; Priebe and Lisberger, 2002; Priebe et al., 2002; Van Wezel and Britten, 2002; Kohn and Movshon, 2003; Krekelberg et al., 2006a). This led us to investigate whether response adaptation could be the underlying origin of the acceleration signals.

Figure 2 shows example neurons with and without an effect of acceleration condition on the neuronal speed tuning. If adaptation were the mechanism behind the speed tuning changes, one would expect that neurons that show a strong effect of adaptation should also show a large effect of acceleration on speed tuning. To quantify this, we defined adaptation strength as the strength of the response to the preferred speed in the last 300 ms relative to the strength of the response in the first 300 ms. Figure 6 shows the distribution of preferred speed shifts as a measure for the speed tuning change (acceleration vs deceleration) relative to this adaptation strength. There was a significant correlation between the two measures (r = 0.47; p < 0.001). In other words, the more a neuron adapted during constant speed stimulation, the bigger the shift of preferred speed caused by the acceleration profile of the stimulus.

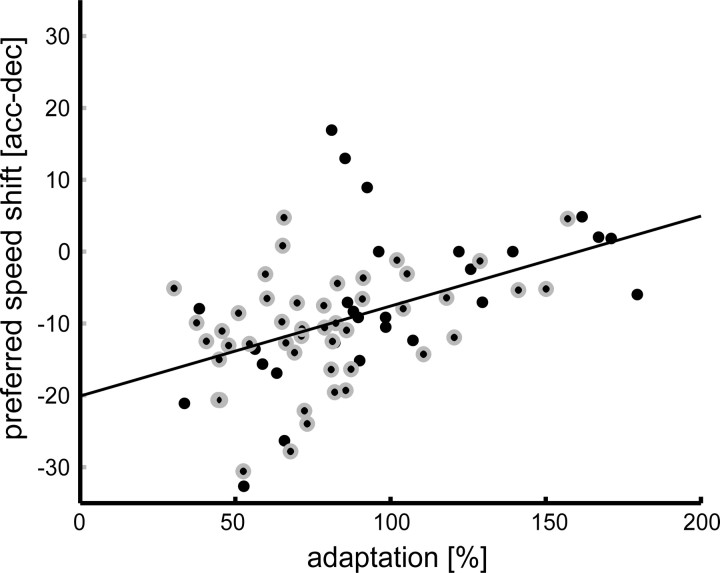
Figure 6.

Relationship between preferred speed shift [acceleration − deceleration (acc − dec); y-axis] and strength of adaptation effect (x-axis) (n = 75). Adaptation is defined as reduction of firing rate to a certain percentage of the initial response (for details, see Results). Small values thus represent strong adaptation effects; values around 100% represent cells that do not show adaptation. Each dot depicts the respective value for one cell. Black dots with a gray annulus represent cells that were significantly speed sensitive in the three conditions (n = 46). The solid line is a linear regression through the data points. The two measures were significantly positively correlated (Pearson correlation, r = 0.47; p < 0.001), neurons with a strong effect of adaptation tended to have a bigger preferred speed shift.

This analysis clearly suggests that adaptation could play an important role in generating acceleration signals. Because of the nature of our stimuli, however, the amount of adaptation was not the same for each stimulus speed in the accelerating versus decelerating conditions. These conditions spanned the same range of speeds, but slow speeds, for example, were presented early in acceleration trials and late in deceleration trials; i.e., the length of adaptation differed for the two conditions. This suggests that the results described so far could be related to the difference in adaptation time. However, if stimulus presentation time were the only source of the effects, one would expect that the response strength to 32°/s stimulus speed, i.e., the speed at the center of the stimulation interval that occurs in both ramp conditions after the same stimulus duration, should be indistinguishable. We thus determined the responses per trial per neuron in the two conditions in a response window from 29°/s to 36°/s. Statistical analysis revealed that 21% of all speed-sensitive neurons (23 of 108) had significantly different spike rates within this window for acceleration versus deceleration conditions (rank sum test, p < 0.05). At least for these neurons, motion adaptation time alone cannot account for the speed history effects.

This analysis excludes the possibility that adaptation time is the sole reason for a difference in firing rates. Adaptation in MT, however, is a complex process that does not depend solely on the time since stimulus onset, but also on the relationship between the stimulus and the speed tuning curve of the cell (Krekelberg et al., 2006a). For instance, the largest amount of adaptation is typically found for stimulus speeds that fall on the flanks of the speed tuning curve. This suggests that a difference in response to an accelerating versus decelerating stimulus at a given test speed could be caused by the fact that one of these stimuli has spent more time on the flank of a speed tuning curve before reaching the test speed.

We investigated this possibility with a stochastic model of individual cells' responses. For each cell, we used the recorded firing rates in 50 ms bins in each of the trials and for each of the constant speeds, to construct a return map. This map tabulates the probability that, for a given constant speed stimulus, a bin with a response of x Hz is followed by a bin with a response of y Hz. Such a return map captures the entire (adaptation) dynamics of a cell for a given stimulus speed, and the collection of seven maps (one for each speed) additionally captures the speed tuning. In essence, these maps represent our complete (stochastic) knowledge of the speed/time response dynamics of a neuron. An example of the return map of a single neuron for one stimulus speed is shown in Figure 7A.

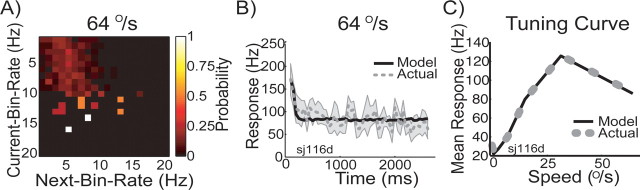
Figure 7.

Stochastic model of MT responses. A, Example of a return map for neuron sj116d for stimulus speed of 64°/s. We computed such a return map for each of the seven stimulus speeds (other speeds not shown). Probability of observing a particular firing rate is color coded: white corresponds to a high probability, and black corresponds to a low probability. The y-axis depicts the rate found in a given time bin, and the x-axis refers to the rate found in the next time bin. For example, when the neuron fired with ∼16 Hz to a stimulus moving at 64°/s, there was a high probability that it would fire with ∼6 Hz in the next bin (i.e., 50 ms later). B, Comparison of the temporal response profile of model prediction and actual neuronal response. Response rate (y-axis) is plotted against time of stimulation (x-axis). The gray dashed line represents the mean response of the neuron sampled in 50 ms bins. The gray area around the mean depicts the SD of the response over trials. The model prediction is shown by the black line; it captures both the initial onset and the more sustained part of the response. C, Comparison between actual speed tuning curve (gray dotted line) of neuron sj116d and the tuning curve prediction of the model for this particular neuron (black solid line). Mean response (y-axis) is plotted against the speed of the stimulus (x-axis). The model prediction lies almost perfectly on top of the measured tuning curve.

To simulate the time course of the response of such a model neuron, we started by choosing the starting firing rate to equal the average response of the real cell in the first bin. The firing rate for the next bin in the time course was then drawn randomly following the probability distribution in the return map. This process was repeated to simulate the entire 2500 ms time course (50 bins of 50 ms). For Figure 7B, we simulated 1000 trials and averaged the response per bin over all trials to generate a predicted average time course (solid line). The dashed line shows the actual average response of the neuron. Clearly, the model captures both the initial rapid adaptation and prolonged sustained response of the neuron. To determine a model speed tuning curve, we calculated these model responses for each of the seven constant speeds and determined the average over the whole time course for each speed, just as we did for the real neural responses. Tuning curves based on model simulations (solid) and the average response of the real cell (dashed) are shown in Figure 7C and matched perfectly.

To assess the goodness of fit between simulated time courses and actual courses, we calculated the model residuals: the difference between actual average response and the simulated response for each speed and each time bin. To take the inherent neuronal variability into account, we expressed this as a Z-score by dividing the residuals by the SD of the actual firing rate over trials. For the simulations of the constant speed data (on which the model was based), the median of this residual distribution was 0. This shows that the model did not have a bias. Most importantly, we found that 98% of the data points had a Z-score between 1 and −1; hence 98% of data points were predicted to within a single SD from their actual value. This modeling exercise shows that the stochastic return map accurately captures a neuron's response as a function of time and speed.

Next, we investigated whether these model dynamics, based solely on the responses to constant speeds, also capture the response dynamics observed during accelerating and decelerating sweeps. Simply following the procedure used for the constant speed simulations, we chose the first time bin to equal the first bin of the actual response to an accelerating or decelerating stimulus and then simulated a time course using the stochastic return map. At each point in time, we used the return map based on the speed that corresponded most closely to the speed that was on the retina one time bin earlier. This 50 ms shift accounts for the expected neural transmission latencies. In other words, for a decelerating stimulus, we started the simulation using the return map derived from the 64°/s constant speed stimulus. Once the stimulus reached a speed nearer to 32°/s than to 64°/s, we continued the simulation with the return map based on the 32°/s constant speed stimulus, etc., until the lowest speed was reached.

Figure 8 shows such a simulated response for an accelerating stimulus (solid line) compared with the actual average response to an accelerating stimulus (dashed line) for the same neuron shown in Figure 7. The model captured the dynamics of the response to an accelerating stimulus to within an SD. Figure 8B shows the simulation of a decelerating stimulus based on the same model. Again, the model simulations closely match the average response of the cell. To assess the goodness of fit, we again determined the Z-scored residuals. The median of the residuals for the acceleration or deceleration stimuli was 0, and 96% of data points had a Z-score between −1 and 1. In other words, a model based purely on the speed tuning and (adaptation) dynamics for constant speeds provided a good description of the response to accelerating and decelerating stimuli.

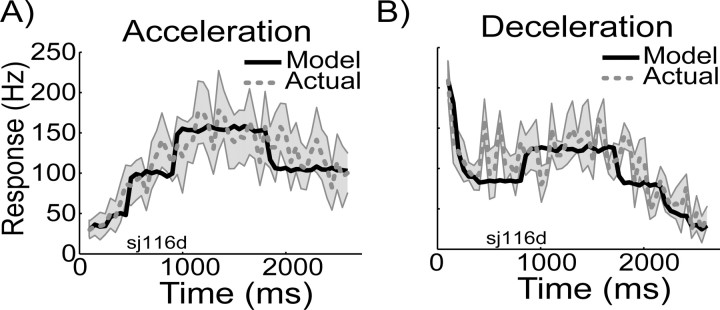
Figure 8.

Model prediction versus actual response profiles for acceleration (A) and deceleration (B) stimulus conditions. Neuronal response in hertz is plotted against stimulus time in milliseconds. The model prediction based on the speed-specific return maps (for more details, see Results) are plotted as black solid lines, and the actual measured mean responses (±SD) over the 50 ms bins are shown in gray. Note that the x-axis depicts time; i.e., slow speeds occur early in the acceleration condition (A), but late in the deceleration condition (B). The model predictions capture the main response patterns in both conditions. The sudden transitions in the modeled response represent transitions from using one constant speed return map to the next. The sharpness of the transition is caused by the limited sampling of the full range of speeds by the seven constant speed conditions.

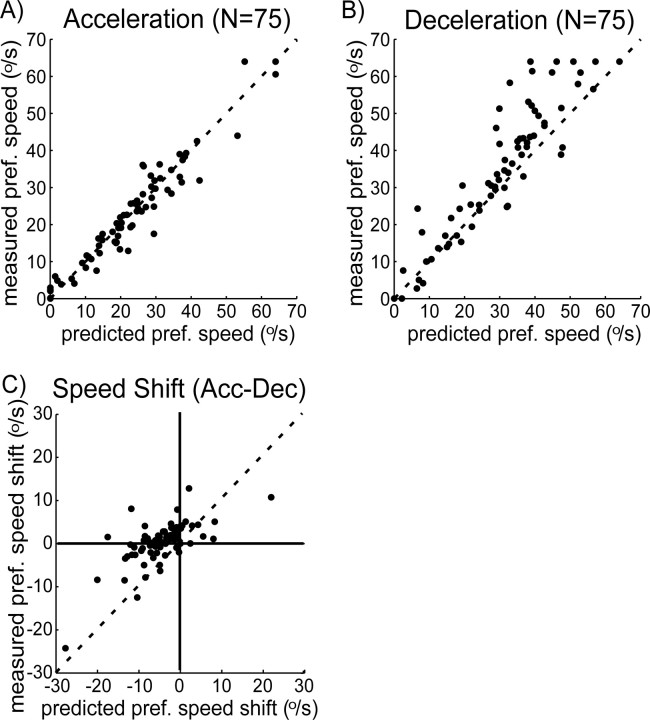
Figure 9 shows a comparison between measured and predicted preferred speeds for all neurons. Both for acceleration (A) and for deceleration (B), the actual preferred speeds were well predicted by the model. Systematic errors can be seen in the deceleration conditions for cells with high preferred speeds. Most likely, this is because of the fact that we recorded no constant speed responses between 32 and 64°/s. As a consequence, the model response for a speed in this range had to be based on the (nearest) recordings, at 32 and 64°/s.

Figure 9.

Predicted (x-axis) versus measured (y-axis) preferred (pref.) speed for acceleration (A) and deceleration (B) ramp conditions. Each dot depicts the preferred speed values for one cell. The dashed line is the line of identity. For both conditions, the dots tend to fall in a small margin around the line of identity, indicating that model and measurement provide similar preferred speed estimates for the cells. C, The preferred speed differences [acceleration (Acc) vs deceleration (Dec)] for the measured data (y-axis) plotted against the predictions of the model. Measured and model data are significantly correlated (Pearson correlation, r = 0.74; p < 0.001).

As a final test of the model, we investigated whether it could explain the speed shifts of Figure 4. Indeed, we found that the model predicted that 73% of cells would have a reduction in preferred speed for accelerating versus decelerating speed ramps (median predicted shift, 9.3°/s). These predictions agree well with the recorded shifts (Fig. 4) (79% cells shift to lower preferred speeds; median shift, 7.1°/s). To illustrate this on a cell-by-cell basis, Figure 9C plots the shift in preferred speed for the recorded data against the shift in preferred speed in the model. It should be noted that the uncertainty in these model predictions (being the difference of the two model predictions of A and B) is large. Moreover, the systematic errors in the deceleration condition discussed above also result in a systematic error in the predicted shift. Nevertheless, the predicted and actual shifts are significantly correlated (r = 0.74; p < 0.001)

Discussion

We showed that a majority of neurons in macaque area MT was sensitive for speed when presented with a visual stimulus that gradually changed its speed. The speed tuning curve of most neurons depended markedly on the speed stimulus history: in an acceleration context the preferred speed of the neurons shifted to lower and in a deceleration context to higher speeds compared with the preference during constant speed stimulation. Using a support vector machine, we showed that the responses of these neurons provided reliable information on both speed and acceleration of the stimuli used in our paradigms. Our model shows that the origin of these signals is a difference in adaptation state that results from following a different trajectory through speed–space. There is no need to assume the existence of a response mechanism that explicitly depends on acceleration. The encoding of stimulus acceleration (even the complete speed history) is a consequence of adaptation that depends on stimulus speed.

In the following sections, we first compare our results to previous studies, then discuss the consequences of our findings for the perception of speed and acceleration, and, last, discuss the role of adaptation as a mechanism to encode temporal stimulus context.

Previous studies

Two papers that investigate acceleration-related signals in the response of MT neurons have been published. They used very similar experimental paradigms; one was in anesthetized macaques (Lisberger and Movshon, 1999), the other in awake, fixating macaques (Price et al., 2005). Our overall conclusions are quite similar to these studies; acceleration changes MT responses, and adaptation (or gain control) can explain these changes.

An important difference with our study, however, is that those studies used a specific stimulus sequence in which acceleration, constant speed, and deceleration always followed each other in the same order. This fixed order of acceleration states makes differences in response among the three states difficult to interpret; the deceleration stimuli were always presented to cells that must already have adapted significantly. Given this design, it is not surprising that deceleration responses are lower than acceleration responses, but these differences cannot be uniquely attributed to differences in stimulus acceleration. Price et al. (2005) also reported an increase in preferred speeds for decelerating stimuli but no shift in preferred speed for accelerating conditions. We believe that this asymmetry is attributable to their asymmetric stimulus design. Using our stimulus design, with randomly interleaved acceleration and deceleration phases, the shifts in preferred speed for accelerating stimuli are mirror images of the shifts for decelerating stimuli.

Our stimulus paradigm allowed us to compare responses to identical speeds (32°/s) and identical adaptation duration, but different acceleration signs. Under these conditions, 21% of cells still showed a different response to acceleration versus deceleration. This shows that adaptation duration alone cannot account for the differences in response. Together with the knowledge that adaptation depends on the speed of the stimulus (Krekelberg et al., 2006a), this led us to a model with speed-dependent adaptation profiles. This model predicted the response profiles of the neurons to smoothly changing stimuli based solely on the response profiles measured for constant stimulus speeds. Unlike previous models (Lisberger and Movshon, 1999), the neurons in this model have no explicit acceleration dependence.

Speed perception

We found that 92% of MT neurons were significantly speed sensitive when assessed with a traditional constant speed approach, and a smaller percentage were significantly speed sensitive during acceleration (63%) and deceleration (80%). Although this difference could in part be a result of the different statistical tests used to assess speed tuning (see Materials and Methods), the performance of the linear classifier also suggests that it is more difficult to extract veridical speed information from the MT responses to a changing speed stimulus. This may explain why speed discrimination is impaired when two stimuli rapidly follow each other (McKee, 1981; Mateeff et al., 2000).

Relative to the preferred speed determined with constant speed stimuli, the majority of neurons had a lower preferred speed in the acceleration condition and a higher preferred speed in the deceleration condition. If MT neurons are labeled lines for the percept of speed, the shift in preferred speed we found should lead to a change in the percept of speed. In the labeled line model, labels are constant and identified with the preferred speed of a cell; only “votes” for the label (i.e., the neural response) can change. This results in a reversal between neural shifts in the response and perceptual shifts; a lower preferred speed leads to an increased perceived speed (Krekelberg et al., 2006a,b). Hence, if the labeled line view is correct, our data predict that accelerating stimuli, with reduced preferred speeds, should lead to an overestimation of speed. Conversely, decelerating stimuli, with increased preferred speeds, should lead to an underestimation of speed. We are not aware of any direct tests of this prediction.

Acceleration perception

We showed that area MT responses provide information on the acceleration of smoothly changing stimuli. Our approach was relatively coarse: we only tested three accelerations: positive acceleration (24.2°/s²), constant motion (0°/s²), and negative acceleration (−24.2°/s²), and showed that our population of MT neurons could be used to distinguish these acceleration states. Price et al. (2005) found that ∼50% of MT cells showed a significant variation in firing across acceleration rates ranging from 60°/s² to 2400 °/s². This percentage of cells is clearly lower than the percentage significantly sensitive to speed [which was 100% for the 10–240°/s speed range of Price et al. (2005)]. This suggests that, consistent with the low level of acceleration sensitivity of human subjects (Schmerler, 1976; McKee, 1981; Snowden and Braddick, 1991; Werkhoven et al., 1992), fewer neurons are acceleration tuned than speed tuned, and the acceleration tuning of MT neurons is broad.

We showed that a linear decoding of the population activity in area MT would allow an observer to correctly assign speed and acceleration to our stimuli in 68% of trials. Whether these signals are sufficient to explain the full scale of behavioral sensitivity to acceleration remains an open question. However, we consider this quantitative assessment of the acceleration and speed information present in the MT population conclusive evidence of the presence of acceleration signals. In our opinion, there is no tension between this statement and our conclusion that acceleration responses are based on speed-dependent adaptation. The first is a statement of information, the second a statement of mechanism. The fact that speed-dependent adaptation explains why acceleration signals arise in MT does not mean that those signals are “just” adaptation.

What the mechanistic explanation in terms of adaptation suggests, however, is that the acceleration signal is not invariant to all changes in the stimulus or speed history. In other words, the model suggests that different speed histories that lead to the same cumulative amount of adaptation could be perceived as having the same acceleration. The absence of an explicit and invariant acceleration detection mechanism may be another reason why human acceleration discrimination is poor compared with speed discrimination (Gottsdanker, 1956; Snowden and Braddick, 1991; Werkhoven et al., 1992).

Adaptation as a mechanism to encode stimulus context

Adaptation is commonly seen as a way to conserve energy by reducing the number of spikes and/or to optimally transmit information by adjusting the neuronal response properties to the changing statistics of the input (for review, see Kohn, 2007). Our analysis here suggests an additional role for adaptation: when the strength of adaptation depends on a stimulus feature of interest, adaptation creates signals that encode stimulus context. In our case, speed-dependent adaptation results in the encoding of speed context (acceleration vs deceleration). A general hysteresis in contrast adaptation alone (Bonds, 1991) could not account for our results, but it could analogously result in the encoding of contrast-history in the neural response.

Conclusion

Our data confirmed that the responses of area MT neurons can signal not only information on the current speed of a moving and smoothly changing stimulus but also on the acceleration sign of the stimulus. We searched for a mechanism that could be used to construct this acceleration information and found that speed-dependent adaptation profiles are sufficient to explain the generation of the acceleration signals in MT.