Endpoint Stiffness of the Arm Is Directionally Tuned to Instability in the Environment

Abstract

It has been shown that humans are able to selectively control the endpoint impedance of their arms when moving in an unstable environment. However, directional instability was only examined for the case in which the main contribution was from coactivation of biarticular muscles. The goal of this study was to examine whether, in general, the CNS activates the sets of muscles that contribute to selective control of impedance in particular directions. Subjects performed reaching movements in three differently oriented unstable environments generated by a robotic manipulandum. After subjects had learned to make relatively straight reaching movements in the unstable force field, the endpoint stiffness of the limb was measured at the midpoint of the movements. For each force field, the endpoint stiffness increased in a specific direction, whereas there was little change in stiffness in the orthogonal direction. The increase in stiffness was oriented along the direction of instability in the environment, which caused the major axis of the stiffness ellipse to rotate toward the instability in the environment. This study confirms that the CNS is able to control the endpoint impedance of the limbs and selectively adapt it to the environment. Furthermore, it supports the idea that the CNS incorporates an impedance controller that acts to ensure stability, reduce movement variability, and reduce metabolic cost.

Introduction

In activities of daily living, we normally move and manipulate objects in our environment. These interactions are unstable if external perturbations or internal errors are amplified by the environment (Burdet et al., 2006). For example, when using a screwdriver the force needed to drive the screw would fluctuate as a result of inherent signal-dependent noise (Harris and Wolpert, 1998; Jones et al., 2002; Hamilton et al., 2004; Osu et al., 2004). Movement produced by variations in the direction of the applied force (van Galen and van Huygevoort, 2000; Van Beers et al., 2004) could cause the screwdriver to slip, creating an unstable interaction. The neuromuscular system must compensate for such environmental instability to successfully perform the task.

Many tasks that humans perform, especially those involving tool use, are inherently unstable (Rancourt and Hogan, 2001). The viscoelastic properties of muscle contribute significantly to stability because they resist perturbations without delay. Hogan (1984, 1985) postulated that an important function of groups of antagonist muscles was the regulation of the mechanical impedance of a joint. Increasing cocontraction of antagonist muscles stabilizes the joint (Milner and Cloutier, 1993; Milner, 2002). The coactivation of antagonistic muscle pairs may also counteract the effect of signal-dependent noise when muscle force increases (van Galen and de Jong, 1995; Osu et al., 2004; Selen et al., 2005). The cocontraction of different muscle pairs can potentially control the orientation of the limb endpoint impedance (Hogan, 1984, 1985), although Mussa-Ivaldi et al. (1985) found only a global increase in the size of the endpoint stiffness without any change in orientation. Only recently was the ability to control the orientation of the endpoint stiffness independently of endpoint force convincingly demonstrated (Burdet et al., 2001; Franklin et al., 2004). These and other studies (Gribble and Ostry, 1998; Takahashi et al., 2001; Perreault et al., 2002; Osu et al., 2003; Darainy et al., 2004; Hinder and Milner, 2005; Milner and Franklin, 2005) have provided evidence that an impedance controller is incorporated in the CNS. The impedance controller is an internal model of the stability of the environment that generates the appropriate motor commands to selectively control the limb impedance required to achieve stability.

Our previous work investigating impedance control during movement examined only one orientation of instability. The increase in endpoint stiffness was interpreted as occurring primarily through the coactivation of biarticular muscles (Franklin et al., 2003b). However, if a general impedance controller exists, the CNS should be able to match changes in endpoint stiffness to arbitrary changes in the orientation of the instability. In the horizontal plane, desired changes in the orientation of the endpoint stiffness can theoretically be produced by combinations of changes in activation of three muscle groups: single-joint shoulder muscles, single-joint elbow muscles, or double-joint muscles (McIntyre et al., 1996). The particular combination of muscle groups will depend on the limb geometry.

To investigate the ability of the neuromuscular system to control the orientation of the endpoint impedance, subjects made reaching movements in three unstable force fields designed so that the orientation of the instability in each force field corresponded to the direction in which a particular set of muscles could increase endpoint stiffness. The prediction was that in each case, the endpoint stiffness would increase in the corresponding direction and that an increase in the activation of the corresponding muscles would be observed.

Materials and Methods

Eight healthy, right-handed subjects (age, 20–34) participated in the study (four male and four female). The experiments were approved by the institutional ethics committee and subjects gave informed consent. For the second electromyographic activity (EMG) recording portion of the experiment, five of the eight subjects (three male and two female) participated.

Effect of cocontracting muscle pairs on endpoint stiffness.

Simulations were performed to investigate the effects of cocontracting antagonistic pairs of muscle groups on endpoint stiffness geometry. Because endpoint stiffness depends on limb geometry, the simulation was restricted to the midpoint of outward reaching movements for comparison with experimental measurements made at the same location (Burdet et al., 2001; Franklin et al., 2003a). Endpoint stiffness is composed of both joint stiffness and geometric stiffness (Franklin and Milner, 2003). Although the contribution of geometric stiffness to endpoint stiffness is a function of endpoint force and geometry of the limb, the contribution of joint stiffness is purely a function of muscle activation. The joint stiffness (R) is composed of four elements that in turn can be expressed in terms of three muscle stiffness parameters (McIntyre et al., 1996):

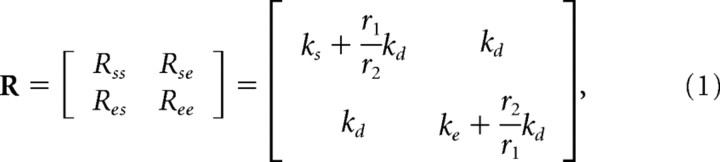where R_ss is the stiffness at the shoulder produced by muscles crossing the shoulder joint, R_se is the stiffness at the shoulder produced by the biarticular muscles, R_ee is the stiffness at the elbow produced by muscles crossing the elbow joint, R_es is the stiffness at the elbow produced by the biarticular muscles, k_s is the single-joint shoulder muscle stiffness, k_d is the double-joint muscle stiffness, k_e is the single-joint elbow muscle stiffness, r₁ is the moment arm of the biarticular muscles at the shoulder, and r₂ is the moment arm of the biarticular muscles at the elbow. This formulation is only valid when considering stiffness attributable to intrinsic muscle properties. In general, stiffness measurements will also include reflex contributions, which can result in the off-diagonal terms of the joint stiffness matrix being unequal. With the assumption that the moment arms at the shoulder and elbow of the biarticular muscles are equal, an increase in cocontraction of muscle pairs relative to that of null field (NF) movements would produce changes in joint stiffness that can be modeled as follows:

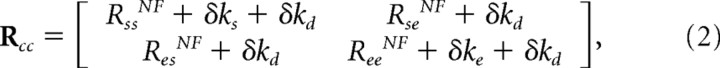where the δk_s, δk_d, and δk_e terms indicate a change in the joint stiffness produced through the cocontraction of the muscle pairs. The means of the joint stiffness terms in the NF for five subjects (Burdet et al., 2001) were used as the baseline. This mean NF joint stiffness (R^NF) was [50.4 20.5; 30.0 24.1] N · m/rad. Individual terms of the joint stiffness matrix were then selectively increased by changing δk_s, δk_d, and δk_e to simulate the cocontraction of specific muscle pairs. To simulate selective coactivation of only single-joint shoulder, biarticular, or single-joint elbow muscles, δk_s, δk_d, or δk_e, respectively, was set to 20 N · m/rad, while the other parameters were set to 0 N · m/rad. Coactivation of all muscle pairs was simulated by simultaneously setting all three terms to 20 N · m/rad. Finally, to simulate coactivation of both single-joint elbow and biarticular muscles, δk_d was set to 20 N · m/rad, and δk_e was set to 10 N · m/rad. The joint stiffness matrix was transformed to endpoint stiffness via equation 4 of McIntyre et al. (1996) and plotted using the singular value decomposition method (Gomi and Osu, 1998).

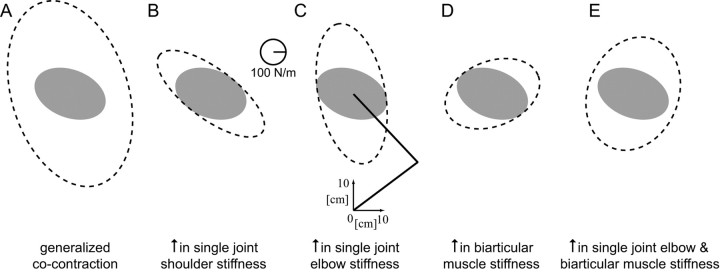
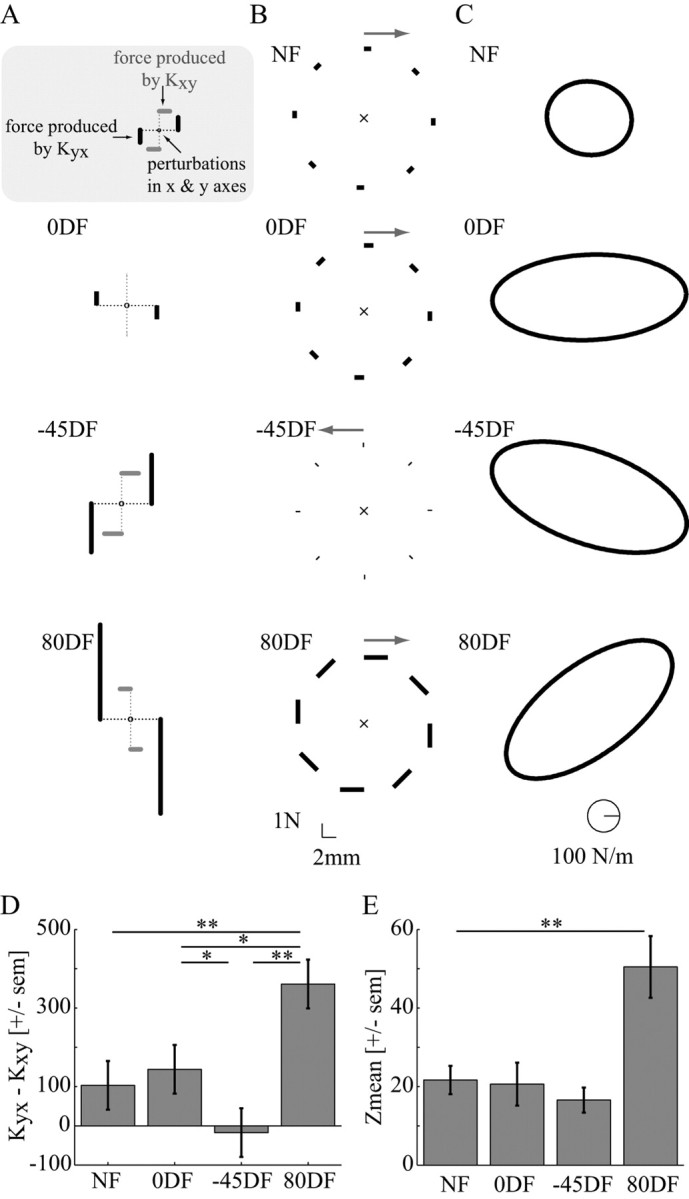
Increasing the activation of all pairs of muscles results in a global increase in the stiffness as others have previously suggested (Mussa-Ivaldi et al., 1985), but it also produces a change in orientation (Fig. 1A). The cocontraction of single-joint shoulder muscles (Fig. 1B) increases the stiffness primarily along the −45/135° axis with no increase in the orthogonal direction. Increasing the stiffness of the single-joint elbow muscles (Fig. 1C) increases the endpoint stiffness along the 90/−90° axis compared with NF stiffness. A simulated increase in the biarticular muscle activity produces a selective increase in stiffness approximately along the 0/180° axis while producing little change in the orthogonal direction (Fig. 1D). By appropriately varying the cocontraction levels of these muscle pairs, endpoint stiffness can be increased in selected directions. For example, by combining single-joint elbow and biarticular muscle cocontraction, the stiffness increases in the 80° direction (Fig. 1E). However, it is not known whether such control can be achieved in practice, because it depends critically on the ability to independently control the levels of muscle activation. As more muscle pairs are activated to the same level, the increase in stiffness becomes more isotropic. Note that the increases in the endpoint stiffness illustrated in Figure 1 only hold for the particular geometry of the limb at the midpoint of the movement used in this experiment. For different geometrical configurations, each muscle pair would produce somewhat different changes in the endpoint impedance.

Figure 1.

Simulated changes in endpoint stiffness that would result from increasing the cocontraction of various muscle pairs. The mean NF stiffness ellipse for five subjects was used for baseline joint stiffness values (filled gray ellipse). Details of the simulations are given in Materials and Methods. The simulations were performed using the limb posture shown by the stick figure of the arm (C). A, Endpoint stiffness produced by global cocontraction of all muscles. B, Endpoint stiffness produced by cocontracting single-joint shoulder muscles. C, Endpoint stiffness produced by cocontracting single-joint elbow muscles. D, Endpoint stiffness produced by cocontracting biarticular muscles. E, Endpoint stiffness produced by cocontracting single-joint elbow and biarticular muscles.

Apparatus.

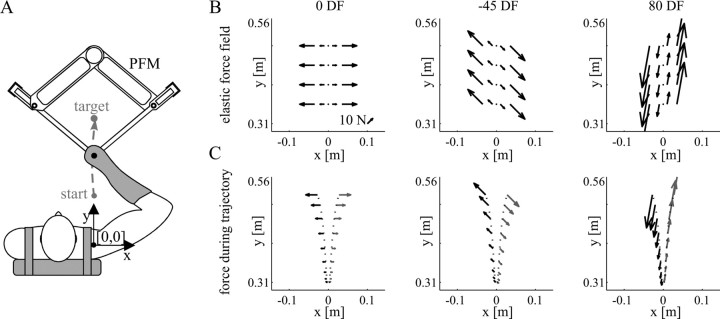
Subjects were seated in a chair with their trunk held against the back of the chair by a shoulder harness. A custom-molded thermoplastic cuff was used to restrict motion of the wrist and firmly attach the subject to the manipulandum. The subject's forearm, along with the cuff, was secured to a beam in the horizontal plane. The forearm, cuff, and beam were coupled to the handle of the parallel-link direct drive air-magnet floating manipulandum (PFM) (Fig. 2A). Motion was thus restricted to a single degree of freedom at both the shoulder and elbow joints in the horizontal plane, where the positive x and positive y directions correspond to the right and forward of the subject, respectively. Details of the PFM and setup were described previously by Gomi and Kawato (1997).

Figure 2.

Experimental setup. A, The subject's right arm was attached to the handle of the PFM with a custom-fitted thermoplastic cuff. Reaching movements were performed from a start position located at [0, 31] cm relative to the shoulder to a target located at [0, 56] cm. The PFM applied either a computer-controlled force field or controlled displacements to estimate stiffness during movement. B, Force produced by the three force fields: 0DF, −45DF, and 80DF (left to right). The force depended on the x-position of the subject's hand. As the hand position deviated either to the left or the right of the straight path joining the start and end targets, the force produced by the PFM increased. The direction in which the force pushed the hand was different for each field. C, Sample force patterns for two trajectories in each force field. Slightly diverging trajectories (shown in black dotted lines) result in widely different force patterns on the hand (compare black and gray arrows).

Subjects performed point-to-point reaching movements from a start circle to an end circle, located 31 and 56 cm, respectively, directly in front of the subject's shoulder joint. A table blocked the subject's view of the manipulandum and the subject's arm. The current position of the hand and the start and end circles were projected from the ceiling onto the table as visual feedback for the subjects. A computer monitor displayed information about whether the completed movement was successful or not. A successful movement was one in which the movement duration was 0.6 ± 0.1 s, finished within the 2.5-cm-diameter end circle, and was completed without crossing the safety boundaries, 5 cm to either side of the y-axis. The force field reverted to the NF if the safety boundary was crossed.

Procedure.

Subjects were asked to perform point-to-point reaching movements in an NF and three different types of divergent force fields (DFs) (Fig. 2B). Each DF created negative stiffness in a different direction. If a subject performed a straight movement along the center line of the workspace (y-axis), then no force was applied by the PFM. However, if the subject deviated from the y-axis, the DF applied a force away from the y-axis, along the direction of negative stiffness, proportional to the deviation in the x-axis. The general equation for the DF was as follows:

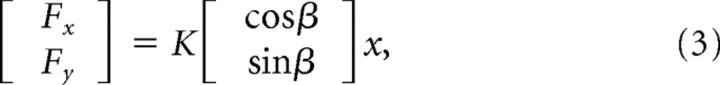where K is a scaling factor for the strength of the fields in N/m to adjust the difficulty of the task for each subject. F_x and F_y are the forces applied by the PFM in the x and y directions, respectively. The fields created a divergent instability along the β = 0, −45, and 80° directions and were scaled for each subject such that the task was difficult but not overly so. These three force fields are referred to as 0DF, −45DF, and 80DF. For two female subjects, the scaling factor K was 300, 425, and 806 N/m for the 0DF, −45DF, and 80DF force fields, respectively. For three male subjects and the other female subject, the scaling factor K was 400, 565, and 863 N/m, respectively, for the 0DF, −45DF, and 80DF force fields. For the two remaining male subjects, the scaling factor K was set at 450, 636, and 1151 for the 0DF, −45DF, and 80DF force fields. These DF directions were selected based on the predictions shown in Figure 1 that selective activation of distinct muscle groups could produce the endpoint stiffness needed to compensate for the instability in the environment.

The expectation was that subjects would selectively adapt the endpoint stiffness such that it increased only in the direction of the instability in the environment (Burdet et al., 2001). However, there are other possible adaptation mechanisms that would also compensate for the instability. Subjects could generally increase the overall size of the endpoint stiffness in all directions. Such an isotropic increase in stiffness would resist the perturbing effects of the force field in all directions and ensure successful movements. However, our previous work suggests that although this strategy may occur early in learning (Franklin et al., 2004), after training, subjects selectively increase the stiffness in the direction of the instability (Burdet et al., 2001; Franklin et al., 2003a, 2004). In these previous experiments, the direction of the instability (perpendicular to the direction of the movement) was in the same direction as the error signal that produced this force. In the current experiment, subjects could also adapt to all three DF fields by simply increasing the stiffness along the x-axis (perpendicular to the movement). In theory, by doing this the error would be driven to zero, and no forces would be applied to the hand. If this was the case, after adaptation the endpoint stiffness in all three unstable fields would be similar.

Learning.

All subjects practiced making movements in the NF on at least one day before the experiment. These training trials were used to accustom the subjects to the equipment and to the movement speed and accuracy requirements. Each force field was learned on a different day, often with several days separating training in one force field from another. Subjects first practiced in the NF, after which their endpoint stiffness was estimated. The order of training in the three DF force fields was randomized across subjects. For each force field, two procedures were conducted on the same day: learning, followed by stiffness estimation. During learning, subjects first completed 30 successful movements in the NF, after which the DF was activated, although no information was provided to the subjects about when activation of the DF would occur. Subjects then made movements in the DF until 100 successful trials were completed. There was a short break before the stiffness estimation.

Stiffness estimation.

Details of the method and analysis for the stiffness estimation were described previously by Burdet et al. (2000). Briefly, subjects first completed 20 successful trials in whichever force field was being tested. After this, an additional 160 successful trials were completed in the force field, of which 80 trials were randomly selected for stiffness estimation. On each of these trials, a 300 ms displacement was applied near the midpoint of the movement in one of eight equally spaced directions, encompassing the full 360°. The displacement consisted of a smooth 100 ms ramp-up, 100 ms hold, and a smooth 100 ms ramp-down segment. The average force and displacement measured during the final 80 ms of the hold period were used to estimate the two-by-two endpoint stiffness matrix K by linear regression using the following equation:

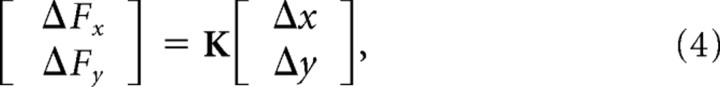where ΔF_x and ΔF_y are the mean change in endpoint force and Δx and Δy are the mean change in displacement in the x and y directions, respectively. The endpoint stiffness can be represented as an ellipse (Mussa-Ivaldi et al., 1985). Singular value decomposition of the stiffness matrix K was used to determine the size, shape, and orientation of the stiffness ellipses (Gomi and Osu, 1998).

Electromyography.

On a separate day, the surface EMG of six arm muscles was measured during movement in each of the three DFs and the NF. Five of the subjects (two female and three male) who had previously taken part in the learning and stiffness experiments participated. EMG was recorded in a separate session from the stiffness experiments so that training and testing in all force fields could be performed on the same day to permit quantitative comparison of the electrical activity of the muscles for the different force fields. Subjects performed movements in each of the three DFs with the order of force field presentation randomized. In all cases, subjects first completed 30 successful movements in the NF, after which they completed 100 successful movements in one of the DFs. Subjects took a short break and then repeated this for the other two DFs. The EMG electrodes remained in place for the duration of the experiment.

Surface EMG was recorded from two monoarticular shoulder muscles: pectoralis major and posterior deltoid; two biarticular muscles: biceps brachii and long head of the triceps; and two monoarticular elbow muscles: brachioradialis and lateral head of the triceps. EMG was recorded using pairs of silver–silver chloride surface electrodes. The electrode locations were chosen to maximize the signal from a particular muscle while avoiding cross talk from other muscles. The skin was cleansed with alcohol and prepared by rubbing electrode paste into the skin. This was removed with a dry cloth, and the pregelled electrodes were attached to the skin and secured with tape. The electrode spacing was ∼2 cm. The impedance of each electrode pair was tested to ensure that it was <10 kΩ. The EMG signals were Butterworth bandpass filtered between 25 Hz and 1.0 kHz and sampled at 2.0 kHz.

The final 20 successful NF trials and final 40 successful DF trials were analyzed. The EMG was rectified and averaged across trials creating a single time-varying measure of electrical activity for each muscle in each force field. A measure of the relative change in muscle activation after adaptation to the DF compared with the NF level was calculated over consecutive 100 ms intervals as follows:

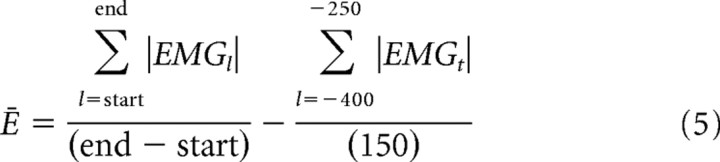where the mean value between −400 and −250 ms before movement onset was assumed to represent background noise and was subtracted. The relative increase in the muscle activation (ΔĒ_i), over the ith interval, was then calculated as follows:

where the NF EMG (Ē_i^NF) was subtracted from the DF EMG (Ē_i^FF) calculated over the same interval and divided by the average NF EMG over the entire 600 ms movement (Ē_0–600^NF). To be able to compare the change in EMG in one muscle to the change in another muscle, the relative change (RC) in the activation of each muscle (m) was calculated as follows:

Because we were interested in the contribution of muscle pairs (single-joint shoulder, biarticular, or single-joint elbow) to endpoint stiffness, RC for the two contributing muscles was summed. RC was computed over 100 ms intervals from the start of the movement (t = 0) to 100 ms after the end of the movement (t = 700). Statistical analysis was performed using the general linear model in SPSS 10.0 (SPSS, Chicago, IL) to perform ANOVA and ANCOVA on the data. Statistical significance was considered at the 0.05 level. Note that this grouping of muscle pairs (single-joint shoulder, biarticular, and single-joint elbow) is not intended to imply that cocontraction can only occur by such pairwise contraction. For example, a subject could cocontract pectoralis major, long head of triceps, and brachioradialis such that the joint torques remained unchanged, which would be represented as equal increases in the RC sums for all muscle pairs. However, grouping the activation into these muscle pairs provides important information, because changes in activation of either muscle in the pair produce the same change in the endpoint stiffness (Fig. 1). Therefore, analyzing changes in muscle activation according to this classification scheme affords straightforward interpretation about how the CNS controls endpoint stiffness through the selected pattern of muscle coactivation.

Results

Hand paths

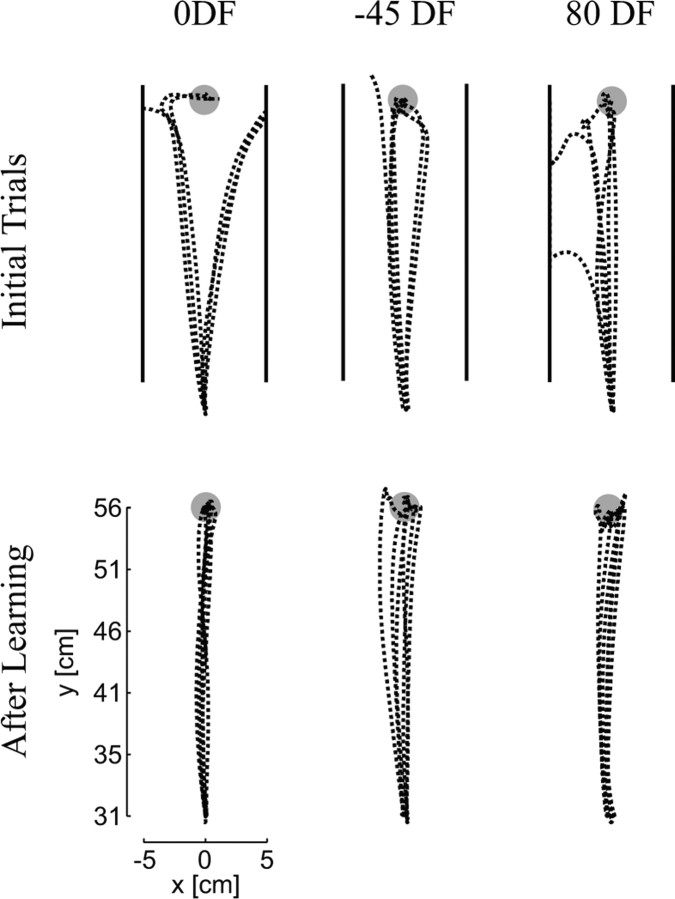
Initial trials performed by the subjects in all three DFs resulted in perturbed movements (Fig. 3). Depending on the particular force field, the hand could be perturbed to the right or left as well as accelerated or decelerated along the direction of movement in the case of the −45DF and 80DF. With practice, subjects adapted to the force fields and learned to make relatively straight, smooth movements. By the end of learning, subjects were able to consistently perform successful movements in all three force fields. The trajectories in the DFs after learning were similar to those in the NF. The average ± SD numbers of trials that subjects performed in the learning phase of the experiment were 141 ± 36 in the 0DF, 124 ± 10 in the −45DF, and 135 ± 31 in the 80DF.

Figure 3.

Trajectories before and after training. Initial trials in the 0DF, −45DF, and 80DF force fields were perturbed away from the straight path toward the target causing the hand to move outside of the safety zone (located at 5 cm to either side of the x-axis and represented by the solid back lines in the figure). Each field perturbed the arm in a slightly different direction. After training in the force fields for 75–150 trials, subjects were able to make straight (or gently curved) movements to the final target without being perturbed.

Endpoint stiffness ellipses

The endpoint stiffness was estimated using linear regression across the individual trials for each force field. The mean r² value for this linear regression, which estimates how well the stiffness matrix explains the variance across all of the different force and position measurements, was 0.57. The r² values were consistent across the four force fields ranging from 0.51 to 0.62. To examine possible differences in the goodness of fit across the fields, an ANOVA was performed. There was no significant main effect (p = 0.07), and no significant differences were found using a post hoc test. A related question is how well the stiffness matrix truly represents the different force measurements made in the eight directions. To examine how well the four-element stiffness matrix represents the restoring force to perturbations in each of the eight directions, the mean force response for each direction was calculated as the product of the stiffness matrix and the displacement vector of the hand and entered into a regression against the measured force. In this case, the mean r² value ranged from 0.92 to 0.96 across the four force fields. The slopes of the relationships (±95% confidence intervals) were close to 1 (NF, 0.90 ± 0.046; 0DF, 0.94 ± 0.034; −45DF, 0.93 ± 0.033; 80DF, 0.89 ± 0.039). This fit was consistent across all of the fields. These results indicate that the stiffness matrix accounts for most of the variance in the mean force responses to the perturbations.

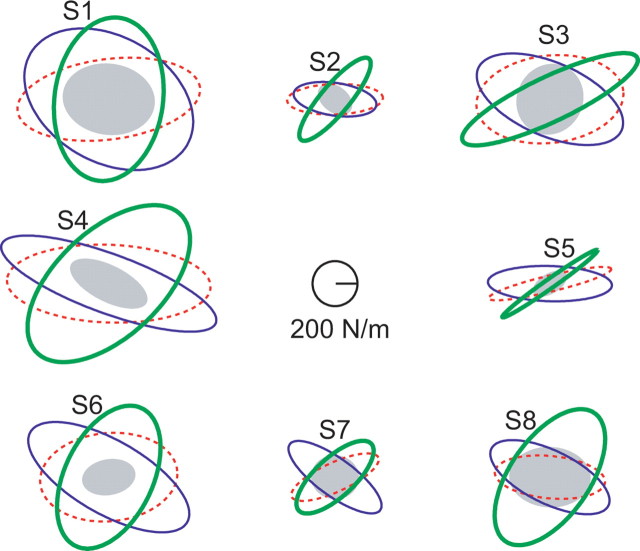
The stiffness after adaptation to each of the DFs was larger than the NF stiffness (Fig. 4). However, the increase in endpoint stiffness was not simply a global increase. The stiffness appeared to increase primarily in one direction with a much smaller increase in the orthogonal direction, which rotated the stiffness ellipse toward the direction of the environmental instability. This suggests that the subjects had selectively increased stiffness in the direction of the instability in the environment.

Figure 4.

Endpoint stiffness was adapted differently in each force field. The stiffness ellipses for each of the eight subjects (S1–S8) participating in the study are shown for each of the four force fields (NF, filled gray; 0DF, dotted red; −45DF, blue; 80DF, thick green). Relative to the NF stiffness, the stiffness measured in the divergent force fields is larger and more anisotropic. The direction of the increased stiffness for each unstable force field is similar across all of the subjects. These directions are close to the directions of instability in the environment.

Changes in the shape and orientation of the stiffness ellipse are compared in Figure 5. The shape of an ellipse is defined as the ratio of the minimum eigenvalue to the maximum eigenvalue. Therefore, a shape of 1 represents a circle, whereas a shape of 0 defines a line. The subjects' endpoint stiffness in the DF was less isotropic than in the NF (i.e., the mean values were 0.40, 0.40, and 0.42 for the 0DF, −45DF, and 80DF, respectively, compared with 0.70 for the NF). The change in the shape of the endpoint stiffness was tested using an ANOVA (with a main effect of force field type and a random factor of subjects). After finding a significant main effect of force field type (p < 0.001), a post hoc test (Dunnett's t) was used to determine whether the shape of endpoint stiffness in each of the divergent force fields was significantly different from that in the NF. A significant difference was found for all three DFs, indicating that the stiffness ellipses became more anisotropic after adaptation (0DF, p < 0.001; −45DF, p < 0.001; 80DF, p = 0.001).

Figure 5.

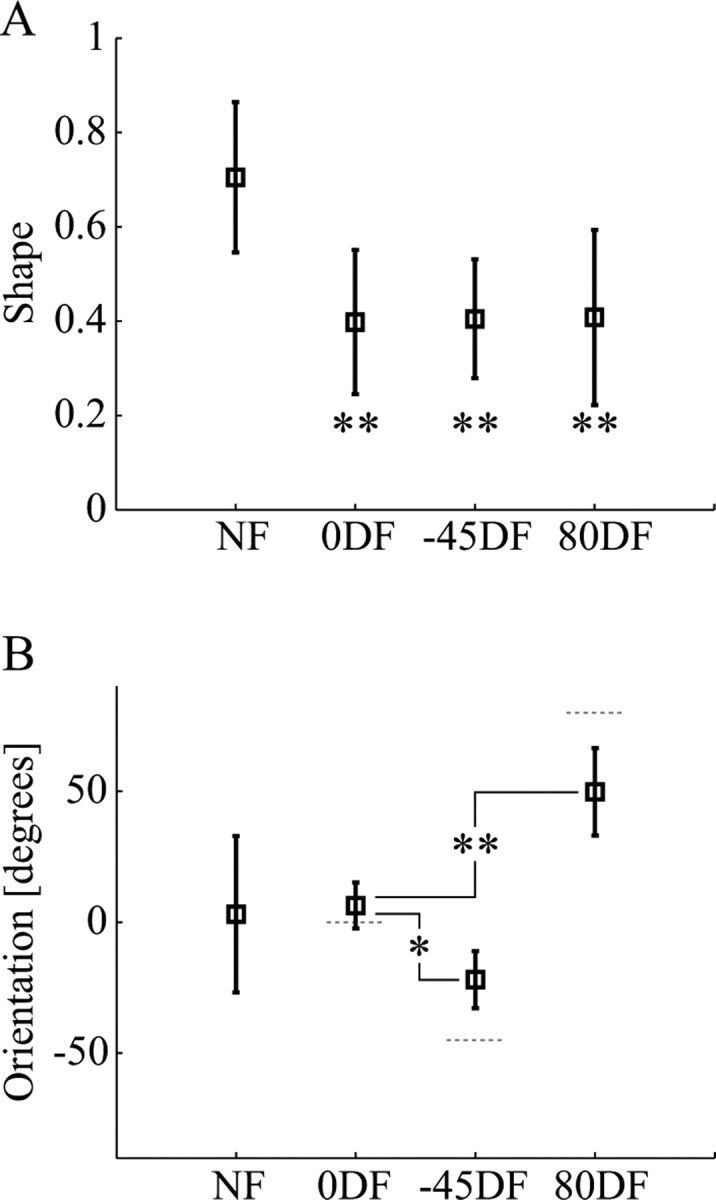
The characteristics of the endpoint stiffness were modified according to the instability in the environment. A, Changes in the shape of the endpoint stiffness ellipse in the four environments. Compared with the stiffness ellipse in the NF force fields, the stiffness ellipses in all three divergent fields were significantly more anisotropic, indicating that the endpoint stiffness had been selectively increased in a particular direction. Mean values across eight subjects with error bars indicating the SD are shown. Statistics indicate the results of Dunnett's t post hoc test of the difference relative to the NF (**p < 0.001). B, The orientation of the endpoint stiffness ellipse in the four environments. The variability in orientation of the NF stiffness is illustrated by the large SD. After subjects adapted to a divergent force field, the orientation shifted closer to the direction of the instability. Compared with the orientation of the 0DF stiffness ellipse, the −45DF stiffness ellipse rotated significantly in the counterclockwise direction, whereas the 80DF stiffness ellipse rotated significantly in the clockwise direction. Statistics indicate the results of Dunnett's t post hoc test of the difference relative to the DF (*p < 0.05; **p < 0.001). The orientation of the force field is indicated with the gray dotted line for each of the divergent fields.

Orientation is defined as the direction of the major stiffness axis relative to the x-axis (Gomi and Osu, 1998). The mean orientation of the NF stiffness was 3.0°. However, there was a large variability in the NF stiffness orientation. Some of this variability can be attributed to the relatively isotropic nature of the NF stiffness ellipse. As the ellipse becomes more isotropic, small changes in the eigenvalues produce relatively large changes in orientation. However, there was also intersubject variability. The NF stiffness ellipses of several subjects were markedly eccentric but did not have a consistent orientation. The 0DF stiffness was oriented close to the direction of instability (mean, 6.4°). The orientation of the −45DF and 80DF stiffness was less closely aligned with the instability, although in each case there was a sizeable rotation of the mean orientation toward the direction of the instability (i.e., −22.0° for the −45DF and 51.6° for the 80DF). An ANOVA (with a main effect of force field type and a random factor of subjects) was performed. After finding a significant main effect of force field type (p < 0.001), a post hoc test (Dunnett's t) was used to determine whether the orientation of endpoint stiffness for the −45DF and 80DF was different from the orientation of the 0DF stiffness. The final endpoint stiffness after adaptation to the −45DF and 80DF force fields was significantly rotated relative to the orientation of the 0DF stiffness (p = 0.028 and p = 0.001, respectively).

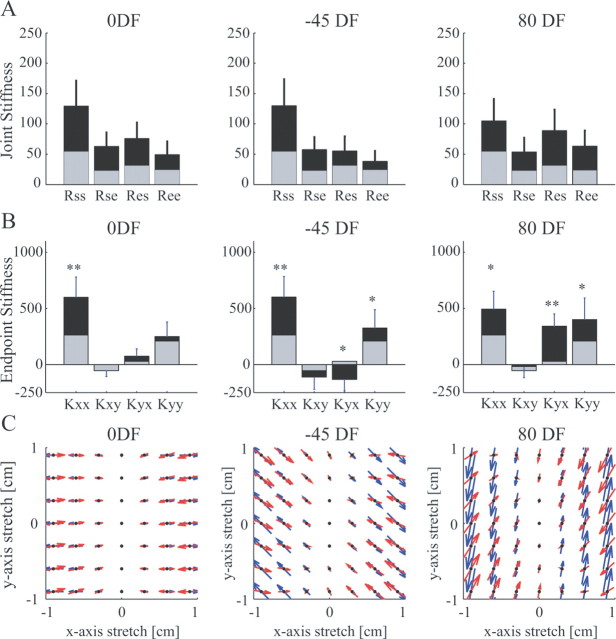
The joint stiffness matrix (Fig. 6A) was calculated from the Cartesian stiffness matrix by means of the standard transformation involving the Jacobian matrix (McIntyre et al., 1996). Comparison of the terms in the matrix can provide some information about the way in which the limb stiffness was modified. A simple ratio of the R_ss to the R_ee was computed for each field. This ratio can provide information about the relative contributions of muscles crossing either the shoulder or elbow joints to the overall stiffness. However, because the biarticular muscles can contribute in different extents to all four terms of the matrix, depending on the moment arms, it is not a measure of the separate effects of the three muscle groups. Differences in this ratio across force fields were analyzed using an ANOVA with random effect of subjects and main effect of force field. The significant main force field effect (p < 0.001) was further examined using Tukey's honestly significant difference (HSD) post hoc test. The ratio (R_ss/R_ee) for the NF (2.33) and the 0DF (2.79) was not significantly different (p = 0.223). However, the ratio for the −45DF (3.65) was significantly higher than for any of the other three force fields (NF, p < 0.001; 0DF, p = 0.007; 80DF, p < 0.001), indicating that the shoulder stiffness had increased relatively more than the elbow stiffness. Conversely, the ratio for the 80DF (1.65) was significantly lower than for the other three fields (NF, p < 0.038; 0DF, p < 0.001; −45DF, p < 0.001), indicating that the elbow stiffness had increased more than the shoulder stiffness.

Figure 6.

Changes in the stiffness after force field adaptation relative to NF stiffness. A, Mean joint stiffness across subjects. Each panel shows the mean values for one of the divergent fields (black bars) compared with the NF (gray bars). Error bars give the SD across the eight subjects. B, Mean endpoint stiffness across subjects. Each panel shows the mean values for one of the divergent fields (black bars) compared with the NF (gray bars). Error bars give the SD across the eight subjects. Differences relative to NF stiffness were statistically tested using a paired t test (*p < 0.05; **p < 0.001). C, Change in endpoint stiffness after adaptation relative to the NF stiffness (ΔK = K_FF − K_NF) represented as a force field under the assumption that the endpoint stiffness is independent of perturbation size is shown with the red arrows. Force vectors are plotted as a function of hand displacement, where the middle of the force vector (black dot) is the hand displacement value. Underneath, shown in blue arrows, the environmental force field imposed in the experiment is shown for the same set of hand displacements.

The cross-joint stiffness terms (R_es and R_se) were also analyzed. Biarticular muscles contribute equally to these two terms of the stiffness matrix, whereas uniarticular muscles do not contribute at all, so differences between these two terms can indicate directional asymmetry of cross-joint reflex responses (Hogan, 1985; Mussa-Ivaldi et al., 1985). A measure of the asymmetry was obtained by taking the differences between the two values and dividing by the mean value: (R_se − R_es)/[(R_se + R_es)/2]. Statistics were then performed on this measure, which was calculated separately for each subject in each force field. Mean values differed across force fields (NF, −0.29; 0DF, −0.20; −45DF, 0.07; 80DF, −0.51). A one-sample t test was performed for each force field (with Bonferroni correction for the four multiple comparisons, significant differences were considered only at the p < 0.0125 level), which demonstrated that for the NF, 0DF, and 80DF the mean values were significantly different from zero (one sample t test; p = 0.001, p = 0.003, and p < 0.001, respectively), but not for the −45DF (p = 0.512). Thus, for three of the four force fields, the R_es term was larger than the R_se term. Differences across the fields were compared using a post hoc test (Tukey's HSD). This mean value for the 80DF was significantly different from the value for both the 0DF (p = 0.041) and the −45DF (p < 0.001). The mean value for the NF was also significantly different from that for the −45DF (p = 0.014). These results indicate that there were significant differences in the cross-joint stiffness terms across the force fields.

The elements of the Cartesian stiffness matrix after adaptation to each divergent force field were compared with the NF values (Fig. 6B). Statistics were performed using a paired t test comparing each stiffness matrix element after adaptation to the corresponding value under the NF. The 0DF produces instability only in the x-direction. Appropriately, the greatest increase occurred in the K_xx term (p = 0.0003), which represents the restoring force in the x-direction caused by a perturbation in the x-direction. No significant change occurred in the other three terms (K_xy, p = 0.95; K_yx, p = 0.07; K_yy, p = 0.32). The stiffness after adaptation to the −45DF force field also changed relative to the NF stiffness but with a different pattern. Both the K_xx and K_yy terms increased relative to the NF (p = 0.0003 and p = 0.03, respectively). There was no significant change in the K_xy term (p = 0.13), but there was a significant decrease (p = 0.004) in the K_yx term, which represents the restoring force in the y-direction caused by a displacement in the x-direction. A similar effect was seen after adaptation to the 80DF. Both the K_xx (p = 0.002) and K_yy (p = 0.008) terms increased relative to the NF stiffness, whereas the K_xy term exhibited no change (p = 0.21). However, the K_yx term increased significantly relative to the NF (p = 0.0003).

The effect of the changes in endpoint stiffness were plotted as a force field (Fig. 6C) to illustrate how much the force would increase in response to perturbations of different amplitudes in different directions. In the 0DF, this force field is aligned in the x-direction. Similarly, in the −45DF and the 80DF fields, the force field is oriented along the −45 and 80° directions, respectively. By representing the change in endpoint stiffness as a force field, the change in the subjects' mechanical response to perturbation can be compared with the environmental force field. In each force field, the endpoint stiffness creates a restoring force that fairly closely matches the size and direction of the applied force field, particularly for small displacements. This shows that these changes in the endpoint stiffness acted to selectively compensate for the instability.

Symmetric and antisymmetric stiffness

The endpoint stiffness can be decomposed into two components: a symmetric component (conservative) and an antisymmetric component (rotational) (Mussa-Ivaldi et al., 1985). The symmetric or conservative component can be produced by a combination of passive, intrinsic, or symmetric reflexive stiffness. However, the antisymmetric component, which arises from differences in the cross-joint terms, is considered to be attributable mainly to asymmetric heteronymous reflexive responses (Hogan, 1985). A large antisymmetric term, therefore, is taken to indicate that there is a significant reflex contribution to the overall stiffness (although lack of a significant antisymmetric term does not prove that there is no reflex component). The endpoint stiffness of the limb was tuned toward the direction of instability in the environment (Figs. 4, 6C). Part of this change in the orientation occurred through the adaptation of the K_yx term of the endpoint stiffness (Fig. 7A). Although this term changed little after adaptation to the 0DF, for the −45DF and 80DF the K_yx term was increased in opposite directions to offset the disturbing force of the environmental field. In contrast, the K_xy term changed little from the NF after adaptation.

Figure 7.

Symmetric and antisymmetric components of endpoint limb stiffness. A, Effect of the change in cross-terms of the endpoint stiffness matrix (K_xy and K_yx). For each of the three divergent force fields, the resulting change in the cross-terms relative to the original NF stiffness was calculated. The force (solid line) resulting from a 1 cm displacement (dotted line) was calculated for each of the ΔK_xy (gray) and ΔK_yx (black) terms. The K_xy terms after adaptation were not significantly different from the NF values and produced only small changes in force. Although the ΔK_yx did not produce large forces in the 0DF field, it produced opposite effects in each of the −45DF and 80DF fields. These forces were directed to resist the oppositely directed forces from the divergent force field. B, The mean antisymmetric components of the limb stiffness for all four force fields. The force created by the antisymmetric component in response to a 10 mm displacement is displayed for eight equally spaced directions (calibration shown at the bottom). At the top of each figure, an arrow displays the direction of this curl component. C, The mean symmetric endpoint stiffness for each of the four force fields. The calibration is shown at the bottom of the figure. D, The difference in the cross-terms of the stiffness matrix (K_yx − K_xy) is shown after adaptation to each force field. It is this difference that gives rise to the antisymmetric components of the endpoint stiffness. Statistics indicate the results of Tukey's HSD post hoc test. (*p < 0.05; **p < 0.001). E, The relative contribution of the antisymmetric component of the endpoint stiffness compared with the overall symmetric forces. The Z_mean and SEM are shown for each of the four force fields. Statistics indicate the results of the Dunnett's t post hoc test testing the difference of each group from the NF results (**p = 0.001).

The mean antisymmetric and symmetric stiffnesses across subjects were determined for each of the four force fields (Fig. 7B,C). The antisymmetric component was clockwise for three of the four fields (NF, 0DF, and 80DF) but slightly counterclockwise for the −45DF stiffness. The symmetric stiffness was still oriented toward the direction of the instability in the force field. This illustrates that both the conservative and nonconservative forces cause the expansion of the stiffness ellipse in the appropriate direction to adapt to the environmental instability.

Differences in the cross-terms of the stiffness matrices after adaptation to the environments were examined by calculating the difference between the K_yx and K_xy terms. Statistical significance was examined using an ANOVA (main effect force field, random effect subjects). A significant main effect (p < 0.001) was further examined with Tukey's HSD post hoc test. Neither in the 0DF nor in the −45DF was the cross-term significantly different from in the NF (p = 0.89 and p = 0.18, respectively). However, there was a significant difference in the cross-term after adaptation to the −45DF (p = 0.044) relative to the 0DF. Finally, the results in the 80DF were different from all force fields (NF, p = 0.001; 0DF, p = 0.005; −45DF, p < 0.001). Therefore, the differences between the cross-term components of the stiffness were different after adaptation to each unstable force field.

The overall contribution of the asymmetric stiffness to the total stiffness was examined by estimating Z_mean, the square root of the ratio of the determinant of the antisymmetric stiffness to the determinant of the symmetric stiffness (Mussa-Ivaldi et al., 1985). Expressed as a percentage, we found the following Z_mean values (mean ± SD of eight subjects) for stiffness under the four conditions: NF, 21.7 ± 10.1; 0DF, 20.6 ± 15.4; −45DF, 16.6 ± 9.0; 80DF, 50.4 ± 22.2. Differences in Z_mean across force fields were tested using an ANOVA (with a main effect of force field type and a random factor of subjects). After a significant main effect of force type (p < 0.001), a post hoc test (Dunnett's t) was used to determine whether the Z_mean in each of the divergent force fields was significantly different from that in the NF. The 0DF and −45DF were not significantly different from the NF results (p = 0.99 and p = 0.80, respectively). A significant difference was found only for the stiffness in the 80DF field (p = 0.001).

Electromyographic activity

The muscle activation patterns were examined during a single day of experiments in which subjects relearned all three divergent force fields in a random order. To be able to attribute differences in the muscle activation to coactivation of muscles rather than changes in the phasic muscle activation patterns, it was necessary to confirm that subjects were performing similar movements in all force fields. The same trials used in the EMG analysis were used to compare joint angles and joint velocities at eight positions in the movement. For each variable, an ANOVA was performed to examine the differences with main factors of force field, position in the movement, and random effect of subjects. There were no significant effects of the force field (shoulder angle, 0.61; elbow angle, 0.76; shoulder angular velocity, 0.33; elbow angular velocity, 0.44) or the interaction effect of force field and position (shoulder angle, 0.33; elbow angle, 0.92; shoulder angular velocity, 0.46; elbow angular velocity, 0.79). These results indicate that similar movements were made in all three force fields. Any differences in the muscle activation patterns, therefore, could be attributed to coactivation rather than changes in the feedforward reciprocal activity due to differences in the trajectory. Because the EMG analysis is based on the average activity of multiple trials rather than trial-by-trial changes in muscle activation, it does not rule out differences in asymmetrical reflex responses or triggered responses depending on the force field. However, previous work [Franklin et al. (2003a), their Fig. 9] suggests that these reflexive and triggered responses contribute only a small amount of the overall EMG change relative to the null field activity.

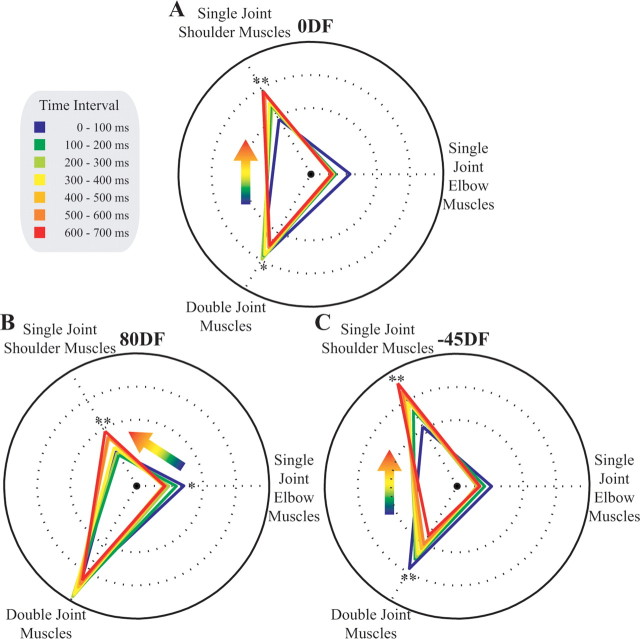
Figure 9.

The relative increase in EMG changes during movement. A, Changes in muscle activity over time in the 0DF. The relative change in the muscle activity is shown for each 100 ms time interval during the movement. As the hand moved away from the body, the difference in biarticular muscle activity decreased, and that of single-joint shoulder muscle activation increased, relative to NF activity. This can be seen as a smooth transformation in the location and shape of the triangle representing the relative muscle contributions. B, Changes in muscle activity over time in the 80DF. C, Changes in muscle activity over time in the 45DF. Both showed similar patterns to changes in the 0DF. Significant differences in the relative EMG activity for the shoulder, elbow, or biarticular muscles throughout the movement were tested with an ANCOVA with interval as the covariate. Significant main effects of the covariate are indicated (*p < 0.05; **p < 0.001). Under conditions in which one muscle group significantly decreased its relative activity over the interval while another muscle group increased its relative activity, this change is shown with the colored arrow. The figure shows the average results across all five subjects.

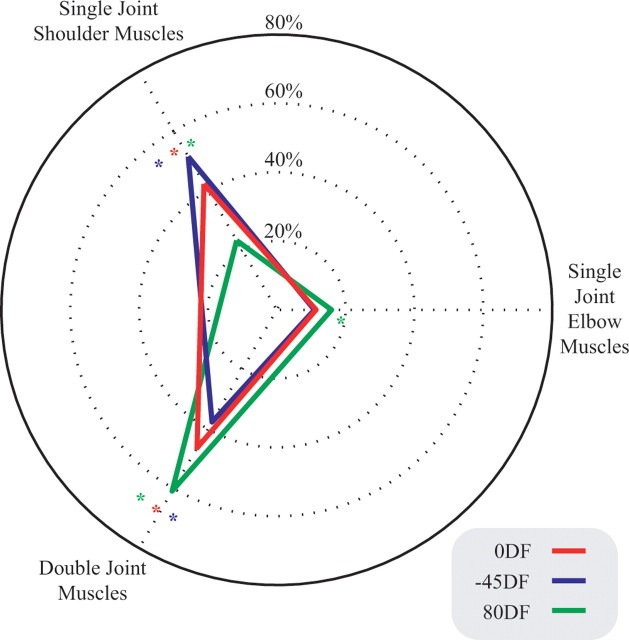
The change in muscle activity relative to the NF was tested for a main effect of force field using ANOVA (main effect force field, main effect interval, random effect subjects). When a main effect was found, a post hoc test (Tukey's HSD) was used to determine whether any of the three force fields were significantly different from the others (p < 0.05). The change in activation for each muscle pair, relative to the NF, is shown in Figure 8. A significant main effect of force field was found for all three muscle pairs: shoulder (p < 0.001), biarticular (p < 0.001), and elbow (p = 0.002). A post hoc test for the shoulder muscle activation found that the activity was significantly different in all three force fields (p < 0.001 for all comparisons). A post hoc test for the biarticular muscle activation also found that the activity was significantly different in all three force fields (0DF compared with −45DF, p = 0.003; p < 0.001 for all other comparisons). Finally, a post hoc test on the elbow muscle activity found a significant increase for 80DF compared with both the 0DF (p = 0.013) and the −45DF (p = 0.002) but no significant difference between the 0DF and −45DF (p = 0.821). To summarize the results, the single-joint shoulder muscle activation increased the most in the −45DF and the least in the 80DF. The opposite effect was seen in the biarticular muscle pair, in which the largest increase occurred in the 80DF, whereas the smallest effect was seen in the −45DF. For the single-joint elbow muscles, the largest increase in muscle activation occurred in the 80DF, with no difference between the 0DF and −45DF. Because the change in muscle activity was expressed as a ratio of NF activity, it cannot be quantitatively related to muscle force or stiffness.

Figure 8.

Unique changes in EMG during movements in each of the three unstable force fields. For each force field, the increase in muscle pair activity relative to NF activity has been plotted as a percentage such that the total change in activity for the three muscle pairs sums to 100%. For each muscle pair, a significant difference for a given force field compared with the other force fields, as determined using post hoc analysis (Tukey's HSD), is indicated in the corresponding color (*p < 0.05). The figure shows the average values for the five subjects.

As subjects extend their arm during the movement, the lateral stiffness of the arm decreases, and the contribution of different muscle groups to endpoint stiffness changes as a result of the changing geometry of the arm. Muscle activity was quantified during 100 ms intervals from the start of the movement (0 ms) until 100 ms after the end of the movement (700 ms). As the subjects extended the arm, the muscle activation pattern changed in all three force fields (Fig. 9). In general, the difference in muscle activation, with respect to the NF, decreased for the single-joint elbow and double-joint muscles, whereas it increased for the shoulder muscles. For each muscle pair and force field, an ANCOVA (covariate interval, random effect subjects) was used to determine whether the difference in muscle activation with respect to the NF changed significantly from the beginning to the end of the movement. It was considered significant if the covariate term was significant at the 0.05 level. In the 0DF, there was a significant increase for the single-joint shoulder muscles with progression in the movement (p < 0.001), whereas a significant decrease occurred in the double-joint muscles (p = 0.002). No significant effect was seen in the single-joint elbow muscles (p = 0.067). In the 80DF, the same effect was also seen: increase in shoulder muscle activity (p < 0.001), a decrease in the activity of double-joint muscles (p < 0.001), and no significant effect in the single-joint elbow muscles (p = 0.385) as the interval of movement changed. In the −45DF, whereas the shoulder muscle activity increased with interval during the movement (p = 0.001), the elbow muscle activity decreased (p = 0.023), and no significant effect was seen in the biarticular muscles (p = 0.175). In all three force fields, the relative activity of the shoulder muscles increased toward the end of the movements.

Discussion

We investigated the ability of the neuromuscular system to control the direction of the impedance of the arm during movement. Subjects adapted to three differently oriented position-dependent unstable force fields. We found that the endpoint stiffness increased in all three cases relative to the NF. It became more anisotropic and was oriented closer to the direction of the imposed instability. This demonstrates that the neuromuscular system attempts to selectively increase the impedance in the direction of instability rather than globally. The pattern of muscle coactivation, relative to the NF, was modified as subjects moved from a proximal to distal posture in a way that suggested compensation for the effect of the changing geometry of the arm on stability. This provides compelling evidence for the existence and utility of an impedance controller in the CNS.

Control over endpoint impedance

When antagonistic muscles are simultaneously activated, the stiffness of the joint can increase with little or no change in the joint torque (Hogan, 1984), suggesting that limb impedance could be controlled by the CNS (Hogan, 1985). Lacquaniti and colleagues (Lacquaniti and Maioli, 1987; Lacquaniti et al., 1991, 1992, 1993) showed that the CNS controls the joint impedance through both anticipatory and reflexive responses during catching. Furthermore, the CNS is able to control the shape and orientation of the endpoint stiffness ellipse of the arm during movements in an unstable environment (Burdet et al., 2001; Franklin et al., 2003a). The increased stiffness in the direction of instability was found to scale with the degree of environmental instability (Franklin et al., 2004).

Our previous studies used a force field that principally required compensatory coactivation of the biarticular muscles (Franklin et al., 2003b, 2004). Whether other muscle pairs could also be selectively coactivated to control the impedance of the limb was unknown and was investigated in the present study. Control of endpoint stiffness orientation has been investigated for a fixed posture in which subjects were provided with visual feedback of the muscle activity levels (Gomi and Osu, 1998) or the endpoint stiffness ellipse (Perreault et al., 2002) or resisted perturbations in specific directions (Darainy et al., 2004). Relatively small changes in orientation were observed [i.e., 19.8° (Perreault et al., 2002), 30° (estimated from figures) (Gomi and Osu, 1998), and 30° (Darainy et al., 2004)] compared with our study (∼70°, on average).

One possible reason why we observed a greater change in the orientation of the stiffness ellipse is that the responses during movement may be caused by transient changes in the impedance similar to that during ball catching (cf. Lacquaniti and Maioli, 1989), which are not sustained during posture. Another possibility is that different populations of neurons are used for controlling the muscle activation patterns during movement and posture (Kurtzer et al., 2005). It is also likely that training with appropriate error signals is important. In two of the previous studies, there were no proprioceptive error signals (Gomi and Osu, 1998; Perreault et al., 2002). Furthermore, the duration of training was short compared with the current study. In the third study, subjects trained over a period of 3 d, resisting directed force pulses (Darainy et al., 2004). Endpoint stiffness gradually increased in the approximate direction of the force pulses and was reduced in the orthogonal direction. However, the force impulse was relatively small (0.6 N · s), which may not have provided an optimal error signal.

Margin of stability

Our previous work showed that the net stiffness (limb stiffness − environment stiffness) was approximately equal to NF stiffness (Burdet et al., 2001; Franklin et al., 2004), suggesting that the CNS maintains a constant margin of stability. In the current experiments, although the direction of the stiffness ellipse was not aligned precisely with the force field instability, the change in the endpoint stiffness relative to the original NF stiffness was precisely aligned (Fig. 6). This suggests that the change in endpoint stiffness was effected to maintain the same margin of stability (Burdet et al., 2001, 2006).

Feedforward changes in muscle activation

After adaptation, the movements rarely deviated much from the straight-line trajectory (Fig. 3). It is likely that stabilization was achieved by feedforward control to increase cocontraction and straighten the trajectory. Although cocontraction and stiffness increase early in the learning (Franklin et al., 2003b), it is only as subjects also learn to straighten the trajectory that performance improves. When the learning is complete, the joint torques and kinematics are similar in all force fields. It is only the change in the endpoint stiffness that is different.

Selective coactivation of different muscle groups (biarticular muscles for the 0DF, shoulder muscles for the −45DF, and a combination of biarticular and elbow muscles for the 80DF) was assumed to be necessary to achieve the predicted changes in orientation of the endpoint stiffness, which was generally supported by the data. In the −45DF field, the muscle activation increased primarily in the single-joint shoulder muscles. There were much smaller increases in the activity of the biarticular and single-joint elbow muscles. In the 80DF field, there was a similar increase in the activation of the biarticular and elbow muscles and a much smaller increase for the single-joint shoulder muscles. In the 0DF, the increase in the activity of single-joint elbow muscles was similar to the −45DF, whereas there was a larger increase in the biarticular muscles and a smaller increase in the single-joint shoulder muscles. Although this is consistent with the findings of previous studies showing that there can be independent coactivation of shoulder and elbow muscles (Gribble and Ostry, 1998), it is clear that the increased stiffness was not produced by a change in the coactivation of only a single muscle pair. It appears that there are limits to the selectivity of muscle coactivation. The simulation (Fig. 1) used to predict the effects of selective cocontraction on endpoint stiffness also has limitations. A number of assumptions were made, including assumptions about moment arms and single equivalent muscles, which are likely to be inaccurate.

As the geometry of the arm changes during movement, the contribution of particular muscles to the endpoint stiffness changes. For example, when the arm is in a relatively extended position in front of the body, an increase in stiffness restricted to the x-direction can only be achieved by increasing the activation of single-joint shoulder muscles. With the arm in a more flexed position, the same change in endpoint stiffness can be produced by biarticular muscles alone. It was, therefore, expected that as subjects extended the arm there would be a greater increase in the activity of the single-joint shoulder muscles. This is exactly what was observed. For all three force fields, the relative change in single-joint shoulder muscle activity was enhanced as subjects extended their arm. This suggests that the stiffness of the arm is controlled throughout the movement to achieve the desired stability

Feedback contributions to impedance control

There is some evidence, particularly for the −45DF and 80DF force fields, that the CNS may modify the gains to the heteronymous reflex responses as part of the adaptation. For these two force fields, the off-diagonal terms of the joint stiffness matrix changed relative to the values in the null field. In the case of −45DF, they became more symmetric, whereas they became less symmetric in the case of the 80DF. The major increase in the cross-joint stiffness occurred in the R_es term, which relates to stretch of the proximal shoulder muscles exciting the more distal elbow muscles. Such proximal-to-distal effects have been reported under static conditions (Smeets and Erkelens, 1991).

Feedforward and feedback contributions to impedance control

Although it is still not clear to what degree impedance control depends on feedforward changes in the motor command (Gribble and Ostry, 1998) compared with possible “feedforward” changes in feedback loop gain (Gomi et al., 2002), it is clear that the CNS is able to tune the endpoint impedance of the limb when moving repetitively in unstable environments. Although it is not known where this adaptation takes place, studies investigating changes in brain activity have shown that the cerebellum is highly active in the manipulation and control of unstable objects (Milner et al., 2006, 2007). There is also evidence from single-cell recording studies in monkeys that cerebellar activity is modulated during coactivation of antagonist muscles (Smith, 1981; Frysinger et al., 1984; Wetts et al., 1985). Presumably by using information about errors from repetitive trials, the brain gradually forms an internal model of the stability of the external environment and learns a time-varying pattern of muscle activation that ensures stability and accuracy while limiting the metabolic cost of the action. The brain can learn to control different groups of antagonist muscles to produce an ideal response to the environmental instability.