An Energy Budget for the Olfactory Glomerulus

Abstract

Energy demands are becoming recognized as an important constraint on neural signaling. The olfactory glomerulus provides a well defined system for analyzing this question. Odor stimulation elicits high-energy demands in olfactory glomeruli where olfactory axons converge onto dendrites of olfactory bulb neurons. We performed a quantitative analysis of the energy demands of each type of neuronal element within the glomerulus. This included the volumes of each element, their surface areas, and ion loads associated with membrane potentials and synaptic activation as constrained by experimental observations. In the resting state, there was a high-energy demand compared with other brain regions because of the high density of neural elements. The activated state was dominated by the energy demands of action potential propagation in afferent olfactory sensory neurons and their synaptic input to dendritic tufts, whereas subsequent dendritic potentials and dendrodendritic transmission contributed only a minor share of costs. It is proposed therefore that afferent input and axodendritic transmission account for the strong signals registered by 2-deoxyglucose and functional magnetic resonance imaging, although postsynaptic dendrites comprise at least one-half of the volume of the glomerulus. The results further suggest that presynaptic inhibition of the axon terminals by periglomerular cells plays an important role in limiting the range of excitation of the postsynaptic cells. These results provide a new quantitative basis for interpreting olfactory bulb activation patterns elicited by odor stimulation.

Introduction

Odor stimulation elicits high-energy demands in activated glomeruli of the olfactory bulb, as shown by the 2-deoxyglucose (2-DG) method (Sharp et al., 1975, 1977), and subsequently by functional magnetic resonance imaging (fMRI) (Yang et al., 1998; Xu et al., 2003). Direct observations of increases in blood flow within the capillaries of a glomerulus activated by odor stimulation have been made by two-photon microscopy (Chaigneau et al., 2003). The changes in the microvasculature that are registered by intrinsic imaging (Mori et al., 1999) are also related to energy demands. These and other studies have shown that the glomeruli are activated to different degrees by different odor molecules, producing spatial patterns within the glomerular layer that represent the different features of the stimulating odor molecules.

A key question in interpreting the activation of a given glomerulus is the extent to which the energy demands are attributable to the afferent synapses from the olfactory receptor neurons (ORNs), reflecting the activation of the ORNs converging on a given glomerulus, or to the postsynaptic dendrites within the glomerulus, reflecting the first steps in processing the input, or to centrifugal fibers, reflecting the activity of brainstem systems in modulating these intraglomerular interactions. An early clue to these relative contributions was the observation of a high 2-DG signal in the overlying olfactory nerve layer near activated glomeruli, suggesting that a significant part of the glomerular signal could be attributable to the preterminal axons and axon terminals within the glomerulus (Sharp et al., 1977). It is also known that the postsynaptic dendrites within the glomerulus are themselves presynaptic, forming dendrodendritic connections with each other (Pinching and Powell, 1971; Shepherd, 1971), and therefore would also be expected to contribute significantly to the signal (Sharp et al., 1977). To identify activity restricted to the afferents, methods for loading the ORNs with voltage-sensitive or Ca²⁺-sensitive dyes have been used (Wachowiak and Cohen, 2001). These results have been consistent with a strong contribution from the axon terminals, but the relative contributions of afferents versus dendritic processes have not been assessed.

To give insight into the cellular basis of glomerular signals and thus of odor maps, and to guide future experiments, we introduce a different approach by constructing an energy budget. This method has proven of value in assessing the energy demands of different neuronal elements in the mammalian retina (Ames et al., 1992; Ames, 2000), in the fly compound eye (Laughlin, 1994), and in the cerebral cortex (Attwell and Laughlin, 2001). The olfactory bulb, with its rigid lamination, distinct cell types, and prominent glomeruli, is an attractive subject for this approach (Shepherd et al., 2004). Here, we construct an energy budget for the olfactory glomerulus of the rat. The results provide quantitative estimates of the energy demands of the main neural elements in an activated glomerulus and give insights into their relative contributions to glomerular activation and odor maps. They further provide estimates of the energy costs of information processing in the olfactory pathway that can be compared with the retina, and with the microcircuits of the cerebral cortex.

Materials and Methods

Overall quantitative approach

Based on a previous study (Attwell and Laughlin, 2001), the energy requirements of the glomerulus were first assessed in relation to basic cellular mechanisms involved in resting and active states. We distinguished between the energy demands of morphologically distinct elements within the glomerulus, which we refer to as canonical neural compartments. We derived the energy demands for each compartment by adapting to our needs the calculations made by Attwell and Laughlin for corresponding compartments in the cerebral cortex. We next performed quantitative estimates of the total volumes of the compartments and numbers of synapses within one glomerulus. The volumes then permitted calculations of the total surface areas on which the population energy demands were based. In Results, we apply these calculations to derive the total energy demands of each type of neuronal compartment for different degrees of activation of the olfactory receptor (OR) cells. The supplemental material (available at www.jneurosci.org) provides the full details of each step.

We focus on the rat, for which quantitative data on the olfactory pathway are most abundant, allowing a comparison with mouse and other mammalian species (quantitative data are summarized in supplemental Table S2, available at www.jneurosci.org as supplemental material).

Elements of the glomerular circuitry

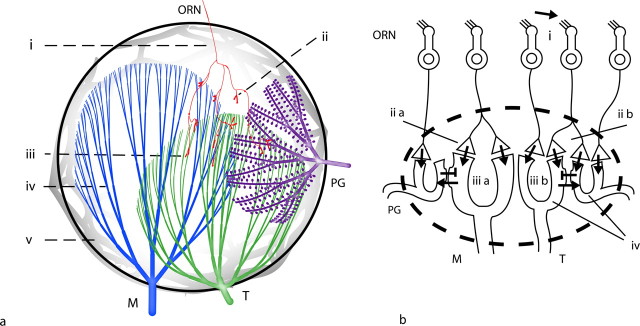
The canonical neuronal compartments for computing the energy requirements of signaling within a glomerulus, beginning with the incoming ORN axons, are as follows: unmyelinated receptor cell axon, preterminal axon, presynaptic axon terminal, and presynaptic and postsynaptic dendritic tuft of mitral (M), tufted (T), and periglomerular (PG) cells. In addition, associated glial processes are considered (Fig. 1 a).

Figure 1.

Organization of the olfactory glomerulus. a, The neuronal compartments within a glomerulus. i, Unmyelinated ORN axon; ii, preterminal ORN axon; iii, presynaptic ORN axon terminal; iv, presynaptic and postsynaptic dendritic tuft of M, T, and PG cells; v, network of glial elements. b, Basic circuits in the olfactory glomerulus. i, ORN cilia project into the epithelium. Their membrane-bound odor receptors are activated through odor molecules (arrow). ii, ORN axons target M, T, and PG cells in the glomerulus via excitatory axodendritic synapses. A given axon might converge its input onto a single dendritic tuft (ii a) or distribute its input onto several receiving cells (ii b). iii, Dendrodendritic synapses between PG and M/T cells. PG cells make inhibitory contacts, and M/T cells make excitatory synapses. Dendrodendritic synapses might be established between cells that receive distinct (iii a) or similar (iii b) sensory input. iv, Synaptic input gives rise to dendritic action potentials/EPSPs.

The neuronal circuit for odor processing that we consider the basis for our calculations originates at the level of the epithelium where odor molecules interact with olfactory receptors expressed in olfactory nerve cell cilia (Fig. 1 b) (for review, see Shepherd et al., 2004). Olfactory nerve cells expressing the same odor receptor converge their axons onto a glomerulus, ramifying on entrance and targeting M/T and PG cell dendritic tufts with excitatory glutamergic synapses. M/T and PG cells interact via dendrodendritic synapses: PG cell dendrites project GABAergic synapses onto M/T cell dendrites, whereas M/T cell dendrites make glutamergic contacts onto PG cell dendrites. PG cells also make GABAergic synapse onto ORN axonal terminals. [The population of neurons termed PG cells forms a heterogeneous group with varying properties (for review, see Kosaka and Kosaka, 2005). To simplify, we consider the subgroup of GABAergic interneurons that receive excitatory input from ORN axons and M/T dendrites, and in turn inhibit ORN axonal terminals and M/T cell dendrites.]

Basic costs of ion transport across the membrane

We are most interested in the signaling-related demands of olfactory neurons (ONs), which include the transport of ions across the cell membrane. Throughout the text, we will need to convert ionic flux in and out of the cell into the cost of restoring the original state. For simplification, we consider only two types of membrane pumps in our calculations. The first is the Na⁺/K⁺ pump that extrudes three Na⁺ and imports two K⁺, requiring one ATP. Therefore, the ATP requirements of the pumps can be estimated to be one-third of the Na⁺ ion load. The second type is the ATP-dependent Ca²⁺ pump that extrudes one Ca²⁺ at a cost of one ATP, after the influx at a postsynaptic site or after a Ca²⁺ spike. Calcium can also be removed by the Na⁺/Ca²⁺ exchanger without energy requirement, but the 3:1 exchange ratio means that Na⁺ must be extruded by the Na⁺/K⁺ pump, requiring again one ATP per Ca²⁺ ion (cf. Attwell and Laughlin, 2001).

Canonical energy calculations

Energy requirements of the resting glomerulus.

Energy demands in the resting state were divided by Attwell and Laughlin (2001) into vegetative processes and signaling-related activities. Vegetative activities include the metabolism of proteins, lipids, and oligonucleotides; cellular transport mechanisms; and proton leak in mitochondria. Attwell and Laughlin suggested basal demands of 0.2 μmol of ATP g⁻¹s⁻¹ in cortical tissue. Because the cell somata (and therefore somatic and nuclear activities) are generally located outside the glomerulus, we assume a lower estimate of 0.05–0.1 μmol of ATP g⁻¹s⁻¹ (see section 1 of supplemental material, available at www.jneurosci.org). Signaling-related processes during resting state relate to the maintenance of the resting membrane potential and they create significant energy demands because ions need to be transported against the electrochemical gradient. The magnitude of ion transfer varies for the different neural elements depending on their membrane resistance and their resting potential. For simplification, axonal, dendritic, and glial elements within the glomerulus are considered isopotential, and the demands are calculated per entire element (see section 2 of supplemental material, available at www.jneurosci.org). In summary, for the part of the ORN axon that is within the glomerulus, we estimate energy demands of 1.75 × 10⁶ ATP s⁻¹ to run the Na⁺/K⁺ pump at rest. The mitral cell dendritic tuft requires 7.37 × 10⁸ ATP s⁻¹. The tufted cell dendritic tuft has slightly lower demands of 3.87 × 10⁸ ATP s⁻¹, reflecting the higher input resistance of the smaller cell size. The even more compact PG cell requires only 0.65 × 10⁸ ATP s⁻¹ per tuft to maintain the resting potential. Glomerular astrocytes, however, form a syncytium through electrical coupling that significantly decreases the input resistance of each cell, as documented through intracellular recordings and dye staining (De Saint Jan and Westbrook, 2005). From comparisons of the coupling of passive hippocampal astrocytes with comparable input resistance (Schools et al., 2006), we assume that up to 20 astrocytes associated with a single glomerulus are electrically coupled, and we derive a minimal cost of 1.4 × 10⁹ ATP s⁻¹ to run the Na⁺/K⁺ pumps of the glial network. Note that the resting demands of the whole glial syncytium are only one order of magnitude higher than the resting demands of a single dendritic tuft.

Energy requirements of an action potential in the olfactory axon.

We adapt the calculations of Attwell and Laughlin (2001) for action potential (AP) propagation in cortical axons to the olfactory axons (see section 3 of supplemental material, available at www.jneurosci.org). Assuming a voltage excursion of 125 mV, we derive a flux of 31,200 Na⁺ per square micrometer of membrane surface area per action potential, corresponding to energy demands of 10,400 ATP per square micrometer. From this, we estimate the costs of action potentials traveling the full length of the axons and their branches within the glomerulus.

Energy demands at the axodendritic synapse.

Our assumptions concerning the stoichiometry and signaling-related costs of primary afferent synapses are based on direct electrophysiological and anatomical evidence. Where not available, we have used parameters of cortical cells as used by Attwell and Laughlin (2001), or we have inferred reasonable parameters through comparison with cortical synapses, taking into account differences in volume.

Presynaptic energy demands at the axodendritic synapse.

In the terminal boutons, the energy requiring properties relate to presynaptic Ca²⁺ entry and restoration by the Ca²⁺ pump, and vesicle release and recycling. These steps are dominated by the Ca²⁺ pump, amounting to ∼12,400 ATP/vesicle (see section 4 of supplemental material, available at www.jneurosci.org).

Postsynaptic energy demands at the axodendritic synapse.

The axon terminals are glutamatergic, releasing vesicles containing glutamate, which act on postsynaptic glutamate receptors on the bulbar dendrites.

The non-NMDA receptors activated by one vesicle allow ∼200,000 Na⁺ ions to enter, and require one-third as many ATP (67,000) for the Na⁺/K⁺ pump to extrude.

The NMDA receptors bring in 180,000 Na⁺ and 10,000 Ca²⁺ per vesicle. Extruding the ions requires 70,000 ATP. In addition, mGluRs may act to release intracellular Ca²⁺ via IP₃. Attwell and Laughlin (2001) suggest that ∼3000 ATPs are required to pump the Ca²⁺ back into the endoplasmic reticulum, including a small amount to resynthesize IP₃. In sum, the total postsynaptic receptor energy demands (approximately one-third of the Na⁺ load plus the costs for Ca²⁺ extrusion) amount to a total of 140,000 ATP per vesicle (see section 5 of supplemental material, available at www.jneurosci.org).

Glutamate recycling energy demands.

The steps include astrocytic glutamate uptake, astrocytic glutamate metabolism, export of glutamate to neurons, packaging of glutamate into vesicles (see section 6 of supplemental material, available at www.jneurosci.org). A total of 3.33 ATP is needed to recycle each glutamate molecule. For 4000 glutamate molecules in a vesicle released and repackaged, a total of ∼13,000 ATP is needed. This is an order of magnitude less than the energy required by the postsynaptic receptor response itself.

Presynaptic inhibition at ORN terminals.

Glutamate release at ORN terminals is inhibited by GABA released from postsynaptic PG cells, which interacts with metabotropic GABA_B receptors. Estimated demands at the axonal terminal and the dendritic release side are 15,400 ATP per vesicle (see section 7 of supplemental material, available at www.jneurosci.org).

Energy requirements of a backpropagating action potential in bulbar dendrites.

The excitatory postsynaptic response activates an action potential in the postsynaptic neuron, which backpropagates into the dendritic tuft. This involves both Na⁺ and Ca²⁺ ions, resulting in total energy demands for dendritic backpropagating action potential (bAP) propagation of ∼10,900 ATP per AP per square micrometer (see section 8 of supplemental material, available at www.jneurosci.org). The energy costs of bAPs are higher than those of APs in olfactory axons because of the extra demands of restoring the Ca²⁺ gradient.

Presynaptic and postsynaptic energy demands at dendrodendritic synapses.

A special property of the olfactory glomerulus, not believed to be present in the cerebral cortex, is that the dendrites are presynaptic as well as postsynaptic. Dendrodendritic terminals are activated by local EPSPs and bAPs after afferent action potentials. As in axonal terminals, we estimate presynaptic costs of 12,400 ATP per vesicle (see section 9 of supplemental material, available at www.jneurosci.org). On the postsynaptic side, we assume that synapses from M/T dendrites onto PG cell dendrites are excitatory, with demands of 13,000 molecules ATP per vesicle glutamate, as in the case of the axodendritic synapses. In contrast, PG dendrites are inhibitory onto M/T dendrites. We estimate the number of Cl⁻ entering the postsynaptic mitral/tufted cell per release of one vesicle GABA_A to be ∼80,000 chloride ions. Assuming an active chloride transport mechanism for restoring ionic concentrations (a Cl⁻-ATPase), total costs for chloride ion extrusion amount to 80,000 ATP per vesicle GABA (see section 10 of supplemental material, available at www.jneurosci.org).

GABA recycling energy demands.

As in the case of glutamate, there are several steps involved in recycling GABA, including astrocytic and neuronal GABA uptake, GABA metabolism, export to neurons, and GABA packaging. Recycling of one GABA molecule requires approximately three ATP per molecule. With an estimated 4000 GABA molecules per vesicle, we obtain 12,000 molecules ATP per vesicle (see section 11 of supplemental material, available at www.jneurosci.org). This is approximately one-fifth of the postsynaptic receptor response itself.

Energy requirements of EPSP and calcium spike in PG cell dendrites.

The activation of dendrodendritic synapses leads to glutamatergic release onto PG cells. In the PG cell, the excitatory input causes an EPSP with ΔV = 10 mV and a subsequent calcium spike with ΔV = 30 mV (Murphy et al., 2005). We calculate a Na⁺ influx of 3 × 10⁵ ions during the EPSP, and a Ca²⁺ influx of 950 ions per square micrometer during the calcium spike, giving total energy demands for ion removal of 10⁵ ATP plus 950 ATP per square micrometer membrane surface area in each cell (see section 12 of supplemental material, available at www.jneurosci.org).

Calculation of population volumes.

We estimated the demands of basic cellular mechanisms involved in the resting and active state. These values are used for calculating the energy requirements under different functional conditions in Results. Before this could be done, quantitative estimates of the sizes, branching patterns, and numbers of the neural elements had to be obtained to arrive at the demands of the neural ensemble within one glomerulus (see section 13 of supplemental material, available at www.jneurosci.org). In the process, we needed to ascertain that the populations of elements gave volumes that were appropriate to the average size of a glomerulus. We next summarize these calculations, which become the basis for the estimates of the surface areas of the elements underlying the energy demands of each of the populations.

Volume of a glomerulus.

A 80 μm diameter sphere, such as a glomerulus in the rat, has a volume given by V = 4/3 π r ³ ≈ 270,000 μm³.

Volume of presynaptic axonal elements.

We have derived a model of the ORN axonal tree based on camera lucida reconstructions and exhaustive work on axon morphology by Klenoff et al. (1998) (Fig. 2 a). From this, we can estimate the volumes of ORN axonal branches, preterminal segments, and synaptic terminals within the glomerulus. With 4500 ORN axons on average converging onto a single glomerulus, their total volumes amount to ∼85,000 μm³. This is ∼30% of the total glomerular volume, and close to the estimate of 29% by Kasowski et al. (1999) based on electron-microscopical observations.

Figure 2.

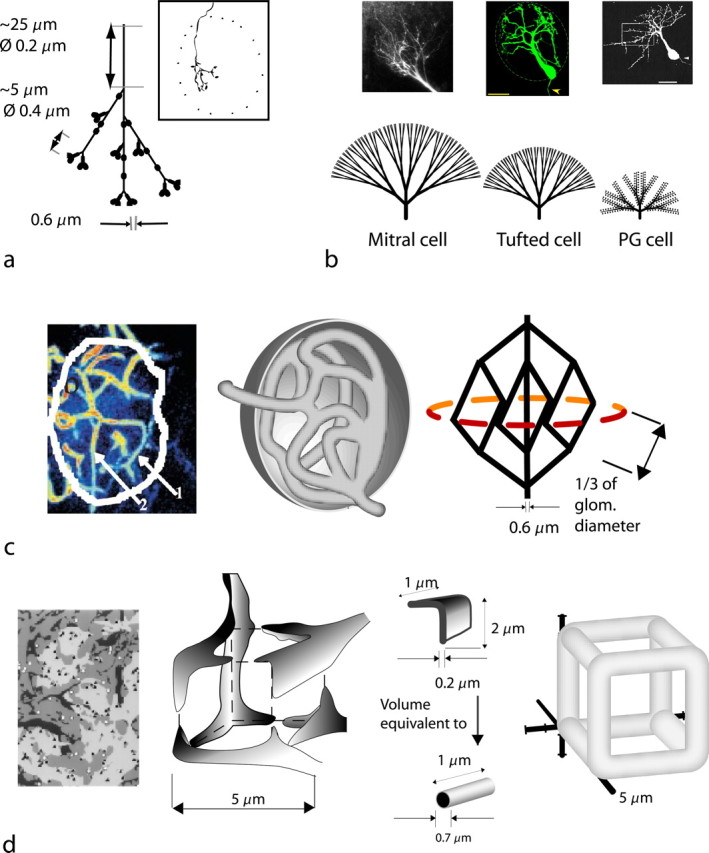
Simplifications of functional glomerular compartments for volume and surface estimations. a, Model of the average intraglomerular olfactory receptor neuron axon derived from morphological studies [inset, camera lucida reconstruction from a 21-d-old rat (Klenoff and Greer, 1998)]. The initial segment of the axon undergoes successive branching as shown. Overall branch length averages 200 μm, and there are ∼25 synaptic terminals (en passant varicosities and synaptic terminals) per axon. The area spanned by the axonal tree is relatively narrow. b, Morphology of the bulbar dendrites. Top left, Mitral cell dendritic tuft (courtesy of W. R. Chen). Bottom left, Branching pattern of mitral cell dendritic tuft. Top middle, Tufted cell tuft. Scale bar, 20 μm (courtesy of W. R. Chen). Bottom middle, Branching pattern of tufted cell dendritic tuft. Top right, Confocal reconstruction of biocytin-filled PG cell. Scale bar, 25 μm (from McQuiston and Katz, 2001). Bottom right, Branching pattern of PG cell dendritic tuft. c, Glomerular vascular supply. Left, Imaging of the capillary network within a single glomerulus by two-photon microscopy (from Chaigneau et al., 2003). Middle, Freehand representation of the capillary network. Right, Formal representation of the capillary network. d, Glomerular glial compartments. Far left, Distribution of astroglial sheets (dark gray) in glomerulus derived from two-photon microscopy (from Chao et al., 1997). Medium gray, Dendrites; light gray, sensory axons. Middle left, Simplified representation of glial process compartment (freehand representation). Middle right, Representation of sheet-like astroglial processes as volume-equivalent cylindrical edges of the compartment. Far right, Formal cube representation of a glial compartment.

Volume of dendritic elements.

Three types of neuron contribute dendrites to a glomerulus: the large mitral cell, medium-size tufted cells, and small periglomerular cells. It is known that M and T cells have a primary dendrite which, at its terminus at the glomerular border, sends off multiple branches, which then ramify in a bifurcating manner. The simplifying approach taken here is to represent the origin of the tree in a canonical form, and adjust the branching tree to the three cell types (Fig. 2 b). Consensus observations suggest that the M cell dendritic tuft extends mostly across the glomerulus. For 25 mitral cells per glomerulus, our calculations give a total volume of ∼40,000 μm³, in other words, ∼15% of the glomerular volume.

For the T cell, we scale the radius of its dendritic tuft to three-fourths of the radius of an M cell dendritic tuft. Assuming 60 tufted cells per glomerulus, we derive a volume of 55,000 μm³, taking up ∼20% of the glomerular space.

For the PG cells, we scale the radius of the tuft to one-half the radius of a mitral cell dendritic tuft. We take into account that the two most distal branching levels are covered with dendritic spines (cf. Pinching and Powell, 1971; McQuiston and Katz, 2001), which add to dendritic volume and surface area. For 100 PG cells per glomerulus, we derive a total volume of ∼27,000 μm³, in other words, ∼10% of the glomerular volume. In comparison, the ORN axons account for ∼85,000 μm³, and the bulbar dendrites account for ∼125,000 μm³. Thus, the relative volumes are ∼2:3, and together they take up ∼80% of the glomerular space. This is similar to the impression given by the results of Kasowski et al. (1999) of the relative amounts of glomerular neuropil occupied by presynaptic and postsynaptic elements. These results for volumes suggest that the estimates of the lengths and diameters of the two types of element (axons and dendrites) are qualitatively consistent, and that together the elements could fit into a large (80-μm-diameter) glomerulus with some room to spare. They thus can be used for calculations of the surface areas to estimate the energy demands of signaling events. Before this could be done, the additional volumes of glia and vasculature needed to be included.

Vascular volumes.

The capillary network traversing the glomerulus was reconstructed based on two-photon imaging results from Chaigneau et al. (2003) and from electron-microscopic images from Kasowski et al. (1999). Both sources agree that on average seven capillaries are distributed over any given cross section of the entire glomerulus, enabling us to derive a formal branching pattern of intraglomerular capillaries (Fig. 2 c). This representation allows us to approximate the volume of the capillary bed in a glomerulus to 15,000 μm³, or ∼6% of the glomerular volume.

Astroglial volumes.

The volumes of glial elements were calculated based on imaging data that suggest a formal network of thin, sheet-like processes within the glomerulus whereas all the astrocyte cell bodies are located superficially (Chao et al. 1997). In a simplified model of the network, the glial processes demarcate cubic compartments with an edge length of ∼4 μm (Fig. 2 d). Given a glomerular volume of 270,000 μm³, we have ∼4000 compartments per glomerulus; the boundary of glial processes takes up ∼20,000 μm³, or ∼8% of the glomerular volume.

Sum of population volumes.

The total volume of the glomerular inventory that we estimated adds to ∼245,000 μm³, or ∼90% of the glomerular space, and is thus compatible with the overall volume constraint.

Calculations of population surface areas.

Given the morphologies of the participating elements, we can next calculate their specific surface membrane areas (see section 14 of supplemental material and supplemental Table S2, available at www.jneurosci.org as supplemental material). These surfaces contain the ion channels for action potential propagation and, combined with synaptic requirements, were the basis for the calculations of energy requirements related to signaling. With 25 mitral, 60 tufted, and 100 PG cell tufts per glomerulus, the total surface area of bulbar dendrites combine to 470,000 μm². In comparison, the 4500 ORN axons account for 920,000 μm². Thus, the relative surface areas of axonal versus dendritic elements are ∼2:1. Note that this is much larger than the 2:3 ratio for volumes because of the generally larger diameters of the dendritic branches, which give lower surface-to-volume ratios. This potentially tilts the balance of energy demands within the glomerulus toward the axons.

Calculations of dendritic synaptic densities.

From Kasowski et al. (1999), we estimate the densities of axodendritic and dendrodendritic synapses on M, T, and PG cells dendrites. Values range from 0.3 to 0.4 synapses/μm², depending on cell type. The ratio of axodendritic to dendrodendritic synapses is 5:1, reflecting the high convergence of ORN axons.

Concentration–response model.

For each neural element, we have so far quantified its surface area and its synaptic density, enabling us to calculate the energy demands associated with its activation. To predict total glomerular energy demands in response to different odor concentrations, we use a simple mathematical model of the activation of each cell population. A detailed description is provided in section 17 of supplemental materials (available at www.jneurosci.org).

The backbone of the model is the relationship between odor concentration, ORN responses, and target cells responses. It is based on three crucial assumptions.

First, the ORNs converging to the same glomerulus have different response thresholds. This has been documented in recent studies of ORNs in the mouse (Grosmaitre et al., 2006) and directly implies that ORN recruitment is a function of odor concentration.

Second, the number of M/T/PG cells responding to an odor stimulus is a function of odor concentration. This is inferred from the observation that total glomerular activation increases with odor concentration (Stewart et al., 1979; Meister and Bonhoeffer, 2001), and from unpublished results from our group indicating that a minimal number of (simultaneous) stimulated ORNs stimuli is needed to activate a given target cell (A. V. Masurkar, W. R. Chen, personal communication), hence implying that target cell recruitment is a step function of ORN recruitment.

Third, the firing frequency of recruited target cells increases with odor concentration. This has been documented in studies of M/T tuning to different odor concentrations (Imamura et al., 1992).

From assumptions 1–3, we confirm the mathematical description of target cell recruitment suggested previously (van Drongelen et al., 1978) and adapt it to the rat olfactory system.

Model of ORN response.

We assume that the mean firing frequency of olfactory receptor neurons expressing the same olfactory receptor is a direct measure of relative odor concentration and can be approximated with Michaelis–Menten kinetics (Meister et al., 2001) as follows:

Here, R is the mean firing rate, R _max is the maximal firing rate (saturation), C is the odor concentration, and K _i is the half-saturating concentration of that odor. The sigmoid concentration–response curve describes the overall transduction mechanism, including ligand binding to olfactory receptors and second messenger cascade. Because firing thresholds and excitability are varying between individual receptors (Grosmaitre et al., 2006), the mean firing rate is not sufficient to describe the range of responses. We have used a Poisson distribution of response frequencies (van Drongelen et al., 1978) such that higher odor concentrations correspond to both higher mean firing frequencies and a greater proportion of responding receptor cells. The proportion of receptor neurons that respond with at least one spike is as follows:

where T is the time interval of response.

Model of target cell response.

The target cells of ORN input are mitral, tufted, and PG cells. We assume that the response of a target cell depends on the number of active receptor cells that converge onto it, and on the number of axonal inputs that are necessary to elicit one action potential. We describe the proportion of target cells that respond with at least one spike after OR activation with the following:

where K is the convergence ratio of receptor cell axons onto a single cell, and m is the number of axonal inputs necessary to evoke an action potential. Based on quantitative data on synaptic connectivity, we use different axonal convergence ratio K for each cell type. The parameter m was introduced based on our experimental observation suggesting that the response of glomerular target cells to the stimulation of the ORN fascicle is a step function depending on the number of axons recruited. We use different values of m to reflect varying degrees of electrotonic compactness.

Model of GABAergic inhibition.

To model the effect of intraglomerular inhibition on the glomerular response to an odor stimulus directly succeeding another (e.g., in the case of two consequent sniffs), we made two simplifying assumptions.

First, the inhibitory response of the PG cell population to sensory input decreases the excitability of M/T cell dendrites, as well as the release probability of glutamate at ORN presynapses onto PG and M/T cells (Aroniadou-Anderjaska et al., 2000; McGann et al., 2005). Second, the strength of inhibition is proportional to the mean firing rate of the PG cells, such that a higher odor concentration results in a greater level of inhibition.

Both presynaptic and dendrodendritic inhibition can be taken into account by raising the parameter m in Equation 3. A higher value of m corresponds to a lower impact of a single axonal AP on the target cell.

Application of the model.

For the energy calculations, we are interested in the glomerular response to one sniff. The numbers and firing rates of receptor cells, principal neurons, and interneurons that are active per sniff can be derived from Equations 2 and 3 and be used to calculate energy demands for different odor concentrations. The time interval T we allow for ORN response per sniff is 60 ms (Duchamp-Viret et al., 2000), because simple odors can be distinguished in <200 ms (Uchida and Mainen, 2003; Abraham et al., 2004). The mean firing frequency of the ORNs ranges from r = 0 Hz to R _max = 150 Hz, for a relative odor concentration of zero to 1 (saturation). Under these conditions, the target cells respond with 0–10 spikes per stimulus, which is within the range of experimental results (Luo and Katz, 2001; Cang and Isaacson, 2003; McQuiston and Katz, 2001). To estimate the energy costs of dendrodendritic signaling, we assume that each mitral and tufted cell interacts with on average five PG cells (Murphy et al., 2005). We further assume a probability of 0.75 for transmitter release at dendrodendritic synapses, whereas the release probability at axodendritic synapses is initially 0.8 (Murphy et al., 2004) but is gradually reduced through presynaptic inhibition by PG cells by up to 50% (Murphy et al., 2005), a function of the number of PG cells that have been activated previously. Note that we need the values of release probability to estimate the energy costs at synaptic terminals.

Based on this model, total energy demands and the distribution of energy usage as a function of relative odor concentration are given in Results.

Results

The energy budget for a resting glomerulus

The in vivo glomerulus may never be totally inactive, but by assuming the ideal case of zero activity we can establish a minimal energy budget that sustains resting membrane potentials as well as vegetative needs.

Basal demands turn out to be dominated by the maintenance of resting membrane potentials. Given 4500 axonal branching trees, 20 astrocytes, and the dendritic tufts of 100 PG cells, 60 tufted cells, and 25 mitral cells, a resting glomerulus with a diameter of 80 μm has specific ATP demands of 0.27 μmol g⁻¹s⁻¹. Nonsignaling-related, or vegetative, cellular activities add 0.05–0.1 μmol ATP g⁻¹s⁻¹ to the basal energy consumption rate of the glomerulus.

In sum, total ATP demands of a resting glomerulus amount to ∼0.4 ATP g⁻¹s⁻¹, with corresponding oxygen demands of 75 μm s⁻¹. These resting demands are at the upper end of the range of measured consumption rates in resting neural tissues, such as 25–84 μm O₂ s⁻¹ in the cerebrum of anesthetized rats (Cohen et al., 2002; Shimoji et al., 2004).

The energy budget for an activated glomerulus

We are interested in the share that each neuronal compartments has in signaling costs, and in the effect that increasing activation has on the distribution of energy usage. Furthermore, we compare our calculations to physiological values of energy consumption, to put realistic constraints on the response of the glomerulus.

Based on Materials and Methods, we calculate the energy demands of the populations of elements within a glomerulus for a sequence of events, starting with activation of the ORN axons, as in the case of a shock delivered to an ON nerve bundle, or through an odor stimulus. The least activation would be an AP in a single axon, but because its impact cannot be distinguished from spontaneous firing, we consider a simultaneous AP in 1% of ORN axons as an arbitrary lower limit of activation. In contrast, maximal activation approximates the case of a volley in all of the ORN axons to a given glomerulus. This is unlikely to be achievable experimentally, because labeled axons in gene-targeted animals (Mombaerts, 1996) show that the bundles arrive from different directions. However, calculation of maximal activation (100% of ORN axons) compared with minimal activation (1% of ORN axons) will give us a range for intermediate physiological levels of input.

We first investigate the energy demands of the glomerulus in the ideal case of a single synchronous input volley from the ORN axons, comparable with electrophysiological stimulation of ORN nerve bundles in the rat olfactory bulb (Chen et al., 1997). For simplicity, we include a probability of 1.0 for vesicle release and postsynaptic receptor activation. In a second step, we use the concentration–response model described in Materials and Methods to estimate energy demands through odor stimulation during a single sniff, which is often considered the natural “unit of olfactory processing” (Kepecs et al., 2006; Scott, 2006). Energy demands for one sniff can then be scaled to different levels of activation, that is, odor concentrations, and to different sniffing rates per second. We also investigate the effect of different levels of inhibition on overall costs, and we consider variations in the probability of vesicle release and postsynaptic receptor activation.

Energy demands attributable to ON activation by electrophysiological stimulation

Upper limit of activation

We estimate energy demands of the glomerulus in the case of a single synchronous input volley from 100% of the axon population (see section 15 of supplemental material, available at www.jneurosci.org). An action potential in all ORNs axons converging onto the glomerulus requires a total of 1.1 × 10¹⁰ ATP for propagation and neurotransmitter release, whereas the activation of all postsynaptic receptor sites on mitral, tufted, and PG cell tufts creates energy demands requirements of 1.6 × 10¹⁰ ATP per action potential. This is ∼1.5 as much ATP as for the axonal elements. Thus, although the surface areas are weighted in favor of the axons, the numbers of synapses come to dominate the energy demands. This is mainly attributable to the fact that each afferent axon gives rise to on average 26 synapses (Klenoff et al., 1998). This divergence is a critical factor in determining the ratio between axonal energy demands and postsynaptic energy demands.

Although the afferent postsynaptic receptor demands are dominant, they still are a direct measure of the afferent axonal input, in contrast to the energy required for additional processing by the dendrodendritic circuits within the glomerulus. We next estimate these requirements.

We assume that all mitral, tufted, and PG cells are being activated and respond with one consequent bAP in each dendritic tuft (Chen et al., 1997). From Materials and Methods, we derive total dendritic energy demands of 5.6 × 10⁹ ATP per bAP. This is a third of postsynaptic receptor demands after an axonal input volley, attributable to the high density of axodendritic synapses, such that, per surface area, the energy demands of synaptic transmission exceed the costs of action potential propagation.

Depolarization of PG cell dendrites evokes retrograde GABA release onto ORNs terminals. We estimate energy demands in the GABAergic PG cell terminals of 4.5 × 10⁸ ATP per bAP. This is almost two orders less than the demands of the postsynaptic receptor response. Later, we will investigate the effect of inhibition on total costs.

The dendritic bAPs in M/T and PG cells activate dendrodendritic synapses. There are approximately one-sixth as many dendrodendritic synapses as axodendritic synapses in the glomerulus (Kasowski et al., 1999). An estimated 65% of these dendrodendritic synapses project from PG onto mitral/tufted cells and are considered GABAergic. The remaining one-third of dendrodendritic synapses are thought to be excitatory connections from mitral/tufted cells onto PG dendrites that cause EPSPs and consecutive Ca²⁺ spikes in PG cells.

We estimate total presynaptic energy demands for all dendrodendritic synapses, excitatory and inhibitory, of 2.6 × 10⁸ ATP per bAP. This is approximately one order less than the presynaptic energy demands of all axodendritic synapses, and one-half the demands of retrograde GABA release from PG cells onto ORNs terminals. We expect such differences because the costs are proportional to the number of synapses involved.

The postsynaptic receptor demands for all dendrodendritic synapses, and depolarizing effects in PG cells, amount to 2.2 × 10⁹ ATP per axonal input volley. This is ∼10 times the cost at the dendritic presynaptic terminals, but only one-tenth of the postsynaptic receptor demands at the axodendritic synapses.

Total costs for neurotransmitter recycling (2.2 × 10⁹ ATP) in axodendritic and dendrodendritic signaling are one order less than total postsynaptic receptor demands.

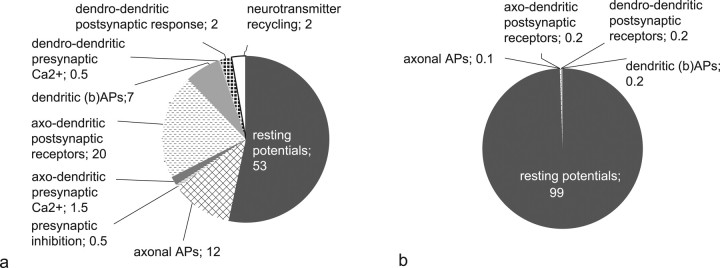
In sum, total signaling costs in response to activation of all of the 4500 axons entering a glomerulus amount to ∼4 × 10¹⁰ ATP. Approximately three-fourths can be attributed to the costs of axonal propagation and axodendritic synaptic transmission, and one-fourth to dendritic potentials and dendrodendritic synaptic transmission.

Thus, signaling costs in the olfactory glomerulus appear to be dominated by afferent input and the associated postsynaptic receptor response, as reflected in the relative distribution of energy usage (Fig. 3 a, without vegetative costs). Despite the active properties of dendrites, and extensive dendrodendritic signaling, the energy required for further processing by the dendrodendritic circuits amounts to only one-third of the demands of presynaptic axonal input and postsynaptic receptor response.

Figure 3.

Energy demands of the activated glomerulus after electrophysiological stimulation of the olfactory nerve bundle. a, Distribution of ATP usage in the glomerulus for an activation of 1% of the ORN axons. b, Distribution of ATP usage in the glomerulus for an activation of 100% of the ORN axons.

With one input volley per second, signaling costs account for <50% of total signaling-related energy demands per second, 53% being attributable to resting potential requirements. The sum of signaling-related and vegetative demands correspond to an ATP consumption rate of 0.6 μmol of ATP g⁻¹s⁻¹. This is within the range of 0.3–1.2 μmol of ATP g⁻¹s⁻¹ that has been documented for neural tissues (cf. Sokoloff, 1977) and approximates a glucose consumption rate of 16 μm per second, and oxygen demands of 100 μm per second.

Lower limit of ON activation

We estimate energy demands of the glomerulus in the case of a single synchronous input volley from 1% of the axon population (see section 16 of supplemental material, available at www.jneurosci.org). In addition to the steps taken above, we needed to make assumptions about the connectivity to derive the energy demands of the response. The assumptions are presented in detail in the supplemental material (available at www.jneurosci.org). In sum, we assume the initial response to 1% axonal input consists in the activation of one mitral, one tufted, and one PG cell. We further assume that five PG cells are fully activated through dendrodendritic input from the mitral and tufted cell.

For a lower limit of activation, we derive signaling costs of 4.7 × 10⁸ ATP per input volley, which is little more than 1% of the resting energy demands per second of the glomerulus. The relative distribution of energy usage illustrates the dominant role of the resting potential demands for this level of activation (Fig. 3 b, without vegetative costs).

Energy demands attributable to ON activation by odor stimulation

With the simple concentration–response model described in Materials and Methods, we calculate the energy demands per sniff for varying levels of receptor activation (corresponding to relative odor concentration), as composed of presynaptic and postsynaptic costs in axonal and dendritic elements, and of costs derived from neurotransmitter recycling. Together with the requirements of the resting state (without vegetative costs), we derive energy demands per second.

We explore the range of four orders of relative odor concentration (i.e., from 10⁻⁴ to 1, or from 0.01 to 100%), which is close to the natural span a single glomerulus responds to (Meister and Bonhoeffer, 2001).

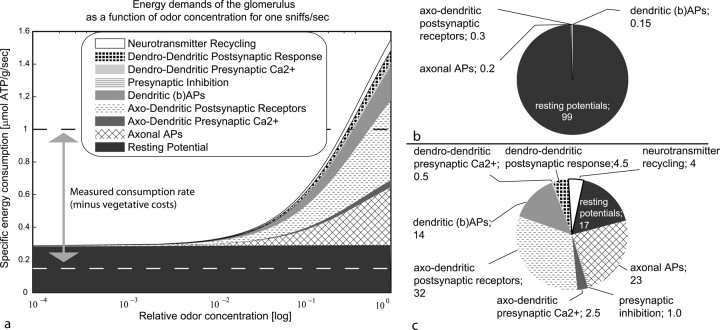
Our model allows six main observations. First, the demands for the maintenance of the resting potential dominate at low odor concentrations (Fig. 4 a). This is consistent with the estimates for the lower limit of electrophysiological stimulation (compare Fig. 3 b).

Figure 4.

Odor stimulation of the glomerulus with one sniff per second. a, Absolute energy demands for each neuronal compartments as a function of odor concentration derived from the concentration–response model. Results are shown for the case that the costs, but not the effects of intraglomerular inhibition, are taken into account. b, Relative distribution of ATP usage in a for an activation of 1% of the ORNs. c, Relative distribution of ATP usage in a for an activation of 100% of the ORNs.

Second, without inhibitory action, signaling costs increase steeply with odor concentration, to the extreme that energy demands are higher than the consumption rates usually measured in neuronal tissues (Fig. 4 b).

Third, the main factor that dominates the increase in energy demands is the postsynaptic receptor response (i.e., glutamate-mediated ion influx, of the bulbar dendrites) (Fig. 4 c). This is in line with our estimates for the upper limit of electrophysiological stimulation and in agreement with Attwell and Laughlin (2001), who found that the postsynaptic receptor response plays a major role in cortical signaling costs. At a rate of one sniff per second, the postsynaptic receptor response contributes little more than 0.3% to total costs when odor concentrations is low but causes nearly one-third of total demands in the fully activated state.

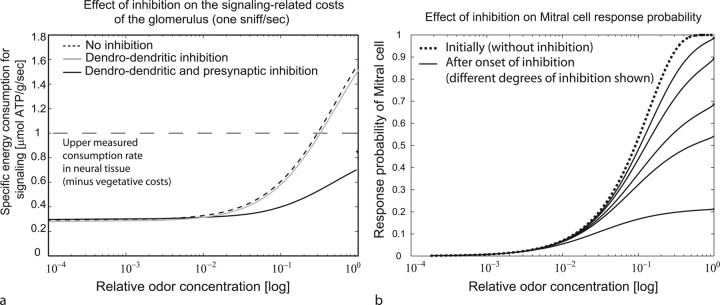
Fourth, because the postsynaptic receptor response to ORN input plays a major role in energy consumption, dendrodendritic inhibition, which reduces dendritic processing, has limited impact on the development of overall costs, whereas presynaptic inhibition of ORN terminals has the potential to cut energy demands significantly (Fig. 5 a).

Figure 5.

The effect of intraglomerular inhibition on energy demands. a, Probability of mitral cell response during initial sniff when the effects of intraglomerular inhibition have not yet set in (dotted line) and during subsequent sniff for various degrees of intraglomerular inhibition (solid lines); the stronger the inhibition, the more gentle the slope. b, Effect of presynaptic versus dendrodendritic inhibition on the signaling cost.

Fifth, in our model both dendrodendritic and presynaptic inhibition increases nonlinearly with rising axonal input. Our results suggest that this strategy allows a high sensitivity for low odor concentration, when inhibition has not yet a strong effect, whereas for higher concentrations the inhibitory action prevents overexcitability of the glomerulus (Fig. 5 b).

Sixth, considering the delayed action of the metabotropic receptors involved in presynaptic inhibition, our results suggest an initially high excitability (and corresponding extremely high-energy demands) of the glomerulus, especially for high sniffing rates, when the odor is encountered first and inhibition has not yet set in fully. Depending on the strength of the inhibitory action, the excitability during subsequent sniffs can then be scaled to lower levels (Fig. 5 b).

Different distributions of energy demands in the resting and active states

Based on the analysis presented thus far, we finally show that the distribution of energy demands in the glomerulus is characteristic for its state of activity, ranging from the resting state to full activation. The energy demands of the resting glomerulus are composed of vegetative and signaling-related ATP expenses. These two add up to 0.37 μmol of ATP g⁻¹s⁻¹, which is 1.5 times the value for cortical tissue (Attwell and Laughlin, 2001), although we assume relatively low vegetative costs because the cell somata are located outside the glomerulus. This difference is attributable to the high density of neural elements in the glomerulus. From the population numbers derived in Materials and Methods, the glomerular volume holds 1.5 × 10¹⁰ neural elements per cm³, namely axons, dendritic tufts, and glial processes. This value is almost 100 times greater than the average cell density in the neocortex (Braitenberg and Schuez, 1998). The estimated resting demands of glial elements in the glomerulus, however, amount to <4% of total basal energy demands, which is lower than the value calculated for cortical tissues (Attwell and Laughlin, 2001). This difference is attributable to the assumed high degree of electrical coupling among glomerular astrocytes.

In summary, although the glomerulus consists of a high density of both neural and glial elements, the neural elements dominate the energy demands of the resting state, which are relatively high compared with other neural tissues.

The energy demands of the activated glomerulus build on the resting state, adding the costs arising from action potentials in the afferent ORN axons, synaptic transmission, and from the postsynaptic membrane response in bulbar dendrites. The impact of each factor depends on the level of receptor nerve stimulation and intraglomerular inhibition. To analyze the impact of these factors, we focused on two levels at which reasonably accurate estimates of the active elements could be made. To investigate very low levels of activation, presumably near threshold, we assumed 1% axonal activation. This imposes relatively limited energy demands; resting potential demands still comprise ∼99% of overall ATP consumption (Figs. 3 b, 4 b). The implication of this result is that sensitivity to low levels of odor in the ambient air can be achieved at low additional cost.

For comparison, we examined maximal axonal activation in two ways. In a first approach, we considered the effect of a single input volley through brief electrophysiological stimulation of all olfactory axons to a glomerulus. In this case, resting potential demands still accounted for ∼55%, whereas the rise in total costs was mainly attributable to axonal APs (12%) and postsynaptic receptor responses (∼22%). Instead of taking population response probabilities as a basis of calculations, precise numbers of activated cells were derived from the limited data available on axonal convergence rates and dendrodendritic connectivity. This approach did not provide for scaling the postsynaptic response to intermediate levels of activation because this would require an exact circuit diagram of the intraglomerular network. When future experiments clarify the network architecture, we will be able to refine our calculations.

In a second approach, we modeled the rise of glomerular activation during a sniff by assuming nonlinear response probabilities of presynaptic and postsynaptic cell populations. This allowed multiple responses and the recruitment of responding cells with rising levels of odor concentration. In this case, maximal activation drives up the demands of axonal APs to 23%, and of postsynaptic receptor responses to 32% of total costs, such that they both exceed resting potential demands (17%) (Figs. 3 a, 4 a.c).

In both cases of strong activation, we find that dendritic potentials and dendrodendritic synaptic transmission accounted for a minor part (9 and 19%, respectively) of the costs of full activation, despite the fact that dendritic elements take up at least one-half the volume in the glomerulus. From our calculation, it has become clear that two main factors shift the balance of energy consumption toward ORN axonal propagation and axodendritic synaptic transmission: axonal convergence and axodendritic synaptic density, respectively. The first factor translates into the 2:1 ratio of axonal to dendritic membrane surface areas, and the second into the 5:1 ratio of axodendritic to dendrodendritic synapses. Thus, the distribution of energy demands reflects the convergence of axonal input onto a single glomerulus.

We further observe that, even for a single sniff, axonal and postsynaptic demands risk exceeding physiological sustainable levels. Balanced against this are several properties: First is the well known adaptation that occurs in olfactory receptor cells in response to prolonged or rapidly repeated odor stimulation. This effect would also be found at the sniffing rate of up to 8 Hz in the rat (Youngentob et al., 1987; Kepecs et al., 2006). In addition, there is evidence that a mechanism of input control operates within the glomerulus (Aroniadou-Anderjaska et al., 2000). We therefore incorporated a form of delayed, presynaptic inhibition of axonal input that allows maintaining a high sensitivity at low receptor excitation, while suppressing overexcitation at higher levels of excitation, such that the range of tolerable input strengths is enlarged (Fig. 5 b).

The implications of this distribution of energy usage will be dealt with in Discussion.

Discussion

In the present work, we exploited the specific properties of a single rat olfactory glomerulus to determine the relative and absolute contributions of its functional compartments to energy demands. In contrast to previous analyses of the energy budget of the neocortex in rodents (Ames, 2000; Attwell and Laughlin, 2001; Laughlin and Sejnowski, 2003; Lennie, 2003), we had the advantage of focusing on a well defined system in which the sequence of neuronal signaling is known in detail, thus putting realistic constraints on connectivity and activation parameters. Importantly, estimation of membrane surface areas that are the sites of energy-demanding ions flows was facilitated by the spherical structure of the glomerulus, imposing boundaries on cell volumes and numbers. Our thorough review of experimental data specific to the olfactory glomerulus warrants, we propose, the extrapolation of our results to the whole ensemble of glomeruli in the olfactory bulb, affecting in particular the interpretation of functional imaging data from the odor-activated glomerular layer.

Supply of energetic substrates to the olfactory glomerulus

Our results show that maintenance and activation of the olfactory glomerulus are comparatively energy-intensive states. How do the anatomy and physiology of the glomerular layer account for sufficient supply of metabolites, particularly after the sudden, localized rise in energy demands in odor-activated glomeruli? Adaptations at several levels of bulbar organization become apparent from experimental results. First, the density of capillaries within glomeruli is higher than in the ORN layer and other regions of the olfactory bulb (Chaigneau et al., 2003), suggesting an elevated capacity for blood supply. Moreover, the blood flow within this capillary network is modulated in an odor- and glomerulus-specific manner on olfactory receptor stimulation (Chaigneau et al., 2003), indicating a fine control of local vascular response that matches the blood flow to differing glomerular energy demands. Furthermore, the lattice-like distribution of glial processes within the glomerulus provides an infrastructure that connects neuronal and vascular elements. This suggests that glomerular astrocytes mediate functional neurovascular coupling, as has been shown for astrocytic processes in culture and in vivo (for review, see Magistretti and Pellerin, 1999; Girouard and Iadecola, 2006; Jakovcevic and Harder, 2007). The glomerular glial processes seem conveniently placed to monitor neuronal activity (cf. De Saint Jan and Westbrook, 2005), adapt the local blood flow in response, and deliver bloodborne metabolic substrates, or their derivatives, to recipient neuronal cells.

Gain control in the activated olfactory glomerulus

Our analysis of the distribution of energy demands in the activated olfactory glomerulus shows that total costs of axonal propagation and axodendritic synaptic transmission increase significantly with rising olfactory receptor stimulation and are capable of tripling the basal glomerular consumption rate. However, it has been observed that blood flow, which supplies oxygen and glucose, increases a moderate 10–30% nearby odor-activated glomeruli (Chaigneau et al., 2003). This large discrepancy between calculated and observed increases suggests the existence of gain control mechanisms that either prevent excessive energy demands and limit the vascular response or, conversely, match the glomerular demands to vascular capacities. Given the dominance of afferent input in generating energy costs, the glomerular circuitry provides an effective means of curbing metabolic demands, namely restricting ORN axonal input. Experimental studies show that presynaptic inhibition through GABA_B release from PG cells back onto axodendritic synapses reduces afferent ORN input by limiting the increase in calcium concentration in ORN terminals during odor stimulation (Vucinic et al., 2006) and suppressing neurotransmission from ORN to M/T cells and PG cells (Aroniadou-Anderjaska et al., 2000). Our concentration–response model suggests that this mechanism is indeed capable of significantly reducing glomerular response and overall glomerular costs. This is comparable with gain control in the retina, where the presynaptic regulation of transmitter release from photoreceptor output synapses prevents saturation and shifts the operating curve to match the range of input signals (Laughlin, 1994).

In addition to presynaptic inhibition, axonal input can be restricted directly at its source by downregulating the response of the olfactory receptor neuron to strong odorant stimuli using economical second messenger systems such as intracellular Ca²⁺ and local NO release (Breer and Shepherd, 1993).

In sum, restriction of axonal input effectively reduces glomerular activation and can be implemented at several sites. According to our calculations of the distribution of energy demands and to our concentration–response model, the restriction of postsynaptic potentials, for example, through dendrodendritic inhibition, will be less effective in reducing overall energy demands.

From a coding standpoint, it is difficult to assess the optimal degree of gain control in early olfactory processing because little is known about information coding across the glomerular neuron population (Laurent, 1999). As information is distributed to brain areas for higher-order processing, the code may become sparser (Laurent, 2002) and be represented by the 1% of active neurons, as proposed for energy-efficient coding in neocortex (Levy and Baxter, 1996; Attwell and Laughlin, 2001; Lennie, 2003).

Energy demands and odor maps in the olfactory bulb

How are the findings of our energy budget relevant to the interpretation of activity maps of the olfactory bulb, obtained by 2-DG, fMRI, or intrinsic imaging? Only a minor share of energy demands is attributable to dendrodendritic synaptic transmission and dendritic potentials, suggesting that glomerular activity maps mainly reflect energy demands that are related to afferent input, particularly axonal action potentials and postsynaptic receptor responses. However, although processes with high energetic costs are likely to be the main recipients of metabolic substrates, it is conceivable that the activities underlying activity maps, such as blood flow or glucose metabolism, are regulated by processes that contribute only a minor share to overall costs. Indeed, recent experimental studies have directly linked functional imaging signals to neurotransmitter release, a process that has comparatively low energetic demands (Attwell and Laughlin, 2001), as also demonstrated by our calculations. In particular, changes in cerebral blood flow are unaffected by changes in principal cell spiking frequency but are sensitive to afferent excitatory synaptic activity (Thomsen et al., 2004). Consistent with this interpretation, intrinsic optical signals are positively correlated with glutamate release and uptake through astrocytes (Gurden et al., 2006). The blood oxygen level-dependent (BOLD) signal used in fMRI as well as the glucose metabolism rate observed with 2-DG have also been associated with glutamate signaling (Attwell and Iadecola, 2002; Logothetis and Wandell, 2004; Magistretti, 2006). All these findings suggest that activity patterns in the olfactory glomerular layer reflect vascular responses to synaptic glutamate release, possibly mediated through astrocytes. Because of the superior number of afferent excitatory synapses compared with dendrodendritic excitatory synapses, we further conclude that the activity patterns mostly represent glutamergic input from olfactory receptor neurons to the glomerulus. Interestingly, our calculations indicate that, in this case, the functional signal is coupled to the process that directly precedes the most energy demanding activity, namely the postsynaptic receptor response (plus any subsequent postsynaptic activities), as if to prepare the system for upcoming high metabolic substrate demands.

These considerations support the initial interpretation of the 2-DG signals (Sharp et al., 1975, 1977) that the glomerular foci mainly reflect the differential activation of olfactory receptor cells rather than postsynaptic processing. Experiments with dye loading of olfactory receptor cells confirmed this interpretation (Wachowiak and Cohen, 2001). The same argument applies to the unlikely contribution of centrifugal fiber input to the initial glomerular patterns. However, it is known that olfactory bulb responsiveness to food odors is higher in hungry animals (Pager et al., 1972), as is the corresponding signal seen in fMRI studies of the bulb (F. Q. Xu, unpublished data). Current studies are aimed at determining the extent to which this attentional effect represents the actions of centrifugal fibers or the levels of sensory input in the different states.

Our results also have relevance to the analysis of the signals in 2-DG and fMRI studies of the olfactory bulb compared with other brain regions. The signal after odor stimulation appears to be stronger than seen with natural activity in other parts of the brain (Yang et al., 1998). Our quantitative analysis is consistent with the interpretation that this reflects the high degree of convergence of the unimodal input to a given glomerulus.

Outlook

The present work demonstrates the importance of a quantitative analysis of complete neural circuits for the understanding of network architecture and the interpretation of activity-related signals. Such a theoretical approach can bridge the gap between observations on the level of a single cell that are common in experimental neuroscience, and the global view on neuronal tissue activity through functional imaging techniques. Based on a thorough analysis of local processes, predictions of the behavior of a whole neural system can be put forward and serve as inspiration and guidance for experimental work. For example, our investigation of the functional compartments in a single olfactory glomerulus suggests that bulbar odor activity patterns derived from BOLD, 2-DG, or intrinsic optical signals mainly visualize afferent input from epithelial olfactory receptor neurons. Based on our findings, we predict that if future experimental work succeeds in monitoring the output activity of the principal glomerular cells, qualitative differences to the input-dominated odor maps should reflect the intermediate processing activity of the glomerulus.