Mitochondrial and Plasma Membrane Potential of Cultured Cerebellar Neurons during Glutamate-Induced Necrosis, Apoptosis, and Tolerance

Abstract

A failure of mitochondrial bioenergetics has been shown to be closely associated with the onset of apoptotic and necrotic neuronal injury. Here, we developed an automated computational model that interprets the single-cell fluorescence for tetramethylrhodamine methyl ester (TMRM) as a consequence of changes in either ΔΨ_m or ΔΨ_p, thus allowing for the characterization of responses for populations of single cells and subsequent statistical analysis. Necrotic injury triggered by prolonged glutamate excitation resulted in a rapid monophasic or biphasic loss of ΔΨ_m that was closely associated with a loss of ΔΨ_p and a rapid decrease in neuronal NADPH and ATP levels. Delayed apoptotic injury, induced by transient glutamate excitation, resulted in a small, reversible decrease in TMRM fluorescence, followed by a sustained hyperpolarization of ΔΨ_m as confirmed using the ΔΨ_p-sensitive anionic probe DiBAC₂(3). This hyperpolarization of ΔΨ_m was closely associated with a significant increase in neuronal glucose uptake, NADPH availability, and ATP levels. Statistical analysis of the changes in ΔΨ_m or ΔΨ_p at a single-cell level revealed two major correlations; those neurons displaying a more pronounced depolarization of ΔΨ_p during the initial phase of glutamate excitation entered apoptosis more rapidly, and neurons that displayed a more pronounced hyperpolarization of ΔΨ_m after glutamate excitation survived longer. Indeed, those neurons that were tolerant to transient glutamate excitation (18%) showed the most significant increases in ΔΨ_m. Our results indicate that a hyperpolarization of ΔΨ_m is associated with increased glucose uptake, NADPH availability, and survival responses during excitotoxic injury.

Introduction

Glutamate excitotoxicity is an important contributor to neuronal loss associated with ischemic, traumatic, and seizure-induced brain injury (Choi, 1994). Prolonged glutamate receptor overactivation results in a rapid necrotic neuronal injury that is known to be highly dependent on excessive Ca²⁺ uptake leading to a loss of mitochondrial bioenergetics, ionic homeostasis, and cellular integrity (Choi, 1987; Tymianski et al., 1993a; Budd and Nicholls, 1996b; White and Reynolds, 1996; Stout et al., 1998; Vergun et al., 1999; Ward et al., 2000). Transient glutamate receptor activation, in contrast, can trigger a delayed apoptotic neuronal injury characterized by nuclear condensation, cell shrinkage, and a delayed collapse of mitochondrial bioenergetics and Ca²⁺ homeostasis hours after the initial excitation (Ankarcrona et al., 1995; Budd et al., 2000; Luetjens et al., 2000; Ward et al., 2000, 2006). The sequestration of Ca²⁺ within the mitochondrial matrix has been reported to play an integral role in excitotoxic injury (Budd and Nicholls, 1996b; Wang and Thayer, 1996; White and Reynolds, 1997; Stout et al., 1998; Brocard et al., 2001; Ward et al., 2005), resulting in an early impairment of mitochondrial ADP phosphorylation (Kushnareva et al., 2005).

The mitochondrial membrane potential (ΔΨ_m) is the central parameter controlling the accumulation of Ca²⁺ within the mitochondrial matrix, respiration, and ATP synthesis (Nicholls and Ferguson, 1992; Nicholls and Budd, 2000; Nicholls, 2002). The fluorescent membrane-permeant cationic probe tetramethylrhodamine methyl ester (TMRM) has become one of the most frequently used probes in the analysis of ΔΨ_m in intact cells because of its minimal phototoxicity, low photobleaching, and the ability to use it in both a quenched (aggregated probe) and nonquenched (no aggregation of probe) mode (Ehrenberg et al., 1988; Nicholls and Ward, 2000; Buckman et al., 2001; Gerencser and Adam-Vizi, 2005). Previously, we have successfully used TMRM in the quenched mode to monitor mitochondrial function during glutamate-induced injury in cerebellar granule neurons (Ward et al., 2000) identifying a sensitivity of TMRM to changes in ΔΨ_m and the plasma membrane potential (ΔΨ_p). Indeed, the relative contribution of key changes in ΔΨ_m and ΔΨ_p after glutamate excitation have previously been difficult to define (Ankarcrona et al., 1995; Khodorov et al., 1996; White and Reynolds, 1996; Kiedrowski, 1998; Prehn, 1998; Stout et al., 1998; Keelan et al., 1999; Nicholls and Ward, 2000). In this study, we set out to investigate the complex changes that occur at the ΔΨ_m and ΔΨ_p level in relation to changes in neuronal metabolism and define how alterations in these parameters correlate with neuronal injury and survival after glutamate excitation. We have expanded on a computational model for interpreting whole-cell TMRM fluorescence (Ward et al., 2000; Nicholls, 2006) allowing for the rapid, automated, and impartial assessment of changes in ΔΨ_m and ΔΨ_p at a single-cell level and subsequent statistical analysis. From this, we have identified significant alterations in ΔΨ_m and ΔΨ_p that are paralleled with key modifications to neuronal metabolism that directly relate to neuronal outcome (necrosis, apoptosis, and tolerance) after glutamate excitation.

Materials and Methods

Materials.

Fetal calf serum and minimal essential medium were from Invitrogen (Paisley, Strathclyde, UK). Glutamate, glycine, and all other reagents were from Sigma (Poole, Dorset, UK). Fluo-4 AM, DiBAC₂(3), and TMRM were purchased from Invitrogen (Bio Sciences, Dun Laoghaire, Ireland).

Preparation of primary cerebellar granule neurons.

Cerebellar granule neurons were prepared as described previously (Ward et al., 2000) with minor modifications. Cerebella from 7-d-old Wistar rats of both sexes were dissected and pooled. The tissue was placed in 20 ml of filter sterilized PBS supplemented with 0.25 mg/ml trypsin and incubated at 37°C for 20 min. Trypsinization was terminated by the addition of an equal volume of filter-sterilized PBS supplemented with 0.05 mg/ml soybean trypsin inhibitor, 3 mm MgSO₄, and 30 U/ml DNase I. The neurons were then triturated, and the resulting neurons were resuspended in supplemented culture medium. Cells were then plated on poly-l-lysine-coated glass coverslips, glass Willco (Amsterdam, The Netherlands) dishes, 6-well plates, and 24-well plates at 1 × 10⁶ cells per milliliter and maintained at 37°C in a humidified atmosphere of 5% CO₂/95% air.

Confocal microscopy.

Cerebellar granule neurons on Willco dishes were loaded with TMRM (30 nm) only or coloaded with Fluo-4 AM (3 μm) for 30 min at 37°C (in the dark) in experimental buffer [containing (in mm) 120 NaCl, 3.5 KCl, 0.4 KH₂PO₄, 20 2-[(2-hydroxy-1,1-bis(hydroxymethyl)ethyl)amino]ethanesulfonic acid N-[Tris(hydroxymethyl)methyl]-2-aminoethanosulfonic acid (Tes), 5 NaHCO₃, 1.2 Na₂SO₄, 1.2 CaCl₂, 1.2 MgCl₂, and 15 glucose, pH 7.4]. The Willco dishes with cells were washed in fresh medium after loading before being mounted in a nonperfusion (37°C) holder and placed on the stage of an LSM 510 Meta Zeiss (Oberkochen, Germany) confocal microscope. No MgCl₂ was present in buffers for experiments that involved the addition of glutamate. For glutamate-induced apoptosis, neurons were exposed to glutamate and glycine (100 and 10 μm) for 5 min, and (+)-5-methyl-10,11-dihydro-5H-dibenzo[a,d]cyclohepten-5,10-imine maleate (MK-801; 10 μm; Sigma) and 2,3-dioxo-6-nitro-1,2,3,4-tetrahydrobenzoquinoxaline-7-sulfonoamide (NBQX; 10 μm; Sigma) were added to block glutamate receptor activation. In the model of glutamate-induced necrosis, MK-801 and NBQX were not added. Fluo-4 AM was excited at 488 nm with an argon laser (1%), and the emission was collected through a 505–550 nm barrier filter; TMRM was excited at 543 nm with a helium neon laser (3%), and the emission was collected through a 560 nm long-pass filter. Images were collected at 15 s intervals during glutamate excitation and every 5 min during the rest of the experiment, and the resulting fluorescent images were processed using MetaMorph Software version 7.1, release 3 (Molecular Devices, Berkshire, UK).

DiBAC₂(3) is a fluorescent probe that has been successfully used to characterize changes in ΔΨ_p (Freedman and Novak, 1989). Here, cerebellar granule neurons were incubated with an experimental buffer containing 1 μm DiBAC₂(3) for 30 min at 37°C. A concentration of 1 μm DiBAC₂(3) was also present in the experimental buffer. DiBAC₂(3) is a bis-barbituric acid oxonol compound that partitions into the membrane as a function of membrane potential. Hyperpolarization causes extrusion of the dye and decreased fluorescence, whereas depolarization causes enhanced fluorescence. Fluorescence was monitored with an LSM 510 (Zeiss) confocal microscope. The probe was excited at 488 nm with an argon laser (1%), and the emission was collected through a 530–600 nm barrier filter. Images were collected at 15 s intervals during additions [glutamate, oligomycin, carbonyl cyanide p-(trifluoromethoxy) phenylhydrazone (FCCP)] and every 2 min throughout the rest of the experiment. The resulting fluorescent images were processed using MetaMorph software.

Computational modeling.

We have used MATLAB software (version 7.0; Mathworks, Cambridge, UK) for the creation of an automated computational model for the analysis of single-cell fluorescence responses for monovalent cationic probes [TMRM, tetramethylrhodamine ethyl ester (TMRE), rhodamine-123] in populations of cells providing rapid predictive output on changes in ΔΨ_p and ΔΨ_m for large data sets. Previous models have been restricted by the manual fitting of parameters, limited flexibility within the parameters, and low throughput of data sets. This model provides automated output for large data sets with minimal parameter fitting.

This model, as in previous models (Ward et al., 2000; Nicholls, 2006), was based on the Nernstian equilibration of a generic membrane-permeant monovalent cation c⁺ (TMRM, TMRE, rhodamine-123). The equilibration concentration for free c⁺ in the extracellular medium, cytosol, and mitochondrial matrix at 37°C results in the relationships described below:

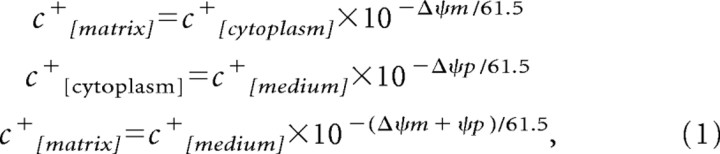where ΔΨ_p and ΔΨ_m are the plasma and mitochondrial membrane potentials and the divisor 61.5 is the value (in millivolts) for RT/F log(2) at 37°C. Re-equilibration of the cytosolic and extracellular compartment attributable to changes in the potentials of ΔΨ_p and ΔΨ_m are taken into account by assuming a first-order flux between the extracellular medium and the cytosol:

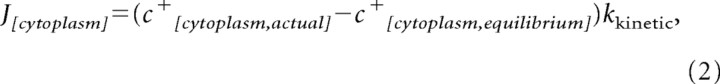where k_kinetic is a constant proportional to the permeability of the c⁺ probe across the plasma membrane. The equilibration effects between the mitochondria and the cytosol are assumed as immediate. From this, we obtain the whole-cell fluorescence f_[cell] as the sum of the cytosolic and mitochondrial matrix signals by taking into consideration the distinct behavior attributable to quenching of the fluorescence signal within the mitochondria with the quench threshold concentration c⁺_[quench]:

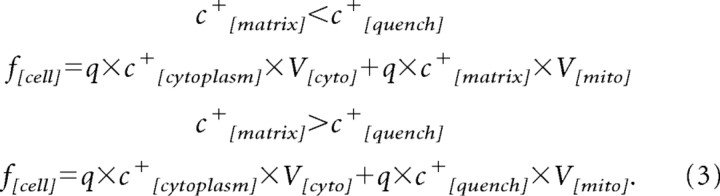Here, q is the quantum yield of the probe with V_[cyto] and V_[mito] denoting the cytosolic and mitochondrial volume.

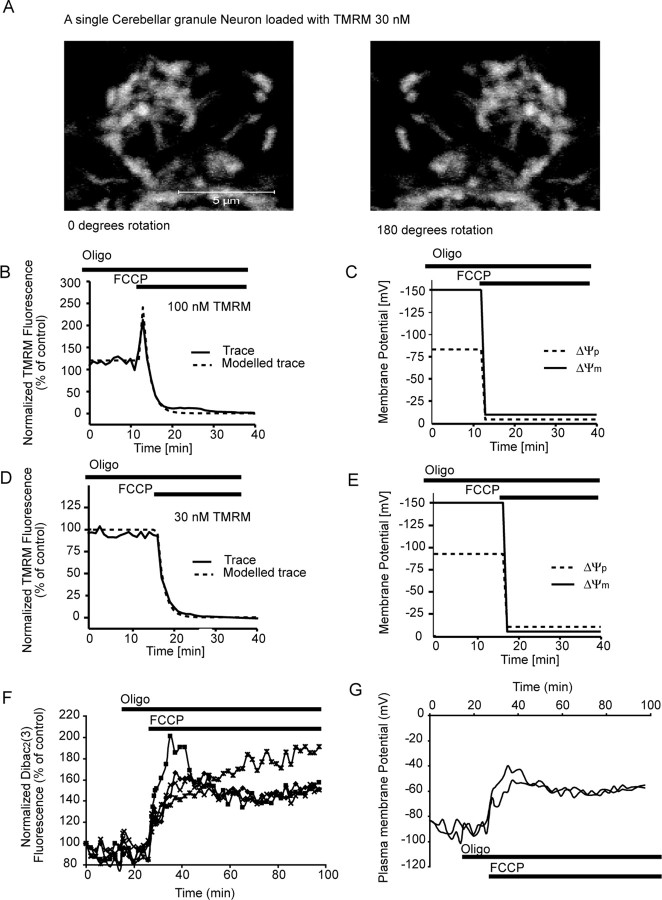
To provide a more accurate model, we re-evaluated the mitochondrial volume (V_[mito]) within the neurons as well as the rate constant k_kinetic for TMRM (see Fig. 2) and implemented the model into MATLAB. A Newton routine for fitting the membrane potentials to the experimental fluorescent traces was implemented to avoid the need and bias of manual parameter fitting. The mitochondrial volume within the neurons (6.2 ± 0.8% SEM) was determined by using the Zeiss LSM 510 confocal microscope to create high-resolution z-stacks (80 × 0.2 μm steps, 0.8 μm optical slice) of TMRM-loaded neurons (see Fig. 2A). The rate constant k_kinetic was determined as 0.008 s⁻¹ by remodeling the redistribution of TMRM after the induction of mitochondrial depolarization by the protonophore FCCP in the presence of oligomycin in both the quenched and unquenched mode (see Fig. 2B,D). Because of variation in both the kinetic constant and the mitochondrial volume between neurons, we included them into the set of parameters for the subsequent fitting routine with an allowed variation of 0.008 ± 0.001 s⁻¹ and 6.2 ± 1.7%, respectively.

Figure 2.

Characterization of TMRM fluorescence in cerebellar granule neurons with high-resolution single-cell confocal microscopy. A, Cerebellar granule neurons were loaded with 30 nm TMRM, and the mitochondrial volume (17.6 ± 1.5 μm³; 6.2 ± 0.8%; n = 9) was determined by measuring the volume of individual mitochondria within the neurons after the acquisition of high-resolution z-stacks with an LSM 510 confocal microscope. B, D, Neurons loaded with 100 nm TMRM (B) and 30 nm TMRM (D) were exposed to FCCP (2 μm) in the presence of oligomycin (2 μg/ml) and monitored over a 60 min period. C, E, Using MATLAB software, the traces in B and D were modeled, and the changes in both ΔΨ_m and ΔΨ_p were established for these control experiments (all experiments were performed 3 times in different cultures). F, Cerebellar granule neurons were loaded with the ΔΨ_p-sensitive probe DiBAC₂(3) (1 μm) and exposed to oligomycin (2 μg/ml), followed by FCCP (2 μm). A rapid increase in fluorescence (depolarization of ΔΨ_p) was associated with the addition of FCCP (traces are representative of those obtained from 3 separate experiments). G, Representative traces for modeled changes in ΔΨ_p (A) for neurons exposed to oligomycin (2 μg/ml) and FCCP (2 μm). Oligo, Oligomycin.

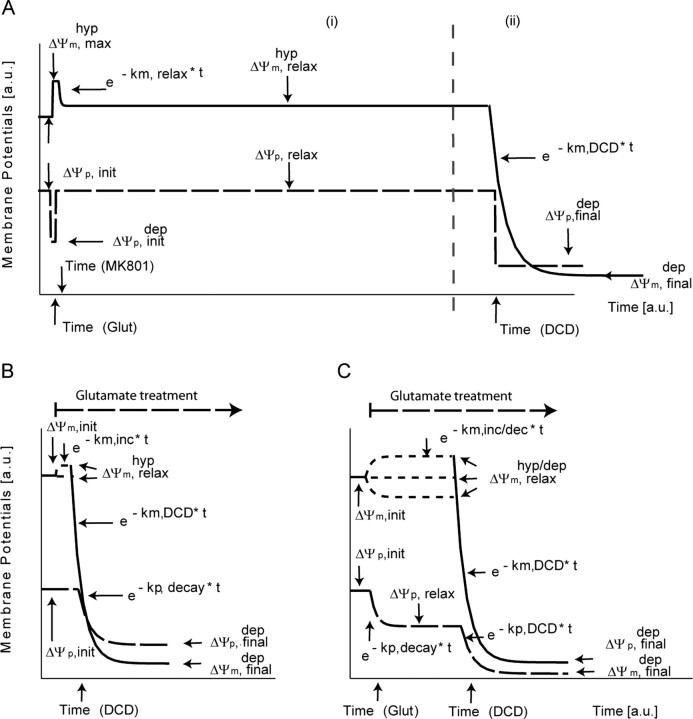
Parameter fitting was implemented using the built-in Newton-based root-finding algorithm FITCURVE of MATLAB, allowing for up to 50,000 iterations. To pose biological restrictions on the fits, we assumed a functional behavior for the time course of (ΔΨ_p) and (ΔΨ_m) as given in Figure 1 with parameters subject to fitting within a given range (supplemental Table 1, available at www.jneurosci.org as supplemental material) (Ward et al., 2000; Dussmann et al., 2003; Nicholls, 2006). For the apoptotic model (Fig. 1A), we assumed an initial depolarization (ΔΨ_p,initial) of the plasma membrane being present between the onset of glutamate and the addition of MK-801, returning to a higher value (ΔΨ_p,relax) [−83 mV (Nicholls, 2006)] rapidly after the addition of the antagonist. Moreover, to render the change of experimental fluorescence, we allowed ΔΨ_m to vary to a distinct value (ΔΨ^Hyp_m,max) at the time of glutamate addition and then to exponentially relax (constant k_relax) to a certain rate (ΔΨ^Hyp_{m, relax}). During the collapse of ΔΨ_m and the onset of apoptosis, we assumed a variant (ii) of our model allowing for exponential decay of both potentials (k_m,DCD, k_p,DCD) to a final, remnant value (ΔΨ_p,final, ΔΨ_m,final) after the onset of injury (t_DCD).

Figure 1.

Potential models and fitting parameters for MATLAB-based analysis. The figure depicts the assumed functional behavior of ΔΨ_m (solid line) and ΔΨ_p (dashed line) that is used for fitting the TMRM fluorescent responses as taken from biological assumptions described in Materials and Methods. Parameters subject to fitting (potential values, decay constants) are indicated by arrows. A, Potential model for the apoptotic cells showing hyperpolarizion of ΔΨ_m only (i) and showing hyperpolarization of ΔΨ_m with a secondary collapse (ii). B, Necrotic model; monophasic response. C, Necrotic model; biphasic response. a.u., Arbitrary units; hyp, hyperpolarizion; max, maximum; dep init, initial depolarization; dep final, final depolarization; inc, increase; dec, decay; Glut, glutamate; DCD, delayed calcium deregulation.

For the monophasic necrotic model (Fig. 1B), we assumed a permanent initial depolarization of the plasma (ΔΨ_p,final) and mitochondrial membrane (ΔΨ_m,final) with the decay constants k_{p, decay}, k_{m, decay}, respectively. For the biphasic necrotic model (Fig. 1C), we allowed for a change of the mitochondrial membrane (ΔΨ_m,_relax^Hyp/Dep, k_m,inc/dec) and a decay of the plasma potential (ΔΨ_p,relax, k_p,_decay) after onset of continuous glutamate lasting and before the decay of both potentials, at the time point of injury (t_DCD).

For computational modeling of the DiBAC₂(3) responses, we assumed the measured fluorescence F_initial, F_actual(t) proportional to the cytosolic concentration of the dye with the Nernstian equation:

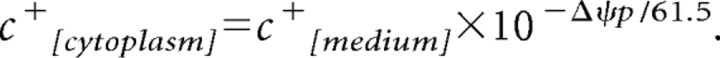We obtained the following:

Epi-fluorescence NADPH microscopy.

Seven- to 8-d-old cerebellar granule neurons on Willco dishes were loaded with TMRM (30 nm) for 30 min at 37°C (in the dark), in experimental buffer. The Willco dishes with cells were washed in fresh medium after loading before being mounted in a nonperfusion (37°C) holder and placed on the stage of a Zeiss Axiovert 200M microscope. During experiments, cells were treated as described above (see Confocal microscopy). NADPH auto fluorescence as well as TMRM fluorescence was observed using an Axiovert 200M inverted microscope equipped with a 63×, 1.4 numerical aperture oil-immersion objective (Zeiss), dichroic beam splitters, and filter wheels in the excitation and emission light path containing the appropriate filter sets (NADPH: excitation, 375 ± 25 nm; emission, 448 ± 32 nm; TMRM: excitation, 530 ± 21 nm; emission, 592 ± 22 nm; filters and dichroic mirrors were made by Semrock, Rochester, NY). Emission and bright-field images were recorded using a back-illuminated, cooled EM CCD camera (Ixon BV 887-DCS; Andor, Belfast, UK). The imaging setup was controlled by MetaMorph software.

ATP luciferase assays.

Cerebellar granule neurons were maintained on poly-d-lysine (5 μg/ml)-coated 24-well plates for 7–8 d before use. The culturing medium was replaced with an experimental buffer (in mm: 120 NaCl, 3.5 KCl, 0.4 KH₂PO₄, 20 TES, 5 NaHCO₃, 1.2 Na₂SO₄, 1.2 CaCl₂, and 15 glucose, pH 7.4), and the neurons were excited with glutamate/glycine for 5 min or continuously (100 and 10 μm) and lysed at the times indicated. In separate experiments, cerebellar granule neurons were exposed to combinations of oligomycin (2 μg/ml), FCCP (2 μm), and MK-801 (10 μm) and maintained for 30 min before being lysed. The neurons were lysed using a hypotonic lysis buffer (Tris-acetate buffer, pH 7.75). Fifty microliters of the sample and 50 μl of the luciferin–luciferase reaction kit (ENLITEN ATP Assay System Bioluminescence Detection kit; Promega, Southampton, UK) for ATP were reacted to quantify ATP content. The amount of ATP was determined by a concentration standard curve, and ATP content values were normalized according to the protein concentration for each sample (moles ATP/μg protein).

Glucose uptake assay.

Cerebellar granule neurons were maintained on poly-d-lysine (5 μg/ml)-coated 96-well plates for 7–8 d before use. The culturing medium was then replaced with an experimental buffer (in mm: 120 NaCl, 3.5 KCl, 0.4 KH₂PO₄, 20 TES, 5 NaHCO₃, 1.2 Na₂SO₄, 1.2 CaCl₂, and 1 glucose, pH 7.4) minus MgCl₂. The cerebellar granule neurons were treated with glutamate/glycine (100 and 10 μm) for 10 min (37°C) or exposed to sham conditions (experimental buffer). The excitation buffer was replaced with buffer minus glucose and containing 100 μm 2-deoxyglucose and ³H-2-deoxyglucose. ³H-2-deoxyglucose is taken up by neurons through the glucose transporters; however, it is not fully metabolized by the neuron and is retained within the cell. The neurons were maintained for 20 min in the experimental buffer containing the ³H-2-deoxyglucose; the buffer was then removed, and the neurons were washed twice with cold buffer minus glucose before the addition of 100 μl of scintillation fluid. The plates were left for 20 min on ice before reading on a Matrix-96 beta counter (Packard, Grove, IL). All conditions were repeated six times per experiment, and the same experiment was performed in at least three different cultures.

Statistics.

Data are given as means ± SEM. For statistical comparison, one-way ANOVA followed by Tukey's test were used. p values <0.05 were considered to be statistically significant. Data for ΔΨ_m, ΔΨ_p and the onset of neuronal injury were plotted using Origin 7 software (OriginLab, Northampton, MA) a linear regression was preformed on the data, and the R² value was calculated for each data set.

Results

Characterization and computational modeling of whole-cell TMRM fluorescence in cerebellar granule neurons

Cellular TMRM fluorescence is not only highly dependent on the changes in both ΔΨ_p and ΔΨ_m but is also directly related to the total mitochondrial volume within the cell (Ward et al., 2000; Dussmann et al., 2003; Nicholls, 2006). Therefore, a stringent determination of the mitochondrial volume was performed in cerebellar granule neurons. High-resolution z-stacks with 0.2 μm steps were taken of three fields of neurons, and the cellular volume (296.9 ± 32.9 μm³) and the mitochondrial volume (17.6 ± 1.5 μm³) were determined for each neuron (Fig. 2A). The mitochondrial volume (6.2 ± 0.8%) was found to be larger than that described previously (Ward et al., 2000; Nicholls, 2006)

To determine the rate constant (k_kinetic) for the redistribution of TMRM, several control experiments were performed (Fig. 2B,C). The protonophore FCCP (2 μm) was added to neurons loaded with TMRM in the presence of oligomycin (2 μg/ml) to uncouple ΔΨ_m, and the fluorescent signals were monitored for neurons in both the quenched (Fig. 2B) and nonquenched (Fig. 2D) mode. From the redistribution of the probe after the addition of FCCP, we established a kinetic constant for the redistribution of TMRM of 0.008 s⁻¹.

The MATLAB-based computational model was used to interpret the changes in TMRM fluorescence in response to the addition of FCCP/oligomycin and provide output on changes in ΔΨ_m and ΔΨ_p. Surprisingly, in the modeled traces (Fig. 2C,E) the expected rapid collapse in ΔΨ_m after the addition of FCCP was also closely paralleled with a rapid collapse of ΔΨ_p. To validate these findings, we used the ΔΨ_p-sensitive fluorescent probe DiBAC₂(3) to monitor changes in ΔΨ_p after the addition of oligomycin and FCCP (Fig. 2F,G). A rapid and prolonged increase in DiBAC₂(3) fluorescence after the addition of FCCP that reflected a substantial depolarization of ΔΨ_p (Fig. 2F,G) was observed.

In addition to monitoring TMRM and DiBAC₂(3) fluorescent responses, changes in Ca²⁺ dynamics (Fluo-4) and neuronal ATP levels were monitored within the neurons after the addition of FCCP in the presence of oligomycin (Fig. 3). A rapid collapse of Ca²⁺ homeostasis was identified within the neurons after exposure to the protonophore FCCP (Fig. 3A). The collapse in Ca²⁺ homeostasis (Fig. 3A) after the addition of FCCP was completely blocked by the NMDA antagonist MK-801 (Fig. 3B). The addition of oligomycin alone had no significant impact on neuronal ATP levels (Fig. 3); however, oligomycin plus FCCP resulted in a significant decrease (*p < 0.01) in ATP levels that was blocked by the presence of the NMDA antagonist MK-801 (Fig. 3C). These results suggest that any Ca²⁺ entering the neuron is the direct result of NMDA receptor overactivation attributable to glutamate release from the presynaptic terminals. Because the ATP synthase inhibitor oligomycin was present throughout (Fig. 3), energy restrictions alone could not account for the release of glutamate. This is intriguing in that it suggests presynaptic, polarized mitochondria play a key role in the regulation of glutamate within the synapse.

Figure 3.

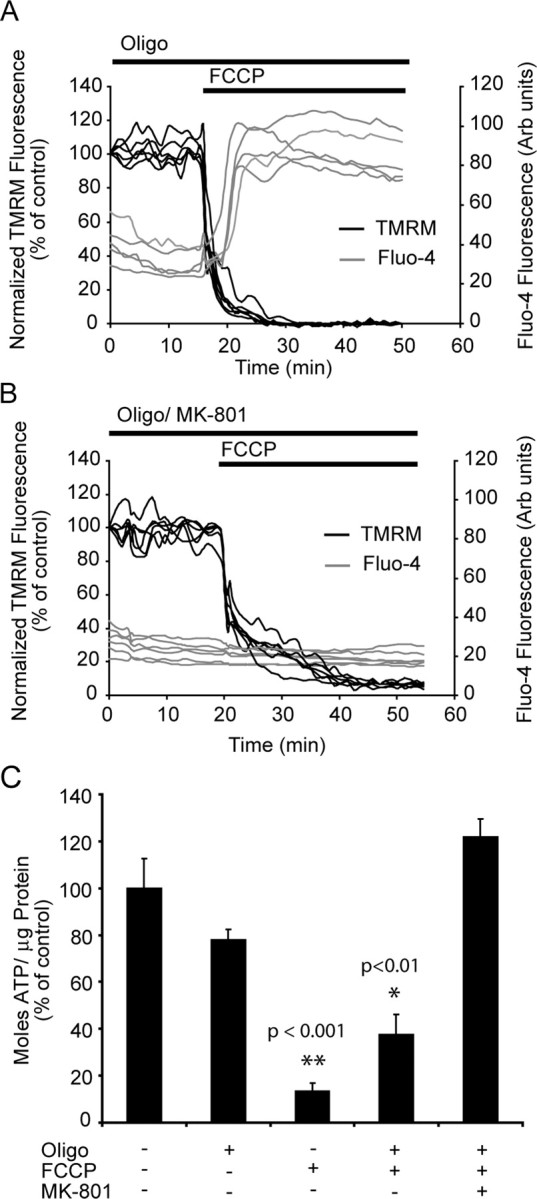
Protonophore addition induces a rapid collapse of Ca²⁺ homeostasis that is blocked with MK-801. A, B, Neurons were loaded with TMRM (30 nm) and Fluo-4 (3 μm) for 30 min at 37°C and exposed to FCCP (2 μm) in the presence of oligomycin (2 μg/ml) with (A) or without (B) MK-801 (10 μm). A rapid increase in cytosolic Ca²⁺ accompanied the FCCP addition in neurons that did not have MK-801 present (experiments were repeated 3 times for each condition, with similar results). C, Neurons were treated with a combination of FCCP (2 μm), oligomycin (2 μg/ml), and MK-801 (10 μm) for 30 min, and ATP levels were measured moles ATP/μg protein. All data were normalized to control values for comparison between experiments (experiments were performed in triplicate in 3 separate cultures;**p < 0.001; *p < 0.01 difference from control). Error bars indicate SEM. Oligo, Oligomycin; Arb units, arbitrary units.

Characterization of ΔΨ_m and ΔΨ_p during necrotic cell injury induced by prolonged glutamate excitation in cerebellar granule neurons

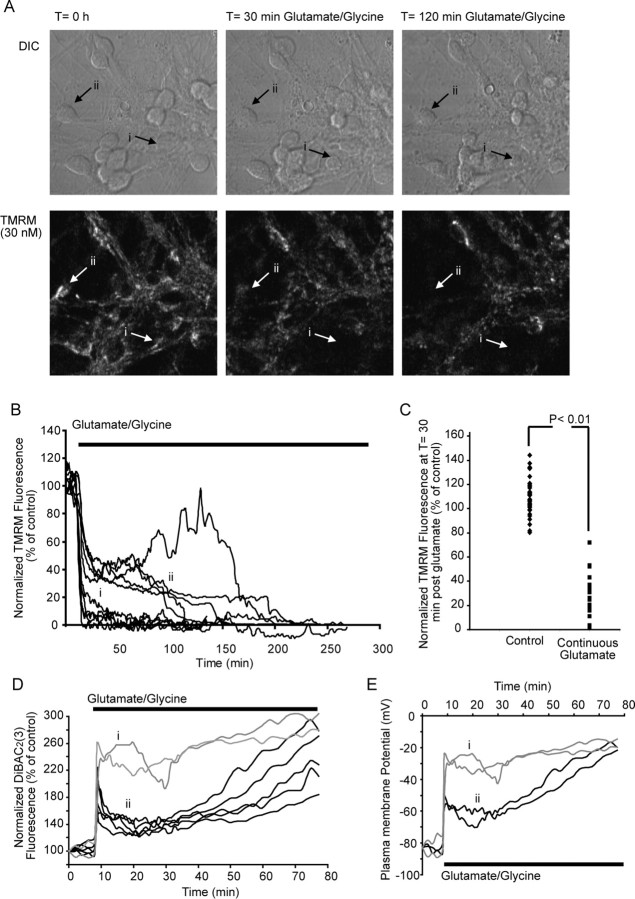
We have previously characterized a model of excitotoxic necrosis in cerebellar granule neurons induced by prolonged glutamate excitation (Castilho et al., 1998, 1999; Ward et al., 2000). In agreement with previous studies, we identified two major subgroups of neurons after prolonged glutamate excitation: (1) neurons that underwent a rapid collapse of ΔΨ_m (5–20 min) (Fig. 4A,B) with monophasic loss (33.1%) of TMRM fluorescence, rapid loss of Ca²⁺ homeostasis, and neuronal swelling; and (2) neurons that underwent a delayed neuronal injury (15 min to 4 h) (Fig. 4A,B, ii) with a biphasic drop (63.4%) in TMRM fluorescence, a delayed loss of Ca²⁺ homeostasis, neuronal swelling, and early membrane lysis (Ward et al., 2000; Ward et al., 2005).

Figure 4.

Prolonged glutamate excitation induces a rapid loss of ΔΨ_m and early necrotic injury in cerebellar granule neurons. Cerebellar granule neurons plated on Willco dishes were loaded with 30 nm TMRM and continuously exposed to glutamate/glycine (100 μm/10 μm). TMRM fluorescence was then monitored over time, and images were taken at 1 min intervals. A, Differential interference contrast (DIC) and TMRM fluorescent images were chosen at selected time points (0, 30, and 120 min during glutamate excitation) from a representative experiment. B, Representative traces for whole-cell TMRM fluorescence in neurons during prolonged glutamate excitation. Two major subgroups were identified: traces that show a rapid collapse of ΔΨ_m (i) and traces that show a partial recovery of ΔΨ_m, followed by a secondary collapse of ΔΨ_m (ii). C, Whole-cell TMRM fluorescence in control neurons after 30 min and neurons treated with glutamate for 30 min. p < 0.001, difference between TMRM fluorescence for control neurons and neurons after 30 min continuous glutamate excitation (control, n = 39; necrotic, n = 63). D, Cerebellar granule neurons were loaded with the ΔΨ_p-sensitive probe DiBAC₂(3) (1 μm) and continuously exposed to glutamate/glycine (100 μm/10 μm). Neurons undergo a rapid monophasic (i) collapse of ΔΨ_p or a biphasic (ii) collapse of ΔΨ_p (traces are representative of those obtained from 3 separate experiments). E, Representative traces for modeled changes in ΔΨ_p (C) for neurons undergoing a rapid monophasic (i) collapse of ΔΨ_p or a biphasic (ii) collapse of ΔΨ_p when continuously exposed to glutamate/glycine (100 μm/10 μm).

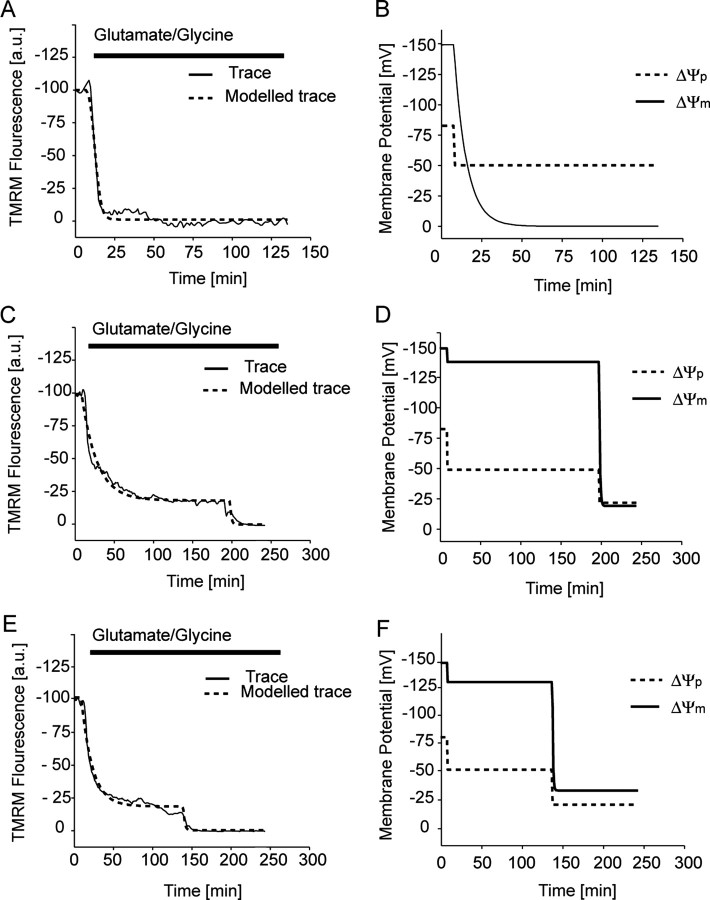
From the data obtained (Fig. 4), we used the MATLAB-based computational model (Fig. 1B,C) for the high throughput assessment of the TMRM fluorescence responses to define potential changes in ΔΨ_m and ΔΨ_p. Representative traces from neurons exposed to glutamate are shown from separate (Fig. 5A,C,E) experiments and modeled output traces for ΔΨ_m and ΔΨ_p determined for each (Fig. 5B,D,F): (1) neurons that entered a rapid necrotic cell death with a monophasic decrease in ΔΨ_m and ΔΨ_p after glutamate excitation (Fig. 5A) and (2) neurons that entered a delayed necrotic injury (Fig. 5C,E) with a biphasic decrease in ΔΨ_m and ΔΨ_p. The rate at which neurons entered the second phase of injury varied considerably (15 min to 4 h) between neurons and cultures; however, all neurons entered a necrotic-like injury with a rapid swelling of the neuron and loss of cellular integrity shortly after the collapse of ΔΨ_m.

Figure 5.

Computational modeling of TMRM traces for neurons during prolonged glutamate excitation. Cerebellar granule neurons plated on Willco dishes were loaded with 30 nm TMRM and continuously exposed to glutamate/glycine (100 μm/10 μm). TMRM fluorescence was then monitored over time, and images were taken at 2 min intervals. A, Representative TMRM fluorescent trace (solid line) and fitted trace (dashed line) for a neuron that had a rapid monophasic response during glutamate induced necrosis. C, E, Representative TMRM fluorescent traces and fitted traces for neurons that have a biphasic response during glutamate-induced necrosis. B, D, F, Modeled changes in both ΔΨ_p (dashed lines) and ΔΨ_m (solid line) for the fitted traces in figures A, C, and E, respectively. TMRM (A, C, E) traces are representative of traces obtained from eight separate experiments from different cultures. a.u., Arbitrary units.

To validate that the modeled ΔΨ_p responses above (Fig. 5B,D,F) were accurate, we directly monitored ΔΨ_p with the plasma membrane-sensitive probe DiBAC₂(3) (Fig. 4D). Again, two major groups of neurons were identified: neurons that underwent a rapid collapse of ΔΨ_p (Fig. 4D, i) and neurons that underwent a secondary loss of ΔΨ_p (Fig. 4D, ii). When the DiBAC₂(3) responses were modeled using the MATLAB software and the predictive changes in ΔΨ_p were calculated (Fig. 4E), the values for ΔΨ_p were found to be similar to those predicted form the modeled TMRM data (Fig. 5B,D,F). Therefore, it would appear that MATLAB-based computational models can accurately determine changes in both ΔΨ_m and ΔΨ_p from TMRM responses alone.

Hyperpolarization of ΔΨ_m in apoptotic neurons after transient glutamate receptor excitation

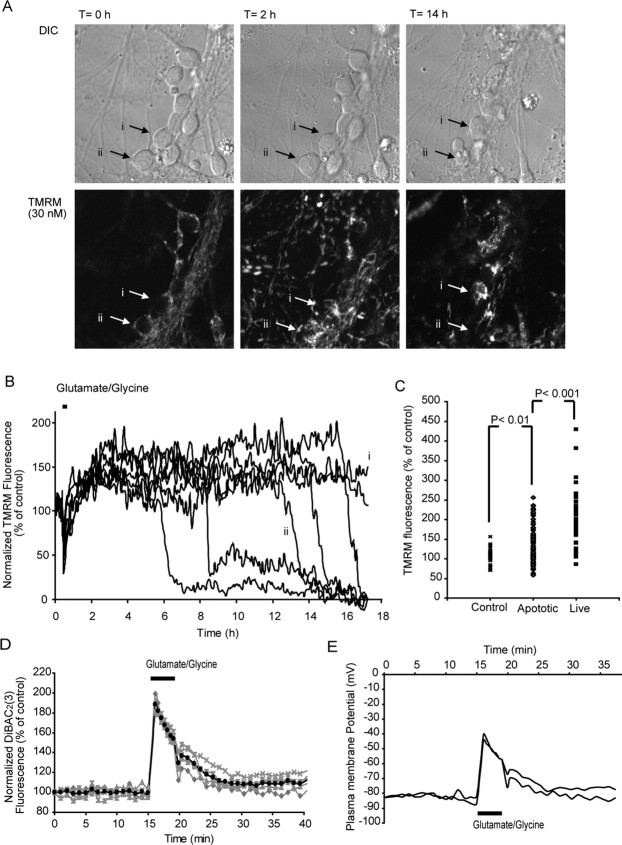
Transient excitotoxicity results in a delayed neuronal injury that has mitochondrial dysfunction intricately linked with injury onset (Lankiewicz et al., 2000; Luetjens et al., 2000; Ward et al., 2000, 2006). Here, cerebellar granule neurons were stimulated for 5 min with glutamate/glycine, allowed to recover, and monitored over a 24 h period (Ward et al., 2006). After transient glutamate excitation, only 2.9% of the neurons underwent rapid necrotic injury with an early loss of ΔΨ_m (46.2 ± 16.7 min), neuronal swelling, and early membrane lysis. However, the majority of neurons monitored (78.8%) displayed a delayed loss of ΔΨ_m (11.8 ± 0.8 h), cell shrinkage, and condensation of the nucleus within a 24 h period. An additional 18.2% survived this injury and retained a hyperpolarized ΔΨ_m and normal cellular morphology for at least 24 h (Fig. 6A,B).

Figure 6.

Transient glutamate excitation results in a hyperpolarization ΔΨ_m and a late apoptotic injury in cerebellar granule neurons. Cerebellar granule neurons plated on Willco dishes were loaded with 30 nm TMRM and exposed to glutamate/glycine (100 μm/10 μm) for 5 min. TMRM fluorescence was then monitored over time, and images were taken at 5 min intervals. A, Differential interference contrast (DIC) and TMRM fluorescent images were chosen at selected time points (0 min, 2 h, and 14 h after glutamate) from a representative experiment. B, Representative traces for whole-cell TMRM fluorescence in neurons during prolonged glutamate excitation. Two major subgroups are shown: traces that show a secondary collapse of ΔΨ_m downstream of excitation (i) and traces that show a collapse of ΔΨ_m within 24 h (ii). C, Whole-cell TMRM fluorescence in control neurons after 120 min and neurons 120 min after glutamate excitation. p < 0.01, difference between TMRM fluorescence for control neurons and apoptotic neurons 120 min after transient glutamate excitation; p < 0.001 difference between TMRM fluorescence for apoptotic neurons 120 min after transient excitation compared with neurons that survive for >24 h after glutamate excitation (control, n = 39; apoptotic, n = 134; live, n = 31). D, Cerebellar granule neurons were loaded with the ΔΨ_p-sensitive probe DiBAC₂(3) (1 μm) and transiently (5 min) exposed to glutamate/glycine (100 μm/10 μm). Fluorescence recovers close to pre-exposure levels (average response dark trace) after the addition of glutamate (traces are representative of those obtained from 3 separate experiments). E, Representative traces for modeled changes in ΔΨ_p for neurons transiently exposed to glutamate.

The MATLAB-based model was used (Fig. 1A) to interpret the changes in TMRM fluorescence for populations of individual neurons and provide output on changes in ΔΨ_m and ΔΨ_p during and after transient glutamate excitation. In the majority of neurons (97.1%), a transient depolarization of ΔΨ_p was associated with glutamate receptor overactivation with values for ΔΨ_p returning to prestimulation levels within a relatively short (5–15 min) period of time (Fig. 7B,D,F,H). Interestingly, the values for ΔΨ_m after glutamate excitation were found to be significantly higher (p < 0.001) than before glutamate excitation (Fig. 7B,D,F,H). Similar to the previous experiments, the output on the changes in ΔΨ_m and ΔΨ_p deducted from the computational analysis of the TMRM responses were validated with the ΔΨ_p-sensitive probe DiBAC₂(3). An increase in DiBAC₂(3) fluorescence was associated with the initial glutamate excitation (ΔΨ_p depolarization) (Fig. 6D); after inhibition of glutamate receptor overactivation, the fluorescence recovered to prestimulation levels with no hyperpolarization of the ΔΨ_p (lower fluorescence than baseline) identified (Fig. 6D). Interestingly, when the DiBAC₂(3) responses were calculated using MATLAB software and the predictive changes in ΔΨ_p were calculated (Fig. 6E), the values for ΔΨ_p were again found to be similar to those predicted from the modeled TMRM data (Fig. 7B,D,F,G). What is most significant from these results is the fact that the increase in TMRM fluorescence after glutamate excitation (Figs. 6, 7) is almost entirely attributable to a hyperpolarization of ΔΨ_m with little or no contribution from changes in ΔΨ_p (Fig. 6D,E).

Figure 7.

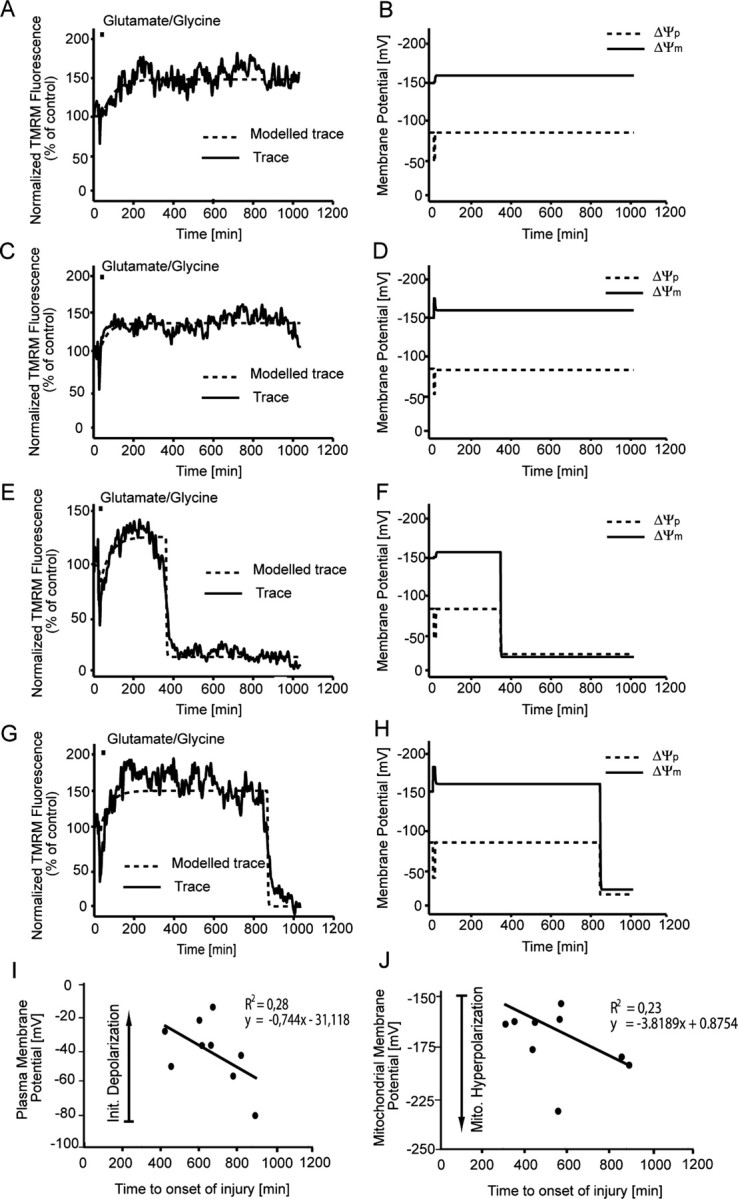
Computational modeling of TMRM traces for cerebellar granule neurons after transient glutamate excitation. Cerebellar granule neurons plated on Willco dishes were loaded with 30 nm TMRM and exposed to glutamate/glycine (100 μm/10 μm) for 5 min. TMRM fluorescence was then monitored over time, and images were taken at 5 min intervals. A, C, Representative TMRM fluorescent traces (solid line) and fitted traces (dashed lines) for neurons that undergo apoptosis after transient glutamate excitation. E, G, Representative TMRM fluorescent traces and fitted traces for neurons that do not undergo apoptosis after transient glutamate excitation. B, D, F, H, Modeled changes in both ΔΨ_p (dashed lines) and ΔΨ_m (solid line) for the fitted traces in A, C, E, and F, respectively. TMRM traces (A, C, E, G) are representative of traces obtained from eight separate experiments from different cultures. I, The fitted initial depolarization of ΔΨ_p during glutamate excitation is plotted against the onset of injury (collapse of TMRM signal; n = 5 populations of neurons). J, The fitted maximum mitochondrial hyperpolarization of ΔΨ_m against onset of injury after glutamate excitation (n = 5 populations of neurons).

Hyperpolarization of ΔΨ_m is a predictor of survival time and tolerance to transient glutamate receptor excitation

Statistical analysis of the MATLAB-based computational model was performed to investigate whether changes in ΔΨ_m and ΔΨ_p after transient glutamate receptor overactivation could predict downstream injury or survival. Two major phases of change were determined during transient glutamate excitation: (1) the extent of the initial depolarization of ΔΨ_p during the glutamate excitation phase and (2) the hyperpolarization of ΔΨ_m after the excitation phase (Figs. 6, 7). When the single-cell data from a number of neuronal populations were characterized, correlations between the onset of injury (collapse of ΔΨ_m within the neuron) and changes in ΔΨ_m and ΔΨ_p could be established. A strong correlation was identified (r² = 0.28; n = 5 neuronal populations) between the extent of the initial depolarization and the onset of neuronal injury in individual population subsets (Fig. 7I), with a large depolarization of ΔΨ_p during the initial glutamate excitation phase associated with a more rapid onset of injury. The second and possibly more interesting correlation defined (r² = 0.23; n = 5 neuronal populations) is that between the extent of hyperpolarization after transient excitation within a population of cells and the onset of injury (Fig. 7J), with those neurons having a more pronounced hyperpolarization of ΔΨ_m during the recovery phase surviving longer. On further analysis of the TMRM fluorescence for those neurons that tolerated the glutamate insult, we identified that those neurons tolerant to transient glutamate excitation had a significantly (p < 0.001) higher TMRM fluorescence (202.8 ± 19.2; n = 31) than neurons that underwent apoptosis (Fig. 6C). These data suggest that the extent of the hyperpolarization of ΔΨ_m (increase in TMRM fluorescence) after transient glutamate excitation is more closely associated with neuronal survival rather than injury.

Enhanced glucose uptake and NADPH availability in response to transient glutamate excitation

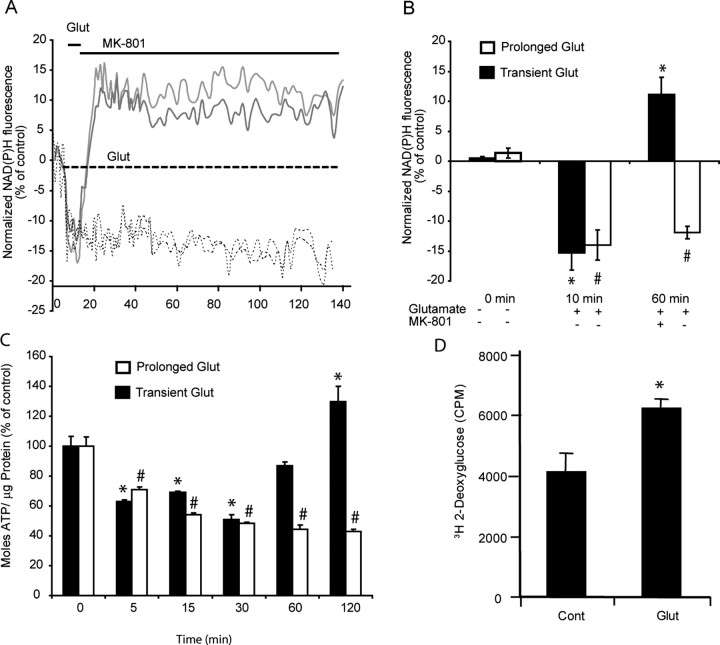
Because an increased ΔΨ_m is highly suggestive of alterations in neuronal metabolism, we investigated how glucose uptake, NADPH production, and neuronal ATP levels may be altered in relation to glutamate excitation. Prolonged glutamate excitation (dashed line) resulted in a significant (^#p < 0.01) rapid and continuous decrease in both neuronal NADPH (Fig. 8A,B) and ATP (Fig. 8C) levels within the neurons. However, transient glutamate excitation (solid line) resulted in a transient decrease in both neuronal NADPH and ATP levels that was followed by a significant (*p < 0.01) and sustained increase in both (Fig. 8A,B) NADPH and ATP. This increase in NAHPD and ATP levels was also coupled to a significant increase in glucose uptake (Fig. 8D) as measured with ³H-2-deoxyglucose. These alterations in neuronal metabolism, in particular the NADPH levels that could be determined in real time, closely paralleled the hyperpolarization of ΔΨ_m identified after transient glutamate excitation (Figs. 6B, 7).

Figure 8.

Glutamate (Glut) induced changes in neuronal NADPH, ATP, and glucose uptake. Cerebellar granule neurons plated on Willco dishes were exposed to glutamate/glycine (100 μm/10 μm) continuously (dashed line) or for 5 min (solid line) before termination of NMDA receptor activation with MK-801 (10 μm). A, B, NADPH autofluorescence was monitored over time (A) and at selected time points (0, 10, and 60 min; B) chosen before, during, and after glutamate excitation for statistical analysis. (At least 5 cells were analyzed per experiment, and the experiment was repeated in three different cultures. ^#p < 0.01; *p < 0.01, difference from respective control.) C, Cerebellar granule neurons plated in 24-well plates were exposed to glutamate/glycine (100 μm/10 μm) for 5 min or continuously, and their ATP content was measured (moles ATP/μg protein) at the times indicated. Data are represented as percentage of control response (n = 3 experiments in triplicate; ^#p < 0.01; *p < 0.01, difference from respective control). D, Cerebellar granule neurons plated in 96-well plates were exposed to glutamate/glycine (100 μm/10 μm) for 10 min and washed, and the medium was replaced with buffer containing ³H-2-deoxyglucose for 20 min. The cells were washed twice, and the ³H-2-deoxyglucose was measured in a Matrix-96 beta counter for 20 min. Data are presented as counts per minute (CPM) for control (washed neurons) and glutamate-treated neurons (6 wells were examined per condition per experiment and repeated in 3 separate cultures; *p < 0.01). Error bars indicate SEM.

Discussion

Computational modeling of ΔΨ_m and ΔΨ_p from TMRM fluorescent traces

Cationic fluorescent probes (TMRM, TMRE, rhodamine-123, JC-1) are an invaluable tool for monitoring mitochondrial function in intact cells during excitotoxic injury (Khodorov et al., 1996; White and Reynolds, 1996; Kiedrowski, 1998; Prehn, 1998; Stout et al., 1998; Ward et al., 2000; Buckman et al., 2001). However, because of the complex nature of these probes and their sensitivity to changes in both ΔΨ_m and ΔΨ_p, the fluorescence responses obtained have often been misinterpreted because of an overestimation of changes in ΔΨ_m by underestimating the significance of changes in ΔΨ_p on the total cellular fluorescence (Nicholls and Ward, 2000; Ward et al., 2000). Here, we have successfully created an automated MATLAB-based computational model that uses the sensitivity of TMRM fluorescence to changes in both ΔΨ_m and ΔΨ_p providing predictive output on changes in ΔΨ_m and ΔΨ_p, removing the need for additional plasma membrane indicators or manual parameter fitting. Using the plasma-sensitive probe DiBAC₂(3) (Ehrenberg et al., 1988; Gonzalez and Maher, 2002), we have validated the sensitivity and accuracy of the computational model created in predicting changes in ΔΨ_p. With this technology, we have been able to evaluate changes that occur at a ΔΨ_m and ΔΨ_p level in models of glutamate-induced necrosis, apoptosis, and tolerance, providing us with novel insights into the bioenergetic/metabolic mechanisms associated with glutamate regulation and glutamate-induced injury and tolerance.

Effects of “mitochondrial” toxins on ΔΨ_p, Ca²⁺ uptake, and glutamate release

In control experiments (Fig. 3), a combination of the ATP synthase inhibitor oligomycin and the protonophore FCCP were used to collapse ΔΨ_m in neurons, a technique routinely used to nullify mitochondrial function within neurons (Stout et al., 1998; Ward et al., 2005). The addition of oligomycin alone resulted in only minor changes in ΔΨ_m and neuronal ATP levels; however, the addition of FCCP resulted in the expected collapse of ΔΨ_m that was coupled with an unexpected decrease in ΔΨ_p, loss of Ca²⁺ homeostasis, and a significant decrease in neuronal ATP levels. Because the addition of the NMDA receptor antagonist MK-801 blocked these events, it implies that a depolarization of synaptic mitochondria was sufficient to induce glutamate release. Presynaptic mitochondria have a functional role in the regulation of Ca²⁺ (Yang et al., 2003; Brown et al., 2006; Ly and Verstreken, 2006; Mironov and Symonchuk, 2006) within synaptic vesicles; indeed, recent studies have shown that the endoplasmic reticulum (ER) and mitochondria bidirectionally exchange Ca²⁺ within the synapse and that Ca²⁺ released from the ER or mitochondria is sufficient to evoke exocytosis (Mironov and Symonchuk, 2006). If synaptic mitochondria are highly involved in the regulation of synaptic Ca²⁺ (Mironov and Symonchuk, 2006), a mitochondrial depolarization and reversal of the Ca²⁺ uniporter would provide sufficient Ca²⁺ to enable glutamate exocytosis to occur. Yang et al. (2003) also identified that Ca²⁺ released from mitochondria through the mitochondrial Na⁺–Ca²⁺ exchanger is sufficient to induce synaptic glutamate release. Additionally, Budd and Nicholls (1996a) previously characterized a protonophore releasable pool of Ca²⁺ within neurons. Therefore, it appears that the manipulation of ΔΨ_m with mitochondrial toxins may alter Ca²⁺ sequestration within synaptic mitochondria and thereby alter glutamate regulation within the synapse.

Glutamate-induced necrosis

The injury identified during prolonged glutamate excitation in this study is very much in agreement with previous studies including work performed by ourselves (Ankarcrona et al., 1995; White and Reynolds, 1996; Prehn, 1998; Stout et al., 1998; Ward et al., 2000), with prolonged glutamate excitation resulting in a monophasic or biphasic collapse of ΔΨ_m, paralleled with a decrease in ΔΨ_p, rapid neuronal swelling, and early membrane lysis. Prolonged glutamate excitation also resulted in the rapid decay of ATP as a consequence of the increased activity of both the Na⁺/K⁺ and Ca²⁺ ATPases at the plasma membrane.

What is intriguing from the data presented here is the biphasic DiBAC₂(3) responses (Fig. 4E) during glutamate excitation, where the loss of ΔΨ_p is not a single event but appears to be a slowly developing process. So what may induce a slow loss of ΔΨ_p? The preservation of a polarized plasma membrane is dependent on the regulation of ionic homeostasis by Na⁺/K⁺ and Ca²⁺ ATPases, as well as the Na⁺/Ca²⁺ exchanger. During glutamate excitation, a high concentration of Ca²⁺ is retained within the cytosol and mitochondrial matrix (Tymianski et al., 1993a; Budd and Nicholls, 1996b; Stout et al., 1998; Brocard et al., 2001; Ward et al., 2005). This prolonged increase in cytosolic and mitochondrial Ca²⁺ has been shown to increase calpain activity (Siman et al., 1989; Faddis et al., 1997; Lankiewicz et al., 2000), and it has been suggested that this increased calpain activation leads to cleavage of the Na⁺/Ca²⁺ exchanger, resulting in the progressive disruption of cellular homeostasis (Bano et al., 2005). Additionally, the activation of TRP (transient receptor potential) channels, post glutamate excitation, may also play an integral part in the development of this secondary, slow ΔΨ_p depolarization (Aarts et al., 2003).

Glutamate-induced apoptosis and tolerance

In contrast to the necrotic injury induced by prolonged glutamate excitation, transient glutamate excitation resulted in a reversible depolarization of ΔΨ_p that was followed by a prolonged hyperpolarization of ΔΨ_m, with the subsequent collapse of both ΔΨ_m and ΔΨ_p, cell shrinkage and nuclear condensation occurring hours downstream of the initial excitation (Lankiewicz et al., 2000; Luetjens et al., 2000; Ward et al., 2000). Using the MATLAB-based computational model, we were able to detect changes in both ΔΨ_m and ΔΨ_p relative to injury onset for populations of single cells after transient glutamate excitation. A correlation was identified between the extent of the initial depolarization of ΔΨ_p during the glutamate excitation phase and the onset of injury within neurons, with those neurons having a more pronounced depolarization of ΔΨ_p during the excitation phase entering a more rapid cell death. Previous studies have identified that excitotoxic injury is highly dependent on the duration and intensity of glutamate/NMDA receptor overactivation (Choi, 1987; Tymianski et al., 1993b; Sattler et al., 1998). Because of the variability in the initial ΔΨ_p depolarization identified after glutamate excitation in this study, it is evident that there are marked variations in the type and number of glutamate/NMDA receptors present at the plasma membrane between neurons within a “homogenous” culture.

The most significant findings in this study involve the relationship between the hyperpolarization of ΔΨ_m, the changes in neuronal metabolism, and neuronal survival after transient glutamate excitation. A hyperpolarization of ΔΨ_m has previously been described in hippocampal neurons exposed to staurosporine (Poppe et al., 2001) and 30 min oxygen glucose deprivation (Iijima et al., 2003), and also in primary rodent cortical neurons (Perry et al., 2005) after the induction of the regulatory protein Tat (transactivator of transcription) by HIV-1. The increase in ΔΨ_m identified was associated with the onset of apoptotic injury, as is true for the majority of neurons in this study. Here, we could rapidly interpret the TMRM fluorescent responses for a number of populations of single-cell data with the MATLAB-based computational model. From this, a positive correlation was established between ΔΨ_m and neuronal survival, with neurons displaying a more pronounced hyperpolarization of ΔΨ_m surviving longer, a correlation that may have been inadvertently missed in previous studies (Poppe et al., 2001; Iijima et al., 2003; Perry et al., 2005). Additionally, the MATLAB-based analysis allowed us to identify a subset of neurons tolerant to glutamate excitation that had a significantly higher hyperpolarization of ΔΨ_m than apoptotic neurons after transient glutamate excitation.

Why does a hyperpolarization of ΔΨ_m promote or indicate survival? Glutamate excitation results in an early and rapid depletion in neuronal ATP levels (Atlante et al., 1996; Almeida et al., 1998). To counteract this loss of ATP, neurons can increase their capacity to provide extra fuel, NADPH/FADH₂, to meet the energy demands within the cell (Shuttleworth et al., 2003; Brennan et al., 2006). Because glutamate excitation results in the accumulation of Ca²⁺ within the mitochondrial matrix (Budd and Nicholls, 1996b; Wang and Thayer, 1996), the activation state of mitochondrial dehydrogenases will be altered increasing proton extrusion (Hansford, 1994a,b). We have previously identified that mitochondria retain Ca²⁺ within the mitochondrial matrix after transient glutamate excitation (Ward et al., 2005), which may lead to a prolonged alteration in dehydrogenase activity. What is evident in this study is that after glutamate excitation, the energetic state within neurons undergoing apoptosis or that are tolerant to the stimulus does not return to the prestimulus resting state, with a sustained increased ΔΨ_m that is coupled with increased glucose uptake and NADPH availability within the neurons.

Our key finding that neurons with an increased ΔΨ_m (and capacity to increase mitochondrial substrates NADPH and FADH₂) after glutamate excitation survive longer or tolerate the stimulus is also supported by Vergun et al. (2003), who have shown that an inhibition of glycolysis is sufficient to induce a hypersensitivity of primary cortical neurons to glutamate excitation. It would therefore appear that the injury or tolerance induced is a function of the availability of ATP within the cell, with any variability between responses dictated by the ability of each neuron to produce ATP, a finding that may have a significant impact for our understanding of neuronal conditioning and tolerance.