Subthreshold Dendritic Signal Processing and Coincidence Detection in Dentate Gyrus Granule Cells

Abstract

Although dendritic signal processing has been extensively investigated in hippocampal pyramidal cells, only little is known about dendritic integration of synaptic potentials in dentate gyrus granule cells, the first stage in the hippocampal trisynaptic circuit. Here we combined dual whole-cell patch-clamp recordings with high-resolution two-photon microscopy to obtain detailed passive cable models of hippocampal granule cells from adult mice. Passive cable properties were determined by direct fitting of the compartmental model to the experimentally measured voltage responses to short and long current pulses. The data are best fit by a cable model with homogenously distributed parameters, including an average specific membrane resistance (R_m) of 38.0 kΩ cm², a membrane capacitance (C_m) of 1.0 μF cm⁻², and an intracellular resistivity (R_i) of 194 Ω cm. Computational analysis shows that signal propagation from somata into dendrites is more efficient in granule cells compared with CA1 pyramidal cells for both steady-state and sinusoidal voltage waveforms up to the gamma frequency range (f_50% of 74 Hz). Similarly, distal synaptic inputs from entorhinal fibers can efficiently depolarize the somatic membrane of granule cells. Furthermore, the time course of distal dendritic synaptic potentials is remarkably fast, and temporal summation is restricted to a narrow time window in the range of ∼10 ms attributable to the rapid dendritic charge redistribution during transient voltage signals. Therefore, the structure of the granule cell dendritic tree may be critically important for precise dendritic signal processing and coincidence detection during hippocampus-dependent memory formation and retrieval.

Introduction

Granule cells of the dentate gyrus form the first stage of the trisynaptic circuit within the hippocampal formation (Lisman, 1999). They fire action potentials (APs) in a highly specific manner that is dependent on behavioral paradigms, such as spatial exploration and object recognition during a delayed non-match-to-sample task (Jung and McNaughton, 1993; Wiebe and Stäubli, 1999). The sparse and environment-specific activity of granule cells is believed to be important for the precise separation of different entorhinal input patterns (Chawla et al., 2005; Leutgeb et al., 2007). Although dendritic integration of excitatory and inhibitory synaptic inputs is an important elementary step in this process (Treves and Rolls, 1992; Lisman, 1999), our knowledge about dendritic signal processing in granule cells is only rudimentary.

Dendritic integration and propagation of synaptic potentials is shaped by several factors, including the morphological structure of the dendritic tree and passive membrane properties such as the specific membrane resistance (R_m), the specific membrane capacitance (C_m), and the intracellular resistivity (R_i) (Rall et al., 1992; Gulledge et al., 2005). Dendritic cable properties were extensively studied in hippocampal and neocortical pyramidal cells by combining whole-cell patch-clamp recordings with three-dimensional (3D) morphological reconstructions of the dendritic tree (Major et al., 1994; Stuart and Spruston, 1998; Trevelyan and Jack, 2002; Golding et al., 2005). Furthermore, simultaneous recordings with two patch-clamp electrodes from soma and dendrites were used to directly constrain the intracellular resistivity R_i in cortical pyramidal cells (Stuart and Spruston, 1998; Golding et al., 2005).

Based on these data, detailed compartmental models were developed, which allowed realistic computational analysis of dendritic signal processing. Because of differences in neuronal morphology and membrane properties, the studies revealed substantial differences in steady-state voltage attenuation from the soma into distal dendritic branches, which was relatively low for CA3 pyramidal cells (≤20%) (Major et al., 1994) and much larger in CA1 and neocortical pyramidal cells (up to 90%) (Stuart and Spruston, 1998; Golding et al., 2005). Remarkably, attenuation of synaptic potentials from dendrites toward the soma was pronounced in all of these principal cells with up to 300-fold reduction of the EPSP amplitude in CA1 pyramidal neurons (Golding et al., 2005). This shows that the electrotonic structure of neurons has a large impact on synaptic communication.

Similarly, compartmental cable models of hippocampal granule cells were developed by combining intracellular microelectrode recordings with horseradish peroxidase staining (Turner and Schwartzkroin, 1983; Turner, 1984a). However, microelectrode recordings have severe technical limitations and introduce shunt artifacts especially pronounced in small cell types (Durand, 1984; Spruston and Johnston, 1992). Therefore, a compartmental model based on patch-clamp recordings would be necessary for realistic computational analysis of dendritic signal processing in granule cells.

Here we combined dual patch-clamp recordings at the soma or simultaneous somatic and dendritic recordings to study the intracellular propagation of transient voltage signals in adult mouse hippocampal granule cells. After biocytin filling, the cells were three-dimensionally reconstructed using two-photon microscopy and spatial deconvolution. We thereby obtained detailed compartmental cable models for computational analysis of dendritic signal processing. This analysis revealed major differences between hippocampal granule and pyramidal cells, emphasizing that the structure of neurons shapes function.

Materials and Methods

Slice preparation.

Transverse 350-μm-thick slices were cut from the hippocampus of 2- to 4-month-old C57BL/6 mice using a custom-made vibratome (Geiger et al., 2002; Bischofberger et al., 2006a). Animals were kept in an oxygenated chamber for 10 min, anesthetized with isoflurane, and subsequently killed by decapitation, in accordance with institutional guidelines. For the dissection and the storage of the slices, a solution containing 87 mm NaCl, 25 mm NaHCO₃, 2.5 mm KCl, 1.25 mm NaH₂PO₄, 25 mm glucose, 75 mm sucrose, 7 mm MgCl₂, and 0.5 mm CaCl₂ (equilibrated with 95% O₂/5% CO₂) was used. Slices were incubated at 35°C for 30 min and subsequently stored at room temperature.

Electrophysiology.

Slices were superfused with a physiological extracellular solution containing 125 mm NaCl, 25 mm NaHCO₃, 2.5 mm KCl, 1.25 mm NaH₂PO₄, 25 mm glucose, 2 mm CaCl₂, 1 mm MgCl₂, 10 μm CNQX, and 10 μm bicuculline methiodide (equilibrated with 95% O₂/5% CO₂). Mature granule cells of the dentate gyrus were identified using infrared differential interference contrast (IR-DIC) video microscopy. Dual whole-cell recordings were performed at either the soma or a somatic and dendritic location of the same cell. For dendritic recordings, 100 μm Alexa594 (Invitrogen, Carlsbad, CA) was added to the intracellular solution, and patch-clamp recordings were obtained from terminal dendritic expansions resulting from the slicing procedure (diameter, ≈2 μm) (Shu et al., 2006). After ∼5 min, the fluorescently labeled soma was identified using a back-illuminated cooled-frame-transfer CCD camera (EBFT 512; Princeton Instruments, Trenton, NJ). The excitation light source (Polychrome II with 75 W xenon lamp; T.I.L.L. Photonics, Munich, Germany) was coupled to the epifluorescent port of the microscope [Axioskop FS2 (Zeiss, Jena, Germany); 60× water immersion objective (Olympus Optical (Tokyo, Japan)] via a light guide. To minimize bleaching, the intensity of the excitation light (550 nm) was reduced to 10%. The filter combination for excitation and emission comprised a beam splitter (FT580) and an emission filter (long-pass 590) from Zeiss.

Patch pipettes (6–10 MΩ for somatic recordings, 15 MΩ for dendritic recording) were pulled from thick-walled borosilicate glass (outer diameter, 2.0 mm; inner diameter, 0.6 mm). Voltage signals were measured with either two Axopatch 200A amplifiers in “I-clamp fast” mode or a Multiclamp 700A (Molecular Devices, Palo Alto, CA) amplifier, filtered at 10 kHz, and digitized at 20 kHz using a CED 1401 interface (Cambridge Electronic Design, Cambridge, UK). Current pulses were generated using a homemade data acquisition software (FPulse) running under Igor 5.02 (WaveMetrics, Lake Oswego, OR). Pipettes were filled with a solution containing the following (in mm):120 K-gluconate, 20 KCl, 10 EGTA, 2 MgCl₂, 2 Na₂ATP, 0.3 NaGTP, 1 Na₂ phosphocreatine, and 10 HEPES, pH 7.2. Pipette capacitance was compensated. Bridge balance was used to compensate the series resistance of 20–40 MΩ (somatic recordings) or ∼50 MΩ (dendritic recording) and monitored continuously. Recordings were performed at 22–24°C.

Data analysis.

For each cell, 120–600 baseline-subtracted voltage traces were scaled with the injected current, and the average of all traces was calculated. The baseline was calculated as the mean voltage during a 60 ms period preceding the pulse. The membrane time constant was estimated from a linear fit to a semilogarithmic plot of the voltage decay after the end of a 500 ms hyperpolarizing current pulse. For the linear regression in Figure 2, an algorithm that minimizes the sum of squared differences in x and y direction was used. All analysis was done using C-Stimfit (C.S.-H.), Excel (Microsoft, Seattle, WA), and Prism 3.0 (GraphPad Software, San Diego, CA). Value are given as mean ± SEM.

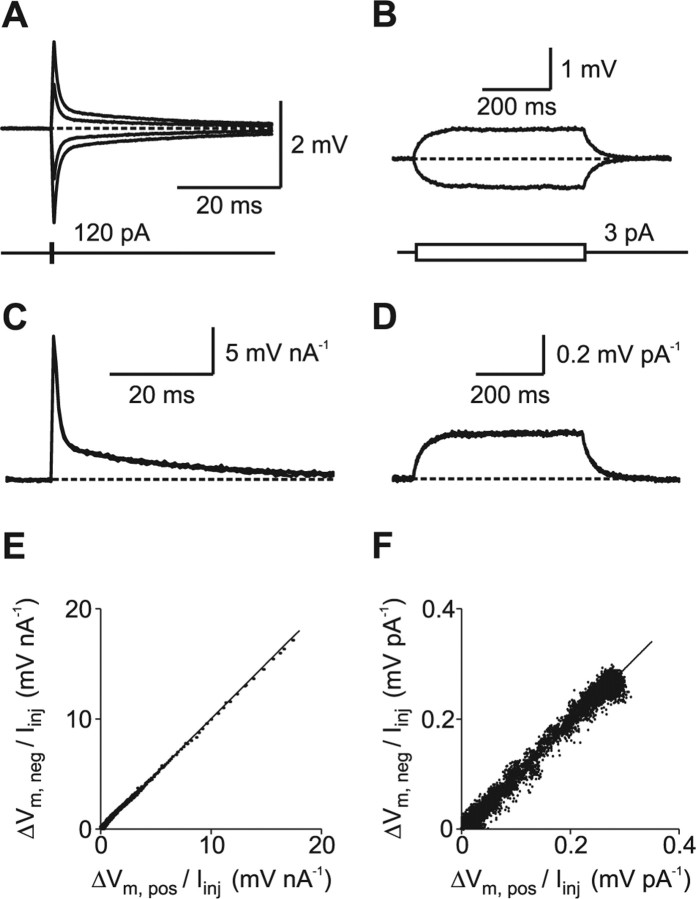
Figure 2.

Linear membrane properties near the resting membrane potential. A, Voltage responses to brief current injections with different amplitudes (0.5 ms; −120, −60, +60, and + 120 pA). Resting potential was −80 mV (dashed line). B, Voltage responses to long current injections (500 ms; −3 and +3 pA). C, D, The voltage responses to short and long current injections were scaled with the injected current amplitude and superimposed to study linearity. The superposition of the scaled traces indicates that both short and long voltage transients scale linearly with current within the tested voltage range. E, The scaled voltage response to a negative short current pulse was plotted against the scaled voltage response to a positive short pulse during a 200 ms time interval, including the peak amplitudes. The line shows a bidirectional linear fit to the data (slope, 1.00). F, Same as in E for the long current pulse during a 500 ms time interval (slope, 0.99).

Biocytin labeling and morphology.

Cells were filled with biocytin (1–2 mg/ml) during whole-cell recording and subsequently fixed with 4% paraformaldehyde in 0.1 m PBS. After washing, tissue sections were incubated with fluorescein isothiocyanate-conjugated avidin-D (2 μl/ml; Vector Laboratories, Burlingame, CA) and 0.3% Triton X-100 during 24 h at 4°C. To minimize tissue shrinkage and distortion, the fixed slices were not dehydrated or resliced. Furthermore, slices were placed in the middle of a Teflon ring (350 μm thickness) to minimize compression by the coverslip and embedded in Prolong Antifade Gold (Invitrogen). Fluorescence was analyzed with two-photon microscopy using a pulsed titanium:sapphire laser (Chameleon-XR tuned to 790 nm; Coherent, Santa Clara, CA) attached to a Zeiss LSM 510 that was equipped with a 20×/0.75 numerical aperture (NA) or a 40×/1.3 NA oil-immersion objective. The morphology of the cells was reconstructed from a stack of 400–600 images (voxel size, 0.14–0.21 μm in the x–y plane; 0.3–0.5 μm along the z-axis). To improve spatial resolution, a deconvolution algorithm was used that directly constructs the point-spread function from the collected datasets (AutoDeblur X; AutoQuant Imaging, Troy, NY). Dendrites, soma, and axon were traced within the three-dimensional image stack using a semiautomated filament tracing software (Imaris 4.5; Bitplane, Zürich, Switzerland).

Cable modeling.

Passive cable models were obtained using NEURON 5.8 or 5.9 (Carnevale and Hines, 2006) running either under Linux (SUSE 10.0) or Unix (IBM AIX 5L 5.1). The digitized morphological data were exported in NEURON format. Spines were counted using a two-dimensional image projection along the z-axis, and the resulting density was corrected for spines hidden by the dendritic shaft. Assuming radial symmetry, we multiplied spine density with a correction factor f: f = π/(π − 2α) with the angle α = arcsin[r/(r + l)], where r is the radius of the dendritic shaft and l = 1.25 μm is the average spine length (Hama et al., 1989). In four of eight cells, we could not accurately determine the exact number of spines on all dendrites, either because dendrites were running parallel to the z-axis or because the signal-to-noise ratio was not sufficiently large. In these cases, we assigned representative spine densities from neighboring dendrites of the same cell. “Collapsed” spines were implemented into the model by scaling R_m and C_m of spine-bearing compartments to account for the additional membrane surface area that was assumed to be 1.2 μm² per single spine (Hama et al., 1989). When spines were explicitly modeled (see Figs. 4D, 7D), they consisted of a neck (length, 0.75 μm; diameter, 0.18 μm) and a head (length, 0.50 μm; diameter, 0.50 μm) (Hama et al., 1989) unless specified differently, resulting in a membrane surface area of 1.2 μm² per spine.

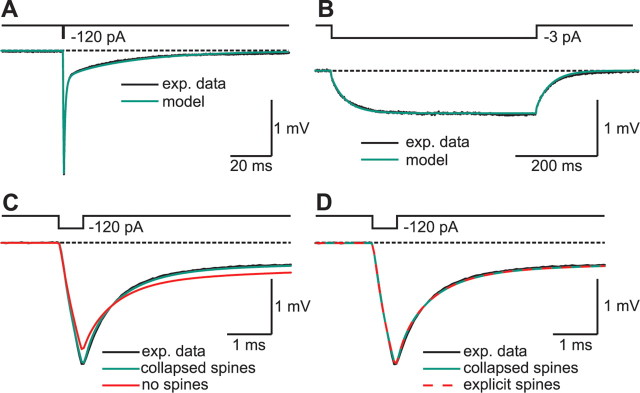
Figure 4.

Detailed morphology is necessary to reproduce electrophysiological responses of granule cells. A, Voltage response of the cell (black) and the passive cable model (green) to a brief current pulse (0.5 ms, −120 pA). The cable model was obtained by fitting the response of the model to the experimental data, varying R_m, C_m, and R_i. Spines were implemented into the model by scaling R_m and C_m within a dendritic segment according to the measured spine density. B, Voltage response of the cell (black) and the passive cable model (green) to a sustained current injection (500 ms, −3 pA). C, Same as in A, plotted at expanded timescale. In addition, the voltage response of a model without spines (red) was fitted to the data. In the model without spines, neither the fast nor the slow components of the voltage transients could be reproduced. D, Modeling of all 5797 spines explicitly as individual compartments, consisting of a head and a neck, did not obviously improve the results of the fit (red dashed trace), indicating that the electrical properties of spines can be adequately represented by scaling R_m and C_m of spine-bearing dendritic compartments (green trace).

Figure 7.

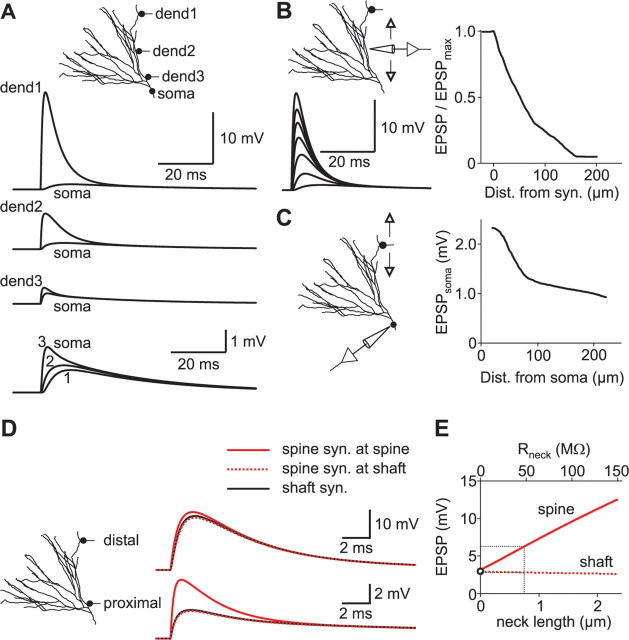
Dendrosomatic attenuation of excitatory synaptic potentials. A, Local and somatic voltage responses to excitatory postsynaptic conductance changes in distal (dend1), middle (dend2), and proximal (dend3) dendrites were simulated. Traces at the bottom show the somatic responses at higher magnification. B, Left, A single EPSP was elicited in a distal dendrite. Traces show voltage transients from different locations along a path from the dendrite to the soma. Right, The relative amplitude of the EPSP (EPSP/EPSP_max) is plotted against distance from the synapse. C, Left, Single EPSPs were elicited at different locations along a path between a distal dendrite and the soma, and EPSP amplitudes were measured at the soma. Right, The somatic EPSP amplitude is plotted against the distance of the synapse from the soma. D, EPSPs evoked in spines and dendritic shafts were compared. Left, Single EPSPs were evoked in either distal or proximal parts of the dendritic tree. Right, Single EPSPs evoked in distal (top traces) and proximal (bottom traces) dendrites. Synapses were either placed on spine heads (red traces) or directly on the adjacent dendritic shaft (black traces). Spine neck length was 0.75 μm. E, EPSPs were evoked in a proximal spine with varying neck length, and the resulting EPSP amplitudes were plotted against both neck length and axial neck resistance (R_neck). The open circle corresponds to a synapse that was placed directly on the dendritic shaft. The black dotted lines correspond to a neck length of 0.75 μm, as used in D.

Segment length was adjusted according to the “d_lambda rule” (Carnevale and Hines, 2006) as follows. The alternating current (AC) length constant λ_AC at 1 kHz was calculated for each section, and the number of segments per section (nseg) was increased until the length of segments was below 3.3% of λ_AC. Further increasing nseg by a factor of 3 had no effect on the results of the simulations. The integration time step was fixed to 10 μs. Frequency-dependent voltage attenuation was computed using the impedance tools built into NEURON (Carnevale et al., 1997).

R_m, C_m, and R_i were obtained by direct least-squares fitting of the response of the model to the experimental data in NEURON using the built-in “Brent's principal axis” algorithm that minimizes the sum of squared errors (χ²). To constrain model parameters, voltage responses to short (0.5 ms) current pulses were used (Turner, 1984a; Clements and Redman, 1989; Rall et al., 1992), and χ² was calculated during a period of 100 ms starting at the onset of the current pulse. The initial phase (3.5 ms) representing the fast charge redistribution was weighted by a factor of 10 to increase the contribution of R_i to the goodness of the total fit. In three cells, we additionally included long current pulses (500 ms) into the fit. This changed the best-fit parameters by only 5.2 ± 3.2% in these three cells. For cable models based on dual somatic recordings, only traces from the voltage recording electrode (not from the current injection electrode) were used. For the cable model based on a simultaneous somatodendritic recording (see Fig. 5), voltage responses from both electrodes were used for the fit. However, fits to transients recorded with the current injection electrode were started 2.5 ms after termination of the current pulses to avoid artifacts attributable to pipette capacitance and series resistance compensation.

Figure 5.

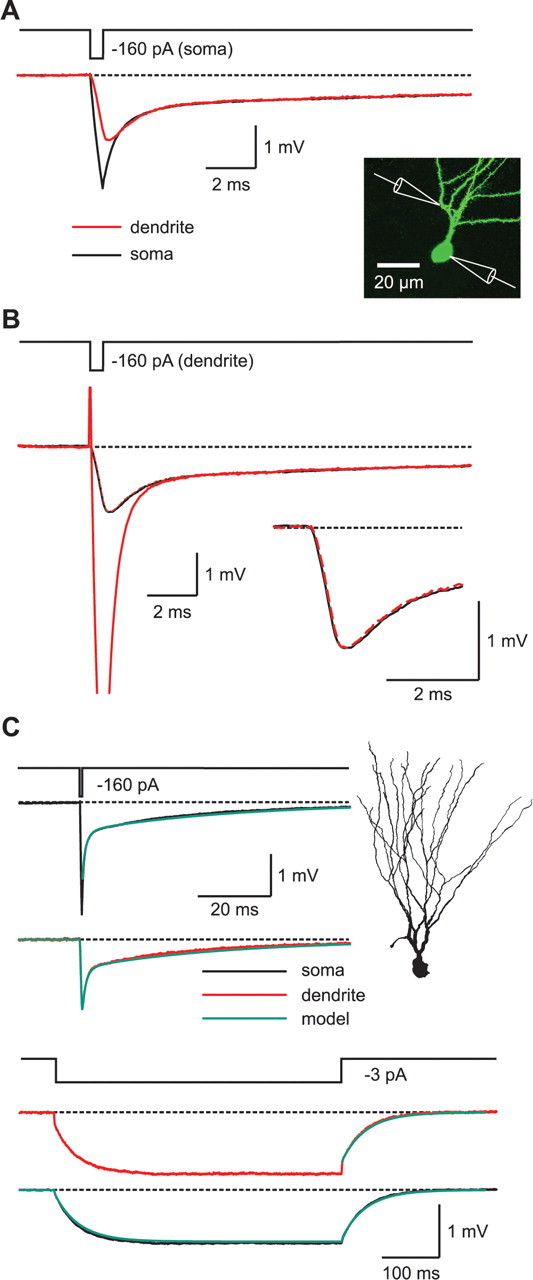
Simultaneous somatic and dendritic recordings directly show the intracellular charge redistribution during transient voltage pulses. A, Voltage response at the soma (black) and at a dendrite ∼50 μm from the center of the soma (red) when a brief current pulse (0.5 ms, −160 pA) was applied to the soma. B, Voltage response at the dendrite (red) and at the soma (black) when a brief current pulse (0.5 ms, −160 pA) was applied to the dendrite. The reciprocal dendritic recording from A is plotted superimposed as a red dashed line. The inset shows the location of the somatic and the dendritic pipettes. C, Passive cable model obtained from a simultaneous somatodendritic recording. Either brief (top traces) or sustained (bottom traces) current injections were applied to the soma or the dendrite (0.5 ms, −160 pA or 500 ms, −3 pA, respectively). The voltage responses of the cell to these injections were recorded at both the soma (black) and the dendrite (red).

To account for the effects of the analog low-pass Bessel filter (f_c of 10 kHz) used for data acquisition, we tested the effects of digitally filtering simulated data during the fit procedure with a four-pole Bessel filter. When comparing the results of a fit using filtered data with a fit using unfiltered data, none of the fit parameters had changed by >1.6%. To estimate statistical errors in the fit parameters, we used a bootstrap method, as described previously for cable models of Purkinje cells (Roth and Häusser, 2001). In brief, we analyzed 100 bootstrap replications of the original dataset to obtain 100 best-fit parameters for R_m, C_m, and R_i for each cell. These parameter sets were then used to calculate the statistical SD and the coefficient of variation (CV) of the best-fit parameters.

To test for inhomogenous distribution of the membrane resistance, we introduced a varying R_m for dendrites and soma similar to what was used for neocortical and CA1 pyramidal cells (Stuart and Spruston, 1998; Golding et al., 2005). In brief, R_m changed with distance (d) from the soma according to the following function: R_m (d) = R_end + (R_som− R_end)/(1 + exp[(d − d_half)/k]), with R_m approaching R_som at the soma and R_end at the terminal dendritic membrane (Golding et al., 2005). The half-maximal distance d_half and the slope k were fixed to 50 μm similar to the pyramidal cell models, and R_som and R_end were fitted as free parameters. To test for contribution of the axonal R_m, the same distribution was used with R_end representing the specific membrane resistance at the distal end of the axon.

To estimate the effects of recording temperature on properties of cable models, we scaled our passive membrane parameters, which had been obtained at 22–24°C, by Q₁₀ values previously estimated for layer 2/3 pyramidal cells (Trevelyan and Jack, 2002). Assuming a temperature difference of 10°C, we used Q₁₀ values of 0.51 for R_m, 0.96 for C_m, and 0.80 for R_i.

Although thick-walled pipette glass and capacitance compensation were used, a residual capacitive component of the pipette tips might contribute to the recorded voltage signals (Roth and Häusser, 2001). Therefore, pipette tips were incorporated into the model. Their capacitance per unit length was included as an additional free parameter into the fits, and their total axial resistance was adjusted so that it matched the series resistance (Roth and Häusser, 2001). Pipette models had a length of 1 mm, an initial diameter of 1 μm, and a final diameter of 128 μm. Best-fit values for the total capacitance of our pipette models were always close to 0 (0.26 ± 0.20 pF; n = 8), indicating that the capacitance of the used pipette glass was well compensated during the experiments.

Synaptic simulations.

Synaptic conductance changes were simulated using the sum of two exponential functions with τ_rise = 0.2 ms and τ_decay = 2.5 ms (Colquhoun et al., 1992; Geiger et al., 1995), a reversal potential of 0 mV, and peak conductances of 1 nS (see Fig. 7) or 0.1 nS (see Fig. 8). When a voltage clamp was simulated at the soma of a granule cell model, synaptic conductance changes with these kinetics led to somatic voltage-clamp currents that decayed with time constants between 3.9 ms (proximal synapses) and 7.4 ms (distal synapses), which is in close agreement with published data of EPSCs in dentate gyrus granule cells obtained under whole-cell voltage-clamp conditions (Keller et al., 1991). The CA1 pyramidal cell models (Golding et al., 2005) were downloaded from http://www.northwestern.edu/neurobiology/faculty/spruston/sk_models/JP_2005/Attenuation.zip. To create an isopotential cell without any fast charge redistribution (see Fig. 8B), R_i was set to 10⁻⁹ Ω cm to avoid numerical problems that would have resulted from setting it to 0.

Figure 8.

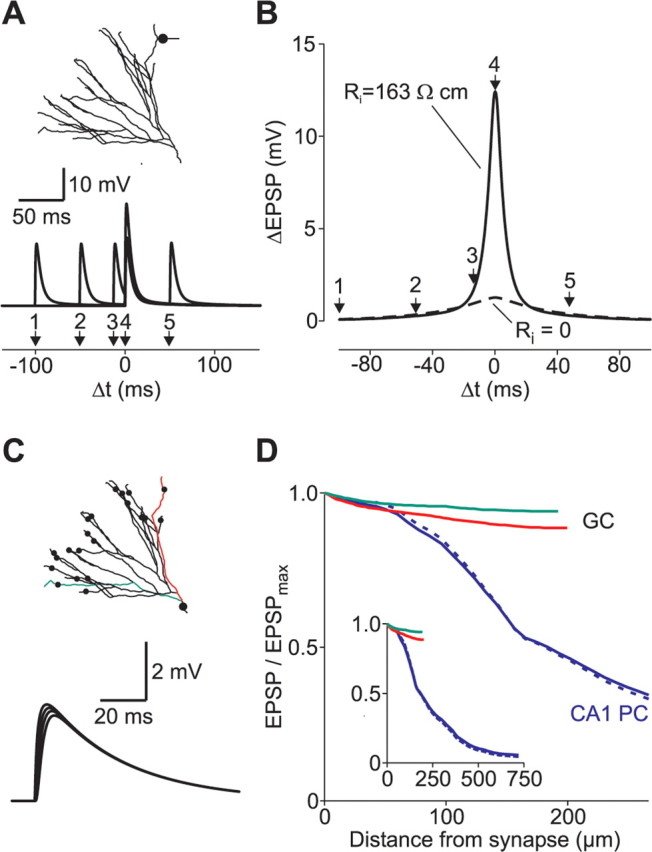
Temporal and spatial summation of coincident synaptic potentials. A, Two EPSPs were evoked at the same synaptic site in a distal dendrite at different time intervals to analyze temporal summation. B, Local differences in EPSP peak amplitudes measured at the synaptic site were plotted against the time interval between the two simulated synaptic events (solid line). The width of the summation window at half-maximal amplitude was 10.6 ms. When R_i was set to 0, the initial charge redistribution was abolished. This enlarged the width at half-maximal amplitude to 56.8 ms (dashed line). C, Twenty-two distal synapses were activated simultaneously (black circles). Traces show examples of voltage transients from different locations along the red dendrite. D, EPSP peak amplitudes at different dendritic locations were normalized to the maximal amplitude at the synaptic site (EPSP_max) and plotted against distance from synapse. The green and red curves correspond to the green and red dendrites of the granule cell (GC) depicted in C. The blue traces show the attenuation in a CA1 pyramidal cell (PC) when multiple synapses are activated (model taken from Golding et al., 2005). Synaptic kinetics were either set to the same values as for the granule cell model (blue solid line; τ_rise of 0.2 ms; τ_decay of 2.5 ms) or adopted from the original publication by Golding et al. (blue dashed line; τ_rise of 0.5 ms; τ_decay of 5 ms).

Results

Linear voltage responses to small current injections

We performed dual-pipette patch-clamp recordings from the soma of mature hippocampal granule cells in brain slices from 2- to 4-month-old adult mice (Fig. 1A). To avoid recording from newly generated immature granule cells, we focused on the outer regions of the granule cell layer (Schmidt-Hieber et al., 2004). Passive membrane properties were analyzed at the resting potential of granule cells (V_m of −80.4 ± 1.3 mV; n = 8), by injecting rectangular current pulses via one of the two patch pipettes. Only voltage responses that were recorded with the other electrode were used for analysis (Fig. 1B). By separating the current injection from the voltage recording site, we avoided artifacts arising from series resistance and pipette capacitance compensation that would otherwise have distorted the initial phase of the voltage transient (Fig. 1B). This is particularly important because only a precise estimate of the initial fast charge redistribution allows the accurate determination of the intracellular resistivity, R_i (Major et al., 1994; Thurbon et al., 1998; Roth and Häusser, 2001).

Figure 1.

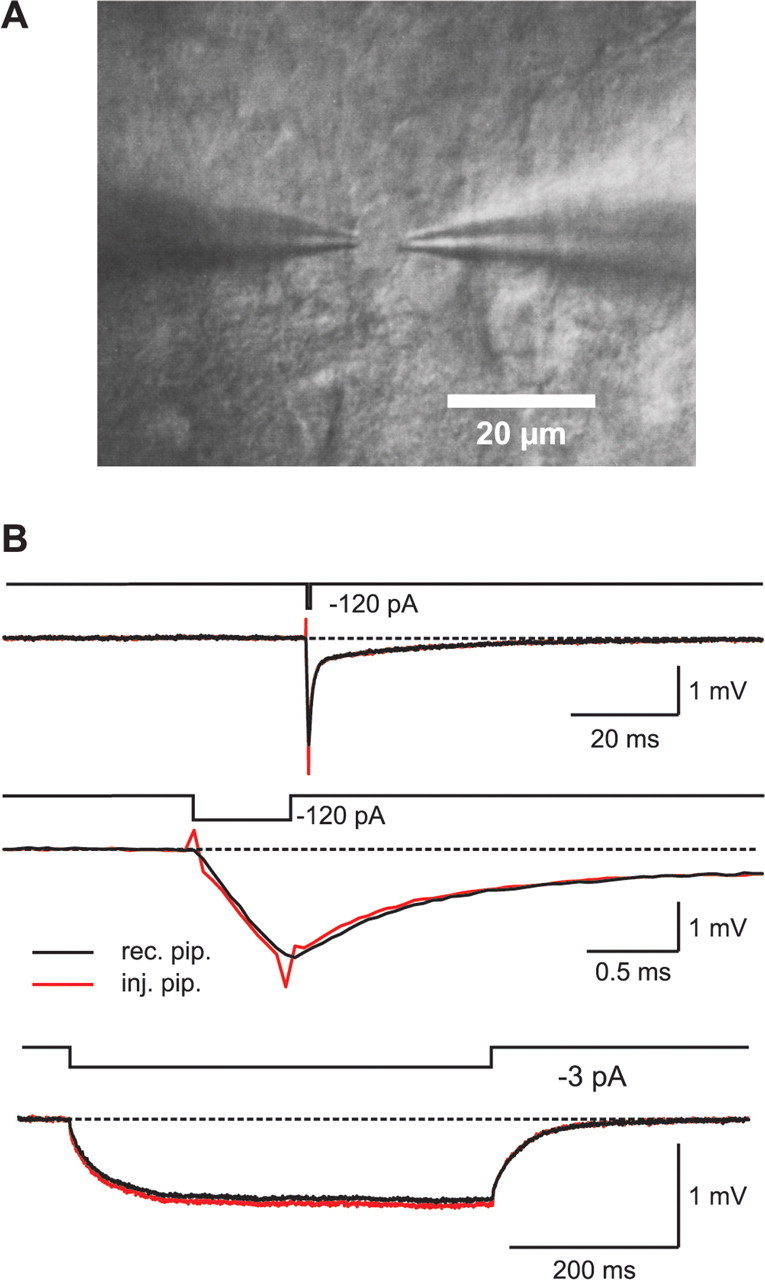
Double-somatic whole-cell recordings from hippocampal granule cells. A, IR-DIC image of two patch pipettes attached to a granule cell soma. B, Top traces, Voltage responses to a brief (0.5 ms, −120 pA) current pulse, recorded either with the current injecting pipette (red trace) or with the pipette that was used only for voltage recording (black trace). Middle traces, Same as above, at expanded timescale. Bottom traces, Voltage responses to a long (500 ms, −3 pA) current pulse.

Injection of small and long hyperpolarizing current pulses (500 ms) (Fig. 1B) revealed an average input resistance of R_N = 308 ± 26 MΩ and a membrane time constant of τ_m = 37.2 ± 2.6 ms (n = 8). These values are very similar to those reported previously for mature granule cells in the adult hippocampus (Spruston and Johnston, 1992; St. John et al., 1997; Schmidt-Hieber et al., 2004).

As a prerequisite for passive cable models, the voltage response has to scale linearly with the injected current. To test whether voltage-dependent conductances were activated, we injected either short (0.5 ms, −160 to +160 pA) or long (500 ms, −6 to +6 pA) current pulses, leading to small voltage changes (Fig. 2A,B) in the range of approximately ±5 and ±2 mV around the resting membrane potential, respectively. The different voltage responses were scaled with the injected current and plotted superimposed. As shown in Figure 2, C and D, no signs of nonlinearity, such as inward rectification or sag, could be found for small voltage transients, consistent with previous reports (Spruston and Johnston, 1992; St. John et al., 1997; Lübke et al., 1998).

To quantify the linearity of negative and positive voltage responses, we scaled the recorded voltage traces with the injected current and plotted the values of the negative pulses against the values measured at corresponding time points during positive pulses (Fig. 2E,F). When a linear fit was applied to these data, the slope of the regression line was 0.99 ± 0.01 (n = 8) for the short and 0.98 ± 0.00 (n = 3) for the long pulses, respectively. Hence, voltage-dependent conductances were not activated within the tested voltage range around resting membrane potential.

High-resolution morphological reconstruction

To obtain high-resolution, 3D morphological data, cells were filled with biocytin during recordings and subsequently labeled with FITC-conjugated avidin (Fig. 3). Fluorescence signals were detected with a two-photon microscope to enable fluorescence excitation and signal detection from deep parts of the tissue block (Fig. 3A). Thereby, it was possible to perform high-resolution whole-mount reconstructions of deep granule cells with fully preserved dendritic trees without resectioning the tissue block after fixation. After acquisition and deconvolution of the 3D image stacks, physical integrity of the dendritic tree was checked and dendrites were reconstructed using an automated filament tracing software (Fig. 3B). After visual inspection of the resulting morphology, obvious errors were manually corrected according to the measured fluorescence data.

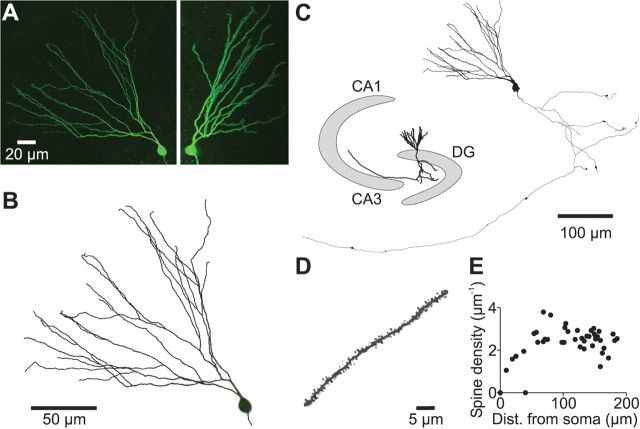
Figure 3.

Three-dimensional reconstruction of soma, axon, and dendrites of granule cells. A, Merged images of a stack of 350 optical sections obtained with a two-photon microscope (left, x–y projection; right, y–z projection). A deconvolution algorithm was used to improve resolution. The cell was filled with biocytin during whole-cell recording and subsequently labeled with FITC–avidin. B, Overlay of the reconstructed dendritic tree (black lines) and the original fluorescence data (gray). To obtain objective morphological data, the majority of the dendrites (∼80%) was reconstructed using an automated filament tracing software; the remaining dendrites were traced manually. C, Shape plot of the morphological data exported into NEURON. The inset shows the approximate position of the cell within the hippocampus. DG, Dentate gyrus. D, A typical spine-bearing dendrite from a different cell at high magnification. E, Spine density on all of the dendrites of the cell was plotted against distance of the center of the dendrite from the soma.

Reconstructed granule cells had on average 32 ± 3 dendritic branches and a total dendritic length of 2264 ± 133 μm (n = 8). The diameters of the dendrites ranged from 1.51 ± 0.11 μm in proximal to 0.73 ± 0.04 μm (n = 8) in distal dendritic compartments. These diameter estimates were very similar to the values obtained with electron microscopy for adult rat granule cells ranging from 1.4 to 0.7 μm in proximal and distal dendritic compartments, respectively (Hama et al., 1989). As the dendrites were densely covered by synaptic spines, we further obtained estimates of spine density by counting spines on two-dimensional projection images of the dendrites (Fig. 3D). After correcting numbers for spines hidden by the dendritic shaft (see Materials and Methods), an average spine density of 2.39 ± 0.06 μm⁻¹ (n = 8) was obtained, very similar to what was reported for rat dentate gyrus granule cells using electron microscopy (Hama et al., 1989). Thus, dendritic spines substantially increase the total membrane surface area to 191 ± 7% (n = 8 cells) of its value without spines. Spines were incorporated into the models by scaling R_m and C_m of spine-bearing dendrites appropriately.

Detailed cable models accurately reproduce fast and slow voltage transients

To obtain estimates of the passive membrane parameters R_m, C_m, and R_i, we fitted the voltage responses of the model to both short and long current pulses to the experimental data. Using uniform parameter distributions throughout the cell, both the fast and the slow components of voltage transients could faithfully be reproduced (Fig. 4A,B). When spines were omitted from the model, an accurate fit of the experimental data could not be obtained (Fig. 4C). Because spines were implemented in our model by scaling the parameters that depend on membrane surface area, this phenomenon could not be explained if spines increased the area uniformly by a constant factor throughout the cell. Instead, the increase in membrane surface area was larger in more distal compartments attributable to two different factors. First, the relative contribution of individual spines is dependent on the membrane area per unit length and therefore on the diameter of the dendritic shaft ranging from 1.51 μm in proximal to 0.73 μm in distal dendritic compartments. Second, the density of spines is nonhomogenously distributed, resulting in spine correction factors ranging from 1.7 ± 0.1 to 2.3 ± 0.1 (n = 8) in proximal and distal compartments, respectively.

These findings emphasize the importance of an exact morphological reconstruction, ideally based on high-resolution imaging techniques. On average, passive membrane parameters obtained from eight cable models were as follows: R_m = 38.0 ± 2.3 kΩ cm², C_m = 1.01 ± 0.03 μF cm⁻², and R_i = 194 ± 24 Ω cm (Table 1). To assess statistical errors, a bootstrap method was used (Roth and Häusser, 2001). Analyzing 100 bootstrap replications of the original dataset revealed that the CV for R_m was 3.7% and the CV for C_m and R_i was only 1.6 and 1.9%, respectively (Table 1). This indicates that the fitted parameters of the model cells are well constrained by the experimental data. Furthermore, C_m converged to values that were similar to those measured in nucleated patches as the specific membrane capacitance for neuronal and non-neuronal cell membranes (0.9–1.0 μF cm⁻²) (Gentet et al., 2000). Finally, the membrane time constant predicted by the models τ_m = R_m C_m = 38.4 ms is close to the experimentally measured value of τ_m = 37.2 ± 2.6 ms (n = 8) and close to previous estimates of τ_m in adult hippocampal granule cells using patch-clamp recordings (25–43 ms) (Spruston and Johnston, 1992; St. John et al., 1997).

Table 1.

Best-fit parameters obtained for different granule cells

	Rm (kΩ cm2)	CV (%)	Cm (μF cm−2)	CV (%)	Ri (Ω cm)	CV (%)	Surface area (1000 μm2)	Number of spines
Cell 1	39.3	3.1	0.89	1.1	225	0.4	12.1	4933
Cell 2	41.7	3.8	0.96	1.0	198	1.5	17.6	6830
Cell 3	44.9	7.6	0.90	3.3	93	2.2	14.0	6089
Cell 4	44.7	4.3	1.05	1.0	218	0.9	11.8	4494
Cell 5a	24.9	4.0	1.06	0.9	140	1.4	14.4	5942
Cell 6a	36.1	2.5	1.10	2.7	320	3.1	10.1	3091
Cell 7a	36.4	3.0	1.00	1.0	163	1.2	15.8	5797
Cell 8	35.8	1.1	1.14	1.8	191	4.2	10.9	4925
Mean ± SEM	38.0 ± 2.3	3.7	1.01 ± 0.03	1.6	194 ± 24	1.9	13.3 ± 0.9	5262 ± 410

The electrophysiological data were obtained with double recordings from the soma except for cell 8, for which somatodendritic double recordings were used. Stochastic error attributable to recording noise was assessed using a bootstrap method, and variability of best-fit parameter values is given by the CV. Surface area includes somatic, dendritic, axonal, and spine membrane.

^aCells with a long reconstructed axon reaching the CA3 area.

By using double patch-clamp recordings to separate the current injection from the voltage recording electrode, we were able to also fit the rapid initial part of the transient voltage signals (Fig. 4), which reflects intracellular charge redistribution and essentially constrains R_i (Rall et al., 1992; Roth and Häusser, 2001). To directly determine R_i in other cell types, double recordings from dendrites and somata were used (Stuart and Spruston, 1998; Roth and Häusser, 2001; Golding et al., 2005). As granule cells have particularly thin dendrites (diameter of ≈0.7–1.5 μm), direct dendritic recordings with conventional patch pipettes are not possible. Therefore, we used a modified approach to further analyze dendritic cable properties. We performed simultaneous recordings from the soma and artificial terminal dendritic expansions that arose from the slicing procedure, similar to what has been described for simultaneous somato-axonal recordings (Fig. 5) (Shu et al., 2006).

Simultaneous somatodendritic recordings during brief somatic current injections revealed that the fast initial component is strongly attenuated, whereas the slow component has a similar amplitude and time course (Fig. 5A), showing that the initial component is attributable to a rapid intracellular charge redistribution (Rall et al., 1992). In contrast to double recordings from pyramidal cells (Stuart and Spruston, 1998; Golding et al., 2005), the somatic and dendritic traces apparently converge during the late phase of the transient, suggesting a similar specific membrane resistance R_m in granule cell soma and dendrites. We also injected brief current pulses into the dendrite and recorded dendritic and somatic voltage responses (Fig. 5B). The dendritic voltage transient was substantially larger on dendritic current injection because of the higher local input impedance. Nevertheless, the somatic and dendritic transients rapidly converged, suggesting homogenous distribution of membrane properties. The comparison of the somatic transient evoked by dendritic injection (Fig. 5B, continuous black line) with the dendritic transient obtained with somatic injection (Fig. 5B, dashed red line) shows that the propagated responses were virtually identical. The symmetry against interchanging input and recording positions is a characteristic feature of linear electrical systems and has been shown to apply to passive dendritic trees with complex morphology as well (Major et al., 1993). The result of this reciprocity test therefore indicates that propagation occurred in a linear system, further demonstrating that voltage-dependent conductances were not activated.

After reconstruction of the full 3D morphology, we obtained a passive cable model from a somatodendritic recording (Fig. 5C). The final model (R_m = 35.8 kΩ cm², C_m = 1.14 μF cm⁻², and R_i = 191 Ω cm) could well reproduce the voltage responses to both short and long current pulses in the somatic and dendritic compartment. In contrast to neocortical and CA1 pyramidal cells, dendritic and somatic responses in granule cells were well reproduced by a homogenous distribution of cable parameters (Stuart and Spruston, 1998; Golding et al., 2005). To further test for inhomogeneity, we introduced independent somatic and dendritic membrane resistances R_som and R_end as free parameters in the model (see Materials and Methods). However, the quality of the fit improved only insignificantly, as quantified by a relatively small reduction of χ² by 3.3%, indicating that a homogenous distribution of model parameters is sufficient to reproduce the subthreshold voltage propagation in dentate gyrus granule cells, similar to what has been found in cerebellar Purkinje cells and spinal motoneurons (Thurbon et al., 1998; Roth and Häusser, 2001).

Granule cells are electrotonically compact at frequencies up to the gamma range

For detailed analysis of subthreshold dendritic signal processing, we first performed a comparative computational analysis of the steady-state voltage attenuation in models of granule cells and CA1 pyramidal cells (published by Golding et al., 2005) (Fig. 6). Steady-state voltage attenuation from the granule cell soma into the distal dendrites was small (88.4 ± 0.8% of the somatic voltage response at an average distance of ∼210 μm from soma; n = 8 cells) (Fig. 6A). This corresponds to an average electrotonic distance of L = 0.50 ± 0.02, indicating that granule cells are electrotonically compact. In contrast, voltage attenuation from the soma into distal dendrites of CA1 pyramidal cells was much more pronounced (15.2 ± 9% of the somatic voltage response at an average distance of ∼720 μm from soma; n = 3) because of a different geometry, lower R_m, and high expression levels of I_h channels (Fig. 6, blue) (Golding et al., 2005).

Figure 6.

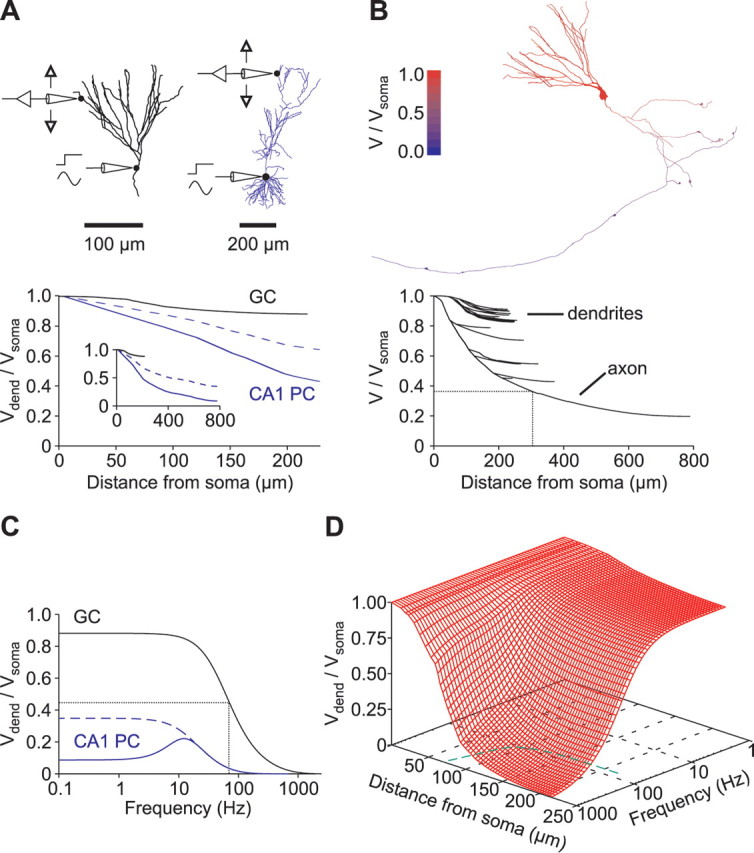
Somatofugal voltage propagation along granule cell dendrites and axons. A, Steady-state voltage attenuation. Top, Granule cell (GC) (left) and CA1 pyramidal cell (PC) morphology (right) (taken from Golding et al., 2005). Bottom, Steady-state voltage attenuation (V_dend/V_soma) is plotted against distance from soma. Voltage attenuation in the CA1 pyramidal cell was measured in either the presence (solid blue line) or absence (dashed blue line) of I_h. The inset shows the same plot with a longer distance axis. B, Left, The color code indicates steady-state voltage attenuation (red, no attenuation; blue, complete attenuation). Right, Steady-state voltage attenuation of all compartments is plotted against distance from the granule cell soma. The dotted lines indicate where axonal voltage has decayed to e⁻¹ of the somatic value. C, Voltage attenuation (V_dend/V_soma) in a distal dendrite is plotted against the frequency of the sinusoidal command voltage at the soma. The same cells as in A were used. The dotted lines indicate where the ratio has decreased to its half-maximal value (f_50%). Voltage attenuation in the CA1 pyramidal cell was measured either in the presence (solid blue line) or in the absence (dashed blue line) of I_h. Note the resonance maximum at ∼12 Hz when I_h is present. D, Attenuation is plotted against both frequency and distance from soma (red grid). The dashed green line on the bottom plane is a plot of the critical frequencies (f_50%) against distance from soma.

In three of eight cells, the axon was well preserved within the brain slice and was reconstructed into the CA3 region in which mossy fiber boutons terminate onto CA3 pyramidal cells (Fig. 3C) (Bischofberger et al., 2006b). Simulations showed that varying R_m in the axon by a factor of two (see Materials and Methods) had only little influence on voltage responses recorded at the soma. The voltage transients during short current pulses changed on average by 0.004 ± 0.002 mV (n = 3), corresponding to ∼0.2% of the peak amplitude per twofold increase in axonal R_m. Therefore, R_m in the full extent of the axon might not be constrained by our fitting procedure. Nevertheless, if we assume a homogenous distribution of parameters throughout the somatodendritic and axonal domain, simulations of voltage attenuation along the granule cell axon revealed a length constant of 296 μm (Fig. 6B). Therefore, in the CA3 region, at 500 μm distance from the soma, steady-state voltage would still be 25% of its somatic value (Fig. 6B), indicating that somatic subthreshold potentials can propagate to presynaptic terminals to modulate transmitter release, consistent with recent findings (Alle and Geiger, 2006; Shu et al., 2006).

We next examined the attenuation of sinusoidal voltage waveforms in our cable models. When the frequency of somatic voltage signals was progressively increased, the voltage amplitude measured at the tips of all distal dendrites decreased to 50% of its steady-state value at a critical frequency (f_50%) of 74 ± 4 Hz (n = 8 cells), close to the upper spectral limit of hippocampal gamma oscillations (30–80 Hz) (Penttonen et al., 1998). This is substantially higher than the critical frequency measured in distal apical dendrites using models of CA1 pyramidal cells (18 ± 2 Hz in dendrites of the apical tuft if I_h was absent; n = 3 model cells) (Fig. 6C). To test the filtering behavior of more proximal granule cell dendrites, we measured frequency-dependent voltage attenuation at various locations along the dendritic tree (Fig. 6D). Propagation of oscillating potentials above the gamma frequency range was confined to dendrites that were <100 μm away from the soma. These simulations suggest that granule cell dendrites very effectively promote somatodendritic voltage propagation but act as low-pass filters for transient voltage signals with high-frequency components above the gamma range.

Because the recordings for the CA1 pyramidal cell models were obtained at a higher temperature than our models, we tested for the effects of temperature by scaling our passive membrane parameters with Q₁₀ values previously reported for layer 2/3 pyramidal cells (Trevelyan and Jack, 2002) (see Materials and Methods). However, there was only a small increase in steady-state attenuation in granule cells dendrites at ∼34°C (82.7 ± 1.1 vs 88.4 ± 0.8% of the somatic voltage response). Furthermore, the critical frequency for the dendritic propagation of sinusoidal voltage waveforms was even slightly higher (f_50% of 102 ± 4 vs 74 ± 4 Hz), further emphasizing the difference between granule and pyramidal cells. Taken together, cable properties of dentate gyrus granule cells appear to be substantially different from those of hippocampal CA1 pyramidal cells.

Fast initial charge redistribution shapes synaptic integration

To study the integration of synaptic potentials within the dendritic tree, we simulated excitatory synaptic inputs at different dendritic locations. Single glutamatergic synapses with a peak conductance of 1 nS and a reversal potential of 0 mV were placed on distal, middle, or proximal parts of the dendritic tree (Fig. 7A). The local response varied strongly depending on the synaptic location: whereas distal synaptic conductance changes led to a local depolarization of 18.9 mV, proximal events only caused a local depolarization of 3.1 mV, showing that the local charging of the cell membrane is strongly dependent on synapse location. As the distal EPSPs are attenuated during propagation toward the soma (Fig. 7B), the differences were less pronounced when the EPSP amplitude was measured at the soma rather than locally (Fig. 7A,C). Thus, the longer propagation distance of distal synaptic events appears to be outbalanced by a higher local input impedance, leading to similar dendrosomatic charge transfer for different synapses throughout the dendritic tree, a phenomenon that has been termed “passive normalization” (Jaffe and Carnevale, 1999). These data indicate that even distal synaptic inputs can effectively depolarize the granule cell soma.

The time course of the somatic EPSPs, however, appears to be strongly dependent on synapse location (Fig. 7A): distally evoked EPSPs (dend1) showed a slow rise time (t_20–80) of 3.6 ms (20–80%) and a monoexponential decay with a time constant of 36.4 ms, very similar to τ_m (36.5 ms in this granule cell). In contrast, the rise time of proximally evoked EPSPs (dend3) was much faster (t_20–80 of 0.8 ms), and the decay followed a biexponential time course with fast and slow time constants (τ_f) = 3.6 ms (18% of amplitude) and τ_s = 35.1 ms (82% of amplitude), respectively. This indicates that proximal synaptic inputs depolarize the somatic cell membrane to a similar extent as distal synaptic inputs; however, the temporal control of the somatic voltage is different (Turner, 1984b; Geiger et al., 1997; Roth and Häusser, 2001).

The kinetic differences of the local dendritic EPSPs are even more pronounced. The proximal EPSP had a local rise time of t_20–80 = 0.6 ms and a biexponential decay with an amplitude-weighted time constant of τ_w = 20.6 ms (dend3). In contrast, the distal dendritic EPSP showed a much faster time course (t_20–80 of 0.6 ms and τ_w of 8.8 ms; dend1) attributable to strong local charging of the dendritic cell membrane and rapid subsequent charge redistribution.

Excitatory synapses on granule cells are located on dendritic spines with different morphologies (Hama et al., 1989). To assess the influence of synaptic spines on shape and passive propagation of EPSPs, we simulated synaptic conductance changes located either on spine heads or on the adjacent dendritic shaft (Fig. 7D) (Turner, 1984b). A typical spine was modeled with a neck (length, 0.75 μm; diameter, 0.18 μm) and a head (length, 0.5 μm; diameter, 0.5 μm) according to electron microscopy data (Hama et al., 1989), resulting in an axial neck resistance (R_neck) of 44.7 MΩ. In a distal dendrite, the ratio of EPSP amplitudes in the spine head and in the adjacent dendritic shaft was only 111% (Fig. 7D, top traces). However, in a proximal dendrite, attenuation by the spine neck was more pronounced, with an amplitude ratio of 214% (Fig. 7D, bottom traces).

Placing synapses directly on the dendritic shaft rather than on spine heads had only very little influence on EPSP waveforms recorded at the dendritic shaft, with an amplitude difference of <4% for both distal and proximal synaptic conductance changes (Fig. 7D, continuous black vs red dotted traces). Because the morphology of spine necks shows substantial variations (Hama et al., 1989), we also varied the spine neck resistance by changing the neck length from 0 to 2 μm at a proximal synapse (Fig. 7E). Surprisingly, the EPSP amplitude in the shaft was only slightly affected. The amplitudes decreased approximately linearly with increasing neck length, corresponding to an attenuation of 4.7%/μm or 7.1%/100 MΩ. Therefore, an increased neck length of 2 μm or a reduced neck diameter of 0.1 μm would be necessary to attenuate the dendritic EPSP amplitude by ∼10%. This relatively small attenuation might be related to the increase in input impedance with larger neck resistance, again leading to a larger local EPSP amplitude in the spine, more efficient charge transfer, and thereby to passive normalization of the EPSP amplitude against spine neck resistance. Thus, for most of the excitatory synapses onto granule cells, the electrical properties of the spines will affect the somatic EPSP amplitude by <10%.

As long as voltage-dependent conductances are not activated, our data are consistent with the view that spines may represent biochemically but not electrically isolated compartments (Turner, 1984b; Nimchinsky et al., 2002). However, large synaptic potentials might preferentially activate voltage-gated conductances in dendritic spines. Taken together, excitatory synaptic inputs in granule cell dendrites can efficiently depolarize granule cell somata, essentially independent of the distance to the soma and the shape of postsynaptic spines. However, the time course of proximal and distal synaptic potentials is substantially different attributable to the rapid dendritic charge redistribution.

Temporal and spatial integration of synaptic potentials

Because distal EPSPs decay much faster than the membrane time constant, temporal summation of dendritic EPSPs might also be restricted to short time intervals. To quantify the time window for temporal summation of dendritic voltage transients, we simulated two synaptic events separated by time intervals of variable duration at distal dendritic sites. The temporal summation was quantified as the increment ΔEPSP relative to the amplitude of a single EPSP and plotted against the time interval in Figure 8, A and B. When the original R_i, as determined by the fitting procedure, was used, the window for temporal summation had a half-width of 10.8 ± 0.5 ms (n = 8 cells). To estimate the contribution of the initial charge redistribution in shaping the time window, these simulations were repeated in the same model but with R_i set to 0, thereby creating an isopotential cell. In this model, the time window had a half-width of 58.1 ± 2.8 ms. Using the original R_i, the summation of the EPSP amplitude measured at the soma had a similar half-duration of 70.7 ± 3.2 ms (n = 8), indicating that the initial charge redistribution narrowed the time window of local dendritic EPSP summation to 15% of the somatic EPSP-summation time window.

We next examined the spatial summation of simultaneously active distributed synaptic inputs in granule cells. Synapses with a conductance of 0.1 nS were placed on each distal dendrite of the granule cells (Fig. 8C). In this case, there was only little voltage attenuation, especially when compared with the CA1 pyramidal cell model: the EPSP amplitude at the soma was on average 78 ± 4% (n = 8 cells) of the local EPSP amplitudes at the sites of synaptic conductance changes versus 4.5% obtained in simulations with the CA1 model (Fig. 8C,D). Scaling passive parameters in granule cells to account for the effects of the different recording temperatures had only a minor effect on the estimate of attenuation (76 ± 4%). These data indicate that the fast initial charge redistribution within the granule cell dendritic tree leads to a marked attenuation of single, distal synaptic potentials and to a remarkably narrow time window for dendritic EPSP summation. At the same time, multiple simultaneously active glutamatergic synapses can depolarize the entire cell homogenously with relatively small attenuation.

Discussion

The present results provide a detailed analysis of the passive signal propagation within the dendritic tree of hippocampal granule cells using dual somatic and dendritic whole-cell patch-clamp recordings. We report that granule cells are electrotonically much more compact than hippocampal pyramidal cells, leading to faithful propagation of somatic voltage waveforms toward distal dendrites and to effective depolarization of the somatic membrane by proximal and distal synaptic inputs. Nevertheless, dendritic synaptic potentials show a remarkably rapid time course, much faster than the membrane time constant, enabling local dendritic information processing with high temporal precision.

Detailed cable model of dentate gyrus granule cells

By combining two-photon microscopy with 3D deconvolution, we were able to generate three-dimensional datasets that allowed precise tracing of the dendritic tree of adult mouse dentate gyrus granule cells. By fitting small voltage responses to brief and long current pulses, we were able to constrain a passive cable model with homogenously distributed parameters (R_m = 38.0 kΩ cm², C_m = 1.01 μF cm⁻², and R_i = 194 Ω cm), which is fundamentally different from granule cell models obtained previously using sharp microelectrodes (e.g., R_m of 2–4 kΩ cm²) (Durand et al., 1983; Turner and Schwartzkroin, 1983). Using dual patch-clamp whole-cell recordings, we were able to avoid several sources of artifacts. First, because the seal resistance was always larger than ∼5 GΩ, we could avoid leakage of current via somatic shunt conductances (I ≤ 0.2 pA during a 1 mV pulse). Second, transient voltage responses could be used from the very beginning of the current injection pulse, because capacitive artifacts were prevented by separating the current injection from the voltage recording pipette. Finally, in one case, we were able to develop a compartmental model after performing a somatodendritic double recording, which allowed direct experimental analysis of the intracellular voltage propagation.

The characteristic time course of the voltage responses in granule cells further indicates that the parameters are well defined by the experimental data: because the initial charge redistribution is mostly completed within the first 5 ms (Figs. 4, 5), it is temporally well separated from the slower spatially homogenous decay of the membrane potential back to baseline with the membrane time constant τ_m = R_m C_m. Furthermore, the amplitude of the slow component is strongly dependent on the specific membrane capacitance, suggesting that R_m and C_m are uniquely determined (Rall, 1977). An additional constraint is given by the initial charge redistribution, which reflects the equalization of voltage differences between different cellular compartments (Fig. 5). Because the time course of this equalization is strongly dependent on R_i (Rall et al., 1992), all three fitted parameters were well constrained by different aspects of the recorded voltage transients.

The obvious separation of the initial fast and the late slow component decaying with a monoexponential time course was also reported for cerebellar Purkinje cells, which were also shown to be electrotonically compact (Roth and Häusser, 2001). In contrast, neocortical and CA1 pyramidal cells have much larger dendritic trees, are less compact, and do not show this pronounced separation of fast and slow components (Stuart and Spruston, 1998; Golding et al., 2005). These findings indicate that the ratio of the time constant of the slow decay (τ_m) and the fast time constants (τ_n) in different types of neurons is dependent on the electrotonic length L of the dendrites, as predicted by linear cable theory (Rall et al., 1992). For a uniform passive equivalent cylinder, these ratios can be explicitly calculated as τ_m/τ_n = 1 + (nπ/L)² (n = 1, 2, 3…) (Rall, 1977).

Frequency-dependent signal propagation

In contrast to previous models, we found that steady-state attenuation of voltages in granule cell dendrites is remarkably small. The smaller voltage decay from the soma toward the distal dendrites of only ∼12% is very likely attributable to a higher specific membrane resistance R_m of 38.0 kΩ cm², which is substantially larger than what was reported previously (2–4 kΩ cm²) (Durand et al., 1983; Turner and Schwartzkroin, 1983; Turner, 1984a). It is also larger than what was described more recently for dendrites of CA1 pyramidal cells (10–32 kΩ cm²) (Golding et al., 2005), indicating different voltage attenuation in hippocampal granule cells versus pyramidal cells.

By using a CA1 pyramidal cell model published by Golding et al. (2005), we could directly compare dendritic voltage propagation in apical dendrites of the two different types of neurons and found substantial differences. First, steady-state voltage attenuation in granule cells was smaller at similar distances from the soma. Second, because the physical length of pyramidal cell dendrites was approximately three times larger, voltage attenuation toward distal dendrites was dramatically larger in pyramidal cells (15% of V_soma) compared with granule cells (88% of V_soma). Finally, propagation of sinusoidal voltage waveforms with different frequencies was also more effective in granule cells with half-maximal attenuation at four times higher frequencies (f_50% of 74 Hz vs 18 Hz in pyramidal cells). These data indicate that somatic voltage control of distal dendrites, on which entorhinal synaptic inputs terminate in both cell types, is remarkably different.

Dendritic coincidence detection

Because of the powerful voltage attenuation in pyramidal cell dendrites, it was suggested that distal synaptic inputs may only influence somatic output if dendritic voltage-gated conductances are activated (Magee and Johnston, 1995; Golding et al., 2005). Furthermore, the large electrotonic distance of dendritic inputs from the soma is believed to increase the computational power of individual neurons by restricting dendritic voltage changes to parts of the dendritic tree. For example, local dendritic coincidence detection was shown to be important for initiation of dendritic spikes and induction of synaptic plasticity (Softky, 1994; Golding et al., 2002; Williams and Stuart, 2002). Although granule cells have relatively short dendrites and are electrotonically compact, local dendritic coincidence of synaptic potentials might also be important. According to our analysis, dendritic EPSPs show a large amplitude and remarkably brief time course attributable to a high local input impedance and a rapid intracellular charge redistribution. If distal synaptic inputs are activated within a narrow time window of less than ∼10 ms, they will sum up and effectively depolarize the dendritic membrane potential. As a consequence, activation of dendritic voltage-dependent Ca²⁺ channels (Blaxter et al., 1989) and NMDA receptors (Lin et al., 2006) will depend on highly coincident synaptic potentials.

The precise amplitude and time course of excitatory synaptic currents in granule cell dendrites is not known. However, the amplitude of the synaptic conductance might be in the range of 0.1–1 nS, as has been estimated for quantal conductance changes at other hippocampal glutamatergic synapses (Jonas et al., 1993; Stricker et al., 1996; Magee and Cook, 2000). Furthermore, the time course is likely to be dominated by the deactivation of granule cell AMPA receptors, which was shown to be in the range of ∼2.5 ms (Colquhoun et al., 1992; Geiger et al., 1995). Our simulations indicate that an excitatory conductance with a peak amplitude of 1 nS and an exponential decay with a time constant of 2.5 ms evokes a local dendritic EPSP amplitude of ∼20 mV, attenuating to ∼1 mV at the soma. This was essentially independent of whether synapses were placed on the dendritic shaft or on spines, because the electrical properties of synaptic spines attenuated the dendritic EPSPs by <10%. This would indicate that few synapses activated within a narrow time window of <10 ms may be able to relieve voltage-dependent Mg²⁺ block and trigger local dendritic Ca²⁺ influx via NMDA receptors, known to be important for the induction of synaptic plasticity (Golding et al., 2002; Lin et al., 2006).

Functional significance of subthreshold dendritic signal propagation

The high-frequency voltage propagation in the granule cell dendrites might be important for temporal signal processing in the hippocampus. It was shown that hippocampal granule cells and pyramidal cells fire APs in a specific temporal relationship to the theta rhythm when the animal passes through the place field of the cell (Jung and McNaughton, 1993; O'Keefe and Recce, 1993). When the animal is in the center of the place field of a given neuron, this neuron fires APs earlier in the theta cycle than neurons with adjacent place fields (Skaggs and McNaughton, 1996; Skaggs et al., 1996). For temporal coding with high fidelity, neurons with the same place field should fire exactly at the same time, which might be coordinated by inhibitory interneurons firing in the gamma frequency range (30–80 Hz) (Penttonen et al., 1998; McBain and Fisahn, 2001; Csicsvari et al., 2003; Bartos et al., 2007). In particular, it was reported that synchronization of gamma oscillations in the entorhinal cortex and the hippocampus might be correlated with successful learning and memory retrieval (Fell et al., 2001). The properties of the granule cell dendritic tree support precise temporal integration of inhibitory and excitatory synaptic inputs during gamma oscillations.

Furthermore, hippocampal granule cells are believed to be important for the separation of similar entorhinal input patterns during spatial exploration (Chawla et al., 2005; Leutgeb et al., 2007), and pattern separation is known to be dependent on the ability to detect correlations in the input space (Treves and Rolls, 1992). According to our data, coincident activation of dendritic synaptic inputs may locally activate dendritic NMDA receptors important for synaptic plasticity. Therefore, synaptic plasticity might be specifically induced by consistently coactive inputs. Conversely, granule cells are compact, and distal EPSPs show only moderate attenuation compared with hippocampal pyramidal cells (Golding et al., 2005). Together, the high specificity and the large efficacy of synaptic connections will reliably discharge a minimal subset of neurons (Chawla et al., 2005), supporting pattern separation in the hippocampus.

In conclusion, the morphological and electrotonic structure of hippocampal granule cells strongly shapes neuronal function. The effective signal propagation up to the gamma frequency range and the short temporal window for EPSP summation in the range of ∼10 ms might be important for both temporal coding and the unique representation of memory items within the hippocampal network.