Frequency Control of Motor Patterning by Negative Sensory Feedback

Abstract

The sensory system plays a key role in the generation of behavior by providing the nervous system with information about the environment and feedback about body movements such that motor output can continuously be adapted to changing circumstances. Although the effects of sensory organs on nervous system function have been demonstrated in many systems, the impact of sensory activity has rarely been studied in conditions in which motor output and sensory activity can interact as they do in behaving animals. In such situations, emergent properties may surface and govern the characteristics of the motor system.

We studied the dynamics of sensorimotor interaction with a combination of electrophysiological experiments and computational modeling in the locust flight pattern generator, including its sensory components. The locust flight motor output is produced by a central pattern generator that interacts with phasic sensory feedback from the tegula, a proprioceptor that signals downstroke movement of the wing. We modeled the flight control system, and we tested the model predictions by replacing tegula feedback in the animal with artificial feedback through computer-controlled electric stimulation of the appropriate sensory nerves.

With reference to the cycle frequency in the locust flight rhythm, our results show that motor patterns can be regulated via the variation of sensory feedback loops. In closed-loop conditions, tegula feedback strength determines cycle frequency in the model and the biological preparation such that stronger feedback results in lower frequencies. This regulatory mechanism appears to be a general emergent property of negative feedback systems.

Introduction

The perception of external conditions and internal states represents one of the essential tasks of the nervous system. Feedback from peripheral sensors adapts ongoing behavior to the requirements of the environment or the body (review in Pearson, 1986). In many systems with rhythmic motor output, phasic sensory feedback even produces substantial parts of the pattern characteristics and is thus regarded as an integral part of the rhythm generating machinery (Pearson, 2004). Although the effects of sensory organs on motor circuits have been demonstrated in many systems, the idiosyncratic dynamics created by the interaction of sensory activity and pattern generator in behaving animals have only rarely been elucidated. We here show that motor patterns can be regulated via the variation of sensory feedback loops, in principle, and that this mode is implemented in pattern generators. We demonstrate this for a particular feature of the locust flight pattern generator, namely its cycle frequency.

When characterizing sensory organs, the classic emphasis is on how sensory signals alter motor output, or the information flow toward that output, in an open-loop situation, that is, with sensory activity remaining unaffected by motor output. The dynamical components, which are determined by the interaction of motor and sensory activities, are disregarded in these investigations. In behaving animals, and thus closed-loop situations, in contrast, emergent system properties may surface and govern the functional characteristics of the system.

We investigated such emergent properties of sensorimotor interaction using the locust flight pattern generator and its sensory components. Flight motor output is produced by a central pattern generator (cpg) of ∼80 interneurons located in the thoracic ganglia. In the isolated CNS, elevator (wing upstroke) and depressor (wing downstroke) motor neuron discharges alternate with a frequency of ∼10 Hz. In intact animals, interactions between cpg and proprioceptive feedback play an important role in the functionally adequate patterning of motor activity (Wolf and Pearson, 1988). The tegula, a proprioceptive sense organ on the wing, has proven to be of particular importance for the generation of a functional flight rhythm and resulting aerodynamic forces (Wolf and Pearson, 1988; Wolf, 1993). The tegula is activated by the downstroke movement of the wing and accelerates the initiation of elevator activity, therefore speeding up the wing beat rhythm (Büschges and Pearson, 1991).

Here, we show a novel emergent property of proprioceptive feedback. Changes in feedback strength regulate the frequency of the cpg in behaviorally relevant closed-loop conditions. We demonstrate this by modeling the locust flight cpg at different levels of complexity and by applying realistic tegula feedback to these models. To test the model prediction, we deliver computer-controlled artificial sensory feedback to the biological preparation. Our results indicate that the obtained frequency regulation is not restricted to the flight control network and the specifics of tegula feedback but rather represent a general feature of negative feedback loops. We thus provide evidence that variation of sensory feedback regulates centrally generated rhythms and that this mode of pattern regulation has general applicability.

Materials and Methods

Animals and preparation.

All experiments were performed at room temperature (∼22°C) on adult locusts, Locusta migratoria (L.), obtained from a laboratory culture at the University of Ulm. Animals were mounted ventral side up to a fork-shaped holder by their thoracic sternites, and the thoracic ganglia were exposed (details by Wolf and Pearson, 1987). Standard recording techniques were used (Robertson and Pearson, 1982). In all experiments, the forewing tegulae were removed by transecting their bases. Flight was elicited by directing a wind stream onto the animal's head. Measurements were made after the end of this wind stimulus, when the locust had settled into stable flight.

Recording and stimulation.

The activity of the depressor muscle 97 (first basalar muscle of the forewing) (Burrows, 1996) was monitored with electromyographic (EMG) recordings. The fact that there is a time lag (7–8 ms) between the onset of EMG activity in hindwing and forewing muscles was taken into account for data analysis and model implementation.

To stimulate hindwing tegula afferents, the nerve branches arising from both hindwing tegulae (N1C1a) (Fig. 1A,B) were transected and stimulated with extracellular hook electrodes. For recording the compound action potential of the tegula afferents, a second hook electrode was placed on nerve N1C (Fig. 1B, top). In closed-loop experiments and in experiments in which we recorded intracellularly from interneurons and motor neurons, we stimulated N1C to activate the tegula afferents (Fig. 1B, bottom). Because N1C1a and N1C both contain the axons of the tegula afferents, we considered them equally suited for activating tegula input for the purpose of the present study (for specificity of tegula stimulation in N1C, see Pearson and Wolf, 1988). We stimulated the hindwing tegulae because their effects on the flight pattern are stronger and more reliable than those of the forewing tegulae and because the hindwing tegulae contribute to the control of both hindwing and forewing movements, whereas the organs of the forewings are of minor, if any, importance in the context considered here (Büschges et al., 1992; Fischer and Ebert, 1999).

Figure 1.

Techniques. A, Schematic outline of the locust mesothoracic and metathoracic ganglia, viewed in horizontal projection. Filled arrows mark stimulation sites on the bilaterally symmetric afferent tegula nerves N1C1a (open-loop experiments). Open arrows mark the stimulation sites on N1C (closed-loop and intracellular recording experiments). N1–N5, Roots of nerves 1–5. B, Top, Schematic drawings of electrode placements for extracellular stimulation of tegula nerve N1C1a and simultaneous extracellular recording of compound action potential on N1C. Bottom, During intracellular recording of interneurons and motor neurons, N1C was stimulated. C, EPSPs elicited by tegula input in model interneuron 301 at different synaptic strengths. The time constant of decay (7 ms) was unaffected by synaptic strength.

Trains of several voltage pulses (pulse duration, 0.1 ms) were delivered at a repetition rate of 220 Hz to mimic a natural discharge of the receptor organs (Wolf, 1993). Although in open-loop conditions the duration of the stimulus train was 25 ms, it depended on the corresponding cycle period (cp) in closed-loop conditions (see below). In the latter experiments, the calculation of the tegulae feedback was performed in real time with Spike2 (version 5.14; Cambridge Electronic Design, Cambridge, UK) and a 1401plus analog-to-digital board (Cambridge Electronic Design). Intracellular recordings were made using an NPI NEC 10L (NPI, Tamm, Germany) amplifier in bridge or single-electrode discontinuous current-clamp mode.

Evaluation of data.

Data were recorded on computer hard disk using Spike2 (version 5.03–5.14; Cambridge Electronic Design) and a 1401plus analog-to-digital board (Cambridge Electronic Design). Data were analyzed using the Spike2 script language. Individual scripts are available at http://www.neurobiologie.de/spike2. Final figures were prepared with CorelDraw (version 12.0 for Windows; Corel, Ottawa, Ontario, Canada). Graphics and statistics (Student's t test and paired samples t test) were generated using Excel (Microsoft, Seattle, WA). Data are presented as means ± SD. N refers to the number of animals, and n gives the number of trials. For all statistical tests, significance with respect to controls is indicated in the figures using the following symbols: *p < 0.05; **p < 0.01.

The cp of the flight rhythm was defined as the duration between the onset of a depressor burst and the onset of the subsequent burst. Cycle frequency was defined as the 1/cp. Mean values for all rhythm-related parameters were determined from measurements of at least 10 consecutive cycles.

To measure the difference in cycle frequency between flight with and without tegula stimulation, we averaged the cycle frequency of the last four cycles before the onset of a stimulus sequence and compared it with the average of the third and fourth cycles after stimulus onset. The latter measurement was taken, because the effect of tegula stimulation increased during the initial wing beat cycles and reached a steady-state after approximately the third cycle. Alternatively, we used the average of the last four cycles of a flight sequence with tegula stimulation and compared it with the averaged third and fourth cycles after the end of the stimulation. To compare different animals, data were normalized to the mean cycle frequency of flight sequences without tegula stimulation and then averaged.

Simulation.

The locust flight pattern generator was modeled with the simulation environment madSim (Stein and Ausborn, 2004; Straub et al., 2004). madSim is freely available at http://www.neurobiologie.de/madsim. Neurons possessed standard morphology and passive properties according to Ekeberg et al. (1991). Active membrane properties were implemented according to modified Hodgkin–Huxley equations (Table 1) (Hodgkin and Huxley, 1952; Ekeberg et al., 1991). Each ionic current j is represented as the product of the driving force (E_j − V_m), maximum conductance G_j, activation a, and inactivation b:

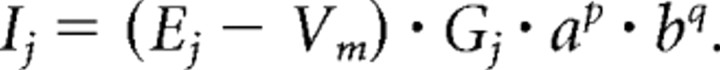In this equation, V_m represents the membrane potential and E_j the reversal potential of current j. Values between 0 and 1 may be assigned to a and b, whereas the exponents p and q may take integer values.

Table 1.

Ion channel parameters

Channel type	Notation	Power	Equilibrium potential (mV)	Maximum conductance (μS)	α			β
					A	V0	s	A	V0	s
Fast Na+	m (activation)	p = 3	50	10	1	−40	−1	−0.06	−49	20
	h (inactivation)	q = 1	50	10	−0.2	−40	1	0.0007	−40	2
Inward rectifier (K+)	n (activation)	p = 4	−90	30	0.02	−31	−0.8	−0.005	−28	0.4

A, Rate constant (mV/ms); V₀, half-maximum potential (mV); s, step width (mV).

The activation a and the inactivation b of each current are described by first-order differential equations of the following form:

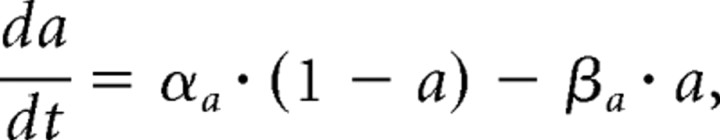where α_a is the rate by which the gates switch from a closed to an open state, and β_a is the rate for the reverse process. α_a is voltage dependent and is of the following form:

where V₀ is the half-maximum potential, A is the rate constant, and s is the step width of the curve. β_a follows the same equation, except for β of the inactivation gate of the fast sodium channel (β_h), which is of the following form:

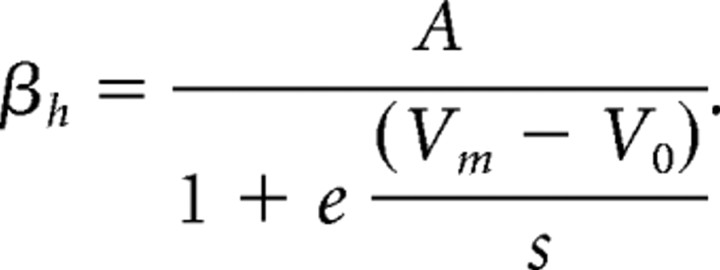Because most of these parameters have not been measured in the animal, we adjusted the model properties such that the overall input/output relationships of specific neurons matched those in the animal [e.g., change in spike frequency during current injection (H. Wolf, unpublished data)]. Care was taken to keep intrinsic neuron properties in the physiological range, as estimated by experimental data.

The synaptic parameters (i.e., time course and conduction delay) in the model were adjusted by matching recorded and simulated postsynaptic potential (PSP). When the time courses of PSPs had been experimentally determined, the time-to-peak and the time constant of decay of the model PSPs were adjusted using exponential rise and decay functions. Synaptic strength, however, cannot be deduced from experimental findings for several reasons. For instance, there exist several copies of each interneuron, and, in electrophysiological recordings, only one of them is monitored. It was thus assumed that the combined actions of several synapses onto all copies of a given interneuron were functionally similar to changes in the synaptic strength onto a single copy of the model interneuron. The time courses of the PSPs were not influenced by the imposed amplitude modulation, because it depended on exponential rise and decay functions. Figure 1C demonstrates this for interneuron 301.

Tegula model.

The tegulae were modeled as a single afferent neuron. Its activity was controlled by either current injection (open-loop condition) or the activity of the depressor unit (closed-loop condition). For the latter, the transfer functions of tegula activation and duration of tegula activity were derived from Fischer et al. (2002) and Hedwig and Becher (1998).

The latency of tegula activation is correlated to the wing beat period (Fischer et al., 2002) such that the onset of tegula activity is almost phase-locked to the beginning of the downstroke movement (a combination of phase-dependent activation and fixed time latency). At the same time, motor activity and wing position are tightly correlated at any given wing beat period during unperturbed flight (Hedwig and Becher, 1998). Thus, the onset of tegula activity essentially depends on the timing of the depressor motor neuron discharge. From the above data, we derived a mathematical description for tegula activation in our model cpg. The latency of tegula activation depended on the timing of the depressor unit (corresponding to motor neuron 112) and was a function of cycle period (see Fig. 3C). The transfer function included the time needed for muscle activation by the motor neuron, muscle contraction, wing movement, and tegula activation.

Figure 3.

Tegula feedback in the model. A, Synaptic connections between model tegula and cpg neurons. Neurons without annotation represent unidentified interneurons or identified cpg interneurons with inhibitory synaptic contacts to other cpg interneurons. EL, Elevator unit; DEP, depressor unit. B, Phase–response curve of the model cpg with tegula stimulation. Similar to the biological situation, tegula input caused a type 0 reset of the flight rhythm. sp, Stimulus phase; ΔP/P, phase–response curve. C, Interaction between cpg and proprioceptive tegula feedback. Both the latency between motor neuron discharge and onset of tegula activity, and the duration of the tegula activity are functions of cycle period. Latency included the time required for activation and contraction of the muscles, for wing movement, and for the activation of the tegula afferents. la, Latency; d, duration; cp, cycle period. The two equations describe the dependency of latency and discharge duration on cycle period. D, Comparison of depressor and elevator activity in the model, without (left) and with (right) tegula feedback in closed-loop conditions. In the latter situation, onset and duration of tegula activity depended on depressor motor discharge, and cycle frequency was higher than without tegula feedback.

The duration of the tegula burst is related to cycle period (Fischer et al., 2002). The transfer function describing burst duration was estimated by using experimental data (see Fig. 3C) (Fischer et al., 2002) (H. Wolf and H. Fischer, unpublished data).

Phase–response curves.

Phase–response curves are a compact way of capturing the functional significance of a discrete input to an oscillatory system (Abramovich-Sivan and Akselrod, 1998). They show the change in oscillator period elicited by inputs occurring at different phases in the rhythm (Wolf and Pearson, 1988; Prinz et al., 2003). Tegula stimuli (5 spikes; 220 Hz firing frequency) were given at phases from 0 to 1 in 0.1 increments. Phase zero was assigned to the first spike in each depressor burst. For a tegula discharge beginning at time t after the start of the preceding depressor burst, the stimulus phase was defined as t/P, with P being the period of the free-running rhythm. The period change ΔP caused by tegula stimulation was defined as the time difference between (1) the start of the first depressor burst after tegula activation had commenced and (2) the time at which this burst would have started without tegula stimulation. Thus, if the first depressor burst occurred earlier than in the unperturbed rhythm, ΔP is negative. If the first depressor burst was delayed, ΔP assumes a positive value. A classical phase–response curve is obtained when the normalized period change (ΔP/P) is plotted against the stimulus phase (t/P).

Definition of threshold and tegula feedback strength.

In the biological system, stimulus threshold (T) during tegula stimulation was determined by the appearance of a compound action potential on nerve 1C (see Figs. 1B, 5A). This convention had also been used in previous studies (Wolf, 1993) to test the response of the flight system to tegula perturbation. At threshold amplitude, tegula stimulation causes a type 0 reset (Winfree, 2001) of the flight rhythm (Wolf and Pearson, 1988) (see Fig. 2A). In the model, the threshold T was defined as the level of synaptic strengths that caused a type 0 reset of the model flight rhythm. The definitions of threshold for the biological system and the model were thus considered comparable.

Figure 5.

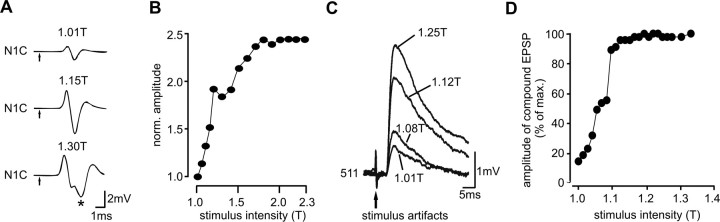
Changes in synaptic strength of tegula feedback; locust preparation. A, Original recordings from nerve N1C, during stimulation of the more distal tegula nerve N1C1a with different stimulus amplitudes (1.01T, 1.15T, and 1.3T). Arrows mark time of stimulation. With increasing stimulus intensities, the amplitude of the compound action potential increased and a second component appeared (*). B, The amplitude of the compound action potential is plotted against stimulus intensity. Amplitudes were normalized to the amplitude recorded at 1T. C, Increasing stimulus voltage increased the amplitude of the EPSP elicited in interneuron 511 by tegula input. Four sample traces are superimposed; stimulus intensity is indicated. D, The amplitude of the compound EPSP elicited in interneuron 511 is plotted against stimulus voltage. Amplitudes were normalized to the maximum amplitude (8 stimulus presentations averaged; data from 1 sample recording shown, similar data obtained in 62 recordings).

Figure 2.

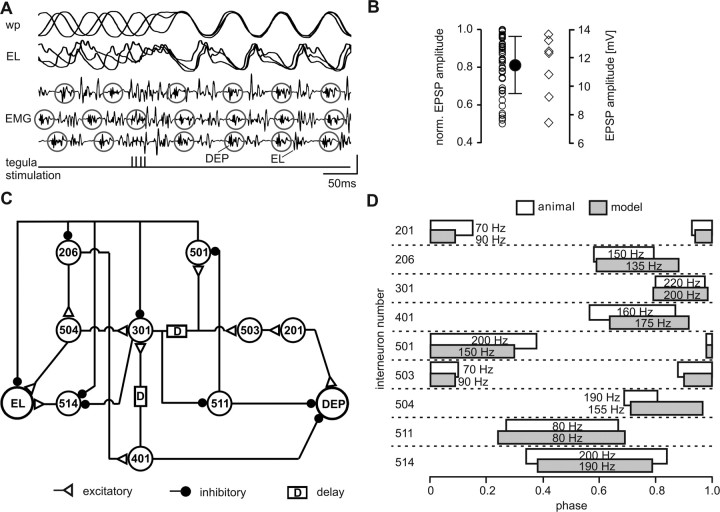
Tegula feedback in the locust and the cpg model. A, Wing positions (wp; top trace) and intracellular recording of an elevator motor neuron (EL; second trace) during tegula stimulation. Three consecutive stimulus presentations are superimposed. Stimuli were given at different phases of the rhythm. The corresponding EMG recordings [illustrating the activity of depressor (DEP) and EL muscles] are shown separately (middle 3 traces). Circles indicate depressor bursts. Tegula stimulation (bottom trace; reference for superposition) synchronized wing position and the appearance of depressor bursts and thus reset the rhythm. Vertical calibration bar, 10 mV. B, Amplitudes of EPSPs (ordinates) that occurred during flight episodes between phases 0.3 and 0.4. Left (open circles), EPSPs were normalized to the maximum amplitude in each of 12 flight episodes; filled circle, average and SD. Right (diamonds), Data from a single flight episode; amplitudes in millivolts. C, Synaptic connectivity of model flight cpg network. EL, Elevator unit; DEP, depressor unit; D, synaptic connection with delay (corresponding to polysynaptic pathway); numbers represent names of interneurons. D, Phase of cpg interneuron activity in flying animals (white bars) and in the model oscillator (gray bars). Numbers indicate interneuron identity; average firing frequencies during a burst are given.

In experiments with tethered locusts, changes in stimulus amplitude (voltage) resulted in corresponding changes in the amplitude of tegula PSPs in flight interneurons and motor neurons (see Fig. 5C). Stimulus voltage was thus used as a measure for the strength of the proprioceptive feedback provided by the tegula (Pearson and Wolf, 1988). In the model, feedback strength was determined by the level of synaptic conductances of the tegula connections. Comparable with the stimulus voltage in the biological system, the strength of the synaptic connections in the model determined the amplitude of the tegula PSP in postsynaptic neurons.

Simplified model.

In this model, the interaction between sensory feedback and cpg was tested by providing a continuously charged capacitance with negative feedback (see Fig. 7A). The capacitance represented the excitation of the depressor motor neurons and possessed a time constant for charging of 10 ms. Negative feedback was either implemented using the tegula transfer functions (see Fig. 3C) or a constant delay and duration. Once activated, the feedback introduced a negative input current into the capacitance. Feedback strength was varied between 1 and 750 (relative units), whereas all other parameters were kept constant.

Figure 7.

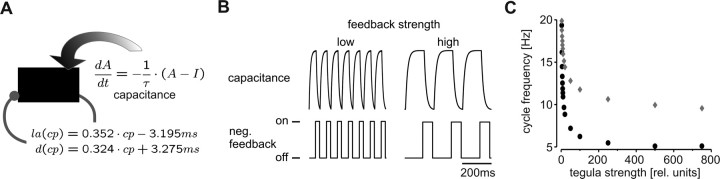
The simplified model. A, Schematic representation of the simplified model. The charge of the capacitance represents the excitation level of the depressor motor neurons. τ, Time constant of charge; I, difference in current, between the tonic positive charge applied throughout the simulation and the feedback. Onset and duration of the feedback current were calculated according to the equations indicated. la, Latency of onset; d, duration. B, Oscillations observed in the voltage of the capacitance with low (left, 5 units) and high (right, 500 units) feedback strengths. C, Cycle frequencies in the simplified model are plotted against feedback strength. Black, Latency and duration of the negative feedback depended on cycle period (according to the tegula transfer functions given in Fig. 3C). Gray, Latency and duration were kept constant.

Results

Effects of tegula proprioceptive feedback on the flight rhythm

During flight, the tegula signals the downstroke movement of the wing. Its activity has a profound impact on the flight rhythm. Whenever the tegula is activated, it resets the rhythm (prematurely with regard to the centrally generated rhythm) and, by doing so, speeds up the rhythm (Wolf and Pearson, 1988; Büschges and Pearson, 1991). The former finding is exemplified in Figure 2A, in which we electrically stimulated the tegula afferents in animals with otherwise disabled tegulae, while recording activity of the depressor muscle. Independent of the stimulus phase, tegula stimulation elicited a depressor discharge after a fixed latency and thus started a new flight cycle. In these experiments, we used a fixed stimulus amplitude of 1.2T (see Materials and Methods). Previous publications (Wolf and Pearson, 1988) characterized the reset elicited by the tegula as a “strong” (type 0) (Winfree, 2001) reset. The effect of the tegula on the motor pattern is thus profound.

We further observed that there was considerable variation in the amplitude of tegula-elicited PSPs in flight motor neurons in the phase range in which the tegula is usually active during flight (between phase 0.3 and 0.4) (Fischer et al., 2002). For example, the amplitude of the tegula-elicited EPSP in elevator motor neurons could vary during a single flight episode by up to 46% at a constant phase (Fig. 2B, open circles and diamonds). On average, the normalized EPSP amplitude was 0.81 ± 0.15 (n = 42 in 12 flight episodes) (Fig. 2B, filled circle). These observations were consistent in 12 animals and recordings of different metathoracic elevator motor neurons.

Model of the flight central pattern generator

According to Figure 2A and previous reports (Wolf, 1993), the main effect of the tegula is to reset the flight rhythm. In this light, the question arises why the output strength of the tegula afferents is variable. Because EPSP size cannot be altered experimentally in the animal, we approached this question by modeling the flight cpg.

For simulation, we chose to represent each identified neuron of the core central pattern generator by one functional unit based on modified Hodgkin–Huxley equations (see Materials and Methods). The underlying network structure (Fig. 2C) was based on the locust flight cpg model of Grimm and Sauer (1995) and on previous electrophysiological analyses (Robertson and Pearson, 1985). In addition, synaptic inhibition from neurons 301 and 501 onto neuron 514 was implemented to obtain appropriate phasing of 514. Although most flight interneurons exist in more than one copy [bilateral pairs of neurons within a given ganglion (Robertson and Pearson, 1983) and segmental homologs (Robertson et al., 1982)], it proved to be sufficient to represent each homolog group by a single neuron to generate a reliable and realistic flight motor pattern (Grimm and Sauer, 1995). Different from Grimm and Sauer (1995), who modeled the influence of neuron 301 onto 501 as a delayed excitation, we represented this connection in a physiologically more accurate way as disynaptic pathway with neuron 301 inhibiting in a graded manner the tonic release of inhibitory transmitter from neuron 511, as hypothesized by Robertson and Pearson (1985). Because the onset of the depressor motor output was used to calculate the timing of the tegula input (see below), we implemented a fictive depressor unit representing the activity of the different depressor motor neurons. The restriction to one unit was acceptable because there is no functional difference between the motor neurons that drive the different depressor muscles (Hedwig and Pearson, 1984) on the level of basic pattern generation (as opposed to flight steering, etc.). To provide adequate input to the depressor motor neuron unit, neurons 503 and 201 were integrated into the network with their established network connections (Fig. 2C). Similar to the depressor unit, a single elevator unit represented the motor output of all elevator motor neurons.

In our simulation, we tuned intrinsic and synaptic parameters of each neuron such that the resulting firing frequencies, as well as the phase relationships and duty cycles during flight, corresponded to those in the animal (Fig. 2D). The time constants of rise and decay of the PSPs in interneurons were adjusted (see Materials and Methods) to match experimental findings. In the model, flight was initiated by raising the membrane potential of interneurons 206, 511, and 514 above threshold. These are the interneurons that either receive depolarizing input from wind-sensitive projections in the brain descending to the thoracic ganglia (neuron 206) (Reichert and Rowell, 1986; Rowell and Reichert, 1986; Kien and Heichele, 1993) or that participate in rhythm generation but do not receive excitatory input from other cpg neurons (neurons 511 and 514). As a result, the modeled network generated oscillatory activity that was very similar to a deafferented (i.e., without any sensory feedback) (Wilson, 1961) flight rhythm, with a cycle frequency of 9.73 Hz (cycle period, 103 ms) (Fig. 3D, left).

To test the validity of our model, we also probed its response to two different types of perturbation. (1) Robertson and Pearson (1983) demonstrated that one of the characteristic network responses to a strong tonic depolarization of interneuron 301 is a decrease in cycle period. When we performed the same test in the model network, we observed that, in agreement with the physiological data, the cycle period of the model rhythm decreased from 103 ms before current injection to 52 ms during depolarization of interneuron 301. (2) In contrast, a tonic depolarization of interneuron 501 was shown to slow down the flight rhythm (Robertson and Pearson, 1983) to a cycle period of ∼250 ms. In the model, we found that tonic depolarizing current delivered to neuron 501 caused the cycle period of the flight rhythm to increase from 103 to 243 ms.

Proprioceptive feedback in closed-loop conditions speeds up the rhythm

In the animal, the tegula is activated by the downstroke of the wing and provides proprioceptive sensory information about timing and velocity of that cycle segment to the flight pattern generator. In the model, the tegula was represented by a single neuron, with a firing frequency of 220 Hz when activated (Wolf and Pearson, 1988). All known synaptic connections from the tegula onto flight cpg neurons were implemented (Fig. 3A) (Büschges et al., 1992; Wolf, 1993). Most importantly, the strength and the timing of the tegula synapses were adjusted separately for each postsynaptic neuron (see Materials and Methods) such that the network response to tegula input corresponded to the response of the flight cpg in the animal. As a measure for network performance, we used the phase–response curve (Fig. 3B), which illustrates the relationship between the timing of tegula stimulation and the effect on the flight rhythm (see Materials and Methods). These measurements were performed in open-loop conditions, i.e., the onset and the duration of the tegula activity did not depend on cycle period. Despite the numerous nonlinearities of the model, we obtained a linear relationship between stimulus phase and phase–response (Fig. 3B). This demonstrates that each tegula stimulus train initiated an independent new flight cycle (type 0 reset; Winfree, 2001), as was shown for tegula input to the biological flight pattern generator (Fig. 2A) (Wolf and Pearson, 1988).

In closed-loop conditions, in contrast, as occur in the animal, the activation of the tegula is strictly correlated to the activity of the depressor motor neurons and muscles (Hedwig and Becher, 1998; Fischer et al., 2002). We used this fact to incorporate a mathematical model of tegula activation into our model cpg (Fig. 3C) (for details, see Materials and Methods). Consequently, the onset and the duration of the tegula burst became functions of cycle period and of depressor activity in particular. The firing frequency was kept at 220 Hz, thus mimicking the situation in intact flying locusts. As a result of this realistic tegula feedback, the flight rhythm generated by the model network sped up and the cycle frequency increased from 9.73 to 17.48 Hz (cycle period from 103 to 57 ms) (Fig. 3D), which closely resembles the main effects of the tegulae in the animal (Büschges and Pearson, 1991).

Modulation of proprioceptive feedback strength regulates the speed of the model rhythm

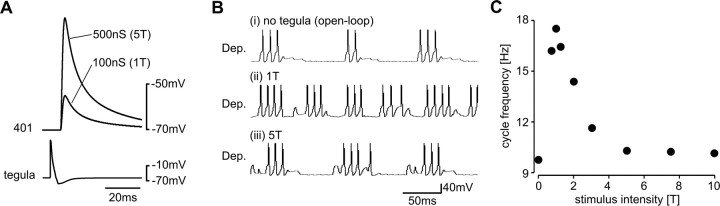
In the animal, the strength of the tegula input onto the flight cpg is not constant but rather changes even during short flight episodes (Fig. 2B). To test the impact of such changes in functionally relevant closed-loop conditions, we varied the synaptic conductances of the tegula synapses onto model interneurons and motor neurons. The strengths of all synapses were altered in equal steps. The set of synaptic conductances that was used to obtain the phase–response curve (Fig. 3B) was defined as the threshold value T. The following variations of synaptic strengths were used: 0.75T, 1.0T, 1.25T, 2T, 3T, 5T, 7.5T, and 10T. Figure 4A shows the resulting increase of PSP amplitude in the cpg neuron 401. Here, synaptic strength was increased from 100 nS (1T) to 500 nS (5T).

Figure 4.

Changes in synaptic strength of tegula feedback; model oscillator. A, The amplitude of PSPs elicited in flight interneurons by tegula input increased with synaptic strength. Superposition of EPSPs in interneuron 401, recorded at two different synaptic strengths. B, Motor output (depressor unit) of the model network at different tegula feedback strengths (closed-loop condition). i, Isolated cpg without tegula feedback; ii, with synaptic strength of tegula feedback at 1T; and iii, at 5T. C, Cycle frequency of the model oscillator (closed-loop conditions) is plotted against tegula feedback strength. Suprathreshold stimulation with 1T increased cycle frequency compared with the isolated cpg. With increasing tegula strength, the cycle frequency decreased again until it approached values close to those obtained in the isolated cpg.

Along with the increase in tegula strength, the cycle frequency of the motor pattern decreased compared with activation of the tegula with 1T. In Figure 4B, three situations are compared. (1) Without tegula activity, the flight rhythm was generated by the cpg only and thus cycle frequency was low (Fig. 4Bi). (2) When the strength of tegula input was set to 1T and tegula feedback depended on motor activity of the depressor unit (closed-loop), cycle frequency increased and the flight rhythm sped up (Fig. 4Bii). (3) Interestingly, with higher feedback strength (5T), the flight rhythm slowed down again (Fig. 4Biii), to cycle frequencies that were close to those obtained without tegula stimulation. In Figure 4C, the cycle frequencies are given for all tested tegula feedback strengths. After a rapid increase to 17.48 Hz (57 ms) with a tegula strength of 1T, cycle frequency decreased gradually to 10.15 Hz (98 ms) at 10T. The model thus predicted that variations in proprioceptive feedback strength, that is, in the strength of the feedback loop represented by the tegula input, can regulate the speed of the rhythm.

The strength of proprioceptive feedback regulates the speed of the flight rhythm in the animal

To test the above predictions of the model, we performed experiments on tethered flying animals. We severed all tegulae and replaced input from the hindwing organs with computer-generated feedback (see Materials and Methods) (Fig. 1A,B). As a means to vary the strength of tegula feedback, we changed stimulus voltage. Because the tegula comprises ∼75 sensory cells (Kutsch et al., 1980), higher stimulus voltages recruit larger numbers of sensory units (Pearson and Wolf, 1988). This was most obvious when monitoring the compound action potential on nerve 1C (Fig. 5A) that was elicited by the stimulus and represents the combined activity of all recruited tegula axons. The stimulus amplitude at which the compound action potential first appeared was defined as stimulus threshold T. When we increased stimulus voltage, the amplitude of the compound action potential increased and a second component appeared in the shape of the compound action potential (Fig. 5A, * at 1.3T), which indicated the activation of tegula afferents with smaller diameters and longer conduction delays (Kutsch et al., 1980; Pearson and Wolf, 1988). Figure 5B illustrates the change in the (normalized) amplitude of the compound action potential with increasing stimulus intensities.

Along with an increase in the amplitude of the compound potential in nerve 1, larger PSPs were elicited in the synaptic targets of the tegula. Figure 5, C and D, demonstrates this for flight interneuron 511. In Figure 5C, a superposition of the EPSPs elicited by tegula stimulation with four different stimulus intensities is shown. The EPSPs elicited by stimulation with 1.25T exhibited approximately five times the amplitude of the one elicited by stimulation with 1.01T. In the graph of Figure 5D, EPSP amplitudes were normalized to the maximum amplitude that was reached with tegula stimulation. Similar responses were found in 62 recordings of flight interneurons and motor neurons. In conclusion, changing stimulus voltage proved to be a useful tool for altering the strength of the proprioceptive feedback provided by the tegula (Pearson and Wolf, 1988).

When we activated the computer-generated model of the tegula during flight episodes, the onset and the duration of the tegula stimulus depended on the cycle period of the previous flight cycle. As a reference for cycle period, electromyograms of depressor muscle 97 were recorded. Onset and duration of the tegula stimulus were dynamically altered in each cycle (Fig. 6A) according to the equations shown in Figure 3C (see also Materials and Methods). As was to be expected, the flight rhythm sped up whenever the tegula stimulus was enabled with stimulus voltages close to 1T (Fig. 6B). When the stimulus was turned off for several cycles, the cycle frequency of the rhythm gradually decreased. In the example shown in Figure 6B–D, stimulus threshold was 0.75 V. The cycle frequency increased significantly from 10.32 ± 0.65 Hz without stimulation to 13.13 ± 0.37 Hz during suprathreshold stimulation with 0.75 V (9 ≤ n ≤ 11; p < 0.01) (Fig. 6D).

Figure 6.

Tegula feedback controls cycle frequency. A, Dynamic adjustment of tegula stimulation. The latency of onset (black bars), the duration of the stimulus train delivered to the tegula afferents, and thus the number of pulses per train (gray numbers) depended on the period of the previous wing beat cycle. Sample cycles with three different cycle periods are shown. cp was determined by the onset of depressor motor neuron discharge, as monitored in EMG recordings of muscle 97. Tegula stimulus trains had a frequency of 220 Hz. B, Instantaneous cycle frequency in closed-loop conditions, as monitored by a depressor EMG recording, with and without tegula stimulation. Tegula feedback strength 1T (0.75 V). cf, Cycle frequency; dep., depressor EMG; teg., tegula stimulation. Vertical calibration bar: 10–14 Hz. C, Same as B but with a tegula feedback strength of 2T (1.5 V). D, Histogram plotting cycle frequency against stimulus voltage; data are from one animal. Threshold for tegula activation 0.75 V. At this stimulus voltage, cycle frequency increased significantly compared with subthreshold stimulation (subthr.); further increasing stimulus voltages elicited significantly slower cycle frequencies. *p < 0.05; **p < 0.01. E, In some animals, cycle frequencies at high stimulus voltages dropped below those obtained without tegula activation. Experimental situation and data presentation as in B. Dashed lines mark cycle frequency without tegula stimulation. Vertical calibration bar: 10–15 Hz. F, Average change in cycle frequency is plotted against stimulus voltage (N = 9 animals). The average threshold for activation of tegula afferents, T, was 0.5 V. At this stimulus voltage, cycle frequency was significantly larger than during subthreshold stimulation or during stimulation with large amplitudes. *p < 0.05; **p < 0.01.

In contrast, when we increased stimulus intensity to 1.5 V (2T), almost no change in cycle frequency occurred (Fig. 6C) when stimulation was turned on. A more quantitative approach revealed that, with increasing stimulus voltages, the cycle frequency decreased compared with stimulation at threshold level (Fig. 6D), until no difference to subthreshold stimulation could be observed (stimulus voltage, 1.5 V). This was strikingly similar to the findings in the model cpg (Fig. 4B,C) and thus supported the prediction obtained with the modeling approach.

In four of the nine tested animals, cycle frequency at high stimulus intensities even dropped below the cycle frequency recorded during subthreshold stimulation and flight sequences without stimulation, respectively. Figure 6E demonstrates this for a stimulus intensity of 2T. Whereas stimulation with 1T sped up the rhythm compared with control (left), stimulation with 2T slowed down the rhythm (right).

A comparison of the average changes in cycle frequency recorded in all experimental animals (Fig. 6F) confirmed the above observations in selected individuals. Although activating the tegula with stimulus voltages right above threshold increased the cycle frequency by up to 15%, this increase diminished with higher stimulus voltages.

In conclusion, the results of our experiments support the prediction of the model flight pattern generator, namely, that the strength of proprioceptive tegula feedback determines the frequency of the flight rhythm.

Simplified model of proprioceptive feedback

The fact that feedback strength determines the speed of the motor pattern may be an intrinsic property of the flight motor network, or it may be an emergent property of the proprioceptive feedback loop. To decide between these two possibilities, we simplified the model, particularly with regard to the representation of the cpg. In this reduced model, the excitation of the depressor motor neurons was represented by a capacitance that was continuously charged by positive current (Fig. 7A). Sensory feedback was implemented in the same way as in the Hodgkin–Huxley model of the flight cpg and in the experiments, that is, with the transfer functions given in Figure 3C. Cycle period was defined as the time between two identical capacitance levels of consecutive cycles. For this, we arbitrarily chose a level of 50% of the maximum charge. The latency of feedback activation was then calculated in reference to this point in time. Once activated, the feedback introduced a negative input current into the capacitance that exceeded the tonic positive current. The feedback thus caused a drop in the capacitive charge. On the basic level of rhythmogenesis, this negative feedback loop is functionally equivalent to tegula feedback in the animal, in which the tegula is triggered when the network switches into the depressor state and thus shuts down depressor discharge and initiates elevator activity. The feedback was switched off after its duration (as calculated according to the equations given in Fig. 3C) was completed, and the capacitance resumed positive charging attributable to the tonic current input. When the threshold level was reached again, a new cycle started. This simple model exhibited stable oscillations with a frequency depending on the selected parameters.

In our model, the capacitance had a time constant of charge of 10 ms, and a tonic input current of 2 (relative units) was applied throughout the duration of the simulation. A feedback strength of 5 resulted in stable oscillations with a frequency of 15.09 Hz (Fig. 7B, left). When we altered feedback strength to 500, while keeping all other parameters constant, we observed that cycle frequency dropped to 5.56 Hz (Fig. 7B, right). In general, the speed of the rhythm depended on feedback strength in a way such that higher feedback strengths resulted in lower cycle frequencies (Fig. 7C, black). This dependence had a form similar to the ones obtained in the Hodgkin–Huxley model and in the behaving animal. This indicates that the observed frequency regulation by the tegula was not an idiosyncratic characteristic of the locust flight motor network but rather a general property of feedback systems of the present form.

Indeed, frequency regulation had not even depended on the specifics of the tegula transfer functions. We initially used cycle period to calculate latency and duration of tegula activity. In the simulation shown in Figure 7C (gray), in contrast, the parameter cycle period was preassigned a value of 50 ms, resulting in a constant latency and duration of the feedback. We still obtained a similar correlation between feedback strength and cycle frequency, which indicates that the control of the speed of a rhythmic motor pattern by the modulation of feedback strength is a general feature of negative (sensory) feedback systems.

Discussion

It is a common view that central pattern generators are primarily responsible for generating the motor patterns underlying rhythmic behavior and that feedback from peripheral sensors functions in modulating these pattern generating networks. This view is certainly adequate for systems in which the elimination of sensory feedback has little or no impact on the motor pattern [e.g., in lamprey (Grillner et al., 1995) and Tritonia swimming (Getting, 1983) and others (for review, see Pearson, 1986)]. However, in many systems, the function of the pattern generating networks is restructured, and substantial parts of the pattern characteristics are produced by phasic sensory feedback, a fact that is reflected in a significant change of the motor pattern after deafferentation (Cang and Friesen, 2002; Pearson, 2004; Kristan et al., 2005). This essentially means that phasic sensory feedback must be regarded as an integral part of the rhythm generating machinery.

The dynamics created by the interaction of sensory activity and cpg have not yet been elucidated in most systems. We here show that centrally generated rhythms can be regulated via variation of sensory feedback loops and that this mode is actually implemented in the regulation of a particular feature of the locust flight rhythm, namely its cycle frequency. In open-loop conditions, the tegula resets the rhythm, a feature also reflected in our Hodgkin–Huxley model of the flight cpg (Fig. 3B). In addition to this profound impact on the motor output, tegula feedback strength is altered during flight (Fig. 2B). The cpg model predicted that such an alteration would result in a frequency regulation of the cpg output in closed-loop conditions (Fig. 4C). We verified this prediction in the biological preparation by altering feedback strength in an artificially closed-loop system (Fig. 6F). Surprisingly, higher feedback strengths resulted in lower cpg frequencies. The regulation of cpg speed by the modulation of feedback strength appears to be a general feature of negative sensory feedback (Fig. 7C).

In the locust flight system, the generation of burst activity in cpg neurons is strongly influenced by tegula feedback, which in turn depends on wing movement and thus on the activity of cpg neurons. Investigations using classical approaches provided detailed knowledge about tegula activation, its synaptic connections to flight interneurons and motor neurons, as well as a phenomenological understanding of the functions of this proprioceptor. Unfortunately, emergent properties of the intact system cannot be studied in this way, because the dynamics of sensorimotor interaction are necessarily disregarded. We, therefore, used a combination of electrophysiological experiments and computational modeling with artificially closed tegula feedback loops. Tegula discharge was dependent on the momentary motor output, and feedback strength could be altered in this artificially closed loop.

The strength of sensory feedback is subject to phasic as well as task-dependent modulation in many systems. For example, mechanosensory neurons receive presynaptic inputs that modulate the effectiveness of their synaptic transmission to postsynaptic neurons (presynaptic inhibition) (for review, see Rudomin et al., 1998). Task-specific modulation has been studied extensively for motor networks and pattern selection from rhythm generating circuitry, with the finding that most motor networks are highly flexible (Earhart and Stein, 2000; Lieske et al., 2000; Nusbaum and Beenhakker, 2002; Kristan et al., 2005; Hawkins et al., 2006). Task-specific modulation affects all elements of the pattern generating networks investigated so far and at many different levels. Given the fact that sensory feedback, and tegula feedback in particular, is an integral part of the pattern generating machinery, it is conceivable that task-specific modulation of sensory activity may occur and contribute to the regulation, and possibly to the selection, of motor patterns.

cpg and tegula model

The pattern generator underlying locust flight is one of the best described pattern generating networks. At the same time, knowledge about the constitutive pattern generating mechanisms is basic, which means that we are presently unable to describe its behavior with a particular type of oscillator (e.g., relaxation oscillators and the like) (Izhikevich, 2006). We therefore chose to represent each identified cpg neuron by one functional unit, which allowed us to avoid any assumptions regarding the oscillatory characteristics of the network. Rather, we implemented into our model as many experimental results as possible, such as network connectivity, PSP time constants, firing frequencies, and phase relationships. In support of this approach, recent findings (Golowasch et al., 2002; Prinz et al., 2004; Schulz et al., 2006) have stressed the fact that the response characteristics of the network, rather than its exact composition, define the important characteristics of behavior.

The oscillatory activity of our model was very similar to the deafferented flight rhythm (Fig. 2D) and well in the range of properties exhibited by its biological counterpart. Only interneuron 504 was different in its phasing from the biological neuron, the evident reason being that the presynaptic neurons that terminate its discharge are not known. This was, however, irrelevant for network function, because the interneurons postsynaptic to 504 exhibited correct phasing. The plausibility of the network was further validated by comparing the effects of current injections into single model and biological interneurons (301, 501). The model network showed realistic responses to such perturbations. One obvious difference between the model and the animal is that the model does not exhibit the gradual decrease in wing beat frequency observed in tethered flying animals. The reasons for this decrease are not clear, but waning effects of neuromodulators and central excitation (which remains constant in the model) have been implicated (Ramirez and Pearson, 1991).

Because locusts are neurogenic flyers, the contractions of the flight muscles directly reflect motor neuron activity. In addition, the activation of the tegula is related to the resulting wing beat movement (Hedwig and Becher, 1998; Fischer et al., 2002). These correlations allowed us to describe the duration of tegula activity and the delay of its onset as linear functions of cycle period (Fig. 3C). In closed-loop conditions, realistic activity patterns of the tegula model in the flight cycle were achieved in both the model and electrophysiological experiments (Figs. 3D, 6B).

Regulation of cpg frequency as an emergent property of proprioceptive sensory feedback

Our tegula model was sufficient to reproduce the main effects of the tegula, such as a type 0 reset of the flight rhythm in open-loop conditions (Fig. 3B) (Winfree, 2001), a shortening of the depression–elevation delay, and an increase in cycle frequency when the feedback loop between cpg and sensory feedback was closed (Fig. 3D) (Büschges and Pearson, 1991). Sensory organs that reset motor patterns are generally assumed to affect the timing of phase transitions of the pattern and thus major aspects of the respective behavior (such as walking, swimming, respiration, and feeding) (for review, see Pearson, 1993). In the locust, the reset of the rhythm and the excitation of the elevators correspond to an earlier onset of wing elevation, leading to an aerodynamically adequate phase transition from downstroke to upstroke movement (Wolf, 1993). Our results indicate that proprioceptive feedback additionally serves the regulation of motor pattern speed. We provide evidence for this interpretation by both modeling (Figs. 4C, 7C) and electrophysiological (Fig. 6F) experiments. In support of this view, changes of tegula synaptic strength occur during flight (Fig. 2B). These changes may arise from several sources, among them presynaptic inhibition of the afferent terminals (Büschges and Wolf, 1999). Feedback strength may also vary, however, attributable to changes in tegula spike activity during variations in wing movement. Tegula discharge amplitude is positively related to the angular velocity of the downstroke movement over a broad range of velocities (Fischer et al., 2002). Thus, because slower flight cycles produce smaller angular velocities (Fischer et al., 2002), tegula activity gets weaker as the flight rhythm slows down. Considering the capability of the tegula feedback to regulate the speed of the rhythm, a weakening of tegula discharge may well increase the speed of the flight rhythm, thus working toward a homeostatic regulation of wing stroke frequency.

Intriguingly, we observed in several animals that tegula stimulation at high stimulus intensities decreased cycle frequency to values even below those recorded without tegula feedback (Fig. 6E, right). This indicates that the function of tegula feedback is not to speed up the flight rhythm relative to the deafferented situation (that never occurs in normal animals, anyway) but rather to stabilize cycle frequency to a certain range, depending on feedback strength. This is also evident when cycle frequencies are monitored during flight with and without proprioceptive feedback. Without feedback, cycle frequencies tend to decline steadily and flight episodes are usually rather short, terminating when cycle frequencies drop below 8–10 Hz. With tegula feedback present, cycle frequencies are more stable (Fig. 6C) and flight episodes last longer.

We show that the ability of sensory feedback to regulate the frequency of the motor pattern is no peculiarity of the locust flight control network but rather a general feature of negative feedback. We demonstrate this for a feedback model in which a continuously charged capacitor (representing the central part of the network) was equipped with negative feedback (Fig. 7). Frequency regulation in this simple model was similar to the one obtained in the Hodgkin–Huxley model and in the animal, even when latency and duration of the feedback were constant and thus independent of cycle period. One obvious difference between the cpg model and the simplified model is that the latter does not show the initial increase in cycle frequency at low stimulus strengths. Because the network model incorporates a cpg whereas the simplified model does not, it is conceivable that interactions between cpg and tegula feedback determine the initial increase but are dominated by the tegula feedback at higher feedback strengths. High feedback strengths result in a stronger activation of all elevator parts of the network, which forces the network to remain longer in the elevator phase and ultimately leads to a delayed depressor activation and thus longer cycle periods.

Considering the general applicability of the frequency control mechanisms in this study and the fact that modulation of the strength of negative feedback loops is a widespread phenomenon in motor control (Clarac and Cattaert, 1996; Büschges and El Manira, 1998), one can assume that this mechanism of regulating cycle frequency is common in animals.