The Neural Coding of Stimulus Intensity: Linking the Population Response of Mechanoreceptive Afferents with Psychophysical Behavior

Abstract

How specific aspects of a stimulus are encoded at different stages of neural processing is a critical question in sensory neuroscience. In the present study, we investigated the neural code underlying the perception of stimulus intensity in the somatosensory system. We first characterized the responses of SA1 (slowly adapting type 1), RA (rapidly adapting), and PC (Pacinian) afferents of macaque monkeys to sinusoidal, diharmonic, and bandpass noise stimuli. We then had human subjects rate the perceived intensity of a subset of these stimuli. On the basis of these neurophysiological and psychophysical measurements, we evaluated a series of hypotheses about which aspect(s) of the neural activity evoked at the somatosensory periphery account for perception. We evaluated three types of neural codes. The first consisted of population codes based on the firing rate of neurons located directly under the probe. The second included population codes based on the firing rate of the entire population of active neurons. The third included codes based on the number of active afferents. We found that the response evoked in the localized population is logarithmic with stimulus amplitude (given a constant frequency composition), whereas the population response across all neurons is linear with stimulus amplitude. We conclude that stimulus intensity is best accounted for by the firing rate evoked in afferents located under or near the locus of stimulation, weighted by afferent type.

Introduction

The three low-threshold mechanoreceptive afferents found in the glabrous skin of macaque [slowly adapting type 1 (SA1), rapidly adapting (RA), and Pacinian (PC)] are sensitive to different types of stimulation (Talbot et al., 1968; Johansson and Vallbo, 1979b; Freeman and Johnson, 1982a,b). SA1 afferents are most responsive to statically indented stimuli or to low-frequency vibratory stimuli, whereas PC afferents are exquisitely sensitive to high-frequency vibrations (>100 Hz). RA afferents are sensitive to vibrations at intermediate frequencies. Although the three afferent types have been implicated in different aspects of tactile perception [SA1 in form and texture perception; RA in microslip, flutter and motion perception; and PC in the perception of microtextures (Hollins and Bensmaia, 2007) and of textures explored through a tool (Yoshioka et al., 2007) (for review, see Johnson, 2001)], all three populations of afferents respond to most natural stimuli, albeit to different degrees. Thus, the nervous system must either sift through or integrate information conveyed through these three sensory channels to form a coherent percept.

In the present study, we investigated the neural mechanisms underlying the tactile perception of stimulus intensity. The perceived intensity of sinusoids in the low- to intermediate-frequency range has been shown to increase linearly with stimulus intensity (Stevens, 1968; Franzén, 1969; Verrillo et al., 1969) whereas the firing rates evoked in individual peripheral afferents do not (Mountcastle et al., 1969). Johnson (1974) set out to elucidate the neural code of perceived intensity by reconstructing the response evoked in a population of RA afferents by 40 Hz vibrations at various intensities (also see Cohen and Vierck, 1993b). He tested several putative codes, including (but not limited to) the mean population firing rate and the total number of active fibers, and concluded that any aspect of the neural discharge that increased linearly with intensity could account for the psychophysical behavior. Several codes could not be rejected based on his psychophysical and neurophysiological data.

Here, we sought to elaborate on Johnson's study in two ways. First, we presented a variety of stimuli (sinusoidal, diharmonic, and noise stimuli) that vary not only in their intensity but also in their frequency composition. Such an assortment of stimuli is likely to constrain theories of the underlying neural code to a greater extent than would a more limited stimulus set. Second, we characterized the activity evoked in the three populations of mechanoreceptive afferents to assess the extent to which each afferent type contributes to perceived intensity. Following Johnson's approach, we then evaluated the extent to which predictions derived from each of a set of putative neural codes accounts for subjective estimates of perceived intensity. An important assumption underlying this approach is that a linear relationship exists between the aspect of the neural activity that is relevant to the subjective experience (in this case, perceived intensity) and the subjective experience itself (Johnson et al., 2002). Finally, we discuss the implications of the present neurophysiological findings to the central mechanisms of intensity coding.

Materials and Methods

Apparatus

Two different simulators were used to deliver well controlled vibratory stimuli. High-frequency stimuli were delivered with a Mini-Shaker (Type 4810; Brüel and Kjaer, Nærum, Denmark) driven by a power amplifier (Type 2706; Brüel and Kjaer). Low-frequency vibrations were delivered using a custom-made Chubbuck motor (Chubbuck, 1966), driven by a servo-controlled amplifier and equipped with a high-precision linear variable displacement transducer (LVDT) with micrometer-resolution. The input voltage to both amplifiers, under computer control, was generated using a digital-to-analog card (PCI-6229; output rate = 20 kHz; National Instruments, Austin, TX).

Mini-Shaker movements were monitored using an accelerometer (Type 8702B50M1; Kistler Instrument Corporation, Amherst, NY) with a dynamic range of ±50 × g. The threaded stud on the top of the accelerometer was mounted directly to the Mini-Shaker motor, and the stud of the stylus was attached to the bottom of the accelerometer. The output of the accelerometer was amplified and conditioned using a piezotron coupler (Type 5134A; Kistler Instrument Corporation) and then digitized (PCI-6229; sampling rate = 20 kHz; National Instruments). The same analog-to-digital card was used to digitize the output of the LVDT.

The contactor consisted of a steel-tipped stylus fixed to both the table of the Chubbuck and the threaded bottom of the accelerometer on the Mini-Shaker. The stylus was 175 mm long with a radius of 12.5 mm and a weight of 12.5 g. The stylus was machined out of Carbon Afferent and Ultem (GE, Pittsfield, MA), a light-weight and rigid polyimide thermoplastic resin. The stylus was outfitted with a steel tip, embedded into the hollow shaft, and secured with a setscrew. The steel tip introduced an additional 3.2 g and 15 mm to the stylus. The tip of the stylus was flat and had a diameter of 1 mm (cf. Freeman and Johnson, 1982b).

The effect of environmental vibrations was minimized using a floating table (Type MICRO-g; Technical Manufacturing Corporation, Peabody, MA), on which the entire experimental setup (including the animal) was placed. The motors were held securely and could be coarsely positioned using a heavy-duty multiaxis Linhof camera positioning system (Linhof Präzisions-Systemtechnik, Munich, Germany), which was also secured to the floating table. A Newport ball bearing linear stage (UMR8.51; Newport Corporation, Irvine, CA) was bolted onto the end of the Linhof system to finely position the motors along the z-axis (i.e., into the skin). Finally, the motors were secured onto the stage using a custom-built clamp.

The Chubbuck displacement sensor was calibrated using an Optodyne laser interferometer (LDS 1000; Optodyne, Compton, CA), capable of measuring absolute displacement to submicrometer resolution. The actual position, as measured by the interferometer, was regressed onto the output of the position sensor. The Chubbuck has a linear frequency response up to ∼50 Hz with a slow roll-off with further increases in frequency. To compensate for the amplitude roll-off, we ran the Chubbuck through a wide range of amplitudes at each of the frequencies used in the experiment. From the cross-correlation between desired and actual motor positions, we found the peaks of the sinusoids at each frequency–amplitude pair and determined the actual amplitude achieved. We then fit the measured amplitudes to the commanded amplitudes for each frequency using second-order polynomials. We also implemented phase compensation using a lookup table at each frequency. This compensation was critical in generating accurate diharmonic waveforms with prespecified phase relationships.

Analogous compensation procedures were implemented for the Mini-Shaker using the output of the accelerometer as feedback to generate the desired acceleration signals.

Because the Chubbuck stimulator provides a force output, we also measured the forces exerted on the skin during vibratory stimulation and found that these ranged from nearly 0 to 25 × g (pressure = 0.32 N/mm²).

Stimuli

Stimuli varied widely in their frequency content and amplitude and included simple sinusoidal, diharmonic, and noise stimuli. The Mini-Shaker was used to deliver stimuli that included frequency components >100 Hz, and the Chubbuck was used to deliver all other stimuli.

Sinusoids.

Sinusoids were presented at 1, 5, 10, 25, 60, 100, 150, 200, 250, 300, 400, 500, 600, 800, and 1000 Hz. At 1 Hz, amplitudes ranged from 5 to 360 μm, zero-to-peak; at 10 Hz, from 2.5 to 130 μm; at 100 Hz, from 0.5 to 130 μm; at 1000 Hz, from 0.17 to 8 μm. The stimulus duration was either five stimulus cycles or 0.1 s, whichever was longer. At each frequency, amplitudes were incremented in equal logarithmic steps over the total range.

Diharmonic stimuli.

Diharmonic stimuli were specified using the following expression:

where A₁ and A₂ are the amplitudes of the low- and high-frequency components, respectively, ω₁ and ω₂ are the two frequencies (ω₁ < ω₂), and φ is the phase of the high-frequency component relative to that of the low-frequency component. The (ω₁, ω₂) frequency pairs are shown in Table 1. Component amplitudes ranged from 2 to 125 μm if their frequency was <100 Hz, from 2 to 100 μm at 100 and 125 Hz, and from 0.1 to 5 μm at 1000 Hz. The phase φ took on one of four values: 0, π/2, π, or 3π/2. The stimulus duration was either five stimulus cycles (i.e., five cycles of the low-frequency component) or 0.1 s, whichever was longer. The amplitudes of the two frequency components were incremented in equal logarithmic steps over their respective ranges.

Table 1.

Frequency pairs in the set of diharmonic stimuli

ω1(Hz)	ω2(Hz)
5	10, 15, 25, 50, 100
10	20, 30, 50, 100
25	50, 75, 125, 250, 500, 1000
50	150, 250, 500, 1000
100	200, 300, 500
200	400, 600, 1000
400	800

Bandpass noise stimuli.

Stimuli were generated by first creating wide-band noise, then bandpass filtering it to the specified frequency range. Each noise stimulus was then scaled to a set of predetermined rms amplitudes, namely 0.5, 1, 5, 10, and 50 μm. The bandpass cutoff frequencies of the noise stimuli are shown in Table 2. The duration of all noise stimuli was 1 s.

Table 2.

Low- (f₁) and high- (f₂) frequency cutoffs for the noise stimuli

f1 (Hz)	f2 (Hz)
5	10, 25, 50, 100
25	50, 125, 250, 500
50	100, 250, 500, 1000

Each stimulus was preceded and followed by a period of no stimulation to reduce the effects of vibratory adaptation (Bensmaia et al., 2005b; Leung et al., 2005) and to allow us to establish the spontaneous firing rates of each afferent (which were typically near zero). The interstimulus interval was 100 ms for sinusoidal and diharmonic stimuli and 1 s for noise stimuli.

Subjects

The nine psychophysical subjects (four females and five males), all students or employees at Johns Hopkins University, were paid for their participation. They ranged in age from 19 to 24 years. Consent was obtained from each subject. The Human Subjects Institutional Review Board of Johns Hopkins University approved the experiments.

Neurophysiology

All experimental protocols complied with the guidelines of the Johns Hopkins University Animal Care and Use Committee and the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Single-unit recordings were made from the ulnar and median nerves of two anesthetized macaque monkeys (Macaca mulatta) using standard methods (Talbot et al., 1968). Standard procedures were used to classify mechanoreceptive afferents according to their responses to step indentations and vibratory stimulation (Talbot et al., 1968; Freeman and Johnson, 1982b). An afferent was classified as SA1 if it produced sustained firing in response to a step indentation. It was classified as RA if it had a small receptive field (RF) and responded only to the onset and offset of an indentation. It was classified as PC if (1) it was vigorously activated by air blown gently over the hand; (2) it was activated by transmitted vibrations produced by tapping on the hand restraint; and (3) its receptive field was large. The point of maximum sensitivity of the afferent (or hotspot) was located on the skin using a handheld probe and then marked with a felt-point pen. The stimulator probe was centered on the hotspot of the afferent to the extent possible (PC RFs do not have clear hotspots). The tip of the probe was fixed with cyanoacrylate glue to the skin at its resting position, i.e., with no preindentation.

Psychophysics

The subjects' arm rested on a padded arm-rest, and their view of the stimulator was obstructed by a curtain. Subjects wore earphones playing pink noise to eliminate auditory cues. The stimulator assembly was placed on a separate platform than that on which the armrest was fixed to isolate the subject from unwanted vibrations. Before each experimental block, the stimulus probe was lowered until it just contacted the skin. Subjects were presented with 74 vibratory stimuli (selected as described in Results) presented in pseudorandom order. On each trial, subjects produced magnitude estimates of perceived intensity on a ratio scale. If the stimulus was imperceptible, they were to assign to it the number 0. In a given experimental block, the first rating was arbitrary (unless the stimulus was not perceived). They were instructed to produce a number twice as large if the next stimulus felt twice as intense, or a number one-half as large if the stimulus felt one-half as intense. They were encouraged to use decimals or fractions if they deemed it necessary. The stimulus duration was 1 s. In the first experimental block, subjects rated a subset of 20 stimuli for practice. The practice block was followed by five experimental blocks in which archival data were collected. Psychophysical ratings were normalized by the mean rating obtained in each experimental block then averaged across blocks and subjects. In one of the experimental blocks, the probe tip was glued to the skin to mimic the stimulus conditions used in the neurophysiological recordings. The presence or absence of glue had no effect on subjects' ratings: The correlation between the mean ratings obtained in the glued and unglued conditions was 0.98; a paired t test revealed that the difference between the sets of ratings was nil (t₍₇₃₎ = 0, p = 1).

Results

We recorded neural responses from 12 SA1, 17 RA, and 8 PC afferents with RFs on the glabrous surface of the hand. Figure 1 shows representative afferent responses to five presentations of a 20 Hz sinusoid at different amplitudes. Individual afferents produced highly consistent responses across presentations of the same stimulus, whereas responses varied substantially across afferent types or even across afferents of a given type. For instance, in response to a 20 Hz sinusoid of amplitude 35 μm, four RA afferents responded robustly with one impulse per cycle, another seven fired less than once per cycle, and the remaining four failed to respond entirely. All afferents were probed at their point of maximum sensitivity (except for PC afferents, which lack a defined hotspot) so this variability in the neural response cannot be ascribed to differences in the locus of stimulation relative to the afferent's RF. Note that, as stimulus intensity increased, more afferents were recruited, i.e., produced a response above their spontaneous activity (which was typically nil). Furthermore, within the subpopulations of active fibers, entrainment increased with increased stimulus amplitude.

Figure 1.

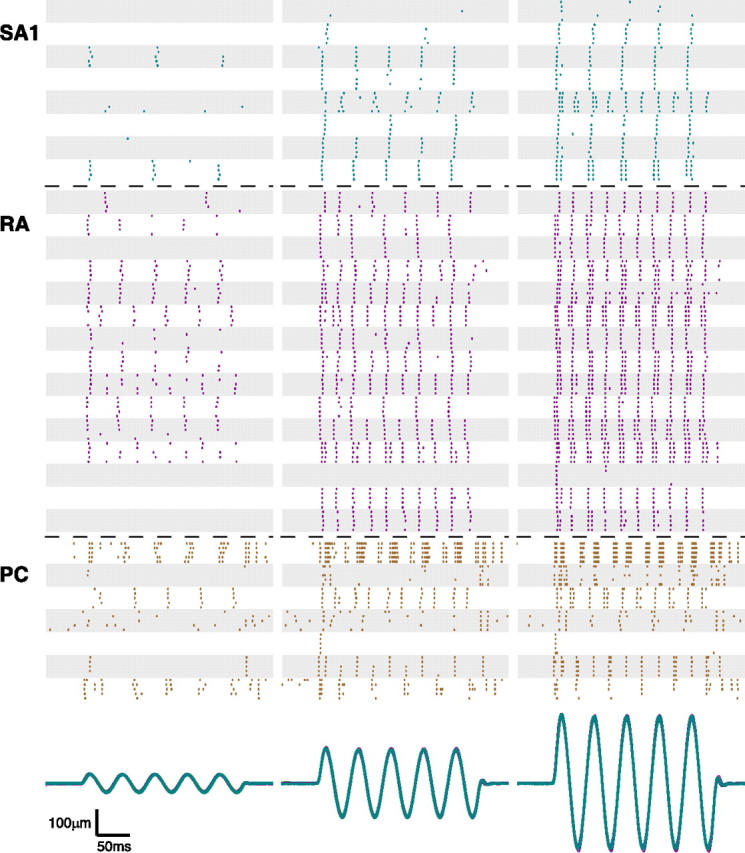
Spike-time rasters showing the responses of 8 SA1 (cyan), 15 RA (magenta), and 7 PC (brown) afferents to a 20 Hz sinusoid with amplitudes of 35 (left), 130 (center), and 250 μm (right). Each alternating shaded and unshaded patch corresponds to the responses of a given afferent to five presentations of the same stimulus. The bottom traces show the stimulus position as a function of time for all of the stimulus presentations.

Whenever possible, we created specific compensations for specific frequencies across a wide range of amplitudes (as described above), but this technique becomes impractical for stimuli requiring a larger set of frequencies, such as bandpass noise. For those stimuli, we created a frequency filter: We measured the Chubbuck's frequency and phase response up to 200 Hz and acquired the motor transfer function. We then used the inverted frequency and phase response curves, interpolated or decimated to match the stimulus sample size, to compensate complex stimuli. The frequency filter was also used to generate bandpass noise. Frequency filters produced less accurate compensation than the frequency and phase compensation described above, but we were still able to faithfully reproduce the desired waveforms (Figs. 1, 2, bottom panels).

Figure 2.

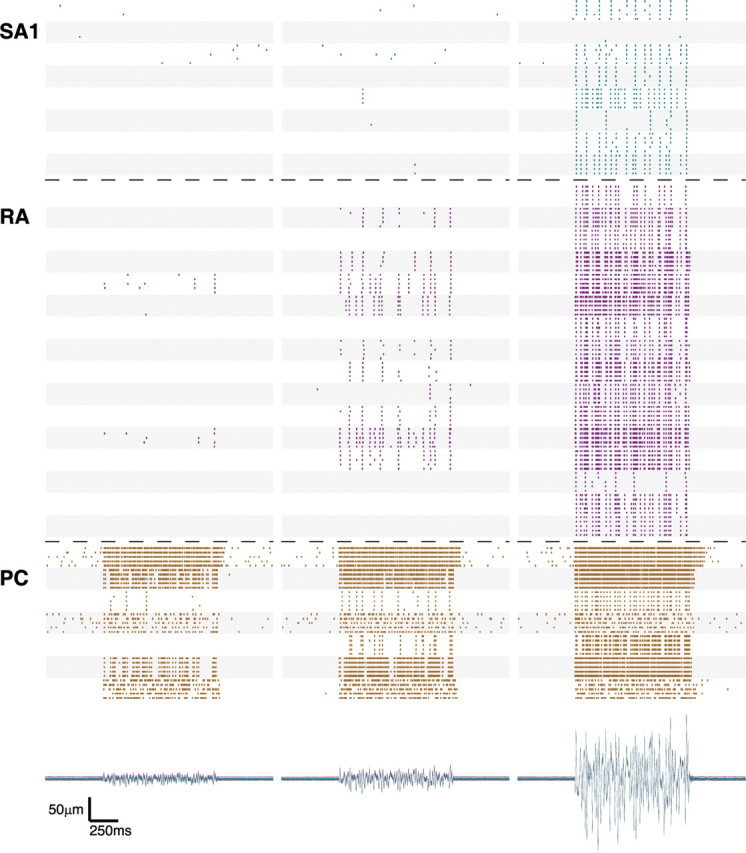
Spike-time rasters showing the responses of 8 SA1 (cyan), 16 RA (magenta), and 7 PC (brown) afferents to bandpass noise (5–100 Hz) with rms amplitudes of 5 (left), 10 (center), and 50 (right) μm. Each alternating shaded and unshaded patch corresponds to the responses of a given afferent to five presentations of the same stimulus. The bottom traces show the stimulus position as a function of time for all of the stimulus presentations. From the almost complete overlap of the traces, it can be seen that the stimulus was remarkably consistent across recording days.

When presented with a (5–100 Hz) (this notation denotes the low- and high-frequency cutoffs of a noise stimulus) bandpass noise stimulus, mechanoreceptive afferents also responded in an intensity-dependent manner, both in terms of firing rates and total number of active afferents (Fig. 2). This is seen most clearly in the responses of RA afferents: Only 2 of 16 RA afferents responded to noise with an rms amplitude of 5 μm, whereas 10 of 16 afferents responded to the 10 μm noise with mean rates ranging from 2 to 17 impulses per second, and 16 of 16 afferents responded to the 50 μm noise with mean rates ranging from 7 to 64 impulses per second. As was seen in responses to sinusoids, a wide variability in sensitivity was observed across afferents of a given type. A difference in absolute sensitivity across afferent types is also readily apparent: at an rms amplitude of 5 μm, the noise stimulus readily evoked robust responses from PC afferents yet failed to elicit more than a handful of spikes from SA1 or RA afferents; in response to the 10 μm noise, some RA afferents were active, but SA1 afferents were still relatively silent; all afferent types responded robustly to the 50 μm stimulus.

From the raster plots shown in Figures 1 and 2, it can be seen that at least two aspects of the afferent response changed with stimulus intensity: the firing rate evoked in individual afferents and the total number of active afferents within each population of afferents.

Individual rate–intensity functions

To probe the relationship between stimulus parameters and afferent firing rates, we first examined how the impulse rate evoked in individual afferents varied with stimulus intensity. For the harmonic stimuli (sinusoidal and diharmonic stimuli), we measured the response evoked by the stimulus in its steady state. Thus, we did not count spikes evoked during cycles that occurred during the on or off ramps (and the stimulus duration was adjusted accordingly). For diharmonic stimuli, stimulus cycles were determined on the basis of the lower-frequency component contained in the stimulus.

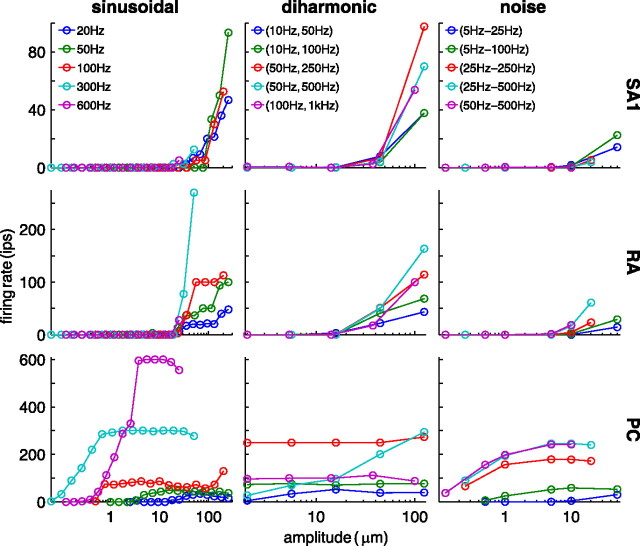
Figure 3 shows the rate–intensity functions obtained from three typical afferent fibers (one per afferent type) grouped according to frequency content: each trace corresponds to a particular frequency (sinusoidal), pair of frequencies (diharmonic), or pair of bandpass cutoff frequencies (noise). The impulse rate evoked in each afferent type tends to increase as stimulus intensity increases, but the rate at which each afferent does so depends both on the afferent type and the frequency content of the stimulus. For example, the PC afferent is highly sensitive to high-frequency sinusoids (100, 300, and 600 Hz), responding even at submicrometer amplitudes, whereas the SA1 and RA afferents do not respond to these stimuli until amplitudes almost two orders of magnitude higher. Conversely, PC responses to the low-frequency sinusoid (20 Hz) are weaker than their SA1 and RA counterparts. Furthermore, absolute thresholds (the minimum amplitude to evoke a response) and the slopes of the rate–intensity functions are virtually independent of frequency for the SA1 afferents (i.e., the traces tend to overlap), whereas these are highly frequency dependent for the PC fiber. RA responses exhibit intermediate frequency dependence.

Figure 3.

Rate–intensity functions obtained from a typical SA1 (top), RA (middle), and PC (bottom) afferent for a subset of sinusoidal (left), diharmonic (center), and noise (right) stimuli. For the diharmonic stimuli, each trace corresponds to the pair of frequencies specified in the legend; rates are plotted as a function of the amplitude of the low-frequency component (the relative amplitudes of the high-frequency components depend on their frequency; see Materials and Methods); for the noise stimuli, each trace shows afferent responses to stimuli with the low- and high-frequency cutoffs specified in the legend. ips, Impulses per second.

Mechanoreceptive afferents often exhibit entrained responses to sinusoidal stimuli (i.e., an integral number of impulses per cycle) over wide ranges of amplitudes (Talbot et al., 1968; Johnson, 1974; Bensmaia et al., 2005b). This phenomenon is clearly shown in the PC afferent's response to the high-frequency sinusoids (100, 300, and 600 Hz); for instance, at 300 Hz, the afferent responds at 300 impulses per second (once per cycle) for stimulus amplitudes ranging from 4.2 through 85 μm. Thus, this afferent's firing rate provides no information about stimulus intensity over this range of amplitudes. Indeed, this is a common problem: the PC response is entrained over the range of amplitudes tested for several diharmonic stimuli. This phenomenon is not exclusive to PC afferents; for example, the RA afferent entrains to 20 and 100 Hz sinusoids over a range of amplitudes. Obviously, entrainment plateaus are not seen in afferent responses to noise stimuli because of their aperiodic nature.

Mean rate–intensity functions

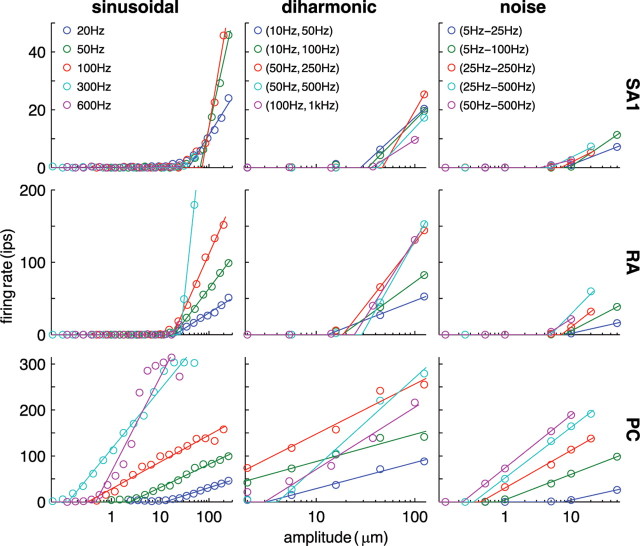
As mentioned above, differences in stimulus intensity cannot be resolved by an individual afferent over the range of intensities spanned by that afferent's entrainment plateau. Thus, given that perceived intensity is a monotonic function of stimulus intensity (for sinusoids at least) (Talbot et al., 1968; Johnson, 1974), single mechanoreceptive afferents provide insufficient information to code for stimulus intensity (cf. Johnson, 1974). However, impulse rates evoked by a given stimulus differ greatly within and across afferents types (Figs. 1, 2). We therefore examined the relationship between the mean firing rate evoked in each afferent type and stimulus intensity (Fig. 4). To obtain the mean rate–intensity functions, we averaged the rate evoked by each stimulus across repetitions and afferents, for each afferent type individually.

Figure 4.

Mean rate–intensity functions obtained from SA1, RA, and PC afferents for the three types of stimuli. Open circles correspond to neural data, and the solid lines denote the predicted firing rates (fit using Eq. 2). ips, Impulses per second.

In contrast to responses of individual afferents, mean responses exhibit little to no entrainment [PC responses to 600 and 800 Hz sinusoids seem to exhibit an entrainment plateau at the high stimulus intensities. However, few PC afferents responded at those frequencies and intensities (n = 3), so this feature is likely not present in the response of a larger sample.] because entrainment plateaus occur over different ranges of amplitudes for different afferents (data not shown). Indeed, mean rate increases monotonically with stimulus intensity for all afferent types for all stimuli. The dependence of PC firing rates on the frequency content of the stimulus is still evident in the mean firing rates: PC afferents are highly sensitive to high-frequency stimuli, responding to 100, 300, and 600 Hz sinusoids at amplitudes <1 μm (their mean absolute threshold is almost two orders of magnitude lower than that of SA1 and RA afferents) but not at the low frequencies. The same frequency dependence can be observed in PC responses to diharmonic and noise stimuli (Fig. 4); indeed, stimuli that include high-frequency components tend to yield lower thresholds. Mean rate–intensity functions for SA1 and RA afferents are more clustered, suggesting that these populations are less sensitive to the frequency composition of the stimuli. In Figure 4, data obtained from stimuli differing only in the relative phase of the high-frequency component relative to that of the low-frequency component (φ in Eq. 1) were averaged together, because phase was found to have no effect on firing rate (as predicted from Bensmaia and Hollins, 2000) (Fig. 5).

Figure 5.

Comparison of the rate intensity functions obtained for five diharmonic stimuli at four relative phases (φ = 0, π/2, π, and 3π/2). The different traces of each color correspond to stimuli that differ only in phase. Relative phase had no effect on firing rate for any stimulus in any afferent type. ips, Impulses per second.

We fit the rate–intensity data obtained from each group of stimuli (whose frequency content was constant) with a rectified logarithmic function:

where a is the effective stimulus amplitude in micrometers, α is the slope of the linear portion of the function, β is the log threshold (i.e., the logarithm of the minimum amplitude that will, on average, activate an afferent of that type), and f(a) is the mean firing rate evoked in that population of afferents (in impulses per second) by a stimulus of amplitude a. The slopes and threshold parameters, α and β, were fit, using a least-squares method, to data obtained from stimuli sharing the same frequency content. The fitted rectified log functions are plotted along with the rate–intensity data in Figure 4. According to this mathematical formulation, then, the activity of an afferent will remain at zero until the effective amplitude becomes larger than some threshold, at which point the rate will increase as a logarithmic function of amplitude. As can be seen from Figure 4, rectified log functions provided close fits for the rate–intensity functions: the mean coefficients of determination (R²) for functions fit to sinusoidal, diharmonic, and noise stimuli were 0.97, 1.0, and 0.99, respectively.

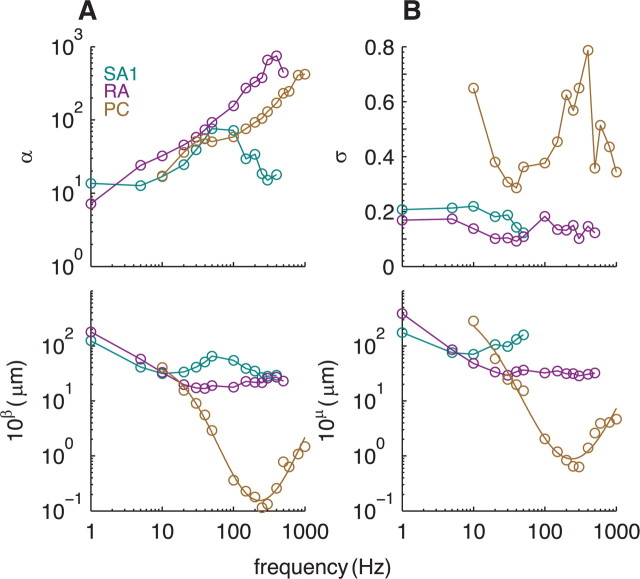
We examined the slopes and thresholds, α and β, of the rectified logarithmic functions obtained from responses to sinusoids and considered how these varied with frequency (Fig. 6A). The frequency dependence of threshold parameter β conformed with previous measurements of absolute threshold (Talbot et al., 1968; Freeman and Johnson, 1982a; Johansson et al., 1982): PC afferents yielded a characteristic U-shaped threshold-frequency relationship; the RA threshold-frequency function was also U-shaped (for frequencies through 400 Hz), although considerably shallower. Finally, SA1 thresholds exhibited a complex relationship with stimulus frequency. The slopes of the rate–intensity functions, α, also varied across afferent types: slopes increased monotonically for PC afferents and, over a wide range, for RA afferents, whereas slopes for SA1 afferents were an inverted U-shaped function of stimulus frequency. The respective relationships of α and β to stimulus frequency further illustrate the differences in spectral sensitivity across afferent types.

Figure 6.

A, Parameters α and β as a function of frequency. Parameter β [converted to micrometers from log(μm)] is an estimate of the mean absolute threshold of each afferent type at each frequency. Parameter α denotes the mean rate of rise of the firing rate as a function of increments in log(amplitude) of the stimulus. Parameters for a given frequency are shown only if stimuli at the two highest intensities at that frequency evoked a mean rate of at least 5 impulses/s; otherwise, parameter estimates are unreliable. B, Parameters μ and ς as a function of frequency. Parameter μ [converted to micrometers from log(μm)] is an estimate of the amplitude at which the probability that an afferent of a given type will become active is 0.5. Parameter ς denotes the slope of the sigmoid [in log(μm)⁻¹]. Sigmoid parameters for a given frequency are shown only if the stimulus at the highest intensity at that frequency activated at least 50% of the afferents; otherwise, parameter estimates are unreliable.

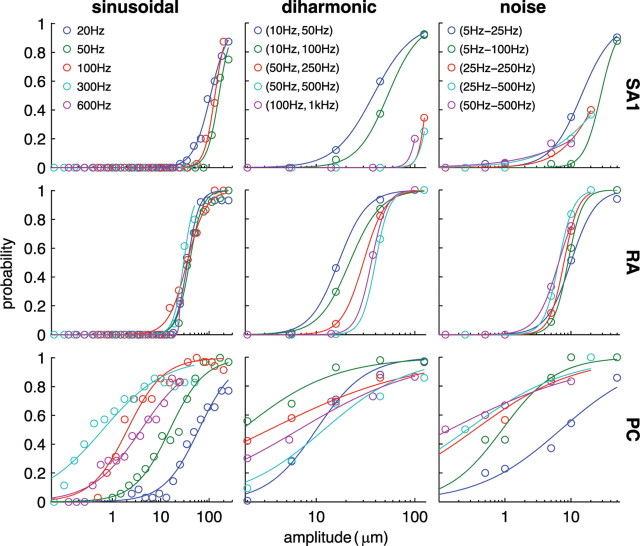
Recruitment–intensity functions

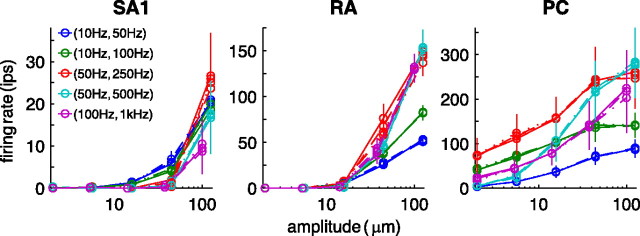
As we have already seen, modulation of the firing rate of individual afferents is but one way in which the peripheral neural response reflects stimulus intensity. Indeed, an increasing number of afferents is recruited as the stimulus intensity increases (Figs. 1, 2). To better understand this aspect of the neural response, we investigated the relationship between stimulus intensity and the probability that an individual neuron of a given type will fire (Fig. 7). To calculate this firing probability, we counted the number of trials for which a neuron fired at a rate that was at least 10% greater than its baseline rate, defined as the mean firing rate during periods in which no stimulus was presented. The baseline rate was zero or near zero for most SA1 and RA afferents and some PC afferents (Figs. 1, 2).

Figure 7.

Mean probability–intensity functions obtained from SA1, RA, and PC afferents for the three types of stimuli. Open circles correspond to neural data, and solid lines denote predicted probabilities (fit using Eq. 3).

As one might expect, recruitment–intensity functions share similarities with their firing-rate counterparts: both are modulated by stimulus frequency in qualitatively similar ways. For instance, the frequency dependence of PC responses is evident in the recruitment functions (as it was in the mean-rate functions), whereas the weaker frequency dependence of SA1 and RA response stands in clear contrast. (Interestingly, the SA1 recruitment functions for diharmonic stimuli are much more divergent than are the corresponding firing-rate functions. In other words, the firing rate evoked in individual SA1 afferents or in a population of SA1 afferents does not seem to depend on stimulus frequency, but the number of active SA1 afferents does.) However, the two quantities are not interchangeable. For instance, recruitment of PC afferents by a 100 Hz sinusoid saturates at 10 μm, yet the mean firing rate in this population continues to increase up through 200 μm. RA recruitment shows a similar disparity: recruitment saturates at ∼60 μm at all stimulus frequencies, but the mean firing rate continues to increase as amplitude increases through 200 μm. The slopes of RA mean rate and recruitment functions for sinusoids are also different: recruitment increases at essentially the same rate for all the sinusoids, whereas the slopes of the rate–intensity functions are frequency dependent. Thus, the hypothesis that the peripheral neural code for stimulus intensity is based on afferent recruitment would likely yield divergent predictions from one positing that firing rate is the relevant quantity.

To characterize how recruitment was modulated by stimulus frequency, a standard sigmoid was fit to the recruitment–intensity functions:

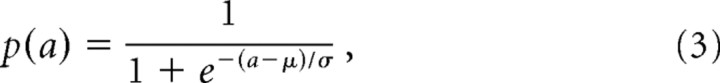where p(a) is the probability that an afferent will become activated at amplitude a (when the stimulator is placed over its hotspot), and μ and ς are free parameters (fit, using a least-squares method, to data obtained from groups of stimuli sharing the same frequency content). As can be seen from Figure 7, the sigmoids provided nearly perfect fits for the recruitment–intensity functions: The mean coefficients of determination for functions fit to sinusoidal, diharmonic, and noise stimuli were 0.98, 0.99, and 0.97, respectively.

Figure 6B shows the parameter values of the sigmoids fit to sinusoids as a function of frequency. The frequency dependence of parameter μ was similar to that of β (see Eq. 2), whereas the slope of the sigmoid, ς, did not vary systematically with frequency (particularly for SA1 and RA afferents), in contrast to the slope of the rectified log function, α. The differential behavior of parameters ς and α further demonstrates that these two aspects of the neural response (and putative neural codes) are not equivalent.

Magnitude estimates of perceived intensity

To investigate the neural code underlying vibrotactile intensity, we measured the perceived intensity of a carefully selected subset of the stimuli presented in the neurophysiological experiments. To the extent possible, we selected stimuli that evoked divergent responses across afferent types to characterize the relative contributions of the three populations of afferents to the coding of vibrotactile intensity. Note that, at the extreme, if SA1, RA, and PC responses to a set of stimuli are perfectly correlated, it is impossible to disentangle their relative contributions. Stimuli were delivered using a single stimulator, the Chubbuck, so that subjects could rate all of the stimuli within each experimental block; presenting stimuli (in pseudorandom order) with two stimulators was impractical. The use of the Chubbuck as the lone stimulator constrained the stimulus set to vibrations whose frequency content did not exceed 100 Hz, the maximum frequency at which the Chubbuck performed nearly perfectly.

The psychophysical stimulus set comprised 74 stimuli (24 sinusoids, 40 diharmonic stimuli, and 10 noise stimuli, each with unique frequency–amplitude combinations). The mean impulse rates evoked in SA1 and RA afferents by these stimuli were highly correlated (R² = 0.76); RA and PC responses were more divergent (R² = 0.53), with many PC afferents responding to stimuli that failed to excite RA afferents; SA1 and PC afferents differed substantially in their response (R² = 0.23), again with a number of stimuli evoking responses in PC but not SA1 afferents. That the various stimuli excited the three afferent types to varying degrees suggested that the stimulus set would allow us to assess the relative contributions of the three populations of afferents to perceived intensity.

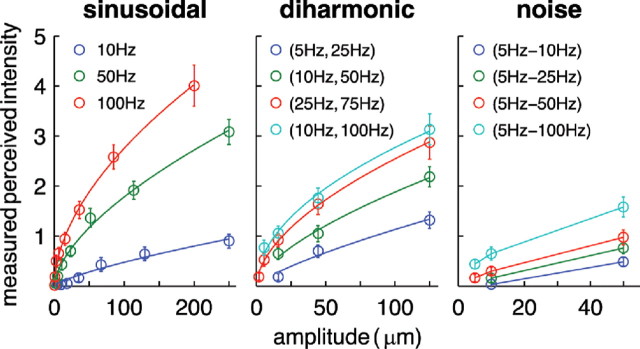
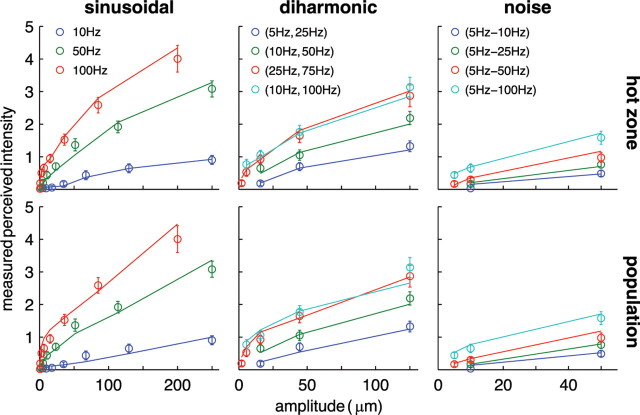
The nine subjects were highly consistent in producing ratings of perceived intensity. The median correlation between the mean ratings produced by one subject and those produced by another is 0.92 (minimum correlation = 0.85). For all three stimulus categories (sinusoidal, diharmonic, and noise stimuli), the perception of intensity varied with both the frequency content and amplitude of the vibrations (Fig. 8). For sinusoidal and diharmonic stimuli, the relationship between perceived and actual intensity is reasonably well approximated by a power function (not enough bandpass noise stimuli shared the same frequency content to justify fitting a function). Frequency content appears to be a significant factor in determining perceived intensity: the sinusoid with the highest frequency, diharmonic with the highest component frequency, and bandpass noise with the highest upper frequency cutoff all yielded the highest ratings within their group.

Figure 8.

Ratings of perceived intensity, averaged across subjects, for a subset of sinusoidal (left), diharmonic (center), and noise (right) stimuli. For the diharmonic stimuli, ratings are plotted as a function of the amplitude of the low-frequency component (the relative amplitudes of the high-frequency components depend on their frequency; see Materials and Methods). We only included groups of stimuli that comprised at least two stimuli sharing the same frequency content and differing only in amplitude. The sinusoidal and diharmonic stimuli are fit with power functions. For sinusoids, exponents are 0.75, 0.61, and 0.54 at 10, 50, and 100 Hz, respectively; for diharmonic stimuli, the exponents are 0.76, 0.64, 0.56, and 0.50 for (5 Hz, 25 Hz), (10 Hz, 50 Hz), (25 Hz, 75 Hz), and (10 Hz, 100 Hz), respectively. The mean correlation between predicted and observed perceived intensity was 0.99 for both sinusoidal and diharmonic stimuli. No exponent was fit to the data obtained from noise stimuli because there were too few data points per stimulus group (each group sharing bandpass frequencies).

Neural codes for perceived intensity

The primary objective of the present study was to establish the neural code underlying perceived intensity [following Johnson (1974)]. It has been suggested that the relevant aspect of neural activity should exhibit a linear relationship with the subjective experience to which it gives rise (Johnson et al., 2002); thus, the pattern of psychophysical ratings (Fig. 8) should be consistent with the neural quantity predicated by any viable neural code.

Firing rate of afferents whose RFs are located under the probe

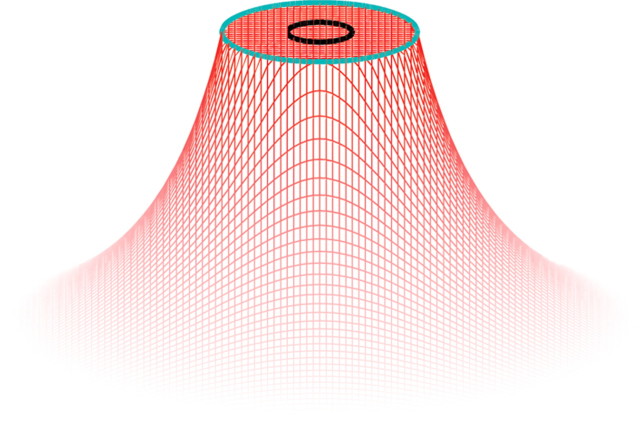
The first and most straightforward predictor of perceived intensity is the mean evoked rate in each population of afferents. Two assumptions underlie this peripheral code for perceived intensity: (1) Only afferents whose RFs are located under or near the stimulating probe (i.e., are located in the “hot zone”) (see Fig. 10) contribute to the perceived intensity of the stimulus. (2) A sufficient number of afferents (∼10 or more) have RFs located in the hot zone such that their activity is better approximated by mean rate–intensity functions (Fig. 4) than by individual rate–intensity functions (Fig. 3).

Figure 10.

Spatial distribution of the effective amplitude, A(r), of the stimulus; A(r) drops off as an inverse square function of distance beyond an annulus 1 mm away from the probe edge (see Eq. 3). The black contour indicates the location and extent of the contactor (r = 0.5 mm). The term “hot zone” refers to the area under this blue contour, an area over which the effective amplitude is constant at A₀.

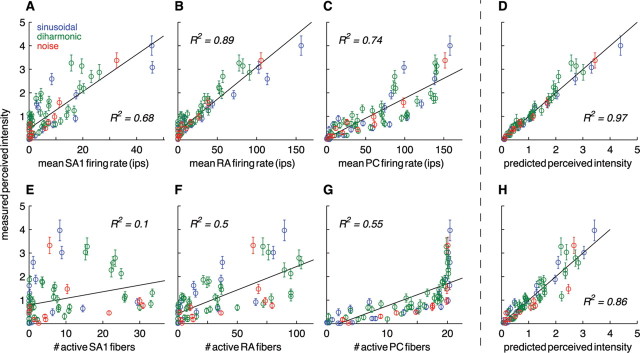
To assess the viability of this putative code, we plotted the mean rate evoked in each afferent population against the mean perceived intensity for all the stimuli used in the psychophysical experiment (Fig. 9A–C). The mean rate evoked in SA1 afferents was moderately predictive of the intensity ratings (Fig. 9A) (R² = 0.68); however, SA1 afferents failed to respond to a number of stimuli to which nonzero ratings were ascribed. The mean firing rate of RA afferents was a good linear predictor of perceived intensity (Fig. 9B) (R² = 0.89), but these fibers also failed to respond to a number of palpable stimuli. Finally, PC rates were highly but not perfectly correlated with intensity ratings (Fig. 9C) (R² = 0.74).

Figure 9.

A–C, Perceived intensity ratings plotted against the mean firing rate evoked in SA1 (A), RA (B), and PC (C) afferents. D, Predictions derived from the multiple regression of perceived intensity on the population firing rates in the three types of afferents. The three slope coefficients (β_SA1 = 0.29, β_RA = 0.36, and β_PC = 0.46) are highly significant (p < 0.001), indicating that all three types of mechanoreceptive afferents contribute to perceived intensity. E–G, Perceived intensity versus the number of active SA1 (E), RA (F), and PC (G) afferents. As can be seen, PC recruitment is a poor code for perceived intensity because it saturates at low stimulus intensities. H, Relationship between the measured perceived intensity and the predicted perceived intensity from the multiple regression model. ips, Impulses per second.

These results suggest that the mean response evoked in a population of mechanoreceptive afferents of a single type, whose RFs are located in the hot zone, does not account for all aspects of perceived intensity. One possibility is that information from all three afferent populations combines to yield a unified percept of intensity. To evaluate this hypothesis, we performed a multiple regression of perceived intensity ratings on the mean firing rates of the three afferent types. We found that the regression model produced exceptionally accurate predictions of perceived intensity (Fig. 9D) (R² = 0.97). Importantly, the slope coefficients for SA1 (β_SA1 = 0.25) (here, we report the standardized regression coefficient), RA (β_RA = 0.36), and PC (β_PC = 0.46) afferents were all highly significant (t₍₇₀₎ = 5.0, 5.4, and 11.2 for SA1, RA, and PC afferents, respectively; p < 0.001). This analysis suggests, then, that the firing rate evoked in mechanoreceptive afferents whose RFs are located at or near the locus of stimulation (in the hot zone) relate the necessary information about stimulus intensity to mediate perception. Furthermore, the responses in all three types of afferents determine the perceived intensity of the stimulus.

Population firing rate

The weighted mean activity in all three types of mechanoreceptive afferents can account for 97% of the variance in the intensity ratings. As noted above, however, this analysis is based solely on the activity of afferents whose RFs are in the hot zone. In fact, it has been shown that a stimulus excites afferents that are not directly under the stimulus probe (Johnson, 1974; Cohen and Vierck, 1993a): vibrations produced at the locus of stimulation propagate across the skin and also activate afferents whose RFs are nearby. Specifically, Johnson (1974) found that the effective amplitude of a vibratory stimulus, i.e., the stimulus amplitude experienced by a mechanoreceptor embedded in the skin, drops off as an inverse square of the distance between the locus of stimulation and the location of the mechanoreceptor. Thus, the effective amplitude of the stimulus at a distance r from the probe center, A(r), is approximately

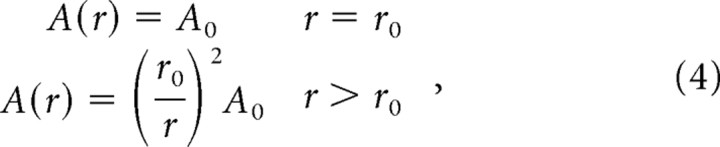where A₀ is the amplitude of the stimulus at the locus of stimulation, r₀ is the radius of the probe + 1 mm (cf. Johnson, 1974) (note that this is an empirically determined relationship). In other words, an afferent whose RF is located at distance r from the center of the stimulator contactor responds to the stimulus as if a vibration of amplitude A(r) was delivered over its hot spot. Using this relationship, we reconstructed the stimulus at any point on the glabrous skin with respect to the stimulator tip (Fig. 10).

The relationship described by Johnson (1974) was based on the activity of a population of RA afferents. The coarse spatial structure of SA1 and RA RFs is similar (Johansson, 1978), and the model is likely applicable to both afferent types. The spatial properties of PC afferents are very different from those of SA1 and RA afferents, however. First, their RFs are an order of magnitude larger (mean area = 101 mm² vs 11 and 13 mm² for SA1 and RA afferents, respectively) (Johansson and Vallbo, 1980). Furthermore, a PC afferent's sensitivity is relatively homogenous over its RF [Johansson (1978), their Fig. 7]. In fact, when testing a PC afferent, the stimulator probe was placed somewhere within this sensitive zone but not necessarily in the “hottest” spot of the RF because the latter was difficult to locate. For these reasons, when estimating the population response of PC afferents, we assumed that these afferents have large homogeneous RFs; the best estimate of the PC population response, then, is the mean response (Fig. 4) multiplied by the estimated number of active afferents.

To infer the neural activity produced by a stimulus in a population of SA1 or RA afferents, we required a function that relates the response of a typical (or average) afferent to the intensity of the stimulus. The rate–intensity functions shown in Figure 4 satisfy this condition: indeed, the response evoked by a stimulus averaged across afferents is a reasonable estimate of the expected value of the firing rate evoked in a single afferent by that stimulus. To describe the relationship between firing rate and intensity, we used rectified logarithmic functions (Eq. 2) fit to groups of stimuli with the same frequency content (see above). Whether these functions capture the behavior of the afferents outside of this range is immaterial as we never extrapolated beyond the range of intensities used (In fact, it is unlikely that these functions are adequate across all intensities as firing rates likely saturate at high intensities).

We then expressed the spike rate evoked by a stimulus of amplitude A₀ in an afferent whose RF is located at distance r from the locus of stimulation by substituting A(r) (from Eq. 4) for a (in Eq. 2):

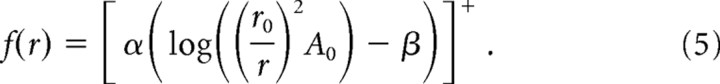From these functions (and for purposes of integration, see below), we worked backwards to determine the maximum distance at which the stimulus is able to activate the afferent, r_max [i.e., the distance at which f(r) = 0]:

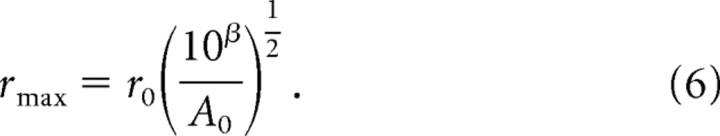For example, a 100 Hz, 85 μm sinusoid will activate SA1 afferents up to a distance of 1.6 mm and RA afferents up to a distance of 3.3 mm away from the locus of stimulation; a 100 Hz, 200 μm sinusoid will excite SA1 afferents up to a distance of 2.5 mm and RA afferents up to a distance of 5 mm.

To reconstruct the population response, we first assumed that all points on the skin surface at a distance r from the probe are stimulated at the same effective stimulus amplitude [A(r); see Eq. 4]. Based on this assumption, we expressed the firing rate, F_annulus(r), for the set of afferents whose point of maximum sensitivity lies within an infinitesimally thin annulus of radius r centered on the probe:

where f(r) is the expected value of the firing rate (in impulses per second per millimeter per afferent) at distance r from the center of the stimulator probe, and ρ is the innervation density of the afferent type (in units per square millimeter). We then integrated the expression for F_annulus(r) over r from the edge of the probe contactor + 1 mm to a distance away from the contactor at which the stimulus no longer evokes a response (as determined using Eq. 6):

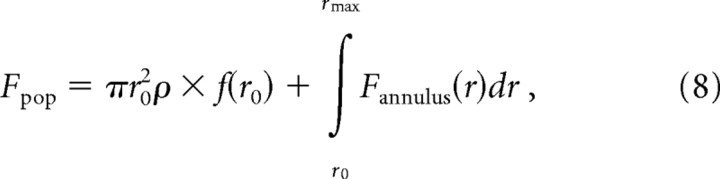where f(r₀) is the firing rate of afferents whose hotspot is located under the probe (or within 1 mm of its edge) and are therefore stimulated at an effective amplitude of A₀. Expanding the nested functions within the integral yields the following expression:

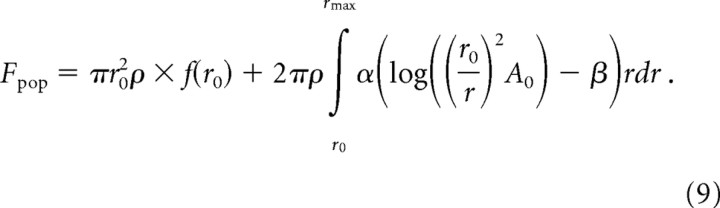The population rate can then be divided into two components: (1) the total firing rate of afferents whose RFs are located within a circular area of radius r₀ under and around the stimulus probe and (2) the firing rates of afferents outside this region, expressed as an integral of successive annuli expanding outwards away from the edge of the probe. The solution of Equation 9 is as follows:

where r_max is the maximum distance away from the hot spot at which the stimulus will evoke an action potential in this population of afferents. Substituting for r_max (from Eq. 6), Equation 10 becomes the following:

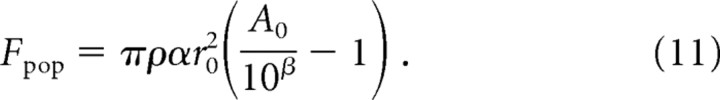Thus, although mean afferent firing rates are logarithmic with stimulus amplitude, population firing rates for SA1 and RA afferents exhibit a linear relationship with stimulus amplitude (A₀).

The PC population response was estimated by multiplying the mean evoked firing rate by the estimated number of PC afferents whose RFs overlap the contactor area. The latter was estimated by computing the area of a circle whose radius was equal to the mean radius of a PC RF (5.7 mm) (cf. Johansson, 1978) and multiplying the resulting area by the innervation density of PC afferents in human skin (0.2 units/mm²) (cf. Johansson and Vallbo, 1979b).^a

F_pop, derived for SA1 and RA responses, was then used to predict perceived intensity in a multiple regression model. The overall goodness of fit of this model is nearly identical to that obtained with mean firing rates (R² = 0.96). However, the hot-zone model more closely captures the fine structure of the psychophysical data than does the population-rate model (Fig. 11). As described above, the predicted perceived intensity (solid lines) was computed by using the output of Equation 2 (with values of α and β shown in Fig. 6) as input to the multiple regression model with a single set of regression coefficients. Although these coefficients were computed by pooling together results obtained using different stimulus frequencies, the predicted perceived intensities are remarkably accurate at all stimulus frequencies. Furthermore, the mean SA1 and RA firing rates are highly correlated with their population-rate counterparts (r = 0.92 and 0.92 for SA1 and RA afferents, respectively), despite the fact that one measure is linear with amplitude and the other logarithmic.

Figure 11.

Predictions of perceived intensity derived from the hot-zone model (top) and from the population-rate model (bottom) for sinusoidal, diharmonic, and noise stimuli. Although both models capture the coarse structure of the psychophysical data, the hot-zone predictions match the data even in their details. This is particularly evident for the low-frequency sinusoidal and diharmonic stimuli.

Number of active afferents

Next, we assessed whether the recruitment of afferents could serve as a code for intensity [following Johnson (1974)]. As shown in Figure 7, the recruitment of afferents directly under the probe is a function that saturates at relatively low stimulus amplitudes, suggesting that the number of active afferents under the probe cannot determine the perceived intensity. However, as discussed above, a stimulus propagates across the skin and excites afferents whose RFs are located away from the contact area. Using a similar approach as that used to estimate the population firing rate, we estimated the total number of afferents activated by a given stimulus, then assessed whether this quantity could determine perceived intensity.

To estimate afferent recruitment, we first characterized the probability that an afferent (of a given type) would be activated by the stimulus as a function of its intensity. The recruitment–intensity functions were then used as estimates of the probability that an afferent of a given type would become active (that its activity would increase by at least 10% over its baseline rate).

The probability that a given afferent whose hotspot is located at distance r from the locus of stimulation is activated by a stimulus of amplitude A₀ can then be derived by substituting a (from Eq. 3) with the expression for A(r) (from Eq. 4):

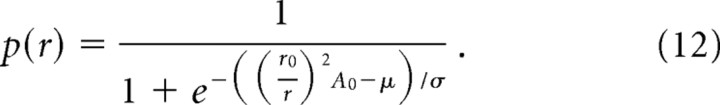To model the number of active afferents across the population, we again assumed that all points on the skin surface at a distance r from the stimulus probe are stimulated at the same effective stimulus amplitude A(r). Again, we defined the total number of active afferents per millimeter, P_annulus(r), about an infinitesimally thin annulus of distance r, as follows (see Eq. 7):

where ρ is the innervation density of the afferent type (in units per square millimeter). To calculate the total number of active afferents of a given type over the skin surface we used the following relationship:

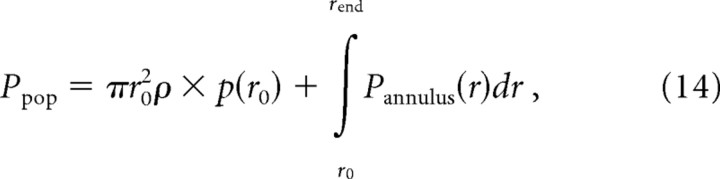where r₀ is the radius of the probe and r_end is an arbitrary upper endpoint of the integral chosen such that p(a) at this distance approaches zero (r_end = 50 mm). Expanding the nested functions within the integral yields an expression analogous to Equation 9, namely:

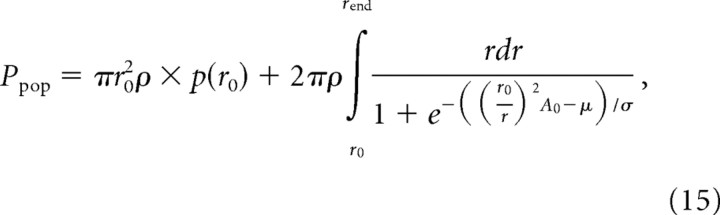where A₀ is the amplitude of the stimulus at the locus of stimulation. This integral does not have an analytical solution, so we used recursive adaptive Simpson quadrature to solve it over the specified endpoints.

For reasons detailed above, the number of active PC afferents was derived by multiplying p(a) by the number of PC afferents whose RF overlaps the contact area (as described above).

The numbers of active SA1, RA, and PC afferents are, individually, poor predictors of perceived intensity (R² = 0.10, 0.50, and 0.55 for SA1, RA, and PC afferents, respectively) (Fig. 9E–G). When perceived intensity ratings is regressed onto P_pop, the model fit is somewhat poorer than that obtained from the firing-rate model (Fig. 9H) (R² = 0.86). Again, the slope coefficients for SA1 (β_SA1 = −0.84), RA (β_RA = 1.3), and PC (β_PC = 0.28) afferents are all highly significant (t₍₇₀₎ = −8.7, 12.0, and 4.8 for SA1, RA, and PC afferents, respectively; p < 0.001). Note that the slope coefficient for SA1 afferents is significantly negative, indicating that the perceived intensity decreases as more SA1 afferents are recruited, an implausible phenomenon. Although the goodness of fit of the firing-rate and recruitment models are comparable (the small difference in goodness of fit may be attributed to differential inaccuracies in the underlying population estimates), the peculiarity of the SA1 regression coefficient weakens the case for population recruitment as a neural code for perceived intensity.

Discussion

Neural coding of stimulus intensity

In this study, we characterized the relationship between two aspects of the neural response (firing rate and number of active afferents) and stimulus intensity. We then assessed the extent to which a set of peripheral neural codes can account for perceived intensity (Table 3). One of our primary assumptions was that the relevant aspect of neural activity should exhibit a linear relationship with the subjective experience to which it gives rise (Johnson et al., 2002).

Table 3.

Summary of neural codes

Hypothesis tested	Outcome
(1) Firing rate of individual afferents (SA1, RA, PC)	Rejected because individual rate-intensity functions comprise long entrainment plateaus
(2) Mean firing rate of individual afferents	SA1, R2 = 0.68
	RA, R2 = 0.89
	PC, R2 = 0.74*
(3) Weighted firing rate of three afferent types located under the probe	R2 = 0.97
(4) Number of afferents of each type activated under the probe	Rejected because number of afferents recruited plateaus at low stimulus intensities (Fig. 4)
(5) Estimated total firing rate of each afferent type	SA1, R2 = 0.56
	RA, R2 = 0.80
	PC, R2 = 0.74*
(6) Estimated weighted firing rate of three afferent types	R2 = 0.96
(7) Estimated total number of afferents of each type activated by the stimulus	SA1, R2 = 0.10
	RA, R2 = 0.51
	PC, R2 = 0.54
(8) Estimated weighted number of active afferents	R2 = 0.86

*Codes are identical.

We eliminated the first hypothesis (that perceived intensity is determined by the firing rate in individual afferents) because rate–intensity functions for individual afferents exhibit entrainment plateaus, over which the neural response does not change, whereas perceived intensity increases monotonically with stimulus intensity (compare Figs. 3, 8). Codes based on the responses of single afferent types (hypotheses 2, 5, and 7 corresponding to mean rate, total population firing rate, and total population recruitment, respectively) could not be rejected outright. Indeed, these hypotheses did not yield dramatically erroneous predictions (as does, for instance, the first hypothesis) so they cannot be said to have been falsified (Popper, 1959). However, all of these codes yield significantly poorer predictions than do codes that involve input from all three afferent types, which constitutes evidence that all three populations of afferents mediate the perception of stimulus intensity. We eliminated the fourth hypothesis because recruitment functions saturate at low stimulus intensities, whereas the psychometric functions do not (compare Figs. 7, 8). We also evaluated the hypothesis that the rate at which synchronized spikes impinge on neurons that receive afferent input determines perceived intensity (see supplemental material, available at www.jneurosci.org).

Thus, three hypothetical neural codes account linearly for the psychophysical ratings (3, 6, and 8): the firing rates of afferents located under the probe, weighted by afferent type; the total population firing rate, weighted by afferent type; and the total number of active afferents, weighted by afferent type. We showed that the two viable firing-rate hypotheses (3 and 6) can only be distinguished on the basis of small deviations of their predictions from the psychophysical data (Fig. 11). Although the recruitment code (8) provides good predictions of the perceived intensity, it is improbable, because it makes the unlikely prediction that perceived intensity decreases as more SA1 afferents are recruited. We thus favor the hypothesis that perceived intensity is determined by the firing rate evoked in the three main populations of mechanoreceptive afferents, weighted by afferent type.

According to hypothesis 3, only afferents whose RFs are located under or near the contact area (i.e., the area over which the effective amplitude is the actual amplitude of the stimulus) (Fig. 10) contribute to the perceived intensity of the stimulus. In the present experiment, the contactor and surrounding area spanned ∼7 mm². In humans, ∼5 SA1 and 10 RA afferents will have RFs whose centers are located in this region; another 20 PC afferents will have RFs that overlap the center of the contactor (using densities from Johansson and Vallbo, 1979a).

The relative innervation densities of the three types of mechanoreceptive fibers differ across body regions, even across different regions in the hand (Johansson and Vallbo, 1979a), as do psychophysical thresholds (Johansson and Vallbo, 1979b). An interesting question is whether the perceived intensity of vibratory stimuli varies as a function of body region or whether it remains constant across the body surface. If the weighting of the activity of the three receptor types is constant across body regions, the present model predicts that perceived intensity would vary according to relative innervation density. Another possibility is that this weighting varies across the body surface to maintain perceptual constancy for stimulus intensity.

Both the hot-zone hypothesis (3) and the population-rate hypothesis (6) match the psychophysical data well, with the hot-zone hypothesis producing slightly better predictions. Additional experiments will be required to establish which of these two codes (population or hot zone) underlies the perception of intensity. Moreover, how stimulus intensity is represented in cortex is unclear [but see de Lafuente and Romo (2005, 2006)]. That simple coding mechanisms such as the ones proposed here can account for perception is particularly striking given the nonlinear and dynamic nature of cortical processing (Moore et al., 1999; Kohn and Whitsel, 2002; Sripati et al., 2006). For instance, vibratory stimulation has been shown to evoke a pattern of activation in primary somatosensory cortex that becomes more spatially restricted over time (Simons et al., 2007). An intriguing possibility is that this spatial funneling of the cortical response may reflect a network dynamic that culminates in the activation of a population of neurons whose RFs are confined to the hot zone: the initially wide-spread cortical response, evoked by input from the entire population of mechanoreceptive afferents activated by the stimulus (Fig. 10), becomes confined to the population of neurons with RFs overlapping the hot zone; it is then this population of neurons that convey information about stimulus intensity. The phenomenon of central adaptation also constitutes a dynamic change in the responses of cortical neurons to vibratory stimuli: indeed, cortical responses to extended suprathreshold vibratory stimulation decrease over time (O'Mara et al., 1988; Whitsel et al., 2003), a phenomenon that is explained only in part by adaptation in the responses of peripheral afferents (Bensmaia et al., 2005b) [however, given the time course of the spatial funneling and of peripheral and central adaptation (Leung et al., 2005), the degree to which these phenomena influenced our results is not clear]. Thus, many questions remain as to the neural coding of intensity in cortex; these questions, however, are beyond the scope of the present study. Nevertheless, a major conclusion of this study is that signals from three submodalities, which convey information about different aspects of the stimulus (i.e., form, motion and vibration), are integrated to form a coherent percept of stimulus intensity.

Role of slowly adapting type 2 afferents

A fourth type of afferent, slowly adapting type 2 (SA2), traditionally believed to terminate in Ruffini corpuscles (although see Pare et al., 2003), is found in the glabrous skin of humans but not macaques and responds to vibratory stimulation (Merzenich and Harrington, 1969; Gynther et al., 1992). Whether this afferent type contributes to perceived intensity is unclear. However, there is little direct evidence that it contributes to vibrotaction [for a counterargument, see Bolanowski et al. (1988)]. For instance, microstimulation of single SA2 afferents does not produce any conscious sensation, much less a vibratory percept, whereas microstimulation of the other three afferent types yields sensations ranging from pressure, to taps, to vibrations, the nature of which depends both on the frequency of the electrical impulses and the type of mechanoreceptive afferent stimulated (Ochoa and Torebjörk, 1983). Regardless, if SA2 afferents do contribute to the perception of stimulus intensity, their influence must be small because responses from the three other afferent types account for 97% of the variance in ratings of perceived intensity.

The psychophysics of perceived intensity

In a number of psychophysical studies, subjects were presented with sinusoidal stimuli varying in frequency and amplitude and produced ratings of subjective intensity (Stevens, 1968; Franzén, 1969; Verrillo et al., 1969; Marks, 1979; Hollins and Roy, 1996). Perceived intensity was modeled as a simple power function of stimulus intensity (Stevens, 1968; Franzén, 1969) or as a two-branched function, with the second branch a power function (Verrillo et al., 1969; Hollins and Roy, 1996). The slope of the function has been found to decrease with stimulus frequency in some cases (Stevens, 1968; Franzén, 1969) but not others (Verrillo et al., 1969; Hollins and Roy, 1996) [this decrease in psychophysical exponent may be attributed to an enhancement in the PC response (see supplemental material, available at www.jneurosci.org)]. According to the present model, however, the perceived intensity of sinusoids is a three-branched logarithmic or linear function of stimulus intensity: the first branch corresponds to stimuli the perception of which is mediated by a single population of afferents (the most sensitive population at that stimulus frequency); the second branch corresponds to stimuli mediated by the two most sensitive populations of afferents; and the third corresponds to stimuli mediated by all three populations of afferents. Because the slope and threshold parameters of the rectified log functions differ across afferent types, the slopes of the three branches will differ: the slope of the first branch is determined entirely by the properties of a single afferent population, but the slopes of the other two branches are determined by specific combinations of the three populations of afferents.

Neural coding of stimulus frequency

That two waveforms are perceived as being equally intense does not imply that they are indistinguishable. For instance, low-frequency diharmonic stimuli varying only in the phase of the high-frequency component relative to that of the low-frequency component have been shown to be discriminable (Bensmaia and Hollins, 2000), although these evoke identical firing rates in the three afferent types (Fig. 5). Furthermore, the discriminability of sinusoidal, diharmonic, and triharmonic waveforms cannot be predicted on the basis of intensity cues alone but rather is a function of both the intensive and temporal properties of the stimuli (Bensmaia et al., 2005a). Given the present results, it is unlikely that the perception of frequency is simply based on the mean firing rates of mechanoreceptive afferents, although frequency may be coded with a mean rate code in primary somatosensory cortex (Salinas et al., 2000). There are two other coding hypotheses that must be considered if frequency is not coded by rate at the periphery. First, the temporal profile of the afferent response has been shown to be shaped to a large degree by the temporal properties of the stimulus. For instance, sinusoids evoke periodic responses, whereas noise stimuli do not (compare Figs. 1, 2). Second, because the three populations of mechanoreceptive afferents have different frequency sensitivity profiles, the relative activation of each population of afferents could carry information about the frequency content of the stimulus (Roy and Hollins, 1998).

Conclusion

The study by Johnson (1974) was one of the first to investigate the role of population coding in sensory perception. One of his major conclusions was that perception is based on the activity of populations of neurons rather than on that of single neurons. Here we extend his findings and conclude that perception of a simple quantity such as intensity is based not only on the activity of a single population of afferents, but on the activity of all mechanoreceptive afferents. Furthermore, the present study provides a mathematical framework to evaluate hypotheses about the neural coding of stimulus intensity, which may lead to a deeper understanding of submodality convergence and the integration of stimulus information over the skin surface.