Spatial Organization of Neuronal Population Responses in Layer 2/3 of Rat Barrel Cortex

Abstract

Individual pyramidal neurons of neocortex show sparse and variable responses to sensory stimuli in vivo. It has remained unclear how this variability extends to population responses on a trial-to-trial basis. Here, we characterized single-neuron and population responses to whisker stimulation in layer 2/3 (L2/3) of identified columns in rat barrel cortex using in vivo two-photon calcium imaging. Optical detection of single action potentials from evoked calcium transients revealed low spontaneous firing rates (0.25 Hz), variable response probabilities (range, 0–0.5; mean, 0.2 inside barrel column), and weak angular tuning of L2/3 neurons. On average, both the single-neuron response probability and the percentage of the local population activated were higher in the barrel column than above septa or in neighboring columns. Within the barrel column, mean response probability was highest in the center (0.4) and declined toward the barrel border. Neuronal pairs showed correlations in both spontaneous and sensory-evoked activity that depended on the location of the neurons. Correlation decreased with increasing distance between neurons and, for neuronal pairs the same distance apart, with distance of the pair from the barrel column center. Although neurons are therefore not activated independently from each other, we did not observe precisely repeating spatial activation patterns. Instead, population responses showed large trial-to-trial variability. Nevertheless, the accuracy of decoding stimulus onset times from local population activity increased with population size and depended on anatomical location. We conclude that, despite their sparseness and variability, L2/3 population responses show a clear spatial organization on the columnar scale.

Introduction

The representation and extraction of salient features of sensory input cannot be understood solely on the basis of single-neuron response properties (deCharms and Zador, 2000; Petersen et al., 2002). Rather, the capacity of cortical areas to accurately convey sensory information to downstream targets depends critically on population response properties measurable only with simultaneous observation of multiple neurons (Averbeck et al., 2006). Several studies reported repeated activation of neuronal sequences, albeit with variable precision and under different conditions (Abeles et al., 1993; Hahnloser et al., 2002; Ikegaya et al., 2004; Ji and Wilson, 2007; Luczak et al., 2007). In light of large single-cell variability, it remains unclear to what extent the same subsets of neurons are activated in local populations during repeated presentations of a simple sensory stimulus. Even weak pairwise correlations among neurons might imply strongly correlated network states (Schneidman et al., 2006). Modeling studies indicate that unambiguous detection of stable repeating patterns is difficult, in particular when they are sparse and short-lived, and that they may require simultaneous sampling from >1000 neurons (Izhikevich et al., 2004). In addition, although repeating motifs of high similarity have been found in spontaneous subthreshold membrane potential fluctuations in vivo (Ikegaya et al., 2004), these were not deterministic but instead were stochastic (Mokeichev et al., 2007).

Recent advances in labeling techniques with calcium indicators (Stosiek et al., 2003) combined with in vivo two-photon microscopy now enable simultaneous optical recordings from populations of neurons with single-cell and single-spike resolution (Kerr et al., 2005). Importantly, all neurons within a given local area can be monitored, whether they are spiking or not (Kerr et al., 2005), and their locations (both absolute and relative to each other) can be determined. So far, in vivo two-photon calcium imaging has been used to study the functional organization of sensory responses in mammalian visual cortex (Ohki et al., 2005, 2006) and in the visual and the olfactory system of zebrafish (Niell and Smith, 2005; Yaksi and Friedrich, 2006). Here we characterize sensory-evoked responses in populations of neurons in layer 2/3 (L2/3) of rat primary somatosensory cortex (S1). We focus on the anatomically well defined regions in S1 known as “barrel columns,” which are arranged in the same geometric order as the facial whiskers forming a somatotopic map (Woolsey and Van der Loos, 1970; Simons, 1978). Although L4–L2/3 connections are strong and reliable (Feldmeyer et al., 2002; Silver et al., 2003), individual neurons within L2/3 respond only sparsely to vigorous stimulation of the whiskers (Ahissar et al., 2001; Brecht et al., 2003; Celikel et al., 2004; de Kock et al., 2007). Although anatomy and synaptic physiology of the cortical circuits within the barrel cortex are well known (Petersen, 2003), we still lack an understanding of how whisker deflections are represented at the population level. Key but open questions are as follows. How are population responses spatially organized within barrel columns, i.e., on the scale of tens of micrometers? How do they differ between the center of a barrel column and septal regions? How variable are response patterns from one trial to the next?

In this study, we characterize the spatial and functional organization of neuronal population responses to whisker stimulation. We find that population responses to whisker deflection are highly variable but clearly show higher response probabilities, higher pairwise correlations, and larger information content inside the principal barrel column as opposed to the surrounding septal and barrel regions. We do not find, however, any directional map for angle of whisker deflection within L2/3. Thus, the barrel column is functionally heterogeneous, and the location of neurons on a fine spatial scale dictates population responsiveness and therefore impacts on sensory coding.

Materials and Methods

Animal preparation.

All experimental procedures were performed according to the animal welfare guidelines of the Max-Planck-Society. Thirteen Wistar rats (postnatal day 25–35) were anesthetized with urethane (1–2 g/kg body weight, i.p.). The animal skull was exposed and cleaned, and a metal plate was attached with dental acrylic cement. A 2- to 3-mm-wide craniotomy was opened above barrel cortex centered on bregma −2.5 mm and lateral 5.5 mm. The exposed cortex was superfused with warm normal rat Ringer's (NRR) solution (in mm): 135 NaCl, 5.4 KCl, 5 HEPES, and 1.8 CaCl₂, pH 7.2 with NaOH. The craniotomy was filled with agarose [type III-A (Sigma, St. Louis, MO); 1% in NRR] and covered with an immobilized glass coverslip.

Intrinsic optical imaging.

Functional maps of the barrel cortex were determined using intrinsic optical imaging (Grinvald et al., 1986). The cortical surface was illuminated with red light (630 nm interference filter) while stimulating a single whisker (10 deflections of 1–2° amplitude in the ventrodorsal direction at 5 Hz). Reflectance images were acquired using an Imager 3001 lab interface (Optical Imaging, Rehovot, Israel) with a Dalsa (Waterloo, Ontario, Canada) CCD camera (type 1M60) equipped with a lens pair of a 135 mm and a 50 mm focal length objective [numerical aperture (NA) 0.46, 2.7× magnification]. Images were acquired at 5 Hz frame rate using 3 × 3 binning (312 × 308 pixels, 15 μm pixel size). Relative reflectance changes (ΔR/R) were calculated by dividing the entire frame series through the average image of 10 prestimulus frames. Off-line analysis included additional 3 × 3 spatial binning. Intrinsic signals were averaged over 16 trials, which generated a spot approximately the size of a single column (∼350 μm diameter). Consistency of the barrel field map was validated by stimulating neighboring whiskers and by postmortem histology (see below). The surface blood vessel pattern was imaged for reference using green illumination (546 nm).

Fluorescence labeling and two-photon imaging.

Multicell bolus loading of neocortical cells with the calcium indicator Oregon Green BAPTA-1 (OGB-1) AM (Invitrogen, Carlsbad, CA) was performed in superficial layer 2 as described (Stosiek et al., 2003; Kerr et al., 2005). Astrocytes were labeled with sulforhodamine 101 (Nimmerjahn et al., 2004). Two-photon imaging was performed using a custom-built two-photon laser-scanning microscope (excitation wavelength, 870 nm; laser model Mira 900-F laser; Verdi-10 pump; Coherent, Santa Clara, CA). Fluorescence images of 64 × 128 pixels were acquired through a 20× water-immersion objective lens (0.95 NA; Olympus Optical, Tokyo, Japan) at 11–16 Hz frame rate (1–1.5 ms line duration).

Electrophysiology.

Patch-clamp recordings were performed from OGB-1-loaded L2/3 neurons in cell-attached configuration with a glass pipette containing NRR solution. Neurons were visually targeted using the two-photon microscope. Open pipette resistance was 4–6 MΩ. Cell-attached signals were recorded using an Axoclamp 2-B amplifier (Molecular Devices, Palo Alto, CA) and digitized using a CED power1401 data acquisition board (Cambridge Electronic Design, Cambridge, UK).

Whisker stimulation.

An individual whisker was deflected using a custom-built multidirectional piezoelectric stimulator (Simons, 1983). The stimulator was attached to a whisker 5 mm from its base, and the whisker was deflected 5.7° (500 μm amplitude) for 500 ms using relatively high-velocity (onset and offset, ∼570°/s) ramp-and-hold movements (Bruno and Sakmann, 2006). Deflections were applied randomly in eight directions in 45° increments relative to the horizontal alignment of the rows. Typically, we applied 35 blocks of such stimuli to the whisker (between 200 and 400 total stimuli). Interstimulus time interval ranged from 3 to 6 s. For controls, all the same criteria were used as stated above, but the piezoelectric stimulator was unplugged from the amplifier.

Histology and barrel field reconstruction.

Rats were perfused transcardially with phosphate buffer followed by 4% paraformaldehyde. The cortex was cut tangentially in 100 or 200 μm vibratome sections and stained for cytochrome oxidase (Land and Simons, 1985). The barrel field was reconstructed using a bright-field microscope attached to a Neurolucida system (MicroBrightField, Colchester, VT). The pial vasculature and large radial blood vessels were traced to align histological reconstructions of the barrel field with the intrinsic optical signals and large field-of-view two-photon images. In all experiments with cytochrome oxidase staining (n = 7 animals), the center of mass (determined from the cytochrome oxidase stain) of the principal whisker (PW)-related barrel column overlaid with the spot center (center of mass) obtained from intrinsic optical imaging. From this set of experiments, we calculated the average barrel field size, expressing the position of barrel column borders as fractions of the distance between neighboring barrel column centers (BCCs). In these fractional coordinates, there was little variation in barrel size from one cytochrome c stain to the next (SD of 3.21%; n = 7). In experiments without cytochrome oxidase staining, barrel borders were then placed at the determined average fractional distance between neighboring intrinsic optical imaging spots.

Barrel-centered maps showing the position of all neurons relative to the center of the PW-related column were obtained by aligning the PW-related BCCs from all experiments. For each experiment, the barrel field was rotated such that the BCC in the succeeding row and the same arc lay in the same direction (to the right). For experiments in which an E row whisker had been stimulated, a rotation was made such that the D row BCC lay in the opposite direction (to the left). Borders for the neighboring barrel columns along the row, and arc axes were calculated for these maps by averaging over all experiments after the above alignment procedure.

Data analysis.

OGB-1 fluorescence signals were analyzed in regions of interest from well focused cell bodies (whose diameters as a function of focal plane position were nearly maximal) because out-of-focus neurons showed a reduced signal-to-noise lowering spike detection reliability. Before imaging each population, the focal plane was passed above, below, and through the cell bodies, and the maximum diameter for each neuron was determined. The focal plane was then chosen to give the greatest number of neurons at near-maximal diameter. Signals were expressed as relative fluorescence changes (ΔF/F) after subtracting background from unstained blood vessels. Action potential (AP)-evoked calcium transients were detected using a template matching algorithm, taking advantage of their characteristic shape with a sharp rise followed by an exponential decay (Kerr et al., 2005). Specifically, data points within a moving window (spanning from 3 s before to 2 s after each putative calcium transient) were fitted to a function including an offset and an exponential curve with amplitude A and τ = 380 ms starting at t = 0. The fitted amplitudes were thresholded at 8.7% ΔF/F to yield the peak times of AP-related calcium transients. Threshold and decay time constant were optimized so that imaging data best matched the electrophysiology data. Because each neuron is scanned once per imaging frame (every 64 or 96 ms), optical and electrophysiological spike detection times varied on average by half a frame. Spike detection rate was determined as the fraction of optically detected spikes from all spike events during the entire imaging period (typically 2.44 min).

The responses of each neuron were tested for specificity with respect to deflection angle using two methods. First, we calculated the ratio of the maximal response over all angles to the mean response over all angles (“max/mean response”) and corrected the statistical bias of this observed value as an estimator for the true max/mean. Bias correction was performed by subtracting the max/mean response expected for the same number of stimulus-evoked AP responses in the case of no angular preference. The bias value was estimated numerically for a neuron with n stimulus-evoked AP responses by assigning these n responses randomly across all eight deflection angles and recalculating the max/mean response; the mean result from 10,000 such random reassignments was defined as the bias. We also tested the stimulus responses of each neuron directly against the null hypothesis that the frequency of a stimulus-evoked transient occurred with equal probability for all eight deflection angles, using a generalized version of Fisher's exact test (Cantor, 1979). These two measures showed a strong negative association (supplemental Fig. 3D, available at www.jneurosci.org as supplemental material), whereas the association when bias correction was not performed was much weaker.

Pairwise correlations for onset responses between two neurons i and j were calculated as Pearson's correlation coefficient of the binary response vectors d_i and d_j (i,j = 1… N, with N the number of stimulations applied). Vector components were set to 1 if an AP-evoked calcium transient occurred in the first two image frames after stimulation and to 0 otherwise.

We used a simple inference algorithm to decode stimulus onset times and whisker deflection angles from neural activity in populations of up to 14 neurons. We first randomly classified blocks of continuous imaging (144 s each) as “training data” used to determine parameters and “testing data” used to quantify decoding performance. Training data were used to calculate peristimulus time histograms (PSTHs) for all neurons (time bins, 96 ms), which were concatenated into a single vector v (or in the case of deflection angle decoding, separate vectors v _θ for the eight angles used). Peristimulus time windows were chosen from −0.5 to 1 s and from 0 to 0.7 s for decoding of onset times and deflection angles, respectively. For decoding of stimulus onset times, we then passed a 1.5 s window over the testing data, and for each imaging frame i at the center of the window concatenated the windowed data for all neurons into a single vector R(i). Next, we calculated the correlation with the PSTH for the windowed data surrounding each center frame: c(i) = ρ(v(i), R(t)). Finally, we decoded as onset times all frames i such that c(i) > α, for some threshold α. Note that, for each dataset, the performance of the algorithm was tested for a wide range of α values (see Results). For decoding of deflection angle, all stimuli were randomly divided into training and testing data. PSTHs were calculated and concatenated into separate vectors v _θ for each angle using training data, and all single-trial population responses R in the testing data were then concatenated and compared with each vector v _θ. For each stimulus, the angle argmax_θ(ρ(R, v _θ)) whose PSTH was most correlated to the data were then posited as the deflection angle by the decoder.

We calculated the mutual information (Shannon, 1948) between the binary function W(i), indicating whether a stimulus onset occurred during imaging frame i, and the binary function G(i), indicating whether our inference algorithm decoded a stimulus for frame i:

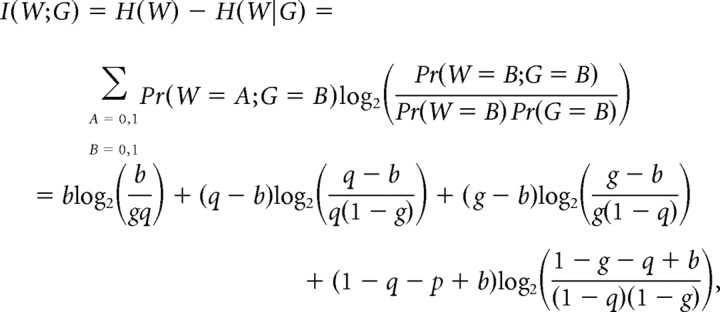where Pr denotes probability, g is the fraction of imaging frames that are assigned stimuli by the decoding algorithm, q is the fraction of imaging frames in which a stimulus actually occurred, and b is the fraction in which a stimulus occurred and was successfully decoded. I was normalized by the total entropy of the stimulus H(W) to give a percentage. For onset time decoding, I was calculated for all values of α (see Results). Information from five-neuron populations was calculated as a mean over all possible selections of five neurons in each imaged population, and the correlation threshold α = 0.08 was used for the decoding of stimulus onset times.

When no information is truly present and the decoding consists of random guessing, b will on average equal gq but will show some statistical fluctuation in finite datasets. However, because I(W; G) can never be negative, there is a slight upward bias in I for random guessing that depends on g, q, b, and the total number of imaging frames n. We therefore examined whether such bias affects our analysis. On average, stimuli were delivered once per 4.05 s, so we fix q = 0.096/4.05 = 0.237. Because each neuron used in information analyses received at least 200 stimuli, we consider the bias in mutual information for the case of 200 stimuli over 810 s of recording time, or n = 8439 time bins of 96 ms each (increasing the amount of data decreases the bias). Given g, q, and n, the probability distribution for b is

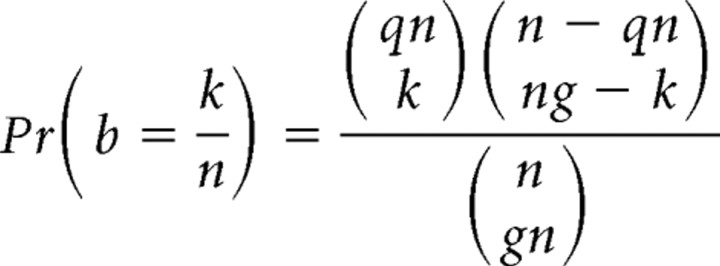for all integers k such that max(0, n(q + g − 1)) ≤ k ≤ min(nq, ng).

This distribution and the formula above determine the full distribution of I as a function of p, which we calculated explicitly and stored for g = 0, 1/n, 2/n,… 1. This analysis revealed that the bias, i.e., the expected value of I given random guessing with probability g, is maximized at g = 0.04, at which point I/H(W) = 0.05%. Because this worst-case estimate of bias is 37 times smaller than the information decoded from the activity of single neurons, we conclude that bias in our information measure did not affect our results.

Results

Optical detection of sensory-evoked spikes in L2/3 of identified barrel columns

In each experiment, we first determined the topographic layout of the barrel field by using intrinsic optical imaging (Grinvald et al., 1986) (Fig. 1 A). We then optically recorded from L2/3 neurons bulk loaded with calcium-sensitive dye (OGB-1) in the area corresponding to a particular principal whisker (Fig. 1 A). Anatomical location was verified postmortem histologically (see Materials and Methods). Neurons were divided into three groups: those localized above the L4 barrel corresponding to the stimulated whisker (PW-related neurons), those above L4 septal regions (septum-related neurons), and those above the L4 barrels surrounding the PW-related barrel [surround whisker (SW)-related neurons]. The average borders of the barrel- and septum-related regions were obtained from anatomical and histological analysis, yielding 203 ± 22 μm (mean ± SD) for the mean radial distance from the PW-related BCC to the barrel–septum border and 273 ± 62 μm from the PW-related BCC to the border of SW-related barrel columns.

Figure 1.

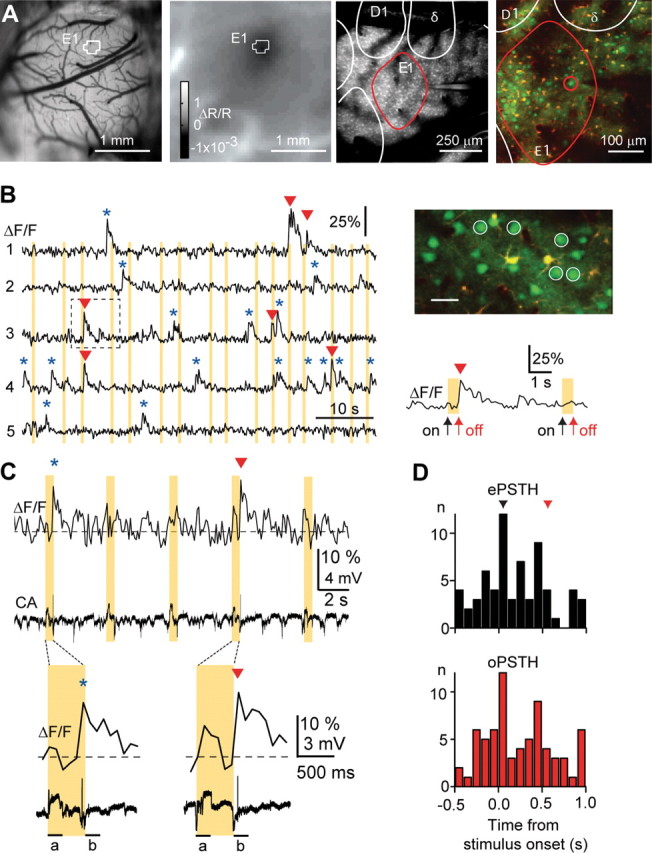
Sensory-evoked calcium transients in identified E1 barrel column. A, Left, Craniotomy over somatosensory cortex. Middle left, Intrinsic optical signal after stimulation of E1 whisker showing the resulting “spot.” The outline of the darkest pixels is overlaid in both images indicating the position of E1 barrel column. Middle right, Close-up view of the E1 area from a low-resolution two-photon image. Barrel field outlines obtained from cytochrome c staining are overlaid. Note the pipette tip on the right side. Right, L2/3 neurons (green) and astrocytes (yellow) stained with calcium indicator and sulforhodamine 101, respectively, in the E1 area and the surrounding tissue. A neuron within the E1 barrel border (red) was targeted with a patch electrode for cell-attached recording. B, Calcium measurement from a population of neurons from a different experiment than in A (scale bar, 30 μm). Fluorescence traces from five simultaneously recorded PW-related L2/3 neurons showing spontaneous (blue asterisks) and sensory-evoked (red arrowheads) calcium transients. Calcium transients were classified as sensory evoked if the initial fluorescence rise and peak occurred within 200 ms after either the onset (away from resting position) or the offset (return to resting position) of the whisker deflection. Note that not all whisker deflections evoke calcium transients. Yellow bars indicate stimulation periods. An example calcium transient associated with offset stimulation is shown on expanded timescale. C, Simultaneous cell-attached (CA) recording and fluorescence measurement from the L2/3 neuron from the E1 area shown in B. A spontaneous (blue asterisks) and a stimulus-evoked (red arrowhead) spike and their associated calcium transients are expanded in the bottom. The spontaneous spike fell outside the 200 ms time windows used to classify spikes as onset (window a) or offset response (window b). D, Electrically (top, ePSTH) and optically (bottom, oPSTH) determined PSTH for the same neuron and the same trials. Only five false positives resulted for 16 min continuous imaging and 231 stimuli in this experiment. Arrows depict bins that contain responses to whisker stimulation.

We performed calcium measurements from neurons located in L2/3 (somata 130–273 μm below the pia; 170 ± 31 μm, mean ± SD) as described previously (Kerr et al., 2005). Sensory stimulation using 500 ms whisker deflections elicited brief calcium transients of similar shape to spontaneous calcium transients (Fig. 1 B) (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). To confirm that we could detect calcium transients evoked by single APs as in previous work (Kerr et al., 2005), we obtained targeted cell-attached recordings from five neurons in five animals (Fig. 1 C,D) (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). More than 90% (93 ± 2.2%, mean ± SEM) of electrically recorded spikes were optically detected, and the spike extraction routine produced false positives only at a low rate [once every 75 s of imaging; 0.0133 ± 0.0033 Hz, ∼5% of spontaneous firing rates (see below); n = 5, mean ± SEM]. Because we imaged continuously for 144 s and stimulated between 30 and 40 times during this period, only 8–11% of the imaging frames could contain evoked spikes (0.2 s for onset and 0.2 s for offset). For cell-attached datasets including sensory stimulation, false positives and nondetected spikes (false negatives) occurred outside of the time bins associated with stimulus periods (data not shown). Furthermore, PSTHs collected from simultaneous electrical and optical recordings were similar (Fig. 1 D), with no significant difference in the total number of spikes for both onset and offset bins (p = 0.36, paired t test, n = 5 neurons). Differences in individual bin numbers are explained by the uncertainty in determining spike times from the fluorescence measurement at low temporal resolution. We conclude that sensory-evoked spiking activity in L2/3 of identified barrel columns can be reliably measured using population calcium imaging.

Spatial organization of spiking activity

We examined the spatial organization of L2/3 neuronal responses by analyzing the occurrence of AP-evoked calcium transients as a function of location and, within the principal barrel column, of radial distance from the BCC (Fig. 2) (populations of 4–17 neurons, 254 neurons in total, 13 animals). Overall, response probabilities to whisker stimulation were below 0.5 and showed considerable variation at all locations (Fig. 2 A,B). Despite this variability, barrel-centered maps pooled from several experiments illustrate that PW-related neurons showed larger onset and offset response probabilities compared with septum- and SW-related neurons (Fig. 2 C). On average, PW-related neurons responded to 19.2 ± 1.0% of stimulus onset deflections (range of 0.8–48%, mean ± SEM; n = 153 neurons, 22 populations, 12 animals). This result was confirmed by cell-attached recordings (17.8 ± 2.5%, mean ± SEM; n = 5; p = 0.63, Mann–Whitney test). Compared with PW-related neurons, the response probability was lower for septum-related (13.6 ± 1.0%, mean ± SEM) and SW-related (14.9 ± 1%, mean ± SEM) neurons (Fig. 2 D). The difference between PW- and septum-related neurons was highly significant (p < 0.005), whereas the other differences were marginally significant (p = 0.10 for PW- vs SW-related; p = 0.18 for septum- vs SW-related; Kruskal–Wallis nonparametric ANOVA, p < 0.01, followed by pairwise Wilcoxon's rank sum tests). Responses to stimulus offset showed similar location dependence but were smaller (PW-related, 14.0 ± 0.8%; septum-related, 11.0 ± 0.9%; SW-related, 11.8 ± 1.0%, mean ± SEM). Consistent with a previous report (Brecht et al., 2003), L2/3 neurons thus preferentially responded to onset over offset deflections (supplemental Fig. 2, available at www.jneurosci.org as supplemental material).

Figure 2.

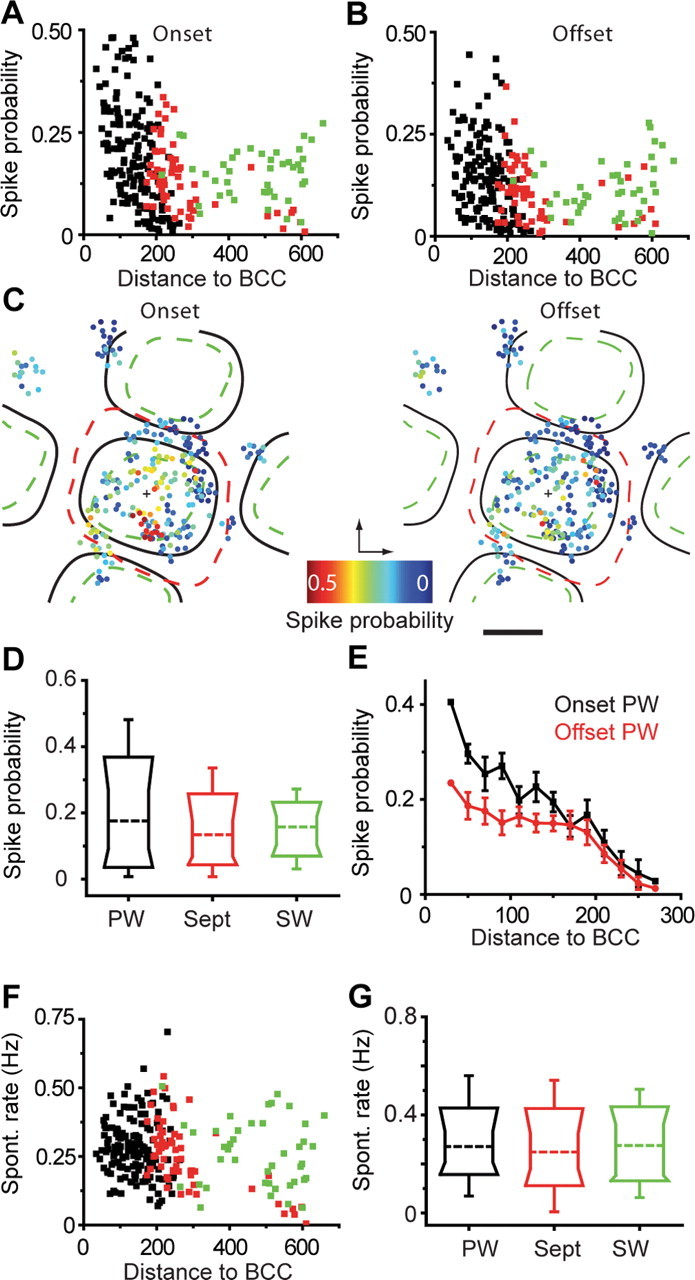
Sensory-evoked responses are pronounced in PW-related regions. A, Probability of spiking response to whisker deflection onset as a function of distance from the PW-related BCC in PW-related (black), septum-related (red), and SW-related (green) neurons. B, As in A, showing responses to deflection offset. C, Spatial map of response probability for whisker deflection onset (left) and offset (right) pooled for all populations and overlaid after alignment to barrel centers. Minimum (green dashed line), maximum (red dashed line), and average (black lines) barrel column borders are shown. Arcs run vertically, rows run horizontally, and black crosses indicate BCC. Scale bar, 200 μm. D, Distribution of onset responses for PW-related, septum (Sept)-related, and SW-related neurons. Box representations show median (broken line), 10th, 25th, 75th, and 90th percentiles and range. E, Mean probability of spiking response in PW-related neurons to whisker deflection onset (black) and offset (red) as a function of distance from BCC. Error bars show SEM. F, Spontaneous rate of calcium transients as a function of distance from BCC; colors as in A. G, Distribution of spontaneous activity for PW-related, septum-related, and SW-related neurons.

Within the principal barrel, mean response probabilities (calculated in 20 μm bins) were highest at the BCC and decreased steadily with radial distance from BCC for both stimulus onset and offset (Fig. 2 E). Onset responses were significantly higher within a 50 μm of the BCC (0.31 ± 0.06) compared with onset responses within 50 μm of barrel column border (0.15 ± 0.1, mean ± SD; p = 0.0002). No spatial clustering was observed in the barrel-centered maps for either response probability (Fig. 2 C) or on–off preference (supplemental Fig. 2, available at www.jneurosci.org as supplemental material).

In addition, we analyzed the spatial organization of spontaneous calcium signals. On average, spontaneous activity was comparable in the three groups of neurons (Fig. 2 F,G) (PW-related, 0.28 ± 0.01 Hz; septum-related, 0.25 ± 0.02 Hz; SW-related, 0.26 ± 0.02 Hz, respectively; mean ± SEM; n = 195 neurons, 13 animals; p = 0.20, three-way nonparametric ANOVA). Optically collected mean spontaneous spiking rates were not significantly different from those recorded electrically (0.24 ± 0.04 Hz, mean ± SEM; n = 5 animals; p = 0.18 optical vs electrical). Unlike response probabilities the spontaneous firing rates were not higher at the BCC compared with the barrel edge (Fig. 2 F) (p = 0.55).

Overall, our results confirm low spontaneous and evoked spike rates in L2/3 neurons and extend these findings by showing a fine-scale spatial organization of evoked but not spontaneous activity according to the underlying barrel cortex structure. Within barrel columns, there is a decrease of spiking probability with radial distance from the BCC, but no apparent local clusters of highly active neurons were found.

Weak angular tuning of barrel- and septum-related L2/3 neurons

Both thalamic neurons and cortical L4 neurons show tuning to the angle of whisker deflection (Simons and Carvell, 1989; Bruno et al., 2003; Timofeeva et al., 2003). Given that L2/3 neurons receive major excitatory input from L4, we next investigated the dependence of L2/3 neuronal responses on stimulation angle. Stimulating the principal whisker randomly in eight directions produced variable responses, with some neurons responding mainly to one direction whereas others responded equally to all directions (Fig. 3 A–C). Quantification of angular tuning in the imaged populations presents a challenge, because many neurons responded infrequently to whisker stimulation. Traditional measures of angular tuning, such as max/mean response (Brumberg et al., 1996; Andermann and Moore, 2006), as well as more recently proposed measures (Kida et al., 2005) involve dividing by overall response rates, leading to large values when the number of stimulus-evoked AP responses is small. Consequently, low response rates will produce high tuning values even in neurons whose responses do not significantly depend on stimulation angle. The expected max/mean response in the absence of angular tuning is termed the “bias” and depends on the total number of AP responses evoked by stimulation. To estimate the bias for each neuron, the responses for each neuron were randomly redistributed over the eight angles (averaged over 10,000 shuffles; see Materials and Methods). We then subtracted this bias from the observed max/mean response for each neuron (Fig. 3 D), leading to a measure of angular tuning not biased by the response rate (supplemental Fig. 3A, available at www.jneurosci.org as supplemental material). On average, the resulting measure will be 0 given no angular tuning in excess of chance and up to 7 for responses to only one deflection angle over many stimuli. After bias correction, max/mean values were mostly close to 0 (Fig. 3 E). Average values among PW-related neurons were 0.017 ± 0.027 for stimulus onset and 0.12 ± 0.037 for offset, septum-related neurons averaged 0.067 ± 0.069 for onset and 0.058 ± 0.062 for offset, and no significant difference in angular tuning strength was found between PW barrel- and septum-related neurons for either onset or offset (p > 0.2, t test or Wilcoxon's rank sum test). The finding that max/mean responses were on average only slightly higher than the expected value in the absence of angular tuning suggests that angular tuning among L2/3 neurons is weak.

Figure 3.

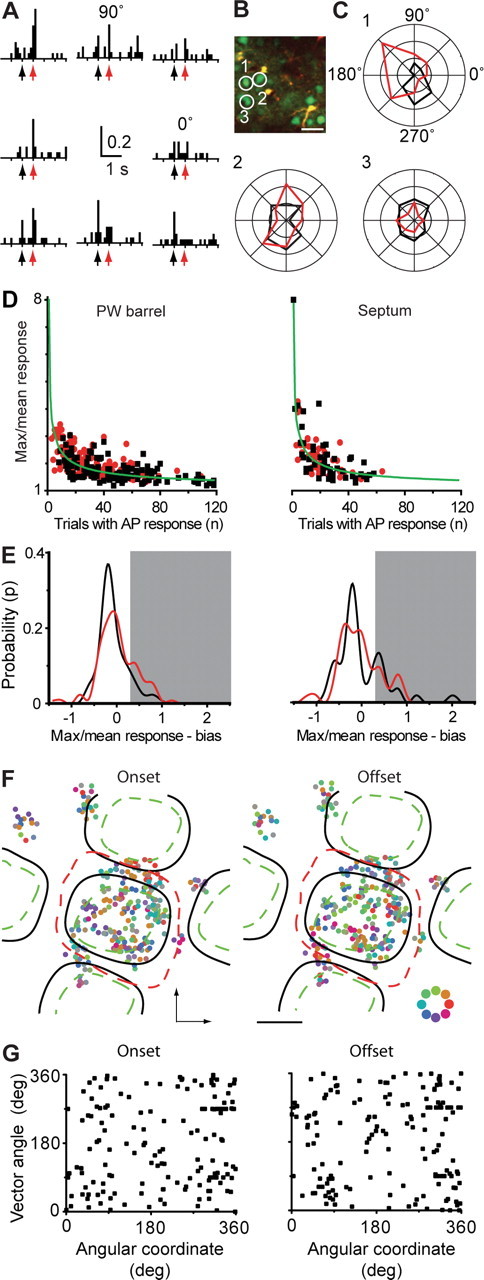
Heterogeneous population response to angular whisker deflection. A, Average activity of one neuron in response to 223 whisker deflections in eight directions (0–315°). Arrows depict onset (black) and offset (red) deflection (neuron 1 in B and C). B, Image of neurons (green) and astrocytes (orange) located within barrel column borders. Scale bar, 30 μm. C, Polar plots of mean percentage responses of the same neurons depicted in B to randomly deflecting the principal whisker in eight different directions (onset deflections in black; offset deflections in red; 223 deflections; circles in units of 10% response probability). D, Scatter plots showing max/mean response versus the number of stimuli leading to AP responses for each PW-related (n = 130; left) and septum-related (n = 54; right) neuron (onset in black; offset in red). The max/mean response is defined as the ratio of maximum spike probability from all eight stimulation angles to mean response probability for all angles. The bias, defined as the max/mean response expected for a neuron with no angular preference and a given number of observed APs, is shown in green. E, Probability distribution of bias-corrected max/mean response for both PW-related (left) and septum-related (right) neurons (0.02 bin width; onset in black; offset in red; see Materials and Methods). Distributions interpolated using cubic spline. Neurons consistently responding only to one direction display values >0, up to a theoretical maximum of 7. Neurons responding evenly to all angles display 0. Shaded region corresponds to values >0.30, the value corresponding to a tuning p value of 0.1 in a linear regression (supplemental Fig. 3D, available at www.jneurosci.org as supplemental material). F, Spatial map of angular tuning. The maximal-response direction of each neuron was color coded (color scale, bottom right) and plotted on an averaged barrel-centered map for deflection onset (left) and offset (right). Minimum (green dashed line), maximum (red dashed line), and average (black lines) barrel borders are shown. Arcs run vertically, rows run horizontally, and black crosses indicate BCC. Scale bar, 200 μm. G, Angle of directional tuning vector as a function of angular anatomic coordinate for all PW-related neurons.

In addition to directly quantifying angular tuning strength for each neuron, we identified neurons exhibiting angular tuning at a given level of statistical significance. We used an exact test of significance incorporating the full set of the stimulus responses of each neuron to yield the significance level (p value), at which the responses of the neuron can be said to depend on angle (see Materials and Methods). Unlike max/mean and similar measures, these p values do not frequently produce values indicating strong tuning for nontuned neurons that respond rarely and do not require bias correction (supplemental Fig. 3B, available at www.jneurosci.org as supplemental material). However, unlike the bias-corrected max/mean responses, these p values do not explicitly quantify the strength of the angular tuning of a neuron: low p values can correspond to either strongly tuned, poorly sampled neurons or weakly tuned, well sampled neurons and tend toward 0 for even the weakest angular tuning given a sufficient number of stimuli.

From the total population of PW-related neurons, 14 and 21% showed a statistically significant angular tuning to deflection onset and offset, respectively (supplemental Fig. 4A, available at www.jneurosci.org as supplemental material) (tuning with p < 0.05 considered significant; exact test of significance; see Materials and Methods). For septum-related neurons, the fractions showing significant tuning were 15 and 10% for onset and offset, respectively (supplemental Fig. 4A, available at www.jneurosci.org as supplemental material). This suggests that 10–20% of L2/3 neurons display direction selectivity independent of their anatomical location. Consistently, 10–20% of neurons within individual populations on average were activated by whisker deflection at each individual angle, regardless of position relative to underlying barrels (data not shown; mean of 0.13 ± 0.02; no difference between each angle; p = 0.23; n = 13 animals).

Tuning p values showed a strong linear relationship with max/mean responses after bias correction (supplemental Fig. 3C, available at www.jneurosci.org as supplemental material). Performing a linear regression, we estimated that on average tuning p values <0.1 correspond to bias-corrected max/mean responses >0.30. This allowed us to estimate a minimum value for the statistical significance of bias-corrected max/mean responses (Fig. 3 E, shaded gray box). Although not all neurons with bias-corrected max/mean values >0.30 had tuning p values <0.1 (supplemental Fig. 3C, available at www.jneurosci.org as supplemental material), this threshold provides a criterion for estimating the significance of bias-corrected max/mean values, connects the two quantifications of direction preference, and provides a more intuitive picture of angular tuning in the set of neurons observed. A few neurons with significant angular tuning p values actually have negative max/mean responses after bias correction because the p value is more informative at smaller sample sizes, especially when the responses of a single angle do not dominate (for example, a neuron responding to 12 trials per angle with three AP responses for four angles and 0 for the other four angles yields a p value of 0.028, an uncorrected max/mean response of 2, and a bias of 2.29).

We also examined whether responses to angular tuning are spatially organized inside the barrel column. Pooled color-coded maps for maximal response direction showed a dispersed distribution of angular preference with no clear directional map for either onset or offset (Fig. 3 F). This result was confirmed by analyzing the directional preference as a function of the angular coordinate of its position. In contrast to a recent publication that reported directional preference maps using this same analysis (Andermann and Moore, 2006), we found no significant relationship between the preferred stimulation angle and the angular coordinate for PW-related neurons (Fig. 3 G), even when considering only significantly “tuned” neurons (supplemental Fig. 4B, available at www.jneurosci.org as supplemental material).

We conclude that angular tuning of L2/3 neurons is generally weak, with only a minority of neurons displaying significant directional selectivity and no clear direction-preference maps.

Large variability of population responses

Given the low response probability and weak angular tuning of individual L2/3 neurons, we next asked how sparse and variable sensory responses are on a population level from one trial to the next. Within individual populations, the fraction of neurons showing AP-evoked calcium transients largely fluctuated from trial to trial, ranging from 0 to near 100% (Fig. 4 A–C). On average, 20.5 ± 2.1% of neurons within PW-related populations were activated by onset deflections (n = 22 PW-related populations, 13 animals, average of 8 neurons per population; mean ± SEM) (Fig. 5 A). Significantly lower fractions were activated in other areas (p = 0.03, ANOVA), and subsequent pairwise comparisons showed that the decrease was significant for septum-related populations (13.1 ± 1.4% activation; n = 14 populations, 7 neurons per population; p = 0.01, t test) but not for SW-related populations (16.0 ± 1.7%; n = 8 populations, 7.8 neurons per population; p = 0.23, t test). Offset deflections activated a smaller fraction of neurons in the same populations (14.4 ± 1.4, 10.1 ± 1.3, and 12.6 ± 1.4% for PW-, septum-, and SW-related, respectively, mean ± SEM). As a comparison, we analyzed traces of spontaneous activity that were recorded as if stimuli had been applied using the exact same criteria used to stimulate the whisker but removing the stimulator power supply (see Materials and Methods). These control conditions on average yielded lower fractions of neurons when compared with responses to whisker stimulation from the same populations. Unlike evoked responses, these spontaneous controls were not significantly different between areas (Fig. 5 A) (7.3 ± 1.8, 7.0 ± 0.6, and 7.3 ± 0.7 for PW-, septum-, and SW-related, respectively; n = 13 animals; p = 0.98). The fraction of neurons activated could depend on the size of the subpopulation imaged. We therefore analyzed the probability distribution of the activated fraction for populations of 5–12 neurons (n = 13 animals) for both stimulated (“evoked”) and nonstimulated (“spontaneous”) trials (Fig. 5 B). All distributions were well approximated with a decreasing exponential function [accounting for nearly all the variability according to the Kullback–Leibler divergence criterion (Cover and Thomas, 1991)]. For the same populations, the exponential coefficient derived from fits (slope of the log plot) was significantly less for evoked than for spontaneous events (median of −3.91 compared with −7.7; p < 0.0001, Wilcoxon's rank sum test), demonstrating the increased likelihood of neuronal activation during whisker deflection. Despite variability in the exponential coefficient, there was no significant correlation with population size (Spearman's rank correlation coefficient of 0.125; p > 0.5; n = 22 populations, range of 5–17 neurons). Most importantly, we compared the fraction of activated neurons to the theoretical outcome if each neuron was assumed independent with its individual response probability (Fig. 5 B, black dotted lines, for 10-neuron populations) (n = 6 animals). The theoretical curves had a multinomial shape clearly deviating from the experimentally determined exponential distribution by several orders of magnitude for higher fractions of neurons active. This finding indicates that neurons cannot be viewed as independent units and that neuronal responses show some degree of correlation.

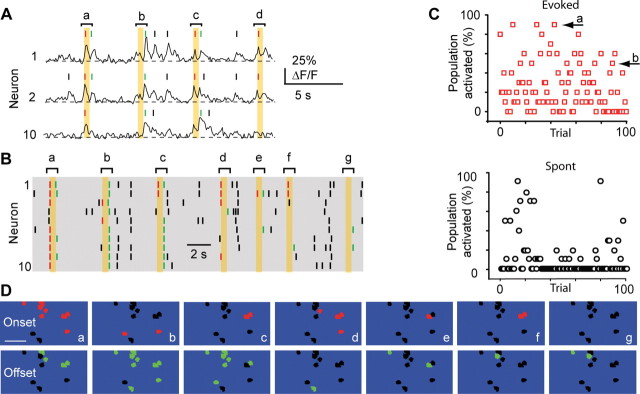
Figure 4.

Variability of population response. A, Calcium traces from three neurons showing spontaneous activity (black dashes) and responses to onset (red dashes) and offset (green dashes) whisker deflection for four single trials (orange boxes, trials a–d). B, Raster plot for seven consecutive deflections in 10 neurons (including same neurons as in A; a–d same trials as shown in B). C, Percentage of neurons in a PW-related population that were activated during 100 subsequent whisker onset deflections (left, red squares) or during spontaneous control trials (right, black circles). Arrows indicate occurrences of 90% (a) and 50% (b) activated. D, Spatial location of neurons in example B. Colored neurons depict active neurons in response to onset (red, top) or offset (green, below) whisker deflection. Neurons that were not active are show in black. Scale bar, 50 μm. Note that onset c repeats in onset response f.

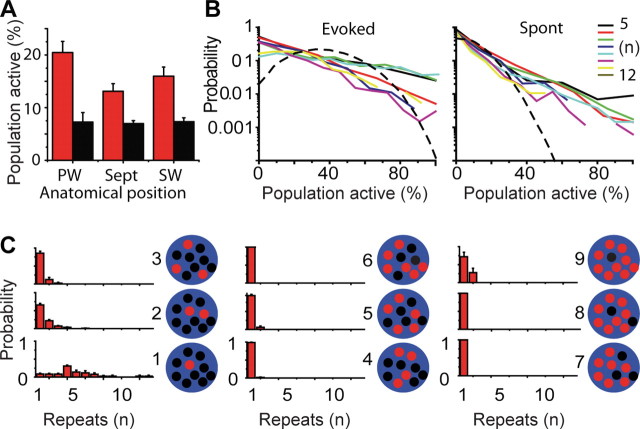
Figure 5.

Distribution of percentage of neurons activated is exponential for small populations. A, Average fraction of activated neurons in response to onset whisker stimulation (red bars) and during spontaneous activity (black bars) in PW-, septum (Sept)-, and SW-related populations. B, Probability histogram of percentage of population activated from single whisker deflections (left) and during spontaneous (Spont) activity (right) for populations of different sizes (ranging from 5 to 12 neurons) compared with predicted probability based on independence and measured response probabilities from populations containing 10 neurons. Note log₁₀ scale. C, Average probability distributions of the number of repeated activations of exact-same subsets of neurons over multiple trials. All trials with a given fraction of neurons active (Fig. 4 C, a and b) were searched for repeating spatial patterns in which the exact same neurons were active and inactive (Fig. 4 D, c and f) in response to whisker stimulation (n = 4 animals, 800 total stimulations), and distributions of the number of exact repetitions were calculated. Numbers to the right of each distribution indicate how many neurons were active in the pattern of a possible 10 neurons. Note that diagrams depict how many neurons were active (red) and not active (black) in each distribution of a total of 10 possible neurons. Patterns that occur only once appear in the repeats, 1 bin.

Correlated activity could result in repeated activation of the same neuronal subsets that could not be predicted from the probabilities of individual neuron firing. We therefore analyzed how similar activation patterns were from one trial to the next taking into account active and nonactive neurons within the field of view. Identical repeats of patterns occurred infrequently (Fig. 4 D, onset deflections c and f). In most cases, the exact subset of activated neurons changed from trial to trial. Figure 5 C shows an analysis of the likelihood of exact repeats with variable numbers of active neurons for four 10-neuron populations (n = 4 animals, 200 stimuli per population). Even for groups involving the same number of active neurons, the specific subset of active neurons typically differed from one response to the next so that most of the observed patterns were unique, occurring only once (79 ± 5% for evoked patterns, 71 ± 5% for spontaneous controls; mean ± SEM; n = 4 animals; p = 0.11; data not shown). Repeated activation of the same patterns was exceptional and occurred mainly in cases involving low numbers of active neurons.

We conclude that the high variability of whisker responses observed at the single-neuron level extends to the level of small local populations. The likelihood of repeated activation of the same set of neurons was very low. Nevertheless, the observed distributions for the active percentage of neuronal populations indicate that local groups of neurons do not act independently. Having identified this departure from independence in neuronal populations, we next proceeded to examine correlated activity in individual neuronal pairs.

Pairwise correlation between neurons depends on location

We quantified pairwise correlations of neuronal activity for almost 700 neuronal pairs during both spontaneous and evoked activity. Correlations were calculated for binary onset responses from pairs of neurons within the same field of view (see Materials and Methods). Averaged over all pairs regardless of the field-of-view location relative to the BCC, correlations were already present during spontaneous activity but increased significantly for evoked responses (Fig. 6 C) (0.15 ± 0.11 vs 0.17 ± 0.13, mean ± SD; n = 13 animals, 1047 pairs; p < 0.01, Wilcoxon's rank sum test). For both evoked and spontaneous activity, PW-related neuronal pairs had higher correlations than septum-related pairs (evoked, 0.20 ± 0.13 and 0.16 ± 0.12, respectively; spontaneous, 0.17 ± 0.09 and 0.13 ± 0.07, respectively; mean ± SD; n = 691 pairs; p = 0.019 evoked, p = 0.002 spontaneous, Wilcoxon's rank sum tests).

Figure 6.

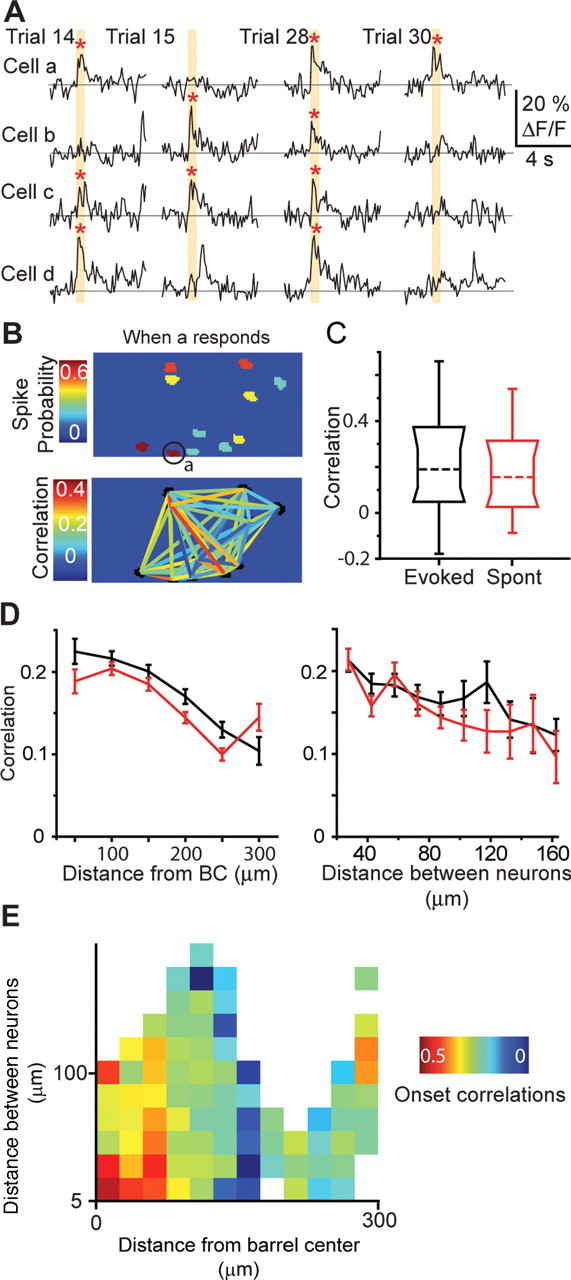
Pairwise correlations depend on location. Whisker deflection increases the correlation between pairs of neurons and is dependent on both distance between neurons and distance from BCC. A, Calcium transients from four simultaneously imaged neurons during four trials of on and off whisker deflection (orange box). Red asterisks represent calcium transients detected as being action potential generated (see Materials and Methods). B, Pseudocolored representation of a population with each neuron colored as a function of correlation when neuron a responds to whisker deflection (top). Correlation between all neurons within the field of view (bottom). C, Comparison of pairwise correlations from evoked and spontaneous (Spont) activity for neurons pooled from all PW related populations. Represented is median (broken line), 10th, 25th, 75th, and 90th percentiles and range. D, Pairwise correlations for both evoked (black) and spontaneous (red) as a function of neuronal pair distance from BCC (left) and distance between neurons (right) for all PW-related neuronal populations. E, Plot of the dependence of pairwise correlations on distance between neurons and on distance from BCC.

We therefore further examined how pairwise correlations depended on (1) the mean distance of the neuronal pairs from the PW-related BCC and (2) the distance between the neurons in each pair. For both evoked and spontaneous activity, pairwise correlations were highest near the BCC and significantly decreased with increasing mean distance from the BCC (Fig. 6 D, left) (Spearman's rank correlation coefficient of −0.30 for both evoked and spontaneous transients; p < 0.0001). Pairwise correlation also significantly decreased with distance between neurons for evoked activity in PW-related pairs (Fig. 6 D, right) (Spearman's rank correlation coefficient of −0.10; p = 0.02), suggesting that, during sensory stimulation, neighboring neurons may be bound together by common inputs. The decrease of correlation with increasing interneuron distance was not significant in septum-related pairs (−0.04, p = 0.63; data not shown), but this may simply be attributable to the weakness of the association and the fact that fewer septum-related pairs were recorded. Interneuron distance was not a confounding factor in the comparison of correlation in PW-related and septum-related pairs, because the average distance across all simultaneously recorded pairs was the same in both regions (PW-related, 60 ± 32; septum-related, 57 ± 30; mean ± SD; p = 0.27, t test). Similarly, the effect of distance to BCC on correlation was not simply a result of the fact that pairs close to the BCC are limited in interneuron distance, for two reasons. First, when considering only neuronal pairs with interneuron distance <40 μm, a decrease in correlation with increasing distance from BCC is still observed (Fig. 6 E). Second, among PW-related pairs, multiple linear regression of correlation against distance between neurons and distance from BCC showed that distance to BCC has two to three times more effect on evoked correlations than distance between neurons (regression coefficient of 0.0008 vs 0.0003 μm⁻¹).

We conclude that activity in L2/3 neuronal pairs is weakly correlated and that the amount of correlation during sensory stimulation is predominantly determined by the location of neurons within the barrel field structure, being strongest at the PW-related BCC and decreasing with distance. In addition, there is a dependence on cell-to-cell distance, suggesting that correlation not only depends on the location relative to the distribution of axonal afferents but also on the common share of inputs.

Information content depends on location

Given the dependence of pairwise correlation on location within the barrel column, the question arises whether this relationship extends to the population level when considering information content. To address this question, we analyzed how well stimulus occurrence and angle of whisker deflection can be decoded from the activity pattern in neuronal populations using a simple classifier routine (see Materials and Methods).

First, we analyzed the accuracy of a decoder of neuronal activity that determined the time points at which a stimulus occurred. For each population (consisting of all or a subset of neurons in the field of view), imaging was divided into 144 s blocks, and 75% of these were randomly selected as training data to estimate the mean PSTHs. For the remaining 25% (testing data), stimulus times were decoded by comparing population activity in a moving window to the mean population activity evoked by the stimulus in the training data and finding the time points at which the correlation exceeded a threshold α (see Materials and Methods). Clearly, the results of decoding procedure depend on the choice of α. Lower values of α increase the total number of onsets but increase the number of false positives. Higher values of α minimize false positives but lead to a low stimulus detection rate. Rather than choosing one particular value for α, we calculated detection rate and false-positive rate for many values of α to produce receiver operator characteristic (ROC) curves for the decoding of stimulus onset time (Fig. 7 A) (1–14 neurons, n = 13 animals, 30 populations).

Figure 7.

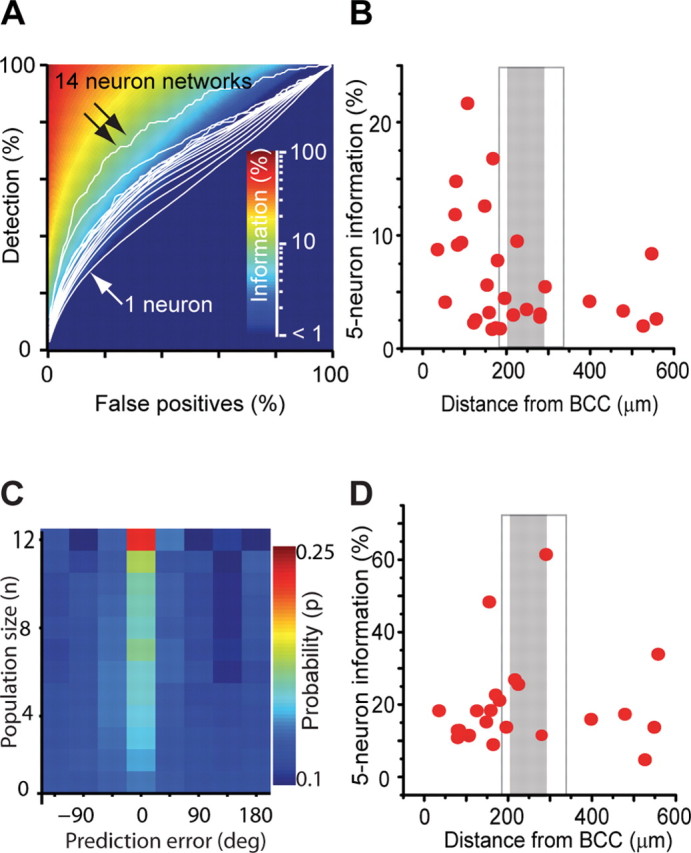
Stimulus representation in local populations depends on location. A, Mean detection rate (white contours) as a function of false-positive rate for populations containing between one neuron (single arrow) and 14 neurons (double arrow). For each combination of detection rate and false-positive rates, the percentage of information captured by the decoder is color coded. B, Average decoded information (α = 0.08) for five-neuron populations as a function of distance from BCC. Each point corresponds to an average of all possible randomly selected five-neuron combinations from within a single population of simultaneously recorded neurons (n = 29 populations). Distance from BCC was calculated as a mean over all neurons in the population to the center of the intrinsic imaging spot. A significant association was observed (p = 0.02). C, Probability distribution (p) of angle decoding error (in degrees) for increasing population size (n). The peak at zero error for larger population sizes indicates improving accuracy (n = 26 populations). D, Average decoded information for deflection angle from five-neuron populations as a function of distance from BCC. Each point corresponds to an average of all possible randomly selected five-neuron combinations from within a single population of simultaneously recorded neurons (n = 22 populations). Distance to BCC was calculated as a mean over all neurons in the population. No significant association was observed (p = 0.21).

For each population, we then determined the maximum percentage of total information decoded by our algorithm over all values of α, quantified by the mutual information between the true and decoded stimuli, and normalized by the stimulus entropy to give a value between 0 and 100% (see Materials and Methods), which we term the “decoded information.” Decoded information of 100% would be achieved only when all onset times are correctly detected with no false positives (Fig. 7 A, top left corner). In the other extreme case, if population activity provided no information about stimulus onsets, the false-positive rate would equal or exceed the detection rate and the decoded information would be 0% (Fig. 7 A, dark blue region, bottom right). A major advantage of quantifying the information through a decoding algorithm, as opposed to directly measuring the mutual information between the stimulus and the neural activity, is that true and decoded stimuli are described by simple discrete probability distributions, resulting in a manageable and unbiased information measure (see Materials and Methods). The obvious disadvantage of this approach, however, is that we cannot be sure we have chosen an optimal decoding scheme, so the decoded information must be taken as a lower bound on the information present in the neural activity.

Our analysis revealed that, for all population sizes, the detection rate was in excess of the false-positive rate (3432 different combinations of subsets of neurons analyzed from 30 populations with 1–14 neurons; n = 13 animals). For a single neuron, this difference was small (Fig. 7 A, bottom white ROC curve) (1.85% decoded information), but it grew steadily as the number of neurons included in the analyzed population increased (top white ROC curves, e.g., 4.04% for five-neuron populations). Thus, over all imaged populations, the decoded information steadily increased with population size (supplemental Fig. 5, available at www.jneurosci.org as supplemental material). Over all five-neuron subpopulations (taking into account all possible combinations among all simultaneously imaged populations), we found a clear spatial dependence, with the most reliable decoding of stimulus occurrences in the PW-related populations. Although decoded information varied considerable among subpopulations at the same distance from the PW-related BCC, overall decoded information significantly decreased with distance from the BCC (Spearman's rank correlation coefficient of −0.42; p = 0.02; n = 22 populations, 13 animals) and was further diminished in septum-related populations (Fig. 7 B). For this analysis, we chose five-neuron populations to strike a balance between population size and number of neural populations available.

Given the weak angular tuning observed, we also tested how reliably a deflection angle could be decoded from neuronal population activity. Training data consisted of 90% of all stimuli, chosen randomly, whereas the remaining 10% of stimuli was used as testing data to measure decoding performance (only populations with at least 15 trials per angle were used). The angle whose mean population response in the training data most resembled a single population response in the testing data was decoded as the most likely stimulus angle. Using single neurons, deflection angle was decoded with 13.7 ± 0.3% (mean ± SEM) accuracy, only slightly above the chance level of 12.5% (range of 0.08–0.18). As the size of the population analyzed increased, the probability of a correct decoding increased, exceeding 17% for 10 neurons (supplemental Fig. 5, available at www.jneurosci.org as supplemental material). Accordingly, the likelihood of small errors increased with population size, whereas larger angle errors became less likely (Fig. 7 C). For five-neuron populations, decoded information about stimulus angle did not decrease with distance from the PW-related BCC and was not significantly diminished in the septum-related populations (Fig. 7 D) (Spearman's rank correlation coefficient of 0.21; p = 0.35; n = 12 animals).

We conclude that the accuracy of decoding both stimulus onset and angle from activity patterns in L2/3 populations increases with population size. The spatial dependence of stimulus representation in L2/3, however, varies for the different features. Although angle decoding showed no dependence on distance from the PW-related BCC, information content about stimulus occurrence was highest near the BCC and showed a clear spatial organization. Population responses in cortical L2/3 thus are functionally heterogeneous with the location with respect to the underlying barrel field structure as a major determinant.

Discussion

Our study sheds light on the complexity of somatosensory L2/3 neuronal population responses to single whisker deflections. Our main findings are as follows: (1) sparseness of spiking in L2/3 neurons, both during spontaneous activity and in response to whisker stimulation; (2) spatial organization of response probability and pairwise correlations are determined by position relative to underlying barrel cortex structure; (3) the absence of precisely repeating stimulus-evoked spike patterns in local neuronal populations; and (4) dependence of stimulus representation on size and location of local populations.

For >250 L2/3 neurons, we found low response probabilities to whisker stimulation ∼0.2 APs per stimulus (no response above 0.48 APs per stimulus). In addition, we confirmed low spontaneous spiking rates (∼0.2–0.3 Hz) as observed in our previous study (Kerr et al., 2005). These results rely on the ability to detect single AP-evoked calcium transients in well focused cell bodies (Kerr et al., 2005; Sato et al., 2007), which we confirmed here using simultaneous electrical recordings. In addition, after optimization of the spike detection variables using cell-attached recordings, we used the same threshold for quantifying spike detection fidelity by rerunning all of the cell-attached recordings through the algorithm with a set threshold. This threshold was then applied to all non-cell-attached data, including both stimulus-evoked and spontaneous activity. Furthermore, because we image continuously for extended periods of time (144 s) and not just episodically around the stimulus (0.4 s window), all of the false-positive and false-negative spikes occurred outside of the stimulus detection window during cell attached recordings. The response probabilities obtained from our imaging approach are consistent with values obtained from electrical recordings in barrel cortex (Ahissar et al., 2001; Margrie et al., 2002; Brecht et al., 2003; Petersen et al., 2003) but with larger samples. Several studies using extracellular recordings have reported much higher response probabilities to whisker deflection (Armstrong-James et al., 1992; Glazewski and Fox, 1996) (see also Shoham et al., 2006). More recently, extracellular studies have found comparable number of spikes per stimulus to the present study using tetrodes (Celikel et al., 2004) or juxtacellular recordings that minimize neuronal selection bias (de Kock et al., 2007). Because L2/3 receives distinct afferent inputs (Bureau et al., 2006), it might also be necessary to further discriminate between L2 and deep L3 in future studies. Another potential source for differences in spike rates could be that neurons might be tuned for stimuli other than used here. However, we used a standardized, ramp-and-hold deflection of a single whisker (Simons, 1983; Bruno et al., 2003; Kida et al., 2005; Bruno and Sakmann, 2006), which has to be considered a strong stimulus because it is close to saturation (Pinto et al., 2000) and can be detected by awake behaving animals (Stuttgen et al., 2006). Furthermore, several studies indicate that cortical neuron spike rates are comparably low in awake animals (Margrie et al., 2002; Crochet and Petersen, 2006; Lee et al., 2006). We thus conclude that the barrel cortex is sparsely active, with L2/3 neurons responding to whisker deflection in a highly variable, unreliable manner. This suggests that it is necessary to study activity patterns trial by trial at the level of well identified neuronal populations.

Using two-photon imaging in combination with intrinsic optical imaging is a powerful tool to study the fine-scale functional organization of the neocortex (Ohki et al., 2005, 2006). Here, we used these methods combined with postmortem anatomical reconstruction of L4 barrels to accurately determine spatial maps of neuronal activity, which cannot be achieved using extracellular population recording techniques. For both onset and offset of whisker deflections, we found higher response probabilities in PW-related neurons than in septum-related neurons. Among PW-related neurons, response probabilities were highest near the BCC and decreased with radial distance.

Neurons generally displayed weak angular tuning that was not bound by underlying barrel borders. Because L4 barrels contain clusters of neurons in which neighboring neurons have similar directional preferences (Bruno et al., 2003) and because the axons of these neurons project vertically to L2/3 (Lubke et al., 2003), it has been suspected that supragranular neurons may also be directionally organized. Despite their strong vertical orientation, L4 afferents densely innervate the entire width of the column (Lubke et al., 2003). This substantial divergence/convergence, along with other cortical inputs, may render L2/3 cells less directionally tuned than their afferent inputs.

Indeed, in contrast to a recent extracellular study proposing the existence of a somatotopic map of whisker motion direction (Andermann and Moore, 2006), we found no relationship between anatomical position and direction selectivity. The reasons for this discrepancy are not clear but could be partly attributable to different recording techniques or different cortical depths of recorded neurons. However, the difference was likely not attributable to an overall lack of tuning among our neurons, because the max/mean responses we observed (1.95 ± 0.05 onset, 2.14 ± 0.05 offset, before bias correction, mean ± SEM) were only slightly lower than those reported by this study (2.32 ± 0.14, mean ± SEM). Because nearby neurons were often observed to have opposite tuning preferences (Fig. 3 E), interpolating the preferences of individual units into a direction map over large areas of the barrel column may be problematic. Our findings are more comparable with the “speckled distribution” of direction-selective neurons in L2/3 of rat visual cortex (Ohki et al., 2005).

Another key finding of our study is that correlations between neuronal pairs depend on location with respect to the functional topography. Pairwise correlations were significantly higher in PW-related neuronal pairs compared with both septum- and SW-related pairs. In addition, correlation strength within the PW-related area decreased with mean distance from the PW-related BCC and also with distance between neurons. These results are consistent with the idea that barrel-related and septum-related neurons receive input from different sources (Lubke et al., 2003; Shepherd et al., 2005; Bureau et al., 2006), with different amplitude and time course (Brecht et al., 2003). A simple explanation for our findings is that dendritic input fields are likely to show the greatest overlap for neurons that are in close vicinity to each other (supplemental Fig. 6, available at www.jneurosci.org as supplemental material). In addition, because afferent fibers to L2/3 are predominantly arranged vertically and confined to the principal barrel column (Lubke et al., 2003), neuronal pairs near the BCC will receive the largest common share of inputs. For neuronal pairs located at barrel column edges, dendrites will also extend into surrounding septal regions, in which they will receive less input arriving from the principal L4 barrel and therefore show less overall correlation (supplemental Fig. 6, available at www.jneurosci.org as supplemental material).

The concept of precise activation of sequences of neuronal ensembles in response to sensory stimulation or during repetitive tasks is central to many hypotheses of cortical function (Richmond et al., 1990, 1999; Abeles et al., 1993; Prut et al., 1998; Gerstein, 2004). Here, we found very few repeats in response to whisker deflections, in contrast to previous studies that showed rich spatial (Ikegaya et al., 2004) and temporal (Luczak et al., 2007) structure even during spontaneous activity. However, a more recent study has conclusively shown that such pattern repeats can appear in stochastic, shuffled data at chance level (Mokeichev et al., 2007). With this in mind, we compared evoked population responses to spontaneous controls and found no significant difference in repeated pattern occurrence. It is possible that neurons within a local neighborhood are not in the same functional neuronal ensemble (Izhikevich et al., 2004). Sampling from much larger neuronal populations (Göbel et al., 2007) might reveal more widely distributed neuronal assemblies in response to sensory input, but, given the low response rate observed in the present study, this will be achieved only if single-AP detection accuracy can be maintained.

The finding of a low probability of pattern repeats might be predicted for small populations from the variable and low response probability of neurons. Regardless of the population size, however, our analysis revealed an exponential distribution of the fraction of population activated, which cannot be reconciled with a model assuming independent units, each responding with its own probability. Rather, neuronal responses have to be assumed to depend on each other (or common inputs), consistent with our finding of pairwise correlations among neurons. Pairwise correlation of neuronal spiking activity provides additional information unavailable in the spiking of single neurons and is directly related to the efficacy of neuronal codes (Averbeck et al., 2006). In particular, even weak pairwise correlations as found here may be sufficient to explain most of the deviation of multineuron responses from independence (Schneidman et al., 2006). Many coding models, however, assume high spontaneous spiking rates in the range of 1–100 Hz (but see Shamir and Sompolinsky, 2006), and, in many experimental data, the spatial relationship between neurons was not known. Using a large set of neuronal pairs with known spatial relationships, we demonstrated here that correlations depend on the exact location of neurons relative to the anatomical organization of the cortical area. This finding may be an important consideration in models of sensory-evoked responses in silico.

The feasibility of decoding stimulus information from sparsely active neuronal populations demonstrates that sparse activity can nevertheless be a potentially efficient coding strategy (Olshausen and Field, 2004). Many sensory and motor systems are thought to use sparse coding strategies that rely on discrete spike bursts (Hahnloser et al., 2002; Laurent, 2002) and timing of single spikes (Petersen et al., 2002). In line with these studies, we found that individual L2/3 neurons in isolation cannot represent the features of whisker deflection but rather cooperate as a population to encode multiple features sparsely across the principal barrel (for neuronal groups, the decoded information is a lower bound on the information present in neural activity, but, for single neurons, it is unlikely that a more sophisticated “decoding strategy” would produce better results). Each feature is encoded by many neurons, and each neuron holds information about several stimulus features (Swindale, 2000). Because L2/3 neurons are functionally well positioned to integrate inputs from various sources (Ahissar et al., 2001; Lubke et al., 2003; Shepherd et al., 2005), such a coding strategy might allow for efficient coding of multiple features of whisker deflection and in addition might facilitate integration of information from the surrounding whiskers (Lebedev et al., 2000), thereby increasing the amount of information and the number of features that can be represented in L2/3.