The Properties and Implications of NMDA Spikes in Neocortical Pyramidal Cells

Abstract

Integration of synaptic input in dendritic trees is a nonlinear process in which excitatory input may elicit spikes localized within the branch receiving input. In addition to membrane current-driven events, a type of dendritic spike has recently been described that instead depends on NMDA receptor current. These NMDA spikes enable superlinear integration among inputs targeted close together on a single branch. Here a compartment model of a layer 5 pyramidal cell was used to examine the mechanisms underlying NMDA spikes and to test properties not directly accessible experimentally. The results indicate the following: initiation of an NMDA spike in a tertiary dendrite in 1 mm [Mg²⁺] requires an NMDA conductance density equivalent to 6–8 nS within a 25-μm-long dendritic subsegment; dendritic membrane currents are not required for NMDA spike production; and targeted dendritic (but not somatic) inhibitory input is exquisitely suited to veto an NMDA spike if it arrives within a 30 ms window in time. Finally, an analysis of the spatial density of NMDA conductance required for NMDA spike production implies that, at least up to the age (postnatal day 35) that these events have been observed, most of the excitatory synaptic conductance arriving at pyramidal cells is NMDA mediated.

Introduction

The conceptualization of excitatory synaptic input has evolved over the last 50 years. Once envisioned as a linear summation of plusses and minuses, Rall (1964) showed that the effect of synaptic conductances depends on their location with respect to each other, with nearby inputs combining sublinearly in a passive dendritic structure. Subsequently, dendritic membrane was revealed to be electrically active (Spencer and Kandel, 1961; Llinás et al., 1968), and now the effect of excitatory input is recognized to involve a complex interaction with dendritic membrane currents (Traub and Llinás, 1977, 1979; Johnston et al., 1996; Yuste and Tank, 1996; Rhodes, 1999), making summation in dendritic trees a highly nonlinear phenomenon the properties of which are just beginning to be unraveled.

Another kind of nonlinearity in the summation of synaptic input has been identified recently, a so-called “NMDA spike,” involving interaction between synapses coactivated in close spatial proximity along a single fine dendritic segment (Schiller et al., 2000; Ariav et al., 2003; Polsky et al., 2004). These events are triggered in vitro by focally applied input, they depend on NMDA current, and they can generate a highly superlinear summation of inputs enabling sets of afferent fibers that terminate in proximity to have much greater impact together than the sum of their separate effects. The somatic EPSP produced by NMDA spikes can exceed 10 mV (Schiller et al., 2000; Polsky et al., 2004), and so several of these events can together be expected to readily prompt somatic firing.

Many basic biophysical questions regarding this potentially important phenomenon have not yet been addressed. For example, to assess whether NMDA spikes are plausibly produced in response to physiological stimuli, it is relevant to ask how much NMDA conductance they require. Does the required conductance imply a physiologically sensible number of coactive spines given the apparently restricted area of input? Does AMPA current boost the event? In what manner are NMDA spikes boosted by the dendritic membrane currents? What is the effect of dendritic inhibition on these events, and how does that effect depend on the relative timing and location of inhibitory and excitatory inputs? Is somatic inhibition effective in preventing NMDA spike or in blocking their efficacy? Can NMDA spikes on separate branches together cause somatic firing? Because of the limitations inherent in manipulating synaptic inputs, it is difficult to quantitatively address these issues experimentally. Accordingly, in the present work, the foregoing questions have been addressed in the setting of a compartment simulation of a layer 5 intrinsically bursting pyramidal cell. The results suggest that NMDA spikes are exquisitely controlled by targeted dendritic inhibition, whereas somatic inhibition is comparatively ineffective in either suppressing the events or blocking their efficacy. Analysis of the NMDA conductance density required for NMDA spikes supports the hypothesis that up to the age [at least postnatal day 35 (P35)] at which NMDA spikes are observed, most of the excitatory synaptic conductance arriving at pyramidal cells is NMDA mediated, and therefore many excitatory synapses may be silent (Isaac et al., 1995; Liao et al., 1995).

Materials and Methods

Compartment model.

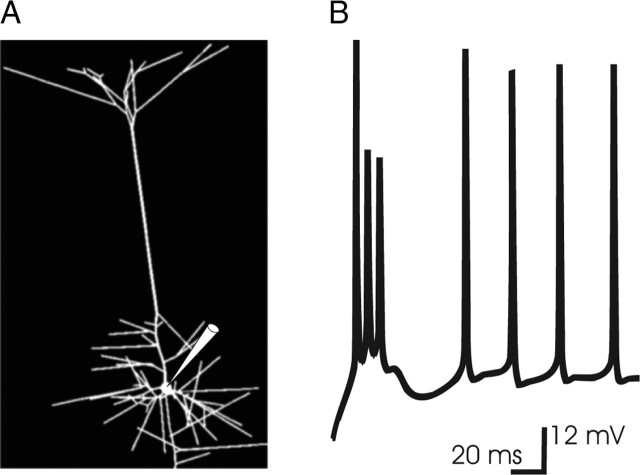
A compartment model (Rall, 1964) of layer 5 thick-trunked pyramidal cell was derived from the Neurolucida file of a cell reconstructed at P28 (kindly supplied by Dr. M. Larkum, University of Bern, Bern, Switzerland). Compartments were defined by branch bifurcations and further constrained to be no more than 50 μm in length. The resulting model cell comprised 166 individual compartments (Fig. 1A) and incorporated conventional values of passive electrotonic parameters as follows: R_i,150 Ωcm; C_m, 1.0 μF/cm²; R_m, 50 kΩcm². The thick proximal dendritic segments abutting the soma, as well as the first 125 μm of trunk, lacked spines. On all other dendritic segments, the membrane area contributed by spines was accounted for by increasing capacitance per unit area, C_m, and decreasing membrane resistance, R_m, by the proportionate increase in surface area attributable to the spines (Holmes and Woody, 1989), with spine area estimated to be 1.4 μm² and density of two spines per micrometer length per micrometer diameter (Larkman, 1991). Thus, for those segments that incorporated spines, C_m (R_m) was multiplied (divided) by 1.92, as the proportionate increase in membrane area per micrometer length per micrometer diameter being (two spines × 1.4 μm² per spine)/π μm² = 0.92. It is worth noting that the adopted values of R_m and R_i may be on the higher side of the physiological range. In simulations of NMDA spikes with lower values (R_m and R_i of 10,000 Ωcm² and 70 Ωcm, respectively), the mechanisms of NMDA spike generation were unchanged, but the lower values were associated with an increase in threshold NMDA conductance required for the generation of NMDA spikes (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). In this respect, the conclusions regarding the threshold amount of NMDA conductance required to produce these events may be conservative.

Figure 1.

A, The morphology of the model layer 5 cell. A layer 5 cell from rat barrel cortex at P28 filled with biocytin and reconstructed using the Neurolucida reconstruction system was kindly supplied by Dr. M. Larkum. The model cell comprised 166 individual compartments. The segment receiving synaptic input was subdivided further into subsegments no more than 23 μm in length, so that the local variation of voltage along the fine segment receiving input could be modeled and the voltage-dependent gating of localized NMDA conductance could be computed. The pipette points to the soma. B, Response of the model cell to current step injection at the soma. The dendritic and somatic distribution of ionic conductances (see Materials and Methods) were adjusted so that the physiological response to current step injection at the soma was approximated, according to previous work (Rhodes and Gray, 1994). The branches of this model cell contained sufficient Ca²⁺ density (densities for all channels are shown in Table 1) so that the first somatic spike triggered a sustained Ca²⁺-driven depolarization in the basal branches that in turn drove a multispike burst in the soma, as described previously (Rhodes and Gray, 1994). With the rise in [Ca²⁺] associated with this dendritic Ca²⁺-driven depolarization, [Ca²⁺]-gated K⁺ (K_Ca) curtailed the dendritic depolarization, so that at this magnitude of current injection, subsequent somatic spikes did not trigger bursts; instead, a single spike was accompanied by a small afterdepolarizing potential, which is one characteristic firing mode of this cell type (McCormick et al., 1985). The response is to an 0.8 nA current step from rest (−71 mV).

Dendritic ionic channel conductance density distribution.

A density distribution of Na, Ca_L, K_Ca, K_A, K_mAHP, K_DR, and I_h conductances was established that enabled this model cell to produce characteristic intrinsic responses to current step (Fig. 1B), according to previous work modeling this cell (Rhodes and Gray, 1994; Rhodes, 1999; Rhodes and Llinás, 2001), in which details of current kinetics may be found. The distribution of dendritic ionic conductances included Na⁺ conductance density (12 mS/cm²) in the basal dendrites consistent with the measurements of Antic (2003), along with high-threshold Ca²⁺ densities of 6–12 mS/cm², adequate to drive the bursts characteristic of this cell type (McCormick et al., 1985; Rhodes and Gray, 1994). The distribution of ionic conductance densities specified in Table 1 was used for all that were simulated, unless specifically noted otherwise. In Table 1, conductance density (in millisiemens per square centimeter) refers to that applicable when channel open probability is 100%.

Table 1.

Channel conductance density^a distribution in the model layer 5 intrinsically bursting pyramidal cell

Region	Na	K DR	CaL	K A	K Ca	I h
Soma	400	60	6	5	2	0
Adjacent to soma	150	20	6	5	1.8	0
Basal dendrites	12	2	8	5	2.4	0
Proximal apical	20	2	8	5	2.4	0
Distal apical	15	2	4	5	1.2	0.5
End segments	6	2	6	5	1.8	0
Tuft	4	1	3	5	0.9	0

The apical dendritic densities indicated pertain to the most proximal and most distal compartments in the apical dendrite (excluding the tuft), with the density in intervening compartments linearly interpolated between them.

^aIn all cases, the density is expressed in mS/cm² and refers to the density applicable when all channels are open.

To assess whether dendritic Ca²⁺ conductance was importantly involved in either the initiation or the subsequent course of NMDA spikes, the generation of these events was examined with the density of dendritic high-threshold Ca²⁺ conductance set at 0, 2, 4, 8, and 12 mS/cm². The results indicated that although not required for NMDA spike production, dendritic Ca²⁺ current (much more than dendritic Na⁺ current) can extend (or curtail, via the activation of Ca²⁺-gated K⁺ currents) the duration of NMDA spikes. In all instances when dendritic Ca²⁺ channels were present in the stimulated branch, dendritic Ca²⁺ entry accompanied the NMDA spike.

[Ca²⁺] dynamics.

Cytosolic [Ca²⁺] was computed with a fast endogenous buffer and a membrane-bound pump. With this system, a somatic spike caused a [Ca²⁺] transient in dendritic membrane of several hundred nanomolar, decaying to rest with τ ≈ 60 ms, consistent with the measurement of this process (Schiller et al., 1995; Helmchen et al., 1996). Details of ionic current and Ca²⁺ buffer and pump kinetics can be found in Rhodes and Llinás (2001). Temperature in the simulations was 35°C, as in the in vitro experiments (Polsky et al., 2004) to which this work primarily refers.

Synaptic stimulation.

To simulate the effect of focal stimulation, a dendritic basal branch segment was chosen (several were used to compare NMDA spike thresholds and somatic efficacies) and then broken into subsegments no more than 23 μm in length. Preliminary results (data not shown) indicated that subdivision into small compartments was required for the accurate simulation of voltage-gated responses to synaptic input into the long, narrow (diameter, ∼0.7 μm), tertiary basal branches on which much spine input arrives (Larkman 1991) because of pronounced attenuation of voltage with distance within those end segments. Simulations were performed with [Mg²⁺] at either 1.0 mm [the concentration used in Polsky et al. (2004)] or 2.0 mm. With the latter, the threshold NMDA conductance required to elicit an NMDA spike was ∼25% greater, but the results were otherwise the same. AMPA-, NMDA-, and GABA-type synaptic conductances were then applied in a chosen subsegment or subsegments and individually varied, as described in Results, to study thresholds and magnitude effects.

Kinetics for the synaptic currents were as follows:

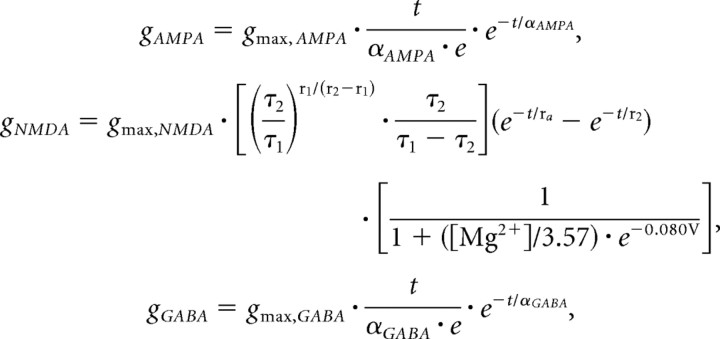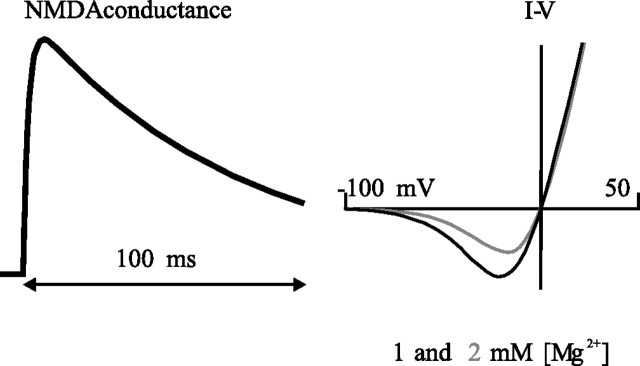
where g_max,AMPA, g_max,NMDA, and g_max,GABA refer to the maximal conductances of the respective currents at their peak (in the case of the NMDA conductance without regard for the [Mg²⁺] block), with voltage in millivolts, time in milliseconds, and [Mg²⁺] in millimolar. α_AMPA and α_GABA control the rate of rise and fall of the respective α functions (Rall, 1964), here 2 and 5 ms, respectively, and τ₁ and τ₂ are the binding and unbinding time constants related to the action of the NMDA receptor, here 2.04 and 75.2 ms, respectively (Jahr and Stevens, 1990). The time course of the NMDA conductance and the I–V curve for the current at [Mg²⁺] of 1 and 2 mm are illustrated in Figure 2.

Figure 2.

The kinetics of the NMDA channel. Left, NMDA conductance as a function of time after synaptic activation at time 0, with the blockade caused by Mg²⁺ neglected (i.e., as if in 0 [Mg²⁺]). The time course indicates a fast rise and much slower fall, reflecting the binding and unbinding time constants of 2 and 75 ms, respectively (kinetics in Materials and Methods). Right, I–V curves applicable for 1 and 2 mm [Mg²⁺], the levels at which the simulations were conducted. The curves indicate a reversal of 0 mV and current magnitude peaking at approximately −7 and −15 mV, respectively, for 1 and 2 mm [Mg²⁺].

Throughout this work, the value of synaptic conductance refers to the total contributed from all stimulated synapses, measured at the peak of the conductance time course and, in the case of NMDA conductance, absent voltage-dependent block. As in vitro, stimulation protocol in simulation was often a pair of stimuli, typically 20 ms apart. Neither receptor saturation nor desensitization was accounted for in computing the response to the second pulse (Mainen et al., 1999). Simulation of responses to longer trains will presumably require incorporation of a receptor population model to account for saturation, along with a more detailed kinetic model of the NMDA receptor in which desensitization is addressed, both of which are beyond the present scope of this work. Although facilitation and refractoriness are both operative at intracortical spine contacts at 20 ms interspike intervals (Thomson, 2003), the effects were not incorporated, nor was release modeled stochastically. Because pyramid–pyramid synapses in cortex generally exhibit net paired-pulse depression (Thomson, 2003), revision of this work to incorporate synapse dynamics will increase the predicted NMDA conductance required for production of NMDA spikes. Also not accounted for here is the recently described slow component of the voltage-dependent unblock of the NMDA receptor (Vargas-Caballero and Robinson, 2003; Kampa et al., 2004), the effect of which would also be to reduce the amount of NMDA conductance available to drive the NMDA spike event. Thus, at least with respect to more accurate biophysical models of release dynamics and NMDA unblock, the conclusions presented here regarding the predicted magnitude of the average NMDA conductance per synapse and the NMDA/AMPA ratio may be conservative.

Both the location and spread of synaptic input was systematically varied to study the effects of position and focality of input on threshold and efficacy. The effects of TTX and Cd²⁺ were simulated by setting the Na⁺ and Ca_L conductances, respectively, to zero. Inhibitory conductance was systematically varied both in its position in the dendritic tree relative to the excitatory input, and in the relative latency between inhibitory and excitatory input arrival. Simulations were done using custom-built simulation software used in previous compartment-modeling work (Rhodes and Gray, 1994; Rhodes, 1999; Rhodes and Llinás, 2001).

Results

Simulated NMDA spikes are produced by a sustained dendritic plateau localized to the dendritic segment receiving input

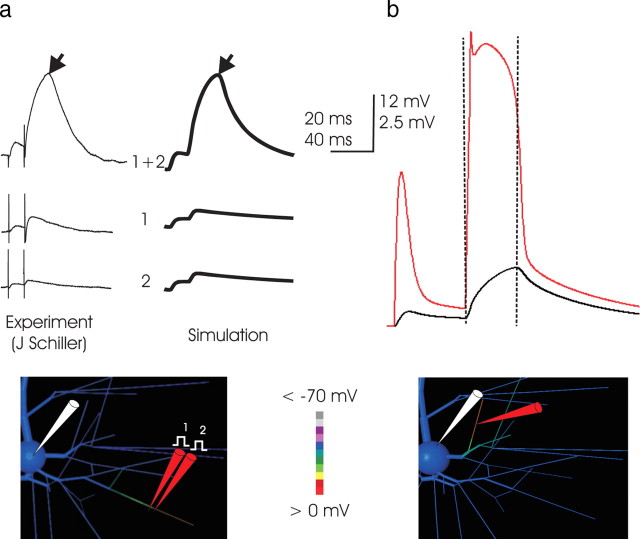
In simulation, a high density of NMDA conductance concentrated within a small region of a distal branch produced an event (Fig. 3a) closely corresponding to the NMDA spike observed with focal stimulation in vitro (Schiller et al., 2000; Schiller and Schiller, 2001; Polsky et al., 2004; Milojkovic et al., 2004). Both in vitro and in simulation, small subthreshold responses from two individual stimuli, when applied together, could produce an event much larger than their sum, indicating the activation of NMDA and membrane currents. In simulation, as in vitro, the somatic response was characterized by two phases: the first, a near-exponential charging of somatic voltage, abruptly giving way to exponential decay (Fig. 3b, dashed lines). Observation of voltage throughout the dendritic tree during simulation made it clear that the charging phase of the somatic event corresponded to a sustained dendritic depolarization ∼60 mV in amplitude that lasted for at least 25 ms and was confined largely to the segment receiving input (Fig. 3b) (Milojkovic et al., 2004), which therefore ohmically drove the somatic EPSP. The sharp transition from charging to decay in the soma corresponded to an abrupt collapse of the dendritic depolarization, whereupon the somatic voltage exponentially relaxed toward rest. For a given synaptic conductance, the somatic amplitude varied with the location of the dendritic NMDA spike, but its two-part form, with distinct charging and decay phases, did not.

Figure 3.

a, Simulation of focal stimulation experiments eliciting NMDA spikes. Left, In vitro (traces courtesy of J. Schiller, Technion), the superlinearity inherent in NMDA spikes is demonstrated by placing two stimulation electrodes in very close proximity and closely apposite a fine basal branch and stimulating with a pair of inputs at 50 Hz. The small somatic EPSP elicited by activation of either electrode individually (bottom traces) is belied by a voltage deflection far greater than their sum when their effect is combined, which demonstrates highly superlinear summation. The same phenomenon occurs in the simulation, when synaptic conductance is applied to two adjacent 23-μm-long dendritic subcompartments, first in turn and then together. In both simulation and in vitro, the somatic EPSP reflects a charging phase that gives way abruptly to a relaxation phase (demarcation at black arrows). The location of simulated stimulation is depicted in the inset, with dendritic voltage at the peak of the NMDA spike coded in color; the corresponding in vitro location is not known. The voltage color scale here applies to the model cell inset in all subsequent Figures. Timescale applies to both measured and simulated traces, but voltage scale of in vitro records (which includes stimulation artifact not present in the simulation) is scaled slightly to normalize peak amplitude. Note the approximately fivefold increase in amplitude of the somatic EPSP associated with the superthreshold event, indicating that the currents responsible for its production are much greater than the AMPA current primarily responsible for the amplitude of the first EPSP. The responses here correspond to 1 nS AMPA and 6 nS NMDA conductance for each of the two inputs, and these and subsequent simulations are performed with the dendritic ionic channels present as detailed in Materials and Methods and Table 1. b, The NMDA spike is caused by a broad but abruptly initiated and terminated dendritic spike. In this and subsequent Figures, unless noted otherwise, voltage at the dendritic loci is plotted in the color matched to the “pipette” in the drawing (here in red) along with the somatic trace in black. In this example (input to a proximal basal end segment; location illustrated in the inset), the simulated NMDA spike is associated with and driven by a dendritic event of ∼60 mV in amplitude, which is triggered immediately on stimulation, quickly reaches a peak voltage of approximately −10 mV, and collapses abruptly after ∼25 ms. The time of collapse of the dendritic event (vertical dashed lines) is coincident with the demarcation between charging and relaxation of the voltage trace in the soma, a shape characteristic of NMDA spikes in vitro (Schiller et al., 2000; Schiller and Schiller, 2001; Polsky et al., 2004) (left). Its shape at the soma is caused by the approximately square outline of voltage in the dendritic segment, with a rapid rate of rise, a long period at maximum voltage, and a rapid collapse. The isolated nature of the NMDA spike in the dendrites is evident in the screen shot of the model cell (voltage coded in color; scale from −70 to 0 mV) of the basal arbor of the dendritric tree that was taken during the apex of the event. Depolarization is much higher in the segment receiving input, particularly from the site of input outward to its distal end, than elsewhere in the branch.

A threshold of ∼8–10 nS NMDA conductance concentrated within a 25 μm dendritic region is required for production of a simulated NMDA spike

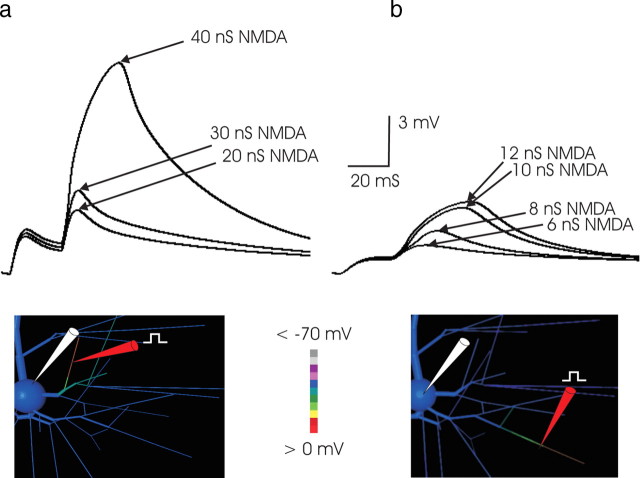
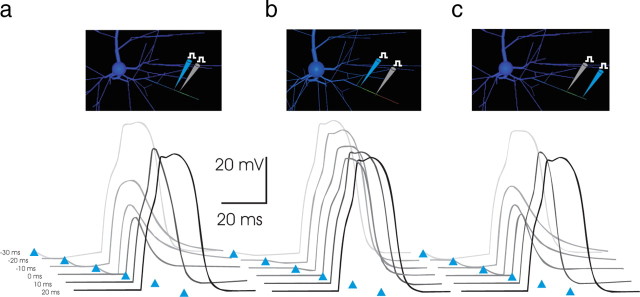
How much NMDA conductance is required for an NMDA spike? The answer bears on the question of how many coactive synapses are required to produce these events and hence on the convergence requirements for their occurrence with natural stimulation in vivo. In the simulations, threshold depended on the location of input and the degree to which the input was spatially concentrated, indicating that any estimation of threshold is relative to those parameters. Inputs near the soma did not trigger NMDA spikes, even when substantial (>50 nS) NMDA conductance was applied, consistent with the experimental observation that focal synaptic stimulation did not elicit NMDA spikes within a 70 μm radius spherical region surrounding the soma (Schiller et al., 2000). Threshold declined as the distance from the soma and the input impedance of the dendritic location increased; as a result, when the values of the passive electrotonic parameters R_i and R_m were changed, corresponding changes (of opposite direction) in threshold NMDA conductances were observed (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). In 2 mm [Mg²⁺], the threshold amount of NMDA conductance required for generation of an NMDA spike was ∼35 nS in a proximal basal branch (Fig. 4a) but as little as 10 nS when concentrated within a 25-μm-long section of fine tertiary basal dendrite (Fig. 4b), declining to 6–8 nS with 1 mm [Mg²⁺] [the concentration used in Polsky et al. (2004) and used here in Figs. 8–10], illustrating a relationship between threshold and external [Mg²⁺]. A short distance of interaction between two focal inputs was observed, limited to ∼50 μm, suggesting that dendritic EPSPs decline to a small fraction of their size at the site of input within this distance. This “interaction distance” compared well with that reported experimentally (40 μm) (Polsky et al., 2004) and provided indirect evidence suggesting that axial attenuation in the simulated tertiary dendritic branches was similar to that measured. [Because threshold varied by location along the tertiary branch, an interaction distance measurement is not valid unless the input is somehow adjusted to account for its location, perhaps with the local threshold or input impedance as a normalizing factor. For this reason, a rigorous characterization of interaction distance would require separate analysis, which is outside the present scope of this work. Although the interaction distances reported here and in Polsky et al. (2004) are in rough agreement, both should be considered in light of the foregoing caveat.] The simulation results imply the fine-grained segmentation of input space addressable in the pyramidal cell dendritic tree noted by Schiller and coworkers (Schiller and Schiller, 2001; Polsky et al., 2004). Concentrating the input into a region <25 μm did not reduce the NMDA conductance required, suggesting that within this distance there is full cooperativity among synaptic inputs.

Figure 4.

a, Threshold for NMDA spike generation was much higher in proximal branches. In this example, in 2 mm [Mg²⁺] and with a 25 ms paired-pulse interval, nearly 40 nS of NMDA was required to produce an NMDA event. The greater threshold correlated with the lower input impedance of the more proximal branch. Here, AMPA conductance was 3 nS. Larger AMPA conductance values increased the EPSP amplitude of the first EPSP but did not reduce the level of NMDA conductance required to trigger a regenerative event. Substantially higher levels of AMPA conductance were inconsistent with the first versus second EPSP amplitude ratio observed in paired-pulse protocols in vitro (compare Fig. 3a, left traces). The site of stimulation in this example was ∼70 μm from the soma. For stimulation at more proximal loci, an NMDA spike could not be elicited, consistent with the corresponding observations with focal extracellular stimulation in vitro (Schiller et al., 2001). b, The minimum amount of NMDA conductance required to produce an NMDA spike in 2 mm [Mg²⁺]was ∼10 nS. Synaptic conductance was applied to a 23 μm subsegment of a fine tertiary basal branch, the center of which was ∼211 μm from the cell body. These high-impedance distal tertiary segments supported the generation of an NMDA spike with the lowest threshold. The regenerative nature of the event is illustrated by the large jump in the somatic EPSP when synaptic conductance was increased incrementally from 8 to 10 nS. Once threshold was reached, the subsequent increase in NMDA conductance had a smaller effect. For all stimuli, the AMPA component of synaptic conductance was 2 nS. In all Figures and throughout the text, conductance values refer to conductance at peak, without any Mg²⁺ blockade. The threshold NMDA conductance at this location declined to ∼6 nS when external [Mg²⁺] was decreased from 2 mm (the concentration in the simulation depicted in this Figure) to 1 mm.

Figure 8.

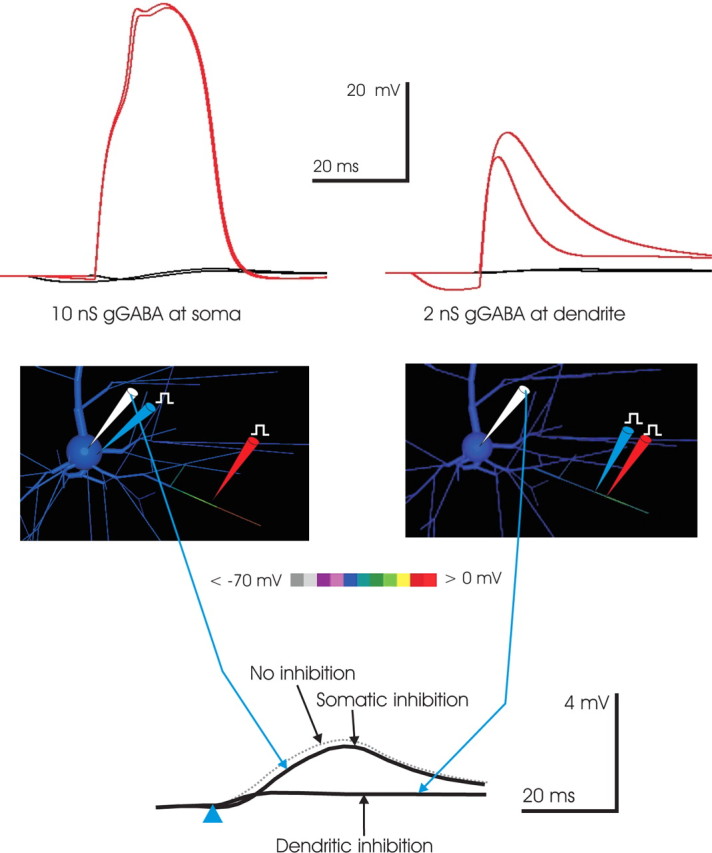
Targeted dendritic inhibition is more effective than somatic inhibition in controlling NMDA spikes. A superthreshold synaptic conductance (2 nS AMPA and 8 nS NMDA; in 1 mm [Mg²⁺]) was applied to a 23 μm subsegment in the middle of a distal basal branch (red pipette at location in inset). The effect of 10 nS GABA conductance applied at the soma (left, top) was compared with that of 2 nS GABA conductance applied at the dendrite in a 23 μm subsegment abutting the location of excitatory input (right, top). In both cases, the effect of the inhibitory conductance was examined when it arrived both coincidentally with the excitatory input and 15 ms in advance of it. The input applied to the soma (left, top) had a negligible effect on the NMDA spike proceeding in the dendritic branch receiving input, whereas an inhibitory conductance just 20% as large targeted to the activated branch quenched the NMDA spike, even when the inhibition arrived 15 ms before the excitatory input. The results illustrate both the relative ineffectiveness of even large-magnitude somatic inhibition and the efficacy of spatially targeted inhibition in quenching NMDA spikes. Bottom, Targeted dendritic inhibition was more effective than somatic inhibition in controlling the somatic EPSP. To test whether somatic inhibition was more effective than dendritic in controlling the somatic EPSP, the excitatory input (red pipette) used in the top right was applied, with 2 nS GABA conductance (blue pipette) applied either to the soma (top) or the dendrite just abutting the site of input (bottom) (inhibition arrives coincidently with excitation, at time indicated by blue arrowhead). The somatic EPSP amplitude peak was 1.9 mV when inhibition was present, a decrement in peak amplitude of ∼0.35 mV when compared with the 2.25 mV EPSP produced when no inhibition was applied (dashed gray trace); however, when the same inhibitory conductance was targeted to the dendrite, the somatic EPSP was just 0.4 mV, reflecting the priority of preventing the NMDA spike rather than, instead, blocking its effect with somatic inhibition. The result suggests that even inhibition impinging directly on the cell body has much less of an effect on the somatic EPSP than dendritic inhibition targeted to the excited branch.

Figure 9.

a, A 35 ms time window for inhibitory suppression of an NMDA spike. To examine the degree of temporal coincidence required for inhibition to be effective in suppressing an NMDA spike, the latency of inhibition relative to arrival of excitation was varied from −30 to +30 ms. Arrival time of inhibitory conductance is indicated by the blue arrowheads, with earliest latencies represented by the lightest shades of gray. The excitatory and inhibitory conductance magnitudes (2 nS AMPA, 8 nS NMDA, and 2 nS GABA, respectively; in 1 mm [Mg²⁺]) were as in Figure 8b, with the inhibitory conductance applied 23 μm proximal to the excitation (blue pipette in inset). Inhibitory input arriving up to 20–25 ms before the excitation, a time period that is sensitive to the time course of the inhibitory conductance (see Materials and Methods), was effective in preventing the NMDA spike at these conductance magnitudes. Inhibition arriving 5–10 ms after the arrival of excitation abruptly quenched the NMDA spike ongoing, curtailing its impact. Thus, with these parameters, a 35 ms window existed in time, most of which precedes excitation, during which targeted dendritic inhibition effectively suppressed the triggering of an NMDA spike. b, c, Inhibition is most effective in suppressing NMDA spikes when targeted to the distal tip. To ascertain whether the colocalization of inhibition with excitation was necessary for its effectiveness, the same paradigm as a was used but with the inhibition applied within the same tertiary branch, but either more proximal or distal to the location of excitatory conductance. Locations of inhibition (blue pipette) and excitation (gray pipette) are as shown in inset. Surprisingly, inhibition at the proximal end (b), near the bifurcation, was relatively ineffective in curtailing the NMDA spike, regardless of latency. In contrast, inhibition applied to the distal-most tip (c) was at least as effective as when it was colocalized with excitation.

Figure 10.

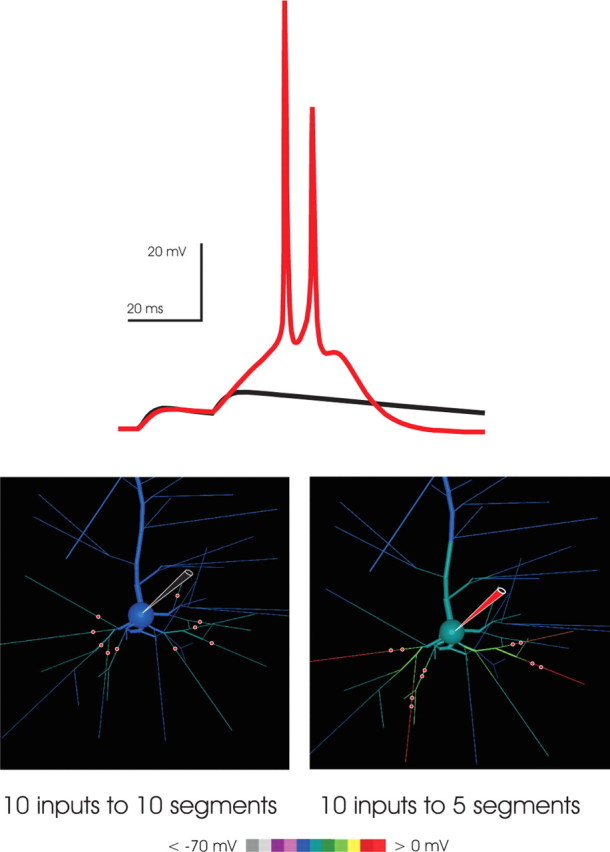
NMDA spikes amplify the efficacy of spatially convergent synaptic input. To examine whether spatially convergent input was amplified by NMDA spikes, a set of 10 identical inputs (each 1 nS AMPA and 5 nS NMDA) was distributed in two alternative patterns: distributed, where each input arrived on a distinct branch, as shown in the bottom left, or paired, where the same 10 inputs were paired in 5 groups of 2, each of the 5 pairs arriving at one of the 10 branches. In both cases, the presynaptic activation was a pair of pulses at 20 ms interspike intervals. In the distributed case, the first EPSP was slightly larger than in the paired case, reflecting reduced driving force saturation (Rall, 1964); however, in the paired case, the second EPSP triggered NMDA spikes in three of the five branches receiving input. Their effect, in turn, powerfully drove the neuron to fire a burst. In contrast, the second EPSP in the distributed case was similar to the first. The result demonstrates that NMDA spikes are powerful drivers of neuronal output and therefore are mechanisms for the amplification of suitable, spatially convergent input.

AMPA synaptic input is not necessary for the production of simulated NMDA spikes

Most of the synaptic conductance in pyramidal cell spine synapses is thought to be composed of AMPA receptor current. Is at least some AMPA current required for production of an NMDA spike? With AMPA current eliminated in simulations, an NMDA spike could still be readily produced (Fig. 5a), supporting the prediction that AMPA conductance is not required for the production of simulated NMDA spikes; however, the threshold amount of NMDA conductance required for the NMDA spike reduced when AMPA conductance was eliminated (data not shown), suggesting that colocalized AMPA facilitates induction of an NMDA spike, presumably by boosting dendritic depolarization and thus opening the NMDA channels that drive the event. Once a small amount of AMPA conductance was present (typically, 10–20% of threshold NMDA conductance was sufficient), adding more did not further reduce the threshold density of NMDA conductance required to produce an NMDA spike. It is concluded that AMPA current plays a nonessential facilitatory role in the generation of NMDA spikes.

Figure 5.

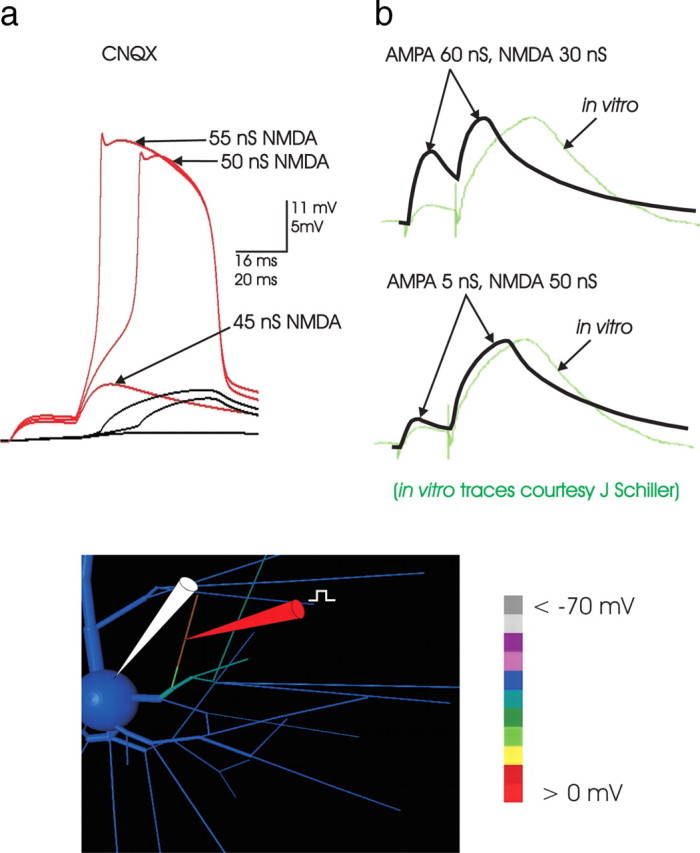
a, NMDA spikes can be elicited without AMPA current. With all AMPA conductance inactivated (as in a CNQX experiment in slice), NMDA spikes could still be produced. In this example, in 2 mm [Mg²⁺], synaptic input was distributed over an entire 65 μm end-segment (indicated by the location of the dendritic electrode in the image inset), with normal threshold ∼45 nS total NMDA conductance. Absent all synaptic AMPA current, the NMDA spike still occurred. The three somatic traces (black) represent 65, 70, and 75 nS total NMDA conductance applied and distributed evenly across the 65 μm segment. Thus, without AMPA to assist in reaching local threshold, the amount of NMDA conductance required to elicit the NMDA spike increased to ∼70 nS, suggesting that although the AMPA current does not drive the NMDA spike, it assists in its initiation. A further increase in AMPA did not decrease the NMDA conductance threshold, reflecting the observation that AMPA did not participate in driving the NMDA spike once it was initiated. b, The shape of the NMDA spike. To examine whether high levels of AMPA could substitute in part for NMDA conductance to produce an event resembling an NMDA spike, sufficient AMPA conductance was applied to a basal branch so that the EPSP amplitude in the soma was that of a large NMDA event (right, top trace; same stimulation and dendritic recording location as in Figure 4a). In the paired-pulse protocol, the resulting EPSP shapes were compared with those in a simulated event in which synaptic NMDA conductance predominated (below). An overlay with a recorded NMDA spike (green trace; courtesy of J. Schiller) was made in both cases; the time scales of the simulated and recorded events are the same, although the amplitude scale of the recorded event was adjusted slightly to normalize peak amplitude to facilitate the comparison of shape. Clearly, the shape of recorded paired-pulse responses are more consistent with simulated events in which NMDA is the dominant synaptic current. The ratio of amplitude of the first and second pulse observed experimentally (∼1:5) is not consistent with an AMPA-dominated event. The comparison of shape as well as relative amplitude of the elicited EPSPs suggests that AMPA is a relatively small component of the currents driving the NMDA spike (see Discussion).

AMPA synaptic input cannot produce simulated NMDA spikes

Clearly AMPA current is not necessary, but at high enough levels can it be sufficient to trigger NMDA spikes? To address this question, the amount of AMPA conductance was varied over a wide range, up to the level at which AMPA conductance alone produced a somatic EPSP of 10 mV. In no case did AMPA-dominated synaptic input produce an effect at the soma resembling that of an NMDA spike. The characteristic shape of the somatic EPSP associated with the dendritic NMDA spike in vitro (with a charge-up phase abruptly giving way to exponential relaxation toward rest; compare Fig. 2) was never evident when AMPA was the dominant synaptic current. Although the dendritic Na⁺ and Ca²⁺ ionic conductances (up to 12 mS/cm² each) integrated into this model cell were fully activated by intense AMPA current, the intrinsic membrane conductances did not produce a dendritic event of sufficient duration to be responsible for the somatic EPSP signature of NMDA spikes. [It remains possible that with different Ca²⁺ current kinetics, a prolonged dendritic event could be triggered by AMPA synaptic input and thereby produce a somatic EPSP resembling that associated with an NMDA spike; however, voltage-gated Ca²⁺ channels in dendrites cannot be the primary driver of NMDA spikes, because Schiller et al. (2000) demonstrated that the events can be elicited in Cd²⁺ with synaptic stimulation achieved by laser uncaging of glutamate.] The simulation results suggest that the shape of the somatic EPSP associated with an NMDA spike cannot be produced by AMPA in conjunction with dendritic membrane currents.

The large ratio of second-to-first EPSP amplitude in paired-pulse stimulation implies that most of the conductance activated synaptically is NMDA mediated

The ratio of second-to-first somatic EPSPs observed in vitro in response to paired-pulse stimulation protocols (Polsky et al., 2004) implies the unexpected conclusion that NMDA must comprise most of the synaptic conductance at the synapses activated by the focal stimulation protocol used in vitro. As has been noted, threshold paired-pulse focal stimulation in vitro (Schiller et al., 2000; Schiller and Schiller, 2001; Polsky et al., 2004) in rats aged up to P35 typically produces a small first EPSP followed by a much larger second EPSP, with the ratio between second and first EPSP amplitude often fivefold or more. This ratio was exhibited only in simulations of focal stimulation when a large NMDA conductance was accompanied by a smaller AMPA conductance and seems to be most consistent with an NMDA/AMPA ratio of approximately more than fivefold (Fig. 5b, bottom panel). When AMPA was comparable with or larger than NMDA conductance (Fig. 5b, top panel), first and second amplitudes were similar. The most parsimonious interpretation of these observations is that the substantial variation between first and second EPSP amplitude suggests that on those dendritic branches where NMDA spikes can be produced there is substantially more NMDA than AMPA conductance available at excitatory synapses on rat neocortical pyramids, at least until the age (P35) through which NMDA spikes have been reported (see Discussion).

Dendritic Na⁺ current reduces synaptic threshold but does not contribute to the NMDA spike once it is initiated

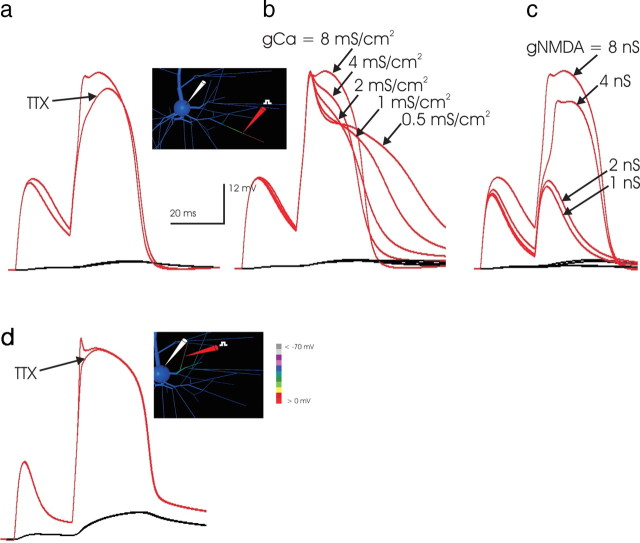
Although experiments using laser uncaging of glutamate in TTX (Schiller et al., 2000) have established that NMDA spikes do not depend on Na⁺ current, it remains possible that the Na⁺ channels that populate the basal dendrites of layer 5 pyramidal cells (Rhodes and Gray, 1994; Antic, 2003) could be involved in driving the event under control conditions. To test this possibility, superthreshold paired-pulse stimulation was applied in control conditions, and the response was compared with that after all Na⁺ channels were turned off. The results indicated that dendritic Na⁺ current reduces the threshold stimulation level, which is consistent with the behavior of this system in vitro (Schiller et al., 2000). In simulations, a 20% threshold increase was typical, remarkably similar to the 29% increase in threshold observed in TTX in vitro by Schiller et al. (2000). This correspondence indicates that the contribution of dendritic Na⁺ current to the initiation of an NMDA spike in the simulation was close to that observed physiologically and supports the plausibility of the Na⁺ conductance density chosen for the basal dendrites in the model cell.

An overlay of the simulated dendritic voltage trace at the site of synaptic stimulation in the two conditions (control and TTX) indicated that dendritic Na⁺ current contributed primarily to the initial peak voltage of the dendritic NMDA event (Fig. 6a); however, once the NMDA spike was initiated, dendrite Na⁺ currents boosted neither amplitude nor width and accordingly had a negligible effect on the somatic EPSP. The same effect was observed when the NMDA spike was instead triggered in a proximal branch (Fig. 6d). It was concluded that dendritic Na⁺ current reduces threshold synaptic input but otherwise plays a negligible role in the generation of NMDA spikes.

Figure 6.

a, The simulated NMDA spike is not dependent on dendritic Na⁺ current. To examine whether the Na⁺ conductance in the basal dendrites of the simulated pyramidal cell (Rhodes and Gray, 1994; Rhodes et al., 1995; Antic, 2003) might be responsible for the initiation or generation of NMDA spikes, Na⁺ channels were turned off in the simulation, and synaptic input of 1 nS AMPA and 4 nS NMDA (∼33% above threshold here) was applied to each of two adjacent 23 μm subsegments at the location indicated on the inset, with 1 mm [Mg²⁺]. As in the corresponding TTX experiment in vitro (Schiller et al., 2000), dendritic Na⁺ current was not required for production of the NMDA spike. A comparison of the simulated response to that in control conditions indicates that the involvement of Na⁺ current is limited to the beginning of the NMDA spike and does not control its duration. The small boost at the beginning of the event was consistent with the finding (Schiller et al., 2000) that threshold NMDA conductance was slightly lowered by the presence of Na⁺ (observed in simulation; data not shown). It was concluded that, like AMPA, Na⁺ conductance boosts initiation but thereafter has a limited role in the generation of simulated NMDA events. Accordingly, at threshold levels of input (data not shown), application of TTX required an increase in synaptic NMDA conductance, as seen in vitro (Schiller et al., 2000). b, Dendritic Ca²⁺ conductance affects the duration and amplitude of NMDA spikes. High-threshold Ca²⁺ current exists in layer 5 intrinsically bursting pyramidal cell dendrites and is instrumental in driving the bursts in simulations of this cell type (Rhodes and Gray, 1994). To address whether dendritic Ca²⁺ current participated in either the initiation or generation of NMDA spikes, it was eliminated in the simulation, here done in 1 mm [Mg²⁺], and a suprathreshold input (applied at the location shown in the inset, with a synaptic conductance of 1 nS AMPA and 4 nS NMDA to each of two adjacent 23 μm compartments) was applied, in 1 mm [Mg²⁺]. The level of dendritic high-threshold Ca conductance was then systematically varied. Although the NMDA spike could be produced at any level of dendritic Ca²⁺ current, consistent with an experimental report in vitro (Schiller et al., 2000), in simulations Ca²⁺ current did contribute importantly to the amplitude and width of the NMDA spike events. Interestingly, at low levels of gCa density, the NMDA spike lengthened because of the reduced effect of Ca²⁺-gated K⁺ currents. It is concluded that Ca²⁺ contributes importantly to driving NMDA spikes and that Ca²⁺-gated K⁺ currents can also shape their duration. c, The NMDA spike is much more sensitive to NMDA conductance magnitude. The comparative sensitivity of NMDA spikes to NMDA conductance was examined by varying that parameter while both the dendritic Na⁺ and Ca²⁺ conductance levels were at the highest levels used in a and b. The NMDA spike was not produced below a minimum level of NMDA conductance, regardless of the presence of dendritic Na⁺ and Ca²⁺ sufficient to make the branch highly intrinsically excitable, illustrating the predominant role of NMDA current in these events, even within intrinsically excitable dendrites. d, NMDA spikes in more proximal branches show similarly limited involvement of dendritic Na⁺ channels. The role of Na⁺ current in the generation of the NMDA spike was examined in a proximal branch in the same manner as in a. Here a larger synaptic conductance was necessary because of the lower input impedance of the proximal branch, and the amplitude of the somatic EPSP was much greater. Despite these differences, here again the elimination of Na⁺ currents curtailed neither the amplitude nor the duration of the NMDA spike, further supporting the conclusion that although Na⁺ currents may reduce the threshold synaptic amplitude that is required (data not shown), they play a minor role in the generation of NMDA spikes.

Dendritic high-threshold Ca²⁺ channels amplify NMDA spike amplitude but are not required for NMDA spike generation

A different picture emerged with respect to the role of dendritic high-threshold Ca²⁺ current. Consistent with the findings reported in vitro in the presence of TTX and Cd²⁺ (Schiller et al., 2000), NMDA spikes could still be produced in the simulation when both Na⁺ and Ca²⁺ currents were turned off (data not shown). To systematically assess the effect of the density of dendritic Ca²⁺ conductance, a stereotyped suprathreshold NMDA spike stimulus was applied, and dendritic gCa density varied over a wide range (Fig. 6b). As dendritic gCa went from 8 mS/cm² (a level enabling the simulated cell to generate intrinsically bursting spike output) to 4 mS/cm² (a level at which the model cell produced regular spiking output; data not shown), there was a decline in the duration for which peak NMDA spike amplitude was sustained; however, at lower levels of dendritic gCa, the duration of the NMDA spike extended, implying a role for K_Ca currents in terminating the dendritic event (Cai et al., 2004). Thus, although the simulations were consistent with the in vitro observation that NMDA spikes do not require dendritic Ca²⁺ currents (Schiller et al., 2000), they also indicate that dendritic Ca²⁺ current participates importantly in driving, and via Ca²⁺-gated K⁺ channels in terminating, the NMDA spike; however, although dendritic Ca²⁺ current plays a role in the simulated NMDA spike, a comparison of the relative sensitivity of the event with NMDA conductance (Fig. 6c) demonstrated that in the simulations, as in vitro (Schiller et al., 2000), these events were most sensitive to NMDA conductance.

The conclusion that dendritic high-threshold Ca²⁺ currents are an important component of the NMDA spike differs from those reached in the simulations reported in Schiller et al. (2000), who concluded that NMDA current is the predominant charge carrier. The model cell used in the simulations reported in that study, however, incorporated a very low dendritic high-threshold Ca²⁺ conductance density (0.02 mS/cm²), far below the dendritic Ca²⁺ conductance (6–8 mS/cm²) required to produce intrinsically bursting characteristics in the simulated layer 5 cell (Rhodes and Gray, 1994). It is therefore likely that those simulations may underestimate the role of dendritic Ca²⁺ (and Ca²⁺-gated K⁺) current in shaping NMDA spikes.

Sensitive control of NMDA spikes by dendritic inhibition

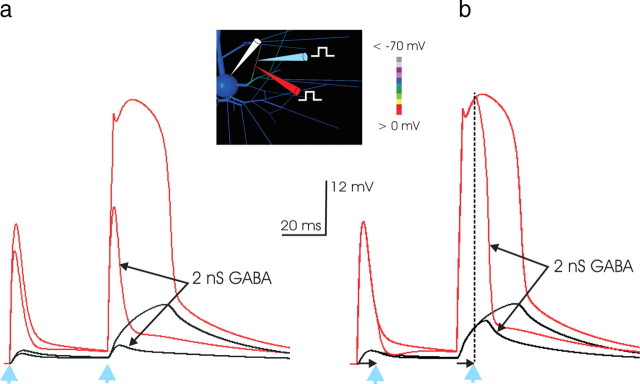
What is the effect of dendritic inhibition on an NMDA spike? The ideal in vitro experiment (e.g., focal application of inhibitory input coincident with superthreshold excitatory input under conditions wherein the inputs may be controlled separately) has not yet been conducted. In the simulation, this question was first addressed by application of an inhibitory conductance with GABA_A-type kinetics colocalized with focal excitatory input. The results revealed extremely sensitive control of NMDA events by colocalized inhibition, reminiscent of that reported for the control of dendritic Ca²⁺ spikes in vitro (Miles et al., 1996; Tsubokawa and Ross, 1996; Kamondi et al., 1998). Even when the synaptic conductance driving the NMDA event was much larger, and with substantial densities of depolarizing Na⁺ and Ca²⁺ currents in the dendritic membrane, a much smaller (in some cases exceeding 20-fold) inhibitory conductance could completely prevent the NMDA spike (Fig. 7a). In the example shown, a 2 nS inhibitory conductance, plausibly produced by just one or two inhibitory synapses, could veto an NMDA spike driven by 50 nS of NMDA current along with depolarizing membrane currents. Moreover, the NMDA event was not a powerful regenerative entity that, once initiated, could not be stopped. Inhibitory input arriving 10 ms after the initiation of the NMDA spike, in the middle of its time course, abruptly terminated the event, with the somatic EPSP following suit with a short time lag (Fig. 7b). Thus, the simulations find that NMDA spikes are extraordinarily vulnerable to dendritic inhibition, suggesting implications for the interplay of specific spatiotemporal patterns of dendritic excitation and inhibition in neocortical circuitry.

Figure 7.

a, Dendritic inhibition powerfully and precisely curtails NMDA spikes. To examine the effect of inhibitory input, a small amount (2 nS in this example) of inhibitory conductance was applied to the same dendritic segment; its location is shown in the inset. Here a large excitatory stimulus (50 nS NMDA and 5 nS AMPA; in 2 mm [Mg²⁺]) was used that, unchecked by inhibition, produced a large dendritic event and a 12 mV somatic EPSP. Remarkably, the 25-fold smaller inhibitory input prevented the NMDA spike from occurring. Thus, these simulations indicate that a small amount of appropriately located inhibitory input is capable of vetoing NMDA spikes when applied with branch-specific precision. The location of the inhibitory and excitatory stimulation is indicated by the blue and red pipettes, respectively. In this and Figure 8, the time of onset of the two inhibitory stimuli is indicated by the blue arrowheads below the time axis. b, Inhibition is effective even after the NMDA spike is underway. A 2 nS inhibitory conductance is applied to the same segment receiving 50 nS NMDA input, but in this case it arrives 10 ms after the arrival of excitatory input (time indicated by vertical dashed line). Although the dendritic spike is fully developed at this time, the small inhibitory input abruptly quenches the unfolding dendritic NMDA spike, and as a consequence it greatly curtails the somatic EPSP. The decrease in the somatic EPSP begins a few milliseconds after the inhibitory input arrives and corresponds to the rapidity of the decrement of the event in the basal dendrites. Thus, inhibition colocated to the same segment as the excitatory input can abruptly quench an NMDA spike, even after it is under way.

Dendritic inhibition is much more effective than somatic inhibition in controlling NMDA spikes and their effect at the soma

Synaptic inhibition targets both somata and dendrites of pyramidal cells and often issues from target-specific interneurons. It is therefore of interest to compare the effectiveness of somatic versus dendritic inhibition in controlling the effect of NMDA spikes. To do so, synaptic excitation sufficient to trigger an NMDA spike was applied to a tertiary basal branch, and a fixed quantity of inhibitory conductance was applied either to the soma or to the dendritic branch receiving excitatory input. A 2 nS dendritic GABAergic conductance in the dendrite suppressed the dendritic NMDA spike completely, so that a dendritic EPSP resembling a passive AMPA-only current was produced (Fig. 8). Although dendritic inhibition concurrent with and after excitation was found to be very effective previously, here the efficacy of dendritic inhibition was still evident with inhibition applied 15 ms before the excitatory input, demonstrating a window in time preceding excitation during which dendritic inhibition is effective (Fig. 9).

In contrast to the effectiveness of dendritic inhibition, even a fivefold greater inhibitory conductance applied to the soma had a negligible effect on the dendritic profile of the NMDA spike (Fig. 8, left, top panel). The results indicate that somatic inhibition does not affect the dendritic NMDA spike event. Thus, production of NMDA spikes in the dendrites is largely isolated from the effect of the somatic inhibition common in cortical circuits.

Targeted dendritic inhibition is more effective than somatic inhibition in controlling the somatic EPSP

The preceding observations addressed the dendritic EPSP, without reference to the net resulting somatic voltage excursion. It is generally believed that somatic inhibition is so-targeted to maximize the effectiveness of inhibitory input in offsetting the effect of excitation in the summation of inputs that is supposed to take place in neurons. Thus, it might have been that although it does not affect the generation of a dendritic NMDA spike, somatic inhibition can nevertheless effectively suppress the resulting somatic EPSP and therefore the effect of the dendritic event. To examine this proposition, an identical amount of inhibitory conductance was applied either to the soma or alternatively to the dendritic locus of synaptic excitation, and the resulting somatic EPSP was compared. With no inhibition, the excitatory input produced an NMDA spike and a 2.3 mV somatic EPSP. With direct somatic inhibition of 2 nS, the dendritic excitation triggered a dendritic NMDA spike (Fig. 8a, left), and a 1.9 mV somatic EPSP was produced (Fig. 8b); however, when the same inhibitory conductance was instead targeted to the branch receiving input, the NMDA spike was quenched, a dendritic EPSP resembling an AMPA event was produced (Fig. 8a, right), and only a 0.4 mV somatic EPSP resulted. The result indicates that targeted dendritic inhibition can be much more effective than somatic inhibition in suppressing the efficacy of excitatory synaptic input.

A 30–35 ms time window primarily before excitation within which dendritic inhibition quenches NMDA spikes

The previous results showed that temporally and spatially coincident inhibition quenches NMDA spikes and suggested that inhibition arriving both 15 ms before and 10 ms after the excitatory stimulus could be effective as well. Inhibition arriving before excitation suppressed an NMDA spike, whereas inhibition arriving after excitation abruptly quenched a spike that was already unfolding. How far this window in time extends, both forward and backward, has considerable implications for the interplay between targeted dendritic inhibition and dendritic spikes during the operation of cortical circuitry. To more fully characterize the window in time within which inhibition was effective, the relative latency of the excitatory and inhibitory input, here arriving in adjacent 23 μm compartments in the middle of a basal end segment (Fig. 9a, inset), was varied across a 60 ms window of time. A superthreshold excitatory conductance was applied to a segment of a tertiary basal branch, and 2 nS of colocalized inhibitory conductance was applied over a range of latencies up to 30 ms before and after the excitation (Fig. 9a). With a GABA_A-type conductance in the form of an α function (α = 5 ms), inhibition arriving 20–25 ms before excitation was effective in blocking NMDA spike generation (although with these kinetics, the inhibitory conductance had declined to 20% of its peak after 20 ms). Thus, the results suggested that that temporal coincidence is not a requirement for inhibition to be effective, but rather that there exists an asymmetric window in time weighted before but extending a short while after the arrival of excitation during which inhibition suppresses NMDA spikes.

Variation in the effectiveness of inhibitory dendritic input with position along the excited branch

The results presented so far assume that dendritic inhibition is colocalized with excitation. Thus, in Figures 7 and 8, both excitatory and inhibitory conductances were applied to abutting (or the same) 23 μm subcompartments in a 170-μm-long end-segment in the basal arbor. If such spatial colocalization is required for dendritic inhibition to be effective, then just a very specific set of distinct inhibitory fibers will be capable of interaction with NMDA spikes activated by a specific set of afferent fibers. To examine this issue, excitation was applied to a 23 μm compartment situated near the midpoint of a tertiary dendritic basal branch, and the relative location of an inhibitory conductance was varied, as was the relative latency of arrival of inhibition and excitation. When located in the subsegment abutting the excitation, either proximal or distal to the site of excitatory input, the effect of inhibition was indistinguishable from that when inhibition was colocalized to the compartment receiving excitation (data not shown), which suggests that inhibition and excitation readily interact across 25–30 μm in the narrow (0.7 μm diameter) dendritic terminal segment.

When inhibition was moved more proximal to the site of excitation but was still within the tertiary branch receiving input, however, its effect diminished precipitously (Fig. 9b, top). Although inhibitory conductance positioned at branch bifurcation points has been considered strategically situated to block the excitatory effect of synaptic input by shunting the passive spread of charge (Rall, 1964), the branch nexus does not prove to be the most effective location for inhibitory conductance to control dendritic NMDA spikes. This was the case for all relative latencies examined (compare Fig. 9b, top); of course, inhibition applied to a sister dendritic branch or to a more distantly separated area of the dendrite would have considerably less impact on the NMDA spike.

In contrast, application of inhibition to the distal tip of the segment receiving input was remarkably effective in quenching the NMDA spike (Fig. 9b, bottom). This effectiveness occurred even when the intrinsic membrane conductances in the branch were turned off (result not shown), suggesting that the effectiveness of inhibition at the tip is a feature of the electrotonic geometry of the tertiary segment rather than related to an interaction with the active conductances present in the dendritic membrane.

The efficacy of spatially focal excitatory input is highly amplified by NMDA spikes

The somatic EPSP associated with NMDA spikes in single basal branches ranged from ∼2 to 10 mV in the examples above (compare Figs. 3, 4), with its magnitude increasing with the proximity of the excited branch to the soma. In all cases, the somatic EPSP associated with an NMDA spike was both larger in amplitude and longer in duration than that produced by a just subthreshold input (compare Fig. 3a), indicating that the regenerative NMDA current amplifies the somatic signal associated with a given synaptic input. To demonstrate the impact of this amplification in the generation of spike output, the efficacy of a set of 10 identical synaptic inputs was compared when distributed in two alternative patterns: in the first, each synapse arrived at a distinct tertiary branch (the distributed case), whereas in the second, the 10 synapses were grouped into 5 pairs of 2, with the inputs in each pair spaced ∼25 μm apart (the paired case). In both cases, the synaptic locations (Fig. 10, left panel) were all approximately equally proximate to the soma, and the synapses were activated by a pair of pulses with a 20 ms interspike interval.

The size of the first somatic EPSP produced by the barrage of 10 synapses was slightly larger in the distributed case, reflecting the observation (Rall, 1964) that in a passive dendritic tree, driving force saturation favors the efficacy of distributed inputs. This also confirmed that the arrangement of input locations in the paired case did not inherently favor its efficacy; however, with the arrival of the second input, three of the five segments activated by the paired input produced NMDA spikes. The outcome was a much more powerful activation of the simulated cell that promptly resulted in the production of a burst of output. In contrast, in the distributed case, the second input produced an EPSP no bigger than the first, and the neuron did not fire. This marked discrepancy in input–output efficacy between the two spatial patterns of input occurred even though the NMDA content of each synapse in the distributed and paired cases was identical. Thus, under input conditions suitable for the production of NMDA spikes, spatial pairing transforms synaptic events that are shaped primarily by AMPA current into dendritic spikes dominated by NMDA current that are much larger and of longer duration, resulting in more powerful neuronal drive.

Discussion

Summary

In this paper, simulations of NMDA spikes (Schiller et al., 2000) were developed in a compartment model of a layer 5 pyramidal cell. In the simulations, as in vitro, NMDA spikes were associated with branch-localized regenerative depolarizations that do not propagate but rather passively drive their dendritic neighborhood and the soma and then collapse abruptly. These events were primarily driven by NMDA current, notwithstanding the presence of considerable Na⁺ and Ca²⁺ conductance density in the simulated dendrites, and as such have the distinction of being a synaptically driven dendritic spike, thereby linking a specific pattern of synaptic input to the occurrence of a sustained branch-limited depolarization. In addition to providing a means for clustered input to more powerfully drive the target cell (Schiller and Schiller, 2001), this mechanism affords the possibility of a direct association between the joint arrival of a set of inputs on a tertiary branch and cellular events gated by a sustained dendritic depolarization, such as induction of synaptic plasticity.

The simulations were used to estimate the minimum amount of NMDA conductance required to drive these events, and they showed ∼6–8 nS (in 1 mm [Mg²⁺]) was adequate when input was confined to a 30 μm subsegement of a tertiary branch, with implications further analyzed below. It was demonstrated that the production of NMDA spikes amplifies the efficacy of a given set of inputs when organized into subsets targeting distinct tertiary branches (Mel, 1992; Schiller and Schiller, 2001), which enabled a read-out of specific subsets of available coactive afferent fibers, a mechanism well suited to the self-organization of higher-order features. Finally, the simulations revealed that a disproportionately small, local inhibitory conductance can veto an NMDA spike if it arrives within 20–25 ms before excitation or can quench it 5–10 ms after initiation, indicating that dendritic inhibition gates NMDA spikes on a branch-specific level.

Simulation of NMDA spikes required an NMDA/AMPA ratio of >1

How many spines are activated by focal stimulation, and what is the consequent NMDA conductance per spine implied by the above results? The density of spines on the basal branches of layer 5 pyramids [2 per micrometer length per micrometer diameter; P28 rat (Larkman, 1991)] suggests that ∼40 spines exist on a typical (0.7 μm diameter) 30 μm subsegment. Optical imaging at single spine resolution suggests that a minority of these synapses are contacted by axons activated by a single focal stimulating electrode (T. Oertner, personal communication), and paired recording experiments in cortex indicate a release probability at excitatory synapses of <50% (Thomson, 2003). Together these observations imply that focal stimulation activates 5–10 spines at most, which together must furnish the 8 nS synaptic NMDA conductance driving a threshold NMDA spike, suggesting a minimum average NMDA conductance of 0.8–1.6 nS per spine; however, published miniature EPSC measurements suggest several-fold lower NMDA conductance at single release sites (Myme et al., 2003). How then can such a small number of spines contribute the NMDA conductance that the simulations indicate is required to drive the NMDA spike?

A related paradox is presented by the large second–first EPSP amplitude ratio observed in vitro (Polsky et al., 2004) in response to paired-pulse stimulation (compare Fig. 3). Extensive simulations with varying synaptic AMPA/NMDA peak conductance ratios (compare Fig. 5b) suggested that the observed paired-pulse amplitude ratio was inconsistent with the hypothesis that AMPA current is the major contributor to the synaptic current that is evoked. The alternative possibility that the second EPSP is largely driven by membrane (rather than synaptic) currents is made implausible by the experiments (Schiller et al., 2000) eliciting these events in bath containing both TTX and Cd²⁺.

Both of the foregoing paradoxes may be parsimoniously resolved by the conjecture that the excitatory synapses onto pyramidal cells in rat cortex, at least to the age (P35) through which NMDA spikes have been reported, consist of two populations: one is AMPA dominated and therefore more accessible to experimental observation, and the other is NMDA dominated and silent, like those reported in juvenile hippocampal pyramidal cells (Isaac et al., 1995; Liao et al., 1995). The requirement that the average NMDA conductance among the synapses activated by focal stimulation is no less than 0.8 nS, along with the small (<0.5 nS) NMDA conductance that is conventionally observed, suggests that the subpopulation of silent synapses must have an average NMDA conductance exceeding 1 nS and perhaps far more if the silent synapses comprise a small minority of the synapses that are activated.

These hypotheses ostensibly conflict with published reports finding that silent synapses are present in early postnatal rat cortex but are greatly diminished by P14 (Rumpel et al., 1998); however, many experiments measuring synaptic currents using minimal stimulation or connected pairs inherently self-select connections that are mediated by AMPA current and so may undersample silent synapses. It is tempting to speculate that the hypothesized silent synapses correspond to a recently characterized transient population of spines that have been reported to be prevalent in rat cortex in the first month or two of postnatal life (Grutzendler et al., 2002; Trachtenberg et al., 2002). These spines, which rapidly form and withdraw, might be dominated by a very large NMDA conductance until the occurrence of events associated with their stabilization.

It should be noted that if a large NMDA conductance in silent synapses is to be consistent with the smaller NMDA conductance found in the AMPA-containing synapses observed using conventional methods, then a mechanism must exist to remove NMDA receptors on the “AMPA-fication” of the silent synapses. Although an AMPA-fication-triggered reduction in NMDA in silent synapses has not yet been observed, it should be straightforwardly possible to elicit long-term potentiation in a silent synapse with standard methods and then to monitor the NMDA component over a long period of time to examine whether AMPA-fication of silent synapses is accompanied by the predicted eventual reduction of NMDA receptor conductance.

Nonsynaptic NMDA receptors activated by glutamate diffusion present an alternative mechanism for NMDA spike generation

The foregoing analysis assumes that activation of glutamate receptors caused by transmitter release triggered by focal stimulation is restricted to synapses; however, it is also possible that such stimulation induces glutamate diffusion outside the synapse, so-called “spillover,” so that synaptically released glutamate also activates nonsynaptic receptors in the neighborhood of the stimulated synapses. If this occurs, then the fast desensitization of AMPA receptors (Colquhoun et al., 1992) would enhance the comparative preference with which NMDA receptors are activated by glutamate diffusing out of the cleft. Thus, extrasynaptic NMDA receptors, either in conjunction with or in place of silent synapses, may provide an alternative mechanism underlying the generation of NMDA spikes, and it will remain for subsequent experiments to assess this possibility.

Long-lasting branch-specific inhibition of NMDA spikes

The simulation results indicated that NMDA spikes are exquisitely sensitive to inhibition, such that merely 2 nS of targeted inhibitory input, conceivably from a small handful of terminals, can readily veto an NMDA spike driven by a >10-fold greater excitatory conductance. Thus, interneurons are capable of very precisely and selectively blocking these events and their consequences. The long (35 ms) time window within which targeted dendritic inhibition can suppress or quench an NMDA spike suggests, at least in the absence of the synaptic background of the in vivo state not addressed in this simulation, that tight temporal arrival precision is not required for dendritic inhibition to be effective. Moreover, the results suggest that GABA_B-mediated dendritic inhibition, which is longer lasting than the GABA_A-type inhibition modeled above (Thomson and Destexhe, 1999), could prevent a branch from being capable of sustaining an NMDA spike for a long period of time. The intriguing possible role for dendritic GABA_B inhibition in determining which branches are able to generate NMDA spikes invites further study, both in experiments and in simulation.

Implications of NMDA spikes for the specification of cortical circuit connectivity

The present results, if confirmed by direct experiments, have a number of computational implications. Perhaps the most compelling is the possibility that NMDA spikes are integrally involved in the “wiring-up” process during which, in prenatal and early postnatal life, internal and sensory signals afferent to the cortex participate in sculpting specific synaptic connectivity in cortical and thalamocortical circuits. Thus, when a set of axons converge in close proximity on a dendritic branch within a suitable window in time and trigger an NMDA spike in that branch, the powerful branch-limited depolarization and Ca²⁺ influx associated with the NMDA spike (compare Fig. 3) could drive the induction of synapse strengthening and stabilization at those coactive synapses; of course, this mechanism would strongly favor the strengthening of sets of afferent fibers that converge in close proximity on a single branch. Coordinated control of this branch event via appropriately targeted and timed inhibition could be a feature that self-organizes in concert with the excitatory connectivity, although the experimental basis for such a process remains to be established. Whether NMDA spikes play such a conjectured role in circuit specification is an inviting topic for further study, as is an examination of the age dependency of NMDA spikes themselves. Are the events limited to a transient early plastic era in synapse formation, perhaps associated with a profusion of silent synapses highly enriched in NMDA conductance? Do the specific connectivity patterns established during the early period of sensory experience then stabilize and remain throughout adulthood? Alternatively, are NMDA spikes also produced in adulthood, and are they therefore also playing a role in adult learning and sensory encoding? It remains for future experimental work to reject or confirm these possibilities. Then, if appropriate, simulations and experiments can proceed in tandem to explore the consequences for cortical circuit formation and function.