A Model of Biological Motion Perception from Configural Form Cues

Abstract

Biological motion perception is the compelling ability of the visual system to perceive complex human movements effortlessly and within a fraction of a second. Recent neuroimaging and neurophysiological studies have revealed that the visual perception of biological motion activates a widespread network of brain areas. The superior temporal sulcus has a crucial role within this network. The roles of other areas are less clear. We present a computational model based on neurally plausible assumptions to elucidate the contributions of motion and form signals to biological motion perception and the computations in the underlying brain network. The model simulates receptive fields for images of the static human body, as found by neuroimaging studies, and temporally integrates their responses by leaky integrator neurons. The model reveals a high correlation to data obtained by neurophysiological, neuroimaging, and psychophysical studies.

Introduction

The visual motion generated by human actors is complex because the body comprises many degrees of freedom. Despite the complexity and diversity of the visual stimulus, humans can easily recognize the movements and gestures of others.

Many studies that investigated the perception of human movement used point-light walker stimuli (Johansson, 1973). These stimuli consist of 12 point lights that are attached to the joints of an otherwise invisible human body. Point-light walkers allow to investigate the impact of the different features of a walking human figure. Generally, these features can be divided in local and global features of motion and form and the dynamics of global motion and form.

Global motion can theoretically be derived from a suitable integration of local motion signals of the trajectories of the point lights over time (Webb and Aggarwal, 1982; Hoffman and Flinchbaugh, 1982; Giese and Poggio, 2003). Alternatively, the visual system may analyze the global form that is sparsely available in the stimulus at each point in time. Although this information is insufficient to recognize a walker from a single frame (Johansson, 1973), temporal integration of the sparse form information may allow the identification of a walker (Chen and Lee, 1992; Beintema and Lappe, 2002; Beintema et al., 2006).

The superior temporal sulcus (STS) has often been implied in the perception of biological motion (Bonda et al., 1996; Oram and Perrett, 1996; Puce et al., 1998; Grossman et al., 2000; Vaina et al., 2001; Beauchamp et al., 2002; Santi et al., 2003; Thompson et al., 2005). Because it receives input from form and motion areas, it is in a prime location to integrate form and motion processing (Oram and Perrett, 1996; Vaina et al., 2001; Beauchamp et al., 2002). The role of other brain areas is less clear.

Some studies found selective activation of the middle temporal gyrus (MT) (Vaina et al., 2001; Ptito et al., 2003) and the kinetic occipital area (KO) (Vaina et al., 2001; Santi et al., 2003), which are believed to process local motion signals. Other studies reported activation of these areas not different from a “scrambled walker” control stimulus, which presented dots with identical motion signals but randomized spatial arrangement that did not depict a human figure (Grossman et al., 2000; Downing et al., 2001). The extrastriate body area (EBA) is activated by static images of the human body (Downing et al., 2001). EBA is also stronger activated by point-light walkers than by a scrambled control stimulus (Downing et al., 2001; Grossman and Blake, 2002). Thus, although the role of the STS in biological motion recognition is undisputed, the contribution of signals feeding into the STS is currently not clear.

We are particularly interested in the possible contribution of form processing to biological motion recognition and present a model for its perception. The model is based on global, configural form information only and uses neurally plausible assumptions. We compared the performance of the model with data from functional magnetic resonance imaging (fMRI), neurophysiological, and psychophysical studies. The results demonstrate that perception of biological motion, even from point-light walkers, can be achieved by the analysis of global form recognition over time.

Materials and Methods

The model

Background and motivation.

Classical point-light walkers were introduced by Johansson (1973) and comprise 12 point lights attached to the joints of an otherwise invisible human body. Point-light stimuli limit information about the walker’s body structure. The visible points provide information about the joint positions, but the connections between them are absent. A single static picture of a point-light walker is insufficient to induce the percept of a human figure in naive observers (Johansson, 1973). When the stimulus is in motion, the individual dots provide fully correct motion signals. Therefore, many studies have concluded that biological motion perception is derived from local motion signals. For instance, Mather et al. (1992) presented a point-light walker embedded in randomly moving noise dots. Subjects viewed the stimulus frames that alternated with a mask consisting of blank frames. The duration of the mask was varied (60–100 ms). Direction discrimination in noise was not possible if stimulus frames and blank interstimulus frames alternated. Mather et al. concluded that local motion detectors that are disturbed by the blank frames are essential to recognize biological motion. Neri et al. (1998) argued in a similar way. They used biological motion or simple translatory motion as a stimulus and asked subjects to detect the stimulus in noise. The results showed no differences for detection of the two stimuli. Both revealed a linear increase of threshold for increasing stimulus dots. Performance threshold for discriminating the walking direction of a biological motion stimulus in noise, however, increased nonlinearly with the number of stimulus dots. Neri et al. (1998) concluded from the first experiment that the common information of the two stimuli (that is motion) is the driving force for biological motion perception. These biological motion filters are flexibly adapted to the stimulus, as reflected in the nonlinearity revealed by the second experiment. Early computational considerations also focused on local motion signals. Johansson (1973) and Cutting (1981) hierarchically reconstructed the human figure from common pendular movements of neighboring dots. The recent computational model of Giese and Poggio (2003) integrates local motion signals and local form signals in independent processing pathways to reconstructed templates of human motion. Only the motion processing pathway of this model was able to reconstruct a human body from point-light walkers.

The reliance on local motion signals is called into question by some observations in neurological patients. Vaina et al. (1990) studied a patient with bilateral lesions including area MT. This patient had severe difficulties in low-level motion integration tasks but no problems identifying biological motion displays. McLeod et al. (1996) reported that patient LM, who lacked all motion perception after a stroke (Zihl et al., 1983), was able to recognize action from point-light biological motion stimuli. Her ability to see biological motion was lost, however, when the stimulus was embedded in noise. Vaina et al. (2002) described a patient that had difficulties integrating local motion signals into a coherent motion percept or to perceive structure from motion but could recognize point-light biological motion. These three cases demonstrate that biological motion perception is possible even when general motion analysis is impaired.

To study biological motion perception in the absence of local motion signals in healthy observers, Beintema and Lappe (2002) developed point-light walkers in which point lifetime was limited to a single animation frame. In these stimuli, 98% of the local motion information is removed (Beintema et al., 2006), yet naive observes readily recognized a walking human figure from these stimuli. Moreover, when observers had to identify the orientation of the walking figure, the addition of local motion signals by increasing the lifetime of the point lights did not aid performance. Beintema et al. (2006) showed similar results for a different biological motion task, namely the discrimination of forward from backward walking. Also in this task, which clearly involves the global motion direction of the figure, local motion signals did not contribute to task performance. Beintema et al. suggested that biological motion perception here was driven by the analysis of the variation of the form of the figure over time. These results prompted us to develop a model of biological motion perception from global form analysis.

Shiffrar et al. (1997) previously emphasized the importance of global form analysis for interpreting biological motion. They presented stick figures of walking humans seen through apertures. Despite the ambiguous motion signals through the apertures, subjects recognized the human figure easily. Chatterjee et al. (1996) showed that form information in biological motion could override local motion signals. They presented a two-photograph series of human movements and asked subjects to report the apparent motion path. Subjects reported the biomechanically consistent path rather than the shortest path, which would be reported if subjects used only local apparent motion signals.

Bertenthal and Pinto (1994) provided additional evidence for an involvement of global form analysis in biological motion perception. They presented point-light walkers surrounded by noise dots. The motion trajectories of the noise dots were identical to those of the walker dots; only the global spatial configuration was different for walker and noise. Despite the identical motion signals in the noise, subjects could still recognize the walking figure. Bertenthal and Pinto argued that “the perception of structure in a point-light walker does not require the prior detection of individual features or local relations.”

The above studies indicate that form analysis of the human body is involved in biological motion recognition. However, it is also clear that biological motion perception is a special function that goes beyond simple form (or motion) analysis. For instance, findings in patients have shown that biological motion perception can be impaired despite intact motion and form perception. Batelli et al. (2003) studied three patients with lesions in the parietal cortex. Although their ability in low-level motion tasks was normal, they were unable to perceive biological motion. Batelli et al. explained this with deficits in attention allocation. Schenk and Zihl (1997) examined stroke patients with lesions in the parietal cortex. In some patients, the perception of biological motion as an isolated stimulus was possible but became impossible when a segregation from the background was necessary. Another study revealed that patients could have normal object and motion recognition performances without perceiving a form in a biological motion stimulus (Cowey and Vaina, 2000). Vaina and Gross (2004) studied four patients with brain damage caused by strokes. All of them were unable to recognize a walker from a point-light figure. They had normal object recognition rates and only partial motion deficits but were impaired on recognition of objects from degraded incomplete information. These patients had damage to STS and were presumably unable to integrate the given information to a percept of biological motion. The specific impairment of biological motion recognition despite intact from and motion processing argues for a separate integration stage in which signals that support biological motion analysis are integrated to achieve the percept.

Recent fMRI studies provided more insight into the neural correlates of biological motion perception. These studies almost uniformly report activation of STS when subjects viewed biological motion displays (Puce et al., 1998; Grossman et al., 2000; Vaina et al., 2001; Beauchamp et al., 2002; Santi et al., 2003; Peuskens et al., 2005; Thompson et al., 2005). STS gets input from both motion and form processing areas.

fMRI studies reported selective activation of motion-sensitive areas KO and MT (Vaina et al., 2001; Santi et al., 2003; Peuskens et al., 2005), although other studies found that the activation of MT and KO is not specific to biological motion (Grossman et al., 2000; Downing et al., 2001). Grossman et al. (2005) reported that transcranial magnetic stimulation to knock-out MT activity did not influence the perception of biological motion, whereas transcranial magnetic stimulation (TMS) over STS impaired the perception of biological motion. Other studies found selective activation in form areas such as the fusiform gyrus or the occipital face area (OFA) (Vaina et al., 2001; Grossman and Blake, 2002; Michels et al., 2005; Peelen and Downing, 2005). Beauchamp et al. (2003) showed that point-light displays of human actions activate the ventral temporal cortex, although this activation is less strong than for whole-body displays. Michels et al. (2005) used different biological motion stimuli that varied in the amount of available motion and form information. Activation levels in areas sensitive to processing static human form depended strongly on the amount of structural information in the stimuli but not on local motion signals. This suggests that form processing areas are recruited for biological motion perception.

Specific form processing areas and the STS are also driven by static images of the human body (Beauchamp et al., 2002). These activations are increased when motion is added (Beauchamp et al., 2003). The EBA shows selective responses to static pictures of human bodies and of stick figures (Downing et al., 2001). However, the role of EBA in perceiving point-light displays remains unclear. Downing et al. (2001) observed a stronger activation for biological motion displays than for scrambled nonhuman figures with identical motion signals. They attributed this signal increase to the engagement of attention driven by the presence of a body configuration. Also, Grossman and Blake (2002) found that EBA responds stronger to biological motion stimuli than to the scrambled controls. Peelen and Downing (2005) reported significant activation in fusiform face area (FFA) for human bodies shown without a head.

Thompson et al. (2005) presented displays of walking mannequins that were either intact or with the limbs and torso scrambled. Stimuli were either completely visible or partially occluded. Activation in STS was always greater for the intact walkers than for the scrambled walkers regardless of whether parts of the body were occluded or not. Thompson et al. concluded that processing of biological motion in STS is driven by configural processing of the walking stimulus rather than tracking the movement of individual limbs. This provides means to process biological motion even in the case of occlusion.

Outline of the model.

From the above studies, we can, for the purpose of our model, derive three assumptions. First, biological motion may be inferred from form analysis without local motion processing. Second, form analysis in some areas of the ventral stream is selective for the shape of the static human body. Third, biological motion perception is a specialized process that combines the analysis of the global form of the human body with its global motion. Our model follows these assumptions. It uses form sensitivity and processes biological motion in two stages, a static and a dynamic form stage. Leaky integrator neurons of the second stage dynamically integrate the output of neural template cells from the first stage. These template cells are formed by Gaussian response functions that simulated receptive fields for human bodies.

Figure 1shows a schematic overview of the model. We assume a library of upright static template cells of human walkers that are implemented in a view-based template-matching approach. The three-dimensional configuration of a walking human body is represented by a collection of two-dimensional postures. We assume that this view-based approach is invariant to size and position of the perceived object, similar to the properties of neurons in higher areas of the ventral stream (Logothetis et al., 1995; Tanaka, 1996). Alternatively, the model may be made adaptable to the size of the stimuli by a preoperating process that resizes stimuli to the required template size. However, size invariance is not an issue for the present paper because the stimuli were always presented at a constant size.

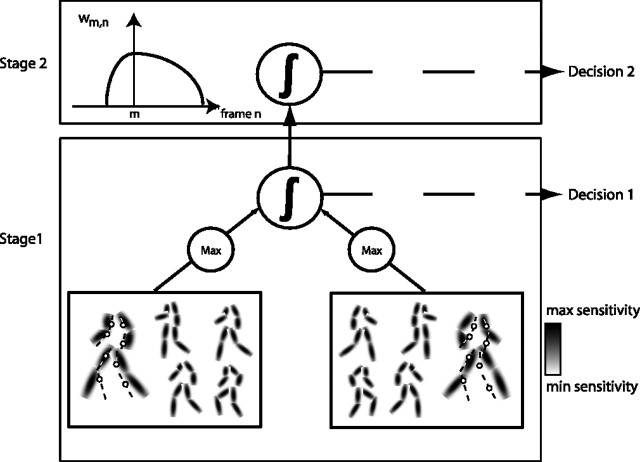
Figure 1.

Illustration of the model. Stage 1 consists of template cells for whole-body postures. Two sets of template cells represent walking to the left and walking to the right, respectively. Each set comprises static postures, with Gaussian response functions indicated by the shaded areas. The dots indicate the stimulus that is compared with the template by each template cell at each time step of stimulation. The dashed lines are only for illustration and not shown in the real stimulus. In each set, a winner-takes-all process selects the cell with maximum output at each time step. From the temporal integration of these maximum responses in the two sets, a decision about stimulus orientation is achieved as a first stage of analysis. This stage of analysis does not consider the temporal order of the stimulus postures. Analysis of temporal order is deferred to stage 2 and provides information for a decision on global motion aspects of the stimulus. This analysis is achieved by weighting the temporal differences between two consecutively selected frames (m,n) by the function w_m,n (inset). This function weights adjacent frames more strongly than frames that are temporally separate. In addition, the function is asymmetric such that it weights frames that are in the preferred direction of the cell more strongly than frames that are in the temporally opposite direction.

We generated the template cells from recordings of the movements of nine human walkers (aged 20–29 years; five males). The individuals walked normally on a catwalk with sensors attached to their major joints (head, shoulders, elbows, wrists, hips, knees, and ankles) while a motion tracking system (MotionStar; Ascension Technology, Burlington, VT) recorded their movements at 95 Hz sampling rate. To reduce noise, we filtered the tracking data by averaging three successive data points of each sensor. If necessary, additional data points of the walking sequence were obtained by interpolation between the filtered recording data. Then, each of the nine walking sequences was divided in temporally equal intervals to obtain a set of 50 sequential body configurations for each walker. The recorded joint positions for each configuration were connected in the anatomically correct way to obtain stick figures of a common walking sequence. These stick figures formed the basis of the body template cells of the model. Each such body template cell is selective for a particular body posture. The cells response to a biological motion stimulus is derived from the total of the responses to the individual stimulus dots. The response to a dot near a particular position on the body is assumed to be maximal if the dot is located on the body and drops off with a Gaussian function of distance of the dot to the nearest point on the body (Fig. 1). Because our study is intended to investigate the contribution of global form, our model treats the body as a global figure without explicitly taking into account local stimulus features (orientation and motion). This is different from previous models, which combine local features hierarchically into a percept of a human body (Johansson, 1973; Cutting, 1978; Giese and Poggio, 2003).

We used two different sets of template cells: one for a walker oriented and moving to the right and one for a walker oriented and moving to the left. Differential activity within those two sets is used for decisions in the discrimination tasks we describe below.

In each set, the nine different walkers redundantly represented each of the 50 static postures for a total of 450 templates.

The model consists of two stages: a first stage for the analysis of the form (posture) of the walker and a second stage for the analysis of the global motion (postural change) of the walker (Fig. 1). Our choice of different stages for these tasks is partly motivated by the above mentioned fMRI studies, which showed different selectivities for static and moving human bodies and, in part, by differences observed between biological motion tasks. For instance, Vaina et al. (2001) showed that identical displays of biological motion might activate different brain regions depending on the task. When the subjects had to discriminate between the shape of the walking pattern and a scrambled control stimulus, different regions were activated than for judging the overall motion direction of the dots. Results of Beintema et al. (2006) also suggested a task-specific analysis of biological motion stimuli. When subjects were asked to identify the direction in which a point-light walker faced (left or right), they mainly used information about the shape of the figure. When asked to discriminate between forward and backward walking point-light figures, subjects used also information about the global motion of the stimulus. These results argue for a task-dependent analysis of a biological motion stimulus as implemented in the different stages of the model.

Stage 1.

At the onset of stimulation, the first stimulus frame is present in stage 1. This frame is compared with the templates of each of the template cells. Each dot of the stimulus frame contributes to the response of the cell weighted by the distance to the nearest part of the body. Each cell sums the responses for all single dots to obtain an overall response measure to this stimulus frame (Eq. 1):

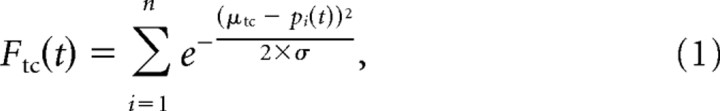where F_tc(t) denotes the output of the template cell tc at the time t. The outputs of the template cells were obtained by weighting the shortest distance between a stimulus dot and a limb of the template with a Gaussian function. p_i gives the position of the stimulus dot I, and μ_tc denotes the limb position in the template cell with the shortest distance to the stimulus dot. σ is the width of the receptive field of the template cells that is defined by the Gaussian weights.

This template-matching procedure is done independently for both sets of template cells. A winner-takes-all mechanism selects the maximum output within each set and feds it into a leaky integrator (Eq. 2). The template-matching procedure is repeated for each stimulus frame independently of the preceding one, and the maximum outputs of both sets are fed into two leaky integrators. The activities u_1,2 of the integrators are computed from

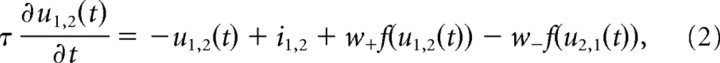where τ = 10 ms, u_1,2 denotes the activities in the decision stage 1 for the two sets of templates, and i_1,2 denotes the bottom-up inputs from both sets of template cells to the decision stage 1 as defined by the maximum outputs of the template cells in Equation 1:

The lateral interaction between the two integrators is given by f(u_1,2(t)), with f a sigmoid function that integrates the state of the two integrators:

with

In Equation 2, lateral interaction is weighted by w₊ and w₋, which denote the weights for lateral excitation and inhibition between the states u_1,2.

The activities u_1,2 provide a decision criterion for a left/right discrimination in stage 1. The maximum activity over the total trial duration of both kinds of template cells is taken for a decision of the model. The excitatory and inhibitory weights w₊ and w₋ are free parameters of the model that will be fixed in a single simulation later (see below, Parameter fits).

Stage 2.

The model in stage 1 does not explicitly consider the temporal order of the stimulus frames. This is implemented in stage 2. We assume that the recognition of one frame influences the expectation of the next frame:

where τ is 10 ms, v_1,2 denotes the activities in the decision stage 2 for the possible responses 1,2, and u is the bottom-up input from stage 1. w_n,m weights the difference between selected frame n and previously selected frame m (Fig. 1). This function should be asymmetric in time because it is intended to generate a preference for one movement direction over the other. We chose

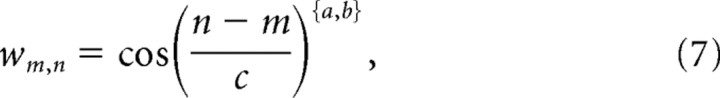with a for n − m ≤ 0, b otherwise.

Experimental methods

We tested the model by comparing its results with neurophysiological, fMRI, and psychophysical data from the literature. In doing so, we adapted the stimulus settings of the corresponding experiments. We conducted additional psychophysical experiments to test model predictions. Here, we used similar experimental settings as described by Beintema and Lappe (2002) and Beintema et al. (2006). In the following, we provide a brief description of the stimulus and the procedure. Additional information can be obtained from those publications.

Tasks

The experiments involved either of two discrimination tasks: a direction task or a forward/backward task. In the direction task, the walker was presented either facing to the left or to the right. The subject had to report the walkers facing orientation. In the forward/backward task, the walker was presented in left or right orientation and either with a normal forward gait or in backward motion, in which case the frames of the walking sequence were displayed in reverse order. The subjects had to report whether the stimulus walked forward or backward.

Stimulus

The stimulus was generated by a computer program and imitated the movements of a walking human (Cutting, 1978). For the model simulations, it is important to realize that the stimulus never exactly matches any of the nine recorded templates of real walkers, because it presumably does not exactly match the motions of a real walker to a human observer. In the original program by Cutting, the human body was depicted by light-points attached to the major joints of an otherwise invisible body. Beintema et al. modified this stimulus such that it consisted of a variable number of points (one to eight), each with a randomly chosen position on the limbs. Each point was relocated to a new randomly chosen position on the limbs after every single frame of the animation sequence. This stimulus allows to study the perceptual mechanisms of biological motion in conditions with near-absent local motion signals, thus focusing on the role of form information. We used this stimulus in the experiments described below. The number of dots present in each stimulus frame (one to eight), the duration of presentation of each stimulus frame (10–200 ms), and the lifetime of each dot (one to eight frames) are parameters that influence the amount of form and global motion present in the stimulus (Beintema and Lappe, 2002; Beintema et al., 2006). The parameters used in each of our experiments are described in the respective section.

Experimental procedure

Stimuli were presented on a monitor with a resolution of 1280 × 1024 pixels and a display size of 30 × 40 cm. The monitor refresh rate was 100 Hz. Unless indicated otherwise, a single stimulus frame was presented for a duration of 50 ms (five monitor frames), and a total trial lasted for 1.6 s, i.e., one walking cycle.

The stimulus covered a field of 5 × 10° and consisted of white dots (5 × 5 pixels) on a black background. Trials were presented in random order, and the stimulus position had a randomly chosen spatial offset to avoid spatial cues.

Four and five subjects (two female) participated in each experiment. They were between 26 and 35 years of age and had normal or corrected-to-normal vision. All subjects were students or members of the department and experienced in psychophysical experiments. Subjects were seated 60 cm in front of the monitor and viewed the stimulus binocularly. Subjects had to indicate their decision in the respective discrimination task by pressing one of two buttons in front of them after the stimulus presentation.

Simulation procedure

We compared the performance of the model with existing data and with data obtained in new experiments. For existing data, we mimicked the stimuli described in the corresponding study. For new psychophysical experiments, we used identical stimuli for model simulations and experimental tasks.

Each simulation run consisted of 150 trials with stimuli with randomly chosen starting phases in the walking cycle. The model computed activation levels for these stimuli in stage 1 [u_1,2(t)] and in stage 2 [v_1,2(t)]. At each model stage, we compared activation levels for both possible decisions (left/right and forward/backward) and used them for the decision in the respective perceptual tasks on a trial-by-trial basis. We then calculated the proportion of correct answers over all trials.

To simulate physiological experiments, we compared the stimulus-induced activity in model stages 1 and 2 with that induced by a respective control. Stimulus-induced activity in each stage was computed as the activity of the maximally active leaky integrator [u₁(t) or u₂(t) in stage 1; v₁(t) or v₂(t) in stage 2] averaged over the duration of the stimulus. This activation of the model cannot be directly compared with activation levels in fMRI experiments, however, because the scaling between the two is not known. We can therefore only compare relative activity differences between conditions. This was done by first normalizing the model activity to the fMRI activity in one condition and then comparing model activation and fMRI activation in the other condition.

Parameter fits

The model stage 1 contains two adjustable parameters, namely the excitatory and inhibitory weights, w₊ and w₋ (Eq. 2). To estimate the values of these parameters, we conducted a psychophysical experiment and fitted the model to the psychophysical data (Fig. 2). The obtained fit was then used for all additional simulations in this study.

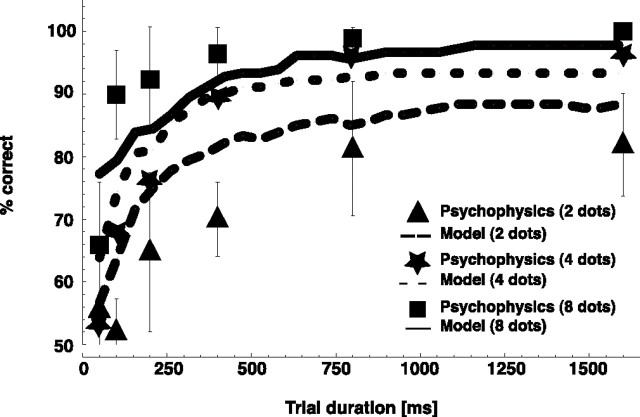
Figure 2.

Psychophysical data used to fix the free parameters of stage 1 and evaluate the optimum fit of the model. Shown are correct responses as a function of total trial duration for two, four, and eight points per stimulus frame in a direction task. Psychophysical data are presented as mean ± SE.

Because model stage 1 is concerned with form analysis, the experiment focused on stimulus properties that influence form information. First, we manipulated the number of dots per stimulus frame (two to eight) to examine the influence of form information per stimulus frame. Second, we varied the form information per trial by varying the stimulus duration (100–1600 ms).

Subjects were asked to report the orientation (left or right) of the walker. The model solved the task by matching the stimulus frames to either template cells for a walker oriented to the right or template cells for a walker oriented to the left. We varied the free parameters so that the model simulations fitted optimally (in terms of least squares) to the psychophysical data for the condition of eight points per frame. The parameters (w₊ = 6.8; w₋ = 4.0) were then fixed for all experiments and simulations reported in this study.

We also tested whether the choice of fit data influenced the model. Fitting results for other conditions with two or four dots per stimulus frame resulted in the same parameter set. Thus, the results do not rely on the kind of fitting or the data we chose for fitting.

Figure 2 displays observer percentage correct and model simulation results for eight, four, and two dots per frame. The observer data for eight points per frame were used to adjust the weights of the model. Data from the four and two dot conditions provide an estimate of how well the parameter fit generalizes. The data reveal a clear relationship between form information and performance of the human observers (Fig. 2). Our form-based model matches these data with high accuracy for all parameters (form per frame/overall form). Although inspection of Figure 2 suggests that for short durations the model does slightly better than the mean of the human observers for two points and slightly worse for eight points per frame, there were no statistically significant differences between model and psychophysical data at any number of points (one-sample t test).

Stage 2 contains three free parameters (a, b, c). These parameters were combined to one adjustable factor (w_m,n), which determines the expected frame order of the model. To estimate the value of this parameter, we used a forward/backward discrimination task with eight dots per stimulus frame and varied the amount of form information by varying the total trial duration between 100 and 1600 ms. Unlike the direction task, the forward/backward task cannot be solved solely by spatial analysis (Beintema et al., 2006). Because the order of the selected frames has to be taken into account, the temporal integration in stage 2 is crucial.

Human subjects were asked to discriminate between a walker moving forward or backward. The model solved the forward/backward task by analyzing, in stage 2, the temporal order of the template cells that were most strongly activated in stage 1 by the sequential stimulus frames. The model used the outputs in stage 2 for an expected forward movement compared with an expected backward movement as the decision criterion to solve the task.

The results from human observers (Fig. 3) were used to fit the free parameter of stage 2 of the model (w_m,n in Eq. 6). This best-fitting weighting function was then used for all simulations reported in this paper.

Figure 3.

Psychophysical data used to fix the free parameter of stage 2 and evaluate the optimum fit of the model. Shown are correct responses as a function of total trial duration for eight points per stimulus frame in a forward/backward task. Psychophysical data are presented as mean ± SE.

Results

Direction task

Beintema and Lappe (2002) and Beintema et al. (2006) asked subjects to discriminate between a walker facing to the right and a walker facing to the left. They manipulated the number of stimulus dots, the duration of each trial, and the amount of motion signals. Recognition rates depended strongly on the available form information but not on motion signals. Furthermore, recognition rates depended on the number of dots per frame (i.e., form information per frame) and on trial duration (i.e., overall form information per trial). However, across all experiments, the recognition rates were constant if the product of trial duration and number of dots was constant, i.e., when the total number of stimulus dots presented during the trial was constant (Beintema et al., 2006). The model is generally consistent with this because its recognition rates critically depended on the number of stimulus dots presented during the trial (compare with Fig. 2). However, the model relies on spatiotemporal integration of form information. This predicts that performance should also depend on the speed with which new information is acquired. Therefore, we conducted an experiment in which we manipulated the information rate of the stimulus by varying the duration each frame was displayed.

Total stimulus duration and walking speed were kept constant. For long frame duration, therefore, the walker remained in one static posture for some time and then changed its posture in a large step to another posture. For short frame durations, the walking sequence was sampled rapidly and appeared smooth. Thus, dynamic sampling of the walking sequence is different for different frame durations as the dynamical change from one displayed posture to the next postures varies.

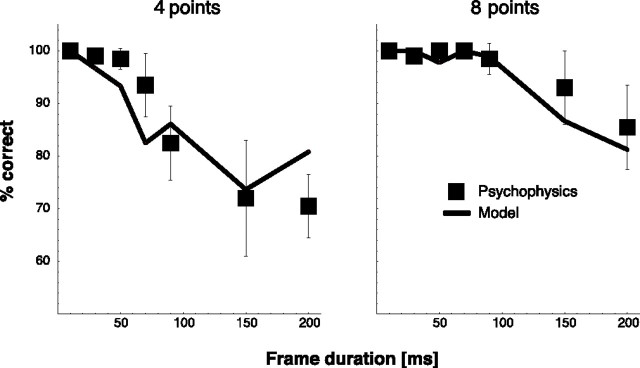
We presented four or eight points per frame and varied frame duration from 10 to 200 ms. Figure 4shows the results for human observers separately for the four dots-per-frame and the eight dots-per-frame condition. Both graphs show a decrease of performance for prolonged frame durations. The decrease is stronger and begins earlier in the four dots-per-frame condition.

Figure 4.

Correct responses as a function of the duration of a single frame for four (left) and eight (right) points per stimulus frame in a direction task. Psychophysical data are presented as mean ± SE.

The model solves the task by matching the stimulus frames to the template cells for walking to the right and to the template cells for walking to the left and integrating the outputs dynamically. For prolonged frame duration, fewer frames are available within the integration time of the leaky integrator. Therefore, the model performance decreases. The decrease of model performance replicates the psychophysical data accurately. For prolonged frame durations, recognition rates drop in a similar way as in the psychophysical data. The model also replicates the stronger and earlier drop of recognition rate for four dots per frame. This supports our hypothesis that form information is integrated over a fixed temporal period. Thus, the results of the direction discrimination task reveal a dependence of recognition rates on form information per frame, form information per trial, and form information per time period.

Forward/backward task

The model simulations and psychophysical results in the direction task provided evidence that the recognition rates depend on form information per time period. The direction task may be performed using only form information (Beintema et al., 2006). The forward/backward discrimination task cannot be solved solely by spatial analysis. In this task, both stimuli (moving forward and moving backward) comprised exactly the same set of frames. In one condition, the frames were presented in forward moving temporal order and, in the other condition, in reversed temporal order. Thus, the temporal properties of the stimulus are crucial.

Beintema et al. investigated the influence of different parameters in this task. We used the same task and compared model predictions for this task with the data from Beintema et al. (2006) and to additional psychophysical experiments reported below. We varied the dynamic behavior in two ways. First, by keeping the total trial duration constant and varying the duration a single frame is presented (variation of frame duration). Second, by manipulating dynamic behavior by varying the walking speed. Here, the number of frames per trial was kept constant and trial duration varied with the duration each frame was presented.

For the first simulation, we adapted psychophysical data of Beintema et al. (2006). A stimulus with eight points per frame was presented, and the duration of a stimulus frame was varied between 30 and 200 ms. Total stimulus duration was kept constant and always contained one full step cycle. Thus, for longer frame durations, the number of frames was reduced and the change of posture between frames was increased to keep the walking speed constant. The task was to discriminate between a walker moving forward and a walker moving backward.

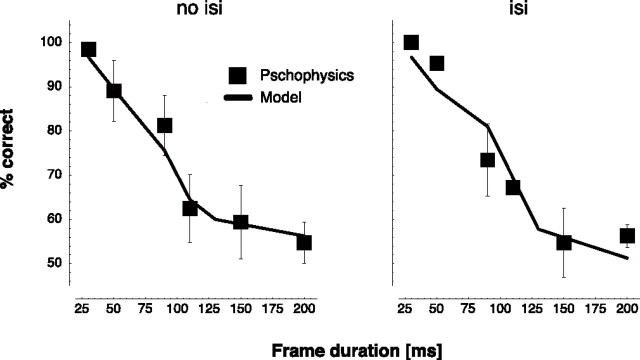
The data are shown in Figure 5(left). For smoother presentations (shorter frame durations), the walking direction was recognized more easily. For longer frame durations, the walking direction was harder to discriminate, at 200 ms frame duration just above chance level. The model showed the same behavior as the human observers in that study.

Figure 5.

Correct responses as a function of frame duration for eight points per stimulus frame in the forward/backward task. Frames are presented for the indicated duration (no isi condition; left) or for 20 ms followed by a blank period for the remainder of the frame duration (isi condition; right). Psychophysical data are presented as mean ± SE. Psychophysical data are adapted from Beintema et al. (2006).

To further rule out a contribution of local motion detectors to the recognition process, Beintema et al. (2006) repeated this experiment with a blank interstimulus interval (isi) between stimulus frames similar to Mather et al. (1992). Each frame was presented for only 20 ms, and the remaining time of the frame duration was filled with a blank frame. The psychophysical data for the isi condition (Fig. 5, right) was not different from that of the no isi condition (Beintema et al., 2006).

We compared the behavior of the model also with these psychophysical data. In principle, the model should be unaffected by the additional blank intervals because it does not rely on local motion signals and thus should not be influenced by the manipulation of local motion signals in the isi condition. However, for the model, there is a difference between the two conditions in the reduced presentation time of stimulus frames in the isi condition. During the blank interval, activation in the template cells drops. The results in Figure 5 (right) show similarity between model and human observers also in the isi condition. In agreement with the psychophysical data, the model showed only negligible differences between the isi and the no isi conditions. These results imply that the forward/backward task can be solved by spatiotemporal analysis of form information. The model simulations fit the psychophysical data in the absence of local motion analysis.

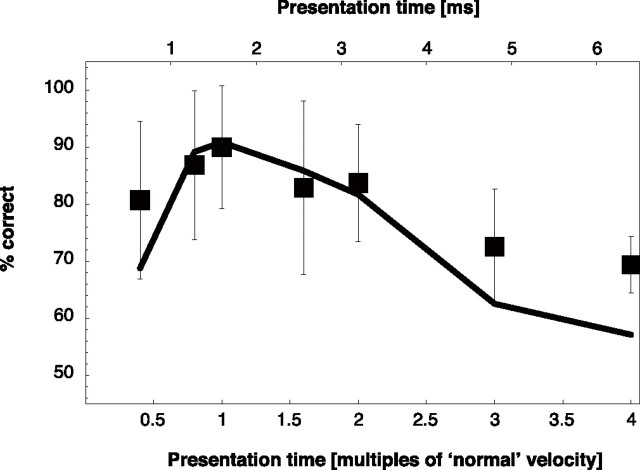
Next, we tested the influence of walking speed on the model behavior and compared the results with psychophysical data in a new experiment. We presented a stimulus with eight points per frame. We kept the number of frames constant (32 frames) and varied the presentation duration of each stimulus frame (20–200 ms). This resulted in slow or fast walking speed. Thus, the overall form information per trial (number of dots per frame × number of frames) was kept constant, but the amount of information within a certain temporal integration period and the total duration of the stimulus varied.

Figure 6shows the results. The human observers reveal a maximum in recognition rate for normal walking speed. Recognition rates decrease for higher and lower walking speeds. This is not unexpected because there is a certain preferred speed associated with a particular walking pattern (Giese and Lappe, 2002). The model simulations also show a decline in performance as the walking speed becomes different from the canonical walking speed. Activation levels of the template cells cannot reach their maximum level if presentation times are short. For long presentation times, the outputs of the template cells will no longer be integrated effectively because of the limited integration period.

Figure 6.

Correct responses as a function of the walker’s velocity for eight points per stimulus frame in the forward/backward task. Psychophysical data are presented as mean ± SE.

Discrimination in noise

So far, we investigated the perception of biological motion with an isolated stimulus. Neri et al. (1998) reported a remarkable efficiency of human observers in the temporal integration of biological motion in noise. They presented a point-light walker with a variable number (one to six) of simultaneously visible dots located on the joints of the walker. The dots kept this joint position for two frames before disappearing and relocating to a new joint location. Therefore, each dot provided useful local motion signals for two frames. The walker was embedded in a random noise mask of dots that changed position in every frame. This stimulus was presented on one side of a fixation dot. The other side displayed the same noise dots plus the number of dots of the walker in random position. Human observers had first to determine in a two-alternative forced-choice task the correct presentation side of the stimulus. After correct detection, they had to discriminate between the walking directions of the stimulus or, in another condition, the coherence of the stimulus. In this coherence task (Mather et al., 1992), the upper and lower parts of the stimulus were shown in either the same (coherent) or opposite (incoherent) direction. Subjects had to decide whether the stimulus was coherent or not. Neri et al. determined noise thresholds for 75% correct recognition rates in the detection and the discrimination task. In agreement with previous results (Barlow, 1997), they found that the relationship between number of stimulus dots and number of noise dots is linear for the detection of the biological motion stimulus. In the case of discriminating walking direction, the relationship was nonlinear, featuring a more rapid increase of performance with increasing number of stimulus dots.

We simulated the discrimination performance of the model for a stimulus surrounded by random dot noise. We adapted the stimulus of Neri et al. (1998) such that one to six dots per frame were presented simultaneously on the major joints of the body. They moved on this position for two frames before they were redrawn on a new joint. For a fixed number of stimulus dots, we varied the number of noise dots within a window of six by 4.5 times the size of the stimulus. Model simulations were run with these stimuli in the direction and coherence tasks.

For the coherence task, the model applied the same steps as in the discrimination task but separately for the upper and lower parts of the body. The templates were, therefore, subdivided into templates for the upper body (arms) and the lower body (legs). This resulted in two final decisions of the model, one for each body part. Comparing these two decisions resulted in the overall decision whether the walker was coherent or incoherent.

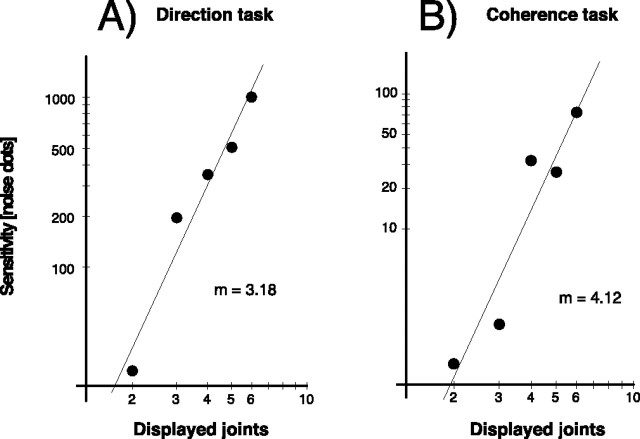
We fitted the levels of correct response to a sigmoid function and determined the threshold for 75% correct responses. These values were plotted in a log–log diagram, and slopes of linear regression were determined analogously to Neri et al. (Fig. 7). The results reveal a slope steeper than 1, consistent with the human data. The slope for discrimination of the walking direction is 3.18. This is in the range of the two subjects in the study by Neri et al., which had slopes of 2.55 and 4.23. In accordance with Neri et al., the slope in the coherence task was even steeper (4.12). This is similar to the value Neri et al. obtained from one subject (4.48). We conclude that the template-matching approach is able to reproduce the spatial integration properties for discrimination in noise.

Figure 7.

Point-light walkers were presented embedded in a variable number of noise dots. The figure shows the thresholds of the model for 75% correct discrimination between the walker’s directions as a function of the number of points per stimulus frame. The results are shown for the direction (A) and coherence (B) tasks (for details on this task, see Results). m denotes the slope of the linear regression of the data.

A similar conclusion was reached by Lee and Wong (2004), who proposed a template-matching algorithm based on the distance of dots to the joints, not the body segments. The neurally plausible approach of our model is able to replicate the psychophysical data also quantitatively. Cutting et al. (1988) investigated the efficiency of various noise masks on the perception of point-light displays. Detection rates decreased if stimulus dots and noise dots revealed identical motion trajectories. Cutting et al. proposed that the observer’s performance included at least two parts: a “filtering task that ignored ∼ of the display area” and a second “organizational task.” Bertenthal and Pinto (1994) showed that, even in noise dots with motion trajectories identical to the motion trajectories of the stimulus dots, the global structure of the stimulus is preserved. These results indicate that segmentation and solving the task do not necessarily rely on the same information. Neri et al. (1998) showed that detection threshold increased with local motion information. Our model showed that the recognition process can be explained by global form analysis.

In agreement with Cutting et al. (1988), we, therefore, suggest that perception of biological motion in noise comprises a preoperating segmentation process and a recognition process fulfilled by template matching. The segmentation process may be supported by form cues if the density of the stimulus dots is higher than the density of the noise dots. Also, motion signals may help to segment the stimulus from the background even when they are not needed for the recognition process itself (Beintema and Lappe, 2002). Our model assumes a first stage that extracts form. It may be supplemented by a preprocessing stage that uses motion cues for segmentation, but, importantly, the motion cues themselves are not passed to the first stage of the model.

Neuronal activities

Studies in humans and nonhuman primates suggest a specialized network for the visual perception of biological motion. This network comprises areas of the visual system (Bonda et al., 1996; Oram and Perrett, 1996; Puce et al., 1998; Grossman et al., 2000; Vaina et al., 2001; Beauchamp et al., 2002; Santi et al., 2003; Thompson et al., 2005) and the mirror-neuron system (Buccino et al., 2001; Saygin et al., 2004; Sakreida et al., 2005). The interrelations between these areas and the specific role of each area are not fully understood. Electrophysiological studies in nonhuman primates have found neurons in the superior temporal polysensory area (STP) selective for biological motion (Oram and Perrett, 1994; Oram and Perrett, 1996). In humans, the presumably homolog of monkey area STP, the STS, has been linked to biological motion in positron emission tomography studies (Bonda et al., 1996) and in fMRI studies (Grossman et al., 2000; Vaina et al., 2001). STS receives input from both form and motion processing areas, but the functional involvement of these connections in biological motion perception is not known. In this section, we compare simulations of model cells with data from monkey area STP.

Stage 1 of the model consists of two types of cells that encode either walking to the right or to the left (Fig. 1). Figure 8(top left) shows response rates of the two stage 1 cells over time after the stimulus is applied. For the one cell (gray line), the stimulus is in preferred direction. For the other cell (black line), the stimulus is in opposite direction. The activity for both types of cells shows an initial rapid increase. After ∼50 ms, the cell with the nonpreferred direction becomes suppressed by inhibitory interactions from the cell with the preferred directions. Both cell responses settle on these respective asymptotic response levels for as long as the stimulus is present.

Figure 8.

Top left, Simulated activity of the two cells of model stage 1 that encode forward walking. The stimulus was a leftward oriented walker with eight points per frame. The light gray line shows the cell with preference for the stimulus orientation, and the black line shows the cell with preference for the opposite orientation. Top right, Simulated activity in model stage 2 for a stimulus facing to the left and moving forward. The light gray line shows the cell with the preference for forward movement, and the black line shows the cell with the preference for backward movement. Both activities are simulated for 150 different trials. Bottom left, Single-cell recordings from a neuron that responds selectively to a particular combination of body orientation and walking direction (e.g., a walker oriented to the left and moving forward), while a forward moving stimulus was presented either with the preferred orientation or with an orientation that was opposite to the preferred orientation. Bottom right, Single-cell recordings from a neuron that responds selectively to a particular combination of body orientation and walking direction. Stimuli were presented with a fixed-body orientation but opposite walking directions. Figures adapted with permission from Oram and Perrett (1996).

Figure 8 (top right) shows the responses of two cells from stage 2 of the model. In this case, the stimulus presented forward walking. One cell (gray line) was selective for forward walking. The other cell (black line) was selective for backward walking. The cells show the same qualitative behavior as cells from stage 1, but activity in the nonpreferred direction decreases more slowly than in stage 1. Also, the differences between both cell types are smaller for stage 2 than for stage 1.

Oram and Perrett (1996) recorded the responses of neurons in anterior STP of the macaque monkey when the monkey viewed real walking humans. In one condition, they recorded spike intensity from cells that discriminate between the directions the walking body faces (Fig. 8, bottom left). This task corresponds to the direction task in our model. In another condition, they recorded cells while the walker was facing in the preferred direction of the cell and walked either forward or backward (Fig. 8, bottom right). This is similar to the forward/backward task used in our model simulations.

In the direction task, the model simulations show the same behavior as the cell recordings. Both stage 1 and stage 2 show a rapid increase of activity for the preferred stimulus. Closer examination reveals that the more rapid decrease in stage 1 matches the electrophysiological data even better than the simulations in model stage 2.

In the model, the two types of cells can discriminate walking direction within 100–200 ms. This is in accordance with the results of Oram and Perrett (1996), who showed that neurons respond selectively to biological motion stimuli with specific form and orientation from 119 ms after stimulus onset.

The forward/backward task comprises both form recognition and global motion analysis. The model analyzes global motion in stage 2. Therefore, we compare electrophysiological data for this forward/backward walking only with stage 2 predictions (Fig. 8, top right). Here, too, the model shows a rapid increase as the neuronal data. Also, it shows weaker activity for the nonpreferred walking direction, similar to the electrophysiological data.

Functional MRI data

We are interested in the contributions of STS and form processing areas to the perception of biological motion. STS activity was found in many fMRI studies (Oram and Perrett, 1996; Puce et al., 1998; Grossman et al., 2000; Vaina et al., 2001; Beauchamp et al., 2002; Santi et al., 2003; Thompson et al., 2005). The contribution of form processing areas to biological motion perception is less clear. Because our model is based on form analysis and does not use local motion signals, we will focus in this section on contributions from form processing areas. Activation of form processing areas has been found in many fMRI studies of biological motion analysis (Downing et al., 2001; Vaina et al., 2001; Grossman and Blake, 2002; Beauchamp et al., 2003; Ptito et al., 2003; Santi et al., 2003; Michels et al., 2005; Thompson et al., 2005). Point-light walkers activate FFA (Vaina et al., 2001; Grossman and Blake, 2002; Santi et al., 2003; Michels et al., 2005), which is believed to process form information. Point-light walkers also activate EBA (Downing et al., 2001; Grossman and Blake, 2002; Michels et al., 2005), which is characterized by sensitivity to static images of human figures (Downing et al., 2001).

The model uses static template cells in stage 1 that are combined for temporal order analysis in stage 2. Possible neural correlates may be EBA or FFA, which are sensitive to static postures of human bodies (Downing et al., 2001; Peelen and Downing, 2005) for stage 1 and area STS, which is sensitive to the global motion of a point-light walker (Grossman et al., 2000; Vaina et al., 2001) for stage 2. We computed model predictions of activation levels at the two model stages for different kinds of stimuli and compared the results with experimental data reported for these areas.

Grossman and Blake (2002) recorded fMRI blood oxygenation level-dependent (BOLD) responses to a stimulus that consisted of 12 point lights that depicted a human walker, and they compared them with BOLD responses to a scrambled control stimulus. In the scrambled control stimulus, the 12 dots had the same motion trajectories as in the biological motion stimulus, but the starting positions of the dots were randomized. Thus, the motion path of any dot is consistent with one of the walker dots while the spatial structure of the stimulus is destroyed so that it does not resemble the human form any longer. Grossman and Blake measured BOLD activity in EBA and STS as subjects viewed the biological motion or the scrambled stimulus. They found a slight increase of activation for biological motion over control in EBA and a strong and significant difference in STS. Downing et al. (2001) also mentioned a significant increase of activation in EBA for point-light walkers compared with controls.

We simulated the experiments with the same stimuli as Grossman and Blake and compared the outputs of the stages 1 and 2 of the model with the results for EBA and STS (Fig. 9). We normalized model data to the maximum of the signal change in the fMRI data. The results of the model simulations are in accordance with the fMRI data. Biological motion stimuli revealed more activation than the scrambled control stimuli in both model stages. The difference between biological motion and control was significant in stage 2 (t = 4.5; p < 0.01, independent t test) but only a trend (p = 0.07) in stage 1. Activity in both model stages matches quantitatively the differences in EBA and STS (Fig. 9).

Figure 9.

Simulated activity in model stages 1 and 2 compared with fMRI data obtained from EBA and STS for normal and scrambled presentation of the stimulus. Results are presented as mean ± SE. fMRI data are adapted from Grossman and Blake (2002). **p < 0.01.

Our model thus exhibits a higher activation level for biological motion than for scrambled stimuli. Stimuli that depict a walker simply match the templates better than a scrambled arrangement of dots. However, from the outline of our model, it is clear that the amount of difference between scrambled and normal depends on the exact way of “scrambling” the stimulus. The more similar the structure of the scrambled walker in a single frame is to the structure of the human body, the more activation the scrambled stimulus elicits. For instance, scrambling the starting phases of the dot movements (Grossman and Blake, 2002; Michels et al., 2005) has a less deteriorating effect on the spatial structure than scrambling the spatial positions of all dots from the walker (Vaina et al., 2001) and should lead to a smaller activity difference. Furthermore, if the single frames of the stimulus were intact but the temporal order of the frames was randomized, the model would make the counter-intuitive prediction that this temporal scrambling does not affect activation levels in stage 1, nor should it affect performance in the direction task. Recently, Hirai and Hiraki (2006) investigated the influence of spatial and temporal scrambling of biological motion stimuli on event-related potentials (ERPs). In accordance with our model predictions, they found that the temporal scrambling had only a negligible influence on the ERP, whereas spatial scrambling decreased the ERP strongly. It would be interesting to test, in an fMRI study, whether different brain areas such as EBA, FFA, and STS are affected by the temporal scrambling.

Peuskens et al. (2005) tested a stimulus that consisted of the motion of an articulated skeleton, but the skeleton was unlike that of a human. Our model would ignore the apparent levers and axles in the “articulated walker” because they would not fit the template. It would thus treat the articulated walker like other scrambled walkers and would show a lower response when compared with the normal walker.

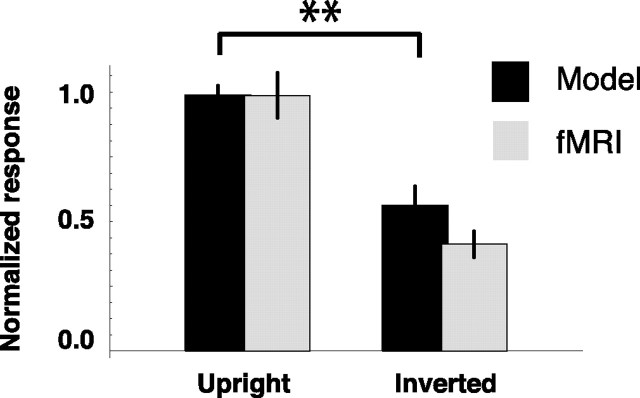
In a previous study, Grossman and Blake (2001) explored the orientation specificity of biological motion in the fMRI BOLD signal. It is well known that perception of biological motion is impaired for upside-down walkers (Sumi, 1984; Pavlova and Sokolov, 2000; Grossman and Blake, 2001; Grossman et al., 2005) (but see Shipley, 2003). Grossman and Blake (2001) recorded neural activity in STS when subjects viewed a canonical (upright) point-light walker or an inverted (upside-down) display of this figure. They found that the response to an inverted walker was approximately half that of an upright walker. We presented both stimuli (upright and inverted) to the model and analyzed the output in stage 2 (Fig. 10). In accordance with the results of Grossman and Blake (2001), inverted walkers evoked significantly lower responses than upright walkers in the model (independent t test, t = 3.8; p < 0.01). The reason for this is that, in our model, only template cells for upright walkers exist. These template cells match an upright point-light walker more accurately than an inverted point-light walker, consistent with the common explanation for viewer-centered orientation specificity of biological motion perception (Reed et al., 2003; Troje, 2003). However, even the poor matches between the upside-down stimuli and the upright templates did elicit some activity in the model as they did in STS. According to the model, this residual activity is still consistent with the assumption of upright only templates. In agreement with the fMRI data, model simulations at stage 2 revealed that inverted and scrambled walkers evoked only approximately half the response of normal biological motion (inverted, 57%; scrambled, 53%). In model stage 1, we found that inverted walkers evoked only 51% of the response to normal biological motion, whereas scrambled walkers reached 75% of the response evoked by normal biological motion. The reason is that the deviations from the templates of the model are even larger for the inverted walker than for a scrambled walker. Therefore, stage 1 responds less to inverted than to scrambled walkers. Stage 2, however, also takes into account whether the sequence of best-matching templates is in accord with a consistent walking motion. Because both the inverted and the scrambled stimulus would essentially lead to a sequence of false matches, there is little consistent temporal order in either condition, and the activation levels drop to similarly low values for both scrambled and inverted walkers.

Figure 10.

Simulated activity in model stage 2 compared with fMRI data obtained from STS for upright and inverted presentation of the stimulus. Results are presented as mean ± SE. fMRI data are adapted from Grossman and Blake (2001). **p < 0.01.

Recent TMS results indeed suggest that STS encodes only upright biological walkers but not inverted walkers. Applying TMS over STS impaired the perception of upright biological motion but not the perception of inverted biological motion (Grossman et al., 2005).

In the experiments above, we simulated data from studies that used classical Johansson point-light walkers with light points attached to the major joints. Additionally, we compared model simulations with results of an fMRI study that used the stimulus of Beintema and Lappe (2002) and that compared walking with static stimuli (Michels et al., 2005). This fMRI study applied four different stimuli. First, they used the classical walker computed by the algorithm of Cutting (1978) with the dots on the joints of the stimuli (classical walker moving). The second stimulus consisted of a static posture of this stimulus presented for the same duration as the moving stimulus (classical walker static). The third stimulus depicted a walking figure with the dots reallocating on the skeleton each frame. This is the stimulus introduced by Beintema and Lappe (2002) and used in the psychophysical simulations of direction and forward/backward tasks presented above. To distinguish it from the classical walker, we will call this stimulus the “sequential position” (SP) walker. For the last stimulus, Michels et al. used a static posture of the SP stimulus with the dots changing their position on the static posture frame by frame (SP walker static).

These four stimuli were also applied in model simulations. Activation levels were computed in the model and compared with the activation levels in the fMRI study. Differences between activations in different conditions were tested for significance with independent t tests. Activation levels and significance levels are reported in Figures 11 and 12. Figure 11 shows the comparison of activity in model stage 1 with fMRI data obtained from EBA and FFA. Figure 12 shows the results from model simulations in stage 2 compared with fMRI data obtained from STS.

Figure 11.

Comparison of simulated activities in model stage 1 with fMRI data obtained from EBA and the FFA/OFA complex. fMRI data are adapted from Michels et al. (2005). Dashed lines and * indicate differences between model simulations for the different conditions, and solid lines and * indicate differences between model simulations and fMRI data within one condition. Classic Walker refers to the stimulus introduced by Cutting (1978), and SP-Walker refers to the stimulus of Beintema and Lappe (2002) (for details, see Results). *p < 0.05; **p < 0.01.

Figure 12.

Comparison of simulated activities in model stage 2 with fMRI data from area STS (Michels et al., 2005). Dashed lines and * indicate differences between model simulations for the different conditions, and solid lines and * indicate differences between model simulations and fMRI data within one condition. Classic Walker refers to the stimulus introduced by Cutting (1978), and SP-Walker refers to the stimulus of Beintema and Lappe (2002) (for details, see Results). *p < 0.05; **p < 0.01.

Statistical analysis for stage 1 revealed that the model predicts increased activity for both SP walker conditions (moving and static) compared with both classical walker conditions. Michels et al. (2005) reported the same statistical differences between the single conditions for both EBA and FFA. Only in EBA and FFA did the SP walker conditions evoke higher activity than for any classical walker condition.

The comparison between model and fMRI data within each condition revealed a significantly higher activity in EBA for the SP walker moving condition compared with the model prediction. Model predictions and fMRI data differed for the classical walker static. Here, the model predicts a disproportionate activity for the static condition compared with the fMRI data. In the classic walker static condition, a single frame of the stimulus is displayed for the entire trial duration, whereas in the three other conditions, stimulus dot positions are refreshed every 50 ms. It is likely that fMRI activation in the classic walker static condition is lower because activity is not sustained over the entire trial as a result of the fatigue of the neuronal response (Grill-Spector et al., 2006). Such mechanisms are not present in the model, and, therefore, the model response is larger.

The comparison of stage 2 with fMRI data revealed that, among all areas, the best correlation is observed between stage 2 and STS. Here, the model predicts that activity for the classical walker static condition is significantly lower than for all other conditions. The same results were reported by Michels et al. (2005) for STS. In addition, the model shows a significantly increased activity for the SP walker static condition compared with the classical walker moving condition. Michels et al. (2005) observed only a trend that did not reach statistical significance (p < 0.09).

The comparison of model and fMRI data within each condition revealed that the model overestimates activity for the classical walker static condition also in stage 2. As specified above, this discrepancy can be explained by the fatigue of the BOLD signal, which is missing in the model.

In summary, the model reveals a high correlation of its stage 1 to EBA and FFA/OFA with a slightly better match for FFA/OFA than for EBA. For stage 2, we found a high correlation between model and STS.

Discussion

Biological motion perception from dynamic form

We developed a neurally plausible model of biological motion perception that dynamically integrates the activity of template cells of static postures of the human body. The first stage of the model analyzes only the form information in each sequential frame of the stimulus without knowledge of the temporal order. Local as well as global motion analysis is excluded. The second stage performs global motion analysis by explicitly analyzing the temporal order of the selected frames. The first stage stands for pure form analysis as in the task of direction discrimination. In experiments using this direction task, we varied the contribution of form information and the influence of global motion. All data could be accurately replicated by the model solely exploiting form information. This indicates that direction discrimination tasks do not necessarily need global motion information.

In the forward/backward discrimination task, global motion analysis had to be involved because the frames and their available form information were identical. Only their temporal order differed. The model computes this global motion in stage 2 by analyzing the frame order based on comparing the current most active template with an intrinsic expectancy. We again varied the amount of form information and the dynamics by changing stimulus duration and velocity. This expectancy combined with the form information transferred from stage 1 accounted for all of data that used the forward/backward task.

Our model approach is consistent with perceptual investigations that showed that a global analysis underlies the perception of human motion from line drawings or whole-body photographs (Shiffrar and Freyd, 1990; Chatterjee et al., 1996; Shiffrar et al., 1997). These studies uniformly stressed the importance of orientation and form cues for biological motion perception. We extend these conclusions to point-light walkers. We found that the form information in a single frame is not enough information to solve biological motion tasks, but temporal integration within an appropriate time window can provide the required information.

The model could also account for psychophysical experiments conducted in interfering noise (Neri et al., 1998). We regard a form-based template-matching model as a possible explanation for the differences observed for discrimination of translatory and biological motion. This supports the conclusion of Neri et al. who considered “very sensitive, but flexible, mechanisms” as an explanation for their findings.

The cortical network for biological motion analysis

Our form-based model was inspired by various findings from neurological patients that suffered from the loss of motion perception but could see biological motion (Vaina et al., 1990, 2002; McLeod et al., 1996). The recent surge in functional imaging studies of biological motion allows us to draw comparisons of the model with parts of the cortical network of biological motion perception. Among this network, STS is believed to be crucially involved in the perception of biological motion because it has been found in imaging (Bonda et al., 1996; Puce et al., 1998; Grossman et al., 2000; Vaina et al., 2001; Beauchamp et al., 2002; Thompson et al., 2005) and electrophysiological investigations (Oram and Perrett, 1994; Oram and Perrett, 1996), and it has been functionally implied from lesion studies (Cowey and Vaina, 2000; Vaina and Gross, 2004).

The data produced by our template-matching model predicted activity in areas sensitive to static postures of human bodies. Comparison of the model predictions with fMRI data from EBA showed a high correlation between model and experimental data. Moreover, the model predicted that the activation is higher for normal biological motion than the activity for the scrambled control (Downing et al., 2001; Grossman and Blake, 2002). However, the neural implementation of the model does not have to be restricted to EBA. Peelen and Downing (2005) also found selective activity for human bodies in the mid-fusiform gyrus, and Grossman and Blake (2002) reported that point-light walkers significantly elicited more activation in FFA than scrambled control stimuli. Comparison of model predictions for different types of walker stimuli with fMRI results (Michels et al., 2005) revealed high similarities to activities in EBA and the FFA/OFA complex. This supports our idea that this step of the model analysis may be implemented in form processing areas. The model simulations suggest that EBA, or other areas sensitive to static postures, can be involved in the network of biological motion perception. Puce et al. (2003) reported similar results for face perception. Line drawings of faces activated the fusiform gyrus more than scrambled line drawings. Therefore, we suggest that areas such as EBA or FFA are candidates for the neural implementation of model stage 1. The results imply that tasks such as the direction task, which does not necessarily involve global motion analysis (Beintema et al., 2006), can be solved by form analysis in this area.

We compared the model simulations of neural activity in stage 2 with fMRI studies of STS activation (Grossman et al., 2001; Grossman and Blake, 2002; Michels et al., 2005). The results imply that the role of STS differs from EBA or other areas processing form information. The differences between the activation levels for normal and scrambled control stimuli in EBA and model stage 1 were multiplied in STS and stage 2. The differences at stage 1 were deferred to stage 2 and reinforced by the temporal analysis conducted at stage 2. From our model simulations, we hypothesize that the additional global motion that is necessary to solve forward/backward tasks is processed in STS and that the impression of global motion can be derived from the dynamic change of static postures, processed in EBA or FFA. That is, in contrast to EBA, STS involves global motion analysis.

The model also predicts that the spatial structure of the stimulus has a strong influence on activity in STS. This is consistent with Thompson et al. (2005), who found that STS activation is driven by the spatial configuration of the stimulus. The hypothesis is also supported in fMRI studies by Grossman and Blake (2002) for spatially scrambled walkers and by Grossman and Blake (2001) for inverted walkers. Also, Hirai and Hiraki (2006) revealed that the amplitude of event-related potentials elicited by point-light biological motion is mainly dependent on the spatial structure of the walker rather than on the temporal structure of the dot movement. Temporal structures would be useful for local motion detectors, whereas the spatial configuration is useful if the stimulus is mainly processed by global form analysis.

The STS also receives input from motion-sensitive areas of the brain and features general motion sensitivity (Ungerleider and Desimone, 1986; Boussaoud et al., 1990). Thus, it is conceivable that low-level motion signals contribute to biological motion processing, although our model would not seem to require them. In the literature, there is surprisingly little direct evidence that low-level motion signals contribute to biological motion perception (for a discussion, see Beintema et al., 2006). Inactivation of motion processing area MT does not interfere with biological motion perception (Grossman et al., 2005). Some studies revealed selective activation of area KO when biological motion is compared with scrambled control stimuli (Vaina et al., 2001; Santi et al., 2003). A pathway through area KO may allow residual motion perception in patients with lesions of MT (Casile and Giese, 2005). However, other studies reported that KO showed no selectivity to biological motion versus these control stimuli (Grossman et al., 2000).

Other computational studies

Only a few computational studies have investigated the influence of dynamics and form information on the perception of biological motion. Troje (2002) proposed a model to identify the gender of a walking person from different viewing angles applying a principal component analysis. The results revealed that omitting information about the spatial structure of the walker by averaging over all walker stimuli corrupts performance. However, leaving out the dynamical component decreases recognition rates even more strongly. We report the same findings for our simpler discrimination tasks: omitting structural information leads to a decrease of performance and even to a stronger decrease if information about the dynamics is decreased.

Lee and Wong (2004) proposed a template-matching model similar to ours, but they used point-light displays as templates instead of stick figures. Their model could also account for the nonlinear relationship between number of stimulus dots and number of noise dots reported by Neri et al. (1998). Our model provides an improvement because it also quantitatively replicates the psychophysical results.

Similar to our approach, Giese and Poggio (2003) assumed snapshots of human walking as the basis for a temporal order analysis. These snapshots are presumably implemented in STS and selectively activated by different human motion patterns. The snapshot neurons get input from motion processing pathways via areas MT and KO and also from form processing areas. In both cases, however, the information is extracted from the stimulus in a local-to-global bottom-up manner. For the case of point-light stimuli, Giese and Poggio proposed that only the motion-analyzing areas are able to lead to the reconstruction because the stimulus is devoid of local form cues such as local orientation. Our model shows that the template matching can be achieved by appropriate global form analysis. Our template-matching method can also explain why areas such as EBA and FFA show a higher activation level for point-light walkers than for their scrambled versions.

The model uses a set of templates that was recorded from movements of humans and is therefore restricted to these templates of human gait perception. In the human brain, it is likely that the templates are generated by a learning processes. Implementation of such a learning process might be possible as an additional aspect for the model and may be interesting to explore. Moreover, templates for different movements or different articulation structures (such as four-legged locomotion of animals) might be learned and used. In this way, the model may in future work be extended from human gait perception to the perception of other biological motion stimuli