Receptive Field Properties of Neurons in the Early Visual Cortex Revealed by Local Spectral Reverse Correlation

Abstract

We introduce a novel class of white-noise analyses, named local spectral reverse correlation (LSRC), which is capable of revealing various aspects of visual receptive field profiles that were undetectable previously in a single simple measurement. The method is based on spectral analyses in a two-dimensional spatial frequency domain for spatially localized areas within and around their receptive fields. Extracellular single-unit recordings were performed for area 17 and 18 neurons in anesthetized cats. A dynamic dense noise pattern was presented in which the pattern covered an area two to three times larger than the classical receptive field. Spike trains were then cross-correlated with frequency spectra of localized noise pattern to obtain spatially localized selectivity maps in the two-dimensional frequency domain. Our findings are as follows. (1) The new LSRC method allows measurements of two-dimensional frequency tunings and their spatial extent even for cells with substantial nonlinearity. (2) A small subset of neurons shows spatial inhomogeneity in the two-dimensional frequency tunings. (3) In addition to facilitatory response profiles, we can also visualize suppressive profiles localized both in space and spatial frequency domains. Our results suggest that the new analysis technique can be a powerful tool for measuring visual response profiles that contain inhomogeneity in space, as well as for studying neurons with substantial nonlinearities. These features make the method particularly suitable for studying response profiles of neurons in early as well as intermediate extrastriate visual areas.

Introduction

Various mapping methods, in particular those that use a reverse correlation analysis, have been very effective in providing detailed receptive fields of neurons in early stages of the visual pathway (Jones and Palmer, 1987; DeAngelis et al., 1993; Reid et al., 1997). However, some aspects of receptive field properties cannot be measured easily by the currently available methods. These include the so-called cross-orientation suppression (Morrone et al., 1982; Bonds, 1989), surround suppression (Hubel and Wiesel, 1968; Dreher, 1972), and possible local variations of tuning properties within a receptive field. Once we go beyond these early areas, mapping receptive fields of neurons in the extrastriate visual areas are expected to be even more difficult. How would one go about measuring receptive fields of downstream cells that collect input from early visual cortical neurons? To acquire selectivity to complex visual features, the extrasriate neurons might collect spatially inhomogeneous inputs from these early-stage filters, meaning that the filter properties (e.g., orientation and spatial frequency tunings) are not uniform over their receptive fields but are different greatly to define selectivities to curved contours (Gallant et al., 1993, 1996; Pasupathy and Connor, 2001). To extend the reverse correlation method for studying details of the early visual cortical areas and for possible uses in extrastriate areas, we have developed a new class of white-noise analysis, named local spectral reverse correlation (LSRC). The purposes of this study are to validate the new LSRC analysis and to examine details of previously invisible response properties including the extent and nature of spatial inhomogeneity, if any, of cells in the early visual cortex.

The LSRC method uses a wide-area, two-dimensional dynamic white-noise sequence similar to those used in previous studies (Reid et al., 1997). However, the key novel idea is in calculating the cross-correlations between the spike train and amplitude spectra of spatially windowed (hence localized in analysis) noise sequence. By doing this, we can acquire the response profiles of the cell in a two-dimensional frequency domain for subfields within and around the receptive field. We have applied this procedure for cells in the early visual cortex of cats and found the following. (1) The LSRC method allows measurements of two-dimensional frequency tunings and their spatial extent for both simple and complex cells, whereas conventional space-domain reverse correlation with dense noise does not reveal first-order responses for complex cells. (2) A small subset of neurons exhibits spatial inhomogeneity in the two-dimensional frequency tunings. (3) In addition to facilitatory response profiles, we can also visualize suppressive profiles localized both in space and spatial frequency domains, which cannot be revealed by a standard reverse correlation procedure. Computational investigations also reveal that the new method is highly effective even in cases in which high thresholds prevent a cell from responding to individual local optimal stimuli alone. Our results suggest that the new analysis technique can be a powerful tool for measuring visual receptive filed profiles that contain inhomogeneity in space, as well as for studying neurons with substantial nonlinearities.

Materials and Methods

All recordings were made from adult cats weighing between 1.5 and 3.7 kg. All animal care and experimental guidelines conformed to those established by the National Institutes of Health and were approved by the Osaka University Animal Care and Use Committee.

Surgical procedure.

Detailed procedures have been described in our recent publication (Nishimoto et al., 2005). Briefly, each cat was anesthetized with isoflurane (2.5–3.5% in O₂) after initial preanesthetic doses of hydroxyzine (atarax; 2.5 mg) and atropine (0.05 mg). Electrocardiogram electrodes and a rectal temperature probe were inserted, and a femoral vein was catheterized. Then, cefotiam hydrochloride (Panspolin; 8.3 mg) and dexamethasone sodium phosphate (Decadron; 0.4 mg) were administered. Subsequently, a tracheostomy was performed, and a tracheal tube was inserted. Then, the animal’s head was secured in a stereotaxic device with the use of ear and mouth bars and clamps on the orbital rim. Tips of the ear bars were coated with local anesthetic gel (Lidocaine). Anesthesia was then switched to sodium thiopental (Ravonal; given continuously at 1.0–1.5 mg/kg/h). After stabilization of anesthesia, paralysis was induced with a loading dose of gallamine triethiodide (10–20 mg), and the animal was placed under artificial respiration at the rate of 20–30 strokes per minute. The respiration rate and stroke volume were adjusted to maintain end-tidal CO₂ between 3.5 and 4.3%. Artificial respiration was performed with a gas mixture of 70% N₂O and 30% O₂. The infusion fluid thereafter contained Ravonal, gallamine triethiodide (10 mg/kg/h), and glucose (40 mg/kg/h) in Ringer’s solution. A craniotomy was then performed directly above the central representation of the visual field in the visual area 17 or 18 (Horsley-Clarke P4 L2.5 for recordings of A17 and A3 L3 for recordings of A18). The dura was dissected away to allow insertion of microelectrodes. We used tungsten microelectrodes (5 MΩ; A-M Systems, Everett, WA) for recording spike activity extracellularly. Typically, two electrodes were used to increase the chance of encountering cells, and they were mounted in parallel in a single protective guide tube and driven by a common microelectrode drive (Narishige, Tokyo, Japan). After lowering the electrodes to the cortical surface, agar was used to protect the cortex, and melted wax was applied over the agar to create a sealed chamber for stabilization. Body temperature was maintained near 38.3°C with the use of a servo-controlled heating pad. Pupils were dilated with atropine (1%), and nictitating membranes were retracted with phenylephrine hydrochloride (Neosynesin; 5%). Contact lenses of appropriate power with 4 mm artificial pupils were positioned on each cornea.

To record the activity of single units, electrical signals from the microelectrodes were amplified (10,000×) and bandpass filtered (300–5000 Hz). Then spike sorting was achieved using a custom-built spike sorter (Ohzawa et al., 1996), in which each spike was sorted by their waveforms and time-stamped with 40 μs resolution.

Visual stimulation.

All of the experiment control functions and generations of visual stimuli were performed using custom-written software on two Windows personal computers. Visual stimuli were generated by a dedicated personal computer and displayed on a cathode ray tube display (GDM-FW900; a resolution of 1600 × 1024 pixels, refreshed at 76 Hz; Sony, Tokyo, Japan). The animal saw the display through a custom-built haploscope, which allowed dichoptic presentations of visual stimuli to the left and right eyes separately using 800 × 1024 pixel areas of the display. The distances (total length of light paths) between the screen and the eyes were set to 57 cm, subtending the visual field of 23° (horizontal) × 30° (vertical) for each eye. All measurements were performed for the dominant eye.

For each cell we encountered, we have presented a dynamic two-dimensional noise array (Fig. 1A). The area covered by the noise array is typically two to three times larger than the classical receptive fields in width and height (typical ranges are from 12 × 12° to 20 × 20°). The noise array consists of 51 × 51 elements, in which the luminance of each element is bright (∼90 cd/m²), dark (∼3 cd/m²), or equal to the mean luminance of the display (∼47 cd/m²). The noise array is redrawn with a new noise pattern every 26 ms (two video frames). Typically, 10 blocks of the noise arrays (a total of 68,400 frames, or 30 min) are presented to obtain sufficient number of spikes for data analysis.

Figure 1.

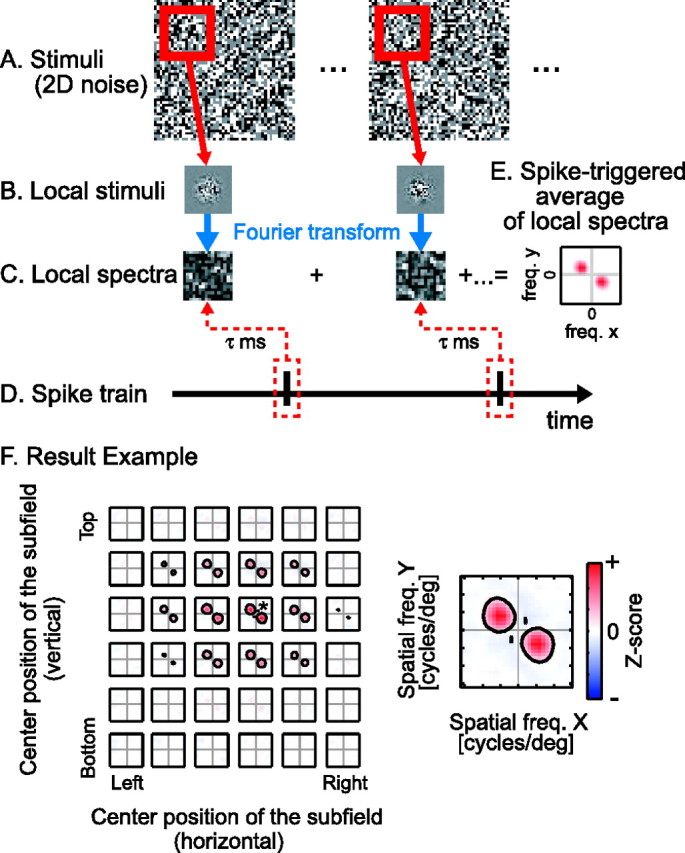
A, Schematic diagram of the LSRC procedure (see Materials and Methods for details). C–E, By calculating a cross-correlation between the spike train (D) and spectra of Gaussian-windowed stimuli (C), we obtain a two-dimensional frequency tuning for the given subfield (E). F, By changing iteratively the center position of the Gaussian window, we can obtain a spatial matrix of the two-dimensional frequency tunings, corresponding to the matrix of localized areas of analysis shown in B. The strongest local spectral tuning map is indicated by an asterisk and is shown enlarged on the right. In each of these spectral maps, facilitatory and suppressive responses are shown by red and blue, respectively, according to the scale bar (suppression is essentially absent for this neuron). These conventions are used for subsequent figures. By nature of the Fourier transform, the tunings are symmetric about the origin. 2D, Two-dimensional; freq., frequency; deg, degree.

Data analysis.

To obtain two-dimensional frequency tunings for spatially localized areas, we have performed a LSRC. LSRC is an application of the standard spike-triggered average techniques (de Boer and Kuyper, 1968; Jones and Palmer, 1987). In the conventional space–time receptive field mapping, a spike-triggered average of stimuli itself (Fig. 1A) is calculated in the space–time domain. In LSRC, instead, we calculate a spike-triggered average of the amplitude spectra of a given subfield of the noise array (Fig. 1C) to obtain a two-dimensional frequency tuning for the given subfield (Fig. 1E). By interpreting the two-dimensional frequency tuning (Fig. 1E) as a polar coordinate representation, we obtain a joint spatial frequency and orientation profile. The distance from the origin to the peak of the excitation (shown in red in Fig. 1E) indicates the optimal spatial frequency for the local subfield of the receptive field. Similarly, the angle of the line connecting the origin and the excitation peak (with the horizontal axis) depicts the optimal orientation for the local subfield.

By systematically changing positions of the subfield for calculating the spectra, we can obtain a matrix of two-dimensional frequency tunings (Fig. 1F), in which each element of the matrix contains the two-dimensional frequency tunings for the given subfield. Therefore, the final matrix of frequency tunings describes the tuning profile of the cell as a function of position (x, y) as well as spatial frequency and orientation in a joint manner. Note that we use Z-score values for representing the response strength in these spectral receptive field profiles throughout this report, to take variability and statistical significance of responses into account (see below). Z-score values may be negative, which may be interpreted as a reduction of activities below the baseline level.

The subfields were windowed by a two-dimensional Gaussian function, and the frequency spectra were calculated by the standard fast Fourier transform algorithm with zero padding (Press et al., 1992). The center of the window was stepped typically by σ of the Gaussian function, where σ is the SD.

We have calculated spike-triggered averages of stimulus local spectra for correlation delays from 0 to 150 ms in 15 ms steps. Then, the optimal correlation delay was determined as the delay for which the signal amplitude was maximal. Typical optimal correlation delays were 45 or 60 ms.

The average number of spikes for our population of cells was 7421 spikes per 30 min stimulation. The SD of the mean is 8225 spikes per 30 min. The minimum and maximum were 1073 and 51,013 spikes, respectively.

Statistical examination.

To evaluate the significance of the spike-triggered signals, we calculated the average and SD (noise level) of signals using shuffled correlations. We obtained the shuffled correlations by calculating cross-correlations between spike trains and shifted (unpaired) stimulus blocks. The mean and the SD of the shuffled correlations were then used to normalize the original spike-triggered signals into Z-score representations. To reduce a computational burden, we assume that the noise level is identical for a sequence of random pattern of any given subfield and spatial frequency. Therefore, for each neuron, we calculate a set of mean and SD values of the shuffled correlations and use it as parameters for normalizing all spike-triggered signals for the neuron. The statistical significance of signals was examined by the Z-score, corrected for multiple comparisons by the Bonferroni’s method. The degree of freedom for the Bonferroni’s correction is set to the number of subfields multiplied by the number of noise elements within ±1 σ of the analyzing Gaussian window. Black curves in the LSRC plot indicate contours for p = 0.05.

Results

Here, we present two sets of results. One is from a set of simulation studies of the LSRC method, conducted to validate our new method itself and to examine how to interpret the results. The other is an experimental result of the LSRC analysis applied for visual neurons in the early visual cortex.

Simulation study

To examine whether the LSRC method works correctly to reveal spatially localized selectivity, results from a set of simulation studies are presented. We have calculated responses of several kinds of model neurons (Fig. 2) to white-noise stimuli and analyzed the response profile of these neurons by the LSRC method as well as a standard reverse correlation procedure (Jones and Palmer, 1987; DeAngelis et al., 1993; Reid et al., 1997).

Figure 2.

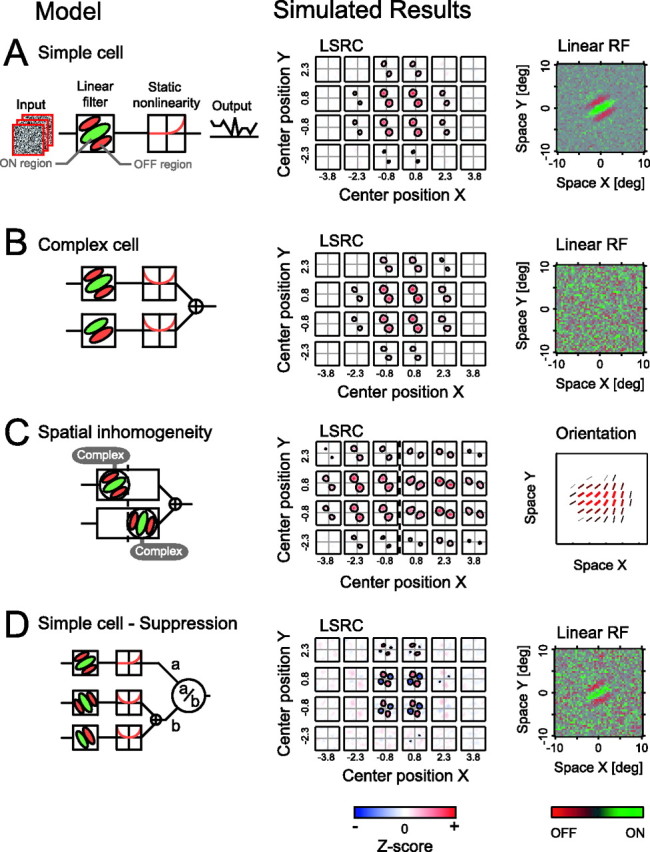
Results are shown of simulations conducted for four types of model neurons. The leftmost drawings depict structures of the models, and the right drawings show the simulated results from the LSRC and the standard reverse correlation analyses. In linear receptive field (RF) maps shown in the rightmost column, ON and OFF subregions are indicated by green and red, respectively, according to the scale bar at the bottom. The linear receptive fields in these simulations and experiments are obtained from the same data set as that used for LSRC. The vertical dashed lines in C indicate the border between the two complex cell components comprising the final output. D, a and b represent facilitatory and suppressive inputs, respectively. deg, Degree.

Simple and complex cells

Figure 2A shows the structure of a model simple cell, together with results of the LSRC analysis and a linear receptive field profile obtained by the standard reverse correlation analysis. The instantaneous responses of the model simple cell are calculated by a linear filtering stage (a Gabor function), followed by a static nonlinearity (a power-law, half-wave rectification). For this model simple cell and other cell types shown in Figure 2, simulations are performed by using a rate-coding model (Troyer et al., 1998) in which the output of the model is a scalar value that corresponds to the firing rate of the model neuron. The output value of the cell in Figure 2A is thus given by the following:

where LF(x,y) is a weighting function (linear filter), S_t(x,y) is a two-dimensional stimulus sequence, and Pos[v] is a half-rectification function, where Pos[v] = v for v > 0 and Pos[v] = 0 otherwise.

Because our scope is limited to the spatial aspect of receptive fields in this study, the temporal dynamics of responses are not considered. Instead, the model was instantaneous and generated one output value for each stimulus frame. Furthermore, instead of generating spikes and computing spike-triggered average of stimuli, equivalent cross-correlation may be computed by multiplying each stimulus frame (or each local spectral amplitude for the case of LSRC) by the output of the model and summing the resulting patterns for all stimulus frames shown to the model cell. This computational procedure applies to both LSRC and standard space-domain reverse correlation analyses.

The results of the LSRC analysis on the model cell responses, shown as a matrix of selectivity in a two-dimensional frequency domain, show the position and spatial extent of the receptive field profile indicated by the limited number of maps with significant excitations. Note also that we can obtain the orientation and spatial frequency selectivity for each localized subfield, allowing us to examine the possible variations of these tuning properties within the receptive field. The recovered linear receptive field profile (Fig. 2A, right), as expected, shows a spatial structure consisting of ON and OFF regions as originally set in the linear stage of the model neuron.

Figure 2B shows results of another simulation for a model complex cell. Our model complex cell is based on the standard energy model (Adelson and Bergen, 1985; Pollen et al., 1989; Ohzawa et al., 1990; Emerson et al., 1992). Because complex cells do not possess spatially separated ON and OFF subregions, a standard reverse correlation procedure does not reveal any spatial structure (Fig. 2B, right). On the other hand, the LSRC method can visualize the position and spatial extent of response profile as well as two-dimensional frequency tunings as in the case of the simple cell. The ability to visualize the response profile of cells even with substantial nonlinearity, like complex cells, is one of the advantages of the LSRC method not available for the standard reverse correlation procedure. Although the spike-triggered average of stimuli (i.e., the output of the standard reverse correlation procedure) will be zero if the underlying nonlinearity is “symmetric” as in the energy model (Simoncelli et al., 2004), LSRC can reveal response profiles for both symmetric and asymmetric types of nonlinearities because the analysis is based on the absolute values of the spectral components.

Spatial inhomogeneity

Can the LSRC method reveal a response profile of neurons, if the selectivities are not homogeneous within their receptive field? This is an important question related to whether LSRC can reveal the profiles of the next-level neurons beyond complex cells, which may be organized to collect from neurons tuned to different parameters. To address this question, we modeled a spatially inhomogeneous neuron in which the orientation selectivity differs depending on the spatial position within the receptive field (Fig. 2C). The model neuron sums the output of two model complex cells (Fig. 2C, left), in which these two components differ in their preferred orientation by 45° and in their spatial positions of the receptive fields. As shown in the simulated result, LSRC can successfully recover the spatial inhomogeneity of the response profile. The two-dimensional frequency tuning for a subfield centered at (−2.3, 0.8), for example, shows a preference to the orientation of 30°, whereas the preferred orientation for a subfield centered at (2.3, 0.8) is 75°. These are exactly the configurations defined in the model. However, note that in the middle of these two locations, we see a tuning profile that is a mixture of those of the original component units and that gives an appearance as if the orientation tuning shifts smoothly over space. This is attributable to a smoothing or blurring effect resulting from the size of the Gaussian window used to compute the spectra. This is a generally applicable limitation for any localized spectral methods in which there is a trade-off between the resolution in the frequency domain and the original domain. Therefore, one limitation of the LSRC method is that an abrupt boundary in tuning parameters, such as orientation, will not be detected as such without using a smaller window size and consequently sacrificing the spectral resolution.

Suppressive profiles

In Figure 2D, we have examined the effect of suppressive components. Our model neuron consists of a simple cell-like facilitative component and a divisive, cross-orientation suppression [a special case of a model by Heeger (1992)]. The suppressive component is modeled as a complex cell-like energy unit because the suppressive effects are known to be phase invariant (DeAngelis et al., 1992). The results show that, although the standard reverse correlation reveals only the linear receptive field (Fig. 2D, right), LSRC shows spatial and spectral positions of suppression (blue areas), in which stimulus energy in the corresponding positions reduces the output of the model neuron. We also simulated a subtractive type of the suppression and found that LSRC can also reveal the subtractive type of suppressions (data not shown).

Overcoming high threshold and nonlinearities for studying higher-order neurons

Several previous studies show that cells selective to complex visual stimuli cannot generally be activated by stimulations using only a part of their optimal stimuli (Tanaka et al., 1991; Pasupathy and Connor, 2001; Ito and Komatsu, 2004). A possible neural mechanism that could explain this phenomenon is that the spiking threshold and nonlinearities are so large that individual parts of appropriate stimuli shown alone cannot achieve the excitation necessary for eliciting spikes. Rather, visual stimuli must contain the essential parts simultaneously in order for the summed excitation to overcome the spiking threshold. This type of nonlinearity is thought to be a source of the problem in mapping response profiles in a part-by-part manner using elementary stimuli such as a bar or a patch of grating (Pollen et al., 2002). The LSRC method may, at least partly, overcome this difficulty. Because large visual areas over the receptive field are always stimulated, by random chance, near optimal combinations of multiple local features can appear in the sequences. Because the white noise for different spatial areas are uncorrelated, the response profiles could be mapped for each local area. This means that the knowledge of selectivities of individual parts of the receptive fields may be obtained from a set of stimuli that covers the entire area.

To examine whether LSRC possesses these desired features for mapping response profiles, even in the situation that partial stimulations cannot reveal them, we have conducted an additional simulation study as illustrated in Figure 3. The model neuron (Fig. 3A) is similar to the spatially inhomogeneous neuron as in Figure 2C but has a high spiking threshold that makes the cell unresponsive unless strong excitations are given. The result demonstrates that, although partial stimulations cannot reveal response profiles in a reliable manner (Fig. 3C), the full stimulations covering the entire receptive field reveal significant response profiles for each localized area (Fig. 3B). These results indicate that LSRC is a highly promising method for overcoming difficulties of mapping receptive field profiles of neurons that combine output of other neurons in a complex manner, without using assumptions regarding the specific details of the combination.

Figure 3.

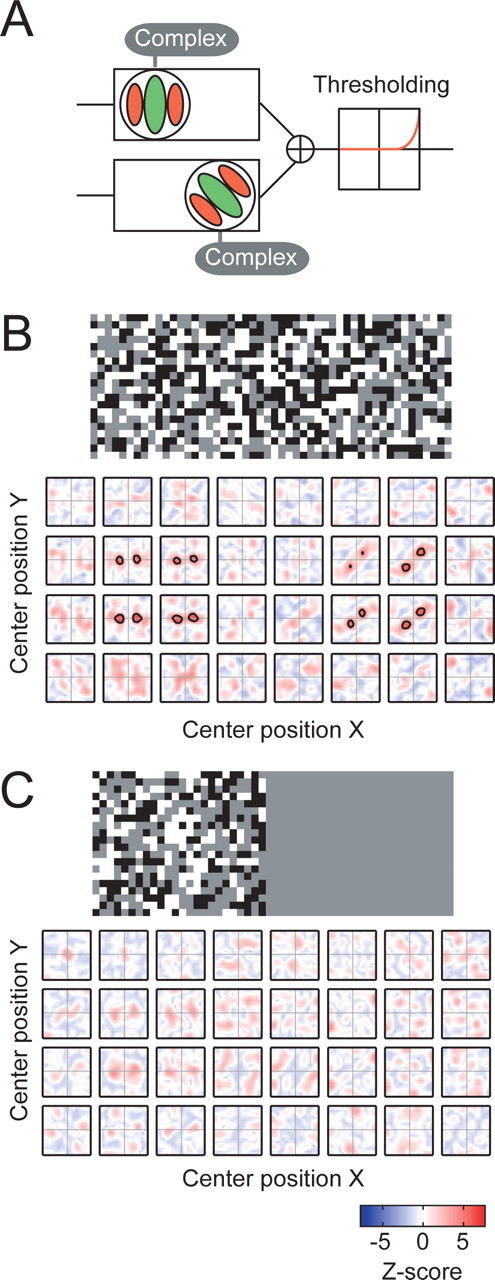
Benefits of the LSRC analysis in studying a higher-order neuron with high threshold are illustrated by simulation. A, Schematic diagram for a model neuron. The model is a spatially inhomogeneous neuron with two complex-type subunits as in Figure 2C, but the subunits have a relatively high firing threshold that prevent the cell from firing unless strong excitatory input is given. The simulations of the LSRC analysis were conducted for two different conditions: B, Full-field noise array that stimulates both subunits simultaneously. C, Half-field noise array in which the right half of the stimuli was masked, providing stimulation of only one of the two subunits. The neuron does not respond unless the entire receptive field is stimulated.

In summary, the simulation studies confirm that (1) LSRC can reveal two-dimensional frequency tunings and their spatial position and extent for both simple and complex cells, (2) LSRC can recover spatially inhomogeneous receptive field profiles, and (3) LSRC can also visualize suppressive profiles localized both in space and spatial frequency domains. Below, we apply the analysis for visual neurons in the cat early visual cortex.

Physiological study

The LSRC analyses were completed for a total of 193 cells (154 cells from area 17 and 34 cells from area 18, in 20 cats). The cortical area of recording is judged based on the coordinates of the electrode penetrations. Of these 193 cells, additional spatial frequency tuning measurements using drifting grating stimuli could be completed with sufficient reliability for 148 neurons. Seventy-seven of these cells were classified as simple, and 71 cells were classified as complex, according to the standard criteria (Skottun et al., 1991; Li et al., 2003; Priebe et al., 2004).

Local spectral selectivity

Figure 4 shows examples of the results for the LSRC and the standard reverse correlation analyses applied for a simple cell (Fig. 4A–C) and a complex cell (Fig. 4D–F) in area 17. These two types of analyses are conducted on the same data set for this and other cells. Although the standard reverse correlation procedure applied for the simple cell (Fig. 4C) yields a space–domain receptive field profile, that for the complex cell (Fig. 4F) shows no structure in this domain. In contrast, results of the LSRC analyses (applied to the same data) show clear response profiles, the two-dimensional frequency tunings as well as the spatial position and extent, for the both simple and complex cells. The spatial extent of the complex cell shows a horizontal elongation that is neither perpendicular nor parallel to the preferred orientation of the cell. The two-dimensional frequency tunings appear similar for all the profiles that contain signals, suggesting that the preferred orientation and spatial frequency is homogeneous throughout the receptive filed for these two cells.

Figure 4.

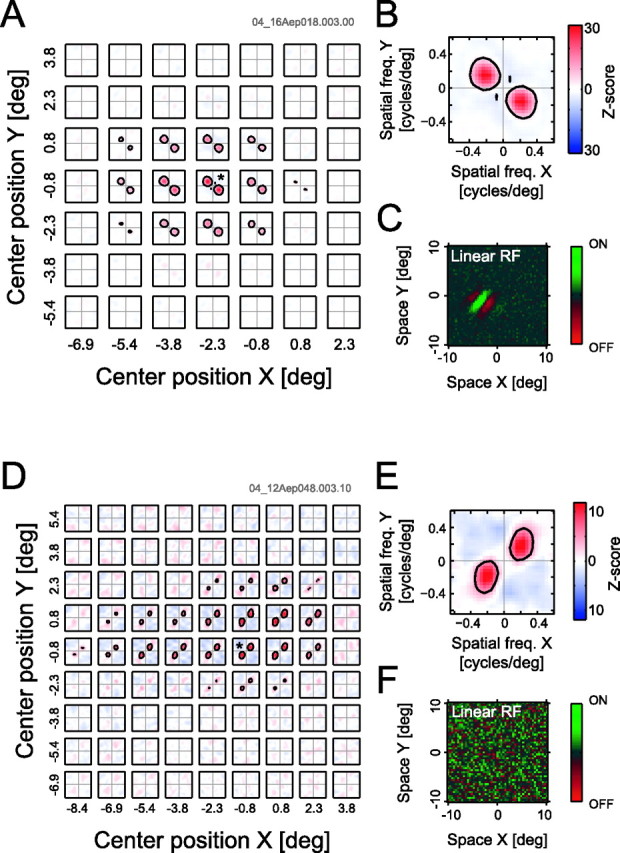
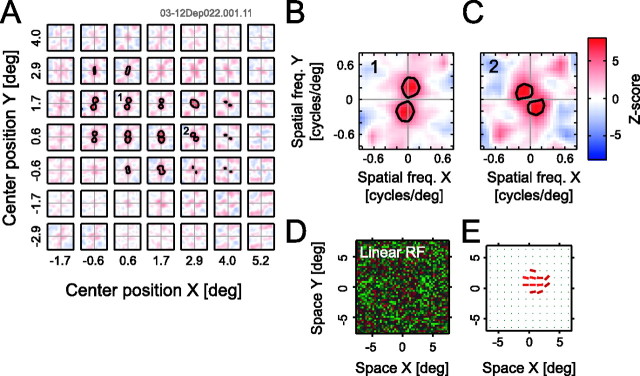
Local spectral selectivities are depicted for a simple (A–C) and a complex (D–F) cell. A, A spatial matrix of local spectral selectivity maps for a simple cell in area 17. Each individual plot shows a tuning property in a two-dimensional spatial frequency domain for the corresponding spatial subfield. The spectral selectivity maps are arranged to reflect the spatial positions of the corresponding subfields. B, A detailed profile of the most responsive subfield indicated by an asterisk in A. C, A linear receptive field profile calculated from the same data as for A. D–F, Data for a complex cell in area 17 in the same format as that for A–C. deg, Degree; freq., frequency; RF, receptive field.

The spatial homogeneity of the two-dimensional profile, however, is not always the case. Figure 5 shows another example for a complex cell in area 17. This cell shows a clear spatial inhomogeneity of the tuning characteristics within the receptive field. As seen in Figure 5, B and C, the two-dimensional frequency tunings differ substantially depending on the subfield location, in that the optimal orientation and spatial frequency differ substantially depending on the regions in which stimuli are presented. Figure 5E depicts a spatial arrangement of orientation tunings for each subfield. Assuming that response amplitude of the cell is dependent on the weighted sum of local features, a stimulus containing a curvature would be optimal for this cell. Although we did not test the neuron with such stimuli directly, this may mean that visual processing of complex features found in the higher-order areas (Gallant et al., 1993, 1996; Hegde and Van Essen, 2000; Pasupathy and Connor, 2001; Ito and Komatsu, 2004) is started, at least partly, in the early visual cortex.

Figure 5.

Local spectral tuning data are shown of a cell that exhibits substantial spatial inhomogeneity of orientation and spatial frequency tuning within its receptive field. A, Local spectral selectivities for a complex cell in area 17. B, C, Detailed tuning properties in A, as indicated by numbers (1 and 2). D, A linear receptive field (RF) profile of the cell. E, A spatial arrangement of orientation tunings obtained from A, in which the orientation of the bars indicates the preferred orientation of the corresponding subfields. Only the data for subfields that contain significant signals are shown (p < 0.01; Bonferroni corrected). This cell was nondirection selective, based on a test with conventional drifting grating stimuli. deg, Degree; freq., frequency.

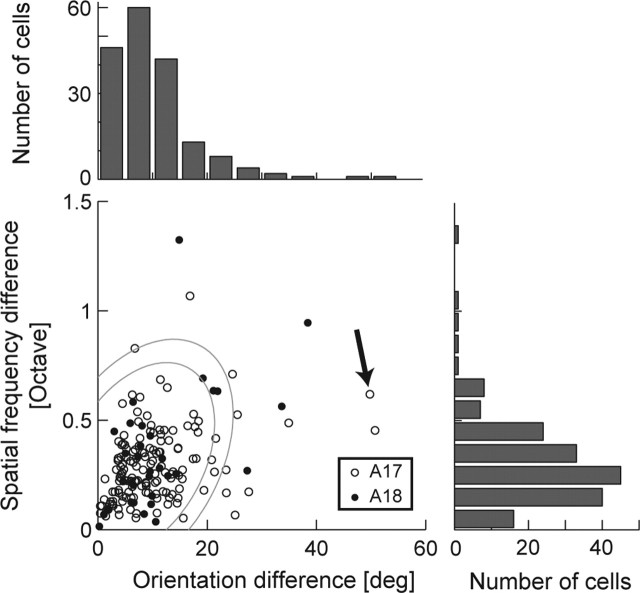
How prevalent are the neurons with spatial inhomogneity in the early visual cortex? To address this question, we summarize the degree of spatial inhomogneity of orientation and spatial frequency tunings for our population of cells (Fig. 6). For each neuron, we have calculated the maximum difference of optimal parameters, both for orientation and spatial frequency, among profiles of subfields that contain significant signals (p < 0.01; Bonferroni corrected). Most of the cells in the early visual cortex show generally homogeneous profiles as in Figure 4, and only a small subset of cells shows the spatial inhomogeneity as shown in Figure 5 (this cell is indicated by a black arrow in Fig. 6). There is no significant difference in distributions of maximum differences for both parameters (orientation and spatial frequency) between areas 17 and 18 (two-sample Wilcoxon test; p > 0.1).

Figure 6.

A population summary is shown of the spatial inhomogeneity of tuning parameters across the receptive fields. The horizontal axis indicates the maximum difference of the preferred orientations among multiple local spectral tuning maps. The vertical axis indicates the same for spatial frequency. Open and filled symbols indicate data for cells in area 17 (A17) and area 18 (A18), respectively. The arrow indicates the cell shown in Figure 5. For this figure, 178 neurons with bandpass spatial frequency tuning profiles and with more than two significant frequency domain maps are included for computing differences of tuning parameters. Two ellipses represent 95 and 99% confidence limits of variations from simulations as a control, assuming homogeneous properties (see Results for details). deg, Degree.

Care must be used, however, in interpreting the apparent inhomogeneities shown in Figure 6. This is because intrareceptive field variations of filtering properties may arise simply because of our procedure in examining the profile using small analyzing windows. For instance, if an analysis window is too small and covers only a part of an ON region of a simple cell receptive field, the resulting spectrum would primarily be that of the Gaussian analysis window itself, which is low-pass, not bandpass as expected from the entire receptive field. Therefore, such artifacts of the procedure may cause apparent intrareceptive field variations of tuning parameters for both spatial frequency and orientation.

To examine how much intrareceptive inhomogeneities the LSRC procedure itself might induce, we have performed simulations using a model simple cell as in Figure 2A. Specifically, model simple cells with Gabor-shaped spatial receptive field profiles were tested using the LSRC procedure, and the methodologically induced variations were examined. We have simulated 1000 model cells, each of which has different parameters selected randomly from the physiologically realistic ranges. Table 1 shows the range of parameters we have used for the simulations based on our physiological data. For each model cell, we have performed the LSRC procedure and calculated maximum variations of optimal parameters for both orientation and spatial frequency, as we performed for the real data. The mean variations for simulated cells are 7.2° for orientation and 0.32 octaves for spatial frequency. The ellipses in Figure 6 show 95 and 99% confidence limits of variations determined by the simulations. We also performed a similar test using model complex cells, but the trend is essentially identical to the case of the simple cell models (data not shown). The result indicates that the most of the small variations within these ellipses are indistinguishable from variations induced by the LSRC procedure itself. Clearly, however, there were cells, even in the early visual cortex, that exhibited large intrareceptive field variations of tuning parameters, which cannot be attributed to the methodological factors.

Table 1.

Simulation parameters for estimating inhomogeneities of methodological origin

	Carrier orientation (°)	Envelope orientation (°)	Carrier phase (°)	Spatial frequency (cycles/stimulus area)	Envelope sigma	Envelope aspect ratio
Minimum	0	0	0	3.0	1.5/SF*0.7	0.7
Maximum	180	180	360	4.5	1.5/SF*1.3	1.3

Ranges of parameters are shown for simulations for determining confidence intervals of interreceptive field variations (see Fig. 6), that might be induced because of the LSRC procedure. See Results for details. SF, Spatial frequency.

Measurement of phase dependency

So far, our primary concern has been the analyses of the spike-triggered averages of the absolute spectral amplitude, and the spatial phase dependency has been ignored. However, Fourier transforms contain information not only of spectral amplitude for each frequency component, but also that of phase. To use all of the information available with the LSRC method, we now extend the method to include both the amplitude and the phase. Because the phase dependence is the key feature that separates simple cells from complex cells (Movshon et al., 1978a; De Valois et al., 1982), incorporating phase information to the LSRC method will allow us to analyze these conventional cell types from a new perspective.

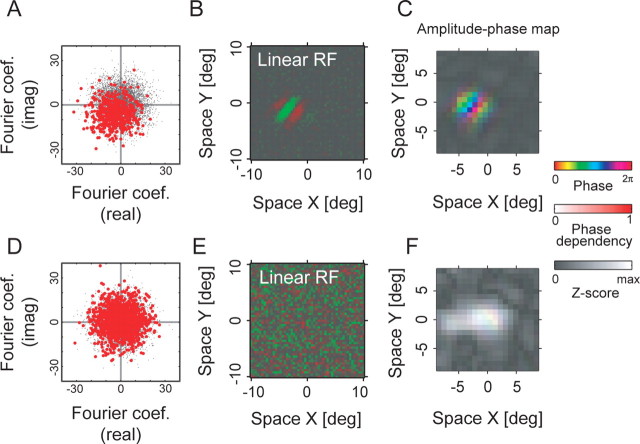
To gain an understanding on how phase dependence may be extracted from the data, we must first clarify how phase dependence metrics are defined statistically based on individual spike data and stimulus frames. The red dots in Figure 7, A and D, show distributions of unaveraged Fourier coefficients for spike-triggered stimuli (for the optimal correlation delay) for the simple and complex cells shown in Figure 4, respectively. These distributions are for the optimal spatial frequency, orientation, and position (i.e., the conditions corresponding to the peaks of Figure 4, B and E). Because a Fourier coefficient is a complex number, each coefficient is plotted as a point on a two-dimensional complex plane with a real and an imaginary component. In this domain, the distance and angle of the dot from the origin indicate the amplitude and spatial phase, respectively, of a sine wave of the given frequency that is contained in the relevant region of the stimulus.

Figure 7.

Spatial phase sensitivities are calculated for a simple cell (A–C) and a complex cell (D–F). A, Fourier coefficients for the maximally effective spatial frequency component in stimuli that led to spikes are shown (red dots) for the optimal correlation delay of 45 ms. The centroid of red dots is offset from the origin indicating selectivity for a given phase. For estimating the distribution for the noise stimuli themselves, Fourier coefficients for the same frequency component are also shown for all frames of the subfield of noise sequence (gray dots). Only the coefficients for one frequency component for the maximally responsive subfield are used. B, Spatial receptive field map obtained by a standard reverse correlation procedure. C, Spatial structure of the phase dependency. The optimal spatial phase, PSI (see Results), and signal amplitude of the LSRC analysis are represented as hue, saturation, and brightness, respectively. D–F, The same as A–C, but for a complex cell. The two cells are the same as those shown in Figure 4. For C and F, the maximum values for the Z-scores were 34.1 and 17.5, respectively. coef., Coefficient; imag, imaginary; deg, degree; RF, receptive field; max, maximum.

Note that the centroid of red points in Figure 7A is biased toward the bottom left side. This corresponds to the fact that the simple cell tends to respond to stimuli of a particular phase and tends not to respond to the anti-phase stimuli. For comparison, if we plot Fourier components for all stimulus frames for the corresponding condition without regard for spikes from the neuron, we obtain a distribution depicted by gray dots in Figure 7A (there are more gray dots than red ones). The distribution is unbiased with respect to the origin, indicating that the noise stimulus sequence contain a homogeneous distribution of Fourier components with respect to spatial phase. On the other hand, the complex cell did not show such phase dependency as illustrated in Figure 7D, where the distribution of red dots, the spike-triggered Fourier coefficients, is unbiased and centered nearly exactly at the origin. The distribution of gray points are hidden behind the red dots in Figure 7D.

Therefore, the magnitude of the phase dependency can be determined from the bias in the distribution of Fourier coefficients for spike-triggered stimuli in the complex domain. We quantify the bias by calculating a vector sum of the spike-triggered Fourier coefficients and define the phase selectivity index (PSI), for each frequency and position, as follows:

where f_spike are spike-triggered Fourier coefficients, f_total are the Fourier coefficients for the entire stimuli, n_spike is the number of spikes, and n_total is the number of total frames in the entire stimulus sequence. The PSI should be high when a cell responds in a phase-dependent manner as in Figure 7A and is close to 0 when there is no phase dependency as Figure 7D.

By using the PSI, we can obtain a spatial map of phase dependency together with the signal magnitude. Such a map allows us to examine possible spatial variations, if any, of local phase sensitivity within a given receptive field. Figure 7, C and F, shows spatial “amplitude-phase” maps for the simple and complex cells, respectively. In these plots, the signal magnitude for each subfield is represented as luminance, whereas the PSI and the preferred spatial phase are shown as saturation and hue, respectively. In these representations, only the PSI values for a fixed (optimal) spatial frequency were used. Spatial variations of the phase dependency for the simple cell can be seen by its map with highly saturated colors in Figure 7C. A similar map for the complex cell (Fig. 7F) consists of points with highly desaturated (almost white) colors, because the cell shows little phase dependency.

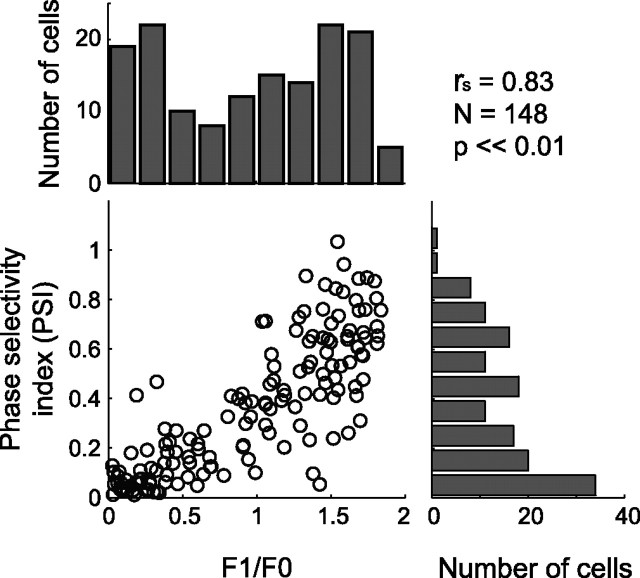
The PSI should have a close relationship to the conventional classification of the simple and complex cell. To what extent is the PSI correlated with the modulation ratio (Skottun et al., 1991; Li et al., 2003; Priebe et al., 2004), the standard criteria for classifications of simple and complex cells? Figure 8 summarizes the result. In this figure, only the PSI value for the spatial position with maximal Z-score is used for each neuron. There is a significant correlation between the PSI and the modulation ratio (p ≪ 0.01; test for Spearman’s correlation coefficients). Therefore, our result opens a possibility of classifying simple and complex cell types based on the dense noise mapping data alone, which was not possible previously because the linear receptive field profiles typically do not show any structure and are indistinguishable noise for many complex cells (Fig. 7E).

Figure 8.

A relationship is shown between the PSI and the conventional modulation ratio (F1/F0). The histograms at the top and the right show distributions of these indices separately. There is a significant correlation between the PSI and F1/F0 ratio (p < 0.01; test for the Spearman’s correlation coefficient).

Profiles of suppression

The LSRC analysis can also visualize suppressive profiles of visual neurons, as suggested by the simulation study (Fig. 2D). Figure 9A–D shows an example cell that exhibits clear suppressive components. Although the linear receptive field (Fig. 9C) only captures the facilitatory profile, LSRC reveals the existence of both facilitatory and suppressive components as indicated by the red and blue regions, respectively, in Figure 9, A and B. The suppression appears to be strongest at an orientation approximately orthogonal to that for facilitation. However, we should use caution in interpreting the results regarding how the suppression is organized as a function of stimulus orientation. Figure 9D shows an orientation tuning profile obtained from a conventional drifting grating test. Responses to the off-peak orientation are less than the spontaneous discharge rate of the neuron, which is a reflection of the suppressive effect. However, this suppression seems to be present for virtually all orientations, except for the peak, and not just for the orientation orthogonal to the optimal (DeAngelis et al., 1992). The LSRC analyses calculate the net sum of facilitation or suppression for each frequency and thus can only visualize whichever is stronger. Therefore, it should be noted that we cannot discriminate the following possibilities apart: whether the suppressive effects exist for all orientations of the frequency range overlapped to the facilitatory one or whether they exist just for orientations nearly orthogonal to the optimal.

Figure 9.

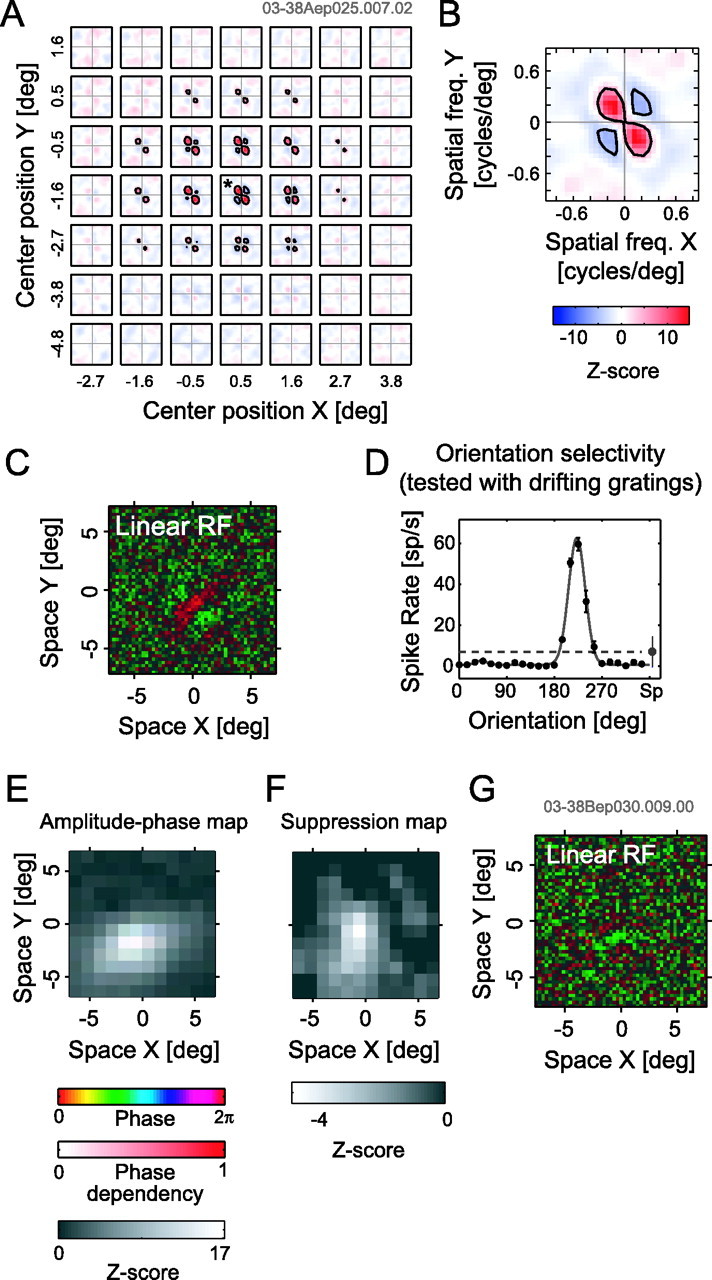
Data from cells with suppressive responses are shown for two complex cells in area 18. A, A result of the LSRC analysis. The reddish regions (Z-score >0) indicate facilitatory components, whereas the bluish regions (Z-score <0) show suppressive components. B, Magnified tuning for a local spectral map, indicated by an asterisk in A. C, Linear receptive field profile. D, An orientation tuning curve obtained by a conventional drifting grating test. The dashed horizontal line indicates the spontaneous firing rate. E–G, Data from another neuron. E, Amplitude and phase map for facilitatory responses in the same format as that of Figure 7, C and F. The facilitation was evaluated at the spatial frequency and orientation of 0.33 cycles/degree and 18°. F, Suppression map is shown using the Z-score only. The suppression was evaluated at the spatial frequency and orientation of 0.23 cycles/degree and 117°. G, Linear receptive field for the second neuron. deg, Degree; freq., frequency; RF, receptive field.

Even with the limitations noted above, the ability of the LSRC method for mapping the degree and spatial parameters of suppression in addition to facilitation would be useful in general for examining potentially inhomogeneous properties of the response profile of the cell. Figures 9E–G shows another example cell exhibiting a form of inhomogeneity, in that spatial areas for facilitation (E) and suppression (F) are not exactly overlapped. The facilitation and the suppression were evaluated at different spatial frequencies and orientations where each was most predominant. Although the facilitatory area appears to be elongated horizontally, the suppressive area shows a vertical elongation and is smaller than that for the facilitation. The smaller spatial extents for the suppression are consistent with findings of a previous study (DeAngelis et al., 1992).

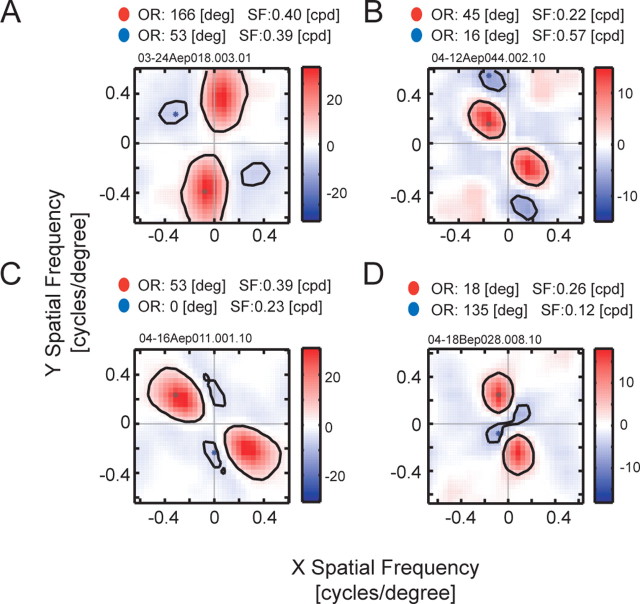
Figure 10 shows two-dimensional frequency tuning profiles of four cells that exhibit strongest suppressions among our data. The optimal frequency for suppression is neither always orthogonal in the orientation nor identical in their spatial frequency to the facilitatory peak (Fig. 10B). Although several previous reports have also pointed out that optimal spatial frequencies for facilitation and suppression are not always identical (Bonds, 1989; DeAngelis et al., 1992), determining parameters for the optimal suppressive stimuli has been quite difficult based on one-dimensional tests. For example, to obtain the suppressive spatial frequency tuning, one had to select an orientation for the suppressive stimulus and vary its spatial frequency. With such tests, even a strong suppression like the one shown in Figure 10B could have easily been missed because both the optimal suppressive orientation and spatial frequency are different from the typical values of these parameters. Two-dimensional tests in the joint orientation and spatial frequency domain, such as those used by Ringach et al. (2002) and ours, are generally required for accurately determining optimal parameters of suppression. It is somewhat puzzling that, among our population of cells, only 10 of 193 cells showed significant suppressive profiles (t test with Bonferroni’s correction; p < 0.01). Previous work based on superimposed drifting sinusoidal gratings (plaid) stimuli seems to find some degree of cross-orientation suppression for most neurons (DeAngelis et al., 1992). It might be related to the difference in the type of stimuli used (dense noise vs plaids), because it is known that response profiles, especially the suppressive profiles, are different depending on the class of stimuli used to acquire tuning profiles (David et al., 2004). It may also be related to the fact that we use Bonferroni’s correction for quantitative estimates of the strength of facilitation and suppression. This correction may have been too conservative. Another point we should consider is that uncovering suppression depends on the mean firing rate of the cell to the noise stimulus. In any case, our sample size does not allow summaries of the relationship between the facilitatory and suppressive parameters of these neurons. Resolution of these issues requires comparative studies of suppression using both dense noise and grating stimuli.

Figure 10.

Two-dimensional spatial frequency tunings are shown for four additional cells that exhibit significant suppressions in the LSRC analysis. A, A two-dimensional spatial frequency tuning for the subfield with the strongest suppression for a complex cell in area 17. B, A similar tuning map for a simple cell in area 17. C, D, Similar plots for two complex cells in area 17. OR, Orientation; SF, spatial frequency; deg, degree; cpd, cycles per degree.

Discussion

Relationship to previous studies

Previous methods for mapping receptive fields and stimulus selectivities of neurons have certain advantages but also suffer from various shortcomings. For example, standard dense noise receptive field mapping generally allows measurements of first-order receptive fields, making it suitable for mapping simple cell receptive fields (Alonso et al., 2001). However, mapping attempts generally fail for complex cells and neurons in higher-order visual areas with substantial nonlinearities. Although it is theoretically possible to measure second- and higher-order receptive field maps, the amount of time required for measurements generally becomes prohibitively long in practice. Therefore, despite the advantage of having the least number of assumptions about what visual features neurons may be sensitive to, the white-noise stimuli have only been moderately effective. Alternative approaches, adopted by the majority of recent studies, have been based on a finite set of computationally generated complex stimuli rich in curved elements, such as non-Cartesian gratings (Gallant et al., 1993, 1996) and curvature-direction stimuli (Pasupathy and Connor, 2001). Although these analyses have been very effective in revealing key stimulus features that excite neurons, the stimulus sets are inherently finite, and assumptions about possible domains of selectivities are built into the stimuli implicitly. Ideal stimulus sets therefore would be those (1) with infinite possible configurations, (2) minimum assumptions, and (3) applicability for all cell types and possible neural connections. LSRCs have many of such ideal properties and could provide an experimental framework for revealing selectivity to the complex visual features.

Recently, several groups have shown that neurons in the primary visual cortex can be described as a set of spatiotemporal linear filters, and these underlying filters can be estimated by conducting a spike-triggered covariance (STC) technique (Touryan et al., 2002; Rust et al., 2004, 2005). The STC and LSRC analyses seem to share several desirable features, especially in that both of these techniques attempt to reveal filtering profiles underlying the responses of neurons and that both of them use white-noise sequences. A notable advantage of LSRC would be its efficiency. Although the LSRC procedure is essentially a first-order approximation of filtering profiles, the STC procedure belongs to a class of second-order approximations and thus need more spikes to map underlying properties. Practically speaking, whereas STC requires several tens of thousands of spikes to generate response profiles of reasonable signals (Rust et al., 2005), LSRC needs only a few thousands of spikes to obtain significant signals, and we could obtain excellent profiles with as few as ∼5000 spikes. In our recording sessions (two-dimensional white-noise stimulation in anesthetized cats), we rarely encounter cells that elicit several tens of thousands of spikes within a typical recording time of ∼30 min. Therefore, LSRC may be applicable to a wider variety of visual areas than STC, especially the areas where the white-noise sequences could elicit relatively a small number of spikes.

Inhomogeneity of response profiles

One of our key motivations for developing LSRC was to find possible spatial inhomogeneities of response profiles, such as local variations of preferred orientations within a given receptive field, that could serve to produce selectivities to complex visual features, particularly those with curved elements. By applying LSRC to cells in the early visual cortex, we found two types of spatial inhomogeneities: (1) a small subset of neurons shows local variations of preferred orientation and spatial frequency within their receptive field; and (2) spatial extents for facilitatory and suppressive components are not always overlapped exactly. Although the proportion of neurons that possess spatial inhomogeneities is not large in the early visual cortex, the existence of these classes of cells may, nevertheless, mean that the processing of complex object features begins at this stage. It would also supply baseline data for selectivity variations within the receptive fields in the early visual cortex, which would be valuable in constraining possibilities of building up downstream neurons that are much more selective to local feature combinations.

Parameter selections in the LSRC analysis

In this study, we have performed the LSRC measurements with relatively high-density stimuli (dot size, 0.2–0.4°) to ensure the ability to reveal receptive field structures tuned to high spatial frequency components. The Nyquist frequency for our typical configurations is 1.25–2.5 cycles/degree, which is reasonably higher than the frequency that is known to be signaled by cells in the early visual cortex of cats (Movshon et al., 1978b; Zhou and Baker, 1994). Although, theoretically, we could use even smaller dots to increase the Nyquist frequency, the average power within each frequency band (thus ability to elicit spikes) would decrease for stimuli consisting of small dots. Trials would be needed to determine reasonable ranges of dot density when applying LSRC to other visual areas.

In the LSRC procedure, we are able to choose arbitrarily the position, size, and steps of the Gaussian window (i.e., the area over which the spectrum is computed) after the experiments are completed. This is one of the advantages of the LSRC method, because we need not be concerned about the exact position and boundary of the receptive field during the experiments. In other words, the spatial parameters of the analysis may be optimized post hoc via trials on the data. These features make LSRC particularly suitable for recordings via large multielectrode arrays. Receptive fields of many cells recorded from such electrodes may span a substantial area of the visual field as well as being tuned to a wide range of parameters. However, in the analyses, we should choose carefully the size of the window. If the size is too small, we cannot acquire proper response profiles for low spatial frequency spectra. On the other hand, if the window size is too large, we lose spatial resolutions. We selected our size of analysis such that the analysis window covers at least a half of the period of the optimal spatial frequency within 1 σ of the Gaussian if the cell shows clear bandpass profiles in their spatial frequency tunings. In rare cases in which neurons had a low-pass spatial frequency tuning, we used the σ value corresponding to one-fifth of the mapped area.

Possible applications and limitations

In this study, we have limited our scope only to the spatial aspects of receptive field profiles, and the LSRC analyses were performed only in the two-dimensional spatial frequency domain. However, the LSRC analysis can naturally be extended to include the temporal domain for studying response profiles in a joint three-dimensional (two-dimensional spatial and a temporal) frequency domain. Because there is physiological evidence that temporal property of cross-orientation inhibition is different from the facilitatory profile (Allison et al., 2001), it is of interest to examine whether the suppression and facilitation could be mapped separately in the three-dimensional frequency domain.

It is natural to think of the applications of LSRC for cells in the higher-order visual areas, such as V2 and V4. Because the cells in these areas are known to respond to more complex stimuli (Gallant et al., 1993, 1996; Pasupathy and Connor, 2001; Ito and Komatsu, 2004), it is of interest to examine how local spectral response profiles are organized for cells in these areas. However, the current LSRC method is probably not applicable to neurons with strong position invariance such as those in the inferotemporal cortical area (Ito et al., 1995; Tanaka, 1996), because tunings for given oriented segments are not tied to specific locations within the receptive field in these areas.

The area MT is another candidate for the application of LSRC. There is a well known model for MT pattern motion-selective neurons (Movshon et al., 1986) by Simoncelli and Heeger (1998). In their model, MT neurons are constructed by summing output of V1 neurons satisfying the constraints for a given velocity. The spatiotemporal LSRC analysis, as describe above, should be able to provide response profiles in the three-dimensional joint domain (spatial frequency, orientation, and temporal frequency) and thus could be used to assess the validity of the model directly, extending the work by Perrone and Thiele (2001). Position invariance is expected for responses of MT neurons. However, it is not a limitation in this case, because LSRC is not used to detect spatial inhomogeneity. Instead, it is used to determine whether the spatiotemporal frequency domain receptive field of MT neurons has a planar organization as proposed by Simoncelli and Heeger (1998).

In conclusion, LSRC is a highly general and efficient method for characterizing neurons in intermediate-stage visual areas beyond the primary visual cortex. The use of random noise stimuli, with the minimum of assumptions about what the cells might be “looking for,” makes the LSRC method particularly suitable for multielectrode, multicell recordings. This is because, at least for initial bulk characterizations, it is desirable not to optimize stimulus parameters only for a selected set of neurons. Therefore, our study provides a basis on which the results from other areas may be compared with respect to inhomogeneities of tuning properties within receptive fields.