The Dynamics of Spatiotemporal Response Integration in the Somatosensory Cortex of the Vibrissa System

Abstract

Spatiotemporal response integration across the neural receptive field (RF) is a general feature of sensory coding and has an important role in shaping responses to naturalistic stimuli. In the primary somatosensory cortex of the rat vibrissa pathway, such integration across the vibrissa array strongly shapes the coding of spatiotemporally distributed deflections. Using a spatiotemporal paired-pulse paradigm, this study revealed that fundamentally different types of pairwise interactions have similar qualitative behavior but that the magnitude, latency, and precision of the neural responses depend on the specific RF components being engaged. In all cases, however, increase in the suppression of response magnitude accompanied a lengthening of latency and a decrease in response precision. Furthermore, nonlinear interactions evoked by stimulation of multiple RF subregions strongly influence both response magnitude and timing to more complex sequences. Despite their complexity, such response interactions are highly predictable from elementary pairwise interactions. To understand the functional role of spatiotemporal interactions in coding, we developed a response model that incorporated the experimentally measured modulations in response magnitude, latency, and precision induced by cross-vibrissa interactions. Simulations of a simplified textural discrimination task indicate that spatiotemporal interactions enhance discrimination under certain stimulus time scales. This improvement follows from a nonlinear response property that acts to restore the neural response in the face of suppression. Together, the present findings highlight the role of response integration in shaping single-cell responses and provide predictions about how changes in response parameters influence coding accuracy.

Introduction

Rats and other rodents use arrays of facial vibrissae to actively discriminate between surface features in the external world with a high degree of accuracy (Guic-Robles et al., 1989; Carvell and Simons, 1990, 1995). The resulting multi-vibrissa deflections, underlying the animal's tactile perception, possess spatiotemporal correlations shaped by dynamics of active whisking, vibrissa anatomy, and the mechanics of vibrissa-surface interface. Given that thalamocortical receptive fields (RFs) typically span multiple vibrissae (Simons, 1978; Armstrong-James et al., 1987), spatiotemporally distributed deflections engage multiple RF subregions and produce complex temporal patterns of neuronal activity. Understanding how spatiotemporally distributed stimuli are encoded is therefore essential to the study of sensory processing in the vibrissa system. Interactions between RF subregions are common to visual (Gilbert et al., 1990; Nelson, 1991), auditory (Brosch and Schreiner, 1997), and other somatosensory (Gardner and Costanzo, 1980a,b; Laskin and Spencer, 1979) pathways and likely serve an important role in view of the highly correlated structure of the sensory world. However, the resulting interplay between excitatory and inhibitory mechanisms is still not fully understood. Here, we use the rat vibrissa pathway to determine how the dynamics of response integration shape responses to spatiotemporally distributed stimuli.

Several studies have shown that responses to deflections of the vibrissa at the center of the RF of a somatosensory cortex (SI) neuron [i.e., the primary vibrissa (PV)] interact with the responses to other vibrissae in the RF [i.e., the adjacent vibrissae (AV)]. The suppressive effect of these interactions causes a single deflection to attenuate the response to a second over a wide time scale (10–200 ms) (Simons, 1985; Simons and Carvell, 1989; Brumberg et al., 1996; Kleinfeld and Delaney, 1996; Mirabella et al., 2001). The observed cortical dynamics likely arise from several sources: (1) inhibitory feedback between the thalamic ventroposterior medial nucleus (VPM) and reticular nucleus (nRT), with subsequent feedforward relay from the VPM; (2) depression of the thalamocortical synapse; and (3) intracortical inhibition. Regardless of the biophysical substrates, pairwise interactions caused by a single vibrissa reflect the interplay between functionally excitatory and inhibitory RF components (Zhu and Connors, 1999) and give rise to more complex, yet predictable, responses with the presentation of additional stimuli (Webber and Stanley, 2004).

This study addressed the question of how SI cells encode spatiotemporally distributed stimuli. The resulting responses were strongly influenced by cross-vibrissa interactions. In particular, the addition of even one spatial component (an AV) dramatically altered the single-cell frequency response from that measured with sole stimulation of the PV. Suppression of the spike-count response was strongly correlated with both an increase in the latency and a reduction in the temporal precision of the response. Moreover, a model using the observed pairwise interactions accurately predicted the responses to single- and paired-vibrissa stimuli. This model demonstrated that, over certain time scales, the cross-vibrissa interactions characterized here enhance the discriminability of distributed patterns. This improvement is attributable to a nonlinearity that partially lowers the amount of response suppression. Together, the findings highlight the importance of spatiotemporal interactions to the coding of distributed deflection patterns, which may be critical in the natural environment.

Materials and Methods

Surgical preparation.

All procedures were approved by the Animal Care and Use Committee at Harvard University and were in agreement with guidelines established by the National Institutes of Health. See the study by Webber and Stanley (2004) for a detailed description of experimental methods. Briefly, female albino rats (250–330 g; Sprague Dawley) were sedated with 2% vaporized isoflurane and anesthetized with sodium pentobarbital (50 mg/kg, i.p., initial dose); supplemental doses (typically 12 mg/kg/h) (Zhu and Connors, 1999) were given as needed to maintain a light level of anesthesia, confirmed by observations of heart rate, respiration, and eyelid/pedal reflexes to averse stimuli (toe or tail pinch). After initial anesthesia, the animal was mounted on a stereotaxic device (Kopf Instruments, Tujunga, CA) in preparation for the surgery and subsequent recordings. After the initial midline incision on the head, tissue and skin were resected, and connective tissue was removed. A small craniotomy (∼2 mm in diameter) was made over the barrel field (stereotaxic coordinates: 1.0–4.0 mm caudal to the bregma, 3.0–7.0 mm lateral to the midline) (Paxinos and Watson, 1998). The dura was left intact. A dam was created with bone wax around the craniotomy, and the cortex was covered with mineral oil solution to stabilize the recording and provide additional protection for the cortical surface. After the recording session, the animal was killed with an overdose of sodium pentobarbital.

Electrophysiology.

Single-unit extracellular recordings were obtained using single tungsten microelectrodes (3–7 MΩ; FHC, Bowdoinham, ME). All recorded cells resided at depths of 500–1200 μm, commensurate with cortical layers III–V. Both data acquisition and actuator control were performed using C++ routines written within the LabWindows acquisitions/control software environment (National Instruments, Austin, TX). Neuronal signals were amplified (A-M Systems, Sequim, WA) and subsequently acquired using a National Instruments signal conditioning unit that fed into an analog-to-digital board (sampling at 20 kHz/channel) in a data acquisition computer. Standard template matching techniques and physiologically plausible refractory periods were used to identify and sort spikes (Lewicki, 1998): a threshold was used to acquire candidate spike waveforms, and several parameters of the putative spike (e.g., waveform peak and trough, time to peak, and time to trough) were then used to assign action potentials to single-cell clusters. For all recorded neurons, spontaneous activity was collected before the beginning of the stimulus trials and again after all stimuli were presented. Cortical RFs were determined manually by identifying all vibrissa that elicited spiking responses for each recorded cell. The PV was identified as the whisker generating maximal responses. All analyses were performed with routines written in Matlab (Mathworks, Natick, MA) and C programming languages.

From a total of 40 units, only cells (n = 30) classifiable as regular-spike units (RSUs) are reported in this study. Based on latency analyses (PV, 7.8 ± 1.5 ms; AV, 11 ± 2 ms), all included cells are likely to reside in monosynaptic thalamocortical recipient zones. Additional criteria for their selection and inclusion, listed below, were consistent with those used by studies that target RSUs in SI: (1) stability of baseline responses to PV and AV deflections over the duration of the experiment, used to ensure consistency over the long (∼3 h) recording interval; (2) width of action potentials (typically 1.5 ms) (McCormick et al., 1985), used to exclude putative inhibitory units [i.e., the fast spiking units (FSUs)]; (3) extracellular responses to, at most, 1–2 AVs (Simons and Carvell, 1989; Brumberg et al., 1996), to ensure that the neuron did not reside in the septa; and (4) shifts in response latency during periodic stimulation by up to a factor of 3, again implying that they likely do not reside in the septa (Ahissar et al., 2000, 2001). Within this group of RSUs, examination of PV and AV response latencies revealed that recordings were likely from layers receiving monosynaptic thalamic inputs, which include layers II/III–VI (Woolsey and Van der Loos, 1970; Jensen and Killackey, 1987; Lu and Lin, 1993).

The average RSU spontaneous activity is slightly <3 Hz (see Results). This value is somewhat higher but still within the range previously reported by studies on anesthetized animals (∼1–3 Hz) (Brumberg et al., 1996; Higley and Contreras, 2003; Ego-Stengel et al., 2004). The small discrepancy can arise from a number of factors. Variations in the level of anesthesia are known to affect the spontaneous firing rates, thus accounting for some of the observed discrepancy. Furthermore, given the likely presence of both supragranular and infragranular RSUs in the data set, laminar variation of spontaneous activity may also explain the higher observed spontaneous rates. Regardless of spontaneous activity and laminar position, all units exhibited qualitatively similar behaviors in response to stimuli.

Vibrissa stimulation.

A pair of multi-layered piezoelectric bending actuators (range of motion, 1 mm; bandwidth, 200 Hz; Polytec PI, Auburn, MA) produced independent PV and AV stimulations for each recorded cell. Deflections were calibrated using a photo-diode circuit, by determining the relationship between command voltage steps and the resulting deflection amplitudes and velocities. Calibration of the two stimulators was performed using a slotted infrared switch (QVA11134, Fairchild Semiconductor), analogous to the method described by other studies (Andermann et al., 2004; Arabzadeh et al., 2005). Briefly, as the tip of the actuator interrupts the path of the infrared beam, the output voltage of the optical switch changes in direct proportion to the tip displacement. This change in voltage was subsequently transformed to the corresponding change in actuator displacement using the linear relationship between small changes in beam occlusion and output voltage (also determined experimentally).

Actuators were placed 10 mm from the face, and each of the two vibrissae was inserted into a 4 cm section of a 20 μl glass pipette that was fixed to the end of the actuator (∼0.57° per 100 μm deflection). For one subset of cells (n = 12), ramp-and-hold pairwise sequences were presented using square-waves of variable duration (amplitude, 400 μm; rise time = fall time, 2 ms) (see Fig. 1B). Pulse deflections (see Fig. 1B) consisting of exponential rising and falling phases (99% rise time = 99% fall time, 5 ms; amplitude, 600 μm) were used for the rest of the recorded cells (n = 18). These stimuli are identical to those described previously in the literature (Ahissar et al., 1997; Hartings and Simons, 1998; Hartings et al., 2003; Khatri et al., 2004). The resulting average deflection velocity, as measured by the average rate of rise to maximum amplitude, was ∼200 mm/s for square-wave transients and ∼120 mm/s for the pulse stimuli. Measurement of pipette deflections revealed that poststimulus oscillations (i.e., ringing) of the piezoelectric actuator consisted of a maximum overshoot of, at most, 100 μm for pulse stimuli and 200 μm for square-wave stimuli and decayed with a time constant of <20 ms.

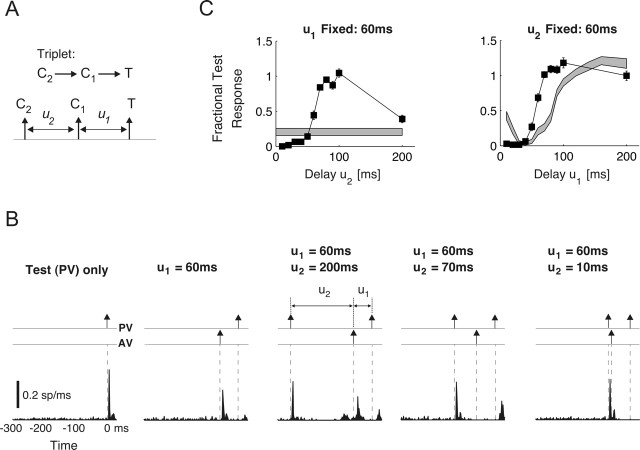
Figure 1.

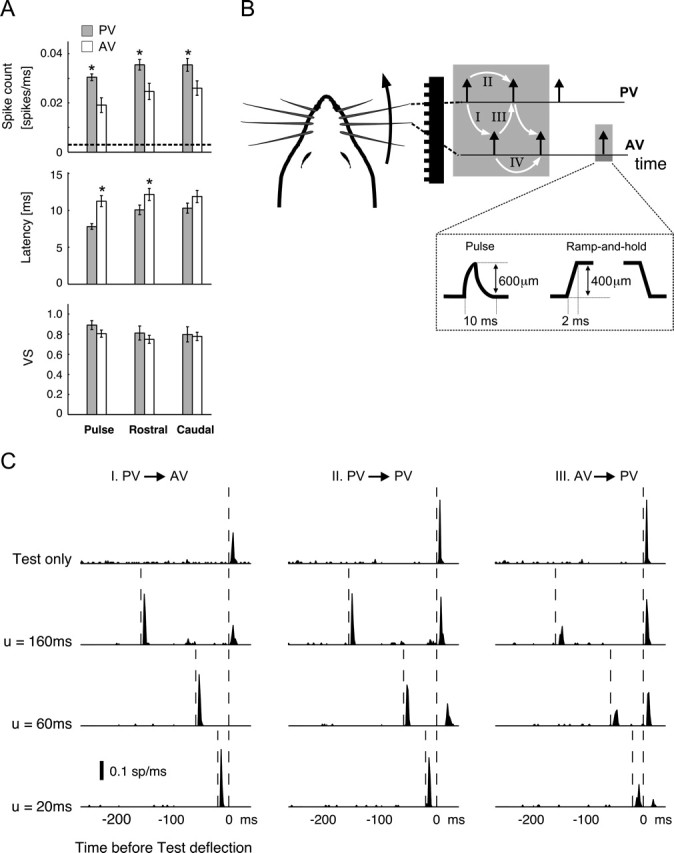
Pairwise interactions for a multi-vibrissa stimulus. A, From top to bottom, bar plots illustrate the averaged spike count, latency, and VS of isolated PV (gray bars) and AV (open bars) responses to the three types of stimuli used in this study. Error bars denote ±1 SEM. The asterisks mark the cases in which the difference between PV and AV measurements was significant (p < 0.05 in all cases; t test). B, Schematic of whisking geometry and evoked contact times for a PV–AV pair over a corrugated surface. White arrows and the corresponding labels I–IV identify four types of pairwise interactions that are experimentally measured here (I, PV→AV; II, PV→PV; III, AV→PV; IV, AV→AV). Additionally, the dashed box illustrates the amplitudes and time courses of both pulse and ramp-and-hold stimuli used in the study. C, Example of pairwise interactions for an individual cell. Each column shows the response to a particular pairwise sequence at three values of interdeflection delay u. In each column, the first row shows the first-order (baseline) deflection response. Rows 2–4 represent responses to deflection pairs with u = 160, 60, and 20 ms, respectively. All PSTHs are shown with time bins of 2 ms. Vertical dashed lines represent deflection times. The AV→AV interaction is not shown here because of its similarity to the PV→PV response for this cell; see Figure 2 for a summary of all pairwise responses (including AV→AV).

Because of the brief and transient nature of stimuli presented, stimulus times used in subsequent computations were taken to be the times at which deflection onsets occurred. All deflections were in the rostrocaudal axis for both stimulus types. For square-wave stimuli, PV movements in the rostral and caudal directions were distinguished as PVr and PVc, respectively. Similar notation is used for AV movements. In the case of pulse stimuli, the rising phase was always in the rostral direction. Therefore, these stimuli are only denoted by the type of the vibrissa that was moved (i.e., PV or AV). In all cases, the AV was immediately caudal to the PV.

Conditioning-test sequences for square-wave stimuli consisted of the following: I, PVr→Avr; II, PVr→PVc; III, AVr→PVc. For sequences I and III, the duration of the ramp-and-hold deflection was fixed at 500 ms, ensuring that the response to the rising (i.e., ON) edges would be unaffected by the subsequent falling edges (i.e., the OFF transients). The duration of the ramp-and-hold stimuli for the PVr→PVc sequence, however, varied over a wide range (see below). We therefore confirmed that the ON response in these cases was not significantly different from that measured in the absence of the following OFF deflection. OFF deflections therefore did not likely interfere with the measurement of the response to the previous ON stimuli. Pulse sequences consisted of the following four variations: I, PV→AV; II, PV→PV; III, AV→PV; IV, AV→AV. The conditioning-test time delays were varied over the following ranges: 10–160, 240, and 260 ms for the PV→PV, PVr→PVc, and AV→AV sequences and 0–100, 120, 140, 160, and 200 ms for the AV→PV, AVr→PVc, PV→AV, and PVr→AVr pairs. More interdeflection interval (IDI) values were used for the measurement of the PV–PV and AV–AV pairs compared with the PV–AV and AV–PV sequences. This was attributable to the fact that prediction computations (described in Results) required the greater number of measurements for the iso-vibrissa pairs. For stimulus triplets, the C₂→C₁→T sequences consisted of PV→AV→PV for pulse stimuli and of PVr→AVr→PVc for square-wave deflections. Periodic stimuli were presented for 25 repeats using only the pulse stimuli (see Results for a description of the frequencies and inter-vibrissa phases used).

For each stimulus pair or triplet, 60 repeats of the sequence were presented at a repetition frequency of 1 Hz. In contrast, significantly longer intervening delays (10 s) were placed between repeats of the periodic stimuli to minimize the effects of synaptic adaptation occurring over longer time scales than those addressed in this study (Chung et al., 2002). Together, presentation of the entire stimulus battery lasted approximately 3 h, limiting both the study to units that were stable over this relatively long period and the cell yield per animal.

Because responses using pulse and square-wave stimuli were very similar in magnitude and time course, for simplicity only, single-cell recordings from pulse stimuli are shown in Results. As also indicated in Results, however, all group analyses include all recorded cells (i.e., using both pulse and square-wave stimuli).

Response measures.

Peristimulus time histograms (PSTHs) in response to repeated presentations of the stimulus were generated using a time resolution of 2 ms. To quantify response magnitude, the average spike-count response over the 3–30 ms poststimulus interval was computed as the area under the PSTH curve. This window was chosen on the basis of the following two considerations: (1) RSU responses to deflections typically have only a short latency component (with PV responses having delays as low as 7 ms); and (2) possible intracortical contributions to AV responses (Armstrong-James et al., 1991; Fox et al., 2003) can lead to slightly longer latencies in such cases (up to ∼20–30 ms).

The response to a stimulus pair demonstrates the simplest type of spatiotemporal interaction. In this case, the response to the second deflection (termed the test) is attenuated as a function of the temporal separation between the two stimuli. The conditioning-test ratio (CTR) curve (defined in Fig. 2A) was used to quantify the attenuation of the test spike count response relative to its unattenuated (baseline) value. Previous studies (Simons and Carvell, 1989; Fanselow and Nicolelis, 1999; Webber and Stanley, 2004) have shown a sigmoidal form for the dependence of CTR curves on the IDI u. We therefore used the following parametrization to fit all measured CTR curves:

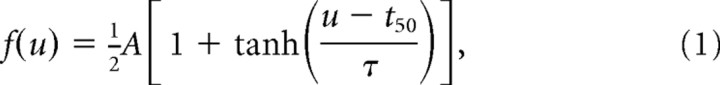where parameters {A, t₅₀, τ} were estimated through least-squares fits. Importantly, this parametrization is valid for IDIs longer than 5–10 ms. For shorter delays, cross-vibrissa interactions may, in fact, facilitate the test response (Shimegi et al., 1999). In the general case consisting of multiple preceding conditioning stimuli {C₁, … C_n}, the change in test response was defined identically. In this case however, the measured ratio is referred to as the fractional test response, to distinguish it from the more simple pairwise interaction.

Figure 2.

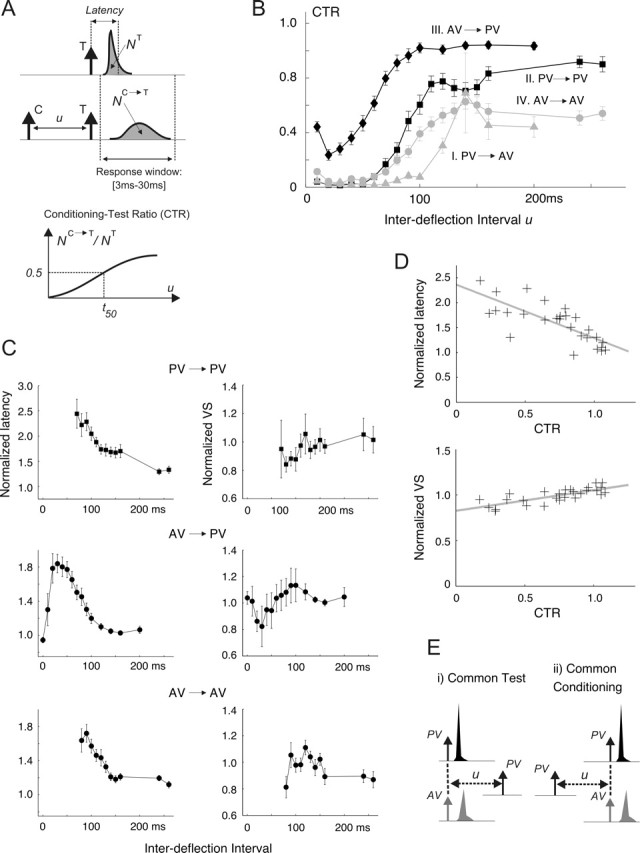
The effects of pairwise interactions on the deflection response. A, The CTR was computed for a range of IDIs by (1) computing the spike-count response to the test (T) stimulus (N^C→T) in presence of a preceding conditioning (C) deflection and (2) normalizing this quantity by the response measured when T is presented in isolation (N^T). Spike count is computed as the area under the measured PSTHs over the 3–30 ms poststimulus time window. Latency represents the center of mass of the PSTH. VS quantifies the precision of the PSTH response and is defined in Materials and Methods (see Response measures). B, Average CTR measurements for pulse stimuli: I, PV→AV (gray triangles); II, PV→PV (black squares); III, AV→PV (black diamonds); IV, AV→AV (gray circles). Error bars represent 1 SEM, computed with n = 18. Qualitatively similar results were obtained using square-wave stimuli (n = 12). C, Both the latency and the VS of test responses in the presence of the conditioning stimulus are normalized to the values measured for the test presented in isolation. The resulting normalized latency (left column) and VS (right column) curves are shown for the PV→PV, AV→PV, and AV→AV interactions. The corresponding results for PV→AV are not shown because the majority of the estimates were unreliable as a result of the typically small AV responses (see text). D, The top scatter plot shows the relationship between the CTR value and the normalized latency of the PV response; PV→PV and AV→PV data are combined, so that each point on this plot corresponds to an average measurement at a given IDI. The x-coordinate of the point is the population-averaged (n = 18) CTR value at that IDI; its y-coordinate represents the corresponding population-averaged normalized latency. The gray line shows the linear regression of the latency ratio onto the CTR value (r = −0.76; p < 1e-4; y = −1.08x + 2.36). The bottom scatter plot illustrates an analogous relationship between the CTR value and the normalized test VS (r = 0.77; p < 1e-4; y = 0.23x + 0.83). E, Conditioning→test sequences are divided into two groups. i, Common test stimulus (left). For pulse stimuli, these consist of PV→PV and AV→PV. ii, Common conditioning stimulus (right), which for pulse stimuli considered here consist of PV→PV and PV→AV. A similar grouping can also be made using the AV→AV as the basis for comparison (in place of PV→PV).

In addition to response magnitude, the timing of single-cell responses was studied with two measures: (1) the latency was defined as the average time delay between the stimulus and evoked spikes and was computed as the center of mass of the single-cell PSTH in the 3–30 ms poststimulus time window; (2) vector strength (VS) (Goldberg and Brown, 1969) quantifies how strongly the spikes time-lock to the stimulus and therefore reflects the temporal precision of the response. Given a sequence of stimuli and the corresponding spike times,

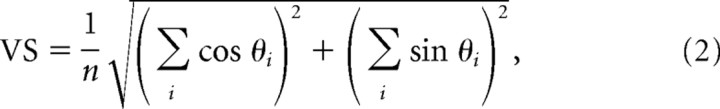where θ_i = 2πt_i/T, t_i is the latency of the ith spike relative to the latest stimulus, and T is the duration of the poststimulus response window (here 27 ms). Similar to the VS measure used by Higley and Contreras (2006), this short window ensures that both magnitude and timing measures correspond to the same time interval.

Limits imposed on texture discrimination.

To understand how cross-vibrissa interactions influence the accuracy with which spatiotemporal deflection patterns are coded, we used ideal-observer analysis in conjunction with a rate-coding model based on the observed response properties. A simple and intuitively plausible definition of coding accuracy is the ability of an ideal observer to discriminate between two geometrically similar surfaces. In our analysis, the underlying task consists of distinguishing between two deflection patterns, generated by vibrissa movements (with velocity v) over idealized periodic surfaces (S₁ and S₂; gratings separated by d and d + Δd, respectively). Single-trial observations of the simulated response of an RSU to the evoked deflections are used to compute the minimum probability of discrimination error achieved by an ideal observer.

Figure 7B illustrates the idealized vibrissa-surface interaction model, similar to that described by Mehta and Kleinfeld (2004), used to generate single- and paired-vibrissa punctate deflection patterns. For a given geometry of whisking, the resulting single- and paired-vibrissa contact times are used in conjunction with a response model (described below) to generate the associated RSU firing rate. The response to a deflection at time t′ exhibits a history dependence that is a result of cross-vibrissa interactions. In keeping with the prediction paradigm (see Results), a scalar variable, x(t′), is sufficient for the prediction of the response in question. Because this variable incorporates all of the history dependence exhibited by an RSU, it represents the “state” of the thalamocortical pathway. At a physiological level, it is reflective of both the intrinsic properties of an RSU and of the properties of the impinging thalamocortical network. For a sequence of deflections, the state x(t′) is taken to be the fractional test response to a stimulus at time t′. In fact, one result of this study is that knowledge of the fractional test response (itself a measure of response magnitude) is also sufficient for an accurate prediction of response latency and precision (as described by VS).

Figure 7.

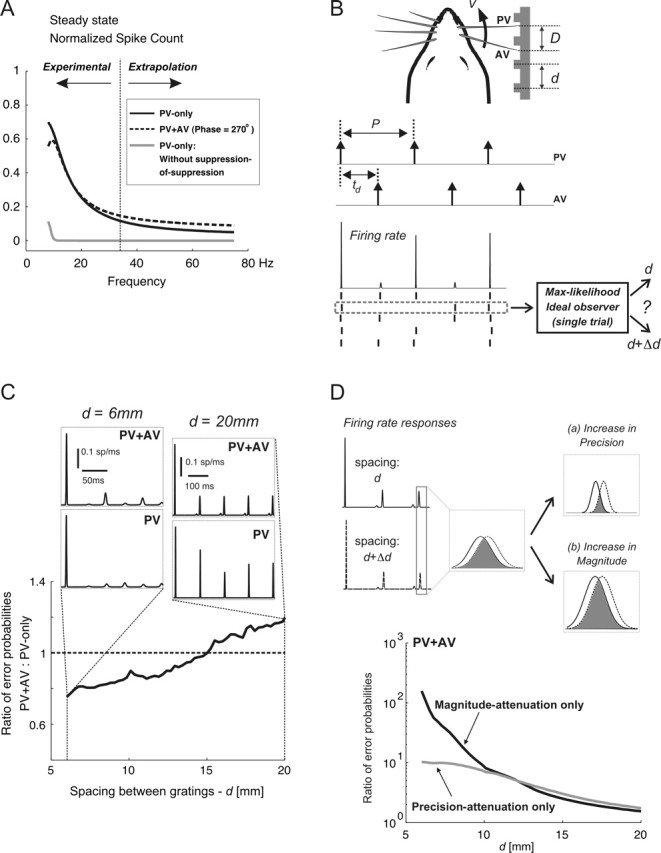
Limits to discrimination performance for single- and two-vibrissa stimuli. A, Simulated normalized PV spike counts in response to PV-only (solid line) and paired-vibrissa (dashed line; PV–AV phase, 270°) stimuli; all simulations were based on the response model described in Results. The CTR curves used in simulations were obtained by parametrically fitting sigmoidal functions to population-averaged CTR curves. The gray curve shows the simulated PV-only response in the absence of suppression-of-suppression. The range of frequencies for which the response model was verified experimentally, along with the range over which the model was extrapolated are labeled as Experimental and Extrapolation, respectively. B, The whisking model generates idealized single- and paired-vibrissa pulse deflections characterized by their occurrence times. With simple geometrical considerations, the stimulation period P and the PV–AV time delay t_d are expressed as follows: P = d/v and t_d = (D mod d)/v, where d, v, and D represent the grating spacing, vibrissa-tip velocity, and inter-vibrissa separation, respectively. For a given geometry and the resulting deflection times, the model described in Materials and Methods generates a pair of firing-rate responses corresponding to surface gratings of d and d + Δd; an example of the firing rate and response rasters is shown. Next, an ideal observer matches the spiking response to the texture that most likely gave rise to that response. C, This plot shows, as a function of grating spacing, the ratio of P_error with two vibrissae to that obtained using only the PV. In all cases, Δd = 0.05 mm. Qualitatively similar results were obtained for other Δd values, although absolute performance improved with increasing Δd (data not shown). D, Changes in P_error as a result of spatiotemporal interactions are attributed to changes in response precision (a) and response magnitude (b). The firing rate responses evoked by spacings of d and d + Δd are shown on the left; the responses to a single stimulus cycle are considered in more detail. For a pair of equally likely surfaces, P_error based on single-trial observations (spikes) of a single response cycle scales with the extent of temporal overlap between the two firing rates; this overlap is shown by the shaded area. An increase in response precision reduces the temporal overlap between the pair of responses (a). In contrast, an increase in response magnitude (b) does not change the fractional overlap between the two responses. It lowers P_error by increasing the likelihood of observing one or more spikes in response: without spikes, P_error is at its maximum (i.e., one-half).

As explained in Results (see Eq. 10), the resulting trajectory of x(t′) is predictable from (1) preceding stimulus times {t_i} and (2) a nonlinear function of the CTR curves, which characterize pairwise interactions between subsequent deflections. Figure 1B shows that combined PV and AV movements result in four types of cross-vibrissa interactions (and thus require the specification of four CTR curves). The following CTR parametrizations are based on experimental measurements (see Results and Fig. 2B): I, PV→AV (A = 0.4, t₅₀ = 120 ms, τ = 30 ms); II, PV→PV (A = 0.8, t₅₀ = 80 ms, τ = 30 ms); III, AV→PV (A = 1, t₅₀ = 50 ms, τ = 30 ms); IV, AV→AV (A = 0.4, t₅₀ = 80 ms, τ = 30 ms). For a sequence of deflection times, the prediction paradigm described in Results allows for the computation of the trajectory of x(t). In turn, the predicted firing rate R̂(t) results from x(t) according to the following relationship:

where R_o is the background firing rate (set to 3 Hz, the average rate observed experimentally) and R̃(t − t_i) represents the first-order PSTH response to a single isolated deflection at time t_i. In turn, the resulting firing rate R̂(t) generates spikes according to a Poisson process. Refractory effects were neglected in this approximation because of (1) the low intrinsic RSU firing rates under experimental conditions, (2) the relatively few number of spikes in response to a deflection (on average less than one), and (3) the relatively long time scale between deflections (in all cases, stimulus periods are >5 ms). As will be subsequently described, our data showed that suppression of the response magnitude also led to an increase in latency and a decrease in response precision. To model the latter two effects on PV and AV responses in the most general way, it was important that our choice for the PSTH template allowed for independent variation of the mean latency and precision. A simple function meeting this criterion that was, nevertheless, sufficiently similar to observed responses is the following Gaussian template:

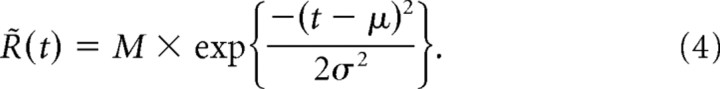The constant M is chosen such that the average number of spikes equals 0.75 for PV responses and 0.5 for AV responses (close to the average measured magnitudes). All parameters were chosen on the basis of the similarity of the resulting waveforms to experimentally measured PSTH responses. Parameters μ and σ, respectively, define the average latency and SD of the spike times relative to the stimulus. It is important to note both μ and σ change with the state variable x, as described below.

Experimental measurements indicate that the average latency of PSTH response increases with increasing levels of response suppression (i.e., with decreasing x values). This effect is well described by the following empirical relationship (fitted via least-squares regression) (see Fig. 2D, top): μ(x) = μ_o × (−1.08x + 2.36), where μ_o equals 8 ms for PV stimuli and 12 ms for AV stimuli. Similarly, it was found that σ increases with decreasing x values. An empirical fit between the measured x and VS values indicated the following relationship: VS(x) = VS_o × (0.23x + 0.83) (see Fig. 2D, bottom). Here, VS_o stands for the measured vector strength of the response in the absence of any preceding deflections. The VS_o values used for PV and AV responses in the simulations were the same as the average values measured experimentally (see Fig. 1A, bottom). The linear dependence between x and VS, in conjunction with the relationship between σ and the VS for a Gaussian PSTH, led to the model for the variation of σ with x.

For a given pair of surfaces {S₁, S₂} and a fixed whisking geometry, the resulting single-cell firing rates R̂_S1(t) and R̂_S2(t) are computed using the above response model. During one trial, an ideal maximum-likelihood observer (Green and Swets, 1966) working with spikes over the interval [0, t] achieves the minimum probability of discrimination error P_error, which for small Δd can be approximated as follows (Rieke et al., 1997):

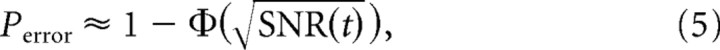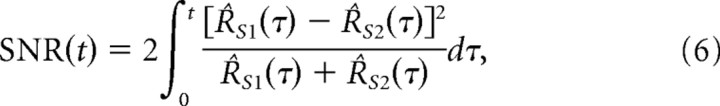and Φ(·) is the cumulative distribution function for a standard Gaussian random variable. Because of the underlying dissimilarity in their geometry (e.g., their spacings), the two surfaces lead to different firing rates (i.e., average responses). Heuristically, the error associated with attributing an observed spike train to one of the two candidate firing rates stems from the stochastic nature of spike generation. The “signal-to-noise” ratio term [i.e., SNR(t)] incorporates this uncertainty together with the average difference in observed responses (i.e., the difference in firing rates) to yield an estimate of the reliability of discrimination. Equation 5 and 6 show that the probability of discrimination error decreases as the dissimilarity between the two instantaneous firing rates grows (i.e., as the underlying surfaces become increasingly dissimilar).

Because of the variations in geometric parameters across animals and whisking bouts, the measure of error was computed and averaged over a range of experimentally measured vibrissa tip velocities (v) (Carvell and Simons, 1990) and plausible inter-vibrissa separations (D) to obtain the mean probability of error that is reported in Results. The resulting PV–AV time delays (t_d) (see Fig. 7B) include the range of delays (10–25 ms) expected from behavioral studies (Sachdev et al., 2001).

Results

Responses to both pulse and square-wave deflections of the PV and the caudal AV were recorded from individual RSUs in the SI. As exemplified by the single-cell PSTH shown in Figure 1C (top row), firing rates in response to both PV and AV stimuli had short latencies (<15 ms in all cases) and were temporally sharp. In addition to the PSTH, three other response metrics were used to quantify RSU responses (see Materials and Methods and Fig. 2A): (1) the response magnitude consisted of the average spike counts in a 3–30 ms poststimulus window; (2) the latency was defined as the average latency of the PSTH relative to the time of stimulus; and (3) the VS quantified the average spread of spike times about their mean and therefore represented the temporal precision of the response; a response having the maximum VS value (of 1) represents infinitely precise spikes after a deflection. Figure 1A shows the averaged measured values for spike count, latency, and VS across the population of cells for both PV and AV stimuli (including both pulse and ramp-and-hold deflections). The background firing rate was 3 ± 2 Hz (mean ± SEM), as shown by the dashed line in Figure 1A. Both spontaneous and stimulus-induced firing rates are consistent with previously reported values (Simons, 1978, 1985; Simons and Carvell, 1989), and in all cases isolated deflections evoked significantly larger responses than the background rate (p < 0.05; t test).

Poststimulus suppression has qualitatively similar features for all multi-vibrissa interactions

Spatiotemporal interactions between the constituent deflections of a spatiotemporally distributed stimulus shape the resulting response in an important way. In the simplest case, a pairwise interaction modulates the response to a deflection as a function of the intervening delay between it and a single preceding stimulus. Figure 1B illustrates an idealized sequence of contacts, along with the resulting pairwise interactions (white arrows) for a PV–AV pair located in the same row. The paired-vibrissa stimulus contains four types of pairwise interactions (white arrows): I, PV preceding AV (PV→AV); II, PV preceding PV (PV→PV); III, AV preceding PV (AV→PV); IV, AV preceding AV (AV→AV). Each column in Figure 1C shows the pairwise interaction between responses to a different stimulus pair for a sample cell (from left to right: I, II, and III). Within each column, the top plot shows the response to the second stimulus presented in isolation, referred to as the first-order response. The following three plots present the recorded response to both deflections as the IDI (symbolized by u) progressively shortens (from top to bottom: 160, 60, and 20 ms). Vertical dashed lines indicate the relative times of the stimulus pair. For each recorded cell, all pairwise interactions evoked qualitatively similar attenuations of the response to the second deflection in the pair: with regard to response magnitude, short IDIs caused maximal suppression of the response (measured by reductions in both the peak and total power of the firing rate), whereas longer IDIs led to progressively lesser attenuation. In addition, pairwise interactions modified the temporal profile of responses. Corresponding to increasing amounts of response suppression with decreasing IDIs, the response latency increased whereas the temporal precision of the evoked PSTH response decreased (compare, for example, the response to the second PV stimulus for PV→PV with IDI = 160 ms to the case when IDI = 60 ms).

Previous studies have also used the above paradigm to quantify the influence of a past stimulus [i.e., the conditioning stimulus (C)] on the response to a test (T) input (Simons, 1985; Nelson, 1991). CTR curves (see Fig. 2A and Materials and Methods) provide a measure of the time course of recovery of the test response from second-order suppression. Generalizing from the single-cell case described above (Fig. 1C), Figure 2B shows the average CTR curves across all recorded cells [I, PV→AV (gray triangles); II, PV→PV (black squares); III, AV→PV (black diamonds); AV→AV (gray circles)]. As shown by the sigmoidal shape of the resulting curves, dynamics of recovery from poststimulus suppression were qualitatively similar for all C→T combinations.

Despite the similarities described above, there are systematic differences between CTRs corresponding to different C→T sequences. On average, the AV→PV CTR (black diamonds) displayed the quickest recovery (Fig. 2B). In comparison, test responses for the PV→PV (black squares) and AV→AV (gray circles) sequences displayed progressively longer recovery time scales. It is important to note that the PV→AV interaction (gray triangles), showing the longest time scale, did not fully recover even for the longest delay studied (260 ms), thus signifying that pairwise interactions can shape the response over a large range of interstimulus deflections.

In addition to modulations in response magnitude, poststimulus suppression also affects the temporal profile of responses. Figure 2A shows this change schematically, whereby the presence of a conditioning deflection reduced the magnitude of the test response, increased its latency, and decreased its VS (i.e., reduced its precision). Figure 2C shows the population-averaged variations in both response latency and VS with IDI for three types of pairwise interactions (left column, normalized latency; right column, normalized VS). Analogous to the CTR measure, the normalized latency shown here is defined as the latency of the test response divided by that measured when the test is presented in isolation. Normalized VS values are defined identically. It is important to note that, because small response magnitudes gave rise to inaccurate estimates of timing, latency and VS values at time points having an averaged CTR value of <0.1 are not shown. Following this line of reasoning, variation of latency and VS with IDI for the PV→AV sequence is not shown because only a small number of IDIs led to CTR values >0.1 (Fig. 2B, gray triangles).

The trend for the three other pairwise sequences is that test response latency is longer than the baseline case for short IDIs (i.e., the normalized latency is larger than unity) but recovers to its baseline value as the IDI lengthens (i.e., the ratio tends toward 1 with increasing IDI) (Fig. 2C, left column). Comparison of the latency curve for each pairwise interaction with the corresponding CTR curve (Fig. 2B) reveals that CTR and normalized latency values were strongly anti-correlated (r = −0.76; p < 1e-4; see also the scatter plot and the regression line in Fig. 2D, top).

The precision of deflection responses also decreased slightly as a result of poststimulus suppression. As shown by Figure 2C (right column), short IDIs tend to correspond to test responses having slightly lower VS values relative to their baseline responses. However, the normalized VS recovers to 1 with increasing IDIs. Figure 2D (bottom) shows the high correlation between the CTR and normalized VS on a population-averaged basis (r = 0.77; p < 1e-4; the gray line represents the best-fit relationship between the CTR and VS ratio).

Suppression depends on the strength of conditioning and test responses

Figure 2B also shows that the various CTR curves have different time courses, indicating that pairwise attenuations are functions of the types of constituent conditioning and test stimuli. To investigate the potential dependence of CTR recovery time on the constituent deflections, the stimuli were grouped into two categories: (1) those with a common test stimulus and (2) those sharing the same conditioning deflection (see Fig. 2E for a schematic).

For the group consisting of stimuli sharing a common test (Fig. 2E, i), the following comparisons were made: PV→PV versus AV→PV (for pulse stimuli) and PVr→PVc versus AVr→PVc (for square-wave deflections). As mentioned above, the CTR curves in Figure 2B show that for a common test stimulus (here a PV deflection), recovery from suppression attributable to a conditioning PV deflection is longer than that evoked by an AV deflection (compare the PV→PV and AV→PV CTR curves). This result suggests that for a common test stimulus, deflections of the PV tend to evoke a longer-lasting suppression than do stimuli evoked by adjacent vibrissa. This relationship (measured for both pulse and square-wave stimuli) is valid on both cell-averaged and cell-by-cell bases [p < 0.001; n = 30; permutation test (Siegel and Castellan, 1988)]. Moreover, a cell-by-cell analysis revealed a significant correlation (r = 0.71; p < 0.001; n = 30; permutation test) between (1) the ratio of the first-order response to a PV pulse to that of an AV and (2) the ratio of the PV→PV recovery time (as measured by the associated t₅₀ parameter) to that of the AV→PV sequence. This correlation leads to the inference that the recovery time from stimulus-evoked suppression scales with the magnitude of the conditioning response. Moreover, in view of the correlations between response magnitude (i.e., the CTR value) and both latency and VS (Fig. 2D), it follows that as the strength of the conditioning stimulus increases, the resulting test response shows progressively longer latencies (i.e., the latency ratios are >1) and degraded precision (i.e., the normalized VS values are <1).

A similar conclusion holds for the case in which the C→T sequences share a common conditioning deflection (Fig. 2E, ii). In this case, the comparison was made between the PV→PV and PV→AV pairs for pulse stimuli and between the PVr→PVc and PVr→AVr pairs for square-wave stimuli. From the CTR curves in Figure 2B (shown for pulses only), it can be seen that recovery from suppression is longer for PV→AV pairs than it was for PV→PV stimuli. This observation suggests that for a common conditioning stimulus, PV test responses tend to recover from suppression more quickly than do test responses evoked by the adjacent vibrissa. This relationship, measured for both pulse and square-wave stimuli, was validated on both a cell-averaged and cell-by-cell bases (p < 0.001; n = 30; permutation test). However, a cell-by-cell analysis similar to the one described above did not demonstrate a significant correlation between the magnitude of the test response and the time scale of recovery. Although not explicitly discussed here, analogous results for both cases discussed above (common conditioning and common test) also hold when the AV→AV interaction is the basis for comparison (however, refer to Fig. 2B for a visual comparison).

Nonlinear interactions induce suppression-of-suppression

Rich spatiotemporal patterns of deflections across pairs of vibrissae give rise to correspondingly more complex response interactions than observed for the pairwise effects considered above. In such cases, the response to each stimulus influences future activity not limited to the immediately following deflection response. As conceptualized by the white arrows in Figure 1B, the activity attributable to each deflection influences the response to the subsequent stimulus, and thus the influence of one stimulus propagates through the responses to future stimuli in a non-trivial manner.

Propagation of spatiotemporal interactions can be most easily observed using a three-deflection sequence that results in the combination of two pairwise interactions. The triplet C₂→C₁→T shown in Figure 3A evokes a third-order interaction between responses to two conditioning stimuli (C₂ and C₁) and one test stimulus. Figure 3B exemplifies how the effects of C₂→C₁ combine with those attributable to C₁→T to shape the test response.

Figure 3.

Nonlinear response interactions. A, Schematic of stimulus triplet. For the sequence C₂→C₁→T, the test response is measured under two scenarios. First, delay u₁ was fixed at 60 ms, and u₂ varied over the range 0–200 ms in 10 ms increments. Next, u₂ was fixed at 60 ms as u₁ varied over the same range. B, PSTH responses for the sequence C₂→C₁→T (specifically, PV→AV→PV) for different values of delay u₂. The leftmost plot shows the first-order test (PV) response. To its right, the response to the pairwise sequence AV→PV is shown (u₁ = 60 ms). The next three plots show the response to the third-order sequence PV→AV→PV as the delay u₁ was fixed at 60 ms, whereas u₂ equaled 200, 70, and 10 ms, respectively. C, The third-order normalized spike counts (fractional test response curves) for the cell shown in B are shown as functions of u₂ (left, ▪; u₁ = 60 ms) and of u₁ (right, ▪; u₂ = 60 ms). Error bars show ±1 SEM. The gray bands represent the corresponding measurements (and their associated uncertainties) for the second-order sequence C₁→T over the same delay range u₁ and u₂ (mean ± 1 SEM).

The leftmost plot in Figure 3B shows the first-order response to a PV test deflection: comparison between this baseline and the responses to more complex sequences reflect changes brought on by response interactions. The next panel to the right shows the second-order response to the sequence AV→PV for an intervening delay of u₁ = 60 ms. For the case shown, the preceding AV deflection (1) almost completely suppresses the response to the following PV pulse, (2) slightly lowers the measured precision (VS), and (3) lengthens the average response latency.

The next three panels illustrate the response to the PV→AV→PV triplet for u₁ fixed at 60 ms and delay u₂ taking progressively lower values. For u₂ = 200 ms, the AV deflection is placed outside the temporal range of suppression evoked by the initial conditioning (PV) stimulus. The corresponding test response in this situation is also very similar to the measured value for the AV→PV case (i.e., the response magnitude is suppressed, whereas the response latency is increased from its baseline value). When the initial PV deflection occurs sufficiently close (e.g., u₂ = 70 ms), the response to the subsequent AV stimulus is nearly eliminated. In contrast, the suppression associated with the AV→PV sequence is significantly reduced, as observed by the sizable increase in test response magnitude (compare the response to the PV deflection occurring at time 0 in the second panel with those in the third and fourth panels). This effect would not result if the second-order interaction attributable to AV→PV were independent from the past history of inputs. A further decrease in u₂ placed the subsequent AV and PV deflections within the range of suppression evoked by the initial PV input and eliminated their corresponding responses (Fig. 3B, fifth panel).

The effect of the C₂→C₁→T sequence on the test response was studied in more detail by varying each delay in the pair (u₁, u₂) while holding the other fixed. The resulting fractional test response (nomenclature used to distinguish from the CTR) was computed as the ratio of the test response, measured in the presence of C₂ and C₁, to its first-order value. Figure 3C shows the fractional test response (▪) as a function of u₂ (left; u₁ fixed at 60 ms), and of u₁ (right; u₂ fixed at 60 ms). In each case, the surrounding gray band represents the measured CTR induced by the C₁→T sequence in isolation (mean ± 1 SEM). Figure 3C clearly shows the “suppression-of-suppression” phenomenon described (top left plot; u₂ values greater than ∼70 ms) as large upward deviations of the third-order responses from the second-order (CTR) value. For u₂ values less than ∼50 ms, the earliest PV deflection directly suppresses the responses to the following two deflections, as evidenced by the portion of the curve below the gray band. Suppression-of-suppression, by increasing the response magnitude, also shortens response latency and raises the precision of response in a way that is consistent with measurements of second-order interactions (Fig. 2D).

On a cell-by-cell basis, and over a large range of both u₁ and u₂ delays, the resulting third-order response significantly deviates from that expected if only pairwise effects were relevant (p < 0.05; two-sided Wilcoxon signed rank test). Additionally, the population-averaged third- and second-order response magnitudes were significantly different over the majority of delays considered. Furthermore, the correlation between response magnitude (CTR) and normalized test latency remained very strong (u₁ fixed: r = −0.8, p < 0.002; u₂ fixed: r = −0.86, p < 0.002). The corresponding correlation between the CTR and normalized VS was indeterminate for the fixed u₂ case (r = −0.2; p < 0.57) but remained very strong for the fixed u₁ measurements (r = 0.85; p < 0.001). Our results therefore indicate that response magnitude is an accurate predictor of response latency and, to a good extent, of response precision (measured by VS).

Pairwise effects predict more complex interactions

As schematized by Figure 1B, history dependence in response to stimulus patterns more complex than pairs can be viewed as the effective combination of pairwise interactions between the preceding stimuli. Figure 4A (top) illustrates the constituent pairwise elements for the simplest case, consisting of the C₂→C₁→T triplet. For C₂, C₁, and T stimuli occurring at times t − (u₁ + u₂), t − u₁, and t, respectively, the recorded fractional test response, denoted here as x(t), depends only on the delay variables u₁ and u₂ and thus can be written x(u₁, u₂). Figure 4A (bottom) illustrates a contour plot example of this function. The value of the resulting x(u₁, u₂) is constant along each curve (i.e., contour) and is specified as a number within the corresponding contour. Dashed horizontal and vertical lines represent directions along which only one of the delay variables changes, whereas the other is fixed (horizontal line, u₁ fixed; vertical line, u₂ fixed). Importantly, the net effect on the test response attributable to the constituent pairwise interactions is a predictable function and is given as follows:

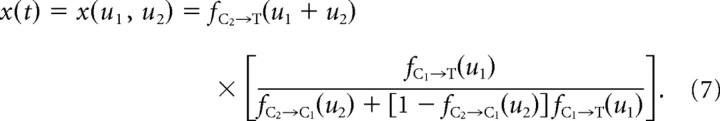Terms of the form f_X→Y(u) represent the measured pairwise CTR for the stimulus sequence X→Y, evaluated at the intervening delay u. Heuristically, Equation 7 represents two distinct influences on the T response (see also the schematic diagrams in Fig. 4A). The first, represented by the right term of the product, captures the change in the C₁→T interaction because of the presence of the preceding C₂ deflection. For large intervening delays u₂, influence of C₂ is negligible, and the C₁→T interaction is the only influence on the test response [i.e., as f_C2→C1(u₂)→ 1, the fraction inside the brackets tends to f_C1→T(u₁)]. For progressively decreasing values of u₂, ever larger suppression of the C₁ response also lowers the suppressive effect of C₁ on the T response. This effect underlies the release from suppression demonstrated by Figure 3. Second, the left term in Equation 7quantifies the direct second-order influence of C₂ on the test response. As expected, this effect increases in strength for decreasing delays between C₂ and T (i.e., for values of u₁ + u₂ less than ∼100 ms). The net effect of these two influences can be seen in the contour plot of x(u₁, u₂) in Figure 4A. For small u₂ values, suppression attributable to C₂ effectively eliminates the responses to the ensuing two deflections. In the other extreme, large u₂ values effectively eliminate any suppressive effects attributable to C₂ on the test response. The suppression-of-suppression phenomenon occurs for intermediate values of u₂, in which the C₁ response is suppressed because of C₂, so that the net suppression on the test response is effectively lifted.

Figure 4.

Prediction of nonlinear interactions from constituent second-order effects. A, Schematic representing the constituent second-order interactions that combine to form the effective third-order fractional test response to the sequence C₂→C₁→T. The predicted response is a function of the two constituent delays u₁ and u₂ and is shown through a contour plot for an example case. B, Agreement between measured (black line with ▪) and predicted (gray line) Fractional test responses is shown for pulse stimuli, as functions of both u₂ (left) and u₁ (right). Error bars represent SEMs of the measured values. Over the population of cells, the coefficients of correlation between measured and predicted third-order responses of a single-cell were (mean ± SEM) 0.82 ± 0.03 for u₁ = 60 ms and 0.77 ± 0.05 for the u₂ = 60 ms case.

Figure 4B demonstrates the agreement between measured (▪; error bars represent SEM) and predicted (gray line) responses to the C₂→C₁→T pulse triplet for the same cell shown in Figure 3, B and C (left, u₁ fixed at 60 ms; right, u₂ fixed at 60 ms). Over the entire population of cells (including both pulse and ramp-and-hold deflection responses), accurate predictions of third-order fractional test responses were obtained using simpler second-order measurements; the coefficients of correlation between predicted and measured curves were 0.82 ± 0.03 for u₁ fixed at 60 ms and 0.77 ± 0.05 for u₂ fixed at 60 ms (mean ± SEM). Given the strong correlation between CTR values and the corresponding normalized latencies and VSs (for both second- and third-order stimuli), it is important to note that predictability of third-order response magnitudes from simpler pairwise interactions means that response timing (i.e., latency and precision) is also predictable from these same CTR curves.

Spatiotemporal interactions significantly influence the dynamics of response adaptation

Results up to this point demonstrate that responses to more complex deflection sequences are shaped by combinations of multiple pairwise interactions. Under active exploration, the precise patterns across the vibrissa array are determined by several factors, including the properties of surface, vibrissa anatomy, and dynamics of whisking. Although naturalistic textures likely evoke aperiodic patterns that are significantly more complicated than the idealized pulses studied here, it is, nevertheless, useful to consider periodic pulse deflections to (1) understand the basic properties of response transformations in the SI and (2) make comparisons with previous studies. In fact, the general principle described here has also been shown to be an important factor in shaping the response to complex, aperiodic single-vibrissa stimuli (Webber and Stanley, 2004). To investigate the time course of adapting responses and higher-order interactions between responses to multiple deflections in close temporal succession, periodic pulse trains were presented using (1) only the PV and (2) both the PV and AV for varying periods and PV–AV time delays t_d (Fig. 5A). Note that for one cycle of the two-vibrissa stimulus, the time delay t_d corresponds to variable u₂ defined in Figure 3A.

Figure 5.

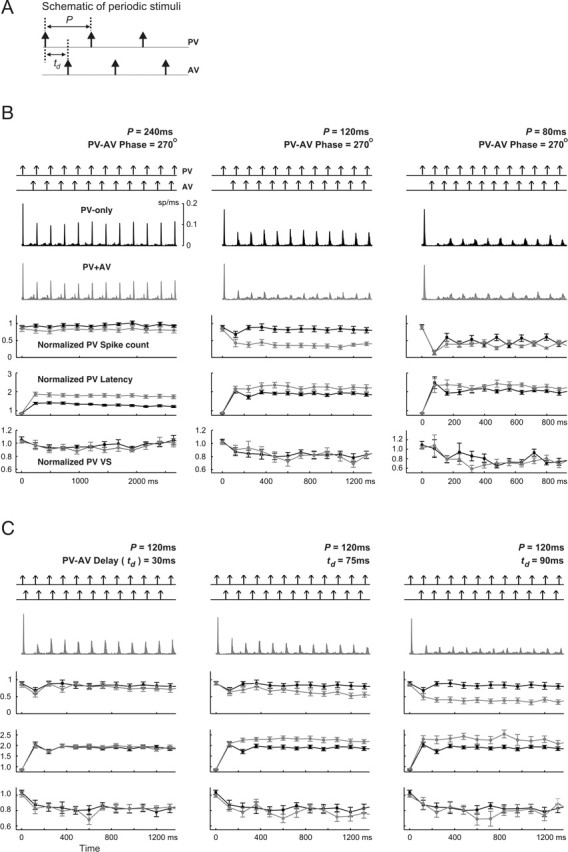
Frequency and phase dependence of transient responses to periodic stimuli. A, Schematic of periodic stimuli. For PV-only cases, stimulation period P took five values: 240, 120, 80, 60, and 30 ms. For the two-vibrissa case, first the PV–AV phase delay was fixed at 270°, whereas the period ranged over the same values as above. Next, the stimulation period was fixed at 120 ms, whereas the PV–AV time delay t_d varied over the range 30–90 ms in 15 ms increments. B, Each column represents results from a distinct stimulation pattern (from left to right: 240, 120, and 80 ms). For each column, the top panel in each plot represents the periodic pulse deflections and the middle two panels show the average firing rate for all cells (n = 18) in response to PV-only and two-vibrissa (PV and AV) stimuli (top plot, PV-only response, black; bottom plot: response to PV and AV, gray). The next three panels show, respectively, the normalized spike counts, latencies, and VSs of PV responses evoked by single (black) and combined (gray) PV–AV deflections. Error bars represent ±1 SEM. C, Dependence of transient responses on the PV–AV time delay for a stimulation period of 120 ms. Results for t_d = 30, 75, and 90 ms are shown in the left, middle, and right columns, respectively. For each column, the order of the panels is the same as that described in B.

Figure 5B shows the resulting transient responses, averaged over all cells, to periodic PV-only and combined PV and AV stimulus trains (from left to right: periods of 240, 120, and 80 ms). As shown by both the instantaneous firing rate and fractional PV spike counts, the overall level of response suppression for the PV-only stimulus increased with increasing frequency. Corresponding to this increase in suppression, the latency of PV-only responses also increased by a factor of ∼2, and the corresponding VSs slightly decreased to below their baseline values. Responses evoked by paired-vibrissa deflections exhibited analogous changes with increasing stimulus frequency (in Fig. 5B, see the firing rates and transient behavior of normalized spike count, latency, and VS, all shown in gray). Therefore, both single- and paired-vibrissa responses undergo greater amounts of response suppression with increasing stimulus frequencies.

For a given stimulation frequency, Figure 5B also shows that paired-vibrissa stimulation leads to more response suppression relative to the PV-only case. This difference is most clear for a stimulation period of 120 ms (middle column; compare gray curves for PV–AV responses with the black representing PV-only measurements). Increased suppression evoked by PV–AV deflections also gave rise to longer response latencies than those attributable to the PV-only case. In all cases, however, the difference in response precision between the paired-vibrissa and PV-only stimuli was weaker for the periods shown (Fig. 5B, last row). This difference grew for shorter deflection periods not shown in Figure 5 (but see Fig. 6A, top right, for the behavior of response VS as a function of frequency).

Figure 6.

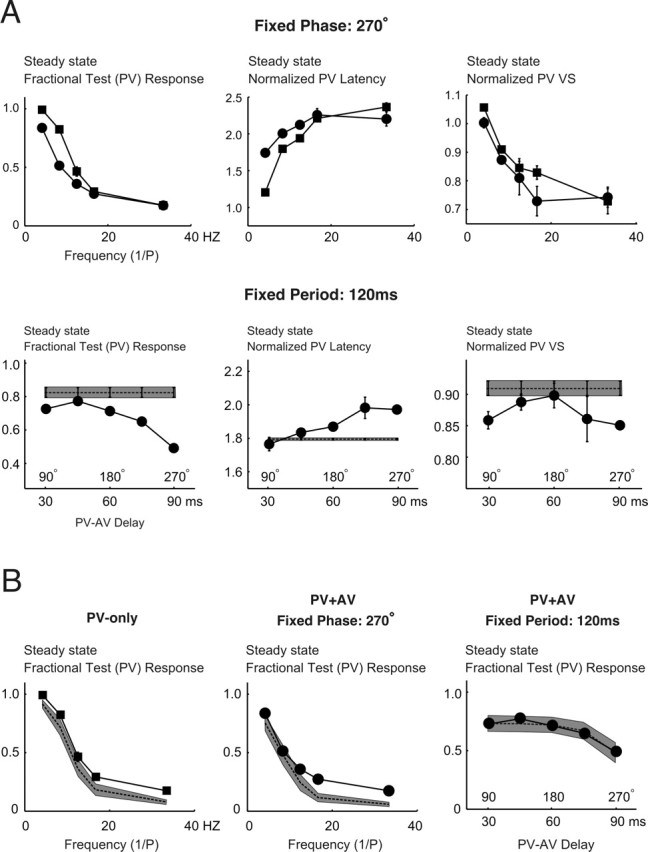
Frequency and phase dependence of steady-state responses to periodic stimuli. A, The top row shows a comparison between three aspects of steady-state PV response (from left to right: spike count, latency, and VS) to single- and multi-vibrissa deflections as a function of frequency (PV-only, ▪; PV–AV with phase delay fixed at 270°, •). All measures represent averages over n = 18 cells, with error bars representing ±1 SEM. Similarly, the bottom row shows the corresponding measurements of PV responses as a function of the PV–AV time delay for a fixed stimulation period of 120 ms. The horizontal axes represent the PV–AV delay as both time (i.e., t_d, in millisecond) and phase (i.e., 360° × t_d/P). B, Predictability of steady-state responses for single- and multi-vibrissa periodic stimuli. From left to right, the plots consist of the following: (1) steady-state responses for PV-only stimuli as a function of frequency; (2) steady-state responses for paired-vibrissa stimuli as a function of frequency (phase is fixed at 270°); and (3) steady-state responses for paired-vibrissa stimuli as a function of varying PV–AV time-delay (period fixed at 120 ms). For each plot, the solid line represents the experimentally measured averaged response. The dashed lines represent the averaged predictions (for all cells). The gray areas are the regions of uncertainty (±1 SEM) for the predictions.

With a fixed period, changes in the PV–AV time delay t_d also caused significant deviations of the paired-vibrissa response from the PV-only case. Figure 5C shows transient spike count responses (gray curves) to a combined PV and AV stimulus with a period of 120 ms (∼8 Hz) for varying PV–AV delays (from left to right: 30, 75, and 90 ms). For comparison, fractional PV responses to a 120 ms periodic single-vibrissa stimulus (black; seen also in the middle column of Fig. 5B) are also shown on the same plot. As the PV–AV time delay grew larger, increased response suppression led both the steady-state and transient PV response magnitude to become increasingly smaller than the corresponding single-vibrissa values. Once more, this increase in response suppression relative to the PV-only case corresponded to a greater lengthening of response latency for the paired-vibrissa deflections. The corresponding response precision, moreover, decreased slightly more than it did for the PV-only responses. Because of cross-vibrissa suppression, AV responses were significantly smaller during the transient response period than PV-induced activity (as seen from firing rates in response to two-vibrissa stimulations). Fractional AV responses are therefore not shown.

The above results demonstrate that, depending on the timing of multi-vibrissa deflections, cross-vibrissa interactions can significantly attenuate the resulting responses. However, as shown by the responses to the triplet sequence (Fig. 3), response interactions are not always suppressive and, in fact, lead to response enhancement for a range of interdeflection times. The relative amount of response suppression has a significant role in the coding of deflection patterns, as described below (see below, Spatiotemporal interactions constrain discrimination between patterns).

To better illustrate the difference between responses in the single- and multi-vibrissa cases, steady-state PV fractional responses are shown in Figure 6A. The top left plot illustrates the single-vibrissa (▪) and two-vibrissa (•; PV–AV phase fixed at 270°) steady-state normalized spike count PV responses as a function of frequency, averaged over all cells. It can be seen that up to ∼12–17 Hz (i.e., a period of 60–80 ms), single- and multi-vibrissa stimuli produced different steady-state responses. In general, the two-vibrissa frequency response was even more low-pass in character compared with the PV-only case. The observed steady-state normalized PV response latencies and VSs were consistent with what would be predicted on the basis of the spike count response. Average response latency increased with stimulus frequency for both single- and two-vibrissa stimuli (see middle plot in the top row), with single-vibrissa responses having shorter latencies at frequencies up to ∼17 Hz. This discrepancy between PV-only and combined PV–AV responses corresponds to the difference in the steady-state spike count up to 17 Hz. Also as a result of increased response suppression evoked by combined PV–AV deflections, the steady-state VS of PV responses decreases with increasing frequencies but asymptotes at a fraction (∼0.7–0.8) of its original value (Fig. 6A, top row, right plot). The differential increase in response suppression attributable to combined PV–AV deflections compared with the PV-only case is also reflected by the slightly lower precision of the two-vibrissa stimuli. As expected from the transient behavior shown in Figure 5, the combined PV–AV frequency response also depended strongly on the relative latency between PV and AV contacts and not simply on the total number of contacts within the experimental interval. The bottom row of Figure 6A shows the dependence of steady-state PV response on the PV–AV time delay (•; period fixed at 120 ms), along with the observed single-vibrissa response with a period of 120 ms (▪). For this fixed frequency case, as the PV–AV time delay increased, the two-vibrissa response showed significantly more attenuation of the steady-state PV spike count than the single-vibrissa case (left plot). This is presumably because the AV-evoked attenuation became more pronounced as the intervening delay between an AV deflection and a subsequent PV deflection decreased. This rise in response suppression also corresponds to increases in response latency (middle plot) and to slight decreases in response precision (right plot).

Steady-state responses are predictable from pairwise interactions

The prediction method outlined earlier for third-order responses can also be generalized for arbitrary two-vibrissa sequences. Note that the state prediction of Equation 7 can be written in a more general form:

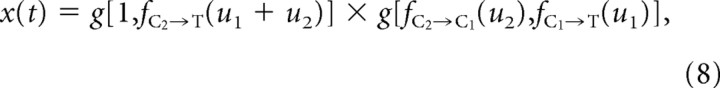where

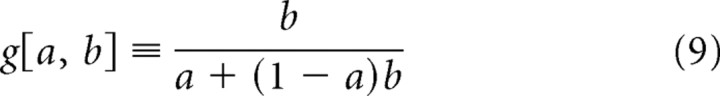For a mixed sequence of PV and AV deflections at times {t₁, t₂, … t_n}, the fractional response x(t_k) to a deflection at time t_k ∈ {t₁, t₂, … t_n} can be expressed through the following recursion:

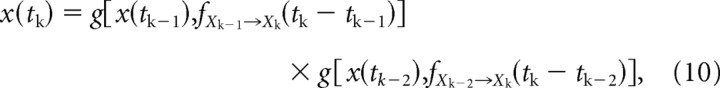with the following initial conditions:

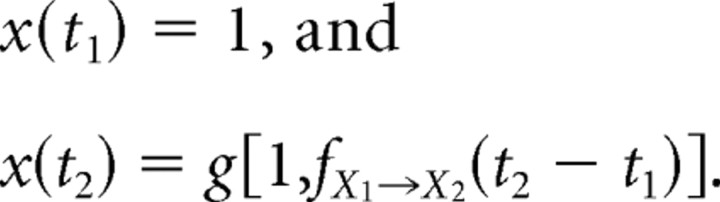Symbols of type X_m denote the type of stimulus presented at time t_m. As before, the function f_X→Y(·) represents the resulting CTR due to an X→Y sequence. The fractional response x(t_k) is, likewise, defined as done previously for third-order responses.

Figure 6B shows that steady-state responses to single- and multi-vibrissa contacts can be well predicted from second-order measures: from left to right, the plots show the measured (solid lines) and predicted (dashed lines) steady-state responses for single-vibrissa, two-vibrissa (fixed-phase), and two-vibrissa (fixed-period) cases, averaged over all cells. The closeness of predictions to measured responses can be seen by the overlap of the measured responses with the region of uncertainty associated with the predictions (gray bands; ±1 SEM).

Simple measurements of second-order interactions [i.e., CTR curves represented by the f_X→Y(·) terms in Eq. 10] can therefore be used to predict responses to more complicated deflection sequences. As such, specification of the underlying dynamics of the second-order attenuation is, to a large extent, sufficient to characterize the response to more complex stimuli. Furthermore, the strong correlations between the magnitude of response suppression and changes in both response latency and precision imply that both magnitude and timing aspects of the response are predictable from second-order measurements.

Spatiotemporal interactions constrain discrimination between patterns

Our findings indicated that cross-vibrissa interactions may act in two distinctly different ways. As shown by the responses to periodic single- and paired-vibrissa stimuli (Figs. 5, 6A), cross-vibrissa interactions significantly attenuated the magnitude of the response, increased its latency, and degraded its temporal precision relative to single-vibrissa stimulation. Yet, Figure 3 also shows that in other cases, the same interactions effectively lowered response attenuation through suppression-of-suppression. This nonlinear mechanism therefore improved the relay of high-frequency stimuli by increasing both the magnitude and temporal precision of the response: the effect of shortening response latency on the accuracy of coding is not readily apparent. Figure 7A shows the two distinct effects of cross-vibrissa interactions on the steady-state response as a function of frequency. First note that responses to both single-vibrissa (solid black line) and paired-vibrissa (dashed line) deflections attenuated with increasing frequency because lowered IDIs led to increased response suppression. The PV-only response had a larger magnitude over all frequencies compared with the hypothetical response curve simulated from dynamics that did not incorporate suppression-of-suppression (gray curve). This difference indicated that single-vibrissa stimulation resulted in significant reductions in response suppression compared with the response expected if response suppression accumulated without the nonlinear dynamics that account for the suppression-of-suppression. Second, relative to PV-only stimuli, paired-vibrissa deflections (PV–AV phase, 270°) evoked larger responses over frequencies greater than ∼30 Hz. This increase, shown by the crossover between the dashed and solid curves, can also be attributed to the greater degree of suppression-of-suppression for PV–AV responses relative to the PV-only case. As shown previously, the relative increase also corresponds to higher response precision for the PV–AV case. The difference between PV–AV and PV-only responses persisted for a wide range of PV–AV time delays, although the crossover point varied as a function of PV–AV phase (simulation results not shown).

Importantly, such observations suggest that limits to coding accuracy depend on the time scales of spatiotemporal interactions. Given the accuracy of the response model in predicting experimental observations, we next used it to understand the functional consequences of cross-vibrissa interactions for coding. Using an intuitive measure, we quantified the probability of error for a maximum-likelihood ideal observer in distinguishing between two stimuli with similar periods, on the basis of single-trial spiking responses (see Materials and Methods). A comparison between the performance of this observer using paired-vibrissa deflections relative to the performance using PV-only stimuli allowed us to evaluate how cross-vibrissa interactions shape the accuracy of single-neuron coding. It should be emphasized that the results described here are intended for qualitative conclusions regarding the role of spatiotemporal interactions in the rate coding of single- and paired-vibrissa patterns. As explained in the Discussion, actual performance levels in behavioral settings also depend on a variety of factors, such as the complex mechanics of vibrissa-surface contacts that are currently not well understood.

Figure 7B depicts the geometric model [similar to that presented by Mehta and Kleinfeld (2004)] used to generate stimuli evoked by single- and paired-vibrissa motion over idealized periodic textures. For fixed values of periodic spacing d, inter-vibrissa separation D, and whisker tip velocity v, the resulting single- and two-vibrissa periodic deflections can be characterized through the same parameters used for experimental measurements presented earlier (Fig. 5A): (1) the stimulation period P and (2) the PV–AV time delay t_d; the legend to Figure 7B describes the dependence of these variables on the underlying geometry. The single- and paired-vibrissa deflections were used in conjunction with a rate-coding model (based on experimentally observed interactions; see Materials and Methods) to generate RSU responses and incorporate cross-vibrissa interactions. Using observed ranges for whisking velocity and inter-vibrissa spacing (Carvell and Simons, 1990), the resulting responses within a window of 500 ms were used to compute the probability of error in distinguishing between a pair of periodic gratings with spacings d and d + Δd.

Figure 7C shows the ratio of the probability of discrimination error in the paired-vibrissa case relative to that computed using single-vibrissa sensation. Experimental observations (Figs. 5, 6) revealed a range of deflection frequencies and PV–AV time delays for which cross-vibrissa interactions cause greater response attenuation (and hence longer latency and lower precision) relative to PV-only responses. The simulations also show the same behavior for d approximately >15 mm. The right inset column in Figure 7C (d = 20 mm, D = 15 mm, v = 167 mm/s) shows such an example; these parameters evoke a deflection period of 120 ms and a PV–AV phase delay of 270°, the same as that shown by the rightmost data point in the right bottom plot of Figure 6A. Cross-vibrissa interactions for d > 15 mm also led to higher probabilities of discrimination error for paired-vibrissa stimuli relative to the PV-only case. As exemplified by the right inset (d = 20 mm), the presence of small AV response magnitudes in the d > 15 mm range does not imply that combined PV–AV observations necessarily result in superior discrimination compared with the PV-only case. Rather, cross-vibrissa dynamics over this range of frequencies and relative PV–AV time delays reduce the discriminability of paired-vibrissa responses compared with PV-only observations.

For smaller texture spacings (d < 15 mm, and hence higher-frequency stimuli), however, paired-vibrissa observations led to improved performance relative to single-vibrissa sensation. As exemplified by the left inset column in Figure 7C (d = 6 mm, D = 15 mm, v = 167 mm/s), cross-vibrissa dynamics result in lesser attenuation of PV–AV response magnitudes compared with the PV-only case. The resulting paired-vibrissa responses therefore have higher magnitudes (spike counts), shorter latencies, and higher precision (shown by a lower temporal spread) than their single-vibrissa counterparts and result in higher discrimination accuracy. These results highlight the fact that, because of spatiotemporal interactions, the underlying time delay between PV and AV deflections has an important role in shaping two-vibrissa responses and the encoding of deflection information.

We have shown that a decrease in the suppression of response magnitude accompanies both a decrease in response latency (by up to a factor of 3) and a rise in response precision. The result shown in Figure 7C addresses the question of how such changes influence the accuracy of coding for deflection patterns. Single-trial discriminability between a pair of stimuli directly scales with the extent of the dissimilarity between the evoked instantaneous firing rates (see Eq. 5 in Materials and Methods). Using the response to one stimulus cycle, Figure 7D provides a heuristic for how changes in response magnitude and precision affect discriminability. The magnified view of the responses to a pair of similar textures (with spacings of d and d + Δd, respectively) depicts the responses to a single stimulus cycle. The temporal overlap (marked by the shaded area) is directly related to the probability of discrimination error (based on responses to a deflection). This fact follows because decrease in temporal overlap increases the dissimilarity between the two firing rate responses. In the event of suppression-of-suppression, there will be increases in both precision and magnitude. The former change [shown by itself (a)] reduces the probability of error by decreasing the temporal overlap between the two responses. Increasing the response magnitude [also shown in the absence of other effects (b)], however, decreases the probability of error indirectly: the amount of overlap between the two responses (measured as a fraction of the total area under a response) does not change with an increase in response magnitude. Yet, the rise in the average number spikes implies that there will be an increase in the fraction of trials during which a spike is available for discrimination. This increase leads to an increase in probability of correct discrimination, because the probability of error in the case in which there is no spike is at its maximum (equaling 0.5). It should also be noted that the latency shifts of the responses to the texture pair were always almost equal. As described below, this observation implies that latency shifts did not influence discrimination error.

To disentangle how changes in response magnitude and timing (latency and precision) affect discrimination performance, each of these effects were, in turn, selectively excluded from the stimulations. The elimination of latency changes did not influence the performance in the discrimination task; the underlying rationale for this observation is that because of the similarity of response suppression evoked by spacings of d and d + Δd, both responses were displaced by nearly equal latencies and, as such, there was no change in their dissimilarity. We therefore only considered changes in magnitude and precision. When the dependence of response precision on suppression is excluded, the ratio of the resulting probability of error to that when all factors are accounted for (Fig. 7D, bottom plot, black line) remains above unity for all d values. A similar result holds when the dependence of response magnitude on suppression is excluded (Fig. 7D, bottom plot, gray line). These observations imply that changes in both response precision and magnitude are significant to constraining the probability of correct discrimination. However, changes in response precision generally had the largest influence on the probability of discrimination error (Fig. 7D, bottom plot, compare black and gray curves).

Discussion

The present study characterized the dynamics of responses to temporally distributed stimuli. An important result of this study is that decreases in response magnitude as a result of cross-vibrissa interactions are correlated with reductions in response precision and with increases in response latency. Beyond the seemingly simple suppression caused by pairwise interactions, strongly nonlinear interactions existed in the form of suppression-of-suppression and led to complex response profiles for trains of single- and paired-vibrissa deflections. The time scale of response interactions, together with that of the stimulus, strongly shaped single-cell response properties, including the measured frequency response characteristics. Pairwise interactions were sufficient for the prediction of the magnitude (and therefore also of the precision and latency) of the response to more complex deflection sequences. Using an experimentally based response model along with idealized vibrissa-surface contacts, we showed that suppression-of-suppression led to more accurate discrimination by increasing both the precision and magnitude of the response.

Physiological origins of within- and cross-vibrissa interactions

Anatomical and electrophysiological studies have identified several likely sources for the interactions studied here. First, subcortical contribution to cross-vibrissa interactions initially appear in the VPM thalamus, because both the primary trigeminal afferents and their downstream brainstem neurons do not generally exhibit poststimulus response suppression (Simons, 1985; Sosnik et al., 2001; Deschênes et al., 2003). The intrathalamic feedback loop between a VPM barreloid and nRT neurons responsive to a common PV (Desîlets-Roy et al., 2002) mediates self-inhibition of the neurons in each barreloid (Spacek and Lieberman, 1974; Harris and Hendrickson, 1987; Pinault et al., 1995). Such a mechanism can partially account for cross-vibrissa suppression, because a fraction of VPM neurons extend dendrites into adjacent barreloids (Desîlets-Roy et al., 2002; Varga et al., 2002) and synapses onto afferent axons from the nRT (Varga et al., 2002). However, previous work has indicated that the average magnitude of cross-vibrissa interactions at the VPM cannot account for the totality of observed cortical poststimulus suppression (Simons and Carvell, 1989). In addition, VPM neurons exhibit the nonlinear suppression-of-suppression much less frequently than do SI cells (R. M. Webber and G. B. Stanley, unpublished observations). Therefore, additional response transformations likely augment the cross-vibrissa interactions originating from the VPM.

Any response suppression generated by intrathalamic mechanisms is augmented within SI by thalamocortical synaptic depression during repetitive firing (Chung et al., 2002). Thalamocortical synapses in layer III depress in response to a stimulus pair (Gil et al., 1997), and similar mechanisms may be relevant to layer IV thalamocortical synapses.

Intracortical mechanisms likely play an important part in giving rise to cross-vibrissa interactions. AV-evoked surround suppression in layer IV has been shown to be highly sensitive to the activity of GABA_A receptors (Kyriazi et al., 1996, 1998), indicating that intrabarrel inhibitory circuits are important to the formation of surround suppression. Fox et al. (2003) further illustrated that inactivation of a barrel eliminates the representation of the corresponding vibrissa from the surround RFs of neighboring barrels. This finding suggests that intracortical connections are also necessary for the presence of surround RFs in layer IV.

Regardless of the source for cross-vibrissa interactions, the suppression-of-suppression likely results in a nonlinearity that is observable at the level of the intracellular potential. Pairwise attenuation of the test response by itself is not evidence for the existence of a nonlinearity. Rather, the IPSP after a conditioning stimulus may lead to a hyperpolarization that linearly adds to the EPSP after the test input. This scenario, however, predicts an accumulation of the suppression for additional inputs, inconsistent with our findings. In contrast, Higley and Contreras (2003) demonstrate that poststimulus suppression, in addition to reducing the EPSP after a stimulus, reduces the following IPSP in a divisive manner.

The dynamics of pairwise interactions

Despite qualitative similarities between the dynamics of all second-order interactions, the time course of postexcitatory suppression depends on the strength and type of the constituent stimuli. Consistent with previous findings (Brumberg et al., 1996), a PV conditioning deflection evoked greater suppression than did the AV. In fact, there exists a high positive correlation between the magnitude of the conditioning response and the time course of recovery (r = 0.71; p < 0.001). Similar analyses revealed that the response to a PV deflection recovered from suppression more quickly than did an AV-evoked test response. However, it was unclear whether this difference in recovery times was a result of differences in the nature of the stimulus (i.e., a PV vs an AV) or of differences in response magnitude.

Significance of spatiotemporal interactions in coding

In this study, we investigated three response parameters likely to be relevant to coding in SI: (1) the average spike count, or equivalently, the firing rate over a given time window; (2) latency; and (3) temporal precision. To determine the dynamic range for rate coding, several studies have characterized the single-vibrissa frequency response of thalamocortical neurons. Cortical adaptation limits the accuracy of coding by firing rate for frequencies higher than ∼4 Hz (Ahissar et al., 2001; Chung et al., 2002; Garabedian et al., 2003; Khatri et al., 2004; Webber and Stanley, 2004). Our results extend these findings by characterizing SI responses to paired-vibrissa deflections as a function of both frequency and phase. Using ideal-observer analysis, we also showed that suppression-of-suppression enhances discrimination by increasing the response magnitude over a range of frequencies.

Recent work suggests that the temporal precision of the response (measured by the VS) remains constant (Khatri et al., 2004) or displays a bandpass behavior with a peak in the range of whisking frequencies (Garabedian et al., 2003). Responses exhibiting such effects can enhance stimulus discriminability in the whisking frequency range and beyond (Moore, 2004). However, our results indicate that response precision declines slightly with the accumulation of suppression, consistent with observations by Higley and Contreras (2006). The discrepancy may result from several factors, such as the choice of anesthetics (sodium pentobarbital here vs halothane and urethane), the interval over which VSs were measured, and the method of recording [single vs multiple units in the study by Garabedian et al. (2003)]. Importantly, we showed that reduction in the temporal precision of the response is highly detrimental to the accuracy of coding by single neurons. Our results imply that all factors that increase the magnitude and precision of the response also improve coding accuracy, as also suggested by Moore (2004).

Here, we also observed an increase in response latency (by up to a factor of 3) with increasing response suppression. Similar but somewhat smaller increases in response latency for neurons in the lemniscal pathway have been reported previously (Ahissar et al., 2000, 2001). We found that changes in response latency did not appreciably affect the probability of discrimination error (see Results). Still, given that the observed latency shifts were larger than the typical PSTH width, response latency is likely an important factor for coding in other contexts.

Our results highlight the role of interstimulus time intervals in shaping discrimination performance. Object contact can evoke interdeflection time delays in the range 10–25 ms (Sachdev et al., 2001). Our experimental and simulation results show that, depending on the PV–AV phase, this range of time delays can lead to response suppression or partial removal of suppression. For relatively large spacings, single-vibrissa discrimination is more accurate than paired-vibrissa performance. This is attributable to the fact that, for this range of spacings, PV–AV time delays, on average, lead to increased attenuation for paired-vibrissa stimuli relative to the PV-only case. In contrast, smaller spacings (and hence higher frequencies) led to greater suppression-of-suppression for the paired-vibrissa case, thus leading to improvements for discrimination using the vibrissa pair. Interestingly, Carvell and Simons (1995) found that the performance of rats in discriminating between two rough textures markedly improves when using two vibrissae instead of one. This finding, although for smaller surface spacings than considered here, is nevertheless consistent with our results for small spacings.

To link the present findings with coding in naturalistic settings requires additional considerations. First, textures evoke continuous deflections (Hartmann et al., 2003; Neimark et al., 2003; Arabzadeh et al., 2005) that typically have smaller amplitudes and velocities than those used here. This study, rather, emphasizes how temporal and spatial (over one or two locations) aspects of stimuli combine to shape the resulting responses and, ultimately, coding accuracy. In this context, the present results are expected to be valid for frequencies less than ∼100–200 Hz. Higher values may lead to response facilitation between subsequent inputs (Shimegi et al., 1999; Ego-Stengel et al., 2004), a factor not studied here. In contrast, naturalistic textures can evoke deflection frequencies as high as 600–700 Hz (Neimark et al., 2003). Additionally, both response magnitude and precision (the latter, at least for fast-spiking units) show tuning to frequencies as high as several hundred hertz (Andermann et al., 2004; Moore and Andermann, 2006). These facts indicate that the vibrissa pathway is capable of encoding stimulus frequencies in a wider range than considered here.

Second, only a limited subset of spatial inputs (namely, the PV and the caudal AV) were considered, whereas the spatial RF of an SI neuron is typically broader, especially in its subthreshold extent (Moore and Nelson, 1998). Together with the caudal AV, additional spatial components shape the functional properties of SI spatiotemporal RFs. An important and logical extension of the present work is to determine whether the simple dynamics of pairwise interactions studied here combine to form the complete spatiotemporal RF.

Third, awake states differ from the anesthetized condition in at least two respects: (1) the time course of response interactions is shorter (Fanselow and Nicolelis, 1999; Castro-Alamancos, 2004), thus possibly aiding the representation of high-frequency stimuli; and (2) the magnitude of response to isolated deflections is lower because of an elevated baseline level of adaptation (Castro-Alamancos, 2004). A related caveat is that the anesthetic used here enhances and mimics the action of GABA at the GABA_A receptor complex, decreasing excitability at both cortical and subcortical stages. Given the role of intracortical inhibition in forming surround suppression, the observed time course and magnitude of cross-vibrissa interactions are likely to be affected by barbiturate anesthesia.

Together, the results and paradigm presented here are broadly applicable both to more complex stimuli and to other modalities. Within the vibrissa pathway, we suggest that the prediction method outlined here for a PV–AV pair is generalizable to patterns incorporating additional vibrissae, velocities, and directions. Predictability of responses to complex stimuli using simpler, experimentally measured interactions suggests that the response model developed here captures a fundamental aspect of cortical dynamics. More generally, the universality of response integration within sensory systems means that understanding the role of spatiotemporal interactions is imperative to the study of sensory coding and promises insight into features common to many sensory pathways and modalities.