Influence of Response Variability on the Coding Performance of Central Gustatory Neurons

Abstract

We explored how variability in responding to taste stimuli could impact the signaling of taste quality information by neuron types and individual cells in the nucleus of the solitary tract. One hundred sixty-two neurons recorded from anesthetized rats were grouped using multivariate analysis of taste responses to the following (in m): 0.5 sucrose, 0.1 NaCl, 0.01 HCl, and 0.01 quinine-HCl. Neurons fell into one of three groups corresponding to cell types that responded optimally to sucrose, NaCl, or HCl. A statistical model was used to examine whether responses observed among neurons within each group could be correctly attributed to the optimal stimulus or another tastant on the basis of spike count. Results revealed poor classification performance in some cases attributable to wide variations in the sensitivities of neurons that compose a cell type. This outcome leads us to question whether neuron types could faithfully encode a single taste quality. We then theoretically explored whether a hypothetical observer of individual neurons could discriminate between spiking rates to different tastants during the first second of stimulus processing. Spike rate was found to be an unreliable predictor of stimulus quality for each neuron tested. However, additional analyses suggested that taste stimuli could be identified by a reader that attends to the relative spiking activities of different kinds of neurons in parallel. Rather than assigning meaning to individual neurons or categories of them, central gustatory circuits may signal quality information using a strategy that involves the relative activities of neurons with different sensitivities to tastants.

Introduction

How is information about taste quality (e.g., sweet, salty, sour, and bitter) represented by activity in the nervous system? This question lies at the center of a long-standing debate in the field of gustatory neurobiology. Early neurophysiological studies revealed that gustatory neurons in several species are sensitive to stimuli representing more than one taste quality. These data led to the idea that taste quality information is encoded by relative patterns of activity generated across a population of neurons (Pfaffmann, 1959; Erickson, 1963). This “across-neuron pattern” theory of taste coding accommodates the multiple sensitivities of taste cells and proposes that individual neurons contribute to the representation of more than one taste quality. Conversely, some data have been interpreted to support the notion that a particular stimulus quality is encoded by the activation of one of a few discrete types of gustatory neurons. In this theory of coding, known as “labeled line,” cells with a common optimal (i.e., best) stimulus are purportedly dedicated to represent the qualitative features of only this stimulus (Pfaffmann, 1974; Pfaffmann et al., 1976). Labeled-line theory requires that activity within a given type of neuron is both necessary and sufficient to represent a single stimulus quality. Interest in this latter model of coding has been kindled by the results of recent molecular and genomic studies of taste receptors. These investigations have shown that receptors for sweet, amino acid, and bitter tastants are expressed in nonoverlapping populations of taste bud cells (TBCs) in oral epithelia (Adler et al., 2000; Nelson et al., 2001). Based in part on these data, it has been proposed that a given taste quality is represented by the activation of one of a few discrete neural channels (Mueller et al., 2005; Scott, 2004; Zhang et al., 2003; Zhao et al., 2003).

Although the across-neuron pattern and labeled-line theories provide different accounts of the mechanism of gustatory coding, both theories can be applied to accommodate most datasets (Scott and Giza, 2000; Katz et al., 2002a). In the present investigation, a combination of experimental and theoretic techniques is used to explore the information-handling limits of central gustatory neurons as imposed by variability in responding to different tastants. We then use knowledge of these limits to infer how neural circuits for taste could be organized to encode information about stimulus quality. Here we analyze taste responses to stimuli humans describe as sweet, salty, sour, or bitter that were electrophysiologically recorded from neurons in the nucleus of the solitary tract (NST) in anesthetized rats. The NST is the first central synapse for taste information processing in mammals. It was evaluated whether the responses of purported functional groups of neurons and individual neurons themselves are reliable indicators of stimulus quality.

Materials and Methods

Our analysis proceeds in two phases. Phase 1 focuses on understanding the fidelity of gustatory neuron types in the NST by examining the extent to which “channel” responses to different stimuli overlap, as indexed by variability in responding to tastants across neurons that compose a given cell type. Here, we evaluate whether random responses to optimal or sideband (i.e., non-optimal) stimuli observed among such neurons could be correctly classified on the basis of response amplitude. The benefits (i.e., identifying true positives) and costs (i.e., reporting false positives) in doing so are characterized using a statistical model known as receiver operating characteristic (ROC) analysis (Green and Swets, 1966). The outcome here has implications for understanding whether the pooled activity of neurons that compose a cell type could be taken as a reliable indicator of stimulus quality. In phase 2, we investigate rate coding by individual NST neurons. Here, ROC analysis is used to characterize how variability in the firing rate of a single cell could impact the ability of its spike output to discriminate between different taste stimuli.

Phase 1: analysis of neuron types.

In phase 1, we analyze taste responses from a large number of NST neurons, some drawn from our files (Lemon et al., 2003, 2004; Lemon and Di Lorenzo, 2002) and others newly recorded. All neurons were sampled from naive adult male Sprague Dawley rats under urethane anesthesia. For newly acquired cells, details of the surgical and recording procedures have been reported previously (Lemon et al., 2003, 2004; Lemon and Smith, 2005). Briefly, conventional single-unit electrophysiological methods were used to record trains of action potentials from gustatory neurons in the NST. Action potentials generated by an individual neuron were identified using a waveform template-matching algorithm (Spike 2/Power 1401 acquisition system; Cambridge Electronic Design, Cambridge, UK). The single-unit nature of the recordings was evidenced by a refractory period (∼2 ms) in spike-interval histograms. Digital records of spike trains were analyzed off-line.

For all neurons, taste responses were evoked by applying stimulus solutions to an oral field that always included at least the anterior tongue and palate. Taste buds in these areas are innervated by cranial nerve VII, which critically mediates behavioral discriminations among taste stimuli in rats (Spector and Grill, 1992; Spector et al., 1997; St. John and Spector, 1998; Kopka et al., 2000; Geran et al., 2002). Neural responses to four stimuli were considered (in m): 0.5 sucrose, 0.1 NaCl, 0.01 HCl, and 0.01 quinine-HCl, respectively categorized as sweet, salty, sour, or bitter by humans. Tastant solutions were made from reagent-grade stock dissolved in laboratory-grade purified water. The chosen concentrations of stimuli evoke half-maximal responses in the rat chorda tympani nerve (Ganchrow and Erickson, 1970), which is the branch of cranial nerve VII that innervates the anterior tongue.

Taste responses were expressed as the average number of spikes evoked in 1 s corrected for spontaneous discharge. A measure of response profile entropy (Smith and Travers, 1979) was calculated for each neuron to quantify its breadth of responsiveness across stimuli. Entropy is defined as follows:

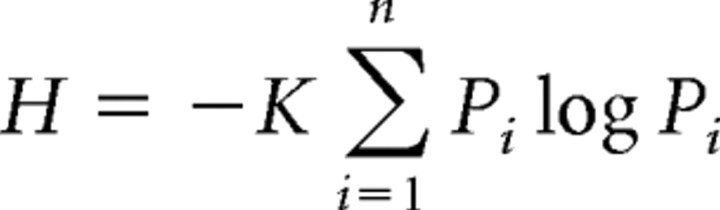where P_i represents the response to the ith stimulus expressed as a proportion of the total response to n stimuli, and K is a scaling constant; K = 1.661 for n = 4. The value of H ranges from a minimum of 0 to a maximum of 1. A neuron that responds to only one stimulus of four would achieve H = 0 (i.e., no uncertainty as to which stimulus produced a response), whereas a cell that responds equally well to all stimuli would result in H = 1 (i.e., maximum uncertainty).

Neurons were categorized into types using hierarchical cluster analysis (HCA). This approach has been used in other studies to group gustatory neurons with similar response properties into classes that presumably serve a particular function in the processing of taste information (Frank et al., 1988; Scott and Giza, 1990). The outcome of HCA typically suggests neuronal groupings that are similar to those that would be derived if one used a “best-stimulus” classification scheme (i.e., categorizing neurons into types based on the stimulus that evokes the highest relative rate of firing) (Smith et al., 1983a,b; Chang and Scott, 1984; Frank et al., 1988; Nakamura and Norgren, 1991). However, HCA provides a more comprehensive approach to defining neuronal groupings because neurons can be categorized based on similarities/dissimilarities among responses to each stimulus under consideration. Input to HCA consisted of a distance matrix representing pairwise neuronal response profile dissimilarity, where 1 − Pearson’s product-moment correlation (r) served as the distance metric. This analysis was performed using the Statistica software package (StatSoft, Tulsa, OK). The “unweighted pair–group average” amalgamation schedule was used.

For each neuron type, we used ROC analysis to evaluate whether randomly observed responses to optimal and sideband stimuli could be correctly classified as such based on knowledge of the mean spike count to each stimulus. ROC analysis offers several advantages for evaluating spike data of the kinds presented in this manuscript. Foremost, ROC analysis does not depend on a single response–decision threshold. In ROC analysis, every possible decision threshold is considered and an estimate of the performance that would be expected across a range of thresholds can be computed. One can intuit that this feature has value for evaluating the spiking activities of sensory neurons because it is, of course, unknown as to what decision threshold the brain might adopt to read neural responses. Moreover, ROC analysis provides a “distribution-free” method to compare distributions of events. Unlike standard parametric statistical tests, ROC analysis does not assume that the distributions are Gaussian and have equal variance (Green and Swets, 1966). The shapes of the frequency distributions analyzed here would suggest that both of these conditions are not met across all comparisons. Any statistical analysis of these distributions must therefore not rely on the assumption of normality or fixed variance. Thus, ROC analysis provides a useful and appropriate statistical method to explore the response properties of gustatory neurons. All ROC analyses herein were conducted using SPSS (SPSS, Chicago, IL) or the ROCR toolkit for the R computing language (Sing et al., 2004; Venables et al., 2004).

As used in phase 1, ROC analysis provides a method to index the degree of similarity among responses to different stimuli in a neuron type (i.e., a neural “channel”). As an extreme example, classification performance that is near perfect (100% correct) would indicate little overlap in the responses of neurons to a given optimal and sideband stimulus. Assuming a sufficient difference between response distributions, a finding of this sort might suggest that the pooled output of these cells could be used to represent the optimal stimulus relative to the sideband stimulus in question. Conversely, classification performance near chance (50% correct) reflects a high degree of overlap between responses to two stimuli among cells that compose a neuron type.

Caution must be assumed with regard to interpreting the outcome of ROC analysis as applied in phase 1 as an estimate of the discriminative capacity of a neural channel. Our data concerning neuron types only pertains to the influence of across-neuron variability in predicting stimulus quality and does not contain measurement of within-neuron response variability, that is, variability in how individual neurons themselves respond to taste stimuli. Because both sources of variance potentially influence the coding performance that could be achieved by attending to the pooled signal of a group of neurons, within-neuron response variability must be taken into account to effectively estimate discriminative capacity. Moreover, it must also be considered that the nervous system could very well read out stimulus quality by attending to neurons on an individual basis rather than lumping their activities into an aggregate signal. Experiments in phase 2 aimed to address these issues.

Phase 2: analysis of rate coding by individual gustatory neurons.

To characterize the accuracy by which the firing rate of an individual neuron conveys information about taste quality, we started by recording trains of action potentials evoked over many presentations of the following (in m): 0.5 sucrose, 0.1 NaCl, 0.01 HCl, and 0.01 quinine-HCl. We attempted to stimulate each cell at least six times with each tastant. On each trial, deionized water was applied to the tongue and palate for 5 s, immediately followed by a stimulus for 5 s and then a 10 s deionized water rinse. Cells were allowed to return to baseline levels of spontaneous activity before the next trial. Stimuli were tested in pairs, with presentation order alternated across trials.

For each evoked spike train, the time interval between sequential action potentials [i.e., the interspike interval (ISI)] was repeatedly sampled during the first second of taste responding, in which response onset was defined as the time of occurrence of the first spike that was at least 300 ms beyond stimulus onset. The reciprocal of each ISI was calculated to derive an estimate of the instantaneous firing rate (IFR) (Cheng and Wasserman, 1996) of the neuron at the point in time at which the ISI under consideration terminated. IFRs were expressed in units of spikes per second. For each neuron, IFR streams measured over multiple trials were pooled to build frequency distributions of spike rates evoked by each stimulus. ROC analysis was used to quantitatively estimate the performance by which a hypothetical observer of individual neurons could use knowledge of these frequency distributions to discriminate between firing rates produced by different taste stimuli.

Here it is assumed that an individual neuron signals the presence of its most effective (i.e., reference) stimulus when activated, as indexed by the mean IFR. Thus, a downstream reader of an NST neuron must know the reference stimulus attached to this cell along with the distribution of firing rates evoked by this stimulus. When the neuron is under gustatory drive, the reader would compute a firing rate distribution to compare with the known distribution to make a decision about whether or not the input was produced by the reference stimulus. The present model explores the plausibility of this decoding strategy by using ROC analysis to compare firing rate distributions to different stimuli in individual cells. It is evaluated whether a hypothetical observer of the IFR could reliably discriminate between randomly drawn firing rates to the reference and another stimulus by always reporting that the larger rate was produced by the reference stimulus. The theoretic approach used here to study rate coding by gustatory neurons is similar to that used in other investigations of information coding by spike intervals and instantaneous firing rates in visual and proprioceptive neurons (Werner and Mountcastle, 1963; Wilson et al., 1988; Kiani et al., 2005). The present model does not attend to the ordering of the spike intervals but only the spacing between spikes, which is inversely proportional to the firing rate of a neuron. This is tied to the present evaluation of whether information about stimulus quality lies in the source of a taste message: could quality information be read out by attending to which cells are active? The present statistical model may, of course, be unrelated to the mechanism the nervous system would use to read the activities of gustatory neurons. However, this model has implications for understanding whether or not different taste stimuli produce reliably different spiking rates in individual cells.

Results

General response characteristics

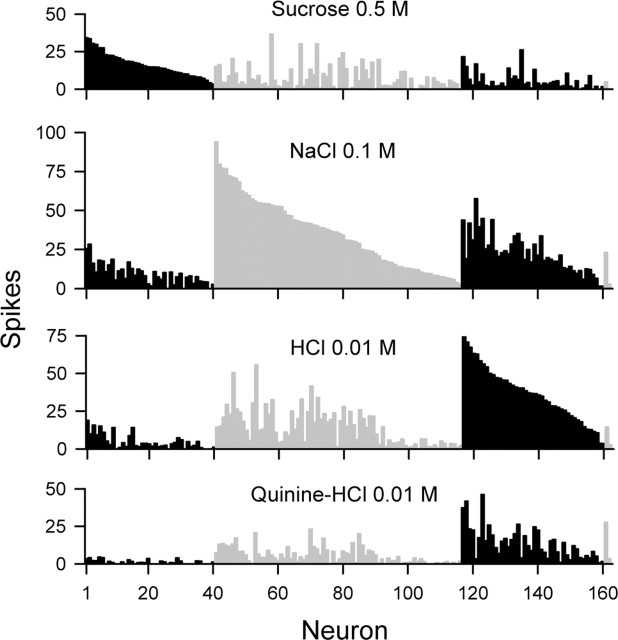
Our dataset was composed of 162 rat NST neurons, 122 drawn from our files (76 cells from Lemon et al., 2003, 2004; 46 cells from Lemon and Di Lorenzo 2002; used here with the consent of P. M. Di Lorenzo, Binghamton University, Binghamton, NY), and 40 cells newly recorded from 28 rats. On the basis of the number of spikes evoked by the four stimuli, 40 neurons responded best to sucrose, 76 responded best to NaCl, 44 responded best to HCl, and two quinine-best neurons were included in our sample. The response profile for each neuron is displayed in Figure 1. Neurons were generally broadly responsive across stimuli (H̄ = 0.75 ± 0.01 SE; mean spontaneous discharge, 1.9 ± 0.2 spikes), as observed in other studies of NST gustatory neurons (McCaughey and Scott, 2000; Di Lorenzo et al., 2003; Di Lorenzo and Victor, 2003; Cho et al., 2004).

Figure 1.

Across-neuron patterns of response evoked by each taste stimulus across 162 NST neurons recorded from anesthetized rats. For each plot, spike count (average number in 1 s) is represented along the ordinate, and neurons are segregated from left to right along the abscissa into best-stimulus groups (sucrose-, NaCl-, HCl-, and quinine-best, respectively), as denoted by black and halftone bars. Cells are rank ordered within each group according to magnitude of responding to their best stimulus.

Phase 1: analyses of neuron types

Cells were categorized into types using HCA, the results of which are depicted graphically by the dendrogram in Figure 2A. Based on responses to sucrose, NaCl, HCl, and quinine, this analysis revealed four types of gustatory neurons. Mean levels of activation produced by optimal and sideband stimuli in each of three neural types are shown in Figure 2B. It can be seen that type S neurons (n = 48; H̄ = 0.72 ± 0.03; mean spontaneous discharge, 0.5 ± 0.1 spikes) responded optimally to sucrose but were also strongly activated by NaCl. Type N neurons (n = 63; H̄ = 0.73 ± 0.02; mean spontaneous discharge, 1.9 ± 0.3 spikes) responded optimally to NaCl and showed good sensitivity to HCl. Type H cells (n = 49; H̄ = 0.83 ± 0.01; mean spontaneous discharge, 3.2 ± 0.4 spikes) responded optimally to HCl but were also responsive to NaCl and quinine. The two quinine-best cells (H̄ = 0.86 ± 0.04; mean spontaneous discharge, 2.7 ± 1.3 spikes) in our sample were identified as an independent group by HCA (response profile is not shown in Fig. 2B). Quinine-best neurons are not as common as other types of cells in the rodent brainstem (Smith et al., 1983a; McCaughey and Scott, 2000; Di Lorenzo et al., 2003; Lemon et al., 2003; Lemon and Smith, 2005), and the low n of this group precluded any meaningful analyses.

Figure 2.

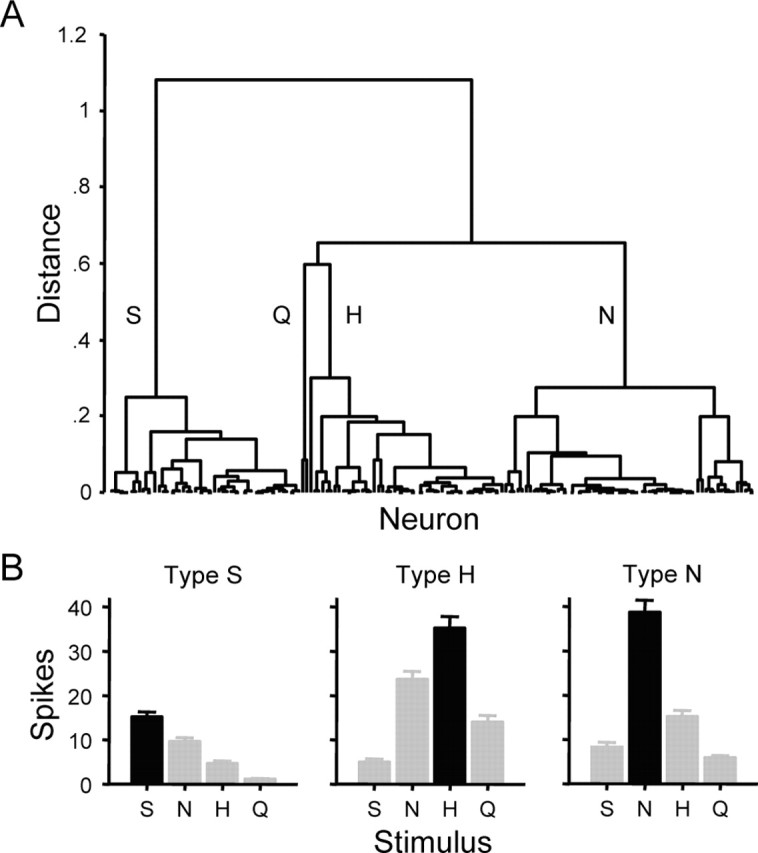
Neural groups defined using multivariate analysis. A, Dendrogram representing the results of hierarchical cluster analysis applied to categorize the neurons shown in Figure 1 into cell types based on similarities among their response profiles. Linkage distance is represented along the ordinate, and individual neurons are represented along the abscissa. Neural types defined by this analysis are denoted by labels: S, sucrose-oriented (n = 48); Q, quinine-oriented (n = 2); H, HCl-oriented (n = 49); and N, NaCl-oriented (n = 63). B, Mean responding to each stimulus in neural types S, H, and N. Bars show mean number of spikes in 1 s ± SE. Spike counts (average spikes in 1 s ± SE) follow. Neural type S: S, 15.2 ± 1.1; N, 9.6 ± 0.9; H, 4.6 ± 0.7; Q, 1.2 ± 0.2. Neural type H: S, 5.0 ± 0.7; N, 23.6 ± 1.9; H, 35.2 ± 2.6; Q, 14.0 ± 1.5. Neural type N: S, 8.3 ± 1.1; N, 38.7 ± 2.7; H, 15.1 ± 1.4; Q, 5.8 ± 0.6.

In phase 1, ROC analysis was applied to categorize taste responses in neuron types. ROC analysis compares two histograms of the kinds shown in Figure 3A. Here, these distributions describe the frequency of occurrence of responses to the optimal stimulus and sideband stimuli across NST neurons of a given cell type. For the present analysis, the response distribution produced by the optimal stimulus served as the reference to which each sideband (i.e., secondary) distribution was compared. A series of response criteria (β₀, β₁, …, β_n) were applied to each pair of distributions (Fig. 3A). These criteria ranged in value from 0 spikes to 1 spike greater than the maximum spike count elicited by the optimal stimulus among all cells of the type under evaluation. Criteria were varied from β₀ to β_n in 1 spike increments. Two values were calculated from the response distributions at each criterion based on the decision rule that a spike count that exceeds β_i announces the presence of the optimal stimulus. First, the number of true-positive responses (“hits”) was determined by identifying neurons in which the response to the optimal stimulus was greater than β_i. Expressing this count as a proportion of the total number of neurons yielded the hit rate at β_i. Second, because NST neurons are generally multisensitive across stimulus qualities, in a proportion of neurons, responses to the sideband stimulus exceeded certain values of β. In these individual cases, the response produced by sideband would be attributed to the optimal stimulus by the decision rule, leading to false-positive classification (i.e., a “false alarm”). The false alarm rate at β_i was calculated by dividing the number of neurons that registered this error by the total. Finally, the hit rate was plotted against the false alarm rate for every possible value of β resulting in a function known as the ROC curve (Fig. 3B).

Figure 3.

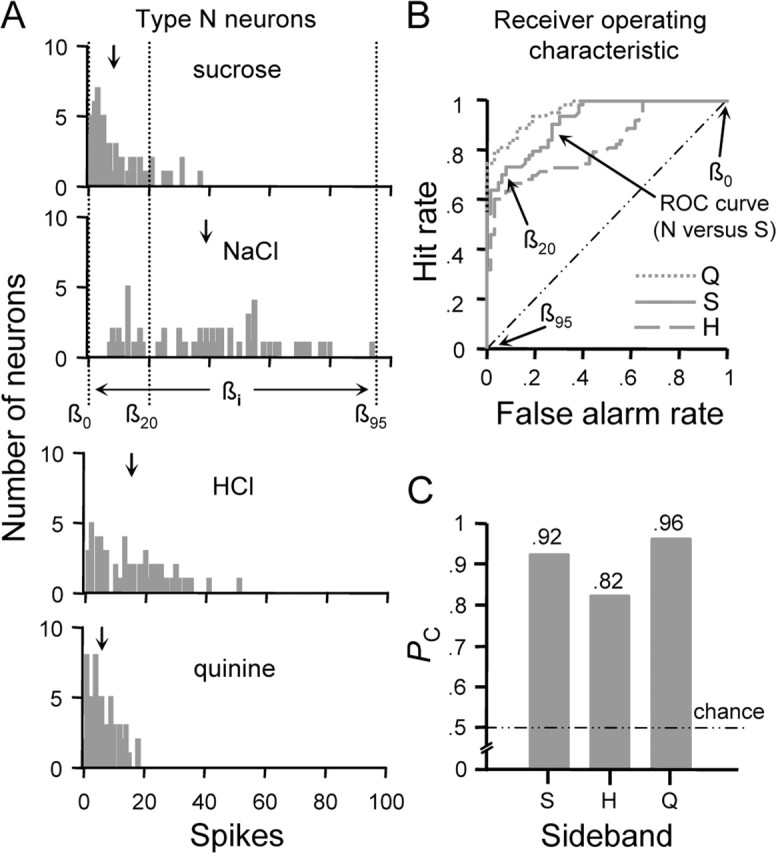
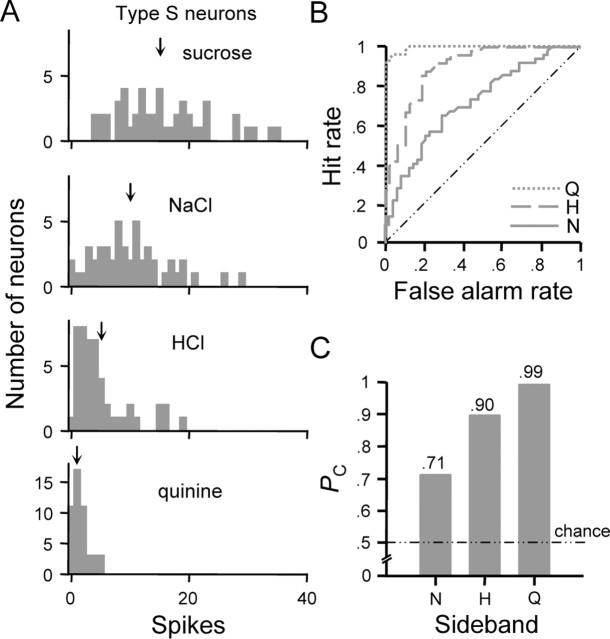
ROC analysis as applied to classify responses observed among type N neurons. A, Distributions showing the number of type N neurons (ordinate) that responded to each stimulus at each spike count (abscissa). Downward arrows above each distribution indicate the mean spike count across all cells. For the sucrose and NaCl distributions, three arbitrary criterion levels (β₀, β₂₀, and β₉₅) and the range over which criteria were varied (← β_i →) to compute the ROC function for this comparison are shown. B, Family of ROC curves describing the relationship between the classification hit rate (ordinate) and false alarm rate (abscissa) for responses to optimal and sideband stimuli in neural type N. Legend denotes the sideband stimulus response distribution compared with that for NaCl to compute each ROC function. Diagonal represents the ROC function that would be observed if the hit and false alarm rates were equal at each criterion. Coordinates along the ROC curve for the NaCl versus sucrose comparison that denote the hit and false alarm rates calculated at the selected values of β in A are marked by arrows. C, Profile showing probabilities (ordinate) that randomly observed responses to NaCl and a given sideband stimulus (abscissa) could be correctly classified on the basis of response amplitude. Each probability (P_C) is given by the normalized area under the corresponding ROC curve in B. Chance performance (P_C = 0.50) is indicated by the dotted/dashed line. S, Sucrose; H, HCl; N, NaCl; Q, quinine.

It has been shown that the area under the ROC curve corresponds to the probability that random true-positive and false-positive events could be correctly classified in a two-alternative, forced-choice psychophysical paradigm (Green and Swets, 1966). This metric has also been adapted for use in neurophysiological studies (Bradley et al., 1987; Newsome et al., 1989; Vogels and Orban, 1990; Britten et al., 1992). Here, the area under the ROC curve provides an estimate of the probability that randomly observed optimal and sideband stimulus responses could be correctly classified on the basis of their amplitude. This probability, P_C, meaningfully ranges from 0.5 to 1. For example, ROC analysis applied to two response distributions that are identical would result in P_C = 0.5, corresponding to a 50% chance of correctly classifying responses as drawn from one distribution or the other. At the opposite extreme, ROC analysis applied to completely nonoverlapping response distributions would yield P_C = 1. In this case, perfect classification performance could be achieved by a binary classifier that adopts any criterion threshold that lies between the two distributions.

Let us first apply this analysis to neural type N. Distributions of spike counts evoked by each stimulus across type N cells are shown in Figure 3A. ROC functions describing the efficiency by which randomly observed optimal and sideband responses could be correctly classified on the basis of amplitude are shown in Figure 3B. The area under each ROC curve (i.e., P_C) is represented by the profile in Figure 3C. It was found that responses to NaCl could be reliably classified relative to those evoked by sucrose (P_C = 0.92) or quinine (P_C = 0.96). A maximum probability of correct classification of 0.82 was found with regard to responses produced by NaCl and HCl. It must be considered that a decrease in the concentration of NaCl (e.g., 0.01 m) would shift the NaCl distribution to the left. Such a shift would induce a larger amount of overlap in the response distributions for NaCl and HCl, thus reducing P_C without affecting the qualitative features of NaCl. Rodents perceive the tastes of NaCl and HCl as perceptually independent as shown by learned-generalization and operant conditioning experiments (Morrison, 1967; Nowlis et al., 1980).

Distributions of firing rates evoked by the optimal stimulus and sideband stimuli in type H neurons are shown in Figure 4A. The ROC functions for optimal/sideband comparisons in this cell type are plotted in Figure 4B; P_C for each comparison is given by the profile in Figure 4C. Responses produced by HCl and sucrose in type H neurons could be reliably classified (P_C = 0.95). A probability of correct classification of 0.85 was observed with regard to responses produced by HCl and quinine. Poor classification performance was observed for responses to HCl and NaCl (P_C = 0.70), which is attributable to widely overlapping variation in the sensitivities of type H neurons to these stimuli (Fig. 4A). Because there is substantial overlap between response distributions to HCl and NaCl and rodents perceive these stimuli as unique (Morrison, 1967; Nowlis et al., 1980), it is questionable as to whether the output of neuron type H could represent exclusively the qualitative features of acidic stimuli.

Figure 4.

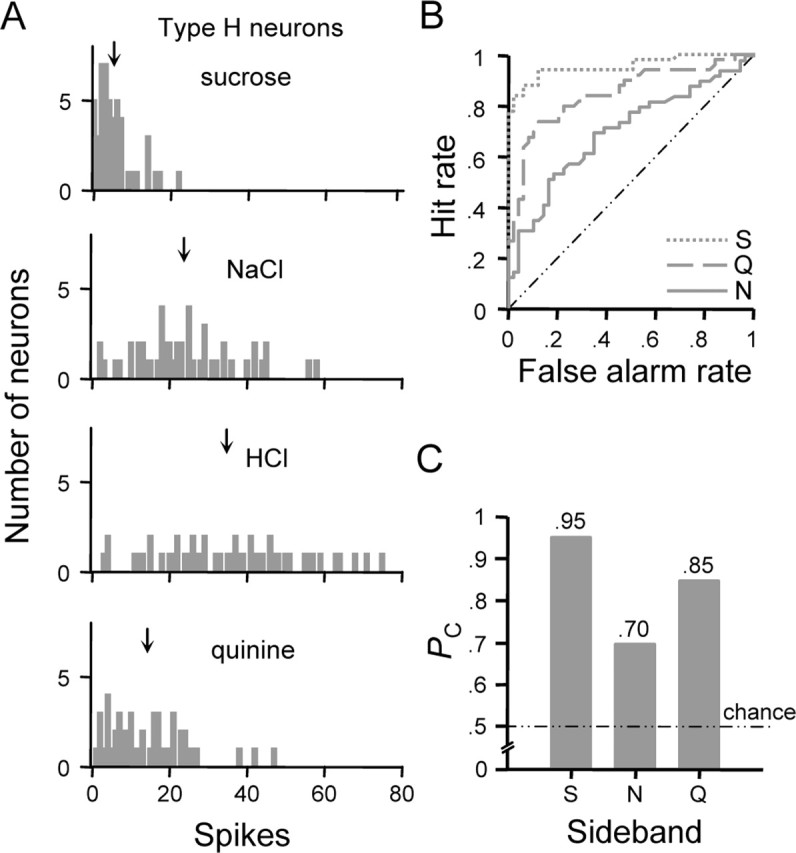
ROC analysis as applied to classify responses observed among type H neurons. A, Frequency distributions showing the number of neurons (ordinate) that responded to each stimulus at each spike count (abscissa). ↓, Mean spike count. B, Family of ROC curves describing the relationship between the classification hit rate (ordinate) and false alarm rate (abscissa) observed at each criterion level for responses to optimal and sideband stimuli in neural type H. Legend denotes the sideband stimulus response distribution compared with that for HCl to compute each ROC function. C, Profile showing probabilities (P_C, ordinate) that randomly observed responses to HCl and a given sideband stimulus (abscissa) could be correctly classified on the basis of response amplitude. S, Sucrose; N, NaCl; Q, quinine.

Figure 5A shows response distributions for spike counts elicited by each stimulus in type S neurons. The family of ROC curves that reflects variability in how neurons of this class respond to sucrose relative to other stimuli is shown in Figure 5B. Corresponding values of P_C are represented in Figure 5C. Responses produced by sucrose could be reliably classified relative to those evoked by HCl (P_C = 0.90) or quinine (P_C = 0.99). However, responses produced by sucrose and NaCl in cell type S could be, at best, poorly classified (P_C = 0.71), which is attributable to a high degree of variability in how neurons of this class respond to these stimuli. This variation results in responses distributions to sucrose and NaCl that substantially overlap. Thus, one could intuit that small adjustments in stimulus concentration could render near equivalent mean responses in neuron type S to sucrose and NaCl, stimuli that are perceived as perceptually independent by rats as indexed by behavioral studies (Morrison, 1967; Nowlis et al., 1980).

Figure 5.

ROC analysis as applied to classify responses observed among type S neurons. A, Frequency distributions showing the number of neurons (ordinate) that responded to each stimulus at each spike count (abscissa). ↓, Mean spike count. B, Family of ROC curves describing the relationship between the classification hit rate (ordinate) and false alarm rate (abscissa) observed at each criterion level for responses to optimal and sideband stimuli in neural type S. Legend denotes the sideband stimulus response distribution compared with that for sucrose to compute each ROC function. C, Profile showing probabilities (P_C, ordinate) that randomly observed responses to sucrose and sideband stimuli (abscissa) could be correctly classified on the basis of spike count. H, HCl; N, NaCl; Q, quinine.

ROC analyses were also performed on neuron types defined using best-stimulus classification, although results only slightly differed from those presented above. Considering the worst-case optimal/sideband comparison, a maximum probability of correct classification of 0.79 was found with regard to responses to NaCl and HCl in NaCl-best neurons, which is similar to P_C observed for this comparison in neural type N. As with neural type H, responses to HCl and NaCl in HCl-best neurons could only be poorly classified (P_C = 0.73). A probability of correct classification of 0.76 was found for responses to sucrose and NaCl in sucrose-best neurons. Although P_C for this comparison is slightly greater than that observed for type S cells, a small reduction in the concentration of sucrose or increase in the concentration of NaCl would result in greater overlap of these response distributions in sucrose-best neurons, reducing classification performance.

Phase 2: modeling rate coding by individual gustatory neurons

Experiments in phase 2 explored how the discriminative abilities of individual neurons would be impacted by variability in firing rate when under gustatory drive. These experiments were performed on 16 neurons included in analyses in phase 1. Spike trains were recorded from each neuron over multiple presentations of each tastant, making 378 total stimulus trials available for analysis in phase 2. For each cell, ROC analysis was used to estimate the probability that a hypothetical observer of the IFR could correctly discriminate between responses to the reference stimulus and secondary tastants using knowledge of the mean IFR. Although mean IFR tends to overestimate spike count per unit time (Lansky et al., 2004), these measures typically covary, as found across all trials (r = +0.91; p < 0.05).

ROC analysis as applied here proceeded in a manner similar to the description of this technique for phase 1 with several differences. Foremost, the input to this analysis consisted of distributions of firing rates measured from a single neuron. The stimulus that elicited the highest mean IFR for a given neuron was used as the reference to which the secondary stimuli were compared. The response criterion (β) was varied from 0 to the maximum firing rate in 1 Hz increments. At β_i, the hit rate was calculated as the proportion of IFRs that exceeded criterion for the reference stimulus, whereas the false alarm rate was tallied as the proportion of IFRs that exceed criterion for the secondary stimulus. The hit rate was plotted as a function of the false alarm rate at each β to produce the ROC curve. In this case, the area under this curve provides an estimate of the probability that a hypothetical observer of the neuron under study could correctly discriminate between spike rates to two stimuli. This probability, P_D, meaningfully ranges from 0.5 (chance performance) to 1 (perfect discrimination). Here it was assumed that P_D = 0.75 represents the just-noticeable difference (JND) threshold between spiking rates to different taste stimuli; P_D < 0.75 represented no detectable difference (cf. Bradley et al., 1987; Vogels and Orban, 1990).

Figure 6 shows the application of this model to an individual NST gustatory neuron, the sampling of which is described in Figure 6A. This neuron responded most effectively to sucrose but nearly as well to NaCl, as reflected by the average number of spikes evoked in 1 s (Fig. 6B) and by the mean IFR over six trials (Fig. 6C). Cosensitivity to sucrose and NaCl is commonly observed in sweet-oriented NST neurons [i.e., cells classified as sucrose-best or type S (Figs. 1, 2)]. A family of ROC curves describing the efficiency of rate coding by this neuron is shown in Figure 6D. The area under each ROC curve (i.e., P_D) is represented by the “neurometric” profile in Figure 6E, which gives the discrimination performance that could be had by an observer attending to the IFR of this cell. Assuming a difference threshold of P_D = 0.75 (i.e., the JND), the observer could reliably discriminate between firing rates evoked by sucrose and HCl or quinine (P_D > 0.75) but would fail to discriminate those produced by sucrose and NaCl (P_D < 0.75) (Fig. 6D,E).

Figure 6.

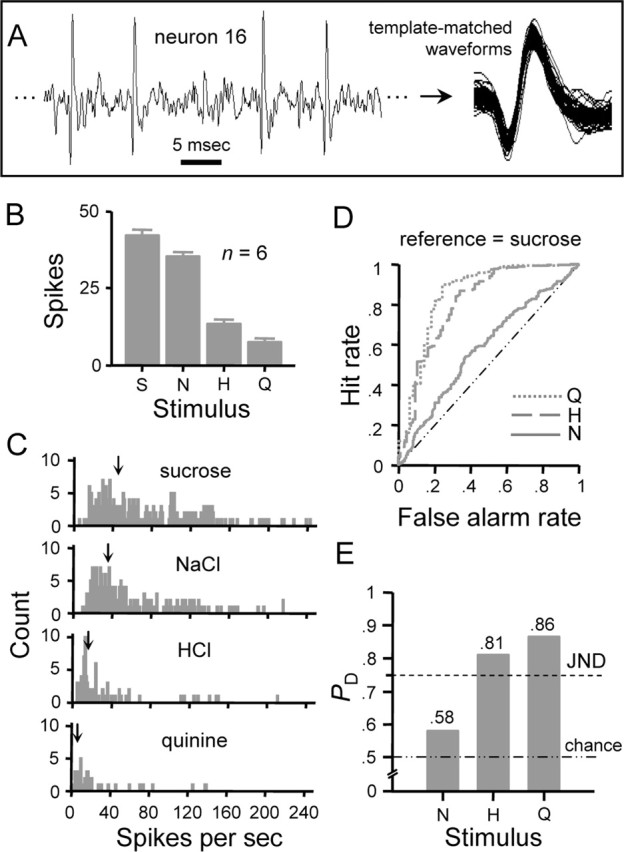
Rate coding performance of an individual NST gustatory neuron. A, Spiking activity sampled from neuron 16 (Table 1) when under gustatory drive. Spikes that arose from individual neurons were identified using a waveform template-matching algorithm. B, Response profile showing the average ± SE number of spikes produced by each stimulus in 1 s over six trials. C, Frequency distributions showing the number of observations (ordinate) of instantaneous firing rates (abscissa) to the four stimuli. Each distribution was built using sequential interspike intervals (s⁻¹) acquired during the first second of evoked responding over six stimulus presentations. ↓, Mean spike rate. D, Family of curves describing the outcome of ROC analysis applied to pairs of distributions in C. For this neuron, the distribution produced by sucrose (i.e., the most effective stimulus) was compared with that for each secondary stimulus. Resulting ROC curves are indicated by the legend according to the secondary stimulus. Each curve describes the relationship between the hit rate (ordinate) and false alarm rate (abscissa) observed at each response criterion level. The dashed/dotted diagonal line represents the ROC curve that would be had if one distribution was compared against itself (i.e., equal hit and false alarm rates at each criterion). E, Neurometric profile showing probabilities (ordinate) that an observer of the instantaneous firing rate in this neuron could use knowledge of the means of the distributions in C to correctly discriminate between spike rates to sucrose and each secondary stimulus, which are listed along the abscissa. Each probability, P_D, is given by the area under the corresponding ROC curve in D. A criterion of 75% correct discrimination (P_D = 0.75) represents the JND between responses to sucrose and a secondary stimulus (dashed line). Chance discrimination performance (P_D = 0.50) is indicated by the dotted/dashed line. S, Sucrose; H, HCl; N, NaCl; Q, quinine.

Figure 7 shows the analysis of rate coding in an additional neuron, which responded most effectively to NaCl and relatively well to HCl and quinine but not sucrose (Fig. 7B,C). ROC analysis indicates that an observer reading the IFR of this cell could discriminate between firing rates produced by NaCl and sucrose (P_D > 0.75) but would fail to discriminate those evoked by NaCl and HCl (P_D < 0.75) (Fig. 7D,E). Discrimination performance for firing rates evoked by NaCl and quinine was found to lie at the difference threshold (P_D = 0.75), although it is likely that reduced performance would be observed if a slightly lower concentration of NaCl were tested (e.g., 0.03 m).

Figure 7.

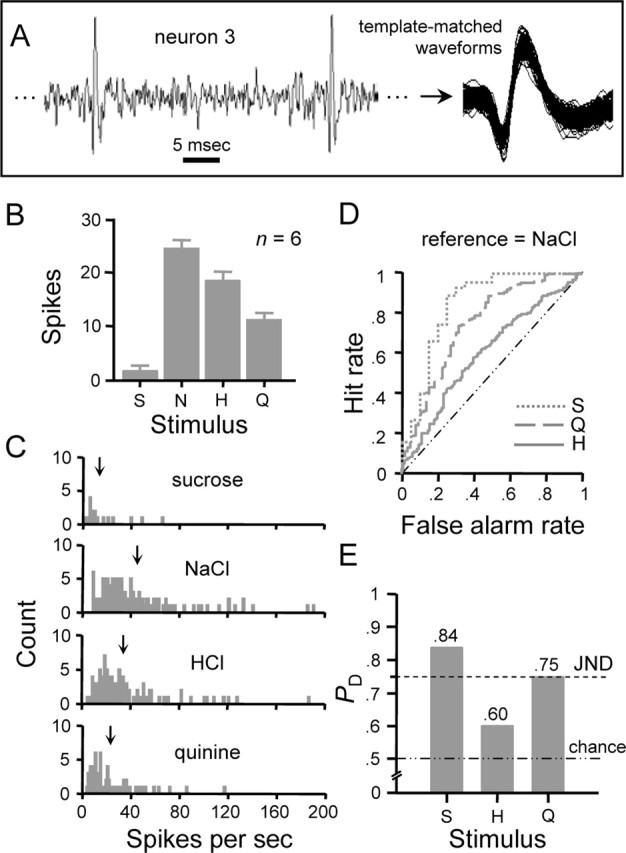
Rate coding performance of an individual NST gustatory neuron. A, Spiking activity sampled from neuron 3 (Table 1) when under taste drive. Template-matched spikes are also shown. B, Response profile showing the average ± SE number of spikes produced by each stimulus in 1 s over six trials. C, Frequency distributions of instantaneous firing rates to the four stimuli built over six presentations of each stimulus. ↓, Mean spike rate. D, Family of curves describing the outcome of ROC analysis applied to pairs of distributions in C. For this neuron, the distribution produced by NaCl was compared with that for each secondary stimulus. Resulting ROC curves are indicated by the legend according to the secondary stimulus. Each curve describes the relationship between the hit rate (ordinate) and false alarm rate (abscissa) observed at each response criterion level. E, Neurometric profile showing probabilities (ordinate) that an observer of the instantaneous firing rate in this neuron could use knowledge of the means of the distributions in C to correctly discriminate between responses to NaCl and each secondary stimulus, which are listed along the abscissa. Each probability, P_D, is given by the area under the corresponding ROC curve in D. P_D = 0.75, JND between responses to NaCl and a secondary stimulus (dashed line). P_D = 0.50, chance discrimination performance (dotted/dashed line). S, Sucrose; H, HCl; N, NaCl; Q, quinine.

A failure to discriminate between firing rates to the reference stimulus and the most effective secondary stimulus was observed for 15 of 16 neurons tested in phase 2 (P_D < 0.75) (Table 1). If we further consider these cells according to which group they were assigned to by HCA in phase 1, six cells were of type H (H̄ = 0.85 ± 0.03; mean spontaneous discharge, 3.2 ± 0.8 spikes), six were type N (H̄ = 0.79 ± 0.04; mean spontaneous discharge, 2.0 ± 1.1 spikes), and four were type S (H̄ = 0.79 ± 0.08; mean spontaneous discharge, 0.2 ± 0.2 spikes). As shown in Table 1, spike rates to HCl and NaCl could not be reliably discriminated in type H cells. Spike rates to NaCl and sucrose or HCl could not be reliably discriminated in five of six type N neurons. For the one exceptional cell, the probability of correctly discriminating between spike rates to NaCl and HCl was found to be equal to the difference threshold (P_D = 0.75), and it is likely that detection performance would drop below this level if small adjustments in stimulus concentration were made (e.g., slightly reducing the concentration of NaCl). Finally, the decision rule that sucrose always produces a faster spike rate than NaCl could not be used to reliably distinguish between responses to these stimuli in type S cells.

Table 1.

Posterior probabilities for correctly discriminating between spike rates evoked by different tastants (i.e., P_D) for each neuron tested in phase 2

Neuron	Cell type	Traditional best stimulus	Most effective stimulus (S1)	2nd most effective stimulus (S2)	PD S1 versus S2
1	H	HCl	NaCl	HCl	0.57
2	H	NaCl	NaCl	HCl	0.56
3	H	HCl	NaCl	HCl	0.60
4	H	HCl	NaCl	HCl	0.54
5	H	HCl	HCl	NaCl	0.55
6	H	HCl	HCl	NaCl	0.53
7	N	NaCl	NaCl	Sucrose	0.70
8	N	NaCl	NaCl	HCl	0.56
9	N	NaCl	NaCl	HCl	0.75
10	N	NaCl	NaCl	Sucrose	0.71
11	N	NaCl	NaCl	Sucrose	0.60
12	N	HCl	NaCl	Sucrose	0.64
13	S	Sucrose	NaCl	Sucrose	0.62
14	S	Sucrose	Sucrose	NaCl	0.67
15	S	Sucrose	Sucrose	NaCl	0.67
16	S	Sucrose	Sucrose	NaCl	0.58

Neurons are denoted in the first column by an integer, and the neuron type (S, N, or H) to which each was assigned by multivariate analysis in phase 1 is given in the second column. The best stimulus for each cell as determined using a common method (net spikes per 5 s stimulus period) is indicated in column three. For each neuron, the most and second most effective stimuli, as determined by the mean IFR during the first second of taste responding, are, respectively, indicated in columns four and five. P_D as computed by ROC analysis of spike rate distributions to these stimuli is given in column six. Bold indicates P_D ≥ 0.75.

The outcome of our statistical model indicates that stimuli of different taste qualities elicit similar firing rates during the first second of stimulus processing in individual gustatory neurons representative of each NST cell type. This suggests that a reader of the firing rates of individual neurons could not reliably identify sucrose, NaCl, or HCl by attaching a message about each stimulus to dedicated neurons and attending to which of these cells are active. The nervous system could be faced with a similar dilemma if it adopted this stimulus decoding strategy. Moreover, poor discrimination performance, at best, would likely also result if the spike outputs of neurons of a type were pooled, yet rats readily distinguish among sucrose, NaCl, and HCl in learned-generalization and operant conditioning experiments (Morrison, 1967; Nowlis et al., 1980). Although NST neurons that responded optimally to quinine were not available for analysis in phase 2, such neurons do not respond differentially, as indexed by spike count, to bitter stimuli relative to tastants of other quality categories, such as Na⁺ salts (Lemon and Smith, 2005), suggesting that the firing rate of such neurons would also poorly signal stimulus quality.

If the firing rate of individual gustatory neurons provides equivocal information about taste quality, how is this message carried by neural activity? Pfaffmann et al. (1976) proposed that the ambiguity about stimulus quality that arises from the multisensitive nature of gustatory neurons could be resolved through a comparison of the activities of multiple cells with different response properties. In example, let us assume two hypothetical neurons, i and j, where each cell responds to stimulus x and y. Suppose that neuron i responds more strongly to stimulus x than neuron j, but that j responds greater to stimulus y. A reader attending to both cells could use the following rules to know the stimulus: x is present when the response in i is larger than j (i.e., i > j) and y when i < j. A similar hypothetical model has been used to explore the detection of visual motion by cortical neurons (Newsome et al., 1989; Britten et al., 1992).

We investigated the plausibility of such a model for taste by using ROC analysis to compare firing rate distributions to each stimulus between pairs of NST neurons. The resulting area under the ROC curve provided an estimate of the probability than an observer of the IFR in these neurons could reliably discriminate whether one cell fires faster than the other when under the drive of a particular stimulus. Here we assume that all neurons are representative of those that would be encountered in a single animal. Figure 8 shows the outcome of this analysis as applied to neurons 5 (n₅) and 7 (n₇) in Table 1. In this figure, the IFR distributions sampled from these neurons under each stimulus condition are shown to the left, and the outcome of ROC analysis of each pair of distributions is shown to the right. In each analysis, the distribution with the larger absolute mean spike rate was used as the reference. Let us first consider responding to sucrose between these neurons. Assuming a difference threshold of 0.75, an observer with knowledge of the means of the sucrose firing rate distributions could reliably categorize responses randomly drawn from each distribution as produced by either neuron, as P_D > 0.75. This is taken to indicate that neurons n₅ and n₇ fire at noticeably different rates when under the drive of sucrose, with n₇ firing detectably faster than n₅. Applying this same logic to the other stimuli, these neurons respond similarly to NaCl (P_D < 0.75), but n₅ responds to HCl and quinine at a faster rate than n₇ (P_D > 0.75).

Figure 8.

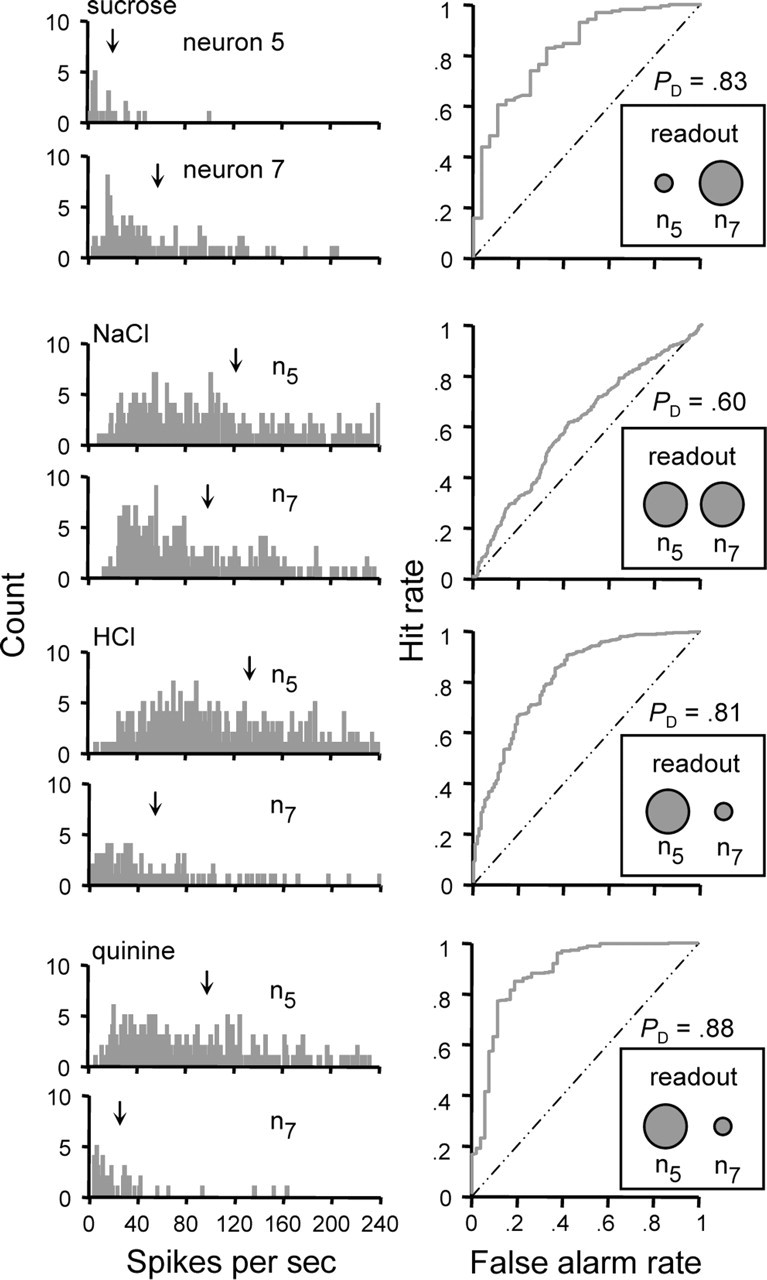
Decoding stimulus input by comparing firing rates between two differently tuned neurons in parallel. The left column shows frequency distributions of instantaneous firing rates to each stimulus observed for neurons 5 (n₅) and 7 (n₇) from Table 1. ↓, Mean spike rate. For each stimulus, ROC analysis was used to estimate the probability that a hypothetical observer of the firing rates of these neurons could use knowledge of their mean firing rates to correctly categorize responses as produced by one cell or the other. This probability, P_D, is given by the area under the ROC curve. The curve computed for each stimulus is shown in the right column. The outcome of this procedure bears on if two neurons fire at similar or reliably different rates to a given stimulus. Assuming a difference threshold of 0.75, the observer could reliably discriminate between responses in neurons 5 and 7 when under the drive of sucrose (P_D > 0.75). This suggests that sucrose elicits detectably different firing rates in these neurons, with n₇ responding noticeably faster than n₅ (i.e., n₅ < n₇, indicated by the size of the circles in the “readout” inset). Following this logic, n₅ = n₇ for NaCl, and n₅ > n₇ for HCl and quinine. A reader of these two neurons in parallel with a priori knowledge of the stimulus associated with each response relationship could use this information to categorize the stimuli tested here in a manner that, to a certain degree, agrees with rodent perceptual categorizations of these stimuli as shown in learned-generalization and conditioning experiments.

The outcome of this procedure suggests that a reader of these neurons in parallel could reliably report that they respond at different or similar firing rates depending on which stimulus is used to drive them. What is more, assuming a priori knowledge of the stimulus associated with each response relationship, this reader could categorize the stimuli tested here in a manner that, to a certain degree, agrees with rat behavioral categorizations of these tastants. Learned-generalization and operant conditioning studies have shown that rodents recognize the taste of sucrose or NaCl as unique out of the group of stimuli we tested (Morrison, 1967; Nowlis et al., 1980). However, in these same behavioral experiments, rodents tend to generalize to a certain degree between the tastes of HCl and quinine, indicating that these stimuli elicit a common qualitative feature. Following these behavioral data, a reader that attends to the spiking activities of the neurons in Figure 8 could know that sucrose is present when n₇ responds at a detectably greater firing rate than n₅ (i.e., n₅ < n₇), that NaCl is present when n₅ and n₇ respond at the same rate (n₅ = n₇), and that the stimulus is HCl or quinine when n₅ responds at a noticeably faster rate than n₇ (i.e., n₅ > n₇). Because the relationship n₅ > n₇ is observed for both for both HCl and quinine, the reader would generalize between these stimuli, as do rodents. Sucrose, NaCl, HCl, and quinine were found to produce this particular pattern of relative spiking relationships in 10 additional pairs of neurons (data shown in Fig. 9) (see following text).

Figure 9.

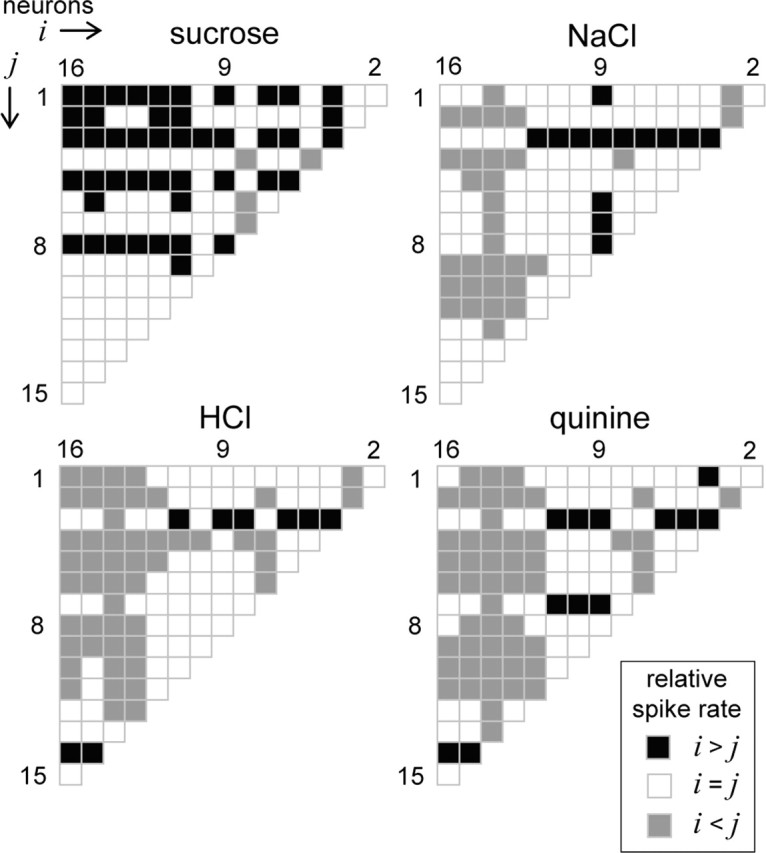
Decoding stimulus input by comparing firing rates among multiple neurons considered in parallel. Each half-matrix describes for a stimulus the pattern of relative spiking relationships that emerged across all possible pairs of NST neurons in our sample of 16 (Table 1). Neurons are sequentially ordered into vectors i and j along the columns and rows, respectively, of the half-matrices. Each matrix element is color coded to reflect the relative spiking relationship (legend) observed between a particular pair of cells, as determined by ROC analysis of spike rate distributions. For this analysis, the distribution of the neuron with the higher absolute mean spike rate was used as the reference, and the resulting probability of correct discrimination, P_D, was compared with a difference threshold of 0.75 to determine the direction of the relative spiking relationship. It can be seen that sucrose, NaCl, HCl, and quinine produce unique patterns of relative spiking among these cells. A priori knowledge of the pattern of relative responding associated with each stimulus could, in principle, be used to discriminate among these stimuli.

Learned-generalization tasks provide an assessment of perceived similarity between stimuli but do not necessarily reflect whether or not two stimuli could be discriminated (Heyer et al., 2004). Although rodents indeed generalize to a certain degree between the tastes of HCl and quinine, such generalization is not complete (Morrison, 1967; Nowlis et al., 1980), which could suggest that rodents perceive these tastants as similar but not identical. Assuming this to be so, we postulated that a reader of NST neurons might resolve differences between HCl, quinine, and other stimuli by considering relative spiking relationships among several neurons in parallel. Figure 9 shows for each stimulus a half-matrix that graphically describes such relationships among all possible pairs of neurons in our sample of 16. Each element within a half-matrix is color coded to reflect the relative spiking relationship observed between a particular pair of neurons under the drive of a given stimulus (see legend), as determined by ROC analysis applied to spike rate distributions between these cells. For each ROC analysis, P_D was compared with a difference threshold of 0.75 to determine the relative spiking relationship. As examples, when under the drive of sucrose, neuron 9 generated spikes at a detectably faster rate than neuron 1, denoted by a blackened matrix element for this comparison in Figure 9, whereas neuron 4 responded detectably faster than neuron 8, as indicated by a halftone element. It can be seen in Figure 9 that different taste stimuli produced unique relative spiking relationships among NST neurons during the first second of stimulus processing. Our analytic approach reliably estimates these relationships as data were sampled over multiple trials. A downstream processor of these cells that reads the relative spiking relationships among them and knows the stimulus associated with each pattern of relationships could, in principle, discriminate among the stimuli tested here. What is more, the processor could compute these discriminations making use of the relative activities of only a small number of cells with different tuning properties, as shown in Figure 10.

Figure 10.

Decoding stimulus input by comparing firing rates among a small number of neurons considered in parallel. Each half-matrix describes the pattern of relative spiking (legend) that was observed to sucrose, NaCl, HCl, and quinine among six neurons (Table 1; two cells were randomly drawn from each cell type) using the same approach as presented in Figure 9. As with Figure 9, a priori knowledge of the stimulus associated with each pattern of relative responding could be used to discriminate among these stimuli. However, these data show that such discriminations could, in principle, be computed making use of the activities of relatively few cells.

Discussion

Analyses in phase 1 indicate that NST neurons that belong to a purported functional neural group vary widely in their sensitivities to taste stimuli. This is evidenced by ROC analysis indicating that, in some cases, responses to optimal and sideband stimuli observed among such cells could not be reliably classified on the basis of response magnitude. For example, responses to HCl and NaCl in neurons of type H and those to sucrose and NaCl in neurons of type S could be classified only poorly at best. These results suggest that stimuli of different taste qualities produce similar levels of activation across cells within each group, which questions whether the aggregate signal of such neurons could faithfully encode a single stimulus quality. Experiments in phase 2 explored how variability in the spiking activities of individual NST neurons drawn from each cell type could impact their abilities to signal information about stimulus quality. Here, ROC analysis was used to explore whether or not a hypothetical observer could reliably discriminate between firing rates to different stimuli in individual neurons during the first second of stimulus processing. Spike rate was found to be an unreliable predictor of stimulus quality for each neuron tested. Thus, it might prove difficult, if not impossible, for a downstream processor of NST neurons to decode stimulus quality by attaching taste messages to dedicated groups of cells or individual neurons and simply reporting the message assigned to a unit when activated. Conversely, the tastants tested here were found to produce unique relative firing relationships among several NST neurons considered in parallel, as shown by ROC analysis of spike rate distributions between neurons under the drive of each stimulus. A reader of these cells that attends to this information and has a priori knowledge of the stimulus associated with each pattern of relative responding could discriminate among sucrose, NaCl, HCl, and quinine, prototypical stimuli of basic taste qualities. Moreover, under this decoding strategy, it was shown that the activities of a small number of cells may, in principle, be sufficient to arrive at a judgment about stimulus quality.

Experiments in phase 2 used the IFR measured during the first second of taste responding to estimate the coding performance of individual neurons. This length of time was chosen to balance allowing sufficient data for the statistical model while focusing on the initial phasic period of the neuronal response, which is particularly important in the representation of taste quality information. For example, rats can detect and respond appropriately to different taste stimuli in <1 s (Halpern and Tapper, 1971; Scott, 1974). Cross-adaptation procedures, which produce diminished taste sensation, result in reduced responding in gustatory nerves primarily during the transient phase (Smith and Frank, 1972). These data indicate that critical and likely sufficient information about stimulus quality is carried by the earliest portion of the phasic component of the neuronal response. For some neurons, this period may only correspond to several action potentials maximum when under gustatory drive. Thus, the coding performance of gustatory neurons during the initial transient phase of responding may be more meaningfully indexed by the rate of action potential generation, as performed here, rather than the absolute number of spikes produced per trial. Although the stimuli tested here evoked different numbers of spikes in many cells (Figs. 6, 7), one must consider that concentrations of perceptually different stimuli can typically be matched to produce equivalent numbers of spikes in gustatory neurons (Scott and Giza, 2000). For example, although the neuron in Figure 6 responds best to sucrose as given by the mean number of spikes per trial (Fig. 6B), this cell could be made to respond equivalently to sucrose and NaCl, for example, by slightly adjusting the concentrations of these stimuli (e.g., decrease the sucrose concentration or increase the NaCl concentration). A similar situation arises for spike counts produced by NaCl and HCl for the cell shown in Figure 7. Given that small adjustments in concentration would not affect the qualitative features of these stimuli and could also result in a changeable “best” stimulus in many cells, the mean spike count, along with the mean firing rate, of a gustatory neuron is a poor indicator of stimulus quality.

Our analyses of pairs and small ensembles of neurons conducted in phase 2 indicate that information about taste quality could be carried by the relative activities of different gustatory neurons considered in parallel (Figs. 8–10). This idea is beyond the scope of labeled-line theory, which would not permit any approach that considers the relative activities of different neurons but along the lines of a neural pattern code for taste, in which the activity of any one cell is only meaningful when taken in the context of its neighbors (cf. Erickson, 1963; Pfaffmann et al., 1976; Smith and St. John, 1999; Scott and Giza, 2000). However, the present model differs from the common conceptualization of pattern theory in gustation, which has been primarily based on the degree of pairwise correlation between activity profiles produced by different tastants across a large number of gustatory neurons. Under this framework, discriminability between two stimuli is inversely proportional to the degree of correlation between their patterns produced across a population of cells (Erickson et al., 1965). In contrast, a processor using the parallel comparison strategy presented here could decode stimulus input making use of the activities of only a few NST neurons with different tuning properties, as shown in Figure 10. That the relative spiking activities of a small number of cells could, in principle, be sufficient to compute discriminations among tastants and that the response properties of these cells would be common to many other neurons in the NST might suggest that there exists a good deal of redundancy and amplification of tastes messages under this coding strategy. One can intuit that the relative spiking relationships observed here could be invariant to changes in stimulus concentration assuming that the relative sensitivities of neurons remained consistent, although this remains to be empirically assessed. It is also important to emphasize that the neurons analyzed here were sampled from different rats. To more effectively explore this model of taste coding would require spike data from several simultaneously recorded neurons, ideally sampled from an awake and behaving animal performing a gustatory discrimination task. Nevertheless, the idea that perceptual judgments could be based on the activities of a small number of neurons has been proposed for visual processing. In monkeys performing visual motion discrimination tasks, psychophysical threshold and the shape of the psychometric function can be accounted for by comparisons between the activities of individual visual cortical neurons and hypothetical cells with different tuning properties (Newsome et al., 1989; Britten et al., 1992).

The recent discoveries of the T1r and T2r taste receptors for sweets, amino acids, and bitter stimuli have provided insight into mechanisms of taste processing in the periphery. These receptors exist in nonoverlapping subsets of TBCs, which has been interpreted as evidence of cellular specificity to a single stimulus quality (Adler et al., 2000; Nelson et al., 2001; Scott, 2004). Mice engineered to express receptors for a normally tasteless compound in TBCs that harbor T1r sweet or T2r bitter receptors display corresponding preference or aversion of this ligand (Zhao et al., 2003; Mueller et al., 2005). These molecular findings have been argued to indicate that different taste qualities are encoded along labeled neuronal lines (Zhang et al., 2003; Zhao et al., 2003; Scott, 2004; Mueller et al., 2005). However, the perceptual consequences that follow the activation of specific categories of TBCs ultimately arise from the activities of central neurons downstream. These consequences would follow regardless of how central gustatory circuits are organized to handle and encode input from taste receptors. The present results indicate that, rather than assigning meaning to individual neurons, central gustatory circuits could effectively encode quality information by the relative activities of multiple kinds of cells with different sensitivities to taste stimuli. Moreover, the temporal features of spike trains in individual NST neurons (Di Lorenzo and Victor, 2003) and time-dependent changes in firing rate within ensembles of cortical neurons (Katz et al., 2002a,b) have also been suggested to convey information about taste. The gustatory neural code could be both spatial and temporal by nature, with both features synergistically increasing the information-handling capacity of the taste network in the brain. Such coding capacity could be necessary to, for example, give rise to fine perceptual differences among similar yet distinct tastants, such as the sugars sucrose and maltose, which are discriminable by rats (Spector et al. 1997), and to integrate or multiplex information related to other aspects of taste stimuli such as texture and temperature, stimulus features that modulate activity in gustatory neurons (Travers and Smith, 1984; Ogawa et al., 1988; Verhagen et al., 2003; Kadohisa et al., 2004). Whether the brain indeed adopts algorithms to encode gustatory information along such parameters remains an open question.