Two Psychophysical Channels of Whisker Deflection in Rats Align with Two Neuronal Classes of Primary Afferents

Abstract

The rat whisker system has evolved into in an excellent model system for sensory processing from the periphery to cortical stages. However, to elucidate how sensory processing finally relates to percepts, methods to assess psychophysical performance pertaining to precise stimulus kinematics are needed. Here, we present a head-fixed, behaving rat preparation that allowed us to measure detectability of a single whisker deflection as a function of amplitude and peak velocity. We found that velocity thresholds for detection of small-amplitude stimuli (<3°) were considerably higher than for detection of large-amplitude stimuli (>3°). This finding suggests the existence of two psychophysical channels mediating detection of whisker deflection: one channel exhibiting high amplitude and low velocity thresholds (W1), and the other channel exhibiting high velocity and low amplitude thresholds (W2). The correspondence of W1 to slowly adapting (SA) and W2 to rapidly adapting (RA) neuronal classes in the trigeminal ganglion was revealed in acute neurophysiological experiments. Neurometric plots of SA and RA cells were closely aligned to psychophysical performance in the corresponding W1 and W2 parameter ranges. Interestingly, neurometric data of SA cells fit the behavior best if it was based on a short time window integrating action potentials during the initial phasic response, in contrast to integrating across the tonic portion of the response. This suggests that detection performance in both channels is based on the assessment of very few spikes in their corresponding groups of primary afferents.

Introduction

The whisker-to-barrel pathway is widely studied as a model system of tactile information processing (Sachdev et al., 2001). But although the rodent whisker system has received considerable attention for almost 100 years (Vincent, 1912), little effort has been directed toward establishing psychophysical tasks to investigate the relation between neural activity and perceptual processes (Johnson et al., 2002). Designing such tasks is challenging because of the difficulty of applying spatiotemporally precise stimuli to awake behaving rats while precluding nonvibrissal stimulus sources (such as cutaneous receptors or the small perioral sinus hairs) under conditions which allow for the assessment of psychophysical parameters. Psychophysical studies conducted so far mostly used nonrestrained, freely moving rats sampling stimuli by using their own body and whisker movements (Carvell and Simons, 1990, 1995; Harvey et al., 2001; Krupa et al., 2001). Hutson and Masterton (1986) are the only investigators so far who attempted to quantify psychophysical detection thresholds with varying kinematic deflection parameters; however, rats in that study were free to move their head, and control of whisker deflection generated by air streams did not reach the level of stimulus control deemed necessary: micrometer precision at a millisecond time scale. The relative coarseness of stimulus application that is characteristic for previous behavioral studies stands in stark contrast to the high spatiotemporal precision of stimuli used for electrophysiological investigations in anesthetized animals. Because such studies demonstrate highly sensitive responses of first-order trigeminal ganglion (TG) neurons (Gibson and Welker, 1983), and temporal precision of responses in the submillisecond range (Jones et al., 2004), it seems highly demanded that psychophysical investigations of the whisker system use stimuli with a spatiotemporal precision matching that resolution. Here, we present a novel method of assessing psychophysical detection thresholds in operantly conditioned, head-fixed rats using highly precise whisker deflections. We find that large-amplitude stimuli require much lower peak velocities to be detectable than small-amplitude stimuli. In analogy to the primate tactile system (Bolanowski et al., 1988), this finding is suggestive of the existence of two psychophysical channels of differing sensitivity ranges. In psychophysics, the term “channel” is used to designate subsystems that sample different regions of the energy spectrum to which the system is responsive (Gescheider et al., 2004). In the human tactile system, four such channels were identified for the glabrous skin (Bolanowski et al., 1988) and aligned to the four cutaneous mechanoreceptors and their associated nerve fibers (Mountcastle et al., 1967). Similarly, we could identify the neural correlates of the psychophysical channels in acute unit recordings from the trigeminal ganglion: two neuronal subclasses, slowly (SA) and rapidly adapting (RA) neurons, demonstrate response properties predicted from the two-channel hypothesis. We believe that this approach will facilitate a detailed characterization of the perceptual qualities of the rat vibrissal system.

Materials and Methods

All experimental and surgical procedures were performed in accordance with standards of the Society for Neuroscience and the German Law for the Protection of Animals. Subjects were six (psychophysics) and nine (neurophysiology) male Sprague Dawley rats (Harlan Winkelmann, Borchen, Germany), aged 12–16 weeks.

Surgery to implant the head mount.

Anesthesia was introduced with a combination of ketamine and xylazine (100 and 10 mg/kg body weight, respectively) injected intraperitoneally, and maintained with isoflurane (1–2%). The rat was positioned in a stereotaxic apparatus, the skull was exposed, and holes were drilled for placement of 11 stainless steel screws. Screws were embedded in dental cement (FLOWline; Heraeus Kulzer, Hanau, Germany). Additionally, a mounting screw turned upside down was placed in the head mount. For EMG recordings, Teflon-insulated silver wires (0.003″ bare, 0.0055″ coated; AM Systems, Carlsborg, WA) were inserted into the left whisker pad and soldered to a connector embedded in the head mount. The wound was treated with antibiotic ointment and sutured. Analgesia and warmth was provided after surgery. After surgery, the rats were allowed to recover for at least 10 d before habituation training commenced. Rats were housed individually and kept under a 12 h light/dark cycle (lights off at 10:00 A.M.) with water and food available ad libitum except for the periods of water restriction. During the period of behavioral testing, the rats were water-restricted for 5 d per week. Drops in body weight, monitored daily, were prevented by supplementary water.

Whisker stimulation.

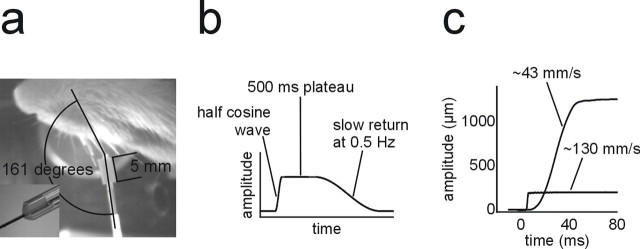
Whisker stimulators were constructed from piezo actuators (Physik Instrumente, Karlsruhe, Germany). A thin glass capillary (Science Products, Hofheim, Germany) was glued to the actuator. The opening at the free end was reduced to a size of 225 μm with dental cement enveloping a small plastic tube which was taken out after hardening of the cement (Fig. 1a, inset).

Figure 1.

Method for precise stimulus application. a, Rat and whisker stimulator viewed from above to illustrate measurements of the distance of the capillary tip to the base of the whisker and the angle between capillary and whisker. Inset, Close-up to show the point of insertion of the whisker into the narrowed opening of the capillary tip. b, Illustration of stimulus construction. c, Calibration traces of two exemplary stimuli with medium (43 mm/s) and high (130 mm/s) peak velocities. The amplitude of ringing after the high-velocity deflection trace is the highest observed in the stimulus set used in this study.

Voltage commands were programmed in LabVIEW (National Instruments, Austin, TX); each stimulus was composed of a fast half cosine wave followed by a 500 ms plateau and another half cosine wave at 0.5 Hz for a very slow return (Fig. 1b). The frequencies of the half cosine waves at stimulus onset were adjusted at each of five amplitudes to yield five different velocities. The range of kinematic parameters covered were 110 to 1100 μm for amplitude, and 5.4 to 130.9 mm/s for velocity. These values correspond to 1 to 12° and 62 to 1500°/s, respectively, if applied 5 mm from the whisker base.

The stimulators were calibrated at the outset of the study with a modified phototransistor sampled at 50 kHz with 1 μm precision (H21A1; Fairchild Semiconductor, South Portland, ME), and an optoelectronic measurement device (laser emitter and detector, resolution 1.4 ms, 11 μm; PAS 11 MH; Hama Laboratories, Redwood City, CA).

Three of 47 stimuli displayed some ringing after stimulus offset at a maximum peak-to-peak amplitude of 7 μm (<0.1°). Importantly, the peak velocity of the after-oscillations did not exceed 20 mm/s (230°/s) for any of the three stimuli although clear signs of detectability at these amplitudes were visible only if the peak velocity exceeded two to three times this value (with nonringing stimuli). Figure 1c shows two exemplary calibration traces, the smaller of which displays the stimulus with the largest after-oscillations used in this study.

To ensure precise whisker stimulation, the relative position of the stimulator to the rat’s snout was monitored via a video camera from above, and a picture was taken before each individual session (Fig. 1a). Using a 5 mm comparison snippet attached to the glass capillary, the distance of the capillary tip to the base of the whisker was adjusted to 5 mm with a precision of ±1 mm. To ensure that the stimulator immediately engaged the whisker at stimulus onset, the capillary and the whisker were tilted against each other at an angle between 155 and 175° such that the vibrissa rested against the inside wall of the capillary (Fig. 1a). Furthermore, care was taken to stimulate the whisker in its null position (i.e., at resting angle relative to the face).

Experimental setup.

To allow for precise whisker stimulation without contamination of body and head movements, the rat was placed in a restraining box, and the head was fixed using the mounting screw to a metal bracket above the exit of the restraining box (Welsh, 1998). The restraining box was put inside an experimental chamber with light- and sound-absorbing enclosing. A spout was positioned in front of the rat’s snout for water delivery. To the left of the animal’s head, a moveable laboratory-built metallic arm was mounted, holding the whisker stimulator. At the beginning of each training session, the whisker C1 was attached to the stimulator. Deflections were always in the rostral-to-caudal direction. Licking movements were detected using the interruption of an infrared beam by tongue protrusion. The rat was constantly monitored using an infrared-light sensitive camera mounted inside the experimental chamber. EMG recordings were done using an extracellular amplifier (MultiChannel Systems, Reutlingen, Germany) at a sampling frequency of 5 kHz. Voltage traces were digitally full-wave rectified and low-pass filtered (10 Hz) offline to yield an envelope trace.

Behavioral task.

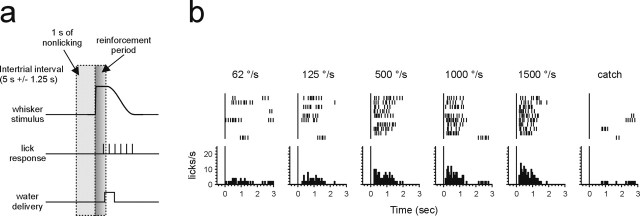
Rats were habituated to the experimental situation by subjecting them to a systematic desensitization procedure for 2–3 weeks after which all animals tolerated head-fixation without any sign of stress. They were then put on water restriction and conditioning commenced. Initially, animals were trained to lick on a fixed-interval schedule of 0.5 s that was incremented step-wise to 5 s. Next, a well detectable rectangular deflection applied to a single whisker served as the discriminative stimulus and occurred every 5 ± 1.25 s. The first lick emitted within 500 ms after its onset [reinforcement period (see Fig. 2a, dark gray field)] yielded water reinforcement. To discourage random licking during the intertrial interval, a period of 1 s without licking was required before a new stimulus would be delivered (Fig. 2a, light gray field). In case the animal licked during that period, the scheduled delivery of the next stimulus was delayed by 1 s. Once the rat would emit lick response at a short latency (<500 ms) to the rectangular deflection in 90% of traces, psychophysical testing began.

Figure 2.

The psychophysical paradigm. a, Illustration of the psychophysical paradigm. b, Licking behavior during a single session. Each tick in the raster plot indicates a lick at the water spout. Peristimulus time histograms below show overall responses to a given stimulus. In this session, five different types of whisker deflections [same amplitude (12°), differing velocities] were presented plus catch trials in which no stimulus was presented and licking was not reinforced.

Psychophysical testing was conducted using the method of constant stimuli. In one session, four to 10 stimuli of identical amplitude but differing peak velocities were presented in pseudorandom order, each of them for 10 times. In addition, a “catch” stimulus was included, in which no deflection of the whisker occurred, but lick responses in a time window of 500 ms were recorded to yield a measure of chance performance. Over the entire course of the experiment, each stimulus type was presented to the rat at least 50 times. To avoid frustration of the rat confronted with many subthreshold stimuli, easily detectable reference stimuli (medium-amplitude pulses) were interspersed with the stimuli of interest. The response to these stimuli also served to monitor the overall performance of the animal. Sessions in which responses to the reference stimulus were <70% were not included in the sample. To ensure that rats responded to tactile input only, white noise (∼80 dB) was presented during sessions. None of the animals responded consistently in control sessions that were identical to experimental sessions, except that the whisker was detached from the stimulator, assuring that nonvibrissal cues did not play a role for their performance.

Electrophysiological recordings.

Rats were anesthetized as described above and placed in a stereotaxic frame. A craniotomy was performed to expose the right cerebral hemisphere, which was then gently aspirated to visualize the trigeminal ganglion at the base of the skull. After careful hemostasis, the dura overlying the ganglion was teased away, and laboratory-built pulled and ground glass-coated platinum tungsten electrodes (80 μm shank diameter; 23 μm diameter of the metal core; free tip length ∼8 μm; impedance, 3–6 MΩ; Thomas Recording, Giessen, Germany) were lowered until units responding to manual whisker stimulation were encountered. Bandpass filtered (300–10,000 Hz) voltage traces were recorded at a 20 kHz sampling rate using an extracellular amplifier (MultiChannel Systems). At the end of the experiment, the rat was killed with an overdose of pentobarbital.

Selection of units and analyses.

Once a unit with sufficient spike amplitude was isolated, the receptive field characteristics (responsive whisker and directional preference) was assessed using a hand-held rod. As reported previously (Lichtenstein et al., 1990), slowly adapting units (for classification, see below) often showed directional preference. Only those units that exhibited a strong response for horizontal rostrocaudal stimulus directions were included in the sample. After attaching the piezo bender to the responsive whisker in the same manner as done in the awake animals, a subset of the whisker deflection stimuli used in the psychophysical experiments was applied. This subset included five of the six stimulus amplitudes (1, 2, 4, 8, 12°) and five of the seven peak velocities (62, 250, 500, 1000, 1500°/s), yielding a total of 25 different stimuli. Ten presentations per stimulus were presented in pseudorandom order at an interstimulus interval of 1.5 s.

All analyses were done offline. First, stimulation artifacts and occasional multiunit activity was sorted out by an automated spike-sorting algorithm (Hermle et al., 2005). Sorting results were checked by the experimenter by visually comparing spike trains with raw traces. Only clear single-unit spike trains entered the present data set. Then, units were classified as slowly adapting if activity to a fast, high-amplitude deflection (12°, 1500°/s) was sustained longer than 25 ms after stimulus onset. Alternatively, in case the neuron was quiescent at this time, it was classified as rapidly adapting. Because SA neurons are known to occasionally display phasic responses to some directions of deflection (Lichtenstein et al., 1990), the possibility that SA cells could erroneously be included into the RA group had to be considered. We, therefore, manually checked whether the cell responded tonically to other directions of deflection and did not include it as RA in case it did. Second, response parameters across our stimulus set of the cells that we classified as RA were very homogenous and were well separated from those that we classified as SA (see Results). This fact validates our classification criterion. For instance, in the parametric range in which SAs usually show phasic responses (low velocities), the spike count of SA cells was well separated from the ones of the RA group. The latter generated a maximum of 1.2 spikes/stimulus in response to high-amplitude stimuli of the lowest velocity, whereas the same stimulus with no exception triggered >4.6 spikes/stimulus in cells within the SA group. Another example is the fact that none of the presumed RA cells displayed any obvious modulation by change of amplitudes whereas each and every cell classified as SA did. In summary, we conclude that RA pool contamination with SA cells can be excluded with high probability.

The peristimulus time histogram (PSTH) was calculated as spike renewal function using a bin width of 0.1 ms and integration window of 1 ms (Abeles, 1982). For RA units, spike counts per stimulus were determined by integrating the PSTH from 0 to 250 ms poststimulus time. For SA responses, the first step was to determine the time of maximal firing rate during the transient response using the PSTH smoothed with a moving Gaussian (50 bins). Integration windows of different lengths were centered at the time of maximum firing rate and the spikes were counted by integration of the nonfiltered PSTH in this window.

Statistics.

Response probability of a single subject was calculated as the mean response rate from at least five sessions using a given stimulus type. Statistical comparisons of behavior group data were made using the nonparametric Friedman test. The principal range of kinematic parameters tested was 1–12° amplitude and 62–1500°/s velocity. Because not all of the six rats were confronted with the full stimulus set for practical reasons, and because we used a related-samples test for higher statistical power, statistical comparisons are not based on all six animals, but on three to four, depending on parameter set. Despite the low power inherent in small-sample studies, effect sizes were so large that the small sample size did not pose a major constraint. In addition, data from the four animals in which most of the parametric range was explored were analyzed on an individual basis using the nonparametric Kruskal–Wallis test. Because the main trends reported here were identical for all animals, Figure 3, b and c, shows data from all six rats (plots depict mean response probabilities; error bars represent SEM). Neurophysiological data with number of spikes or peak firing rate as dependent variables were analyzed with two-way ANOVA, with amplitude (five levels) and velocity (five levels) as factors. In addition to p values, standardized effect sizes (η²) are given. η² varies between 0 and 1 and represents the amount of explained variance by a given factor or by their interaction. To disentangle the roles of velocity and acceleration in the neurophysiological data, multiple regression analyses with two independent variables were computed (velocity and acceleration or amplitude and acceleration). The square of the multiple correlation coefficient, R², reflects the amount of variance explained by the independent variables. Semipartial correlations reveal the correlation of an independent and a dependent variable in the equation when the correlation of the independent with another independent is controlled for. Again, its square (r²) indicates the amount of explained variance. All calculations were done in Matlab 7.0 (MathWorks, Natick, MA).

Figure 3.

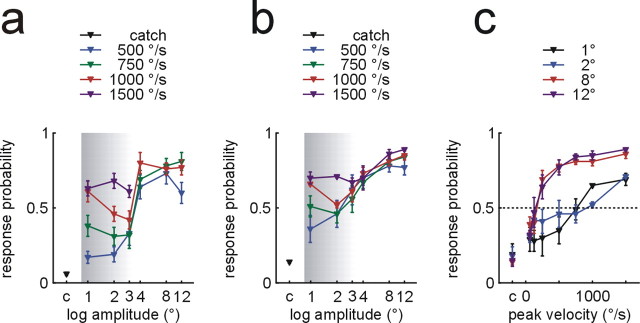
Psychophysical performance. a, Mean response probability ± SEM for one example animal. Curves represent isovelocity sets, varying in amplitude. Velocities from 62 to 250°/s are omitted for clarity. Shaded area highlights amplitude range in which peak velocity had a significant effect in determining the detection probability. b, Same as a but averages across data from four animals. c, Mean response probability ± SEM for four animals. Curves represent isoamplitude stimulus sets, varying in peak velocity. Dotted line indicates 50% performance. c, Catch trials.

Results

General observations

Lick responses recorded during a typical behavioral session are depicted in Figure 2b. The probability to emit licks increased with increasing stimulus peak velocity. After training, all animals broke the light beam at latencies of ∼250 ms to well detectable stimuli. In the over-trained state of the animals, at which the psychophysical testing was performed, whisker movements rarely occurred. If they did, the movements were of low amplitude and short duration. Large amplitude rhythmic whisking (characteristic for exploration) was never observed. EMG activity of the whisker pad recorded in one animal confirmed this impression (data not shown). The fact that head-fixed rats dramatically decrease whisking activity (if not explicitly reinforced for whisker movements) has been reported by other investigators (Gao et al., 2003). Mean catch trial performance ranged between 12 and 18% and does not differ between sets (p = 0.881; data not shown).

Psychophysics

Mean response probability for one example subject is shown in Figure 3a (velocities from 62 to 250°/s have been omitted for clarity in Figure 3, a and b, but are contained in the statistical analysis). Each line represents an “isovelocity set” of stimuli (i.e., stimuli in which the peak velocity remained constant). The four curves overlap at 4, 8, and 12°, but characteristically dissociate at smaller amplitudes (gray shaded area). This phenomenon is also visible in group data (Fig. 3b). Comparisons across amplitudes for isovelocity sets of medium velocities indicate better performance at higher amplitudes (Fig. 3b) (250, 500, 750, and 1000°/s; p = 0.017, p = 0.012, p = 0.017, p = 0.059, respectively). Detectability at the extremes of peak velocities tested showed rather constant performance: either high with high velocities (Fig. 3b) (1500°/s, p = 0.355) or low with low velocities (62, 125°/s; p = 0.399, p = 0.21, respectively) (data not shown in Fig. 3a,b). Thus, although amplitude of whisker deflection determines detectability at medium velocities, it seems insufficient for detection when peak velocity is low (<250°/s) and irrelevant when peak velocity is high (1500°/s).

Next, we concentrate on the trajectories of the curves with peak velocities between 500 and 1500°/s. It is obvious from Figure 3, a and b, that detection curves obtained with different isovelocity stimulus sets behave in a bimodal manner dependent on the amplitude. At low amplitudes (1–3°) (Fig. 3a,b, gray shaded area) peak velocity matters because the detection curves largely diverge. In contrast, the curves follow virtually the same trajectories for higher amplitudes indicating no contribution of peak velocity to detection in this range. Accordingly, response probabilities for peak velocities at 500–1500°/s (Fig. 3b) differ at small amplitudes (1°, p = 0.029; 2°, p = 0.058) but not at larger amplitudes (3°, p = 0.308; 4°, p = 0.284; 8°, p = 0.758; 12°, p = 0.392). Thus, peak velocity contributes differently to detectability at small versus large whisker deflections.

In Figure 3b, not all peak velocities have been included for illustration purposes. Therefore the low velocity threshold at large amplitudes was not captured. This can be more easily appreciated if the detection curves are plotted across peak velocity (Fig. 3c). Depicted in this way, the curves correspond to “isoamplitude sets” of stimuli and directly depict the contribution of peak velocity to detection probability (we omitted the amplitude sets close to the border of the two ranges, 3 and 4°, because interindividual variability of this border did not permit a clear picture). Although both the low-amplitude curves and the high-amplitude curves increase with peak velocity (1°, p = 0.012; 2°, p = 0.012; 8°, p = 0.009; 12°, p = 0.009), the point at which detection probability reaches 0.5 (from here on referred to as “velocity threshold”) clearly differs (∼125°/s for large amplitude; ∼750°/s for small amplitudes).

In summary, we found that a stimulus amplitude of ∼3° divided detectability into two qualitatively different modes. Small stimuli (<3°) were detected only at high peak velocities (∼750°/s), whereas large stimuli (>3°) were detected at substantially lower peak velocities (∼125°/s) (Fig. 3c). Thus, we suggest the existence of two psychophysical channels defined by both amplitude and velocity. The first channel (W1) responds to large amplitude and slow velocities, whereas the second channel (W2) responds already to small amplitudes but requires higher peak velocities (Fig. 3a,b, gray area). As estimated from Figure 3, b and c, the threshold activation for W1 would be ∼3° and ∼125°/s, whereas the threshold for W2 is <1° (not assessed by the present stimulus range) and ∼750°/s.

This pattern of results for aggregated data were closely matched in analyses of individual performance data. The performance of all animals increased significantly as a function of velocity at each tested amplitude from 1–12° (all p values < 0.05). Performance curves for isoamplitude sets were statistically distinguishable between large (8 and 12°) and small (1 and 2°) amplitudes (8 and 12° vs 1 and 2°; all p values < 0.05) but not within either large or small amplitudes (1 vs 2° and 8 vs 12°; all p values > 0.4). Thus, both group and individual data support the notion of two different sensitivity ranges.

Trigeminal ganglion recordings

Next, we tested whether the two proposed psychophysical channels can be assigned to the well described neuronal classes of SA and RA primary afferents in TG. Known response profiles of TG cells to stimuli similar to ours (Shoykhet et al., 2000) led us to hypothesize that W1 is based on SA, and W2 on RA primary afferents. However, the neurometric curves by Shoykhet et al. (2000) covered only about a third of the amplitude range covered by us (them: 2.5 to 6°; us: 1 to 12°) and did not report an amplitude threshold for SA cells. Moreover, these authors used very high velocities (minimum of 1000°/s) that were suprathreshold at all amplitudes tested by us (our velocity range extended from 62 to 1500°/s). Therefore, their data set was not sufficient to confirm or disprove alignment of our presumed subsystems with RA and SA cells.

Single-unit data in anesthetized animals were assessed while stimulating a whisker in an identical manner as in the psychophysical experiments. Our total sample comprises 57 single units of which 14 were classified as SA and 43 as RA. Of the RA units, 16 responded to a wide range of stimuli contained in our stimulus set; they were used to extract the neurometric data presented below. The remaining 27 RA units exclusively responded to step-like deflections (exhibiting highest velocities, but not usable to extract precise kinematic parameters because of mechanical limitations) and were not further analyzed.

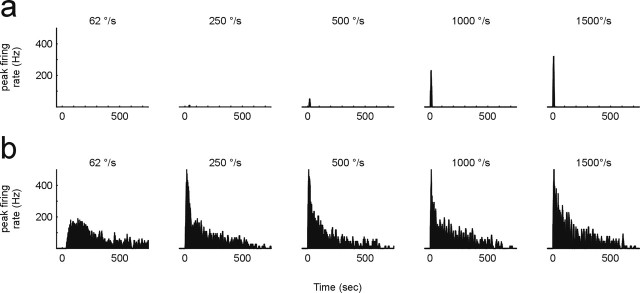
Figure 4 shows typical responses of RA and SA units to a high isoamplitude stimulus set (12°). RA cells gave responses to stimuli at higher peak velocities but only rarely to stimuli at lower peak velocities (Fig. 4a). Uniformly, the response profile was a fast transient (consisting of one to six spikes maximally lasting to 22.5 ms after stimulus onset). Applying the same stimuli, SA units already responded at lower peak velocities with clearly discernible phasic and tonic responses (Fig. 4b). Typically, the phasic response increased with increasing peak velocity in contrast to the tonic portion that was expressed in a more uniform way across different peak velocities.

Figure 4.

Typical PSTHs of TG neurons. a, RA TG neuron. b, SA TG neuron. Both PSTHs were constructed from 10 presentations of a large-amplitude (12°) stimulus at five different velocities.

Plotting the number of poststimulus spikes generated by RA units across the entire stimulus set fully confirmed the prediction drawn from the characteristics of W2. RA activity increases as a function of velocity (F = 51.8; df = 4; p = 2.3 × 10⁻³⁴; η² = 0.37) but not amplitude (F = 1.85; df = 4; p = 0.12; η² = 0.02) or their interaction (F = 0.76; df = 16; p = 0.74, η² = 0.03). Furthermore, robust RA activity (>0.5 spikes/stimulus) is present only at velocities higher than 500°/s, as observed with W2, and this holds regardless of amplitude (Fig. 5a,b).

Figure 5.

Neurometric plots of RA population responses (total spike count within 250 ms after stimulus onset) as function of peak velocity (a, curves represent isoamplitude sets) and amplitude (b, curves represent isovelocity sets). All graphs plot means ± SEM.

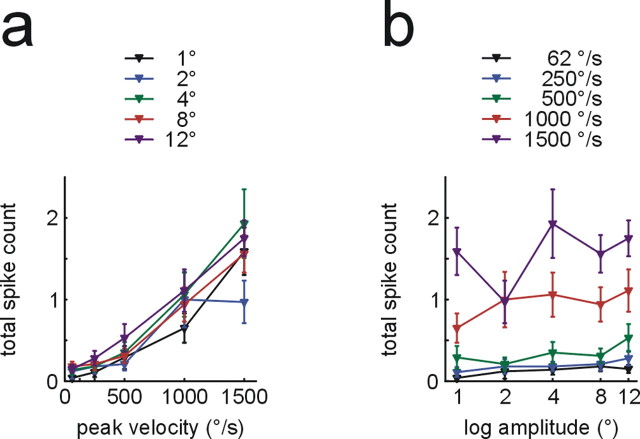
Our first approach to measure SA activity was analogous to the one used with RA cells. However, spike counts (that included the tonic response phase) yielded a less reassuring reflection of our predictions, in this case drawn from W1. SA spike counts readily captured the amplitude threshold typical of W1; they showed a sharp increase with amplitudes 4° or higher. Accordingly, SA spike count increased as a function of amplitude (F = 39.3; df = 4; p = 2.2 × 10⁻²⁶; η² = 0.35) but not velocity (F = 0.13; df = 4; p = 0.973; η² < 0.01) or their interaction (F = 0.08; df = 16; p = 1; η² < 0.01). However, the measure completely failed to reflect the velocity threshold at ∼125°/s which was characteristic of rats’ detection probability in this parameter range (Fig. 6a,b; compare Figs. 3c, 6a).

Figure 6.

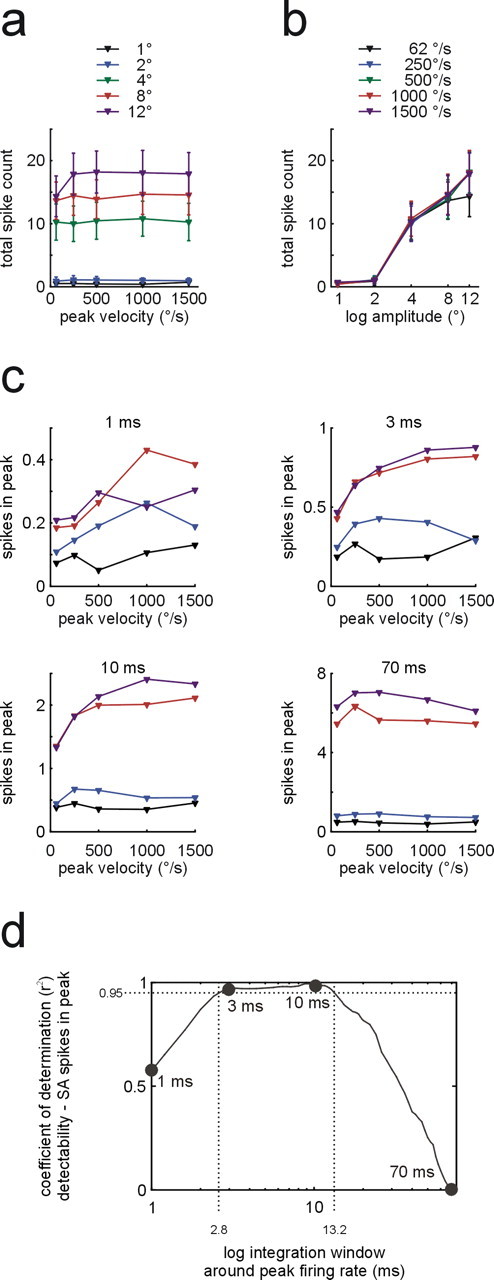
Neurometric plots of SA population responses. a, b, Total spike count within 250 ms after stimulus onset as function of peak velocity (a, curves represent isoamplitude sets; means ±1 SEM) and amplitude (b, curves represent isovelocity sets; both graphs plot means ± SEM). c, Isoamplitude sets (color coded as in a) showing number of spikes in a window around peak firing rate of the transient response as a function of peak velocity. The four panels show results for four different integration window sizes (1, 3, 10, 70 ms). d, Coefficient of determination (variance in detection probability explained by SA spikes counts) as a function of integration window size. Dots indicate the corresponding example plots in c. The dotted lines demarcate the range of window sizes in which >95% of the variance was explained by SA peak spike count.

In search for an alternative approach to fit the SA responses to the psychometric curve, we found that maximal firing rates obtained from the transient phase in smoothed PSTHs yielded a near-perfect match (data not shown). To arrive at spike counts as unit of measurement we had to find the optimal width of the window in which to integrate the PSTH. To this end, the unfiltered PSTH was integrated in windows of varying length which were centered on the time of maximum firing rate (as found in smoothed PSTHs). Next, the correlation of SA spike count and detection probability (in W1, i.e., using the means of responses to 8 and 12° stimulus amplitude) was calculated and the coefficient of determination (r²) was plotted against the width of the integration window. It turned out that windows of 2.8–13.2 ms length yield neurometric curves that explain >95% of the variance of the psychometric data (Fig. 6d). On either side of this optimal range, the fit worsened steeply. Figure 6c shows the resulting neurometric plots for one integration window below (1 ms), two inside (3 and 10 ms), and one above (70 ms) the optimal range. In summary, the neurometric curve based on the transient SA response predicted the psychometric curve much better than the neurometric curve based on the total response dominated by the tonic portion. We therefore, suggest that the detection based on SA responses relies on very few spikes, generated during the transient response, rather than integrating spikes within long intervals.

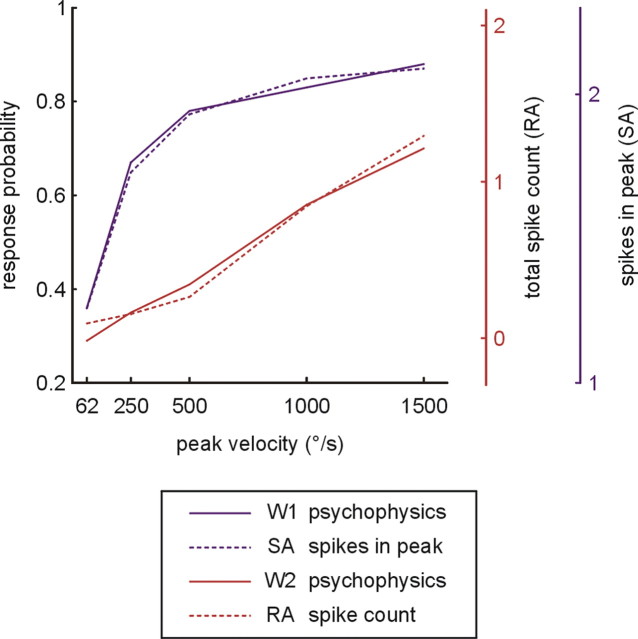
To further illustrate the correspondence of psychometric and neurometric data in the parametric ranges spanned by W1 and W2, we plot SA responses well contained within the W1 range (mean peak firing rates with 1 and 2° amplitudes across all peak velocities) and RA responses well contained within the W2 range (mean spike counts with 8 and 12° amplitudes across all peak velocities) together with detection probability (Fig. 7). The near-perfect match of psychophysical and neurometric data strongly suggest that detectability in W1 is predominantly determined by SA responses, whereas in W2 it is mainly based on RA responses. It is further noteworthy that the spike counts associated with threshold performance (0.5 detection probability) are low and quite comparable for SA and RA units [SA: 1.8 spikes at integration width of 9.2 ms (Fig. 7) but 0.7 spikes at 3 ms, the lower end of optimal integration widths; RA: 0.7 spikes].

Figure 7.

Overlay of psychometric and neurometric curves. Psychometrics, Mean response probabilities for W1 (average of 8 and 12°, blue) and W2 (average of 1 and 2°, red) as a function of peak velocity (left ordinate). Neurometrics, Peak spike count of SA population in the W1 range (average of 8 and 12°, second right ordinate, blue), and spike count of RA population in W2 range (average of 1 and 2°, first right ordinate, red). Peak spike counts for SA cells were calculated with an integration window size of 9.2 ms, in which the coefficient of determination reached its maximum (compare Fig. 6d). Psychometric and neurometric curves show very similar trajectories (compare Figs. 3–6). To allow the direct comparison of axes values, the scaling (translation and expansion) was done as to match the curves optimally.

Coding of kinematic parameters in the whisker system

An obvious question is which kinematic parameter determines the detectability of whisker deflection. The stimuli used here contain sets of stimuli that potentially disentangle peak velocity and acceleration (isovelocity sets). However, the discontinuity of detectability (at ∼3°) and the suggested existence of two channels render this approach problematic as the question of coding has to be asked in the restricted parametric ranges that activate one channel but not the other. Unfortunately, because of technical reasons, the amplitude range is limited in the present set of stimuli, most severely so for the important range of small amplitude, fast stimuli (W2; see Materials and Methods). It turned out that with behavioral data based on these restricted parametric ranges, the problem cannot be resolved. A possible solution, however, is the availability of neurometric data from RA and SA cells across the entire amplitude range. The evidence, presented above, that these separable neuronal responses underpin the two channels, opens the possibility to address the question of coding of kinematic parameters by looking at the neurometric data of each class of primary afferents.

RA spike count correlates positively with both peak velocity and acceleration with the first being a clearly better predictor of spike counts (r²_vel = 0.35; r²_accel = 0.08). Because peak velocity and acceleration do not show a fixed relationship within our set of stimuli, we can disentangle their relative contribution using semipartial correlations in the context of multiple regression [recall that our stimuli were designed to allow independent variation of these kinematic parameters by manipulating amplitude accordingly (i.e., there exist stimulus sets in which peak velocity is kept constant whereas peak acceleration varies)]. Using both kinematic parameters as predictors of RA spike count, a rather strong multiple correlation resulted (R² = 0.36). Semipartial correlations revealed a substantial independent contribution of peak velocity (r² = 0.29) but none for peak acceleration (r² = 0.01), a strong indication that RA cells code for peak velocity but do not reflect peak acceleration. For SA spike counts, we only considered the measurements extracted from the transient response because the total spike count did not match the psychophysical data. Using an integration width of 9.2 ms, the semipartial correlations were r² = 0.14 for amplitude, r² = 0.09 for velocity, and r² < 0.01 for acceleration. In summary, peak velocity rather than peak acceleration determines the spike counts of RA and SA that are related closest to the detectability of whisker deflection.

Discussion

How does neuronal activity give rise to perception? A sufficient answer to this question requires that the transformations from physically precise stimuli to specific neuronal activity, and finally to central representations that give rise to the percept are known. Although the rat whisker system lets us study the transformations from stimuli to central representation in minute detail on the level of molecules, neurons, and highly defined microcircuits, the relationship to perception has been elusive. We set out to complement the whisker model system by relating specific perceptual capabilities to neuronal activity. Psychophysical properties of whisker stimulation in rats have been assessed early on (Vincent, 1912; Schiffman et al., 1970). It has been shown that rats are capable of amazingly fine discriminations of surfaces (Guic-Robles et al., 1989; Carvell and Simons, 1990) and apertures (Krupa et al., 2001), and that discrimination of textures and object forms are optimized by active scanning movements (Carvell and Simons, 1995; Harvey et al., 2001; Prigg et al., 2002). Finally, the detectability of 1–3° whisker deflections applied by a sinusoidally modulated air stream (at 0.1–32 Hz) in mobile rats was demonstrated in the only study so far that attempted to use parameterized whisker deflections (Hutson and Masterton, 1986). However, none of these studies achieved the precision of stimulus control that is needed to causally relate physical properties of the stimulus to neuronal activity and to the percept. To optimize stimulus control, we have taken advantage from a head restraint preparation (Hentschke et al., 2006) that allowed us to apply stimuli 5 mm from the face using a piezo bender in a highly controlled way, a device that has been a standard for precise whisker stimulation in acute experiments for decades (Simons, 1983).

The whisker system uses two psychophysical channels

Based on the psychometric curves, we were able to subdivide the two-dimensional parametric space into four subregions delineated by an amplitude of ∼3° and a velocity of ∼750°/s. Below 3°, only peak velocities >750°/s could be detected consistently (W2), whereas >3°, peak velocities <750°/s (down to 125°/s) were sufficient for detection (W1). In the two remaining parametric subspaces, detection probability was either very low (<3°, <750°/s) or consistently high (>3°, >750°/s). Detailed comparison of the psychometric curves with neurometric data from primary afferents in the TG revealed a near-perfect match of SA activity to detectability in W1, whereas RA activity matched the detectability in W2, yielding the first demonstration of two independent psychophysical channels in the rat whisker system. It should be noted, however, that additional channels might exist that were not detected in the present study, either because they were masked by more sensitive ones, or are responsive outside the tested parameter range as discussed above.

Several studies suggest that in humans, SA-I fibers (coupled to Merkel cell receptors), unlike RA afferents, require a higher number of spikes to elicit a sensation (Talbot et al., 1968; Ochoa and Torebjork, 1983; Vallbo et al., 1984). Our results suggest a similar coding strategy in the rat whisker system. We found that the close match between psychometric and neurometric curves (Fig. 7) was achieved only if transient rather than sustained portions of SA responses were considered. Inclusion of the tonic response portion of SA cells into the neurometric measure not only failed to improve the match with psychophysics, but rather seriously deteriorated it (compare Fig. 6). Thus, very few spikes in a narrow time window between ∼3–10 ms may elicit a sensation. This implies that those central instances of the somatosensory system that give rise to the animals’ percept may not receive (or use) the tonic portion of SA response. Supporting this notion, it has been found that SA encode dynamic kinematic parameters at a high temporal precision (Jones et al., 2004). Moreover, inhibitory mechanisms and/or synaptic depression at higher stages of signal processing lead to high-pass filtering of cortical tactile signals (Carvell and Simons, 1988; Swadlow, 1995; Moore and Nelson, 1998; Zhu and Connors, 1999; Ahissar et al., 2000; Chung et al., 2002), and responses in the barrel cortex were observed to reflect the initial timing of thalamic afferent input rather than the total number of spikes (Pinto et al., 2000). In many natural contexts, the availability of sensory stimuli is short and there is pressure to initiate behavioral decisions in a limited time span (Johansson and Birznieks, 2004). Presumably, such constraints have helped to evolve strategies applied by many sensory systems to extract relevant information from fairly low numbers of spikes (for review, see Rieke et al., 1999). The temporal characteristics of the short nonrepetitive tactile stimuli as used here fall into this class, but it has to be borne in mind that coding strategies may be task or situation dependent and may differ for stimuli that are immanently stretched over time (Luna et al., 2005).

Conclusions

It is the major result of this study that perception in the rat whisker system displays similar principles of organization as the tactile sensing with finger tips in primates. As in primates, the whisker system relies on independent psychophysical channels defined by the association of specific sensitivity ranges (i.e., presumptive differing perceptual qualities) with respective response characteristics of the primary afferent. In humans, perception of different surfaces via the tactile modality is mediated through four such psychophysical channels (Bolanowski et al., 1988). To fully exploit the similarities in organization of rodent whisker and primate finger-tip systems revealed here, the following issues have to be brought forward in future studies. First, the possible association of receptor classes to psychophysical channels has to be elucidated. At least six different types of nerve endings exist at the hair follicle (Ebara et al., 2002) and may represent the basis for such association. Second, specific behavioral functions have to be attributed to the psychophysical channels. In primates such functions (e.g., perception of texture and form, skin motion, hand formation, and distant vibration) have been successfully associated with certain psychophysical channels (Johnson et al., 2000). In contrast, it is unclear if and how suggested functions of the whisker system [e.g., texture discrimination (Carvell and Simons, 1990), distance measurement (Szwed et al., 2006)] are related to psychophysical channels. Third, the central representations giving rise to subjective experience have to be identified (de Lafuente and Romo, 2005). The realistic possibility that, in rats, relatively early stages in processing (e.g., barrel cortex activity with its exquisitely well studied microcircuits) are directly related to perception is an exciting prospect in terms of the quest of how detailed neurophysiological processes relate to perception.