Control of Fast-Reaching Movements by Muscle Synergy Combinations

Abstract

How the CNS selects the appropriate muscle patterns to achieve a behavioral goal is an open question. To gain insight into this process, we characterized the spatiotemporal organization of the muscle patterns for fast-reaching movements. We recorded electromyographic activity from up to 19 shoulder and arm muscles during point-to-point movements between a central location and 8 peripheral targets in each of 2 vertical planes. We used an optimization algorithm to identify a set of time-varying muscle synergies, i.e., the coordinated activations of groups of muscles with specific time-varying profiles. For each one of nine subjects, we extracted four or five synergies whose combinations, after scaling in amplitude and shifting in time each synergy independently for each movement condition, explained 73–82% of the data variation. We then tested whether these synergies could reconstruct the muscle patterns for point-to-point movements with different loads or forearm postures and for reversal and via-point movements. We found that reconstruction accuracy remained high, indicating generalization across these conditions. Finally, the synergy amplitude coefficients were directionally tuned according to a cosine function with a preferred direction that showed a smaller variability with changes of load, posture, and endpoint than the preferred direction of individual muscles. Thus the complex spatiotemporal characteristics of the muscles patterns for reaching were captured by the combinations of a small number of components, suggesting that the mechanisms involved in the generation of the muscle patterns exploit this low dimensionality to simplify control.

Introduction

To generate the appropriate muscle activation patterns for controlling fast-reaching movements, as for many other motor tasks, the CNS has to take into account the dynamic behavior of the musculoskeletal system. Knowledge of musculoskeletal dynamics is necessary to implement a feedforward controller that can launch the arm in the appropriate direction before sensory information can drive error-correcting controls through feedback loops (Gottlieb, 1996; Gribble and Ostry, 1999; Sainburg et al., 1999). How this knowledge is incorporated in the motor commands is a long-standing question in motor control. Our working hypothesis is that the CNS incorporates implicitly yet efficiently the knowledge of the dynamic behavior of the musculoskeletal system necessary for generating the appropriate muscle patterns through the organization of muscle synergies. In our formulation, a muscle synergy comprises the coordinated activations of groups of muscles with specific time-varying profiles (d'Avella et al., 2003). We hypothesize that each synergy is independently scaled in amplitude and shifted in time and that the muscle activations derived from different synergies are combined linearly. This model is compatible with the idea of rule-based, feedforward control of dynamic joint torque (Gottlieb et al., 1997) and with the idea of local basis function approximation of the complex nonlinear transformations required to construct an inverse model (Mussa-Ivaldi and Giszter, 1992; Mussa-Ivaldi, 1997; Wolpert and Kawato, 1998); however, this model also introduces an explicit formulation of a mechanism for muscle pattern generation. Such a mechanism does not require an analytical representation of the musculoskeletal dynamics (Schweighofer et al., 1998; Todorov and Jordan, 2002), yet it might provide a biologically plausible, low-dimensional representation of the motor output without the storage and learning problems of a direct representation of each possible muscle pattern.

In this study, we show that combinations of a small number of time-varying muscle synergies capture the organization of the muscle patterns observed during fast-reaching movements in different directions. Although the muscle activation waveforms of these movements have been characterized (Wadman et al., 1980; Karst and Hasan, 1991; Flanders et al., 1994, 1996), their spatiotemporal organization, simultaneously across muscles and time, has not yet been described. For each subject, we used an optimization algorithm to identify four or five time-varying synergies whose combinations explained a large fraction of the total data variation for many point-to-point movements, including those with different endpoints, different loads, or different forearm postures, as well as for more complex reaching movements involving velocity reversals and via-points. The modulation in amplitude and time of the synergy recruitment captured the changes in shape of the activation waveforms of the individual muscles. Moreover, recruitment amplitudes of the synergies were directionally tuned, and the tuning was better characterized by a cosine function and had a preferred direction less variable across conditions than the tuning of individual muscles. Finally, the organization of muscle patterns for movements with multiple phases, such as the reversal and via-point movements, was captured by the recruitment of sequences of the synergies used for point-to-point movements.

Materials and Methods

Our aim was to identify the spatiotemporal characteristics of the muscle activity patterns used to perform fast-reaching movements in various conditions. We recorded electromyographic (EMG) activity and hand kinematics during point-to-point movements between a central location and one of eight peripheral locations arranged on a circle, either in the sagittal plane or in the frontal plane. These movements were performed with different loads on the hand (experiment 1) or with different postures of the forearm (experiment 2). We also studied more complex reaching movements (experiment 3): movements from one location, either at the center or at the periphery, to a second location and back to the first location in a continuous movement (reversal movements) and movements from one peripheral location to a second peripheral location through the central location (via-point movements).

Experimental design and apparatus.

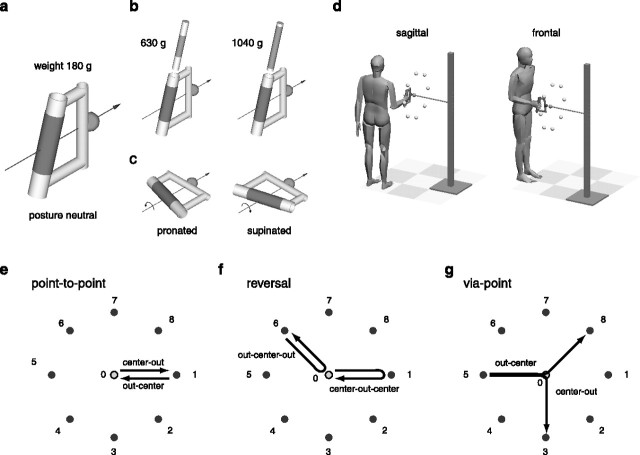
Standing subjects gripped a handle with their right hand and were instructed to move a sphere (diameter, 4 cm) attached to the handle from a start location to a target location and, in experiment 3, from a start location to an intermediate location (via-point) to a target location. The handle (see Fig. 1a) was constructed with two cylinders: one for gripping (diameter, 4 cm; covered with tennis grip tape) and one with the sphere attached on its side. The two cylinders were coplanar, with their symmetry axes at an angle of 16°, so that the axis of the cylinder with the sphere was perpendicular to the forearm axis when the subject gripped the other cylinder while keeping a natural posture of the wrist with a slight ulnar deviation. When the handle was being gripped, the sphere was aligned along the forearm axis with its center at a distance of 12 cm from the center of the gripping area. In experiments 1 and 3, the subjects were instructed to keep the handle vertical, thus imposing a neutral posture with respect to forearm rotation. In experiment 1, the weight of the handle was varied by inserting a tightly fitting cylinder filled with small lead spheres into the gripping cylinder (see Fig. 1b). Two different loads were used so that the total weight of the handle varied among three levels: 180, 630, and 1040 g. In experiment 2, the subjects were instructed to perform reaching movements with the unloaded handle (weight, 180 g) and to vary the forearm posture by rotating the handle into a horizontal orientation after either a clockwise or a counterclockwise rotation (see Fig. 1c). Thus the forearm posture varied among three conditions: neutral, pronated, and supinated.

Figure 1.

Experimental apparatus and conditions. Subjects gripped a custom-made plastic handle with a reference sphere attached on its side (a). In experiment 1, the weight of the handle was varied by inserting a load (b) into the gripping cylinder, thus requiring the subject to carry one of three weights (180, 630, and 1040 g). In experiment 2, subjects were instructed to hold the handle either vertically or horizontally (c) after either a clockwise or counterclockwise rotation of the forearm, thus requiring one of three forearm postures (neutral, pronated, and supinated). Standing subjects performed fast-reaching movements from a fixed starting position (corresponding to a posture with the arm vertical along the body and the forearm horizontal) to eight targets in the sagittal plane and eight targets in the frontal plane (center-out movements) and fast-reaching movements from the peripheral targets back to the starting position (out-center movements) (d,e). In experiment 3, subjects also performed reaching movements with a reversal (f) and through a via-point (g) with the unloaded handle in the neutral posture.

Nine right-handed subjects (age range, 27–40 years) participated in the experiments after giving informed consent. Three subjects (1, 2, and 3) performed experiment 1, three subjects (4, 5, and 6) performed experiment 2, and three subjects (7, 8, and 9) performed experiment 3. All experimental protocols conformed to the Declaration of Helsinki on the use of human subjects in research. Subjects performed blocks of movements from one start location to a target location, directly (point-to-point movements) or through a via-point (reversal and via-point movements), either in the sagittal or in the frontal plane (see Fig. 1d). Subjects were instructed to reach using only their arm and to minimize trunk movements. The start location was marked by a sphere whose location was adjusted so that the arm was approximately in a parasagittal plane, with the upper arm vertical along the trunk and the forearm horizontal. For the four subjects (1, 2, 4, and 5; apparatus 1; see Table 1) who performed only point-to-point movements, the target locations were marked by a sphere positioned by an experimenter. For the remaining five subjects (apparatus 2), the start, target, and via-point locations were marked by transparent spheres mounted on a supporting structure and illuminated from inside by a light-emitting diode. In all cases, the peripheral targets were positioned approximately on a circle of 30 cm of radius centered in the start location and at eight different locations (see Fig. 1e–g) separated by ∼45°. Because subjects performed both center-out and out-center point-to-point movements, for each movement direction (e.g., upward) there were two movements with a different endpoint (e.g., the center-out movement to target 7 and the out-center movement from target 3).

Table 1.

Summary of types of experimental apparatus, types of kinematic data, and muscles recorded for each subject

Experiment	1			2			3
Subject	1	2	3	4	5	6	7	8	9
Apparatus	1	1	2	1	1	2	2	2	2
Endpoint position recording (Fastrak)	+	+	+	+	+	+	+	+	+
Arm kinematics recording (Optotrak)	–	–	+	–	–	+	+	+	+
Biceps brachii, short head (BicShort)	+	+	+	+	+	+	+	+	+
Biceps brachii, long head (BicLong)	+	+	+	+	+	+	+	+	+
Brachialis (Brac)	+	+	+	+	+	+	+	+	+
Pronator Teres (PronTer)	+	+	+	+	+	+	–	+	+
Brachioradialis (BrRad)	+	+	+	+	+	+	+	+	+
Triceps brachii, lateral head (TrLat)	+	+	+	+	+	–	+	+	+
Triceps brachii, long head (TrLong)	+	+	+	+	+	+	+	+	+
Triceps brachii, medial head (TrMed)	–	–	+	–	–	+	+	+	+
Deltoid, anterior (DeltA)	+	+	+	+	+	+	+	+	+
Deltoid, medial (DeltM)	+	+	+	+	+	+	+	+	+
Deltoid, posterior (DeltP)	+	+	+	+	+	+	+	+	+
Pectoralis major, clavicular (PectClav)	+	+	+	+	+	+	+	+	+
Pectoralis major, sternal (PectInf)	–	–	–	–	–	+	+	+	+
Trapezius, superior (TrapSup)	+	+	+	+	+	+	+	+	+
Trapezius, medial (TrapMed)	–	–	+	–	–	–	+	+	+
Trapezius, inferior (TrapInf)	+	+	–	+	+	+	+	+	+
Latissimus dorsi (LatDors)	+	+	+	+	+	+	+	+	+
Teres Major (TeresMaj)	+	+	+	+	+	+	+	+	+
Infraspinatus (InfraSp)	+	+	+	+	+	+	+	+	+

For experiments 1 and 2, each experiment consisted of repeated blocks of trials (five for all subjects with the exception of subjects 4 and 5, who performed four blocks, all performed in a single session) for each one of the six combinations of two planes of movements and three weights (experiment 1) or three forearm postures (experiment 2). Each block included one center-out movement and one out-center movement for each one of the 8 peripheral targets for a total 48 movement conditions per plane. Each trial started after the subject reached the start position, with a “ready” signal followed by a “start” signal (computer-generated tones; 1 s delay), after which the subject was free to choose when to move but was instructed to move fast and accurately to the target and to remain at the target location for at least 1 s (target “hold” period). A trial was considered successful if the subject performed the movement with a duration (defined as the interval in which the endpoint speed was >10% of its maximum speed) <400 ms, stopped within a distance of 10 cm from the target center, and held the final position for at least 1 s. Subjects were given auditory feedback after an unsuccessful movement, and all unsuccessful movements were repeated. Start and target reference positions were defined as the position of the sphere on the subject’s handle, measured during a calibration at the beginning of each experimental session. In experiment 1, these reference positions were measured with the handle sphere close (<1 cm) to the start or target sphere. In experiment 2, the reference positions were on a plane parallel to the plane containing the start and target spheres and shifted a few centimeters from it to allow for movements with the rotated handle. Subjects sat and rested at will between blocks and showed no sign of fatigue throughout the experiment.

In experiment 3, for each plane of movement there were 80 distinct movement conditions: 16 point-to-point movements (1 center-out and 1 out-center for each one of the 8 peripheral targets), 16 reversal movements (1 with the first phase center-out and 1 with the first phase out-center for each one of the 8 peripheral targets), and 48 via-point movements (8 out-center movements for the first phase for each of the 8 peripheral targets, each followed by 1 of 6 center-out movements for the second phase, corresponding to angle of movement from first to second phase of ∼135°, 90°, 45°, −45°, −90°, and −135°). These 80 movement conditions were randomly subdivided in 2 blocks with 40 conditions each, and each condition was repeated 5 times for a total of 10 blocks for each plane of movement. Reversal and via-point trials were considered successful if the movement duration was between 500 and 700 ms. This interval was chosen so that the mean duration of each phase of the reversal and via-point movements would match the typical duration (∼300 ms) (see Table 2) of a point-to-point movement.

Table 2.

Summary of endpoint kinematics for point-to-point movements common to all experiments (mean ± SD)

Experiment	Subject	Plane	Movement duration (ms)	Maximum speed (m/s)	Movement distance (cm)
1	1	fr	219 ± 29	2.15 ± 0.28	26.8 ± 1.8
		sa	279 ± 55	1.83 ± 0.32	26.8 ± 1.7
	2	fr	251 ± 41	1.92 ± 0.26	27.6 ± 1.6
		sa	303 ± 53	1.63 ± 0.31	27.2 ± 2.1
	3	fr	287 ± 26	2.01 ± 0.20	32.0 ± 1.2
		sa	291 ± 41	1.58 ± 0.38	23.5 ± 2.7
2	4	fr	205 ± 36	2.56 ± 0.45	27.3 ± 3.3
		sa	293 ± 58	2.02 ± 0.53	29.2 ± 5.0
	5	fr	225 ± 37	2.53 ± 0.34	29.2 ± 2.5
		sa	282 ± 48	1.89 ± 0.40	27.0 ± 3.0
	6	fr	242 ± 26	2.12 ± 0.23	29.9 ± 1.1
		sa	282 ± 50	1.92 ± 0.43	29.7 ± 1.8
3	7	fr	267 ± 36	2.13 ± 0.30	30.4 ± 1.3
		sa	288 ± 38	2.10 ± 0.39	31.5 ± 2.2
	8	fr	276 ± 31	1.94 ± 0.28	30.4 ± 1.8
		sa	288 ± 28	1.79 ± 0.26	28.8 ± 1.5
	9	fr	262 ± 37	2.05 ± 0.27	30.5 ± 1.6
		sa	304 ± 48	1.82 ± 0.35	30.3 ± 2.1

fr, Frontal; sa, sagittal.

Data acquisition.

The position of the handle gripped by the subject and the activity of muscles involved in shoulder and elbow movements were recorded during all experiments. In the experiments performed with apparatus 1, the position and orientation of three markers placed on the subject’s wrist, shoulder, and handle and one marker placed on the experimenter’s (target) handle were acquired with an electromagnetic motion-tracking system (Fastrak; Polhemus, Colchester, VT). Each marker was sampled at 30 Hz with a spatial resolution of <4 mm in each direction, as estimated with a calibration performed within the workspace used in the experiment. In the experiments performed with apparatus 2, the position and orientation of one Fastrak marker in the subject’s handle was recorded at 120 Hz, and the positions of five to seven additional markers were recorded at 120 Hz with an optical motion tracking system (Optotrak 3020; Northern Digital, Waterloo, Ontario, Canada) with an accuracy of <0.1 mm in each direction. Two of these additional markers were placed on the handle, one was placed on the wrist (over the styloid process of the ulna), one was placed on the elbow (over the lateral epicondyle), and one was placed on the upper arm (at the proximal end close to the head of the humerus). In the case of subject 6, who performed experiment 2, three markers instead of a single one were placed on the wrist (two over the styloid process of the radius with different orientations and one lateral to the styloid process of the ulna) to record the wrist position with the forearm in the three different postures. In all experiments, the EMG activity of up to 19 muscles (see Table 1) was recorded with active bipolar surface electrodes (DE 2.1; Delsys, Boston, MA). Each electrode consisted of two parallel silver bars (10 mm spacing) and a differential preamplifier (gain, 10; rms noise, 1.2 μV; common-mode rejection ratio, >80 dB) housed in a compact case (41 × 20 × 5 mm). Each electrode was taped on the muscle belly and connected to an amplifier (Bagnoli-16; Delsys) where the EMG signal was bandpass filtered (20–450 Hz) and amplified (total gain, 1000). For each muscle, correct electrode placement was tested by asking the subject to perform a number of maneuvers involving both free movements and isometric contractions (Kendall et al., 1993) and then observing the expected activation patterns.

Data acquisition and experiment control were performed on a workstation with custom software written in LabView (National Instruments, Austin, TX). EMG data were digitized continuously during each block (1 kHz sampling rate; PCI-6035E; National Instruments). Kinematic data were synchronized with the EMG data by logging the time of each sample (indicated by a synchronization transistor-transistor logic pulse generated by the Fastrak and Optotrak control units) on a counter (100 kHz clock; PCI-6602; National Instruments) synchronized with the EMG acquisition clock. Fastrak data were processed on-line to compute movement time and target accuracy and to provide auditory feedback to the subject regarding unsuccessful trials. The experiment control program logged the times of all relevant behavioral events.

Data analysis.

All analyses were performed with custom software written in Matlab (Mathworks, Natick, MA). For each block, the continuous EMG and tracker recordings were subdivided into segments corresponding to successful movements starting at the time of the ready signal (1 s before the start signal) and ending at the end of the hold period (1 s after target acquisition).

Endpoint kinematics.

We used the position and orientation data from the subject’s handle Fastrak marker and the measured geometric parameters of the handle to compute the position of the sphere attached to the handle used as the endpoint reference position. These position data were low-pass filtered [finite impulse response (FIR) filter; 15 Hz cutoff; zero-phase distortion; Matlab “fir1” and “filtfilt” functions] and differentiated to compute tangential velocity and speed. For each movement, we measured the following: movement onset time, movement end time, movement duration, maximum speed and its time of occurrence, movement vector (in space), and movement direction (in the plane of movement). Movement onset and movement end were identified as the times in which the speed profile superceded 10% of its maximum. Movement duration was defined as the interval between movement onset and movement end. The movement vector was computed as the difference between final and initial positions. For each experimental condition, because the endpoint moved essentially on a plane (either sagittal or frontal), we computed the projection of the movement vector (in space) on the plane of movement identified by the first two principal components of all the movement vectors for that condition. For movements in the sagittal plane, the movement direction was measured as the angle of rotation from the direction of a horizontal, forward movement around the laterally directed axis perpendicular to the movement plane. Thus a movement directed upward had a 90° direction and a movement backward had a 180° direction. For movements in the frontal plane, the movement direction was measured as the angle of rotation from a medially directed horizontal movement around the axis perpendicular to the movement plane directed forward. Thus a movement directed upward had a 90° direction and a movement directed laterally had a 180° direction.

Joint kinematics.

In the experiments performed with apparatus 2, the positions of the shoulder, elbow, and wrist markers were used to estimate shoulder adduction, shoulder flexion, shoulder external rotation, and elbow flexion angles. The coordinates of the Optotrak markers were first rotated in a Cartesian reference frame, with the gravitational acceleration along the z-axis, by means of a calibration of the direction of the gravitational acceleration based on the measurement of two markers attached to a pendulum. The marker position data were then low-pass filtered (fifth-order Butterworth filter; FIR filter; 12 Hz cutoff; zero-phase distortion; Matlab “butter” and filtfilt functions), and the four joint angles were computed (see Fig. 3b) as the angles associated with a sequence of rotations of the shoulder joint (adduction, flexion, and external rotation) and the elbow joint (flexion). Angular velocities and accelerations were computed by numerical differentiation.

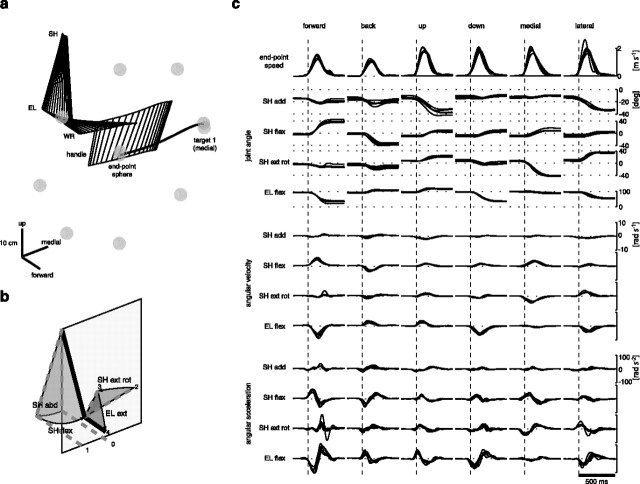
Figure 3.

Example of joint kinematics of point-to-point movements. Joint rotation angles for the shoulder and the elbow joints were computed from the position in space of three markers placed on the arm and forearm. a, The stick figure shows the orientation in space of the upper arm, forearm, and gripping cylinder handle during one movement from the central location to target 1 in the frontal plane (the positions of the central location, of the eight peripheral targets, and of the endpoint at the onset and end of the movement are indicated by gray spheres). SH, Shoulder; EL, elbow; WR, wrist. b, Three shoulder angles (adduction, flexion, and external rotation) and one elbow angle (flexion) were computed as the angles associated with the sequence of single-axis rotations necessary to reach the posture from a reference posture (0–4). Note that a positive shoulder abduction (SH abd), corresponding to a negative shoulder adduction (SH add), is illustrated in the figure. c, Endpoint speed, joint angles, velocities, and accelerations for five repetitions of six center movements in the sagittal and frontal plane (subject 3; 180 g load; neutral posture). flex, Flexion; ext rot, external rotation; rad, radius; deg, degree.

EMG preprocessing.

The EMGs for each trial were digitally full-wave rectified, low-pass filtered (FIR filter; 20 Hz cutoff; zero-phase distortion; Matlab fir1 and filtfilt functions), and integrated over 10 ms intervals. All trials in each experimental condition were then aligned on the time of movement onset and averaged (see Fig. 4). In a few cases (Table 1), some muscles showed a change in signal amplitude during the experimental session (indicated by –), likely resulting from a partial detachment of the electrode from the skin, and those muscles were removed from further analysis.

Figure 4.

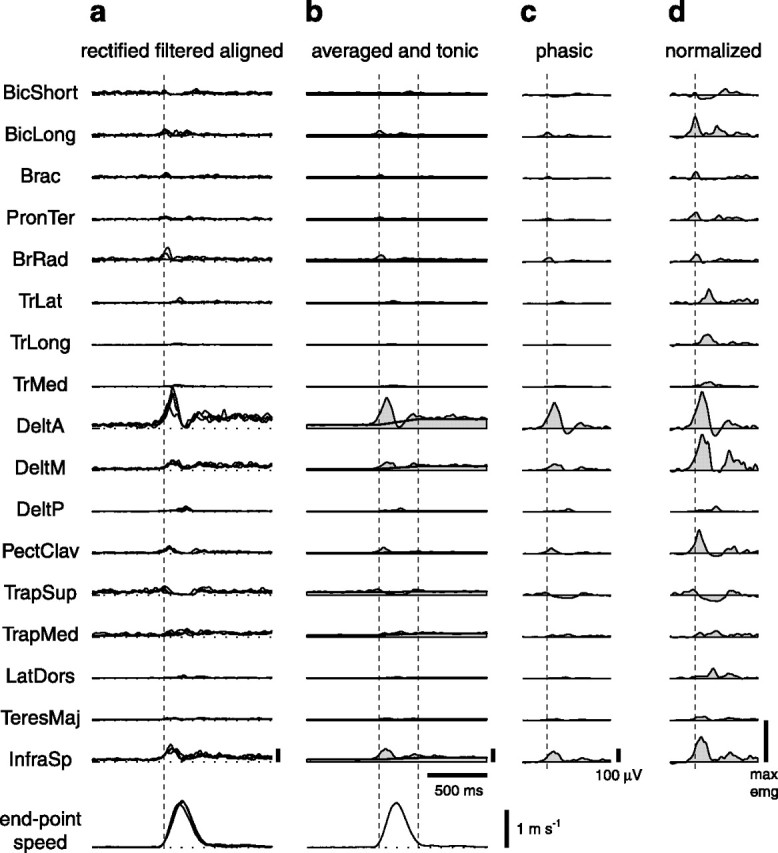
Estimation of phasic EMG patterns. The rectified and filtered EMGs for all repetitions of the same movement (a) were aligned to the time of movement onset and averaged (b, thin line and shaded area). For each muscle, the phasic EMG waveform (c) was constructed by subtracting a linear ramp from the tonic level of that muscle before movement onset to the tonic level after movement end (b, thick line) to the average EMG. Each muscle was then normalized to the maximum of that muscle over all conditions (d) (see Materials and Methods). Abbreviations for muscles are shown in Table 1.

Phasic EMG patterns.

The muscle activities involved in reaching movements in vertical planes are responsible for balancing gravitational forces, for maintaining postural stability, and for accelerating and decelerating the arm to change hand position. Flanders and collaborators (Flanders and Herrmann, 1992; Buneo et al., 1994) have shown that it is possible to dissociate a component of the EMG signal related to holding the arm at specific posture (“tonic”) from one related to the movement (“phasic”). We focused our analysis on the phasic component of the muscle patterns, and we used a subtraction procedure to remove the tonic component from the EMG waveforms. In accordance with Flanders’ data, we modeled the tonic component as a constant muscle activation level before and after the movement and as a linear ramp between two constant levels during the movement. We estimated the activity of each muscle at the initial and final postures by averaging the integrated EMGs from ready time up to 200 ms before movement onset (initial tonic level) and from 200 ms after movement end to the end of the hold period (final tonic level). We then subtracted from the waveform of each muscle the constant initial level from the beginning of the trial up to movement onset, a linear ramp between initial and final levels up to movement end, and the constant final level from movement end to the end of the trial. This procedure was used for all types of reaching movements, including reversal and via-point movements. After subtraction, a phasic waveform could assume negative values, which corresponded to an estimated tonic activation higher than the observed EMG level. Finally, we restricted the time interval considered for further analysis to the samples included between 200 ms before movement onset and 200 ms after movement end, and we normalized the amplitude of each sample for each subject and muscle to the amplitude of the largest sample in that muscle over all conditions.

Muscle synergy extraction.

We modeled the construction of a phasic muscle pattern by the combination of N time-varying muscle synergies as follows:

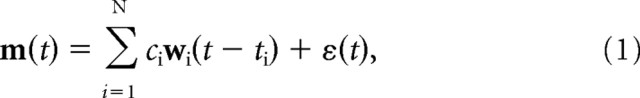where m(t) is a vector of real numbers, each component of which represents the phasic activation of a specific muscle at time t; w_i(τ) is a vector representing the muscle activations for the i-th synergy at time τ after the synergy onset; t_i is the time of synergy onset; c_i is a non-negative scaling coefficient; and ε(t) is noise.

We used a modified version of the optimization algorithm that we introduced recently (d'Avella et al., 2003) to identify a set of muscle synergies and their onset times and scaling coefficients that reconstructed the entire set of phasic muscle patterns in a dataset with minimum error. The algorithm is initialized by choosing random values for N synergies of a specific duration (500 ms corresponding to 50 samples of integrated EMGs), and it proceeds by iterating the following three steps: (1) given a set of synergies, find the synergy onset times for each trial by a matching pursuit procedure (Mallat and Zhang, 1993; d'Avella and Bizzi, 2005); (2) given a set of synergies and their onset times, find the non-negative scaling coefficients for each trial by non-negative least squares (Matlab function “lsqnonneg”); and (3) given the onset times and the scaling coefficients for all the trials, update the synergies according to the gradient descent on the error function as follows:

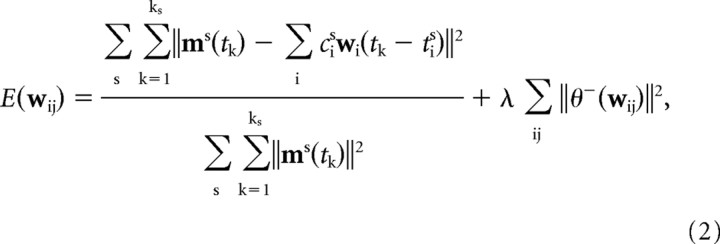where w_ij = w_i(τ_j) and θ ⁻(w) sets to zero all positive components of w; s runs over trials (movements); k_s is number of time samples in trial s; t_k is the time of the k-th sample in each trial; and c^s_i and t^s_i are the amplitude and timing coefficients for the i-th synergy in trial s.

The matching pursuit procedure essentially consists of an iterative search for a set of time-shifted synergies that best match the data. For each trial, the instances of each synergy obtained by using all possible time-shifts are compared with the data, and the instance with the highest normalized scalar product is selected and subtracted from the data. This search is then repeated among the remaining synergies by using the data residual.

As a consequence of the tonic activity subtraction, the phasic EMG waveforms can have negative values, and thus we could not use the original error minimization procedure based on a non-negative matrix factorization approach (d'Avella et al., 2003). We used instead a gradient descent minimization to update the synergies (step 3) with an error function that penalizes both inaccurate reconstructions (first term in Eq. 2) and large negative values in the identified synergies (second term). The denominator in the first term represents the squared norm of the entire dataset, and it was used to simplify the setting of the gradient descent parameters across different datasets (i.e., different subjects) by normalizing the contribution of the reconstruction error to the total error. The penalty term for negative synergy components was motivated by two considerations. First, as for other factorization methods, the decomposition of a set of muscle patterns as combinations of time-varying muscle synergies is not necessarily unique. In fact, there might be transformations of the basis elements, i.e., synergies, and associated transformation of the coefficients, which together provide alternative solutions that explain the data as well as the original bases. For example, in the case of factor analysis (Basilevsky, 1994), the basis vectors (factor loadings) can be rotated arbitrarily to obtain a new, equivalent factor structure, and this arbitrariness is usually removed by choosing some additional criterion such as maximizing the variance of the squared normalized factor loadings (varimax rotation). In the case of the time-varying synergy decomposition, because the basis elements are sequences of muscle activation vectors that can be shifted in time by an arbitrary number of samples, the solution is not invariant under a rotation of the synergies; however, a synergy rotation can lead to a new, different solution that approximates the data with a level of accuracy similar to that of the original solution. Thus the penalty term for negative synergy components in the cost function reduces this arbitrariness by constraining the algorithm to identify a set of synergies with minimal negative components among the sets that explain the data equivalently well. Second, large negative activation waveforms do not have a simple physiological interpretation. A negative deflection in the muscle waveform of one synergy can be interpreted as inhibitory influence acting on the motoneuronal pool excitation deriving from other synergies and from postural control; however, the amount of inhibition sufficient to completely silence a muscle, being equal to the amount of excitation driving the tonic activity of the muscle, is typically much smaller than the peak phasic activity. Thus one would expect a maximum negative deflection in the synergy waveforms to be a small fraction of the waveform peak amplitude.

We used a convergence criterion of five consecutive iterations for which the decrease in the error was <10⁻⁴. To minimize the probability of finding local minima, for each N, we repeated the optimization 10 times and selected the solution with the lowest error. In one subject (subject 3), the step size in the gradient descent update rule was set to 2 after testing values of this parameter ranging from 0.5 to 10 and choosing the value associated with the lowest error. The trade-off parameter (λ) between the two terms of Equation 2 was set to 0.05 after testing values from 0 to 0.5 in the same subject and choosing the minimum value for which the minimum of the normalized synergy waveforms was above −0.3, i.e., representing a moderate amount of inhibition.

Measures of synergy reconstruction goodness.

Because the EMG patterns and the residuals of the reconstruction of the patterns by synergy combinations are multivariate time-series, a measure of the goodness of the reconstruction, typically a ratio of two variances, must be defined using a multivariate measure of data variability. We used the “total variation” (Mardia et al., 1979), defined as the trace of the covariance of the muscle activations, to define a multivariate R² measure as follows:

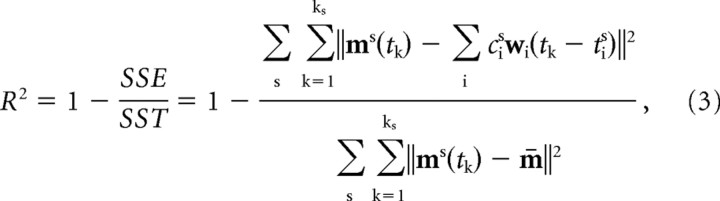where SSE is the sum of the squared residuals, and SST is the sum of the squared residual from the mean activation vector (m̄), i.e., the total variation multiplied by the total number of samples (K = Σ_s k_s). Thus R² represents the fraction of total variation accounted for by the synergy reconstruction. Although this measure is a global indicator of the goodness of reconstruction (operating over all trials), it is also useful to define a goodness of reconstruction measure for individual trials. If we use the same R² value restricted to one trial, we are comparing the residual of that trial with the data variation over that trial, which may vary considerably across trials. Thus the same residual error would have a very different R² value in a trial with a small amplitude modulation of the muscle waveforms and in a trial with a large modulation. We therefore defined a measure of the goodness of the reconstruction of a single trial based on the total variation (across all trials) per unit sample as follows:

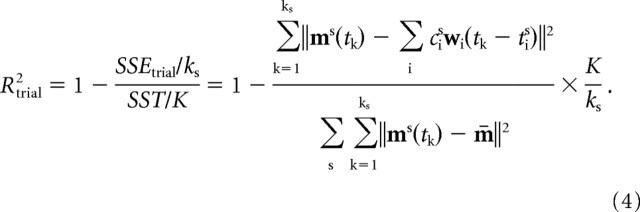With this definition, the global R² is the mean of the R_trial² values weighted by their duration.

Selection of the number of synergies.

The number of extracted synergies N is a parameter of the model, and thus we repeated the extraction with a number of synergies ranging from 1 to 8. We selected a specific number of synergies for further analysis according to a procedure based on the dependence of the amount of total variation explained (R²) on N. If the data were generated by combinations of N* synergies and no noise was added, a set with N > N* synergies would not explain more variation in the data than the set with N* synergies, because it already explains 100% of the data variation. When a certain amount of noise is added, the set with N* synergies would explain <100% of the data variation, and the synergy sets with N > N* synergies would explain larger fractions of the data variation; however, the variation captured by the model with N > N* in addition to the variation captured by the model with N = N* represents only variation attributable to noise. Thus, under the assumption that the random variation attributable to noise is smaller that the structured variation attributable to the synergy combinations, we expect the R² curve to change slope at N = N*. Therefore, we examined the R² versus N plot to estimate the correct number of synergies. This procedure is analogous to the “scree test” commonly used for the selection of the number of factors in factor analysis (Cattell, 1966) and has been shown to be adequate for identifying the correct number of non-negative synchronous muscle synergies (Tresch et al., 2006). We also used a quantitative criterion for the selection of the number of synergies. Under the further assumption that for N > N* each of the additional synergies captures an equal amount of noise-generated variation, we expect the R² curve to follow a straight line for N ≥ N*. A similar assumption underlies the Bartlett’s test, another commonly used test for the selection of the number of factors in factor analysis (Bartlett, 1950). We used a linear regression procedure (Cheung et al., 2005) to identify the value of N after which the R² curve is essentially straight. We performed a series of linear regressions, starting from a regression on the entire R² curve and progressively removing the smallest N value from the regression interval. We then compared the mean square residual errors of the different regressions and selected as the optimal number of synergies N* the first N value corresponding to a regression line from N to N^max with a mean square error <10⁻⁴.

Significance of extracted synergies.

We verified that the structure of the identified synergies did not result from a bias built into the extraction method with a simulation. We compared the R² value for the reconstruction of the actual data by the combinations of the identified synergies with the R² value for the reconstruction of structureless simulated data by the combinations of synergies extracted from those simulated data. We generated structureless data with the same empirical amplitude distribution and smoothness of the observed data by randomly reshuffling the samples independently for each muscle and then low-pass filtering the reshuffled samples (10 Hz cutoff). The reshuffling procedure consisted of generating a random permutation of an index vector (running from 1 to the total number of samples; Matlab function “randperm”) for each muscle and then reordering the samples using the permutated index. We then constructed a simulated dataset with the same number of trials and with the same duration of each trial as the observed data. For each observed dataset, we simulated 50 datasets and repeated the same synergy extraction procedure used for the observed data. We estimated the significance (p < 0.05) by computing the 95th percentile of the R² distribution for simulated data.

Synergy fit to point-to-point, reversal, and via-point EMGs.

We tested the robustness of the synergy model by reconstructing the muscle patterns in one dataset with the synergies extracted from a different dataset. To determine the amplitude and timing coefficients that best reconstruct a set of point-to-point EMG patterns given a set of synergies, we ran one iteration of steps 1 and 2 of the synergy extraction algorithm after initializing the synergies to the given set. We used this procedure in the analysis of experiments 1 and 2 for reconstructing the muscle patterns recorded during movement with additional loads and with pronated or supinated forearm postures with the synergies extracted from the pattern for point-to-point movements with the unloaded handle and a neutral forearm posture. We also used this procedure to fit data from individual trials with the synergies extracted from averaged muscle patterns to perform a statistical analysis of synergy modulation across conditions. For each subject, plane of movement, and synergy, we studied the effect of direction (eight levels), load or posture (three levels), and endpoint (two levels) and their interactions on the synergy amplitude coefficients with a three-way ANOVA (Matlab function “anovan”). In the case of reversal and via-point movements, in which there are two distinct kinematic phases, each associated with a peak in the endpoint tangential velocity, we used a slightly different fitting procedure. Assuming that in these more complex reaching movements each synergy may be recruited more than once during each movement, we again ran one iteration of the first two steps of the extraction algorithm to fit the synergies to the novel dataset but we modified step 1 to allow for multiple instances of the same synergy to be recruited in each movement. To prevent excessive temporal overlap of the same synergy, we introduced a refractory period of 100 ms (10 samples) in the matching pursuit procedure used to determine the synergy onset times (d'Avella and Bizzi, 2005). In summary, we reconstructed each phasic EMG pattern observed during reversal or via-point movements with a sequence of two or more instances of each one of the time-varying muscle synergies extracted from point-to-point movements; each instance was independently scaled in amplitude and shifted in time.

Synergy set comparison.

The cosine of the angle between two synergies was used as a measure of their similarity. This was defined as the maximum of the normalized scalar products between the two time-varying synergies shifted by k₁ and k₂ samples over all possible relative delays (k₁ − k₂) [for details, see d'Avella et al. (2003)].

To compare synergies extracted from different subjects, we grouped them using a hierarchical cluster analysis. We used the similarity between a pair of synergies (s_ij), computed with the subset of muscles common to all subjects, to define a distance measure (d_ij = 1 − s_ij) and to create a hierarchical cluster tree from all synergy pairs (Matlab function “linkage” with the “average” distance method, i.e., using as distance between two clusters the average distance between all pairs of objects across the two clusters). We then partitioned the tree with the minimum number of clusters for which there was no more than one synergy from the same subject in each cluster. Finally, in each cluster, we identified the element with the highest mean similarity with all other elements and used this mean similarity to quantify the mean similarity in a cluster. We also defined a similarity index (S) between two synergies, as a value ranging from 1, in the case of identical synergies, to 0, for a similarity at chance level, as follows:

where s_data is the similarity between the two synergies and s_chance is the mean similarity between 500 pairs of random synergies. We simulated random synergies by sampling the empirical distribution of the activation amplitude of each muscle in the dataset from which the synergies were extracted, constructing sequences of random data with the same length as the synergy duration, and low-pass filtering the resulting sequences (10 Hz cutoff) to match the smoothness in the actual synergies. We then estimated the significance (p < 0.05) of the similarity index from the distribution of the similarities between random synergies.

Directional tuning of synergy amplitude coefficients.

To characterize the directional dependence of the synergy amplitude coefficients in each load or posture and endpoint condition, we used multiple linear regression (Matlab function “regress”) to fit the following model:

where θ is the movement direction, c is the synergy amplitude coefficient, and β₀ is an offset parameter. We then rewrote Equation 6, in terms of amplitude

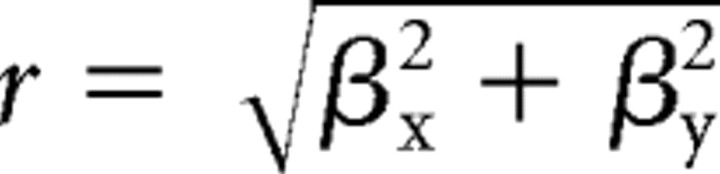and preferred direction

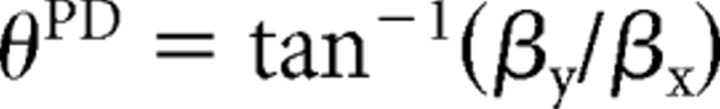of the cosine tuning function, as follows:

The goodness-of-fit was quantified with an R² value, and its significance was tested with an F test. Finally, to compare the angular dispersion of the preferred direction of the synergy amplitude coefficient tuning across conditions with the angular dispersion of the preferred direction of the activation of individual muscles, for each muscle and each trial we computed the maximum integrated EMG activity in a 100 ms window sliding across the entire trial (Flanders et al., 1996), and we fit these data with the same procedure used for the synergy amplitude coefficients. Then, for each plane of movement, synergy, or muscle, we compared the angular deviation (Batschelet, 1981) of the preferred direction across the six different conditions (three loads or postures and two endpoints).

Fit of point-to-point shifted EMGs to reversal and via-point patterns.

We compared the reconstruction of reversal and via-point muscle patterns by the combinations of the muscle synergies extracted from point-to-point patterns with the reconstruction obtained by fitting the muscle patterns of the two point-to-point movement corresponding to the two separate phases of the reversal and via-point movements, each shifted in time to align the tangential velocity peaks. For each subject and plane of movement and for each averaged, phasic reversal and via-point muscle pattern, we first shifted in time the averaged, phasic patterns of point-to-point movement between the start location and intermediate location of the reversal or via-point movement and of the point-to-point movement between the intermediate location and the target location so that the times of peak tangential velocity in the point-to-point movements matched the times of the first and second peak in the tangential velocity of the reversal or via-point movement. We then found two non-negative amplitude scaling coefficients for the two shifted point-to-point patterns that minimized reconstruction error, using a non-negative least squares minimization algorithm (Matlab function “lsqnonneg”).

Results

Nine subjects, subdivided in three groups of three subjects, performed different sets of fast-reaching movements in vertical planes. All groups performed a set of point-to-point movements between a central position and eight targets in the frontal plane and eight targets in the sagittal plane while holding a handle with the forearm in a neutral posture (Fig. 1a,d,e). Subjects in the first group also performed the same set of point-to-point movements with two different loads inserted in the handle (experiment 1) (Fig. 1b), and those in the second group performed the movements with two different forearm postures (experiment 2) (Fig. 1c). Subjects in the third group, in addition to the point-to-point movements with the handle unloaded and the forearm in a neutral posture, performed more complex reaching movements involving a velocity reversal or a via-point (experiment 3) (Fig. 1f,g). We first characterized the spatiotemporal organization of the muscle patterns for the common set of point-to-point movements by identifying, for each subject in each group, a set of time-varying muscle synergies. We then tested whether those synergies could reconstruct the muscle patterns observed in all other conditions.

Endpoint and joint kinematics

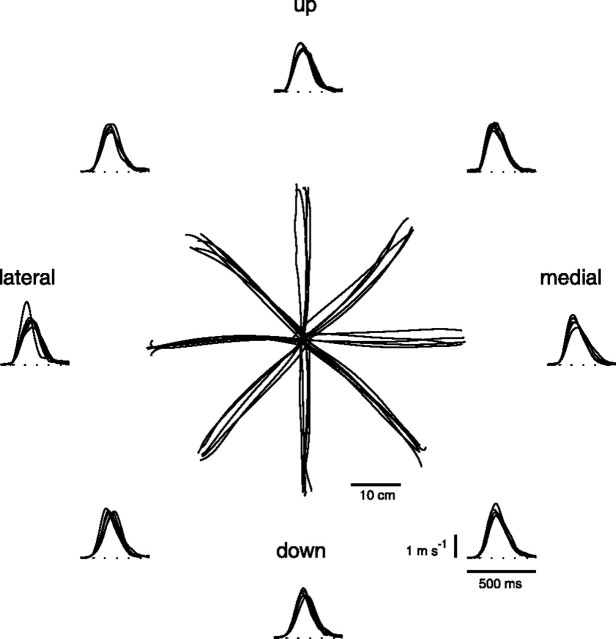
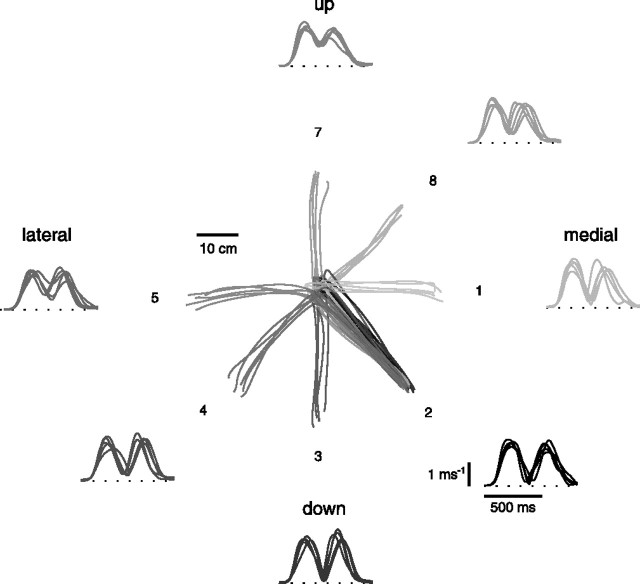
The endpoint trajectories, for all point-to-point movements, were approximately straight, with bell-shaped speed profiles (Fig. 2). For the point-to-point movements common to all experiments, the mean movement duration ranged, across subjects and planes, from 202 to 304 ms; the mean maximum speed ranged from 1.58 to 2.56 m/s; and the mean movement distance ranged from 23.4 to 32.0 cm (Table 2). The direction of movement had a significant effect on movement kinematics in most cases (movement duration, 13 of 18 cases; two-way ANOVA; movement duration vs movement direction and movement endpoint; p < 0.05; maximum speed, 11 of 18 cases; movement distance, 12 of 18 cases). The movement endpoint (peripheral target vs central target) did not have a significant effect in most cases (movement duration, 14 of 18 cases; p > 0.05; maximum speed, 16 of 18 cases; movement distance, 12 of 18 cases), but it had a significant interaction with the direction of movement in many cases (movement duration, 7 of 18 cases; p < 0.05; maximum speed, 9 of 18 cases; movement distance, 13 of 18 cases).

Figure 2.

Example of endpoint kinematics of point-to-point movements. Trajectories and tangential velocity profiles of the endpoint are shown for five repetitions of fast center-out movements to eight targets in the frontal plane (subject 3; 180 g load; neutral forearm posture).

In five subjects, we also recorded the position in space of the upper arm and forearm, from which we estimated shoulder and elbow rotation angles (Fig. 3a,b). The joint rotations required to perform straight endpoint movements involved changes in all of the shoulder angles (adduction, flexion, and external rotation) and elbow angles (flexion). For example (Fig. 3), upward and downward movements were accomplished mainly by elbow flexion and elbow extension, respectively, but they also involved rotations at the other joints, as indicated by their relatively high angular accelerations.

Phasic muscle patterns

We characterized the phasic muscle activation waveforms using a subtraction procedure. We recorded the EMG activity from up to 19 muscles acting on the shoulder and elbow joints, and we averaged the activation waveforms for each muscle across different repetitions after aligning each trial on the time of movement onset (Fig. 4). We then subtracted the postural component of each muscle activation waveform so that the resulting phasic waveforms represented the muscle activity responsible for accelerating and decelerating the arm. Because of the subtraction, the phasic activity could assume negative values, indicating that in some phases of movement for specific muscles, the activity necessary for moving the arm was less than that for holding a static posture against gravity. A qualitative analysis of the phasic EMG waveforms indicated that each muscle had a specific and gradual modulation of its activation amplitude and timing as a function of movement direction, in accordance with previous reports (Flanders et al., 1994, 1996).

Muscle synergies

For many muscles, the shape of the muscle activation waveform appeared preserved, after scaling in amplitude and shifting in time, across some of the directions. This observation suggests that the phasic waveforms of each individual muscle result from one or a few common waveforms that are scaled in amplitude and delayed in time, depending on the movement direction (Flanders, 1991). We sought to go beyond the characterization of individual muscles and to identify spatiotemporal relationships among the activation waveforms of all the recorded muscles, which are invariant across all conditions.

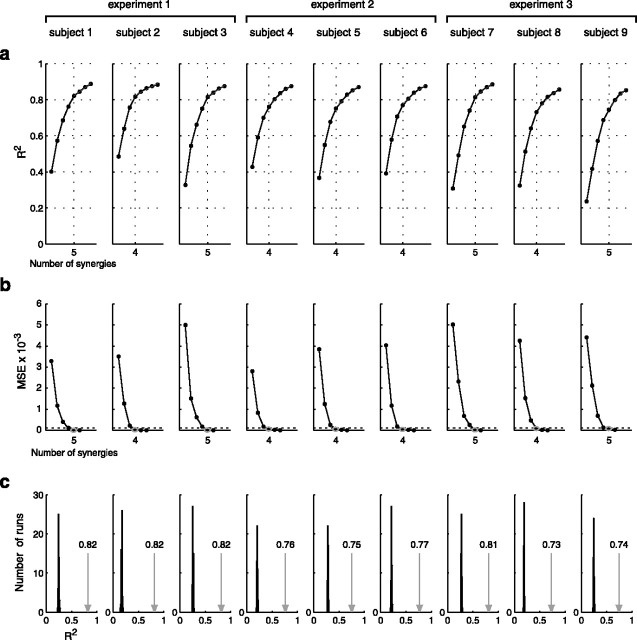
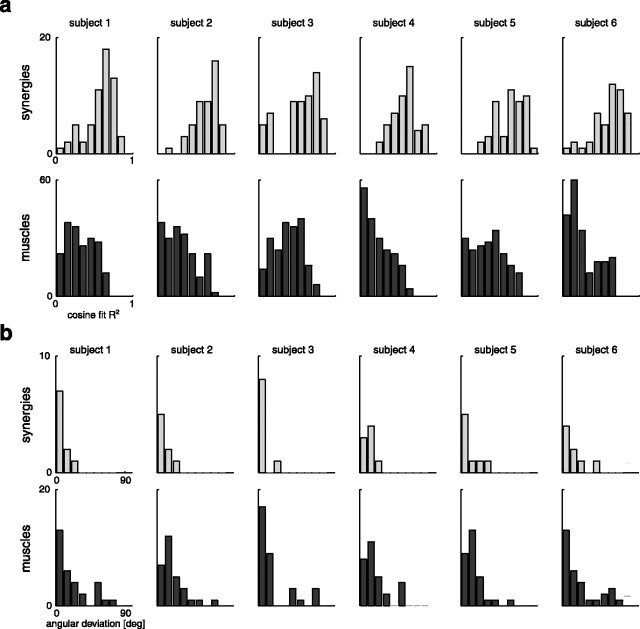
Using the averaged and integrated phasic EMG patterns for all movements of each subject, we extracted sets of time-varying synergies with a number of synergies ranging from one to eight. We selected the number of synergies to consider for further analysis as a compromise between model parsimony and accuracy. We observed that the curve showing the amount of data variation explained by the model (R²) as a function of the number of extracted synergies (Fig. 5a) has a change in slope at four or five, depending on the subject. The existence of a “knee” in the R² curve indicated that synergy sets with more elements than the number of synergies at the knee point explained only a small additional fraction of the total data variation. Furthermore, for all subjects, the portion of the R² curve to the right of the knee appeared straight, suggesting that, under the assumption of isotropic noise (i.e., contributing equally to the different synergies), additional synergies explain an equal amount of random variation attributable to noise. We also used a linear regression procedure to quantitatively validate the choice of the number of synergies (Fig. 5b) (see Materials and Methods). The R² values for the sets with four synergies (subjects 2, 4, 5, 6, and 8) ranged from 0.73 (subject 8) to 0.82 (subject 2). The R² values for the sets with five synergies (subjects 1, 3, 7, and 9) ranged from 0.74 (subject 9) to 0.82 (subjects 1 and 3).

Figure 5.

Synergy extraction. a, Total variation explained as a function of the number of extracted synergies. The curve showing the percentage of the total variation explained by the synergy combinations (R²) as a function of the number of extracted synergies has a change in slope at four or five synergies (dotted vertical line) depending on the subject (different columns). b, Selection of number of synergies. For each subject, the number of synergies to consider for further analysis was determined as the number for which the mean squared error (MSE) of a linear regression of the portion of the R² curve starting from a given number of synergies (1–6) up to the end of the curve (8 synergies) drops below 10⁻⁴ (dashed horizontal line). c, Significance of extracted synergies. Each histogram shows the distribution of the R² values for the reconstruction of simulated, structureless data with synergies extracted from those simulated data over 50 simulation runs, compared with the R² value for the reconstruction of the real runs with the synergies extracted from them (arrow) (see Materials and Methods).

We verified that the extracted synergies captured significant features in the data and did not result from a bias in the method by performing a simulation (see Materials and Methods). The R² value for the reconstruction of the data with the extracted synergies was significantly higher than the R² values obtained from the reconstruction of simulated, structureless data with the same number of synergies extracted from those simulated data (Fig. 5c), indicating that the structure of the extracted synergies expressed a real spatiotemporal organization in the data.

The five synergies extracted from subject 3 (Fig. 6) illustrate the basic features of the synergies extracted from all subjects. Each synergy represents the activation of all the muscles for a duration of 500 ms, with a specific subset of muscles activated more vigorously within each synergy and many muscles recruited by more than one synergy. The first synergy (W₁) has a synchronous burst of activation in all the muscles, with mainly a flexion action on the elbow (both heads of biceps brachii, brachialis, bracoradialis, and pronator teres); in muscles that elevate the scapula (superior and medial trapezius); and in one monoarticular elbow extensor (lateral triceps brachii). A few muscles in the first synergy also show an early negative activation (deltoid anterior and medial), which corresponds to a decrease or inactivation of the postural activity of those muscles during movement. The second synergy (W₂) has a early negative activation of superior trapezius, followed by a sequence of two positive bursts in the three heads of triceps brachii (elbow extensors), with a positive activation of the long head of biceps brachii in between the two triceps bursts. The third synergy (W₃) has a strong positive activation of two shoulder flexors (anterior deltoid and pectoralis), a shoulder abductor (medial deltoid), a shoulder external rotator (infraspinatus), and superior trapezius. The temporal profile of these activation waveforms is essentially biphasic, with a larger initial peak. Other muscles in this synergy (triceps and latissimus dorsi) have a weaker activation peaking at the time of the valley in the activation profile of the biphasic muscles. The activation profile of medial and posterior deltoid, medial trapezius, and infraspinatus in the fourth synergy (W₄) is also positive and biphasic. In addition, this synergy shows a single positive activation peak in lateral and long triceps and a weak negative activation of pectoralis. Finally, the fifth synergy (W₅) has positive activation of three shoulder extensors (posterior deltoid, latissimus dorsii, and teres major), with opposite shoulder rotation actions (external for deltoid and internal for the other two); a simultaneous a negative activation in anterior and medial deltoid, superior trapezius, and infraspinatus; and a delayed positive activation of the elbow flexors and of medial deltoid. In summary, each one of the five synergies extracted from subject 3 has a specific spatiotemporal organization with distinct groups of muscles being activated or inactivated at different times. Moreover, although each synergy is characterized by the synchronous activation of a set of anatomically synergist muscles, as for the elbow flexors in W₁ and the elbow extensors in W₂, each synergy also includes muscles acting on different joints and with an asynchronous activation. Finally, for each synergy we have computed the mean activation waveform across muscles (Fig. 6, bottom row) to help visualize the synergy recruitment timing in Figures 7, 8, and 14.

Figure 6.

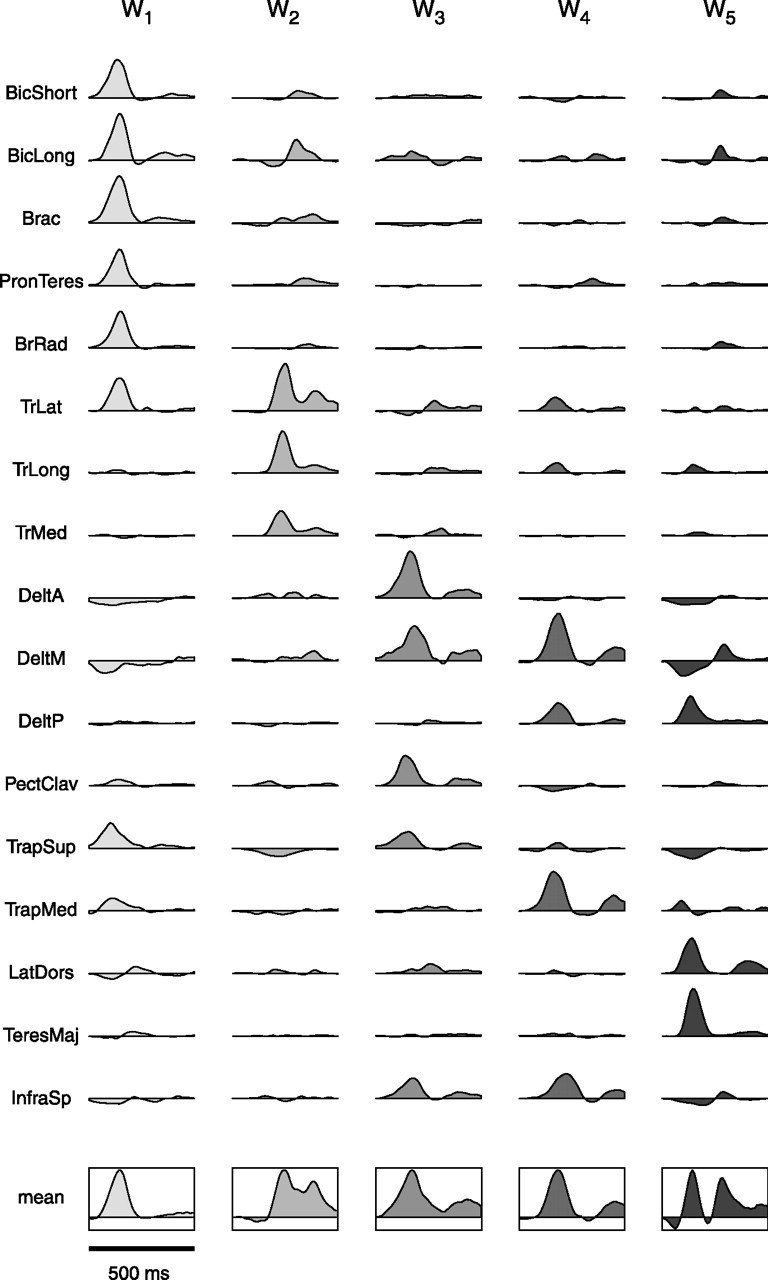
Five time-varying synergies extracted from the muscle patterns of subject 3. Each synergy (W₁ to W₅) represents the activation of all of the muscles for 500 ms, with a specific set of muscle activation waveforms for each synergy. The last row shows the mean muscle activation waveform for each synergy (framed in a rectangle). Abbreviations for muscles are shown in Table 1.

Figure 7.

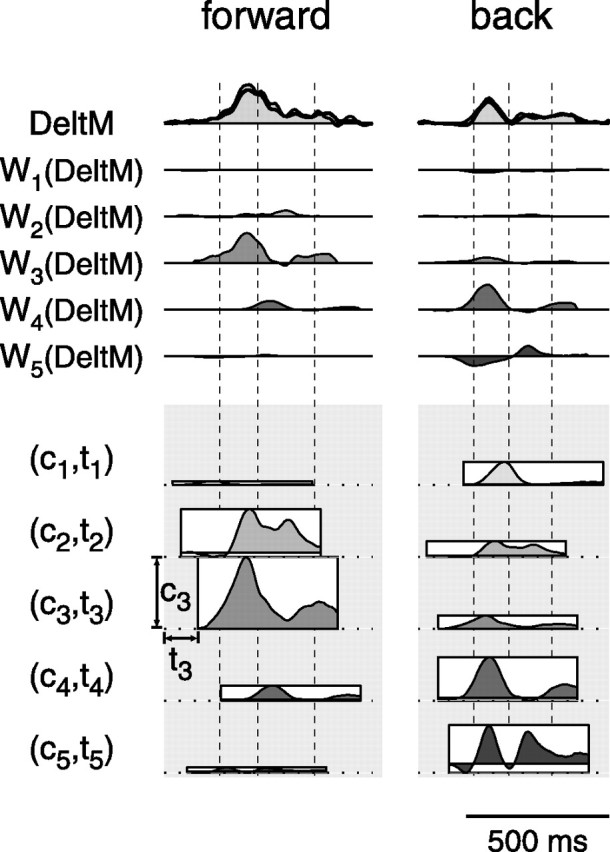
Synergy combination mechanism. The reconstruction of a single muscle activation waveform [medial deltoid (DeltM); first row, thin line and shaded area] in two different movements (different columns; subject 3; center-out; 180 g load) illustrates the mechanism used to construct muscle patterns through the combination of time-varying synergies. For each movement, the synergy activation waveform for each of the five synergies (2nd to 6th row, labeled W₁ to W₅; corresponding to the five waveforms in the DeltM row of Fig. 6) are scaled in amplitude and shifted in time according to movement-specific coefficients (c_i and t_i; i = 1, …, 5; see Materials and Methods) and summed together (first row, thick line). The values of the coefficients are illustrated in the bottom panel using five rectangles. The height of each rectangle represents the amplitude coefficient for one synergy; its horizontal position corresponds to the time of the synergy recruitment. The profile inside each rectangle represents the mean of the muscle activation waveforms in the synergy (Fig. 6, bottom row), and it is shown only to better visualize the synergy recruitment timing. Note how the activation of the same muscle in different movements depends on the recruitment of different synergy combinations (mainly W₂ and W₃ in forward movements; mainly W₄ and W₅ in backward movements). Moreover, the specific shape and timing of the muscle activation waveform depend on the amplitude scaling and time shifting of the different synergy waveforms.

Figure 8.

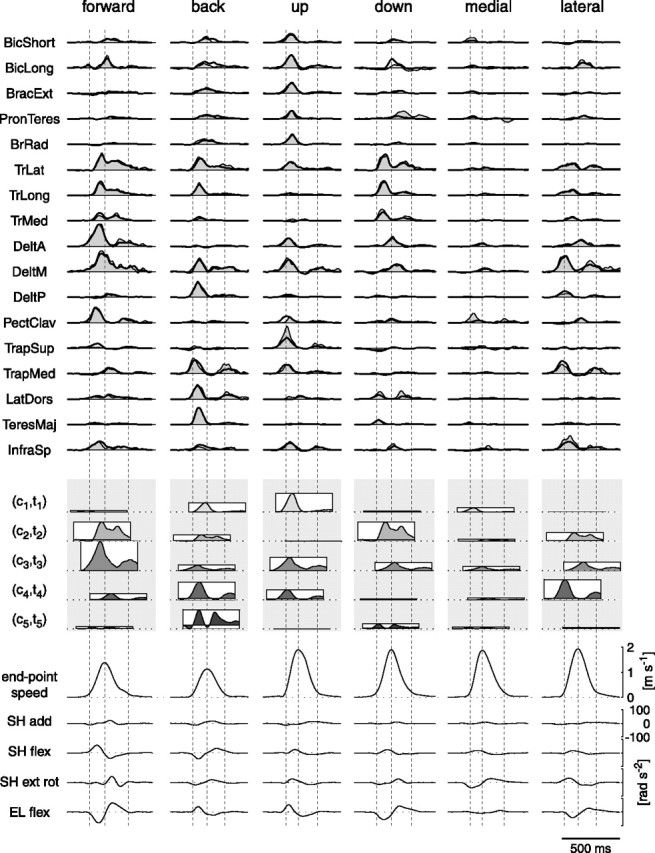
Example of reconstruction of the muscle patterns by synergy combination across movement conditions. The averaged, rectified, filtered, and integrated phasic EMGs are reconstructed by scaling in amplitude and shifting in time five time-varying synergies (Fig. 6). The observed data (top panel, thin line and shaded area) and their reconstruction (thick line) as combinations of the five synergies (where the amplitude and timing coefficients are illustrated by the height and position of rectangles, as in Fig. 7) are shown for two directions in the sagittal plane (forward and back), two directions common to sagittal and frontal planes (up and down), and two directions in the frontal plane (medial and lateral) (subject 3; center-out; 180 g load). For each direction, dashed vertical lines represent the movement onset time, the time of maximum speed, and movement end time. The bottom panel shows the endpoint speed profiles and the angular accelerations for each movement. SH, Shoulder; EL, elbow; rad, radius; add, adduction; flex, flexion; ext rot, extension rotation. Abbreviations for muscles are shown in Table 1.

Figure 14.

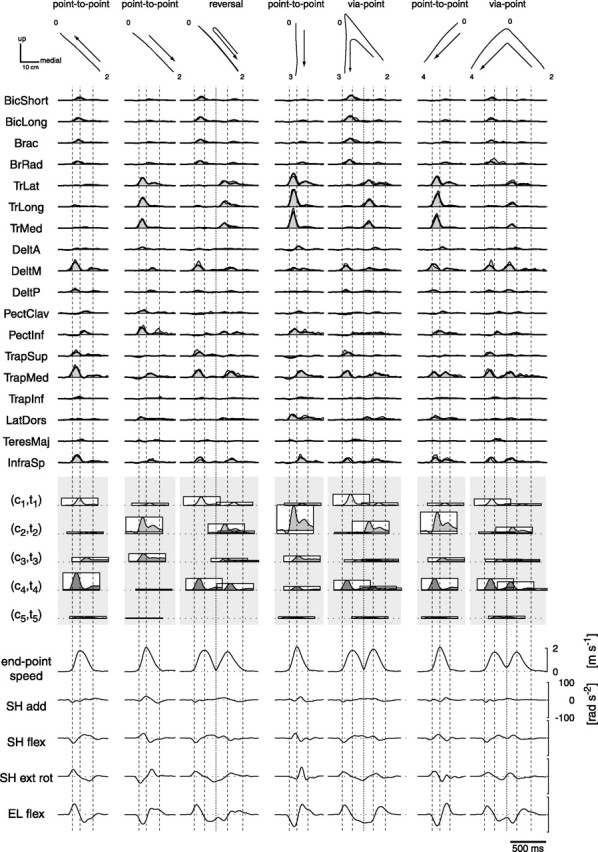
Example of reversal and via-point muscle pattern reconstruction with point-to-point synergies. Trajectories, averaged phasic muscle patterns, synergy reconstruction, synergy combination coefficients, endpoint tangential velocity, and angular accelerations are shown (different rows) for one reversal movement (3rd column) and two via-point movements (5th and 7th columns) with the same first phase (as in the point-to-point movement in the 1st column) and different second phases (as in the point-to-point movements in the 2nd, 4th, and 6th columns). The muscle patterns for the more complex movements resemble a superposition, after time shift, of the patterns for point-to-point movements but with changes in the amplitude and time of individual muscles. SH, Shoulder; EL elbow; add, adduction; flex, flexion; ext rot, external rotation; rad, radius. Abbreviations for muscles are shown in Table 1.

Reconstruction of muscle patterns by synergy combinations

The reconstruction of the activation waveform for a single muscle illustrates the synergy combination mechanism (Fig. 7). For each movement, the five synergy waveforms for that muscle (Fig. 6, DeltM) are scaled in amplitude and shifted in time according to specific coefficients (see Materials and Methods) and summed together to generate the complete muscle activation waveform. Across movements, the different activation waveforms for that muscle are generated with different amplitude and timing coefficients.

In most cases, the muscle patterns for all movement directions and conditions were accurately reconstructed by the combinations of the synergies identified in each subject, when appropriately scaled in amplitude and shifted in time. The example of the muscle patterns for six center-out movements of subject 3 (Fig. 8, top, thin line and shaded area) and the reconstruction of these patterns (top, thick line) by the combinations of the five synergies presented above (Fig. 6) illustrates the level of reconstruction accuracy achieved by the synergy model. The R_trial² value (fraction of the total variation per sample explained in a trial; see Materials and Methods) for the reconstruction of each one of the six patterns of the example ranged from 0.76 (down) to 0.85 (medial). Across all subjects and conditions, the R_trial² values ranged from 0.40 to 0.94 (median, 0.80). In general, the model captured the basic shape of the muscle waveforms even when the reconstruction was not perfect. For example, the observed waveform for latissimus dorsi in the down direction (Fig. 8, fourth column) has a biphasic profile with two peaks, the first peak larger than the second and aligned with movement onset time (first dashed vertical line). The reconstructed waveform for the same muscle (thick line) has a lower amplitude than the observed waveforms, but it has a very similar temporal profile.

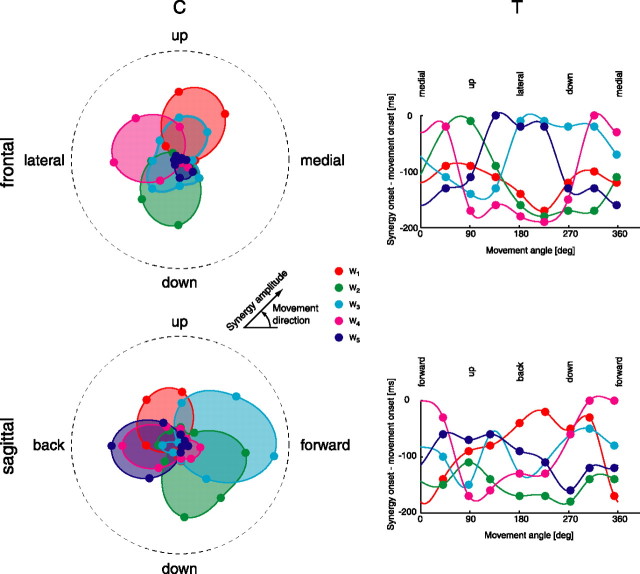
Synergy directional tuning

The amplitude coefficients of each synergy had a distinctive directional tuning. For the eight center-out movements in the frontal plane of subject 3, the amplitude coefficient for the first synergy (W₁) was maximal for upward-medial movements, and it gradually decreased for movement away from this direction (Fig. 9, top left, red). The second synergy (W₂) was maximally recruited for downward movements (top left, green). The third synergy (W₃) had a broad tuning with maxima for both upward-medial and downward-lateral movements (top left, cyan). The fourth synergy (W₄) was tuned for lateral movements (top left, magenta). The fifth synergy (W₅) was weakly recruited in this condition, but it showed a clear downward-medial directional preference (top left, blue). Similarly, the amplitude coefficients for eight center-out movements in the sagittal plane of subject 3 showed a specific directional tuning. In this plane, the first synergy was maximally active for upward-backward movements (bottom left, red), the second synergy was active for directions ranging from down to forward (bottom left, green), and the third synergy was tuned for forward movements. The fourth and the fifth synergies had similar directional dependences, with maximal activation for backward movements (bottom left, magenta and blue). Finally, in many cases the dependence of the amplitude coefficient on the movement direction was unimodal, and it resembled a cosine function with a positive offset.

Figure 9.

Synergy directional tuning. Synergy amplitude coefficients (C, left column) and timing coefficients (T, right column) for movements in the frontal (top row) and sagittal (bottom row) planes are shown for subject 3 (center-out; 180 g load; neutral posture). In both amplitude polar plots (left column) and timing plots (right column), the eight values of the coefficients for each synergy (colored dots) are connected by a periodic cubic spline interpolation curve. deg, Degree.

The synergy onset times were also modulated with movement direction. In the frontal plane, the onset of the first synergy occurred progressively earlier, with respect to the movement onset, as the direction of movement turned away from the direction of maximum recruitment amplitude (around 70° upward from the medial direction) (Fig. 9, top right, red). In contrast, the recruitment of the second synergy was early for movements in and around the direction of maximal recruitment (downward, around 250°) and progressively later going toward upward movements (90°) (top right, green). The onset of the third synergy was early for upward directions (around the first amplitude peak) and late for downward directions (around the second amplitude peak) (top right, cyan). The timing of the fourth and fifth synergies had a modulation similar to that of the second synergy: early for movements in the direction of maximal activation (160° and 260°, respectively) and late for movements toward the opposite direction (top right, magenta and blue). In the sagittal plane, the onset time of the first synergy, starting from the direction of maximal activation (around 130°), shifted later toward more posterior directions and earlier toward anterior directions (bottom right, red). The modulation of the second synergy in the sagittal plane was similar to its modulation in the frontal plane but with a smaller modulation depth: early for downward movements and late for upward movements (bottom right, green). The onset of the third synergy showed a gradual shift toward earlier times, moving from downward, to forward (direction of maximal activation), to upward (bottom right, cyan). The fourth and fifth synergy, in contrast to the similarity in their amplitude modulation, had opposite timing modulations: the onset of W₄ shifted from early to late going from upward, to backward, to downward (bottom right, magenta), whereas the onset of W₅ shifted from late to early across the same range of directions (bottom right, blue).

Comparison across subjects

In most cases, the synergies extracted from different subjects were remarkably similar. To compare synergies extracted from different subjects, we partitioned the set of 40 synergies extracted from all subjects into six clusters (labeled A–F), according to their similarity, with a clustering algorithm (Fig. 10a,b) (see Materials and Methods). The first five clusters contained, in the same order, the five synergies of subject 3 (Fig. 6). Clusters A, C, and D each contained synergies from every subject. Cluster B contained synergies from eight of the nine subjects; cluster E contained synergies from three; and cluster F contained synergies from two. Thus the first four clusters grouped synergies representing a spatiotemporal organization common to all subjects. The muscle activation waveforms of the synergies in clusters A–D (Fig. 10c) show many of the distinctive features of synergies 1–4 of subject 3 (Fig. 6). Specifically, all synergies in cluster A have a burst of activation in elbow flexor muscles and in superior trapezius. A burst of activation in elbow extensor muscles and a negative activation in superior trapezius followed by a smaller burst in elbow flexor muscles are common to all the synergies in cluster B. Cluster C has a characteristic activation of anterior deltoid and pectoralis followed by a smaller activation of latissimus dorsii. Finally, an activation of medial deltoid, posterior deltoid, and infraspinatus is common to all synergies of cluster D.

Figure 10.

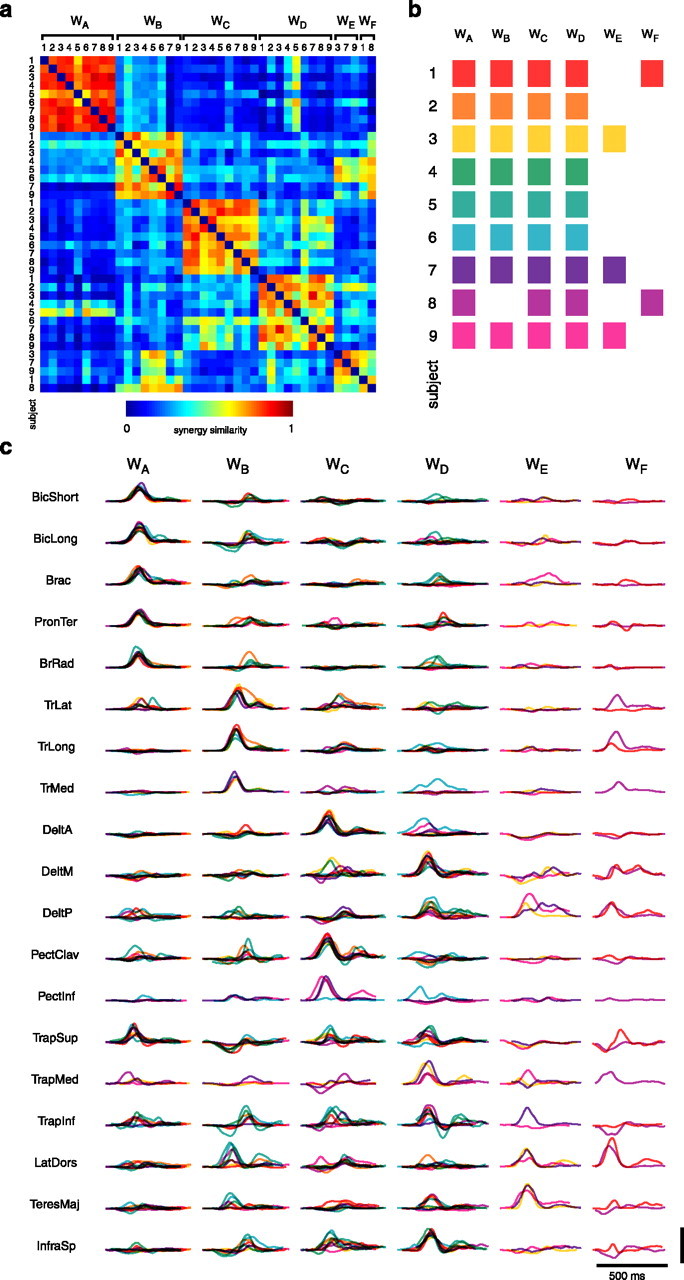
Synergy comparison across subjects. We used a hierarchical clustering algorithm to group the 40 synergies extracted from all nine subjects into groups according to their similarity. The hierarchal cluster tree generated from the similarity matrix (a) was partitioned into six clusters (b) representing the minimum number of clusters for which there was no more than one element from the same subject in each cluster. The synergies in each cluster (c) show common distinctive features (see Results). In b and c, each subject is identified by a different color.

We quantified the degree of similarity within each cluster by identifying the element with the highest mean similarity and by computing a similarity index constructed to normalize the similarity with the similarity expected by chance (see Materials and Methods). Cluster A had a mean similarity between the synergy extracted in subject 7 and the other eight synergies in the cluster of 0.85 and a mean similarity index of 0.65, with all eight pairs significantly similar (p < 0.05). Cluster B had a mean similarity 0.73 and a mean similarity index of 0.40 (most similar element from subject 8; all seven pairs significantly similar). For cluster C, the mean similarity was 0.78 and the mean similarity index was 0.43 (most similar element from subject 2; all eight pairs significantly similar); for cluster D, the mean similarity was 0.72 and the mean similarity index was 0.31 (most similar element from subject 7; five of eight pairs significantly similar); and for cluster E, the mean similarity was 0.77 and the mean similarity index was 0.39 (subject 7; all two pairs significantly similar). Finally, for cluster F, with only two elements, the similarity was 0.67 and the similarity index was 0.32 (significantly higher than chance).

Synergy generalization across dynamic and postural conditions

If the synergies extracted from point-to-point movements with the unloaded handle and neutral forearm posture do not simply represent a parsimonious yet arbitrary fit of the EMG waveform variability across movement directions but, instead, capture a set of spatiotemporal components used to generate the EMG patterns, we expect those synergies to be able to reconstruct the muscle patterns observed in different conditions. We tested this prediction by evaluating the accuracy of the synergy reconstruction when a load was added at the arm endpoint (experiment 1) and when the posture of the forearm was changed (experiment 2). For each subject in the first group, we fit the phasic muscle patterns recorded during point-to-point movements performed with two loads inserted in the handle (total weight, 630 and 1040 g) and used the synergies extracted from the same set of the movements performed with the unloaded handle (180 g). For the subjects in the second group, we fit the patterns recorded during point-to-point movement performed with the forearm pronated and supinated.

In experiment 1, movement duration and maximum speed were significantly affected by the changes in load in most cases (five of six subject and movement plane combinations for movement duration; three-way ANOVA; movement duration vs direction, endpoint, and load; p < 0.05; six of six cases for maximum speed) but movement distance was not (six of six cases; p > 0.05). Movement duration increased with load (positive difference between the mean with the larger load and the mean with the smaller load in 13 of 18 comparisons across the three load levels in 6 cases; p < 0.05; post hoc comparison with Tukey honestly significant difference correction) and maximum speed decreased (negative mean difference in 17 of 18 comparisons). In experiment 2, movement direction, maximum speed, and movement distance were affected by the forearm posture in most cases (four of six cases for movement duration, four of six cases for maximum speed, and five of six cases for movement distance; three-way ANOVA; direction, speed, or distance vs direction, endpoint, and load; p < 0.05). Thus in both experimental manipulations, load and posture affected the movement kinematics.

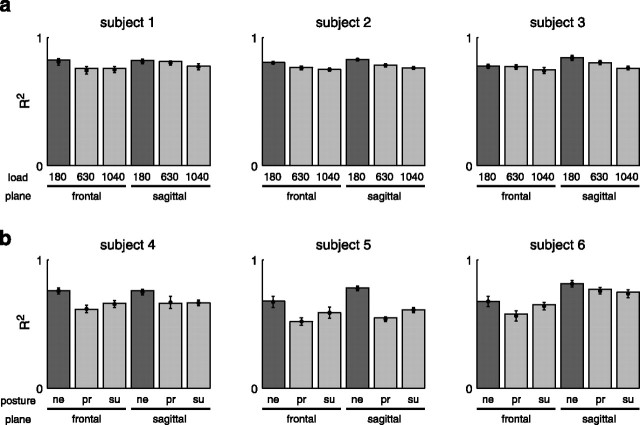
The accuracy in the reconstruction of the muscle patterns by the synergy combinations in most manipulated conditions was close to that observed for the data used in the synergy extraction. In experiment 1, the reconstruction R² value for both load conditions and planes of movement (Fig. 11a) was always >0.75 and with a maximum decrement with respect to the unloaded condition of 0.06. In experiment 2, the minimum R² (Fig. 11b) was 0.52 with the pronated forearm posture and 0.59 with the supinated forearm posture. The maximum R² reduction was 0.24 for the pronated posture and 0.17 for the supinated posture (both for subject 5 in the sagittal plane). Thus for all subjects and in both experiments, the synergy combinations explained a large fraction of the data variation in a condition different from the one used for the synergy identification.

Figure 11.

Robustness of synergies across dynamic and postural conditions. The fraction of total data variation explained by the reconstruction of the data collected with different loads (a, experiment 1; 180, 630, and 1040 g) and different forearm postures (b, experiment 2; ne, neutral; pr, pronated; su, supinated) with the synergies extracted from point-to-point patterns with the unloaded handle and neutral posture (light gray bars) is close to the fraction of the total data variation explained by the reconstruction of the data used for the synergy extraction (dark gray bars), indicating a significant degree of generalization across dynamic and postural conditions. The mean and SD of the R² values obtained over 100 subsets of 50% of the trials that were randomly selected in each condition (bootstrap statistics) are superimposed over the bar representing the R² values for 100% of the trials.

Robustness of synergy directional tuning

We then examined the robustness of the synergy directional tuning across experimental conditions. To perform a statistical analysis of the dependence of the synergy recruitment amplitude on the experimental conditions, we used data from individual trials. For each subject in experiments 1 and 2, we fit the synergies extracted from the averaged phasic EMG patterns recorded with the unloaded handle and a neutral forearm posture to the phasic EMG patterns of individual trials of all conditions. The direction of movement had a highly significant effect on the amplitude coefficients for all subjects, all planes of movements, and all synergies (p < 0.001; three-way ANOVA; synergy amplitude coefficient vs movement direction, endpoint, and load or posture). In most cases in experiment 1, there was also a significant effect of the movement endpoint (center-out vs out-center; 27 of 28 synergy and plane combinations in three subjects; p < 0.01) and load (22 of 28, p < 0.05; 18 of 28, p < 0.01) and a significant interaction between direction and endpoint (28 of 28, p < 0.05). In experiment 2 (different forearm postures), there was a significant effect of endpoint (17 of 24, p < 0.01), forearm posture (18 of 24, p < 0.05; 14 of 24, p < 0.01), and a significant interaction of direction and endpoint (21 of 24, p < 0.05; 16 of 24, p < 0.01).

We characterized the directional tuning of the amplitude coefficients by fitting the dependence of the coefficients on the movement direction with a cosine function for each subject, plane of movement, endpoint, and load or posture (see Materials and Methods). For experiments 1 and 2, this function captured well the directional tuning of the amplitude coefficients in most cases. The cosine tuning was not significant (F test; p > 0.05) in only 3 of the 60 cases (two planes, five synergies, two endpoints, and three loads) for subject 1, in 11 of 60 cases for subject 3 (five synergies), and in 2 of 48 cases for subject 6 (four synergies). It was significant (p < 0.05) in all cases for the remaining three subjects. The median of the distribution of the R² values of the cosine fit was 0.63 for subject 1, 0.67 for subject 2, 0.60 for subject 3, 0.60 for subject 4, 0.67 for subject 5, and 0.68 for subject 6 (Fig. 12a, top row). In comparison, we fit the dependence of the activation of individual muscles (integrated EMG amplitude of the largest 100 ms burst; see Materials and Methods) on the movement direction and found that the median of the distribution of the R² values was significantly lower for all subjects (subject 1, 0.30; subject 2, 0.28; subject 3, 0.39; subject 4, 0.20; subject 5, 0.36; subject 6, 0.29; Wilcoxon rank sum test; p < 10⁻⁶) (Fig. 12a, bottom row). Thus the directional tuning of the synergy amplitude coefficients was better characterized in each plane, endpoint, and load or posture condition by a cosine function than the directional tuning of the peak burst amplitude of individual muscles.

Figure 12.

Cosine tuning for synergy amplitude coefficients and for largest muscle bursts. In most cases, the dependence of the synergy amplitude coefficients on the direction of movement was well captured by a cosine function with an offset (see Materials and Methods). The distribution of R² values of the cosine fit over all conditions (3 loads or postures times; 2 endpoints) and synergies (a, top row, light gray bars) had a median, for each subject in experiment 1 (subjects 1–3) and experiment 2 (subjects 4–6), significantly higher than the median of the distribution of the R² values of the cosine fit, over all conditions and muscles, of the amplitude of the largest 100 ms EMG burst (a, bottom row, dark gray bars). Moreover, the preferred direction of the cosine tuning was less variable, across conditions, for the synergies than for the muscles. The distribution of the angular deviations, across load or posture and endpoint conditions, for each synergy and plane of movement (b, top row, light gray bars) had a smaller median than the distribution of the angular deviations for each muscle and plane (b, bottom row, dark gray bars). deg, Degree.

We then observed that the preferred direction of the cosine fit of the amplitude coefficient of each synergy in most cases did not change significantly with changes in load, posture, and endpoint. For all cases with at least two conditions with a significant cosine tuning, we computed the angular deviation of the tuning preferred direction (see Materials and Methods). The angular deviation was <20° for most synergies and planes (9 of 10 for subject 1; 7 of 8 for subject 2; 9 of 10 for subject 3; 7 of 8 for subject 4; 6 of 8 for subject 5; and 6 of 8 for subject 6; total 43 of 51 = 84%) (Fig. 12b, top row). In contrast, the preferred directions of the directional tuning of individual muscles had a larger angular dispersion. The angular deviation of the preferred direction for individual muscles (Fig. 12b, bottom row) was <20° in 124 of the 185 cases (muscle, plane, and subject combinations, 67%), and the median value of the distribution of all angular deviations was significantly larger for individual muscles than for synergies (Wilcoxon rank sum test; p < 10⁻⁴). Thus the preferred direction of the synergy amplitude coefficients were less affected by the changes in load, posture, and movement endpoint than the preferred direction of the activation amplitude of individual muscles.

Sequences of point-to-point synergies during reversal and via-point reaching

We then tested whether the muscle synergies identified in point-to-point movements were specific for that task or whether they generalized to more complex tasks. In particular, we attempted to reconstruct reaching movements involving multiple kinematic phases by combinations of the synergies extracted in point-to-point movements. A group of three subjects (experiment 3) performed, in addition to the basic set of point-to-point movements, reaching movements from one start location (either central or peripheral) to a target location and back to the same start location in a continuous movement (reversal) and from a peripheral start location to a different peripheral target location through the central location (via-point).

The tangential velocity profiles for reversal and via-point movements had two distinct peaks (Fig. 13). The movement duration was approximately two times the duration of point-to-point movements, and the maximum tangential velocity of both peaks was close to the maximum of the tangential velocity of point-to-point movements (Table 3). The averaged, phasic muscle activation waveforms for reversal and via-point movements generally showed a complex sequence of peaks and valleys that, by a first qualitative analysis, resembled the superposition of the waveforms of the muscle patterns of the corresponding point-to-point movements, each shifted in time to align the tangential velocity peaks (Fig. 14); however, many of the muscle activation waveforms were modulated in amplitude and timing with respect to the point-to-point waveforms, and these changes were different across muscles. For example, in the reversal movement from an inferior-medial location (position 2) to the center (position 0) and back to the same location (subject 7; frontal plane) (Fig. 14, third column), the activation of the elbow extensors (triceps brachii) in the second phase of the movement appears reduced in amplitude with respect to the activation observed in the point-to-point movement from the center to position 2 (second column). In contrast, the activation of medial trapezius and infraspinatus appears increased in the reversal movement with respect to the point-to-point movement.

Figure 13.

Example of reversal and via-point movement endpoint kinematics. Trajectories and tangential velocity profiles of the endpoint are shown for five repetitions of reversal and via-point movements starting from a medial-inferior position on the frontal plane (location 2), reaching the central position, and either returning to the same start position (reversal, darkest lines) or reaching different targets located at an angle ranging from 135° (location 3) to −135° (location 1) with the exception of 0° (via-point, progressively lighter gray lines going from negative to positive deviation angles). All tangential velocity profiles show two distinct maxima.

Table 3.

Summary of endpoint kinematics for reversal and via-point movements in experiment 3 (mean ± SD)

Subject	Type	Plane	Movement duration (ms)	Maximum speed, first peak (m/s)	Maximum speed, second peak (m/s)
7	Rev	fr	605 ± 16	2.04 ± 0.11	1.78 ± 0.11
		sa	602 ± 39	1.97 ± 0.18	1.90 ± 0.25
	Via	fr	580 ± 16	1.95 ± 0.16	1.68 ± 0.06
		sa	573 ± 15	1.90 ± 0.19	1.77 ± 0.08
8	Rev	fr	579 ± 13	1.91 ± 0.07	1.91 ± 0.09
		sa	596 ± 33	1.71 ± 0.23	1.80 ± 0.32
	Via	fr	567 ± 15	1.88 ± 0.09	1.82 ± 0.02
		sa	586 ± 11	1.62 ± 0.16	1.54 ± 0.07
9	Rev	fr	565 ± 17	2.10 ± 0.12	1.79 ± 0.11
		sa	594 ± 26	1.89 ± 0.25	1.71 ± 0.26
	Via	fr	534 ± 14	1.98 ± 0.19	1.73 ± 0.05
		sa	583 ± 14	1.75 ± 0.18	1.55 ± 0.12

Rev, Reversal; Via, via-point; fr, frontal; sa, sagittal.

For each subject in experiment 3, we used the muscle synergies identified in point-to-point movements to reconstruct the muscle patterns observed during reversal and via-point movements. To capture the multiple phases in the muscle patterns of these more complex movements, we fit the patterns to allow for the recruitment of each point-to-point synergy more than one time per movement (see Materials and Methods). We found that the level of accuracy of the reconstruction was close to that for the point-to-point movements used in the synergy extraction. The reconstruction R² value, across subjects and planes of movement, was always >0.61 for reversal movements and >0.57 for via-point movements (Fig. 15a). The largest R² decrement with respect to the point-to-point R² was 0.15 for reversal movements and 0.19 for via-point movements (both for subject 8; sagittal plane). Moreover, we found that the independent modulation, in amplitude and time, of the individual instances of each synergy, in the sequence of two or more used to reconstruct each reversal and via-point movement, captured the changes in the observed muscle patterns with respect to the corresponding point-to-point patterns better than the best fit of those specific point-to-point patterns. In the example of the reversal movement from position 2 to the center and back (Fig. 14, third column), the first synergy (W₁) is recruited during the first phase with an amplitude similar to that in the corresponding point-to-point movement (position 2 to center; first column) but the fourth synergy (W₄) is recruited in the first phase with a lower amplitude than in the point-to-point movement. In the second phase, the amplitude of the second synergy (W₂) is reduced but that of W₄ is increased with respect to the center-out point-to-point movement to position 2 (second column). Thus the muscle pattern for this reversal movement cannot be simply generated by the amplitude modulation of the patterns for the two corresponding point-to-point movements. In general, we compared the distribution of the R_trial² values (fraction of the total variation per sample explained in each trial) for the reconstruction of the reversal and via-point EMG patterns with the synergy combinations to the distribution for the reconstruction by fitting each pattern with the corresponding point-to-point movements, shifted in time to align the tangential velocity peaks (see Materials and Methods). For both reversal and via-point movements, in each subject the median of the distribution of R_trial² differences was significantly larger than zero (Wilcoxon signed rank test; p < 10⁻²). In summary, the muscle patterns for reaching movement with more than one phase were reconstructed by a sequence of point-to-point synergies, each recruited with amplitude and timing coefficients coarsely similar to those used for the corresponding point-to-point movements but finely adjusted to meet the specific demands of these more complex movements.

Figure 15.

Robustness of point-to-point synergies for reversal and via-point movements. a, The fraction of total data variation explained by the reconstruction of the reversal and via-point data (experiment 3) with the synergies extracted from point-to-point muscle patterns (light gray bars) is close to the fraction of the total data variation explained by the reconstruction of the point-to-point data used for the synergy extraction (dark gray bars), suggesting that complex movements are constructed by sequencing and modulating the same synergies used for point-to-point movements. For each condition, the superimposed mean and SD are obtained from bootstrap statistics as in Figure 11. b, The distribution of the differences between the fraction of the total data variation per unit sample explained in each reversal and via-point trial by the synergy reconstruction and the reconstruction obtained by fitting the corresponding point-to-point muscle patterns, shifted in time to align the tangential velocity peaks, has a median significantly higher than zero, indicating that the point-to-point muscle patterns are adjusted by modulating individual synergies to generate these more complex movements. ptp, Point-to-point; rev, reversal; via, via-point.

Discussion

We have shown that the combinations of four or five time-varying muscle synergies, appropriately scaled in amplitude and shifted in time, explain to a large extent the spatiotemporal characteristics of the phasic muscle patterns recorded during fast point-to-point reaching movements in vertical planes across many different conditions as well as during more complex reversal and via-point reaching movements. Each synergy comprises the coordinated activations of specific muscle groups, generally including one or two synchronous bursts of some muscles, acting at one or more joints, and various asynchronous activation and deactivation profiles for other muscles. We also found that the synergy amplitude coefficients were directionally tuned, in most cases according to a cosine tuning function, with a preferred direction varying across conditions significantly less than the preferred direction of the directional tuning of individual muscles.

Our decomposition algorithm is similar to other procedures used to analyze the muscle activity patterns, such as principal component analysis or factor analysis (Patla, 1985; Davis and Vaughan, 1993; Olree and Vaughan, 1995; Merkle et al., 1998; Weijs et al., 1999; Ivanenko et al., 2003, 2004; Krishnamoorthy et al., 2003), independent component analysis (McKeown, 2000; Hart and Giszter, 2004), and non-negative matrix factorization (Tresch et al., 1999; Saltiel et al., 2001; Ting and Macpherson, 2005), all of which allow complex spatiotemporal patterns to be expressed as combinations of a limited number of components; however, these other procedures decompose the time-varying multidimensional muscle activity into combinations of synchronous synergies (vectors with the same dimension as the number of muscles) multiplied by a set of time-varying coefficients (vectors with the same dimension as the number of samples). Here, instead, the decomposition of the muscle patterns into time-varying synergies captured fixed relationships among the muscle activation waveforms across muscles and time. In contrast, synchronous synergies can capture the spatial structure in the patterns (d'Avella and Bizzi, 2005), but any fixed temporal relationship can be recovered only indirectly from the time-series of the combination coefficients associated with each synchronous synergy, and more than one synergy is required to express a fixed asynchronous activation. For example (Fig. 16), the reconstruction of the activation of five muscles generated by the combination of two time-varying synergies, each representing a fixed asynchronous activation, may require up to five synchronous synergies. Moreover, given a set of synergies, the time-varying model provides a more parsimonious description of the muscle patterns than a synchronous model. In fact, one amplitude and one timing parameter per time-varying synergy are sufficient to describe a muscle pattern, whereas the complete time-series of the combination coefficients must be specified with synchronous synergies.

Figure 16.

Differences between time-varying and synchronous synergies. A simple simulation illustrates the fact that invariant temporal relationships among muscle bursts can be captured explicitly by time-varying muscle synergies but only implicitly by synchronous synergies. Three distinct muscle patterns (center panel, gray areas) are generated by combining two time-varying synergies (left panel; W₁ and W₂) with different amplitude scaling (c_i) and time shifting (t_i) coefficients (top panel; represented, as in Figs. 7 and 13, by the height and position of different rectangles). These patterns are then decomposed with a non-negative matrix factorization algorithm (Lee and Seung, 2001) to extract synchronous synergies. Because no noise was added to the patterns, the R² reaches 1 at five synergies (bottom right panel), i.e., five synchronous synergies (right panel, black horizontal bars; each column is a vector representing the muscle activation balance of each synchronous synergy) are required to reconstruct the patterns (central panel, thick black line). These synchronous synergies capture the synchronous amplitude relationships characteristic of the generating time-varying synergies, but they cannot capture the whole spatiotemporal organization. The temporal organization in the muscle patterns is expressed only indirectly by the organization of the time-varying scaling coefficients for the synchronous synergies (bottom panel).

Our findings explain many characteristics of the muscle patterns for reaching as the result of the combination of a few muscle synergies. Flanders and collaborators have shown that, in the muscle patterns for reaching in vertical planes, common phasic waveforms are scaled in amplitude and delayed in time for different directions (Flanders, 1991), and they show a gradual shift in the burst timing and a directional tuning of the burst amplitude with multiple peaks (Flanders et al., 1994, 1996). We have extended those observations by showing that the characteristics of each individual muscle waveform are related to the waveforms of all the other muscles because they are organized into muscle synergies. We expect that our approach would give similar insight into the construction of the muscle patterns for arm movements in the horizontal plane (Wadman et al., 1980; Karst and Hasan, 1991; Scott, 1997) as well as the step-tracking movements of the wrist (Hoffman and Strick, 1990, 1999). Our findings might also provide a new interpretation for the observation that the dynamic muscle torques at the shoulder and elbow during reaching movements are related almost linearly to each other, and their relative scaling changes regularly with movement direction (Gottlieb et al., 1997). A qualitative analysis of the synergy structure suggests that each synergy might generate a biphasic torque profile at one joint or, synchronously, at two or more joints. Thus the activation of one synergy would produce an almost linear relationship between torques. Moreover, in modulating the amplitude balance for two or more synergies across movement directions (Fig. 9), the balance in the corresponding torque profiles would also change, and hence the slope of the linear relation would depend on direction.

The decomposition of the muscle patterns as combinations of a few muscle synergies not only provides a concise description of the variations of the patterns across conditions but also suggests a mechanism for their generation. Such a mechanism might represent an implementation of a feedforward controller based on simple rules expressed in terms of dynamic joint torques (Gottlieb et al., 1997). In this way, the CNS might simplify the problem of constructing an inverse model of the arm dynamics by building a map of goals into a low-dimensional set of synergy recruitment parameters; however, a synergy-based feedforward controller may operate together with a feedback controller and a postural controller (Gottlieb, 1996; Bhushan and Shadmehr, 1999; Sainburg et al., 1999). A feedback controller might also organize its motor output through muscle synergies, and it would be interesting to compare the spatiotemporal organization of the muscle patterns observed during responses to arm perturbations and during reaching. Moreover, because sensory feedback appears to convey information about the whole limb (Poppele et al., 2002) rather than individual sensors, there might be a tight relationship between sensory and motor synergies.

How and where might time-varying muscle synergies be implemented in the CNS? The model predicts a synergy control signal distributed to many motoneuronal pools and transformed into muscle-specific activation waveforms. Several studies on spinalized or decerebrated frogs and cats (Tresch et al., 1999; Kargo and Giszter, 2000; Saltiel et al., 2001; Hart and Giszter, 2004; Lemay and Grill, 2004) indicate that the vertebrate spinal cord is capable of organizing muscle synergies and of flexibly combining them to generate various motor behaviors. In mammals, and particularly in primates, the control of reaching movements also involves the cerebral cortex, the cerebellum, and the basal ganglia. One possibility is that the supraspinal structures recruit and modulate spinally organized synergies (Lukashin et al., 1996; Todorov, 2000) through descending low-dimensional synergy control signals that diverge and are temporally patterned in the spinal network. Either a dedicated spinal circuitry or the same spinal circuitry involved in the generation of rhythmical arm movements (Zehr and Hundza, 2005) might be responsible for this transformation; however, the pyramidal cells in the motor areas of the cerebral cortex influence (Fetz and Cheney, 1980; McKiernan et al., 1998; Park et al., 2004) or are related to (Holdefer and Miller, 2002) multiple muscles and are interconnected thorough intracortical collaterals (Huntley and Jones, 1991; Schneider et al., 2002). Thus muscle synergies also might be directly encoded by the intrinsic and corticospinal pattern of connectivity of pyramidal cells in the cortex. The idea of a cortical representation of muscle synergies is not in conflict with the idea of a cortical representation of kinematic features, because the recruitment of muscle synergies is also related to those features, as we have shown here for fast-reaching movements. The directional tuning of the activity of cortical units in motor and premotor areas (Georgopoulos et al., 1982; Schwartz et al., 1988) might correspond to the directional tuning of the synergy recruitment. The observation that the preferred direction of the synergy recruitment is less affected by changes in load, posture, and endpoint than the individual muscles suggests that muscle synergy encoding represents an intermediate stage of the transformation of kinematic parameters, known to be encoded in premotor and parietal areas, into muscle activations. Units, particularly in the primary motor cortex, that show a small change in preferred direction but a significant modulation in amplitude (Kakei et al., 1999) might encode synergy amplitude coefficients. In contrast, units with a preferred direction that changes with load (Kalaska et al., 1989), posture (Scott and Kalaska, 1997; Kakei et al., 1999), and initial position (Caminiti et al., 1990) might encode the muscle activation output resulting from the combined influence of two or more synergies. Moreover, although the synergy recruitment might originate in the precentral cortical areas, the fact that the ability to compensate for the interaction torques appears to be dependent on the integrity of the cerebellum (Bastian et al., 1996; Topka et al., 1998) suggests that the complete specification of the synergies, in particular their temporal patterning, requires the corticocerebellar loops.

In conclusion, the key and novel insight into the mechanisms involved in the mapping of motor goals into muscle patterns provided by our results is that the complexity and variability of the motor output can result from the flexible and task-dependent combination of a small number of spatiotemporal components. Although we have shown this for the phasic muscle patterns of fast-reaching movements, future investigations will test whether similar conclusions also hold for the postural components of the muscle patterns and for movements at different speeds.